Rechenübungen zur Physik I im WS 2009/2010
|
|
|
- Carsten Hofmann
- vor 5 Jahren
- Abrufe
Transkript
1 Rechenübungen zur Physik I im WS 2009/ Klausur (Abgabe Fr , Uhr N7) Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. (ID 2) ist: 122 Hinweise: Studentenausweis: Hilfsmittel: Lösungen: Zusatzblätter: Toilette: Handy: Bei Unklarheiten: zur Kontrolle bereitlegen Schreibzeug blau, schwarz, grün + 1 beschriebenes Blatt (Fremdsprachigen ist ein Wörterbuch erlaubt) beidseitig auf Aufgabenblätter unbedingt mit laufender Nummer (ID 2, siehe oben) versehen Lösungen zu verschiedenen Aufgaben auf verschiede Blätter immer nur 1 Person ausschalten, einpacken Hilfestellungen nur an alle Teilnehmer
2 Aufgabe 1) Stoß gegen Oszillator 15 Punkte 5/3/7 Drei Kugeln haben die gleiche Masse m. Die Kugeln (2) und (3) sind durch eine masselose Feder miteinander verbunden und befinden sich zunächst in Ruhe. Die entspannte Feder hat die Länge a 0 und die Federkonstante ist k. Die Kugel (1) gleitet reibungsfrei mit der Geschwindigkeit v 1 auf die Kugel (2) zu und stößt diese zur Zeit t=0 zentral und elastisch. Der Stoß von (1) und (2) sei kurz, so dass es während dem Stoß zu keiner Verformung der Feder kommt. Vernachlässigen sie alle Reibungskräfte und die Ausdehnung der Kugeln. a) Geben Sie die Koordinaten des Schwerpunkts X 123 des gesamten Systems sowie des Schwerpunktes X 23 des Kugelpaares (2) und (3) in Abhängigkeit der Zeit an. b) Wie groß ist die Schwingungsenergie E S des Kugelpaares (2).(3)nach dem Stoß? c) Berechnen Sie den zeitlichen Verlauf des Abstandes x 23 der Kugeln (2) und (3).
3 Aufgabe 2) Zwei Satelliten 14 Punkte 6/9 Ein Satellit der Masse 2m befindet sich in einer kreisförmigen Umlaufbahn (Radius R) um die Erde. Durch eine Explosion wird der Satellit in zwei identische Bruchstücke geteilt, wobei das erste eine tangentiale Beschleunigung erfährt, die seine Geschwindigkeit um einen Faktor 2 erhöht. Nehmen Sie an, dass die Explosion selbst keinen Massen- oder Impulsverlust verursacht. a) Bestimmen Sie die jeweiligen Gesamtenergien der beiden Satelliten nach der Explosion. Beschreiben Sie qualitativ ihre Bahnen. b) Bestimmen Sie die minimale Entfernung des zweiten Bruchstückes von der Erde. (Hinweis: Sie erhalten eine quadratische Gleichung, die Sie am besten für die maximale Geschwindigkeit des Bruchstückes lösen.
4 Aufgabe 3) Pendelscheibe 15 Punkte 2/4/4/3/2 Eine Metallscheibe mit Masse m, Innenradius r i und Außenradius r a wird am Rand aufgehängt und führt Schwingungen um diesen Aufhängepunkt A aus, wobei die Rotationsachse senkrecht zur Scheibe liegt. a) Wie lautet der Steinersche Satz für das Trägheitsmoment eines Körpers? b) Wie groß ist das Trägheitsmoment der Scheibe bzgl. der Rotationsachse durch den Aufhängepunkt am Scheibenrand? c) Geben Sie die Bewegungsgleichung für die Auslenkung φ der Scheibe an. d) Geben Sie einen Ausdruck für die Schwingungsperiode der Scheibe bei kleinen Auslenkwinkeln an. e) Wie verändert sich diese Periode falls bei gleicher Scheibenmasse der Innenradius immer größer wird?
5 Aufgabe 4 ) Heizung 10 Punkte 7/3 Ein Zimmer habe das Volumen V. Die Zimmerluft werde durch ein Gas mit f Freiheitsgraden beschrieben bei einem Druck p. Es wird bei konstantem Druck von der Temperatur T 0 auf T 1 erwärmt. Wegen des Druckausgleichs entweicht ein Teil der Luft durch Tür- und Fensterritzen. a) Nehmen Sie an, dass das Gas im Zimmer als ein ideales Gas betrachtet werden kann. Berechnen Sie wie viel Energie für die Erwärmung der Zimmerluft verbraucht wird. b) Das Entweichen der Luft führt zu einem Energieverlust im Zimmer. Vergleichen Sie die Energie des Gases im Zimmer vor und nach dem Aufheizen.
6 Aufgabe 5) Atomstrahlofen 15 Punkte 11/4 In einem Ofen mit Volumen V werden n mol Wasserdampf (H 2 O) auf die Temperatur T erhitzt. Diese Temperatur ist so hoch, dass man annehmen kann, dass der Wasserdampf vollständig in die atomaren Bestandteile H und O mit molaren Massen m H =1g und m O =16g zerfällt. In der Wand befindet sich ein kleines Loch mit Querschnittsfläche S, durch das die Teilchen entweichen. Die normalisierte Geschwindigkeitsverteilung für die Bewegung in einer Dimension lautet: (2-1) 1/2 2 m mv f ( v) = exp. 2π kbt 2kBT a) Bestimmen Sie die Ströme I H = Nɺ H und IO = Nɺ O (Teilchen pro Sekunde) der durch das Loch entweichenden H- und O-Atome. b) Begründen Sie, warum das Verhältnis I H /I O =8 ist.
7 Aufgabe 6 ) Kreisprozess 12 Punkte 4/6/2 Ein ideales Gas durchläuft folgende Schritte: 1 2 : Isochore Erhöhung des Drucks durch Erwärmung 2 3: Adiabatische Entspannung 3 1: Isobare Volumenreduktion Die Wärmekapazitäten C V und C P seien konstant. a) Tragen Sie die Zustandsänderungen des Gases in ein V-p-Diagramm ein. b) Wie hängen die zu- und abgeführten Wärmemengen von den Eckpunkten des Prozesses ab? Wärmemengen: Q, Q, Q ( p V ) ( p V ) ( p V ) Eckpunkte:,,,,, c) Bei dem Prozess wird Wärme in Arbeit umgewandelt. Welche Arbeit: A = W12 W23 W31 wird gemäß dem 1. Hauptsatz insgesamt vom System abgegeben? Berechnen Sie den Wirkungsgrad: als Funktion der Temperaturen T1, T2 und T 3. A η = zugeführte Wärme d) An welchem Punkt (p,v) des Prozesses ist die Temperatur am tiefsten? (2-2) (2-3) (2-4) (2-5)
8
Rechenübungen zur Physik I im WS 2009/2010
 Rechenübungen zur Physik I im WS 2009/200. Klausur (Abgabe Di 5.2.09, 0.00 Uhr N7) Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. (ID ) ist: 22 Hinweise: Studentenausweis: Hilfsmittel: Lösungen:
Rechenübungen zur Physik I im WS 2009/200. Klausur (Abgabe Di 5.2.09, 0.00 Uhr N7) Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. (ID ) ist: 22 Hinweise: Studentenausweis: Hilfsmittel: Lösungen:
Rechenübungen zum Physik Grundkurs 2 im SS 2010
 Rechenübungen zum Physik Grundkurs 2 im SS 2010 1. Klausur (Abgabe Mi 2.6.2010, 12.00 Uhr N7) Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. (ID1) ist: 122 Hinweise: Studentenausweis: Hilfsmittel:
Rechenübungen zum Physik Grundkurs 2 im SS 2010 1. Klausur (Abgabe Mi 2.6.2010, 12.00 Uhr N7) Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. (ID1) ist: 122 Hinweise: Studentenausweis: Hilfsmittel:
Rechenübungen zur Physik 1 im WS 2011/2012
 Rechenübungen zur Physik 1 im WS 2011/2012 1. Klausur Fr 16.12.2011 12.00-15.00 Uhr N5/N7 Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. ID1= 250 Hinweise: Studentenausweis: Hilfsmittel: Lösungen:
Rechenübungen zur Physik 1 im WS 2011/2012 1. Klausur Fr 16.12.2011 12.00-15.00 Uhr N5/N7 Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. ID1= 250 Hinweise: Studentenausweis: Hilfsmittel: Lösungen:
Rechenübungen zum Physik Grundkurs 2 im SS 2010
 Rechenübungen zum Physik Grundkurs 2 im SS 2010 2. Klausur (Abgabe: Do 16.9.2010 12.00 Uhr Neue Aula) Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. ID2= 122 Hinweise: Studentenausweis: Hilfsmittel:
Rechenübungen zum Physik Grundkurs 2 im SS 2010 2. Klausur (Abgabe: Do 16.9.2010 12.00 Uhr Neue Aula) Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. ID2= 122 Hinweise: Studentenausweis: Hilfsmittel:
Teilnehmer-Nr: Integrierter Kurs I. 2. Klausur, WiSe 2010/ März 2011
 Integrierter Kurs I 2. Klausur, WiSe 2010/2011 03. März 2011 Name: Gruppenleiter: Aufgabe Punkte 1 / 5 2 /16 3 /10 4 /13 5 /10 6 /12 7 / 8 8 / 6 insgesamt (max. 80) 1. Gravitationskraft (5 Punkte) Im Jahr
Integrierter Kurs I 2. Klausur, WiSe 2010/2011 03. März 2011 Name: Gruppenleiter: Aufgabe Punkte 1 / 5 2 /16 3 /10 4 /13 5 /10 6 /12 7 / 8 8 / 6 insgesamt (max. 80) 1. Gravitationskraft (5 Punkte) Im Jahr
Rechenübungen zur Physik 1 im WS 2011/2012
 Rechenübungen zur Physik 1 im WS 011/01. Klausur Fr. März 01 9.00-1.00 Uhr N/N6 Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. ID= 99 Hinweise: Studentenausweis: Hilfsmittel: Lösungen: Zusatzblätter:
Rechenübungen zur Physik 1 im WS 011/01. Klausur Fr. März 01 9.00-1.00 Uhr N/N6 Name, Vorname: Geburtstag: Ihre Identifizierungs-Nr. ID= 99 Hinweise: Studentenausweis: Hilfsmittel: Lösungen: Zusatzblätter:
Aufgabensammlung. Experimentalphysik für ET. 2. Erhaltungsgrößen
 Experimentalphysik für ET Aufgabensammlung 1. Erhaltungsgrößen An einem massenlosen Faden der Länge L = 1 m hängt ein Holzklotz mit der Masse m 2 = 1 kg. Eine Kugel der Masse m 1 = 15 g wird mit der Geschwindigkeit
Experimentalphysik für ET Aufgabensammlung 1. Erhaltungsgrößen An einem massenlosen Faden der Länge L = 1 m hängt ein Holzklotz mit der Masse m 2 = 1 kg. Eine Kugel der Masse m 1 = 15 g wird mit der Geschwindigkeit
Abschlussprüfung an Fachoberschulen im Schuljahr 2002/2003
 Abschlussprüfung an Fachoberschulen im Schuljahr 00/00 Haupttermin: Nach- bzw. Wiederholtermin: 0.09.00 Fachrichtung: Technik Fach: Physik Prüfungsdauer: 10 Minuten Hilfsmittel: Formelsammlung/Tafelwerk
Abschlussprüfung an Fachoberschulen im Schuljahr 00/00 Haupttermin: Nach- bzw. Wiederholtermin: 0.09.00 Fachrichtung: Technik Fach: Physik Prüfungsdauer: 10 Minuten Hilfsmittel: Formelsammlung/Tafelwerk
Musterlösung zur Abschlussklausur PC I Übungen (27. Juni 2018)
 1. Abkühlung (100 Punkte) Ein ideales Gas (genau 3 mol) durchläuft hintereinander zwei (reversible) Zustandsänderungen: Zuerst expandiert es isobar, wobei die Temperatur von 50 K auf 500 K steigt und sich
1. Abkühlung (100 Punkte) Ein ideales Gas (genau 3 mol) durchläuft hintereinander zwei (reversible) Zustandsänderungen: Zuerst expandiert es isobar, wobei die Temperatur von 50 K auf 500 K steigt und sich
Allgemeines Gasgesetz. PV = K o T
 Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
Probeklausur zur Vorlesung Physik I (WS 09/10)
 Modalitäten zur Klausur: Bitte legen Sie Ihren Personalausweis und Studentenausweis sichtbar auf den Tisch. Beschriften Sie jedes Blatt mit Name und Vorname. Benutzen Sie für jede Aufgabe das vorgesehene
Modalitäten zur Klausur: Bitte legen Sie Ihren Personalausweis und Studentenausweis sichtbar auf den Tisch. Beschriften Sie jedes Blatt mit Name und Vorname. Benutzen Sie für jede Aufgabe das vorgesehene
Thermodynamik I Klausur 1
 Aufgabenteil / 100 Minuten Name: Vorname: Matr.-Nr.: Das Aufgabenblatt muss unterschrieben und zusammen mit den (nummerierten und mit Namen versehenen) Lösungsblättern abgegeben werden. Nicht nachvollziehbare
Aufgabenteil / 100 Minuten Name: Vorname: Matr.-Nr.: Das Aufgabenblatt muss unterschrieben und zusammen mit den (nummerierten und mit Namen versehenen) Lösungsblättern abgegeben werden. Nicht nachvollziehbare
Klausur Physik für Chemiker
 Universität Siegen Naturwissenschaftlich-Technische Fakultät Department Physik Winter Semester 2018 Prof. Dr. Mario Agio Klausur Physik für Chemiker Datum: 18.3.2019-10 Uhr Name: Matrikelnummer: Einleitung
Universität Siegen Naturwissenschaftlich-Technische Fakultät Department Physik Winter Semester 2018 Prof. Dr. Mario Agio Klausur Physik für Chemiker Datum: 18.3.2019-10 Uhr Name: Matrikelnummer: Einleitung
Aufgabe 1 - Schiefe Ebene - (10 Punkte)
 - schriftlich Klasse: 4AW (Profil A) - (HuR) Prüfungsdauer: Erlaubte Hilfsmittel: Bemerkungen: 4h Taschenrechner TI-nspire CAS Der Rechner muss im Press-to-Test-Modus sein. Formelsammlung Beginnen Sie
- schriftlich Klasse: 4AW (Profil A) - (HuR) Prüfungsdauer: Erlaubte Hilfsmittel: Bemerkungen: 4h Taschenrechner TI-nspire CAS Der Rechner muss im Press-to-Test-Modus sein. Formelsammlung Beginnen Sie
Übungen Theoretische Physik I (Mechanik) Blatt 7 (Austeilung am: , Abgabe am )
 Übungen Theoretische Physik I (Mechanik) Blatt 7 (Austeilung am: 7.9.11, Abgabe am 14.9.11) Beispiel 1: Stoß in der Ebene [3 Punkte] Betrachten Sie den elastischen Stoß dreier Billiardkugeln A, B und C
Übungen Theoretische Physik I (Mechanik) Blatt 7 (Austeilung am: 7.9.11, Abgabe am 14.9.11) Beispiel 1: Stoß in der Ebene [3 Punkte] Betrachten Sie den elastischen Stoß dreier Billiardkugeln A, B und C
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti.
 (c) Ulm University p. 1/1 Grundlagen der Physik 2 Schwingungen und Wärmelehre 14. 05. 2007 Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik Universität Ulm (c) Ulm University p.
(c) Ulm University p. 1/1 Grundlagen der Physik 2 Schwingungen und Wärmelehre 14. 05. 2007 Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik Universität Ulm (c) Ulm University p.
Aufgaben zur Übungsklausur zur Vorlesung Einführung in die Physik für Natur- und Umweltwissenschaftler v. Issendorff, WS2013/
 Aufgaben zur Übungsklausur zur Vorlesung Einführung in die Physik für Natur- und Umweltwissenschaftler v. Issendorff, WS013/14 18.1.013 Diese Aufgaben entsprechen der Abschlußklausur, für die 1 ¾ Stunden
Aufgaben zur Übungsklausur zur Vorlesung Einführung in die Physik für Natur- und Umweltwissenschaftler v. Issendorff, WS013/14 18.1.013 Diese Aufgaben entsprechen der Abschlußklausur, für die 1 ¾ Stunden
Fakultät für Physik der LMU
 Fakultät für Physik der LMU 21.02.2013 Klausur zur Vorlesung E1: Mechanik für Studenten der Physik für das Lehramt an Gymnasien und im Nebenfach (6 ECTS) Wintersemester 2012/13 Prof. Dr. Joachim O. Rädler
Fakultät für Physik der LMU 21.02.2013 Klausur zur Vorlesung E1: Mechanik für Studenten der Physik für das Lehramt an Gymnasien und im Nebenfach (6 ECTS) Wintersemester 2012/13 Prof. Dr. Joachim O. Rädler
Nachklausur 2003 Physik I (Mechanik)
 Institut für Experimentelle Kernphysik WS2003, 8-10-03, 10 00 13 00 Nachklausur 2003 Physik I (Mechanik) Priv. Dozent Dr. M. Erdmann, Dr. G. Barker Name/Vorname : Matrikelnummer : Fachsemester : Übungsgruppe
Institut für Experimentelle Kernphysik WS2003, 8-10-03, 10 00 13 00 Nachklausur 2003 Physik I (Mechanik) Priv. Dozent Dr. M. Erdmann, Dr. G. Barker Name/Vorname : Matrikelnummer : Fachsemester : Übungsgruppe
Theoretische Physik: Mechanik
 Ferienkurs Theoretische Physik: Mechanik Sommer 2013 Probeklausur Technische Universität München 1 Fakultät für Physik 1 Kurze Fragen [20 Punkte] Beantworten Sie folgende Fragen. Für jede richtige Antwort
Ferienkurs Theoretische Physik: Mechanik Sommer 2013 Probeklausur Technische Universität München 1 Fakultät für Physik 1 Kurze Fragen [20 Punkte] Beantworten Sie folgende Fragen. Für jede richtige Antwort
T 300K,p 1,00 10 Pa, V 0, m,t 1200K, Kontrolle Physik Leistungskurs Klasse Hauptsatz, Kreisprozesse
 Kontrolle Physik Leistungskurs Klasse 2 7.3.207. Hauptsatz, Kreisprozesse. Als man früh aus dem Haus gegangen ist, hat man doch versehentlich die Kühlschranktür offen gelassen. Man merkt es erst, als man
Kontrolle Physik Leistungskurs Klasse 2 7.3.207. Hauptsatz, Kreisprozesse. Als man früh aus dem Haus gegangen ist, hat man doch versehentlich die Kühlschranktür offen gelassen. Man merkt es erst, als man
Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung.
 Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung. Nullter und Erster Hauptsatz der Thermodynamik. Thermodynamische
Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung. Nullter und Erster Hauptsatz der Thermodynamik. Thermodynamische
Übungsblatt 13 Physik für Ingenieure 1
 Übungsblatt 13 Physik für Ingenieure 1 Othmar Marti, (othmarmarti@physikuni-ulmde 1 00 1 Aufgaben für die Übungsstunden Schwingungen 1 Zuerst nachdenken, dann in Ihrer Vorlesungsmitschrift nachschauen
Übungsblatt 13 Physik für Ingenieure 1 Othmar Marti, (othmarmarti@physikuni-ulmde 1 00 1 Aufgaben für die Übungsstunden Schwingungen 1 Zuerst nachdenken, dann in Ihrer Vorlesungsmitschrift nachschauen
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Prof. Dr. U. Schollwöck Sommersemester 2013
 Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
(b) Schritt I: freie adiabatische Expansion, also ist δw = 0, δq = 0 und damit T 2 = T 1. Folglich ist nach 1. Hauptsatz auch U = 0.
 3 Lösungen Lösung zu 65. (a) Siehe Abbildung 1. (b) Schritt I: freie adiabatische Expansion, also ist δw 0, δq 0 und damit. Folglich ist nach 1. Hauptsatz auch U 0. Schritt II: isobare Kompression, also
3 Lösungen Lösung zu 65. (a) Siehe Abbildung 1. (b) Schritt I: freie adiabatische Expansion, also ist δw 0, δq 0 und damit. Folglich ist nach 1. Hauptsatz auch U 0. Schritt II: isobare Kompression, also
Schwingungen. a. Wie lautet die Gleichung für die Position der Masse als Funktion der Zeit? b. Die höchste Geschwindigkeit des Körpers.
 Schwingungen Aufgabe 1 Sie finden im Labor eine Feder. Wenn Sie ein Gewicht von 100g daran hängen, dehnt die Feder sich um 10cm. Dann ziehen Sie das Gewicht 6cm herunter von seiner Gleichgewichtsposition
Schwingungen Aufgabe 1 Sie finden im Labor eine Feder. Wenn Sie ein Gewicht von 100g daran hängen, dehnt die Feder sich um 10cm. Dann ziehen Sie das Gewicht 6cm herunter von seiner Gleichgewichtsposition
Vordiplomsklausur Physik
 Institut für Physik und Physikalische Technologien der TU-Clausthal; Prof. Dr. W. Schade Vordiplomsklausur Physik 22.Februar 2006, 9:00-11:00 Uhr für die Studiengänge Mb, Inft, Ciw, E+R/Bach. (bitte deutlich
Institut für Physik und Physikalische Technologien der TU-Clausthal; Prof. Dr. W. Schade Vordiplomsklausur Physik 22.Februar 2006, 9:00-11:00 Uhr für die Studiengänge Mb, Inft, Ciw, E+R/Bach. (bitte deutlich
9. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 8. Dezember 2009
 9. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 8. Dezember 009 Aufgabe 9.1: Doppelfeder Eine Kugel wird im Schwerefeld der Erde zwischen zwei Federn mit
9. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 8. Dezember 009 Aufgabe 9.1: Doppelfeder Eine Kugel wird im Schwerefeld der Erde zwischen zwei Federn mit
Klausur zur Vorlesung Physik I für Chemiker (WS 2017/18)
 Universität Siegen Wintersemester 2017/18 Naturwissenschaftlich-Technische Fakultät Department Physik Klausur zur Vorlesung Physik I für Chemiker (WS 2017/18) Datum: Dienstag, 13.02.2017, 10:00-12:00 Prof.
Universität Siegen Wintersemester 2017/18 Naturwissenschaftlich-Technische Fakultät Department Physik Klausur zur Vorlesung Physik I für Chemiker (WS 2017/18) Datum: Dienstag, 13.02.2017, 10:00-12:00 Prof.
2. Klausur zur Theoretischen Physik I (Mechanik)
 2. Klausur zur Theoretischen Physik I (echanik) 09.07.2004 Aufgabe 1 Physikalisches Pendel 4 Punkte Eine homogene, kreisförmige, dünne Platte mit Radius R und asse ist am Punkt P so aufgehängt, daß sie
2. Klausur zur Theoretischen Physik I (echanik) 09.07.2004 Aufgabe 1 Physikalisches Pendel 4 Punkte Eine homogene, kreisförmige, dünne Platte mit Radius R und asse ist am Punkt P so aufgehängt, daß sie
Experimentalphysik EP, WS 2011/12
 FAKULTÄT FÜR PHYSIK Ludwig-Maximilians-Universität München Prof. O. Biebel, PD. W. Assmann Experimentalphysik EP, WS 0/ Probeklausur (ohne Optik)-Nummer:. Februar 0 Hinweise zur Bearbeitung Alle benutzten
FAKULTÄT FÜR PHYSIK Ludwig-Maximilians-Universität München Prof. O. Biebel, PD. W. Assmann Experimentalphysik EP, WS 0/ Probeklausur (ohne Optik)-Nummer:. Februar 0 Hinweise zur Bearbeitung Alle benutzten
Probeklausur zur Vorlesung PN I Einführung in die Physik für Chemiker und Biologen Priv. Doz. Dr. P. Gilch
 Name: Martrikelnr.: Semester: Biologie Chemie Probeklausur zur Vorlesung PN I Einführung in die Physik für Chemiker und Biologen Priv. Doz. Dr. P. Gilch 12. 2. 2007 Bitte schreiben Sie Ihren Namen auf
Name: Martrikelnr.: Semester: Biologie Chemie Probeklausur zur Vorlesung PN I Einführung in die Physik für Chemiker und Biologen Priv. Doz. Dr. P. Gilch 12. 2. 2007 Bitte schreiben Sie Ihren Namen auf
Physik 2 (B.Sc. EIT) 2. Übungsblatt
 Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Vordiplomsklausur in Physik Mittwoch, 23. Februar 2005, :00 Uhr für den Studiengang: Mb, Inft, Geol, Ciw
 Institut für Physik und Physikalische Technologien 23.02.2005 der TU Clausthal Prof. Dr. W. Daum Vordiplomsklausur in Physik Mittwoch, 23. Februar 2005, 09.00-11:00 Uhr für den Studiengang: Mb, Inft, Geol,
Institut für Physik und Physikalische Technologien 23.02.2005 der TU Clausthal Prof. Dr. W. Daum Vordiplomsklausur in Physik Mittwoch, 23. Februar 2005, 09.00-11:00 Uhr für den Studiengang: Mb, Inft, Geol,
Theoretische Physik: Mechanik
 Seite 1 Theoretische Physik: Mechanik Blatt 4 Fakultät für Physik Technische Universität München 27.09.2017 Inhaltsverzeichnis 1 Trägheitsmoment & Satz von Steiner 2 2 Trägheitstensor einer dünnen Scheibe
Seite 1 Theoretische Physik: Mechanik Blatt 4 Fakultät für Physik Technische Universität München 27.09.2017 Inhaltsverzeichnis 1 Trägheitsmoment & Satz von Steiner 2 2 Trägheitstensor einer dünnen Scheibe
O. Sternal, V. Hankele. 5. Thermodynamik
 5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
Klausur, Sommer 2007, Physik 1+2
 D-MATH/D-PHYS/D-CHEM Prof. G. Dissertori Studienjahr WS06/07 - SS07 ETH Zürich Klausur, Sommer 2007, Physik 1+2 Füllen Sie als erstes den untenstehenden Kopf mit Name und Legi-Nummer aus. Bitte beachten
D-MATH/D-PHYS/D-CHEM Prof. G. Dissertori Studienjahr WS06/07 - SS07 ETH Zürich Klausur, Sommer 2007, Physik 1+2 Füllen Sie als erstes den untenstehenden Kopf mit Name und Legi-Nummer aus. Bitte beachten
Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: , Abgabe am )
 Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: 14.09.11, Abgabe am 1.09.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Übungen Theoretische Physik I (Mechanik) Blatt 8 (Austeilung am: 14.09.11, Abgabe am 1.09.11) Hinweis: Kommentare zu den Aufgaben sollen die Lösungen illustrieren und ein besseres Verständnis ermöglichen.
Übungsblatt 2 ( )
 Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 01 Übungsblatt (11.05.01) 1) Geschwindigkeitsverteilung eines idealen Gases (a) Durch welche Verteilung lässt sich die Geschwindigkeitsverteilung
Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 01 Übungsblatt (11.05.01) 1) Geschwindigkeitsverteilung eines idealen Gases (a) Durch welche Verteilung lässt sich die Geschwindigkeitsverteilung
Musterlösung 2. Klausur Physik für Maschinenbauer
 Universität Siegen Sommersemester 2010 Fachbereich Physik Musterlösung 2. Klausur Physik für Maschinenbauer Prof. Dr. I. Fleck Aufgabe 1: Freier Fall im ICE Ein ICE bewege sich mit der konstanten Geschwindigkeit
Universität Siegen Sommersemester 2010 Fachbereich Physik Musterlösung 2. Klausur Physik für Maschinenbauer Prof. Dr. I. Fleck Aufgabe 1: Freier Fall im ICE Ein ICE bewege sich mit der konstanten Geschwindigkeit
Der Zustand eines Systems ist durch Zustandsgrößen charakterisiert.
 Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Probeklausur STATISTISCHE PHYSIK PLUS
 DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
Schriftliche Vordiplomprüfung Physik
 Schriftliche Vordiplomprüfung Physik Prof. T. Esslinger / Prof. R. Monnier Dated: Mittwoch, 17. September 2003, 9:00 12:00 Uhr) Aufgaben I. ELEKTRON IM MAGNETFELD Ein Elektron Ladung e, Masse m) bewegt
Schriftliche Vordiplomprüfung Physik Prof. T. Esslinger / Prof. R. Monnier Dated: Mittwoch, 17. September 2003, 9:00 12:00 Uhr) Aufgaben I. ELEKTRON IM MAGNETFELD Ein Elektron Ladung e, Masse m) bewegt
Probeklausur zur T1 (Klassische Mechanik)
 Probeklausur zur T1 (Klassische Mechanik) WS 006/07 Bearbeitungsdauer: 10 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
Probeklausur zur T1 (Klassische Mechanik) WS 006/07 Bearbeitungsdauer: 10 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
Beachten sie bitte die Punkteverteilung
 Tutor oder Tutorium: Semester: Fachrichtung: Beachten sie bitte die Punkteverteilung Aufgabe Punkte 1 7 2 11 3 6 4 9 5 7 Gesamt 40 Nützliche Formeln und Konstanten: Volumenelement Zylinderkoordinaten:
Tutor oder Tutorium: Semester: Fachrichtung: Beachten sie bitte die Punkteverteilung Aufgabe Punkte 1 7 2 11 3 6 4 9 5 7 Gesamt 40 Nützliche Formeln und Konstanten: Volumenelement Zylinderkoordinaten:
Hilfsmittel sind nicht zugelassen, auch keine Taschenrechner! Heftung nicht lösen! Kein zusätzliches Papier zugelassen!
 Physik / Klausur Anfang WS /3 Heift / Kurtz Name: Vorname: Matrikel-Nr: Unterschrift: Formeln siehe letzte Rückseite! Hilfsmittel sind nicht zugelassen, auch keine Taschenrechner! Heftung nicht lösen!
Physik / Klausur Anfang WS /3 Heift / Kurtz Name: Vorname: Matrikel-Nr: Unterschrift: Formeln siehe letzte Rückseite! Hilfsmittel sind nicht zugelassen, auch keine Taschenrechner! Heftung nicht lösen!
Klausur Experimentalphysik I
 Universität Siegen Winter Semester 2017/2018 Naturwissenschaftlich-Technische Fakultät Prof. Dr. Mario Agio Department Physik Klausur Experimentalphysik I Datum: 21.3.2018-10 Uhr Name: Matrikelnummer:
Universität Siegen Winter Semester 2017/2018 Naturwissenschaftlich-Technische Fakultät Prof. Dr. Mario Agio Department Physik Klausur Experimentalphysik I Datum: 21.3.2018-10 Uhr Name: Matrikelnummer:
Allgemeine Gasgleichung und technische Anwendungen
 Allgemeine Gasgleichung und technische Anwendungen Ziele i.allgemeine Gasgleichung: Darstellung in Diagrammen: Begriffsdefinitionen : Iso bar chor them Adiabatische Zustandsänderung Kreisprozess prinzipiell:
Allgemeine Gasgleichung und technische Anwendungen Ziele i.allgemeine Gasgleichung: Darstellung in Diagrammen: Begriffsdefinitionen : Iso bar chor them Adiabatische Zustandsänderung Kreisprozess prinzipiell:
Thermodynamische Hauptsätze, Kreisprozesse Übung
 Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene)
 Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene) Wir haben gesehen, dass ein sogenanntes 'ideales Gas' durch die Zustandsgleichung pv = νr T [1] beschrieben wird; wir wollen nun verstehen, welchen
Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene) Wir haben gesehen, dass ein sogenanntes 'ideales Gas' durch die Zustandsgleichung pv = νr T [1] beschrieben wird; wir wollen nun verstehen, welchen
Schriftliche Vordiplomprüfung Physik Wiederholungsprüfung
 Schriftliche Vordiplomprüfung Physik Wiederholungsprüfung Prof. T. Esslinger (Dated: Mittwoch, 5. Februar 4, 9: Uhr) Aufgaben I. IONEN IN EINER FALLE Eine Falle für elektrisch geladene Ionen wird durch
Schriftliche Vordiplomprüfung Physik Wiederholungsprüfung Prof. T. Esslinger (Dated: Mittwoch, 5. Februar 4, 9: Uhr) Aufgaben I. IONEN IN EINER FALLE Eine Falle für elektrisch geladene Ionen wird durch
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 1/13/14) Dozent: J. von Delft Übungen: B. Kubala Klausur zur Vorlesung T1: Theoretische Mechanik, SoSe 008 (3. Juli 007) Bearbeitungszeit:
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 1/13/14) Dozent: J. von Delft Übungen: B. Kubala Klausur zur Vorlesung T1: Theoretische Mechanik, SoSe 008 (3. Juli 007) Bearbeitungszeit:
Experimentalphysik EP, WS 2012/13
 FAKULTÄT FÜR PHYSIK Ludwig-Maximilians-Universität München Prof. O. Biebel, PD. W. Assmann Experimentalphysik EP, WS 0/3 Probeklausur (ohne Optik)-Nummer: 7. Januar 03 Hinweise zur Bearbeitung Alle benutzten
FAKULTÄT FÜR PHYSIK Ludwig-Maximilians-Universität München Prof. O. Biebel, PD. W. Assmann Experimentalphysik EP, WS 0/3 Probeklausur (ohne Optik)-Nummer: 7. Januar 03 Hinweise zur Bearbeitung Alle benutzten
Klausur Technische Mechanik C
 Klausur Technische Mechanik C 8/7/ Name: Matrikel: Studiengang: Hinweise: - Die Prüfungszeit beträgt zwei Stunden - Erlaubte Hilfsmittel sind: Formelsammlungen, Deckblätter der Übungsaufgaben und Taschenrechner
Klausur Technische Mechanik C 8/7/ Name: Matrikel: Studiengang: Hinweise: - Die Prüfungszeit beträgt zwei Stunden - Erlaubte Hilfsmittel sind: Formelsammlungen, Deckblätter der Übungsaufgaben und Taschenrechner
Aufgabe Max.Pkt. Punkte Visum 1 Visum Total 62
 D-PHYS Prof. Dr. M. Carollo Semester HS10 ETH Zürich Prüfung Physik I (24. August 2011) Füllen Sie als erstes den untenstehenden Kopf mit Name und Legi-Nummer aus, und kreuzen Sie Ihre Studienrichtung
D-PHYS Prof. Dr. M. Carollo Semester HS10 ETH Zürich Prüfung Physik I (24. August 2011) Füllen Sie als erstes den untenstehenden Kopf mit Name und Legi-Nummer aus, und kreuzen Sie Ihre Studienrichtung
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
10. Thermodynamik Der erste Hauptsatz Der zweite Hauptsatz Thermodynamischer Wirkungsgrad Der Carnotsche Kreisprozess
 Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Übungen zu Experimentalphysik 2 für MSE
 Physik-Department LS für Funktionelle Materialien SS 208 Übungen zu Experimentalphysik 2 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. olker Körstgens, Sebastian Grott, Julian Heger, Dr. Neelima Paul,
Physik-Department LS für Funktionelle Materialien SS 208 Übungen zu Experimentalphysik 2 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. olker Körstgens, Sebastian Grott, Julian Heger, Dr. Neelima Paul,
Thermodynamik 1 Klausur 08. September 2016
 Thermodynamik 1 Klausur 08. September 2016 Bearbeitungszeit: 150 Minuten Umfang der Aufgabenstellung: 7 nummerierte Seiten Alle Unterlagen zur Vorlesung und Übung sowie Lehrbücher und Taschenrechner sind
Thermodynamik 1 Klausur 08. September 2016 Bearbeitungszeit: 150 Minuten Umfang der Aufgabenstellung: 7 nummerierte Seiten Alle Unterlagen zur Vorlesung und Übung sowie Lehrbücher und Taschenrechner sind
Vorlesung Physik für Pharmazeuten PPh Wärmelehre
 Vorlesung Physik für Pharmazeuten PPh - 07 Wärmelehre Aggregatzustände der Materie im atomistischen Bild Beispiel Wasser Eis Wasser Wasserdampf Dynamik an der Wasser-Luft Grenzfläche im atomistischen Bild
Vorlesung Physik für Pharmazeuten PPh - 07 Wärmelehre Aggregatzustände der Materie im atomistischen Bild Beispiel Wasser Eis Wasser Wasserdampf Dynamik an der Wasser-Luft Grenzfläche im atomistischen Bild
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases. f=5 Translation + Rotation. f=7 Translation + Rotation +Vibration. Wiederholung
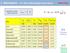 1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
Abschlussprüfung an Fachoberschulen im Schuljahr 2002/2003
 Abschlussprüfung an Fachoberschulen im Schuljahr 00/00 Haupttermin: Nach- bzw. Wiederholtermin: 0.06.00 Fachrichtung: Technik Fach: Physik Prüfungsdauer: 10 Minuten Hilfsmittel: - Formelsammlung/Tafelwerk
Abschlussprüfung an Fachoberschulen im Schuljahr 00/00 Haupttermin: Nach- bzw. Wiederholtermin: 0.06.00 Fachrichtung: Technik Fach: Physik Prüfungsdauer: 10 Minuten Hilfsmittel: - Formelsammlung/Tafelwerk
06/02/12. Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise:
 Prof Dr-Ing Ams Klausur Technische Mechanik C 06/0/1 Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: - Die Prüfungszeit beträgt zwei Stunden - Erlaubte Hilfsmittel
Prof Dr-Ing Ams Klausur Technische Mechanik C 06/0/1 Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: - Die Prüfungszeit beträgt zwei Stunden - Erlaubte Hilfsmittel
PC-Übung Nr.3 vom
 PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler
 TU München Reinhard Scholz Physik Department, T33 Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler http://www.wsi.tum.de/t33/teaching/teaching.htm Übung in Theoretischer Physik B (Thermodynamik)
TU München Reinhard Scholz Physik Department, T33 Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler http://www.wsi.tum.de/t33/teaching/teaching.htm Übung in Theoretischer Physik B (Thermodynamik)
II. Wärmelehre. II.2. Die Hauptsätze der Wärmelehre. Physik für Mediziner 1
 II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
Thermodynamische Hauptsätze, Kreisprozesse Übung
 Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 4.09.00 Inhaltsverzeichnis Inhaltsverzeichnis Thermodynamische Hauptsätze. Aufgabe :..................................... Aufgabe :.....................................
Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 4.09.00 Inhaltsverzeichnis Inhaltsverzeichnis Thermodynamische Hauptsätze. Aufgabe :..................................... Aufgabe :.....................................
Klausur zur Vorlesung E1: Mechanik für Lehramtskandidaten und Nebenfächler (6 ECTS)
 Fakultät für Physik der LMU 13.02.2012 Klausur zur Vorlesung E1: Mechanik für Lehramtskandidaten und Nebenfächler (6 ECTS) Wintersemester 2011/2012 Prof. Dr. Joachim O. Rädler, PD Dr. Bert Nickel und Dr.
Fakultät für Physik der LMU 13.02.2012 Klausur zur Vorlesung E1: Mechanik für Lehramtskandidaten und Nebenfächler (6 ECTS) Wintersemester 2011/2012 Prof. Dr. Joachim O. Rädler, PD Dr. Bert Nickel und Dr.
Physik 2 Hydrologen et al., SoSe 2013 Lösungen 3. Übung (KW 19/20) Carnot-Wärmekraftmaschine )
 3. Übung KW 19/20) Aufgabe 1 T 4.5 Carnot-Wärmekraftmaschine ) Eine Carnot-Wärmekraftmaschine arbeitet zwischen den Temperaturen und. Während der isothermen Expansion vergrößert sich das Volumen von auf
3. Übung KW 19/20) Aufgabe 1 T 4.5 Carnot-Wärmekraftmaschine ) Eine Carnot-Wärmekraftmaschine arbeitet zwischen den Temperaturen und. Während der isothermen Expansion vergrößert sich das Volumen von auf
Übungsaufgaben zur E1 / E1p Mechanik, WS 2016/17. Prof. J. O. Rädler, PD. B. Nickel Fakultät für Physik, Ludwig-Maximilians-Universität, München
 Übungsaufgaben zur E1 / E1p Mechanik, WS 2016/17 Prof. J. O. Rädler, PD. B. Nickel Fakultät für Physik, Ludwig-Maximilians-Universität, München Blatt 11: Gekoppelter Oszillator, Hydrostatik & Gase Ausgabe:
Übungsaufgaben zur E1 / E1p Mechanik, WS 2016/17 Prof. J. O. Rädler, PD. B. Nickel Fakultät für Physik, Ludwig-Maximilians-Universität, München Blatt 11: Gekoppelter Oszillator, Hydrostatik & Gase Ausgabe:
Klausur zur Vorlesung Thermodynamik
 Institut für Thermodynamik 18. März 2011 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
Institut für Thermodynamik 18. März 2011 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
Aufgaben zur Experimentalphysik II: Thermodynamik
 Aufgaben zur Experimentalphysik II: Thermodynamik Lösungen William Hefter - 5//8 1. 1. Durchmesser der Stahlstange nach T : D s D s (1 + α Stahl T) Durchmesser der Bohrung im Ring nach T : D m D m (1 +
Aufgaben zur Experimentalphysik II: Thermodynamik Lösungen William Hefter - 5//8 1. 1. Durchmesser der Stahlstange nach T : D s D s (1 + α Stahl T) Durchmesser der Bohrung im Ring nach T : D m D m (1 +
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik. SCHRIFTLICHE PRÜFUNG zur VU Modellbildung am
 Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik SCHRIFTLICHE PRÜFUNG zur VU Modellbildung am 8..04 Arbeitszeit: 0 min Name: Vorname(n): Matrikelnummer: Note: Aufgabe 3 4
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik SCHRIFTLICHE PRÜFUNG zur VU Modellbildung am 8..04 Arbeitszeit: 0 min Name: Vorname(n): Matrikelnummer: Note: Aufgabe 3 4
Experimentalphysik EP, WS 2013/14
 FAKULTÄT FÜR PHYSIK Ludwig-Maximilians-Universität München Prof. J. Schreiber, PD. W. Assmann Experimentalphysik EP, WS 2013/14 Probeklausur (ohne Optik)-Nummer: 7. Januar 2014 Hinweise zur Bearbeitung
FAKULTÄT FÜR PHYSIK Ludwig-Maximilians-Universität München Prof. J. Schreiber, PD. W. Assmann Experimentalphysik EP, WS 2013/14 Probeklausur (ohne Optik)-Nummer: 7. Januar 2014 Hinweise zur Bearbeitung
A. v = 8.9 m/s B. v = 6.3 m/s C. v = 12.5 m/s D. v = 4.4 m/s E. v = 1.3 m/s
 Aufgabe 1: Wie schnell muss ein Wagen in einem Looping mit 8 m Durchmesser am höchsten Punkt sein, damit er gerade nicht herunterfällt? (im Schwerefeld der Erde) A. v = 8.9 m/s B. v = 6.3 m/s C. v = 12.5
Aufgabe 1: Wie schnell muss ein Wagen in einem Looping mit 8 m Durchmesser am höchsten Punkt sein, damit er gerade nicht herunterfällt? (im Schwerefeld der Erde) A. v = 8.9 m/s B. v = 6.3 m/s C. v = 12.5
Übungen zu Lagrange-Formalismus und kleinen Schwingungen
 Übungen zu Lagrange-Formalismus und kleinen Schwingungen Jonas Probst 22.09.2009 1 Teilchen auf der Stange Ein Teilchen der Masse m wird durch eine Zwangskraft auf einer masselosen Stange gehalten, auf
Übungen zu Lagrange-Formalismus und kleinen Schwingungen Jonas Probst 22.09.2009 1 Teilchen auf der Stange Ein Teilchen der Masse m wird durch eine Zwangskraft auf einer masselosen Stange gehalten, auf
Theoretische Physik: Mechanik
 Ferienkurs Theoretische Physik: Mechanik Sommer 2013 Übung 4 - Angabe Technische Universität München 1 Fakultät für Physik 1 Trägheitstensor 1. Ein starrer Körper besteht aus den drei Massenpunkten mit
Ferienkurs Theoretische Physik: Mechanik Sommer 2013 Übung 4 - Angabe Technische Universität München 1 Fakultät für Physik 1 Trägheitstensor 1. Ein starrer Körper besteht aus den drei Massenpunkten mit
Nachklausur zur Vorlesung Physik I für Chemiker (WS 2017/18)
 Universität Siegen Wintersemester 2017/18 Naturwissenschaftlich-Technische Fakultät Department Physik Nachklausur zur Vorlesung Physik I für Chemiker (WS 2017/18) Datum: Montag, 19.03.2017, 10:00-12:00
Universität Siegen Wintersemester 2017/18 Naturwissenschaftlich-Technische Fakultät Department Physik Nachklausur zur Vorlesung Physik I für Chemiker (WS 2017/18) Datum: Montag, 19.03.2017, 10:00-12:00
Thermodynamik 1 Klausur 12. März Alle Unterlagen zu Vorlesung und Übung sowie Lehrbücher und Taschenrechner sind als Hilfsmittel zugelassen.
 Institut für Energie- und Verfahrenstechnik Thermodynamik und Energietechnik Prof. Dr.-Ing. habil. Jadran Vrabec ThEt Thermodynamik 1 Klausur 12. März 2014 Bearbeitungszeit: 150 Minuten Umfang der Aufgabenstellung:
Institut für Energie- und Verfahrenstechnik Thermodynamik und Energietechnik Prof. Dr.-Ing. habil. Jadran Vrabec ThEt Thermodynamik 1 Klausur 12. März 2014 Bearbeitungszeit: 150 Minuten Umfang der Aufgabenstellung:
Aufgabe 1: (18 Punkte)
 MODULPRÜFUNG TECHNISCHE MECHANIK IV (PO 2004) VOM 26.07.2011 Seite 1 Aufgabe 1: (18 Punkte) Zwei Massenpunkte m 1 = 5 kg und m 2 = 2 kg sind durch ein dehnstarres und massenloses Seil über eine reibungsfrei
MODULPRÜFUNG TECHNISCHE MECHANIK IV (PO 2004) VOM 26.07.2011 Seite 1 Aufgabe 1: (18 Punkte) Zwei Massenpunkte m 1 = 5 kg und m 2 = 2 kg sind durch ein dehnstarres und massenloses Seil über eine reibungsfrei
Vordiplomsklausur Physik
 Institut für Physik und Physikalische Technologien der TU-Clausthal; Prof. Dr. W. Schade Vordiplomsklausur Physik 22.Februar 2006, 9:00-11:00 Uhr für die Studiengänge Mb,Mb-Mech, Inft, Ciw, E+R/Bach. (bitte
Institut für Physik und Physikalische Technologien der TU-Clausthal; Prof. Dr. W. Schade Vordiplomsklausur Physik 22.Februar 2006, 9:00-11:00 Uhr für die Studiengänge Mb,Mb-Mech, Inft, Ciw, E+R/Bach. (bitte
ETH-Aufnahmeprüfung Herbst Physik U 1. Aufgabe 1 [4 pt + 4 pt]: zwei unabhängige Teilaufgaben
![ETH-Aufnahmeprüfung Herbst Physik U 1. Aufgabe 1 [4 pt + 4 pt]: zwei unabhängige Teilaufgaben ETH-Aufnahmeprüfung Herbst Physik U 1. Aufgabe 1 [4 pt + 4 pt]: zwei unabhängige Teilaufgaben](/thumbs/64/51931310.jpg) ETH-Aufnahmeprüfung Herbst 2015 Physik Aufgabe 1 [4 pt + 4 pt]: zwei unabhängige Teilaufgaben U 1 V a) Betrachten Sie den angegebenen Stromkreis: berechnen Sie die Werte, die von den Messgeräten (Ampere-
ETH-Aufnahmeprüfung Herbst 2015 Physik Aufgabe 1 [4 pt + 4 pt]: zwei unabhängige Teilaufgaben U 1 V a) Betrachten Sie den angegebenen Stromkreis: berechnen Sie die Werte, die von den Messgeräten (Ampere-
a) Welche der folgenden Aussagen treffen nicht zu? (Dies bezieht sind nur auf Aufgabenteil a)
 Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Vordiplomsklausur Physik
 Institut für Physik und Physikalische Technologien der TU-Clausthal; Prof. Dr. W. Schade Vordiplomsklausur Physik 14.Februar 2006, 9:00-11:00 Uhr für den Studiengang: Maschinenbau intensiv (bitte deutlich
Institut für Physik und Physikalische Technologien der TU-Clausthal; Prof. Dr. W. Schade Vordiplomsklausur Physik 14.Februar 2006, 9:00-11:00 Uhr für den Studiengang: Maschinenbau intensiv (bitte deutlich
Grundlagen der Physik II
 Grundlagen der Physik II Othmar Marti 05. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 05. 07. 2007 Klausur Die Klausur
Grundlagen der Physik II Othmar Marti 05. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 05. 07. 2007 Klausur Die Klausur
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
Klausur Montag, Bitte ankreuzen:
 Nicht vom Studierenden auszufüllen! Punkte Note Thema Punkte Kz Diff. Kz Diff. C.T. Mechanik, Schwingungen und Wellen Elektrizitätslehre und Optik Thermodynamik Datum Einsicht Kz Summe Punkte Klausur Montag,
Nicht vom Studierenden auszufüllen! Punkte Note Thema Punkte Kz Diff. Kz Diff. C.T. Mechanik, Schwingungen und Wellen Elektrizitätslehre und Optik Thermodynamik Datum Einsicht Kz Summe Punkte Klausur Montag,
Wiederholungsklausur
 PN1 Einführung in die Physik für Chemiker 1 Prof. J. Lipfert WS 2014/15 Wiederholungsklausur Wiederholungsklausur Name: Matrikelnummer: Bitte schreiben Sie Ihren Namen auf jede Seite und legen Sie Ihren
PN1 Einführung in die Physik für Chemiker 1 Prof. J. Lipfert WS 2014/15 Wiederholungsklausur Wiederholungsklausur Name: Matrikelnummer: Bitte schreiben Sie Ihren Namen auf jede Seite und legen Sie Ihren
4 Thermodynamik mikroskopisch: kinetische Gastheorie makroskopisch: System:
 Theorie der Wärme kann auf zwei verschiedene Arten behandelt werden. mikroskopisch: Bewegung von Gasatomen oder -molekülen. Vielzahl von Teilchen ( 10 23 ) im Allgemeinen nicht vollständig beschreibbar
Theorie der Wärme kann auf zwei verschiedene Arten behandelt werden. mikroskopisch: Bewegung von Gasatomen oder -molekülen. Vielzahl von Teilchen ( 10 23 ) im Allgemeinen nicht vollständig beschreibbar
Aufgaben zur Wärmelehre
 Aufgaben zur Wärmelehre 1. Ein falsch kalibriertes Quecksilberthermometer zeigt -5 C eingetaucht im schmelzenden Eis und 103 C im kochenden Wasser. Welche ist die richtige Temperatur, wenn das Thermometer
Aufgaben zur Wärmelehre 1. Ein falsch kalibriertes Quecksilberthermometer zeigt -5 C eingetaucht im schmelzenden Eis und 103 C im kochenden Wasser. Welche ist die richtige Temperatur, wenn das Thermometer
Abschlussprüfung an Fachoberschulen im Schuljahr 2000/2001
 Abschlussprüfung an Fachoberschulen im Schuljahr 2000/2001 Haupttermin: Nach- bzw. Wiederholtermin: 2.0.2001 Fachrichtung: Technik Fach: Physik Prüfungsdauer: 210 Minuten Hilfsmittel: Formelsammlung/Tafelwerk
Abschlussprüfung an Fachoberschulen im Schuljahr 2000/2001 Haupttermin: Nach- bzw. Wiederholtermin: 2.0.2001 Fachrichtung: Technik Fach: Physik Prüfungsdauer: 210 Minuten Hilfsmittel: Formelsammlung/Tafelwerk
Fakultät für Physik der LMU
 Fakultät für Physik der LMU 11.04.2013 Nachholklausur zur Vorlesung E1: Mechanik für Studenten der Physik für das Lehramt an Gymnasien und im Nebenfach (6 ECTS) Wintersemester 2012/13 Prof. Dr. Joachim
Fakultät für Physik der LMU 11.04.2013 Nachholklausur zur Vorlesung E1: Mechanik für Studenten der Physik für das Lehramt an Gymnasien und im Nebenfach (6 ECTS) Wintersemester 2012/13 Prof. Dr. Joachim
Hinweis: Geben Sie für den Winkel α keinen konkreten Wert, sondern nur für sin α und/oder cos α an.
 1. Geschwindigkeiten (8 Punkte) Ein Schwimmer, der sich mit konstanter Geschwindigkeit v s = 1.25 m/s im Wasser vorwärts bewegen kann, möchte einen mit Geschwindigkeit v f = 0.75 m/s fließenden Fluß der
1. Geschwindigkeiten (8 Punkte) Ein Schwimmer, der sich mit konstanter Geschwindigkeit v s = 1.25 m/s im Wasser vorwärts bewegen kann, möchte einen mit Geschwindigkeit v f = 0.75 m/s fließenden Fluß der
Klausur zur Vorlesung E1: Mechanik für Studenten mit Nebenfach Physik (6 ECTS)
 Fakultät für Physik der LMU 23.02.2017 Klausur zur Vorlesung E1: Mechanik für Studenten mit Nebenfach Physik (6 ECTS) Wintersemester 2016/2017 Prof. Dr. Joachim O. Rädler, PD Dr. Bert Nickel Name:... Vorname:...
Fakultät für Physik der LMU 23.02.2017 Klausur zur Vorlesung E1: Mechanik für Studenten mit Nebenfach Physik (6 ECTS) Wintersemester 2016/2017 Prof. Dr. Joachim O. Rädler, PD Dr. Bert Nickel Name:... Vorname:...
Einführung in die Physik
 Einführung in die Physik für Pharmazeuten und Biologen (PPh) Mechanik, Elektrizitätslehre, Optik Übung : Vorlesung: Tutorials: Montags 13:15 bis 14 Uhr, Liebig-HS Montags 14:15 bis 15:45, Liebig HS Montags
Einführung in die Physik für Pharmazeuten und Biologen (PPh) Mechanik, Elektrizitätslehre, Optik Übung : Vorlesung: Tutorials: Montags 13:15 bis 14 Uhr, Liebig-HS Montags 14:15 bis 15:45, Liebig HS Montags
Klausur Physik 1 (GPH1) am
 Name, Matrikelnummer: Klausur Physik 1 (GPH1) am 9.2.04 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel: Beiblätter zur Vorlesung Physik 1 ab
Name, Matrikelnummer: Klausur Physik 1 (GPH1) am 9.2.04 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel: Beiblätter zur Vorlesung Physik 1 ab
Thermodynamik I Klausur SS 2010
 Thermodynamik I Klausur 00 Prof. Dr. J. Kuck, Prof. Dr. G. Wilhelms Aufgabenteil / 00 Minuten/eite Name: Vorname: Matr.-Nr.: Das Aufgabenblatt muss unterschrieben und zusammen mit den (nummerierten und
Thermodynamik I Klausur 00 Prof. Dr. J. Kuck, Prof. Dr. G. Wilhelms Aufgabenteil / 00 Minuten/eite Name: Vorname: Matr.-Nr.: Das Aufgabenblatt muss unterschrieben und zusammen mit den (nummerierten und
Klassische Experimentalphysik I (Mechanik) (WS 16/17)
 Klassische Experimentalphysik I (Mechanik) (WS 16/17) http://ekpwww.physik.uni-karlsruhe.de/~rwolf/teaching/ws16-17-mechanik.html Klausur 2 Anmerkung: Diese Klausur enthält 9 Aufgaben, davon eine Multiple
Klassische Experimentalphysik I (Mechanik) (WS 16/17) http://ekpwww.physik.uni-karlsruhe.de/~rwolf/teaching/ws16-17-mechanik.html Klausur 2 Anmerkung: Diese Klausur enthält 9 Aufgaben, davon eine Multiple
Wichtig!!!! Nur klare, übersichtliche Lösungen werden gewertet!!!! Alle Lösungen immer erst allgemein bestimmen, dann einsetzen!
 ÜBUNGEN ZUR EINFÜHRUNG IN DIE PHYSIK I WS 2008/09 PROBEKLAUSUR 05.12.2008 Kennwort :... Übungsgruppe (Tag/Uhrzeit) Kennzahl : nur für die Korrektoren: Studienziel (bitte ankreuzen): Aufgabe Punkte Physik
ÜBUNGEN ZUR EINFÜHRUNG IN DIE PHYSIK I WS 2008/09 PROBEKLAUSUR 05.12.2008 Kennwort :... Übungsgruppe (Tag/Uhrzeit) Kennzahl : nur für die Korrektoren: Studienziel (bitte ankreuzen): Aufgabe Punkte Physik
