Theoretische Informatik für Wirtschaftsinformatik und Lehramt
|
|
|
- Fanny Kalb
- vor 5 Jahren
- Abrufe
Transkript
1 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Entscheidungsprobleme Priv.-Doz. Dr. Stefan Milius Theoretische Informatik Friedrich-Alexander Universität Erlangen-Nürnberg SS / 43
2 Gliederung 1 Lernziele 2 Grundbegriffe 3 Unentscheidbare Probleme 4 Semi-entscheidbare Probleme 5 Zusammenfassung 2 / 43
3 Worum geht es in diesem Abschnitt? Entscheidungsprobleme Probleme mit nur zwei möglichen Lösungen: Ja oder Nein Frage: Gibt es für jedes solche Problem einen Algorithmus? Berühmtes unentscheidbares Problem: Halteproblem Kann ein Algorithmus feststellen, ob ein gegebenes Programm terminiert oder nicht? Damit lassen sich weitere Entscheidungsprobleme als unentscheidbar nachweisen. 3 / 43
4 Lernziele die Konzepte Entscheidbarkeit, Unentscheidbarkeit, Semi-Entscheidbarkeit beispielbezogen erklären können die Unentscheidbarkeit des Halteproblems erläutern können Methoden für Unentscheidbarkeitsbeweise: 1 Satz von Rice anwenden können 2 Sprache auf eine andere Sprache reduzieren können 4 / 43
5 Entscheidungsprobleme (I) Entscheidungsprobleme sind Probleme, die nur zwei mögliche Lösungen haben: Ja oder Nein. Beispiel: Primzahlproblem Eingabe: Natürliche Zahl n N Aufgabe: Entscheiden, ob n eine Primzahl ist. Bemerkung: Der Problembegriff wird verwendet für eine ganze Klasse gleichartiger Einzelprobleme: Ist 1 eine Primzahl?, Ist 2 eine Primzahl?,... Beispiel: Wortproblem einer formalen Sprache Zu jeder formalen Sprache L Σ ist das zugehörige Wortproblem: Eingabe: w Σ Aufgabe: Entscheiden, ob w L oder nicht. 5 / 43
6 Modellierung von Entscheidungsproblemen Durch geeignete Kodierung lässt sich jedes Entscheidungsproblem in ein Wortproblem umwandeln. Beispiel Kodierung natürlicher Zahlen als Wörter über Σ = {0,..., 9} (Dezimaldarstellung) Primzahlen bilden dann eine formale Sprache: PRIMES Σ Primzahlproblem = Wortproblem für PRIMES. 6 / 43
7 Entscheidungsverfahren und Semi-Entscheidungsverfahren Im Folgenden: Algorithmen für Entscheidungsprobleme Man unterscheidet: Entscheidungsverfahren: Algorithmus, der für alle Eingaben terminiert und die korrekte Antwort Ja oder Nein liefert Semi-Entscheidungsverfahren: Algorithmus, der für jede Eingabe, für die die korrekte Antwort Ja lautet, mit der korrekten Antwort Ja terminiert und der für jede Eingabe, für die die korrekte Antwort Nein lautet, entweder mit der Antwort Nein oder gar nicht terminiert 7 / 43
8 Entscheidbarkeit Entscheidungsproblem als Wortproblem von L Σ : Eingabe: w Σ Aufgabe: Entscheiden, ob w L gilt oder nicht. Formalisierung (zur Erinnerung): Eine Sprache L Σ heißt entscheidbar, wenn es eine TM M = (Q, Σ, Γ, δ, z 0, E) gibt, die auf jede Eingabe w Σ terminiert w genau dann akzeptiert, wenn w L gilt. (M akzeptiert w falls: z 0 w M αz +β mit α, β Γ, z + E akzeptierender Zustand und αz + β finale Konfiguration.) Alternativ: Eine Sprache L Σ heißt entscheidbar, falls die totale charakteristische Funktion χ L : Σ {0, 1} von L berechenbar ist: { 1, falls w L χ L (w) = 0, sonst 8 / 43
9 Entscheidbarkeit im Maschinenmodell Veranschaulichung der Entscheidbarkeit im Maschinenmodell bei jeder Eingabe rechnet die Maschine eine endliche Zeit und gibt dann Ja oder Nein aus Ausgeben : Ja = Halten in einem akzeptierenden Zustand Nein = Halten in einem nicht akzeptierenden Zustand 9 / 43
10 Unentscheidbarkeit Formalisierung (zur Erinnerung, Fortsetzung): Eine unentscheidbare Sprache ist eine Sprache, die nicht entscheidbar ist. Anschauliche Interpretation: Eine Eigenschaft auf einer Menge heißt entscheidbar (auch: rekursiv), wenn es ein Entscheidungsverfahren für sie gibt. Ein Entscheidungsverfahren ist ein Algorithmus (oder eine Turing-Maschine), der (bzw. die) für jedes Element der Menge beantworten kann, ob es die Eigenschaft hat oder nicht. Wenn es ein solches Entscheidungsverfahren nicht gibt, dann nennt man die Eigenschaft unentscheidbar. 10 / 43
11 Entscheidungsprobleme (II) Beispiel Informelles Entscheidungsproblem (bzw. algorithmische Aufgabe): ( ) Entscheide (für beliebig gegebene n, m), ob die natürlichen Zahlen n und m teilerfremd sind. Formale Repräsentation: durch die Menge {(n, m) N 2 n und m sind teilerfremd} Kodierung: über dem Alphabet {, } durch die formale Sprache L tf = { n m {, } n, m N; n und m sind teilerfremd} 11 / 43
12 Entscheidungsprobleme (III) Beispiel (Fortsetzung) L tf ist im Sinne der formalen Definition entscheidbar TM, die L tf entscheidet, kann verstanden werden als ein algorithmisches Verfahren zur Lösung von ( ) Informell: das Entscheidungsproblem ( ) ist entscheidbar Algorithmus für ( ): Lies m, n; for k := 2 to min(m, n) do if k teilt m und n then halte und gib Nein aus endif enddo Gib Ja aus. Das Prädikat k teilt m und n ist total und berechenbar für m, n > 1 und alle 1 < k min(m, n). 12 / 43
13 Programme als Eingabe von Programmen Beispiele Algorithmen werden mithilfe von Programmen notiert Programme können als Wörter über einem geeigneten Alphabet kodiert werden Programme können dann selbst wieder Eingabe für einen Algorithmus sein (eventuell nach vorheriger Umkodierung als natürliche Zahl durch Gödelisierung ) kommt in der Informatik häufiger vor Compiler, Interpreter Interessante Frage: Kann ein Programm P 1, das ein anderes Programm P 2 als Eingabe erhält, entscheiden, ob das übergebene Programm P 2 eine bestimmte (nicht triviale) semantische Eigenschaft aufweist? 13 / 43
14 Das Halteproblem Berühmtes und oft betrachtetes Problem! Allgemeines Halteproblem (H): Eingabe: Programm P, Eingabe x für P Aufgabe: Entscheiden, ob P auf Eingabe x nach endlich vielen Schritten terminiert. Spezielles Halteproblem bzw. Selbstanwendungsproblem (SANW): Eingabe: Programm P Aufgabe: Entscheiden, ob P mit sich selbst als Eingabe nach endlich vielen Schritten terminiert. Für manche Programme leicht: z.b.: LOOP-Programme terminieren auf jede Eingabe Frage: Gibt es einen Algorithmus, der (Nicht-)Terminierung eines gegebenen Programms in endlicher Zeit feststellt? 14 / 43
15 Halteproblem für Turingmaschinen (I) Formalisierung: Allgemeines Halteproblem für TM: Eingabe: Codewort c(m) der (deterministischen) TM M, Eingabewort w Σ Aufgabe: Entscheiden, ob M auf Eingabe w terminiert Spezielles Halteproblem für TM: Eingabe: Codewort c(m) der TM M Aufgabe: Entscheiden, ob M auf Eingabe c(m) terminiert Also Wortprobleme der folgenden formalen Sprachen: L halt = {c(m)w M TM, die auf w hält} L sanw = {c(m) M TM, die auf c(m) hält} 15 / 43
16 Das spezielle Halteproblem (I) Satz 9.1 L sanw ist unentscheidbar. Beweis: durch Widerspruch. Annahme: L sanw ist entscheidbar. Dann existiert eine TM M sanw, die L sanw entscheidet. Mit M sanw baue eine neue TM M: M hält genau dann, wenn M sanw hält und nicht akzeptiert (falls M sanw hält und akzeptiert, hält M nicht) M : c(m) M sanw spez. Halteproblem Ja Endlosschleife Nein M hält und akzeptiert 16 / 43
17 Das spezielle Halteproblem (II) Beweis (Fortsetzung): M : c(m) M sanw spez. Halteproblem Ja Endlosschleife Nein M hält und akzeptiert Frage: Hält M bei Eingabe von c( M) oder nicht? Falls ja: M sanw hält auf c( M) und akzeptiert M hält nicht auf c( M). Widerspruch! Falls nein: M sanw hält auf c( M) und akzeptiert nicht M hält und akzeptiert c( M). Widerspruch! Fazit: Annahme falsch, d.h. L sanw nicht entscheidbar. 17 / 43
18 Reduktionen (I) Ziel jetzt: aus der Unentscheidbarkeit von L sanw weitere Unentscheidbarkeitsresultate gewinnen. Dazu argumentiere: 1 Wenn man Problem L 2 lösen könnte, dann könnte man auch L 1 lösen (Reduktionsschritt). 2 Dann ist L 2 mindestens so schwierig wie L 1. (Notation: L 1 L 2 ) 3 L 1 ist jedoch unentscheidbar. 4 Also: L 2 auch unentscheidbar. 18 / 43
19 Reduktionen (II) Definition Seien Σ ein Alphabet und L 1, L 2 Σ zwei Sprachen. L 1 heißt reduzierbar auf L 2, wenn es eine totale, berechenbare Funktion f : Σ Σ gibt, so dass für alle w Σ gilt: w L 1 f (w) L 2. (Schreibweise: L 1 L 2 oder auch f : L 1 L 2.) Informell bedeutet L 1 L 2 : L 2 mindestens so unentscheidbar ist wie L / 43
20 Reduktionen (III) Anschaulich: wenn f : L 1 L 2, dann kann man aus einer TM M L2, die L 2 akzeptiert und einer TM, die f berechnet eine TM M L1 bauen, die L 1 akzeptiert: 20 / 43
21 Reduktionen (IV) Satz 9.2 Seien Σ ein Alphabet, L 1, L 2 Σ. Es sei L 1 L 2. Ist L 2 entscheidbar, so ist auch L 1 entscheidbar. Ist L 1 unentscheidbar, so ist auch L 2 unentscheidbar. Methode, um die Unentscheidbarkeit eines (als Sprache kodierten) Problems L zu zeigen: finde eine geeignete unentscheidbare Sprache L (z.b. spezielles Halteproblem) finde eine geeignete Funktion f zur Reduktion von L auf L und beweise (Korrektheit der Reduktion): 1 f total und berechenbar 2 w L f (w) L Dann folgt aus Satz 9.2: L ist unentscheidbar 21 / 43
22 Das allgemeine Halteproblem Satz 9.3 Das allgemeine Halteproblem ist unentscheidbar. Beweis: durch Reduktion des speziellen Halteproblems: L sanw L halt Definiere f : Σ Σ : { c(m)c(m) falls w = c(m) für TM M f (w) = 0 sonst 1 f ist total und berechenbar (Syntaxcheck w? = c(m) ; dann c(m) kopieren) 2 w L sanw w = c(m) für TM M, die auf c(m) hält f (w) = c(m)c(m) für TM M, die auf c(m) hält f (w) L halt. 22 / 43
23 Spezielles Wortproblem für eine fest gegebene Grammatik Spezielles Wortproblem für die (fest vorgegebene) Grammatik G = (V, Σ, P, S): Eingabe: w Σ Aufgabe: Entscheide, ob w von der Grammatik G erzeugt wird. Satz 9.4 Das spezielle Wortproblem für eine Chomsky-Grammatik ist (im Allgemeinen) unentscheidbar. Für spezielle (eingeschränkte) Grammatiken ist das Wortproblem aber entscheidbar. (z.b. für kontextfreie Grammatiken) 23 / 43
24 Allgemeines Wortproblem für Grammatiken Folge: Eingabe: Aufgabe: auch das allgemeine Wortproblem für Grammatiken ist unentscheidbar. (Code einer) Grammatik G und Wort w Σ Entscheide, ob w von G erzeugt wird oder nicht. 24 / 43
25 Entscheidungsprobleme für kontextfreie Grammatiken CYK-Algorithmus zeigt: das allgemeine Wortproblem für kontextfreie Grammatiken ist entscheidbar. Einige unentscheidbare Probleme für kontextfreie Sprachen: Satz 9.5 Folgende Probleme für gegebene kontextfreie Grammatiken G 1, G 2 sind unentscheidbar: a) Schnittproblem: Ist L(G 1 ) L(G 2 ) =? b) Äquivalenzproblem: Ist L(G 1 ) = L(G 2 )? c) Ist L(G 1 ) = Σ? (Σ Terminalalphabet mit Σ 2; für Σ = 1 ist jedes kontextfreie L schon regulär) Zum Vergleich: für reguläre Sprachen sind diese Probleme entscheidbar! 25 / 43
26 Satz von Rice Jede nicht triviale Eigenschaft von berechenbaren Funktionen (oder formalen Sprachen) ist unentscheidbar. Trivial heißt eine Eigenschaft, wenn alle oder keine berechenbare Funktion (oder formale Sprache) die Eigenschaft hat. Satz 9.6: Satz von Rice Sei R die Klasse aller Turing-berechenbaren Funktionen und sei S R mit S R. Dann ist die folgende formale Sprache unentscheidbar: L S = {c(m) die von der TM M berechnete Funktion liegt in S} 26 / 43
27 Satz von Rice (Anwendungsbeispiel) Beispiel Betrachte das Problem: Eingabe: c(m) für TM M (die f : Σ Σ berechnet) Aufgabe: Entscheiden, ob f (w) immer gerade Zahl ist oder nicht. Als formale Sprache: L even = {c(m) M TM, die f berechnet mit: f (w) gerade für alle w Σ } Dann gilt: L even = L S für S = {f f : Σ Σ berechenbar und f (w) gerade w Σ } S nicht trivial (d.h. S R), denn: f 1 (w) = ε liegt in S; f 2 (w) = 1 liegt nicht in S = wegen Satz von Rice ist L even = L S unentscheidbar. 27 / 43
28 Satz von Rice (für formale Sprachen) Satz 9.7: Satz von Rice (für formale Sprachen) Sei S eine nicht leere, echte Teilmenge der Menge aller formalen Sprachen. Dann ist die folgende formale Sprache unentscheidbar: Beispiel L S = {c(m) M ist TM und L(M) liegt in S}. Die folgende Sprache ist unentscheibar: L = {c(m) die TM M akzeptiert keine Eingabe} Setze S = { }. Dann ist S nicht triviale Eigenschaft, denn: S und S enthält nicht alle Sprachen. 28 / 43
29 Postsches Korrespondenzproblem (I) Das Alphabet Σ sei fest vorgegeben Postsches Korrespondenzproblem (PCP): Eingabe: endliche Folge von Paaren nicht leerer Wörter (v 1, w 1 ), (v 2, w 2 ),..., (v k, w k ) v i, w i Σ +, i = 1,..., k Aufgabe: Entscheiden, ob es eine nicht-leere Folge i 1,..., i n (1 i j k für j = 1,..., n) von Indizes gibt, so dass gilt: v i1 v i2... v in = w i1 w i2... w in Die Folge i 1,..., i n der Indizes heißt Lösung des Problems. 29 / 43
30 Postsches Korrespondenzproblem (II) Beispiel 1 Gegeben seien die Paare (1, 101), (10, 00), (011, 11) mit v 1 = 1; v 2 = 10; v 3 = 011 w 1 = 101; w 2 = 00; w 3 = 11 Das PCP besitzt in diesem Fall die Lösung I 1 = (1, 3, 2, 3), denn: v 1 v 3 v 2 v 3 = = = = w 1 w 3 w 2 w 3 30 / 43
31 Postsches Korrespondenzproblem (III) Beispiel 2 Gegeben seien die Paare (001, 0), (01, 011), (01, 101), (10, 001) mit v 1 = 001; v 2 = 01; v 3 = 01; v 4 = 10 w 1 = 0; w 2 = 011; w 3 = 101; w 4 = 001 Das PCP besitzt in diesem Fall die Lösung I 1 = (2, 4, 3, 4, 4, 2, 1, 2, 4, 3, 4, 3, 4, 4, 3, 4, 4, 2, 1, 4, 4, 2, 1, 3, 4, 1, 1, 3, 4, 4, 4, 2, 1, 2, 1, 1, 1, 3, 4, 3, 4, 1, 2, 1, 4, 4, 2, 1, 4, 1, 1, 3, 4, 1, 1, 3, 1, 1, 3, 1, 2, 1, 4, 1, 1, 3). Diese besteht schon aus 66 Paaren und zeigt die Komplexität des Problems. 31 / 43
32 Postsches Korrespondenzproblem (IV) Satz 9.8 Das Postsche Korrespondenzproblem ist (im Allgemeinen) unentscheidbar. Bemerkung: PCP wird ebenfalls als Ausgangsproblem für weitere Unentscheidbarkeitsaussagen benutzt Reduktion von PCP auf Problem P = P auch unentscheidbar Zum Beispiel unentscheidbare Grammatikprobleme wie: Eingabe: Zwei (codes von) Chomsky-Grammatiken G 1 und G 2 Aufgabe: Entscheiden ob L(G 1 ) L(G 2 ) =. (siehe z.b. Schöning) 32 / 43
33 Semi-entscheidbare Probleme (I) Erinnerung: Was heißt semi-entscheidbar? Semi-Entscheidbarkeit ist schwächerer Begriff als Begriff der Entscheidbarkeit Eine Sprache L Σ heißt semi-entscheidbar, wenn es eine TM M gibt, so dass w L genau dann gilt, wenn M w akzeptiert. Alternativ: Eine Sprache L Σ heißt semi-entscheidbar, wenn die partielle charakteristische Funktion χ : Σ {0, 1} von L berechenbar ist: { 1, falls w L χ L(w) = undefiniert sonst. 33 / 43
34 Semi-Entscheidbarkeit im Maschinenmodell Veranschaulichung der Semi-Entscheidbarkeit im Maschinenmodell bei jeder Eingabe rechnet die Maschine und gibt falls w L gilt nach endlicher Zeit ja aus falls die Antwort nein lauten müsste, kann es sein, dass die Maschine nie terminiert (oder sie gibt nach endlicher Zeit nein aus) Folge: man kann sich nie sicher sein, ob die Maschine nicht doch irgendwann ja ausgeben wird, da die Antwortzeit nicht beschränkt ist 34 / 43
35 Semi-entscheidbare Probleme (II) Frage: sind einige der zuvor betrachteten unentscheidbaren Probleme wenigstens semi-entscheidbar? Antwort: Ja, das ist der Fall. 35 / 43
36 Semi-Entscheidbarkeit des speziellen Halteproblems Satz 9.9 Das spezielle Halteproblem ist semi-entscheidbar. Beweis: Benutze die universelle TM M u wie folgt: 1 bei Eingabe von w, prüfe ob w = c(m) für eine TM M (falls nicht, halte und akzeptiere w nicht; sonst weiter bei 2) 2 simuliere mit M u die TM M auf Eingabe c(m) 3 halte und akzeptiere genau wenn M u hält (und dabei akzeptiert oder nicht akzeptiert) Analog: Satz 9.10 Das allgemeine Halteproblem ist semi-entscheidbar. 36 / 43
37 Semi-Entscheidbarkeit des Wortproblems Erinnerung: Satz 6.6 a) Zu jeder TM M gibt es eine Chomsky-Grammatik G mit L(G) = L(M). b) Zu jeder Chomsky-Grammatik G gibt es eine TM M mit L(M) = L(G). Daraus folgt die Semi-Entscheidbarkeit des speziellen Wortproblems für Grammatiken: Satz 9.11 Ist G eine Chomsky-Grammatik, so ist L(G) semi-entscheidbar. 37 / 43
38 Semi-entscheidbar und rekursiv aufzählbar (I) Definition Eine nicht-leere Sprache L Σ heißt rekursiv aufzählbar, falls L = oder falls es eine totale und berechenbare Funktion f : N Σ gibt, so dass L = {f (0), f (1), f (2),... } Sprechweise: f zählt L auf. (Man beachte, dass f (i) = f (j) zulässig ist.) Satz 9.12 Eine Sprache ist rekursiv aufzählbar genau dann, wenn sie semi-entscheidbar ist. 38 / 43
39 Semi-entscheidbar und rekursiv aufzählbar (II) Beweis von Satz 9.12: (hier nur = ; andere Richtung = ohne Beweis) Sei L ist rekursiv aufzählbar mittels Funktion f. Semi-Entscheidungsverfahren: input(x); for n := 0, 1, 2, 3,... do if f (n) = x then output(1) endif endfor 39 / 43
40 Äquivalente Aussagen Folgerung: Die folgenden Aussagen sind äquivalent für L Σ : L ist semi-entscheidbar. L ist rekursiv aufzählbar. L = L(M) für eine Turingmaschine M. χ L ist Turing-/WHILE-berechenbar. L ist Definitionsbereich einer berechenbaren Funktion. L ist Wertebereich einer berechenbaren Funktion. L ist vom Typ / 43
41 Nicht semi-entscheidbare Probleme Erinnerung: Satz 6.3 Sei Σ ein Alphabet. Es gibt Funktionen f : Σ Σ, die nicht berechenbar und Sprachen L Σ, die nicht semi-entscheidbar (und damit auch nicht entscheidbar) sind. Beispiel 1: Äquivalenzproblem für Turing-Maschinen L equiv = {c(m 1 )c(m 2 ) M i (i = 1, 2) TM mit L(M 1 ) = L(M 2 )} Tatsächlich hat man im Bereich der unentscheidbaren Probleme eine ganze Hierarchie von (unendlich vielen) Unentscheidbarkeitsgraden mit immer unentscheidbareren Problemen. Die (semi-)entscheidbaren Probleme bilden gerade den untersten Grad dieser Hierarchie. 41 / 43
42 Ein nicht semi-entscheidbares Problem Beispiel 2: Die Sprache L code Die folgende formale Sprache ist nicht semi-entscheidbar: L code = {c(m) M ist TM mit c(m) L(M)}. Beweis: durch Widerspruch. Annahme: L code ist semi-entscheidbar. Also existiert eine TM M mit L( M) = L code. Setze w := c( M). Es gilt w L code oder w L code. 1. Fall: w L code Dann gilt wegen Def. von L code : w L( M) = L code. Widerspruch! 2. Fall: w L code Dann gilt: w L( M) = L code. Widerspruch! Also: Annahme ist falsch! Somit ist L code nicht semi-entscheidbar. 42 / 43
43 Zusammenfassung 1 Lernziele 2 Grundbegriffe 3 Unentscheidbare Probleme 4 Semi-entscheidbare Probleme 5 Zusammenfassung 43 / 43
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
Entscheidungsprobleme
 Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge U Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge U Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Entscheidungsprobleme
 Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge M Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge M Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
2.5 Halteproblem und Unentscheidbarkeit
 38 25 Halteproblem und Unentscheidbarkeit Der Berechenbarkeitsbegriff ist auf Funktionen zugeschnitten Wir wollen nun einen entsprechenden Begriff für Mengen einführen Definition 255 Eine Menge A Σ heißt
38 25 Halteproblem und Unentscheidbarkeit Der Berechenbarkeitsbegriff ist auf Funktionen zugeschnitten Wir wollen nun einen entsprechenden Begriff für Mengen einführen Definition 255 Eine Menge A Σ heißt
Theoretische Informatik Mitschrift
 Theoretische Informatik Mitschrift 9. Berechenbarkeit, Entscheidbarkeit, Aufzählbarkeit 9.1 Grundbegriffe bereits gezeigt: Spracherkennung durch Turingmaschine = Berechnung der semi-charakteristischen
Theoretische Informatik Mitschrift 9. Berechenbarkeit, Entscheidbarkeit, Aufzählbarkeit 9.1 Grundbegriffe bereits gezeigt: Spracherkennung durch Turingmaschine = Berechnung der semi-charakteristischen
Unentscheidbarkeit. Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: Komplexitätstheorie und effiziente Algorithmen
 Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Prof. Barbara König Übungsleitung: Henning Kerstan & Jan Stückrath Worum geht
Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Prof. Barbara König Übungsleitung: Henning Kerstan & Jan Stückrath Worum geht
Theoretische Informatik für Wirtschaftsinformatik und Lehramt
 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Universelle Turingmaschinen und Church sche These Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander
Theoretische Informatik für Wirtschaftsinformatik und Lehramt Universelle Turingmaschinen und Church sche These Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander
Das Halteproblem für Turingmaschinen
 Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Halteproblem/Kodierung von Turing-Maschinen
 Halteproblem/Kodierung von Turing-Maschinen Unser Ziel ist es nun zu zeigen, dass das sogenannte Halteproblem unentscheidbar ist. Halteproblem (informell) Eingabe: Turing-Maschine M mit Eingabe w. Frage:
Halteproblem/Kodierung von Turing-Maschinen Unser Ziel ist es nun zu zeigen, dass das sogenannte Halteproblem unentscheidbar ist. Halteproblem (informell) Eingabe: Turing-Maschine M mit Eingabe w. Frage:
Falls H die Eingabe verwirft, so wissen wir, dass M bei Eingabe w nicht hält. M hält im verwerfenden Haltezustand. Beweis:
 1 Unentscheidbarkeit 2 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 #include char *s="include
1 Unentscheidbarkeit 2 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 #include char *s="include
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17.November 2011 INSTITUT FÜR THEORETISCHE 0 KIT 17.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17.November 2011 INSTITUT FÜR THEORETISCHE 0 KIT 17.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Beispiel: NTM. M = ({q 0,q 1,q 2 }, {0, 1}, {0, 1, #},δ, q 0, #, {q 2 }) q 2
 Beispiel: NTM M = ({q 0,q 1,q 2 }, {0, 1}, {0, 1, #},δ, q 0, #, {q 2 }) 0,1,R 0,0,R q0 1,0,R q1 #,#,R q2 0,0,L Zustand 0 1 # q 0 {(1, R, q 0 )} {(0, R, q 1 )} q 1 {(0, R, q 1 ),(0, L, q 0 )} {(1, R, q
Beispiel: NTM M = ({q 0,q 1,q 2 }, {0, 1}, {0, 1, #},δ, q 0, #, {q 2 }) 0,1,R 0,0,R q0 1,0,R q1 #,#,R q2 0,0,L Zustand 0 1 # q 0 {(1, R, q 0 )} {(0, R, q 1 )} q 1 {(0, R, q 1 ),(0, L, q 0 )} {(1, R, q
Der Satz von Rice. Dann ist C(S) eine unentscheidbare Menge.
 Der Satz von Rice Satz: Sei R die Klasse der (Turing-) berechenbaren Funktionen, S eine nichttriviale Teilmenge von R und C(S) ={w Mw berechnet eine Funktion aus S}. Dann ist C(S) eine unentscheidbare
Der Satz von Rice Satz: Sei R die Klasse der (Turing-) berechenbaren Funktionen, S eine nichttriviale Teilmenge von R und C(S) ={w Mw berechnet eine Funktion aus S}. Dann ist C(S) eine unentscheidbare
Ausgewählte unentscheidbare Sprachen
 Proseminar Theoretische Informatik 15.12.15 Ausgewählte unentscheidbare Sprachen Marian Sigler, Jakob Köhler Wolfgang Mulzer 1 Entscheidbarkeit und Semi-Entscheidbarkeit Definition 1: L ist entscheidbar
Proseminar Theoretische Informatik 15.12.15 Ausgewählte unentscheidbare Sprachen Marian Sigler, Jakob Köhler Wolfgang Mulzer 1 Entscheidbarkeit und Semi-Entscheidbarkeit Definition 1: L ist entscheidbar
Satz von Rice. Lemma 39
 Unentscheidbarkeit Satz von Rice Das nächste Resultat zeigt, dass jede Eigenschaft der von einer Turing-Maschine berechneten Funktion unentscheidbar ist. Das bedeutet, es gibt keine Methode, mit der man
Unentscheidbarkeit Satz von Rice Das nächste Resultat zeigt, dass jede Eigenschaft der von einer Turing-Maschine berechneten Funktion unentscheidbar ist. Das bedeutet, es gibt keine Methode, mit der man
Unentscheidbarkeit. 1. Wann sind Sprachen unentscheidbar? 1, A 0, A } = {
 Unentscheidbarkeit 1. Wann sind Sprachen unentscheidbar? Eine Menge A heisst entscheidbar, falls die charakteristische Funktion von A, nämlich A : {0,1}, berechenbar ist, d.h. gilt: A = { 1, A 0, A } Eine
Unentscheidbarkeit 1. Wann sind Sprachen unentscheidbar? Eine Menge A heisst entscheidbar, falls die charakteristische Funktion von A, nämlich A : {0,1}, berechenbar ist, d.h. gilt: A = { 1, A 0, A } Eine
Reduktionen. Formalisierung von Sprache A ist nicht schwerer als Sprache B.
 Reduktionen Formalisierung von Sprache A ist nicht schwerer als Sprache B. Idee: Algorithmus/DTM für B kann genutzt werden, um A zu entscheiden/akzeptieren. WS 2018/19 Reduktionen 1 Zwei einfache Sprachen
Reduktionen Formalisierung von Sprache A ist nicht schwerer als Sprache B. Idee: Algorithmus/DTM für B kann genutzt werden, um A zu entscheiden/akzeptieren. WS 2018/19 Reduktionen 1 Zwei einfache Sprachen
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 11 15. Juli 2010 Einführung in die Theoretische
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 11 15. Juli 2010 Einführung in die Theoretische
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Unentscheidbarkeitssätze der Logik
 Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Einführung in die Theoretische Informatik Tutorium IX
 Einführung in die Theoretische Informatik Tutorium IX Michael R. Jung 16. & 17. 12. 2014 EThI - Tutorium IX 1 1 Entscheidbarkeit, Semi-Entscheidbarkeit und Unentscheidbarkeit 2 EThI - Tutorium IX 2 Definitionen
Einführung in die Theoretische Informatik Tutorium IX Michael R. Jung 16. & 17. 12. 2014 EThI - Tutorium IX 1 1 Entscheidbarkeit, Semi-Entscheidbarkeit und Unentscheidbarkeit 2 EThI - Tutorium IX 2 Definitionen
Universelle Turingmaschinen
 Universelle Turingmaschinen bisher: zum Erkennen einer rekursiven Sprache L wurde jeweils eine spezielle dtm M L angegeben jetzt: konstruieren feste dtm ( universelle Turingmaschine ), die als Eingabe
Universelle Turingmaschinen bisher: zum Erkennen einer rekursiven Sprache L wurde jeweils eine spezielle dtm M L angegeben jetzt: konstruieren feste dtm ( universelle Turingmaschine ), die als Eingabe
Wie man eine Sprache versteht
 Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
Grundlagen der Programmierung (Vorlesung 24)
 Grundlagen der Programmierung (Vorlesung 24) Ralf Möller, FH-Wedel Vorige Vorlesung Anwendung im Bereich Compilerbau Inhalt dieser Vorlesung Turing-Maschinen Berechenbarkeitstheorie, Halteproblem Lernziele
Grundlagen der Programmierung (Vorlesung 24) Ralf Möller, FH-Wedel Vorige Vorlesung Anwendung im Bereich Compilerbau Inhalt dieser Vorlesung Turing-Maschinen Berechenbarkeitstheorie, Halteproblem Lernziele
THEORETISCHE INFORMATIK UND LOGIK
 THEORETISCHE INFORMATIK UND LOGIK 4. Vorlesung: Das Halteproblem und Reduktionen Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 19. April 2017 Ankündigung Wegen großer Nachfrage wird eine
THEORETISCHE INFORMATIK UND LOGIK 4. Vorlesung: Das Halteproblem und Reduktionen Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 19. April 2017 Ankündigung Wegen großer Nachfrage wird eine
Theoretische Informatik I
 Theoretische Informatik I Einheit 4.3 Eigenschaften von L 0 /L 1 -Sprachen 1. Abschlußeigenschaften 2. Prüfen von Eigenschaften 3. Grenzen der Sprachklassen Sprachklassen Semi-entscheidbare Sprache Sprache,
Theoretische Informatik I Einheit 4.3 Eigenschaften von L 0 /L 1 -Sprachen 1. Abschlußeigenschaften 2. Prüfen von Eigenschaften 3. Grenzen der Sprachklassen Sprachklassen Semi-entscheidbare Sprache Sprache,
Lösung zur Klausur. Grundlagen der Theoretischen Informatik im WiSe 2003/2004
 Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Theoretische Informatik und Logik Übungsblatt 1 (2016S) Lösung
 Theoretische Informatik und Logik Übungsblatt (26S) en Aufgabe. Sei L = {w#w r w {, } }. Geben Sie eine deterministische Turingmaschine M an, welche die Sprache L akzeptiert. Wählen Sie mindestens einen
Theoretische Informatik und Logik Übungsblatt (26S) en Aufgabe. Sei L = {w#w r w {, } }. Geben Sie eine deterministische Turingmaschine M an, welche die Sprache L akzeptiert. Wählen Sie mindestens einen
Grundlagen der Theoretischen Informatik Musterlösungen zu ausgewählten Übungsaufgaben
 Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Carlos Camino Einführung in die Theoretische Informatik SS 2015
 Themenüberblick Dies ist eine Art Checkliste für die Klausurvorbereitung. Zu jedem Thema im Skript sind hier ein paar Leitfragen aufgelistet. Besonders nützlich sind die Tabellen und Abbildungen auf den
Themenüberblick Dies ist eine Art Checkliste für die Klausurvorbereitung. Zu jedem Thema im Skript sind hier ein paar Leitfragen aufgelistet. Besonders nützlich sind die Tabellen und Abbildungen auf den
Berechenbarkeit und Komplexität
 Berechenbarkeit und Komplexität Prof. Dr. Dietrich Kuske FG Theoretische Informatik, TU Ilmenau Wintersemester 2010/11 1 Organisatorisches zur Vorlesung Informationen, aktuelle Version der Folien und Übungsblätter
Berechenbarkeit und Komplexität Prof. Dr. Dietrich Kuske FG Theoretische Informatik, TU Ilmenau Wintersemester 2010/11 1 Organisatorisches zur Vorlesung Informationen, aktuelle Version der Folien und Übungsblätter
Theoretische Informatik
 Theoretische Informatik Lektion 10: Entscheidbarkeit Kurt-Ulrich Witt Wintersemester 2013/14 Kurt-Ulrich Witt Theoretische Informatik Lektion 10 1/15 Inhaltsverzeichnis Kurt-Ulrich Witt Theoretische Informatik
Theoretische Informatik Lektion 10: Entscheidbarkeit Kurt-Ulrich Witt Wintersemester 2013/14 Kurt-Ulrich Witt Theoretische Informatik Lektion 10 1/15 Inhaltsverzeichnis Kurt-Ulrich Witt Theoretische Informatik
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik. SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch
 Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch 3. Teilklausur 25. 07. 2007 Persönliche Daten bitte gut leserlich
Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch 3. Teilklausur 25. 07. 2007 Persönliche Daten bitte gut leserlich
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik 0 KIT 17.05.2010 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik nationales Forschungszentrum Vorlesung in am
Theoretische Grundlagen der Informatik 0 KIT 17.05.2010 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik nationales Forschungszentrum Vorlesung in am
1 Eine Menge M Σ heißt (rekursiv) aufzählbar genau. 2 Die Familie aller aufzählbaren Mengen wird mit RE
 Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 9 Entscheidbarkeit und Aufzählbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 5. Mai 2014 Definition 1 Eine Menge M Σ heißt (rekursiv)
Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 9 Entscheidbarkeit und Aufzählbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 5. Mai 2014 Definition 1 Eine Menge M Σ heißt (rekursiv)
Informatik III - WS07/08
 Informatik III - WS07/08 Kapitel 5 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 5 : Grammatiken und die Chomsky-Hierarchie Informatik III - WS07/08 Kapitel 5 2 Definition
Informatik III - WS07/08 Kapitel 5 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 5 : Grammatiken und die Chomsky-Hierarchie Informatik III - WS07/08 Kapitel 5 2 Definition
Übungsblatt 1. Lorenz Leutgeb. 30. März 2015
 Übungsblatt Lorenz Leutgeb 30. März 205 Aufgabe. Annahmen ohne Einschränkungen: P Σ und P Γ. Per Definitionem der Reduktion: P P 2 f : Σ Γ wobei f total und berechenbar, genau so, dass: w Σ : w P f(w)
Übungsblatt Lorenz Leutgeb 30. März 205 Aufgabe. Annahmen ohne Einschränkungen: P Σ und P Γ. Per Definitionem der Reduktion: P P 2 f : Σ Γ wobei f total und berechenbar, genau so, dass: w Σ : w P f(w)
Die Unentscheidbarkeit extensionaler Eigenschaften von Turingmaschinen: der Satz von Rice
 Die Unentscheidbarkeit extensionaler Eigenschaften von Turingmaschinen: der Satz von Rice Holger Arnold Dieser Text befasst sich mit der Frage, unter welchen Bedingungen das Problem, zu bestimmen, ob die
Die Unentscheidbarkeit extensionaler Eigenschaften von Turingmaschinen: der Satz von Rice Holger Arnold Dieser Text befasst sich mit der Frage, unter welchen Bedingungen das Problem, zu bestimmen, ob die
Turing: prinzipielle Berechenbarkeit Abschnitt 4.2. Turingmaschinen: DTM Abschnitt 4.2. DTM: Akzeptieren und Entscheiden Abschnitt 4.
 Kap. 4: Berechnungsmodelle Turingmaschinen 4.2 Turing: prinzipielle Berechenbarkeit Abschnitt 4.2 Kap. 4: Berechnungsmodelle Turingmaschinen 4.2 Turingmaschinen: DTM Abschnitt 4.2 DTM = DFA + unbeschränkter
Kap. 4: Berechnungsmodelle Turingmaschinen 4.2 Turing: prinzipielle Berechenbarkeit Abschnitt 4.2 Kap. 4: Berechnungsmodelle Turingmaschinen 4.2 Turingmaschinen: DTM Abschnitt 4.2 DTM = DFA + unbeschränkter
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Formale Sprachen. Script, Kapitel 4. Grammatiken
 Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprache bedeutend für die Syntaxdefinition und -analyse von Programmiersprachen Automaten
Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprache bedeutend für die Syntaxdefinition und -analyse von Programmiersprachen Automaten
Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt:
 5.2 Linear beschränkte Automaten Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt: (q, c, d) δ(q, ) = c =. Ein Leerzeichen wird also nie durch ein anderes
5.2 Linear beschränkte Automaten Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt: (q, c, d) δ(q, ) = c =. Ein Leerzeichen wird also nie durch ein anderes
Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016)
 Technische Universität Berlin, Berlin, 28.07.2016 Name:... Matr.-Nr.:... Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016) Einlesezeit: Bearbeitungszeit: Max.
Technische Universität Berlin, Berlin, 28.07.2016 Name:... Matr.-Nr.:... Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016) Einlesezeit: Bearbeitungszeit: Max.
GTI. Hannes Diener Juli. ENC B-0123,
 GTI Hannes Diener ENC B-0123, diener@math.uni-siegen.de 4.-9. Juli 1 / 29 Entscheidungsprobleme und Halteproblem In diesem Kapitel wollen wir uns an Stelle von Berechenbarkeit von Funktion, welche bei
GTI Hannes Diener ENC B-0123, diener@math.uni-siegen.de 4.-9. Juli 1 / 29 Entscheidungsprobleme und Halteproblem In diesem Kapitel wollen wir uns an Stelle von Berechenbarkeit von Funktion, welche bei
Inhalt Theoretische Informatik WS17/18
 Inhalt Theoretische Informatik WS17/18 (nach Modulbeschreibung) Formale Sprachen Wortersetzungssysteme Grammatiken Chomsky-Hierarchie (für Grammatiken und Sprachen) abstrakte Maschinenmodelle zur Akzeptanz
Inhalt Theoretische Informatik WS17/18 (nach Modulbeschreibung) Formale Sprachen Wortersetzungssysteme Grammatiken Chomsky-Hierarchie (für Grammatiken und Sprachen) abstrakte Maschinenmodelle zur Akzeptanz
Algorithmentheorie 8. Vorlesung
 Algorithmentheorie 8. Vorlesung Martin Dietzfelbinger 1. Juni 2006 1.7 Die Churchsche These Der intuitive Berechenbarkeitsbegriff wird durch die Formalisierung TM-Berechenbarkeit, also Rekursivität von
Algorithmentheorie 8. Vorlesung Martin Dietzfelbinger 1. Juni 2006 1.7 Die Churchsche These Der intuitive Berechenbarkeitsbegriff wird durch die Formalisierung TM-Berechenbarkeit, also Rekursivität von
Informatik III. Arne Vater Wintersemester 2006/ Vorlesung
 Informatik III Arne Vater Wintersemester 2006/07 11. Vorlesung 30.11.2006 1 Beziehungen zwischen den Sprachen Jede reguläre Sprache ist eine kontextfreie Sprache. Jede kontextfreie Sprache ist eine entscheidbare
Informatik III Arne Vater Wintersemester 2006/07 11. Vorlesung 30.11.2006 1 Beziehungen zwischen den Sprachen Jede reguläre Sprache ist eine kontextfreie Sprache. Jede kontextfreie Sprache ist eine entscheidbare
Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet.
 Rückschau 12.11.04 Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet. Wir haben das Prinzip der Diagonalisierung eingeführt und mit DIAG eine erste nicht rek. aufz. Sprache
Rückschau 12.11.04 Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet. Wir haben das Prinzip der Diagonalisierung eingeführt und mit DIAG eine erste nicht rek. aufz. Sprache
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 7.07.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 7.07.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 16.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 16.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Ein Induktionsbeweis über Schuhgrößen
 Was ist FALSCH an folgendem Beweis? Behauptung: Ein Induktionsbeweis über Schuhgrößen Alle Teilnehmer dieser Vorlesung haben gleiche Schuhgröße. Wir formalisieren diese Aussage, um einen Induktionsbeweis
Was ist FALSCH an folgendem Beweis? Behauptung: Ein Induktionsbeweis über Schuhgrößen Alle Teilnehmer dieser Vorlesung haben gleiche Schuhgröße. Wir formalisieren diese Aussage, um einen Induktionsbeweis
Theorie der Informatik
 Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V7, 3.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V7, 3.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Theoretische Informatik: Berechenbarkeit und Formale Sprachen
 Prof. Dr. F. Otto 26.09.2011 Fachbereich Elektrotechnik/Informatik Universität Kassel Klausur zur Vorlesung Theoretische Informatik: Berechenbarkeit und Formale Sprachen SS 2011 Name:................................
Prof. Dr. F. Otto 26.09.2011 Fachbereich Elektrotechnik/Informatik Universität Kassel Klausur zur Vorlesung Theoretische Informatik: Berechenbarkeit und Formale Sprachen SS 2011 Name:................................
Präsenzübung Berechenbarkeit und Komplexität
 Lehrstuhl für Informatik 1 WS 2013/14 Prof. Dr. Berthold Vöcking 28.01.2014 Kamal Al-Bawani Benjamin Ries Präsenzübung Berechenbarkeit und Komplexität Musterlösung Name:...................................
Lehrstuhl für Informatik 1 WS 2013/14 Prof. Dr. Berthold Vöcking 28.01.2014 Kamal Al-Bawani Benjamin Ries Präsenzübung Berechenbarkeit und Komplexität Musterlösung Name:...................................
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12 Die Turingmaschine Schreib- Lese-Kopf Arbeitsband mit Eingabe x 1 x i x n Steuereinheit
Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12 Die Turingmaschine Schreib- Lese-Kopf Arbeitsband mit Eingabe x 1 x i x n Steuereinheit
Nachklausur zur Vorlesung
 Lehrstuhl für Theoretische Informatik Prof. Dr. Markus Lohrey Grundlagen der Theoretischen Informatik Nachklausur Nachklausur zur Vorlesung Grundlagen der Theoretischen Informatik WS 2016/17 / 27. Februar
Lehrstuhl für Theoretische Informatik Prof. Dr. Markus Lohrey Grundlagen der Theoretischen Informatik Nachklausur Nachklausur zur Vorlesung Grundlagen der Theoretischen Informatik WS 2016/17 / 27. Februar
Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion
 Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 26. November 2007 Semi-Entscheidbarkeit
Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 26. November 2007 Semi-Entscheidbarkeit
Referat rekursive Mengen vs. rekursiv-aufzählbare Mengen
 Kapitel 1: rekursive Mengen 1 rekursive Mengen 1.1 Definition 1.1.1 informal Eine Menge heißt rekursiv oder entscheidbar, wenn ihre charakteristische Funktion berechenbar ist. 1.1.2 formal Eine Menge A
Kapitel 1: rekursive Mengen 1 rekursive Mengen 1.1 Definition 1.1.1 informal Eine Menge heißt rekursiv oder entscheidbar, wenn ihre charakteristische Funktion berechenbar ist. 1.1.2 formal Eine Menge A
2. Klausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2017/2018
 2. Klausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2017/2018 Hier Aufkleber mit Name und Matrikelnummer anbringen Vorname: Nachname: Matrikelnummer: Beachten Sie: Bringen Sie
2. Klausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2017/2018 Hier Aufkleber mit Name und Matrikelnummer anbringen Vorname: Nachname: Matrikelnummer: Beachten Sie: Bringen Sie
Theoretische Grundlagen der Informatik. Vorlesung am 16. November INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik 0 16.11.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu KIT-Gedenkfeier für
Theoretische Grundlagen der Informatik 0 16.11.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu KIT-Gedenkfeier für
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Klausur SoSe Juli2018
 Universität Osnabrück/ FB6 / Theoretische Informatik Prof. Dr. M. Chimani Informatik D: Einführung in die Theoretische Informatik Klausur SoSe 2018 9. Juli2018 Haupttermin, Prüfungsnr. 1007049 Gruppe:
Universität Osnabrück/ FB6 / Theoretische Informatik Prof. Dr. M. Chimani Informatik D: Einführung in die Theoretische Informatik Klausur SoSe 2018 9. Juli2018 Haupttermin, Prüfungsnr. 1007049 Gruppe:
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 1-13. Sitzung Dennis Felsing dennis.felsing@student.kit.edu http://www.stud.uni-karlsruhe.de/~ubcqr/2010w/tut gbi/ 2011-01-31 Turingmaschinen 1 Turingmaschinen Wiederholung
Grundbegriffe der Informatik Tutorium 1-13. Sitzung Dennis Felsing dennis.felsing@student.kit.edu http://www.stud.uni-karlsruhe.de/~ubcqr/2010w/tut gbi/ 2011-01-31 Turingmaschinen 1 Turingmaschinen Wiederholung
Kontextfreie Sprachen
 Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
3. Klausur Einführung in die Theoretische Informatik Seite 1 von Welches der folgenden klassischen Probleme der Informatik ist entscheidbar?
 3. Klausur Einführung in die Theoretische Informatik Seite 1 von 14 1. Welches der folgenden klassischen Probleme der Informatik ist entscheidbar? A. Gegeben eine kontextfreie Grammatik G. Gibt es ein
3. Klausur Einführung in die Theoretische Informatik Seite 1 von 14 1. Welches der folgenden klassischen Probleme der Informatik ist entscheidbar? A. Gegeben eine kontextfreie Grammatik G. Gibt es ein
Reduktion / Hilberts 10. Problem
 Reduktion / Hilberts 10. Problem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 9. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Reduktion / Hilberts 10. Problem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 9. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Ist eine algorithmische Problemstellung lösbar und wenn ja, mit welchen Mitteln? was ist eine algorithmische Problemstellung?
 Überblick 1. reguläre Sprachen endliche Automaten (deterministisch vs. nichtdeterministisch) Nichtregularität 2. Berechenbarkeit Registermaschinen/Turingmaschinen Churchsche These Unentscheidbarkeit 3.
Überblick 1. reguläre Sprachen endliche Automaten (deterministisch vs. nichtdeterministisch) Nichtregularität 2. Berechenbarkeit Registermaschinen/Turingmaschinen Churchsche These Unentscheidbarkeit 3.
Reduzierbarkeit und das Post'sche Korrespondenzproblem
 Reduzierbarkeit und das Post'sche Korrespondenzproblem Agenda Motivation Reduzierbarkeit Definition Bedeutung Post'sches Korrespondenzproblem (PKP) Modifiziertes Post'sches Korrespondenzproblem (MPKP)
Reduzierbarkeit und das Post'sche Korrespondenzproblem Agenda Motivation Reduzierbarkeit Definition Bedeutung Post'sches Korrespondenzproblem (PKP) Modifiziertes Post'sches Korrespondenzproblem (MPKP)
Theoretische Informatik 1
 Theoretische Informatik 1 Die Komplexitätsklasse P David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Äquivalenz von RM und TM Äquivalenz, Sätze Simulation DTM
Theoretische Informatik 1 Die Komplexitätsklasse P David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Äquivalenz von RM und TM Äquivalenz, Sätze Simulation DTM
Akzeptierende Turing-Maschine
 Akzeptierende Turing-Maschine Definition: Eine akzeptierende Turing-Maschine M ist ein Sechstupel M = (X, Z, z 0, Q, δ, F ), wobei (X, Z, z 0, Q, δ) eine Turing-Maschine ist und F Q gilt. Die von M akzeptierte
Akzeptierende Turing-Maschine Definition: Eine akzeptierende Turing-Maschine M ist ein Sechstupel M = (X, Z, z 0, Q, δ, F ), wobei (X, Z, z 0, Q, δ) eine Turing-Maschine ist und F Q gilt. Die von M akzeptierte
Entscheidbarkeitsfragen
 Entscheidbarkeitsfragen Wir haben eine Reihe von Problemen, die wir auf die verschiedenen Sprachklassen anwenden können, etwa das folgende: Wortproblem: Gegeben eine Sprache L und ein Wort x. Frage: Gilt
Entscheidbarkeitsfragen Wir haben eine Reihe von Problemen, die wir auf die verschiedenen Sprachklassen anwenden können, etwa das folgende: Wortproblem: Gegeben eine Sprache L und ein Wort x. Frage: Gilt
Durchschnittsleerheitsproblem (DLP)
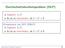 1 Durchschnittsleerheitsproblem (DLP) Gegeben: L, L. Es ist zu entscheiden, ob L L = Komplement von DLP (DNLP) Gegeben: L, L. Es ist zu entscheiden, ob L L Durchschnittsleerheitsproblem (DLP) 2 Nichtentscheidbarkeit
1 Durchschnittsleerheitsproblem (DLP) Gegeben: L, L. Es ist zu entscheiden, ob L L = Komplement von DLP (DNLP) Gegeben: L, L. Es ist zu entscheiden, ob L L Durchschnittsleerheitsproblem (DLP) 2 Nichtentscheidbarkeit
Die Reduktion Hilberts 10. Problem
 Die Reduktion Hilberts 10. Problem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 8. November 2010 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Die Reduktion Hilberts 10. Problem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 8. November 2010 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Übungsblatt 3. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 3 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 21. November 2017 Abgabe 5. Dezember 2017, 11:00 Uhr
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 3 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 21. November 2017 Abgabe 5. Dezember 2017, 11:00 Uhr
Entscheidbare und unentscheidbare Probleme
 Entscheidbare und unentscheidbare Probleme Slide 1 Entscheidbare und unentscheidbare Probleme Hans U. Simon (RUB) mit Modifikationen von Maike Buchin (RUB) Lehrstuhl Mathematik und Informatik Homepage:
Entscheidbare und unentscheidbare Probleme Slide 1 Entscheidbare und unentscheidbare Probleme Hans U. Simon (RUB) mit Modifikationen von Maike Buchin (RUB) Lehrstuhl Mathematik und Informatik Homepage:
6.4 Entscheidbarkeit. nein sein müssen, ist klar. THEO 6.4 Entscheidbarkeit 205/307 c Ernst W. Mayr
 6.4 Entscheidbarkeit Wortproblem Leerheit Äquivalenz Schnittproblem Typ 3 ja ja ja ja DCFL ja ja ja nein (*) Typ 2 ja ja nein (*) nein Typ 1 ja nein (*) nein nein Typ 0 nein (*) nein nein nein (*) Diese
6.4 Entscheidbarkeit Wortproblem Leerheit Äquivalenz Schnittproblem Typ 3 ja ja ja ja DCFL ja ja ja nein (*) Typ 2 ja ja nein (*) nein Typ 1 ja nein (*) nein nein Typ 0 nein (*) nein nein nein (*) Diese
Informatik III. Arne Vater Wintersemester 2006/ Vorlesung
 Informatik III Arne Vater Wintersemester 2006/07 10. Vorlesung 24.11.2006 1 Turingmaschinen Informatik III 9. Vorlesung - 2 Turingmaschinen Eine (deterministische 1-Band) Turingmaschine (DTM) wird beschrieben
Informatik III Arne Vater Wintersemester 2006/07 10. Vorlesung 24.11.2006 1 Turingmaschinen Informatik III 9. Vorlesung - 2 Turingmaschinen Eine (deterministische 1-Band) Turingmaschine (DTM) wird beschrieben
7. Übung TGI. Lorenz Hübschle-Schneider, Tobias Maier INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS. 1 Lorenz Hübschle-Schneider, Tobias Maier
 7. Übung TGI Lorenz Hübschle-Schneider, Tobias Maier INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS 1 Lorenz Hübschle-Schneider, Tobias Maier KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft
7. Übung TGI Lorenz Hübschle-Schneider, Tobias Maier INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS 1 Lorenz Hübschle-Schneider, Tobias Maier KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft
PROBEKLAUSUR SoSe 2016
 Die Anzahl der Aufgaben, das Punkteschema, die Themenschwerpunkte, etc. können sich in der echten Klausur unterscheiden! Universität Osnabrück/ FB6 / Theoretische Informatik Prof. Chimani, Beyer Informatik
Die Anzahl der Aufgaben, das Punkteschema, die Themenschwerpunkte, etc. können sich in der echten Klausur unterscheiden! Universität Osnabrück/ FB6 / Theoretische Informatik Prof. Chimani, Beyer Informatik
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 15.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 15.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundkurs Theoretische Informatik
 Grundkurs Theoretische Informatik Eine anwendungsbezogene Einführung - Für Studierende in allen Informatik-Studiengängen Bearbeitet von Gottfried Vossen, Kurt-Ulrich Witt 6., erweiterte und überarbeitete
Grundkurs Theoretische Informatik Eine anwendungsbezogene Einführung - Für Studierende in allen Informatik-Studiengängen Bearbeitet von Gottfried Vossen, Kurt-Ulrich Witt 6., erweiterte und überarbeitete
Kontextfreie Sprachen
 Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Unentscheidbare Probleme bei formalen Sprachen
 Unentscheidbare Probleme bei formalen Sprachen Maximilian Zagler 22.01.2008 Freie Universität Berlin, Institut für Informatik Proseminar Theoretische Informatik WS 07/08 Dozent: Prof. Dr. Helmut Alt 1
Unentscheidbare Probleme bei formalen Sprachen Maximilian Zagler 22.01.2008 Freie Universität Berlin, Institut für Informatik Proseminar Theoretische Informatik WS 07/08 Dozent: Prof. Dr. Helmut Alt 1
1 Algorithmische Grundlagen
 1 Algorithmische Grundlagen Klocke/17.03.2003 1.1 1.1 Begriffsklärung Fragen Begriffsklärungen Abstraktionsebenen für Algorithmen und Datenstrukturen Algorithmus Qualität von Algorithmen Klocke/17.03.2003
1 Algorithmische Grundlagen Klocke/17.03.2003 1.1 1.1 Begriffsklärung Fragen Begriffsklärungen Abstraktionsebenen für Algorithmen und Datenstrukturen Algorithmus Qualität von Algorithmen Klocke/17.03.2003
Kapitel: Die Chomsky Hierarchie. Die Chomsky Hierarchie 1 / 14
 Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: Komplexitätstheorie und effiziente Algorithmen. Wintersemester 2011/12
 Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Prof. Barbara König Übungsleitung: Henning Kerstan & Jan Stückrath Barbara König
Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Prof. Barbara König Übungsleitung: Henning Kerstan & Jan Stückrath Barbara König
Aufgabentypen: Spickerblatt: kontextfrei (Typ 2): zusätzlich: u ist eine!"# v 1
 Info4 Stoff Aufgabentypen: Grammatik CH einordnen NFA DFA Grammatik Chomsky-NF CYK-Algorithmus: Tabelle / Ableitungsbäume Grammatik streng kf. Grammatik Grammatik Pumping Lemma Beweis, dass Gr. nicht reg,
Info4 Stoff Aufgabentypen: Grammatik CH einordnen NFA DFA Grammatik Chomsky-NF CYK-Algorithmus: Tabelle / Ableitungsbäume Grammatik streng kf. Grammatik Grammatik Pumping Lemma Beweis, dass Gr. nicht reg,
Unentscheidbare Probleme: Diagonalisierung
 Unentscheidbare Probleme: Diagonalisierung Prof Dr Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Oktober 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Unentscheidbare Probleme: Diagonalisierung Prof Dr Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Oktober 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Unentscheidbarkeit von Problemen mittels Turingmaschinen
 Unentscheidbarkeit von Problemen mittels Turingmaschinen Daniel Roßberg 0356177 Roland Schatz 0355521 2. Juni 2004 Zusammenfassung In dieser Arbeit befassen wir uns mit der Unentscheidbarkeit von Problemen
Unentscheidbarkeit von Problemen mittels Turingmaschinen Daniel Roßberg 0356177 Roland Schatz 0355521 2. Juni 2004 Zusammenfassung In dieser Arbeit befassen wir uns mit der Unentscheidbarkeit von Problemen
Rekursive Aufzählbarkeit Die Reduktion
 Rekursive Aufzählbarkeit Die Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Rekursive Aufzählbarkeit Die Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Dank. Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Beispiel einer nicht berechenbaren Funktion: Busy Beaver
 Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Theorie der Informatik
 Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Dank. Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Akzeptierbarkeit und Entscheidbarkeit. Teil V.
 Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
