Tutorium: Analysis und lineare Algebra. Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen
|
|
|
- Wolfgang Albert
- vor 5 Jahren
- Abrufe
Transkript
1 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen
2 Steven Köhler mathe.stevenkoehler.de 2
3 Die Regeln von de l Hospital I Der Typ 0 0 Es sei I ein Intervall und x 0 2 I. Die Funktionen f und g seien fäur alle x 2 I mit x 6= x 0 di erenzierbar. Es gelte g(x) 6= 0 und g 0 (x) 6= 0 fäur alle x 2 I, x 6= x 0. Ferner sei lim f(x) = lim g(x) =0. x!x 0 x!x 0 Dann gilt: lim x!x 0 μ f(x) g(x) = lim x!x 0 μ f 0 (x) ; g 0 (x) falls der rechte Grenzwert existiert bzw. gleich +1 oder 1 ist. Analog fäur x!1. 3
4 Die Regeln von de l Hospital II Der Typ 1 1 Es sei I ein Intervall und x 0 2 I. Die Funktionen f und g seien fäur alle x 2 I mit x 6= x 0 di erenzierbar. Es gelte g(x) 6= 0 und g 0 (x) 6= 0 fäur alle x 2 I, x 6= x 0. Ferner sei lim f(x) = lim g(x) = 1. x!x 0 x!x 0 Dann gilt: μ f(x) lim x!x 0 g(x) μ f 0 (x) = lim ; x!x 0 g 0 (x) falls der rechte Grenzwert existiert bzw. gleich +1 oder 1 ist. Analog fäur x!1. 4
5 Die Regeln von de l Hospital III Der Typ 0 1 Es seien lim x!x 0 f(x) = 0 und lim x!x 0 g(x) = 1. Dann gilt: ³ lim f(x) g(x) x!x 0 = lim x!x 0 Ã! f(x) 1 g(x) = lim x!x 0 Ã! g(x) 1 : f(x) 5
6 Die Regeln von de l Hospital IV Der Typ 1 1 Es sei lim x!x 0 f(x) = lim x!x 0 g(x) = 1. Dann gilt: ³ lim f(x) g(x) x!x 0 = lim x!x 0 Ã 1 g(x) 1 f(x) 1 f(x)g(x)! : 6
7 Die Regeln von de l Hospital V Die Typen 0 0,1 1 und 1 0 ² Typ 0 0 : Es seien lim x!x 0 f(x) = 0 und lim x!x 0 g(x) =0. ² Typ 1 1 : Es seien lim x!x 0 f(x) =1und lim x!x 0 g(x) = 1. ² Typ 1 0 : Es seien lim x!x 0 f(x) = 1 und lim x!x 0 g(x) =0. Dann gilt: ³ g(x) ³ f(x) lim f(x) = lim e g(x) ln = e x!x 0 x!x 0 lim g(x) ln f(x) x!x 0 : 7
8 Die Regeln von de l Hospital VI Aufgabe Bestimme die folgenden Grenzwerte ² lim x 1 x x!1 μ ² lim x!0 ² lim x!0 1 ln (x +1) 1 x μ 2 x 1. 3x 2 8
9 Reihen s 1 = a 1 s 2 = a 1 + a 2 s 3 = a 1 + a 2 + a 3 s 4 = a 1 + a 2 + a 3 + a 4. s n = nx a i = a 1 + a 2 + :::+ a n i=1 Man nennt die Folge (s n ) n2n eine Reihe. Die Summe s n = n P hei¼t n-te Partialsumme der Reihe, die Summanden a i Glieder der Reihe. a i i=1 hei¼en 9
10 Harmonische Reihen Man nennt die folgende (divergente) Reihe die harmonische Reihe: 1X i=1 1 i = ::: Generell werden Reihen der Form 1X i=1 1 i = ::: als harmonische Reihen bezeichnet. Diese konvergieren fäur >1 und divergieren fäur 1. 10
11 Geometrische Reihen Man nennt Reihen der folgenden Form geometrische Reihen: 1X q i =1+q + q 2 + ::: i=0 Diese konvergieren fäur q < 1unddivergieren fäur q 1. FÄur q < 1lÄasst sich der Grenzwert wie folgt berechnen: lim n!1 Ã X n! q i i=0 = 1 1 q : Dies folgt unmittelbar aus der geometrischen Summenformel nx i=0 q i = 1 qn+1 1 q : 11
12 Das Majorantenkriterium Es sei 1P i=0 b i eine konvergente Reihe mit nichtnegativen Gliedern b i,d.h.b i 0fÄur alle i =1; 2;:::. Ist dann 1 P i=0 a i eine Reihe, fäur die ja i j b i fäur alle i =1; 2;::: gilt, so konvergiert auch die Reihe 1 P i=0 a i. Man nennt die Reihe 1 P i=0 b i eine konvergente Majorante. 12
13 Das Quotientenkriterium I Gegeben sei eine Reihe 1 P endlich viele i. i=0 a i mit a i 6=0fÄur alle bis auf häochstens Die Reihe konvergiert (und zwar sogar absolut), falls es ein i 0 0undeinq mit 0 <q<1gibt,sodassfäur alle i i 0 gilt: a i+1 a i q<1: Die Reihe divergiert, falls es ein i 0 0 gibt, so dass fäur alle i i 0 gilt: a i+1 a i 1: 13
14 Das Quotientenkriterium II Gegeben sei eine Reihe 1 P i=0 a i mit a i 6=0fÄur alle bis auf häochstens endlich viele i. Danngilt: a Ist lim i+1 i!1 a i < 1, so konvergiert die Reihe absolut. a Ist lim i+1 i!1 a i > 1, so divergiert die Reihe. a Ist lim i+1 i!1 a i = 1, ist keine Aussage zur Konvergenz mäoglich. 14
15 Das Wurzelkriterium I Die Reihe konvergiert (und zwar sogar absolut), falls es ein i 0 0 und ein q mit 0 <q<1gibt,sodassfäur alle i i 0 gilt: i q a i q<1: Die Reihe divergiert, fallseseini 0 0 gibt, so dass fäur alle i i 0 gilt: i q a i 1: 15
16 Das Wurzelkriterium II Gegeben sei eine Reihe 1 P i=0 a i mit a i 6=0fÄur alle bis auf häochstens endlich viele i. Danngilt: i Ist lim q a i!1 i < 1, so konvergiert die Reihe absolut. i Ist lim q a i!1 i > 1, so divergiert die Reihe. i Ist lim q a i!1 i = 1, ist keine Aussage zur Konvergenz mäoglich. 16
17 Das Leibnizsche Kriterium Eine Reihe 1 P i=0 1 iai mit a i 0istkonvergent,wenn a i eine monotone Nullfolge ist, d.h., wenn a 0 a 1 a 2 ::: sowie a i! 0gilt. 17
18 Potenzreihen Eine Potenzreihe ist ein Ausdruck der Form 1X a i x i = a 0 + a 1 x + a 2 x 2 + :::: i=0 Eine Potenzreihe kann als \unendliches Polynom" aufgefasst werden. 18
19 Konvergenzradius I Zu jeder Potenzreihe 1 P R 2 i=0 a i x i gibt es eine Zahl R mit n o r 2 R : r 0 [ n o 1 ; so dass die Potenzreihe fäur alle x mit x < R (absolut) konvergiert und fäur alle x mit x >Rdivergiert. Die Zahl R wird als Konvergenzradius der Reihe bezeichnet. 19
20 Konvergenzradius II Der Konvergenzradius kann sowohl mit dem Quotienten- als auch mit dem Wurzelkriterium berechnet werden: R = lim a n n!1 a n+1 R = bzw. lim n!1 1 q an n 20
21 Taylorpolynome I Die Funktion f sei im Intervall [a; b] (n + 1)-mal di erenzierbar und die (n+1)-te Ableitung sei stetig auf [a; b]. Es gelte 0 2 (a; b). Dann folgt fäur alle x 2 [a; b]: n P f(x) =T n (x)+r n (x): f Dabei ist T n (x) = (k) (0) k! x k das n-te Taylorpolynom (an der k=0 Stelle x 0 =0)undfÄur das Restglied (in Integralform) gilt: R n (x) = 1 n! Z x 0 (x t) n f (n+1) (t) dt: 21
22 Taylorpolynome II Einige Taylor-Polynome der Funktion sin. 22
23 Taylorreihen I Die Funktion f sei im Intervall a; b beliebig oft di erenzierbar. Es gelte 0 2 a; b. Dann hei¼t die Potenzreihe 1X k=0 f (k) (0) k! x k die Taylorreihe von f. Genauer gesagt handelt es sich um die Taylorreihe mit dem Entwicklungspunkt x 0 = 0. Statt Taylorreihe sagt man auch Taylor-Entwicklung. Allgemein: 1X k=0 f (k) (x 0 ) k! x x0 k 23
24 Taylorreihen II Aufgabe Bestimme eine Taylorreihe fäur die Funktion f(x) = sinh(2x). Aufgabe Bestimme eine Taylorreihe fäur die Funktion f(x) = cosh(2x). 24
25 Funktionen mit mehreren Variablen Beispielfunktion: f(x; y) =cos p x sin (y) 25
26 Bestimmung des Gradienten I ZunÄachst werden die stationäaren Stellen der Funktion bestimmt: Dazu wird der Gradient grad f(x 1 ;x 2 ;:::;x n ) gebildet und gleich 0 gesetzt. grad f(x 1 ;x 2 ;:::;x n ) = ³ df dx 1 ; df dx 2 ;:::; = (0; 0;:::;0) df dx n 26
27 Bestimmung des Gradienten II Dies läasst sich auch wie folgt schreiben: df dx 1 (x) = 0 df dx 2 (x) = 0. df (x) dx n = 0 Die LÄosungen x (i) dieses Gleichungssystem sind die gesuchten stationäaren Stellen. Diesewerdenauchkritische Stellen genannt. 27
28 Aufstellen der Hesse Matrix I Anschlie¼end werden die Hesse-Matrizen H i wie folgt erstellt: H i = 0 df dx 2 1 ³x (i) df ³ (i) x dx 2 dx 1. df ³ dx n dx 1 x (i) df ³ (i) x dx 1 dx 2 df dx 2 2 ³x (i). df ³ (i) x dx n dx 2 df ³ dx 1 dx n df ³ dx 2 dx n..... df dx 2 n x (i) x (i) ³x (i) 1 C A 28
29 Aufstellen der Hesse Matrix II Abschlie¼end muss die De nitheit der Hesse-Matrizen bestimmt werden, um die Art des Extremums zu ermitteln: Dazu werden zunäachst die Abschnittsdeterminanten 1, 2, :::, n bestimmt. Sind alle i > 0 (i 2 f1;:::;ng), so ist die Matrix positiv de nit und es liegt ein Minimum vor. Haben die i ein alternierendes Vorzeichen, beginnend mit "-", ist die Matrix negativ de nit und es liegt ein Maximum vor. Formal ausgedräuckt: 2m+1 < 0und 2m > 0mitm 2 N. 29
30 Aufstellen der Hesse Matrix III Ist die Matrix weder positiv noch negativ de nit, kann ohne weitere Untersuchung keine genaue Aussage getro en werden. Dazu wird z.b. die Bilinearform b Hi benutzt. Diese ist wie folgt de niert: b Hi (x; y) =x H i y T Gibt es nun Vektoren x und y, so dass b Hi (x; x) > 0 und b Hi (y;y) < 0, so ist die Matrix inde nit und es liegt kein Extremum vor. 30
31 Ableiten von Funktionen mit mehreren Variablen ohne Nebenbedingungen Aufgabe Aufgabe Bestimme die Extremstellen von f(x; y) = 6xy + x 2 +2y 3. 31
32 Komplexe Zahlen I Es sei z = a + ib 2 C. Dann hei¼t ² a Realteil von z (Bezeichnung: a =Rez oder a = <z); ² b ImaginÄarteil von z (Bezeichnung: b =Imz oder b = =z); ² jzj = p a 2 + b 2 absoluter Betrag von z; ² z = a ib konjugiert komplexe Zahl zu z. 32
33 Komplexe Zahlen II 33
34 Rechnen mit komplexen Zahlen I Addition & Subtraktion Es seien z 1 = a 1 + ib 1 und z 2 = a 2 + ib 2.Dannist z 1 + z 2 = ³a 1 + a 2 + i ³b 1 + b 2 ; z 1 z 2 = ³a 1 a 2 + i ³b 1 b 2 : 34
35 Rechnen mit komplexen Zahlen II Multiplikation & Division Es seien z 1 = a 1 + ib 1 und z 2 = a 2 + ib 2.Dannist z 1 z 2 = ³a 1 a 2 b 1 b 2 + i ³a 1 b 2 + a 2 b 1 ; z 1 z 2 = μ a1 a 2 + b 1 b 2 a i b2 2 μ a1 b 2 a 2 b 1 a : b2 2 35
36 Polarkoordinatendarstellung I Komplexe Zahlen käonnen alternativ auch mit Hilfe der folgenden Polarkoordinatendarstellung angegeben werden: z = r ³cos ' + i sin ' : Die Bezeichnungen sind bei dieser Darstellung wie folgt: ² r: Betrag von z; ² ': Argument von z. 36
37 Polarkoordinatendarstellung II Es seien z 1 = r 1 (cos ' 1 + i sin ' 1 )undz 2 = r 2 (cos ' 2 + i sin ' 2 ). Dann gilt: z 1 z 2 = r 1 r 2 ³ cos ' 1 + ' 2 + i sin '1 + ' 2 ; z 1 z 2 = r 1 r 2 ³ cos ' 1 ' 2 + i sin '1 ' 2 : 37
38 Die komplexe Exponentialfunktion Eine weitere MÄoglichkeit zur Darstellung komplexer Zahlen ergibt sich durch die Verwendung der komplexen Exponentialfunktion: r ³cos ' + i sin ' = r e i' 38
39 Vielen Dank für die Aufmerksamkeit & Viel Erfolg bei der Klausur 39
Tutorium: Analysis und lineare Algebra
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra. Vorbereitung der Abschlussklausur (Teil 1)
 Tutorium: Analysis und lineare Algebra Vorbereitung der Abschlussklausur (Teil 1) Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Konvergenz, Stetigkeit und Differenzierbarkeit 3 Konvergenz
Tutorium: Analysis und lineare Algebra Vorbereitung der Abschlussklausur (Teil 1) Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Konvergenz, Stetigkeit und Differenzierbarkeit 3 Konvergenz
Tutorium: Analysis und lineare Algebra
 Tutorium: Analysis und lineare Algebra Vorbereitung der Abschlussklausur (Teil 2) Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Determinanten 3 Determinanten Determinanten kleiner Matrizen
Tutorium: Analysis und lineare Algebra Vorbereitung der Abschlussklausur (Teil 2) Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Determinanten 3 Determinanten Determinanten kleiner Matrizen
Tutorium: Analysis und lineare Algebra
 Tutorium: Analysis und lineare Algebra Vorbereitung der Abschlussklausur (Teil 2) Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Komplexe Zahlen 3 Komplexe Zahlen Komplexe Zahlen I Es sei
Tutorium: Analysis und lineare Algebra Vorbereitung der Abschlussklausur (Teil 2) Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Komplexe Zahlen 3 Komplexe Zahlen Komplexe Zahlen I Es sei
Tutorium: Analysis und lineare Algebra. Vorbereitung der Abschlussklausur (Teil 1)
 Tutorium: Analysis und lineare Algebra Vorbereitung der Abschlussklausur (Teil 1) Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Konvergenz Definition der Konvergenz I Eine Folge (a n )
Tutorium: Analysis und lineare Algebra Vorbereitung der Abschlussklausur (Teil 1) Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Konvergenz Definition der Konvergenz I Eine Folge (a n )
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Tutorium: Analysis und lineare Algebra. Konvergenz, Stetigkeit & Differenzierbarkeit
 Tutorium: Analysis und lineare Algebra Konvergenz, Stetigkeit & Differenzierbarkeit Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 2011 Steven Köhler Definition der Konvergenz Eine Folge
Tutorium: Analysis und lineare Algebra Konvergenz, Stetigkeit & Differenzierbarkeit Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 2011 Steven Köhler Definition der Konvergenz Eine Folge
Tutorium: Analysis und lineare Algebra. Vorbereitung der zweiten Bonusklausur (Teil 1)
 Tutorium: Analysis und lineare Algebra Vorbereitung der zweiten Bonusklausur (Teil 1) Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Ungleichungen 3 Ungleichungen Aufgabe 1a a) Bestimme
Tutorium: Analysis und lineare Algebra Vorbereitung der zweiten Bonusklausur (Teil 1) Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Ungleichungen 3 Ungleichungen Aufgabe 1a a) Bestimme
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
Steven Köhler. Tutorium: Analysis und lineare Algebra. Konvergenz, Stetigkeit & Differenzierbarkeit. mathe.stevenkoehler.
 Tutorium: Analysis und lineare Algebra Konvergenz, Stetigkeit & Differenzierbarkeit Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 2011 Steven Köhler Definition der Konvergenz Eine Folge
Tutorium: Analysis und lineare Algebra Konvergenz, Stetigkeit & Differenzierbarkeit Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 2011 Steven Köhler Definition der Konvergenz Eine Folge
Mathematik I - Woche 10
 Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 20/2 R. Steuding (HS-RM) NumAna Wintersemester 20/2 / 20 2. Reihen R. Steuding (HS-RM) NumAna
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 20/2 R. Steuding (HS-RM) NumAna Wintersemester 20/2 / 20 2. Reihen R. Steuding (HS-RM) NumAna
Folgen und Reihen. 1 Konvergenz
 Folgen und Reihen Man betrachte viele Zahlen hintereinander geschrieben. Solche Folgen von Zahlen können durch nummeriert werden. Es entsteht eine Zuordnung der natürlichen Zahlen zu den Gliedern der Folge.
Folgen und Reihen Man betrachte viele Zahlen hintereinander geschrieben. Solche Folgen von Zahlen können durch nummeriert werden. Es entsteht eine Zuordnung der natürlichen Zahlen zu den Gliedern der Folge.
Kapitel 5 Reihen 196
 Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Vorlesung: Analysis I für Ingenieure
 Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
Wenn man eine Folge gegeben hat, so kann man auch versuchen, eine Summe. a 0 + a 1 + a 2 +
 8 Reihen 38 8 Reihen Wenn man eine Folge gegeben hat, so kann man auch versuchen, eine Summe a 0 + a + a 2 + zu bilden. Wir wollen nun erklären, was wir darunter verstehen wollen. Zunächst kann man die
8 Reihen 38 8 Reihen Wenn man eine Folge gegeben hat, so kann man auch versuchen, eine Summe a 0 + a + a 2 + zu bilden. Wir wollen nun erklären, was wir darunter verstehen wollen. Zunächst kann man die
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Folgen und Reihen. Folgen. Inhalt. Mathematik für Chemiker Teil 1: Analysis. Folgen und Reihen. Reelle Funktionen. Vorlesung im Wintersemester 2014
 Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Stroppel Musterlösung , 180min. Aufgabe 1 (3 Punkte) Bestimmen Sie die Determinante der Matrix
 Stroppel Musterlösung 7.., 8min Aufgabe Punkte Bestimmen Sie die Determinante der Matrix A =. Geben Sie alle Lösungen x des homogenen Gleichungssystems Ax = an. Entwicklung nach der ersten Spalte: deta
Stroppel Musterlösung 7.., 8min Aufgabe Punkte Bestimmen Sie die Determinante der Matrix A =. Geben Sie alle Lösungen x des homogenen Gleichungssystems Ax = an. Entwicklung nach der ersten Spalte: deta
2 k k 1 k(k + 1) = 2n+1. n = 0 = k(k + 1) = 2n+1 n n. = 2 n+1 n + 2 (n + 1)(n + 2) + n. (n + 1)(n + 2)
 Prof. Hesse Höhere Mathematik I und II Musterlösung 7. 0. 0, 80min Aufgabe (3 Punkte) Zeigen Sie mit vollständiger Induktion: Für alle n N gilt n k= k k k(k + ) = n+ n +. Induktionsanfang: k= Induktionsschluss
Prof. Hesse Höhere Mathematik I und II Musterlösung 7. 0. 0, 80min Aufgabe (3 Punkte) Zeigen Sie mit vollständiger Induktion: Für alle n N gilt n k= k k k(k + ) = n+ n +. Induktionsanfang: k= Induktionsschluss
Übungsklausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Spickzettel Mathe C1
 Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
Ferienkurs Analysis 1
 Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die
 3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
5. Unendliche Reihen [Kö 6]
![5. Unendliche Reihen [Kö 6] 5. Unendliche Reihen [Kö 6]](/thumbs/92/110553245.jpg) 25 5. Unendliche Reihen [Kö 6] 5.1 Grundbegriffe Definition 1. Es sei k Z und (a i ) i k eine (komplexe) Folge. Unter der unendlichen Reihe a i versteht man die Folge (s n ) n k der Partialsummen s n :=
25 5. Unendliche Reihen [Kö 6] 5.1 Grundbegriffe Definition 1. Es sei k Z und (a i ) i k eine (komplexe) Folge. Unter der unendlichen Reihe a i versteht man die Folge (s n ) n k der Partialsummen s n :=
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu. MC-Fragen Serie 1. Einsendeschluss: Freitag, der :00 Uhr
 D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? (a) Eine divergente Folge ist nicht
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? (a) Eine divergente Folge ist nicht
REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert
![REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert](/thumbs/55/37057337.jpg) Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Mathematik I Herbstsemester 2018 Kapitel 6: Potenzreihen
 Mathematik I Herbstsemester 208 Kapitel 6: Potenzreihen Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 58 6. Potenzreihen Reihen (Zahlenreihen) Konvergenzkriterien für Reihen Notwendiges
Mathematik I Herbstsemester 208 Kapitel 6: Potenzreihen Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 58 6. Potenzreihen Reihen (Zahlenreihen) Konvergenzkriterien für Reihen Notwendiges
Tutorium: Analysis und lineare Algebra. Differentialrechnung. Steven Köhler. mathe.stevenkoehler.de Steven Köhler
 Tutorium: Analysis und lineare Algebra Differentialrechnung Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Differenzenquotient Der Di erenzenquotient ist de niert als f(x) x f(x) f(x 0)
Tutorium: Analysis und lineare Algebra Differentialrechnung Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Differenzenquotient Der Di erenzenquotient ist de niert als f(x) x f(x) f(x 0)
HM I Tutorium 5. Lucas Kunz. 21. November 2018
 HM I Tutorium 5 Lucas Kunz 2. November 208 Inhaltsverzeichnis Theorie 2. Definition.................................... 2.2 Wichtige Reihen................................. 2.3 Absolute Konvergenz..............................
HM I Tutorium 5 Lucas Kunz 2. November 208 Inhaltsverzeichnis Theorie 2. Definition.................................... 2.2 Wichtige Reihen................................. 2.3 Absolute Konvergenz..............................
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Reihen von Zahlen. Inhalt:
 5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
Absolute Konvergenz. Definition 3.8. Beispiel 3.9. Eine Reihe. a n. konvergent ist. Die alternierende harmonische Reihe aber nicht absolut konvergent.
 Definition 3.8 Eine Reihe n=1 a n heißt absolut konvergent, wenn die Reihe konvergent ist. a n n=1 Beispiel 3.9 Die alternierende harmonische Reihe aber nicht absolut konvergent. n=1 ( 1)n 1 n ist zwar
Definition 3.8 Eine Reihe n=1 a n heißt absolut konvergent, wenn die Reihe konvergent ist. a n n=1 Beispiel 3.9 Die alternierende harmonische Reihe aber nicht absolut konvergent. n=1 ( 1)n 1 n ist zwar
Folgen und Reihen. Christoph Laabs, n s k und ist Grenzwert dieser Reihe.
 Folgen und Reihen Christoph Laabs, christoph.laabs@tu-dresden.de Grundlagen Eine Reihe ist darstellbar durch z. B. = a 0 + a + a 2 + a + a 4 +... Ausgesprochen wird das als Summe von von k bis Unendlich.
Folgen und Reihen Christoph Laabs, christoph.laabs@tu-dresden.de Grundlagen Eine Reihe ist darstellbar durch z. B. = a 0 + a + a 2 + a + a 4 +... Ausgesprochen wird das als Summe von von k bis Unendlich.
Prof. Schneider Höhere Mathematik I/II Musterlösung A = x 1 = 6x 1 + x 3 x 2 = 2x 2 x 3 = x 1 + 6x 3
 Aufgabe ( Punkte) a) Bestimmen Sie die Eigenwerte und Eigenvektoren der Matrix 6 A = 6 b) Bestimmen Sie die allgemeine Lösung des Differentialgleichungssystems x = 6x + x 3 x = x x 3 = x + 6x 3 c) Bestimmen
Aufgabe ( Punkte) a) Bestimmen Sie die Eigenwerte und Eigenvektoren der Matrix 6 A = 6 b) Bestimmen Sie die allgemeine Lösung des Differentialgleichungssystems x = 6x + x 3 x = x x 3 = x + 6x 3 c) Bestimmen
Kap. 10: Folgen und Reihen. Eine Funktion a : N Ñ R
 Definition: Zahlenfolge Kap. 10: Folgen und Reihen 10.1 Definition: Zahlenfolge Eine Funktion a : N Ñ R poder Cq heißt reelle (oder komplexe) Zahlenfolge. Man nennt a n apnq das n-te Folgenglied und schreibt
Definition: Zahlenfolge Kap. 10: Folgen und Reihen 10.1 Definition: Zahlenfolge Eine Funktion a : N Ñ R poder Cq heißt reelle (oder komplexe) Zahlenfolge. Man nennt a n apnq das n-te Folgenglied und schreibt
Analysis I. 3. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Selbsteinschätzung Mathe I Dieser Fragebogen wächst Woche für Woche mit.
 Technische Universität Dresden, Institut für Wissenschaftliches Rechnen Dr. Ute Feldmann, Maximilian Becker Selbsteinschätzung Mathe I Dieser Fragebogen wächst Woche für Woche mit. Die 3 Kreise mit Ampelfarben
Technische Universität Dresden, Institut für Wissenschaftliches Rechnen Dr. Ute Feldmann, Maximilian Becker Selbsteinschätzung Mathe I Dieser Fragebogen wächst Woche für Woche mit. Die 3 Kreise mit Ampelfarben
Freie Universität Berlin Wintersemester 11/12 Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke
 Freie Universität Berlin Wintersemester / Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke Musterlösung zum. Übungsblatt zur Vorlesung Mathematik für Physiker I Differenzierbarkeit,
Freie Universität Berlin Wintersemester / Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke Musterlösung zum. Übungsblatt zur Vorlesung Mathematik für Physiker I Differenzierbarkeit,
Reihen, Exponentialfunktion Vorlesung
 Reihen, Exponentialfunktion Vorlesung Marcus Jung 5.03.20 Inhaltsverzeichnis Inhaltsverzeichnis Reihen 3. Denition.................................... 3.2 Konvergenzkriterien für Reihen........................
Reihen, Exponentialfunktion Vorlesung Marcus Jung 5.03.20 Inhaltsverzeichnis Inhaltsverzeichnis Reihen 3. Denition.................................... 3.2 Konvergenzkriterien für Reihen........................
10 Aus der Analysis. Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit
 10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an.
 Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
KLAUSUR. Analysis (E-Technik/Mechatronik/W-Ing) Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf
 KLAUSUR Analysis (E-Technik/Mechatronik/W-Ing).9.7 Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.: Unterschrift: In der Klausur können Sie insgesamt
KLAUSUR Analysis (E-Technik/Mechatronik/W-Ing).9.7 Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.: Unterschrift: In der Klausur können Sie insgesamt
REIHEN. 1. Definition und Konvergenz. Definition (unendliche) Reihe
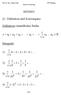 REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
Folgen, Reihen, Potenzreihen, Exponentialfunktion
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
z 2 + 2z + 10 = 0 = 2 ± 36 2 Aufgabe 2 (Lineares Gleichungssystem) Sei die reelle 3 4 Matrix
 Mathematik für Wirtschaftswissenschaftler im WS 03/04 Lösungsvorschläge zur Klausur im WS 03/04 Aufgabe (Komplexe Zahlen (4 Punkte a Berechnen Sie das Produkt der beiden komplexen Zahlen + i und 3 + 4i
Mathematik für Wirtschaftswissenschaftler im WS 03/04 Lösungsvorschläge zur Klausur im WS 03/04 Aufgabe (Komplexe Zahlen (4 Punkte a Berechnen Sie das Produkt der beiden komplexen Zahlen + i und 3 + 4i
Prof. Steinwart Höhere Mathematik I/II Musterlösung A =
 Prof. Steinwart Höhere Mathematik I/II Musterlösung 9.8.6 Aufgabe Punkte a Berechnen Sie die Eigenwerte der folgenden Matrix: A 3 b Es sei 4 A. 8 5 Bestimmen Sie P, P M, und eine Diagonalmatrix D M, so,
Prof. Steinwart Höhere Mathematik I/II Musterlösung 9.8.6 Aufgabe Punkte a Berechnen Sie die Eigenwerte der folgenden Matrix: A 3 b Es sei 4 A. 8 5 Bestimmen Sie P, P M, und eine Diagonalmatrix D M, so,
Grundlagen: Folgen u. endliche Reihen Unendliche Reihen Potenzreihen. Reihen. Fakultät Grundlagen. März 2015
 Fakultät Grundlagen März 015 Fakultät Grundlagen Grundlagen: und endliche Beispiele Geometrische Reihe, Konvergenzkriterien Fakultät Grundlagen Folie: Übersicht Grundlagen: und endliche Artithmetische
Fakultät Grundlagen März 015 Fakultät Grundlagen Grundlagen: und endliche Beispiele Geometrische Reihe, Konvergenzkriterien Fakultät Grundlagen Folie: Übersicht Grundlagen: und endliche Artithmetische
Ferienkurs Analysis 1, SoSe Unendliche Reihen. Florian Beye August 15, 2008
 Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Nachklausur Analysis 2
 Nachklausur Analysis 2. a) Wie ist der Grenzwert einer Folge in einem metrischen Raum definiert? Antwort: Se (a n ) n N eine Folge in dem metrischen Raum (M, d). Diese Folge besitzt den Grenzwert g M,
Nachklausur Analysis 2. a) Wie ist der Grenzwert einer Folge in einem metrischen Raum definiert? Antwort: Se (a n ) n N eine Folge in dem metrischen Raum (M, d). Diese Folge besitzt den Grenzwert g M,
Man schreibt dann lim. = bzw. lim
 Die Funktion f : R R geht für x nach (bzw. ), fallses für allem R + ein t(ε) R + gibt, so dass gilt ist x > t(ε), dann folgt f(x) > M bzw. ist x > t(ε), dann folgt f(x) < M. Man schreibt dann lim x = bzw.
Die Funktion f : R R geht für x nach (bzw. ), fallses für allem R + ein t(ε) R + gibt, so dass gilt ist x > t(ε), dann folgt f(x) > M bzw. ist x > t(ε), dann folgt f(x) < M. Man schreibt dann lim x = bzw.
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 22.11.2016 3. Mächtigkeit und die komplexe Zahlen Komplexe Zahlen Definition Die komplexe Zahlen sind definiert als C = R 2 = R R, mit (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
Universität Freiburg 22.11.2016 3. Mächtigkeit und die komplexe Zahlen Komplexe Zahlen Definition Die komplexe Zahlen sind definiert als C = R 2 = R R, mit (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
Kapitel 3. Reihen und ihre Konvergenz
 Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
D-BAUG Analysis I HS 2015 Dr. Meike Akveld. Clicker Fragen
 D-BAUG Analysis I HS 05 Dr. Meike Akveld Clicker Fragen Frage Der Satz: Dieser Satz ist falsch ist wahr ist richtig weiss ich nicht Es handelt hier um eine sogenannte Paradoxie. Die Paradoxie dieses Satzes
D-BAUG Analysis I HS 05 Dr. Meike Akveld Clicker Fragen Frage Der Satz: Dieser Satz ist falsch ist wahr ist richtig weiss ich nicht Es handelt hier um eine sogenannte Paradoxie. Die Paradoxie dieses Satzes
Mathematische Anwendersysteme Einführung in MuPAD
 Mathematische Anwendersysteme Einführung in MuPAD Tag 6 Folgen Konvergenzkriterien Reihen Potenzreihen 2322004 Gerd Rapin grapin@mathuni-goettingende Gerd Rapin Mathematische Anwendersysteme: Einführung
Mathematische Anwendersysteme Einführung in MuPAD Tag 6 Folgen Konvergenzkriterien Reihen Potenzreihen 2322004 Gerd Rapin grapin@mathuni-goettingende Gerd Rapin Mathematische Anwendersysteme: Einführung
HM I Tutorium 5. Lucas Kunz. 24. November 2016
 HM I Tutorium 5 Lucas Kunz 24. November 206 Inhaltsverzeichnis Theorie 2. Definition einer Reihe.............................. 2.2 Wichtige Reihen................................. 2.3 Limites inferior
HM I Tutorium 5 Lucas Kunz 24. November 206 Inhaltsverzeichnis Theorie 2. Definition einer Reihe.............................. 2.2 Wichtige Reihen................................. 2.3 Limites inferior
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Tutorium: Analysis und Lineare Algebra
 Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
Mathematik IT 3 (Analysis) Probeklausur
 Mathematik IT (Analysis) Probeklausur Datum: 08..0, Zeit: :5 5:5 Name: Matrikelnummer: Vorname: Geburtsdatum: Studiengang: Aufgabe Nr. 5 Σ Punkte Soll 5 9 7 Punkte Ist Lösungen ohne begründeten Lösungsweg
Mathematik IT (Analysis) Probeklausur Datum: 08..0, Zeit: :5 5:5 Name: Matrikelnummer: Vorname: Geburtsdatum: Studiengang: Aufgabe Nr. 5 Σ Punkte Soll 5 9 7 Punkte Ist Lösungen ohne begründeten Lösungsweg
Tutorium: Diskrete Mathematik
 Tutorium: Diskrete Mathematik Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition Als lineare Gleichungssysteme bezeichnet man in der linearen Algebra Gleichungssysteme der folgenden
Tutorium: Diskrete Mathematik Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition Als lineare Gleichungssysteme bezeichnet man in der linearen Algebra Gleichungssysteme der folgenden
Brückenkurs Rechentechniken
 Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Häufungspunkte und Satz von Bolzano und Weierstraß.
 Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
Stroppel Musterlösung , 180min. Aufgabe 1 (4 Punkte) Bestimmen Sie die folgenden Grenzwerte und Funktionengrenzwerte.
 Stroppel Musterlösung 3908, 80min Aufgabe 4 Punkte) Bestimmen Sie die folgenden Grenzwerte und Funktionengrenzwerte a) 4n 3 9 lim b) lim n n + n) n + )5n 4) c) lim x 0 sinlnx + )) sinhx) a) Es ist lim
Stroppel Musterlösung 3908, 80min Aufgabe 4 Punkte) Bestimmen Sie die folgenden Grenzwerte und Funktionengrenzwerte a) 4n 3 9 lim b) lim n n + n) n + )5n 4) c) lim x 0 sinlnx + )) sinhx) a) Es ist lim
1. Aufgabe 8 Punkte. f (x) = (x 2 + 1) e x2. Es gilt. f (x) = 2xe x2 + ( x ) e x2 ( 2x) = 2x 3 e x2.
 1. Aufgabe 8 Punkte Geben Sie die Bereiche, auf denen die Funktion f : R R mit f (x) = (x + 1) e x monoton wachsend oder fallend ist, an, und untersuchen Sie die Funktion auf lokale und globale Extrema.
1. Aufgabe 8 Punkte Geben Sie die Bereiche, auf denen die Funktion f : R R mit f (x) = (x + 1) e x monoton wachsend oder fallend ist, an, und untersuchen Sie die Funktion auf lokale und globale Extrema.
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Modulprüfung Hm 1 & Hm 2
 Seite von 9 Modulprüfung Hm & Hm Hinweise: - Es gibt 9 Aufgaben. Die jeweilige Punktzahl ist angegeben. - Die Maximalpunktzahl ist 56. Zum Bestehen der Klausur sind 4 Punkte hinreichend. - Die Bearbeitungszeit
Seite von 9 Modulprüfung Hm & Hm Hinweise: - Es gibt 9 Aufgaben. Die jeweilige Punktzahl ist angegeben. - Die Maximalpunktzahl ist 56. Zum Bestehen der Klausur sind 4 Punkte hinreichend. - Die Bearbeitungszeit
Übungen Ingenieurmathematik
 Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Analysis 1 für Informatiker (An1I)
 Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
KAPITEL 2. Folgen und Reihen
 KAPITEL 2 Folgen und Reihen 1. Konvergenz und Divergenz Definition 2.1 (Folgen). Eine Abbildung a : N R (bzw. a : N 0 R) nennt man Folge. Statt a : N R schreibt man meist (a n ) n N und a n statt a(n).
KAPITEL 2 Folgen und Reihen 1. Konvergenz und Divergenz Definition 2.1 (Folgen). Eine Abbildung a : N R (bzw. a : N 0 R) nennt man Folge. Statt a : N R schreibt man meist (a n ) n N und a n statt a(n).
1 k = = Sie ist also gerade der Grenzwert der zur Folge (r k 10 k ) k N0 gehörenden Reihe( n
 Die zur Folge ( k ) k N gehörende Reihe ( n k ) n N ist divergent, genauer k =. 2. Dezimalzahlen: Eine Zahl r = r 0,r r 2 r 3 mit r 0 N 0 und r n {0,...,9} für n hat den Wert r = r 0 +r 0 +r 2 00 +...
Die zur Folge ( k ) k N gehörende Reihe ( n k ) n N ist divergent, genauer k =. 2. Dezimalzahlen: Eine Zahl r = r 0,r r 2 r 3 mit r 0 N 0 und r n {0,...,9} für n hat den Wert r = r 0 +r 0 +r 2 00 +...
3. Folgen und Reihen. 3.1 Folgen und Grenzwerte. Denition 3.1 (Folge) Kapitelgliederung
 Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
x k = s k=1 y k = y konvergent. Dann folgt (cx k ) = cx für c K. Partialsummenfolge konvergiert
 4 Reihen Im Folgenden sei K R oder K C. 4. Definition. Es sei (x k ) Folge in K. Wir schreiben x k s und sagen, die Reihe x k konvergiere, falls die sogenannte Partialsummen-Folge s n x k n, 2,... in K
4 Reihen Im Folgenden sei K R oder K C. 4. Definition. Es sei (x k ) Folge in K. Wir schreiben x k s und sagen, die Reihe x k konvergiere, falls die sogenannte Partialsummen-Folge s n x k n, 2,... in K
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
Analysis I. 6. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Klausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 4.3.3 Klausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((4+3+3 Punkte a Welche
Karlsruher Institut für Technologie (KIT Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 4.3.3 Klausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((4+3+3 Punkte a Welche
LS Informatik 4 & Folgen und Reihen. Buchholz / Rudolph: MafI 2 38
 3. Folgen und Reihen Buchholz / Rudolph: MafI 2 38 Kapitelgliederung 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung
3. Folgen und Reihen Buchholz / Rudolph: MafI 2 38 Kapitelgliederung 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung
Prüfungklausur HM 1 (Ing), Lösungshinweise
 Aufgabe : a Welche komplexen Zahlen erfüllen die Gleichung z + i z =? Skizzieren Sie die Lösungsmenge in der Gaussschen Zahlenebene. 6 Punkte b Für welche komplexen Zahlen z gilt (z + i = 8 e π i? Die
Aufgabe : a Welche komplexen Zahlen erfüllen die Gleichung z + i z =? Skizzieren Sie die Lösungsmenge in der Gaussschen Zahlenebene. 6 Punkte b Für welche komplexen Zahlen z gilt (z + i = 8 e π i? Die
Höhere Mathematik II. (Vorlesungskript)
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München Höhere Mathematik II (Vorlesungskript) Univ. Prof. Dr. sc. math. Kurt Marti 2 2 L
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München Höhere Mathematik II (Vorlesungskript) Univ. Prof. Dr. sc. math. Kurt Marti 2 2 L
KAPITEL 9. Funktionenreihen
 KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler. (a) Bestimmen Sie die kartesische Form von Wintersemester 7/8 (..8) z = ( + i)( i) + ( + i). (b) Bestimmen Sie sämtliche komplexen Lösungen
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler. (a) Bestimmen Sie die kartesische Form von Wintersemester 7/8 (..8) z = ( + i)( i) + ( + i). (b) Bestimmen Sie sämtliche komplexen Lösungen
Analysis I Lösung von Serie 14. Um die Inhomogene DGl zu lösen, müssen wir partikuläre Lösungen finden. (a) Wir machen den Ansatz:
 d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
Analysis I. 4. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I 4. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching March 9, 07 Rechnen mit Limites (Bonus) Bemerkung. Die folgenden Situationen sind Problematisch: 0,,, 0 0, 0, 0
Analysis I 4. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching March 9, 07 Rechnen mit Limites (Bonus) Bemerkung. Die folgenden Situationen sind Problematisch: 0,,, 0 0, 0, 0
Folgen, Reihen, Grenzwerte u. Stetigkeit
 Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Folgen. Eine (unendliche) (Zahlen)folge ist eine Abbildung. dann als. notiert, und das wird abgekürzt mit. nennt man die Folgenglieder.
 Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung Statt dann als schreibt man auch oder ähnlich, die Folge wird notiert, und das wird abgekürzt mit. Die nennt man die Folgenglieder. Mathematik
Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung Statt dann als schreibt man auch oder ähnlich, die Folge wird notiert, und das wird abgekürzt mit. Die nennt man die Folgenglieder. Mathematik
Polynomiale Approximation. und. Taylor-Reihen
 Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
3. Potenzreihen. Definition 7.5. Eine unendliche Reihe der Form. a k x k. Es handelt sich also um eine Funktionenreihe mit f k (x) = a k x k.
 3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
Vorlesung Analysis I WS 07/08
 Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
27 Taylor-Formel und Taylor-Entwicklungen
 136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
Aufgabe 1 (Komplexe Zahlen) Berechnen Sie die folgenden komplexe Zahlen:
 Mathematik für Wirtschaftswissenschaftler im SoSe 24 Lösungsvorschläge zur Klausur im SoSe 24 Aufgabe (Komplexe Zahlen) Berechnen Sie die folgenden komplexe Zahlen: z = ( + i) 2 w = + i. Stellen Sie jeweils
Mathematik für Wirtschaftswissenschaftler im SoSe 24 Lösungsvorschläge zur Klausur im SoSe 24 Aufgabe (Komplexe Zahlen) Berechnen Sie die folgenden komplexe Zahlen: z = ( + i) 2 w = + i. Stellen Sie jeweils
Prüfungsfragen zur Theorie
 Prüfungsfragen zur Theorie Formulieren Sie die Monotoniegesetze (Rechenregeln für Ungleichungen)! Satz: Für alle a,b,c,d gilt: a b und c.d a+c b+d Satz: Für alle a,b,c,d + o gilt: a b und c d ac bd 1 Satz:
Prüfungsfragen zur Theorie Formulieren Sie die Monotoniegesetze (Rechenregeln für Ungleichungen)! Satz: Für alle a,b,c,d gilt: a b und c.d a+c b+d Satz: Für alle a,b,c,d + o gilt: a b und c d ac bd 1 Satz:
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu. MC-Fragen Serie 1. Einsendeschluss: Freitag, der :00 Uhr
 D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? Eine divergente Folge ist nicht beschränkt.
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? Eine divergente Folge ist nicht beschränkt.
Anleitung zu Blatt 2, Analysis II
 Fachbereich Mathematik der Universität Hamburg Dr. H. P. Kiani Anleitung zu Blatt 2, Analysis II SoSe 202 Funktionenfolgen, Potenzreihen I Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur
Fachbereich Mathematik der Universität Hamburg Dr. H. P. Kiani Anleitung zu Blatt 2, Analysis II SoSe 202 Funktionenfolgen, Potenzreihen I Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur
a 0 +a 1 x+a 2 x n=0 a n x n := lim
 1 Taylor-Entwicklung 1.1 Potenzreihen Def.: Ein Ausdruck der Form a 0 +a 1 +a +... a n n := lim k k a n n, (1) mit einer (unendlichen) Folge reeller Konstanten a 0,a 1,a,... ( Koeffizienten ) und einer
1 Taylor-Entwicklung 1.1 Potenzreihen Def.: Ein Ausdruck der Form a 0 +a 1 +a +... a n n := lim k k a n n, (1) mit einer (unendlichen) Folge reeller Konstanten a 0,a 1,a,... ( Koeffizienten ) und einer
HM I Tutorien 6 und 7
 HM I Tutorien 6 und 7 Lucas Kunz. Dezember 207 und 8. Dezember 207 Inhaltsverzeichnis Vorwort 2 2 Theorie 2 2. Definition einer Reihe.............................. 2 2.2 Absolute Konvergenz..............................
HM I Tutorien 6 und 7 Lucas Kunz. Dezember 207 und 8. Dezember 207 Inhaltsverzeichnis Vorwort 2 2 Theorie 2 2. Definition einer Reihe.............................. 2 2.2 Absolute Konvergenz..............................
Konvergenz und Divergenz einer unendlichen Reihe. 5-E Ma 2 Lubov Vassilevskaya
 Konvergenz und Divergenz einer unendlichen Reihe 5-E Ma 2 Lubov Vassilevskaya Folgen und Reihen: Beispiele Unter dem Bildungsgesetz einer unendlichen Reihe n i= versteht man einen funktionalen Zusammenhang
Konvergenz und Divergenz einer unendlichen Reihe 5-E Ma 2 Lubov Vassilevskaya Folgen und Reihen: Beispiele Unter dem Bildungsgesetz einer unendlichen Reihe n i= versteht man einen funktionalen Zusammenhang
2 Folgen und Reihen. 2.1 Folgen in C Konvergenz von Folgen. := f(n)
 2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
Vorlesungsprüfung Differential- und Integralrechnung (PHY.C30) Fragenkatalog
 Vorlesungsprüfung Differential- und Integralrechnung (PHY.C30) Fragenkatalog Im folgenden finden Sie eine Liste von typischen Prüfungsfragen für die Vorlesungsprüfung Differential- und Integralrechnung
Vorlesungsprüfung Differential- und Integralrechnung (PHY.C30) Fragenkatalog Im folgenden finden Sie eine Liste von typischen Prüfungsfragen für die Vorlesungsprüfung Differential- und Integralrechnung
Mathematik für Wirtschaftswissenschaftler im WS 12/13 Lösungen zu den Übungsaufgaben Blatt 12
 Mathematik für Wirtschaftswissenschaftler im WS /3 Lösungen zu den Übungsaufgaben Blatt Aufgabe 5 Welche der folgenden Matrizen sind positiv bzw negativ definit? A 8, B 3 7 7 8 9 3, C 7 4 3 3 8 3 3 π 3
Mathematik für Wirtschaftswissenschaftler im WS /3 Lösungen zu den Übungsaufgaben Blatt Aufgabe 5 Welche der folgenden Matrizen sind positiv bzw negativ definit? A 8, B 3 7 7 8 9 3, C 7 4 3 3 8 3 3 π 3
