Heinrich Heine-Universität Düsseldorf Sommersemester Lineare Algebra 1. Vierzehnte & Fünfzehnte Woche,
|
|
|
- Oswalda Küchler
- vor 5 Jahren
- Abrufe
Transkript
1 Fakultät für Mathematik PD Dr Markus Perling Heinrich Heine-Universität Düsseldorf Sommersemester 2014 Lineare Algebra 1 Vierzehnte & Fünfzehnte Woche, Determinanten (Schluß) Das folgende Resultat zeigt, daß die Determinante für jede quadratische Matrix definiert ist und (im Prinzip) ausgerechnet werden kann Satz (Leibniz-Formel): Es sei A = (α ij ) Mat n n (K) Dann gilt: det A = sgn(σ)α σ(1)1 α σ(n)n σ Sym n Die folgenden Aussagen sind wichtige Hilfsmittel zur Berechnung von Determinanten Satz: Es sei A Mat n n (K) Dann gilt: det A = 0 Rang(A) < n Insbesondere gilt also, daß det A 0 genau dann, wenn die Spaltenvektoren von A eine Basis von K n bilden Satz: Es seien A, B Mat n n (K) Dann gilt: det AB = det A det B Satz: Es sei A Mat n n (K) Dann gilt: det A = det A t Satz: Es sei A Mat n n (K) eine Blockmatrix der Form ( ) B C A = 0 (n r) r D wobei B Mat r r (K), C Mat r (n r) (K), D Mat (n r) (n r) (K) Dann gilt: det A = det B det D Wir können diesen Satz per Induktion auf beliebige Matrizen in Blockdiagonalform erweitern: Korollar: Es sei A 1 A 2 A = 0 A t wobei A i Mat ni n i (K) und t i=1 n i = n Dann gilt: det A = t det A i i=1
2 Definition: Es sei A Mat n n (K) und 1, i, j n Dann bezeichne A ij Mat (n 1) (n 1) (K) die Untermatrix von A, die dadurch entsteht, daß die i-te Zeile und die j-te Spalte aus A entfernt werden: α 11 α 1,j 1 α 1,j+1 α 1n α A ij = i 1,1 α i 1,j 1 α i 1,j+1 α i 1,n α i+1,1 α i+1,j 1 α i+1,j+1 α i+1,n α n,1 α n,j 1 α n,j+1 α n,n Weiterhin bezeichnen wir mit A ij := (α kl ), wobei α kl wenn k i, l j α kl = 1 wenn k = i, l = j 0 sonst, bzw α 11 α 1,j 1 0 α 1,j+1 α 1n α i 1,1 α i 1,j 1 0 α i 1,j+1 α i 1,n A ij = α i+1,1 α i+1,j 1 0 α i+1,j+1 α i+1,n α n,1 α n,j 1 0 α n,j+1 α n,n Lemma: Es sei A Mat n n (K) Dann gilt: det A ij = ( 1) i+j det A ij = det(a 1,, a j 1, e i, a j+1,, a n ), wobei a 1,, a n die Spalten von A sind Definition: Es sei A Mat n n (K) Dann setzen wir A # := (α # ij ) Mat n n(k), wobei α # ij := ( 1)i+j det A ji Wir nennen A # die zu A adjungierte Matrix Satz: Es gilt A # A = AA # = det(a)1 n Korollar: Ist A invertierbar, dann gilt: A 1 = 1 det A A# Satz (Laplacescher Entwicklungssatz): Es sei A = (α ij ) Mat n n (K) und 1 j n Dann gilt: n det A = ( 1) i+j α ij det A ij i=1 Man nennt obige Formel auch die Entwicklung nach der j-ten Spalte Via transposition kann man entsprechend auch nach der i-ten Zeile entwickeln Beispiele: 1) Für n = 2 gilt: det A = α 11 α 22 α 12 α 21
3 2) Für n = 3 gilt: det A = α 11 det A 11 α 21 det A 21 + α 31 det A 31 = α 11 α 22 α 33 + α 12 α 23 α 13 + α 13 α 21 α 32 α 11 α 23 α 32 α 12 α 21 α 33 α 13 α 22 α 31 Diese Formel wird auch die Sarrus-Regel genannt Bemerkung: Man mache sich klar, daß zur Berechnung einer Determinante durch die Leibnizformel oder den Entwicklungssatz n! Terme berechnet werden müssen Dies bedeutet, daß diese Formeln für größere n keine praktische Möglichkeit sind, um eine Determinante auszurechnen und daher eher für theoretische Betrachtungen verwendet werden Die entscheidende Eigenschaft, die es erlaubt, Determinanten auszurechnen, ist die Multilinearität Wir haben bereits gesehen, daß eine Möglichkeit darin besteht, die Determinante durch Zeilentransformationen in obere Dreiecksform zu bringen und dann die Diagonalelemente zusammenzumultiplizieren Effiziente Berechnungsmethoden verwenden in der Regel Varianten dieses Verfahrens Korollar (Cramersche Regel): Es sei A GL n (K) und b K n Dann hat das lineare Gleichungssystem Ax = b genau eine Lösung x = (x 1,, x n ) K n, mit für alle 1 i n x i = 1 det A det(a 1,, a i 1, b, a i+1,, a n ) Definition: Zwei Matrizen A, B Mat n n (K) heißen zueinander Konjugiert, bzw ähnlich, wenn es eine Matrix T GL n (K) gibt, so daß gilt B = T AT 1 Sind A und B zueinander konjugiert, dann beobachten wir, daß gilt: det B = det T AT 1 = det T det A det T 1 = det A Definition: Es sei V ein endlich-dimensionaler Vektorraum mit Basis B und f : V V eine lineare Abbildung Dann setzen wir det f := det M B B (f) Ist B eine weitere Basis von V, dann gilt insbesondere, daß MB B zueinander konjugiert sind, da gilt: MB B B (f) = TB MB B (f)tb B, (f) und M B B (f) wobei TB B GL n(k) und T B B Wahl der Basis B ab = (T B B ) 1 Insbesondere hängt somit det f nicht von der 11 Eigenwerte und charakteristisches Polynom Auch in diesem Kapitel sei K stets ein Körper Definition: Es sei V ein endlich-dimensionaler Vektorraum und f : V V eine lineare Abbildung (i) λ K heißt Eigenwert von f, wenn es ein v V \ {0} gibt mit f(v) = λv (ii) Es sei λ K Dann heißt v V \ {0} mit f(v) = λv Eigenvektor zum Eigenwert λ
4 (iii) Wir bezeichnen mit Eig(f, λ) := {v V f(v) = λv} den Eigenraum von f zu λ (iv) Die Menge σ(f) := {λ K Eig(f, λ) {0}} heißt das Spektrum von f Ist A Mat n n (K) gegeben, dann beziehen wir die oben eingeführten Begriffe für die Abbildung φ A : K n K n auch auf A, dh wir sprechen dann von Eigenwert, Eigenraum, Eigenvektor und Spektrum von A Bemerkung: Wir beobachten, daß Eig(f, 0) genau der Kern von f ist Allgemeiner gilt für v V und λ K: f(v) = λv (f λid V )(v) = 0 v Kern(f λid V ) Definition: Es sei V ein endlich-dimensionaler Vektorraum und f : V V eine lineare Abbildung (i) f heißt diagonalisierbar, wenn es eine Basis B von V gibt, so daß MB B (f) eine Diagonalmatrix ist (ii) f heißt trigonalisierbar, wenn es eine Basis B von V gibt, so daß MB B (f) eine obere Dreiecksmatrix ist Ebenso bezeichnen wir eine Matrix A Mat n n (K) als diagonalisierbar (bzw trigonalisierbar), wenn es ein T GL n (K) gibt, so daß T AT 1 eine Diagonalmatrix (bzw eine obere Dreiecksmatrix) ist Abbildung Dann sind folgene Aussagen äquvalent: (i) f ist diagonalisierbar (ii) V besitzt eine Basis von Eigenvektoren von f Definition: Es seien V ein endlich-dimensionaler Vektorraum mit Basis B und f : V V eine lineare Abbildung Dann heißt χ f := det(m B B (f) X1 n ) K[X] das charakteristische Polynom von f Analog bezeichnen wir für A Mat n n (K): das charakteristische Polynom von A Für alle T GL n (K) gilt: χ A := det(a X1 n ) K[X] det(t AT 1 X1 n ) = det(t AT 1 T X1 n T 1 ) = det T (A X1 n )T 1 = det(a X1 n ) Somit hängt insbesondere χ f nicht von der Wahl der Basis B ab Satz: Es sei A Mat n n (K) Die Eigenwerte von A sind genau die Nullstellen von χ A Definition: Die Abbildung Mat n n (K) K, A = (α ij ) n i=1 α ii =: Spur A bezeichnen wir als die Spurabbildung
5 Die Spurabbildung hat folgende Eigenschaften für alle A, B Mat n n (K): (i) Spur(A + B) = Spur A + Spur B (ii) Spur AB = Spur BA (iii) Weiterhin gilt mit T GL n (K): Spur(T AT 1 ) = Spur((AT 1 )T ) = Spur(A) Satz: Es gilt: χ A = ( 1) n X n + a n 1 X n a 0, wobei a n 1 = ( 1) n 1 Spur(A) und a 0 = det A Definition: Es sei V ein Vektorraum und f : V V eine lineare Abbildung Ein Untervektorraum U V heißt f-invariant, wenn gilt f(u) U Lemma: Es seien V ein endlich-dimensionaler Vektorraum, f : V V eine lineare Abbildung und U V ein f-invarianter Untervektorraum Dann gilt: (i) Die Abbildung f V/U : V/U V/U, [v] [f(v)] ist wohldefiniert und linear (ii) Es gilt: χ f = χ f U χ fv /U Abbildung Dann ist f genau dann trigonalisierbar, wenn χ f in Linearfaktoren zerfällt, dh es gibt λ 1,, λ n K, so daß χ f = ( 1) n (X λ 1 ) (X λ n ) Folgender Satz, den wir im Rahmen dieser Vorlesung nicht zeigen können, ist eine der grundlegensten Aussagen überhaupt: Satz (Der Fundamentalsatz der Algebra): Jedes nichtkonstante Polynom in C[X] besitzt eine Nullstelle Als Korollar folgt hieraus, daß jedes nichtkonstante Polynom in C[X] in Linearfaktoren zerfällt Insbesondere ist also jede quadratische Matrix mit komplexen Einträgen trigonalisierbar Definition: Es seien V ein endlich-dimensionaler Vektorraum und f : V V eine lineare Abbildung (i) Eine aufsteigende Kette von Untervektorräumen heißt Fahne in V {0} = V 0 V 1 V 2 V r = V (ii) Gilt dim V = r, dann heißt die Fahne vollständig (dann gilt insbesondere auch dim V i = i für alle 1 i r) (iii) Sind die V i f-invariant, so heißt die Fahne f-invariant Abbildung Dann ist f genau dann trigonalisierbar, wenn es eine vollständige, f- invariante Fahne in V gibt
6 Definition: Es seien A Mat n n (K), λ K Dann gilt χ A = (X λ) k mit k 0 und g(λ) 0 (i) k heißt die algebraische Vielfachheit von λ als Eigenwert von A (ii) dim Eig(f, λ) heißt die geometrische Vielfachheit von λ als Eigenwert von A Analog spricht man auch von der algebraischen bzw geometrischen Vielfachheit einer lineare Abbildung f : V V Lemma: Es seien V ein endlich-dimensionaler Vektorraum und f : V V eine lineare Abbildung Dann ist f genau dann diagonalisierbar, wenn gilt V = Eig(f, λ) λ σ(f) Abbildung Die folgenden Aussagen sind äquivalent: (i) f ist diagonalisierbar (ii) χ f zerfällt in Linearfaktoren und für jeden Eigenwert stimmen algebraische und geometrische Vielfachheit überein Literatur-/Lesevorschläge Jedes beliebige Buch oder sonstige Quelle zur Linearen Algebra
6 Eigenwerte und Eigenvektoren
 6.1 Eigenwert, Eigenraum, Eigenvektor Definition 6.1. Es sei V ein Vektorraum und f : V V eine lineare Abbildung. Ist λ K und v V mit v 0 und f(v) = λv gegeben, so heißt die Zahl λ Eigenwert (EW) von f,
6.1 Eigenwert, Eigenraum, Eigenvektor Definition 6.1. Es sei V ein Vektorraum und f : V V eine lineare Abbildung. Ist λ K und v V mit v 0 und f(v) = λv gegeben, so heißt die Zahl λ Eigenwert (EW) von f,
Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10)
 Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10) Kapitel 15: Eigenwerte und -vektoren Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 5. November 2009) Diagonalisierbarkeit
Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10) Kapitel 15: Eigenwerte und -vektoren Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 5. November 2009) Diagonalisierbarkeit
Eigenwerte und Diagonalisierung
 Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
6 Eigenwerte und Eigenvektoren
 6.1 Eigenwert, Eigenraum, Eigenvektor Definition 6.1. Es sei V ein Vektorraum und f : V V eine lineare Abbildung. Ist λ K und v V mit v 0 und f(v) = λv gegeben, so heißt die Zahl λ Eigenwert (EW) von f,
6.1 Eigenwert, Eigenraum, Eigenvektor Definition 6.1. Es sei V ein Vektorraum und f : V V eine lineare Abbildung. Ist λ K und v V mit v 0 und f(v) = λv gegeben, so heißt die Zahl λ Eigenwert (EW) von f,
2.11 Eigenwerte und Diagonalisierbarkeit
 2.11. EIGENWERTE UND DIAGONALISIERBARKEIT 127 Die Determinante eines Endomorphismus Wir geben uns jetzt einen endlichen erzeugten K-Vektorraum V und einen Endomorphismus ϕ : V V vor. Wir wollen die Determinante
2.11. EIGENWERTE UND DIAGONALISIERBARKEIT 127 Die Determinante eines Endomorphismus Wir geben uns jetzt einen endlichen erzeugten K-Vektorraum V und einen Endomorphismus ϕ : V V vor. Wir wollen die Determinante
5 Diagonalisierbarkeit
 5 Diagonalisierbarkeit Sei V ein K Vektorraum mit einer Basis B = (v 1,..., v n ) Wiederholung aus 2: Sei f : V V K linear. Stelle f(v j ) für j = 1,..., n dar in der Form a 1j Das n Tupel a j =. a nj
5 Diagonalisierbarkeit Sei V ein K Vektorraum mit einer Basis B = (v 1,..., v n ) Wiederholung aus 2: Sei f : V V K linear. Stelle f(v j ) für j = 1,..., n dar in der Form a 1j Das n Tupel a j =. a nj
KAPITEL 8. Normalformen. 1. Blockmatrizen. ,C K m 2 n 1. X = K (m 1+m 2 ) (n 1 +n 2 ) K L. und Y = M N Blockmatrizen mit.
 KAPITEL 8 Normalformen Definition 8.1 (Blockmatrizen). Sind 1. Blockmatrizen A K m 1 n 1,B K m 1 n 2,C K m 2 n 1 und D K m 2 n 2 so nennet man die Matrix X = ( A B C D ) K (m 1+m 2 ) (n 1 +n 2 ) eine Blockmatrix
KAPITEL 8 Normalformen Definition 8.1 (Blockmatrizen). Sind 1. Blockmatrizen A K m 1 n 1,B K m 1 n 2,C K m 2 n 1 und D K m 2 n 2 so nennet man die Matrix X = ( A B C D ) K (m 1+m 2 ) (n 1 +n 2 ) eine Blockmatrix
Lineare Algebra I Lösungsvorschlag
 Aufgabe Lineare Algebra I Lösungsvorschlag Wir bezeichnen mit a, a 2, a 3 Q 4 die Spalten der Matrix A. Es ist 7 a + 2a 2 = 7 4 = 7a 3, und wir sehen im l A = a, a 2, a 3 = a, a 2. Da die Vektoren a und
Aufgabe Lineare Algebra I Lösungsvorschlag Wir bezeichnen mit a, a 2, a 3 Q 4 die Spalten der Matrix A. Es ist 7 a + 2a 2 = 7 4 = 7a 3, und wir sehen im l A = a, a 2, a 3 = a, a 2. Da die Vektoren a und
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 205/6): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 205/6): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2
Lineare Algebra I. Prof. Dr. Daniel Roggenkamp Vorlesung -
 Lineare Algebra I Prof. Dr. Daniel Roggenkamp - 22.Vorlesung - Aus der letzten Vorlesung: Polynome K[t] (p 0, p,, p i K mit p i = 0 i > i 0 für ein i 0 = i 0 p i t i = p 0 + p t + p 2 t 2 + + p i0 t i
Lineare Algebra I Prof. Dr. Daniel Roggenkamp - 22.Vorlesung - Aus der letzten Vorlesung: Polynome K[t] (p 0, p,, p i K mit p i = 0 i > i 0 für ein i 0 = i 0 p i t i = p 0 + p t + p 2 t 2 + + p i0 t i
Ausgewählte Lösungen zu den Übungsblättern 9-10
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Dezember Ausgewählte Lösungen zu den Übungsblättern 9- Übungsblatt
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Dezember Ausgewählte Lösungen zu den Übungsblättern 9- Übungsblatt
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 205): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2 2
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 205): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2 2
Heinrich Heine-Universität Düsseldorf Sommersemester Lineare Algebra 1. Dreizehnte Woche,
 Fakultät für Mathematik PD Dr Markus Perling Heinrich Heine-Universität Düsseldorf Sommersemester 2014 Lineare Algebra 1 Dreizehnte Woche, 272014 9 Der Gauß-Algorithmus (Ende) estimmung des Inversen einer
Fakultät für Mathematik PD Dr Markus Perling Heinrich Heine-Universität Düsseldorf Sommersemester 2014 Lineare Algebra 1 Dreizehnte Woche, 272014 9 Der Gauß-Algorithmus (Ende) estimmung des Inversen einer
1 Darstellungsmatrizen
 Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 14/15 A 1 Darstellungsmatrizen Vereinbarungen für dieses Kapitel: K Körper V und W endlich-dimensionale K-Vektorräume B = {v
Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 14/15 A 1 Darstellungsmatrizen Vereinbarungen für dieses Kapitel: K Körper V und W endlich-dimensionale K-Vektorräume B = {v
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 13. Übung: Woche vom (Lin.Alg.
 Übungsaufgaben 13. Übung: Woche vom 23. 1.-27. 1. 2017 (Lin.Alg. II): Heft Ü 3: 1.1.3; 1.1.7 (a,b); 1.1.8; 1.1.11; 3.4.3 (b); 1.3.3 (c); 1.2.3 (b,d); Hinweis 1: 3. Test (Integration, analyt. Geom.) ist
Übungsaufgaben 13. Übung: Woche vom 23. 1.-27. 1. 2017 (Lin.Alg. II): Heft Ü 3: 1.1.3; 1.1.7 (a,b); 1.1.8; 1.1.11; 3.4.3 (b); 1.3.3 (c); 1.2.3 (b,d); Hinweis 1: 3. Test (Integration, analyt. Geom.) ist
Klausur zur Vorlesung Lineare Algebra II, SoSe 2016,
 Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
5 Minimalpolynom und charakteristisches Polynom
 5 Minimalpolynom und charakteristisches Polynom 5.1 Lemma Sei A K n n. Dann ist λ K genau dann ein Eigenwert von A, wenn det(λe n A) = 0. 5.2 Beispiel ( ) 1 4 i) A = R 1 1 2 2 det(λe 2 A) = λ 1 4 1 λ 1
5 Minimalpolynom und charakteristisches Polynom 5.1 Lemma Sei A K n n. Dann ist λ K genau dann ein Eigenwert von A, wenn det(λe n A) = 0. 5.2 Beispiel ( ) 1 4 i) A = R 1 1 2 2 det(λe 2 A) = λ 1 4 1 λ 1
Heinrich Heine-Universität Düsseldorf Sommersemester Lineare Algebra 1. Zwölfte Woche, Rang(f) := dim Bild(f).
 Fakultät für Mathematik PD Dr Markus Perling Heinrich Heine-Universität Düsseldorf Sommersemester 204 Lineare Algebra Zwölfte Woche, 256204 8 Der Rang einer Linearen Abbildung Auch in diesem Abschnitt
Fakultät für Mathematik PD Dr Markus Perling Heinrich Heine-Universität Düsseldorf Sommersemester 204 Lineare Algebra Zwölfte Woche, 256204 8 Der Rang einer Linearen Abbildung Auch in diesem Abschnitt
3.7 Eigenwerte und Eigenvektoren
 3.7. EIGENWERTE UND EIGENVEKTOREN 123 3.7 Eigenwerte und Eigenvektoren Wir wollen jetzt lineare Endomorphismen durch Matrizen besonders übersichtlicher Gestalt (u.a. mit möglichst vielen Nullen) beschreiben,
3.7. EIGENWERTE UND EIGENVEKTOREN 123 3.7 Eigenwerte und Eigenvektoren Wir wollen jetzt lineare Endomorphismen durch Matrizen besonders übersichtlicher Gestalt (u.a. mit möglichst vielen Nullen) beschreiben,
Lineare Algebra und analytische Geometrie I
 Prof. Dr. H. Brenner Osnabrück WS 2015/2016 Lineare Algebra und analytische Geometrie I Vorlesung 25 J ai décidé d être heureux parce que c est bon pour la santé Voltaire Trigonalisierbare Abbildungen
Prof. Dr. H. Brenner Osnabrück WS 2015/2016 Lineare Algebra und analytische Geometrie I Vorlesung 25 J ai décidé d être heureux parce que c est bon pour la santé Voltaire Trigonalisierbare Abbildungen
Determinanten. Motivation: Man betrachte das lineare Gleichungssystem =. (1) y = Sei o.b.d.a a 0 und c 0. Dann ist (1) äquivalent zu. = ac ad y.
 Determinanten Motivation: Man betrachte das lineare Gleichungssystem [ [ [ a b x u = (1) c d y v Sei obda a und c Dann ist (1) äquivalent zu [ [ ca cb x = ac ad y und ferner zu [ [ ca cb x ad cb y Falls
Determinanten Motivation: Man betrachte das lineare Gleichungssystem [ [ [ a b x u = (1) c d y v Sei obda a und c Dann ist (1) äquivalent zu [ [ ca cb x = ac ad y und ferner zu [ [ ca cb x ad cb y Falls
Eigenwerte, Diagonalisierbarkeit, charakteristisches Polynom
 Eigenwerte, Diagonalisierbarkeit, charakteristisches Polynom Eine Fragestellung, die uns im weiteren beschäftigen wird, ist das Finden eines möglichst einfachen Repräsentanten aus jeder Äquivalenzklasse
Eigenwerte, Diagonalisierbarkeit, charakteristisches Polynom Eine Fragestellung, die uns im weiteren beschäftigen wird, ist das Finden eines möglichst einfachen Repräsentanten aus jeder Äquivalenzklasse
6.3 Eigenwerte. γ ist Eigenwert von T [T] B B γi ist nicht invertierbar.
![6.3 Eigenwerte. γ ist Eigenwert von T [T] B B γi ist nicht invertierbar. 6.3 Eigenwerte. γ ist Eigenwert von T [T] B B γi ist nicht invertierbar.](/thumbs/70/62033901.jpg) Um zu zeigen, dass die irreduziblen Teiler eines reellen Polynoms höchstens den Grad 2 haben, fassen wir nun (x γ) und (x γ) zusammen und stellen fest, dass (x (a + b i))(x ((a b i)) = x 2 2a + (a 2 +
Um zu zeigen, dass die irreduziblen Teiler eines reellen Polynoms höchstens den Grad 2 haben, fassen wir nun (x γ) und (x γ) zusammen und stellen fest, dass (x (a + b i))(x ((a b i)) = x 2 2a + (a 2 +
3 Determinanten, Eigenwerte, Normalformen
 Determinanten, Eigenwerte, Normalformen.1 Determinanten Beispiel. Betrachte folgendes Parallelogramm in der Ebene R 2 : y (a + c, b + d) (c, d) (a, b) x Man rechnet leicht nach, dass die Fläche F dieses
Determinanten, Eigenwerte, Normalformen.1 Determinanten Beispiel. Betrachte folgendes Parallelogramm in der Ebene R 2 : y (a + c, b + d) (c, d) (a, b) x Man rechnet leicht nach, dass die Fläche F dieses
3.5 Trigonalisierbarkeit, verallgemeinerte Eigenräume und Jordansche Normalform
 LinAlg II Version 1 29. Mai 2006 c Rudolf Scharlau 219 3.5 Trigonalisierbarkeit, verallgemeinerte Eigenräume und Jordansche Normalform Das Problem der Normalformen für Endomorphismen handelt kurz gesprochen
LinAlg II Version 1 29. Mai 2006 c Rudolf Scharlau 219 3.5 Trigonalisierbarkeit, verallgemeinerte Eigenräume und Jordansche Normalform Das Problem der Normalformen für Endomorphismen handelt kurz gesprochen
23. Die Jordan sche Normalform
 Chr.Nelius, Lineare Algebra II (SS 2005) 1 23. Die Jordan sche Normalform Wir suchen für einen trigonalisierbaren Endomorphismus unter seinen dreiecksförmigen Darstellungsmatrizen eine Darstellungsmatrix,
Chr.Nelius, Lineare Algebra II (SS 2005) 1 23. Die Jordan sche Normalform Wir suchen für einen trigonalisierbaren Endomorphismus unter seinen dreiecksförmigen Darstellungsmatrizen eine Darstellungsmatrix,
Klausurenkurs zum Staatsexamen (SS 2013): Lineare Algebra und analytische Geometrie 3 Lösungsvorschlag
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 23): Lineare Algebra und analytische Geometrie 3 Lösungsvorschlag 3. Mit Hilfe elementarer Zeilenumformungen sowie der Tatsache, daß sich die Determinante
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 23): Lineare Algebra und analytische Geometrie 3 Lösungsvorschlag 3. Mit Hilfe elementarer Zeilenumformungen sowie der Tatsache, daß sich die Determinante
Lineare Algebra: Determinanten und Eigenwerte
 : und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
: und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
Diagonalisierbarkeit symmetrischer Matrizen
 ¾ Diagonalisierbarkeit symmetrischer Matrizen a) Eigenwerte und Eigenvektoren Die Matrix einer linearen Abbildung ³: Î Î bezüglich einer Basis ( Ò ) ist genau dann eine Diagonalmatrix wenn jeder der Basisvektoren
¾ Diagonalisierbarkeit symmetrischer Matrizen a) Eigenwerte und Eigenvektoren Die Matrix einer linearen Abbildung ³: Î Î bezüglich einer Basis ( Ò ) ist genau dann eine Diagonalmatrix wenn jeder der Basisvektoren
Lineare Algebra. 12. Übungsstunde. Steven Battilana. stevenb student.ethz.ch battilana.uk/teaching
 Lineare Algebra 12. Übungsstunde Steven Battilana stevenb student.ethz.ch battilana.uk/teaching December 14, 2017 1 Erinnerung: Determinanten, Orthogonale/unitäre Matrizen Sei A R 2 2, dann kann die Inverse
Lineare Algebra 12. Übungsstunde Steven Battilana stevenb student.ethz.ch battilana.uk/teaching December 14, 2017 1 Erinnerung: Determinanten, Orthogonale/unitäre Matrizen Sei A R 2 2, dann kann die Inverse
Eigenwerttheorie. Martin Gubisch Lineare Algebra I WS 2007/2008
 Eigenwerttheorie Martin Gubisch Lineare Algebra I WS 27/28 Motivation Gegeben seien ein K-Vektorraum V der Dimension n < und eine K-lineare Abbildung f : V V Wir suchen eine Basis V = v 1,, v n von V,
Eigenwerttheorie Martin Gubisch Lineare Algebra I WS 27/28 Motivation Gegeben seien ein K-Vektorraum V der Dimension n < und eine K-lineare Abbildung f : V V Wir suchen eine Basis V = v 1,, v n von V,
Berechnung der Determinante
 Berechnung der Determinante Verhalten der Determinante unter elementaren Zeilenoperationen: Das Vertauschen zweier Zeilen/Spalten der Matrix A ändert nur das Vorzeichen der Determinante, d.h: i, j {1,...,
Berechnung der Determinante Verhalten der Determinante unter elementaren Zeilenoperationen: Das Vertauschen zweier Zeilen/Spalten der Matrix A ändert nur das Vorzeichen der Determinante, d.h: i, j {1,...,
Karlsruher Institut für Technologie (KIT) WS 2012/13 Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning
 Karlsruher Institut für Technologie (KIT) WS 22/3 Institut für Analysis 28..23 Prof. Dr. Tobias Lamm Dr. Patrick Breuning Höhere Mathematik I für die Fachrichtung Physik 4. Übungsblatt (letztes Blatt)
Karlsruher Institut für Technologie (KIT) WS 22/3 Institut für Analysis 28..23 Prof. Dr. Tobias Lamm Dr. Patrick Breuning Höhere Mathematik I für die Fachrichtung Physik 4. Übungsblatt (letztes Blatt)
6 Hauptachsentransformation
 6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
3.4 Trigonalisierung und Jordansche Normalform
 3.4 Trigonalisierung und Jordansche Normalform Definition 3.4.1. Sei V ein K-Vektorraum, F End K (V ). Ein Unterraum U V heißt F -invariant falls F (U) U. Bemerkung. (1) Falls U V ein F -invarianter Unterraum
3.4 Trigonalisierung und Jordansche Normalform Definition 3.4.1. Sei V ein K-Vektorraum, F End K (V ). Ein Unterraum U V heißt F -invariant falls F (U) U. Bemerkung. (1) Falls U V ein F -invarianter Unterraum
Lineare Algebra. 13. Übungsstunde. Steven Battilana. stevenb student.ethz.ch battilana.uk/teaching
 Lineare Algebra 3. Übungsstunde Steven Battilana stevenb student.ethz.ch battilana.uk/teaching December 29, 27 Erinnerung Satz. Axiomatischer Zugang, Eigenschaften der Determinante. Die Abbildung det :
Lineare Algebra 3. Übungsstunde Steven Battilana stevenb student.ethz.ch battilana.uk/teaching December 29, 27 Erinnerung Satz. Axiomatischer Zugang, Eigenschaften der Determinante. Die Abbildung det :
5.2 Diagonalisierbarkeit und Trigonalisierung
 HINWEIS: Sie finden hier eine vorläufige Kurzfassung des Inhalts; es sind weder Beweise ausgeführt noch ausführliche Beispiele angegeben. Bitte informieren Sie sich in der Vorlesung. c M. Roczen und H.
HINWEIS: Sie finden hier eine vorläufige Kurzfassung des Inhalts; es sind weder Beweise ausgeführt noch ausführliche Beispiele angegeben. Bitte informieren Sie sich in der Vorlesung. c M. Roczen und H.
Lösungsskizze zur Wiederholungsserie
 Lineare Algebra D-MATH, HS Prof. Richard Pink Lösungsskizze zur Wiederholungsserie. [Aufgabe] Schreibe die lineare Abbildung f : Q Q 5, x +x +x x x +x +6x f x := x +x +8x x x +x +x. x +x +5x als Linksmultiplikation
Lineare Algebra D-MATH, HS Prof. Richard Pink Lösungsskizze zur Wiederholungsserie. [Aufgabe] Schreibe die lineare Abbildung f : Q Q 5, x +x +x x x +x +6x f x := x +x +8x x x +x +x. x +x +5x als Linksmultiplikation
Lineare Algebra I Lösungsvorschläge zum 14. Übungsblatt U. Görtz
 Lineare Algebra I Lösungsvorschläge zum 14. Übungsblatt U. Görtz Aufgabe 1 Sei V ein endlich-dimensionaler K-Vektorraum, und seien f und g Endomorphismen von V mit f g = g f. Zeige: a) Sind f und g diagonalisierbar,
Lineare Algebra I Lösungsvorschläge zum 14. Übungsblatt U. Görtz Aufgabe 1 Sei V ein endlich-dimensionaler K-Vektorraum, und seien f und g Endomorphismen von V mit f g = g f. Zeige: a) Sind f und g diagonalisierbar,
Mathematik I. Vorlesung 18. Vielfachheiten und diagonalisierbare Abbildungen. µ λ = dim(eig λ (ϕ))
 Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 18 Vielfachheiten und diagonalisierbare Abbildungen Satz 18.1. Es sei K ein Körper und es sei V ein endlichdimensionaler K- Vektorraum.
Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 18 Vielfachheiten und diagonalisierbare Abbildungen Satz 18.1. Es sei K ein Körper und es sei V ein endlichdimensionaler K- Vektorraum.
Kapitel 4. Determinante. Josef Leydold Mathematik für VW WS 2017/18 4 Determinante 1 / 24
 Kapitel 4 Determinante Josef Leydold Mathematik für VW WS 2017/18 4 Determinante 1 / 24 Was ist eine Determinante? Wir wollen messen, ob n Vektoren im R n linear abhängig sind bzw. wie weit sie davon entfernt
Kapitel 4 Determinante Josef Leydold Mathematik für VW WS 2017/18 4 Determinante 1 / 24 Was ist eine Determinante? Wir wollen messen, ob n Vektoren im R n linear abhängig sind bzw. wie weit sie davon entfernt
Trigonalisierung. Definition. 1) Sei F : V V linear, dim V = n. Dann heißt F trigonalisierbar, wenn es eine Basis B von V gibt sodass a 11 a 12..
 Trigonalisierung Sei F : V V linear und dim V = n. Wir beschäftigen uns jetzt mit der Frage, ob es eine Basis B von V gibt, sodass M B (F ) eine Dreiecksmatrix ist. Definition. ) Sei F : V V linear, dim
Trigonalisierung Sei F : V V linear und dim V = n. Wir beschäftigen uns jetzt mit der Frage, ob es eine Basis B von V gibt, sodass M B (F ) eine Dreiecksmatrix ist. Definition. ) Sei F : V V linear, dim
8 Eigenwerttheorie I 8. EIGENWERTTHEORIE I 139. Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet:
 8. EIGENWERTTHEORIE I 139 8 Eigenwerttheorie I Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet: K[x] = Abb[N, K] = {P ; P = a n x n + a n 1 x n 1 + + a 0 ; a
8. EIGENWERTTHEORIE I 139 8 Eigenwerttheorie I Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet: K[x] = Abb[N, K] = {P ; P = a n x n + a n 1 x n 1 + + a 0 ; a
Lösungsskizzen zur Klausur zur Linearen Algebra II. Definitionen
 Technische Universität Berlin Sommersemester 2008 Institut für Mathematik 18 Juli 2008 Prof Dr Stefan Felsner Andrea Hoffkamp Lösungsskizzen zur Klausur zur Linearen Algebra II Aufgabe 1 (1+1+1 Punkte)
Technische Universität Berlin Sommersemester 2008 Institut für Mathematik 18 Juli 2008 Prof Dr Stefan Felsner Andrea Hoffkamp Lösungsskizzen zur Klausur zur Linearen Algebra II Aufgabe 1 (1+1+1 Punkte)
4 Eigenwerte und Eigenvektoren
 4 Eigenwerte und Eigenvektoren Sei V {0} ein K Vektorraum und f : V V K linear. Definition: Ein Eigenwert von f ist ein Element λ K, für die es einen Vektor v 0 in V gibt, so dass f(v) = λ v. Sei nun λ
4 Eigenwerte und Eigenvektoren Sei V {0} ein K Vektorraum und f : V V K linear. Definition: Ein Eigenwert von f ist ein Element λ K, für die es einen Vektor v 0 in V gibt, so dass f(v) = λ v. Sei nun λ
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 2016
 Name, Vorname Matrikel-Nr. Aufg. Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 206 Bearbeiten Sie bitte
Name, Vorname Matrikel-Nr. Aufg. Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 206 Bearbeiten Sie bitte
7 Determinanten. f i : Mat n n (K) K. j=1 ( 1)i+j a ij D(A ij )
 7 Determinanten Im folgenden betrachten wir quadratische Matrizen. Wir schreiben dabei eine n n Matrix A (über dem Körper K) primär als Zeilenvektor, dessen Elemente die Spalten von A sind; also A = (a
7 Determinanten Im folgenden betrachten wir quadratische Matrizen. Wir schreiben dabei eine n n Matrix A (über dem Körper K) primär als Zeilenvektor, dessen Elemente die Spalten von A sind; also A = (a
Kapitel 11 Eigenwerte und Eigenvektoren
 Kapitel Eigenwerte und Eigenvektoren. Problem der Diagonalisierbarkeit Es sei wieder K gleich R oder. Eine n n)-matrix A mit Koeffizienten aus K wird als diagonalisierbar bezeichnet, wenn es eine invertierbare
Kapitel Eigenwerte und Eigenvektoren. Problem der Diagonalisierbarkeit Es sei wieder K gleich R oder. Eine n n)-matrix A mit Koeffizienten aus K wird als diagonalisierbar bezeichnet, wenn es eine invertierbare
Beispiellösungen zur Klausur Lineare Algebra bei Prof. Habegger
 Beispiellösungen zur Klausur Lineare Algebra bei Prof. Habegger Stefan Lell 2. Juli 2 Aufgabe. Sei t Q und A t = t 4t + 2 2t + 2 t t 2t 2t Mat 3Q a Bestimmen Sie die Eigenwerte von A t in Abhängigkeit
Beispiellösungen zur Klausur Lineare Algebra bei Prof. Habegger Stefan Lell 2. Juli 2 Aufgabe. Sei t Q und A t = t 4t + 2 2t + 2 t t 2t 2t Mat 3Q a Bestimmen Sie die Eigenwerte von A t in Abhängigkeit
Henning Krause Lineare Algebra Julia Sauter SS 2017 Klausur mit Lösungsvorschlag Jan Geuenich
 Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Lineare Algebra I für Mathematiker Lösungen
 Lineare Algebra I für Mathematiker Lösungen Anonymous 24. April 2016 Aufgabe 1 Beantworten Sie bitte die folgenden Fragen. Jeder Vektorraum hat mindestens ein Element. Q ist ein R-Vektorraum (mit der Multiplikation
Lineare Algebra I für Mathematiker Lösungen Anonymous 24. April 2016 Aufgabe 1 Beantworten Sie bitte die folgenden Fragen. Jeder Vektorraum hat mindestens ein Element. Q ist ein R-Vektorraum (mit der Multiplikation
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Scheinklausur, 2. Teil, Lineare Algebra I, WS 2001, Prof. Dr. G. Hiß. Ja oder
 Gruppe A Scheinklausur 2. Teil 15.2.2002 Lineare Algebra I WS 2001 Prof. Dr. G. Hiß Name: Matrikelnummer: Kreuzen Sie bei jeder Frage entweder Ja oder Nein oder nichts an. Auswertung der Multiple-Choice-Aufgaben:
Gruppe A Scheinklausur 2. Teil 15.2.2002 Lineare Algebra I WS 2001 Prof. Dr. G. Hiß Name: Matrikelnummer: Kreuzen Sie bei jeder Frage entweder Ja oder Nein oder nichts an. Auswertung der Multiple-Choice-Aufgaben:
Lineare Algebra und Numerische Mathematik für D-BAUG
 P Grohs T Welti F Weber Herbstsemester 215 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 12 Aufgabe 121 Matrixpotenzen und Eigenwerte Diese Aufgabe ist
P Grohs T Welti F Weber Herbstsemester 215 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 12 Aufgabe 121 Matrixpotenzen und Eigenwerte Diese Aufgabe ist
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz SS 5 4.5.5 Höhere Mathematik II für die Fachrichtung Physik Lösungsvorschläge zum 4. Übungsblatt
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz SS 5 4.5.5 Höhere Mathematik II für die Fachrichtung Physik Lösungsvorschläge zum 4. Übungsblatt
a b Q = b a 0 ) existiert ein Element p Q, so dass gilt: q 1 q 2 = 2 b 1 b 2 a 1 b 2 a 2 b 1 a 1 a 2 b 1 b 2 a 1 b 2 a 2 b 1 a b p = 1 det(q) C 2 2,
 Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
Lineare Algebra und analytische Geometrie I
 Prof Dr H Brenner Osnabrück WS 205/206 Lineare Algebra und analytische Geometrie I Vorlesung 7 Was die Menschen verbin, ist nicht der Glaube, sondern der Zweifel Peter Ustinow Universelle Eigenschaft der
Prof Dr H Brenner Osnabrück WS 205/206 Lineare Algebra und analytische Geometrie I Vorlesung 7 Was die Menschen verbin, ist nicht der Glaube, sondern der Zweifel Peter Ustinow Universelle Eigenschaft der
18 λ 18 + λ 0 A 18I 3 = / Z 2 Z 2 Z Z Z 1
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
2 Ähnlichkeit von Matrizen, Eigenwerte und Eigenvektoren
 2 ÄHNLICHKEIT VON MATRIZEN, EIGENWERTE UND EIGENVEKTOREN 1 19. Mai 2000 2 Ähnlichkeit von Matrizen, Eigenwerte und Eigenvektoren Motivation. Es seien: V ein K-Vektorraum mit dim V = n < und F End V, Φ,
2 ÄHNLICHKEIT VON MATRIZEN, EIGENWERTE UND EIGENVEKTOREN 1 19. Mai 2000 2 Ähnlichkeit von Matrizen, Eigenwerte und Eigenvektoren Motivation. Es seien: V ein K-Vektorraum mit dim V = n < und F End V, Φ,
KLAUSUR ZUR LINEAREN ALGEBRA II 19. Juli 2008
 KLAUSUR ZUR LINEAREN ALGEBRA II 19. Juli 2008 MUSTERLÖSUNG Name: Studiengang: Aufgabe 1 2 3 4 5 6 Summe Punktzahl /50 Allgemeine Hinweise: Bitte schreiben Sie Ihre Lösungen jeweils unter die Aufgabenstellung
KLAUSUR ZUR LINEAREN ALGEBRA II 19. Juli 2008 MUSTERLÖSUNG Name: Studiengang: Aufgabe 1 2 3 4 5 6 Summe Punktzahl /50 Allgemeine Hinweise: Bitte schreiben Sie Ihre Lösungen jeweils unter die Aufgabenstellung
1. Übungsblatt: Lineare Algebra II Abgabe: 8./ in den Übungsgruppen
 Hannover, den 7. Februar 2002 Aufgabe. Übungsblatt: Lineare Algebra II Abgabe: 8./9.4.2002 in den Übungsgruppen (2, 2, 3 Punkte) Der Vektorraum V = C[, ] sei mit dem üblichen Skalarprodukt f, g = f(t)g(t)
Hannover, den 7. Februar 2002 Aufgabe. Übungsblatt: Lineare Algebra II Abgabe: 8./9.4.2002 in den Übungsgruppen (2, 2, 3 Punkte) Der Vektorraum V = C[, ] sei mit dem üblichen Skalarprodukt f, g = f(t)g(t)
Lineare Algebra 2. Lösung zu Aufgabe 7.2:
 Technische Universität Dortmund Sommersemester 2017 Fakultät für Mathematik Übungsblatt 7 Prof. Dr. Detlev Hoffmann 15. Juni 2017 Marco Sobiech/ Nico Lorenz Lineare Algebra 2 Lösung zu Aufgabe 7.1: (a)
Technische Universität Dortmund Sommersemester 2017 Fakultät für Mathematik Übungsblatt 7 Prof. Dr. Detlev Hoffmann 15. Juni 2017 Marco Sobiech/ Nico Lorenz Lineare Algebra 2 Lösung zu Aufgabe 7.1: (a)
Die wichtigste Klasse von Funktionen zwischen Vektorräumen sind die linearen Abbildungen.
 Definition: Lineare Abbildung Lineare Abbildungen Die wichtigste Klasse von Funktionen zwischen Vektorräumen sind die linearen Abbildungen. 8.1 Definition: Lineare Abbildung Eine Funktion f : V Ñ W zwischen
Definition: Lineare Abbildung Lineare Abbildungen Die wichtigste Klasse von Funktionen zwischen Vektorräumen sind die linearen Abbildungen. 8.1 Definition: Lineare Abbildung Eine Funktion f : V Ñ W zwischen
2. Dezember Lineare Algebra II. Christian Ebert & Fritz Hamm. Skalarprodukt, Norm, Metrik. Matrizen. Lineare Abbildungen
 Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Basisprüfung. 18. August 2015
 Lineare Algebra I/II D-MATH, HS 4/FS 5 Prof Richard Pink Basisprüfung 8 August 25 [6 Punkte] Betrachte den reellen Vektorraum R 3 zusammen mit dem Standardskalarprodukt, und die Vektoren 9 3 v := 6, v
Lineare Algebra I/II D-MATH, HS 4/FS 5 Prof Richard Pink Basisprüfung 8 August 25 [6 Punkte] Betrachte den reellen Vektorraum R 3 zusammen mit dem Standardskalarprodukt, und die Vektoren 9 3 v := 6, v
Tutorium: Analysis und Lineare Algebra
 Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 14.5.218 (Teil 2) 9. Mai 218 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 218 Steven Köhler 9. Mai 218 3 c 218
Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 14.5.218 (Teil 2) 9. Mai 218 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 218 Steven Köhler 9. Mai 218 3 c 218
3.3 Eigenwerte und Eigenräume, Diagonalisierung
 3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 42 Normale Endomorphismen Nach Satz 34.1 besitzt eine Isometrie über C eine Orthonormalbasis aus Eigenvektoren
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 42 Normale Endomorphismen Nach Satz 34.1 besitzt eine Isometrie über C eine Orthonormalbasis aus Eigenvektoren
7 Determinanten. D ist alternierend g.d.w. für alle i j gilt:
 7 Determinanten Im folgenden betrachten wir quadratische Matrizen Wir schreiben dabei eine n n Matrix A (über dem Körper K) primär als Zeilenvektor, dessen Elemente die Spalten von A sind; also A = (a
7 Determinanten Im folgenden betrachten wir quadratische Matrizen Wir schreiben dabei eine n n Matrix A (über dem Körper K) primär als Zeilenvektor, dessen Elemente die Spalten von A sind; also A = (a
Übungen zum Ferienkurs Ferienkurs Lineare Algebra für Physiker WiSe 2017/18 Blatt 3 - Lösung
 Technische Universität München Physik Department Pablo Cova Fariña, Claudia Nagel Übungen zum Ferienkurs Ferienkurs Lineare Algebra für Physiker WiSe 207/8 Blatt 3 - Aufgabe : Darstellungsmatrizen Sei
Technische Universität München Physik Department Pablo Cova Fariña, Claudia Nagel Übungen zum Ferienkurs Ferienkurs Lineare Algebra für Physiker WiSe 207/8 Blatt 3 - Aufgabe : Darstellungsmatrizen Sei
4 Determinanten, Eigenwerte, Diagonalisierung, Jordansche Normalform
 Technische Universität München Florian Ettlinger Ferienkurs Lineare Algebra Vorlesung Donnerstag WS 2/2 4 Determinanten, Eigenwerte, Diagonalisierung, Jordansche Normalform 4 Determinanten 4 Definition
Technische Universität München Florian Ettlinger Ferienkurs Lineare Algebra Vorlesung Donnerstag WS 2/2 4 Determinanten, Eigenwerte, Diagonalisierung, Jordansche Normalform 4 Determinanten 4 Definition
7.3 Unitäre Operatoren
 Wir können jeden Operator T wie folgt schreiben: Dabei gilt T = 1 2 (T + T ) + i( 1 2 i (T T )) (T + T ) = T + T sowie ( 1 2 i (T T )) = 1 2 i (T T) = 1 2 i (T T ). Wir können T also in zwei lineare Operatoren
Wir können jeden Operator T wie folgt schreiben: Dabei gilt T = 1 2 (T + T ) + i( 1 2 i (T T )) (T + T ) = T + T sowie ( 1 2 i (T T )) = 1 2 i (T T) = 1 2 i (T T ). Wir können T also in zwei lineare Operatoren
Lineare Algebra und analytische Geometrie I
 Prof. Dr. H. Brenner Osnabrück WS 0/06 Lineare Algebra und analytische Geometrie I Vorlesung... und ein guter Lehrer kann auch einem schlechten Schüler was beibringen Beziehung zwischen Eigenräumen Wir
Prof. Dr. H. Brenner Osnabrück WS 0/06 Lineare Algebra und analytische Geometrie I Vorlesung... und ein guter Lehrer kann auch einem schlechten Schüler was beibringen Beziehung zwischen Eigenräumen Wir
Musterlösungen für die Nachklausur in LinAlg vom
 Musterlösungen für die Nachklausur in LinAlg vom 10.10.16 1. Finden Sie mindestens ) zwei Dreh )Matrizen ) M R 2 2 mit der Eigenschaft 1 0 M = : M = ± 1 1 2 ±1 1 k k 1 k 2. Sei A R 3 3 die Matrix A = 0
Musterlösungen für die Nachklausur in LinAlg vom 10.10.16 1. Finden Sie mindestens ) zwei Dreh )Matrizen ) M R 2 2 mit der Eigenschaft 1 0 M = : M = ± 1 1 2 ±1 1 k k 1 k 2. Sei A R 3 3 die Matrix A = 0
5 Eigenwerte, Eigenvektoren und Diagonalisierbarkeit
 ME Lineare Algebra HT 2008 99 5 Eigenwerte, Eigenvektoren und Diagonalisierbarkeit 5.1 Ein Beispiel zur Motivation Als einfachstes Beispiel eines dynamischen Systems untersuchen wir folgendes Differentialgleichungssystem
ME Lineare Algebra HT 2008 99 5 Eigenwerte, Eigenvektoren und Diagonalisierbarkeit 5.1 Ein Beispiel zur Motivation Als einfachstes Beispiel eines dynamischen Systems untersuchen wir folgendes Differentialgleichungssystem
7.2 Die adjungierte Abbildung
 7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
m 1 Die Bewegung der drei Kugeln wird beschrieben durch das folgende Differentialgleichungssystem x 1 (t) x 2 (t) x 3 (t) k 12 k 12 k 12 k k 23
 Kapitel 5 Eigenwerte 5. Definition und Beispiele Wir sehen uns ein System dreier schwingender Kugeln der Massen m, m und m 3 an, die durch Federn aneinander gekoppelt sein sollen. m k m k 3 m 3 x ( t x
Kapitel 5 Eigenwerte 5. Definition und Beispiele Wir sehen uns ein System dreier schwingender Kugeln der Massen m, m und m 3 an, die durch Federn aneinander gekoppelt sein sollen. m k m k 3 m 3 x ( t x
Sommer 2017 Musterlösung
 Sommer 7 Musterlösung. (5 Punkte) a) Sei V ein Vektorraum über K und sei T End(V ). Geben Sie die Definition eines Eigenwertes von T und zeigen Sie für endlichdimensionales V, dass λ K genau dann ein Eigenwert
Sommer 7 Musterlösung. (5 Punkte) a) Sei V ein Vektorraum über K und sei T End(V ). Geben Sie die Definition eines Eigenwertes von T und zeigen Sie für endlichdimensionales V, dass λ K genau dann ein Eigenwert
6. Normale Abbildungen
 SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
Richie Gottschalk Lineare Algebra I Seite 1. a) Welche der folgenden Ringe sind kommutativ? Es gibt genau einen Unterraum W von V mit dim(w ) = n.
 Richie Gottschalk Lineare Algebra I Seite Aufgabe Im Folgenden sind K immer ein Körper und V ein K-Vektorraum. a) Welche der folgenden Ringe sind kommutativ? K[x] K[x] ist per se ein kommutativer Polynomring.
Richie Gottschalk Lineare Algebra I Seite Aufgabe Im Folgenden sind K immer ein Körper und V ein K-Vektorraum. a) Welche der folgenden Ringe sind kommutativ? K[x] K[x] ist per se ein kommutativer Polynomring.
4.4 Hermitesche Formen
 44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
Lineare Algebra I Zusammenfassung
 Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
Proseminar Lineare Algebra II, SS 11. Blatt
 Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS. Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF
 TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF 07032016-11032016 Inhaltsverzeichnis Inhaltsverzeichnis 1 Lineare Abbildungen 2 11 Homomorphismus 2 12 Kern
TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF 07032016-11032016 Inhaltsverzeichnis Inhaltsverzeichnis 1 Lineare Abbildungen 2 11 Homomorphismus 2 12 Kern
Lineare Algebra - Determinanten und Eigenwerte
 Lineare Algebra - Determinanten und Eigenwerte 26 März 2011 1 Determinanten 11 Definition (Determinanten): Sei K ein Körper und N n 0 Dann nennt man eine durch det : M(n n, K) K, a det(a) definierte Abbildung
Lineare Algebra - Determinanten und Eigenwerte 26 März 2011 1 Determinanten 11 Definition (Determinanten): Sei K ein Körper und N n 0 Dann nennt man eine durch det : M(n n, K) K, a det(a) definierte Abbildung
Musterlösungen zur Linearen Algebra II Weihnachtszettel
 Musterlösungen zur Linearen Algebra II Weihnachtszettel Aufgabe. Welche der folgenden Matrizen 3 0 0 A = 0 4, B = 3, C = 0 0 0 6 0 0 0 sind über R und welche über C diagonalisierbar? Bestimmen Sie dazu
Musterlösungen zur Linearen Algebra II Weihnachtszettel Aufgabe. Welche der folgenden Matrizen 3 0 0 A = 0 4, B = 3, C = 0 0 0 6 0 0 0 sind über R und welche über C diagonalisierbar? Bestimmen Sie dazu
Ferienkurs Lineare Algebra
 Ferienkurs Lineare Algebra Wintersemester 9/ Lösungen Eigenwerte und Diagonalsierbarkeit Blatt Diagonalisierbarkeit. Zeigen sie, dass für eine diagonalisierbare Matrix A folgendes gilt: det(a) = wobei
Ferienkurs Lineare Algebra Wintersemester 9/ Lösungen Eigenwerte und Diagonalsierbarkeit Blatt Diagonalisierbarkeit. Zeigen sie, dass für eine diagonalisierbare Matrix A folgendes gilt: det(a) = wobei
3.3 Das charakteristische Polynom
 LinAlg II Version 1 2. Mai 2006 c Rudolf Scharlau 209 3.3 Das charakteristische Polynom Wir setzen die im vorigen Abschnitt begonnene Untersuchung von Eigenvektoren und Eigenwerten fort und stellen den
LinAlg II Version 1 2. Mai 2006 c Rudolf Scharlau 209 3.3 Das charakteristische Polynom Wir setzen die im vorigen Abschnitt begonnene Untersuchung von Eigenvektoren und Eigenwerten fort und stellen den
Übungen zur Linearen Algebra II, Sommersemester Test, , Gruppe A: Lösung
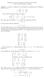 Aufgabe. (5 Punkte) Matrix A C 3 3 : Übungen zur Linearen Algebra II, Sommersemester 0. Test, 9.5.0, Gruppe A: Lösung Bestimmen Sie alle Eigenwerte und Eigenräume der folgenden 8 A 9 6 3 9 Lösung: Charakteristisches
Aufgabe. (5 Punkte) Matrix A C 3 3 : Übungen zur Linearen Algebra II, Sommersemester 0. Test, 9.5.0, Gruppe A: Lösung Bestimmen Sie alle Eigenwerte und Eigenräume der folgenden 8 A 9 6 3 9 Lösung: Charakteristisches
Klausur zu. Lineare Algebra II. Viel Erfolg! Fachbereich Mathematik WS 2012/13 Dr. habil. Matthias Schneider. Bonus Note. Aufgabe
 Klausur zu Lineare Algebra II Fachbereich Mathematik WS 0/3 Dr. habil. Matthias Schneider Aufgabe 3 4 5 6 7 Bonus Note Punktzahl 4 3 3 3 3 0 erreichte Punktzahl Es sind keine Hilfsmittel zugelassen. Die
Klausur zu Lineare Algebra II Fachbereich Mathematik WS 0/3 Dr. habil. Matthias Schneider Aufgabe 3 4 5 6 7 Bonus Note Punktzahl 4 3 3 3 3 0 erreichte Punktzahl Es sind keine Hilfsmittel zugelassen. Die
Lineare Algebra. Wintersemester 2017/2018. Skript zum Ferienkurs Tag Claudia Nagel Pablo Cova Fariña. Technische Universität München
 Technische Universität München Wintersemester 27/28 Lineare Algebra Skript zum Ferienkurs Tag 3-2.3.28 Claudia Nagel Pablo Cova Fariña Wir danken Herrn Prof. Kemper vielmals für seine Unterstützung bei
Technische Universität München Wintersemester 27/28 Lineare Algebra Skript zum Ferienkurs Tag 3-2.3.28 Claudia Nagel Pablo Cova Fariña Wir danken Herrn Prof. Kemper vielmals für seine Unterstützung bei
Serie a) Welche der folgenden Vektoren sind Eigenvektoren der Matrix 1 0 1? 0 1 1
 Prof. Norbert Hungerbühler Serie Lineare Algebra II ETH Zürich - D-MAVT. a Welche der folgenden Vektoren sind Eigenvektoren der Matrix? i (,,. ii (,,. iii (,,. iv (, 3,. v (,,. Ein Vektor v ist Eigenvektor
Prof. Norbert Hungerbühler Serie Lineare Algebra II ETH Zürich - D-MAVT. a Welche der folgenden Vektoren sind Eigenvektoren der Matrix? i (,,. ii (,,. iii (,,. iv (, 3,. v (,,. Ein Vektor v ist Eigenvektor
1. Hausübung ( )
 Übungen zur Vorlesung»Lineare Algebra B«(SS ). Hausübung (8.4.) Aufgabe Es seien σ (3, 6, 5,, 4, 8,, 7) und τ (3,,, 4, 6, 5, 8, 7). Berechnen Sie σ τ, τ σ, σ, τ, die Anzahl der Inversionen von σ und τ
Übungen zur Vorlesung»Lineare Algebra B«(SS ). Hausübung (8.4.) Aufgabe Es seien σ (3, 6, 5,, 4, 8,, 7) und τ (3,,, 4, 6, 5, 8, 7). Berechnen Sie σ τ, τ σ, σ, τ, die Anzahl der Inversionen von σ und τ
TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS. Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF
 TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF 07.03.2016-11.03.2016 Inhaltsverzeichnis Inhaltsverzeichnis 1 Darstellungsmatrizen 2 2 Diagonalisierbarkeit
TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF 07.03.2016-11.03.2016 Inhaltsverzeichnis Inhaltsverzeichnis 1 Darstellungsmatrizen 2 2 Diagonalisierbarkeit
4 Lineare Abbildungen Basisdarstellungen
 4 Lineare Abbildungen Basisdarstellungen (4.1) Seien V,W endlich dimensionale K-Vektorräume, und sei T : V W linear. Sei {v 1,...,v } Basis von V und {w 1,...,w M } Basis von W. Sei T (v j ) = M a kj w
4 Lineare Abbildungen Basisdarstellungen (4.1) Seien V,W endlich dimensionale K-Vektorräume, und sei T : V W linear. Sei {v 1,...,v } Basis von V und {w 1,...,w M } Basis von W. Sei T (v j ) = M a kj w
KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG
 KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG Aufgabe 1 Es sei K ein Körper, V ein K-Vektorraum, und seien v 1,..., v n V (n N). (a) Definieren Sie, wann die endliche Familie v 1,...,
KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG Aufgabe 1 Es sei K ein Körper, V ein K-Vektorraum, und seien v 1,..., v n V (n N). (a) Definieren Sie, wann die endliche Familie v 1,...,
12 Lineare Algebra - Übersicht. Themen: Unterräume Lineare Abbbildungen Gauß-Algorithmus Eigenwerte und Normalformen
 12 Lineare Algebra - Übersicht Themen: Unterräume Lineare Abbbildungen Gauß-Algorithmus Eigenwerte und Normalformen Unterräume Sei X ein Vektorraum über Ã. Eine Teilmenge M X heißt Unterraum von X, wenn
12 Lineare Algebra - Übersicht Themen: Unterräume Lineare Abbbildungen Gauß-Algorithmus Eigenwerte und Normalformen Unterräume Sei X ein Vektorraum über Ã. Eine Teilmenge M X heißt Unterraum von X, wenn
MC-Serie 11: Eigenwerte
 D-ERDW, D-HEST, D-USYS Mathematik I HS 14 Dr. Ana Cannas MC-Serie 11: Eigenwerte Einsendeschluss: 12. Dezember 2014 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung
D-ERDW, D-HEST, D-USYS Mathematik I HS 14 Dr. Ana Cannas MC-Serie 11: Eigenwerte Einsendeschluss: 12. Dezember 2014 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung
