Folien aus der Vorlesung Optimierung I SS2013
|
|
|
- Daniel Holzmann
- vor 5 Jahren
- Abrufe
Transkript
1 Folien aus der Vorlesung Optimierung I SS2013 Dr. Jens Maßberg Institut für Optimierung und Operations Research, Universität Ulm July 10, 2013
2 Datenstrukturen für Graphen und Digraphen Graph Scanning Algorithmus BFS-Bäume Minimum Spanning Trees Kruskal s Algorithm Prim s Algorithm Dijkstra s Algorithmus Moore-Bellman-Ford Algorithmus Floyd-Warshall Algorithmus
3 Inzidenzmatrix b d a f c e ab ac bd be cd ce df ef a 1 1 b c d e f 1 1 Speicheraufwand: O(nm).
4 Adjazenzmatrix b d a f c e a b c d e f a 1 1 b c d e f 1 1 Speicheraufwand: O(n 2 ).
5 Kantenliste b d a f c e (a, b), (a, c), (b, d), (b, e)(c, d), (c, e), (d, f ), (e, f ) Speicheraufwand: O(m log(n)).
6 Adjazenzliste b d a f c e a b c d e f b,c a,d,e a,d,e b,c,f b,c,f d,e Speicheraufwand: O(m log n + n log m).
7 Inzidenzmatrix von Digraphen b d a f c e ab ac bd be cd ce df ef a 1 1 b c d e f -1-1
8 Adjazenzmatrix von Digraphen b d a f c e a b c d e f a 1 1 b 1 1 c 1 1 d 1 e 1 f Speicheraufwand: O(n 2 ).
9 Graph Scanning Algorithmus Input: Ein Graph G/ Digraph D und ein Knoten r von G/D. Output: Die Menge R der Knoten, die in G/D von r aus auf Wegen/gerichteten Wegen erreichbar sind und eine Menge T E(G)/A(D), für die (R, T ) Baum/Arboreszenz mit Wurzel r ist. begin R {r}; Q {r}; T ; l(r) 0; while Q do 1 Wähle v Q; 2 if w V \ R mit e = vw E(G) / e = (v, w) A(D) then Wähle solch ein w; R R {w}; Q Q {w}; T T {e}; l(w) l(v) + 1; end else Q Q \ {v}; end end return (R, T );
10 Graph Scanning Algorithmus
11 Graph Scanning Algorithmus r
12 Graph Scanning Algorithmus r 1
13 Graph Scanning Algorithmus 2 r 1
14 Graph Scanning Algorithmus 3 2 r 1
15 Graph Scanning Algorithmus 3 2 r 1 3
16 Graph Scanning Algorithmus r 1 3
17 BFS-Bäume r 1 2
18 Minimum Spanning Trees a b c d 1 e 6 f 11 g
19 Minimum Spanning Trees a b c d 1 e 6 f 11 g
20 Kruskal s Algorithm Input: Ein zusammenhängender Graph G und eine Kostenfunktion c : E R. Output: Ein Minimum Spanning Tree T f"ur (G, c). begin Sortiere die Kanten von G so, dass c(e 1 ) c(e 2 )... c(e m ) gilt; end T (V (G), ); for i = 1 to m do if T + e i ist ein Wald then T (V (G), E(T ) {e i }); end end return T ;
21 Kruskals s algorithm a b c d 1 e 6 f 11 g
22 Kruskals s algorithm a b c d 1 e 6 f 11 g
23 Kruskals s algorithm a b c d 1 e 6 f 11 g
24 Kruskals s algorithm a b c d 1 e 6 f 11 g
25 Kruskals s algorithm a b c d 1 e 6 f 11 g
26 Kruskals s algorithm a b c d 1 e 6 f 11 g
27 Kruskals s algorithm a b c d 1 e 6 f 11 g
28 Kruskals s algorithm a b c d 1 e 6 f 11 g
29 Kruskals s algorithm a b c d 1 e 6 f 11 g
30 Kruskals s algorithm a b c d 1 e 6 f 11 g
31 Prim s Algorithm Input: Ein zusammenhängender Graph G und eine Kostenfunktion c : E(G) R. Output: Ein Minimum Spanning Tree T. begin W"ahle v V (G); end T ({v}, ); while V (T ) V (G) do Wähle eine Kante xy minimaler Kosten c(xy) mit x V (T ) und y V (G) \ V (T ); end T (V (T ) {y}, E(T ) {e}); return T ;
32 Prim s algorithm a b c d 1 e 6 f 11 g
33 Prim s algorithm a b c d 1 e 6 f 11 g
34 Prim s algorithm a b c d 1 e 6 f 11 g
35 Prim s algorithm a b c d 1 e 6 f 11 g
36 Prim s algorithm a b c d 1 e 6 f 11 g
37 Prim s algorithm a b c d 1 e 6 f 11 g
38 Prim s algorithm a b c d 1 e 6 f 11 g
39 Dijkstra s algorithm Input: Ein Digraph D, c : A(D) R >0 und r V (D). Output: Kürzeste Wege von r zu allen erreichbaren Knoten: (l(v), p(v)) v V (D)\{r}, wobei l(v) = dist (D,c) (r, v) gilt und p(v) ein Vorgänger von v auf einem bzgl. c kürzesten Weg von r nach v ist. Ist v nicht erreichbar, so ist l(v) = und p(v) nicht definiert. begin l(r) 0; for v V (D) \ {r} do l(v) ; 1 R ; while R V (D) do 2 Wähle v V (D) \ R mit l(v) = min{l(w) w V (D) \ R}; 3 R R {v}; for w V (D) \ R mit (v, w) A(D) do if l(w) > l(v) + c((v, w)) then 4 l(w) l(v) + c((v, w)); p(w) v; end end end return (l(v), p(v)) v V (D)\{r} ; 2013 endinstitut für Optimierung und Operations Research, Universität Ulm, Dr. Jens Maßberg
40 Dijkstra s algorithm
41 Dijkstra s algorithm
42 Dijkstra s algorithm
43 Dijkstra s algorithm
44 Dijkstra s algorithm
45 Dijkstra s algorithm
46 Dijkstra s algorithm
47 Dijkstra s algorithm
48 Moore-Bellman-Ford Algorithmus Input: Ein Digraph D, eine konservative Funktion c : A(D) R und s V (D). Output: Wie beim Dijkstra s Algorithm: (l(v), p(v)) v V (D)\{r} wobei l(v) = dist (D,c) (s, v) gilt und p(v) ein Vorgänger von v auf einem kürzesten Weg von s nach v ist. (Ist v nicht erreichbar, so ist l(v) = und p(v) nicht definiert.) begin l(s) 0; for v V (D) \ {s} do l(v) ; end for i = 1 to n(d) 1 do for (v, w) A(D) do if l(w) > l(v) + c((v, w)) then l(w) l(v) + c((v, w)); p(w) v; end end end return (l(v), p(v)) v V (D)\{s} ; end
49 Moore-Bellman-Ford Algorithmus
50 Moore-Bellman-Ford Algorithmus i =
51 Moore-Bellman-Ford Algorithmus 0 i =
52 Moore-Bellman-Ford Algorithmus 0 i =
53 Moore-Bellman-Ford Algorithmus 0 i =
54 Floyd-Warshall Algorithmus Input: Ein Digraph D mit V (D) = [n] und eine konservative Gewichtsfunktion c : A(D) R. Output: Matrizen (l(i, j)) (i,j) [n] 2 und (p(i, j)) (i,j) [n] 2. Hier bei gilt l(i, j) = dist (D,c) (i, j) und für (i, j) [n 2 ] mit l(i, j) < ist (p(i, j), j) die letzte gerichte Kante eines bezüglich c kürzesten gerichteten Weges in D von i nach j.
55 Floyd-Warshall Algorithmus begin for (i, j) A(D) do l(i, j) c((i, j)); p(i, j) i; for i, j V (D) mit i j und (i, j) A(D) do l(i, j) ; for i V (D) do l(i, i) 0; for j = 1 to n do for i = 1 to n do if i j then for k = 1 to n do if k j then if l(i, k) > l(i, j) + l(j, k) then l(i, k) l(i, j) + l(j, k); p(i, k) p(j, k); end end end end end end end
8 Diskrete Optimierung
 8 Diskrete Optimierung Definition 8.1. Ein Graph G ist ein Paar (V (G), E(G)) besteh aus einer lichen Menge V (G) von Knoten (oder Ecken) und einer Menge E(G) ( ) V (G) 2 von Kanten. Die Ordnung n(g) von
8 Diskrete Optimierung Definition 8.1. Ein Graph G ist ein Paar (V (G), E(G)) besteh aus einer lichen Menge V (G) von Knoten (oder Ecken) und einer Menge E(G) ( ) V (G) 2 von Kanten. Die Ordnung n(g) von
EDM, Algorithmen und Graphenspeicherung
 EDM, Algorithmen und Graphenspeicherung 1 Graphenspeicherung Gespeichert werden soll ein Graph G = (V, E) bzw. Digraph D = (V, A). Man beachte: E ( ) V 2 bzw. E V 2 1.1 Adjazenzmatrix Graph G: A = (a vw
EDM, Algorithmen und Graphenspeicherung 1 Graphenspeicherung Gespeichert werden soll ein Graph G = (V, E) bzw. Digraph D = (V, A). Man beachte: E ( ) V 2 bzw. E V 2 1.1 Adjazenzmatrix Graph G: A = (a vw
Algorithmen & Komplexität
 Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Kürzeste Pfade Problem Gegeben Netzwerk: Graph G = (V, E), Gewichtsfunktion w: E N Zwei Knoten: s, t Kantenzug/Weg
Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Kürzeste Pfade Problem Gegeben Netzwerk: Graph G = (V, E), Gewichtsfunktion w: E N Zwei Knoten: s, t Kantenzug/Weg
Grundlagen: Algorithmen und Datenstrukturen
 Grundlagen: Algorithmen und Datenstrukturen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Sommersemester 00
Grundlagen: Algorithmen und Datenstrukturen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Sommersemester 00
Kap. 6.6: Kürzeste Wege
 Kap. 6.6: Kürzeste Wege Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 1./. VO DAP SS 009./9. Juli 009 1 Nachtest für Ausnahmefälle Di 1. Juli 009, 16:00 Uhr,
Kap. 6.6: Kürzeste Wege Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 1./. VO DAP SS 009./9. Juli 009 1 Nachtest für Ausnahmefälle Di 1. Juli 009, 16:00 Uhr,
Algorithmen I. Prof. Jörn Müller-Quade Institut für Theoretische Informatik Web: https://crypto.iti.kit.edu/index.php?
 Algorithmen I Prof. Jörn Müller-Quade 19.6.1 Institut für Theoretische Informatik Web: https://crypto.iti.kit.edu/index.php?id=99 (Folien von Peter Sanders) KIT Institut für Theoretische Informatik 1 Organisatorisches
Algorithmen I Prof. Jörn Müller-Quade 19.6.1 Institut für Theoretische Informatik Web: https://crypto.iti.kit.edu/index.php?id=99 (Folien von Peter Sanders) KIT Institut für Theoretische Informatik 1 Organisatorisches
8.4 Digraphen mit negativen Kantengewichten Grundsätzliches Betrachte Startknoten s und einen Kreis C mit Gesamtlänge < 0.
 8.4 Digraphen mit negativen Kantengewichten 8.4.1 Grundsätzliches Betrachte Startknoten s und einen Kreis C mit Gesamtlänge < 0. k 4 5 1 s 1 3 2 C k 0 k 3 1 1 1 k 1 k 2 v Sollte ein Pfad von s nach C und
8.4 Digraphen mit negativen Kantengewichten 8.4.1 Grundsätzliches Betrachte Startknoten s und einen Kreis C mit Gesamtlänge < 0. k 4 5 1 s 1 3 2 C k 0 k 3 1 1 1 k 1 k 2 v Sollte ein Pfad von s nach C und
Kap. 6.6: Kürzeste Wege
 0.0.00 Nachtest für Ausnahmefälle Kap..: Kürzeste Wege Professor Dr. Lehrstuhl für Algorithm Engineering, LS Fakultät für Informatik, TU Dortmund./. VO DAP SS 00./. Juli 00 Di. Juli 00, :00 Uhr, OH, R.
0.0.00 Nachtest für Ausnahmefälle Kap..: Kürzeste Wege Professor Dr. Lehrstuhl für Algorithm Engineering, LS Fakultät für Informatik, TU Dortmund./. VO DAP SS 00./. Juli 00 Di. Juli 00, :00 Uhr, OH, R.
Algo&Komp. - Wichtige Begriffe Mattia Bergomi Woche 6 7
 1 Kürzeste Pfade Woche 6 7 Hier arbeiten wir mit gewichteten Graphen, d.h. Graphen, deren Kanten mit einer Zahl gewichtet werden. Wir bezeichnen die Gewichtsfunktion mit l : E R. Wir wollen einen kürzesten
1 Kürzeste Pfade Woche 6 7 Hier arbeiten wir mit gewichteten Graphen, d.h. Graphen, deren Kanten mit einer Zahl gewichtet werden. Wir bezeichnen die Gewichtsfunktion mit l : E R. Wir wollen einen kürzesten
Graphalgorithmen 2. Dominik Paulus Dominik Paulus Graphalgorithmen / 47
 Graphalgorithmen Dominik Paulus.0.01 Dominik Paulus Graphalgorithmen.0.01 1 / 7 1 Spannbäume Kruskal Prim Edmonds/Chu-Liu Datenstrukturen Fibonacci-Heap Union/Find Kürzeste Pfade Dijkstra Bellman-Ford
Graphalgorithmen Dominik Paulus.0.01 Dominik Paulus Graphalgorithmen.0.01 1 / 7 1 Spannbäume Kruskal Prim Edmonds/Chu-Liu Datenstrukturen Fibonacci-Heap Union/Find Kürzeste Pfade Dijkstra Bellman-Ford
4.2 Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition 4.2.1
 Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
3.6 Branch-and-Bound-Verfahren
 36 Branch-and-Bound-Verfahren Die Branch-and-Bound -Methode beruht darauf, auf eine intelligente Weise alle zulässigen Lösungen eines kombinatorischen Optimierungsproblems aufzulisten und mit Hilfe von
36 Branch-and-Bound-Verfahren Die Branch-and-Bound -Methode beruht darauf, auf eine intelligente Weise alle zulässigen Lösungen eines kombinatorischen Optimierungsproblems aufzulisten und mit Hilfe von
Wie wird ein Graph dargestellt?
 Wie wird ein Graph dargestellt? Für einen Graphen G = (V, E), ob gerichtet oder ungerichtet, verwende eine Adjazenzliste A G : A G [i] zeigt auf eine Liste aller Nachbarn von Knoten i, wenn G ungerichtet
Wie wird ein Graph dargestellt? Für einen Graphen G = (V, E), ob gerichtet oder ungerichtet, verwende eine Adjazenzliste A G : A G [i] zeigt auf eine Liste aller Nachbarn von Knoten i, wenn G ungerichtet
Datenstrukturen und Algorithmen (SS 2013)
 Datenstrukturen und Algorithmen (SS 2013) Übungsblatt 10 Abgabe: Montag, 08.07.2013, 14:00 Uhr Die Übungen sollen in Gruppen von zwei bis drei Personen bearbeitet werden. Schreiben Sie die Namen jedes
Datenstrukturen und Algorithmen (SS 2013) Übungsblatt 10 Abgabe: Montag, 08.07.2013, 14:00 Uhr Die Übungen sollen in Gruppen von zwei bis drei Personen bearbeitet werden. Schreiben Sie die Namen jedes
Teil 2: Graphenalgorithmen
 Teil : Graphenalgorithmen Anwendungen Definitionen Datenstrukturen für Graphen Elementare Algorithmen Topologisches Sortieren Kürzeste Wege Minimal aufspannende Bäume Problemstellung Algorithmus von Prim
Teil : Graphenalgorithmen Anwendungen Definitionen Datenstrukturen für Graphen Elementare Algorithmen Topologisches Sortieren Kürzeste Wege Minimal aufspannende Bäume Problemstellung Algorithmus von Prim
Erinnerung VL
 Erinnerung VL.6.16 Graphtraversierung (DFS, topologische Sortierung und mehr) Kürzeste Wege: Problemstellung, Algorithmen Analoger Algorithmus Dijkstras Algorithmus: Idee, Korrektheit Heute: mehr zu Dijkstra,
Erinnerung VL.6.16 Graphtraversierung (DFS, topologische Sortierung und mehr) Kürzeste Wege: Problemstellung, Algorithmen Analoger Algorithmus Dijkstras Algorithmus: Idee, Korrektheit Heute: mehr zu Dijkstra,
Datenstrukturen und Algorithmen SS07
 Datenstrukturen und Algorithmen SS0 Datum:.6.200 Michael Belfrage mbe@student.ethz.ch belfrage.net/eth Programm von Heute Minimaler Spannbaum (MST) Challenge der Woche Fibonacci Heap Minimaler Spannbaum
Datenstrukturen und Algorithmen SS0 Datum:.6.200 Michael Belfrage mbe@student.ethz.ch belfrage.net/eth Programm von Heute Minimaler Spannbaum (MST) Challenge der Woche Fibonacci Heap Minimaler Spannbaum
Algorithmen und Datenstrukturen Kapitel 9. und
 Algorithmen und Datenstrukturen Kapitel 9 und Kürzeste Pfade Frank Heitmann heitmann@informatik.uni-hamburg.de 9. Dezember 0 Frank Heitmann heitmann@informatik.uni-hamburg.de / Problemstellung Definition
Algorithmen und Datenstrukturen Kapitel 9 und Kürzeste Pfade Frank Heitmann heitmann@informatik.uni-hamburg.de 9. Dezember 0 Frank Heitmann heitmann@informatik.uni-hamburg.de / Problemstellung Definition
Informatik II, SS 2016
 Informatik II - SS 208 (Algorithmen & Datenstrukturen) Vorlesung 4 (..208) Graphenalgorithmen III Algorithmen und Komplexität Bäume Gegeben: Zusammenhängender, ungerichteter Graph G = V, E Baum: Zusammenhängender,
Informatik II - SS 208 (Algorithmen & Datenstrukturen) Vorlesung 4 (..208) Graphenalgorithmen III Algorithmen und Komplexität Bäume Gegeben: Zusammenhängender, ungerichteter Graph G = V, E Baum: Zusammenhängender,
Kap. 6.5: Minimale Spannbäume ff
 Kap. 6.: Minimale Spannbäume ff Professor Dr. Karsten Klein Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 20. VO 2. TEIL DAP2 SS 2009 2. Juli 2009 SS08 1 Überblick 6.:
Kap. 6.: Minimale Spannbäume ff Professor Dr. Karsten Klein Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 20. VO 2. TEIL DAP2 SS 2009 2. Juli 2009 SS08 1 Überblick 6.:
Definition Ein gerichteter Graph G = (V, E) ist ein Graph von geordneten Paaren (u, v) mit u V und v V.
 Kapitel 4 Graphenalgorithmen 4.1 Definitionen Definition 4.1.1. Der Graph G = (V, E) ist über die beiden Mengen V und E definiert, wobei V die Menge der Knoten und E die Menge der Kanten in dem Graph ist.
Kapitel 4 Graphenalgorithmen 4.1 Definitionen Definition 4.1.1. Der Graph G = (V, E) ist über die beiden Mengen V und E definiert, wobei V die Menge der Knoten und E die Menge der Kanten in dem Graph ist.
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 20 (23.7.2014) All Pairs Shortest Paths, String Matching (Textsuche) Algorithmen und Komplexität Vorlesungsevaluation Sie sollten alle eine
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 20 (23.7.2014) All Pairs Shortest Paths, String Matching (Textsuche) Algorithmen und Komplexität Vorlesungsevaluation Sie sollten alle eine
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen Lerneinheit : Kürzeste Pfade in Graphen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 016.6.01 Einleitung Diese Lerneinheit beschäftigt
Algorithmen und Datenstrukturen Lerneinheit : Kürzeste Pfade in Graphen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 016.6.01 Einleitung Diese Lerneinheit beschäftigt
3. Minimale Spannbäume. Definition 99 T heißt minimaler Spannbaum (MSB, MST) von G, falls T Spannbaum von G ist und gilt:
 3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e),
3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e),
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 17 (8.7.2014) Minimale Spannbäume II Union Find, Prioritätswarteschlangen Algorithmen und Komplexität Minimaler Spannbaum Gegeben: Zus. hängender,
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 17 (8.7.2014) Minimale Spannbäume II Union Find, Prioritätswarteschlangen Algorithmen und Komplexität Minimaler Spannbaum Gegeben: Zus. hängender,
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 02. Mai 2017 [Letzte Aktualisierung: 10/07/2018,
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 02. Mai 2017 [Letzte Aktualisierung: 10/07/2018,
Graphalgorithmen II. Sebastian Ehrenfels Sebastian Ehrenfels Graphalgorithmen II / 44
 Graphalgorithmen II Sebastian Ehrenfels 4.6.2013 Sebastian Ehrenfels Graphalgorithmen II 4.6.2013 1 / 44 Inhalt 1 Datenstrukturen Union-Find Fibonacci-Heap 2 Kürzeste wege Dijkstra Erweiterungen Bellman-Ford
Graphalgorithmen II Sebastian Ehrenfels 4.6.2013 Sebastian Ehrenfels Graphalgorithmen II 4.6.2013 1 / 44 Inhalt 1 Datenstrukturen Union-Find Fibonacci-Heap 2 Kürzeste wege Dijkstra Erweiterungen Bellman-Ford
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 018/19 1. Vorlesung Minimale Spannbäume Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Motivation ) Kantengewichte w : E R >0 ) w(e ) := e E w(e)
1 Algorithmen und Datenstrukturen Wintersemester 018/19 1. Vorlesung Minimale Spannbäume Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Motivation ) Kantengewichte w : E R >0 ) w(e ) := e E w(e)
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Kürzeste Wege Maike Buchin 4. und 6.7.2017 Einführung Motivation: Bestimmung von kürzesten Wegen ist in vielen Anwendungen, z.b. Routenplanung, ein wichtiges Problem. Allgemeine
Vorlesung Datenstrukturen Kürzeste Wege Maike Buchin 4. und 6.7.2017 Einführung Motivation: Bestimmung von kürzesten Wegen ist in vielen Anwendungen, z.b. Routenplanung, ein wichtiges Problem. Allgemeine
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
Berechnung minimaler Spannbäume. Beispiel
 Minimale Spannbäume Definition Sei G pv, Eq ein ungerichteter Graph und sei w : E Ñ R eine Funktion, die jeder Kante ein Gewicht zuordnet. Ein Teilgraph T pv 1, E 1 q von G heißt Spannbaum von G genau
Minimale Spannbäume Definition Sei G pv, Eq ein ungerichteter Graph und sei w : E Ñ R eine Funktion, die jeder Kante ein Gewicht zuordnet. Ein Teilgraph T pv 1, E 1 q von G heißt Spannbaum von G genau
Programm heute. Algorithmen und Datenstrukturen (für ET/IT) Übersicht: Graphen. Definition: Ungerichteter Graph. Definition: Ungerichteter Graph
 Programm heute Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 07 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München 7 Fortgeschrittene Datenstrukturen Graphen
Programm heute Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 07 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München 7 Fortgeschrittene Datenstrukturen Graphen
Kapitel 4: Netzplantechnik Gliederung der Vorlesung
 Gliederung der Vorlesung 1. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege 4. Netzplantechnik 5. Minimal spannende Bäume 6. Traveling Salesman Problem 7. Flüsse in Netzwerken
Gliederung der Vorlesung 1. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege 4. Netzplantechnik 5. Minimal spannende Bäume 6. Traveling Salesman Problem 7. Flüsse in Netzwerken
4. Welchen Zusammenhang gibt es zwischen den Eckengraden und der Anzahl der Kanten eines ungerichteten Graphen?
 Kapitel 7 Graphentheorie Verständnisfragen Sachfragen 1. Was ist ein ungerichteter Graph? 2. Erläutern Sie den Begriff Adjazenz! 3. Erläutern Sie den Eckengrad in einem Graphen! 4. Welchen Zusammenhang
Kapitel 7 Graphentheorie Verständnisfragen Sachfragen 1. Was ist ein ungerichteter Graph? 2. Erläutern Sie den Begriff Adjazenz! 3. Erläutern Sie den Eckengrad in einem Graphen! 4. Welchen Zusammenhang
Bemerkung: Es gibt Algorithmen für minimale Spannbäume der Komplexität O(m + n log n) und, für dünnbesetzte Graphen, der Komplexität O(m log n), wobei
 Bemerkung: Es gibt Algorithmen für minimale Spannbäume der Komplexität O(m + n log n) und, für dünnbesetzte Graphen, der Komplexität O(m log n), wobei { log x = min n N n: log (log ( log(x) )) } {{ } n
Bemerkung: Es gibt Algorithmen für minimale Spannbäume der Komplexität O(m + n log n) und, für dünnbesetzte Graphen, der Komplexität O(m log n), wobei { log x = min n N n: log (log ( log(x) )) } {{ } n
1.Aufgabe: Minimal aufspannender Baum
 1.Aufgabe: Minimal aufspannender Baum 11+4+8 Punkte v 1 v 2 1 3 4 9 v 3 v 4 v 5 v 7 7 4 3 5 8 1 4 v 7 v 8 v 9 3 2 7 v 10 Abbildung 1: Der Graph G mit Kantengewichten (a) Bestimme mit Hilfe des Algorithmus
1.Aufgabe: Minimal aufspannender Baum 11+4+8 Punkte v 1 v 2 1 3 4 9 v 3 v 4 v 5 v 7 7 4 3 5 8 1 4 v 7 v 8 v 9 3 2 7 v 10 Abbildung 1: Der Graph G mit Kantengewichten (a) Bestimme mit Hilfe des Algorithmus
9 Minimum Spanning Trees
 Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
3.2 Generischer minimaler Spannbaum-Algorithmus
 3.2 Generischer minimaler Spannbaum-Algorithmus Initialisiere Wald F von Bäumen, jeder Baum ist ein singulärer Knoten (jedes v V bildet einen Baum) while Wald F mehr als einen Baum enthält do wähle einen
3.2 Generischer minimaler Spannbaum-Algorithmus Initialisiere Wald F von Bäumen, jeder Baum ist ein singulärer Knoten (jedes v V bildet einen Baum) while Wald F mehr als einen Baum enthält do wähle einen
Grundlagen der Algorithmen und Datenstrukturen Kapitel 8
 Grundlagen der Algorithmen und Datenstrukturen Kapitel 8 Christian Scheideler + Helmut Seidl SS 2009 12.06.09 Kapitel 8 1 Graphen Graph G=(V,E) besteht aus Knotenmenge V Kantenmenge E ungerichteter Graph
Grundlagen der Algorithmen und Datenstrukturen Kapitel 8 Christian Scheideler + Helmut Seidl SS 2009 12.06.09 Kapitel 8 1 Graphen Graph G=(V,E) besteht aus Knotenmenge V Kantenmenge E ungerichteter Graph
Teil 2: Graphenalgorithmen
 Teil : Graphenalgorithmen Anwendungen Definitionen Datenstrukturen für Graphen Elementare Algorithmen Topologisches Sortieren Kürzeste Wege Problemstellung Ungewichtete Graphen Distanzgraphen Gewichtete
Teil : Graphenalgorithmen Anwendungen Definitionen Datenstrukturen für Graphen Elementare Algorithmen Topologisches Sortieren Kürzeste Wege Problemstellung Ungewichtete Graphen Distanzgraphen Gewichtete
Algorithmen und Datenstrukturen Kapitel 9. und
 Algorithmen und Datenstrukturen Kapitel 9 Minimale Spannbäume und Kürzeste Pfade Frank Heitmann heitmann@informatik.uni-hamburg.de 9. Dezember 01 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/13
Algorithmen und Datenstrukturen Kapitel 9 Minimale Spannbäume und Kürzeste Pfade Frank Heitmann heitmann@informatik.uni-hamburg.de 9. Dezember 01 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/13
Kürzeste Wege. Ein Startknoten, nichtnegative Gewichte
 Kürzeste Wege Gegeben ein Digraph D = (V, A) mit Bogengewichten c(a). Aufgabe: Finde einen Weg W von einem Knoten zu allen anderen oder zu einem bestimmten mit c(w) minimal. Problem: negative Gewichte
Kürzeste Wege Gegeben ein Digraph D = (V, A) mit Bogengewichten c(a). Aufgabe: Finde einen Weg W von einem Knoten zu allen anderen oder zu einem bestimmten mit c(w) minimal. Problem: negative Gewichte
Effiziente Algorithmen
 Effiziente Algorithmen Martin Hofmann und Jan Johannsen Institut für Informatik LMU München Sommersemester 2002 Graphalgorithmen Grundlegendes Repräsentation von Graphen Breiten- und Tiefensuche Minimale
Effiziente Algorithmen Martin Hofmann und Jan Johannsen Institut für Informatik LMU München Sommersemester 2002 Graphalgorithmen Grundlegendes Repräsentation von Graphen Breiten- und Tiefensuche Minimale
Minimal spannende Bäume
 http://www.uni-magdeburg.de/harbich/ Minimal spannende Fakultät für Informatik Otto-von-Guericke-Universität 2 Inhalt Definition Wege Untergraphen Kantengewichtete Graphen Minimal spannende Algorithmen
http://www.uni-magdeburg.de/harbich/ Minimal spannende Fakultät für Informatik Otto-von-Guericke-Universität 2 Inhalt Definition Wege Untergraphen Kantengewichtete Graphen Minimal spannende Algorithmen
12. Der Algorithmus von Dijkstra. Informatik II für Verkehrsingenieure
 . Der Algorithmus von Dijkstra Informatik II für Verkehrsingenieure Problemstellung Gegeben: Graph G =(V, E, len) mit positiver Kantenfunktion len : E! R 0, Knoten s, t V Mögliche Aufgaben Berechne Distanz
. Der Algorithmus von Dijkstra Informatik II für Verkehrsingenieure Problemstellung Gegeben: Graph G =(V, E, len) mit positiver Kantenfunktion len : E! R 0, Knoten s, t V Mögliche Aufgaben Berechne Distanz
Algorithmen und Datenstrukturen Tafelübung 14. Jens Wetzl 8. Februar 2012
 Algorithmen und Datenstrukturen Tafelübung 14 Jens Wetzl 8. Februar 2012 Folien Keine Garantie für Vollständigkeit und/oder Richtigkeit Keine offizielle Informationsquelle LS2-Webseite Abrufbar unter:
Algorithmen und Datenstrukturen Tafelübung 14 Jens Wetzl 8. Februar 2012 Folien Keine Garantie für Vollständigkeit und/oder Richtigkeit Keine offizielle Informationsquelle LS2-Webseite Abrufbar unter:
2. Das single-source-shortest-path-problem
 . Das single-source-shortest-path-problem Zunächst nehmen wir an, dass d 0 ist. Alle kürzesten Pfade von a nach b sind o.b.d.a. einfache Pfade.. Dijkstra s Algorithmus Gegeben: G = (V, A), (A = V V ),
. Das single-source-shortest-path-problem Zunächst nehmen wir an, dass d 0 ist. Alle kürzesten Pfade von a nach b sind o.b.d.a. einfache Pfade.. Dijkstra s Algorithmus Gegeben: G = (V, A), (A = V V ),
Kürzeste-Wege-Algorithmen und Datenstrukturen
 Kürzeste-Wege-Algorithmen und Datenstrukturen Institut für Informatik Universität zu Köln SS 2009 Teil 1 Inhaltsverzeichnis 1 Kürzeste Wege 2 1.1 Voraussetzungen................................ 2 1.2
Kürzeste-Wege-Algorithmen und Datenstrukturen Institut für Informatik Universität zu Köln SS 2009 Teil 1 Inhaltsverzeichnis 1 Kürzeste Wege 2 1.1 Voraussetzungen................................ 2 1.2
3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel
 3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel EADS 3.1 Konstruktion von minimalen Spannbäumen 16/36
3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel EADS 3.1 Konstruktion von minimalen Spannbäumen 16/36
Maximale s t-flüsse in Planaren Graphen
 Maximale s t-flüsse in Planaren Graphen Vorlesung Algorithmen für planare Graphen 6. Juni 2017 Guido Brückner INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg
Maximale s t-flüsse in Planaren Graphen Vorlesung Algorithmen für planare Graphen 6. Juni 2017 Guido Brückner INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg
Kürzeste Wege in Graphen. Orte mit Straßenverbindungen. Coma I Rolf Möhring
 Kürzeste Wege in Graphen Orte mit Straßenverbindungen Orte als Knoten eines Graphen Straßenverbindungen als Kanten eines Graphen Ungerichteter Graph G = (V,E) Kanten Knoten Knotenmenge V = {,,n} oder {,,n
Kürzeste Wege in Graphen Orte mit Straßenverbindungen Orte als Knoten eines Graphen Straßenverbindungen als Kanten eines Graphen Ungerichteter Graph G = (V,E) Kanten Knoten Knotenmenge V = {,,n} oder {,,n
Kapitel 4: Dynamische Datenstrukturen. Algorithmen und Datenstrukturen WS 2012/13. Prof. Dr. Sándor Fekete
 Kapitel 4: Dynamische Datenstrukturen Algorithmen und Datenstrukturen WS 2012/13 Prof. Dr. Sándor Fekete 4.4 Binäre Suche Aufgabenstellung: Rate eine Zahl zwischen 100 und 114! Algorithmus 4.1 INPUT: OUTPUT:
Kapitel 4: Dynamische Datenstrukturen Algorithmen und Datenstrukturen WS 2012/13 Prof. Dr. Sándor Fekete 4.4 Binäre Suche Aufgabenstellung: Rate eine Zahl zwischen 100 und 114! Algorithmus 4.1 INPUT: OUTPUT:
Lernmodul 7 Algorithmus von Dijkstra
 Folie 1 von 30 Lernmodul 7 Algorithmus von Dijkstra Quelle: http://www.map24.de Folie 2 von 30 Algorithmus von Dijkstra Übersicht Kürzester Weg von A nach B in einem Graphen Problemstellung: Suche einer
Folie 1 von 30 Lernmodul 7 Algorithmus von Dijkstra Quelle: http://www.map24.de Folie 2 von 30 Algorithmus von Dijkstra Übersicht Kürzester Weg von A nach B in einem Graphen Problemstellung: Suche einer
Name:... Vorname:... Matr.-Nr.:... Studiengang:...
 Technische Universität Braunschweig Sommersemester 2013 IBR - Abteilung Algorithmik Prof. Dr. Sándor P. Fekete Dr. Christiane Schmidt Stephan Friedrichs Klausur Netzwerkalgorithmen 16.07.2013 Name:.....................................
Technische Universität Braunschweig Sommersemester 2013 IBR - Abteilung Algorithmik Prof. Dr. Sándor P. Fekete Dr. Christiane Schmidt Stephan Friedrichs Klausur Netzwerkalgorithmen 16.07.2013 Name:.....................................
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide
 Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide Dipl-Math. Wolfgang Kinzner 3.4.2012 Kapitel 3: Minimal aufspannende Bäume und Matroide Minimal aufspannende
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide Dipl-Math. Wolfgang Kinzner 3.4.2012 Kapitel 3: Minimal aufspannende Bäume und Matroide Minimal aufspannende
10. Übung Algorithmen I
 INSTITUT FÜR THEORETISCHE INFORMATIK 1 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft Institut für Theoretische www.kit.edu Informatik Bäume
INSTITUT FÜR THEORETISCHE INFORMATIK 1 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft Institut für Theoretische www.kit.edu Informatik Bäume
Kapitel 4: Minimal spannende Bäume Gliederung der Vorlesung
 Kapitel : Minimal spannende Bäume Gliederung der Vorlesung. Fallstudie Bipartite Graphen 2. Grundbegriffe. Elementare Graphalgorithmen und Anwendungen. Minimal spannende Bäume. Kürzeste Wege. Traveling
Kapitel : Minimal spannende Bäume Gliederung der Vorlesung. Fallstudie Bipartite Graphen 2. Grundbegriffe. Elementare Graphalgorithmen und Anwendungen. Minimal spannende Bäume. Kürzeste Wege. Traveling
Aufgaben zur Klausurvorbereitung
 Vorlesung Graphen und Optimierung Sommersemester 2013/14 Prof. S. Lange Aufgaben zur Klausurvorbereitung Hier finden Sie eine Reihe von Übungsaufgaben, die wir an den beiden Vorlesungsterminen am 29.01.2014
Vorlesung Graphen und Optimierung Sommersemester 2013/14 Prof. S. Lange Aufgaben zur Klausurvorbereitung Hier finden Sie eine Reihe von Übungsaufgaben, die wir an den beiden Vorlesungsterminen am 29.01.2014
Definition Gerichteter Pfad. gerichteter Pfad, wenn. Ein gerichteter Pfad heißt einfach, falls alle u i paarweise verschieden sind.
 3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
SS11 Effiziente Algorithmen 5. Kapitel: Dynamische Programmierung
 SS11 Effiziente Algorithmen 5. Kapitel: Dynamische Programmierung Martin Dietzfelbinger Juni/Juli 2011 FG KTuEA, TU Ilmenau Effiziente Algorithmen SS11 Kapitel 5 Kapitel 5: Dynamische Programmierung Typische
SS11 Effiziente Algorithmen 5. Kapitel: Dynamische Programmierung Martin Dietzfelbinger Juni/Juli 2011 FG KTuEA, TU Ilmenau Effiziente Algorithmen SS11 Kapitel 5 Kapitel 5: Dynamische Programmierung Typische
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 2016/17 19. Vorlesung Kürzeste Wege & Dijkstras Algorithmus Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Wozu kürzeste Wege? 2 3-8 Modellierung
1 Algorithmen und Datenstrukturen Wintersemester 2016/17 19. Vorlesung Kürzeste Wege & Dijkstras Algorithmus Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Wozu kürzeste Wege? 2 3-8 Modellierung
Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl. Beispiele für optimale Greedy-Lösungen
 Wiederholung Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl unabhängig von Subproblemen Optimalität der Subprobleme Beispiele für optimale Greedy-Lösungen Scheduling Problem
Wiederholung Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl unabhängig von Subproblemen Optimalität der Subprobleme Beispiele für optimale Greedy-Lösungen Scheduling Problem
Algorithmen I - Tutorium 28 Nr. 11
 Algorithmen I - Tutorium 28 Nr. 11 13.07.2017: Spaß mit Schnitten, Kreisen und minimalen Spannbäumen Marc Leinweber marc.leinweber@student.kit.edu INSTITUT FÜR THEORETISCHE INFORMATIK (ITI), PROF. DR.
Algorithmen I - Tutorium 28 Nr. 11 13.07.2017: Spaß mit Schnitten, Kreisen und minimalen Spannbäumen Marc Leinweber marc.leinweber@student.kit.edu INSTITUT FÜR THEORETISCHE INFORMATIK (ITI), PROF. DR.
Kapitel 4: Minimale spannende Bäume Gliederung der Vorlesung
 Kapitel : Minimale spannende Bäume Gliederung der Vorlesung. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman
Kapitel : Minimale spannende Bäume Gliederung der Vorlesung. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman
Algorithmen und Datenstrukturen (für ET/IT)
 Algorithmen und Datenstrukturen (für ET/IT) Wintersemester / Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Programm heute 7 Fortgeschrittene Datenstrukturen Such-Algorithmen
Algorithmen und Datenstrukturen (für ET/IT) Wintersemester / Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Programm heute 7 Fortgeschrittene Datenstrukturen Such-Algorithmen
Klausurvorbereitung. 1 Zentrale Begriffe. 2 Bipartite Graphen. 2.1 Begriffe. Vorlesung Graphen und Optimierung Sommersemester 2011 Prof. S.
 Vorlesung Graphen und Optimierung Sommersemester 2011 Prof. S. Lange Klausurvorbereitung Hier finden Sie alle Begriffe, Zusammenhänge und Algorithmen, die mit Blick auf die Klausur relevant sind. Um es
Vorlesung Graphen und Optimierung Sommersemester 2011 Prof. S. Lange Klausurvorbereitung Hier finden Sie alle Begriffe, Zusammenhänge und Algorithmen, die mit Blick auf die Klausur relevant sind. Um es
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 5: Suchalgorithmen Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 20. März 2018 1/91 WIEDERHOLUNG - BÄUME / bin etc home
Algorithmische Graphentheorie Vorlesung 5: Suchalgorithmen Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 20. März 2018 1/91 WIEDERHOLUNG - BÄUME / bin etc home
Fortgeschrittene Netzwerk- und Graph-Algorithmen
 Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Datenstrukturen und Algorithmen. Christian Sohler FG Algorithmen & Komplexität
 Datenstrukturen und Algorithmen Christian Sohler FG Algorithmen & Komplexität 1 Klausur Wichtige Hinweise: 2.7.07, Beginn 9 Uhr Bitte spätestens 8:4 Uhr vor Ort sein Sporthalle + Audimax Informationen
Datenstrukturen und Algorithmen Christian Sohler FG Algorithmen & Komplexität 1 Klausur Wichtige Hinweise: 2.7.07, Beginn 9 Uhr Bitte spätestens 8:4 Uhr vor Ort sein Sporthalle + Audimax Informationen
Informatik II, SS 2018
 Informatik II - SS 2018 (Algorithmen & Datenstrukturen) Vorlesung 15b (13.06.2018) Graphenalgorithmen IV Algorithmen und Komplexität Prims MST-Algorithmus A = while A ist kein Spannbaum do e = u, v ist
Informatik II - SS 2018 (Algorithmen & Datenstrukturen) Vorlesung 15b (13.06.2018) Graphenalgorithmen IV Algorithmen und Komplexität Prims MST-Algorithmus A = while A ist kein Spannbaum do e = u, v ist
Zweizusammenhang und starker Zusammenhang
 .. Zeizusammenhang und starker Zusammenhang Carsten Gutenger Vorlesung Algorithmen und Datenstrukturen WS /. Januar Zeizusammenhang Betrachte ein Netzerk (Graph) Z.B. Computernetzerk, Flug- oder Schienennetzerk
.. Zeizusammenhang und starker Zusammenhang Carsten Gutenger Vorlesung Algorithmen und Datenstrukturen WS /. Januar Zeizusammenhang Betrachte ein Netzerk (Graph) Z.B. Computernetzerk, Flug- oder Schienennetzerk
2. Optimierungsprobleme 6
 6 2. Beispiele... 7... 8 2.3 Konvexe Mengen und Funktionen... 9 2.4 Konvexe Optimierungsprobleme... 0 2. Beispiele 7- Ein (NP-)Optimierungsproblem P 0 ist wie folgt definiert Jede Instanz I P 0 hat einen
6 2. Beispiele... 7... 8 2.3 Konvexe Mengen und Funktionen... 9 2.4 Konvexe Optimierungsprobleme... 0 2. Beispiele 7- Ein (NP-)Optimierungsproblem P 0 ist wie folgt definiert Jede Instanz I P 0 hat einen
15. Elementare Graphalgorithmen
 Graphen sind eine der wichtigste Modellierungskonzepte der Informatik Graphalgorithmen bilden die Grundlage vieler Algorithmen in der Praxis Zunächst kurze Wiederholung von Graphen. Dann Darstellungen
Graphen sind eine der wichtigste Modellierungskonzepte der Informatik Graphalgorithmen bilden die Grundlage vieler Algorithmen in der Praxis Zunächst kurze Wiederholung von Graphen. Dann Darstellungen
Algorithmen und Datenstrukturen 2-1. Seminar -
 Algorithmen und Datenstrukturen 2-1. Seminar - Dominic Rose Bioinformatics Group, University of Leipzig Sommersemster 2010 Outline 1. Übungsserie: 3 Aufgaben, insgesamt 30 28 Punkte A1 Spannbäume (10 8
Algorithmen und Datenstrukturen 2-1. Seminar - Dominic Rose Bioinformatics Group, University of Leipzig Sommersemster 2010 Outline 1. Übungsserie: 3 Aufgaben, insgesamt 30 28 Punkte A1 Spannbäume (10 8
Kapitel 8 Graphenalgorithmen. Minimaler Spannbaum Union-find-Problem Kürzeste Wege
 Kapitel 8 Graphenalgorithmen Minimaler Spannbaum Union-find-Problem Kürzeste Wege Rückblick Graphen Modelle für Objekte und Beziehungen untereinander Personen - Bekanntschaften Ereignisse - Abhängigkeiten
Kapitel 8 Graphenalgorithmen Minimaler Spannbaum Union-find-Problem Kürzeste Wege Rückblick Graphen Modelle für Objekte und Beziehungen untereinander Personen - Bekanntschaften Ereignisse - Abhängigkeiten
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2006 5. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Wdhlg.: Dijkstra-Algorithmus I Bestimmung der
Algorithmen und Datenstrukturen 2 Sommersemester 2006 5. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Wdhlg.: Dijkstra-Algorithmus I Bestimmung der
Kap. 6.5: Minimale Spannbäume
 Kap. 6.5: Minimale Spannbäume Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 19./20. VO DAP2 SS 2009 30.6./2.7.2009 1 Anmeldung zur Klausur 31.07.2009 um 10:15
Kap. 6.5: Minimale Spannbäume Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 19./20. VO DAP2 SS 2009 30.6./2.7.2009 1 Anmeldung zur Klausur 31.07.2009 um 10:15
Kürzeste (billigste) Wege
 Kürzeste (billigste) Wege 1. Kürzeste (billigste) Wege Gerichteter Graph G = (V, E) Kostenfunktion c : E R 1 2 1 3 3 2 4 4 2 6 6 5 3 2 Entfernung zwischen zwei Knoten Kosten eines Wegs P = v 0, v 1,...,
Kürzeste (billigste) Wege 1. Kürzeste (billigste) Wege Gerichteter Graph G = (V, E) Kostenfunktion c : E R 1 2 1 3 3 2 4 4 2 6 6 5 3 2 Entfernung zwischen zwei Knoten Kosten eines Wegs P = v 0, v 1,...,
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 3 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
ADS: Algorithmen und Datenstrukturen 2 Teil 3 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
Erinnerung VL
 Erinnerung VL 7.06.016 Bellman-Ford-Algorithmus (Brute-Force-Suche) Varianten des Kürzeste-Wege-Problems (azyklische Graphen) Ausblick: Routenplanung in Straÿennetzwerken Motivation Minimale Spannbäume
Erinnerung VL 7.06.016 Bellman-Ford-Algorithmus (Brute-Force-Suche) Varianten des Kürzeste-Wege-Problems (azyklische Graphen) Ausblick: Routenplanung in Straÿennetzwerken Motivation Minimale Spannbäume
1 Kürzeste Pfade in Graphen
 Praktikum Algorithmen-Entwurf (Teil 3) 03.11.2011 1 1 Kürzeste Pfade in Graphen Es sei ein gerichteter Graph G = (V, E) mit V = n Knoten, E = m Kanten und Kantengewichten c : E R gegeben. Ein Pfad in G
Praktikum Algorithmen-Entwurf (Teil 3) 03.11.2011 1 1 Kürzeste Pfade in Graphen Es sei ein gerichteter Graph G = (V, E) mit V = n Knoten, E = m Kanten und Kantengewichten c : E R gegeben. Ein Pfad in G
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
5. Bäume und Minimalgerüste
 5. Bäume und Minimalgerüste Charakterisierung von Minimalgerüsten 5. Bäume und Minimalgerüste Definition 5.1. Es ein G = (V, E) ein zusammenhängender Graph. H = (V,E ) heißt Gerüst von G gdw. wenn H ein
5. Bäume und Minimalgerüste Charakterisierung von Minimalgerüsten 5. Bäume und Minimalgerüste Definition 5.1. Es ein G = (V, E) ein zusammenhängender Graph. H = (V,E ) heißt Gerüst von G gdw. wenn H ein
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Prof. Martin Lercher Institut für Informatik Heinrich-Heine-Universität Düsseldorf Teil 9 Graphen Version vom 13. Dezember 2016 1 / 1 Vorlesung Fortsetzung 13. Dezember
Algorithmen und Datenstrukturen Prof. Martin Lercher Institut für Informatik Heinrich-Heine-Universität Düsseldorf Teil 9 Graphen Version vom 13. Dezember 2016 1 / 1 Vorlesung Fortsetzung 13. Dezember
Diskrete Strukturen WS 2005/06. Ernst W. Mayr. 27. Januar Fakultät für Informatik TU München
 WS 2005/06 Ernst W. Mayr Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2005ws/ds/ 27. Januar 2006 Ernst W. Mayr 2.16 Inzidenzmatrix 3. Definitionen für gerichtete Graphen 3.1 Digraph
WS 2005/06 Ernst W. Mayr Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2005ws/ds/ 27. Januar 2006 Ernst W. Mayr 2.16 Inzidenzmatrix 3. Definitionen für gerichtete Graphen 3.1 Digraph
24. Minimale Spannbäume
 Problem Gegeben: Ungerichteter, zusammenhängender, gewichteter Graph G = (V, E, c). 4. Minimale Spannbäume Gesucht: Minimaler Spannbaum T = (V, E ), E E, so dass e E c(e) minimal. Motivation, Greedy, Algorithmus
Problem Gegeben: Ungerichteter, zusammenhängender, gewichteter Graph G = (V, E, c). 4. Minimale Spannbäume Gesucht: Minimaler Spannbaum T = (V, E ), E E, so dass e E c(e) minimal. Motivation, Greedy, Algorithmus
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 2016/17 19. Vorlesung Kürzeste Wege & Dijkstras Algorithmus Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Ergebnisse des 1. Kurztests 14 12 10
1 Algorithmen und Datenstrukturen Wintersemester 2016/17 19. Vorlesung Kürzeste Wege & Dijkstras Algorithmus Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Ergebnisse des 1. Kurztests 14 12 10
Richtig oder falsch? Richtig oder falsch? Richtig oder falsch? Mit dynamischer Programmierung ist das Knapsack- Problem in Polynomialzeit lösbar.
 Gegeben sei ein Netzwerk N = (V, A, c, s, t) wie in der Vorlesung. Ein maximaler s-t-fluss kann immer mit Hilfe einer Folge von höchstens A Augmentationsschritten gefunden werden. Wendet man den Dijkstra-Algorithmus
Gegeben sei ein Netzwerk N = (V, A, c, s, t) wie in der Vorlesung. Ein maximaler s-t-fluss kann immer mit Hilfe einer Folge von höchstens A Augmentationsschritten gefunden werden. Wendet man den Dijkstra-Algorithmus
Algorithmen und Datenstrukturen 13
 19. Juli 2012 1 Besprechung Blatt 12 Fragen 2 Bäume AVL-Bäume 3 Graphen Allgemein Matrixdarstellung 4 Graphalgorithmen Dijkstra Prim Kruskal Fragen Fragen zu Blatt 12? AVL-Bäume AVL-Bäume ein AVL-Baum
19. Juli 2012 1 Besprechung Blatt 12 Fragen 2 Bäume AVL-Bäume 3 Graphen Allgemein Matrixdarstellung 4 Graphalgorithmen Dijkstra Prim Kruskal Fragen Fragen zu Blatt 12? AVL-Bäume AVL-Bäume ein AVL-Baum
25. Minimale Spannbäume
 695 25. Minimale Spannbäume Motivation, Greedy, Algorithmus von Kruskal, Allgemeine Regeln, Union-Find Struktur, Algorithmus von Jarnik, Prim, Dijkstra, Fibonacci Heaps [Ottman/Widmayer, Kap. 9.6, 6.2,
695 25. Minimale Spannbäume Motivation, Greedy, Algorithmus von Kruskal, Allgemeine Regeln, Union-Find Struktur, Algorithmus von Jarnik, Prim, Dijkstra, Fibonacci Heaps [Ottman/Widmayer, Kap. 9.6, 6.2,
Institut für Mathematik Geometrie und Lineare Algebra J. Schönenberger-Deuel. Aufgabe 1. Wir geben nur zwei von sehr vielen möglichen Strategien.
 Lösungen Übung 13 Aufgabe 1. Wir geben nur zwei von sehr vielen möglichen Strategien. a) Strategie 1 (nächster Nachbar): Jedes Mal reist der Reisende vom Punkt, wo er gerade ist, zur nächstgelegenen Stadt,
Lösungen Übung 13 Aufgabe 1. Wir geben nur zwei von sehr vielen möglichen Strategien. a) Strategie 1 (nächster Nachbar): Jedes Mal reist der Reisende vom Punkt, wo er gerade ist, zur nächstgelegenen Stadt,
Algorithmen & Komplexität
 Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Kapitel 4: Datenstrukturen Kapitel 4.2: Union-Find-Strukturen Union-Find-Strukturen Gegeben: Datensätze
Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Kapitel 4: Datenstrukturen Kapitel 4.2: Union-Find-Strukturen Union-Find-Strukturen Gegeben: Datensätze
Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo?
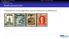 Briefmarkensammeln (Folie 413, Seite 80 im Skript) Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo? Welche Briefmarken für einen 20 fen Brief? Der Greedy-Algorithmus führt nicht
Briefmarkensammeln (Folie 413, Seite 80 im Skript) Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo? Welche Briefmarken für einen 20 fen Brief? Der Greedy-Algorithmus führt nicht

 Laufzeitanalyse (1) demogr. int i=1; for (int j = 1; j
Laufzeitanalyse (1) demogr. int i=1; for (int j = 1; j