Rechnerpraktikum zur Nichtlinearen Optimierung
|
|
|
- August Bauer
- vor 5 Jahren
- Abrufe
Transkript
1 Rechnerpraktikum zur Nichtlinearen Optimierung 9. März März 2016 Sebastian Garreis, B. Sc. Philipp Jarde, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische Optimierung (M1) Garching, 10. März 2016
2 Kursplan Mittwoch, 9. März 2016: Optimierungsverfahren in der unrestringierten Optimierung Vergleich von Konvergenzverhalten einzelner Verfahren Matlab Donnerstag, 10. März 2016: Optimierungsverfahren in der restringierten Optimierung Vorstellen von externer Lösungs-Software Modellieren und Lösen mit AMPL NEOS Freitag, 11. März 2016: Innere-Punkte-Verfahren Installation und Kompilieren größerer Optimierungspakete AMPL und Ipopt
3 P1 - C 60 -Molekül min f (x), f (x) = 1 x R F (x) 2 2. (1) x k+1 = x k + σ k s k, f (x k + σ k s k ) f (x k ) σ k γ f (x k ) T s k.
4 P1 - C 60 -Molekül min f (x), f (x) = 1 x R F (x) 2 2. (1) x k+1 = x k + σ k s k, f (x k + σ k s k ) f (x k ) σ k γ f (x k ) T s k. Gradientenverfahren: s k = f (x k ) = F (x k ) T F (x k ),
5 P1 - C 60 -Molekül min f (x), f (x) = 1 x R F (x) 2 2. (1) x k+1 = x k + σ k s k, f (x k + σ k s k ) f (x k ) σ k γ f (x k ) T s k. Gradientenverfahren: s k = f (x k ) = F (x k ) T F (x k ), Gauß-Newton-Verfahren: F (x k ) T F (x k )s k = F (x k ) T F (x k ) (= f (x k )),
6 P1 - C 60 -Molekül min f (x), f (x) = 1 x R F (x) 2 2. (1) x k+1 = x k + σ k s k, f (x k + σ k s k ) f (x k ) σ k γ f (x k ) T s k. Gradientenverfahren: Gauß-Newton-Verfahren: i s k = f (x k ) = F (x k ) T F (x k ), F (x k ) T F (x k )s k = F (x k ) T F (x k ) (= f (x k )), Newton-Verfahren: [ ] F i (x k )F i (x k ) + F (x k ) T F (x k ) s k = F (x k ) T F (x k ).
7 P2 - Gradienten-, Newton-, inverses BFGS-Verfahren Newton-Verfahren löst unrestringierte Optimierungsprobleme mit quadratischer Zielfunktion in einer Iteration. Keine lokal-quadratische Konvergenz des Newton-Verfahrens ist ein häufiges Indiz für eine Verletzung der hinreichenden Optimalitätsbedingung zweiter Ordnung. Konvergenz-Geschwindigkeit des Gradienten-Verfahren hängt bei quadratischen Funktionen von der Kondition der Matrix ab. Vorteile inverses BFGS-Verfahren : Matrix-Vektor-Multiplikation statt lineares Gleichungssystem, keine 2. Ableitungen notwendig, häufig lokal ähnliches Konvergenzverhalten wie Newton-Verfahren beobachtbar (superlineare Konvergenz).
8 P3 - Problem der Brachistochrone Vergleich von Speicherbedarf und Rechenaufwand: Speicher Flops Gradienten-Verfahren O(n) O(n) Vektor-Vektor-Operationen Newton-Verfahren (dense) O(n 2 ) O(n 3 ) Lösung LGS mit voller Matrix Newton-Verfahren (sparse) O(n) O(n) Lösung LGS mit tridiagonal-matrix
9 P3 - Problem der Brachistochrone Vergleich von Speicherbedarf und Rechenaufwand: Speicher Flops Gradienten-Verfahren O(n) O(n) Vektor-Vektor-Operationen Newton-Verfahren (dense) O(n 2 ) O(n 3 ) Lösung LGS mit voller Matrix Newton-Verfahren (sparse) O(n) O(n) Lösung LGS mit tridiagonal-matrix Bei vielen Problemen lässt sich die Struktur der Hesse-Matrix ausnutzen, um sowohl Speicherbedarf als auch den Rechenaufwand zur Lösung des linearen Gleichungssystems zu reduzieren.
10 Das restringierte Optimierungsproblem min f (x) u. d. N. g(x) 0, h(x) = 0 (2) x Rn mit f : R n R, g : R n R m, h : R n R p glatt genug. KKT-Bedingungen (notwendig, falls eine CQ erfüllt ist): Es gibt λ R m und µ R p mit f ( x) + g( x) λ + h( x) µ = 0 h( x) = 0 λ 0, g( x) 0, λ T g( x) = 0 Die erste Bedingung kann mit Hilfe der Lagrangefunktion L(x, λ, µ) = f (x) + λ T g(x) + µ T h(x) (3) auch als x L( x, λ, µ) = 0 geschrieben werden.
11 Implementierungsaspekte Wie sind die Funktionen gegeben? Explizit oder implizit Ungenauigkeiten Programmiersprachen? Ableitungen? Startpunktwahl Schätzung der Lösung Schätzung der Startmatrizen M k, B k, H k Heuristik
12 Implementierungsaspekte Lösen von Teilproblemen Lineare Gleichungssysteme QPs bei SQP-Verfahren LPs Geschickte Parameterwahl Große Optimierungsprobleme Darstellung von/operationen mit Vektoren und Matrizen Effiziente Operationen und Lösung der Teilprobleme notwendig
13 Optimierungssoftware Je nach Problemstellung (linear, quadratisch, konvex, allgemein, nichtglatt, gemischt-ganzzahlig, unrestringiert, restringiert, Verfügbarkeit der Ableitungen etc.) gibt es andere Löser. Die Eingabe des eigentlichen Problems (der Daten eines Problems) ist unterschiedlich. Überblick über einige Software findet man zum Beispiel hier:
14 AMPL AMPL: Modellierungssoftware Keine eigenen Löser Schnittstellen zu vielen Lösern, Grundlegende Syntax: Jede Anweisung beginnt mit einem Schlüsselwort und endet mit ; Groß- und Kleinschreibung ist wichtig Grundlegende Struktur: model bsp.mod; data bsp.dat; solve; oder commands bsp.com; Anzeige von Lösung x mit display x;
15 AMPL Einfaches Beispiel Problem: max 3x 1 + x 2 u. d. N. x 1 + x 2 4, 2x 1 + 3x 2 6, x 1, x 2 0 x R 2 Zugehörige Modelldatei: var x1; var x2; maximize ziel: 3*x1+x2; subject to nb1: x1+x2 <= 4; subject to nb2: -2*x1+3*x2 <= 6; subject to nb3: x1 >= 0; subject to nb4: x2 >= 0;
16 AMPL Einfaches Beispiel Aufruf des Lösers: option solver minos; solve; MINOS 5.5: optimal solution found. 1 iterations, objective 12 display x1,x2,ziel; x1 = 4 x2 = 0 ziel = 12 Stattdessen kann auch eine Command-Datei aufgerufen werden.
17 AMPL Weitere Features: Mengendefinitionen Parameter (für Data-Datei) Indexmengen-Schreibweise Excel-Schnittstelle viele weitere problemabhängigen Schlüsselwörter nutzbar
18 AMPL Ein etwas komplizierteres Beispiel: set M; # Menge von Bedarfsorten set N; # Menge von Produktionsorten param a i in N >= 0; # Angebotsmengen param b j in M >= 0; # Bedarfsmengen param c i in N, j in M; # Kosten param s i in N, j in M; # Schranken var x i in N, j in M >= 0, <= s[i,j]; minimize kosten: sum i in N, j in M x[i,j]*c[i,j]; #sum j in M, i in N... oder sum i in N sum j in M subject to bedarf j in M: sum i in N x[i,j] = b[j]; subject to angebot i in N: sum j in M x[i,j] = a[i];
19 Los geht s!
Einführung in Softwaretools zur Nichtlinearen Optimierung
 Einführung in Softwaretools zur Nichtlinearen Optimierung 3. April 2017 5. April 2017 Sebastian Garreis, M. Sc. (hons) Johannes Haubner, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl
Einführung in Softwaretools zur Nichtlinearen Optimierung 3. April 2017 5. April 2017 Sebastian Garreis, M. Sc. (hons) Johannes Haubner, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl
Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung
 Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung 18.3.14-20.3.14 Dr. Florian Lindemann Moritz Keuthen, M.Sc. Technische Universität München Garching, 19.3.2014 Kursplan Dienstag, 18.3.2014
Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung 18.3.14-20.3.14 Dr. Florian Lindemann Moritz Keuthen, M.Sc. Technische Universität München Garching, 19.3.2014 Kursplan Dienstag, 18.3.2014
Rechnerpraktikum zur Nichtlinearen Optimierung
 Rechnerpraktikum zur Nichtlinearen Optimierung 9. März 2016 11. März 2016 Sebastian Garreis, B. Sc. Philipp Jarde, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische
Rechnerpraktikum zur Nichtlinearen Optimierung 9. März 2016 11. März 2016 Sebastian Garreis, B. Sc. Philipp Jarde, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische
Kontinuierliche Optimierung
 Kontinuierliche Optimierung Markus Herrich Wintersemester 2018/19 ii Inhaltsverzeichnis 2 Optimalitäts- und Regularitätsbedingungen 1 2.1 Einleitung und Wiederholung.................... 1 2.2 Optimalitätsbedingungen
Kontinuierliche Optimierung Markus Herrich Wintersemester 2018/19 ii Inhaltsverzeichnis 2 Optimalitäts- und Regularitätsbedingungen 1 2.1 Einleitung und Wiederholung.................... 1 2.2 Optimalitätsbedingungen
Seminarvortrag: Trust-Region-Verfahren
 Seminarvortrag: Trust-Region-Verfahren Helena Klump Universität Paderborn Dezember 2012 Helena Klump 1 / 22 Trust-Region-Verfahren Problemstellung Sei die Funktion f : R n R gegeben. Betrachtet wird das
Seminarvortrag: Trust-Region-Verfahren Helena Klump Universität Paderborn Dezember 2012 Helena Klump 1 / 22 Trust-Region-Verfahren Problemstellung Sei die Funktion f : R n R gegeben. Betrachtet wird das
Modellieren mit AMPL
 Modellieren mit AMPL Elisabeth Gassner Mathematische Modelle in den Wirtschaftswissenschaften Prof. R. E. Burkard 27. April 2007 E. Gassner (Mathematische Modelle) AMPL 27. April 2007 1 / 21 Überblick
Modellieren mit AMPL Elisabeth Gassner Mathematische Modelle in den Wirtschaftswissenschaften Prof. R. E. Burkard 27. April 2007 E. Gassner (Mathematische Modelle) AMPL 27. April 2007 1 / 21 Überblick
Rechnerpraktikum zur Optimierung III
 TU München Lehrstuhl Mathematische Optimierung Prof. Dr. M. Ulbrich Dipl.-Math. Florian Lindemann Sommersemester 007 Teil II Rechnerpraktikum zur Optimierung III Für die Bearbeitung des Aufgabenzettels
TU München Lehrstuhl Mathematische Optimierung Prof. Dr. M. Ulbrich Dipl.-Math. Florian Lindemann Sommersemester 007 Teil II Rechnerpraktikum zur Optimierung III Für die Bearbeitung des Aufgabenzettels
Konvexe Optimierung I Sommersemester Kapitel 0
 Sommersemester 2013 Kapitel 0 Jun.-Prof. Dr. Thorsten Raasch Johannes Gutenberg-Universität Mainz Institut für Mathematik 15. April 2013 Konvexe Optimierung Was ist das? Was bedeutet Optimierung? Was bedeutet
Sommersemester 2013 Kapitel 0 Jun.-Prof. Dr. Thorsten Raasch Johannes Gutenberg-Universität Mainz Institut für Mathematik 15. April 2013 Konvexe Optimierung Was ist das? Was bedeutet Optimierung? Was bedeutet
Eine kurze Beschreibung zu AMPL und CPLEX
 Welchen Kuchen backt Bernd Brezel? Lineare Optimierung Eine kurze Beschreibung zu AMPL und CPLEX Prof. Dr. Andrea Walther Institut für Mathematik Universität Paderborn 1 1 Das allgemeines Vorgehen Zur
Welchen Kuchen backt Bernd Brezel? Lineare Optimierung Eine kurze Beschreibung zu AMPL und CPLEX Prof. Dr. Andrea Walther Institut für Mathematik Universität Paderborn 1 1 Das allgemeines Vorgehen Zur
Newton- und und Quasi-Newton-Methoden in der Optimierung. János Mayer
 Newton- und und Quasi-Newton-Methoden in der Optimierung János Mayer 1 GLIEDERUNG Newton-Methode für nichtlineare Gleichungen nichtlineare Gleichungssysteme freie Minimierung. Quasi-Newton-Methoden für
Newton- und und Quasi-Newton-Methoden in der Optimierung János Mayer 1 GLIEDERUNG Newton-Methode für nichtlineare Gleichungen nichtlineare Gleichungssysteme freie Minimierung. Quasi-Newton-Methoden für
Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung
 TU München Lehrstuhl Mathematische Optimierung Prof. Dr. Michael Ulbrich Dipl.-Math. Florian Lindemann Wintersemester 008/09 Blatt 1 Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung Für die
TU München Lehrstuhl Mathematische Optimierung Prof. Dr. Michael Ulbrich Dipl.-Math. Florian Lindemann Wintersemester 008/09 Blatt 1 Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung Für die
TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik. Grundlagen der Nichtlinearen Optimierung. Klausur zur Vorlesung WS 2008/09
 ................ Note I II Name Vorname 1 Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 Obige Angaben sind richtig: Unterschrift der Kandidatin/des Kandidaten 3 TECHNISCHE UNIVERSITÄT
................ Note I II Name Vorname 1 Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 Obige Angaben sind richtig: Unterschrift der Kandidatin/des Kandidaten 3 TECHNISCHE UNIVERSITÄT
Die CUTEr Testbibliothek
 Die CUTEr Testbibliothek Slide 1 Motivation Softwarepakete mit vollkommen verschiedenen Anwendungsschwerpunkten Optimierung entweder nur einer von vielen Schwerpunkten oder sogar nur Nebenprodukt zur Lösung
Die CUTEr Testbibliothek Slide 1 Motivation Softwarepakete mit vollkommen verschiedenen Anwendungsschwerpunkten Optimierung entweder nur einer von vielen Schwerpunkten oder sogar nur Nebenprodukt zur Lösung
Optimierung. Optimierung. Vorlesung 4 Newton und Quasi Newton Verfahren (Teil II) 2013 Thomas Brox, Fabian Kuhn
 Optimierung Vorlesung 4 Newton und Quasi Newton Verfahren (Teil II) 1 Newton Verfahren Taylor Approximation 1. Ordnung von Newton Verfahren! 0 Setze 0und berechne Löse lineares Gleichungssystem für : 2
Optimierung Vorlesung 4 Newton und Quasi Newton Verfahren (Teil II) 1 Newton Verfahren Taylor Approximation 1. Ordnung von Newton Verfahren! 0 Setze 0und berechne Löse lineares Gleichungssystem für : 2
Inhaltsverzeichnis. Innere-Punkte-Verfahren 3. Inhaltsverzeichnis 1
 Inhaltsverzeichnis 1 Inhaltsverzeichnis Innere-Punkte-Verfahren 3 1 Theoretische Grundlagen 3 1.1 Die KKT-Bedingungen........................... 3 1.2 Der zentrale Pfad.............................. 4
Inhaltsverzeichnis 1 Inhaltsverzeichnis Innere-Punkte-Verfahren 3 1 Theoretische Grundlagen 3 1.1 Die KKT-Bedingungen........................... 3 1.2 Der zentrale Pfad.............................. 4
Kapitel 12. Lagrange-Funktion. Josef Leydold Mathematik für VW WS 2017/18 12 Lagrange-Funktion 1 / 28. f (x, y) g(x, y) = c. f (x, y) = x y 2
 Kapitel 12 Lagrange-Funktion Josef Leydold Mathematik für VW WS 2017/18 12 Lagrange-Funktion 1 / 28 Optimierung unter Nebenbedingungen Aufgabe: Berechne die Extrema der Funktion unter der Nebenbedingung
Kapitel 12 Lagrange-Funktion Josef Leydold Mathematik für VW WS 2017/18 12 Lagrange-Funktion 1 / 28 Optimierung unter Nebenbedingungen Aufgabe: Berechne die Extrema der Funktion unter der Nebenbedingung
Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben. Eine kurze Einführung in Quasi Newton Verfahren
 Ergänzungen zu dem Buch Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben von Carl Geiger und Christian Kanzow (Springer Verlag, 1999) Eine kurze Einführung in Quasi Newton Verfahren
Ergänzungen zu dem Buch Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben von Carl Geiger und Christian Kanzow (Springer Verlag, 1999) Eine kurze Einführung in Quasi Newton Verfahren
Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung
 TU München Lehrstuhl Mathematische Optimierung Prof. Dr. Michael Ulbrich Dipl.-Math. Florian Lindemann Wintersemester 2008/09 Blatt 3 Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung P9. Installation
TU München Lehrstuhl Mathematische Optimierung Prof. Dr. Michael Ulbrich Dipl.-Math. Florian Lindemann Wintersemester 2008/09 Blatt 3 Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung P9. Installation
Optimierung für Nichtmathematiker
 Optimierung für Nichtmathematiker Prof. Dr. R. Herzog WS2/ / Inhaltsübersicht 3Einführung in die freie Optimierung 4Orakel und Modellfunktionen 5Optimalitätsbedingungen der freien Optimierung 6Das Newton-Verfahren
Optimierung für Nichtmathematiker Prof. Dr. R. Herzog WS2/ / Inhaltsübersicht 3Einführung in die freie Optimierung 4Orakel und Modellfunktionen 5Optimalitätsbedingungen der freien Optimierung 6Das Newton-Verfahren
Optimierung. Optimierung. Vorlesung 2 Optimierung ohne Nebenbedingungen Gradientenverfahren. 2013 Thomas Brox, Fabian Kuhn
 Optimierung Vorlesung 2 Optimierung ohne Nebenbedingungen Gradientenverfahren 1 Minimierung ohne Nebenbedingung Ein Optimierungsproblem besteht aus einer zulässigen Menge und einer Zielfunktion Minimum
Optimierung Vorlesung 2 Optimierung ohne Nebenbedingungen Gradientenverfahren 1 Minimierung ohne Nebenbedingung Ein Optimierungsproblem besteht aus einer zulässigen Menge und einer Zielfunktion Minimum
Operations Research. Konvexe Funktionen. konvexe Funktionen. konvexe Funktionen. Rainer Schrader. 4. Juni Gliederung
 Operations Research Rainer Schrader Konvexe Funktionen Zentrum für Angewandte Informatik Köln 4. Juni 2007 1 / 84 2 / 84 wir haben uns bereits mit linearen Optimierungsproblemen beschäftigt wir werden
Operations Research Rainer Schrader Konvexe Funktionen Zentrum für Angewandte Informatik Köln 4. Juni 2007 1 / 84 2 / 84 wir haben uns bereits mit linearen Optimierungsproblemen beschäftigt wir werden
Operations Research für Logistik
 Operations Research für Logistik Lineare Optimierung (170.202) Ao. Univ. - Prof. Norbert SEIFTER Dipl. - Ing. Stefanie VOLLAND Sommersemester 2012 Lehrstuhl Industrielogistik Lineare Optimierung Inhalte:
Operations Research für Logistik Lineare Optimierung (170.202) Ao. Univ. - Prof. Norbert SEIFTER Dipl. - Ing. Stefanie VOLLAND Sommersemester 2012 Lehrstuhl Industrielogistik Lineare Optimierung Inhalte:
Optimierung für Nichtmathematiker
 Technische Universität Chemnitz Chemnitz, 19.10.2009 Prof. Dr. C. Helmberg, A. Lau Optimierung für Nichtmathematiker Übung 2 Einführung in die Modellierungssprache AMPL 1. Wir betrachten zunächst das Mozartproblem
Technische Universität Chemnitz Chemnitz, 19.10.2009 Prof. Dr. C. Helmberg, A. Lau Optimierung für Nichtmathematiker Übung 2 Einführung in die Modellierungssprache AMPL 1. Wir betrachten zunächst das Mozartproblem
Veranstaltung und Übung: Optimierungssysteme Modelle, Software, Praxisanwendungen. Uwe Suhl Veronika Waue SS 2008
 Veranstaltung 10033025 und 101053 Übung: Optimierungssysteme Modelle, Software, Praxisanwendungen Uwe Suhl Veronika Waue SS 2008 Organisatorisches Veronika Waue Sprechstunde Mi.11h-12h (R214) E-mail: veronika@waue.net
Veranstaltung 10033025 und 101053 Übung: Optimierungssysteme Modelle, Software, Praxisanwendungen Uwe Suhl Veronika Waue SS 2008 Organisatorisches Veronika Waue Sprechstunde Mi.11h-12h (R214) E-mail: veronika@waue.net
KAPITEL 3. Konvexe Funktionen
 KAPITEL 3 Konvexe Funktionen Sei F R n ein Definitionsbereich und f : F R eine Funktion. Unter dem Epigraphen von f versteht man die Menge epif = {(x, z) R n+1 x F, z R, z f(x)}. Man nennt f konvex, wenn
KAPITEL 3 Konvexe Funktionen Sei F R n ein Definitionsbereich und f : F R eine Funktion. Unter dem Epigraphen von f versteht man die Menge epif = {(x, z) R n+1 x F, z R, z f(x)}. Man nennt f konvex, wenn
Optimierung für Nichtmathematiker
 Optimierung für Nichtmathematiker Prof. Dr. R. Herzog WS2010/11 1 / 1 Inhaltsübersicht 3Einführung in die freie Optimierung 4Orakel und Modellfunktionen 5Optimalitätsbedingungen der freien Optimierung
Optimierung für Nichtmathematiker Prof. Dr. R. Herzog WS2010/11 1 / 1 Inhaltsübersicht 3Einführung in die freie Optimierung 4Orakel und Modellfunktionen 5Optimalitätsbedingungen der freien Optimierung
Optimierung mit Matlab
 Lehrstuhl Mathematik, insbesondere Numerische und Angewandte Mathematik Prof. Dr. L. Cromme Optimierung mit Matlab 1 Optimierungsaufgaben Die allgemeine Aufgabenstellung der Optimierung besteht darin,
Lehrstuhl Mathematik, insbesondere Numerische und Angewandte Mathematik Prof. Dr. L. Cromme Optimierung mit Matlab 1 Optimierungsaufgaben Die allgemeine Aufgabenstellung der Optimierung besteht darin,
1. Hausaufgabenblatt (16.04./ )
 Lehrstuhl Ingenieurmathematik Modul: (Wirtschaftsingenieurwesen/Betriebswirtschaftslehre/Informatik) Sommersemester 2014 1. Hausaufgabenblatt (16.04./23.04.2015) Aufgabe H 1.1 Lösen Sie die linearen Gleichungssysteme
Lehrstuhl Ingenieurmathematik Modul: (Wirtschaftsingenieurwesen/Betriebswirtschaftslehre/Informatik) Sommersemester 2014 1. Hausaufgabenblatt (16.04./23.04.2015) Aufgabe H 1.1 Lösen Sie die linearen Gleichungssysteme
Das Gradientenverfahren
 Das Gradientenverfahren - Proseminar: Algorithmen der Nichtlinearen Optimierung - David Beisel December 10, 2012 David Beisel Das Gradientenverfahren December 10, 2012 1 / 28 Gliederung 0 Einführung 1
Das Gradientenverfahren - Proseminar: Algorithmen der Nichtlinearen Optimierung - David Beisel December 10, 2012 David Beisel Das Gradientenverfahren December 10, 2012 1 / 28 Gliederung 0 Einführung 1
1 Einleitung. f (x) =min! bei x G ={x : g i (x) 0 i I}, (1.1) wobei I. I ={i : i = 1,, m}
 1 1 Einleitung 1.1 Das lineare und das nichtlineare Optimierungsproblem Im vorliegenden Buch werden Optimierungsaufgaben betrachtet, die dadurch charakterisiert sind, dass eine lineare oder nichtlineare
1 1 Einleitung 1.1 Das lineare und das nichtlineare Optimierungsproblem Im vorliegenden Buch werden Optimierungsaufgaben betrachtet, die dadurch charakterisiert sind, dass eine lineare oder nichtlineare
MODULPRÜFUNG MODUL MA 1302 Einführung in die Numerik
 ................ Note Name Vorname 1 I II Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 Obige Angaben sind richtig: Unterschrift der Kandidatin/des Kandidaten 3 TECHNISCHE UNIVERSITÄT
................ Note Name Vorname 1 I II Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 Obige Angaben sind richtig: Unterschrift der Kandidatin/des Kandidaten 3 TECHNISCHE UNIVERSITÄT
MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHE- MIE UND LEBENSMITTELCHEMIE
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHE- MIE UND LEBENSMITTELCHEMIE Differentialrechnung für Funktionen mehrerer
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHE- MIE UND LEBENSMITTELCHEMIE Differentialrechnung für Funktionen mehrerer
Optimale Steuerung 1
 Optimale Steuerung 1 Kapitel 6: Nichtlineare Optimierung unbeschränkter Probleme Prof. Dr.-Ing. Pu Li Fachgebiet Simulation und Optimale Prozesse (SOP) Beispiel: Parameteranpassung für Phasengleichgewicht
Optimale Steuerung 1 Kapitel 6: Nichtlineare Optimierung unbeschränkter Probleme Prof. Dr.-Ing. Pu Li Fachgebiet Simulation und Optimale Prozesse (SOP) Beispiel: Parameteranpassung für Phasengleichgewicht
maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum {j in P} (1/a[j]) * X[j] <= beta; subject to Grenzen {j in P}: 0 <= X[j] <= u[j];
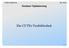
![maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum {j in P} (1/a[j]) * X[j] <= beta; subject to Grenzen {j in P}: 0 <= X[j] <= u[j]; maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum {j in P} (1/a[j]) * X[j] <= beta; subject to Grenzen {j in P}: 0 <= X[j] <= u[j];](/thumbs/64/50698761.jpg) AMPL-Modell für beliebige Produkte (myprod.mod) set P; param a {j in P}; param beta; param c {j in P}; param u {j in P}; var X {j in P}; maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum
AMPL-Modell für beliebige Produkte (myprod.mod) set P; param a {j in P}; param beta; param c {j in P}; param u {j in P}; var X {j in P}; maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum
Rechnerpraktikum zur Optimierung III
 TU München Lehrstuhl Mathematische Optimierung Prof. Dr. M. Ulbrich Dipl.-Math. Florian Lindemann Sommersemester 2007 Teil I Rechnerpraktikum zur Optimierung III P1. Durchhängenes Seil Die senkrechten
TU München Lehrstuhl Mathematische Optimierung Prof. Dr. M. Ulbrich Dipl.-Math. Florian Lindemann Sommersemester 2007 Teil I Rechnerpraktikum zur Optimierung III P1. Durchhängenes Seil Die senkrechten
Einführung in Softwaretools zur nichtlinearen Optimierung (WS 2016/17)
 Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische Optimierung, M1 Sebastian Garreis, M. Sc. (hons) Johannes Haubner, M. Sc. Einführung in Softwaretools zur nichtlinearen
Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische Optimierung, M1 Sebastian Garreis, M. Sc. (hons) Johannes Haubner, M. Sc. Einführung in Softwaretools zur nichtlinearen
Es wird vor allem auf die wesentlichen Ideen der Verfahren eingegangen und weniger auf Details.
 Kapitel 5 Lösungsverfahren Dieses Kapitel gibt einen Überblick über Lösungsverfahren für nichtlineare Optimierungsprobleme. Es wird vor allem auf die wesentlichen Ideen der Verfahren eingegangen und weniger
Kapitel 5 Lösungsverfahren Dieses Kapitel gibt einen Überblick über Lösungsverfahren für nichtlineare Optimierungsprobleme. Es wird vor allem auf die wesentlichen Ideen der Verfahren eingegangen und weniger
Teil II Optimierung. Modellgestützte Analyse und Optimierung Kap. 5 Einführung Optimierung. Peter Buchholz 2006
 Teil II Optimierung Gliederung 5 Einführung, Klassifizierung und Grundlagen 6 Lineare Optimierung 7 Nichtlineare Optimierung 8 Dynamische Optimierung (dieses Jahr nur recht kurz) (9 Stochastische Optimierungsmethoden
Teil II Optimierung Gliederung 5 Einführung, Klassifizierung und Grundlagen 6 Lineare Optimierung 7 Nichtlineare Optimierung 8 Dynamische Optimierung (dieses Jahr nur recht kurz) (9 Stochastische Optimierungsmethoden
Vorlesung Einführung in die Mathematische Optimierung (Wintersemester 2013/14)
 Vorlesung Einführung in die Mathematische Optimierung (Wintersemester 3/) Kapitel : Optimierung ohne Nebenbedingungen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom. Oktober 3) Gliederung
Vorlesung Einführung in die Mathematische Optimierung (Wintersemester 3/) Kapitel : Optimierung ohne Nebenbedingungen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom. Oktober 3) Gliederung
Vorlesung Einführung in die Mathematische Optimierung (Wintersemester 2013/14)
 Vorlesung Einführung in die Mathematische Optimierung (Wintersemester 3/4) Kapitel : Optimierung ohne Nebenbedingungen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom. Oktober 3) Gliederung
Vorlesung Einführung in die Mathematische Optimierung (Wintersemester 3/4) Kapitel : Optimierung ohne Nebenbedingungen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom. Oktober 3) Gliederung
Inhalt. Problemstellung und Überblick. Allgemeine Problemstellung und Terminologie. Überblick über spezielle Klassen von Optimierungsproblemen
 Inhalt Problemstellung und Überblick Allgemeine Problemstellung und Terminologie Überblick über spezielle Klassen von Optimierungsproblemen 40: 40 [40,40] 2.1 Das Optimierungsproblem in allgemeiner Form
Inhalt Problemstellung und Überblick Allgemeine Problemstellung und Terminologie Überblick über spezielle Klassen von Optimierungsproblemen 40: 40 [40,40] 2.1 Das Optimierungsproblem in allgemeiner Form
UVK Verlagsgesellschaft mbh Konstanz mit UVK/Lucius München
 IngolfTerveer Mathematik- Formeln Wirtschaftswissenschaften UVK Verlagsgesellschaft mbh Konstanz mit UVK/Lucius München Inhalt 1 Grundlegende Begriffe 11 1.1 Zahlbereiche 11 1.1.1 Reelle Zahlen 11 1.1.2
IngolfTerveer Mathematik- Formeln Wirtschaftswissenschaften UVK Verlagsgesellschaft mbh Konstanz mit UVK/Lucius München Inhalt 1 Grundlegende Begriffe 11 1.1 Zahlbereiche 11 1.1.1 Reelle Zahlen 11 1.1.2
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Aussagenlogik 4 Lineare Algebra
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Aussagenlogik 4 Lineare Algebra
Konvexe Optimierungsprobleme
 von: Veronika Kühl 1 Konvexe Optimierungsprobleme Betrachtet werden Probleme der Form (P) min x C f(x) wobei f : C R eine auf C konvexe, aber nicht notwendigerweise differenzierbare Funktion ist. Ziel
von: Veronika Kühl 1 Konvexe Optimierungsprobleme Betrachtet werden Probleme der Form (P) min x C f(x) wobei f : C R eine auf C konvexe, aber nicht notwendigerweise differenzierbare Funktion ist. Ziel
FK WMS: Wirtschaftsmathematik 2, Einheit 7/8
 FK WMS: Wirtschaftsmathematik 2, Einheit 7/8 Markus Sinnl 1 markus.sinnl@univie.ac.at http://homepage.univie.ac.at/markus.sinnl basierend auf Folien von Dr. Ivana Ljubic, Mag. Christian Spreitzer und Mag.
FK WMS: Wirtschaftsmathematik 2, Einheit 7/8 Markus Sinnl 1 markus.sinnl@univie.ac.at http://homepage.univie.ac.at/markus.sinnl basierend auf Folien von Dr. Ivana Ljubic, Mag. Christian Spreitzer und Mag.
Mathematische Werkzeuge R. Neubecker, WS 2016 / 2017
 Mustererkennung Mathematische Werkzeuge R. Neubecker, WS 2016 / 2017 Optimierung: Lagrange-Funktionen, Karush-Kuhn-Tucker-Bedingungen Optimierungsprobleme Optimierung Suche nach dem Maximum oder Minimum
Mustererkennung Mathematische Werkzeuge R. Neubecker, WS 2016 / 2017 Optimierung: Lagrange-Funktionen, Karush-Kuhn-Tucker-Bedingungen Optimierungsprobleme Optimierung Suche nach dem Maximum oder Minimum
3 Optimierung mehrdimensionaler Funktionen f : R n R
 3 Optimierung mehrdimensionaler Funktionen f : R n R 31 Optimierung ohne Nebenbedingungen Optimierung heißt eigentlich: Wir suchen ein x R n so, dass f(x ) f(x) für alle x R n (dann heißt x globales Minimum)
3 Optimierung mehrdimensionaler Funktionen f : R n R 31 Optimierung ohne Nebenbedingungen Optimierung heißt eigentlich: Wir suchen ein x R n so, dass f(x ) f(x) für alle x R n (dann heißt x globales Minimum)
Nebenfach Mathematik im Informatik-Studium. Martin Gugat FAU: Friedrich-Alexander-Universität Erlangen-Nürnberg 26.
 Nebenfach Mathematik im Informatik-Studium Martin Gugat martin.gugat@fau.de FAU: Friedrich-Alexander-Universität Erlangen-Nürnberg 26. Oktober 2016 Motivation Die rigorose Analyse von Algorithmen erfordert
Nebenfach Mathematik im Informatik-Studium Martin Gugat martin.gugat@fau.de FAU: Friedrich-Alexander-Universität Erlangen-Nürnberg 26. Oktober 2016 Motivation Die rigorose Analyse von Algorithmen erfordert
Inhaltsverzeichnis. Vorwort Kapitel 1 Einführung, I: Algebra Kapitel 2 Einführung, II: Gleichungen... 57
 Vorwort... 13 Vorwort zur 3. deutschen Auflage... 17 Kapitel 1 Einführung, I: Algebra... 19 1.1 Die reellen Zahlen... 20 1.2 Ganzzahlige Potenzen... 23 1.3 Regeln der Algebra... 29 1.4 Brüche... 34 1.5
Vorwort... 13 Vorwort zur 3. deutschen Auflage... 17 Kapitel 1 Einführung, I: Algebra... 19 1.1 Die reellen Zahlen... 20 1.2 Ganzzahlige Potenzen... 23 1.3 Regeln der Algebra... 29 1.4 Brüche... 34 1.5
Optimieren unter Nebenbedingungen
 Optimieren unter Nebenbedingungen Hier sucht man die lokalen Extrema einer Funktion f(x 1,, x n ) unter der Nebenbedingung dass g(x 1,, x n ) = 0 gilt Die Funktion f heißt Zielfunktion Beispiel: Gesucht
Optimieren unter Nebenbedingungen Hier sucht man die lokalen Extrema einer Funktion f(x 1,, x n ) unter der Nebenbedingung dass g(x 1,, x n ) = 0 gilt Die Funktion f heißt Zielfunktion Beispiel: Gesucht
AMPL Eine kurze Einführung
 AMPL Eine kurze Einführung Sebastian Lohse Juni 2006 Beispiel Modellierung Mengen Parameter Dateneingabe Anzeige Analyse Optionen Script-Files Historisches um 1985 implementiert und seither stetig weiterentwickelt
AMPL Eine kurze Einführung Sebastian Lohse Juni 2006 Beispiel Modellierung Mengen Parameter Dateneingabe Anzeige Analyse Optionen Script-Files Historisches um 1985 implementiert und seither stetig weiterentwickelt
Proseminar Lineare Algebra WS 08/09 Prof. Dr. O. Bogopolski 1. Vortrag: Lineare Gleichungen. am 11. März von Maximilian Wahner
 Proseminar Lineare Algebra WS 08/09 Prof. Dr. O. Bogopolski 1 Vortrag: Lineare Gleichungen am 11. März 2009 von Maximilian Wahner Technische Universität Dortmund Fakultät für Mathematik Proseminar Lineare
Proseminar Lineare Algebra WS 08/09 Prof. Dr. O. Bogopolski 1 Vortrag: Lineare Gleichungen am 11. März 2009 von Maximilian Wahner Technische Universität Dortmund Fakultät für Mathematik Proseminar Lineare
Differenzialrechnung für Funktionen mit mehreren unabhängigen Variablen. Graphentheorie
 Differenzialrechnung für Funktionen mit mehreren unabhängigen Variablen Graphentheorie Differenzialrechnung für Funktionen mit mehreren unabhängigen Variablen Def.: eine Funktion n f :D mit D,x (x,...x
Differenzialrechnung für Funktionen mit mehreren unabhängigen Variablen Graphentheorie Differenzialrechnung für Funktionen mit mehreren unabhängigen Variablen Def.: eine Funktion n f :D mit D,x (x,...x
MATTHIAS GERDTS. Optimierung. Universität der Bundeswehr München Wintertrimester 2014
 MATTHIAS GERDTS Optimierung Universität der Bundeswehr München Wintertrimester 2014 Addresse des Autors: Matthias Gerdts Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München
MATTHIAS GERDTS Optimierung Universität der Bundeswehr München Wintertrimester 2014 Addresse des Autors: Matthias Gerdts Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München
Wir untersuchen in diesem Abschnitt das (lokale) Newton Verfahren zur Lösung eines nichtlinearen Gleichungssystems
 Kapitel 2 Newton Verfahren 2.1 Das lokale Newton Verfahren Wir untersuchen in diesem Abschnitt das (lokale) Newton Verfahren zur Lösung eines nichtlinearen Gleichungssystems F (x) = 0 (2.1) mit einer zumindest
Kapitel 2 Newton Verfahren 2.1 Das lokale Newton Verfahren Wir untersuchen in diesem Abschnitt das (lokale) Newton Verfahren zur Lösung eines nichtlinearen Gleichungssystems F (x) = 0 (2.1) mit einer zumindest
Mit 119 Bildern, 368 Beispielen und 225 Aufgaben mit Lösungen
 Mathematik für Wirtschaftswissenschaftler Ein Lehr- und Übungsbuch für Bachelors 2., aktualisierte Auflage Mit 119 Bildern, 368 Beispielen und 225 Aufgaben mit Lösungen Fachbuchverlag Leipzig im Carl Hanser
Mathematik für Wirtschaftswissenschaftler Ein Lehr- und Übungsbuch für Bachelors 2., aktualisierte Auflage Mit 119 Bildern, 368 Beispielen und 225 Aufgaben mit Lösungen Fachbuchverlag Leipzig im Carl Hanser
Aufgabensammlung zum UK Mathematische Optimierung
 Aufgabensammlung zum UK Mathematische Optimierung Mehrdimensionale Analysis Stetigkeit. Man bestimme den natürlichen Definitionsbereich D f der folgenden Funktionen f: a) f(x, y) = ln(x y ) b) f(x, y)
Aufgabensammlung zum UK Mathematische Optimierung Mehrdimensionale Analysis Stetigkeit. Man bestimme den natürlichen Definitionsbereich D f der folgenden Funktionen f: a) f(x, y) = ln(x y ) b) f(x, y)
9 Optimierung mehrdimensionaler reeller Funktionen f : R n R
 9 Optimierung mehrdimensionaler reeller Funktionen f : R n R 91 Optimierung ohne Nebenbedingungen Ein Optimum zu suchen heißt, den größten oder den kleinsten Wert zu suchen Wir suchen also ein x R n, sodass
9 Optimierung mehrdimensionaler reeller Funktionen f : R n R 91 Optimierung ohne Nebenbedingungen Ein Optimum zu suchen heißt, den größten oder den kleinsten Wert zu suchen Wir suchen also ein x R n, sodass
Inhaltsverzeichnis. Vorwort Kapitel 1 Einführung, I: Algebra Kapitel 2 Einführung, II: Gleichungen... 57
 Vorwort... 13 Vorwort zur 3. deutschen Auflage... 17 Kapitel 1 Einführung, I: Algebra... 19 1.1 Die reellen Zahlen... 20 1.2 Ganzzahlige Potenzen... 23 1.3 Regeln der Algebra... 29 1.4 Brüche... 34 1.5
Vorwort... 13 Vorwort zur 3. deutschen Auflage... 17 Kapitel 1 Einführung, I: Algebra... 19 1.1 Die reellen Zahlen... 20 1.2 Ganzzahlige Potenzen... 23 1.3 Regeln der Algebra... 29 1.4 Brüche... 34 1.5
Nebenfach Mathematik im Informatik-Studium. Martin Gugat FAU: Friedrich-Alexander-Universität Erlangen-Nürnberg 25.
 Nebenfach Mathematik im Informatik-Studium Martin Gugat martin.gugat@fau.de FAU: Friedrich-Alexander-Universität Erlangen-Nürnberg 25. Oktober 2017 Motivation Die rigorose Analyse von Algorithmen erfordert
Nebenfach Mathematik im Informatik-Studium Martin Gugat martin.gugat@fau.de FAU: Friedrich-Alexander-Universität Erlangen-Nürnberg 25. Oktober 2017 Motivation Die rigorose Analyse von Algorithmen erfordert
NICHTRESTRINGIERTE OPTIMIERUNG
 3 NICHTRESTRINGIERTE OPTIMIERUNG Die Aufgabe, mit der wir uns im Folgen beschäftigen werden, ist die Lösung von Minimierungsproblemen der Form minimiere f(x) in R n, (3.1) wobei f : R n R eine gegebene
3 NICHTRESTRINGIERTE OPTIMIERUNG Die Aufgabe, mit der wir uns im Folgen beschäftigen werden, ist die Lösung von Minimierungsproblemen der Form minimiere f(x) in R n, (3.1) wobei f : R n R eine gegebene
Lineare Klassifikationsmethoden
 Verena Krieg Fakultät für Mathematik und Wirtschaftswissenschaften 08. Mai 2007 Inhaltsverzeichnis 1. Einführung 2. Lineare Regression 3. Lineare Diskriminanzanalyse 4. Logistische Regression 4.1 Berechnung
Verena Krieg Fakultät für Mathematik und Wirtschaftswissenschaften 08. Mai 2007 Inhaltsverzeichnis 1. Einführung 2. Lineare Regression 3. Lineare Diskriminanzanalyse 4. Logistische Regression 4.1 Berechnung
Inhaltsübersicht für heute:
 Inhaltsübersicht für heute: Innere-Punkte-Verfahren Lineare Optimierung über Kegeln Second-Order-Cone Programme SOC Anwendung: Regularisierung SOC Anwendung: Klassifizierung, Support-Vektor SOC Anwendung:
Inhaltsübersicht für heute: Innere-Punkte-Verfahren Lineare Optimierung über Kegeln Second-Order-Cone Programme SOC Anwendung: Regularisierung SOC Anwendung: Klassifizierung, Support-Vektor SOC Anwendung:
Mathematik für Wirtschaftswissenschaftler
 Knut Sydsaeter Peter HammondJ Mathematik für Wirtschaftswissenschaftler Basiswissen mit Praxisbezug 2., aktualisierte Auflage Inhaltsverzeichnis Vorwort 13 Vorwort zur zweiten Auflage 19 Kapitel 1 Einführung,
Knut Sydsaeter Peter HammondJ Mathematik für Wirtschaftswissenschaftler Basiswissen mit Praxisbezug 2., aktualisierte Auflage Inhaltsverzeichnis Vorwort 13 Vorwort zur zweiten Auflage 19 Kapitel 1 Einführung,
3 Statische Optimierung: Mit Beschränkungen
 3 Statische Optimierung: Mit Beschränkungen Den nachfolgenden Betrachtungen liegt das statische Optimierungsproblem mit Gleichungsund Ungleichungsbeschränkungen gemäß (.) in der Form min f(x) Kostenfunktion
3 Statische Optimierung: Mit Beschränkungen Den nachfolgenden Betrachtungen liegt das statische Optimierungsproblem mit Gleichungsund Ungleichungsbeschränkungen gemäß (.) in der Form min f(x) Kostenfunktion
Numerisches Rechnen. (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang. Institut für Geometrie und Praktische Mathematik RWTH Aachen
 Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Einführung in Softwaretools zur nichtlinearen Optimierung (WS 2017/18)
 Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische Optimierung, M1 Florian Lindemann, Dr. rer. nat. Daniel Walter, M. Sc. (hons) Einführung in Softwaretools zur nichtlinearen
Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische Optimierung, M1 Florian Lindemann, Dr. rer. nat. Daniel Walter, M. Sc. (hons) Einführung in Softwaretools zur nichtlinearen
Teil 6. Differentialrechnung mehrerer Veränderlicher
 Teil 6 Differentialrechnung mehrerer Veränderlicher 95 96 6.1 Topologie von Mengen Umgebung ε-umgebung eines Punktes x R n : B ε (x) = {y : y x < ε} Umgebung U von x: Menge, die eine ε-umgebung von x enthält
Teil 6 Differentialrechnung mehrerer Veränderlicher 95 96 6.1 Topologie von Mengen Umgebung ε-umgebung eines Punktes x R n : B ε (x) = {y : y x < ε} Umgebung U von x: Menge, die eine ε-umgebung von x enthält
Statistik. Sommersemester Stefan Etschberger. für Betriebswirtschaft, Internationales Management, Wirtschaftsinformatik und Informatik
 Stefan Etschberger für Betriebswirtschaft, Internationales Management, Wirtschaftsinformatik und Informatik Sommersemester 2017 Gliederung 1 : Einführung 2 Differenzieren 2 3 Deskriptive 4 Wahrscheinlichkeitstheorie
Stefan Etschberger für Betriebswirtschaft, Internationales Management, Wirtschaftsinformatik und Informatik Sommersemester 2017 Gliederung 1 : Einführung 2 Differenzieren 2 3 Deskriptive 4 Wahrscheinlichkeitstheorie
1 Einleitung Optimierung in Technik-, Natur- und Wirtschaftswissenschaften Optimierung mit dem Computer
 1 Einleitung...1 1.1 Optimierung in Technik-, Natur- und Wirtschaftswissenschaften... 4 1.2 Optimierung mit dem Computer... 5 1.2.1 Anwendung von Computeralgebrasystemen... 6 1.2.2 Anwendung von EXCEL...
1 Einleitung...1 1.1 Optimierung in Technik-, Natur- und Wirtschaftswissenschaften... 4 1.2 Optimierung mit dem Computer... 5 1.2.1 Anwendung von Computeralgebrasystemen... 6 1.2.2 Anwendung von EXCEL...
Übung 5, Analytische Optimierung
 Übung 5, 5.7.2011 Analytische Optimierung Aufgabe 5.1 Bei der Herstellung von Konserven werden für Boden und Deckel bzw. für den Konservenmantel verschiedene Materialien verwendet, die g 1 = bzw. g 2 =
Übung 5, 5.7.2011 Analytische Optimierung Aufgabe 5.1 Bei der Herstellung von Konserven werden für Boden und Deckel bzw. für den Konservenmantel verschiedene Materialien verwendet, die g 1 = bzw. g 2 =
18.4 Das Newton-Verfahren
 18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
Wirtschaftsmathematik II
 WMS: Wirtschaftsmathematik 2 :: WS 2009/10 Wirtschaftsmathematik II Reinhard Ullrich http://homepage.univie.ac.at/reinhard.ullrich Basierend auf Folien von Dr. Ivana Ljubic October 11, 2009 1 Funktionen
WMS: Wirtschaftsmathematik 2 :: WS 2009/10 Wirtschaftsmathematik II Reinhard Ullrich http://homepage.univie.ac.at/reinhard.ullrich Basierend auf Folien von Dr. Ivana Ljubic October 11, 2009 1 Funktionen
Optimierung für Nichtmathematiker
 Optimierung für Nichtmathematiker Prof. Dr. R. Herzog WS/ / Inhaltsübersicht 3Einführung in die freie Optimierung 4Orakel und Modellfunktionen 5Optimalitätsbedingungen der freien Optimierung 6Das Newton-Verfahren
Optimierung für Nichtmathematiker Prof. Dr. R. Herzog WS/ / Inhaltsübersicht 3Einführung in die freie Optimierung 4Orakel und Modellfunktionen 5Optimalitätsbedingungen der freien Optimierung 6Das Newton-Verfahren
6. Softwarewerkzeuge für die Lineare Programmierung
 6. Softwarewerkzeuge für die Lineare Programmierung Inhalt 6. Softwarewerkzeuge für die Lineare Programmierung GNU Linear Programming Kit Operations Research I Hochschule Bonn-Rhein-Sieg, SS 2013 314 GNU
6. Softwarewerkzeuge für die Lineare Programmierung Inhalt 6. Softwarewerkzeuge für die Lineare Programmierung GNU Linear Programming Kit Operations Research I Hochschule Bonn-Rhein-Sieg, SS 2013 314 GNU
Nichtlineare Optimierung
 Nichtlineare Optimierung Roland Griesse Numerische Mathematik Chemnitzer Skiseminar Gerlosberg, 07. 14. März 2009 Gliederung Konvexe Optimierung 1 Konvexe Optimierung Bedeutung Beispiele Charakterisierung
Nichtlineare Optimierung Roland Griesse Numerische Mathematik Chemnitzer Skiseminar Gerlosberg, 07. 14. März 2009 Gliederung Konvexe Optimierung 1 Konvexe Optimierung Bedeutung Beispiele Charakterisierung
Optimale Steuerung chemischer Batch-Reaktoren Praktikum Nichtlineare Modellierung in den Naturwissenschaften im WS 2012/13
 MÜNSTER Optimale Steuerung chemischer Batch-Reaktoren Praktikum Nichtlineare Modellierung in den Naturwissenschaften im WS 2012/13 Karoline Pelka Christian Schmidt Christoph Große Kracht 5. Februar 2013
MÜNSTER Optimale Steuerung chemischer Batch-Reaktoren Praktikum Nichtlineare Modellierung in den Naturwissenschaften im WS 2012/13 Karoline Pelka Christian Schmidt Christoph Große Kracht 5. Februar 2013
Inhaltsverzeichnis. Vorlesung und Übung Optimierung (WS 2017/2018) Steinböck, Kugi,Institut für Automatisierungs- und Regelungstechnik, TU Wien
 Inhaltsverzeichnis 3 Statische Optimierung mit Beschränkungen 66 3.1 Optimalitätsbedingungen........................... 67 3.1.1 Optimalitätsbedingungen basierend auf zulässigen Richtungen... 67 3.1.2
Inhaltsverzeichnis 3 Statische Optimierung mit Beschränkungen 66 3.1 Optimalitätsbedingungen........................... 67 3.1.1 Optimalitätsbedingungen basierend auf zulässigen Richtungen... 67 3.1.2
Lösungsskizzen zu den Klausuraufgaben zum Kurs 1142 Algorithmische Mathematik. a 0 = 0 =
 Lösungsskizzen zu den Klausuraufgaben zum Kurs 4 Algorithmische Mathematik 4KSL3 6 Punkte Aufgabe. Die Folge (a n ) n N natürlicher Zahlen a n sei rekursiv definiert durch a 0 = 0, a n = a n + n falls
Lösungsskizzen zu den Klausuraufgaben zum Kurs 4 Algorithmische Mathematik 4KSL3 6 Punkte Aufgabe. Die Folge (a n ) n N natürlicher Zahlen a n sei rekursiv definiert durch a 0 = 0, a n = a n + n falls
Optimierung für Wirtschaftsinformatiker: Analytische Optimierung mit Ungleichungsnebenbedingungen
 Optimierung für Wirtschaftsinformatiker: Analytische Optimierung mit Ungleichungsnebenbedingungen Dr. Nico Düvelmeyer Freitag, 8. Juli 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 NLP Aufgabe KKT 2 Nachtrag
Optimierung für Wirtschaftsinformatiker: Analytische Optimierung mit Ungleichungsnebenbedingungen Dr. Nico Düvelmeyer Freitag, 8. Juli 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 NLP Aufgabe KKT 2 Nachtrag
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: b a 2 3a 1
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Chinese Postman Problem Hamiltonsche Graphen und das Traveling Salesman Problem Max-Flow-Min-Cut...151
 Inhaltsverzeichnis 1 Kernkonzepte der linearen Optimierung... 1 1.1 Einführung... 1 1.2 Grundlegende Definitionen... 8 1.3 Grafische Lösung... 10 1.4 Standardform und grundlegende analytische Konzepte...
Inhaltsverzeichnis 1 Kernkonzepte der linearen Optimierung... 1 1.1 Einführung... 1 1.2 Grundlegende Definitionen... 8 1.3 Grafische Lösung... 10 1.4 Standardform und grundlegende analytische Konzepte...
Mathematik 2 für Wirtschaftsinformatik
 für Wirtschaftsinformatik Sommersemester 2012 Hochschule Augsburg Hinreichende Bedingung für lokale Extrema Voraussetzungen Satz D R n konvex und offen Funktion f : D R zweimal stetig partiell differenzierbar
für Wirtschaftsinformatik Sommersemester 2012 Hochschule Augsburg Hinreichende Bedingung für lokale Extrema Voraussetzungen Satz D R n konvex und offen Funktion f : D R zweimal stetig partiell differenzierbar
Rückblick auf die letzte Vorlesung. Bemerkung
 Bemerkung 1) Die Bedingung grad f (x 0 ) = 0 T definiert gewöhnlich ein nichtlineares Gleichungssystem zur Berechnung von x = x 0, wobei n Gleichungen für n Unbekannte gegeben sind. 2) Die Punkte x 0 D
Bemerkung 1) Die Bedingung grad f (x 0 ) = 0 T definiert gewöhnlich ein nichtlineares Gleichungssystem zur Berechnung von x = x 0, wobei n Gleichungen für n Unbekannte gegeben sind. 2) Die Punkte x 0 D
Newton-Verfahren zur gleichungsbeschränkten Optimierung. 1 Gleichungsbeschränkte Optimierungsprobleme
 Newton-Verfahren zur gleichungsbeschränkten Optimierung Armin Farmani Anosheh (afarmani@mail.uni-mannheim.de) 3.Mai 2016 1 Gleichungsbeschränkte Optimierungsprobleme Einleitung In diesem Vortrag geht es
Newton-Verfahren zur gleichungsbeschränkten Optimierung Armin Farmani Anosheh (afarmani@mail.uni-mannheim.de) 3.Mai 2016 1 Gleichungsbeschränkte Optimierungsprobleme Einleitung In diesem Vortrag geht es
Klausur Mathematik II
 Technische Universität Dresden. Juli 8 Institut für Numerische Mathematik Prof. Dr. G. Matthies, Dr. M. Herrich Klausur Mathematik II Modul Dierentialgleichungen und Dierentialrechnung für Funktionen mehrerer
Technische Universität Dresden. Juli 8 Institut für Numerische Mathematik Prof. Dr. G. Matthies, Dr. M. Herrich Klausur Mathematik II Modul Dierentialgleichungen und Dierentialrechnung für Funktionen mehrerer
BWL-Crash-Kurs Mathematik
 Ingolf Terveer BWL-Crash-Kurs Mathematik UVK Verlagsgesellschaft mbh Vorwort 9 1 Aufgaben der Linearen Wirtschaftsalgebra 13 Aufgaben 17 2 Lineare Gleichungssysteme 19 2.1 Lineare Gleichungssysteme in
Ingolf Terveer BWL-Crash-Kurs Mathematik UVK Verlagsgesellschaft mbh Vorwort 9 1 Aufgaben der Linearen Wirtschaftsalgebra 13 Aufgaben 17 2 Lineare Gleichungssysteme 19 2.1 Lineare Gleichungssysteme in
Modul NUME: Numerische Mathematik Einführung
 TU Dresden Fakultät Mathematik Institut für Numerische Mathematik 1 Prof. Dr. A. Fischer WiS 2018/2019 Modul NUME: Numerische Mathematik Einführung 5. Übungsblatt: 10. - 21. Dezember 2018 Aufgabe 18 :
TU Dresden Fakultät Mathematik Institut für Numerische Mathematik 1 Prof. Dr. A. Fischer WiS 2018/2019 Modul NUME: Numerische Mathematik Einführung 5. Übungsblatt: 10. - 21. Dezember 2018 Aufgabe 18 :
Die MATLAB-Funktionen (Beschreibung : Siehe MATLAB-Hilfen)
 Fachbereich Grundlagenwissenschaften Prof. Dr. H. Dathe Numerische Mathematik/Optimierung Eine Einführung in Theorie und Verfahren Die MATLAB-Funktionen (Beschreibung : Siehe MATLAB-Hilfen) linprog Lineare
Fachbereich Grundlagenwissenschaften Prof. Dr. H. Dathe Numerische Mathematik/Optimierung Eine Einführung in Theorie und Verfahren Die MATLAB-Funktionen (Beschreibung : Siehe MATLAB-Hilfen) linprog Lineare
1. Lineare Optimierungsaufgaben (LOA) als Teilklasse konvexer Optimierungsprobleme. f(x) min, x G (1.1) (Legende)
 . Lineare Optimierungsaufgaben (LOA) als Teilklasse konvexer Optimierungsprobleme X Banachraum, wobei X = R n G zulässige Menge des Optimierungsproblems f: G R Zielfunktion f(x) min, x G (.) (Legende)
. Lineare Optimierungsaufgaben (LOA) als Teilklasse konvexer Optimierungsprobleme X Banachraum, wobei X = R n G zulässige Menge des Optimierungsproblems f: G R Zielfunktion f(x) min, x G (.) (Legende)
Nichtlineare Gleichungen, mehrere Unbekannte
 Dritte Vorlesung, 6. März 2008, Inhalt Aufarbeiten von Themen der letzten Vorlesung, und Nichtlineare Gleichungen, mehrere Unbekannte Systeme nichtlinearer Gleichungen Vektor- und Matrixnormen Fixpunkt-Iteration,
Dritte Vorlesung, 6. März 2008, Inhalt Aufarbeiten von Themen der letzten Vorlesung, und Nichtlineare Gleichungen, mehrere Unbekannte Systeme nichtlinearer Gleichungen Vektor- und Matrixnormen Fixpunkt-Iteration,
Fachhochschule München Fakultät 03 FA WS 2011/2012. Diplomvorprüfung in Mathematik I (Lineare Algebra) Fahrzeugtechnik
 Fachhochschule München Fakultät 03 FA WS 20/202 Diplomvorprüfung in Mathematik I (Lineare Algebra) Fahrzeugtechnik Arbeitszeit: 90 Minuten, Hilfsmittel: Formelsammlung, Skripten, Bücher, Taschenrechner
Fachhochschule München Fakultät 03 FA WS 20/202 Diplomvorprüfung in Mathematik I (Lineare Algebra) Fahrzeugtechnik Arbeitszeit: 90 Minuten, Hilfsmittel: Formelsammlung, Skripten, Bücher, Taschenrechner
Seminaraufgabensammlung zur Lehrveranstaltung. Prozessoptimierung 1. 1 Formulieren und Lösen linearer Optimierungsprobleme
 Fachgebiet Simulation und Optimale Prozesse Fakultät für Informatik und Automatisierung Institut für Automatisierungsund Systemtechnik Seminaraufgabensammlung zur Lehrveranstaltung Prozessoptimierung Vorlesender:
Fachgebiet Simulation und Optimale Prozesse Fakultät für Informatik und Automatisierung Institut für Automatisierungsund Systemtechnik Seminaraufgabensammlung zur Lehrveranstaltung Prozessoptimierung Vorlesender:
Klausurrepetitorium ABWL
 Klausurrepetitorium ABWL Planungs- und Südwestfälische Industrie- und Handelskammer 9. August 5 Dr. Friedhelm Kulmann, Sandra Rudolph 9.8.5 Gliederung. Nichtlineare Optimierungsprobleme.. Quadratisches
Klausurrepetitorium ABWL Planungs- und Südwestfälische Industrie- und Handelskammer 9. August 5 Dr. Friedhelm Kulmann, Sandra Rudolph 9.8.5 Gliederung. Nichtlineare Optimierungsprobleme.. Quadratisches
Das Trust-Region-Verfahren
 Das Trust-Region-Verfahren Nadine Erath 13. Mai 2013... ist eine Methode der Nichtlinearen Optimierung Ziel ist es, das Minimum der Funktion f : R n R zu bestimmen. 1 Prinzip 1. Ersetzen f(x) durch ein
Das Trust-Region-Verfahren Nadine Erath 13. Mai 2013... ist eine Methode der Nichtlinearen Optimierung Ziel ist es, das Minimum der Funktion f : R n R zu bestimmen. 1 Prinzip 1. Ersetzen f(x) durch ein
Lineare Gleichungen. Mathematik-Repetitorium. 3.1 Eine Unbekannte. 3.2 Zwei oder drei Unbekannte. 3.3 Allgemeine lineare Gleichungssysteme
 Lineare Gleichungen 3.1 Eine Unbekannte 3.2 Zwei oder drei Unbekannte 3.3 Allgemeine lineare Gleichungssysteme Lineare Gleichungen 1 Vorbemerkung zu Kapitel 1 Gleichungen (Unbekannte) (Variablen, Parameter)
Lineare Gleichungen 3.1 Eine Unbekannte 3.2 Zwei oder drei Unbekannte 3.3 Allgemeine lineare Gleichungssysteme Lineare Gleichungen 1 Vorbemerkung zu Kapitel 1 Gleichungen (Unbekannte) (Variablen, Parameter)
