Neuronale Netze (Konnektionismus)
|
|
|
- Benedict Seidel
- vor 8 Jahren
- Abrufe
Transkript
1 Einführung in die KI Prof. Dr. sc. Hans-Dieter Burkhard Vorlesung (Konnektionismus) sind biologisch motiviert können diskrete, reell-wertige und Vektor-wertige Funktionen berechnen, Einsatz z.b. für Klassifizierungsaufgaben Dynamische Systeme Informationsspeicherung verteilt im gesamten Netz Lernverfahren z.b. Back-Propagation, Evolutionäre Verfahren sind robust bezüglich Verrauschten Daten Ausfall von Teilen des Netzes 2 1
2 Beispiel-Aufgabe: Schrifterkennung Es soll ein Verfahren entwickelt werden, das geschriebenen Zeichen die korrekte Bedeutung zuordnet. können so trainiert werden, dass sie die Aufgabe mit geringer Fehlerrate lösen. Trainieren bedeutet: Anpassung des Verhaltens anhand präsentierter Beispiele. Generalisierung: Das Netz kann so verallgemeinern, dass auch zuvor nicht gesehene Zeichen korrekt klassifiziert werden. 3 Biologisches Vorbild Nervenzelle 4 2
3 Biologisches Vorbild Gehirn mit Neuronen, 20 Typen Axon bis zu 1m lang Gerichtete Reizleitung von Dendriten zu Synapsen Weiterleitung bei hinreichend starker Erregung Jeweils Verbindungen (Synapsen) zu Neuronen Insgesamt Synapsen Schaltzeit 10-3 Sekunden (Computer ) Erfassung einer Szene: 10-1 Sekunden (d.h. ca. 100 Verarbeitungs-Schritte) Hohe Parallelität Lernfähigkeit 5 Modell: (Künstliches) Neuron, Unit McCulloch-Pitts Unit Mehrere Eingänge, 1 (verzweigter) Ausgang Starke Vereinfachung gegenüber natürlichem Neuron 6 3
4 Neuronales Netz Miteinander verknüpfte Neuronen u 1,...,u n Die Verbindungen zwischen Neuronen u j und u i sind gewichtet mit Werten w ji Darstellung der Verknüpfung als Matrix ((w ji )) (mit w ji =0 falls keine Verbindung besteht) 7 Verarbeitung an Einheit u i a j = Aktivierung von Einheit u j ( i=1,..,n ) Bias b i := - a 0 w 0i Gewichtete Summe der Eingänge: in i (a) = w i a + b i = Σ j=0,..,n w ji a i mit w i =(w 1i,,w ni ) und a = (a 1,,a n ) Aktivierungsfunktion (Transferfunktion) g Ausgabe a i = g(in i (a)) = g(σ j=0,..,n w ji a i ) 8 4
5 Eingabe-Funktion in i in i (a) = Σ j=0,..,n Ohne Bias: w ji a i Σ j=1,..,n w ji a i = Skalarprodukt w i a von w i =(w 1i,,w ni ) und a=(a 1,,a n ) = cos(w i, a) w i a = Maß für Ähnlichkeit von w i und a Klassifizierung mittels Schwellwert (bias) b i = - a 0 w 0i : K = { a Σ j=1,..,n w ji a i > b i } = { a Σ j=0,..,n w ji a i > 0 } 9 Lineare Trennung w i a = cos(w i, a) w i a > b i w i a= b i a wi w i a b i w i a> b i 10 5
6 Aktivierungsfunktion g a i = g(in i (a)) = g(σ i=0,..,n w ji a i ) Schaltet Ausgabe ein falls Eingabe hinreichend groß, z.b. (a) Schwellwert (b) Sigmoidfunktion 1/(1+e -x ) (c) Tangens hyperbolicus tanh(x)= (e x -e -x ) /(e x +e -x ) = (e 2x -1)/(e 2x +1) = 1 2/(e 2x +1) (c) 11 Klassifizierung Schwellwertfunktion liefert scharfe Trennung klassische Menge K := { a Σ j=0,..,n w ji a i > 0 } = { a g(in i (a)) > 0 } Sigmoide liefert unscharfe Trennung Fuzzy-Menge (Zugehörigkeitswert) µ(a) := g(in i (a)) 12 6
7 Aktivierungsfunktion g a i = g(in i (a)) = g(σ i=0,..,n w ji a i ) Sigmoidfunktion und tanh sind differenzierbar Flanken als Übertragungsfunktion (z.b. Verstärkung). Angenähert: im mittleren Flanken-Bereich linear im unteren Flankenbereich exponentiell Im oberen Flankenbereich logarithmisch Stärke (Steilheit) modifizierbar als Faktor bei in i (eingehende Gewichte insgesamt modifizieren) Annäherung an Schwellwertfunktion bei starker Steilheit Bias a 0 = -1 und Gewicht w 0i für horizontale Justierung 13 Netzstrukturen Ohne Rückkopplung ( feed forward ) Verarbeitung Eingabevektor Ausgabevektor Typischerweise in Schichten (layer) angeordnet: Eingabeschicht, Ausgabeschicht Verdeckte Schichten (hidden layer) 14 7
8 Netzstrukturen Mit Rückkopplung ( rekurrente Netze ): Dynamisches System mit Möglichkeiten für Stabilisierung (Zustand) Oszillation Chaotischem Verhalten Antwort auf eine Eingabe vom aktuellen Zustand abhängig ( Gedächtnis) 15 Netzstrukturen Ohne Rückkopplung ( feed forward ) Berechnung einer Funktion, z.b. Boolesche Funktionen Mittels Verknüpfung beliebige Boolesche Funktionen darstellbar XOR 16 8
9 Perzeptron Einschichtig, Ohne Rückkopplung Ausgaben eines Neurons mit 2 Eingängen bei sigmoider Aktivierungsfunktion 17 Perzeptron Ausgaben unabhängig voneinander. Ausgabe einer Einheit: a= g(in i (a)) = g(σ i=0,..,n w j a i ) Gleichung einer Hyperebene falls g Schwellwertfunktion: oder Σ i=0,..,n w j a i > 0 w a > b i Nur Darstellung von linear trennbaren Funktionen 18 9
10 Nur linear trennbare Funktionen Σ i=0,..,n w j a i > 0 oder w a > b i XOR ist nicht linear trennbar Analoges Resultat für sigmoide Aktivierungsfunktion 19 Mehrschichtige Netze Die Ausgaben von Netzen können als Eingaben nachgeschalteter Netze verwendet werden. Das ermöglicht komplexeres Verhalten. Alle (stetigen) Funktionen in Netzen mit (zwei) drei verdeckten Schichten darstellbar
11 Lernen Gegeben: Menge F von Funktionen Menge N von Neuronalen Netzen N Gütemaß g: F x N W Gesucht: Verfahren, das zu gegebener Funktion f(x 1,...,x n ) œf durch Auswertung von Beispielen ( Lernen ) ein Netz NœN liefert mit hinreichender Güte g(f,n). i.a. keine genaue Übereinstimmung gefordert, sondern gute Approximation: optimale Güte = minimaler Fehler 21 Lern-Verfahren Gegeben: Funktion f(x 1,...,x n ) Güte g(f,n) definiert über die Fehler der Netzausgabe f(x 1,...,x n ) - N(x 1,...,x n ) Gesucht: Netz N mit optimaler Güte g(f,n). Idee des Lernens: Das Netz wird anhand von (endlich vielen) Trainingsdaten solange modifiziert, bis es auf diesen Daten hinreichend gut arbeitet
12 Generalisierung Annahme: Wenn das Netz auf den Trainingsdaten gut arbeitet, wird es auch für alle anderen Daten gute Ergebnisse liefern. Inductive Bias: Zusätzliche (versteckte) Annahme, durch die die Hypothese gerechtfertigt ist Bei Neuronalen Netzen z.b. Stetigkeitsannahmen (für Lernen stetiger Funktionen) Lineare Trennbarkeit (für Klassifikation mit Perzeptron) 23 Generalisierung Beispiel für Inductive Bias: Beispiele f(0,0) = 0 f(0,1) = 1 f(1,0) = 1 Angelerntes Netz: N (sei korrekt auf Beispielen) Generalsierungsmöglichkeiten: N(1,1) = 0 oder N(1,1) = 1 Perzeptron kann nur verallgemeinern zu N(1,1) =
13 Lern-Verfahren für Eingabe: Beispielmenge B, initiales Netz N 0 Start: k:=0 Schritt k: Falls Güte g(f,n k ) > ε : Exit mit Lösung N k. Andernfalls: N k+1 aus N k berechnen durch Anpassen der Gewichte w ji := w ji + δw ij Heuristik für Anpassung: Optimierung von g(f,n k ) anhand der Lernbeispiele B. (z.b. Fehlerminimierung/Gradientenabstieg) Weiter mit Schritt k Lernformen: Überwachtes Lernen ( supervised learning, mit Lehrer ) Es werden Beispiele korrekter Zuordnungen ausgewertet: B = { [(x d 1,...,x d n), f(x d 1,...,x d n)] d œ D } Eingabe von (x d 1,...,x d n) N k liefert Ausgabe N k (x d 1,...,x d n) Fehler: δ d := f(x d 1,...,x d n) -N k (x d 1,...,x d n) Modifizierung von N k zu N k+1 mittels w ji := w ji + δw ji wobei δw ji proportional zu δ d 26 13
14 Unüberwachtes Lernen ( unsupervised learning, ohne Lehrer ) Es werden Eingabe-Beispiele [x 1,...,x n ] in N verarbeitet. Das Netz soll z.b. Regularitäten (Clusterbildung) erkennen. Mögliche Verfahren: Hebbsche Lernregel: Verbindungen zwischen gleichzeitig aktivierten Neuronen verstärken δw ji proportional zu a i a j ( festigen durch Wiederholung ) Competitive Learning (Winner takes it all): Eingänge hoch aktivierter Neuronen werden verstärkt. 27 Überwachtes Lernen für Perzeptron Gradientenabstieg Idee: Fehler bei Trainingsbeispielen minimieren Summe der Fehlerquadrate: E = g(f,n) = d D ( f(x d 1,...,x d n) - N(x d 1,...,x d n) ) 2 Gradientenabstieg: Korrekturen der Gewichte: w i := w i + δw i ( Delta-Regel ) in Richtung der größten Abnahme des Fehlers E 28 14
15 Gradientenabstieg für Perzeptron Start: k:=0 w i := kleine zufällige Werte, Lernrate η festlegen. Schritt k: Iteration von 1-3 mit Netz N k bis g(n k,f) < ε: 1. Für jedes Trainingsbeispiel d = [ [x d 1,...,x d n], f (x d 1,...,x d n) ]: Fehler δ d := f(x d 1,...,x d n) - N k (x d 1,...,x d n) berechnen. 2. Korrekturwerte der Gewichte w i bestimmen: δw i := η d D δ d x d i 3 Neues Netz N k+1 mit modifizierten Gewichten: w i := w i + δw i Weiter mit Schritt k Gradientenabstieg für Perzeptron Vorzugeben: Anzahl der Neuronen - an Problemgröße angepasst: Dimension des Raumes Initiale Gewichte Fehlerschranke ε Lernrate η bestimmt Stärke der Modifikation Zu kleine Werte: geringe Variation, Gefahr lokaler Minima Zu große Werte: schnelle Variation, am Ende schlechte Konvergenz Simulated annealing: η mit der Zeit verringern 30 15
16 Inkrementeller Gradientenabstieg für P. Bisher: Modifikation bezüglich Gesamtfehler bei allen Beispielen δw i := η d D δ d x d i Jetzt: Einzelmodifikationen für jedes Beispiel δw i := η δ d x d i Vorteile: Schnellere Konvergenz Besseres Verlassen lokaler Minima 31 Inkrementeller Gradientenabstieg für P. Start: k:=0 w i := kleine zufällige Werte, Lernrate η festlegen. Schritt k: Für jedes Trainingsbeispiel d = [ [x d 1,...,x d n], f (x d 1,...,x d n) ]: a) Fehler δ d := f(x d 1,...,x d n)-n k (x d 1,...,x d n) berechnen. b) Korrekturwerte der Gewichte w i bestimmen: δw i := η δ d x d i c) Neues Netz N k mit modifizierten Gewichten: w i := w i + δw i Delta-Regel Falls g(n k,f) < ε : Exit. Sonst N k+1 := N k, weiter mit Schritt k
17 Backpropagation Lernen in mehrschichtigen Netzen Fehler von Ausgabeschicht sukzessive in vorherige Schichten geeignet zurück propagieren Ausgangspunkt: Minimierung der Summe der Fehlerquadrate E = d D ( N(x d 1,...,x d n) - f (x d 1,...,x d n) ) 2 Verfahren: Gradientenabstieg (in Richtung Ableitung der Fehlerfunktion) Ausgabe (i.a. mehrere Neuronen) f (x 1,...,x n ) = [ t 1,...,t k ] Beispiele in der Form d = [ [ x 1,...,x n ], [ t 1,...,t k ] ] 33 Backpropagation Start: k:=0 w ji := kleine zufällige Werte, Lernrate η festlegen. Schritt k: Für jedes Trainingsbeispiel d = [ [ x 1,...,x n ], [ t 1,...,t k ] ]: a) Berechnung N(x d 1,...,x d n) ( Vorwärtspropagierung ) b) Rückwärtspropagierung des Fehlers für Ausgabe-Neuronen sowie schichtweise für innere Neuronen c) Korrekturwerte der Gewichte bestimmen: δw ji d) Gewichte korrigieren: w ji := w ji + δw ji e) Neues Netz N k mit modifizierten Gewichten Falls g(n k,f) < ε : Exit. Sonst N k+1 := N k, weiter mit Schritt k
18 Berechnung der Korrekturwerte f (x 1,...,x n ) = [ t 1,...,t k ] sei der tatsächliche Wert. N(x d 1,...,x d n) = [ o 1,...,o k ] sei die Ausgabe des Netzes, d.h. o u die Ausgabe am Ausgabe-Neuron u Berechnung des Fehlers für Ausgabe-Neuronen u : δ u := o u ( 1- o u ) (t u -o u ) sowie schichtweise für innere Neuronen v : δ v := o v ( 1 - o v ) u w vu δ u δ u ist der Korrekturwert der nachfolgenden Neuronen u Korrekturwerte der Gewichte: δw uv := η δ u a u 35 Lernen für Mehrschichtige Netze Vorzugeben: Anzahl der Schichten und Neuronen pro Schicht an Problemgröße angepasst Initiale Gewichte häufig alle Neuronen zwischen Schichten verbunden Fehlerschranke ε Lernrate η bestimmt Stärke der Modifikation Simulated annealing: η mit der Zeit verringern 36 18
19 Nochmal: Inductive Bias Hypothese für Generalisierung: Wenn das Netz auf den Trainingsdaten gut arbeitet, wird es auch für alle anderen Daten gute Ergebnisse liefern. Grundsätzlich könnte jedes Netz als Ergebnis genommen werden, das die Trainingsbeispiele korrekt verarbeitet. Das Lernverfahren macht aber zusätzliche Annahmen: Bias bzgl. der gelernten Funktionen bzw. Beispiele: - Stetigkeit: Ähnliche Ausgaben bei ähnlichen Eingaben. - Gleichmäßige Interpolation zwischen Trainingsbeispielen. Bias bzgl. der entstehenden Netze: - Gradientenabstieg für Modifikation der Netze 37 Welche Größe des Netzes ist sinnvoll? Viel hilft nicht viel. Anzahl und Größe der Schichten müssen dem Problem entsprechen (eine Spezialisierung der Neuronen auf individuelle Aufgaben erlauben). Untersuchung: Lernen der Binärkodierung in der verborgenen Schicht (nach Mitchell) Aus Mitchell: Machine Learning 38 19
20 Welche Größe des Netzes ist sinnvoll? Entwicklung der Aktivierungen der verborgenen Neuronen während des Lernens 39 Welche Größe des Netzes ist sinnvoll? Gelernte Kodierung der verborgenen Neuronen 40 20
21 Welche Größe des Netzes ist sinnvoll? Anpassung der Gewichte der Eingabe-Neuronen (mit bias) zu einem der verdeckten Neuronen 41 Welche Größe des Netzes ist sinnvoll? Fehler an den Ausgabe-Neuronen während des Lernens 42 21
22 Welche Größe des Netzes ist sinnvoll? Drei verdeckte Neuronen entsprechen genau der Dimension des Problems, weniger oder mehr Neuronen führen zu schlechteren Ergebnissen. Im besten Fall werden die überzähligen Neuronen mit der Zeit ignoriert. 43 Bestimmung der Größe von Netzen Probieren. Zunächst zu viele Neuronen, dann Neuronen mit wenig Einfluss (geringe Gewichte) eliminieren Zunächst zu wenig Neuronen, dann Neuronen hinzufügen (bei schlechter Konvergenz). Evolutionäre Algorithmen
23 Overfitting Anpassung an zu spezielle Beispiele geht zulasten der Generalisierung (insbesondere bei verrauschten Daten) Gegenstrategie: Beispielmenge D aufteilen in Trainingsmenge D T Validierungsmenge D V Abbruch-Kriterium nur beziehen auf D V Kreuzvalidierung: Mehrfache unterschiedliche Aufteilungen von D in D T und D V 45 Overfitting 46 23
24 Overfitting 47 Anwendungen Klassifizierung, z.b. Schriftzeichen Erkennung von Sprachmustern Reaktive Steuerungen Vorteile: Schnelle Berechnung Robust bzgl. Rauschen in Trainingsdaten Robust bzgl. Ausfall von Neuronen 48 24
25 Charakteristika typischer Anwendungen Eingabe: (reell-wertige) Merkmalsvektoren. Merkmale können auch korreliert sein. Daten können verrauscht sein. Ausgabe: diskret/kontinuierlich Vektor Trainingsverfahren: evtl. langwierig, komplex, wiederholte Versuche Anwendung Ausgabewert wird schnell berechnet Schlechte Kommunizierbarkeit Subsymbolischer Ansatz 49 Schrifterkennung Test mit mit Zeichen aus je 20x20 Pixeln in 8 Graustufen. Netz mit 400 Eingabe-Neuronen, 10 Ausgabe-Neuronen. Beste Ergebnisse bei 300 verdeckten Neuronen (1 Schicht). Trainingszeit: 7 Tage, Fehler-Rate: 1,6 % Laufzeit 0,01 Sekunden, Speicherbedarf 0,5 MB Bessere Klassifizierung mit Support-Vektor-Maschinen (SVM): Fehler-Rate: 0,6 % 50 25
26 Rekurrente Netze Netze mit Rückkopplungen. Gedächtnis. Dynamisches System. 51 Aus Steffen Wischmann: Neural dynamics of social behavior: An evolutionary and mechanistic perspective on communication, cooperation, and competition among situated agents. (Dissertation, Bonn 2007) 52 26
27 Rekurrente Netze: 1 Neuron Netze mit Rückkopplungen. Veränderung der Aktivierung auch ohne Eingabe: Oszillation, Konvergenz u.a. möglich. Diskretes Dynamisches System: a(0), a(1), a(2), b w a(t) = g( w a(t-1) + b + e(t) ) e(t) a(t) 53 Rekurrente Netze: 1 Neuron Transferfunktion g(x) = if x<0 then -1 else +1 Gedächtnis: Werte für a(t) -1 e(t) a(t-1) e(t) a(t) = g( 0.5 a(t-1) + e(t) ) 54 27
28 Rekurrente Netze: 1 Neuron Transferfunktion g(x) = if x<0 then -1 else +1 Oszillation: Werte für a(t) a(t-1) a(t) = g( - a(t-1) ) 55 Rekurrente Netze: 1 Neuron Transferfunktion g(x) = tanh(x) a(t) = tanh( -1.5 a(t-1) ) a(0) = 0 a(1) = 0.46 a(2) = a(3) = 0.66 a(4) = a(5) = 0.83 a(6) = a(7) = 0.89 a(8) = -0,69 a(9) = 0.91 a(10) = a(11) = 0.91 a(12) = a(13) =
29 Scilab-Programm // Einzelnes Neuron // Parameterdefinitionen w = 1; // Rückkopplung, gesetzt bei Aufruf D b = 1; // input bzw. bias, gesetzt bei Aufruf D y = 1; // initiale Aktivierung, gesetzt bei Aufruf D n = 20; // Iterationen function [y] = F(x) y = tanh(w*x+b); endfunction // Definition der Übertragungsfunktion function [G] = GraphF() for kx=1:100 G(kx) = F(kx/10-5); end endfunction //Darstellung der Übertragungsfunktion 57 function [y] = IterateF(y, n) idx = size(y,2); for i=1:n y(idx+i) = F( y(idx+i-1) ); write(%io(2), y(idx+i)); x_vals=[y(idx+i-1) y(idx+i-1)]; y_vals=[y(idx+i-1) y(idx+i)]; plot2d(x_vals,y_vals); // Linie von y=x zu neuem Funkionswert x_vals=[y(idx+i-1) y(idx+i)]; y_vals=[y(idx+i) y(idx+i)]; plot2d(x_vals,y_vals); // Linie von Funktionswert zu y=x plot(-4.9,y(idx+i-1), '--mo'); // Funktionswert end endfunction function D(w0,b0,y0) w=w0; b=b0; y=y0; plot2d([1:100]/10-5, GraphF(),rect=[-5,-2,5,2]); // Übertragungsfunktion plot2d([-2:0.01:2],[-2:0.01:2]); // y=x U = IterateF(y,n); endfunction // Iterationen 58 29
30 Plot Scilab-Programm a(0) = 0 a(1) = 0.46 a(2) = a(3) = 0.66 a(4) = a(5) = 0.83 a(6) = a(7) = 0.89 a(8) = -0,69 a(9) = 0.91 a(10) = a(11) = 0.91 a(12) = a(13) = Rekurrente Netze: 1 Neuron Transferfunktion g(x) = tanh(x) b w e(t) a(t) = tanh( w a(t-1) + b + e ) Verhalten in Abhängigkeit von b und w fl Analyse dynamischer Systeme 60 30
31 Diskrete Dynamische Systeme Zustand x t Übergänge x t+1 =f(x t ) Trajektorie/Orbit x 0, x 1, x 2, x 3, x 4, x 5, Fixpunkt x = f(x) Schnittpunkt von y=f(x) mit y=x x t x t+1 f(x) Attraktor: Zustandsmenge, die Trajektorien anzieht (z.b. stabile Fixpunkte) Bassin: Zustandsmenge, die in einen Attraktor führt Repellor: Gegenteil von Attraktor (z.b. instabile Fixpunkte) 61 Diskrete Dynamische Systeme Beispiel: f(x) = x 2 Trajektorie/Orbit x 0, x 02, x 04, x 08, Stabiler Fixpunkt x=0 Bassin -1< x < 1 Instabiler Fixpunkt x=1 bei kleiner Abweichung Konvergenz gegen 0 oder 1.Ableitung: f (x) = 2x Fixpunkt stabil falls f (x) <
32 Diskrete Dynamische Systeme Beispiel: f(x) = rx - rx 2 = rx(1-x) r=4 logistische Funktion betrachten für 0 x 1 0 r r= r= r= Scilab: Logistische Funktion // Logistische Funktion // Parameterdefinitionen r = 1; // Parameter der log. Fkt., gesetzt bei Aufruf D n = 50; // Iterationen y = 0.6; // Startwert, gesetzt bei Aufruf D function [y] = F(x) // Definition der logistischen Funktion y = r*x*(1-x) endfunction function [G] = GraphF() //Darstellung der logistischen Funktion for kx=1:100 G(kx) = F(kx/100); end endfunction 64 32
33 function [y] = IterateF(y, n) Logistische idx = size(y,2); x_vals=[y Funktion y]; y_vals=[0 y]; plot2d(x_vals,y_vals); // Linie von Startwert zu y=x for i=1:n y(idx+i) = F( y(idx+i-1) ); printf('%5.3f \n', y(idx+i)); x_vals=[y(idx+i-1) y(idx+i-1)]; y_vals=[y(idx+i-1) y(idx+i)]; plot2d(x_vals,y_vals); // Linie von y=x zu neuem Funkionswert x_vals=[y(idx+i-1) y(idx+i)]; y_vals=[y(idx+i) y(idx+i)]; plot2d(x_vals,y_vals); // Linie von Funktionswert zu y=x plot(0,y(idx+i), '--mo'); // Funktionswert end endfunction function D(r0,y0) r=r0; y=y0; plot2d([1:100]/100, GraphF(),rect=[0,0,1,1]); // logist. Fkt. plot2d([0:0.01:1],[0:0.01:1]); // y=x U = IterateF(y,n); // Iterationen endfunction 65 Logistische Funktion f(x) = rx - rx 2 = rx(1-x) Fixpunkte (1) x = 0 stabil (Attraktor) für r 1 mit Bassin [0,1] instabil (Repellor) für r>1 (2) x = (r-1)/r für r 1 stabil (Attraktor) für r<3 mit Bassin [0,1] instabil (Repellor) für r>
34 Logistische Funktion f(x) = rx - rx 2 = rx(1-x) Verhalten für r>3 : 3< r < Orbit der Periode 2 ( d.h. Fixpunkt von f(f(x)), x= f(f(x)) ) < r < weitere Aufspaltungen ( Bifurkationen ) Orbits der Perioden 4, 8, 16, < r < 4 i.a. chaotisches Verhalten dazwischen in einigen Abschnitten auch wieder periodisch (z.b. für r=3,84 ) 67 Bifurkationsdiagramm Logistische Funktion lim t x r Feigenbaumdiagramm: 68 Bifurkationsdiagramm der logistischen Funktion (aus Wikipedia) 34
35 Diskrete Dynamische Systeme Attraktor A: Punktmenge, gegen die benachbarte Trajektorien konvergieren Bassin (Attraktorbecken) U: V Punktmenge, die in Attraktor führen A Separatrix: Grenze eines Bassins U A ist Attraktor mit Bassin U, falls - A ist invariant (keine Trajektorie verlässt A) - Für alle offenen V mit AÕVÕU existiert Zeitpunkt T>0 von dem an Trajektorien aus U ganz in V liegen 69 Diskrete Dynamische Systeme Typen von Attraktoren Stabiler Fixpunkt Periodischer Orbit mit Periode n Quasiperiodischer Orbit Chaotischer Attraktor Repellor: Attraktor von f
36 Diskrete Dynamische Systeme Strukturelle Stabilität: Dynamik des Systems bleibt qualitativ unverändert bei Änderung der Systemparameter. Strukturelle Instabilität (Bifurkationen): Kleine Änderungen der Systemparameter führen zu qualitativen Änderungen (z.b. neue Attraktoren) 71 Rekurrente Netze: 1 Neuron Transferfunktion g(x) = tanh(x) b w e(t) a(t) = tanh( w a(t-1) + b + e(t) ) Verhalten in Abhängigkeit von b und w fl Analyse dynamischer Systeme 72 36
37 Rekurrente Netze: 1 Neuron b = e(t) = 0 w a(t) = tanh( w a(t-1) ) 1 < w 2 stabile Fixpunkte 1 instabiler Fixpunkt (x=0) a(t) in Abhängigkeit von a(t-1) Startwert a(0)= Rekurrente Netze: 1 Neuron b = e(t) = 0 w a(t) = tanh( w a(t-1) ) 0 w 1 1 stabiler Fixpunkt (x=0) a(t) in Abhängigkeit von a(t-1) Startwert a(0)=
38 Rekurrente Netze: 1 Neuron b = e(t) = 0 w a(t) = tanh( w a(t-1) ) -1 w < 0 1 stabiler Fixpunkt (x=0) a(t) in Abhängigkeit von a(t-1) Startwert a(0)= Rekurrente Netze: 1 Neuron b = e(t) = 0 w a(t) = tanh( w a(t-1) ) w < -1 1 instabiler Fixpunkt (x=0) 2-periodischer Orbit a(t) in Abhängigkeit von a(t-1) Startwert a(0)=
39 Rekurrente Netze: 1 Neuron w=2, b+e(t) = -2, -1, 0, 1, 2 b w e(t) a(t) = tanh( w a(t-1) + b + e(t) ) a(t) in Abhängigkeit von a(t-1) Startwert a(0)=0 (Hysterese-Verhalten) Rekurrente Netze Mehr dazu in der Vorlesung Mathematische Grundlagen der Wahrnehmung und Sensomotorik (SS08) von Dr. Manfred Hild 78 39
Neuronale Netze (Konnektionismus) Einführung in die KI. Beispiel-Aufgabe: Schrifterkennung. Biologisches Vorbild. Neuronale Netze.
 Einführung in die KI Prof. Dr. sc. Hans-Dieter Burkhard Vorlesung (Konnektionismus) sind biologisch motiviert können diskrete, reell-wertige und Vektor-wertige Funktionen berechnen Informationsspeicherung
Einführung in die KI Prof. Dr. sc. Hans-Dieter Burkhard Vorlesung (Konnektionismus) sind biologisch motiviert können diskrete, reell-wertige und Vektor-wertige Funktionen berechnen Informationsspeicherung
Neuronale Netze (Konnektionismus)
 Einführung in die KI Prof. Dr. sc. Hans-Dieter Burkhard Daniel Göhring Vorlesung (Konnektionismus) sind biologisch motiviert können diskrete, reell-wertige und Vektor-wertige Funktionen berechnen Informationsspeicherung
Einführung in die KI Prof. Dr. sc. Hans-Dieter Burkhard Daniel Göhring Vorlesung (Konnektionismus) sind biologisch motiviert können diskrete, reell-wertige und Vektor-wertige Funktionen berechnen Informationsspeicherung
Einführung in neuronale Netze
 Einführung in neuronale Netze Florian Wenzel Neurorobotik Institut für Informatik Humboldt-Universität zu Berlin 1. Mai 2012 1 / 20 Überblick 1 Motivation 2 Das Neuron 3 Aufbau des Netzes 4 Neuronale Netze
Einführung in neuronale Netze Florian Wenzel Neurorobotik Institut für Informatik Humboldt-Universität zu Berlin 1. Mai 2012 1 / 20 Überblick 1 Motivation 2 Das Neuron 3 Aufbau des Netzes 4 Neuronale Netze
Was bisher geschah Künstliche Neuronen: Mathematisches Modell und Funktionen: Eingabe-, Aktivierungs- Ausgabefunktion Boolesche oder reelle Ein-und
 Was bisher geschah Künstliche Neuronen: Mathematisches Modell und Funktionen: Eingabe-, Aktivierungs- Ausgabefunktion Boolesche oder reelle Ein-und Ausgaben Aktivierungsfunktionen: Schwellwertfunktion
Was bisher geschah Künstliche Neuronen: Mathematisches Modell und Funktionen: Eingabe-, Aktivierungs- Ausgabefunktion Boolesche oder reelle Ein-und Ausgaben Aktivierungsfunktionen: Schwellwertfunktion
Neuronale Netze mit mehreren Schichten
 Neuronale Netze mit mehreren Schichten Lehrstuhl für Künstliche Intelligenz Institut für Informatik Friedrich-Alexander-Universität Erlangen-Nürnberg (Lehrstuhl Informatik 8) Neuronale Netze mit mehreren
Neuronale Netze mit mehreren Schichten Lehrstuhl für Künstliche Intelligenz Institut für Informatik Friedrich-Alexander-Universität Erlangen-Nürnberg (Lehrstuhl Informatik 8) Neuronale Netze mit mehreren
Kapitel LF: IV. IV. Neuronale Netze
 Kapitel LF: IV IV. Neuronale Netze Perzeptron-Lernalgorithmus Gradientenabstiegmethode Multilayer-Perzeptrons und ackpropagation Self-Organizing Feature Maps Neuronales Gas LF: IV-39 Machine Learning c
Kapitel LF: IV IV. Neuronale Netze Perzeptron-Lernalgorithmus Gradientenabstiegmethode Multilayer-Perzeptrons und ackpropagation Self-Organizing Feature Maps Neuronales Gas LF: IV-39 Machine Learning c
Was bisher geschah. Lernen: überwachtes Lernen. biologisches Vorbild neuronaler Netze: unüberwachtes Lernen
 Was bisher geschah Lernen: überwachtes Lernen korrigierendes Lernen bestärkendes Lernen unüberwachtes Lernen biologisches Vorbild neuronaler Netze: Neuron (Zellkörper, Synapsen, Axon) und Funktionsweise
Was bisher geschah Lernen: überwachtes Lernen korrigierendes Lernen bestärkendes Lernen unüberwachtes Lernen biologisches Vorbild neuronaler Netze: Neuron (Zellkörper, Synapsen, Axon) und Funktionsweise
Kapitel LF: IV. Multilayer-Perzeptrons und Backpropagation. Multilayer-Perzeptrons und Backpropagation. LF: IV Machine Learning c STEIN 2005-06
 Kapitel LF: IV IV. Neuronale Netze Perzeptron-Lernalgorithmus Gradientenabstiegmethode Multilayer-Perzeptrons und ackpropagation Self-Organizing Feature Maps Neuronales Gas 39 Multilayer-Perzeptrons und
Kapitel LF: IV IV. Neuronale Netze Perzeptron-Lernalgorithmus Gradientenabstiegmethode Multilayer-Perzeptrons und ackpropagation Self-Organizing Feature Maps Neuronales Gas 39 Multilayer-Perzeptrons und
Praktikum Computational Intelligence 2 Ulrich Lehmann, Johannes Brenig, Michael Schneider
 Praktikum Computational Intelligence 2 Ulrich Lehmann, Johannes Brenig, Michael Schneider Versuch: Training des XOR-Problems mit einem Künstlichen Neuronalen Netz (KNN) in JavaNNS 11.04.2011 2_CI2_Deckblatt_XORbinaer_JNNS_2
Praktikum Computational Intelligence 2 Ulrich Lehmann, Johannes Brenig, Michael Schneider Versuch: Training des XOR-Problems mit einem Künstlichen Neuronalen Netz (KNN) in JavaNNS 11.04.2011 2_CI2_Deckblatt_XORbinaer_JNNS_2
Maschinelles Lernen: Neuronale Netze. Ideen der Informatik Kurt Mehlhorn
 Maschinelles Lernen: Neuronale Netze Ideen der Informatik Kurt Mehlhorn 16. Januar 2014 Übersicht Stand der Kunst im Bilderverstehen: Klassifizieren und Suchen Was ist ein Bild in Rohform? Biologische
Maschinelles Lernen: Neuronale Netze Ideen der Informatik Kurt Mehlhorn 16. Januar 2014 Übersicht Stand der Kunst im Bilderverstehen: Klassifizieren und Suchen Was ist ein Bild in Rohform? Biologische
Gliederung. Biologische Motivation Künstliche neuronale Netzwerke. Anwendungsbeispiele Zusammenfassung. Das Perzeptron
 Neuronale Netzwerke Gliederung Biologische Motivation Künstliche neuronale Netzwerke Das Perzeptron Aufbau Lernen und Verallgemeinern Anwendung Testergebnis Anwendungsbeispiele Zusammenfassung Biologische
Neuronale Netzwerke Gliederung Biologische Motivation Künstliche neuronale Netzwerke Das Perzeptron Aufbau Lernen und Verallgemeinern Anwendung Testergebnis Anwendungsbeispiele Zusammenfassung Biologische
Neuronale Netze (I) Biologisches Neuronales Netz
 Neuronale Netze (I) Biologisches Neuronales Netz Im menschlichen Gehirn ist ein Neuron mit bis zu 20.000 anderen Neuronen verbunden. Milliarden von Neuronen beteiligen sich simultan an der Verarbeitung
Neuronale Netze (I) Biologisches Neuronales Netz Im menschlichen Gehirn ist ein Neuron mit bis zu 20.000 anderen Neuronen verbunden. Milliarden von Neuronen beteiligen sich simultan an der Verarbeitung
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Künstliches binäres Neuron
 Künstliches binäres Neuron G.Döben-Henisch Fachbereich Informatik und Ingenieurwissenschaften FH Frankfurt am Main University of Applied Sciences D-60318 Frankfurt am Main Germany Email: doeben at fb2.fh-frankfurt.de
Künstliches binäres Neuron G.Döben-Henisch Fachbereich Informatik und Ingenieurwissenschaften FH Frankfurt am Main University of Applied Sciences D-60318 Frankfurt am Main Germany Email: doeben at fb2.fh-frankfurt.de
!(0) + o 1("). Es ist damit möglich, dass mehrere Familien geschlossener Orbits gleichzeitig abzweigen.
 Bifurkationen an geschlossenen Orbits 5.4 167 der Schnittabbldung konstruiert. Die Periode T (") der zugehörigen periodischen Lösungen ergibt sich aus =! + o 1 (") beziehungsweise Es ist also t 0 = T (")
Bifurkationen an geschlossenen Orbits 5.4 167 der Schnittabbldung konstruiert. Die Periode T (") der zugehörigen periodischen Lösungen ergibt sich aus =! + o 1 (") beziehungsweise Es ist also t 0 = T (")
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Einführung. Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Vorlesungen zur Komplexitätstheorie. K-Vollständigkeit (1/5)
 Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
6. Bayes-Klassifikation. (Schukat-Talamazzini 2002)
 6. Bayes-Klassifikation (Schukat-Talamazzini 2002) (Böhm 2003) (Klawonn 2004) Der Satz von Bayes: Beweis: Klassifikation mittels des Satzes von Bayes (Klawonn 2004) Allgemeine Definition: Davon zu unterscheiden
6. Bayes-Klassifikation (Schukat-Talamazzini 2002) (Böhm 2003) (Klawonn 2004) Der Satz von Bayes: Beweis: Klassifikation mittels des Satzes von Bayes (Klawonn 2004) Allgemeine Definition: Davon zu unterscheiden
Extrema von Funktionen in zwei Variablen
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Extrema von Funktionen in zwei Variablen Literatur: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen,
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Extrema von Funktionen in zwei Variablen Literatur: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen,
Algorithmen II Vorlesung am 15.11.2012
 Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Approximation durch Taylorpolynome
 TU Berlin Fakultät II - Mathematik und Naturwissenschaften Sekretariat MA 4-1 Straße des 17. Juni 10623 Berlin Hochschultag Approximation durch Taylorpolynome Im Rahmen der Schülerinnen- und Schüler-Uni
TU Berlin Fakultät II - Mathematik und Naturwissenschaften Sekretariat MA 4-1 Straße des 17. Juni 10623 Berlin Hochschultag Approximation durch Taylorpolynome Im Rahmen der Schülerinnen- und Schüler-Uni
Kohonennetze Selbstorganisierende Karten
 Kohonennetze Selbstorganisierende Karten Julian Rith, Simon Regnet, Falk Kniffka Seminar: Umgebungsexploration und Wegeplanung mit Robotern Kohonennetze: Neuronale Netze In Dendriten werden die ankommenden
Kohonennetze Selbstorganisierende Karten Julian Rith, Simon Regnet, Falk Kniffka Seminar: Umgebungsexploration und Wegeplanung mit Robotern Kohonennetze: Neuronale Netze In Dendriten werden die ankommenden
Rekursionen (Teschl/Teschl 8.1-8.2)
 Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Übungsklausur. Bitte wählen Sie fünf Aufgaben aus! Aufgabe 1. Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr.
 Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr. Gert Zöller Übungsklausur Hilfsmittel: Taschenrechner, Formblatt mit Formeln. Lösungswege sind stets anzugeben. Die alleinige Angabe eines
Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr. Gert Zöller Übungsklausur Hilfsmittel: Taschenrechner, Formblatt mit Formeln. Lösungswege sind stets anzugeben. Die alleinige Angabe eines
Grundlagen des Maschinellen Lernens Kap. 4: Lernmodelle Teil II
 1. Motivation 2. Lernmodelle Teil I 2.1. Lernen im Limes 2.2. Fallstudie: Lernen von Patternsprachen 3. Lernverfahren in anderen Domänen 3.1. Automatensynthese 3.2. Entscheidungsbäume 3.3. Entscheidungsbäume
1. Motivation 2. Lernmodelle Teil I 2.1. Lernen im Limes 2.2. Fallstudie: Lernen von Patternsprachen 3. Lernverfahren in anderen Domänen 3.1. Automatensynthese 3.2. Entscheidungsbäume 3.3. Entscheidungsbäume
Softcomputing Biologische Prinzipien in der Informatik. Neuronale Netze. Dipl. Math. Maria Oelinger Dipl. Inform. Gabriele Vierhuff IF TIF 08 2003
 Softcomputing Biologische Prinzipien in der Informatik Neuronale Netze Dipl. Math. Maria Oelinger Dipl. Inform. Gabriele Vierhuff IF TIF 08 2003 Überblick Motivation Biologische Grundlagen und ihre Umsetzung
Softcomputing Biologische Prinzipien in der Informatik Neuronale Netze Dipl. Math. Maria Oelinger Dipl. Inform. Gabriele Vierhuff IF TIF 08 2003 Überblick Motivation Biologische Grundlagen und ihre Umsetzung
Computational Intelligence I Künstliche Neuronale Netze
 Computational Intelligence I Künstliche Neuronale Nete Universität Dortmund, Informatik I Otto-Hahn-Str. 6, 44227 Dortmund lars.hildebrand@uni-dortmund.de Inhalt der Vorlesung 0. Organisatorisches & Vorbemerkungen.
Computational Intelligence I Künstliche Neuronale Nete Universität Dortmund, Informatik I Otto-Hahn-Str. 6, 44227 Dortmund lars.hildebrand@uni-dortmund.de Inhalt der Vorlesung 0. Organisatorisches & Vorbemerkungen.
Tangentengleichung. Wie lautet die Geradengleichung für die Tangente, y T =? Antwort:
 Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Klausur Mathematik 2
 Mathematik für Ökonomen WS 2014/15 Campus Duisburg PD Dr. V. Krätschmer, Fakultät für Mathematik Klausur Mathematik 2 17.02.2015, 12:30-14:30 Uhr (120 Minuten) Erlaubte Hilfsmittel: Nur reine Schreib-
Mathematik für Ökonomen WS 2014/15 Campus Duisburg PD Dr. V. Krätschmer, Fakultät für Mathematik Klausur Mathematik 2 17.02.2015, 12:30-14:30 Uhr (120 Minuten) Erlaubte Hilfsmittel: Nur reine Schreib-
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Der Backpropagation-Algorithmus als Beispiel für Lernalgorithmen künstlicher neuronaler Netze Reinhard Eck 1
 Der Backpropagation-Algorithmus als Beispiel für Lernalgorithmen künstlicher neuronaler Netze 2.04.2006 Reinhard Eck Was reizt Informatiker an neuronalen Netzen? Wie funktionieren Gehirne höherer Lebewesen?
Der Backpropagation-Algorithmus als Beispiel für Lernalgorithmen künstlicher neuronaler Netze 2.04.2006 Reinhard Eck Was reizt Informatiker an neuronalen Netzen? Wie funktionieren Gehirne höherer Lebewesen?
14. Minimale Schichtdicken von PEEK und PPS im Schlauchreckprozeß und im Rheotensversuch
 14. Minimale Schichtdicken von PEEK und PPS im Schlauchreckprozeß und im Rheotensversuch Analog zu den Untersuchungen an LDPE in Kap. 6 war zu untersuchen, ob auch für die Hochtemperatur-Thermoplaste aus
14. Minimale Schichtdicken von PEEK und PPS im Schlauchreckprozeß und im Rheotensversuch Analog zu den Untersuchungen an LDPE in Kap. 6 war zu untersuchen, ob auch für die Hochtemperatur-Thermoplaste aus
4. Dynamische Optimierung
 4. Dynamische Optimierung Allgemeine Form dynamischer Optimierungsprobleme 4. Dynamische Optimierung Die dynamische Optimierung (DO) betrachtet Entscheidungsprobleme als eine Folge voneinander abhängiger
4. Dynamische Optimierung Allgemeine Form dynamischer Optimierungsprobleme 4. Dynamische Optimierung Die dynamische Optimierung (DO) betrachtet Entscheidungsprobleme als eine Folge voneinander abhängiger
Nichtlineare Optimierung ohne Nebenbedingungen
 Kapitel 2 Nichtlineare Optimierung ohne Nebenbedingungen In diesem Abschnitt sollen im wesentlichen Verfahren zur Bestimmung des Minimums von nichtglatten Funktionen in einer Variablen im Detail vorgestellt
Kapitel 2 Nichtlineare Optimierung ohne Nebenbedingungen In diesem Abschnitt sollen im wesentlichen Verfahren zur Bestimmung des Minimums von nichtglatten Funktionen in einer Variablen im Detail vorgestellt
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
BONUS MALUS SYSTEME UND MARKOV KETTEN
 Fakultät Mathematik und Naturwissenschaften, Fachrichtung Mathematik, Institut für Mathematische Stochastik BONUS MALUS SYSTEME UND MARKOV KETTEN Klaus D. Schmidt Ringvorlesung TU Dresden Fakultät MN,
Fakultät Mathematik und Naturwissenschaften, Fachrichtung Mathematik, Institut für Mathematische Stochastik BONUS MALUS SYSTEME UND MARKOV KETTEN Klaus D. Schmidt Ringvorlesung TU Dresden Fakultät MN,
DIFFERENTIALGLEICHUNGEN
 DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
Entscheidungsbäume. Definition Entscheidungsbaum. Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen?
 Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
In konstanten Modellen wird davon ausgegangen, dass die zu prognostizierende Größe sich über die Zeit hinweg nicht verändert.
 Konstante Modelle: In konstanten Modellen wird davon ausgegangen, dass die zu prognostizierende Größe sich über die Zeit hinweg nicht verändert. Der prognostizierte Wert für die Periode T+i entspricht
Konstante Modelle: In konstanten Modellen wird davon ausgegangen, dass die zu prognostizierende Größe sich über die Zeit hinweg nicht verändert. Der prognostizierte Wert für die Periode T+i entspricht
Theoretische Grundlagen der Informatik WS 09/10
 Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Künstliche neuronale Netze
 Künstliche neuronale Netze Eigenschaften neuronaler Netze: hohe Arbeitsgeschwindigkeit durch Parallelität, Funktionsfähigkeit auch nach Ausfall von Teilen des Netzes, Lernfähigkeit, Möglichkeit zur Generalisierung
Künstliche neuronale Netze Eigenschaften neuronaler Netze: hohe Arbeitsgeschwindigkeit durch Parallelität, Funktionsfähigkeit auch nach Ausfall von Teilen des Netzes, Lernfähigkeit, Möglichkeit zur Generalisierung
Anhand des bereits hergeleiteten Models erstellen wir nun mit der Formel
 Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
(λ Ri I A+BR)v Ri = 0. Lässt sich umstellen zu
 Herleitung der oppenecker-formel (Wiederholung) Für ein System ẋ Ax + Bu (B habe Höchstrang) wird eine Zustandsregelung u x angesetzt. Der geschlossene egelkreis gehorcht der Zustands-Dgl. ẋ (A B)x. Die
Herleitung der oppenecker-formel (Wiederholung) Für ein System ẋ Ax + Bu (B habe Höchstrang) wird eine Zustandsregelung u x angesetzt. Der geschlossene egelkreis gehorcht der Zustands-Dgl. ẋ (A B)x. Die
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Funktionsbeschreibung. Lieferantenbewertung. von IT Consulting Kauka GmbH
 Funktionsbeschreibung Lieferantenbewertung von IT Consulting Kauka GmbH Stand 16.02.2010 odul LBW Das Modul LBW... 3 1. Konfiguration... 4 1.1 ppm... 4 1.2 Zertifikate... 5 1.3 Reklamationsverhalten...
Funktionsbeschreibung Lieferantenbewertung von IT Consulting Kauka GmbH Stand 16.02.2010 odul LBW Das Modul LBW... 3 1. Konfiguration... 4 1.1 ppm... 4 1.2 Zertifikate... 5 1.3 Reklamationsverhalten...
V 2 B, C, D Drinks. Möglicher Lösungsweg a) Gleichungssystem: 300x + 400 y = 520 300x + 500y = 597,5 2x3 Matrix: Energydrink 0,7 Mineralwasser 0,775,
 Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
Absolute Stetigkeit von Maßen
 Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Funktion Erläuterung Beispiel
 WESTFÄLISCHE WILHELMS-UNIVERSITÄT WIRTSCHAFTSWISSENSCHAFTLICHE FAKULTÄT BETRIEBLICHE DATENVERARBEITUNG Folgende Befehle werden typischerweise im Excel-Testat benötigt. Die Beispiele in diesem Dokument
WESTFÄLISCHE WILHELMS-UNIVERSITÄT WIRTSCHAFTSWISSENSCHAFTLICHE FAKULTÄT BETRIEBLICHE DATENVERARBEITUNG Folgende Befehle werden typischerweise im Excel-Testat benötigt. Die Beispiele in diesem Dokument
Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. z(t) = at + b
 Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Prüfungszeiten für den Studiengang Bachelor of Science in Psychologie
 Prüfungszeiten für den Studiengang Bachelor of Science in Psychologie Stand: 1.12.2014 Die folgende Übersicht enthält einen Rahmenterminplan für die Prüfungszeiten nach der Änderung der Prüfungsordnung,
Prüfungszeiten für den Studiengang Bachelor of Science in Psychologie Stand: 1.12.2014 Die folgende Übersicht enthält einen Rahmenterminplan für die Prüfungszeiten nach der Änderung der Prüfungsordnung,
Künstliche Intelligenz Maschinelles Lernen
 Künstliche Intelligenz Maschinelles Lernen Stephan Schwiebert Sommersemester 2009 Sprachliche Informationsverarbeitung Institut für Linguistik Universität zu Köln Maschinelles Lernen Überwachtes Lernen
Künstliche Intelligenz Maschinelles Lernen Stephan Schwiebert Sommersemester 2009 Sprachliche Informationsverarbeitung Institut für Linguistik Universität zu Köln Maschinelles Lernen Überwachtes Lernen
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens 1 Organisatorisches Freitag, 05. Mai 2006: keine Vorlesung! aber Praktikum von 08.00 11.30 Uhr (Gruppen E, F, G, H; Vortestat für Prototyp)
Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens 1 Organisatorisches Freitag, 05. Mai 2006: keine Vorlesung! aber Praktikum von 08.00 11.30 Uhr (Gruppen E, F, G, H; Vortestat für Prototyp)
Konzepte der AI Neuronale Netze
 Konzepte der AI Neuronale Netze Franz Wotawa Institut für Informationssysteme, Database and Artificial Intelligence Group, Technische Universität Wien Email: wotawa@dbai.tuwien.ac.at Was sind Neuronale
Konzepte der AI Neuronale Netze Franz Wotawa Institut für Informationssysteme, Database and Artificial Intelligence Group, Technische Universität Wien Email: wotawa@dbai.tuwien.ac.at Was sind Neuronale
Lineare Gleichungssysteme I (Matrixgleichungen)
 Lineare Gleichungssysteme I (Matrigleichungen) Eine lineare Gleichung mit einer Variable hat bei Zahlen a, b, die Form a b. Falls hierbei der Kehrwert von a gebildet werden darf (a 0), kann eindeutig aufgelöst
Lineare Gleichungssysteme I (Matrigleichungen) Eine lineare Gleichung mit einer Variable hat bei Zahlen a, b, die Form a b. Falls hierbei der Kehrwert von a gebildet werden darf (a 0), kann eindeutig aufgelöst
Elementare Bildverarbeitungsoperationen
 1 Elementare Bildverarbeitungsoperationen - Kantenerkennung - 1 Einführung 2 Gradientenverfahren 3 Laplace-Verfahren 4 Canny-Verfahren 5 Literatur 1 Einführung 2 1 Einführung Kantenerkennung basiert auf
1 Elementare Bildverarbeitungsoperationen - Kantenerkennung - 1 Einführung 2 Gradientenverfahren 3 Laplace-Verfahren 4 Canny-Verfahren 5 Literatur 1 Einführung 2 1 Einführung Kantenerkennung basiert auf
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
Aufabe 7: Baum-Welch Algorithmus
 Effiziente Algorithmen VU Ausarbeitung Aufabe 7: Baum-Welch Algorithmus Florian Fest, Matr. Nr.0125496 baskit@generationfun.at Claudia Hermann, Matr. Nr.0125532 e0125532@stud4.tuwien.ac.at Matteo Savio,
Effiziente Algorithmen VU Ausarbeitung Aufabe 7: Baum-Welch Algorithmus Florian Fest, Matr. Nr.0125496 baskit@generationfun.at Claudia Hermann, Matr. Nr.0125532 e0125532@stud4.tuwien.ac.at Matteo Savio,
Maximizing the Spread of Influence through a Social Network
 1 / 26 Maximizing the Spread of Influence through a Social Network 19.06.2007 / Thomas Wener TU-Darmstadt Seminar aus Data und Web Mining bei Prof. Fürnkranz 2 / 26 Gliederung Einleitung 1 Einleitung 2
1 / 26 Maximizing the Spread of Influence through a Social Network 19.06.2007 / Thomas Wener TU-Darmstadt Seminar aus Data und Web Mining bei Prof. Fürnkranz 2 / 26 Gliederung Einleitung 1 Einleitung 2
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Jan Parthey, Christin Seifert. 22. Mai 2003
 Simulation Rekursiver Auto-Assoziativer Speicher (RAAM) durch Erweiterung eines klassischen Backpropagation-Simulators Jan Parthey, Christin Seifert jpar@hrz.tu-chemnitz.de, sech@hrz.tu-chemnitz.de 22.
Simulation Rekursiver Auto-Assoziativer Speicher (RAAM) durch Erweiterung eines klassischen Backpropagation-Simulators Jan Parthey, Christin Seifert jpar@hrz.tu-chemnitz.de, sech@hrz.tu-chemnitz.de 22.
Wir unterscheiden folgende drei Schritte im Design paralleler Algorithmen:
 1 Parallele Algorithmen Grundlagen Parallele Algorithmen Grundlagen Wir unterscheiden folgende drei Schritte im Design paralleler Algorithmen: Dekomposition eines Problems in unabhängige Teilaufgaben.
1 Parallele Algorithmen Grundlagen Parallele Algorithmen Grundlagen Wir unterscheiden folgende drei Schritte im Design paralleler Algorithmen: Dekomposition eines Problems in unabhängige Teilaufgaben.
Behörde für Bildung und Sport Abitur 2008 Lehrermaterialien zum Leistungskurs Mathematik
 Abitur 8 II. Insektenpopulation LA/AG In den Tropen legen die Weibchen einer in Deutschland unbekannten Insektenpopulation jedes Jahr kurz vor Beginn der Regenzeit jeweils 9 Eier und sterben bald darauf.
Abitur 8 II. Insektenpopulation LA/AG In den Tropen legen die Weibchen einer in Deutschland unbekannten Insektenpopulation jedes Jahr kurz vor Beginn der Regenzeit jeweils 9 Eier und sterben bald darauf.
Modulabschlussklausur Analysis II
 Modulabschlussklausur Analysis II. Juli 015 Bearbeitungszeit: 150 min Aufgabe 1 [5/10 Punkte] Es sei a R und f a : R 3 R mit f a (x, y, z) = x cos(y) + z 3 sin(y) + a 3 + (z + ay a y) cos(x) a) Bestimmen
Modulabschlussklausur Analysis II. Juli 015 Bearbeitungszeit: 150 min Aufgabe 1 [5/10 Punkte] Es sei a R und f a : R 3 R mit f a (x, y, z) = x cos(y) + z 3 sin(y) + a 3 + (z + ay a y) cos(x) a) Bestimmen
Aufgaben zur Flächenberechnung mit der Integralrechung
 ufgaben zur Flächenberechnung mit der Integralrechung ) Geben ist die Funktion f(x) = -x + x. a) Wie groß ist die Fläche, die die Kurve von f mit der x-chse einschließt? b) Welche Fläche schließt der Graph
ufgaben zur Flächenberechnung mit der Integralrechung ) Geben ist die Funktion f(x) = -x + x. a) Wie groß ist die Fläche, die die Kurve von f mit der x-chse einschließt? b) Welche Fläche schließt der Graph
Selbstorganisierende Karten
 Selbstorganisierende Karten Yacin Bessas yb1@informatik.uni-ulm.de Proseminar Neuronale Netze 1 Einleitung 1.1 Kurzüberblick Die Selbstorganisierenden Karten, auch Self-Organizing (Feature) Maps, Kohonen-
Selbstorganisierende Karten Yacin Bessas yb1@informatik.uni-ulm.de Proseminar Neuronale Netze 1 Einleitung 1.1 Kurzüberblick Die Selbstorganisierenden Karten, auch Self-Organizing (Feature) Maps, Kohonen-
Wir haben in den vorherigen Kapiteln verschiedene Verfahren zur Regression und Klassifikation kennengelernt (z.b. lineare Regression, SVMs)
 6. Neuronale Netze Motivation Wir haben in den vorherigen Kapiteln verschiedene Verfahren zur Regression und Klassifikation kennengelernt (z.b. lineare Regression, SVMs) Abstrakt betrachtet sind alle diese
6. Neuronale Netze Motivation Wir haben in den vorherigen Kapiteln verschiedene Verfahren zur Regression und Klassifikation kennengelernt (z.b. lineare Regression, SVMs) Abstrakt betrachtet sind alle diese
Neuronale Netze in der Robotik
 Seminarvortrag Neuronale Netze in der Robotik Datum: 18.01.2002 Vortragende: Elke von Lienen Matrikelnummer: 302489 Studiengang: Informatik Inhaltsverzeichnis Einleitung 3 Biologisches Vorbild 4 Künstliche
Seminarvortrag Neuronale Netze in der Robotik Datum: 18.01.2002 Vortragende: Elke von Lienen Matrikelnummer: 302489 Studiengang: Informatik Inhaltsverzeichnis Einleitung 3 Biologisches Vorbild 4 Künstliche
kurze Wiederholung der letzten Stunde: Neuronale Netze Dipl.-Inform. Martin Lösch (0721) Dipl.-Inform.
 kurze Wiederholung der letzten Stunde: Neuronale Netze martin.loesch@kit.edu (0721) 608 45944 Labor Wissensrepräsentation Aufgaben der letzten Stunde Übersicht Neuronale Netze Motivation Perzeptron Multilayer
kurze Wiederholung der letzten Stunde: Neuronale Netze martin.loesch@kit.edu (0721) 608 45944 Labor Wissensrepräsentation Aufgaben der letzten Stunde Übersicht Neuronale Netze Motivation Perzeptron Multilayer
Ausarbeitung des Seminarvortrags zum Thema
 Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Agile Vorgehensmodelle in der Softwareentwicklung: Scrum
 C A R L V O N O S S I E T Z K Y Agile Vorgehensmodelle in der Softwareentwicklung: Scrum Johannes Diemke Vortrag im Rahmen der Projektgruppe Oldenburger Robot Soccer Team im Wintersemester 2009/2010 Was
C A R L V O N O S S I E T Z K Y Agile Vorgehensmodelle in der Softwareentwicklung: Scrum Johannes Diemke Vortrag im Rahmen der Projektgruppe Oldenburger Robot Soccer Team im Wintersemester 2009/2010 Was
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
 9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
Dialognetze. Ziel : Beschreibung von Methoden und Beschreibungstechniken für den Entwurf und die Dokumentation von Dialogabläufen
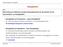 Dialognetze Ziel : Beschreibung von Methoden und Beschreibungstechniken für den Entwurf und die Dokumentation von Dialogabläufen Dialogabläufe auf Fensterebene "grobe Dialogabläufe" d.h. Wechsel zwischen
Dialognetze Ziel : Beschreibung von Methoden und Beschreibungstechniken für den Entwurf und die Dokumentation von Dialogabläufen Dialogabläufe auf Fensterebene "grobe Dialogabläufe" d.h. Wechsel zwischen
Kurzeinführung Moodle
 Kurzeinführung Moodle 1. Einstieg, Kursinhalte, Datei-Download Nachdem Sie sich erfolgreich registriert und eingeloggt haben, gelangen Sie zu Ihrer Hauptseite. Aktivieren Sie Meine Startsteite um Ihren/Ihre
Kurzeinführung Moodle 1. Einstieg, Kursinhalte, Datei-Download Nachdem Sie sich erfolgreich registriert und eingeloggt haben, gelangen Sie zu Ihrer Hauptseite. Aktivieren Sie Meine Startsteite um Ihren/Ihre
Rekursionen. Georg Anegg 25. November 2009. Methoden und Techniken an Beispielen erklärt
 Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
QM: Prüfen -1- KN16.08.2010
 QM: Prüfen -1- KN16.08.2010 2.4 Prüfen 2.4.1 Begriffe, Definitionen Ein wesentlicher Bestandteil der Qualitätssicherung ist das Prüfen. Sie wird aber nicht wie früher nach der Fertigung durch einen Prüfer,
QM: Prüfen -1- KN16.08.2010 2.4 Prüfen 2.4.1 Begriffe, Definitionen Ein wesentlicher Bestandteil der Qualitätssicherung ist das Prüfen. Sie wird aber nicht wie früher nach der Fertigung durch einen Prüfer,
Optimierung für Wirtschaftsinformatiker: Analytische Optimierung ohne Nebenbedingungen
 Optimierung für Wirtschaftsinformatiker: Analytische Optimierung ohne Nebenbedingungen Dr. Nico Düvelmeyer Freitag, 1. Juli 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Einführung und Wiederholung Beispiel
Optimierung für Wirtschaftsinformatiker: Analytische Optimierung ohne Nebenbedingungen Dr. Nico Düvelmeyer Freitag, 1. Juli 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Einführung und Wiederholung Beispiel
1 Part-of-Speech Tagging
 2. Übung zur Vorlesung NLP Analyse des Wissensrohstoes Text im Sommersemester 2008 Dr. Andreas Hotho, Dipl.-Inform. Dominik Benz, Wi.-Inf. Beate Krause 28. Mai 2008 1 Part-of-Speech Tagging 1.1 Grundlagen
2. Übung zur Vorlesung NLP Analyse des Wissensrohstoes Text im Sommersemester 2008 Dr. Andreas Hotho, Dipl.-Inform. Dominik Benz, Wi.-Inf. Beate Krause 28. Mai 2008 1 Part-of-Speech Tagging 1.1 Grundlagen
Aufgabe 1. Zunächst wird die allgemeine Tangentengleichung in Abhängigkeit von a aufgestellt:
 Aufgabe 1 1.1. Bestimmung von D max : 1. Bedingung: x >0 ; da ln(x) nur für x > 0 definiert ist. 2. Bedingung: Somit ist die Funktion f a nur für x > 0 definiert und sie besitzt eine Definitionslücke an
Aufgabe 1 1.1. Bestimmung von D max : 1. Bedingung: x >0 ; da ln(x) nur für x > 0 definiert ist. 2. Bedingung: Somit ist die Funktion f a nur für x > 0 definiert und sie besitzt eine Definitionslücke an
Vorlesungsplan. Von Naïve Bayes zu Bayesischen Netzwerk- Klassifikatoren. Naïve Bayes. Bayesische Netzwerke
 Vorlesungsplan 17.10. Einleitung 24.10. Ein- und Ausgabe 31.10. Reformationstag, Einfache Regeln 7.11. Naïve Bayes, Entscheidungsbäume 14.11. Entscheidungsregeln, Assoziationsregeln 21.11. Lineare Modelle,
Vorlesungsplan 17.10. Einleitung 24.10. Ein- und Ausgabe 31.10. Reformationstag, Einfache Regeln 7.11. Naïve Bayes, Entscheidungsbäume 14.11. Entscheidungsregeln, Assoziationsregeln 21.11. Lineare Modelle,
Anmerkungen zur Übergangsprüfung
 DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
 Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Einführung in Petri-Netze. Modellierung von Abläufen und Prozessen (1) Abhängigkeitsgraphen: Motivation. Petri-Netze
 Einführung in Petri-Netze Modellierung von Abläufen und Prozessen () Motivation Abhängigkeitsgraphen: A B 6 C 5 D Petri-Netze Markierungen Invarianten Credits: L. Priese, H. Wimmel: Petri-Netze, Theoretische
Einführung in Petri-Netze Modellierung von Abläufen und Prozessen () Motivation Abhängigkeitsgraphen: A B 6 C 5 D Petri-Netze Markierungen Invarianten Credits: L. Priese, H. Wimmel: Petri-Netze, Theoretische
Programmiertechnik II
 Analyse von Algorithmen Algorithmenentwurf Algorithmen sind oft Teil einer größeren Anwendung operieren auf Daten der Anwendung, sollen aber unabhängig von konkreten Typen sein Darstellung der Algorithmen
Analyse von Algorithmen Algorithmenentwurf Algorithmen sind oft Teil einer größeren Anwendung operieren auf Daten der Anwendung, sollen aber unabhängig von konkreten Typen sein Darstellung der Algorithmen
Suche in Spielbäumen Spielbäume Minimax Algorithmus Alpha-Beta Suche. Suche in Spielbäumen. KI SS2011: Suche in Spielbäumen 1/20
 Suche in Spielbäumen Suche in Spielbäumen KI SS2011: Suche in Spielbäumen 1/20 Spiele in der KI Suche in Spielbäumen Spielbäume Minimax Algorithmus Alpha-Beta Suche Einschränkung von Spielen auf: 2 Spieler:
Suche in Spielbäumen Suche in Spielbäumen KI SS2011: Suche in Spielbäumen 1/20 Spiele in der KI Suche in Spielbäumen Spielbäume Minimax Algorithmus Alpha-Beta Suche Einschränkung von Spielen auf: 2 Spieler:
Anwendungsbeispiele Buchhaltung
 Rechnungen erstellen mit Webling Webling ist ein Produkt der Firma: Inhaltsverzeichnis 1 Rechnungen erstellen mit Webling 1.1 Rechnung erstellen und ausdrucken 1.2 Rechnung mit Einzahlungsschein erstellen
Rechnungen erstellen mit Webling Webling ist ein Produkt der Firma: Inhaltsverzeichnis 1 Rechnungen erstellen mit Webling 1.1 Rechnung erstellen und ausdrucken 1.2 Rechnung mit Einzahlungsschein erstellen
Programmieren I. Kapitel 7. Sortieren und Suchen
 Programmieren I Kapitel 7. Sortieren und Suchen Kapitel 7: Sortieren und Suchen Ziel: Varianten der häufigsten Anwendung kennenlernen Ordnung Suchen lineares Suchen Binärsuche oder Bisektionssuche Sortieren
Programmieren I Kapitel 7. Sortieren und Suchen Kapitel 7: Sortieren und Suchen Ziel: Varianten der häufigsten Anwendung kennenlernen Ordnung Suchen lineares Suchen Binärsuche oder Bisektionssuche Sortieren
Hinweise zum Ausfüllen der Zeiterfassung
 Hinweise zum Ausfüllen der Zeiterfassung Generelle Hinweise zu Excel Ab Version VSA 4.50 wird die dezimale Schreibweise für Zeiteingaben verwendet. Die Zeiterfassung, die Sie erhalten haben wurde für Excel
Hinweise zum Ausfüllen der Zeiterfassung Generelle Hinweise zu Excel Ab Version VSA 4.50 wird die dezimale Schreibweise für Zeiteingaben verwendet. Die Zeiterfassung, die Sie erhalten haben wurde für Excel
Kevin Caldwell. 18.April 2012
 im Rahmen des Proseminars Numerische Lineare Algebra von Prof.Dr.Sven Beuchler 18.April 2012 Gliederung 1 2 3 Mathematische Beschreibung von naturwissenschaftlich-technischen Problemstellungen führt häufig
im Rahmen des Proseminars Numerische Lineare Algebra von Prof.Dr.Sven Beuchler 18.April 2012 Gliederung 1 2 3 Mathematische Beschreibung von naturwissenschaftlich-technischen Problemstellungen führt häufig
6.2 Scan-Konvertierung (Scan Conversion)
 6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
i x k k=1 i u i x i v i 1 0,2 24 24 0,08 2 0,4 30 54 0,18 3 0,6 54 108 0,36 4 0,8 72 180 0,60 5 1,0 120 300 1,00 2,22 G = 1 + 1 n 2 n i=1
 1. Aufgabe: Der E-Commerce-Umsatz (in Millionen Euro) der fünf größten Online- Shopping-Clubs liegt wie folgt vor: Club Nr. Umsatz 1 120 2 72 3 54 4 30 5 24 a) Bestimmen Sie den Ginikoeffizienten. b) Zeichnen
1. Aufgabe: Der E-Commerce-Umsatz (in Millionen Euro) der fünf größten Online- Shopping-Clubs liegt wie folgt vor: Club Nr. Umsatz 1 120 2 72 3 54 4 30 5 24 a) Bestimmen Sie den Ginikoeffizienten. b) Zeichnen
