Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012
|
|
|
- Martina Waltz
- vor 5 Jahren
- Abrufe
Transkript
1 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1
2 Abgeschlossenheit (Definition) Gegeben sei eine Menge M und ein n-ärer Operator f : M M M. Man sagt, eine Menge M M ist unter f abgeschlossen, wenn für n beliebige Elemente m 1,..., m n M gilt: f (m 1,..., m n ) M. Beispiel: Sei M = N und M = {i i N und i ist gerade}. Sei f der Multiplikationsoperator, d.h. f (x, y) = x y. M ist abgeschlossen unter f, denn das Produkt zweier gerader Zahlen ist wieder eine gerade Zahl. Sei nun g die Operation: g(x) = x/2, wobei / der Ganzzahldivision entspricht. M ist nicht unter der Operation g abgeschlossen. Ein Gegenbeispiel ist: g(6) = 6/2 = 3. Sander Bruggink Automaten und Formale Sprachen 169
3 Wir betrachten hier für die Menge aller regulären Sprachen. Die interessante Frage ist: Falls L 1, L 2 regulär sind, sind dann auch L 1 L 2, L 1 L 2, L 1 L 2, L 1 = Σ \L 1 (Komplement) und L 1 regulär? Kurze Antwort: Die regulären Sprachen sind unter allen diesen Operationen abgeschlossen. Sander Bruggink Automaten und Formale Sprachen 170
4 Abschluss unter Vereinigung Wenn L 1 und L 2 reguläre Sprachen sind, dann ist auch L 1 L 2 regulär. Beweis: Da L 1 und L 2 nach Annahme regulär sind, gibt es reguläre Ausdrücke α 1 und α 2 mit L(α 1 ) = L 1 und L(α 2 ) = L 2. Der reguläre Ausdruck α 1 α 2 erzeugt nun die Sprache L 1 L 2 und von daher ist sie regulär. Sander Bruggink Automaten und Formale Sprachen 171
5 Abschluss unter Produkt/Konkatenation Wenn L 1 und L 2 reguläre Sprachen sind, dann ist auch L 1 L 2 = {w 1 w 2 w 1 L 1, w 2 L 2 } regulär. Beweis: Da L 1 und L 2 nach Annahme regulär sind, gibt es reguläre Ausdrücke α 1 und α 2 mit L(α 1 ) = L 1 und L(α 2 ) = L 2. Der reguläre Ausdruck α 1 α 2 erzeugt nun die Sprache L 1 L 2 und von daher ist sie regulär. Sander Bruggink Automaten und Formale Sprachen 172
6 Abschluss unter der Stern-Operation Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Da L nach Annahme regulär ist, gibt es einen regulären Ausdruck α mit L(α) = L. Der reguläre Ausdruck α erzeugt dann die Sprache L. Da es einen regulären Ausdruck für die Sprache gibt, ist sie regulär. Sander Bruggink Automaten und Formale Sprachen 173
7 Abschluss unter Komplement Wenn L eine reguläre Sprache ist, dann ist auch L = Σ \L regulär. Bemerkung: bei Bildung des Komplements muss immer festgelegt werden, bezüglich welcher Obermenge das Komplement gebildet werden soll. Hier ist das die Menge Σ aller Wörter über dem Alphabet Σ, das gerade betrachtet wird. Sander Bruggink Automaten und Formale Sprachen 174
8 Beweis: Da L nach Annahme regulär ist, gibt es einen DFA M = (Z, Σ, δ, z 0, E) mit T (M) = L. Dieser Automat wird einfach in einen Automaten M für L umgewandelt, indem man die End- und Nicht-Endzustände vertauscht. D.h. M = (Z, Σ, δ, z 0, Z\E). Dann gilt: w L ˆδ(z 0, w) E ˆδ(z 0, w) Z\E w L. Weil es einen DFA M für L gibt, ist L regulär. Sander Bruggink Automaten und Formale Sprachen 175
9 Abgeschlossenheit unter Komplement b z 0 c z 1 a z 2 c z E a b b, c a b a, b, c z 0 c z 1 a z 2 c z E a b b, c a a, b, c Sander Bruggink Automaten und Formale Sprachen 176
10 Abschluss unter Schnitt Wenn L 1 und L 2 reguläre Sprachen sind, dann ist auch L 1 L 2 regulär. Beweis: Es gilt L 1 L 2 = L 1 L 2 und wir wissen bereits, dass reguläre Sprachen unter Komplement und Vereinigung abgeschlossen sind. Sander Bruggink Automaten und Formale Sprachen 177
11 Kreuzproduktkonstruktion Es gibt noch eine direkte Konstruktion. Dabei werden die zwei Automaten für L 1 und L 2 miteinander synchronisiert und quasi parallelgeschaltet. Dies erfolgt durch das Bilden des Kreuzprodukts. Seien M 1 = (Z 1, Σ, δ 1, s 1, E 1 ) und M 2 = (Z 2, Σ, δ 2, s 2, E 2 ) DFAs mit T (M 1 ) = L 1 und T (M 2 ) = L 2. Dann akzeptiert folgender Automat M die Sprache L 1 L 2 : M = (Z 1 Z 2, Σ, δ, (s 1, s 2 ), E 1 E 2 ), wobei δ((z 1, z 2 ), a) = (δ 1 (z 1, a), δ 2 (z 2, a)). M akzeptiert ein Wort w genau dann, wenn sowohl M 1 als auch M 2 das Wort w akzeptieren. Sander Bruggink Automaten und Formale Sprachen 178
12 Warum sind interessant? Zeigen, dass eine Sprache regulär ist. Kompliziertere reguläre Sprachen können aus einfacheren zusammengebaut werden. Zeigen, dass eine Sprache nicht regulär ist. Manchmal ist es z.b. einfacher zu beweisen, dass das Komplement oder der Schnitt einer Sprache mit einer regulären Sprachen nicht regulär ist. Sander Bruggink Automaten und Formale Sprachen 179
13 Algorithmen Algorithmen für Probleme Wir diskutieren nun, ob es Verfahren bzw. Algorithmen gibt, um Fragestellungen bzw. Probleme für reguläre Sprachen zu lösen. Die allgemeine Form der Fragestellungen ist: Gegeben seien reguläre Sprachen L 1, L 2. Gilt für diese Sprachen, dass...? Dabei nehmen wir an, dass reguläre Sprachen als DFAs, NFAs, Grammatiken oder reguläre Ausdrücke gegeben sind. Sander Bruggink Automaten und Formale Sprachen 178
14 Algorithmen für Probleme Algorithmen Probleme Wortproblem: Gegeben eine reguläre Sprache L und w Σ. Gilt w L? Leerheitsproblem: Gegeben eine reguläre Sprache L. Gilt L =? Endlichkeitsproblem: Gegeben eine reguläre Sprache L. Ist L endlich? Schnittproblem: Gegeben zwei reguläre Sprachen L 1, L 2. Gilt L 1 L 2 =? Inklusionsproblem: Gegeben zwei reguläre Sprachen L 1, L 2. Gilt L 1 L 2? Äquivalenzproblem: Gegeben zwei reguläre Sprachen L 1, L 2. Gilt L 1 = L 2? Sander Bruggink Automaten und Formale Sprachen 179
15 Algorithmen für Probleme Algorithmen Wortproblem (w L?) Gegeben sind L und w Σ. Lösung: Bestimme einen DFA M für L und verfolge die Zustandsübergänge von M, wie durch w vorgegeben. Endzustand wird erreicht w L Nicht-Endzustand wird erreicht w L Sander Bruggink Automaten und Formale Sprachen 180
16 Algorithmen für Probleme Algorithmen Leerheitsproblem (L =?) Gegeben ist L. Lösung: Bestimme einen NFA M für L. L = es gibt keinen Pfad von einem Start- zu einem Endzustand. Sander Bruggink Automaten und Formale Sprachen 181
17 Algorithmen für Probleme Algorithmen Endlichkeitsproblem (Ist L endlich?) Gegeben ist L. Lösung: Bestimme einen NFA M für L. L ist unendlich in M gibt es unendlich viele Pfade von einem Start- zu einem Endzustand es gibt einen erreichbaren Zyklus in M, von dem aus wiederum ein Endzustand erreichbar ist. Sander Bruggink Automaten und Formale Sprachen 182
18 Algorithmen für Probleme Algorithmen Schnittproblem (L 1 L 2 =?) Gegeben sind L 1, L 2. Lösung: Bestimme DFAs M 1, M 2 für L 1, L 2 und bilde das Kreuzprodukt von M 1, M 2. Wende dann den Leerheitstest auf das Kreuzprodukt an. Sander Bruggink Automaten und Formale Sprachen 183
19 Algorithmen für Probleme Algorithmen Inklusionsproblem (L 1 L 2?) Gegeben sind L 1, L 2. Lösung: Es gilt L 1 L 2 genau dann, wenn L 1 L 2 =. Da Schnitt und Komplement konstruktiv bestimmbar sind und ein Leerheitstest existiert, kann damit das Inklusionsproblem gelöst werden. Sander Bruggink Automaten und Formale Sprachen 184
20 Algorithmen für Probleme Algorithmen Äquivalenzproblem (L 1 = L 2?) Gegeben sind L 1, L 2. Lösung 1: Bestimme jeweils zu L 1 und L 2 die minimalen DFAs. Wenn die DFAs gleich sind (evtl. nach Umbenennung der Zuständen), dann sind L 1 und L 2 gleich. Lösung 2: Es gilt L 1 = L 2 genau dann, wenn L 1 L 2 und L 1 L 2. Das Inklusionsproblem ist wie wir vorher gesehen haben lösbar. Sander Bruggink Automaten und Formale Sprachen 185
21 Algorithmen für Probleme Algorithmen Effizienzgesichtspunkte: Je nach dem in welcher Darstellung eine Sprache L gegeben ist, kann die Komplexität der oben beschriebenen Verfahren sehr unterschiedlich ausfallen. Beispiel Äquivalenzproblem: L 1, L 2 gegeben als DFAs Komplexität O(n 2 ) (d.h., quadratisch viele Schritte in der Größe der Eingabe) L 1, L 2 gegeben als Grammatiken, reguläre Ausdrücke oder NFAs Komplexität NP-hart Das bedeutet unter anderem: es ist nicht bekannt, wie dieses Problem effizient gelöst werden kann. Mehr zum Thema Komplexität in der Vorlesung Berechenbarkeit und Komplexität im Wintersemester. Sander Bruggink Automaten und Formale Sprachen 186
22 Anwendung: Modellverifikation Programmverifikation mit regulären Sprachen System Spezifikation Modellierung Modellierung endliche Automaten Systemmodell Spezifikationsmodell Model Checker Yes No Sander Bruggink Automaten und Formale Sprachen 187
23 Programmverifikation mit regulären Sprachen Anwendung: Modellverifikation In unserem Fall: Das Systemmodell ist ein NFA Sys, der alle möglichen Systemabläufe akzeptiert. Das Spezifikationsmodell ist ein NFA Spec, der alle erlaubten Systemabläufe akzeptiert. Wir verifizieren eine Sicherheitseigenschaft. Das heißt, das Spec die erlaubte Abläufe des Systems angibt. Wir ermitteln also, ob: L(Sys) L(Spec) Sander Bruggink Automaten und Formale Sprachen 188
24 Programmverifikation mit regulären Sprachen Anwendung: Verifikation Beispiel: wechselseitiger Ausschluss (eng.: mutual exclusion) Wir betrachten zwei Prozesse P 1, P 2, die auf eine gemeinsame Ressource zugreifen wollen. Jeder Prozess hat einen sogenannten kritischen Bereich, in dem auf die Ressource zugegriffen wird. Es darf sich jeweils nur ein Prozess im kritischen Bereich befinden. Es stehen gemeinsame Variable zur Verfügung, über die sich die Prozesse synchronisieren können. Diese Variablen sind jedoch keine Semaphore, d.h., eine atomare Operation, bei der gleichzeitig gelesen und geschrieben wird, ist nicht möglich. Wir möchten zeigen, dass der wechselseitige Ausschluss gewährleistet ist und dass gewisse Fairnessbedingungen (jeder Prozess kommt irgendwann an die Reihe) eingehalten werden. Sander Bruggink Automaten und Formale Sprachen 189
25 Programmverifikation mit regulären Sprachen Anwendung: Verifikation Versuch 1: Beide Prozesse P 1, P 2 verwenden eine gemeinsame Boolesche Variable f, die mit false initialisiert wird. Programmcode für P 1, P 2 while true do 1: if (f = false?) then 2: f := true 3: Betrete kritischen Bereich... 4: Verlasse kritischen Bereich 5: f := false end end Sander Bruggink Automaten und Formale Sprachen 190
26 Programmverifikation mit regulären Sprachen Anwendung: Verifikation Vorgang: Gebe Automaten P 1 und P 2 für die beiden Prozesse an. Gebe einen Automaten F für den Wert der Variable an. Berechne das Kreuzprodukt M Sys der obigen drei Automaten (dieser Automat modelliert das Gesamtverhalten des Systems). Gebe einen Automaten M Spec für die Spezifikation an. Finde heraus, ob L(M Sys ) L(M Spec ). Sander Bruggink Automaten und Formale Sprachen 191
27 Programmverifikation mit regulären Sprachen Anwendung: Verifikation Wir verwenden folgendes Alphabet, bestehend aus den Programm-Befehlen und den Abfragen der Booleschen Variablen: Σ = {(f := true) i, (f := false) i, (f = true?) i, (f = false?) i i {1, 2}} (Synchronisation von Prozess i mit Variable f ) {BkB i, VkB i i {1, 2}} (Prozess i betritt/verläßt kritischen Bereich). Der Index i {1, 2} gibt an, ob die jeweilige Aktion vom ersten oder vom zweiten Prozess ausgeführt wird. Sander Bruggink Automaten und Formale Sprachen 192
28 Anwendung: Verifikation Programmverifikation mit regulären Sprachen Beschreibung der Abläufe eines Prozesses i als endlicher Automat: (f = true?) i i P i 1 (f = false?) i 2 (f := true) i i (f := false) i 3 i 5 VkB i 4 BkB i i mit i = {(f :=true) i, (f :=false) i, (f =true?) i, (f =false?) i BkB j, VkB j } wobei j = 2, falls i = 1, und j = 1, falls i = 2. i Sander Bruggink Automaten und Formale Sprachen 193
29 Anwendung: Verifikation Programmverifikation mit regulären Sprachen Beschreibung der Booleschen Variable f durch einen Automaten: f F (f = false?) 1 (f := false) 1 (f = false?) 1 2 (f := false) 2 (f := true) 1 (f := true) 2 (f := false) 1 (f := false) 2 (f = true?) 1 (f = true?) 2 2 (f := true) 1 (f := true) 2 f mit f = {BkB 1, VkB 1, BkB 2, VkB 2 }. Sander Bruggink Automaten und Formale Sprachen 194
30 Anwendung: Verifikation Programmverifikation mit regulären Sprachen Die Sprache aller Abläufe des Gesamtsystems ist T (P 1 ) T (P 2 ) T (F ). Der Automat WA, der alle Abläufe beschreibt, die den wechselseitigen Ausschluß erfüllen (beide Prozesse sind nicht gleichzeitig im kritischen Bereich) sieht folgendermaßen aus: WA BkB 1 VkB 2 Σ\{VkB 1, BkB 2 } Σ\{BkB 1, VkB 2 } VkB 1 BkB 2 Σ\{BkB 1, BkB 2 } Damit ist zu zeigen T (P 1 ) T (P 2 ) T (F ) T (WA). Sander Bruggink Automaten und Formale Sprachen 195
31 Programmverifikation mit regulären Sprachen Anwendung: Verifikation Kodierung für Grail: (f := true) 1 a (f := true) 2 A (f := false) 1 b (f := false) 2 B (f = true?) 1 c (f = true?) 2 C (f = false?) 1 d (f = false?) 2 D BkB 1 x BkB 2 X VkB 1 y VkB 2 Y Sander Bruggink Automaten und Formale Sprachen 196
32 Programmverifikation mit regulären Sprachen Anwendung: Verifikation Automaten-Dateien: p1.aut, p2.aut, f.aut, wa.aut. Benutzte Grail-Werkzeuge: fmcross aut1 < aut2 > res erzeugt das Kreuzprodukt von aut1 und aut2 und speichert das Ergebnis in res. fmcment aut > res erzeugt das Komplement des aut und speichert es in res. fmenum aut zählt die Wörter in der vom Automaten aut akzeptierten Sprache auf. Sander Bruggink Automaten und Formale Sprachen 197
33 Anwendung: Verifikation Programmverifikation mit regulären Sprachen Die entstehende Sprache ist nicht leer! Es gibt also Abläufe, die die Bedingung des wechselseitigen Ausschluss verletzen. Einer davon ist DdAXax. Übersetzt ins ursprüngliche Alphabet: (f = false?) 2 (f = false?) 1 (f := true) 2 BkB 2 (f := true) 1 BkB 1. Grund für die Verletzung des wechselseitigen Ausschlusses: Es gibt keine atomare Schreib- und Leseoperation. Daher können beide Prozessen nacheinander die Variable auslesen, anschließend setzen beide die Variable und betreten den kritischen Bereich. Der Algorithmus ist also falsch! Sander Bruggink Automaten und Formale Sprachen 198
34 Anwendung: Verifikation Programmverifikation mit regulären Sprachen Versuch 2: Wir betrachten nun das Verfahren zum wechselseitigen Ausschluss von Lamport. Dabei betrachten wir: zwei Prozesse P 1, P 2 mit unterschiedlichem Programmcode und zwei Boolesche Variable f 1, f 2 (beide initialisiert mit false). Sander Bruggink Automaten und Formale Sprachen 199
35 Anwendung: Verifikation Programmverifikation mit regulären Sprachen Prozess P 1 : while true do 1: f 1 := true 2: while (f 2 = true?) do skip end 3: Betrete kritischen Bereich... 4: Verlasse kritischen Bereich 5: f 1 := false end skip : Null-Operation (hat keine Auswirkungen) Sander Bruggink Automaten und Formale Sprachen 200
36 Programmverifikation mit regulären Sprachen Anwendung: Verifikation Prozess P 2 while true do 1: f 2 := true 2: if (f 1 = true?) then do 3: f 2 := false 4: while (f 1 = true?) do skip end else 5: Betrete kritischen Bereich... 6: Verlasse kritischen Bereich 7: f 2 := false end end Sander Bruggink Automaten und Formale Sprachen 201
37 Programmverifikation mit regulären Sprachen Anwendung: Verifikation In diesem Fall betrachten wir folgendes Alphabet Σ: Σ = {(f 1 := false) i, (f 2 := false) i, (f 1 = false?) i, (f 2 = false?) i, (f 1 := true) i, (f 2 := true) i, (f 1 = true?) i, (f 2 = true?) i, BkB i, VkB i i {1, 2}} Sander Bruggink Automaten und Formale Sprachen 202
38 Anwendung: Verifikation Programmverifikation mit regulären Sprachen Automat für den Prozess P 1 : 1 (f 1 := true) 1 (f 2 = false?) (f 2 = true?) 1 BkB 1 P 1 (f 1 := false) 1 5 VkB 1 4 Dabei gilt, dass all mögliche Aktionen von Prozess 2 enthält. Sander Bruggink Automaten und Formale Sprachen 203
39 Anwendung: Verifikation Programmverifikation mit regulären Sprachen Automat für den Prozess P 2 : (f 1 = true?) 2 (f 1 = false?) 2 4 (f 2 := false) 2 1 (f 2 := true) 2 2 (f 1 = true?) 2 3 (f 2 := false) VkB 2 BkB 2 5 (f 1 = false?) 2 P 2 Dabei gilt, dass all mögliche Aktionen von Prozess 1 enthält. Sander Bruggink Automaten und Formale Sprachen 204
40 Programmverifikation mit regulären Sprachen Anwendung: Verifikation Automaten für die beiden Variablen: 1 2 F 1 F 2 (f 1 = false?) 2 1 (f 1 := false) 1 (f 2 = false?) 1 1 (f 2 := false) 2 (f 1 := true) 1 (f 1 := false) 1 (f 2 := true) 2 (f 2 := false) 2 (f 1 = true?) 2 2 (f 1 := true) 1 (f 2 = true?) 1 2 (f 2 := true) = {(f 2 := true) 2, (f 2 := false) 2, (f 2 = true?) 1, (f 2 = false?) 1 BkB 1, BkB 2, VkB 1, VkB 2 Analog für 2. Sander Bruggink Automaten und Formale Sprachen 205
41 Programmverifikation mit regulären Sprachen Anwendung: Verifikation Kodierung für Grail: (f 1 := true) 1 a (f 2 := true) 2 A BkB 1 x (f 1 := false) 1 b (f 2 := false) 2 B BkB 2 X (f 2 = true?) 1 c (f 1 = true?) 2 C VkB 1 y (f 2 = false?) 1 d (f 1 = false?) 2 D VkB 2 Y Jetzt sind die Systemabläufe in den erlaubten Systemabläufe enthalten. Das Protokoll ist also korrekt. Sander Bruggink Automaten und Formale Sprachen 206
42 Programmverifikation mit regulären Sprachen Anwendung: Verifikation Zusammenfassung Verifikation: Wir haben mit Hilfe von endlichen Automaten zwei Protokolle modelliert, die wechselseitigen Ausschluss realisieren sollen. Mit Hilfe der Lösungsverfahren für das Inklusionsbzw. Schnittproblem konnten wir überprüfen, ob diese Protokolle tatsächlich wechselseitigen Ausschluss realisieren. Das bedeutet: die vorgestellten Verfahren können zur Programmverifikation eingesetzt werden. Sander Bruggink Automaten und Formale Sprachen 207
Abschlusseigenschaften. Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Abschlusseigenschaften
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Abgeschlossenheit (Definition) Gegeben sei eine Menge M und ein n-ärer
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Abgeschlossenheit (Definition) Gegeben sei eine Menge M und ein n-ärer
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Ersetzungsverfahren: Grammatiken
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Ersetzungsverfahren: Grammatiken
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Einschub: Kellerautomaten
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Einschub: Kellerautomaten
Theorie der Informatik
 Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Beweisidee: 1 Verwende den Keller zur Simulation der Grammatik. Leite ein Wort. 2 Problem: der Keller darf nicht beliebig verwendet werden, man kann
 Automaten und Formale prachen alias Theoretische Informatik ommersemester 2011 Dr. ander Bruggink Übungsleitung: Jan tückrath Wir beschäftigen uns ab jetzt einige Wochen mit kontextfreien prachen: Kontextfreie
Automaten und Formale prachen alias Theoretische Informatik ommersemester 2011 Dr. ander Bruggink Übungsleitung: Jan tückrath Wir beschäftigen uns ab jetzt einige Wochen mit kontextfreien prachen: Kontextfreie
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2011
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2011 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Wir beschäftigen uns ab
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2011 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Wir beschäftigen uns ab
FORMALE SYSTEME. 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten. TU Dresden, 14. November 2016.
 FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
Kontextfreie Sprachen. Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Kontextfreie Sprachen
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Wortproblem: der CYK-Algorithmus Pumping Lemma für kontextfreie Sprachen
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Wortproblem: der CYK-Algorithmus Pumping Lemma für kontextfreie Sprachen
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
 Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Abschlusseigenschaften
 Abschlusseigenschaften Die Klasse der regulären Sprachen hat eine große Zahl nützlicher Eigenschaften, insbesondere die folgenden Abschlusseigenschaften: Satz: Die Klasse der regulären Sprachen ist abgeschlossen
Abschlusseigenschaften Die Klasse der regulären Sprachen hat eine große Zahl nützlicher Eigenschaften, insbesondere die folgenden Abschlusseigenschaften: Satz: Die Klasse der regulären Sprachen ist abgeschlossen
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2013
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2013 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Reguläre Ausdrücke Wozu
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2013 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Reguläre Ausdrücke Wozu
Algorithmen mit konstantem Platzbedarf: Die Klasse REG
 Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden kann.
 Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Satz (Abschluß unter der Stern-Operation)
 Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Adventure-Problem. Vorlesung Automaten und Formale Sprachen Sommersemester Adventure-Problem
 -Problem Vorlesung Automaten und Formale Sprachen Sommersemester 2018 Prof. Barbara König Übungsleitung: Christina Mika-Michalski Zum Aufwärmen: wir betrachten das sogenannte -Problem, bei dem ein Abenteurer/eine
-Problem Vorlesung Automaten und Formale Sprachen Sommersemester 2018 Prof. Barbara König Übungsleitung: Christina Mika-Michalski Zum Aufwärmen: wir betrachten das sogenannte -Problem, bei dem ein Abenteurer/eine
2.2 Reguläre Sprachen Endliche Automaten
 2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
2.2 Nichtdeterministische endliche Automaten
 2 Endliche Automaten arbeiten und hier kann dann ggf. auch wieder auf die Konstruktion verwiesen werden. Fragen 1. Wie viele Informationen kann man in einem DFA speichern? a) beliebig viele b) endlich
2 Endliche Automaten arbeiten und hier kann dann ggf. auch wieder auf die Konstruktion verwiesen werden. Fragen 1. Wie viele Informationen kann man in einem DFA speichern? a) beliebig viele b) endlich
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit. Zugangsnummer: 9201
 Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Wiederholung Kapitel 3 und 4 http://pingo.upb.de Zugangsnummer: 9201 Dozent: Jun.-Prof. Dr.
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Wiederholung Kapitel 3 und 4 http://pingo.upb.de Zugangsnummer: 9201 Dozent: Jun.-Prof. Dr.
FORMALE SYSTEME. Der Satz von Myhill und Nerode. Automaten verkleinern mit Quotientenbildung. Verschiedene Äquivalenzrelationen
 Automaten verkleinern mit Quotientenbildung Wir betrachten DFAs mit totaler Übergangsfunktion. FORMALE SYSTEME 9. Vorlesung: Minimale Automaten (2) Markus Krötzsch TU Dresden, 9. November 207 C 0 A 0 [A]
Automaten verkleinern mit Quotientenbildung Wir betrachten DFAs mit totaler Übergangsfunktion. FORMALE SYSTEME 9. Vorlesung: Minimale Automaten (2) Markus Krötzsch TU Dresden, 9. November 207 C 0 A 0 [A]
Das Pumping Lemma: Ein Anwendungsbeispiel
 Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
FORMALE SYSTEME. 3. Vorlesung: Endliche Automaten. TU Dresden, 17. Oktober Markus Krötzsch
 FORMALE SYSTEME 3. Vorlesung: Endliche Automaten Markus Krötzsch TU Dresden, 17. Oktober 2016 Rückblick Markus Krötzsch, 17. Oktober 2016 Formale Systeme Folie 2 von 31 Wiederholung Mit Grammatiken können
FORMALE SYSTEME 3. Vorlesung: Endliche Automaten Markus Krötzsch TU Dresden, 17. Oktober 2016 Rückblick Markus Krötzsch, 17. Oktober 2016 Formale Systeme Folie 2 von 31 Wiederholung Mit Grammatiken können
a b b a Alphabet und Wörter - Zusammengefasst Formale Grundlagen der Informatik 1 Kapitel 2 Endliche Automaten und reguläre Sprachen
 Formale Grundlagen der Informatik Kapitel 2 und reguläre Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de 5. April 26 Frank Heitmann heitmann@informatik.uni-hamburg.de /52 Alphabet und Wörter
Formale Grundlagen der Informatik Kapitel 2 und reguläre Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de 5. April 26 Frank Heitmann heitmann@informatik.uni-hamburg.de /52 Alphabet und Wörter
Suche nach einem solchen Kreis. Endlichkeitstest. Vereinigung und Durchschnitt. Abschlusseigenschaften
 Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
3. Vorlesung: Endliche Automaten Markus Kr otzsch Lehrstuhl Wissensbasierte Systeme
 Wiederholung Mit Grammatiken können wir Sprachen beschreiben und sie grob in Typen unterteilen: FORMALE SYSTEME 3. Vorlesung: Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Formale
Wiederholung Mit Grammatiken können wir Sprachen beschreiben und sie grob in Typen unterteilen: FORMALE SYSTEME 3. Vorlesung: Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Formale
Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (ii) ε ist ein regulärer Ausdruck über Σ.
 Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2 Lösungsblatt 2 3. Mai 2 Einführung in die Theoretische Informatik Hinweis:
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2 Lösungsblatt 2 3. Mai 2 Einführung in die Theoretische Informatik Hinweis:
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Beispiel Produktautomat
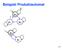 Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
Homomorphismen. Defnition: Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen:
 Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M 2. p 1
 Beispiel Produktautomat p Vereinfachte Konstruktion f. NFAs Seien M,M 2 NFAs f. die Sprachen L und L 2. Konstruktion eines NFAs für L L 2 : Erzeuge Kopien von M und M 2. p q q p 2 Erzeuge neuen Startzustand
Beispiel Produktautomat p Vereinfachte Konstruktion f. NFAs Seien M,M 2 NFAs f. die Sprachen L und L 2. Konstruktion eines NFAs für L L 2 : Erzeuge Kopien von M und M 2. p q q p 2 Erzeuge neuen Startzustand
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 19.
 Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Professur für Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Professur für Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Formale Grundlagen der Informatik 1 Kapitel 5 Abschlusseigenschaften
 Formale Grundlagen der Informatik 1 Kapitel 5 Frank Heitmann heitmann@informatik.uni-hamburg.de 18. April 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/64 NFAs - Grundlagen DFAs vs. NFAs Der
Formale Grundlagen der Informatik 1 Kapitel 5 Frank Heitmann heitmann@informatik.uni-hamburg.de 18. April 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/64 NFAs - Grundlagen DFAs vs. NFAs Der
DisMod-Repetitorium Tag 4
 DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012
 utomaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink utomaten und Formale Sprachen 1 Der CYK-lgorithmus Beispiel
utomaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink utomaten und Formale Sprachen 1 Der CYK-lgorithmus Beispiel
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
Theoretische Informatik für Wirtschaftsinformatik und Lehramt
 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Entscheidungsprobleme Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität Erlangen-Nürnberg
Theoretische Informatik für Wirtschaftsinformatik und Lehramt Entscheidungsprobleme Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität Erlangen-Nürnberg
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
Übersicht. Nebenläufige Programmierung: Praxis und Semantik. Synchronisation (4) Eine untere Schranke für den Platzbedarf
 Übersicht Komplexitätsresultate Aktuelle Themen zu Informatik der Systeme: Nebenläufige Programmierung: Praxis und Semantik Synchronisation (4) Drei Komplexitätsresultate Eine genaue Schranke für den Platzbedarf
Übersicht Komplexitätsresultate Aktuelle Themen zu Informatik der Systeme: Nebenläufige Programmierung: Praxis und Semantik Synchronisation (4) Drei Komplexitätsresultate Eine genaue Schranke für den Platzbedarf
Theorie der Informatik
 Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Model Checking mit Büchi Automaten
 Ingo Weigelt Softwaretechnik 3 16.05.2007 Übersicht 1 Automaten über unendlichen Wörtern ω-automaten Büchi-Automaten 2 Model Checking mit Büchi Automaten Konstruktion von A Konstruktion von A S Leerheitstest
Ingo Weigelt Softwaretechnik 3 16.05.2007 Übersicht 1 Automaten über unendlichen Wörtern ω-automaten Büchi-Automaten 2 Model Checking mit Büchi Automaten Konstruktion von A Konstruktion von A S Leerheitstest
Formale Sprachen und endliche Automaten
 Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Potenzmengenkonstruktion. Vergleich DFAs NFAs. NFA DFA ohne überflüssige Zust. Ansatz nicht praktikabel
 Vergleich DFAs NFAs Frage: Können NFAs nichtreguläre Sprachen erkennen? NEIN Potenzmengenkonstruktion Gegeben: NFA (Q,Σ,q 0,δ,F), konstruiere DFA: Q =P (Q), q 0 = {q 0 }, F ={q q F } Satz T4.4.5: Zu jedem
Vergleich DFAs NFAs Frage: Können NFAs nichtreguläre Sprachen erkennen? NEIN Potenzmengenkonstruktion Gegeben: NFA (Q,Σ,q 0,δ,F), konstruiere DFA: Q =P (Q), q 0 = {q 0 }, F ={q q F } Satz T4.4.5: Zu jedem
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 20.
 Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Theoretische Informatik Mitschrift
 5 Eigenschaften regulärer Sprachen 51: Die Nerode-Relation Theoretische Informatik Mitschrift Definition 51: Sei L * L * * mit L :={u, v * * w *:uw L v w L }heißt Nerode-Relation von L Sei ={0,1}, L= *{00}
5 Eigenschaften regulärer Sprachen 51: Die Nerode-Relation Theoretische Informatik Mitschrift Definition 51: Sei L * L * * mit L :={u, v * * w *:uw L v w L }heißt Nerode-Relation von L Sei ={0,1}, L= *{00}
Unentscheidbare Probleme bei formalen Sprachen
 Unentscheidbare Probleme bei formalen Sprachen Maximilian Zagler 22.01.2008 Freie Universität Berlin, Institut für Informatik Proseminar Theoretische Informatik WS 07/08 Dozent: Prof. Dr. Helmut Alt 1
Unentscheidbare Probleme bei formalen Sprachen Maximilian Zagler 22.01.2008 Freie Universität Berlin, Institut für Informatik Proseminar Theoretische Informatik WS 07/08 Dozent: Prof. Dr. Helmut Alt 1
Berechenbarkeitstheorie 1. Vorlesung
 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Zentrale Themen
Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Zentrale Themen
Informatik IV. Pingo Sommersemester Dozent: Prof. Dr. J. Rothe. J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13
 Informatik IV Sommersemester 2019 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13 Website http://pingo.upb.de/ Code: 1869 J. Rothe (HHU Düsseldorf) Informatik IV 2 / 13 Frage
Informatik IV Sommersemester 2019 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13 Website http://pingo.upb.de/ Code: 1869 J. Rothe (HHU Düsseldorf) Informatik IV 2 / 13 Frage
Theoretische Informatik Kap 1: Formale Sprachen/Automatentheorie
 Gliederung der Vorlesung. Grundbegriffe. Formale Sprachen/Automatentheorie.. Grammatiken.2..3. Kontext-freie Sprachen 2. Berechnungstheorie 2.. Berechenbarkeitsmodelle 2.2. Die Churchsche These 2.3. Unentscheidbarkeit
Gliederung der Vorlesung. Grundbegriffe. Formale Sprachen/Automatentheorie.. Grammatiken.2..3. Kontext-freie Sprachen 2. Berechnungstheorie 2.. Berechenbarkeitsmodelle 2.2. Die Churchsche These 2.3. Unentscheidbarkeit
Grundlagen der Theoretischen Informatik, SoSe 2008
 2. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 1 Einelementiges Alphabet (4 Punkte) (a) Geben
2. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 1 Einelementiges Alphabet (4 Punkte) (a) Geben
Turingmaschinen Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: Komplexitätstheorie und effiziente Algorithmen
 Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Schematische Darstellung einer Turing-Maschine: Kopf kann sich nach links und
Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Schematische Darstellung einer Turing-Maschine: Kopf kann sich nach links und
2.3 Abschlusseigenschaften
 2.3 Abschlusseigenschaften 2.3 Abschlusseigenschaften In diesem Abschnitt wollen wir uns mit Abschlusseigenschaften der regulären Sprachen, d.h. mit der Frage, ob, gegeben eine Operation und zwei reguläre
2.3 Abschlusseigenschaften 2.3 Abschlusseigenschaften In diesem Abschnitt wollen wir uns mit Abschlusseigenschaften der regulären Sprachen, d.h. mit der Frage, ob, gegeben eine Operation und zwei reguläre
Automaten und Formale Sprachen ε-automaten und Minimierung
 Automaten und Formale Sprachen ε-automaten und Minimierung Ralf Möller Hamburg Univ. of Technology Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik, Vieweg Verlag 2 Danksagung
Automaten und Formale Sprachen ε-automaten und Minimierung Ralf Möller Hamburg Univ. of Technology Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik, Vieweg Verlag 2 Danksagung
11.1 Kontextsensitive und allgemeine Grammatiken
 Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Informatik III. Christian Schindelhauer Wintersemester 2006/07 3. Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 3. Vorlesung 02.11.2006 schindel@informatik.uni-freiburg.de 1 Kapitel III Reguläre Sprachen Reguläre Sprachen und Ausdrücke Informatik III
Informatik III Christian Schindelhauer Wintersemester 2006/07 3. Vorlesung 02.11.2006 schindel@informatik.uni-freiburg.de 1 Kapitel III Reguläre Sprachen Reguläre Sprachen und Ausdrücke Informatik III
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit. Zugangsnummer: 3288
 Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Wiederholung Kapitel 2 http://pingo.upb.de Zugangsnummer: 3288 Dozent: Jun.-Prof. Dr. D. Baumeister
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Wiederholung Kapitel 2 http://pingo.upb.de Zugangsnummer: 3288 Dozent: Jun.-Prof. Dr. D. Baumeister
Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 2. Mai HA-Lösung. TA-Lösung
 Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 2. Mai 2016 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 2 Beachten Sie: Soweit
Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 2. Mai 2016 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 2 Beachten Sie: Soweit
Worterkennung in Texten speziell im Compilerbau 20. April Frank Heitmann 2/64
 Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges
Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges
FORMALE SYSTEME. 8. Vorlesung: Minimale Automaten. TU Dresden, 6. November Markus Krötzsch Lehrstuhl Wissensbasierte Systeme
 FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
1 Eliminieren von ɛ-übergängen
 1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
Software Engineering Ergänzung zur Vorlesung
 Ergänzung zur Vorlesung Prof. Dr. Markus Müller-Olm WS 2008 2009 2.6.1 Endliche und reguläre Sprachen Endliche und reguläre Sprache: fundamental in vielen Bereichen der Informatik: theorie Formale Sprachen
Ergänzung zur Vorlesung Prof. Dr. Markus Müller-Olm WS 2008 2009 2.6.1 Endliche und reguläre Sprachen Endliche und reguläre Sprache: fundamental in vielen Bereichen der Informatik: theorie Formale Sprachen
Wie man eine Sprache versteht
 Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
5.2 Endliche Automaten
 114 5.2 Endliche Automaten Endliche Automaten sind Turingmaschinen, die nur endlichen Speicher besitzen. Wie wir bereits im Zusammenhang mit Turingmaschinen gesehen haben, kann endlicher Speicher durch
114 5.2 Endliche Automaten Endliche Automaten sind Turingmaschinen, die nur endlichen Speicher besitzen. Wie wir bereits im Zusammenhang mit Turingmaschinen gesehen haben, kann endlicher Speicher durch
c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} c) {abcabc} d) {abcbc, abc, a} c) {aa, ab, ba, bb} d) {{aa}, {ab}, {ba}, {bb}}
 2 Endliche Automaten Fragen 1. Was ergibt sich bei {a, bc} {de, fg}? a) {abc, defg} b) {abcde, abcfg} c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} 2. Was ergibt sich bei {abc, a} {bc, λ}?
2 Endliche Automaten Fragen 1. Was ergibt sich bei {a, bc} {de, fg}? a) {abc, defg} b) {abcde, abcfg} c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} 2. Was ergibt sich bei {abc, a} {bc, λ}?
Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: Komplexitätstheorie und effiziente Algorithmen. Wintersemester 2011/12
 Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Prof. Barbara König Übungsleitung: Henning Kerstan & Jan Stückrath Barbara König
Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Prof. Barbara König Übungsleitung: Henning Kerstan & Jan Stückrath Barbara König
Nachklausur zur Vorlesung
 Lehrstuhl für Theoretische Informatik Prof. Dr. Markus Lohrey Grundlagen der Theoretischen Informatik Nachklausur Nachklausur zur Vorlesung Grundlagen der Theoretischen Informatik WS 2016/17 / 27. Februar
Lehrstuhl für Theoretische Informatik Prof. Dr. Markus Lohrey Grundlagen der Theoretischen Informatik Nachklausur Nachklausur zur Vorlesung Grundlagen der Theoretischen Informatik WS 2016/17 / 27. Februar
Theoretische Informatik 2 bzw. Formale Sprachen und Berechenbarkeit. Sommersemester Herzlich willkommen!
 Theoretische Informatik 2 bzw. Formale Sprachen und Berechenbarkeit Sommersemester 2012 Prof. Dr. Nicole Schweikardt AG Theorie komplexer Systeme Goethe-Universität Frankfurt am Main Herzlich willkommen!
Theoretische Informatik 2 bzw. Formale Sprachen und Berechenbarkeit Sommersemester 2012 Prof. Dr. Nicole Schweikardt AG Theorie komplexer Systeme Goethe-Universität Frankfurt am Main Herzlich willkommen!
Die Nerode-Relation und der Index einer Sprache L
 Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Grundlagen der Theoretischen Informatik Musterlösungen zu ausgewählten Übungsaufgaben
 Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2 Lösungsblatt 2. Mai 2 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2 Lösungsblatt 2. Mai 2 Einführung in die Theoretische Informatik
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Berechenbarkeits- und Komplexitätstheorie
 Berechenbarkeits- und Komplexitätstheorie Lerneinheit 5: Die Klasse NP Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2015/2016 26.9.2015 Einleitung Thema dieser Lerneinheit
Berechenbarkeits- und Komplexitätstheorie Lerneinheit 5: Die Klasse NP Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2015/2016 26.9.2015 Einleitung Thema dieser Lerneinheit
Frank Heitmann 2/47. 1 Ein PDA beginnt im Startzustand z 0 und mit im Keller. 2 Ist der Automat
 Formale Grundlagen der Informatik 1 Kapitel 5 Über reguläre Sprachen hinaus und (Teil 2) Frank Heitmann heitmann@informatik.uni-hamburg.de 21. April 2015 Der Kellerautomat - Formal Definition (Kellerautomat
Formale Grundlagen der Informatik 1 Kapitel 5 Über reguläre Sprachen hinaus und (Teil 2) Frank Heitmann heitmann@informatik.uni-hamburg.de 21. April 2015 Der Kellerautomat - Formal Definition (Kellerautomat
Maike Buchin 18. Februar 2016 Stef Sijben. Probeklausur. Theoretische Informatik. Bearbeitungszeit: 3 Stunden
 Maike Buchin 8. Februar 26 Stef Sijben Probeklausur Theoretische Informatik Bearbeitungszeit: 3 Stunden Name: Matrikelnummer: Studiengang: Geburtsdatum: Hinweise: Schreibe die Lösung jeder Aufgabe direkt
Maike Buchin 8. Februar 26 Stef Sijben Probeklausur Theoretische Informatik Bearbeitungszeit: 3 Stunden Name: Matrikelnummer: Studiengang: Geburtsdatum: Hinweise: Schreibe die Lösung jeder Aufgabe direkt
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Herzlich willkommen!!!
 Theoretische Informatik 2 Sommersemester 2013 Prof. Dr. Georg Schnitger AG Theoretische Informatik Johann Wolfgang Goethe-Universität Frankfurt am Main Herzlich willkommen!!! 1 / 19 Kapitel 1: Einführung
Theoretische Informatik 2 Sommersemester 2013 Prof. Dr. Georg Schnitger AG Theoretische Informatik Johann Wolfgang Goethe-Universität Frankfurt am Main Herzlich willkommen!!! 1 / 19 Kapitel 1: Einführung
Grundlagen der Informatik. Prof. Dr. Stefan Enderle NTA Isny
 Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
Theoretische Informatik für Wirtschaftsinformatik und Lehramt
 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Eigenschaften regulärer Sprachen Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität
Theoretische Informatik für Wirtschaftsinformatik und Lehramt Eigenschaften regulärer Sprachen Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität
Die mathematische Seite
 Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Grundlagen der Programmierung (Vorlesung 24)
 Grundlagen der Programmierung (Vorlesung 24) Ralf Möller, FH-Wedel Vorige Vorlesung Anwendung im Bereich Compilerbau Inhalt dieser Vorlesung Turing-Maschinen Berechenbarkeitstheorie, Halteproblem Lernziele
Grundlagen der Programmierung (Vorlesung 24) Ralf Möller, FH-Wedel Vorige Vorlesung Anwendung im Bereich Compilerbau Inhalt dieser Vorlesung Turing-Maschinen Berechenbarkeitstheorie, Halteproblem Lernziele
Formale Sprachen. Script, Kapitel 4. Grammatiken
 Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprache bedeutend für die Syntaxdefinition und -analyse von Programmiersprachen Automaten
Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprache bedeutend für die Syntaxdefinition und -analyse von Programmiersprachen Automaten
Informatik 3 Theoretische Informatik WS 2015/16
 2. Probeklausur 22. Januar 2016 Informatik 3 Theoretische Informatik WS 2015/16 Prof. Dr. Peter Thiemann Albert-Ludwigs-Universität Freiburg Institut für Informatik Name: Matrikel-Nr.: Schreiben Sie Ihren
2. Probeklausur 22. Januar 2016 Informatik 3 Theoretische Informatik WS 2015/16 Prof. Dr. Peter Thiemann Albert-Ludwigs-Universität Freiburg Institut für Informatik Name: Matrikel-Nr.: Schreiben Sie Ihren
Carlos Camino Einführung in die Theoretische Informatik SS 2015
 Themenüberblick Dies ist eine Art Checkliste für die Klausurvorbereitung. Zu jedem Thema im Skript sind hier ein paar Leitfragen aufgelistet. Besonders nützlich sind die Tabellen und Abbildungen auf den
Themenüberblick Dies ist eine Art Checkliste für die Klausurvorbereitung. Zu jedem Thema im Skript sind hier ein paar Leitfragen aufgelistet. Besonders nützlich sind die Tabellen und Abbildungen auf den
1. Übungsblatt 6.0 VU Theoretische Informatik und Logik
 . Übungsblatt 6. VU Theoretische Informatik und Logik 25. September 23 Aufgabe Sind folgende Aussagen korrekt? Begründen Sie jeweils Ihre Antwort. a) Für jede Sprache L gilt: L < L (wobei A die Anzahl
. Übungsblatt 6. VU Theoretische Informatik und Logik 25. September 23 Aufgabe Sind folgende Aussagen korrekt? Begründen Sie jeweils Ihre Antwort. a) Für jede Sprache L gilt: L < L (wobei A die Anzahl
Aufgabe Mögliche Punkte Erreichte Punkte a b c d Σ a b c d Σ x1 13
 Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 2003/04 ILKD Prof. Dr. D. Wagner 14. April 2004 2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004 Hier Aufkleber
Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 2003/04 ILKD Prof. Dr. D. Wagner 14. April 2004 2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004 Hier Aufkleber
Einführung in die Computerlinguistik Chomskyhierarchie
 Einführung in die Computerlinguistik Chomskyhierarchie Dozentin: Wiebke Petersen 14. Foliensatz Wiebke Petersen Einführung CL 1 Wiederholung: Formale Grammatik Denition Eine formale Grammatik ist ein 4-Tupel
Einführung in die Computerlinguistik Chomskyhierarchie Dozentin: Wiebke Petersen 14. Foliensatz Wiebke Petersen Einführung CL 1 Wiederholung: Formale Grammatik Denition Eine formale Grammatik ist ein 4-Tupel
Theoretische Informatik und Logik Übungsblatt 1 (2016S) Lösung
 Theoretische Informatik und Logik Übungsblatt (26S) en Aufgabe. Sei L = {w#w r w {, } }. Geben Sie eine deterministische Turingmaschine M an, welche die Sprache L akzeptiert. Wählen Sie mindestens einen
Theoretische Informatik und Logik Übungsblatt (26S) en Aufgabe. Sei L = {w#w r w {, } }. Geben Sie eine deterministische Turingmaschine M an, welche die Sprache L akzeptiert. Wählen Sie mindestens einen
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2011
 Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Endliche Automaten Jörg Roth 101
 Endliche Automaten Jörg Roth 101 Wir wollen im Folgenden die Abschlusseigenschaften regulärer Sprachen betrachten. Fragestellung: Wenn wir reguläre Sprachen haben, welche binären und unären Operationen
Endliche Automaten Jörg Roth 101 Wir wollen im Folgenden die Abschlusseigenschaften regulärer Sprachen betrachten. Fragestellung: Wenn wir reguläre Sprachen haben, welche binären und unären Operationen
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 3 14. Mai 2010 Einführung in die Theoretische
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 3 14. Mai 2010 Einführung in die Theoretische
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Lexikalische Programmanalyse der Scanner
 Der Scanner führt die lexikalische Analyse des Programms durch Er sammelt (scanned) Zeichen für Zeichen und baut logisch zusammengehörige Zeichenketten (Tokens) aus diesen Zeichen Zur formalen Beschreibung
Der Scanner führt die lexikalische Analyse des Programms durch Er sammelt (scanned) Zeichen für Zeichen und baut logisch zusammengehörige Zeichenketten (Tokens) aus diesen Zeichen Zur formalen Beschreibung
Einführung in die Computerlinguistik Chomskyhierarchie
 Einführung in die Computerlinguistik Chomskyhierarchie Dozentin: Wiebke Petersen 14. Foliensatz Wiebke Petersen Einführung CL 1 Wiederholung: Formale Grammatik Denition Eine formale Grammatik ist ein 4-Tupel
Einführung in die Computerlinguistik Chomskyhierarchie Dozentin: Wiebke Petersen 14. Foliensatz Wiebke Petersen Einführung CL 1 Wiederholung: Formale Grammatik Denition Eine formale Grammatik ist ein 4-Tupel
Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni Christian Franz
 Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni 2 Christian Franz Inhaltsverzeichnis Wiederholung: Vorlesung vom 9.6.2... Beispiele für Äquivalenzklassen... 4.5. Minimierung
Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni 2 Christian Franz Inhaltsverzeichnis Wiederholung: Vorlesung vom 9.6.2... Beispiele für Äquivalenzklassen... 4.5. Minimierung
Diskrete Mathematik. Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl
 OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
Formale Methoden 1. Gerhard Jäger 23. Januar Uni Bielefeld, WS 2007/2008 1/18
 1/18 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 23. Januar 2008 2/18 Das Pumping-Lemma Sein L eine unendliche reguläre Sprache über ein endliches Alphabet
1/18 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 23. Januar 2008 2/18 Das Pumping-Lemma Sein L eine unendliche reguläre Sprache über ein endliches Alphabet
Informatik III. Arne Vater Wintersemester 2006/ Vorlesung
 Informatik III Arne Vater Wintersemester 2006/07 10. Vorlesung 24.11.2006 1 Turingmaschinen Informatik III 9. Vorlesung - 2 Turingmaschinen Eine (deterministische 1-Band) Turingmaschine (DTM) wird beschrieben
Informatik III Arne Vater Wintersemester 2006/07 10. Vorlesung 24.11.2006 1 Turingmaschinen Informatik III 9. Vorlesung - 2 Turingmaschinen Eine (deterministische 1-Band) Turingmaschine (DTM) wird beschrieben
