Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 1
|
|
|
- Jasmin Frank
- vor 3 Jahren
- Abrufe
Transkript
1 Studiengang: Matrielnummer: Anz. Blätter: Z Bonus Punte Note Prüfungslausur zum Modul Höhere Mathemati für Ingenieure , Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen aber eine Vorlesungsoder Übungsmitschriften, Formelsammlungen aber eine Lehrbücher, das vorgegebene Formelblatt von Grenzwerten, Reihen, Grundintegralen und Integrationsformeln, zugelassene wissenschaftl. Taschenrechner ein GTR, ein Computer-Algebra-System CAS)). Bearbeiten Sie bitte jede Aufgabe auf einem separaten Blatt bzw. auf separaten Blättern. Das Aufgabenblatt ist mit abzugeben. Vergessen Sie bitte nicht, auf dem Aufgabenblatt und jedem Lösungsblatt Ihre Matrielnummer gut leserlich anzugeben. Der Lösungsweg ist stets anzugeben, er sollte in allen Schritten durch eigene Rechnungen deutlich erennbar, begründet und nachvollziehbar sein. Nur dann ann nach detaillierter Bewertung die volle Puntzahl erreicht werden. Viel Erfolg! Aufgabe : 7 P.) a) Bestimmen Sie in Abhängigeit vom reellen Parameter p) den Grenzwert der Folge a n := p ) n. b) Untersuchen Sie die folgenden Reihen auf Konvergenz und geben sie das verwendete Konvergenzriterium an. Hinweis zu ii): Verwenden Sie das beannte Monotonieverhalten von sinx) auf [0, ]. i) 00 n n= n! ii) ) n+ sin n n= iii) cos n. n= a) Beanntlich gilt für n 0, wenn q <, wenn q = q n divergiert bestimmt), wenn q > divergiert unbestimmt, wenn q. Offenbar gilt stets q := p. Wir haben daher für die Folge a n ) Unbestimmte Divergenz im Falle p =, d. h. p = 0. In diesem Falle alterniert a n zwischen und. Bestimmte Divergenz gegen im Falle p > p > p >, d. h. für p < oder p >. Eine onstante Folge a n ) im Falle p = p = p =, d. h. für p = ±.
2 Konvergenz gegen 0 im Falle p <, d. h. < p < bzw. 0 < p <. Dies bedeutet wiederum 0 < p <, also 0 < p < oder < p < 0. b) i) Die Reihe wird am besten mit dem Quotientenriterium behandelt. Bezeichnen wir die Reihenglieder mit a n = 00n n!, so benötigen wir den Grenzwert q = lim a n+ n a n = lim n 00 n+ n+)! 00 n n! 00 n+ n! = lim n n + )! 00 = lim 00 n n n + = 0. Da q <, liegt Konvergenz vor. ii) Da zunächst für 0 < x < π die Beziehung sin x > 0 gilt, ist offenbar sin > 0, n d. h. sin sind die Beträge der Reihenglieder; deren Vorzeichen wird nur durch n den Fator ) n+ bestimmt, also liegt eine alternierende Reihe vor. In der Nähe der Null genauer gesagt auf [0, π/]) ist die Sinusfuntion außerdem monoton wachsend. Da <, ist also sin < sin, d. h. die n+ n n+ n Beträge der Reihenglieder sind monoton fallend. Schließlich ist wegen der Stetigeit der Sinusfuntion im Nullpunt lim sin ) n n = sin lim = sin 0 = 0, so dass die Beträge der Reihenglieder n n auch eine Nullfolge bilden. Somit ist die Reihe nach dem Leibnizriterium onvergent. ) iii) Es gilt lim cos = cos0) =, die Reihenglieder bilden also eine Nullfolge. Daher ist die notwendige Konvergenzbedingung verletzt, d. h. die Reihe n n divergiert. Aufgabe : 9 P.) Gegeben sei die Funtion fx) = x x 4. a) Bestimmen Sie den Definitionsbereich und untersuchen Sie die Funtion fx) hinsichtlich Nullstellen und Symmetrieverhalten. b) Untersuchen Sie die Grenzwerte von fx) für x ± sowie an eventuell vorhandenen Unstetigeitsstellen. c) Untersuchen Sie das Monotonieverhalten der Funtion fx) und leiten Sie daraus die Art der Extrema an den Stellen x 0 = 0 und x / = ± ab. Berechnen Sie auch die Extremwerte. d) Ermitteln Sie den Wertebereich und sizzieren Sie den Graphen von fx). a) Die Funtion ist definiert für alle x ±, d.h. D f = R \ {±}. Die Stellen x = ± sind Polstellen, da dort der Nenner 0 wird, der Zähler aber nicht.) Die Nullstellen ergeben sich aus fx) = 0 = x = 0 dreifache Nullstelle). Es gilt f x) = x = fx). Deshalb ist die Funtion achsensymmetrisch. Diese Eigenschaft lässt sich im folgenden noch x) 4 ausnutzen.
3 b) Wir untersuchen die Limites für x gegen Polstelle) sowie gegen, der Rest folgt durch Achsensymmetrie der Funtion. [ ] [ ] x lim x x 4 = x =, lim 0 x + x 4 = = x lim x + x 4 = +. Wegen der Achsensymmetrie folgt dann: lim fx) = +, lim x fx) = +, lim x fx) =. x + c) Da die Betragsfuntion an sich nicht überall differenzierbar ist, lösen wir die Betragsstriche auf und betrachten zunächst den Fall x > 0. Dort gilt dann fx) = x x 4 und somit f x) = x x 4) x x x 4) = x x ) x 4) für x > 0. Analog haben wir für negative x fx) = x) x 4 = x x 4 und somit f x) = x x 4) x x x 4) = x x ) x 4) für x < 0. Den Fall x < 0 ann man auch dadurch erhalten, dass aufgrund der Achsensymmetrie die Beziehung f x) = f x) gilt.) Wegen der Gleichheit der lins- und rechtsseitigen Ableitung existiert auch die Ableitung in x = 0 und ist dort gleich 0. Außerdem wird f x) = 0 für x =, d. h. x = ± = ±. Zur Monotonie: Der Ansatz f x) > 0 f monoton wachsend) führt auf die Fälle: i) x > 0 und x ) > 0 x > x > = x, ) ii) x < 0 und x ) < 0 x < x < = x, 0). Also insgesamt: f monoton wachsend für x, 0), ). Analog führt die Bedingung f x) < 0 f monoton fallend in x) auf die Fälle i) x > 0 und x ) < 0 x < x < = x 0, ) ii) x < 0 und x ) > 0 x > x > = x, ). Also ist f monoton fallend für x, ) 0, ). Man hätte auch jeweils nur den Fall x > 0 betrachten und den Rest aus der Achsensymmetrie folgern önnen.) Insgesamt folgt also x 0 = 0 ist loales Maximum da Übergang m.w. m.f.), x / = ± ist loales Minimum da Übergang m.f. m.w.). Die Funtionswerte sind f0) = 0, f± ) =.
4 d) Aus Extrema und Grenzwertverhalten ergibt sich schließlich der Wertebereich W f =, 0] [, + ) siehe Sizze). y 0 x Aufgabe : 0 P.) a) Wie muss a R gewählt werden damit für z = i + a) i) i gilt Rez) = 0? b) Bestimmen Sie alle z C in artesischer algebraischer) Form, für die gilt: iz 4i)z + 8i) = 0. c) Sizzieren Sie die Teilmenge der Gaußschen Zahlenebene, deren Elemente z = x + iy gleichzeitig beide Ungleichungen erfüllen: z z z und Rez ) > Re z) 4. a) z = a + i) i) i )) i also ist Re z = a = 0 a =. = a + i) i) = a + a )i, b) Wir dividieren die Gleichung gleich durch i. Das Produt wird dann 0, wenn einer der beiden Fatoren in Klammern 0 wird Ausmultiplizieren wäre also ontraprodutiv). z 4i = 0: z = 4i = 4e π/+π)i z = e π/4+π)i, = 0,. Dies ergibt die beiden Lösungen z = e iπ/4 = cos π 4 + i sin π ) 4 z = e 5πi/4 =... = i = ) ) + i = + i = 0), = i = ).
5 z + 8i = 0: z = 8i = 8e π/+π)i z = e π/+π/)i, = 0,,. Dies ergibt die drei Lösungen z = e iπ/ = i = 0), z 4 = e 7πi/6 = cos 7π 6 + i sin 7π 6 z 5 = e πi/6 =... = i ) = i = ). ) = i ) = i = ), c) Für die erste Ungleichung erhalten wir durch Ausnutzen der Beziehung z z = z = x + y : z z z z z. Dies beschreibt das Äußere des Einheitsreises mit Rand). Für die zweite Ungleichung ergibt sich mit der Darstellung z = x + iy x, y reell): Rex xyi y ) > x 4 x y > x 4 y < 4 y <. Dies beschreibt den Streifen zwischen den Geraden y = und y = ohne Rand. Insgesamt ergibt sich das folgende Bild. Die gesuchte Puntmenge grün) ist natürlich unbeschränt, so dass hier nur ein Teil gezeichnet werden ann. Die Kreislinie gehört zur Menge, die Geraden y = ± jedoch nicht.) y x Aufgabe 4: 6 P.) Gegeben seien die Funtionen fx) = 5 4x und gx) = 4x )e x. a) Bestimmen Sie jeweils eine Stammfuntion F x) von fx) bzw. Gx) von gx). b) Berechnen Sie den Flächeninhalt der Fläche, die von den Graphen der Funtionen fx) und gx) sowie den Geraden x = und x = 4 eingeschlossen wird. Hinweis: Es gilt fx) < gx) für alle x.
6 c) Untersuchen Sie, ob die uneigentlichen Integrale fx)dx und 4 und geben Sie ggf. deren Werte an. a) Mit der Substitution t = 4x, dt = 4 dx erhält man 5 dx F x) = = 5 t / dt = 5 4x 4 4 t/ = 5 4x. b) fx)dx existieren Man önnte sich auch diret auf die Integrationsformel für verettete Funtionen mit linearer innerer Funtion von unserem Formelblatt berufen.) Das andere Integral ann man mittels partieller Integration mit ux) = 4x, v x) = e x behandeln. Dann ist u x) = 4, vx) = ex. Man erhält Gx) = 4x )e x dx = 4x ) ex 4 e x dx = 4x ) ex ex = 4x ) ex. Integrationsonstanten wurden weggelassen, da jeweils nur eine Stammfuntion gesucht war.) 4 A = gx) fx)) dx = 4x ) ex 5 ) 4 4x = e8 5 5 e 5 ) c) Der Nenner von fx) wird Null, wenn x =. Der Zähler von fx) ist dort nicht 4 Null, so dass eine Polstelle vorliegt. Es handelt sich daher um ein uneigentliches Integral mit einem in einer Umgebung der unteren Integrationsgrenze unbeschränten Integranden. Mit obiger Stammfuntion F gilt /4 fx) dx = lim fx) dx = lim ε 0+ /4+ε ε 0+ ) 4ε 5 = lim ε 0+ = 5, das uneigentliche Integral ist also onvergent. 5 4x /4+ε Im zweiten Fall liegt ein uneigentliches Integral mit unbeschräntem Integrationsintervall vor, hier ist fx) dx = lim A = lim A A fx) dx = lim A 4A ) 5 5 A 4x =, das uneigentliche Integral ist also bestimmt) divergent.
7 Aufgabe 5: 6 P.) a) Bestimmen Sie den Konvergenzbereich der Reihe = x + ). b) Stellen Sie die Funtion f x) = mit Hilfe der geometrischen Reihe als + 4x 8x Potenzreihe dar und folgern Sie daraus die Potenzreihe für f x) = + 4x. Geben Sie den Konvergenzbereich beider Potenzreihen an. c) Bestimmen Sie die Potenzreihe für f x) = ln + 4x ) mittels gliedweiser Integration der geeigneten Potenzreihe aus b) sowie den Konvergenzbereich der Potenzreihe von f x). a) Es gibt verschiedene Möglicheiten, den Konvergenzbereich zu bestimmen. Eine Betrachtung als speziell geometrische Reihe ist nicht möglich. Zur Auswahl stehen die Betrachtung als Zahlenreihe mit dem Quotienten- bzw. Wurzelriterium a) bzw. a)) oder als Potenzreihe a) bzw. a4)). a) Zahlenreihe mit dem Quotientenriterium. Dazu betrachtet man die Reihe als b mit b = x + ). = Bemerung: Die Rechnung würde sich leicht vereinfachen, wenn man b vorher noch zu x + )) = x + ) umformt, die Ergebnisse bleiben natürlich die gleichen.) Anwendung des Quotientenriteriums auf b bedeutet, den Grenzwert des folgenden Quotienten zu bestimmen: b + b = + x + + )+ x + ) = x + )+ + ) x + = x ) + +, also lim b + b = lim + = x + lim + = ) x + = x + lim = x +. Nach dem Quotientenriterium liegt Konvergenz vor, wenn + x + < < x + < 4 < x <, ) und Divergenz, wenn x+ > x+ < oder x+ > ) x < 4 oder x > ). ) Um den Konvergenzbereich zu bestimmen müssen noch die Randpunte betrachtet werden: x = 4 : b = = = 4 + ) = = 4+ ) = ), =
8 diese alternierende Reihe onvergiert nach dem Leibnizriterium, da die Beträge der Reihenglieder b = eine monotone Nullfolge bilden. Dagegen gilt für x = : b = = = + ) = = + ) = =, was die harmonische Reihe ergibt, die divergent ist. Folglich ist der Konvergenzbereich das halboffene Intervall [ 4, ). a) Zahlenreihe mit dem Wurzelriterium. Dazu betrachtet man wiederum die Reihe = b wie unter a), die obige Bemerung gilt hier ebenso. Die Anwendung des Wurzelriteriums auf b bedeutet die Bestimmung des Grenzwerts lim b = lim = x + = x + ) = x + lim lim = x +. Nach dem Wurzelriterium gelten für Konvergenz bzw. Divergenz dieselben Bedingungen an diesen Grenzwert wie in ) und ). Die Randpunte sind wieder ebenfalls wie in a) extra zu betrachten. Betrachtung mittels der speziellen Methoden für Potenzreihen: a) Potenzreihe mit dem Zentrum Entwiclungspunt) a = y 0 = 0. Dazu interpretieren wir die Reihe als = x + ) = a y, = d. h. eine Potenzreihe mit den Koeffizienten a =, der Variablen y = x + und dem Entwiclungspunt y 0 = 0. Dann bestimmt man den Konvergenzradius R = lim a + a. R = lim a a + = lim + ) = lim Dann onvergiert die Potenzreihe a y für = + lim a a + = c mit c = = lim + ) =. y = x + < R = < x + < < x + < < x + < 4 < x <. Auch in diesem Fall müssen die Randpunte x = 4 und x = gesondert betrachtet werden. Wie bei a) erhält man für x = 4 Konvergenz und für x = Divergenz, der Konvergenzbereich ist [ 4, ).
9 a4) Potenzreihe mit Zentrum Entwiclungpunt) a = x 0 = x +) = x+) = a x+) ist eine Potenzreihe in der Variablen = = = x mit dem Zentrum a = x 0 =. Der Konvergenzradius dieser Reihe ist R = lim a = lim = lim + = a + + und damit liegt Konvergenz vor für x ) = x + < < x + < 4 < x <, die Randpunte sind wiederum extra zu betrachten. b) Die geometrische Reihe q onvergiert genau dann, wenn q <. In diesem Falle ist ihre Summe f x) = =0 =0 q =. Deshalb ist q 4x ) = 4x ) = =0 4) x =0 4x = 4 x < x < 4 x <. Die Funtion f x) ist das 8x-Fache von f x). Eine von 0 verschiedene Zahl ann an die Glieder einer Reihe multipliziert bzw. aus dieser herausgezogen) werden, ohne dass sich dabei etwas an der Konvergenz ändert. Daher ist für x 0 f x) = 8xf x) = 8x 4) x = 8 4) x + x <. =0 Für x = 0 ist obige Reihe offensichtlich ebenfalls onvergent und hat die Summe f 0) = 0. c) Es gilt =0 ln + 4x ) ) 8x = + 4x = 8 4) x +, =0 d. h. f ist eine Stammfuntion von f. Da diese Reihe für x < onvergiert, gilt dies auch für die gliedweise integrierte Reihe. Die Randpunte sind dabei wiederum extra zu betrachten. Es gilt für x < : x 8t f x) = + 4t dt = 8 x 4) t + dt = 8 4) t+ x + = 8 0 =0 4) x+ +. =0 Wir betrachten die Randpunte x = ± : ) 4) + ± 8 = 8 ) + + =0 =0 = =0 0 ) + = =0 ) = 8 =0 ) +. =0 0 ) ) +
10 In beiden Fällen ergibt sich also dieselbe alternierende Reihe, die nach dem Leibnizriterium onvergiert, da die Beträge der Reihenglieder eine monotone Nullfolge bilden. Deshalb ist der Konvergenzbereich das abgeschlossene Intervall [, ]. Aufgabe 6: 7 P.) Es seien A = und b = a mit a R. a) Für welche a R ist das lineare Gleichungssystem A x = b lösbar? Ermitteln Sie für diese a die allgemeine Lösung des Gleichungssystems. Geben Sie auch die Lösung des dazugehörigen homogenen Gleichungssystems an. b) Geben Sie den Rang der Koeffizientenmatrix A und für die Fälle a = und a = 5 jeweils den Rang der erweiterten Koeffizientenmatrix an. c) Untersuchen Sie die Spalten von A auf lineare Abhängigeit. Ermitteln Sie eine Basis und die Dimension des von den Spalten von A aufgespannten Unterraums. a) Mittels Gauß-Algorithmus wird zunächst die erweiterte Koeffizientenmatrix in eine Form gebracht, in welcher Aussagen über die Lösbareit möglich sind a a a + 5 Anhand der letzten Zeile erennt man, dass das Gleichungssystem genau dann lösbar ist, wenn a = 5 bei einer Nullzeile auf der linen Seite in der Zeilenstufenform muss auch auf der rechten Seite eine 0 stehen, bzw. der Rang der Koeffizientenmatrix muss gleich dem der erweiterten Koeffizientenmatrix sein vgl. b)). Für a = 5 ermitteln wir jetzt die allgemeine Die Nichtleitunbeannten in den Spalten ohne Leitelemente) werden als freie Parameter angesetzt: x = s, x 4 = t. Dann lösen wir die Leitgleichungen mit den marierten Leitelementen) von unten nach oben auf: x + 4t = 7 = x = 7 4t x + s + 7 4t) + 5s = = x = 9 s + 7t. In Vetorform haben wir die allgemeine Lösung 9 7 x = s 0 + t 0 4, s, t R. 0 0 }{{} Anteil mit freien Parametern ist die allg. Lsg. des homogenen Systems A x= 0
11 Es sei angemert, dass man ggf. die Leitelemente auch in anderen Spalten hätte wählen önnen. Dann wären andere Variable die freien Parameter, und die Lösungsdarstellung würde anders aussehen, insgesamt aber natürlich dieselbe Menge von Vetoren ergeben. b) Der Rang einer Matrix ist ablesbar an der Anzahl der Leitelemente. Für die Koeffizientenmatrix ist er also unabhängig von a immer gleich. Der Rang der erweiteren Koeffizientenmatrix ist im Falle a = gleich, da hier in der letzten Zeile auf der rechten Seite ein weiteres Leitelement 0) steht. Im Falle a = 5 ist er gleich, wie der Rang der Koeffizientenmatrix. c) Die Spalten von A sind linear abhängig, da der Rang von A leiner als die Spaltenzahl ist, oder äquivalent, da das homogene lineare Gleichungssystem nicht nur die triviale Lösung x = 0 besitzt vgl. a)). Mit Determinanten ann man hier nicht argumentieren, da A nicht quadratisch ist.) Eine Basis in dem von den Spalten aufgespannten Unterraum bilden die Spalten, in denen beim Gauß-Algorithmus Leitelemente entstehen, also hier die erste und die dritte Spalte der ursprünglichen Matrix. Die Dimension des Unterraums ist also gleich Anzahl der Basisvetoren). Der Unterraum ist eine Ebene im R. Zusatzaufgabe: Punte) a) Berechnen Sie die Ableitung von fx) = lnx)). b) Weisen Sie mit Hilfe des Integralriteriums unter Benutzung von a)) nach, dass die Reihe nlnn)) onvergiert. a) f x) = n= lnx)) ) = ) lnx)) x = xlnx)). b) Das Integralriterium für Reihen besagt, dass die Reihe und das uneigentliche Integral fx) dx mit fx) = xlnx)) = nlnn)) das gleich Konvergenzverhalten haben, wenn die Funtion fx) = für x < stetig ist offenbar xlnx)) erfüllt), positiv erfüllt, weil lnx) > 0 für x > ) und monoton fallend erfüllt, weil die Funtionen gx) = x und hx) = lnx)) ) monoton wachsend auf [, ) sind und damit fx) monoton fallend) ist. Zur Berechnung des uneigentlichen Integrals ann man verwenden, dass aus a) folgt: ) xlnx)) dx = dx = lnx)) lnx)) + C. Berechnung des uneigentlichen Integrals: dx = lim xlnx)) A = lim A A dx = lim xlnx)) A lna)) + lnx)) ) = ln)) Deshalb onvergiert das uneigentliche Integral und damit auch die Reihe. A ) ln)) <.
Höhere Mathematik für Ingenieure , Uhr (1. Termin)
 Studiengang: Matrikelnummer: 1 3 4 5 6 Z Punkte Note Prüfungsklausur A zum Modul Höhere Mathematik für Ingenieure 1 17.. 14, 8. - 11. Uhr 1. Termin Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche
Studiengang: Matrikelnummer: 1 3 4 5 6 Z Punkte Note Prüfungsklausur A zum Modul Höhere Mathematik für Ingenieure 1 17.. 14, 8. - 11. Uhr 1. Termin Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche
Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 1
 Studiengang: Matrikelnummer: 3 4 5 6 Z Punkte Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 8. 7. 6, 8. -. Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen
Studiengang: Matrikelnummer: 3 4 5 6 Z Punkte Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 8. 7. 6, 8. -. Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen
3. Potenzreihen. Definition 7.5. Eine unendliche Reihe der Form. a k x k. Es handelt sich also um eine Funktionenreihe mit f k (x) = a k x k.
 3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 1
 Studiengang: Matrikelnummer: 3 4 5 6 Z Bonus Punkte Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure.. 7, 3. - 6. Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen
Studiengang: Matrikelnummer: 3 4 5 6 Z Bonus Punkte Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure.. 7, 3. - 6. Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen
Klausur zum Grundkurs Höhere Mathematik I
 Name, Vorname: Studiengang: Matrikelnummer: 2 4 5 6 Z Punkte Note Klausur zum Grundkurs Höhere Mathematik I für BNC, GtB, MB, EC, TeM, VT, KGB, WWT, ESM, FWK, BGi, WiW 22. Februar 2007, 8.00 -.00 Uhr Zugelassene
Name, Vorname: Studiengang: Matrikelnummer: 2 4 5 6 Z Punkte Note Klausur zum Grundkurs Höhere Mathematik I für BNC, GtB, MB, EC, TeM, VT, KGB, WWT, ESM, FWK, BGi, WiW 22. Februar 2007, 8.00 -.00 Uhr Zugelassene
Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 1
 Studiengang: Matrikelnummer: 3 4 5 6 Z Bonus Punkte Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 9.. 08, 3.00-6.00 Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen
Studiengang: Matrikelnummer: 3 4 5 6 Z Bonus Punkte Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 9.. 08, 3.00-6.00 Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen
Analysis I Mathematik für InformatikerInnen II SoSe 12 Musterlösungen zur Prüfungsklausur vom 18. Juli 2012
 Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler. (a) Bestimmen Sie die kartesische Form von Wintersemester 7/8 (..8) z = ( + i)( i) + ( + i). (b) Bestimmen Sie sämtliche komplexen Lösungen
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler. (a) Bestimmen Sie die kartesische Form von Wintersemester 7/8 (..8) z = ( + i)( i) + ( + i). (b) Bestimmen Sie sämtliche komplexen Lösungen
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler Wintersemester 26/7 (2.3.27). (a) Bestimmen Sie die kartesische Form von z = 5i 2i und z 2 = ( ) 9 3 2 2 i. (b) Bestimmen Sie sämtliche
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler Wintersemester 26/7 (2.3.27). (a) Bestimmen Sie die kartesische Form von z = 5i 2i und z 2 = ( ) 9 3 2 2 i. (b) Bestimmen Sie sämtliche
REIHEN. 1. Definition und Konvergenz. Definition (unendliche) Reihe
 REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
Prüfungklausur HM 1 (Ing), Lösungshinweise
 Aufgabe : a Welche komplexen Zahlen erfüllen die Gleichung z + i z =? Skizzieren Sie die Lösungsmenge in der Gaussschen Zahlenebene. 6 Punkte b Für welche komplexen Zahlen z gilt (z + i = 8 e π i? Die
Aufgabe : a Welche komplexen Zahlen erfüllen die Gleichung z + i z =? Skizzieren Sie die Lösungsmenge in der Gaussschen Zahlenebene. 6 Punkte b Für welche komplexen Zahlen z gilt (z + i = 8 e π i? Die
Potenzreihen. Potenzreihen sind Funktionenreihen mit einer besonderen Gestalt.
 Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt. Definition. Ist (a ) eine Folge reeller (bzw. omplexer) Zahlen und x 0 R (bzw. z 0 C), dann heißt die Reihe a (x x 0 ) (bzw.
Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt. Definition. Ist (a ) eine Folge reeller (bzw. omplexer) Zahlen und x 0 R (bzw. z 0 C), dann heißt die Reihe a (x x 0 ) (bzw.
k + k + 1 ( 1) k( k 2 + 2k + 1 k ) f)
 Prof. Dr. L. Schwachhöfer Dr. J. Horst Faultät Mathemati TU Dortmund Musterlösung zum 5. Übungsblatt zur Höheren Mathemati I (P/ET/AI/IT/IKT/MP WS 0/ Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz:
Prof. Dr. L. Schwachhöfer Dr. J. Horst Faultät Mathemati TU Dortmund Musterlösung zum 5. Übungsblatt zur Höheren Mathemati I (P/ET/AI/IT/IKT/MP WS 0/ Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz:
Unendliche Reihen. . n
 Unendliche Reihen Gegeben sei eine Folge (a ) reeller Zahlen. Aus den Gliedern dieser Folge bilden wir eine neue Folge (s n ) von Partialsummen, das bedeutet, s n berechnet sich durch Aufsummieren der
Unendliche Reihen Gegeben sei eine Folge (a ) reeller Zahlen. Aus den Gliedern dieser Folge bilden wir eine neue Folge (s n ) von Partialsummen, das bedeutet, s n berechnet sich durch Aufsummieren der
1. Aufgabe (6 Punkte) Zeigen Sie mit Hilfe der vollständigen Induktion, dass folgende Gleichheit gilt für alle n N, n 2. k (k + 1)! = 1 1 n!.
 . Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
. Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
Probeklausur zur Analysis für Informatiker
 Lehrstuhl A für Mathemati Prof. Dr. R. Stens Aachen, den 28. Januar 20 Probelausur zur Analysis für Informatier Musterlösung Aufgabe Zeigen Sie, dass für alle n N gilt. 2n+ ( ) + Beweis durch vollständige
Lehrstuhl A für Mathemati Prof. Dr. R. Stens Aachen, den 28. Januar 20 Probelausur zur Analysis für Informatier Musterlösung Aufgabe Zeigen Sie, dass für alle n N gilt. 2n+ ( ) + Beweis durch vollständige
Aufgabe 1. Version A Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an.
 Analysis I, WiSe 013/14, 04.0.014 (Ise 1 Aufgabe 1. Version A Multiple Choice (4 Punte. Kreuzen Sie die richtige(n Antwort(en an. a Welche der folgenden Aussagen über Folgen sind sinnvoll und wahr? jede
Analysis I, WiSe 013/14, 04.0.014 (Ise 1 Aufgabe 1. Version A Multiple Choice (4 Punte. Kreuzen Sie die richtige(n Antwort(en an. a Welche der folgenden Aussagen über Folgen sind sinnvoll und wahr? jede
KAPITEL 9. Funktionenreihen. 9.1 Taylor-Reihen Potenzreihen Methoden der Reihenentwicklung Anwendungen...
 KAPITEL 9 Funtionenreihen 9. Taylor-Reihen.................................... 74 9.2 Potenzreihen..................................... 77 9.3 Methoden der Reihenentwiclung.......................... 90
KAPITEL 9 Funtionenreihen 9. Taylor-Reihen.................................... 74 9.2 Potenzreihen..................................... 77 9.3 Methoden der Reihenentwiclung.......................... 90
Wesentliche Sätze (Analysis 1 für Lehramt)
 Wesentliche Sätze (Analysis für Lehramt) Inhaltsverzeichnis Alexander Schmalstieg TU Dortmund, Wintersemester 203/204 Wichtige Formeln 2 Folgen 2 3 Maxima und Suprema 3 4 Gleichmäßige Konvergenz 3 5 Funtionen
Wesentliche Sätze (Analysis für Lehramt) Inhaltsverzeichnis Alexander Schmalstieg TU Dortmund, Wintersemester 203/204 Wichtige Formeln 2 Folgen 2 3 Maxima und Suprema 3 4 Gleichmäßige Konvergenz 3 5 Funtionen
Klausur zur Vorlesung Analysis 1 (240003) 1. Termin: Aufgaben und Lösungen
 Prof Dr M Kaßmann Wintersemester 9/ Faultät für Mathemati Universität Bielefeld Klausur zur Vorlesung Analysis () Termin: 5 Aufgaben Lösungen Aufgaben: Die omplexen Lösungen der Gleichung z = i sind (
Prof Dr M Kaßmann Wintersemester 9/ Faultät für Mathemati Universität Bielefeld Klausur zur Vorlesung Analysis () Termin: 5 Aufgaben Lösungen Aufgaben: Die omplexen Lösungen der Gleichung z = i sind (
HTWD, FB Informatik/Mathematik. Mathematik für Bauingenieure. Wiederholungsaufgaben: Mathematik I
 HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Mathematik I Wiederholung Mathematik für Bauingenieure Wiederholungsaufgaben: Mathematik I Aufgabe : Für die Aussagenverbindung T = (A B) ( A) gebe man
HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Mathematik I Wiederholung Mathematik für Bauingenieure Wiederholungsaufgaben: Mathematik I Aufgabe : Für die Aussagenverbindung T = (A B) ( A) gebe man
Anleitung zu Blatt 4 Analysis I für Studierende der Ingenieurwissenschaften
 Department Mathemati der Universität Hamburg WiSe 20/202 Dr. Hanna Peywand Kiani Anleitung zu Blatt 4 Analysis I für Studierende der Ingenieurwissenschaften Reelle Zahlenreihen 6.2.20 Die ins Netz gestellten
Department Mathemati der Universität Hamburg WiSe 20/202 Dr. Hanna Peywand Kiani Anleitung zu Blatt 4 Analysis I für Studierende der Ingenieurwissenschaften Reelle Zahlenreihen 6.2.20 Die ins Netz gestellten
Potenzreihen. Potenzreihen sind Funktionenreihen mit einer besonderen Gestalt.
 Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
Ferienkurs Analysis 1
 TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienurs Analysis 1 Potenzreihen, Exponentialfuntion, Stetigeit, Konvergenz, Grenzwert Henri Thoma 1.03.014 Inhaltsverzeichnis 1. Potenzreihen:... 1. Exponentialfuntion...
TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienurs Analysis 1 Potenzreihen, Exponentialfuntion, Stetigeit, Konvergenz, Grenzwert Henri Thoma 1.03.014 Inhaltsverzeichnis 1. Potenzreihen:... 1. Exponentialfuntion...
ANALYSIS I. Lösung der Klausur vom 25/02/14. Aufgabe 1
 ANALYSIS I Lösung der Klausur vom 5//4 Aufgabe (a) Das Monotonieriterium für Folgen besagt, dass monoton wachsende nach oben beschränte Folgen (a n ) R onvergent sind. Entsprechendes gilt für monoton fallende
ANALYSIS I Lösung der Klausur vom 5//4 Aufgabe (a) Das Monotonieriterium für Folgen besagt, dass monoton wachsende nach oben beschränte Folgen (a n ) R onvergent sind. Entsprechendes gilt für monoton fallende
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 2017/18, am
 Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
1 k k konvergent? und
 28 Reihen 27 28 Reihen Aufgabe: Sind die Reihen ( + und onvergent? 28. Komplexe Reihen. a Für eine Folge (a in C heißt die Reihe a onvergent, falls die Folge der Partialsummen (s n := n a onvergiert. In
28 Reihen 27 28 Reihen Aufgabe: Sind die Reihen ( + und onvergent? 28. Komplexe Reihen. a Für eine Folge (a in C heißt die Reihe a onvergent, falls die Folge der Partialsummen (s n := n a onvergiert. In
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathemati für Informatier II (Sommersemester 00) Lösungen zu Aufgabenblatt
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathemati für Informatier II (Sommersemester 00) Lösungen zu Aufgabenblatt
1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen:
![1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen: 1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen:](/thumbs/53/30982501.jpg) Klausur zur Analysis I svorschläge Universität Regensburg, Wintersemester 013/14 Prof. Dr. Bernd Ammann / Dr. Mihaela Pilca 0.0.014, Bearbeitungszeit: 3 Stunden 1. Aufgabe [ Punte] Seien X, Y zwei nicht-leere
Klausur zur Analysis I svorschläge Universität Regensburg, Wintersemester 013/14 Prof. Dr. Bernd Ammann / Dr. Mihaela Pilca 0.0.014, Bearbeitungszeit: 3 Stunden 1. Aufgabe [ Punte] Seien X, Y zwei nicht-leere
4x 1 + 2x 2 + 3x 3 = 1, x 2 + ax 3 = 1, ax 2 + x 3 = a 1. 0 a 1 1 Wir führen nun den Gauÿalgorithmus durch:
 Aufgabe 8 Punkte Bestimmen Sie die Lösungsmenge in R in Abhängigkeit von a R des folgenden linearen Gleichungssystems: 4x + x + 3x 3 =, x + ax 3 =, ax + x 3 =. Lösung. Wir schreiben das lineare Gleichungssystem
Aufgabe 8 Punkte Bestimmen Sie die Lösungsmenge in R in Abhängigkeit von a R des folgenden linearen Gleichungssystems: 4x + x + 3x 3 =, x + ax 3 =, ax + x 3 =. Lösung. Wir schreiben das lineare Gleichungssystem
Mehrfach und unendlich oft differenzierbare Funktionen, Potenzreihen
 Kapitel V Mehrfach und unendlich oft differenzierbare Funtionen, Potenzreihen 21 Mehrfache Differenzierbareit und Potenzreihen 22 Die trigonometrischen und die Hyperbelfuntionen 23 Konvexe Funtionen und
Kapitel V Mehrfach und unendlich oft differenzierbare Funtionen, Potenzreihen 21 Mehrfache Differenzierbareit und Potenzreihen 22 Die trigonometrischen und die Hyperbelfuntionen 23 Konvexe Funtionen und
Mathematik IT 3 (Analysis) Probeklausur
 Mathematik IT (Analysis) Probeklausur Datum: 08..0, Zeit: :5 5:5 Name: Matrikelnummer: Vorname: Geburtsdatum: Studiengang: Aufgabe Nr. 5 Σ Punkte Soll 5 9 7 Punkte Ist Lösungen ohne begründeten Lösungsweg
Mathematik IT (Analysis) Probeklausur Datum: 08..0, Zeit: :5 5:5 Name: Matrikelnummer: Vorname: Geburtsdatum: Studiengang: Aufgabe Nr. 5 Σ Punkte Soll 5 9 7 Punkte Ist Lösungen ohne begründeten Lösungsweg
5. Übung zur Analysis II
 Julius-Maximilians-Universität Würzburg Institut für Mathemati Prof. Dr. H. Pabel Christian Lageman, Martin Lamprecht, Ralf Winler Würzburg, den. Juni 006 5. Übung zur Analysis II Sommersemester 006 Lösungshinweise.)
Julius-Maximilians-Universität Würzburg Institut für Mathemati Prof. Dr. H. Pabel Christian Lageman, Martin Lamprecht, Ralf Winler Würzburg, den. Juni 006 5. Übung zur Analysis II Sommersemester 006 Lösungshinweise.)
Höhere Mathematik II. Variante A
 Lehrstuhl II für Mathematik Prof Dr E Triesch Höhere Mathematik II SoSe 5 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter (Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof Dr E Triesch Höhere Mathematik II SoSe 5 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter (Vorder- und Rückseite
7 Integralrechnung für Funktionen einer Variablen
 7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Vorlesung Mathematik WS 08/09. Friedel Bolle. Vorbemerkung
 Vorlesung Mathemati WS 08/09 Vorbemerung Weshalb Mathemati für Öonomen? Das werden Sie selbst sehen im Grundstudium in - Miroöonomie - Statisti - Maroöonomie - BWL: Prodution und dazu in einer Reihe von
Vorlesung Mathemati WS 08/09 Vorbemerung Weshalb Mathemati für Öonomen? Das werden Sie selbst sehen im Grundstudium in - Miroöonomie - Statisti - Maroöonomie - BWL: Prodution und dazu in einer Reihe von
2 a 6. a 4 a Wir führen nun den Gauÿalgorithmus durch: 2 a a 2 4a 2 4a a a 2 2a 0 2 a
 Aufgabe 8 Punkte). Bestimmen Sie die Lösungsmenge in R in Abhängigkeit von a R) des folgenden linearen Gleichungssystem: x + ax + 6x = 4, ax + 4x + ax =, x + 4x =. Lösung. Wir schreiben das lineare Gleichungssystem
Aufgabe 8 Punkte). Bestimmen Sie die Lösungsmenge in R in Abhängigkeit von a R) des folgenden linearen Gleichungssystem: x + ax + 6x = 4, ax + 4x + ax =, x + 4x =. Lösung. Wir schreiben das lineare Gleichungssystem
Unendliche Reihen - I
 Unendliche Reihen - I Zur Wiederholung. Sei eine Folge ( ) N aus R (bzw. C) gegeben (die Folge der Summanden). Die Folge (s n ) n N in der Form Die Reihe mit s n = n heißt unendliche Reihe und wird geschrieben.
Unendliche Reihen - I Zur Wiederholung. Sei eine Folge ( ) N aus R (bzw. C) gegeben (die Folge der Summanden). Die Folge (s n ) n N in der Form Die Reihe mit s n = n heißt unendliche Reihe und wird geschrieben.
Grundlagen der Mathematik (BSc Maschinenbau)
 Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 5.9.7 Grundlagen der Mathematik (BSc Maschinenbau) Aufgabe. (6+8+6 Punkte) a) Zeigen Sie durch Induktion nach n N: n (k ) = n k= b) Stellen Sie die folgenden Mengen
Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 5.9.7 Grundlagen der Mathematik (BSc Maschinenbau) Aufgabe. (6+8+6 Punkte) a) Zeigen Sie durch Induktion nach n N: n (k ) = n k= b) Stellen Sie die folgenden Mengen
Analysis I MATH, PHYS, CHAB. 2 k (2 k ) s = 2 k(1 s) = k=0. (2n 1) n=1. n=1. n n 2. n=1. n=1. = ζ(2) 1 4 ζ(2) = 3 4 ζ(2)
 Prof. D. Salamon Analysis I MATH, PHYS, CHAB HS 204 Musterlösung Serie 7. Der Vollständigeit wegen, zeigen wir zunächst die Konvergenz der Reihendarstellung der ζ-funtion für s >. ζs : n n s 2 + n s 0
Prof. D. Salamon Analysis I MATH, PHYS, CHAB HS 204 Musterlösung Serie 7. Der Vollständigeit wegen, zeigen wir zunächst die Konvergenz der Reihendarstellung der ζ-funtion für s >. ζs : n n s 2 + n s 0
3 a) Berechnen Sie die normierte Zeilenstufenform der Matrix A = normierte Zeilenstufenform:
 1. Aufgabe (9 Punkte) In dieser Aufgabe müssen Sie Ihre Antwort nicht begründen. Es zählt nur das Ergebnis. Tragen Sie nur das Ergebnis auf diesem Blatt im jeweiligen Feld ein. 0 1 3 a) Berechnen Sie die
1. Aufgabe (9 Punkte) In dieser Aufgabe müssen Sie Ihre Antwort nicht begründen. Es zählt nur das Ergebnis. Tragen Sie nur das Ergebnis auf diesem Blatt im jeweiligen Feld ein. 0 1 3 a) Berechnen Sie die
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Mathematik für Sicherheitsingenieure I A
 Prof. Dr. J. Ruppenthal Wuppertal, 3.8.8 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+5+5 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH ist.
Prof. Dr. J. Ruppenthal Wuppertal, 3.8.8 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+5+5 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH ist.
Zulassungsprüfung in Mathematik
 der Deutschen Aktuarvereinigung e V Hinweise: Als Hilfsmittel sind ein Taschenrechner, eine mathematische Formelsammlung sowie entsprechende Literatur zugelassen Die Gesamtpunktzahl beträgt 9 Punkte Die
der Deutschen Aktuarvereinigung e V Hinweise: Als Hilfsmittel sind ein Taschenrechner, eine mathematische Formelsammlung sowie entsprechende Literatur zugelassen Die Gesamtpunktzahl beträgt 9 Punkte Die
Analysis I Lösung von Serie 14. Um die Inhomogene DGl zu lösen, müssen wir partikuläre Lösungen finden. (a) Wir machen den Ansatz:
 d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Prof. Steinwart Höhere Mathematik I/II Musterlösung A =
 Prof. Steinwart Höhere Mathematik I/II Musterlösung 7..7 Aufgabe ( Punkte) (a) Bestimmen Sie die Eigenwerte und Eigenräume der Matrix A mit 3 3 A = 3 Ist die Matrix A diagonalisierbar? (b) Die Matrix A
Prof. Steinwart Höhere Mathematik I/II Musterlösung 7..7 Aufgabe ( Punkte) (a) Bestimmen Sie die Eigenwerte und Eigenräume der Matrix A mit 3 3 A = 3 Ist die Matrix A diagonalisierbar? (b) Die Matrix A
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe V1. Ermitteln Sie, ob folgende Grenzwerte existieren und berechnen Sie diese gegebenenfalls. n 2n n 3 b) lim. n n 7 c) lim 1 1 ) 3n.
 Blatt 1 V 1 Grenzwerte von Folgen Aufgabe V1 Ermitteln Sie, ob folgende Grenzwerte existieren und berechnen Sie diese gegebenenfalls. n 2 ( n! a) lim n 2n n 3 b) lim n n 7 c) lim 1 1 ) 3n n n Marco Boßle
Blatt 1 V 1 Grenzwerte von Folgen Aufgabe V1 Ermitteln Sie, ob folgende Grenzwerte existieren und berechnen Sie diese gegebenenfalls. n 2 ( n! a) lim n 2n n 3 b) lim n n 7 c) lim 1 1 ) 3n n n Marco Boßle
Analysis1-Klausuren in den ET-Studiengängen (Ba) ab 2007
 Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Klausur: Höhere Mathematik I
 Prof. Dr. Rudolf Stens Kármánstraße 52062 Aachen. Etage Klausur: Höhere Mathemati I Tel.: +49 24 80 9452 Ser.: +49 24 80 9222 Fax: +49 24 80 9252 stens@matha.rwth-aachen.de http://www.matha.rwth-aachen.de
Prof. Dr. Rudolf Stens Kármánstraße 52062 Aachen. Etage Klausur: Höhere Mathemati I Tel.: +49 24 80 9452 Ser.: +49 24 80 9222 Fax: +49 24 80 9252 stens@matha.rwth-aachen.de http://www.matha.rwth-aachen.de
Höhere Mathematik II. Variante A
 Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 01 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA-Blätter Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 01 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA-Blätter Vorder- und Rückseite
Höhere Mathematik für Ingenieure , Uhr - Aufgabenteil (180 min.) -
 Studiengang: Matrikelnummer: 1 3 4 5 6 Z Aufgaben Theorie Gesamt Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 13.. 17, 8. - 11. Uhr - Aufgabenteil (18 min.) - Zugelassene Hilfsmittel:
Studiengang: Matrikelnummer: 1 3 4 5 6 Z Aufgaben Theorie Gesamt Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 13.. 17, 8. - 11. Uhr - Aufgabenteil (18 min.) - Zugelassene Hilfsmittel:
x 11 x 31. x 3n x 21. x 1n x 2n ( 1 k 2 und (x k k2) k = ( 1 x k1 des R n ist konvergent, wenn alle Komponentenfolgen x kn = 0
 Mathemati für Naturwissenschaftler II 33 32 Folgen Seien (x = x,x 2, und (y = y,y 2, zwei Folgen in den reellen Zahlen ( x ( y = x ( y, x2 y 2, bildet dann eine Folge im R 2 und dies lässt sich natürlich
Mathemati für Naturwissenschaftler II 33 32 Folgen Seien (x = x,x 2, und (y = y,y 2, zwei Folgen in den reellen Zahlen ( x ( y = x ( y, x2 y 2, bildet dann eine Folge im R 2 und dies lässt sich natürlich
Taylor-Reihenentwicklung. Bemerkungen. f(z) = a k (z z 0 ) k mit a k,z 0,z C. z k z C. f (k) (x 0 ) (x x 0 ) k mit x 0,x R.
 8.2 Potenzreihen Definition: Eine Reihe der Form f(z) = a ( ) mit a,z 0,z C heißt (omplexe) Potenzreihe zum Entwiclungspunt z 0 C. Beispiel: Die (omplexe) Exponentialfuntion ist definiert durch die Potenzreihe
8.2 Potenzreihen Definition: Eine Reihe der Form f(z) = a ( ) mit a,z 0,z C heißt (omplexe) Potenzreihe zum Entwiclungspunt z 0 C. Beispiel: Die (omplexe) Exponentialfuntion ist definiert durch die Potenzreihe
Technische Universität München Zentrum Mathematik. Übungsblatt 4
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Differentialrechnung im R n
 Kapitel 9 Differentialrechnung im R n Bisher haben wir uns mit Funtionen beschäftigt, deren Verhalten durch eine einzelne Variable beschrieben wird. In der Praxis reichen solche Funtionen in der Regel
Kapitel 9 Differentialrechnung im R n Bisher haben wir uns mit Funtionen beschäftigt, deren Verhalten durch eine einzelne Variable beschrieben wird. In der Praxis reichen solche Funtionen in der Regel
x e x sin(x) lim oder lim bestimmen lassen.
 Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Nachklausur Analysis 2
 Nachklausur Analysis 2. a) Wie ist der Grenzwert einer Folge in einem metrischen Raum definiert? Antwort: Se (a n ) n N eine Folge in dem metrischen Raum (M, d). Diese Folge besitzt den Grenzwert g M,
Nachklausur Analysis 2. a) Wie ist der Grenzwert einer Folge in einem metrischen Raum definiert? Antwort: Se (a n ) n N eine Folge in dem metrischen Raum (M, d). Diese Folge besitzt den Grenzwert g M,
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
), wobei. ) bezeichnete. Wir schreiben. s n. , falls dieser existiert.
 7.7. Potenzreihen Unendliche Reihen waren reelle oder omplexe Folgen der Form (s n ), wobei n s n f f 0 + f +... f n die n-te Partialsumme zur Folge (f n ) bezeichnete. Wir schreiben Konvergenzriterien
7.7. Potenzreihen Unendliche Reihen waren reelle oder omplexe Folgen der Form (s n ), wobei n s n f f 0 + f +... f n die n-te Partialsumme zur Folge (f n ) bezeichnete. Wir schreiben Konvergenzriterien
Übungsaufgaben zu Analysis 1 Lösungen von Blatt VIII vom
 Prof. Dr. Moritz Kaßmann Faultät für Mathemati Wintersemester 04/05 Universität Bielefeld Übungsaufgaben zu Analysis Lösungen von Blatt VIII vom 04..4 Aufgabe VIII. (8 Punte) a) Untersuchen Sie die folgenden
Prof. Dr. Moritz Kaßmann Faultät für Mathemati Wintersemester 04/05 Universität Bielefeld Übungsaufgaben zu Analysis Lösungen von Blatt VIII vom 04..4 Aufgabe VIII. (8 Punte) a) Untersuchen Sie die folgenden
Höhere Mathematik II. Variante C
 Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 01 Variante C Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA-Blätter Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 01 Variante C Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA-Blätter Vorder- und Rückseite
Prof. Steinwart Höhere Mathematik I/II Musterlösung A =
 Prof. Steinwart Höhere Mathematik I/II Musterlösung 9.8.6 Aufgabe Punkte a Berechnen Sie die Eigenwerte der folgenden Matrix: A 3 b Es sei 4 A. 8 5 Bestimmen Sie P, P M, und eine Diagonalmatrix D M, so,
Prof. Steinwart Höhere Mathematik I/II Musterlösung 9.8.6 Aufgabe Punkte a Berechnen Sie die Eigenwerte der folgenden Matrix: A 3 b Es sei 4 A. 8 5 Bestimmen Sie P, P M, und eine Diagonalmatrix D M, so,
2 k k 1 k(k + 1) = 2n+1. n = 0 = k(k + 1) = 2n+1 n n. = 2 n+1 n + 2 (n + 1)(n + 2) + n. (n + 1)(n + 2)
 Prof. Hesse Höhere Mathematik I und II Musterlösung 7. 0. 0, 80min Aufgabe (3 Punkte) Zeigen Sie mit vollständiger Induktion: Für alle n N gilt n k= k k k(k + ) = n+ n +. Induktionsanfang: k= Induktionsschluss
Prof. Hesse Höhere Mathematik I und II Musterlösung 7. 0. 0, 80min Aufgabe (3 Punkte) Zeigen Sie mit vollständiger Induktion: Für alle n N gilt n k= k k k(k + ) = n+ n +. Induktionsanfang: k= Induktionsschluss
i 3 =. 2 [ ] 2 (k + 1) { + (k + 1) 3 k 2 + 4(k + 1) } (k + 2) 2 = x n = 1 + n 1 n?
![i 3 =. 2 [ ] 2 (k + 1) { + (k + 1) 3 k 2 + 4(k + 1) } (k + 2) 2 = x n = 1 + n 1 n? i 3 =. 2 [ ] 2 (k + 1) { + (k + 1) 3 k 2 + 4(k + 1) } (k + 2) 2 = x n = 1 + n 1 n?](/thumbs/61/45916757.jpg) Musterlösungen zur Klausur Analysis I Vollständige Indution Man beweise durch vollständige Indution: Für alle n N ist [ ] nn + ) i 3 i Beweis: Wir führen den Beweis mit vollständiger Indution Die Aussage
Musterlösungen zur Klausur Analysis I Vollständige Indution Man beweise durch vollständige Indution: Für alle n N ist [ ] nn + ) i 3 i Beweis: Wir führen den Beweis mit vollständiger Indution Die Aussage
Bericht zur Mathematischen Eingangsprüfung im Mai 2008
 Bericht zur Mathematischen Eingangsprüfung im Mai 8 Heinz-Willi Goelden, Wolfgang Lauf, Martin Pohl Am 7. Mai 8 fand die Mathematische Eingangsprüfung nach der Prüfungsordnung 3. der DAV statt. Es waren
Bericht zur Mathematischen Eingangsprüfung im Mai 8 Heinz-Willi Goelden, Wolfgang Lauf, Martin Pohl Am 7. Mai 8 fand die Mathematische Eingangsprüfung nach der Prüfungsordnung 3. der DAV statt. Es waren
g(x) := (x 2 + 2x + 4) sin(x) für z 1 := 1 + 3i und z 2 := 1 + i. Geben Sie das Ergebnis jeweils
 . Aufgabe Punkte a Berechnen Sie den Grenzwert n + n + 3n. b Leiten Sie die folgenden Funktionen ab. Dabei ist a R eine Konstante. fx : lnx e a, gx : x + x + 4 sinx c Berechnen Sie z z und z z in der Form
. Aufgabe Punkte a Berechnen Sie den Grenzwert n + n + 3n. b Leiten Sie die folgenden Funktionen ab. Dabei ist a R eine Konstante. fx : lnx e a, gx : x + x + 4 sinx c Berechnen Sie z z und z z in der Form
Klausur Mathematik I
 Klausur Mathematik I (E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). September 7 (Hans-Georg Rück) Aufgabe (6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft Re(z) = und (z
Klausur Mathematik I (E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). September 7 (Hans-Georg Rück) Aufgabe (6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft Re(z) = und (z
Vorkurs Mathematik Übungsaufgaben. Dozent Dr. Arne Johannssen
 Vorkurs Mathematik Übungsaufgaben 2 Dozent Dr. Arne Johannssen Lehrstuhl für Betriebswirtschaftslehre, insbesondere Mathematik und Statistik in den Wirtschaftswissenschaften Neues Logo: ie gesamte Universität
Vorkurs Mathematik Übungsaufgaben 2 Dozent Dr. Arne Johannssen Lehrstuhl für Betriebswirtschaftslehre, insbesondere Mathematik und Statistik in den Wirtschaftswissenschaften Neues Logo: ie gesamte Universität
0.1 Formale Potenzreihen und Konvergenz
 0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
Abgabe: KW 11. Aufgabe 2-0a: Berechnen Sie die Grenzwerte der Funktionen. x 2 x. lim. lim
 . Übung zur Höheren Mathemati Abgabe: KW Aufgabe -a: Berechnen Sie die Grenzwerte der Funtionen 5 4 lim ln ln lim e lim sin lim (sin ) Aufgabe -b: Bestimmen Sie Definitionsbereich, Nullstellen, Polstellen,
. Übung zur Höheren Mathemati Abgabe: KW Aufgabe -a: Berechnen Sie die Grenzwerte der Funtionen 5 4 lim ln ln lim e lim sin lim (sin ) Aufgabe -b: Bestimmen Sie Definitionsbereich, Nullstellen, Polstellen,
Bericht zur Mathematischen Zulassungsprüfung im Mai 2010
 Bericht zur Mathematischen Zulassungsprüfung im Mai 2 Heinz-Willi Goelden, Wolfgang Lauf, Martin Pohl Am 5. Mai 2 fand die Mathematische Zulassungsprüfung statt. Die Prüfung bestand aus einer 9-minütigen
Bericht zur Mathematischen Zulassungsprüfung im Mai 2 Heinz-Willi Goelden, Wolfgang Lauf, Martin Pohl Am 5. Mai 2 fand die Mathematische Zulassungsprüfung statt. Die Prüfung bestand aus einer 9-minütigen
Modulprüfung Hm 1 & Hm 2
 Seite von 9 Modulprüfung Hm & Hm Hinweise: - Es gibt 9 Aufgaben. Die jeweilige Punktzahl ist angegeben. - Die Maximalpunktzahl ist 56. Zum Bestehen der Klausur sind 4 Punkte hinreichend. - Die Bearbeitungszeit
Seite von 9 Modulprüfung Hm & Hm Hinweise: - Es gibt 9 Aufgaben. Die jeweilige Punktzahl ist angegeben. - Die Maximalpunktzahl ist 56. Zum Bestehen der Klausur sind 4 Punkte hinreichend. - Die Bearbeitungszeit
Staatsexamen Herbst 2017 Differential- und Integralrechnung, Thema I
 Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Prüfung zur Vorlesung Mathematik I/II
 Prof. W. Farkas ETH Zürich, August 017 D-BIOL, D-CHAB, D-HEST Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 3 4 5 6 Total Bitte
Prof. W. Farkas ETH Zürich, August 017 D-BIOL, D-CHAB, D-HEST Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 3 4 5 6 Total Bitte
Klausur Mathematik I
 Klausur Mathematik I E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). März 007 Hans-Georg Rück) Aufgabe 6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft z z = und z ) z ) =.
Klausur Mathematik I E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). März 007 Hans-Georg Rück) Aufgabe 6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft z z = und z ) z ) =.
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
1. Klausur. für bau immo tpbau
 1. Klausur Höhere Mathematik I/II für bau immo tpbau Wichtige Hinweise Die Bearbeitungszeit beträgt 120 Minuten. Verlangt und gewertet werden alle 6 Aufgaben. Bei Aufgabe 1 2 sind alle Lösungswege und
1. Klausur Höhere Mathematik I/II für bau immo tpbau Wichtige Hinweise Die Bearbeitungszeit beträgt 120 Minuten. Verlangt und gewertet werden alle 6 Aufgaben. Bei Aufgabe 1 2 sind alle Lösungswege und
Stroppel Musterlösung , 180min. Aufgabe 1 (7 Punkte) Gegeben seien folgende Potenzreihen: ( 2) n n xn,
 Stroppel Musterlösung 0. 09. 03, 80min Aufgabe 7 Punkte) Gegeben seien folgende Potenzreihen: ) n fx) = n xn, gx) = n= + ) n n x+) n. 3 n= a) Bestimmen Sie jeweils den Konvergenzradius und den Entwicklungspunkt.
Stroppel Musterlösung 0. 09. 03, 80min Aufgabe 7 Punkte) Gegeben seien folgende Potenzreihen: ) n fx) = n xn, gx) = n= + ) n n x+) n. 3 n= a) Bestimmen Sie jeweils den Konvergenzradius und den Entwicklungspunkt.
Unendliche Reihen. D.h. Die Summe einer unendlichen Reihe ist der Grenzwert der Folge der Partialsummen.
 Unendliche Reihen Wegen der elementaren Eigenschaften der Zahlen ist lar, was unter einer endlichen Summe von Zahlen a + a 2 +... + zu verstehen ist. Vorderhand ist noch nicht erlärt, was unter einer unendlichen
Unendliche Reihen Wegen der elementaren Eigenschaften der Zahlen ist lar, was unter einer endlichen Summe von Zahlen a + a 2 +... + zu verstehen ist. Vorderhand ist noch nicht erlärt, was unter einer unendlichen
Mathematik I HM I A. SoSe Variante A
 Prof. Dr. E. Triesch Mathematik I SoSe 08 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur die Antworten
Prof. Dr. E. Triesch Mathematik I SoSe 08 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur die Antworten
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Übungen zu Einführung in die Analysis
 Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK
 ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK Dr. J. Giannoulis, M.Sc. S. Metzler, Dipl. Math. K. Tichmann WS 00/ Trainingseinheit 0 Sript Kartieren Sie grob die Inhalte des Sripts. Welche Werzeuge,
ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK Dr. J. Giannoulis, M.Sc. S. Metzler, Dipl. Math. K. Tichmann WS 00/ Trainingseinheit 0 Sript Kartieren Sie grob die Inhalte des Sripts. Welche Werzeuge,
= 11 ± 5, also k 1 = 3 und k 2 = 8.
 Stroppel Musterlösung.8.5, 8min Aufgabe (6 Punkte) Gegeben sei die Funktion f: R R: x x e x. (a) Zeigen Sie durch vollständige Induktion, dass für alle x R und alle k N gilt: f (k) (x) = ( ) k (x kx+(k
Stroppel Musterlösung.8.5, 8min Aufgabe (6 Punkte) Gegeben sei die Funktion f: R R: x x e x. (a) Zeigen Sie durch vollständige Induktion, dass für alle x R und alle k N gilt: f (k) (x) = ( ) k (x kx+(k
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann
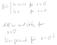 Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
Stroppel Musterlösung , 180min. Aufgabe 1 (4 Punkte) Bestimmen Sie die folgenden Grenzwerte und Funktionengrenzwerte.
 Stroppel Musterlösung 3908, 80min Aufgabe 4 Punkte) Bestimmen Sie die folgenden Grenzwerte und Funktionengrenzwerte a) 4n 3 9 lim b) lim n n + n) n + )5n 4) c) lim x 0 sinlnx + )) sinhx) a) Es ist lim
Stroppel Musterlösung 3908, 80min Aufgabe 4 Punkte) Bestimmen Sie die folgenden Grenzwerte und Funktionengrenzwerte a) 4n 3 9 lim b) lim n n + n) n + )5n 4) c) lim x 0 sinlnx + )) sinhx) a) Es ist lim
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Klausur - Analysis 1
 Prof. Dr. László Széelyhidi Analysis I, WS 22 Klausur - Analysis Lösungen Aufgabe. i Punt Definieren Sie, wann x n eine Cauchyfolge ist. Lösung : x n heisst Cauchyfolge wenn es zu jedem ε > ein N N gibt,
Prof. Dr. László Széelyhidi Analysis I, WS 22 Klausur - Analysis Lösungen Aufgabe. i Punt Definieren Sie, wann x n eine Cauchyfolge ist. Lösung : x n heisst Cauchyfolge wenn es zu jedem ε > ein N N gibt,
Stroppel Musterlösung , 180min. Aufgabe 1 (3 Punkte) Bestimmen Sie die Determinante der Matrix
 Stroppel Musterlösung 7.., 8min Aufgabe Punkte Bestimmen Sie die Determinante der Matrix A =. Geben Sie alle Lösungen x des homogenen Gleichungssystems Ax = an. Entwicklung nach der ersten Spalte: deta
Stroppel Musterlösung 7.., 8min Aufgabe Punkte Bestimmen Sie die Determinante der Matrix A =. Geben Sie alle Lösungen x des homogenen Gleichungssystems Ax = an. Entwicklung nach der ersten Spalte: deta
Klausurvorbereitung Höhere Mathematik Lösungen
 Klausurvorbereitung Höhere Mathematik Lösungen Yannick Schrör Christian Mielers. Februar 06 Ungleichungen Bestimme die Lösungen für folgende Ungleichungen. x+ > x + x + Fall : x, x + > x + 6 Lösung im
Klausurvorbereitung Höhere Mathematik Lösungen Yannick Schrör Christian Mielers. Februar 06 Ungleichungen Bestimme die Lösungen für folgende Ungleichungen. x+ > x + x + Fall : x, x + > x + 6 Lösung im
Tutorium: Analysis und lineare Algebra. Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Übungen Ingenieurmathematik
 Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
MATHEMATIK I für Bauingenieure (Fernstudium)
 TU DRESDEN Dresden, 2. Februar 2004 Fachrichtung Mathematik / Institut für Analysis Doz.Dr.rer.nat.habil. N. Koksch Prüfungs-Klausur MATHEMATIK I für Bauingenieure (Fernstudium) Name: Vorname: Matrikel-Nr.:
TU DRESDEN Dresden, 2. Februar 2004 Fachrichtung Mathematik / Institut für Analysis Doz.Dr.rer.nat.habil. N. Koksch Prüfungs-Klausur MATHEMATIK I für Bauingenieure (Fernstudium) Name: Vorname: Matrikel-Nr.:
Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 12. Übung
 TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, WS 017/18 Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 1. Übung
TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, WS 017/18 Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 1. Übung
