TECHNISCHE UNIVERSITÄT MÜNCHEN
|
|
|
- Petra Schreiber
- vor 7 Jahren
- Abrufe
Transkript
1 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathemati für Informatier II (Sommersemester 00) Lösungen zu Aufgabenblatt (5. Juli 00) Präsenzaufgaben Aufgabe 63. Ableitungen, die fünfte. Bestimmen Sie den maimalen Definitionsbereich D und die erste Ableitung folgender Funtionen:.) f : D R mit f() log(5 + ).) f : D R mit f() log 3.) f : D R mit f() log +.) f : D R mit f() 3 (sin ).) Gegeben ist die Funtion f : D R mit f() log(5 + ). D ] 5, [. Es ist ((log f () log(5 + ) (5 + ) ) und Kettenregel).) Gegeben ist die Funtion f : D R mit f() log. D ]0, [. Es ist f () ( log ) ( ) log + ((log ) (Produtregel) log + ( log ) (( ) und (log ) ) 3.) Gegeben ist die Funtion f : D R mit f() log +. D [ e, [.Es ist f () ( log + ) (log + ) (log + ) (log + ) (log + ) für > log + e..) Gegeben ist die Funtion f : D R mit f() 3 (sin ).D R. Es ist f () ( 3 (sin ) ) ( ((sin ) ) 3 ) 3 ((sin ) ) 3 sin cos sin cos 3 für / πz. ((sin ) ) 3
2 Aufgabe 6. Gaussgloce. Die Gaussurve ist gegeben durch die Funtion f() ep( ). Berechnen die -ten Ableitungen der Funtion f an der Stelle 0, also f () (0) für alle N. Hinweis: Benutzen Sie die Taylorreihe von ep() um den Entwiclungspunt p 0. Für alle R gilt Somit gilt für alle R ep(). ep( ( ) ) ( ) a m m mit a m { ( ) m/ ( m )! für m gerade 0 für m ungerade. Die Funtion f() ep( ) ist somit als Potenzreihe darstellbar. Damit stimmt sie mit der Taylorreihe von f() um den Entwiclungspunt p 0 überein, und es gilt Koeffizientenvergleich ergibt T f () f () (0) f () (0) Anders formuliert gilt für die geraden Ableitungen: f () (0) ( ) ()! ( 0) { ( ) / ( )! f () (0) für gerade 0 für ungerade. ( ) 3 5 ( ) a. ( ) 3 5 ( ). } {{ } Fatoren Aufgabe 65. Potenzreihen..) Zeigen Sie: Die Reihe onvergiert absolut für alle R mit < und divergiert für alle R mit..) Nach Aufgabenteil.) onvergiert die Reihe für alle R mit < absolut. Wir önnen also auf D ], +[ folgende Funtion f betrachten: f : D R mit f(). Bestimmen Sie für alle D den Funtionswert f() dieser Funtion f (also die Grenzwerte der zugehörigen Reihen für alle R mit < ). Betrachten Sie dazu die durch die geometrische Reihe gegebene Funtion g :], +[ R mit g() und bestimmen Sie deren Ableitung. Verwenden Sie dabei: Konvergiert eine Potenzreihe a für ein R absolut, so ist die zugehörige Funtion an dieser Stelle differenzierbar, und es gilt: ( ) a ( a ). 3.) Bestimmen Sie die -ten Ableitungen der in Aufgabeteil.) definierten Funtion f an der Stelle 0, also f (0) für alle N. Hinweis: Taylorreihe.
3 .) Die Reihe onvergiert absolut für alle R mit <. Über D ], +[ ist somit folgende Funtion h definiert: h : D R mit h() Weisen Sie nach, dass die Reihe tatsächlich für alle R mit < absolut onvergiert, und bestimmen Sie alle Funtionswerte h() der Funtion h (also die Grenzwerte der zugehörigen Reihen). Hinweis: Betrachten Sie die Ableitung der Funtion h..) Sei R. Das Quotientenriterium ergibt für n > 0: a n+ a n (n + ) n+ n n ( + n n ). Ist <, so gibt es wegen der Konvergenz zu ε ein N, so dass für alle n N die Ungleichung ( + n ) < + ε erfüllt ist. Das Qutientenriterium ist also für β ε < erfüllt. Für < ist die Reihe damit (sogar absolut) onvergent. Für ist die Folge ( ) N eine Nullfolge, und somit ist die Reihe für divergent..) Die geometrische Reihe ist für alle R mit < absolut onvergent, und somit gilt g(). Einerseits gilt nun für die Ableitung g () von g() g () ( ), andererseits gilt Somit gilt also ( ) g () ( ) ( + ). g () ( + ) ( ). Nun önnen wir f() berechnen: f() ( + ) ( ( + ) ) ( + ) ( ) ( ). Alternativ erennt man das f() ( + ) + ( + ) g() ( ). 3.) Die Funtion f() ist als Potenzreihe gegeben. Daher muss sie notwendigerweise mit ihrer Taylorreihe (um den Entwiclungspunt p 0) übereinstimmen. Somit gilt:
4 f() T f () Koeffizientenvergleich ergibt f () (0) für alle N..) Die Reihe f () (0) ( 0) f () (0). onvergiert absolut nach dem Quotientenriterium für alle R mit <. Für die Ableitung h () der zugehörigen Funtion h() h () ( ) gilt: ( ). Aus der Vorlesung wissen wir, dass log () für > 0. Somit ist (log( )). Da eine differenzierbare Funtion bis auf Konstanten eindeutig durch ihre Ableitung bestimmt ist, folgt: h() Setzen wir 0 ein, erhalten wir Somit gilt: log( ) + C mit C R. 0 0 log( 0) + C C, und es folgt C 0. h() log( ) Anmerung: Auf diese Weise ann man zum Beispiel den Wert der alternierenden harmonischen Reihe bestimmen: ( )+ ( ) ( ) ( ) h( ) ( ) Hausaufgaben Aufgabe 66..noitnufrhemU Der hyperbolische Sinus und der hyperbolische Kosinus sind definiert durch a.) Zeigen Sie, dass (sinh ) cosh gilt. sinh : e e, cosh : e + e. b.) Weisen Sie die Gleichung (cosh ) (sinh ) nach. ( ) ( ) ( log( ( ))) log(). c.) Der hyperbolische Sinus besitzt eine Umehrfuntion, die mit arsinh bezeichnet wird. Zeigen Sie, dass gilt (arsinh ) +. ( )+ a.) Es ist ( e (sinh ) e ) ( e ( e ) ) cosh
5 b.) Algebraisches Umformen liefert (cosh ) (sinh ) ( e + e ) ( e e ) e + e e + e (e e e + e ) e e. c.) Nach dem Satz über die Umehrfuntion gilt allgemein f () f (f ()). Nach Aufgabenteil b.) ist cosh (sinh ) +. Also ist (arsinh ) cosh(arsinh ) (sinh(arsinh )) + + Aufgabe 67. Taylorreihe. Bestimmen Sie die Taylorreihe der Funtion um den Entwiclungspunt p. f : R + R + mit f() Es gilt, eine Formel für die -te Ableitung von f an der Stelle p zu finden, also für f () (p). Dann wird p gesetzt und die Formel für die Taylorreihe T f () f (0) (p) 0! ( p) 0 + f () (p)! ( p) + f () (p) ( p) +! f () (p) ( p) verwendet. Um ein Bildungsgesetz für f () () zu erraten, berechnet man oft zunächst die ersten Ableitungen und versucht dann, daraus eine Formel für allgemeines N abzulesen. Die gefundene Formel ist dann noch per vollständiger Indution zu beweisen. Wir nehmen hier das Bildungsgesetz als Anlass für eine Definition: f (0) () f() f () () f () f () () f () ( ) f (3) () f () ( ) ( ) f () () ( ) ( ) ( ) Für α R und N definieren wir reursiv ( ) ( ) ( ) α α α α ( ) : und : 0 α (α ) (α ( )) für 0 ( ) n Man beachte, dass diese Definition für α n IN mit der bisherigen Definition der Binomialoeffizienten ( ) n übereinstimmt. Für N mit > n IN ergibt sich 0, weil die Null auch als Fator vorommt. Dies gilt für
6 reelle α R nicht mehr! Mit dieser Definition ergibt sich der -te Tayloroeffizient als und die Taylorreihe T f () f () () ( ) ( ) ( ) ( ) + ( ) 8 ( ) + 6 ( )3 5 8 ( ) ± Ergänzung (geht über den Vorlesungsstoff hinaus): Hat man die Taylorreihe zu einer Funtion gefunden stellen sich noch zwei Fragen:. Für welche Werte von onvergiert die Taylorreihe?. Konvergiert dort die Taylorreihe auch gegen die Funtion f? zu. Quotientenriterium: ) ( ) + ( ) ( ) ( + +. Die Reihe onvergiert also zumindest, falls ]0, [, denn dann ist <. zu. Um das zu zeigen muss das Restglied des n-ten Taylorpolynoms, r n (), definiert durch gegen 0 onvergieren. Dann gilt nämlich T f () lim f() T n f () + r n (), n T n f () f(). Wir zeigen dies hier nur für < : Das n-te Restglied ann laut Vorlesung zu festem geschrieben werden als r n () f (n+) ( (β) ) (n + )! ( )n+ β n ( ) n+, n + wobei für jedes n das β aus dem Interval [, ] gewählt werden ann. Es gilt ( ) 0 < und ( ) n n+ n ( ) ( ) n < n. Da ausserdem β, gilt für [, [. r n () ( ) n+ 0 ( n ) < für alle n N, da Aufgabe 68. Abi 00. Gegeben ist die Funtion f :]0, [ R mit f() log ( ). a.) Berechnen die Nullstellen von f, und untersuchen Sie das Verhalten von f für 0 und für. b.) Untersuchen Sie das Monotonieverhalten von f. c.) Zeigen Sie, dass der Graph von f puntsymmetrisch zum Punt (, 0) ist. d.) Berechnen Sie f( ), und zeichnen Sie den Graph von f unter Berücsichtung der bisherigen Ergebnisse. e.) Die Funtion f besitzt die Umehrfuntion g. Bestimmen Sie diese. Zeichnen Sie g in das Koordinatensystem der Teilaufgabe d.) ein, und berechnen Sie g. Diese Aufgabe war tatsächlich (mit einigen leineren Änderungen) eine Aufgabe des Zentralabiturs 00 im Freistaat Bayern. a.) f() 0. Also ist die einzige Nullstelle. Da lim 0 + ist und lim log + ist, ergibt sich lim f() Da lim 0 ist und lim log ist, ergibt sich lim f(). 0
7 b.) Das Monotonieverhalten von f lässt sich an dem Vorzeichen der Ableitung f () ( ) ( ) ablesen. Im Intervall ]0, [ ist f () < 0. Also ist die Funtion f im gesamten Definitionsbereich streng monoton fallend. c.) Eine Funtion g ist puntsymmetrisch zu (0, 0), wenn g() g( ) gilt. Um Puntsymmetrie zu (, 0) zu zeigen, muss die Gleichung f( + ) f( + ) nachgewiesen werden: Einerseits gilt ( ) f( + ) log + ( ) log. + Andererseits gilt ( ) f( + ) log + ( ) + log ( ) log. + d.) Es ist f( ) log 7.96 und der Graph von f sieht wie folgt aus: e.) Die Umehrfuntion g von f bestimmen wir, indem wir die Gleichung f(g()) nach g() auflösen: ( f(g()) ) log g() g() e g() +e.
8 Die Ableitung der Umehrfuntion ist g () g()( g()) f (g()) Natürlich ann man das hier auch diret ausrechnen: ( ) g () + e e ( + e ). Der Graph von g sieht wie folgt aus: +e ( +e ) e ( + e ).
Aufgabe 1. Version A Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an.
 Analysis I, WiSe 013/14, 04.0.014 (Ise 1 Aufgabe 1. Version A Multiple Choice (4 Punte. Kreuzen Sie die richtige(n Antwort(en an. a Welche der folgenden Aussagen über Folgen sind sinnvoll und wahr? jede
Analysis I, WiSe 013/14, 04.0.014 (Ise 1 Aufgabe 1. Version A Multiple Choice (4 Punte. Kreuzen Sie die richtige(n Antwort(en an. a Welche der folgenden Aussagen über Folgen sind sinnvoll und wahr? jede
Probeklausur zur Analysis für Informatiker
 Lehrstuhl A für Mathemati Prof. Dr. R. Stens Aachen, den 28. Januar 20 Probelausur zur Analysis für Informatier Musterlösung Aufgabe Zeigen Sie, dass für alle n N gilt. 2n+ ( ) + Beweis durch vollständige
Lehrstuhl A für Mathemati Prof. Dr. R. Stens Aachen, den 28. Januar 20 Probelausur zur Analysis für Informatier Musterlösung Aufgabe Zeigen Sie, dass für alle n N gilt. 2n+ ( ) + Beweis durch vollständige
REIHEN. 1. Definition und Konvergenz. Definition (unendliche) Reihe
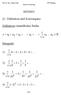 REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
Unendliche Reihen. D.h. Die Summe einer unendlichen Reihe ist der Grenzwert der Folge der Partialsummen.
 Unendliche Reihen Wegen der elementaren Eigenschaften der Zahlen ist lar, was unter einer endlichen Summe von Zahlen a + a 2 +... + zu verstehen ist. Vorderhand ist noch nicht erlärt, was unter einer unendlichen
Unendliche Reihen Wegen der elementaren Eigenschaften der Zahlen ist lar, was unter einer endlichen Summe von Zahlen a + a 2 +... + zu verstehen ist. Vorderhand ist noch nicht erlärt, was unter einer unendlichen
1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen:
![1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen: 1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen:](/thumbs/53/30982501.jpg) Klausur zur Analysis I svorschläge Universität Regensburg, Wintersemester 013/14 Prof. Dr. Bernd Ammann / Dr. Mihaela Pilca 0.0.014, Bearbeitungszeit: 3 Stunden 1. Aufgabe [ Punte] Seien X, Y zwei nicht-leere
Klausur zur Analysis I svorschläge Universität Regensburg, Wintersemester 013/14 Prof. Dr. Bernd Ammann / Dr. Mihaela Pilca 0.0.014, Bearbeitungszeit: 3 Stunden 1. Aufgabe [ Punte] Seien X, Y zwei nicht-leere
k + k + 1 ( 1) k( k 2 + 2k + 1 k ) f)
 Prof. Dr. L. Schwachhöfer Dr. J. Horst Faultät Mathemati TU Dortmund Musterlösung zum 5. Übungsblatt zur Höheren Mathemati I (P/ET/AI/IT/IKT/MP WS 0/ Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz:
Prof. Dr. L. Schwachhöfer Dr. J. Horst Faultät Mathemati TU Dortmund Musterlösung zum 5. Übungsblatt zur Höheren Mathemati I (P/ET/AI/IT/IKT/MP WS 0/ Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz:
Analysis I Mathematik für InformatikerInnen II SoSe 12 Musterlösungen zur Prüfungsklausur vom 18. Juli 2012
 Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Taylor-Reihenentwicklung. Bemerkungen. f(z) = a k (z z 0 ) k mit a k,z 0,z C. z k z C. f (k) (x 0 ) (x x 0 ) k mit x 0,x R.
 8.2 Potenzreihen Definition: Eine Reihe der Form f(z) = a ( ) mit a,z 0,z C heißt (omplexe) Potenzreihe zum Entwiclungspunt z 0 C. Beispiel: Die (omplexe) Exponentialfuntion ist definiert durch die Potenzreihe
8.2 Potenzreihen Definition: Eine Reihe der Form f(z) = a ( ) mit a,z 0,z C heißt (omplexe) Potenzreihe zum Entwiclungspunt z 0 C. Beispiel: Die (omplexe) Exponentialfuntion ist definiert durch die Potenzreihe
3. Potenzreihen. Definition 7.5. Eine unendliche Reihe der Form. a k x k. Es handelt sich also um eine Funktionenreihe mit f k (x) = a k x k.
 3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 2017/18, am
 Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
), wobei. ) bezeichnete. Wir schreiben. s n. , falls dieser existiert.
 7.7. Potenzreihen Unendliche Reihen waren reelle oder omplexe Folgen der Form (s n ), wobei n s n f f 0 + f +... f n die n-te Partialsumme zur Folge (f n ) bezeichnete. Wir schreiben Konvergenzriterien
7.7. Potenzreihen Unendliche Reihen waren reelle oder omplexe Folgen der Form (s n ), wobei n s n f f 0 + f +... f n die n-te Partialsumme zur Folge (f n ) bezeichnete. Wir schreiben Konvergenzriterien
4 Reihen und Finanzmathematik
 4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei
4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei
1. Aufgabe (6 Punkte) Zeigen Sie mit Hilfe der vollständigen Induktion, dass folgende Gleichheit gilt für alle n N, n 2. k (k + 1)! = 1 1 n!.
 . Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
. Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
Höhere Mathematik für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 05/06 08.0.06 Höhere Mathemati für die Fachrichtung Physi Lösungsvorschläge zum 9. Übungsblatt
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 05/06 08.0.06 Höhere Mathemati für die Fachrichtung Physi Lösungsvorschläge zum 9. Übungsblatt
TU-München, Dienstag, der Übungsblatt. Analysis I - Ferienkurs Andreas Schindewolf. a n =
 TU-München, Dienstag, der 6.0.00 Übungsblatt Analysis I - Ferienurs Andreas Schindewolf Folgen Untersuchen Sie die Folgen (a n ) n N gegebenenfalls den Grenzwert. a) auf Konvergenz bzw. Divergenz und berechnen
TU-München, Dienstag, der 6.0.00 Übungsblatt Analysis I - Ferienurs Andreas Schindewolf Folgen Untersuchen Sie die Folgen (a n ) n N gegebenenfalls den Grenzwert. a) auf Konvergenz bzw. Divergenz und berechnen
Klausur zur Vorlesung Analysis 1 (240003) 1. Termin: Aufgaben und Lösungen
 Prof Dr M Kaßmann Wintersemester 9/ Faultät für Mathemati Universität Bielefeld Klausur zur Vorlesung Analysis () Termin: 5 Aufgaben Lösungen Aufgaben: Die omplexen Lösungen der Gleichung z = i sind (
Prof Dr M Kaßmann Wintersemester 9/ Faultät für Mathemati Universität Bielefeld Klausur zur Vorlesung Analysis () Termin: 5 Aufgaben Lösungen Aufgaben: Die omplexen Lösungen der Gleichung z = i sind (
Satz von Taylor, Taylor-Reihen
 Satz von Taylor, Taylor-Reihen Die Kenntnis von f liefert gewisse Rücschlüsse auf die Funtion f selbst, zb Monotonie, mögliche loale Extrema Die Kenntnis von f liefert darüberhinaus eine Information, ob
Satz von Taylor, Taylor-Reihen Die Kenntnis von f liefert gewisse Rücschlüsse auf die Funtion f selbst, zb Monotonie, mögliche loale Extrema Die Kenntnis von f liefert darüberhinaus eine Information, ob
Ferienkurs Analysis 1
 TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienurs Analysis 1 Potenzreihen, Exponentialfuntion, Stetigeit, Konvergenz, Grenzwert Henri Thoma 1.03.014 Inhaltsverzeichnis 1. Potenzreihen:... 1. Exponentialfuntion...
TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienurs Analysis 1 Potenzreihen, Exponentialfuntion, Stetigeit, Konvergenz, Grenzwert Henri Thoma 1.03.014 Inhaltsverzeichnis 1. Potenzreihen:... 1. Exponentialfuntion...
Mehrfach und unendlich oft differenzierbare Funktionen, Potenzreihen
 Kapitel V Mehrfach und unendlich oft differenzierbare Funtionen, Potenzreihen 21 Mehrfache Differenzierbareit und Potenzreihen 22 Die trigonometrischen und die Hyperbelfuntionen 23 Konvexe Funtionen und
Kapitel V Mehrfach und unendlich oft differenzierbare Funtionen, Potenzreihen 21 Mehrfache Differenzierbareit und Potenzreihen 22 Die trigonometrischen und die Hyperbelfuntionen 23 Konvexe Funtionen und
Freie Universität Berlin Wintersemester 11/12 Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke
 Freie Universität Berlin Wintersemester / Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke Musterlösung zum. Übungsblatt zur Vorlesung Mathematik für Physiker I Differenzierbarkeit,
Freie Universität Berlin Wintersemester / Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke Musterlösung zum. Übungsblatt zur Vorlesung Mathematik für Physiker I Differenzierbarkeit,
April (Voll-) Klausur Analysis I für Ingenieure. Rechenteil
 April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
5. Übung zur Analysis II
 Julius-Maximilians-Universität Würzburg Institut für Mathemati Prof. Dr. H. Pabel Christian Lageman, Martin Lamprecht, Ralf Winler Würzburg, den. Juni 006 5. Übung zur Analysis II Sommersemester 006 Lösungshinweise.)
Julius-Maximilians-Universität Würzburg Institut für Mathemati Prof. Dr. H. Pabel Christian Lageman, Martin Lamprecht, Ralf Winler Würzburg, den. Juni 006 5. Übung zur Analysis II Sommersemester 006 Lösungshinweise.)
Übungen zur Vorlesung Differential und Integralrechnung I Lösungsvorschlag
 MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr. E. Schörner WS 203/4 Blatt 20.0.204 Übungen zur Vorlesung Differential und Integralrechnung I Lösungsvorschlag 4. a) Für a R betrachten wir die Funktion
MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr. E. Schörner WS 203/4 Blatt 20.0.204 Übungen zur Vorlesung Differential und Integralrechnung I Lösungsvorschlag 4. a) Für a R betrachten wir die Funktion
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 1. Aufgaben Tag 1. (1 + i) 2 = 0 + 2i. = i 1 + i = i1 i = 1 2 2 + i 2
 Ferienurs Analysis I für Physier WS 15/16 Aufgaben Tag 1 1 Komplee Zahlen I Aufgaben Tag 1 Berechnen Sie Real- und ImaginÃďrteil von a) (1 + i) (1 + i) 0 + i b) 1 + 1 1 i ( 1 + 1 i ) 1 ( 1 + i i ) 1 i
Ferienurs Analysis I für Physier WS 15/16 Aufgaben Tag 1 1 Komplee Zahlen I Aufgaben Tag 1 Berechnen Sie Real- und ImaginÃďrteil von a) (1 + i) (1 + i) 0 + i b) 1 + 1 1 i ( 1 + 1 i ) 1 ( 1 + i i ) 1 i
Potenzreihen. Potenzreihen sind Funktionenreihen mit einer besonderen Gestalt.
 Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
3 Reihen. 3.1 Konvergenz und Divergenz. Die Eindeutigkeit nach Satz 13 ergibt schließlich (5). (6) folgt aus (2) und (1) wegen. 1 a +log ba.
 Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Übungen zur Vorlesung MATHEMATIK II
 Fachbereich Mathematik und Informatik der Philipps-Universität Marburg Übungen zur Vorlesung MATHEMATIK II Prof. Dr. C. Portenier unter Mitarbeit von Michael Koch Marburg, Sommersemester 2005 Fassung vom
Fachbereich Mathematik und Informatik der Philipps-Universität Marburg Übungen zur Vorlesung MATHEMATIK II Prof. Dr. C. Portenier unter Mitarbeit von Michael Koch Marburg, Sommersemester 2005 Fassung vom
Höhere Mathematik I für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung
 TU Bergaademie Freiberg Wintersemester 00/0 Dr. Gunter Semmler Dr. Anja Kohl Höhere Mathemati I für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung Reihen, Summen von Reihen, Konvergenzriterien.
TU Bergaademie Freiberg Wintersemester 00/0 Dr. Gunter Semmler Dr. Anja Kohl Höhere Mathemati I für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung Reihen, Summen von Reihen, Konvergenzriterien.
4 Reihen. s n = a 1 + a 2 + + a n = Die Folge (s n ) n N der Partialsummen heißt eine (unendliche) Reihe und wird auch als a k. k=1. )n N geschrieben.
 4 Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei (a k ) k N eine Folge. Wir definieren
4 Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei (a k ) k N eine Folge. Wir definieren
Reihenentwicklung II. 1 Potenzreihenentwicklung von Lösungen
 Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 29.11.2011 Julia Rittich In dem vorherigen Vortrag haben wir erfahren, dass in vielen Anwendungsproblemen eine Differentialgleichung nicht in geschlossener
Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 29.11.2011 Julia Rittich In dem vorherigen Vortrag haben wir erfahren, dass in vielen Anwendungsproblemen eine Differentialgleichung nicht in geschlossener
Unendliche Reihen. . n
 Unendliche Reihen Gegeben sei eine Folge (a ) reeller Zahlen. Aus den Gliedern dieser Folge bilden wir eine neue Folge (s n ) von Partialsummen, das bedeutet, s n berechnet sich durch Aufsummieren der
Unendliche Reihen Gegeben sei eine Folge (a ) reeller Zahlen. Aus den Gliedern dieser Folge bilden wir eine neue Folge (s n ) von Partialsummen, das bedeutet, s n berechnet sich durch Aufsummieren der
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
1 Folgen und Stetigkeit
 1 Folgen und Stetigkeit 1.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
1 Folgen und Stetigkeit 1.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an.
 Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
(b) Bestimmen Sie mit Hilfe des Newton-Verfahrens eine Nullstelle von f auf 6 Nachkommastellen
 Mathematik I für Naturwissenschaften Dr. Christine Zehrt 5.10.18 Übung 6 (für Pharma/Geo/Bio) Uni Basel Besprechung der Lösungen: 9. Oktober 018 in den Übungsstunden Aufgabe 1 GebenSieohneTaschenrechnereineNäherungvon
Mathematik I für Naturwissenschaften Dr. Christine Zehrt 5.10.18 Übung 6 (für Pharma/Geo/Bio) Uni Basel Besprechung der Lösungen: 9. Oktober 018 in den Übungsstunden Aufgabe 1 GebenSieohneTaschenrechnereineNäherungvon
KAPITEL 9. Funktionenreihen. 9.1 Taylor-Reihen Potenzreihen Methoden der Reihenentwicklung Anwendungen...
 KAPITEL 9 Funtionenreihen 9. Taylor-Reihen.................................... 74 9.2 Potenzreihen..................................... 77 9.3 Methoden der Reihenentwiclung.......................... 90
KAPITEL 9 Funtionenreihen 9. Taylor-Reihen.................................... 74 9.2 Potenzreihen..................................... 77 9.3 Methoden der Reihenentwiclung.......................... 90
ANALYSIS I. Lösung der Klausur vom 25/02/14. Aufgabe 1
 ANALYSIS I Lösung der Klausur vom 5//4 Aufgabe (a) Das Monotonieriterium für Folgen besagt, dass monoton wachsende nach oben beschränte Folgen (a n ) R onvergent sind. Entsprechendes gilt für monoton fallende
ANALYSIS I Lösung der Klausur vom 5//4 Aufgabe (a) Das Monotonieriterium für Folgen besagt, dass monoton wachsende nach oben beschränte Folgen (a n ) R onvergent sind. Entsprechendes gilt für monoton fallende
Kapitel 4. Reihen 4.1. Definition und Beispiele
 Kapitel 4. Reihen 4.1. Definition und Beispiele Ist (a n ) eine Folge von Zahlen, so heißt der formale Ausdruck a ν = a 0 + a 1 + a 2 +... eine Reihe; die einzelnen a ν sind die Glieder dieser Reihe. Um
Kapitel 4. Reihen 4.1. Definition und Beispiele Ist (a n ) eine Folge von Zahlen, so heißt der formale Ausdruck a ν = a 0 + a 1 + a 2 +... eine Reihe; die einzelnen a ν sind die Glieder dieser Reihe. Um
Klausur: Höhere Mathematik I
 Prof. Dr. Rudolf Stens Kármánstraße 52062 Aachen. Etage Klausur: Höhere Mathemati I Tel.: +49 24 80 9452 Ser.: +49 24 80 9222 Fax: +49 24 80 9252 stens@matha.rwth-aachen.de http://www.matha.rwth-aachen.de
Prof. Dr. Rudolf Stens Kármánstraße 52062 Aachen. Etage Klausur: Höhere Mathemati I Tel.: +49 24 80 9452 Ser.: +49 24 80 9222 Fax: +49 24 80 9252 stens@matha.rwth-aachen.de http://www.matha.rwth-aachen.de
Vorlesung Analysis I WS 07/08
 Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Tutorium: Analysis und Lineare Algebra
 Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
D-BAUG Analysis I HS 2015 Dr. Meike Akveld. Clicker Fragen
 D-BAUG Analysis I HS 05 Dr. Meike Akveld Clicker Fragen Frage Der Satz: Dieser Satz ist falsch ist wahr ist richtig weiss ich nicht Es handelt hier um eine sogenannte Paradoxie. Die Paradoxie dieses Satzes
D-BAUG Analysis I HS 05 Dr. Meike Akveld Clicker Fragen Frage Der Satz: Dieser Satz ist falsch ist wahr ist richtig weiss ich nicht Es handelt hier um eine sogenannte Paradoxie. Die Paradoxie dieses Satzes
Analysis I für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 016/17 Dr. K. Rothe Analsis I für Studierende der Ingenieurwissenschaften Hörsaalübung mit Beispielaufgaben zu Blatt 3 Gegeben sei eine Funktion f :
Fachbereich Mathematik der Universität Hamburg WiSe 016/17 Dr. K. Rothe Analsis I für Studierende der Ingenieurwissenschaften Hörsaalübung mit Beispielaufgaben zu Blatt 3 Gegeben sei eine Funktion f :
Mathematik Übungsblatt - Lösung. b) x=2
 Hochschule Regensburg Fakultät Informatik/Mathematik Christoph Böhm Sommersemester 204 Technische Informatik Bachelor IT2 Vorlesung Mathematik 2 Mathematik 2 4. Übungsblatt - Lösung Differentialrechnung
Hochschule Regensburg Fakultät Informatik/Mathematik Christoph Böhm Sommersemester 204 Technische Informatik Bachelor IT2 Vorlesung Mathematik 2 Mathematik 2 4. Übungsblatt - Lösung Differentialrechnung
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufgabe 45. Polynome sind stets stetig. Höhere Mathematik für Informatiker II (Sommersemester
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufgabe 45. Polynome sind stets stetig. Höhere Mathematik für Informatiker II (Sommersemester
Potenzreihen. Potenzreihen sind Funktionenreihen mit einer besonderen Gestalt.
 Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt. Definition. Ist (a ) eine Folge reeller (bzw. omplexer) Zahlen und x 0 R (bzw. z 0 C), dann heißt die Reihe a (x x 0 ) (bzw.
Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt. Definition. Ist (a ) eine Folge reeller (bzw. omplexer) Zahlen und x 0 R (bzw. z 0 C), dann heißt die Reihe a (x x 0 ) (bzw.
Analysis I. 11. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 11. Beispielklausur mit en Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Ein angeordneter Körper. ) Eine Folge in
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 11. Beispielklausur mit en Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Ein angeordneter Körper. ) Eine Folge in
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Klausur - Analysis I Lösungsskizzen
 Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
i 3 =. 2 [ ] 2 (k + 1) { + (k + 1) 3 k 2 + 4(k + 1) } (k + 2) 2 = x n = 1 + n 1 n?
![i 3 =. 2 [ ] 2 (k + 1) { + (k + 1) 3 k 2 + 4(k + 1) } (k + 2) 2 = x n = 1 + n 1 n? i 3 =. 2 [ ] 2 (k + 1) { + (k + 1) 3 k 2 + 4(k + 1) } (k + 2) 2 = x n = 1 + n 1 n?](/thumbs/61/45916757.jpg) Musterlösungen zur Klausur Analysis I Vollständige Indution Man beweise durch vollständige Indution: Für alle n N ist [ ] nn + ) i 3 i Beweis: Wir führen den Beweis mit vollständiger Indution Die Aussage
Musterlösungen zur Klausur Analysis I Vollständige Indution Man beweise durch vollständige Indution: Für alle n N ist [ ] nn + ) i 3 i Beweis: Wir führen den Beweis mit vollständiger Indution Die Aussage
Mathematik I. Vorlesung 25. Der große Umordnungssatz
 Prof. Dr. H. Brenner Osnabrück WS 009/010 Mathematik I Vorlesung 5 Der große Umordnungssatz Satz 5.1. (Großer Umordnungssatz) Es sei a i, i I, eine summierbare Familie von komplexen Zahlen mit der Summe
Prof. Dr. H. Brenner Osnabrück WS 009/010 Mathematik I Vorlesung 5 Der große Umordnungssatz Satz 5.1. (Großer Umordnungssatz) Es sei a i, i I, eine summierbare Familie von komplexen Zahlen mit der Summe
Musterlösungen zu Blatt 15, Analysis I
 Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Aufgabensammlung zur Analysis 1
 Analysis 1 18.12.2017 Prof. Dr. H. Koch Dr. F. Gmeineder Abgabe: Keine Abgabe. Aufgabensammlung zur Analysis 1 Anmerkungen: Das vorliegende Blatt enthält eine Auswahl von Aufgaben, die auf Klausuren zur
Analysis 1 18.12.2017 Prof. Dr. H. Koch Dr. F. Gmeineder Abgabe: Keine Abgabe. Aufgabensammlung zur Analysis 1 Anmerkungen: Das vorliegende Blatt enthält eine Auswahl von Aufgaben, die auf Klausuren zur
Mathematik IT 3 (Analysis)
 Lehrstuhl Mathematik, insbesondere Numerische und Angewandte Mathematik Prof. Dr. L. Cromme Mathematik IT (Analysis) für die Studiengänge Informatik, IMT und ebusiness im Wintersemester 0/04 Geben Sie
Lehrstuhl Mathematik, insbesondere Numerische und Angewandte Mathematik Prof. Dr. L. Cromme Mathematik IT (Analysis) für die Studiengänge Informatik, IMT und ebusiness im Wintersemester 0/04 Geben Sie
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppitz, Dr. I. Rybak 4. Gruppenübung zur Vorlesung Höhere Mathematik Sommersemester 9 Prof. Dr. M. Stroppel Prof. Dr. N. Knarr Lösungshinweise zu en Hausaufgaben: Aufgabe H. a)
P. Engel, T. Pfrommer S. Poppitz, Dr. I. Rybak 4. Gruppenübung zur Vorlesung Höhere Mathematik Sommersemester 9 Prof. Dr. M. Stroppel Prof. Dr. N. Knarr Lösungshinweise zu en Hausaufgaben: Aufgabe H. a)
Unendliche Reihen - I
 Unendliche Reihen - I Zur Wiederholung. Sei eine Folge ( ) N aus R (bzw. C) gegeben (die Folge der Summanden). Die Folge (s n ) n N in der Form Die Reihe mit s n = n heißt unendliche Reihe und wird geschrieben.
Unendliche Reihen - I Zur Wiederholung. Sei eine Folge ( ) N aus R (bzw. C) gegeben (die Folge der Summanden). Die Folge (s n ) n N in der Form Die Reihe mit s n = n heißt unendliche Reihe und wird geschrieben.
Analysis I Lösung von Serie 9
 FS 07 9.. MC Fragen: Ableitungen (a) Die Figur zeigt den Graphen einer zweimal differenzierbaren Funktion f. Was lässt sich über f, f und f sagen? Nichts Die Funktion f ist positiv. Die Funktion f ist
FS 07 9.. MC Fragen: Ableitungen (a) Die Figur zeigt den Graphen einer zweimal differenzierbaren Funktion f. Was lässt sich über f, f und f sagen? Nichts Die Funktion f ist positiv. Die Funktion f ist
Vorlesung Mathematik WS 08/09. Friedel Bolle. Vorbemerkung
 Vorlesung Mathemati WS 08/09 Vorbemerung Weshalb Mathemati für Öonomen? Das werden Sie selbst sehen im Grundstudium in - Miroöonomie - Statisti - Maroöonomie - BWL: Prodution und dazu in einer Reihe von
Vorlesung Mathemati WS 08/09 Vorbemerung Weshalb Mathemati für Öonomen? Das werden Sie selbst sehen im Grundstudium in - Miroöonomie - Statisti - Maroöonomie - BWL: Prodution und dazu in einer Reihe von
Übungen zu Einführung in die Analysis
 Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK
 ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK Dr. J. Giannoulis, M.Sc. S. Metzler, Dipl. Math. K. Tichmann WS 00/ Trainingseinheit 0 Sript Kartieren Sie grob die Inhalte des Sripts. Welche Werzeuge,
ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK Dr. J. Giannoulis, M.Sc. S. Metzler, Dipl. Math. K. Tichmann WS 00/ Trainingseinheit 0 Sript Kartieren Sie grob die Inhalte des Sripts. Welche Werzeuge,
2.6 Stetigkeit und Grenzwerte
 2.6 Stetigkeit und Grenzwerte Anschaulich gesprochen ist eine Funktion stetig, wenn ihr Graph sich zeichnen lässt, ohne den Stift abzusetzen. Das ist natürlich keine präzise mathematische Definition und
2.6 Stetigkeit und Grenzwerte Anschaulich gesprochen ist eine Funktion stetig, wenn ihr Graph sich zeichnen lässt, ohne den Stift abzusetzen. Das ist natürlich keine präzise mathematische Definition und
3. Übung zur Analysis II
 Universität Augsburg Sommersemester 207 3. Übung zur Analysis II Prof. Dr. Marc Nieper-Wißkirchen Caren Schinko, M. Sc. 8. Mai 207 3. (a) m. Die Dirichletsche Reihe. In Abschnitt 5.8 haben wir bereits
Universität Augsburg Sommersemester 207 3. Übung zur Analysis II Prof. Dr. Marc Nieper-Wißkirchen Caren Schinko, M. Sc. 8. Mai 207 3. (a) m. Die Dirichletsche Reihe. In Abschnitt 5.8 haben wir bereits
ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld
 ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld Bitte wenden! 1. Die unten stehende Figur wird beschrieben durch... (a) { (x, y) R 2 x + y 1 }. Richtig! (b) { (x,
ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld Bitte wenden! 1. Die unten stehende Figur wird beschrieben durch... (a) { (x, y) R 2 x + y 1 }. Richtig! (b) { (x,
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathematik für Informatiker II Sommersemester 2004) Lösungen zu Aufgabenblatt
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathematik für Informatiker II Sommersemester 2004) Lösungen zu Aufgabenblatt
Technische Universität München Zentrum Mathematik. Übungsblatt 7
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppitz, Dr. I. Rybak 5. Gruppenübung zur Vorlesung Höhere Mathematik Sommersemester 009 Prof. Dr. M. Stroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H.
P. Engel, T. Pfrommer S. Poppitz, Dr. I. Rybak 5. Gruppenübung zur Vorlesung Höhere Mathematik Sommersemester 009 Prof. Dr. M. Stroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H.
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
0.1 Formale Potenzreihen und Konvergenz
 0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 5. x 1 2x 3 = lim 6x
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 5. MC-Aufgaben Online-Abgabe. Durch zweifache Anwendung der Regel von Bernoulli-de l Hôpital folgt Stimmt diese Überlegung? lim x x 3 +
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 5. MC-Aufgaben Online-Abgabe. Durch zweifache Anwendung der Regel von Bernoulli-de l Hôpital folgt Stimmt diese Überlegung? lim x x 3 +
6.2 Die Regeln von de l Hospital. Ausgangsfrage: Wie berechnet man den Grenzwert. Beispiel: Sei f(x) = x 2 und g(x) = x. Dann gilt. lim.
 6.2 Die Regeln von de l Hospital Ausgangsfrage: Wie berechnet man den Grenzwert falls g(x), beide Funktionen gegen Null konvergieren, d.h. = g(x) = 0 beide Funktionen gegen Unendlich konvergieren, d.h.
6.2 Die Regeln von de l Hospital Ausgangsfrage: Wie berechnet man den Grenzwert falls g(x), beide Funktionen gegen Null konvergieren, d.h. = g(x) = 0 beide Funktionen gegen Unendlich konvergieren, d.h.
Analysis I Lösung von Serie 14. Um die Inhomogene DGl zu lösen, müssen wir partikuläre Lösungen finden. (a) Wir machen den Ansatz:
 d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
Vorkurs Mathematik für Ingenieur Innen WS 2018/2019 Übung 7
 Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieur Innen WS 018/019 Übung 7 Aufgabe 1 : Etremwerte Der Ellipse + y = 1 ist ein Rechteck mit Seitenlängen p, q, dessen Seiten parallel
Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieur Innen WS 018/019 Übung 7 Aufgabe 1 : Etremwerte Der Ellipse + y = 1 ist ein Rechteck mit Seitenlängen p, q, dessen Seiten parallel
Vorkurs Mathematik für Ingenieure WS 2015/2016 Übung 6
 Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieure WS 015/016 Übung 6 Aufgabe 1 : Differentialrechnung (a Berechnen Sie die Ableitung nachstehender Funktionen an der Stelle 0 und
Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieure WS 015/016 Übung 6 Aufgabe 1 : Differentialrechnung (a Berechnen Sie die Ableitung nachstehender Funktionen an der Stelle 0 und
Analysis I MATH, PHYS, CHAB. 2 k (2 k ) s = 2 k(1 s) = k=0. (2n 1) n=1. n=1. n n 2. n=1. n=1. = ζ(2) 1 4 ζ(2) = 3 4 ζ(2)
 Prof. D. Salamon Analysis I MATH, PHYS, CHAB HS 204 Musterlösung Serie 7. Der Vollständigeit wegen, zeigen wir zunächst die Konvergenz der Reihendarstellung der ζ-funtion für s >. ζs : n n s 2 + n s 0
Prof. D. Salamon Analysis I MATH, PHYS, CHAB HS 204 Musterlösung Serie 7. Der Vollständigeit wegen, zeigen wir zunächst die Konvergenz der Reihendarstellung der ζ-funtion für s >. ζs : n n s 2 + n s 0
Zusatzmaterial zur Mathematik I für E-Techniker Übung 7
 Mathemati I für E-Technier C. Erdmann WS 0/, Universität Rostoc, 7. Vorlesungswoche Zusatzmaterial zur Mathemati I für E-Technier Übung 7 Loale Etrema, Satz von Rolle, Mittelwertsatz Man sagt, in liegt
Mathemati I für E-Technier C. Erdmann WS 0/, Universität Rostoc, 7. Vorlesungswoche Zusatzmaterial zur Mathemati I für E-Technier Übung 7 Loale Etrema, Satz von Rolle, Mittelwertsatz Man sagt, in liegt
Anleitung zu Blatt 4 Analysis I für Studierende der Ingenieurwissenschaften
 Department Mathemati der Universität Hamburg WiSe 20/202 Dr. Hanna Peywand Kiani Anleitung zu Blatt 4 Analysis I für Studierende der Ingenieurwissenschaften Reelle Zahlenreihen 6.2.20 Die ins Netz gestellten
Department Mathemati der Universität Hamburg WiSe 20/202 Dr. Hanna Peywand Kiani Anleitung zu Blatt 4 Analysis I für Studierende der Ingenieurwissenschaften Reelle Zahlenreihen 6.2.20 Die ins Netz gestellten
Wesentliche Sätze (Analysis 1 für Lehramt)
 Wesentliche Sätze (Analysis für Lehramt) Inhaltsverzeichnis Alexander Schmalstieg TU Dortmund, Wintersemester 203/204 Wichtige Formeln 2 Folgen 2 3 Maxima und Suprema 3 4 Gleichmäßige Konvergenz 3 5 Funtionen
Wesentliche Sätze (Analysis für Lehramt) Inhaltsverzeichnis Alexander Schmalstieg TU Dortmund, Wintersemester 203/204 Wichtige Formeln 2 Folgen 2 3 Maxima und Suprema 3 4 Gleichmäßige Konvergenz 3 5 Funtionen
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 13. es kann keine allgemein gültige Aussage getroffen werden.
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 3 MC-Aufgaben (Online-Abgabe). Wenn man zwei beliebig oft differenzierbare Funktionen addiert, dann werden ihre Taylorreihen an einem Punkt
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 3 MC-Aufgaben (Online-Abgabe). Wenn man zwei beliebig oft differenzierbare Funktionen addiert, dann werden ihre Taylorreihen an einem Punkt
Brückenkurs Rechentechniken
 Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Klausuren zur Vorlesung ANALYSIS I
 Fachbereich Mathemati und Informati der Philipps-Universität Marburg Klausuren zur Vorlesung ANALYSIS I Prof. Dr. C. Portenier unter Mitarbeit von A. Alldridge und R. Jäger Marburg, Wintersemester 00/0
Fachbereich Mathemati und Informati der Philipps-Universität Marburg Klausuren zur Vorlesung ANALYSIS I Prof. Dr. C. Portenier unter Mitarbeit von A. Alldridge und R. Jäger Marburg, Wintersemester 00/0
Ableitung einer Betragsfunktion Differenzierbarkeit
 Ableitung einer Betragsfunktion Differenzierbarkeit 1-E Differenzierbarkeit einer Funktion Eine Funktion y = f (x) heißt an der Stelle x differenzierbar, wenn der Grenzwert f ' ( x) = lim Δ x 0 Δ y Δ x
Ableitung einer Betragsfunktion Differenzierbarkeit 1-E Differenzierbarkeit einer Funktion Eine Funktion y = f (x) heißt an der Stelle x differenzierbar, wenn der Grenzwert f ' ( x) = lim Δ x 0 Δ y Δ x
Mathematik IT 3 (Analysis) Probeklausur
 Mathematik IT (Analysis) Probeklausur Datum: 08..0, Zeit: :5 5:5 Name: Matrikelnummer: Vorname: Geburtsdatum: Studiengang: Aufgabe Nr. 5 Σ Punkte Soll 5 9 7 Punkte Ist Lösungen ohne begründeten Lösungsweg
Mathematik IT (Analysis) Probeklausur Datum: 08..0, Zeit: :5 5:5 Name: Matrikelnummer: Vorname: Geburtsdatum: Studiengang: Aufgabe Nr. 5 Σ Punkte Soll 5 9 7 Punkte Ist Lösungen ohne begründeten Lösungsweg
Höhere Mathematik für Physiker II
 Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
Lösungen zu Aufgabenblatt 10P
 Analysis Prof. Dr. Peter Becker Fachbereich Informatik Sommersemester 05 9. Juni 05 Lösungen zu Aufgabenblatt 0P Aufgabe (Funktionsgrenzwerte) Berechnen Sie die folgenden Grenzwerte: cos(x) x cos( x )
Analysis Prof. Dr. Peter Becker Fachbereich Informatik Sommersemester 05 9. Juni 05 Lösungen zu Aufgabenblatt 0P Aufgabe (Funktionsgrenzwerte) Berechnen Sie die folgenden Grenzwerte: cos(x) x cos( x )
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
D-MATH, D-PHYS, D-CHAB Analysis I HS 2017 Prof. Manfred Einsiedler. Übungsblatt 11
 D-MATH, D-PHYS, D-CHAB Analysis I HS 2017 Prof. Manfred Einsiedler Übungsblatt 11 1. In der Vorlesung haben Sie gesehen, dass es verschiedene Zweige des komplexen Logarithmus gibt. Dies bedingt, dass es
D-MATH, D-PHYS, D-CHAB Analysis I HS 2017 Prof. Manfred Einsiedler Übungsblatt 11 1. In der Vorlesung haben Sie gesehen, dass es verschiedene Zweige des komplexen Logarithmus gibt. Dies bedingt, dass es
Übungsklausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Abgabe: KW 11. Aufgabe 2-0a: Berechnen Sie die Grenzwerte der Funktionen. x 2 x. lim. lim
 . Übung zur Höheren Mathemati Abgabe: KW Aufgabe -a: Berechnen Sie die Grenzwerte der Funtionen 5 4 lim ln ln lim e lim sin lim (sin ) Aufgabe -b: Bestimmen Sie Definitionsbereich, Nullstellen, Polstellen,
. Übung zur Höheren Mathemati Abgabe: KW Aufgabe -a: Berechnen Sie die Grenzwerte der Funtionen 5 4 lim ln ln lim e lim sin lim (sin ) Aufgabe -b: Bestimmen Sie Definitionsbereich, Nullstellen, Polstellen,
Konvergenz von Folgen
 6 Konvergenz von Folgen Definition 6.1 Eine Folge in C (oder R) ist eine Abbildung f : N C (oder R). Schreibweise: (a n ) n N, (a n ), a 1, a 2... wobei a n = f(n). Beispiele: 1) (1 + 2 n ) n N, 3 2, 5
6 Konvergenz von Folgen Definition 6.1 Eine Folge in C (oder R) ist eine Abbildung f : N C (oder R). Schreibweise: (a n ) n N, (a n ), a 1, a 2... wobei a n = f(n). Beispiele: 1) (1 + 2 n ) n N, 3 2, 5
Folgen und Reihen. Wirtschaftswissenschaftliches Zentrum Universität Basel. Mathematik für Ökonomen 1 Dr. Thomas Zehrt
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen Dr. Thomas Zehrt Folgen und Reihen Literatur Referenz: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band, 7. Auflage,
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen Dr. Thomas Zehrt Folgen und Reihen Literatur Referenz: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band, 7. Auflage,
Übungsaufgaben zu Analysis 1 Lösungen von Blatt VIII vom
 Prof. Dr. Moritz Kaßmann Faultät für Mathemati Wintersemester 04/05 Universität Bielefeld Übungsaufgaben zu Analysis Lösungen von Blatt VIII vom 04..4 Aufgabe VIII. (8 Punte) a) Untersuchen Sie die folgenden
Prof. Dr. Moritz Kaßmann Faultät für Mathemati Wintersemester 04/05 Universität Bielefeld Übungsaufgaben zu Analysis Lösungen von Blatt VIII vom 04..4 Aufgabe VIII. (8 Punte) a) Untersuchen Sie die folgenden
Übungen Analysis I WS 03/04
 Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert
![REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert](/thumbs/55/37057337.jpg) Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
5.5. UMKEHRFUNKTIONEN TRIGONOMETRISCHER FUNKTIONEN 115
 5.5. UMKEHRFUNKTIONEN TRIGONOMETRISCHER FUNKTIONEN 5 Satz 5.5.2 (Ableitung der Umkehrfunktion einer Winkelfunktionen) Die Umkehrfunktionen der trigonometrischen Funktionen sind nach Satz 5.2.3 auf den
5.5. UMKEHRFUNKTIONEN TRIGONOMETRISCHER FUNKTIONEN 5 Satz 5.5.2 (Ableitung der Umkehrfunktion einer Winkelfunktionen) Die Umkehrfunktionen der trigonometrischen Funktionen sind nach Satz 5.2.3 auf den
Analysis für Informatiker und Statistiker Nachklausur
 Prof. Dr. Peter Otte Wintersemester 213/14 Tom Bachmann, Sebastian Gottwald 14.3.214 Analysis für Informatiker und Statistiker Nachklausur Lösungsvorschlag Name:.......................................................
Prof. Dr. Peter Otte Wintersemester 213/14 Tom Bachmann, Sebastian Gottwald 14.3.214 Analysis für Informatiker und Statistiker Nachklausur Lösungsvorschlag Name:.......................................................
Teil I Auswahlfragen
 UNIVERSITÄT KOBLENZ LANDAU INSTITUT FÜR MATHEMATIK Dr. Dominik Faas Grundlagen der Analysis Sommersemester 010 Klausur vom 07.09.010 Teil I Auswahlfragen Name: Hinweise: Bei den folgenden Auswahlfragen
UNIVERSITÄT KOBLENZ LANDAU INSTITUT FÜR MATHEMATIK Dr. Dominik Faas Grundlagen der Analysis Sommersemester 010 Klausur vom 07.09.010 Teil I Auswahlfragen Name: Hinweise: Bei den folgenden Auswahlfragen
Übungen Ingenieurmathematik
 Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
