Trigonometrische Funktionen
|
|
|
- Sven Schulze
- vor 7 Jahren
- Abrufe
Transkript
1 Trigonometrische Funktionen Rainer Hauser September Einleitung 1.1 Der Begriff Funktion Eine Funktion ordnet jedem Element m 1 einer Menge M 1 ein Element m einer Menge M zu. Man schreibt dafür f: M 1 M, m 1 f(m 1 ) = m oder einfach m 1 f(m 1 ), falls die beiden Mengen aus dem Kontext klar sind. Manchmal schreibt man auch x f(x), f(x), x y oder f(x) = y. Die letzten zwei Varianten benutzt man vor allem, wenn man den Graphen einer Funktion in einem Koordinatensystem aufzeichnen will. Die Menge M 1 heisst Definitionsbereich und die Menge derjenigen Elemente m von M, für die es ein m 1 M 1 mit f(m 1 ) = m gibt, heisst Wertebereich. Viele Funktionen in der Mathematik ordnen reellen Zahlen reelle Zahlen zu. Sind alle Elemente des Wertebereiches reelle Zahlen, so kann man einerseits die Nullstellen angeben, also diejenigen Elemente m 1 von M 1, für die f(m 1 ) = 0 gilt, und andererseits die so genannten Extrema bestimmen, also diejenigen Elemente m 1 von M 1, für die f(m 1 ) maximal beziehungsweise minimal im Wertebereich ist. 1. Der Einheitskreis Sind zwei Punkte P 1 und P mit den Koordinaten (x 1, y 1 ) und (x, y ) in einem rechtwinkligen Koordinatensystem gegeben, so ist ihr Abstand d(p 1, P ) = (x x 1 ) + (y y 1 ). Das folgt aus dem Satz von Pythagoras. Die Menge aller Punkte, die vom Ursprung eines rechtwinkligen Koordinatensystems den Abstand 1 haben, nennt man den Einheitskreis. Lässt man einen Punkt auf dem Einheitskreis wandern, so lassen sich seine Koordinaten als Funktion des Winkels im Ursprung darstellen. Das führt zu den trigonometrischen Funktionen. Die trigonometrischen Funktionen im Gradmass.1 Sinus und Cosinus eines Drehwinkels Dreht man einen Strahl s im Koordinatensystem, in dem der Einheitskreis k eingezeichnet ist, um einen Winkel α, und bezeichnet man mit P (x, y) den Punkt, in dem sich s und k schneiden, so ist Sinus und Cosinus durch x = cos α y = sin α (1) über die Koordinaten des Schnittpunktes P (x, y) definiert, die vom Winkel α abhängen. Der Drehwinkel α ist der im Gegenuhrzeigersinn gemessene Winkel zwischen der positiven Seite der x-achse und dem Strahl s. Dreht man den Strahl s, so ändert der Winkel α und der Punkt P (x, y), sodass man sin α und cos α als Funktionen betrachten kann, die einem Winkel eine reelle Zahl zuordnen, und deren Wertebereiche die reellen Zahlen zwischen 1 und +1 sind. 1
2 Sinus und Cosinus sind Funktionen, die einem Winkel im Gradmass eine reelle Zahl zuordnen. Die Zuordnung α sin α heisst Sinusfunktion und die Zuordnung α cos α heisst Cosinusfunktion. Wegen dem Satz von Pythagoras gilt sin α + cos α = 1. (Es hat sich eingebürgert, dass man meist sin α statt sin(α) sowie sin α statt sin(α) schreibt.) Weiter gelten die Beziehungen sin(90 α) = cos(α) cos(90 α) = sin(α) () offensichtlich für Winkel zwischen 0 und 90 sowie die Beziehungen sin(α + 90 ) = cos(α) sin(α ) = sin(α) sin(α + 70 ) = cos(α) sin(180 α) = sin(α) cos(α + 90 ) = sin(α) cos(α ) = cos(α) cos(α + 70 ) = sin(α) cos(180 α) = cos(α) für beliebige Winkel α, wie man mit dreh- und spiegelsymmetrischen Überlegungen leicht sieht. Weil der Strahl s nach einem Drehwinkel von 360 wie bei 0 wieder mit der positiven Seite der x-achse zusammenfällt, gilt sin(α) = sin(α + n 360 ) cos(α) = cos(α + n 360 ) (3) für alle Winkel α und jede Zahl n Z. Die zwei Funktionen sind also periodisch, und die Periode ist 360. Folgende Sinus- und Cosinuswerte kann man sich mit folgendem Trick leicht merken: sin α 0 = = = = 1 = cos α 1 = = = = 0 =. Tangens und Cotangens eines Drehwinkels Tangens und Cotangens lassen sich ebenfalls mit einem Drehwinkel um den Nullpunkt definieren. Es wird aber kein Strahl, sondern die Gerade g gedreht, und die Schnittpunkte des Tangensbeziehungsweise des Cotangensträgers mit einer Koordinatenachse und mit g bestimmt, welchen Wert der Tangens beziehungsweise Cotangens annimmt. Tangens und Cotangens sind Funktionen, die einem Winkel im Gradmass eine reelle Zahl zuordnen. Die Zuordnung α tan α heisst Tangensfunktion und die Zuordnung α cot α heisst Cotangensfunktion. Aus Symmetrieüberlegungen und aus den Strahlensätzen folgt tan α = sin α cos α tan α = 1 cot α cot α = cos α sin α cot α = 1 tan α für alle Winkel α. Für cos α = 0 und für sin α = 0 führen die Formeln (4) zu einer Division durch 0, und die beiden Funktionen sind somit nicht überall definiert. Weil die Gerade g nach einem Drehwinkel von 180 wie bei 0 mit der x-achse zusammenfällt, gilt tan(α) = tan(α + n 180 ) cot(α) = cot(α + n 180 ) (5) für alle Winkel α und jede Zahl n Z. Die zwei Funktionen sind also ebenfalls periodisch, aber die Periode ist 180 wegen sin(α ) = ( 1) sin α und cos(α ) = ( 1) cos α. (4)
3 Wegen den Formeln (4) lassen sich Symmetrieeigenschaften sowie die Werte für 30, 45 und 60 von Sinus und Cosinus ableiten. So nehmen beispielsweise die Tangens- und die Cotangensfunktion offensichtlich den Wert 1 an für α = Trigonometrie im rechtwinkligen Dreieck Um die Trigonometrie auch bei allgemeinen rechtwinkligen Dreiecken, in denen die Hypotenuse nicht die Länge 1, sondern die Länge c hat, anwenden zu können, müssen die Seitenlängen a und b durch c dividiert werden. (Das entspricht einer generellen Massstabänderung, bei der c die neue Einheitslänge wird.) In einem rechtwinkligen Dreieck gibt es zwei spitze Winkel. Beide liegen zwischen einer Kathete und der Hypotenuse, sodass die andere Kathete gegenüber liegt. Deshalb spricht man in Bezug auf diese Winkel von einer Ankathete und einer Gegenkathete und definiert die trigonometrischen Funktionen mit ihrer Hilfe. Die trigonometrischen Funktionen werden im rechtwinkligen Dreieck nicht wie in (1) durch einen Drehwinkel, sondern durch die Beziehungen sin α = Gegenkathete Hypotenuse cos α = Ankathete Hypotenuse tan α = Gegenkathete Ankathete cot α = Ankathete Gegenkathete definiert. Ist wie üblich a die Gegenkathete, b die Ankathete und c die Hypotenuse von α, so bedeutet das sin α = a c cos α = b c (6) im rechtwinkligen Dreieck, und die Beziehungen () stimmen offensichtlich. Rechtwinklige Dreiecke, bei denen zwei unabhängige Grösse (Seiten oder Winkel) gegeben sind, können nicht nur mit Zirkel und Lineal konstruiert, sondern mit den Mitteln der Trigonometrie auch berechnet werden. Dabei helfen der Satz von Pythagoras und die Umkehrfunktionen sin 1 und cos 1..4 Trigonometrie im allgemeinen Dreieck Man kann sogar jedes Dreieck, bei dem genügend Seitenlängen und Winkel gegeben sind, und die man mit Zirkel und Lineal konstruieren kann, mit den Mitteln der Trigonometrie rechnerisch bearbeiten. Dabei gelten die folgenden drei Sätze. In jedem Dreieck mit den Seiten a, b und c sowie den Winkeln α, β und γ gilt sin α a = sin β b = sin γ c a sin α = b sin β = c sin γ gemäss dem Sinussatz. (Im rechtwinkligen Dreieck folgt daraus die Beziehung (6) wegen sin 90 = 1.) (7) Der Sinussatz lässt sich leicht aus (6) beweisen. Für die Winkel α bei der Ecke A und β bei der Ecke B gilt sin α = h b und sin β = h a, woraus einerseits h = a sin β und andererseits h = b sin α folgt. Dividiert man diese Gleichung entweder durch a und b oder durch sin α und sin β und stellt man fest, dass diese Beziehung für beliebige zwei Seiten gilt, so folgt daraus der Sinussatz. Weiter gilt in jedem Dreieck mit den Seiten a, b und c sowie den Winkeln α, β und γ a = b + c bc cos α b = a + c ac cos β c = a + b ab cos γ (8) gemäss dem Cosinussatz. (Das ist eine Verallgemeinerung des Satzes von Pythagoras.) 3
4 Der Cosinussatz lässt sich leicht beweisen. Mit a = h + (c x), b = h +x sowie x = b cos α lassen sich x und h eliminieren. Aus a = (h + x ) + c cx wird so a = b + c bc cos α. Mit der Gleichung b = h + x eliminiert man die beiden Summanden h und x elegant gemeinsam, und mit x = b cos α eliminiert man den noch verbleibenden Faktor x in cx. Mit dem Sinus- und Cosinussatz kann man sämtliche fehlenden Seitenlängen und Winkel in einem allgemeinen Dreieck mit genügend vorgegebenen Angaben berechnen. Sind drei Seitenlängen oder zwei Seitenlängen und der eingeschlossene Winkel gegeben, lassen sich die übrigen Grössen mit dem Cosinussatz bestimmen. Ist hingegen eine Seitenlänge und der gegenüberliegende Winkel sowie eine weitere Grösse gegeben, kommt der Sinussatz zur Anwendung. Sind zwei Winkel bekannt, lässt sich der dritte offensichtlich berechnen, weil die Winkelsumme im Dreieck 180 beträgt. Beispiel: Gegeben seien α = 3, a = 3 cm und c = 5 cm. Konstruiert man dieses Dreieck mit Zirkel und Lineal, gibt das zwei Lösungen wie in der nebenstehenden Abbildung gezeigt. Das muss sich natürlich auch bei der rechnerischen Lösung der Aufgabe zeigen. Mit sin γ = c a sin α = 5 3 sin 3 gemäss Sinussatz gilt sin γ Es gibt es aber zwei Winkel γ 1 6 und γ = 118 mit diesem Sinuswert wegen sin(180 γ) = sin(γ). Für beide Werte gilt β i = 180 α γ i > 0 (mit i {1, }). Die dritte Seitenlänge b lässt sich mit dem Sinus- oder mit dem Cosinussatz bestimmen. Es gibt offensichtlich für die beiden verschiedenen Werte von β auch zwei verschiedene Seitenlängen b. Nicht nur die unbekannten Seitenlängen und Winkel lassen sich rechnerisch bestimmen, sondern auch der Flächeninhalt eines Dreiecks, ohne dass erst die Länge einer Höhe bestimmt werden muss. Sind zwei Seitenlängen und der eingeschlossene Winkel gegeben, so gilt A = 1 bc sin α A = 1 ac sin β A = 1 ab sin γ (9) für den Flächeninhalt A des Dreiecks. Auch dieser Satz lässt sich leicht beweisen. Mit A = 1 hc für die Fläche und h = b sin α für die Höhe senkrecht zur Seite c kann man h eliminieren, womit die Behauptung gezeigt ist. Man kann also mit Hilfe von Sinus und Cosinus in einem Dreieck mit genügend bekannten Seitenlängen und Winkeln die anderen Seitenlängen und Winkel sowie den Flächeninhalt berechnen..5 Peilung Damit ein Schiff einen Hafen anpeilen kann, muss es die Richtung, in der der Hafen liegt, in Bezug auf eine bekannte Richtung wissen. Im Folgenden wird Norden als Bezugsrichtung und die Abweichung im Uhrzeigersinn davon gemessen im Gradmass für die Peilung angenommen. Die Richtung wird dreistellig angegeben. In der nebenstehenden Abbildung ist die Richtung 080 gestrichelt gezeigt. Norden entspricht somit 000, Osten 090, Süden 180 und Westen 70. Für die Richtungen zwischen Norden (N), Osten (E), Süden (S) und Westen (W) haben sich spezielle Bezeichnungen eingebürgert. So nennt man 045 auch einfach Nordosten (NE). Für die Peilung in der Ebene (wie etwa in der Schifffahrt) genügt also ein Winkel. Für die Peilung im Raum (wie etwa in der Luftfahrt) kommt man mit einem Zahlenwert allein nicht mehr aus. 4
5 3 Die trigonometrischen Funktionen im Bogenmass 3.1 Das Bogenmass Neben dem Gradmass gibt es noch andere Möglichkeiten, Winkel zu messen. Eine davon ist das Bogenmass, das die Grösse des Winkels durch die Länge des Bogens angibt, den der Winkel auf dem Einheitskreis herausschneidet. Im Bogenmass entspricht π dem vollen Winkel mit 360 und π einem rechten Winkel. Das Bogenmass lässt sich mit Bogenmass = π 180 Gradmass aus dem Gradmass berechnen, und das Gradmass lässt sich mit Gradmass = 180 π Bogenmass aus dem Bogenmass berechnen. Ist a der Winkel α im Bogenmass gegeben, so ist im Kreissektor b = r a die Länge des Bogens b und A = r a die Fläche A. Mit den obigen Formeln lassen sich diese Grössen ins Gradmass umrechnen. 3. Trigonometrie im Bogenmass Schreibt man sin x statt sin α, so ist Sinus im Bogenmass gemeint. Will man mit einem Taschenrechner, den man vom Gradmass auf Bogenmass umschalten kann, die Sinuskurve berechnen, ergibt das etwa das, was in der nebenstehenden Abbildung gezeigt ist. Die Sinuskurve ist im Nullpunkt praktisch gerade und fällt dort mit der Winkelhalbierenden y = x zusammen. Aus dieser Tatsache folgt, dass sin(x) x für kleine Werte x gilt. Weil in diesem Bereich cos x 1 gilt, lässt sich tan(x) = x aus der Beziehung (4) für den Tangens folgern. Man kann zudem beweisen, dass für 0 < x < π sin x < x < tan x gilt, indem man die Flächen von geeigneten Dreiecken und Kreissektoren betrachtet. Die Symmetrieeigenschaften der trigonometrischen Funktionen hängen nicht davon ab, ob Winkel im Grad- oder im Bogenmass gemessen werden. Es gelten somit sämtliche oben erwähnten Symmetriebeziehungen. Speziell sei aber auf die Zusammenhänge sin( x) = sin(x) cos( x) = cos(x) tan( x) = tan(x) cot( x) = cot(x) für die trigonometrischen Funktionen hingewiesen. Die Cosinusfunktion ist somit eine gerade Funktion, während die Sinus-, Tangens- und Cotangensfunktion ungerade Funktionen sind. Auch die zu (3) und (5) äquivalenten Periodizitätseigenschaften gelten für die trigonometrischen Funktionen im Bogenmass. Die Periode von Sinus und Cosinus ist π, was 360 entspricht, und diejenige von Tangens und Cotangens ist π, was 180 entspricht. 5
6 4 Harmonische Schwingungen 4.1 Periodische Bewegungsabläufe Periodische Vorgänge wiederholen sich nach einer gewissen Zeit, die man deren Periode nennt. Gewisse periodische Bewegungsabläufe lassen sich durch eine Funktion vom Typ f(t) = a sin(b t+c) beschreiben, falls man die Abschwächung durch Reibungsverluste vernachlässigt. Sie werden harmonische Schwingungen genannt. Das Schwingen eines Pendels, eines an einer Feder befestigten Gewichts oder der gezupften Saite eines Musikinstruments sind Beispiele dafür. In der unten stehenden Abbildung ist ein Beispiel für eine harmonische Schwingung gezeigt. Ein an einer Feder befestigter Schreibstift pendelt auf und ab und zeichnet seinen momentanen Ort auf einem Papierband auf, das sich mit konstanter Geschwindigkeit nach links bewegt. Die Frage ist, wie man aus diesem Papierband die Bewegungsgleichung für die schreibende Spitze der Feder bestimmen kann. Der Parameter a ist einfach, denn er folgt unmittelbar aus den Maxima und Minima. Damit muss a = ± sein. Der Parameter b hängt mit der Periode 1. der Schwingung zusammen, und wegen 1. b = π gilt somit b = 5π 3. Aus f(0) = a sin(c) = 1 folgt sin(c) = 0.5, was für c = π 6 gilt. Damit ist f(t) = sin( 5π 3 t + π 6 ) die Bewegungsgleichung. (Man beachte, dass die Parameter a, b und c nicht eindeutig sind, sodass verschiedene Bewegungsgleichungen dieselbe Bewegung beschreiben können, und dass es zwei Stellen pro Periode gibt mit sin(x) = 1, was zu einem falschen Wert für c führen kann. Überprüfen der Gleichung für bekannte Werte wie t = 0. lohnt sich, um sicher zu stellen, dass dies die richtige Gleichung ist.) 4. Nullstellen und Extrema Ist eine harmonische Schwingung als Funktion der Form f(x) = a sin(b x + c) gegeben, so stellt sich die Frage, wie man den zugehörigen Graphen möglichst genau skizzieren kann. Dazu bestimmt man sinnvollerweise erst die Nullstellen und die Extrema. Die Funktion f(x) = sin(x) hat die Nullstellen bei x = n π für alle n Z. Somit hat sin(b x + c) die Nullstellen bei b x + c = n π beziehungsweise, aufgelöst nach x, bei x = n π c b für alle n Z. Die Maxima und Minima liegen in der Mitte zwischen zwei Nullstellen und können damit ebenfalls bestimmt werden. Hat man Maxima, Minima und Nullstellen, kann man den Graphen grob skizzieren. 6
Trigonometrie. In der Abbildung: der Winkel 120 (Gradenmaß) ist 2π = 2π (Bogenmaß).
 Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
1 Einleitung. 2 Sinus. Trigonometrie
 1 Einleitung Die Trigonometrie (trigonon - griechisch für Dreieck) und die trigonometrischen Funktionen sind wichtige mathematische Werkzeuge zur Beschreibung der Natur. In der Physik werden trigonometrische
1 Einleitung Die Trigonometrie (trigonon - griechisch für Dreieck) und die trigonometrischen Funktionen sind wichtige mathematische Werkzeuge zur Beschreibung der Natur. In der Physik werden trigonometrische
KOMPETENZHEFT ZUR TRIGONOMETRIE, II
 KOMPETENZHEFT ZUR TRIGONOMETRIE, II 1. Aufgabenstellungen Aufgabe 1.1. Bestimme alle Winkel in [0 ; 360 ], die Lösungen der gegebenen Gleichung sind, und zeichne sie am Einheitskreis ein. 1) sin(α) = 0,4
KOMPETENZHEFT ZUR TRIGONOMETRIE, II 1. Aufgabenstellungen Aufgabe 1.1. Bestimme alle Winkel in [0 ; 360 ], die Lösungen der gegebenen Gleichung sind, und zeichne sie am Einheitskreis ein. 1) sin(α) = 0,4
Trigonometrie. Mag. DI Rainer Sickinger HTL. v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1
 Trigonometrie Mag. DI Rainer Sickinger HTL v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1 Definition von Sinus, Cosinus und Tangens am Einheitskreis Im rechtwinkligen Dreieck ist der Winkel zwischen
Trigonometrie Mag. DI Rainer Sickinger HTL v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1 Definition von Sinus, Cosinus und Tangens am Einheitskreis Im rechtwinkligen Dreieck ist der Winkel zwischen
f(x nk ) = lim y nk ) = lim Bemerkung 2.14 Der Satz stimmt nicht mehr, wenn D nicht abgeschlossen oder nicht beschränkt ist, wie man z.b.
 Proposition.13 Sei f : D R stetig und D = [a, b] R. Dann ist f(d) beschränkt. Außerdem nimmt f sein Maximum und Minimum auf D an, d.h. es gibt x max D und ein x min D, so dass f(x max ) = sup f(d) und
Proposition.13 Sei f : D R stetig und D = [a, b] R. Dann ist f(d) beschränkt. Außerdem nimmt f sein Maximum und Minimum auf D an, d.h. es gibt x max D und ein x min D, so dass f(x max ) = sup f(d) und
1. Definition der trigonometrischen Funktionen für beliebige Winkel
 1 Trigonometrie 2 1. Definition der trigonometrischen Funktionen für beliebige Winkel In einem Kreis mit Mittelpunkt M(0,0) und Radius r ist der zunächst spitze Winkel α gezeichnet. α legt auf dem Kreis
1 Trigonometrie 2 1. Definition der trigonometrischen Funktionen für beliebige Winkel In einem Kreis mit Mittelpunkt M(0,0) und Radius r ist der zunächst spitze Winkel α gezeichnet. α legt auf dem Kreis
1. Unterteilung von allgemeinen Dreiecken in rechtwinklige
 Trigonometrie am allgemeinen Dreieck Wir können auch die Seiten und Winkel von allgemeinen Dreiecken mit Hilfe der Trigonometrie berechnen. Die einfachste Variante besteht darin, ein beliebiges Dreieck
Trigonometrie am allgemeinen Dreieck Wir können auch die Seiten und Winkel von allgemeinen Dreiecken mit Hilfe der Trigonometrie berechnen. Die einfachste Variante besteht darin, ein beliebiges Dreieck
2.8 Trigonometrische Funktionen (Thema aus dem Bereich Analysis/Geometrie)
 .8 Trigonometrische Funktionen (Thema aus dem Bereich Analysis/Geometrie) Inhaltsverzeichnis Repetition und Einleitung Verhältnisse beim Kreis mit Radius r 3 3 Die Graphen der Sinus- und der Cosinusfunktion
.8 Trigonometrische Funktionen (Thema aus dem Bereich Analysis/Geometrie) Inhaltsverzeichnis Repetition und Einleitung Verhältnisse beim Kreis mit Radius r 3 3 Die Graphen der Sinus- und der Cosinusfunktion
3. Erweiterung der trigonometrischen Funktionen
 3. Erweiterung der trigonometrischen Funktionen 3.1. Polarkoordinaten 1) Rechtwinklige und Polarkoordinaten Üblicherweise gibt man die Koordinaten eines Punktes in der Ebene durch ein Zahlenpaar vor: P(x
3. Erweiterung der trigonometrischen Funktionen 3.1. Polarkoordinaten 1) Rechtwinklige und Polarkoordinaten Üblicherweise gibt man die Koordinaten eines Punktes in der Ebene durch ein Zahlenpaar vor: P(x
Definition von Sinus und Cosinus
 Definition von Sinus und Cosinus Definition 3.16 Es sei P(x y) der Punkt auf dem Einheitskreis, für den der Winkel von der positiven reellen Halbachse aus (im Bogenmaß) gerade ϕ beträgt (Winkel math. positiv,
Definition von Sinus und Cosinus Definition 3.16 Es sei P(x y) der Punkt auf dem Einheitskreis, für den der Winkel von der positiven reellen Halbachse aus (im Bogenmaß) gerade ϕ beträgt (Winkel math. positiv,
Trigonometrie. Mag. DI Rainer Sickinger HTL. v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1
 Trigonometrie Mag. DI Rainer Sickinger HTL v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1 Verschiedene Winkel DEFINITION v 1 Mag. DI Rainer Sickinger Trigonometrie 2 / 1 Verschiedene Winkel Vermessungsaufgaben
Trigonometrie Mag. DI Rainer Sickinger HTL v 1 Mag. DI Rainer Sickinger Trigonometrie 1 / 1 Verschiedene Winkel DEFINITION v 1 Mag. DI Rainer Sickinger Trigonometrie 2 / 1 Verschiedene Winkel Vermessungsaufgaben
Trigonometrie. Geometrie Kapitel 3 MnProfil - Mittelstufe KSOe. Ronald Balestra CH Zürich
 Trigonometrie Geometrie Kapitel 3 MnProfil - Mittelstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch 29. Januar 2012 Inhaltsverzeichnis 3 Trigonometrie 1 3.1 Warum Trigonometrie........................
Trigonometrie Geometrie Kapitel 3 MnProfil - Mittelstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch 29. Januar 2012 Inhaltsverzeichnis 3 Trigonometrie 1 3.1 Warum Trigonometrie........................
Lösungen der Trainingsaufgaben aus. Toolbox Mathematik für MINT-Studiengänge
 Lösungen der Trainingsaufgaben aus Toolbox Mathematik für MINT-Studiengänge 1 Geometrie mit Sinus, Cosinus und Tangens Version 22. Dezember 2016 Lösung zu Aufgabe 1.1 Gemäß Abbildung 1.1 und der Definition
Lösungen der Trainingsaufgaben aus Toolbox Mathematik für MINT-Studiengänge 1 Geometrie mit Sinus, Cosinus und Tangens Version 22. Dezember 2016 Lösung zu Aufgabe 1.1 Gemäß Abbildung 1.1 und der Definition
Trigonometrie. 3. Kapitel aus meinem Lehrgang Geometrie. Ronald Balestra CH St. Peter
 Trigonometrie 3. Kapitel aus meinem Lehrgang Geometrie Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch 17. August 2008 Inhaltsverzeichnis 3 Trigonometrie 46 3.1 Warum Trigonometrie........................
Trigonometrie 3. Kapitel aus meinem Lehrgang Geometrie Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch 17. August 2008 Inhaltsverzeichnis 3 Trigonometrie 46 3.1 Warum Trigonometrie........................
Nullstellen. Häufig interessiert man sich für die Werte der unabhängigen Variable einer Funktion, für die der Funktionswert 0 ist:
 15 y 10 5 5 x 10 15 Nullstellen Häufig interessiert man sich für die Werte der unabhängigen Variable einer Funktion, für die der Funktionswert 0 ist: 98 Sei f : R R eine Funktion. Ist x 0 D(f) eine reelle
15 y 10 5 5 x 10 15 Nullstellen Häufig interessiert man sich für die Werte der unabhängigen Variable einer Funktion, für die der Funktionswert 0 ist: 98 Sei f : R R eine Funktion. Ist x 0 D(f) eine reelle
Ankathete Hypothenuse
 Arbeitsauftrag: Trigonometrische Funktionen Bearbeitet folgendes Blatt und macht Euch mit den Trigonometrischen Funktionen und ihren Eigenschaften vertraut. 1.) Grundlagen - Wiederholung: Trigonometrische
Arbeitsauftrag: Trigonometrische Funktionen Bearbeitet folgendes Blatt und macht Euch mit den Trigonometrischen Funktionen und ihren Eigenschaften vertraut. 1.) Grundlagen - Wiederholung: Trigonometrische
Berechnungen am rechtwinkligen Dreieck Der Einheitskreis. VI Trigonometrie. Propädeutikum Holger Wuschke. 21. September 2018
 Propädeutikum 018 1. September 018 Denition Trigonometrie Die Trigonometrie beschäftigt sich mit dem Messen (µɛτ ρoν) von dreiseitigen (τ ρίγωνo) Objekten. Zunächst gilt in Dreiecken: A = 1 g h Abbildung:
Propädeutikum 018 1. September 018 Denition Trigonometrie Die Trigonometrie beschäftigt sich mit dem Messen (µɛτ ρoν) von dreiseitigen (τ ρίγωνo) Objekten. Zunächst gilt in Dreiecken: A = 1 g h Abbildung:
Aufgaben mit Lösungen zum Themengebiet: Geometrie bei rechtwinkligen Dreiecken
 Übungsaufgaben zur Satzgruppe des Pythagoras: 1) Seiten eines rechtwinkligen Dreiecks Sind folgende Aussagen richtig oder falsch? Verbessere, wenn notwendig! Die Katheten grenzen an den rechten Winkel.
Übungsaufgaben zur Satzgruppe des Pythagoras: 1) Seiten eines rechtwinkligen Dreiecks Sind folgende Aussagen richtig oder falsch? Verbessere, wenn notwendig! Die Katheten grenzen an den rechten Winkel.
Folgende Eigenschaft beschreibt eine gewisse Symmetrie des Funktionsgraphen:
 für alle x [0,2000]. Das Intervall [0,2000] könnte aus ökonomischer Sicht relevant sein, wenn etwa die Maximalauslastung bei 2000 produzierten Waschmaschinen liegt. Folgende Eigenschaft beschreibt eine
für alle x [0,2000]. Das Intervall [0,2000] könnte aus ökonomischer Sicht relevant sein, wenn etwa die Maximalauslastung bei 2000 produzierten Waschmaschinen liegt. Folgende Eigenschaft beschreibt eine
Trigonometrie. Geometrie - Kapitel 3 Sprachprofil - Mittelstufe KSOe. Ronald Balestra CH Zürich
 Trigonometrie Geometrie - Kapitel 3 Sprachprofil - Mittelstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch Name: Vorname: 31. Januar 2013 Überblick über die bisherigen ALGEBRA - Themen:
Trigonometrie Geometrie - Kapitel 3 Sprachprofil - Mittelstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch Name: Vorname: 31. Januar 2013 Überblick über die bisherigen ALGEBRA - Themen:
KREISFUNKTIONEN. Allgemeines
 KREISFUNKTIONEN Allgemeines Um die Graphen der Winkelfunktionen zeichnen und verstehen zu können, ist es wichtig, den Einheitskreis zu kennen. Zunächst stellt man sich einen Kreis mit dem Radius 1 vor.
KREISFUNKTIONEN Allgemeines Um die Graphen der Winkelfunktionen zeichnen und verstehen zu können, ist es wichtig, den Einheitskreis zu kennen. Zunächst stellt man sich einen Kreis mit dem Radius 1 vor.
2.3 Elementare Funktionen
 .3 Elementare Funktionen Trigonometrische Funktionen (Winkelfunktionen) Vorbemerkung. Wir definieren die Winkelfunktionen bezogen auf die Bogenlänge x auf dem Einheitskreis, d.h. für x [0,π]. Alternativ
.3 Elementare Funktionen Trigonometrische Funktionen (Winkelfunktionen) Vorbemerkung. Wir definieren die Winkelfunktionen bezogen auf die Bogenlänge x auf dem Einheitskreis, d.h. für x [0,π]. Alternativ
1 Die Strahlensätze 2. 2 Winkel 3. 3 Rechtwinklige Dreiecke 3. 4 Kreise 6. 5 Trigonometrische Funktionen 8. 6 Kurven in Parameterdarstellung 10
 Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematischer Vorkurs Dr. Thomas Zehrt Geometrie Inhaltsverzeichnis 1 Die Strahlensätze 2 2 Winkel 3 3 Rechtwinklige
Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematischer Vorkurs Dr. Thomas Zehrt Geometrie Inhaltsverzeichnis 1 Die Strahlensätze 2 2 Winkel 3 3 Rechtwinklige
Trigonometrische Funktionen
 Abbildungsverzeichnis Inhaltsverzeichnis Trigonometrische Funktionen Die hier behandelten trigonometrischen Funktionen sind sin, cos, tan, cot. Es zeigt sich, dass die Umkehrfunktionen der trigonometrischen
Abbildungsverzeichnis Inhaltsverzeichnis Trigonometrische Funktionen Die hier behandelten trigonometrischen Funktionen sind sin, cos, tan, cot. Es zeigt sich, dass die Umkehrfunktionen der trigonometrischen
HTBLA VÖCKLABRUCK STET
 HTBLA VÖCKLABRUCK STET Trigonometrie INHALTSVERZEICHNIS 1. WINKELFUNKTIONEN IM RECHTWINKELIGEN DREIECK... 3. BOGENMASS... 3 3. TRIGONOMETRISCHE FUNKTIONEN BELIEBIGER WINKEL... 4 3.1. Einheitskreis (r =
HTBLA VÖCKLABRUCK STET Trigonometrie INHALTSVERZEICHNIS 1. WINKELFUNKTIONEN IM RECHTWINKELIGEN DREIECK... 3. BOGENMASS... 3 3. TRIGONOMETRISCHE FUNKTIONEN BELIEBIGER WINKEL... 4 3.1. Einheitskreis (r =
3.1 Rationale Funktionen
 3.1 Rationale Funktionen EineFunktionf : R R der Formx P(x) Q(x) mit Polynomen P(x), Q(x) heißt rationale Funktion. Der maximale Definitionsbereich von f = P(x) Q(x) Sei x 0 R mit Q(x 0 ) = 0. Ferner sei
3.1 Rationale Funktionen EineFunktionf : R R der Formx P(x) Q(x) mit Polynomen P(x), Q(x) heißt rationale Funktion. Der maximale Definitionsbereich von f = P(x) Q(x) Sei x 0 R mit Q(x 0 ) = 0. Ferner sei
Trigonometrie. Geometrie. Kapitel 3, 4 & 5. MNProfil - Mittelstufe. Ronald Balestra CH Zürich
 Trigonometrie Geometrie Kapitel 3, 4 & 5 MNProfil - Mittelstufe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch 25. März 2019 Überblick über die bisherigen Geometrie - Themen: 1 Ähnlichhkeit 1.1
Trigonometrie Geometrie Kapitel 3, 4 & 5 MNProfil - Mittelstufe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch 25. März 2019 Überblick über die bisherigen Geometrie - Themen: 1 Ähnlichhkeit 1.1
II.1 sin, cos, tan im rechtwinkligen Dreieck und im Einheitskreis
 II.1 sin, cos, tan im rechtwinkligen Dreieck und im Einheitskreis 263/1 a) c = 5 cm; 53,13 ; 36,87 b) b = 12 cm; 22,62 ; 67,38 c) a 4,11 cm; b 5,66 cm; = 54 d) c 7,46 cm; b 6,58 cm; = 62 e) c 1631,73 cm;
II.1 sin, cos, tan im rechtwinkligen Dreieck und im Einheitskreis 263/1 a) c = 5 cm; 53,13 ; 36,87 b) b = 12 cm; 22,62 ; 67,38 c) a 4,11 cm; b 5,66 cm; = 54 d) c 7,46 cm; b 6,58 cm; = 62 e) c 1631,73 cm;
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Wiederhole eigenständig: elementare Konstruktionen nach diesen Sätzen
 1/5 Erinnerung: Kongruenzsätze SSS, SWS, WSW, SsW Wiederhole eigenständig: elementare Konstruktionen nach diesen Sätzen Grundwissen: Elementare Sätze über Dreiecke: o Winkelsumme 180 0 o Dreiecksungleichung
1/5 Erinnerung: Kongruenzsätze SSS, SWS, WSW, SsW Wiederhole eigenständig: elementare Konstruktionen nach diesen Sätzen Grundwissen: Elementare Sätze über Dreiecke: o Winkelsumme 180 0 o Dreiecksungleichung
Funktionen einer reellen Veränderlichen
 KAPITEL Funktionen einer reellen Veränderlichen.1 Eigenschaften von Funktionen........................... 39. Potenz- und Wurzelfunktionen............................ 1.3 Trigonometrische Funktionen.............................
KAPITEL Funktionen einer reellen Veränderlichen.1 Eigenschaften von Funktionen........................... 39. Potenz- und Wurzelfunktionen............................ 1.3 Trigonometrische Funktionen.............................
Spezielle Klassen von Funktionen
 Spezielle Klassen von Funktionen 1. Ganzrationale Funktionen Eine Funktion f : R R mit f (x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, n N 0 und a 0, a 1,, a n R, (a n 0) heißt ganzrationale Funktion n
Spezielle Klassen von Funktionen 1. Ganzrationale Funktionen Eine Funktion f : R R mit f (x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, n N 0 und a 0, a 1,, a n R, (a n 0) heißt ganzrationale Funktion n
Trigonometrie. Winkelfunktionen und Einheitskreis
 Trigonometrie Die Trigonometrie ist die Lehre der Winkel- oder Kreisfunktionen. Die auffälligste Eigenschaften der Funktionen der Trigonometrie ist die Periodizität: Trigonometrische Funktionen zeigen
Trigonometrie Die Trigonometrie ist die Lehre der Winkel- oder Kreisfunktionen. Die auffälligste Eigenschaften der Funktionen der Trigonometrie ist die Periodizität: Trigonometrische Funktionen zeigen
1.4 Trigonometrie I. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 4
 1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
Mathematik W18. Mag. Christina Sickinger. Berufsreifeprüfung. Trigonometrie am rechtwinkligen Dreieck
 Mathematik W18 Mag. Christina Sickinger Berufsreifeprüfung v 0 Mag. Christina Sickinger Mathematik W18 1 / 41 Das Problem v 0 Mag. Christina Sickinger Mathematik W18 2 / 41 Wir wollen das Problem lösen!
Mathematik W18 Mag. Christina Sickinger Berufsreifeprüfung v 0 Mag. Christina Sickinger Mathematik W18 1 / 41 Das Problem v 0 Mag. Christina Sickinger Mathematik W18 2 / 41 Wir wollen das Problem lösen!
Schulmathematik: Lineare Algebra & Analytische Geometrie. Kapitel 2: Trigonometrie. MAC.05043UB/MAC.05041PH, VU im SS 2017
 Schulmathematik: Lineare Algebra & Analytische Geometrie Kapitel 2: Trigonometrie MAC.05043UB/MAC.05041PH, VU im SS 2017 http://imsc.uni-graz.at/pfeiffer/2017s/linalg.html Christoph GRUBER, Florian KRUSE,
Schulmathematik: Lineare Algebra & Analytische Geometrie Kapitel 2: Trigonometrie MAC.05043UB/MAC.05041PH, VU im SS 2017 http://imsc.uni-graz.at/pfeiffer/2017s/linalg.html Christoph GRUBER, Florian KRUSE,
F u n k t i o n e n Trigonometrische Funktionen
 F u n k t i o n e n Trigonometrische Funktionen Jules Antoine Lissajous (*1822 in Versailles, 1880 in Plombières-les-Bains) wurde durch die nach ihm benannten Figuren bekannt, die bei der Überlagerung
F u n k t i o n e n Trigonometrische Funktionen Jules Antoine Lissajous (*1822 in Versailles, 1880 in Plombières-les-Bains) wurde durch die nach ihm benannten Figuren bekannt, die bei der Überlagerung
Trigonometrie aus geometrischer und funktionaler Sicht
 Trigonometrie aus geometrischer und funktionaler Sicht Der Kosinussatz und der Sinussatz: Wenn in einem Dreieck nur zwei Seiten und der eingeschlossene Winkel gegeben sind, oder nur die drei Seiten bekannt
Trigonometrie aus geometrischer und funktionaler Sicht Der Kosinussatz und der Sinussatz: Wenn in einem Dreieck nur zwei Seiten und der eingeschlossene Winkel gegeben sind, oder nur die drei Seiten bekannt
Trigonometrie. bekannte Zusammenhänge. 4-Streckensatz: groß/klein = groß/klein. Zusammenhänge im allgemeinen Dreieck:
 Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
FH Gießen-Friedberg, Sommersemester 2010 Skript 9 Diskrete Mathematik (Informatik) 30. April 2010 Prof. Dr. Hans-Rudolf Metz.
 FH Gießen-Friedberg, Sommersemester 010 Skript 9 Diskrete Mathematik (Informatik) 30. April 010 Prof. Dr. Hans-Rudolf Metz Funktionen Einige elementare Funktionen und ihre Eigenschaften Eine Funktion f
FH Gießen-Friedberg, Sommersemester 010 Skript 9 Diskrete Mathematik (Informatik) 30. April 010 Prof. Dr. Hans-Rudolf Metz Funktionen Einige elementare Funktionen und ihre Eigenschaften Eine Funktion f
Trigonometrie - die Grundlagen in einem Tag
 Trigonometrie - die Grundlagen in einem Tag Fachtage Dezember 2012 an der Kantonsschule Zürich Nord Klasse W3n R. Balestra Name: Vorname: 6. Dezember 2012 Inhaltsverzeichnis 1 Zielsetzung & Ablauf 1 2
Trigonometrie - die Grundlagen in einem Tag Fachtage Dezember 2012 an der Kantonsschule Zürich Nord Klasse W3n R. Balestra Name: Vorname: 6. Dezember 2012 Inhaltsverzeichnis 1 Zielsetzung & Ablauf 1 2
Themen: Strahlensätze, Trigonometrie, trigonometrische Funktionen
 Mathematik Klasse 10c Vorbereitung Klassenarbeit Nr. 3 am 1.3.019 Themen: Strahlensätze, Trigonometrie, trigonometrische Funktionen Checkliste Was ich alles können soll Ich erkennen die Strahlensatzfiguren
Mathematik Klasse 10c Vorbereitung Klassenarbeit Nr. 3 am 1.3.019 Themen: Strahlensätze, Trigonometrie, trigonometrische Funktionen Checkliste Was ich alles können soll Ich erkennen die Strahlensatzfiguren
Lineare Funktionen. Das rechtwinklige (kartesische) Koordinatensystem. Funktionen
 Das rechtwinklige (kartesische) Koordinatensystem Funktionen Funktion: Eine Funktion ist eine eindeutige Zuordnung. Jedem x D wird genau eine reelle Zahl zugeordnet. Schreibweise: Funktion: f: x f (x)
Das rechtwinklige (kartesische) Koordinatensystem Funktionen Funktion: Eine Funktion ist eine eindeutige Zuordnung. Jedem x D wird genau eine reelle Zahl zugeordnet. Schreibweise: Funktion: f: x f (x)
Grundwissen 10. Überblick: Gradmaß rπ Länge eines Bogens zum Mittelpunktswinkels α: b = α
 Grundwissen 0. Berechnungen an Kreis und Kugel a) Bogenmaß Beispiel: Gegeben ist ein Winkel α=50 ; dann gilt: b = b = π 50 0,8766 r r 360 Die (reelle) Zahl ist geeignet, die Größe eines Winkels anzugeben.
Grundwissen 0. Berechnungen an Kreis und Kugel a) Bogenmaß Beispiel: Gegeben ist ein Winkel α=50 ; dann gilt: b = b = π 50 0,8766 r r 360 Die (reelle) Zahl ist geeignet, die Größe eines Winkels anzugeben.
Die Funktionen. Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet.
 Die Funktionen Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de 1 Der Funktionsbegriff Seite 1 2 Die linearen Funktionen Seite 3
Die Funktionen Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de 1 Der Funktionsbegriff Seite 1 2 Die linearen Funktionen Seite 3
Grundwissen. 10. Jahrgangsstufe. Mathematik
 Grundwissen 10. Jahrgangsstufe Mathematik 1 Kreis und Kugel 1.1 Kreissektor und Bogenmaß Kreis Umfang U = π r=π d Flächeninhalt A=π r Kreissektor mit Mittelpunktswinkel α Bogenlänge b= α π r 360 Flächeninhalt
Grundwissen 10. Jahrgangsstufe Mathematik 1 Kreis und Kugel 1.1 Kreissektor und Bogenmaß Kreis Umfang U = π r=π d Flächeninhalt A=π r Kreissektor mit Mittelpunktswinkel α Bogenlänge b= α π r 360 Flächeninhalt
Kapitel 5 Trigonometrie
 Mathematischer Vorkurs TU Dortmund Seite / 7 Schenkel Winkelbereich Scheitel S α Winkel werden in Grad oder im Bogenmaß (auch Rad) angegeben: 360 =. y cot α r = sin α α cos α tan α x Durch diese Betrachtungen
Mathematischer Vorkurs TU Dortmund Seite / 7 Schenkel Winkelbereich Scheitel S α Winkel werden in Grad oder im Bogenmaß (auch Rad) angegeben: 360 =. y cot α r = sin α α cos α tan α x Durch diese Betrachtungen
Bundesgymnasium für Berufstätige Salzburg. Mathematik 4 Arbeitsblatt A 4-4 Winkelfunktionen. LehrerInnenteam m/ Mag. Wolfgang Schmid.
 Schule Bundesgymnasium für Berufstätige Salzburg Thema Mathematik 4 Arbeitsblatt A 4-4 Winkelfunktionen LehrerInnenteam m/ Mag. Wolfgang Schmid Unterlagen Um die Größe eines Winkels anzugeben gibt es verschiedenee
Schule Bundesgymnasium für Berufstätige Salzburg Thema Mathematik 4 Arbeitsblatt A 4-4 Winkelfunktionen LehrerInnenteam m/ Mag. Wolfgang Schmid Unterlagen Um die Größe eines Winkels anzugeben gibt es verschiedenee
Mathematischer Vorkurs NAT-ING II
 Mathematischer Vorkurs NAT-ING II (0.09.03 0.09.03) Dr. Jörg Horst WS 03-04 Mathematischer Vorkurs TU Dortmund Seite / 5 Mathematischer Vorkurs TU Dortmund Seite 6 / 5 Schenkel Winkelbereich Scheitel S
Mathematischer Vorkurs NAT-ING II (0.09.03 0.09.03) Dr. Jörg Horst WS 03-04 Mathematischer Vorkurs TU Dortmund Seite / 5 Mathematischer Vorkurs TU Dortmund Seite 6 / 5 Schenkel Winkelbereich Scheitel S
2 Geometrie und Vektoren
 Geometrie und Vektoren Vorbemerkung: Begriffe wie die folgenden werden hier als bekannt vorausgesetzt: Punkt, Strecke, Strahl, Gerade, Ebene, Kreis, Winkel, rechter Winkel, etc..1 Grundlegende Sätze Satz
Geometrie und Vektoren Vorbemerkung: Begriffe wie die folgenden werden hier als bekannt vorausgesetzt: Punkt, Strecke, Strahl, Gerade, Ebene, Kreis, Winkel, rechter Winkel, etc..1 Grundlegende Sätze Satz
Verlauf Material LEK Glossar Lösungen. Schritt für Schritt erklärt Sinus und Kosinus. Florian Borges, Traunstein VORANSICHT
 Reihe 9 S Verlauf Material Schritt für Schritt erklärt Sinus und Kosinus Florian Borges, Traunstein y 5 6 R ϕ( t ) 7 0 Die Sinusfunktion entsteht durch Projektion eines rotierenden Zeigers auf die y-achse.
Reihe 9 S Verlauf Material Schritt für Schritt erklärt Sinus und Kosinus Florian Borges, Traunstein y 5 6 R ϕ( t ) 7 0 Die Sinusfunktion entsteht durch Projektion eines rotierenden Zeigers auf die y-achse.
Selbsteinschätzungstest Auswertung und Lösung
 Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Aufgabe 1 Vereinfachen Sie die folgenden Ausdrücke soweit wie möglich. Vorsicht: Einige Terme können nicht weiter vereinfacht werden!
 Bachelor Bauingenieurwesen Reto Spöhel Repetitionsblatt BMS-Stoff Mathematik Alle Aufgaben sind ohne Taschenrechner zu lösen! Aufgabe 1 Vereinfachen Sie die folgenden Ausdrücke soweit wie möglich. Vorsicht:
Bachelor Bauingenieurwesen Reto Spöhel Repetitionsblatt BMS-Stoff Mathematik Alle Aufgaben sind ohne Taschenrechner zu lösen! Aufgabe 1 Vereinfachen Sie die folgenden Ausdrücke soweit wie möglich. Vorsicht:
Lösung - Serie 2. D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Welche der folgenden Funktionen ( 1, 1) R sind strikt monoton wachsend?
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie.. Welche der folgenden Funktionen (, R sind strikt monoton wachsend? (a (b (c + 3 (d e (e (f arccos Keine. Auf (, 0] ist strikt monoton
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie.. Welche der folgenden Funktionen (, R sind strikt monoton wachsend? (a (b (c + 3 (d e (e (f arccos Keine. Auf (, 0] ist strikt monoton
FH Gießen-Friedberg, FB 06 (MNI) Lösungen zu Übungsblatt 8 Einführung in die höhere Mathematik 6. Dezember 2006 Prof. Dr. H.-R.
 FH Gießen-Friedberg, FB 06 (MNI) Lösungen zu Übungsblatt 8 Einführung in die höhere Mathematik 6. Dezember 006 Prof. Dr. H.-R. Metz Aufgabe 1 Skizzieren Sie die Funktionen e x, ln(x) = log e (x) und e
FH Gießen-Friedberg, FB 06 (MNI) Lösungen zu Übungsblatt 8 Einführung in die höhere Mathematik 6. Dezember 006 Prof. Dr. H.-R. Metz Aufgabe 1 Skizzieren Sie die Funktionen e x, ln(x) = log e (x) und e
Winkel und Winkelmessung
 4. Trigonometrie Winkel und Winkelmessung Winkel... Teil der Ebene, der von zwei Strahlen ( Schenkeln ) mit gleichem Anfangspunkt ( Scheitel ) begrenzt wird Winkelmessung... Quantitative Erfassung der
4. Trigonometrie Winkel und Winkelmessung Winkel... Teil der Ebene, der von zwei Strahlen ( Schenkeln ) mit gleichem Anfangspunkt ( Scheitel ) begrenzt wird Winkelmessung... Quantitative Erfassung der
Analytische Geometrie I
 Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Differenzial- und Integralrechnung II
 Differenzial- und Integralrechnung II Rainer Hauser Dezember 011 1 Einleitung 1.1 Ableitung Die Ableitung einer Funktion f: R R, x f(x) ist definiert als f (x) = df(x) dx = d f(x + h) f(x) f(x) = lim dx
Differenzial- und Integralrechnung II Rainer Hauser Dezember 011 1 Einleitung 1.1 Ableitung Die Ableitung einer Funktion f: R R, x f(x) ist definiert als f (x) = df(x) dx = d f(x + h) f(x) f(x) = lim dx
Brückenkurs Mathematik zum Sommersemester 2015
 HOCHSCHULE HANNOVER UNIVERSITY OF APPLIED SCIENCES AND ARTS Dipl.-Math. Xenia Bogomolec Brückenkurs Mathematik zum Sommersemester 2015 Übungsblatt 1 (Grundlagen) Aufgabe 1. Multiplizieren Sie folgende
HOCHSCHULE HANNOVER UNIVERSITY OF APPLIED SCIENCES AND ARTS Dipl.-Math. Xenia Bogomolec Brückenkurs Mathematik zum Sommersemester 2015 Übungsblatt 1 (Grundlagen) Aufgabe 1. Multiplizieren Sie folgende
Musterlösungen zu Serie 7
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Musterlösungen zu Serie 7 1. Für jede der vier trigonometrischen Funktionen gilt: Genau in den Nullstellen x k ist y x k = 0 und y x k 0, was bedeutet,
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Musterlösungen zu Serie 7 1. Für jede der vier trigonometrischen Funktionen gilt: Genau in den Nullstellen x k ist y x k = 0 und y x k 0, was bedeutet,
Mathematik. für das Ingenieurstudium. 1 Grundlagen. Jürgen Koch Martin Stämpfle.
 1 Grundlagen www.mathematik-fuer-ingenieure.de 2010 und, Esslingen Dieses Werk ist urheberrechtlich geschützt. Alle Rechte, auch die der Übersetzung, des Nachdruckes und der Vervielfältigung des Werkes,
1 Grundlagen www.mathematik-fuer-ingenieure.de 2010 und, Esslingen Dieses Werk ist urheberrechtlich geschützt. Alle Rechte, auch die der Übersetzung, des Nachdruckes und der Vervielfältigung des Werkes,
Brückenkurs Mathematik. Mittwoch Freitag
 Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Didaktik der Geometrie
 Didaktik der Geometrie 7.1 Didaktik der Geometrie Didaktik der Geometrie 7.2 Inhalte Didaktik der Geometrie 1 Ziele und Inhalte 2 Begriffsbildung 3 Konstruieren 4 Argumentieren und Beweisen 5 Problemlösen
Didaktik der Geometrie 7.1 Didaktik der Geometrie Didaktik der Geometrie 7.2 Inhalte Didaktik der Geometrie 1 Ziele und Inhalte 2 Begriffsbildung 3 Konstruieren 4 Argumentieren und Beweisen 5 Problemlösen
Die Funktion f (x) = e ix
 Die Funktion f (x) = e ix Wir wissen e ix = 1, liegt also auf dem Einheitskreis. Mit wachsendem x läuft e ix immer wieder um den Einheitskreis herum. Die Laufrichtung ist gegen den Uhrzeigersinn (mathematisch
Die Funktion f (x) = e ix Wir wissen e ix = 1, liegt also auf dem Einheitskreis. Mit wachsendem x läuft e ix immer wieder um den Einheitskreis herum. Die Laufrichtung ist gegen den Uhrzeigersinn (mathematisch
Serie 1: Repetition von elementaren Funktionen
 D-ERDW, D-HEST, D-USYS Mathematik I HS 15 Dr. Ana Cannas Serie 1: Repetition von elementaren Funktionen Bemerkung: Die Aufgaben der Serie 1 bilden den Fokus der Übungsgruppen in der zweiten Semesterwoche
D-ERDW, D-HEST, D-USYS Mathematik I HS 15 Dr. Ana Cannas Serie 1: Repetition von elementaren Funktionen Bemerkung: Die Aufgaben der Serie 1 bilden den Fokus der Übungsgruppen in der zweiten Semesterwoche
Trigonometrische Funktionen
 Trigonometrische Funktionen Wir wollen einer Zeichnung und nicht dem Taschenrechner mehrere Sinuswerte entnehmen und graphisch darstellen. Falls c = ist, gilt a = sinα. Die Strecken der Länge liegen auf
Trigonometrische Funktionen Wir wollen einer Zeichnung und nicht dem Taschenrechner mehrere Sinuswerte entnehmen und graphisch darstellen. Falls c = ist, gilt a = sinα. Die Strecken der Länge liegen auf
Mathematische Probleme, SS 2013 Donnerstag $Id: dreieck.tex,v /04/12 15:30:18 hk Exp hk $
 $Id: dreieck.tex,v 1.3 2013/04/12 15:30:18 hk Exp hk $ 1 Dreiecke 1.2 Der Strahlensatz Nachdem wir in der letzten Sitzung rechtwinklige Dreiecke betrachtet haben, kommen wir nun zur Einführung der trigonometrischen
$Id: dreieck.tex,v 1.3 2013/04/12 15:30:18 hk Exp hk $ 1 Dreiecke 1.2 Der Strahlensatz Nachdem wir in der letzten Sitzung rechtwinklige Dreiecke betrachtet haben, kommen wir nun zur Einführung der trigonometrischen
α π r² Achtung: Das Grundwissen steht im Lehrplan! 1. Kreis und Kugel
 Achtung: Das Grundwissen steht im Lehrplan! Tipps zum Grundwissen Mathematik Jahrgangsstufe 10 Folgende Begriffe und Aufgaben solltest Du nach der 10. Klasse kennen und können: (Falls Du Lücken entdeckst,
Achtung: Das Grundwissen steht im Lehrplan! Tipps zum Grundwissen Mathematik Jahrgangsstufe 10 Folgende Begriffe und Aufgaben solltest Du nach der 10. Klasse kennen und können: (Falls Du Lücken entdeckst,
I. Reelle Zahlen GRUNDWISSEN MATHEMATIK - 9. KLASSE
 I. Reelle Zahlen 1. Die Menge der rationalen Zahlen und die Menge der irrationalen Zahlen bilden zusammen die Menge der reellen Zahlen. Nenne Beispiele für rationale und irrationale Zahlen.. Aus negativen
I. Reelle Zahlen 1. Die Menge der rationalen Zahlen und die Menge der irrationalen Zahlen bilden zusammen die Menge der reellen Zahlen. Nenne Beispiele für rationale und irrationale Zahlen.. Aus negativen
1.4 Trigonometrie. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 3
 1.4 Trigonometrie Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 3 2.1 Was sind trigonometrischen Funktionen?.......................... 3 2.2 Die
1.4 Trigonometrie Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 3 2.1 Was sind trigonometrischen Funktionen?.......................... 3 2.2 Die
1 Mengenlehre. Maturavorbereitung GF Mathematik. Aufgabe 1.1. Aufgabe 1.2. Bestimme A \ B. Aufgabe 1.3. Aufgabe 1.4. Bestimme B \ A. Aufgabe 1.
 Maturavorbereitung GF Mathematik Kurzaufgaben 1 Mengenlehre Aufgabe 1.1 Gegeben sind die Mengen A = {1, 2, 3} und B = {2, 3, 6, 8}. Bestimme A B. Aufgabe 1.2 Gegeben sind die Mengen A = {1, 2, 3} und B
Maturavorbereitung GF Mathematik Kurzaufgaben 1 Mengenlehre Aufgabe 1.1 Gegeben sind die Mengen A = {1, 2, 3} und B = {2, 3, 6, 8}. Bestimme A B. Aufgabe 1.2 Gegeben sind die Mengen A = {1, 2, 3} und B
Brückenkurs Mathematik. Dienstag Freitag
 Brückenkurs Mathematik Dienstag 2.0. - Freitag 2.0. Vorlesung 5 Elementare Funktionen Kai Rothe Technische Universität Hamburg Dienstag 9.0. 0 Brückenkurs Mathematik, c K.Rothe, Vorlesung 5 Umkehrfunktion........................
Brückenkurs Mathematik Dienstag 2.0. - Freitag 2.0. Vorlesung 5 Elementare Funktionen Kai Rothe Technische Universität Hamburg Dienstag 9.0. 0 Brückenkurs Mathematik, c K.Rothe, Vorlesung 5 Umkehrfunktion........................
Trigonometrie. Schülerzirkel Mathematik Schülerseminar
 Schülerzirkel Mathematik Schülerseminar Trigonometrie Im Schülerseminar für Schülerinnen und Schüler der Klassenstufen 8 10 wurde die Trigonometrie innerhalb der Einheit über komplexe Zahlen behandelt,
Schülerzirkel Mathematik Schülerseminar Trigonometrie Im Schülerseminar für Schülerinnen und Schüler der Klassenstufen 8 10 wurde die Trigonometrie innerhalb der Einheit über komplexe Zahlen behandelt,
Was bedeutet Trigonometrie und mit was beschäftigt sich die Trigonometrie?
 Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Dr. Günter Rothmeier Kein Anspruch auf Vollständigkeit Elementarmathematik (LH) und Fehlerfreiheit
 WS 8/9 5 7 Elementarmathematik (LH) und Fehlerfreiheit 5. Trigonometrie 5.. Trigonometrische Terme am Einheitskreis 5... Das olarkoordinatensstem Man kann die Lage eines unktes im -dimensionalen Raum folgendermaßen
WS 8/9 5 7 Elementarmathematik (LH) und Fehlerfreiheit 5. Trigonometrie 5.. Trigonometrische Terme am Einheitskreis 5... Das olarkoordinatensstem Man kann die Lage eines unktes im -dimensionalen Raum folgendermaßen
befasst sich mit den Beziehungen zwischen den Seiten und Winkeln in einem Dreieck.
 Trigonometrie Lernziele befasst sich mit den Beziehungen zwischen den Seiten und Winkeln in einem Dreieck. Selbständiges Erarbeiten der Kurztheorie Kenntnis der wichtigsten Begriffe, Definitionen und Formeln
Trigonometrie Lernziele befasst sich mit den Beziehungen zwischen den Seiten und Winkeln in einem Dreieck. Selbständiges Erarbeiten der Kurztheorie Kenntnis der wichtigsten Begriffe, Definitionen und Formeln
1. die ganzen Zahlen, denn 7= 1. a ist diejenige nicht negative Zahl, die quadriert a ergibt: 16 = 4; 0 = = 36 = 25 = e) Grundwissen 9.
 Grundwissen 9. Klasse Quadratwurzel a ist diejenige nicht negative Zahl, die quadriert a ergibt: ( a ) a Die Zahl a unter der Wurzel heißt Radikand. Es gibt keine Quadratwurzel aus einer negativen Zahl.
Grundwissen 9. Klasse Quadratwurzel a ist diejenige nicht negative Zahl, die quadriert a ergibt: ( a ) a Die Zahl a unter der Wurzel heißt Radikand. Es gibt keine Quadratwurzel aus einer negativen Zahl.
1 Dreiecke. 1.1 Rechtwinklige Dreiecke. Mathematische Probleme, SS 2016 Freitag $Id: dreieck.tex,v /04/15 14:02:10 hk Exp $
 $Id: dreieck.tex,v 1.21 20/04/15 14:02:10 hk Exp $ 1 Dreiecke 1.1 Rechtwinklige Dreiecke Am Ende der letzten Sitzung hatten wir begonnen die primitiven pythagoräischen Tripel zu bestimmen, und in einem
$Id: dreieck.tex,v 1.21 20/04/15 14:02:10 hk Exp $ 1 Dreiecke 1.1 Rechtwinklige Dreiecke Am Ende der letzten Sitzung hatten wir begonnen die primitiven pythagoräischen Tripel zu bestimmen, und in einem
Priv. Doz. Dr. A. Wagner Aachen, 19. September 2016 S. Bleß, M. Sc. Analysis. Übungsaufgaben. im Vorkurs Mathematik 2016, RWTH Aachen University
 Priv. Doz. Dr. A. Wagner Aachen, 9. September 6 S. Bleß, M. Sc. Analysis Übungsaufgaben im Vorkurs Mathematik 6, RWTH Aachen University Intervalle, Supremum und Infimum Für a, b R, a < b nennen wir eine
Priv. Doz. Dr. A. Wagner Aachen, 9. September 6 S. Bleß, M. Sc. Analysis Übungsaufgaben im Vorkurs Mathematik 6, RWTH Aachen University Intervalle, Supremum und Infimum Für a, b R, a < b nennen wir eine
Grundlagen. Einteilung der Dreiecke. Besondere Punkte des Dreiecks
 Der Name leitet sich von den griechischen Begriffen Tirgonon Dreieck und Metron Maß ab. ist also die Lehre vom Dreieck, d.h. die Grundaufgabe der besteht darin, aus drei Größen eines gegebenen Dreiecks
Der Name leitet sich von den griechischen Begriffen Tirgonon Dreieck und Metron Maß ab. ist also die Lehre vom Dreieck, d.h. die Grundaufgabe der besteht darin, aus drei Größen eines gegebenen Dreiecks
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Serie 2
 D-MAVT/D-MATL Analysis I HS 017 Dr. Andreas Steiger Serie Die erste Aufgabe ist eine Multiple-Choice-Aufgabe MC-Aufgabe), die online gelöst wird. Bitte schicken Sie Ihre Lösungen zu den Online MC-Fragen
D-MAVT/D-MATL Analysis I HS 017 Dr. Andreas Steiger Serie Die erste Aufgabe ist eine Multiple-Choice-Aufgabe MC-Aufgabe), die online gelöst wird. Bitte schicken Sie Ihre Lösungen zu den Online MC-Fragen
Rechtwinklige Dreiecke konstruieren
 1 Vertiefen 1 Rechtwinklige Dreiecke konstruieren zu Aufgabe Schulbuch, Seite 106 Dreiecke konstruieren a) Konstruiere die Dreiecke mit den Angaben aus der Tabelle. Miss dann die übrigen Maße und vervollständige
1 Vertiefen 1 Rechtwinklige Dreiecke konstruieren zu Aufgabe Schulbuch, Seite 106 Dreiecke konstruieren a) Konstruiere die Dreiecke mit den Angaben aus der Tabelle. Miss dann die übrigen Maße und vervollständige
Aufgaben zum Basiswissen 10. Klasse
 Aufgaben zum Basiswissen 10. Klasse 1. Berechnungen an Kreisen und Dreiecken 1. Aufgabe: In einem Kreis mit Radius r sei α ein Mittelpunktswinkel mit zugehörigem Kreisbogen der Länge b und Kreissektor
Aufgaben zum Basiswissen 10. Klasse 1. Berechnungen an Kreisen und Dreiecken 1. Aufgabe: In einem Kreis mit Radius r sei α ein Mittelpunktswinkel mit zugehörigem Kreisbogen der Länge b und Kreissektor
Dr. O. Wittich Aachen, 12. September 2017 S. Bleß, M. Sc. Analysis. Übungsaufgaben. im Vorkurs Mathematik 2017, RWTH Aachen University
 Dr. O. Wittich Aachen,. September 7 S. Bleß, M. Sc. Analysis Übungsaufgaben im Vorkurs Mathematik 7, RWTH Aachen University Intervalle, Beschränktheit, Maxima, Minima Aufgabe Bestimmen Sie jeweils, ob
Dr. O. Wittich Aachen,. September 7 S. Bleß, M. Sc. Analysis Übungsaufgaben im Vorkurs Mathematik 7, RWTH Aachen University Intervalle, Beschränktheit, Maxima, Minima Aufgabe Bestimmen Sie jeweils, ob
9.5 Graphen der trigonometrischen Funktionen
 9.5 Graphen der trigonometrischen Funktionen 9.5 Graphen der trigonometrischen Funktionen. Unter dem Bogenmass eines Winkels versteht man die Länge des Winkelbogens von auf dem Kreis mit Radius (Einheitskreis).
9.5 Graphen der trigonometrischen Funktionen 9.5 Graphen der trigonometrischen Funktionen. Unter dem Bogenmass eines Winkels versteht man die Länge des Winkelbogens von auf dem Kreis mit Radius (Einheitskreis).
Überblick über die Winkelfunktionen Sinusfunktion
 Überblick über die Winkelfunktionen Sinusfunktion -x2 -x1 x1 x2 Die Funktion x sin x ; x ℝ heißt Sinusfunktion und ihr Graph Sinuskurve. Die Sinusfunktion ist punktsymmetrisch (blau in der Zeichnung) zum
Überblick über die Winkelfunktionen Sinusfunktion -x2 -x1 x1 x2 Die Funktion x sin x ; x ℝ heißt Sinusfunktion und ihr Graph Sinuskurve. Die Sinusfunktion ist punktsymmetrisch (blau in der Zeichnung) zum
Analytische Geometrie II
 Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Funktionen einer reellen Veränderlichen
 KAPITEL Funktionen einer reellen Veränderlichen. Grundbegriffe Definition.. Eine Abbildung oder Funktion f ist eine Zuordnung(svorschrift), die jeder Zahl x aus dem Definitionsbereich D(f) der Funktion
KAPITEL Funktionen einer reellen Veränderlichen. Grundbegriffe Definition.. Eine Abbildung oder Funktion f ist eine Zuordnung(svorschrift), die jeder Zahl x aus dem Definitionsbereich D(f) der Funktion
D-MAVT/D-MATL Analysis I HS 2018 Dr. Andreas Steiger. Serie 2
 D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Steiger Serie Die ersten Aufgaben sind Multiple-Choice-Aufgaben MC), die online gelöst werden. Bitte schicken Sie Ihre Lösungen zu den Online MC-Fragen bis Mittwoch,
D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Steiger Serie Die ersten Aufgaben sind Multiple-Choice-Aufgaben MC), die online gelöst werden. Bitte schicken Sie Ihre Lösungen zu den Online MC-Fragen bis Mittwoch,
Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis
 Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis 1. Eine Rampe hat eine Steigung von 5%. Wie groß ist der Steigungswinkel? 2. Gegeben ist ein rechtwinkliges
Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis 1. Eine Rampe hat eine Steigung von 5%. Wie groß ist der Steigungswinkel? 2. Gegeben ist ein rechtwinkliges
Mathematischer Vorkurs
 Mathematischer Vorkurs Dr. Agnes Lamacz Mathematischer Vorkurs TU Dortmund Seite / 50 Kapitel 5 Mathematischer Vorkurs TU Dortmund Seite 54 / 50 Scheitel S Schenkel α Winkelbereich Winkel werden in Grad
Mathematischer Vorkurs Dr. Agnes Lamacz Mathematischer Vorkurs TU Dortmund Seite / 50 Kapitel 5 Mathematischer Vorkurs TU Dortmund Seite 54 / 50 Scheitel S Schenkel α Winkelbereich Winkel werden in Grad
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
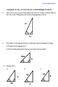 Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
a) Wie hoch ist die Leiter? b) Wie weit stehen die beiden Fußpunkte auseinander? Abbildung 1: Eine Stehleiter
 1. Berechnen Sie die jeweils fehlenden Größen (Winkel α, β und γ, Seiten a, b und c) in den folgenden Dreiecken: a) a = 5 cm, b = 9 cm, γ = 90 b) c = 9 cm, a = 6 cm, γ = 56, 3 (Überlegen Sie zuerst, wo
1. Berechnen Sie die jeweils fehlenden Größen (Winkel α, β und γ, Seiten a, b und c) in den folgenden Dreiecken: a) a = 5 cm, b = 9 cm, γ = 90 b) c = 9 cm, a = 6 cm, γ = 56, 3 (Überlegen Sie zuerst, wo
Trignonometrische Funktionen 6a
 Schuljahr 2015/16 andreas.kucher@uni-graz.at Institute for Mathematics and Scientific Computing Karl-Franzens-Universität Graz Graz, November 23, 2015 Winkelmaße Winkelmaß bis 6. Klasse: Grad (0 360 )
Schuljahr 2015/16 andreas.kucher@uni-graz.at Institute for Mathematics and Scientific Computing Karl-Franzens-Universität Graz Graz, November 23, 2015 Winkelmaße Winkelmaß bis 6. Klasse: Grad (0 360 )
Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 9
 Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 9 Wissen und Können. Zahlenmengen Aufgaen, Beispiele, Erläuterungen N Z Q R natürliche ganze rationale reelle Zahlen Zahlen Zahlen
Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 9 Wissen und Können. Zahlenmengen Aufgaen, Beispiele, Erläuterungen N Z Q R natürliche ganze rationale reelle Zahlen Zahlen Zahlen
Fachdidaktik Mathematik: Mathematik erleben (Teil 1)
 Fachdidaktik Mathematik: Mathematik erleben (Teil 1) Um was es geht? Im folgenden werden Beispiele zum Thema Trigonometrie gezeigt, in denen sich die Schüler aktiv mit einer Aufgabenstellung auseinander
Fachdidaktik Mathematik: Mathematik erleben (Teil 1) Um was es geht? Im folgenden werden Beispiele zum Thema Trigonometrie gezeigt, in denen sich die Schüler aktiv mit einer Aufgabenstellung auseinander
