Jetzt lerne ich Mathematik für die Mittelstufe
|
|
|
- Norbert Otto
- vor 7 Jahren
- Abrufe
Transkript
1 Jetzt lerne ich Mathematik für die Mittelstufe von Dr. rer. nat. Marco Schuchmann, Dipl.-Math.
2 Seite 2
3 Seite 3 Vorwort In diesem Buch werden diverse Themen der Mittelstufe bzw. Sekundarstufe 1 behandelt. Zum Inhalt des Buches gehören: Grundlagen und Rechengesetze zum Umgang mit Variablen, ein Einstieg zum Lösen von linearen Gleichungen, die binomische Formeln, der Satz von Pythagoras sowie der Höhen- und Kathetensatz, der Sinus- und Kosinussatz, Gleichungssysteme, die p-q-formel, Wurzelgleichungen, Bruchgleichungen, Potenzgesetze, Logarithmen und Exponentialgleichungen, Geraden, Parabeln und Exponentialfunktionen. Dabei sind viele Erklärungen, wichtige Hinweise für bestimmte Aufgabentypen, Aufgabenbeispiele mit Lösungstipps und Grafiken im Buch zu finden. Bei allen Beschreibungen steht im Vordergrund, dass diese für Schülerinnen und Schüler möglichst verständlich sind, weshalb auch viele Zwischenschritte bei Umformungen dargestellt werden. Auf den beiden Seiten zum Buch, der Seite und der Seite werden Programme zum Lösen von Aufgaben und zum Erstellen von Graphen bereitgestellt wie auch Übungsaufgaben, Ergänzungen zum Buch und eine Formelsammlung zur Flächen- und Volumenberechnung. Im Sommer 2011 Dr. Marco Schuchmann ( schuchmann@alles-mathe.de)
4 Seite 4
5 Seite 5 Inhaltsverzeichnis 1 Rechnen mit Variablen Zusammenfassen von Termen Das Distributivgesetz Lineare Gleichungen mit einer Unbekannten Potenzgesetze Wurzelgesetze Logarithmen Wurzelgleichungen Bruchgleichungen Binomische Formeln Lineare Gleichungssysteme mit zwei Unbekannten Lineare Gleichungssysteme mit drei oder mehr Unbekannten Trigonometrie Grundlagen Pythagoras Höhensatz und Kathetensatz von Euklid Berechnung von Winkeln und Seiten im rechtwinkligen Dreieck mit Sinus, Kosinus und Tangens Sinussatz Kosinussatz Geraden Parabeln Exponentialfunktionen... 91
6 Seite 6
7 Seite 7 1 Rechnen mit Variablen 1.1 Zusammenfassen von Termen Gleiche Variablen und Produkte gleicher Variablen können zusammengefasst werden, d.h. sie können addiert oder subtrahiert werden: Beispiele: 4a + 3a = 7a 2b 3b = -1b = -b 4a + 3b + 2a 8b = 4a + 2a + 3b 8b = 6a 5b 2x + 3y + 5xy + 9x y = 11x + 2y +5xy 15 8x x = 25 6x 5x 2 + 8xy + 3x 2 + 2xy = 8x xy Bemerkungen: 1) Es gilt das folgende Gesetz (Kommutativgesetz): aÿb = bÿa 2) Damit die Übersicht größer ist, sortiert man aber bei Termen die Variablen alphabetisch. Außerdem kann man den Malpunkt, wie wir es bereits oben getan haben, weg lassen: 4ÿx = 4x 3) Statt 1x schreibt man x. Weiterhin gilt somit: a 1/ 5a 5 ab 4 1/ 4ab a 4 b Aufgaben: a) x + 4x b) 3x 8y + 2x 4y c) 2a + 8b 10a + 12b d) 10xy + 8x + 15xy 2x + 4y e) 9a 2 7a + 2a 2 + 2a f) 5a a + 7
8 Seite 8 Lösungen: a) 5x b) 5x 12y c) -8a + 20b d) 25xy + 6x + 4y e) 11a 2 5a f) 7a Das Distributivgesetz Das Distributivgesetz lautet wie folgt: a(b + c) = ab + ac Beispiele: 4(2x + 3y) = 4ÿ2x + 4ÿ3y = 8x + 12y -(x 2y) = -x + 2y -5(3a 2b) = -15a + 10b a b (a 4 b) / 4 a / 4 b / 4 Ausklammern Das Distributivgesetz wird auch beim Ausklammern verwendet. Dabei werden gemeinsame Teiler ausgeklammert. Z.B. haben bei dem Term 10x + 15y beide Summanden den Teiler 5. Dadurch könnte man für den Term auch 5(10/5x + 15/5y) = 5(2x + 3y) schreiben. Beispiele: 4x + 8y = 4(x + 2y) a = 20(1 + 2a) 4x 2 + 8x = 4x(x + 2) Bemerkungen: 1) Es gilt: xÿx = x 2 xÿxÿx = x 3 2) x 2 sollte nicht mit 2x = x + x verwechselt werden. 3) Beim Zusammenfassen wird das Distributivgesetz verwendet: 4a + 6a = a(4 + 6) = 10a
9 Seite 9 4) Aus dem Distributivgesetz folgt (a + b)(c + d) = ac + ad + bc + bd, d.h. hier muss man insgesamt 4 Produkte bilden. Aufgaben: 1) Löse die Klammern auf und fasse - wenn möglich - zusammen: a) 5(x + 3) b) (-x -4y) c) 4(2a 3b) d) 2x(x + 3y) e) -3(-2a + 3b + c) f) 4(3y + 2z) + 2(3x 5z) g) 5(8a 2b) 5(3a + 4b) h) (4 3x)(2 + 4x) i) (2a 3b )(2a + 3b) 2) Klammere gemeinsame Faktoren aus: a) 5x + 10y b) -15a + 10b c) 6x + 9y + 12z d) 4 8a e) -12a a f) 6x 12xy + 15x 2 g) 25u 30v + 20w Lösungen: 1) a) 5x + 15 b) x + 4y c) 8a 12b d) 2x 2 + 6xy e) 6a 9b 3c f) 12y + 8z + 6x 10z = 6x + 12y 2z g) 40a 10b 15a 20b = 25a 30b h) x 6x 12x 2 = -12x 2 +10x + 8 i) 4a 2 +6ab 6ab 9b 2 = 4a 2 9b 2 2) a) 5(x + 2y) b) 5(-3a + 2b) c) 3(2x + 3y + 4z) d) 4(1 2a) e) 12a(-a + 2) f) 3x(2 4y + 5x) g) 5(5u 6v + 4w)
10 Seite 10 2 Lineare Gleichungen mit einer Unbekannten Wir betrachten die Gleichung: x + 4 = 5 Eine solche Gleichung kann systematisch gelöst werden, indem auf beide Seiten der Gleichung dieselbe Zahl addiert oder subtrahiert wird. Oder man multipliziert beide Seiten (d.h. aber komplett jeweils eine Seite) mit einer Zahl ungleich Null oder dividiert durch diese. Dadurch wird die Lösung nicht verändert und man spricht von einer Äquivalenzumformung. Nun könnte man die obige Gleichung lösen, wenn man von beiden Seite 4 subtrahiert. x = 5 4 x = 1 Man schreibt bei einer solchen Umformung die Zahl, die subtrahiert, addiert, mit der multipliziert oder durch die dividiert wird, hinter einen senkrechten Strich rechts neben die Gleichung (mit der zugehörigen arithmetischen Operation): x + 4 = 5-4 x = 1 Bei der nächsten Gleichung müssen wir durch 4 dividieren: 4x = 20 :4 x = 5 Die Lösung kann man auch in Form einer Lösungsmenge angeben: L = {5} Weitere Beispiele: 2x + 4 = x = 16 :2 Also: L = {8} x = 8-4x + 10 = x = -8 : (-4) x = 2 Also: L = {2}
11 Seite 11 Bei der nächsten Gleichung sollte man (wie oben) alle Terme mit x auf eine Seite bringen und alle ohne x auf die andere. Dividiert wird dann immer zum Schluss. Also: L = {-1} Also: L = {8} 5x + 8 = 6x + 9-6x -x + 8 = 9-8 -x = 1 :(-1) oder ÿ(-1) x = -1 x/4 = 2 ÿ4 (oder :1/4) x = 8 Bei der nächsten Gleichung sollte man erst die Klammer auflösen und danach zusammenfassen, bevor man mit den Umformungen beginnt: Also: L = {-2} 2(x + 4) 2 = x + 4 2x = x 2x + 6 = x -6 2x = 8 + 6x -6x -4x = 8 :(-4) x = -2 Aufgaben: Bestimme die Lösungsmenge: a) 4x = 20 b) x + 9 = 15 c) 2x + 3 = -5 d) -4x - 10 = -30 e) 6x 8 = 3x + 1 f) -2x + 5 = 2x + 21 g) 3(x 4) + x = 8 h) -(2x 5) +2(x + 3) = 4x 1 i) 5x + 9 = 5 + 8x j) 2x = 9x k) -9x (2 4x) = 1/2
12 Seite 12 Lösungen: a) L = {5} b) L = {6} c) L = {-4} d) L = {5} e) L = {3} f) L = {-4} g) L = {5} h) L = {3} i) L = {4/3} j) L = {0} k) L = {-1/2} Bemerkung zu Spezialfällen: Gleichungen können auch keine oder unendlich viele Lösungen besitzen. Hierzu zwei Beispiele: 3x + 4 = 3x + 5-3x 4 = 5 Diese Gleichung ist für keine rationale Zahl (falls die Grundmenge gleich den rationalen Zahlen ist) erfüllt. Die Lösungsmenge ist leer: L = {} 3x + 4 = 3x + 4-3x 4 = 4 Diese Gleichung ist für alle rationale Zahl (falls die Grundmenge gleich den rationalen Zahlen ist) erfüllt: L = Q Falls die Grundmenge die reellen Zahlen bildet, dann wäre natürlich hier L = R. Zum Schluss kommen noch ein paar Aufgaben zum einsetzen in Terme. Soll z.b. in den Term T = -2x + 1 für die Variable x der Wert 3 eingesetzt werden, dann ergibt sich T = -2ÿ3 + 1 = -5. Aufgaben: 1) Berechne T = 3x 2 für: a) x = 1 b) x = -4 c) x = 2/3 2) Berechne T = -2x + 5 für: a) x = -3 b) x = 4 c) x = 1/3
13 Seite 13 Lösungen: 1) a) T = 1 b) T = -14 c) T = 0 2) a) T = 11 b) T = -3 c) T = 13/3 = 4 1/3 (Als gemischte Zahl geschrieben.)
14 Seite 14 3 Wurzeln Die Wurzel aus einer nichtnegativen Zahl a, d.h. a für a 0, ist die nichtnegative Lösung der Gleichung x 2 = a. Bemerkungen: 1) Damit ist 4 = 2, denn 2 2 = 4. Die Zahl unter der Wurzel wird der Radikand genannt. Ein häufig gemachter Fehler bei Wurzel ist der folgende: 4 2. Dies ist falsch! Denn die Gleichung x 2 = 4 hat zwar zwei Lösungen, nämlich 2 und -2, aber die Wurzel aus einer Zahl ist immer die positive Lösung der Gleichung x 2 = a. Sonst könnte man über die Wurzel keine Funktion definieren und die Rechnung 4 9 hätte 4 Ergebnisse, nämlich 2 + 3, 2 3, und ) Es gibt keine reelle Zahl, für die x 2 = -4 wäre. Aus diesem Grund gibt es keine reelle Zahl 4. Für das Wurzelziehen ohne Taschenrechner sollte man einige Quadratzahlen kennen: 2 2 = 4, 3 2 = 9, 4 2 = 16,, 25 2 = 625 Dies dient allerdings nur der Übung, denn die meisten Wurzeln - alleine schon aus den natürlichen Zahlen - ergeben keine natürliche Zahl, nicht mal eine rationale Zahl. Rationale Zahlen sind Zahlen, die man als Bruch (aus ganzen Zahlen) schreiben kann und die dann entweder nach dem Komma irgendwann abbrechen oder periodisch sind. Die Menge der rationalen Zahlen wird mit Q bezeichnet. Beispielsweise ergibt 2 eine irrationale Zahl. Irrationale Zahlen sind Zahlen, die unendlich viele Nachkommastellen besitzen und nicht periodisch sind. Die Menge der irrationalen Zahlen wird mit I bezeichnet. Die irrationale Zahlen und die rationale Zahlen zusammen ergeben die reellen Zahlen, d.h. es gilt R = I» Q. R ist die Menge der reellen Zahlen. Es gilt: 2 = 1, Beispiele für Wurzeln:
15 Seite ,25 1,5 Wird unter der Wurzel (d.h. beim Radikand) das Komma um zwei Stellen verschoben, so ist es beim Ergebnis um eine Stelle verschoben. Dies liegt daran, dass bei Produkten und Quotienten (nicht bei Summen!) die Wurzeln getrennt gezogen werden können: Damit halbieren sich bei den folgenden Beispielen mit rationalen Ergebnissen die Anzahl der Nullen bzw. Nachkommastellen durch das Wurzelziehen: 0,04 0,2 0,0025 0, , ,001 Beispiele für Brüche: Kommen wir nun zum teilweisen Wurzelziehen: Lässt sich der Radikant als ein Produkt aus einer Zahl und einer Quadratzahl (bzw. aus einer Zahl, aus der man durch das Wurzelziehen eine rationale Zahl erhält) darstellen, so kann man teilweise die Wurzel ziehen.
16 Seite 16 Beispiele: x 4 y x 2 y Oder für Quotienten: Bemerkung: x 2 x gilt für x 0, denn beispielsweise ist ( 1) 2 1 und nicht gleich -1. D.h. bei Variablen muss man unter umständen eine einschränkende Bedingung angeben. Man könnte aber auch den Betrag verwenden: x 2 x. Der Betrag ist wie folgt festgelegt: Für x 0 ist x = x und für x < 0 ist x = -x, womit der Betrag einer Zahl immer positiv oder gleich Null ist (für x = 0). Für keine Einschränkung, wohl aber für 4 2 x x benötigt man 6 3 x x, denn x 3 ist für negative x auch negativ. Aufgaben: 1) Ziehe die folgenden Wurzeln: 64 ; 6400 ; 144 ; 2500 ; 0, 81 ; 0, 01 ; 1, 44 ; 0, ) Ziehe teilweise die Wurzel und fasse - wenn möglich - zusammen: 20 ; 72 ; 48 ; 125 ; 500 ; 3) Bestimme die Lösungsmenge: a) x 2 = 25 b) x 2 = -16 c) x 2 16 = ; ; 2 3 a ; a 3 b 2 ; 50 8 ;
17 Seite 17 Lösungen: 1) 8; 80; 12; 50; 0,9; 0,1; 1,2; 0, ) 2 5 ; 6 2 ; 4 3 ; 5 5 ; 10 5 ; ; ; a 3 für a 0; a 2 ab 2 ab a für a 0 und b 0; = 7 2 ; = 1 3 = 3 3) a) x 2 = 25 Also gilt: L = {-5; 5} b) L = {} c) L = {-6; 6} x = 5 oder x = -5 (oft verwendete Schreibweise für die Lösungen: x 1/2 = 5)
18 Seite 18 4 Potenzgesetze (1) a n a m a nm Beispiele: a 3 ÿa 7 = a 10 x 3 ÿy 4 ÿx 2 ÿy 5 = x 5 ÿy 9 4x 8 (-2)x 3 = -8x 11 (2) a a n m nm a (für a 0) Beispiele: 8 a 2 a a 6 a a 3 2 a 3( 2) a 32 a 5 a a 10 4 b b 8 2 a 6 b x y 3 2 2x y 2 5 6x y 2x (oder auch 2 y 3 ) Bemerkung: Für a 0 folgt aus (2): a m 0 I) a 1, also a 0 = 1. m a II) 1 0 a n a n n a a, also 1 n a n a. Somit ist
19 Seite 19 (3) (aÿb) n = a n ÿb n n a a bzw. n b b n Beispiele: (xÿy) 3 = x 3 ÿy 3 0,25 4 ÿ8 4 = (0,25ÿ8) 4 = 2 4 = /8 3 = (16/8) 3 = 2 3 = 8 (4) m n nm a a Beispiele: a a a k 1 2 k1 (k1)(k1) k 1 x x x Für die beiden Gesetzte (3) und (4): ( a b ) (a ) (b ) a 9 b ( 4x ) 4 (x ) 16x 10 Aufgaben: 1) Fasse zusammen: a) x 5 ÿx 3 b) 2y 8 5x 3 y 10 8 x c) 5 x 3 10 x y d) 2 5 x y 8 12x y 3x y 7 e) 4 12
20 Seite 20 12(x y) f) 2 4(x y) g) a 2n+3m ÿ a -4n+2m 8 2) Wende die Potenzgesetze an: a) (2a) 4 b) (x 8 y 3 ) 4 c) (-0,5) 6 ÿ2 6 d) 2 2 a 4 e) (aÿb 4 ) -2 3) Schreibe in wissenschaftlicher Schreibweise: Beispiele: = 1,2345ÿ10000 = 1,2345ÿ10 4 0,00013 = 1,3 / = 1,3ÿ10-4 a) b) 0, c) d) 0,
21 Seite 21 Lösungen: 1) a) x 8 b) 10x 3 y 18 c) x 3 d) x 5 y 5 e) 4x 4 y -5 f) 6 3(x y) Achtung: 6 ( x y) ist allgemein nicht dasselbe wie x 6 + y 6! g) a -2n+5m 2) a) 16a 4 b) x 32 y 12 c) (-1) 6 = 1 d) 16 16a 8 a 8 e) a -2 ÿb -8 3) a) 1,25ÿ10 4 b) 1,25ÿ10-6 c) -8,3ÿ10 5 d) 4ÿ10-8
22 Seite 22 5 Wurzelgesetze (1) n n a a 1/ Beispiele: a ) 1/ 2 a a (Es gilt: 2 a 3 x x 1/ 3 (2) m n a a n / m Beispiele: x 5 10 x 10 / 5 x 2 a 0,75 a 75 /100 a 3 / 4 a 4 3 x 4 1/ 2 1/ 4 1/ 21/ 4 3 / 4 4 x 3 x x x x x n n n (3) a b a b bzw. Beispiele: n a b n n a b x 8 x 2 x 4 4 a a 16 a Teilweises Wurzelziehen: Die Formel (3) wird auch bei dem so genannten teilweisen Wurzelziehen angewandt:
23 Seite 23 Beim teilweisen Wurzelziehen prüft man zunächst, wie man oben sieht (und wie auch im Kapitel Wurzeln beschrieben), welche Quadratzahl Teiler des Radikanten (dieser steht unter der Wurzel) ist und zerlegt dann den Radikanten in Faktoren. m n mn (4) a a Beispiel: a a Bemerkung zur einschränkenden Bedingung: Bei einigen Aufgabenstellungen im Rahmen der Anwendung der Wurzelgesetze kann zusätzlich nach einer einschränkenden Bedingung gefragt werden. Z.B. gilt 4 x 4 x nur für x 0, denn falls x negativ wäre, gilt das Gleichheitszeichen nicht mehr. Beispielsweise würde für x = -1 auf der linken Seite der Gleichung 4 4 ( 1) stehen, was gleich 1 ist und rechts würde -1 stehen, also ein Widerspruch. Somit muss man als Einschränkung x 0 angeben oder man schreibt 4 x 4 x und verwendet den Betrag. Die Gleichung x x gilt für alle reellen Zahlen x, man benötigt hier keine Einschränkung Dies gilt auch für x x. Aufgaben: 1) Schreibe mit Wurzel: x 1/3, a 1/9, b 4/5, c 0,25 2) Schreibe ohne Wurzel (mit gebrochenem Exponenten): 4 x, 3 x 9, 5 x 2 3) Ziehe teilweise die Wurzel (so weit wie möglich): 32, 75, 0, 12, 50000, 45 20, 9, a, x y, 3 a 18 b 10 Lösungen: 1) Mit Wurzel: 3 x, 9 a, 5 x 4 2) Ohne Wurzel: x 1/4, x 9/3 = x 3, x 2/5, 4 c 3) Teilweises Wurzelziehen:
24 Seite ,12 0,04 3 0,04 3 0, = = a 3 10 a x y = x x y y x y x y a b a b b a 6 b 3 3 b Wie man sieht, sollte bei der dritten Wurzel der Exponent durch drei teilbar sein. Bemerkung: Lösung einer Gleichung der Form x n = a (mit xœñ): x 2 16 x = 4 oder x = -4 (also x 1 = 4 und x 2 = -4), denn 4 2 = 16 und (-4) 2 = 16. Also sieht man, dass falls a > 0 und n gerade ist, zwei Lösungen existieren. Wenn a = 0 ist, existiert nur eine Lösung (x = 0) und wenn a < 0 wäre, ergäbe sich keine Lösung: x 4 = -8 hätte keine Lösung. Weitere Beispiele: x 4 = 16 4 x = 2 oder x = -2. x 3 = 8 3 x = 2 Hier gibt es nur eine Lösung, denn (-2) 3 = -8.
25 Seite 25 Somit hätte die Gleichung x 3 = -8 die Lösung x = -2. Die Gleichung x n = a hat für ungerades n also immer genau eine Lösung, selbst wenn a negativ ist. Aufgaben: a) x 3 = b) x 4 = 81 c) 2x = 35 d) x 6 = -1 e) x 2/3 = 4 Lösungen: a) x 3 = x = b) x 4 = 81 4 x = 4 81 Somit ist x = 3 oder x = -3, bzw. x 1 = 3 und x 2 = -3. c) 2x = x 4 = 32 : 2 x 4 = 16 4 Somit ist x = 2 oder x = -2, bzw. x 1 = 2 und x 2 = -2. d) x 6 = -1 6 Keine Lösung! e) x 3/5 = 8 ( ) 5/3 x = 8 5/ =
26 Seite 26 6 Logarithmen Mit einem Logarithmus kann man Gleichungen der Form b = a x lösen (mit a > 0 und b > 0). Zu einem Logarithmus gehört immer eine Basis. log a (x) ist der Logarithmus von x zur Basis a und ist die Umkehrfunktion von a x. Damit gilt log a (a x ) = x. Nun kann man die obige Gleichung durch Anwendung des log a auf beide Seiten lösen: b = a x log a x = log a (b) Damit wäre log 10 (1000) die Lösung der Gleichung 10 x = Es gilt somit log 10 (1000) = 3. Weiterhin gilt: log a (a) = 1 und log a (1) = 0 (da a 0 = 1). Aufgaben: log 2 (4), log 3 (27), log 2 ( 2 ), log 10 (0,001), log 5 (1/25), log 10 ( ), log 3 (1/ 3) Lösungen: log 2 (4) = log 2 (2 2 ) = 2, log 3 (27) = log 3 (3 3 ) = 3, log 2 ( 2 ) = log 2 (2 1/2 ) = 1/2, log 10 (0,001) = log 10 (10-3 ) = -3, log 5 (1/25) = log 5 (1/5 2 ) = log 5 (5-2 ) = -2, log 10 ( ) = 6, log 3 (1/ 3) = log 3 (3-1/2 ) = -1/2 Zu den bekanntesten Logarithmen zählen lg(x) = log 10 (x) und ln(x) = log e (x), wobei e die Euler sche Zahl ist. Es gelten folgende Gesetz (die sich von den Potenzgesetzen ableiten lassen): (1) log a (c x ) = xÿlog a (c) (2) log a (bÿc) = log a (b) + log a (c) (3) log a (b/c) = log a (b) - log a (c) Aus (3) folgt: log a (1/c) = log a (1) log a (c) = - log a (c).
27 Seite 27 Mit dem Gesetz (1) könnte man die Gleichung 5 x = 28 auch ohne den Logarithmus zur Basis 5 lösen und einen beliebigen Logarithmus verwenden: 5 x = 28 lg xÿlg(5) = lg(28) : lg(5) x = lg(28)/lg(5) º 2,070 Damit wäre log 5 (28) das gleiche wie lg(28)/lg(5) oder wie ln(28)/ln(5). Aufgaben: log a (10a), log a (aÿb 3 ), log a (c 4 /d 3 ), log a ( 5 a ), log b c a 5 d, 10000a lg 3 b c Lösungen: log a (10a) = log a (10) + log a (a) = log a (10) + 1 log a (aÿb 3 ) = log a (a) + log a (b 3 ) = 1 + 3ÿlog a (b) log a (c 4 /d 3 ) = log a (c 4 ) - log a (d 3 ) = 4ÿlog a (c) - 3ÿlog a (d) log a ( 5 a ) = log a (a 5/2 ) = 5/2 3 4 b c log a = log 5 a (b 3 ÿc 4 ) - log a (d 5 ) = log a (b 3 ) + log a (c 4 ) - log a (d 5 ) d = 3ÿlog a (b) + 4ÿlog a (c) - 5ÿlog a (d) 10000a lg 3 b c 5 = lg(10000a 5 ) - lg(b 3 ÿc 1/2 ) = lg(10000) + lg(a 5 ) (lg(b 3 ) + lg(c 1/2 )) = 4 + 5ÿlg(a) 3ÿlg(b) 1/2ÿlg(c) Aufgaben: Gesucht ist die Lösung der Gleichung: a) 8 x = 20 b) 5 x+1 = 125 c) 2ÿ3 x = 28 d) 5ÿ3 x = 4 x-2 e) 4 2x+1 = 64 f) log 2 (x+5) = 3
28 Seite 28 Lösungen: a) 8 x = 20 log 8 x = log 8 (20) º 1,441 Falls der Taschenrechner nur eine lg-taste besitzt: 8 x = 20 lg xÿlg(8) = lg(20) :lg(8) x = lg(20)/lg(8) b) 5 x+1 = 125 log 5 x+1 = 3-1 x = 2 c) 2ÿ3 x = 28 :2 3 x = 14 log 3 x = log 3 (14) º 2,402 d) 5ÿ3 x = 4 x+1 log 4 log 4 (5) + xÿlog 4 (3) = x + 1 Nun sollte man alle Terme mit x auf eine Seite bringen und die Zahlen ( ohne x ) auf die andere Seite: Nun x ausklammern: log 4 (5) + xÿlog 4 (3) = x + 1 -x - log 4 (5) xÿlog 4 (3) - x = 1 - log 4 (5) xÿ(log 4 (3) - 1) = 1 - log 4 (5) : (log 4 (3) - 1) x = (1 - log 4 (5) )/ (log 4 (3) - 1) x º 0,7757
29 Seite 29 e) 4 2x+1 = 64 Lösung: x = 1 (klar, da 64 = 4 3 ist, muss 2x+1 = 3 sein) f) log 2 (x+5) = 3 Da log (x) a a x gilt, kann man auf beide Seiten die Funktion f(x) = 2 x anwenden und erhält x + 5 = 2 3, womit die Lösung x = 3 lautet.
30 Seite 30 7 Wurzelgleichungen Bei einer Wurzelgleichung steht die Unbekannte unter einer Wurzel. Beispielsweise wäre x 4 eine Wurzelgleichung. Zum Lösen sollte man immer zunächst versuchen, die Wurzel zu isolieren, damit diese alleine auf einer Seite steht. Dies ist beim oberen Beispiel schon der Fall. Danach quadriert man beide Seiten: x 4 () 2 x = 16 Das Quadrieren ist aber keine Äquivalenzumformung, d.h. die Lösungsmenge ist nach dem Quadrieren nicht unbedingt mehr die gleiche wie vor dem Quadrieren, weshalb man bei Wurzelgleichungen immer eine Probe machen muss, bevor man die Lösungsmange angibt. Würde man z.b. x = 4 auf beiden Seiten quadrieren, so würde sich x 2 = 16 ergeben. Diese neue Gleichung hat nun aber 2 Lösungen, nämlich 4 und -4. Weiteres Beispiel: x 4 () 2 x = 16 Probe (dazu setzt man x = 16 in die ursprüngliche Gleichung ein): 16? 4 Dies ist ein Widerspruch, denn die Wurzel aus 16 ist 4. Damit wäre die Lösungsmenge leer: L = {}. Weitere Beispiele: x Zunächst isolieren wir die Wurzel, bevor wir quadrieren: x x 2 3 () 2 x + 2 = 9-2 x = 7
31 Seite 31 Probe: ? 3 1 = 2 ist richtig! Somit ist x = 7 die Lösung: L = {7} x 8 x 4 () 2 Beim Quadrieren wird, wie beschrieben, immer die komplette Seite quadriert: x + 8 = (x 4) 2 Hier muss die binomische Formel angewendet werden: Nun können wir die p-q-formel anwenden: x + 8 = x 2 8x x 8 0 = x 2 9x + 8 x 1/2 = 9/2 81/ 4 8 9/2 7/2 Also ist x 1 = 8 und x 2 = 1. Wir machen die Probe: Für x = 8: = 4 Somit ist x = 8 eine Lösung. Für x = 1: = -3 Somit ist x = 3 keine Lösung. Es gilt also: L = {8}?? Es gibt auch Wurzelgleichungen, bei denen man zunächst die Wurzeln nicht isolieren kann, wie beispielsweise: x 4 2 x 4 In so einem Fall ist es das Beste, wenn beide Wurzeln (wie hier) auf verschiedenen Seiten stehen. Wir bestimmen die Lösung: x 4 2 x 4 () 2
32 Seite 32 x x 4 2 (Achtung: Links binomische Formel anwenden.) Nun kann man die Wurzel isolieren: 2 2 x x 4 2 x 4 x x = x 4 x - 4 x = x 4 x - 4 x = x 4 -x -8 (*) - 4 x 4 = -12 :(-4) x 4 = 3 () 2 x + 4 = 9-4 x = 5 Bemerkung: Bei (*) hätte man nicht unbedingt durch (-4) teilen müssen, man hätte auch direkt quadrieren können und hätte 16(x+4) = 144 erhalten, da für Produkte (aÿb) 2 = a 2 ÿb 2 gilt. Nun machen wir noch die Probe: = 1 Die Gleichung ist erfüllt und wir kennen die Lösungsmenge: L = {5}? Aufgaben: a) 2x b) 2 x c) 3x 7 1 2x 3 d) 2x 1 2 4x 5 Lösungen: a) L = {4} b) L = {5} c) L = {3} d) L = {1; 5}
33 Seite 33 8 Bruchgleichungen Bei einer Bruchgleichung steht die Unbekannte im Nenner eines Bruches. Beispielsweise: 12 x Bei Bruchgleichungen legt man zunächst den Definitionsbereich fest. Es sind alle reellen Zahlen (oder rationalen Zahlen, je nachdem von welcher Grundmenge man ausgeht) als Lösung möglich, außer die, bei denen der Nenner Null werden würde. Dies wäre hier die 0. Somit ist der Definitionsbereich bekannt: à = R \ {0} (oder à = Q \ {0}) Im Folgenden gehen wir immer von den reellen Zahlen als Grundmenge aus. Lösen können wir die obige Bruchgleichung, wenn wir diese (d.h. beide Seiten der Gleichung) mit dem Nenner multiplizieren, also mit x: ÿx x 12 = 3x :3 x = 4 Nun liegt 4 im Definitionsbereich und ist somit eine Lösung der obigen Gleichung: L = {4} Weitere Beispiele: 6 2 x 1 Der Nenner wird gleich Null, wenn x + 1 = 0 ist bzw. wenn x = -1 ist: à = R \ {-1} 6 2 x 1 ÿ(x + 1) 6 = 2(x + 1) 6 = 2x = 2x :2 x = 2 L = {2}
34 Seite x 1 x 1 Ã = R \ {-1; 1} Wir erhalten: x 1 x 1 ÿ(x + 1)(x - 1) 4 4 (x 1)(x 1) (x 1)(x 1) 3 (x 1)(x 1) x 1 x 1 Jetzt kürzt sich jeweils der Nenner heraus: 4(x - 1) + 4(x + 1) = 3(x 2 1) 8x = 3x 2 3-8x 3x 2 8x 3 = 0 :3 x 2 8/3x 1 = 0 Nun können wir die p-q-formel anwenden: x 1/2 = 4/3 16 / 9 1 4/3 5/3 Also ist x 1 = 3 und x 2 = -1/3. L = {-1/3; 3} Es folgt noch ein letztes Beispiel: 3 1 2x 4 x 2 3 x 2 4 Der Definitionsbereich wird bestimmt, indem wieder geprüft wird, für welche x die Nenner gleich Null werden: 2x + 4 = 0 ergibt x = -2. x 2 = 0 ergibt x = 2. x 2 4 = 0 ergibt x = 2 oder x = -2.
35 Seite 35 Nun ist à = R \ {-2; 2}. Im ersten Nenner (von links) kann man auch 2(x + 2) und in dem Nenner auf der rechten Seite kann man auch (x 2)(x + 2) schreiben (Anwendung der binomische Formel, bzw. Darstellung als Linearfaktoren siehe Bemerkung 2 unten). Dadurch kann man die Gleichung mit 2(x 2)(x + 2) multiplizieren, was dem Hauptnenner entspricht: (x 2) x 2 (x 2)(x 2) ÿ2(x 2)(x + 2) 3(x 2) 1ÿ2(x + 2) = - 3ÿ2 x 10 = x = 4 Also L ={4}. Bemerkungen: 1) Hätte der zweite Bruch auf der linken Seite der Gleichung die Form 1 man ihn mit (-1) erweitern können und hätten erhalten. x x gehabt, so hätte 2) Liegen beispielsweise zwei Nullstellen x 1 und x 2 vor, so kann man die Gleichung (d.h. beide Seiten der Gleichung) mit (x x 1 )(x x 2 ) multiplizieren. Im Beispiel oben hätte somit auch der Faktor (x 2)(x + 2) genügt. Aufgaben: a) 8 4 x 3 b) 5 x 3 8 x 6 c) 4 x 1 x 2 d) x 2 x 1 e) 4 2 x 1 x 1 16 x 2 1
36 Seite 36 Definitionsbereiche und Lösungen: a) Ã = Ñ \ {3}; L ={5} b) Ã = Ñ \ {-6; -3}; L ={2} c) Ã = Ñ \ {-2}; L ={-3; 2} d) Ã = Ñ \ {-2; -1}; L ={-3/2; 2} e) Ã = Ñ \ {-1; 1}; L ={3}
37 Seite 37 9 Binomische Formeln Die folgenden drei Formeln sind als die binomischen Formeln in der Schule bekannt: (1) (a + b) 2 = a 2 + 2ab + b 2 (2) (a - b) 2 = a 2-2ab + b 2 (3) (a + b)(a b) = a 2 - b 2 Durch ausmultiplizieren kann man diese leicht herleiten. Z.B.. (a + b) 2 = (a + b)(a + b) = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2 Beispiele: (x + 5) 2 = x 2 + 2ÿ5ÿx = x x + 25 (x - 2)(x + 2) = x = x 2 4-2ÿ(x -3) 2 = -2ÿ(x 2-2ÿ3ÿx ) =-2x x - 18 (4x + 3y) 2 = (4x) 2 + 2ÿ4xÿ3y + (3y) 2 = 16x xy + 9y x y x 2x y y x 2x y y x y x y x y x y (2x + 3y) 2 (3x - 5y) 2 = 4x xy + 9y 2 (9x 2-30xy + 25y 2 ) = 4x xy + 9y 2 9x 2 +30xy - 25y 2 = -5x xy -16y 2 Wie man sieht, würde bei einem dritten Binom (Formel (3)) die Wurzel verschwinden. Dies kann man bei der folgenden Aufgabe verwenden: Der Nenner soll rational werden (d.h. im Nenner soll keine Wurzel mehr stehen bzw. keine, die eine irrationale Zahl ergäbe): Hier muss man diesen Bruch so erweitern, dass im Nenner das dritte Binom steht:
38 Seite (4 3) (4 3)(4 3) Aufgaben: a) Wende die binomischen Formeln an: (4x + 3) 2 (2x - 9)(2x + 9) -5ÿ(x -4) 2 (-2x + 5y) 2 (-a b) 2 2 x y 2 x 3 y x 3 y (4x - 2y) 2 + 2(x + 5y) 2 b) Rationalisiere den Nenner: 8 4 a a 2 b b Lösungen: a) (4x + 3) 2 = 16x x + 9 (2x - 9)(2x + 9) = 4x ÿ(x - 4) 2 = -5ÿ(x 2 8x + 16) = -5x x - 80 (-2x + 5y) 2 = (5y - 2x) 2 = 25y 2 20xy + 4x 2 (-a b) 2 = (-1) 2 (a + b) 2 = (a + b) 2 = a 2 + 2ab + b x y 2 x 2 2 x y y 4x 4 xy y
39 Seite 39 x 3 y x 3 y = x 2 9y (4x - 2y) 2 + 2(x + 5y) 2 = 16x 2 16xy + 4y 2 + 2(x xy + 25y 2 ) = 18x 2 + 4xy +54y 2 b) a b a b a b a 2a b 2 a b a b a b a b 2 b Bemerkung zur Berechnung von (a + b) n für beliebige (natürliche) Potenzen n: (x + y) 3 könnte man auflösen, wenn man (x + y) 2 (x + y) berechnen würde. Man kann aber auch das so genannte Pascal sche Dreieck verwenden, in dem man die Koeffizienten für beliebige Potenzen ablesen kann. Hier ist das Pascal sche Dreieck bis zur Potenz n = 4 zu sehen: Zur Konstruktion des Pascal schen Dreiecks: Man beginnt mit den oberen drei Einsen und schreibt links und rechts weitere Einsen hin. Danach erhält man jeweils eine Zeile, wenn man zwischen den Einsen links und rechts jeweils die Zahlen in der Spalte darüber addiert. Diese Summe schreibt man dann immer in die Mitte unter den beiden addierten Zahlen. Für n = 2 ergibt sich die 2 aus der Summe der beiden Einsen darüber, u.s.w.. Nun können wir (x + y) 3 berechnen. Wir beginnen in der unteren Summe mit x 3 = x 3 y 0, danach nimmt der Exponent von x um eines ab und der von y um eins zu, bis man bei y 3
40 Seite 40 angelangt ist. Vor die Summanden schreibt man dann die Koeffizienten aus dem Pascal schen Dreieck aus der Zeile für n = 3: (x + y) 3 = 1ÿx 3 + 3ÿx 2 y + 3ÿxy 2 + 1ÿy 3 = x 3 + 3x 2 y + 3xy 2 + y 3 Für (x - y) 3 geht man genauso vor, nur dass hier das Vorzeichen wechselt, wobei man mit einem positiven Vorzeichen beginnt: (x - y) 3 = +1ÿx 3-3ÿx 2 y + 3ÿxy 2-1ÿy 3 = x 3-3x 2 y + 3xy 2 - y 3 Noch ein Beispiel: (2x + 3y) 3 = 1ÿ(2x) 3 + 3ÿ(2x) 2 ÿ3y + 3ÿ2xÿ(3y) 2 + 1ÿ(3y) 3 = 8x x 2 y + 54xy y 3
41 Seite Lineare Gleichungssysteme mit zwei Unbekannten Wie beginnen mit einem Beispiel: Gesucht ist die Lösung des folgenden Gleichungssystems: (I) 2x y = 4 (II) x + y = 5 Hier stehen eine Reihe von Verfahren zur Verfügung. In diesem Beispiel würde sich das Additionsverfahren anbieten. Dabei werden die beiden linken und die beiden rechten Seiten der Gleichungen addiert: (I) + (II) 3x = 9 Die Variable y ist entfallen. Nun können wir die Gleichung nach x auflösen und erhalten x = 3. Diese Lösung können wir nun in (I) oder in (II) einsetzen und erhalten y: In (II) 3 + y = 5-3 y = 2 Also ist x = 3 und y = 2. Im Allgemeinen muss man die Gleichungen (I) und (II) mit geeigneten Zahlen multiplizieren, so dass man dass Additionsverfahren anwenden kann. Beispiel: (I) 3x 4y = 2 (II) 2x + y = 5 Hier könnte man die zweite Gleichung mit 4 multiplizieren, damit nach einer Additino der beiden Gleichungen die Variable y entfällt. Nun können wir addieren: (I) 3x 4y = 2 4ÿ(II) 8x + 4y = 20 (I) + 4ÿ(II) 11x = 22 : 11 x = 2 In (II) einsetzen ergibt: 2ÿ2 + y = 5. Also ist y = 1.
42 Seite 42 Ein weiteres Beispiel: (I) 2x 5y = 3 (II) 3x + 8y = 20 Hier könnte man die zweite Gleichung mit -2 und die erste Gleichung mit 3 multiplizieren. Danach kann man y durch Addition eliminieren. 3ÿ(I) 6x - 15y = 9-2ÿ(II) -6x - 16y = -40 Eine Addition ergibt: -31y = -31, womit y = 1 ist. Setzt man y = 1 z.b. in (I) ein, erhält man: Also ist x = 4 und y = 1. 2x 5 = x = 8 :2 x = 4 Neben dem Additionsverfahren gibt es auch das Subtraktionsverfahren, was sich aber auf das Additionsverfahren zurückführen lässt (wenn man eine Gleichung mit -1 multipliziert). Hätte man oben die Gleichung (II) statt mit -2 mit 2 multipliziert, so könnte man das Subtraktionsverfahren anwenden: 6x - 15y = 9 6x + 16y = y = -31 Es ergibt sich dieselbe Gleichung wie oben. Wenn also zwei Koeffizienten einer Variablen gleich sind, kann man das Subtraktionsverfahren verwenden und bei verschiedenen Vorzeichen das Additionsverfahren. Ist eine der beiden Gleichungen nach einer Variablen aufgelöst, so kann man das Einsetzungsverfahren anwenden: (II) in (I) einsetzen ergibt: (I) 2x 3y = 3 (II) y = x 2 2x - 3ÿ(x 2) = 3 -x + 6 = 3-6 -x = -3 :(-1) x = 3 Nun kann man x = 3 in (II) einsetzen und erhält y = 3 2 = 1.
43 Seite 43 Liegen beide Gleichungen in der nach derselben Variablen aufgelösten Form vor, so kann man das Gleichsetzungsverfahren anwenden: Gleichsetzen ergibt: (I) y = 2x - 4 (II) y = 4x + 4 2x 4 = 4x x = 4x + 8-4x -2x = 8 :(-2) x = -4 Nun kann man x = -4 in (I) oder (II) einsetzen. Wir setzen in (I) ein und erhalten y = 2ÿ(-4) 4 = -12. Die Lösung eines Gleichungssystems mit 2 Unbekannten kann man als Schnittpunkt zweier Geraden interpretieren. Somit kann man die Lösungsmenge wie folgt angeben: L = {(-4; -12)} Im obigen Beispiel sehen die Geraden wie folgt aus:
44 Seite 44 Spezialfälle: Nun könnte es passieren, dass beide Geraden parallel sind. In diesem Fall hätten wir keine Lösung. Wenn beide Geraden aufeinander liegen würden, hätte man unendliche viele Lösungen, nämlich alle Punkte auf der Geraden. Beispiele: (I) y = 2x + 4 (II) y = 2x + 8 Gleichsetzen ergibt: 2x + 4 = 2x + 8-2x 4 = 8 Dies ist ein Widerspruch, womit keine Lösung existiert, was man schon an den Gleichungen hätte sehen können, da sie zwei parallele Geraden beschreiben. Es gilt L = {}. (I) y = 2x + 4 (II) y = 2x + 4 Gleichsetzen ergibt: 2x + 4 = 2x + 4-2x 4 = 4 Die Gleichung ist für alle xœñ erfüllt. Somit wäre die Lösungsmenge durch gegeben. L = {(x; y) y = 2x + 4} Beispiel für Textaufgabe: 2 Cola und 3 Hamburger kosten 9,70. 5 Cola und 8 Hamburger kosten 25,50. Wie viel kostet eine Cola und wie viel ein Hamburger? Zu Beginn muss man die Variablen und deren Bedeutung festlegen. Wir wählen x für den Preis einer Cola und y für den Preis eines Hamburgers. Nun müsste zweimal der Preis für eine Cola und dreimal der Preis für einen Hamburger 9,70 ergeben. So können wir die beiden Gleichungen (bei zwei Variablen bzw. Unbekannten benötigen wir auch zwei Gleichungen) aufstellen, wobei wir ohne Einheiten rechnen: (I) 2x + 3y = 9,7 (II) 5x + 8y = 25,5 Wie müssen uns wieder für eine Variable entscheiden, die wie eliminieren möchten. Wir wählen x. Nun multiplizieren wir die erste Zeile mit 5 und die zweite Zeile mit 2: 5ÿ(I) 10x + 15y = 48,5 2ÿ(II) 10x + 16y = 51 Wir wenden das Subtraktionsverfahren an: 5ÿ(I) 2ÿ(II) -y = - 2,5 : (-1)
45 Seite 45 Dies setzen wir in (I) ein: y = 2,5 2x + 3ÿ2,5 = 9,7 2x + 7,5 = 9,7-7,5 2x = 2,2 :2 x = 1,1 Damit kostet eine Cola 1,10 und ein Hamburger 2,50. Bemerkungen: Man könnte immer mit einem Verfahren auskommen, wenn man zuvor die Gleichungen entsprechend umformt. Beispiel: (I) 5x + 4y = 9 (II) 2x 3y = -1 Hier würde sich eigentlich das Additionsverfahren oder Subtraktionsverfahren anbieten, man könnte aber auch die Gleichungen so umformen, dass man das Einsetzungsverfahren anwenden kann. Dabei würde es sich anbieten, die zweite Gleichung nach x aufzulösen: 2x 3y = -1 +3y 2x = y :2 x = -1/2 + 3/2y Nun könnte man das Einsetzungsverfahren anwenden und in (I) einsetzen. Beim Einsetzungsverfahren könnte man auch nach Vielfachen von x oder y auflösen (d.h. z.b. nach 2x). Beispiel: (I) 2x + 3y = -1 (II) 2x = y + 3 Hier kann man den Term 2x in Gleichung (I) durch y + 3 ersetzen, womit man die Gleichung y y = -1 bzw. 4y + 3 = -1 erhält, die man nach y auflösen kann. Dies könnte man tun, wenn man zunächst Brüche vermeiden möchte. Aufgaben: 1) a) x + y = -1 -x + y = 5 b) 2x + 3y = 11 4x 2y = 14
46 Seite 46 c) 3x + 5y = 4-4x + 8y = 24 d) y = 2x 5 2x + 3y = 9 e) 4x + 3y = 26 4x = 2y + 16 f) x = 2y + 3 x = -4y + 9 2) a) Jenny ist doppelt so alt wie Justin. Bei zusammen sind 18 Jahre alt. Wie alt sind die beiden? b) In 6 Jahren ist Tim doppelt so alt wie Jasmin. Heute ist Tim 18 Jahre älter als Jasmin. Wie alt sind beide heute? Lösungen: 1) a) L = {(-3; 2)} b) L = {(4; 1)} c) L = {(-2; 2)} d) L = {(3; 1)} e) L = {(5; 2)} f) L = {(5; 1)} 2) a) Wir wählen x = Alter Jenny und y = Alter Justin. (I) x = 2y (II) x + y = 18 (I) in (II) einsetzen: 2y + y = 18 3y = 18 :3 y = 6 In (I) einsetzen ergibt x = 12. Also ist Jenny 12 Jahre alt und Justin 6.
47 Seite 47 b) Wir wählen x = Alter Tim (heute) und y = Alter Jasmin (heute). In 6 Jahren ist Tim x + 6 Jahre alt und Jasmin y + 6 Jahre:. (I) x + 6 = 2(y + 6) (II) x = 18 + y Also ist: (I) x + 6 = 2y + 12 (II) x = 18 + y (II) in (I): 18 + y + 6 = 2y + 12 y + 24 = 2y y = 2y 12-2y -y = -12 :(-1) y = 12 Mit (II) ergibt sich x = = 30. Somit ist Tim heute 30 Jahre alt und Jasmin 12. Wenn ihr noch keine quadratischen Gleichungen behandelt habt, dann könnt ihr diesen Punkt überspringen: Beispiel für nichtlineare Gleichungssysteme mit zwei Unbekanten: Die Fläche eines Rechtecks beträgt 40cm 2 und der Umfang 26cm. Wie lange sind die Seien des Rechtecks? Es gilt für die Fläche A eines Rechtecks mit den Seitenlängen a und b: A = aÿb Für dessen Umfang gilt: U = 2a + 2b Wir rechnen ohne Einheiten: (I) aÿb = 40 (II) 2a + 2b = 26 Nun können wir z.b. die Gleichung (I) nach b auflösen: (III) b = 40/a Dies können wir in (II) einsetzen: 2a + 2ÿ40/a = 26 Immer wenn die Unbekannte im Nenner auftaucht, sollte man die Gleichung mit dem Nenner multiplizieren: 2a + 80/a = 26 ÿa 2a = 26a -26a 2a 2 26a + 80 = 0 : 2 a 2 13a + 40 = 0 Diese Gleichung kann man mit der p-q-formel lösen (diese findet ihr unter auf Seite 8 oder im Kapitel Parabeln) und man erhält:
48 Seite 48 a 1 = 5 und a 2 = 8 Mit (III) erhalten wir b 1 = 40/a 1 = 8 und b 2 = 40/a 2 = 5. Somit ist eine Seite 5cm lang und die andere 8cm.
49 Seite Lineare Gleichungssysteme mit drei oder mehr Unbekannten Wir beginnen mit einem Beispiel: (I) 2x - 3y + 2z = 2 (II) x - y + 3z = 8 (III) -3x + 2y + 2z = 7 Zum Lösen diesen Gleichungssystems kann man wie folgt vorgehen: Man wählt, wie bei linearen Gleichungssystemen mit zwei Unbekannten, eine Variable aus, die eliminiert werden soll. Danach führt man zweimal für je zwei Zeilen das Additionsverfahren bzw. Subtraktionsverfahren durch und eliminiert die ausgewählte Variable, wobei insgesamt alle drei Gleichungen verwendet werden müssen. Damit erhält man zwei Gleichungen mit zwei Unbekannten. Wir eliminieren x und subtrahieren von (I) das Zweifache von (II) und danach addieren wir das Dreifache der Gleichung (II) zu (III): (I) - 2ÿ(II) -y - 4z = -14 (*) (III) + 3ÿ(II) -y + 11z = 31 Nun können wir z.b. die beiden neu entstanden Gleichungen subtrahieren (falls wir als nächstes y eliminieren möchten) und erhalten -15z = -45 :(-15) z = 3 Nun können wir z = 3 in eine der beiden Gleichungen mit nur 2 Unbekannten einsetzen. Wir setzen z = 3 in die Gleichung (*) ein und erhalten: -y - 12 = y = -2 : (-1) y = 2 Nun können wir die Lösung für y und z in eine der drei Gleichungen (I), (II) oder (III) einsetzen und erhalten x. Wir setzen in (II) ein: x ÿ3 = 8 x + 7 = 8-7 x = 1 Somit ist x =1, y = 2 und z = 3, also ist L = {(1; 2; 3)}.
50 Seite 50 Analog würde man bei 4 Unbekannten und 4 Gleichungen erst eine Variable eliminieren und aus 4 Gleichungen mit 4 unbekannten 3 Gleichungen mit 3 Unbekannten erhalten. Falls nicht alle Variablen in jeder Gleichung vorkommen, hat man Schritte gespart, wenn man zunächst eine fehlende Variable eliminiert. Z.B. bei: (I) 2y + z = 3 (II) 2x + 3y + z = 7 (III) -2x + 2y + 4z = -2 Hier sollte man x eliminieren. Da die Gleichung (I) kein x enthält muss man nur noch die Gleichungen (II) und (III) addieren und man hat zwei Gleichungen mit zwei Unbekannten y und z. Bemerkung: Den Gauß-Algorithmus zum Lösen linearer Gleichungssystem findet ihr auf Seite 18 unter Dieser wird aber in der dort beschriebenen Version (mit Tableau) oft erst in der Oberstufe behandelt.
51 Seite Trigonometrie 12.1 Grundlagen Die Ecken eines Dreiecks werden üblicherweise mit Großbuchstaben bezeichnet. Dabei beginnt man in einer Ecke mit A und geht von dieser Ecke gegen den Uhrzeigersinn zur nächsten Ecke, die dann mit B bezeichnet wird. Die Seiten gegenüber den Ecken werden dann mit denselben - aber kleinen - Buchstaben bezeichnet. Für die Winkel in den Ecken nimmt man griechische Buchstaben. Bei A steht a ( Alpha ), bei B steht b ( Beta ) und bei C steht g ( Gamma ). Die Winkelsumme in jedem Dreieck beträgt 180 : a + b + g = 180 Sind alle drei Seiten gleich groß, so spricht man von einem gleichseitigen Dreieck. Hier wären dann auch alle Winkel gleich groß. Es gilt dann a = b = g = 60. Bei einem gleichschenkligen Dreieck sind 2 Seiten gleich groß und es stimmen zwei Winkel überein. Wenn z.b. a = b ist, dann wären die Winkel a und b gleich. In diesem Fall nennt man die Seite c die Basis und die Seiten a und b sind die Schenkel.
52 Seite Pythagoras Kommen wir als nächstes zum Satz von Pythagoras. Dieser gilt in rechtwinkligen Dreiecken, d.h. in Dreiecken, bei denen einer der Winkel gleich 90 beträgt. Wenn g = 90 ist, so würde der Satz des Pythagoras wie folgt lauten: c 2 = a 2 + b 2 Die Seite gegenüber dem rechten Winkel heißt Hypotenuse. Wenn g = 90 ist, ist c die Hypotenuse. Die anderen beiden Seiten heißen Katheten. Wenn g = 90 ist, wären die Seiten a und b die Katheten. Allgemein sagt der Satz von Pythagoras, dass das Quadrat der Hypotenuse gleich der Summe der Quadrate der Katheten ist. Wenn a = 90 wäre, würde dann a 2 = b 2 + c 2 gelten, da dann a die Hypotenuse wäre. Die Hypotenuse ist immer die längste Seite im rechtwinkligen Dreieck. Sind nun in einem rechtwinkligen Dreieck zwei Seiten bekannt, so kann die dritte berechnet werden. Beispiele: Es sei g = 90, a = 3cm und b = 4cm. Wir rechnen erst mal ohne Einheiten: a 2 + b 2 = c = c = c 2 25 = c 2 c = 5 Also ist c = 5cm. Wir rechnen noch mal mit Einheiten: a 2 + b 2 = c 2 (3cm) 2 + (4cm) 2 = c 2
53 Seite 53 9cm cm 2 = c 2 25cm 2 = c 2 c = 5cm (Hier benötigen wir nur die positive Lösung, da es sich um Dreiecksseiten handelt.) Es sei g = 90, c = 13cm und b = 12cm. a 2 + b 2 = c 2 a 2 + (12cm) 2 = (13cm) 2 a cm 2 = 169cm 2-144cm 2 a 2 = 25cm 2 a = 5cm Aufgaben: 1) a) g = 90, a = 8m und b = 6m. b) g = 90, a = 2dm und c = 5dm. c) b = 90, a = 3cm und c = 6cm. d) a = 90, a = 1,3m und b = 1,2m. 2) a) Wie groß ist die Diagonale in einem Quadrat mit der Katenlänge 10cm? b) Wie groß ist die Diagonale eines Monitors der 40cm breit und 30cm hoch ist? c) Eine 10m lange Leiter wird an eine Wand gelehnt. Sie soll auf dem Boden einen Abstand von 3m von der Wand haben. Wie hoch kommt man mit dieser Leiter? d) Ein gleichseitiges Dreieck hat eine Seitenlänge von 6cm. Wie groß ist die Höhe? Lösungen: 1) a) c = 10m b) b º 4,58dm c) b º 6,71cm d) c = 0,5m 2) a) d 2 = a 2 + a 2. Dies ergibt d º 14,14cm. Man kann auch direkt eine Formel für die Diagonale im Quadrat mit Seitenlänge a aufstellen: d 2 = 2a 2 d = 2 a
54 Seite 54 b) d 2 = a 2 + b 2. Dies ergibt d = 50cm. c) Die Leiter ist die Hypotenuse (siehe Skizze). Somit gilt: Damit ergibt sich: h 9,54m (10m) 2 = (3m) 2 + h 2
55 Seite 55 d) Wenn a die Seitenlänge ist, so gilt für die Höhe h: Damit ergibt sich: h 5,20cm a 2 = (a/2) 2 + h 2 (6cm) 2 = (3cm) 2 + h 2 Man kann hier auch eine Formel für die Höhe h in einem gleichseitigen Dreieck mit Seitenlänge a aufstellen: a 2 = (a/2) 2 + h 2 a 2 = 1/4a 2 + h 2-1/4a 2 3/4a 2 = h 2 h = 3 / 2 a
56 Seite Höhensatz und Kathetensatz von Euklid Im Folgenden sei g = 90. h ist die Höhe auf c (d.h. h = h c ). Die Höhe teilt die Hypotenuse in zwei Stücke, wobei das unter der Kathete a mit p und das unter der Kathete b mit q bezeichnet wird (siehe obere Grafik). Nun gilt der Höhensatz von Euklid h 2 = pÿq, sowie die Kathetensatz von Euklid: a 2 = cÿp und b 2 = cÿq Es gilt natürlich c = p + q. Außerdem könnte man dreimal den Satz von Pythagoras anwenden: c 2 = a 2 + b 2 a 2 = p 2 + h 2 b 2 = q 2 + h 2 Beispiele: Es sei a = 8cm und c = 10cm. Gesucht sind alle fehlenden Teile (b, p, q und h): Wie müssen eine Formel verwenden, bei der nur eine Unbekannte vorkommen würde, z.b. Pythagoras (im großen Dreieck) oder den Kathetensatz a 2 = cÿp. Wir setzen in den Kathetensatz ein: a 2 = cÿp (8cm) 2 = 10cmÿp 64cm 2 = 10cmÿp :10cm p = 6,4cm
57 Seite 57 Mit p und c kann man immer q berechnen: c = p + q 10cm = 6,4cm + q -6,4cm q = 3,6cm Nun können wir mit dem Höhensatz b berechnen: b 2 = cÿq b 2 = 10cmÿ3,6cm b 2 = 36cm b = 6cm Zuletzt bestimmen wir noch h mit dem Höhensatz: h 2 = pÿq h 2 = 6,4cmÿ3,6cm h 2 = 23,04cm 2 h = 4,8cm Bemerkung: Wie man sieht, muss man sich immer nur eine Gleichung heraussuchen, bei der 2 Größen bekannt sind bzw. nur eine unbekannt ist. Es gibt aber auch Spezialfälle, bei denen dies nicht geht. Beispielsweise wenn p = 6cm und b = 4cm wäre. Hier müsste man zwei Gleichungen aufstellen (wir rechnen hier der Einfachheit halber ohne Einheiten): a 2 = cÿp a 2 = 6c (*) Nun benötigen wir noch eine Gleichung, wo nur a und c fehlt: c 2 = a 2 + b 2 c 2 = a Nun setzen wir (*) in die obige Gleichung ein: c 2 = 6c + 16
58 Seite 58 Wir bringen alles auf eine Seite : c 2 6c 16 = 0 Nun können wir die p-q-formel für quadratische Gleichungen anwenden: c 1/2 = Also ist c 1 = 8 und c 2 = -2, womit c gleich 8cm lang ist. Damit erhalten wir alle anderen Größen: q = c p = 8cm 6cm = 2cm a 2 = cÿp a 2 = 8cmÿ6cm a 2 = 48cm 2 a º 6,93cm h 2 = pÿq h 2 = 6cmÿ2cm h 2 = 12cm 2 h º 3,46cm Aufgaben: Bestimme alle fehlenden Größen: a) p = 9cm, q = 4cm b) a = 9m, c = 15m c) p = 2cm, c = 10cm d) a = 5dm, b = 8dm Lösungen: a) h = 6cm, c = 13cm, a º 10,82cm, b º 7,21cm b) b = 12m, h = 7,2m, p = 5,4m, q = 9,6m c) q = 8cm, a º 4,47cm, b º 8,94cm, h = 4cm d) c º 9,43dm, h º 4,24dm, p º 2,65dm, q º 6,78dm
59 Seite Berechnung von Winkeln und Seiten im rechtwinkligen Dreieck mit Sinus, Kosinus und Tangens Sind in einem rechtwinkligen Dreieck zwei Seiten bekannt, oder eine Seite und ein zusätzlicher Winkel (außer dem, der 90 beträgt), dann kann man alle anderen Seiten und Winkel berechnen. Dazu kann man die trigonometrischen Funktionen Sinus (sin), Kosinus (cos) oder Tangens (tan) verwenden. Hier muss man allerdings noch mal zwischen den beiden Katheten unterscheiden. Die Kathete, die an dem Winkel anliegt, den man berechnen oder verwenden möchte, heißt Ankathete und die andere heißt Gegenkathete. Wenn g = 90 ist, so wäre c die Hypotenuse. Von a aus betrachtet ist dann b die Ankathete (da b an diesem Winkel anliegt) und a die Gegenkathete. Von b aus ist es umgekehrt, denn hier ist a die Ankathete und b die Gegenkathete. Nun gelten folgende Beziehungen zwischen den Winkel und den Seiten: Gegenkathete sin( ) Hypotenuse Ankathete cos( ) Hypotenuse Gegenkathete tan( ) Ankathete D.h. in einem Dreieck mit c als Hypotenuse gilt: sin( ) cos( ) tan( ) a c b c a b sin( ) cos( ) tan( ) b c a c b a
60 Seite 60 Beispiele: g = 90 ; a = 6cm; c = 10cm. Gesucht wird. Wir haben somit die Hypotenuse und eine Kathete gegeben. Von aus betrachtet ist a die Gegenkathete, womit wir den Sinus verwenden: sin( ) 6cm 10cm sin( ) 0,6 sin -1 Wir wenden oben die Umkehrfunktion des Sinus an, um den Winkel zu erhalten: g = 90 ; b = 6cm; = 40. Gesucht wird a. = sin -1 (0,6) º 36,87 Hier sind die beiden Katheten gegeben, was ein Fall für den Tangens ist: a tan( 40 ) ÿ6cm 6cm a = 6cmÿtan(40 ) º 5,03cm a = 90 ; b = 8cm; b = 30 Gesucht wird a. Hier ist a die Hypotenuse und von b aus ist b die Gegenkathete. Wie müssen somit den Sinus verwenden: 8cm sin( 30 ) ÿa a aÿsin(30 ) = 8cm :sin(30 ) 8cm a 16cm sin(30) Gesucht wird x in der nächsten Grafik.
61 Seite 61 x ist hier die Gegenkathete und 50m ist die Länge der Ankathete. Also muss der Tangens verwendet werden: x tan( 20 ) ÿ50m 50m x = 50mÿtan(20 ) º 18,20m Bemerkung: Ist neben dem rechten Winkel ein weiterer Winkel bekannt, so kennt man alle Winkel, denn es gilt allgemein: a + b + g = 180 Wenn nun z.b. 90 ist, dann wäre a + b + 90 = 180, bzw. es gilt dann: a + b = 90 Aufgaben: 1) Berechne alle fehlenden Seiten und Winkel: a) 90 ; a = 8cm; c = 12cm b) 90 ; a = 5dm; a = 40 c) 90 ; b = 5m; a = 30 d) 90 ; a = 5mm; b = 7mm e) a = 90 ; g = 60 ; c = 8m 2) Berechne h und alle Winkel in den Ecken (a ist der Winkel in der Ecke A, ). Es sei a = 12cm; c = 6cm; b = d = 5cm
62 Seite 62 3) Ein Baum wirft einen 5m langen Schatten. Die Sonnenstrahlen treffen unter einem Winkel von 40 auf die Erde auf. Wie hoch ist der Baum? 4) Auf einem Schild steht 5% Steigung. a) Wie groß ist der Neigungswinkel der Straße? b) Wenn man auf dieser Straße 80m fährt, welcher Höhenunterschied ergibt sich dann? Lösungen: 1) a) a º 41,81 ; b º 48,19 ; b º 8,94cm b) b = 50 ; b º 5,96dm; c º 7,78dm c) b = 60 ; a º 2,89m; c º 5,77m d) a º 35,54 ; b º 54,46 ; c = 8,6mm e) b = 30 ; a º 9,24m; b º 4,62m 2) Wegen der Symmetrie des Trapezes (b = d) kann man zunächst x berechnen. Es gilt: 2x + c = a 2x + 6cm = 12cm -6cm 2x = 6cm :2 x = 3cm Somit kann man h über Pythagoras berechnen: Die Lösung ist h = 4cm. b 2 = x 2 + h 2 (5cm) 2 = (3cm) 2 + h 2 Es gilt außerdem (da in dem Dreieck mit den Seiten x, h und d die Seite d die Hypotenuse ist und die Seite x von a aus die Ankathete): cos( ) x d 3cm 5cm
63 Seite 63 Dies ergibt a º 53,13. Wegen der Symmetrie ist b º 53,13. Da auch g = d ist und a + b + g + d = 180 gilt (Winkelsumme im Viereck), ist g = d º 126,87. 3) Die Höhe des Baumes sei h (siehe Grafik). Es gilt: tan( 40 ) h 5m Somit ist h º 4,20m und der Baum ist ca. 4,2m hoch. 4) Skizze: Für die Steigung in Prozent (p) gilt (wenn c die Hypothenuse wäre, ist p = b/aÿ100%): p = tan(a)ÿ100% Also ist 5% = tan(a)ÿ100% und somit tan(a) = 0,05, womit sich a º 2,86 ergibt. Außerdem gilt: sin( ) h 80m Also ist h º 4,00m, womit ein Höhenunterschied von ca. 4m bewältigt wird.
64 Seite Sinussatz Den Sinussatz kann man allgemein in Dreiecken auch ohne rechte Winkel anwenden. Speziell kann man den Sinussatz anwenden, wenn ein Winkel, eine gegenüberliegende Seite und ein weiterer Winkel oder eine weitere Seite bekannt ist. Der Sinussatz besagt, dass das Verhältnis von Seite zu ihrem gegenüberliegenden Winkel in einem Dreieck konstant ist, d.h. es gilt: a b c sin( ) sin( ) sin( ) Somit gilt a b sin( ) sin( ), aber auch a b sin( ), sin( ) wenn man die Gleichung umstellt. Beispiele: Es ist a = 4cm, a = 60 und b = 50, gesucht ist b. 4cm b sin(60) sin(50) ÿsin(50 ) b = 4cm sin(50) 3,54cm sin(60)
65 Seite 65 Es ist g = = 70. Somit könnte man nun c berechnen. Als nächstes sei a = 8cm, c = 5cm, a = 100 gegeben, gesucht ist g. Es gilt: a c sin( ) sin( ) (*) Durch Umstellung der Gleichung kann man zeigen, dass auch sin( ) sin( ) a c gilt. Wir nehmen diese Gleichung, da man nur eine Umformung benötigt, wenn die Unbekannte im Zähler steht. Bei der Gleichung (*) müsste man erst mit sin(a) und sin(g) multiplizieren und dann durch a teilen. sin( 100) sin( ) 8cm 5cm ÿ5cm sin(100) 5cm sin( ) 8cm 0,61550 = sin(g) sin -1 g º 37,99 Bemerkung: Bei der Berechung des Winkels mit dem Sinussatz wird der Taschenrechner einen falschen Winkel ausgeben, wenn der gesuchte Winkel größer als 90 ist. Es gilt z.b.: sin(80 ) = sin(100 ) = 0, Bei sin -1 (0, ) gibt der Taschenrechner 80 aus. Diese Problem kann nicht auftreten, wenn ein gegebener Winkel bereits größer oder gleich 90 ist, oder wenn beispielsweise a, b und a gegeben ist und b a gilt, denn dann muss auch b a sein. Aufgaben: a) a = 8cm; b = 5cm; a = 80 ; b =? b) b = 5cm; a = 50 ; b = 60 ; a =? c) c = 12m; b = 8m; g = 100 ; a =?; b =?; a =? d) a = 8m; b = 75 ; g = 30 ; a =?; b =?; c =? Lösungen: a) b º 37,99 b) a º 4,42cm c) a º 7,66m; a º 38,96 ; b º 41,04 d) b = 8m ; c º 4,14; a = 75 (1. Schritt: a = 180± - 75± - 30±)
66 Seite Kosinussatz Sind zwei Seiten gegeben und der Winkel, der von beiden Seiten eingeschlossen ist, so kann der Kosinussatz verwendet werden. Er kann aber auch verwendet werden, wenn drei Seiten bekannt sind und ein Winkel bestimmt werden soll. Es gilt: a 2 = b 2 + c 2 2ÿbÿcÿcos(a) b 2 = a 2 + c 2 2ÿaÿcÿcos(b) c 2 = a 2 + b 2 2ÿaÿbÿcos(g) Wenn beispielsweise g = 90 wäre, dann würde sich bei der unteren Formel der Satz von Pythagoras ergeben, da cos(90 ) = 0 ist. Beispiele: Gegeben ist b = 4cm, c = 6cm und a = 60, gesucht wird a. a 2 = (4cm) 2 + (6cm) 2 2ÿ4cmÿ6cmÿcos(60 ) a 2 = 52cm 2 48cm 2 ÿcos(60 ) a 2 = 28cm 2 a º 5,29cm Gegeben ist a = 5cm, b = 3cm und c = 7cm, gesucht wird a. (5cm) 2 = (3cm) 2 + (7cm) 2 2ÿ3cmÿ7cmÿcos(a) 25cm 2 = 9cm cm 2 42cm 2 ÿcos(a) 25cm 2 = 58cm 2 42cm 2 ÿcos(a) -58cm 2-33cm 2 = -42cm 2 ÿcos(a) :(-42cm 2 )
67 Seite 67 0, = cos(a) cos -1 a º 38,21 Wir leiten nun noch die Formel zur Berechnung von a her: a 2 = b 2 + c 2 2ÿbÿcÿcos(a) -b 2 -c 2 a 2 b 2 c 2 = -2ÿbÿcÿcos(a) :(-2ÿbÿc) 2 2 a b c 2 b c 2 cos( ) Bzw. nach Erweiterung des Bruches mit (-1): b cos( ) 2 2 c a 2 b c 2 Aufgaben: 1) a) a = 7m; b = 9m; g = 70 ; c =? b) b = 2cm; c = 4cm; a = 50 ; a =? c) a = 6dm; c = 5dm; b = 120 ; c =? d) a = 8m; b = 9m; c = 7m; g =? 2) Ort A ist von Ort C 5km und von Ort B 7km entfernt. Von A aus sieht man die Orte B und C unter einem Winkel von 60. Wie weit sind die Ort B und C voneinander entfernt? Lösungen: a) c º 9,32m b) a º 3,12cm c) c º 9,54dm d) g º 48,19 2) Wir machen zunächst eine Skizze:
Lineare Gleichungssysteme mit zwei Unbekannten
 Lineare Gleichungssysteme mit zwei Unbekannten Wie beginnen mit einem Beispiel: Gesucht ist die Lösung des folgenden Gleichungssystems: (I) 2x y = 4 (II) x + y = 5 Hier stehen eine Reihe von Verfahren
Lineare Gleichungssysteme mit zwei Unbekannten Wie beginnen mit einem Beispiel: Gesucht ist die Lösung des folgenden Gleichungssystems: (I) 2x y = 4 (II) x + y = 5 Hier stehen eine Reihe von Verfahren
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
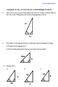 Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Gruber I Neumann. Erfolg in VERA-8. Vergleichsarbeit Mathematik Klasse 8 Gymnasium
 Gruber I Neumann Erfolg in VERA-8 Vergleichsarbeit Mathematik Klasse 8 Gymnasium . Zahlen Zahlen Tipps ab Seite, Lösungen ab Seite 0. Zahlen und Zahlenmengen Es gibt verschiedene Zahlenarten, z.b. ganze
Gruber I Neumann Erfolg in VERA-8 Vergleichsarbeit Mathematik Klasse 8 Gymnasium . Zahlen Zahlen Tipps ab Seite, Lösungen ab Seite 0. Zahlen und Zahlenmengen Es gibt verschiedene Zahlenarten, z.b. ganze
Die Kanten der Grundfläche mit je 7 cm sind die Katheten a und b des rechtwinkligen Dreiecks, die Hypotenuse c ist die gesuchte Bodendiagonale c.
 Aufgabe 1 Schritt 1: Ansatz und Skizze Bei einem Würfel, bei dem ja alle Kantenlängen gleich sind, kannst du mit einer Raumdiagonale, einer senkrechten Kante und einer Decken oder Bodendiagonalen ein rechtwinkliges
Aufgabe 1 Schritt 1: Ansatz und Skizze Bei einem Würfel, bei dem ja alle Kantenlängen gleich sind, kannst du mit einer Raumdiagonale, einer senkrechten Kante und einer Decken oder Bodendiagonalen ein rechtwinkliges
Grundwissen 9. Klasse 9/1. Grundwissen 9. Klasse 9/2
 Grundwissen 9. Klasse 9/. Quadratwurzel Definition: a ist diejenige positive Zahl, deren Quadrat a ergibt: a =a z.b. 5=5 Bezeichnung: Die Zahl a unter der Wurzel heißt Radikand. Radikandenbedingung: a
Grundwissen 9. Klasse 9/. Quadratwurzel Definition: a ist diejenige positive Zahl, deren Quadrat a ergibt: a =a z.b. 5=5 Bezeichnung: Die Zahl a unter der Wurzel heißt Radikand. Radikandenbedingung: a
1. Funktionen. 1.3 Steigung von Funktionsgraphen
 Klasse 8 Algebra.3 Steigung von Funktionsgraphen. Funktionen y Ist jedem Element einer Menge A genau ein E- lement einer Menge B zugeordnet, so nennt man die Zuordnung eindeutig. 3 5 6 8 Dies ist eine
Klasse 8 Algebra.3 Steigung von Funktionsgraphen. Funktionen y Ist jedem Element einer Menge A genau ein E- lement einer Menge B zugeordnet, so nennt man die Zuordnung eindeutig. 3 5 6 8 Dies ist eine
Schritt 1: Bedeutung rationale bzw. irrationale Zahl klären
 Aufgabe 1 Schritt 1: Bedeutung rationale bzw. irrationale Zahl klären Rationale Zahlen sind positive Bruchzahlen Q, ihre Gegenzahlen und die Null. Also alle Zahlen, die als Quotient zweier ganzer Zahlen
Aufgabe 1 Schritt 1: Bedeutung rationale bzw. irrationale Zahl klären Rationale Zahlen sind positive Bruchzahlen Q, ihre Gegenzahlen und die Null. Also alle Zahlen, die als Quotient zweier ganzer Zahlen
Definitions- und Formelübersicht Mathematik
 Definitions- Formelübersicht Mathematik Definitions- Formelübersicht Mathematik Mengen Intervalle Eine Menge ist eine Zusammenfassung von wohlunterschiedenen Elementen zu einem Ganzen. Dabei muss entscheidbar
Definitions- Formelübersicht Mathematik Definitions- Formelübersicht Mathematik Mengen Intervalle Eine Menge ist eine Zusammenfassung von wohlunterschiedenen Elementen zu einem Ganzen. Dabei muss entscheidbar
1. die ganzen Zahlen, denn 7= 1. a ist diejenige nicht negative Zahl, die quadriert a ergibt: 16 = 4; 0 = = 36 = 25 = e) Grundwissen 9.
 Grundwissen 9. Klasse Quadratwurzel a ist diejenige nicht negative Zahl, die quadriert a ergibt: ( a ) a Die Zahl a unter der Wurzel heißt Radikand. Es gibt keine Quadratwurzel aus einer negativen Zahl.
Grundwissen 9. Klasse Quadratwurzel a ist diejenige nicht negative Zahl, die quadriert a ergibt: ( a ) a Die Zahl a unter der Wurzel heißt Radikand. Es gibt keine Quadratwurzel aus einer negativen Zahl.
Kapitel 3. Kapitel 3 Gleichungen
 Gleichungen Inhalt 3.1 3.1 Terme, Gleichungen, Lösungen x 2 2 + y 2 2 3.2 3.2 Verfahren zur zur Lösung von von Gleichungen 3x 3x + 5 = 14 14 3.3 3.3 Gleichungssysteme Seite 2 3.1 Terme, Gleichungen, Lösungen
Gleichungen Inhalt 3.1 3.1 Terme, Gleichungen, Lösungen x 2 2 + y 2 2 3.2 3.2 Verfahren zur zur Lösung von von Gleichungen 3x 3x + 5 = 14 14 3.3 3.3 Gleichungssysteme Seite 2 3.1 Terme, Gleichungen, Lösungen
Mathematik. für das Ingenieurstudium. 1 Grundlagen. Jürgen Koch Martin Stämpfle.
 1 Grundlagen www.mathematik-fuer-ingenieure.de 2010 und, Esslingen Dieses Werk ist urheberrechtlich geschützt. Alle Rechte, auch die der Übersetzung, des Nachdruckes und der Vervielfältigung des Werkes,
1 Grundlagen www.mathematik-fuer-ingenieure.de 2010 und, Esslingen Dieses Werk ist urheberrechtlich geschützt. Alle Rechte, auch die der Übersetzung, des Nachdruckes und der Vervielfältigung des Werkes,
ALGEBRA Lineare Gleichungen Teil 1. Klasse 8. Datei Nr Friedrich W. Buckel. Dezember 2005 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
 ALGEBRA Lineare Gleichungen Teil Klasse 8 Lineare Gleichungen mit einer Variablen Datei Nr. 40 Friedrich W. Buckel Dezember 005 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Inhalt DATEI 40 Grundlagen und ein
ALGEBRA Lineare Gleichungen Teil Klasse 8 Lineare Gleichungen mit einer Variablen Datei Nr. 40 Friedrich W. Buckel Dezember 005 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Inhalt DATEI 40 Grundlagen und ein
Brückenkurs Mathematik. Mittwoch Freitag
 Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Download. Basics Mathe Gleichungen mit Klammern und Binomen. Einfach und einprägsam mathematische Grundfertigkeiten wiederholen.
 Download Michael Franck Basics Mathe Gleichungen mit Klammern und Binomen Einfach und einprägsam mathematische Grundfertigkeiten wiederholen Downloadauszug aus dem Originaltitel: Basics Mathe Gleichungen
Download Michael Franck Basics Mathe Gleichungen mit Klammern und Binomen Einfach und einprägsam mathematische Grundfertigkeiten wiederholen Downloadauszug aus dem Originaltitel: Basics Mathe Gleichungen
) sind keine Terme. Setzt man für die Variable eines Terms eine Zahl ein, so erhält man als Ergebnis wieder eine Zahl. y = 2 3 y = 11
 Wert eines Terms berechnen sind sinnvolle Rechenausdrücke, die aus Zahlen, Variablen, Rechenzeichen und Klammern bestehen können. Setzt man für die Variablen Zahlen ein, so erhält man als Ergebnis wieder
Wert eines Terms berechnen sind sinnvolle Rechenausdrücke, die aus Zahlen, Variablen, Rechenzeichen und Klammern bestehen können. Setzt man für die Variablen Zahlen ein, so erhält man als Ergebnis wieder
1. Vereinfache wie im Beispiel: 3. Vereinfache wie im Beispiel: 4. Schreibe ohne Wurzel wie im Beispiel:
 1. Zahlenmengen Wissensgrundlage Aufgabenbeispiele Gib die jeweils kleinstmögliche Zahlenmenge an, welche die Zahl enthält? R Q Q oder All diejenigen Zahlen, die sich nicht mehr durch Brüche darstellen
1. Zahlenmengen Wissensgrundlage Aufgabenbeispiele Gib die jeweils kleinstmögliche Zahlenmenge an, welche die Zahl enthält? R Q Q oder All diejenigen Zahlen, die sich nicht mehr durch Brüche darstellen
Lö sungen zu Wiederhölungsaufgaben Mathematik
 Lö sungen zu Wiederhölungsaufgaben Mathematik I) Zahlenbereiche. Zu welchem Zahlenbereich (N, Z, Q, R) gehören die folgenden Zahlen: N, Z, Q, R R Q, R N, Z, Q R -7 Z, Q, R -7, Q, R 0 N, Z, Q, R i) Z, Q,
Lö sungen zu Wiederhölungsaufgaben Mathematik I) Zahlenbereiche. Zu welchem Zahlenbereich (N, Z, Q, R) gehören die folgenden Zahlen: N, Z, Q, R R Q, R N, Z, Q R -7 Z, Q, R -7, Q, R 0 N, Z, Q, R i) Z, Q,
Quadratwurzeln. Reelle Zahlen
 M 9. Quadratwurzeln ist diejenige nicht negative Zahl, die quadriert ergibt: Die Zahl unter der Wurzel heißt Radikand: = Quadratwurzeln sind nur für positive Zahlen definiert: 0 25 = 5; 8 = 9; 0,25 = =
M 9. Quadratwurzeln ist diejenige nicht negative Zahl, die quadriert ergibt: Die Zahl unter der Wurzel heißt Radikand: = Quadratwurzeln sind nur für positive Zahlen definiert: 0 25 = 5; 8 = 9; 0,25 = =
Grundlagen Mathematik 7. Jahrgangsstufe
 ALGEBRA 1. Grundlagen Grundlagen Mathematik 7. Jahrgangsstufe Menge der ganzen Zahlen Z = {..., -3, -2, -1, 0, 1, 2, 3,... } Menge der rationalen Zahlen Q = { z z Z und n N } (Menge aller n positiven und
ALGEBRA 1. Grundlagen Grundlagen Mathematik 7. Jahrgangsstufe Menge der ganzen Zahlen Z = {..., -3, -2, -1, 0, 1, 2, 3,... } Menge der rationalen Zahlen Q = { z z Z und n N } (Menge aller n positiven und
Reelle Zahlen, Termumformungen, Gleichungen und Ungleichungen
 2. Vorlesung im Brückenkurs Mathematik 2018 Reelle Zahlen, Termumformungen, Gleichungen und Ungleichungen Dr. Markus Herrich Markus Herrich Reelle Zahlen, Gleichungen und Ungleichungen 1 Die Menge der
2. Vorlesung im Brückenkurs Mathematik 2018 Reelle Zahlen, Termumformungen, Gleichungen und Ungleichungen Dr. Markus Herrich Markus Herrich Reelle Zahlen, Gleichungen und Ungleichungen 1 Die Menge der
Teil 1: Trainingsheft für Klasse 7 und 8 DEMO. Lineare Gleichungen mit einer Variablen. Datei Nr Friedrich W. Buckel. Stand 5.
 ALGEBRA Lineare Gleichungen Teil 1: Trainingsheft für Klasse 7 und 8 Lineare Gleichungen mit einer Variablen Datei Nr. 1140 Friedrich W. Buckel Stand 5. Januar 018 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
ALGEBRA Lineare Gleichungen Teil 1: Trainingsheft für Klasse 7 und 8 Lineare Gleichungen mit einer Variablen Datei Nr. 1140 Friedrich W. Buckel Stand 5. Januar 018 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Quadratwurzeln. ist diejenige nicht negative Zahl, die quadriert ergibt: Die Zahl unter der Wurzel heißt Radikand:
 M 9.1 Quadratwurzeln ist diejenige nicht negative Zahl, die quadriert ergibt: Die Zahl unter der Wurzel heißt Radikand: Quadratwurzeln sind nur für positive Zahlen definiert: 0 25 5; 81 9; 0,25 0,5; 0,0081
M 9.1 Quadratwurzeln ist diejenige nicht negative Zahl, die quadriert ergibt: Die Zahl unter der Wurzel heißt Radikand: Quadratwurzeln sind nur für positive Zahlen definiert: 0 25 5; 81 9; 0,25 0,5; 0,0081
Mathematik. FOS 11. Jahrgangsstufe (technisch) c 2003, Thomas Barmetler Stand: 23. Juli Kontakt und weitere Infos:
 FOS 11. Jahrgangsstufe (technisch) c 2003, Thomas Barmetler Stand: 23. Juli 2004 Kontakt und weitere Infos: www.schule.barmetler.de Inhaltsverzeichnis 1 Wiederholung 5 1.1 Bruchrechnen.............................
FOS 11. Jahrgangsstufe (technisch) c 2003, Thomas Barmetler Stand: 23. Juli 2004 Kontakt und weitere Infos: www.schule.barmetler.de Inhaltsverzeichnis 1 Wiederholung 5 1.1 Bruchrechnen.............................
Quadratwurzeln. ist diejenige nicht negative Zahl, die quadriert. unter der Wurzel heißt Radikand:
 M 9.1 Quadratwurzeln ist diejenige nicht negative Zahl, die quadriert ergibt: Die Zahl unter der Wurzel heißt Radikand: Quadratwurzeln sind nur für positive Zahlen definiert: ; ; ; ; M 9.2 Reelle Zahlen
M 9.1 Quadratwurzeln ist diejenige nicht negative Zahl, die quadriert ergibt: Die Zahl unter der Wurzel heißt Radikand: Quadratwurzeln sind nur für positive Zahlen definiert: ; ; ; ; M 9.2 Reelle Zahlen
Rechnen mit Quadratwurzeln
 9. Grundwissen Mathematik Algebra Klasse 9 Rechnen mit Quadratwurzeln Die Quadratwurzel aus a ist diejenige nichtnegative Zahl aus R, deren Quadrat wieder a ergibt. a nennt man Radikand. Man schreibt dafür
9. Grundwissen Mathematik Algebra Klasse 9 Rechnen mit Quadratwurzeln Die Quadratwurzel aus a ist diejenige nichtnegative Zahl aus R, deren Quadrat wieder a ergibt. a nennt man Radikand. Man schreibt dafür
Über das Rechteck weißt du, dass der Umfang 32 cm beträgt. Die Formel für den Umfang eines Rechtecks lautet 2 2.
 Aufgabe 1 Schritt 1: Skizze und Ansatz Über das Rechteck weißt du, dass der Umfang 32 cm beträgt. Die Formel für den Umfang eines Rechtecks lautet 2 2. Da du außerdem das Verhältnis der Seitenlängen kennst,
Aufgabe 1 Schritt 1: Skizze und Ansatz Über das Rechteck weißt du, dass der Umfang 32 cm beträgt. Die Formel für den Umfang eines Rechtecks lautet 2 2. Da du außerdem das Verhältnis der Seitenlängen kennst,
Mathematikvorkurs. Fachbereich I. Sommersemester Elizaveta Buch
 Mathematikvorkurs Fachbereich I Sommersemester 2017 Elizaveta Buch Themenüberblick Montag Grundrechenarten und -regeln Bruchrechnen Binomische Formeln Dienstag Potenzen, Wurzeln und Logarithmus Summen-
Mathematikvorkurs Fachbereich I Sommersemester 2017 Elizaveta Buch Themenüberblick Montag Grundrechenarten und -regeln Bruchrechnen Binomische Formeln Dienstag Potenzen, Wurzeln und Logarithmus Summen-
1 GRUNDLAGEN 1.4 Massvorsätze und Zehnerpotenzen
 GRUNDLAGEN.4 Massvorsätze und Zehnerpotenzen.4. Zehnerpotenzen Kommt in einem Produkt immer derselbe Faktor vor, so schreibt man das Produkt in der Potenzschreibweise. Zahlen in der Form 0 5 heissen Zehnerpotenzen.
GRUNDLAGEN.4 Massvorsätze und Zehnerpotenzen.4. Zehnerpotenzen Kommt in einem Produkt immer derselbe Faktor vor, so schreibt man das Produkt in der Potenzschreibweise. Zahlen in der Form 0 5 heissen Zehnerpotenzen.
UND MOSES SPRACH AUCH DIESE GEBOTE
 UND MOSES SPRACH AUCH DIESE GEBOTE 1. Gebot: Nur die DUMMEN kürzen SUMMEN! Und auch sonst läuft bei Summen und Differenzen nichts! 3x + y 3 darfst Du NICHT kürzen! x! y. Gebot: Vorsicht bei WURZELN und
UND MOSES SPRACH AUCH DIESE GEBOTE 1. Gebot: Nur die DUMMEN kürzen SUMMEN! Und auch sonst läuft bei Summen und Differenzen nichts! 3x + y 3 darfst Du NICHT kürzen! x! y. Gebot: Vorsicht bei WURZELN und
Terme und Gleichungen
 Terme und Gleichungen Rainer Hauser November 00 Terme. Rekursive Definition der Terme Welche Objekte Terme genannt werden, wird rekursiv definiert. Die rekursive Definition legt zuerst als Basis fest,
Terme und Gleichungen Rainer Hauser November 00 Terme. Rekursive Definition der Terme Welche Objekte Terme genannt werden, wird rekursiv definiert. Die rekursive Definition legt zuerst als Basis fest,
1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: m (ausgesprochen: T von t und m)
 Grundwissen Mathematik 7. Klasse 1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: Ttm (, ) = ( t 5+ 6) 20+ m (ausgesprochen: T von t und m) Ein Term besteht aus
Grundwissen Mathematik 7. Klasse 1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: Ttm (, ) = ( t 5+ 6) 20+ m (ausgesprochen: T von t und m) Ein Term besteht aus
Vorbereitungskurs Mathematik
 Vorbereitungskurs Mathematik Grundlagen für das Unterrichtsfach Mathematik für die Fachhochschulreifeprüfung Zweijährige Höhere Berufsfachschule Berufsoberschule I Duale Berufsoberschule Inhalt 0. Vorwort...
Vorbereitungskurs Mathematik Grundlagen für das Unterrichtsfach Mathematik für die Fachhochschulreifeprüfung Zweijährige Höhere Berufsfachschule Berufsoberschule I Duale Berufsoberschule Inhalt 0. Vorwort...
Quadratwurzeln. ist diejenige nicht negative Zahl, die quadriert. unter der Wurzel heißt Radikand:
 M 9.1 Quadratwurzeln ist diejenige nicht negative Zahl, die quadriert ergibt: Die Zahl unter der Wurzel heißt Radikand: Quadratwurzeln sind nur für positive Zahlen definiert: ; ; ; ; M 9.2 Reelle Zahlen
M 9.1 Quadratwurzeln ist diejenige nicht negative Zahl, die quadriert ergibt: Die Zahl unter der Wurzel heißt Radikand: Quadratwurzeln sind nur für positive Zahlen definiert: ; ; ; ; M 9.2 Reelle Zahlen
Minimalziele Mathematik
 Jahrgang 5 o Kopfrechnen, Kleines Einmaleins o Runden und Überschlagrechnen o Schriftliche Grundrechenarten in den Natürlichen Zahlen (ganzzahliger Divisor, ganzzahliger Faktor) o Umwandeln von Größen
Jahrgang 5 o Kopfrechnen, Kleines Einmaleins o Runden und Überschlagrechnen o Schriftliche Grundrechenarten in den Natürlichen Zahlen (ganzzahliger Divisor, ganzzahliger Faktor) o Umwandeln von Größen
J Quadratwurzeln Reelle Zahlen
 J Quadratwurzeln Reelle Zahlen J Quadratwurzeln Reelle Zahlen 1 Quadratwurzeln Ein Quadrat habe einen Flächeninhalt von 64 cm. Will man wissen, wie lang die Seiten des Quadrates sind, so muss man herausfinden,
J Quadratwurzeln Reelle Zahlen J Quadratwurzeln Reelle Zahlen 1 Quadratwurzeln Ein Quadrat habe einen Flächeninhalt von 64 cm. Will man wissen, wie lang die Seiten des Quadrates sind, so muss man herausfinden,
Lineare Funktionen. Das rechtwinklige (kartesische) Koordinatensystem. Funktionen
 Das rechtwinklige (kartesische) Koordinatensystem Funktionen Funktion: Eine Funktion ist eine eindeutige Zuordnung. Jedem x D wird genau eine reelle Zahl zugeordnet. Schreibweise: Funktion: f: x f (x)
Das rechtwinklige (kartesische) Koordinatensystem Funktionen Funktion: Eine Funktion ist eine eindeutige Zuordnung. Jedem x D wird genau eine reelle Zahl zugeordnet. Schreibweise: Funktion: f: x f (x)
I. Reelle Zahlen GRUNDWISSEN MATHEMATIK - 9. KLASSE
 I. Reelle Zahlen 1. Die Menge der rationalen Zahlen und die Menge der irrationalen Zahlen bilden zusammen die Menge der reellen Zahlen. Nenne Beispiele für rationale und irrationale Zahlen.. Aus negativen
I. Reelle Zahlen 1. Die Menge der rationalen Zahlen und die Menge der irrationalen Zahlen bilden zusammen die Menge der reellen Zahlen. Nenne Beispiele für rationale und irrationale Zahlen.. Aus negativen
MATHEMATIK G9 LÖSEN VON GLEICHUNGEN
 MATHEMATIK G9 LÖSEN VON GLEICHUNGEN Viele mathematische (und naturwissenschaftliche) Probleme lassen sich dadurch lösen, dass man eine Gleichung (oder auch mehrere) aufstellt und diese dann löst. Wir werden
MATHEMATIK G9 LÖSEN VON GLEICHUNGEN Viele mathematische (und naturwissenschaftliche) Probleme lassen sich dadurch lösen, dass man eine Gleichung (oder auch mehrere) aufstellt und diese dann löst. Wir werden
Achsensymmetrie. Konstruktionen M 7.1
 M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
2015, MNZ. Jürgen Schmidt. 2.Tag. Vorkurs. Mathematik WS 2015/16
 Vorkurs Mathematik WS 2015/16 2.Tag Arten von Gleichungen Lineare Gleichungen (und Funktionen) 0 = ax + b (oft als Funktion: y = mx + n) a,b R Parameter m Anstieg, n Achsenabschnitt Quadratische Gleichungen
Vorkurs Mathematik WS 2015/16 2.Tag Arten von Gleichungen Lineare Gleichungen (und Funktionen) 0 = ax + b (oft als Funktion: y = mx + n) a,b R Parameter m Anstieg, n Achsenabschnitt Quadratische Gleichungen
= T 2. Lösungsmenge ist die Menge aller Elemente des Definitionsbereiches D G, die die Gleichung zu einer Wahre Aussage machen.
 Gleichungen Eine Gleichung ist eine Aussage, in der die Gleichheit zweier Terme durch Mathematische Symbol ausgedrückt wird. Dies wird durch das Gleichheitssymbol = symbolisiert G : = T 2 Definitionsmenge
Gleichungen Eine Gleichung ist eine Aussage, in der die Gleichheit zweier Terme durch Mathematische Symbol ausgedrückt wird. Dies wird durch das Gleichheitssymbol = symbolisiert G : = T 2 Definitionsmenge
Stichwortverzeichnis. Symbole. Stichwortverzeichnis
 Stichwortverzeichnis Stichwortverzeichnis Symbole ( ) (Runde Klammern) 32, 66 (Betragszeichen) 32 (Multiplikations-Zeichen) 31 + (Plus-Zeichen) 31, 69 - (Minus-Zeichen) 31, 69 < (Kleiner-als-Zeichen) 33,
Stichwortverzeichnis Stichwortverzeichnis Symbole ( ) (Runde Klammern) 32, 66 (Betragszeichen) 32 (Multiplikations-Zeichen) 31 + (Plus-Zeichen) 31, 69 - (Minus-Zeichen) 31, 69 < (Kleiner-als-Zeichen) 33,
Potenzen, Wurzeln, Logarithmen
 KAPITEL 3 Potenzen, Wurzeln, Logarithmen 3.1 Funktionen und Umkehrfunktionen.............. 70 3.2 Wurzeln............................ 72 3.3 Warum ist a 2 + b 2 a + b?................. 73 3.4 Potenzfunktion........................
KAPITEL 3 Potenzen, Wurzeln, Logarithmen 3.1 Funktionen und Umkehrfunktionen.............. 70 3.2 Wurzeln............................ 72 3.3 Warum ist a 2 + b 2 a + b?................. 73 3.4 Potenzfunktion........................
Brückenkurs Mathematik zum Sommersemester 2015
 HOCHSCHULE HANNOVER UNIVERSITY OF APPLIED SCIENCES AND ARTS Dipl.-Math. Xenia Bogomolec Brückenkurs Mathematik zum Sommersemester 2015 Übungsblatt 1 (Grundlagen) Aufgabe 1. Multiplizieren Sie folgende
HOCHSCHULE HANNOVER UNIVERSITY OF APPLIED SCIENCES AND ARTS Dipl.-Math. Xenia Bogomolec Brückenkurs Mathematik zum Sommersemester 2015 Übungsblatt 1 (Grundlagen) Aufgabe 1. Multiplizieren Sie folgende
Lineare Gleichungssysteme mit 2 Variablen
 Lineare Gleichungssysteme mit 2 Variablen Lineare Gleichungssysteme mit 2 Variablen Einzelne lineare Gleichungen mit zwei Variablen Bis jetzt haben wir nur lineare Gleichungen mit einer Unbekannten (x)
Lineare Gleichungssysteme mit 2 Variablen Lineare Gleichungssysteme mit 2 Variablen Einzelne lineare Gleichungen mit zwei Variablen Bis jetzt haben wir nur lineare Gleichungen mit einer Unbekannten (x)
Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt.
 M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
Achsensymmetrie. Konstruktionen. Mathematik-Grundwissen Klassenstufe 7
 Wissen Achsensymmetrie Beispiel Figuren die an einer Achse a gespiegelt werden nennt man achsensymmetrisch bezüglich a. Die Verbindungsstrecke zwischen zwei achsensymmetrischen Punkten wird durch die Achse
Wissen Achsensymmetrie Beispiel Figuren die an einer Achse a gespiegelt werden nennt man achsensymmetrisch bezüglich a. Die Verbindungsstrecke zwischen zwei achsensymmetrischen Punkten wird durch die Achse
Formelsammlung Mathematik 9
 I Lineare Funktionen... 9.) Funktionen... 9.) Proportionale Funktionen... 9.) Lineare Funktionen... 9.4) Bestimmung von linearen Funktionen:... II) Systeme linearer Gleichungen... 9.5) Lineare Gleichungen
I Lineare Funktionen... 9.) Funktionen... 9.) Proportionale Funktionen... 9.) Lineare Funktionen... 9.4) Bestimmung von linearen Funktionen:... II) Systeme linearer Gleichungen... 9.5) Lineare Gleichungen
Polynomgleichungen. Gesetzmäßigkeiten
 Polynomgleichungen Gesetzmäßigkeiten Werden zwei Terme durch ein Gleichheitszeichen miteinander verbunden, so entsteht eine Gleichung. Enthält die Gleichung die Variable x nur in der 1. Potenz, so spricht
Polynomgleichungen Gesetzmäßigkeiten Werden zwei Terme durch ein Gleichheitszeichen miteinander verbunden, so entsteht eine Gleichung. Enthält die Gleichung die Variable x nur in der 1. Potenz, so spricht
Berufliches Gymnasium Gelnhausen
 Berufliches Gymnasium Gelnhausen Fachbereich Mathematik Die inhaltlichen Anforderungen für das Fach Mathematik für Schülerinnen und Schüler, die in die Einführungsphase (E) des Beruflichen Gymnasiums eintreten
Berufliches Gymnasium Gelnhausen Fachbereich Mathematik Die inhaltlichen Anforderungen für das Fach Mathematik für Schülerinnen und Schüler, die in die Einführungsphase (E) des Beruflichen Gymnasiums eintreten
Reelle Zahlen (R)
 Reelle Zahlen (R) Bisher sind bekannt: Natürliche Zahlen (N): N {,,,,,6... } Ganze Zahlen (Z): Z {...,,,0,,,... } Man erkennt: Rationale Zahlen (Q):.) Zwischen den natürlichen Zahlen befinden sich große
Reelle Zahlen (R) Bisher sind bekannt: Natürliche Zahlen (N): N {,,,,,6... } Ganze Zahlen (Z): Z {...,,,0,,,... } Man erkennt: Rationale Zahlen (Q):.) Zwischen den natürlichen Zahlen befinden sich große
Grundwissensblatt 8. Klasse. IV. Lineare Gleichungen mit zwei Variablen 1. Eigenschaften von linearen Gleichungen mit zwei Variablen
 Grundwissensblatt 8. Klasse IV. Lineare Gleichungen mit zwei Variablen. Eigenschaften von linearen Gleichungen mit zwei Variablen Alle linearen Gleichungen der Form a + by = c (oder auch y = m + t) erfüllen:
Grundwissensblatt 8. Klasse IV. Lineare Gleichungen mit zwei Variablen. Eigenschaften von linearen Gleichungen mit zwei Variablen Alle linearen Gleichungen der Form a + by = c (oder auch y = m + t) erfüllen:
Der Satz des Pythagoras
 Der Satz des Pythagoras Das rechtwinklige Dreieck Jedes rechtwinklige Dreieck besitzt eine Hypotenuse (c), das ist die längste Seite des Dreiecks (bzw. diejenige gegenüber dem rechten Winkel). Die anderen
Der Satz des Pythagoras Das rechtwinklige Dreieck Jedes rechtwinklige Dreieck besitzt eine Hypotenuse (c), das ist die längste Seite des Dreiecks (bzw. diejenige gegenüber dem rechten Winkel). Die anderen
Wurzelgleichungen. 1.1 Was ist eine Wurzelgleichung? 1.2 Lösen einer Wurzelgleichung. 1.3 Zuerst die Wurzel isolieren
 1.1 Was ist eine Wurzelgleichung? Wurzelgleichungen Beispiel für eine Wurzelgleichung Eine Wurzelgleichung ist eine Gleichung bei der in mindestens einem Radikanten (Term unter der Wurzel) die Unbekannte
1.1 Was ist eine Wurzelgleichung? Wurzelgleichungen Beispiel für eine Wurzelgleichung Eine Wurzelgleichung ist eine Gleichung bei der in mindestens einem Radikanten (Term unter der Wurzel) die Unbekannte
Klasse 9+ (Mittelstufe Plus) Hinweise und Lösungen
 Klasse 9+ (Mittelstufe Plus) Hinweise und Lösungen. a) (x + y) (x y) = x + xy + y [x xy + y ] = = x + xy + y x + xy y = 4xy b) z 3 z ) = z + z z z(z ) z (z ) (z 0; ) c) (8a 3 b) = ( 3²a3 b) = 3 4 a 6 b
Klasse 9+ (Mittelstufe Plus) Hinweise und Lösungen. a) (x + y) (x y) = x + xy + y [x xy + y ] = = x + xy + y x + xy y = 4xy b) z 3 z ) = z + z z z(z ) z (z ) (z 0; ) c) (8a 3 b) = ( 3²a3 b) = 3 4 a 6 b
@ GN GRUNDWISSEN MATHEMATIK. Inhalt... Seite
 Inhaltverzeichnis Inhalt... Seite Klasse 5: 1 Zahlen... 1 1.1 Zahlenmengen... 1 1.2 Dezimalsystem... 1 1.3 Römische Zahlen... 1 1.4 Runden... 1 1.5 Termarten... 1 1.6 Rechengesetze... 2 1.7 Rechnen mit
Inhaltverzeichnis Inhalt... Seite Klasse 5: 1 Zahlen... 1 1.1 Zahlenmengen... 1 1.2 Dezimalsystem... 1 1.3 Römische Zahlen... 1 1.4 Runden... 1 1.5 Termarten... 1 1.6 Rechengesetze... 2 1.7 Rechnen mit
Tipps und Tricks für die Abschlussprüfung
 Tipps und Tricks für die Abschlussprüfung Rechentipps und Lösungsstrategien mit Beispielen zu allen Prüfungsthemen Mathematik Baden-Württemberg Mathematik-Verlag Vorwort: Sehr geehrte Schülerinnen und
Tipps und Tricks für die Abschlussprüfung Rechentipps und Lösungsstrategien mit Beispielen zu allen Prüfungsthemen Mathematik Baden-Württemberg Mathematik-Verlag Vorwort: Sehr geehrte Schülerinnen und
Nullstellen. Somit ergibt sich x = 4 oder x = -4, da das Quadrat beider Zahlen 16 ergibt. Man schreibt
 Nullstellen Aufgabe 1 Gegeben ist die folgende quadratische Funktion: Bestimme die Nullstellen. f( x) x² 3 x² 3 : x² 16 16 x² 16 Somit ergibt sich x = 4 oder x = -4, da das Quadrat beider Zahlen 16 ergibt.
Nullstellen Aufgabe 1 Gegeben ist die folgende quadratische Funktion: Bestimme die Nullstellen. f( x) x² 3 x² 3 : x² 16 16 x² 16 Somit ergibt sich x = 4 oder x = -4, da das Quadrat beider Zahlen 16 ergibt.
gebrochene Zahl gekürzt mit 9 sind erweitert mit 8 sind
 Vorbereitungsaufgaben Mathematik. Bruchrechnung.. Grundlagen: gebrochene Zahl gemeiner Bruch Zähler Nenner Dezimalbruch Ganze, Zehntel Hundertstel Tausendstel Kürzen: Zähler und Nenner durch dieselbe Zahl
Vorbereitungsaufgaben Mathematik. Bruchrechnung.. Grundlagen: gebrochene Zahl gemeiner Bruch Zähler Nenner Dezimalbruch Ganze, Zehntel Hundertstel Tausendstel Kürzen: Zähler und Nenner durch dieselbe Zahl
Propädeutikum Mathematik
 Propädeutikum Mathematik Wintersemester 2016 / 2017 Carsten Krupp BBA und IBS Vorkurs Mathematik - Wintersemester 2016 / 2017 Seite 1 Literaturhinweise Cramer, E., Neslehova, J.: Vorkurs Mathematik, Springer,
Propädeutikum Mathematik Wintersemester 2016 / 2017 Carsten Krupp BBA und IBS Vorkurs Mathematik - Wintersemester 2016 / 2017 Seite 1 Literaturhinweise Cramer, E., Neslehova, J.: Vorkurs Mathematik, Springer,
GRUNDWISSEN Seitenhalbierende Konstruktion von Vierecken [nach Lambacher Schweizer 7] [eigene Grafiken]
![GRUNDWISSEN Seitenhalbierende Konstruktion von Vierecken [nach Lambacher Schweizer 7] [eigene Grafiken] GRUNDWISSEN Seitenhalbierende Konstruktion von Vierecken [nach Lambacher Schweizer 7] [eigene Grafiken]](/thumbs/68/58070661.jpg) GRUNDWISSEN Inhalt 5.Gleichungen... 2 5.1. Gleichungen und Lösungen... 2 5.2. Äquivalente Gleichungsumformungen... 2 5.3. Systematisches Lösen einer Gleichungen... 2 5.4. Lineare Gleichungen in Anwendungsaufgaben...
GRUNDWISSEN Inhalt 5.Gleichungen... 2 5.1. Gleichungen und Lösungen... 2 5.2. Äquivalente Gleichungsumformungen... 2 5.3. Systematisches Lösen einer Gleichungen... 2 5.4. Lineare Gleichungen in Anwendungsaufgaben...
Quadratische Gleichungen
 Quadratische Gleichungen Alle aufgezeigten Lösungswege gelten für Gleichungen, die schon vereinfacht und zusammengefasst wurden. Es darf nur noch + vorhanden sein!!! (Also nicht + und auch nicht 3 ; bitte
Quadratische Gleichungen Alle aufgezeigten Lösungswege gelten für Gleichungen, die schon vereinfacht und zusammengefasst wurden. Es darf nur noch + vorhanden sein!!! (Also nicht + und auch nicht 3 ; bitte
Grundwissen Mathematik Klasse 8. Beispiel: m= 2,50 1 = 5,00. Gleichung: y=2,50 x. Beispiel: c=1,5 160=2,5 96=3 80=6 40=240.
 I. Funktionen 1. Direkt proportionale Zuordnungen Grundwissen Mathematik Klasse x und y sind direkt proportional, wenn zum n fachen Wert für x der n fache Wert für y gehört, die Wertepaare quotientengleich
I. Funktionen 1. Direkt proportionale Zuordnungen Grundwissen Mathematik Klasse x und y sind direkt proportional, wenn zum n fachen Wert für x der n fache Wert für y gehört, die Wertepaare quotientengleich
Themenerläuterung. Die wichtigsten benötigten Formeln
 Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
Grundlagen der Mathematik von Ansgar Schiffler - Seite 1 von 7 -
 - Seite von 7 -. Wie lautet die allgemeine Geradengleichung? (Mit Erklärung). Ein Telefontarif kostet 5 Grundgebühr und pro Stunde 8 cent. Wie lautet allgemein die Gleichung für solch einen Tarif? (Mit
- Seite von 7 -. Wie lautet die allgemeine Geradengleichung? (Mit Erklärung). Ein Telefontarif kostet 5 Grundgebühr und pro Stunde 8 cent. Wie lautet allgemein die Gleichung für solch einen Tarif? (Mit
Basistext Lineare Gleichungssysteme. Eine lineare Gleichung mit einer Unbekannten hat die allgemeine Form! #=%
 Basistext Lineare Gleichungssysteme Eine lineare Gleichung mit einer Unbekannten hat die allgemeine Form! #=% Mit zwei Unbekannten gibt es die allgemeine Form:! #+% '=( Gelten mehrere dieser Gleichungen
Basistext Lineare Gleichungssysteme Eine lineare Gleichung mit einer Unbekannten hat die allgemeine Form! #=% Mit zwei Unbekannten gibt es die allgemeine Form:! #+% '=( Gelten mehrere dieser Gleichungen
Variable und Terme A 7_01. Variable sind Platzhalter für Zahlen aus einer vorgegebenen Grundmenge G, z. B. x IN; y ; a Q
 Variable und Terme A 7_01 Variable sind Platzhalter für Zahlen aus einer vorgegebenen Grundmenge G, z B x IN; y ; a Q Jede sinnvolle Zusammenstellung aus Zahlen und Variablen mit Hilfe von Rechenzeichen
Variable und Terme A 7_01 Variable sind Platzhalter für Zahlen aus einer vorgegebenen Grundmenge G, z B x IN; y ; a Q Jede sinnvolle Zusammenstellung aus Zahlen und Variablen mit Hilfe von Rechenzeichen
Stufen- und Wechselwinkel sind genau dann gleich groß, wenn die Geraden g und h parallel sind.
 1 Sätze über Winkel Geradenkreuzung: Zwei Geraden, die sich in einem Punkt schneiden, nennt man eine Geradenkreuzung. α α Nebeneinander liegende Winkel heißen Nebenwinkel, sie β ergeben zusammen stets
1 Sätze über Winkel Geradenkreuzung: Zwei Geraden, die sich in einem Punkt schneiden, nennt man eine Geradenkreuzung. α α Nebeneinander liegende Winkel heißen Nebenwinkel, sie β ergeben zusammen stets
1 Lineare Funktionen. 1 Antiproportionale Funktionen
 Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Propädeutikum Mathematik
 Propädeutikum Mathematik Wintersemester 2017/2018 Carsten Krupp Betriebswirtschaftslehre (BBA) und International Business Studies (IBS)) Vorkurs Mathematik - Wintersemester 2017/2018 Seite 1 Literaturhinweise
Propädeutikum Mathematik Wintersemester 2017/2018 Carsten Krupp Betriebswirtschaftslehre (BBA) und International Business Studies (IBS)) Vorkurs Mathematik - Wintersemester 2017/2018 Seite 1 Literaturhinweise
Was ist eine Gleichung?
 Was ist eine Gleichung? Eine Gleichung ist eine Behauptung. Allerdings nicht irgendeine Behauptung, sondern die Behauptung, dass zwei Dinge gleich sind. Die zwei ''Dinge'' enthalten ein oder mehrere Symbole
Was ist eine Gleichung? Eine Gleichung ist eine Behauptung. Allerdings nicht irgendeine Behauptung, sondern die Behauptung, dass zwei Dinge gleich sind. Die zwei ''Dinge'' enthalten ein oder mehrere Symbole
Grundwissen Mathematik 7. Klasse 7 / 1
 Grundwissen Mathematik 7. Klasse 7 / 1 Achsensymmetrie und Achsenspiegelung - Längentreue: Symmetrische Strecken sind gleich lang. - Winkeltreue: Symmetrische Winkel sind gleich groß. - Der Drehsinn ändert
Grundwissen Mathematik 7. Klasse 7 / 1 Achsensymmetrie und Achsenspiegelung - Längentreue: Symmetrische Strecken sind gleich lang. - Winkeltreue: Symmetrische Winkel sind gleich groß. - Der Drehsinn ändert
Corinne Schenka Vorkurs Mathematik WiSe 2012/13. Die kleineren Zahlbereiche sind jeweils Teilmengen von größeren Zahlbereichen:
 2. Zahlbereiche Besonderheiten und Rechengesetze Die kleineren Zahlbereiche sind jeweils Teilmengen von größeren Zahlbereichen: 2.1. Die natürlichen Zahlen * + besitzt abzählbar unendlich viele Elemente
2. Zahlbereiche Besonderheiten und Rechengesetze Die kleineren Zahlbereiche sind jeweils Teilmengen von größeren Zahlbereichen: 2.1. Die natürlichen Zahlen * + besitzt abzählbar unendlich viele Elemente
Länge eines Vektors und Abstand von zwei Punkten 2. 4 = 6. Skalarprodukt und Winkel zwischen Vektoren
 Länge eines Vektors und Abstand von zwei Punkten Aufgabe Bestimme die Länge des Vektors x. Die Länge beträgt: x ( ) =. Skalarprodukt und Winkel zwischen Vektoren Aufgabe Es sind die Eckpunkte A(; ), B(
Länge eines Vektors und Abstand von zwei Punkten Aufgabe Bestimme die Länge des Vektors x. Die Länge beträgt: x ( ) =. Skalarprodukt und Winkel zwischen Vektoren Aufgabe Es sind die Eckpunkte A(; ), B(
Gleichungen und Ungleichungen
 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme. Kapitel 3 Gleichungen und Ungleichungen linke Seite = rechte Seite Grundmenge: Menge aller Zahlen, die wir als Lösung der Gleichung
Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme. Kapitel 3 Gleichungen und Ungleichungen linke Seite = rechte Seite Grundmenge: Menge aller Zahlen, die wir als Lösung der Gleichung
Gleichungen und Ungleichungen
 Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Gleichungen und Ungleichungen
 Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
MATHEMATIK Grundkurs 11m3 2010
 MATHEMATIK Grundkurs 11m3 2010 Städtisches Gymnasium Leichlingen Zusammenfassende Informationen zum Unterricht ab 29. Oktober 2010 Für jede Doppelstunde ein Kapitel 2 Kapitel 1 Doppelstunde 29.10.2010
MATHEMATIK Grundkurs 11m3 2010 Städtisches Gymnasium Leichlingen Zusammenfassende Informationen zum Unterricht ab 29. Oktober 2010 Für jede Doppelstunde ein Kapitel 2 Kapitel 1 Doppelstunde 29.10.2010
Grundwissen Mathematik
 Grundwissen Mathematik Algebra Terme und Gleichungen Jeder Abschnitt weist einen und einen teil auf. Der teil sollte gleichzeitig mit dem bearbeitet werden. Während die bearbeitet werden, sollte man den
Grundwissen Mathematik Algebra Terme und Gleichungen Jeder Abschnitt weist einen und einen teil auf. Der teil sollte gleichzeitig mit dem bearbeitet werden. Während die bearbeitet werden, sollte man den
Propädeutikum Mathematik
 Propädeutikum Mathematik Sommersemester 2016 Carsten Krupp BBA Seite 1 Literaturhinweise Cramer, E., Neslehova, J.: Vorkurs Mathematik, Springer, 2004 Piehler, Sippel, Pfeiffer: Mathematik zum Studieneinstieg,
Propädeutikum Mathematik Sommersemester 2016 Carsten Krupp BBA Seite 1 Literaturhinweise Cramer, E., Neslehova, J.: Vorkurs Mathematik, Springer, 2004 Piehler, Sippel, Pfeiffer: Mathematik zum Studieneinstieg,
Schritt 1: Koordinaten in die allgemeine Funktionsgleichung einsetzen
 Aufgabe 1a) Schritt 1: S in die Scheitelpunktform einsetzen 0,5 2 Schritt 2: Koordinaten von P einsetzen und a berechnen 2,25 1,5 0,5 2 0,25 Schritt 3: Funktionsterm aufstellen 0,25 0,5 2 als Scheitelpunktform,
Aufgabe 1a) Schritt 1: S in die Scheitelpunktform einsetzen 0,5 2 Schritt 2: Koordinaten von P einsetzen und a berechnen 2,25 1,5 0,5 2 0,25 Schritt 3: Funktionsterm aufstellen 0,25 0,5 2 als Scheitelpunktform,
1.1. Geradengleichung aus Steigung und y-achsenabschnitt
 Version vom 4. Januar 2007 Gleichungen von Geraden in der Ebene 1999 Peter Senn * 1.1. Geradengleichung aus Steigung und y-achsenabschnitt In dieser Form lautet die Gleichung der Geraden wie folgt: g:
Version vom 4. Januar 2007 Gleichungen von Geraden in der Ebene 1999 Peter Senn * 1.1. Geradengleichung aus Steigung und y-achsenabschnitt In dieser Form lautet die Gleichung der Geraden wie folgt: g:
M 9.1. Quadratwurzeln. Wie bezeichnet man die Zahl unter der Wurzel? Für welche Zahlen ist die Wurzel definiert? Berechne: Carina Mittermayer (2010)
 M 9.1 Quadratwurzeln Wie wird definiert? Wie bezeichnet man die Zahl unter der Wurzel? Für welche Zahlen ist die Wurzel definiert? Berechne: M 9.2 Reelle Zahlen Was sind irrationale Zahlen? Nenne vier
M 9.1 Quadratwurzeln Wie wird definiert? Wie bezeichnet man die Zahl unter der Wurzel? Für welche Zahlen ist die Wurzel definiert? Berechne: M 9.2 Reelle Zahlen Was sind irrationale Zahlen? Nenne vier
M 9.1. Quadratwurzeln. Wie bezeichnet man die Zahl unter der Wurzel? Für welche Zahlen ist die Wurzel definiert? Berechne: Carina Mittermayer (2010)
 M 9.1 Quadratwurzeln Wie wird definiert? Wie bezeichnet man die Zahl unter der Wurzel? Für welche Zahlen ist die Wurzel definiert? Berechne: M 9.2 Reelle Zahlen Was sind irrationale Zahlen? Nenne vier
M 9.1 Quadratwurzeln Wie wird definiert? Wie bezeichnet man die Zahl unter der Wurzel? Für welche Zahlen ist die Wurzel definiert? Berechne: M 9.2 Reelle Zahlen Was sind irrationale Zahlen? Nenne vier
Propädeutikum Mathematik
 Propädeutikum Mathematik Wintersemester 2018/2019 Carsten Krupp BBA und IBS Termine: Freitag, 14.09.18 von 9.00-18.00 Uhr Raum 1H.0.01 (Neubau - R100) Montag, 17.09.18 von 9.00 18.00 Uhr Raum 1H.0.01 (Neubau
Propädeutikum Mathematik Wintersemester 2018/2019 Carsten Krupp BBA und IBS Termine: Freitag, 14.09.18 von 9.00-18.00 Uhr Raum 1H.0.01 (Neubau - R100) Montag, 17.09.18 von 9.00 18.00 Uhr Raum 1H.0.01 (Neubau
Propädeutikum Mathematik
 Propädeutikum Mathematik Sommersemester 2018 Carsten Krupp BBA und IBS Termine: Freitag, 23.02.18 von 9.00-18.00 Uhr Raum 1H.0.01 (Neubau - R100) Montag, 26.02.18 von 9.00 18.00 Uhr Raum 1H.0.01 (Neubau
Propädeutikum Mathematik Sommersemester 2018 Carsten Krupp BBA und IBS Termine: Freitag, 23.02.18 von 9.00-18.00 Uhr Raum 1H.0.01 (Neubau - R100) Montag, 26.02.18 von 9.00 18.00 Uhr Raum 1H.0.01 (Neubau
Vierecke. 7.1 Grundwissen Mathematik Geometrie Klasse 7. Drachenviereck: Viereck, bei dem eine Diagonale Symmetrieachse ist
 7.1 Grundwissen Mathematik Geometrie Klasse 7 Vierecke Trapez: Viereck, bei dem zwei Gegenseiten parallel sind gleichschenkliges Trapez: Trapez, bei dem die beiden Schenkel c gleich lang sind (b = d) d
7.1 Grundwissen Mathematik Geometrie Klasse 7 Vierecke Trapez: Viereck, bei dem zwei Gegenseiten parallel sind gleichschenkliges Trapez: Trapez, bei dem die beiden Schenkel c gleich lang sind (b = d) d
Achsensymmetrie. Konstruktionen M 7.1
 M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
Achsensymmetrie. Grundkonstruktionen
 M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
Musteraufgaben zu den Mathematikmodulen Ein Selbsttest
 Musteraufgaben zu den Mathematikmodulen Ein Selbsttest I. Grundlagen der Mathematik I Terme und Gleichungen, elementare Funktionen (bis zu 5 h) Grundsätzliches zum Vereinfachen von Termen und Lösen von
Musteraufgaben zu den Mathematikmodulen Ein Selbsttest I. Grundlagen der Mathematik I Terme und Gleichungen, elementare Funktionen (bis zu 5 h) Grundsätzliches zum Vereinfachen von Termen und Lösen von
Fachbereich I Management, Controlling, Health Care. Mathematikvorkurs. Wintersemester 2017/2018. Elizaveta Buch
 Fachbereich I Management, Controlling, Health Care Mathematikvorkurs Wintersemester 2017/2018 Elizaveta Buch Themenüberblick Montag Grundrechenarten und -regeln Bruchrechnen Prozentrechnung Dienstag Binomische
Fachbereich I Management, Controlling, Health Care Mathematikvorkurs Wintersemester 2017/2018 Elizaveta Buch Themenüberblick Montag Grundrechenarten und -regeln Bruchrechnen Prozentrechnung Dienstag Binomische
2. Die Satzgruppe des Pythagoras
 Grundwissen Mathematik 9. Klasse Seite von 17 1.4 Rechnen mit reellen Zahlen a) Multiplizieren und Dividieren von reellen Zahlen + Es gilt: a b = a b mit ab R, 0 Beispiele: 18 = 36 = 6 14 14 7 = = a a
Grundwissen Mathematik 9. Klasse Seite von 17 1.4 Rechnen mit reellen Zahlen a) Multiplizieren und Dividieren von reellen Zahlen + Es gilt: a b = a b mit ab R, 0 Beispiele: 18 = 36 = 6 14 14 7 = = a a
Vorkurs Mathematik 1
 Vorkurs Mathematik 1 Einführung in die mathematische Notation Konstanten i komplexe Einheit i 2 + 1 = 0 e Eulersche Zahl Kreiszahl 2 Einführung in die mathematische Notation Bezeichner Primzahlen, Zähler
Vorkurs Mathematik 1 Einführung in die mathematische Notation Konstanten i komplexe Einheit i 2 + 1 = 0 e Eulersche Zahl Kreiszahl 2 Einführung in die mathematische Notation Bezeichner Primzahlen, Zähler
2.3 Logarithmus. b). a n = b n = log a. b für a,b 0 ( : gesprochen genau dann bedeutet, dass beide Definitionen gleichwertig sind) Oder log a
 2.3 Logarithmus Bsp. Seite 84 mitte: Wie lange muss man Fr. 10 000.- zu 5,1% anlegen, um Fr. 16 000.- zu erhalten? Lösen Sie die Zinseszinsformel nach q n auf Aus q n erfolgt die Berechnung von n mittels
2.3 Logarithmus Bsp. Seite 84 mitte: Wie lange muss man Fr. 10 000.- zu 5,1% anlegen, um Fr. 16 000.- zu erhalten? Lösen Sie die Zinseszinsformel nach q n auf Aus q n erfolgt die Berechnung von n mittels
Mathematik für die Berufsfachschule II
 Didaktische Jahresplanung: Schnittpunkt Mathematik für die Berufsfachschule II Passgenau zum Lehrplan 2019 Schule: Lehrkraft: Klasse : Schuljahr: Bildungsplan für die Berufsfachschule in Rheinland-Pfalz;
Didaktische Jahresplanung: Schnittpunkt Mathematik für die Berufsfachschule II Passgenau zum Lehrplan 2019 Schule: Lehrkraft: Klasse : Schuljahr: Bildungsplan für die Berufsfachschule in Rheinland-Pfalz;
Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt.
 M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
6 Gleichungen und Gleichungssysteme
 03.05.0 6 Gleichungen und Gleichungssysteme Äquivalente Gleichungsumformungen ( ohne Änderung der Lösungsmenge ).) a = b a c = b c Addition eines beliebigen Summanden c.) a = b a - c = b - c Subtraktion
03.05.0 6 Gleichungen und Gleichungssysteme Äquivalente Gleichungsumformungen ( ohne Änderung der Lösungsmenge ).) a = b a c = b c Addition eines beliebigen Summanden c.) a = b a - c = b - c Subtraktion
GMFH - Gesellschaft für Mathematik an Schweizer Fachhochschulen SMHES - Société pour les Mathématiques dans les Hautes Ecoles Spécialisées suisses
 GMFH - Gesellschaft für Mathematik an Schweizer Fachhochschulen SMHES - Société pour les Mathématiques dans les Hautes Ecoles Spécialisées suisses Mathematik-Referenzaufgaben zum Rahmenlehrplan für die
GMFH - Gesellschaft für Mathematik an Schweizer Fachhochschulen SMHES - Société pour les Mathématiques dans les Hautes Ecoles Spécialisées suisses Mathematik-Referenzaufgaben zum Rahmenlehrplan für die
