67 Grenzwert einer Funktion f in x 0 x 0 [a, b] D(f)
|
|
|
- Felix Fromm
- vor 7 Jahren
- Abrufe
Transkript
1 Grenzwerte Stetigkeit Differentiation einer Funktion (Uneigentliche) Grenzwerte von Zahlenfolgen Nrn Grenzwert einer Funktion f in x 0 x 0 [a, b] D(f) Die Zahl x 0 ist also als Grenzwert erreichbar durch Zahlenfolgen x n, n N, für die (für alle n N) x n D(f) und x n x 0 gilt. Eine Zahl c heißt Grenzwert der Funktion f an der Stelle x 0, wenn für JEDE Folge (x n, n N) mit x n x 0 gilt: f(x n ) c. n n Schreibweisen GW lim x x 0 f(x) = c oder f(x) c für x x 0 Für einen linksseitigen Grenzwert werden nur Folgen mit x n < x 0, für einen rechtsseitigen Grenzwert werden nur Folgen mit x n > x 0 zugelassen. Schreibweisen LGW lim 0 x x 0 Schreibweisen RGW lim 0+ x x 0 + Existieren links- und rechtsseitiger Grenzwert, und sind beide gleich der einen Zahl c, so ist auch der Grenzwert gleich c (und umgekehrt). GW=LGW=RGW Rechenregeln für Grenzwerte wie Nr. 47 Bsp. a 4 3 f(x) LGW FW RGW x x 0 =, f(x) = x für 0 x < 3/4 für x = x 2/3 für < x 2 LGW: lim f(x) = lim x = x x FW: f() = 3/4 RGW: lim f(x) = lim (x 2/3) = /3 x + x Als Sonderfälle für die Stelle x 0 und den (dann uneigentlich genannten) Grenzwert c einer Funktion sind auch die idealen Zahlen ± zugelassen, d.h. der uneigentliche Grenzwerte lim x x0 f(x) = ± (sog. Polstellen) und die Grenzwertbildung lim x f(x) [bzw. lim x f(x)] für alle uneigentlichen Grenzwerte von Folgen x n [bzw. x n ]. Diese Sonderfälle dienen insbesondere der Untersuchung des (asymptotischen) Verhaltens einer Funktion am Rand ihres Definitionsbereiches hierzu mehr nach Nrn. 7 und 75 Bsp. 2 f(x) = /x, D(f) = R >0, lim x 0+ (/x) = +, lim (/x) = 0 x + Mathematik für Ökonomen - Campus Duisburg von 2
2 68 Stetigkeit einer Funktion f in x 0 x 0 [a, b] D(f) Stetigkeit von f in x 0 : LGW = FW = RGW lim f(x) existiert und f(x 0 ) = lim f(x) x x 0 x x0 Linksseitige Stetigkeit von f in x 0 : LGW = FW lim f(x) existiert und f(x 0) = lim f(x) x x 0 x x 0 Rechtsseitige Stetigkeit von f in x 0 : FW = RGW lim f(x) existiert und f(x 0) = lim f(x) x x 0 + x x 0 + Ist f linksseitig stetig in x 0 und rechtsseitig stetig in x 0, so ist f auch stetig in x 0 (und umgekehrt). Ist f an jeder Stelle x 0 D(f) stetig (bzw. linksseitig stetig bzw. rechtsseitig stetig), so heißt f stetig (bzw. linksseitig stetig bzw. rechtsseitig stetig) Bsp. b Die Funktion f aus Bsp. a ist unstetig in x 0 = (wird auch bei keiner anderen Festsetzung des Funktionswertes f() stetig in x 0 = ), wäre aber bei der Festsetzung f() := linksseitig stetig in x 0 = und bei der Festsetzung f() := /3 rechtsseitig stetig in x 0 =. 69 Regeln für stetige Funktionen α R konstant Sind f und g stetig in x 0, dann auch αf, f ± g, f g und, wenn g(x 0 ) 0, f/g. Ist g stetig in x 0 und f stetig in x = g(x 0 ), dann ist f(g(x)) stetig in x 0. Entsprechende Regeln gelten für die linksseitige bzw. rechtsseitige Stetigkeit. 70 Stetigkeit von Grundfunktionen Die Grundfunktionen x, x r (r Q), e x und ln x sind stetig. Damit sind auch Funktionen stetig, die nach obigen Regeln (Nr. 69) aus stetigen Grundfunktionen zusammengesetzt sind. Sie werden sehr selten andere als derartig zusammengesetzte Funktionstypen benötigen. Allerdings wird dabei oft nicht der maximale Definitionsbereich genützt werden, sondern nur ein Stück (Teilintervall). Bei der Zusammensetzung solcher Stücke können an zumindest einigen Nahtstellen Unstetigkeiten auftreten: Stückweise Stetigkeit endlich viele Stücke Eine Funktion, die stückweise (mit angrenzenden Stücken) definiert ist und in jeder Stelle ihres Definitionsbereiches mit Ausnahme mindestens einer Stückgrenze (Nahtstelle) stetig ist, nennen wir stückweise stetig. Mathematik für Ökonomen - Campus Duisburg 2 von 2
3 Funktionen, die bis auf endlich viele Stellen stetig sind, an den Unstetigkeitsstellen aber rechtsseitig stetig sind (und einen linksseitigen Grenzwert besitzen), spielen in vielen Anwendungen eine besondere Rolle. Beispiele hierfür sind Treppenfunktionen wie Rundungsfunktionen [x], x, x und empirische Verteilungsfunktionen/kumul. Häufigkeitsverteilungen Statistik Methode : Einsetzen zur Grenzwertberechnung stetiger Funktionen Oft wird es nicht darum gehen, die Stetigkeit einer Funktion (an einer Stelle x 0 ) nachzuweisen, weil diese Eigenschaft schon aus allgemeinen Regeln gefolgert werden kann. Vielmehr wird umgekehrt das Wissen um die Stetigkeit eines Ausdrucks in x 0 dazu benützt, den Grenzwert dieses Ausdrucks in x 0 auszurechnen, nämlich durch simples Einsetzen von x 0 (verwenden der Definitionsgleichungen der Stetigkeit (Nr. 68). Bsp. 3 a Bsp. 3 b LGW in x 0 = : lim x f(x) = RGW in x 0 = : lim x + f(x) = f(x) = x für 0 x < 3/2 für x = x für < x 2 lim x = = x einsetzen lim x + (x2 2 3 ) = einsetzen = 3 Die Funktion f aus Bsp. 3 a ist wiederum unstetig in x 0 = (wird auch bei keiner anderen Festsetzung von f() stetig in ), wäre aber bei der Festsetzung f() := linksseitig stetig in und bei der Festsetzung f() := /3 rechtsseitig stetig in. Bei ökonomischen Anwendungen hat die Festlegung des Funktionswertes an Unstetigkeitsstellen oft eine inhaltliche Bedeutung Finanzmathematik 7 Stetige Ergänzung einer Funktion f in x 0 Ist x 0 D(f), aber als Grenzwert erreichbar durch Folgen x n D(f), n N, so kann f in x 0 durch seinen Grenzwert in x 0, falls es den gibt, definiert werden: f(x 0 ) := lim f(x) x D(f), x x 0 Der Definitionsbereich von f wird so durch x 0 ergänzt und f ist in x 0 stetig. Linksseitig stetige Ergänzung von f in x 0 : f(x 0 ) := lim f(x) x D(f), x x 0 Rechtsseitig stetige Ergänzung von f in x 0 : f(x 0 +) := lim f(x) x D(f), x x 0 + Mathematik für Ökonomen - Campus Duisburg 3 von 2
4 Als Sonderfälle für die Stelle x 0 und den (dann uneigentlichen) Grenzwert einer Funktion sind wiederum die idealen Zahlen ± zugelassen, d.h. wenn diese (uneigentlichen) Grenzwerte existieren die Ergänzung f(x 0 ±) := lim x x0 ± f(x) = bzw. = und die beiden Grenzwertbildungen f( ) := lim x f(x) bzw. f( ) := lim x f(x). Bsp =, 0 =, ± = 0, e =, e = 0, ln =, ln x ln(0+) =, =. Aber z.b. lim x x =? (Problem:, 0 Nr. 75) 0 Die Exponentialfunktion, eine für ökonomische ( Wachstumsfunktion) und statistische ( Normalverteilung) Anwendungen sehr wichtige Funktion, ist für jedes x R selbst durch einen Grenzwert definiert: e x := lim n n i=0 (xi /i!).! Zwei verschiedene Betrachtungsweisen (siehe auch Taylorpolynome) e x ist die Grenzwertbildung einer Folge f n (x) := n i=0 (xi /i!), n N, von Funktionswerten verschiedener Funktionen für ein festes x R im Gegensatz zur Grenzwertbildung von Folgen f(x n ), n N von Funktionswerten einer festen Funktion f und verschiedenen x n R in Zusammenhang mit der Stetigkeit dieser Funktion f. Die Grenzwerteigenschaft stetiger Funktionen berechtigt dazu, den Funktionswert eines (im Modell) stetigen f an einer rechnerisch ungünstigen oder praktisch nicht realisierbaren Stelle x durch den Funktionswert an einer rechnerisch günstigeren oder praktisch realisierbaren Stelle x 0 abzuschätzen: Näherung für f(x) bei stetigen Funktionen: x x 0 f(x) f(x 0 ) Solche Näherungen können sehr grob sein und sie erfassen nicht die Abhängigkeit der Änderungen von f(x) von den Änderungen von x. Ausgangspunkt einer Marginalanalyse Was mensch genauer haben möchte, ist etwas von der Form f(x) f(x 0 ) c (x x 0 ) also eine Aussage über eine (ungefähre) proportionale Abhängigkeit der Abweichung f(x) f(x 0 ) von kleinen Abweichungen x x 0. Hierbei soll der Proportionalitätsfaktor c allenfalls von der Basisstelle x 0 abhängen. Anders formuliert: Der Differenzenquotient f(x) f(x 0) x x 0 soll für jedes x 0 durch eine einzige Konstante ersetzt werden, die für alle x in der Nähe von x 0 ungefähr gültig ist. Bei differenzierbaren Funktionen wird dies mit dem Grenzwert des Differenzenquotienten c := f (x 0 ) möglich: Mathematik für Ökonomen - Campus Duisburg 4 von 2
5 72 Differenzierbarkeit einer Funktion f in x 0 x 0 [a, b] D(f) liegt vor, wenn der Grenzwert f (x 0 ) := f(x) f(x 0 ) lim x x0 x x 0, die Ableitung von f in x 0 existiert. Entsprechend werden die einseitigen Grenzwerte des Differentialquotienten verwendet: für die rechtsseitige Ableitung f + (x 0) (rechtsseitige Differenzierbarkeit) der rechtsseitige Grenzwert mit x x 0 +, für die linksseitige Ableitung f (x 0) (linksseitige Differenzierbarkeit) der linksseitige Grenzwert mit x x 0. Ist f linksseitig differenzierbar in x 0 und rechtsseitig differenzierbar in x 0, so ist f auch differenzierbar in x 0 (und umgekehrt). Ist f an jeder Stelle x 0 D(f) differenzierbar (bzw. linksseitig differenzierbar bzw. rechtsseitig differenzierbar), so heißt f differenzierbar (bzw. linksseitig differenzierbar bzw. rechtsseitig differenzierbar) Die Grenzwertbildung für die Ableitung berechtigt zu dem 72a marginalen (grenzwertigen) Ansatz: Näherung für f(x) bei differenzierbaren Funktionen an der Basisstelle x 0 f(x) f(x 0 ) f (x 0 ) (x x 0 ) bzw. f(x) f(x 0 ) + f (x 0 ) (x x 0 ) y = f(x 0 ) + f (x 0 ) (x x 0 ) ist die Tangentengleichung an f in (x 0, f(x 0 )) Bsp. 5 f(x) f(x 0 ) x 0 y = f(x 0 ) + f (x 0 ) (x x 0 ) Gerade durch f(x 0 ) mit der Steigung f (x 0 ) x (Einseitige) Differenzierbarkeit impliziert (einseitige) Stetigkeit: Eine in x 0 differenzierbare (bzw. linksseitig differenzierbare bzw. rechtsseitig differenzierbare) Funktion ist auch in x 0 stetig (bzw. linksseitig stetig bzw. rechtsseitig stetig).! vorsicht Die Stetigkeit der Funktion f(x), nicht der Ableitung f (x) folgt die Ableitung wird zwar meist, aber muss nicht stetig sein. Mathematik für Ökonomen - Campus Duisburg 5 von 2
6 73 Differenzierbarkeit von Grundfunktionen Die Grundfunktionen x, x r (r Q), e x und ln x sind in den nachfolgend (als D(f )) angegebenen Bereichen differenzierbar. Damit sind auch Funktionen differenzierbar, die nach folgenden Regeln (Nr. 74) aus differenzierbaren Grundfunktionen zusammengesetzt sind. Bei der Zusammensetzung Differenzierbarkeitsbereiche beachten 73a f(x) D(f) D(f ) f (x) c (konstant) R R 0 2 x R R 0 { für x < 0 für x > 0 3 a x k (k N) R R k x k 3 b x k (k N) R 0 R 0 k x k 4 a x /k (k N gerade) R 0 R >0 k x/k 4 b x /k (k N ungerade) R R 0 4 c x r (r Q) R >0 R >0 r x r 5 ln x R >0 R >0 x 6 a e x R R e x 6 b x α = e α ln x (α R 0 ) R >0 R >0 α x α 6 c b x = e x ln b (b R >0, b ) R R (ln b) b x Fast alle der in ökonomischen Anwendungen betrachteten Funktionen setzen sich unter Verwendung der bei den folgenden Rechenregeln betrachteten Operationen Vielfache [αf(x)], endliche Summen [f(x) ± g(x)], Produkte [f(x) g(x), f(x)/g(x)] und Kompositionen [f(g(x))] aus den obigen Funktionstypen zusammen. (6 b c) sind bereits abstrakte Beispiele für die Anwendung der unten folgenden Kettenregel (KR): Bsp. 6 f(x) = x α = e α ln x, f (x) = e α ln x (α x ) = x α α x = α x α. Für α N oder α Q kennen Sie diese Ableitungsregel, sie gilt auch für beliebiges α R, z.b. ist (x 2 ) = 2 x 2 (= 2 e ( 2 ) ln x ). Für f(x) = b x = e x ln b ist nach (KR): f (x) = e x ln b ln b = b x ln b. Mathematik für Ökonomen - Campus Duisburg 6 von 2
7 74 Regeln für differenzierbare Funktionen α R konstant Sind f und g differenzierbar in x 0, dann auch αf, f ± g, f g und, wenn g(x 0 ) 0, f/g. Ist g differenzierbar in x 0 und f differenzierbar in x = g(x 0 ), dann ist f(g(x)) differenzierbar in x 0. Die Ableitungen ergeben sich (auch) aus den Ableitungen der an der neu zusammengesetzten Funktion beteiligten Funktionen, jeweils an der Stelle x 0 : (αf) = αf konstante Faktoren ausklammern (f ± g) = f ± g Summen gliedweise differenzieren (PR) (f g) = f g + f g Produktregel (QR) (f/g) = (f g f g )/g 2 Quotientenregel (KR) (f(g)) = f (g) g Kettenregel Bei entsprechend rechtsseitigen bzw. linksseitigen Voraussetzungen gelten entsprechende rechtsseitige bzw. linksseitige Regeln, z.b. (PR+) (f g) + = f + g + f g + (KR+) (f(g)) + = f +(g) g + (PR ) (f g) = f g + f g (KR ) (f(g)) = f (g) g Die drei wichtigsten Grundableitungen noch einmal unter Verwendung der Kettenregel (und für die bei Anwendungen meist benötigten Definitionsbereiche) in kompakter Form: z := g(x), z := g (x) 74a f(z) D(f) D((f(z)) ) (f(z)) 7 z α (= e α ln z ) (α R 0 ) R >0 R >0 α z α z 8 ln z R >0 R >0 z z = z /z 9 e z R R e z z Bsp. 7 (a) f(x) = ( + x 2 ) 3, f (x) = 3( + x 2 ) 3 (2x) = 6x( + x 2 ) 2 (b) f(x) = ( + x 2 ) 3/2, f (x) = 3 2 ( + x2 ) 3/2 (2x) = 3x( + x 2 ) 5/2 (c) f(x) = ( + x 2 ) 2, f (x) = 2 ( + x 2 ) 2 (2x) = 2 3/2 x ( + x 2 ) (d) f(x) = ln ( + x 2 ), f (x) = (e) f(x) = e +x2, f (x) = e +x2 (2x) 2 2x + x 2 z z (f) f(x) = ln ( + e +x2 ), f (x) = ( + e+x2 ) + e +x2 = Bsp. 7e e +x2 (2x) + e +x2 Mathematik für Ökonomen - Campus Duisburg 7 von 2
8 Schreibweise f (n) (x), n N 0 für die n-te Ableitung von f Die n-te Ableitung (n ) einer Funktion f ist sukzessive definiert als Ableitung der (n )-ten Ableitung von f (wenn es die Ableitung gibt) Anfang: f (0) (x) := f(x), Schritt : f () (x) := (f (0) ) (x) = f (x), Schritt 2: f (2) (x) := (f () ) (x) = f (x), Schritt n: f (n) (x) := (f (n ) ) (x).. 3. Ableitung werden meist mit f, f, f bezeichnet, dann f (4), f (5)...! vorsicht Verwechseln Sie dies nicht mit der n-ten Potenz einer Funktion, die als f n (x) := (f(x)) n, n N 0 geschrieben wird z.b. ist der Nenner in der Quotientenregel die zweite Potenz g 2 (x 0 ) := (g(x 0 )) 2 von g und nicht die zweite Ableitung g (2) (x 0 ) := g (x 0 ) von g. Erste Anwendungen der Differentiation Hilfsmittel zur Grenzwertberechnung (auch einseitig : x x 0 ± ) 75 L Hôspitalsche Regel Vorauss.: f und g differenzierbar, f und g stetig, x 0 R oder x 0 = durch Folgen x n, n N, aus D(f) D(g) erreichbar, g (x 0 ) 0 sowie f(x 0 ) := lim f(x) und g(x 0 ) := lim f(x) beide gleich Null LHR 0 0 x x 0 x x 0 oder beide gleich LHR Wenn es dann denn Grenzwert lim x x0 f (x)/g (x) gibt, dann gibt es auch den Grenzwert lim x x0 f(x)/g(x) und beide sind gleich: ( f g )(x f(x) 0) := lim x x 0 g(x) = lim f (x) x x 0 g (x) =: (f g )(x 0) Dies kann ggf. auch erst nach wiederholter Anwendung die beiden Grenzwertprobleme 0 0 und lösen. Wegen = 0+ ist dies eigentlich nur ein Problem (Kehrwertbildung in Zähler und Nenner) und kann (aber muss nicht) auch das Grenzwertproblem (0+) = = lösen (/Kehrwert eines Faktors). Bei dem Hilfsmittel LHR gibt es also immer eine zweite Ansatzmöglichkeit wenn die eine das Problem verschärft, kann (aber muss nicht) vielleicht die andere das Problem lösen: Bsp. 8 a Für x ist (ln x)/x nicht definiert. Zähler und Nenner ableiten: x = x ln x 0, also lim x x x = 0 nach LHR. f(x) = (ln x)/x hat also den Grenzwert f( ) := 0. Mathematik für Ökonomen - Campus Duisburg 8 von 2
9 Bsp. 8 b Für x 0+ ist x ln x 0 nicht definiert. Ansatz : x ln x = nicht definiert. Z&N ableiten: x (ln x) 0 0 ( ) (ln x) 2 x = ( x) (ln x) 2 0 nicht definiert Ansatz 2: x ln x = ln x x Bsp. 8 c Gesucht: x ( ) x 2 = x 0, d.h. lim lim x (das Problem hat sich verschärft) nicht definiert. Z&N ableiten: ln x x ln x = lim = 0 mit LHR x 0+ x 0+ x. e x +e x 2 =? Zweimalige Anwendung von (x ) 2 LHR 0 0 liefert: lim e x +e x 2 e = lim x e x e x (x ) 2 x 2(x ) = lim x +e x x 2 = 2 2 =. In Bsp. 8 mehrfach verwendet: Methode Einsetzen (Z&N sind jew. stetig) Die Untersuchung des Vorzeichenverhaltens einer Funktion, speziell: von Ableitungen einer Funktion, liefert einfache Kriterien für Informationen über die Gestalt einer Funktion. Bereiche/Intervalle, über denen eine Funktion (die Ableitung einer Funktion) negative bzw. positive Werte annimmt oder gleich Null ist ( Nullstelle ), werden besonders benannte Bereiche/Stellen: Nullstellen, stationäre Stellen einer Funktion f Eine Stelle x 0 mit f(x 0 ) = 0 heißt Nullstelle von f Eine Stelle x 0 mit f (x 0 ) = 0 heißt stationäre Stelle von f Jede stationäre Stelle x 0 ist eine mögliche Extremstelle von f, die Tangente in f(x 0 ) ist parallel zur x-achse (y = f(x 0 ), Steigung f (x 0 ) = 0) Nullstelle von f : Bestimmung von Urbildern eines Funktionswertes (meist: von Funktionswerten der Umkehrfunktion ). Gegeben: g(x) = c, gesucht: x. Mögliche Methode: Nullstellenberechnung für f(x) = g(x) c Thema 9 Vorz./Nullst. von f : Monotoniebereiche von f und Teil der Extremwertbestimmung für f Vorz./Nullst. von f : Krümmungsbereiche von f und Teil der Extremwertbestimmung für f, Teil der Extremwertbestimmung für f (Wendepunkt für f) Vorzeichen/Nullstellen von f = (f ) liefern also (gleichbedeutend) Monotoniebereiche von f und sind Teil der Extremwertbestimmung für f. Vorzeichen/Nullstellen von f = (f ) = (f ) liefern (gleichbedeutend) Krümmungsbereiche für f, Monotoniebereiche von f... u.s.w: Wir wenden, für unterschiedliche Funktionen, immer wieder die gleichen Methoden an, nur die Interpretation/Benennung ist je nach differentieller Denktiefe eine andere. Mathematik für Ökonomen - Campus Duisburg 9 von 2
10 Wenn unten von Ableitungen in x [a, b] die Rede ist, so sind am Rand x = a (bzw. x = b) die rechtsseitige (bzw. linksseitige) Ableitung gemeint. 76 Monotonie einer differenzierbaren Funktion [Monotonie Nr. 8] f (x) > 0 für alle x [a, b] f ist strikt monoton wachsend über [a, b] f (x) < 0 für alle x [a, b] f ist strikt monoton fallend über [a, b] f (x) 0 für alle x [a, b] f ist monoton wachsend über [a, b] f (x) 0 für alle x [a, b] f ist monoton fallend über [a, b] 77 Extrempunkte einer Funktion f Extremum = Min. oder Max. (x 0, f(x 0 )) heißt lokales Maximum von f, wenn um x 0 herum ein Intervall I gebildet werden kann so, dass f(x 0 ) f(x) für alle x D(f) mit x I. (x 0, f(x 0 )) heißt lokales Minimum von f, wenn um x 0 herum ein Intervall I gebildet werden kann so, dass f(x 0 ) f(x) für alle x D(f) mit x I. Ein lokales Maximum (bzw. Minimum) heißt global, wenn der entsprechende Wertevergleich von f(x 0 ) f(x) (bzw. f(x 0 ) f(x)) für jedes x aus dem Definitionsbereich von f richtig ist. x 0 heißt Extremstelle, f(x 0 ) Extremwert, (x 0, f(x 0 )) Extrempunkt. Zur Untersuchung einer Funktion auf Konkavität/Konvexität werden wir nur das folgende (einfach handhabbare) Kriterium der zweiten Ableitung verwenden. Eine weitere Charakterisierung dient uns als Interpretationshilfe Thema 9 78 Konvexität/Konkavität, Wendepunkt Krümmung Eine Funktion f heißt (strikt) konvex über [a, b], wenn für je zwei Stellen x, x 2 die Verbindungsgerade zwischen den beiden Funktionswerten (strikt) oberhalb der Funktionskurve zwischen x und x 2 liegt. Äquivalent für zweifach differenzierbare Funktionen f: f konvex über [a, b] f (x) 0 x [a, b] f strikt konvex über [a, b] f (x) > 0 x [a, b] Für (strikte) Konkavität wird oben jedes oberhalb durch unterhalb ersetzt, jedes Zeichen durch und jedes Zeichen > durch <. Ein Punkt (x 0, f(x 0 )) an der Stelle x 0 mit Funktionswert f(x 0 ) heißt Wendepunkt, wenn f an der Stelle x 0 seine Krümmung ändert, d.h. von strikter Konvexität zu strikter Konkavität wechselt oder umgekehrt. Mathematik für Ökonomen - Campus Duisburg 0 von 2
11 Kriterien und Methode für über [a, b] mehrfach differenzierbare Funktionen f 79 Extrempunkt- und Wendepunktbestimmung D(f) = [a, b] Berechne f und f über [a, b] 2 Bestimme die strikten Vorzeichenbereiche ± von f in [a, b] Bereich(+): strikte Zunahme von f, Bereich( ): strikte Abnahme von f, ggf. Nullstellen x 0 von f (stationäre Stellen von f) berechnen. 3 Extrempunktbestimmung 3- Lokale Extrema (falls es Stellen x 0 mit f (x 0 ) = 0 gibt): wenn f (x 0 ) < 0, dann ist (x 0, f(x 0 )) lokaler Maximalpunkt, wenn f (x 0 ) > 0, dann ist (x 0, f(x 0 )) lokaler Minimalpunkt, wenn f (x 0 ) = 0, dann ist (zunächst) keine Entscheidung möglich. 3-2 Globale Extrema: Vergleiche f(a) und f(b) und falls es solche überhaupt gibt lokale Extremwerte f(x 0 ). 4 Bestimme die strikten Vorzeichenbereiche ± von f in [a, b] Bereich(+): strikte Konvexität, Bereich( ): strikte Konkavität von f, ggf. Nullstellen x 0 von f (Wendepunktkandidaten für f) berechnen. 5 Wendepunktbestimmung (falls es Stellen x 0 mit f (x 0 ) = 0 gibt) (a) Vergleichskriterium, falls auf Basis von Schritt 4 direkt möglich: bei einem Vorzeichendurchgang +0 von f : konvex/konkav-wp bei einem Vorzeichendurchgang 0+ von f : konkav/konvex-wp (b) Ableitungskriterium (falls es Stellen x 0 mit f (x 0 ) = 0 gibt): wenn f (x 0 ) < 0, dann ist (x 0, f(x 0 )) konvex/konkav-wendepunkt, wenn f (x 0 ) > 0, dann ist (x 0, f(x 0 )) konkav/konvex-wendepunkt, wenn f (x 0 ) = 0, dann ist (zunächst) keine Entscheidung möglich. Schritte 4 5 sind (methodisch) nur die Anwendung von 3 auf f statt auf f. In der Situation f (x 0 ) = 0 = f (x 0 ) kann evtl. die Anwendung von 5 auf f statt auf f Erfolg bringen. Derartig gefundene Extrema/Wendepunkte x 0 für f sind dann auch Extrema/Wendepunkte des ursprünglichen f. [ u.s.w. ] Situationen, in denen die Differentialrechnung nicht so einfach wie in Nr. 79 helfen kann. Solche Funktionstypen werden, Unstetigkeitsstellen Knicke statt mit feineren mathematischen Methoden, oft nur graphisch gelöst (und wenn die Spitzen Funktionen von unbekannten Parametern abhängen für gewisse Szenarios ). Mathematik für Ökonomen - Campus Duisburg von 2
12 Bsp. 9 f(x) = ( + x) ln( + x), D(f) = R 0. Für alle x 0 ist f (x) = ln( + x) + ln() + = > 0, f (x) = ( + x) > 0. Also ist f strikt monoton wachsend, strikt konvex, ohne Maximum, ohne Wendepunkt, globales Minimum ist f(0) = ln = 0. Bsp. 0 f(x) = e (x 2)2 /2, D(f) = [, 5], f (x) = e (x 2)2 /2 (2 x) f(x) f (x) f (x) f (x) = e (x 2)2 /2 (2 x) 2 e (x 2)2 /2 = e (x 2)2 /2 ((2 x) 2 ) Vorzeichen der ersten Ableitung: Da e z > 0 für jedes z ist, bestimmt der Faktor (2 x) das Vorzeichen von f : { > 0, 2 > x, str. wachsend f (x) = = 0, 2 = x, Nullstelle < 0, 2 < x, strikt fallend Lokale Extrema: Da f (2) = < 0, ist x = 2 eine Max-Stelle mit Max-Wert f(2) = : (2, ) ist ein lokaler Max-Punkt. Globale Extrema: f( ) = e 9/2 < globales Min. f(2) = globales Max. f(5) = e 9/2 < globales Min. Vorzeichen der zweiten Ableitung: Da e z > 0 für jedes z ist, bestimmt der Faktor ((2 x) 2 ) das Vorzeichen von f. Vorzeichen dieses Faktors: z.b. so: (2 x) 2 = x 2 4x + 3 hat die Nullstellen x = und x 2 = 3, also ist (2 x) 2 = (x ) (x 3) mit den beiden einzigen Möglichkeiten: oder Ein Testwert (z.b. x = 0: ( )( 3) = 3 > 0) findet die erste Möglichkeit. Damit sind die Bereiche [, ] und [3, 5] für Konvexität (+), und [, 3] für Konkavität ( ), die konvex/konkav-stelle und die konkav/konvex-stelle 3 direkt angegeben. WPunkte: (, f()) und (3, f(3)) mit f() = e /2 = f(3). + 3 Mathematik für Ökonomen - Campus Duisburg 2 von 2
Grenzwerte-Stetigkeit-Differentiation einer Funktion
 Grenzwerte-Stetigkeit-Differentiation einer Funktion Wir betrachten ab jetzt nur noch Funktionen f : D(f) R (Uneigentliche) Grenzwerte von Zahlenfolgen Nrn. 41-45 46 Grenzwert einer Funktion f in x 0 x
Grenzwerte-Stetigkeit-Differentiation einer Funktion Wir betrachten ab jetzt nur noch Funktionen f : D(f) R (Uneigentliche) Grenzwerte von Zahlenfolgen Nrn. 41-45 46 Grenzwert einer Funktion f in x 0 x
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Anwendung der Differentiation in der Marginalanalyse
 Anwendung der Differentiation in der Marginalanalyse Bereits in Thema 5 wurde vorgestellt, wie bei einer (ökonomischen) Funktion f über f(x) f(x 0 ) f (x 0 ) (x x 0 ) proportional die Ableitung an der
Anwendung der Differentiation in der Marginalanalyse Bereits in Thema 5 wurde vorgestellt, wie bei einer (ökonomischen) Funktion f über f(x) f(x 0 ) f (x 0 ) (x x 0 ) proportional die Ableitung an der
x 1 keinen rechtsseitigen Grenzwert x 0+ besitzen. (Analog existiert der linksseitige Grenzwert nicht.)
 Differentialrechnung 1 Grenzwerte Gegeben sei ein Intervall I R, a I {, } und f : I\{a} R. Die Funktion f kann sehr wohl auch an der Stelle x = a erklärt sein, wir wollen aber nur wissen wie sich die Funktion
Differentialrechnung 1 Grenzwerte Gegeben sei ein Intervall I R, a I {, } und f : I\{a} R. Die Funktion f kann sehr wohl auch an der Stelle x = a erklärt sein, wir wollen aber nur wissen wie sich die Funktion
Mathematischer Vorbereitungskurs für das MINT-Studium
 Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
2015, MNZ. Jürgen Schmidt. Vorkurs. Mathematik. Ableiten. Tag WS 2015/16
 Vorkurs 4. Mathematik Ableiten WS 2015/16 Tag Einführendes Beispiel Vernachlässigen wir den Luftwiderstand, so können wir in hinreichender Näherung für den freien Fall eines Körpers s(t) = 5t 2 als Weg-Zeit-Abhängigkeit
Vorkurs 4. Mathematik Ableiten WS 2015/16 Tag Einführendes Beispiel Vernachlässigen wir den Luftwiderstand, so können wir in hinreichender Näherung für den freien Fall eines Körpers s(t) = 5t 2 als Weg-Zeit-Abhängigkeit
Differentiation und Taylorentwicklung. Thomas Fehm
 Differentiation und Taylorentwicklung Thomas Fehm 4. März 2009 1 Differentiation in R 1.1 Grundlagen Definition 1 (Ableitung einer Funktion) Es sei f eine Funktion die auf dem Intervall I R definiert ist.
Differentiation und Taylorentwicklung Thomas Fehm 4. März 2009 1 Differentiation in R 1.1 Grundlagen Definition 1 (Ableitung einer Funktion) Es sei f eine Funktion die auf dem Intervall I R definiert ist.
Anwendungen der Differentialrechnung
 KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
9. Übungsblatt zur Vorlesung Mathematik I für Informatik
 Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Mathematik I Herbstsemester 2018 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Eigenschaften stetiger Funktionen Buch Kap. 2.5
 Eigenschaften stetiger Funktionen Buch Kap. 2.5 Satz 2.6: (Nullstellensatz) Ist f : [a, b] R stetig und haben f (a) und f (b) unterschiedliche Vorzeichen, so besitzt f in (a, b) mindestens eine Nullstelle.
Eigenschaften stetiger Funktionen Buch Kap. 2.5 Satz 2.6: (Nullstellensatz) Ist f : [a, b] R stetig und haben f (a) und f (b) unterschiedliche Vorzeichen, so besitzt f in (a, b) mindestens eine Nullstelle.
HM I Tutorium 9. Lucas Kunz. 19. Dezember 2018
 HM I Tutorium 9 Lucas Kunz 19. Dezember 2018 Inhaltsverzeichnis 1 Theorie 2 1.1 Definition der Ableitung............................ 2 1.2 Ableitungsregeln................................ 2 1.2.1 Linearität................................
HM I Tutorium 9 Lucas Kunz 19. Dezember 2018 Inhaltsverzeichnis 1 Theorie 2 1.1 Definition der Ableitung............................ 2 1.2 Ableitungsregeln................................ 2 1.2.1 Linearität................................
Kapitel 5: Differentialrechnung
 Kapitel 5: Differentialrechnung Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 5: Differentialrechnung 1 / 23 Gliederung 1 Grundbegriffe 2 Abbildungen
Kapitel 5: Differentialrechnung Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 5: Differentialrechnung 1 / 23 Gliederung 1 Grundbegriffe 2 Abbildungen
Übersicht. 1. Motivation. 2. Grundlagen
 Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Anwendungen der Differentialrechnung
 KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
Kapitel 7. Differentialrechnung. Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56
 Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f x = f (x 0 + x) f (x 0 ) x = f (x)
Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f x = f (x 0 + x) f (x 0 ) x = f (x)
Monotonie, Konkavität und Extrema
 Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Monotonie, Konkavität und Extrema
 Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Mathematischer Vorkurs NAT-ING II
 Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
Kurvendiskussion. Mag. Mone Denninger 10. Oktober Extremwerte (=Lokale Extrema) 2. 5 Monotonieverhalten 3. 6 Krümmungsverhalten 4
 Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion.
 4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
Differentialrechnung. Mathematik W14. Christina Sickinger. Berufsreifeprüfung. v 1 Christina Sickinger Mathematik W14 1 / 79
 Mathematik W14 Christina Sickinger Berufsreifeprüfung v 1 Christina Sickinger Mathematik W14 1 / 79 Die Steigung einer Funktion Wir haben bereits die Steigung einer linearen Funktion kennen gelernt! Eine
Mathematik W14 Christina Sickinger Berufsreifeprüfung v 1 Christina Sickinger Mathematik W14 1 / 79 Die Steigung einer Funktion Wir haben bereits die Steigung einer linearen Funktion kennen gelernt! Eine
3 Folgen, Reihen und stetige Funktionen
 Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
Differenzialrechnung
 Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathematischer Vorbereitungskurs für das MINT-Studium
 Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de WS 2016/2017 Vorlesung 7 MINT Mathkurs WS 2016/2017 1 / 20 Stetigkeit einer Funktion (continuity of a
Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de WS 2016/2017 Vorlesung 7 MINT Mathkurs WS 2016/2017 1 / 20 Stetigkeit einer Funktion (continuity of a
Technische Universität München Zentrum Mathematik. Übungsblatt 4
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Mathematik 3 für Informatik
 Gunter Ochs Sommersemester 0 Mathematik 3 für Informatik Hausaufgabenblatt Lösungshinweise ohne Garantie auf Fehlerfeiheit). Seien f ) = { {, falls, falls und f ) =. ln, falls a) Skizzieren
Gunter Ochs Sommersemester 0 Mathematik 3 für Informatik Hausaufgabenblatt Lösungshinweise ohne Garantie auf Fehlerfeiheit). Seien f ) = { {, falls, falls und f ) =. ln, falls a) Skizzieren
Klausur Mathematik 2
 Mathematik für Ökonomen WS 215/16 Campus Duisburg PD Dr. V. Krätschmer, Fakultät für Mathematik Klausur Mathematik 2 16.2.216, 13:3-15:3 Uhr (12 Minuten) Erlaubte Hilfsmittel: Nur reine Schreib- und Zeichengeräte.
Mathematik für Ökonomen WS 215/16 Campus Duisburg PD Dr. V. Krätschmer, Fakultät für Mathematik Klausur Mathematik 2 16.2.216, 13:3-15:3 Uhr (12 Minuten) Erlaubte Hilfsmittel: Nur reine Schreib- und Zeichengeräte.
6 Die Bedeutung der Ableitung
 6 Die Bedeutung der Ableitung 24 6 Die Bedeutung der Ableitung Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung Rückschlüsse über die Funktion f ziehen kann Zunächst
6 Die Bedeutung der Ableitung 24 6 Die Bedeutung der Ableitung Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung Rückschlüsse über die Funktion f ziehen kann Zunächst
Da der Nenner immer positiv ist, folgt. g (x) > 0 2x(2 x) > 0 0 < x < 2 g (x) < 0 2x(2 x) < 0 x < 0 oder x > 2
 Da der Nenner immer positiv ist, folgt g (x) > 0 x( x) > 0 0 < x < g (x) < 0 x( x) < 0 x < 0 oder x > Also ist g auf (0,) streng monoton wachsend sowie auf (,0) und auf (, ) strengmonotonfallend.außerdemistg
Da der Nenner immer positiv ist, folgt g (x) > 0 x( x) > 0 0 < x < g (x) < 0 x( x) < 0 x < 0 oder x > Also ist g auf (0,) streng monoton wachsend sowie auf (,0) und auf (, ) strengmonotonfallend.außerdemistg
{, wenn n gerade ist,, wenn n ungerade ist.
 11 GRENZWERTE VON FUNKTIONEN UND STETIGKEIT 60 Mit anderen Worten, es ist lim f(x) = b lim f (, a)(x) = b, x a x a wobei f (, a) die Einschränkung von f auf (, a) ist. Entsprechendes gilt für lim x a.
11 GRENZWERTE VON FUNKTIONEN UND STETIGKEIT 60 Mit anderen Worten, es ist lim f(x) = b lim f (, a)(x) = b, x a x a wobei f (, a) die Einschränkung von f auf (, a) ist. Entsprechendes gilt für lim x a.
Funktionsgrenzwerte, Stetigkeit
 Funktionsgrenzwerte, Stetigkeit Häufig tauchen in der Mathematik Ausdrücke der Form lim f(x) auf. x x0 Derartigen Ausdrücken wollen wir jetzt eine präzise Bedeutung zuweisen. Definition. b = lim f(x) wenn
Funktionsgrenzwerte, Stetigkeit Häufig tauchen in der Mathematik Ausdrücke der Form lim f(x) auf. x x0 Derartigen Ausdrücken wollen wir jetzt eine präzise Bedeutung zuweisen. Definition. b = lim f(x) wenn
Institut für Analysis WiSe 2018/2019 Prof. Dr. Dirk Hundertmark Dr. Markus Lange. Analysis 1. Aufgabenzettel 14
 Institut für Analysis WiSe 2018/2019 Prof. Dr. Dirk Hundertmark 03.02.2019 Dr. Markus Lange Analysis 1 Aufgabenzettel 14 Dieser Zettel wird in der letzten Übung des Semesters am 08.02.2019 besprochen Aufgabe
Institut für Analysis WiSe 2018/2019 Prof. Dr. Dirk Hundertmark 03.02.2019 Dr. Markus Lange Analysis 1 Aufgabenzettel 14 Dieser Zettel wird in der letzten Übung des Semesters am 08.02.2019 besprochen Aufgabe
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
ε δ Definition der Stetigkeit.
 ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
6 Di erentialrechnung, die Exponentialfunktion
 6 Di erentialrechnung, die Exonentialfunktion 6. Exonentialfunktion Wir führen die Exonentialfunktion ein, die eine stetige Funktion mit folgenden Eigenschaften ist: ex(x + y) =ex(x)ex(y) (8) ex(0) =,
6 Di erentialrechnung, die Exonentialfunktion 6. Exonentialfunktion Wir führen die Exonentialfunktion ein, die eine stetige Funktion mit folgenden Eigenschaften ist: ex(x + y) =ex(x)ex(y) (8) ex(0) =,
Mathematik für Studierende der Biologie Wintersemester 2017/18. Grundlagentutorium 4 Lösungen
 Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
I. Verfahren mit gebrochen rationalen Funktionen:
 I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
Mathematik zum Mitnehmen
 Mathematik zum Mitnehmen Zusammenfassungen und Übersichten aus Arens et al., Mathematik Bearbeitet von Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth
Mathematik zum Mitnehmen Zusammenfassungen und Übersichten aus Arens et al., Mathematik Bearbeitet von Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth
Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 12. Übung
 TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, WS 017/18 Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 1. Übung
TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, WS 017/18 Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 1. Übung
Thema 5 Differentiation
 Thema 5 Differentiation Definition 1 Sei f : D R. Dann ist f im Punkt x 0 differenzierbar, falls f(x) f(x 0 ) x x 0 x x 0 auf der Menge D \ {x 0 } existiert. Der Limes ist dann die Ableitung von f im Punkt
Thema 5 Differentiation Definition 1 Sei f : D R. Dann ist f im Punkt x 0 differenzierbar, falls f(x) f(x 0 ) x x 0 x x 0 auf der Menge D \ {x 0 } existiert. Der Limes ist dann die Ableitung von f im Punkt
Differentialrechnung
 Kapitel 7 Differentialrechnung Josef Leydold Auffrischungskurs Mathematik WS 2017/18 7 Differentialrechnung 1 / 75 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f = f ( 0 + ) f ( 0 ) = f
Kapitel 7 Differentialrechnung Josef Leydold Auffrischungskurs Mathematik WS 2017/18 7 Differentialrechnung 1 / 75 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f = f ( 0 + ) f ( 0 ) = f
Differentialrechnung. Kapitel 7. Differenzenquotient. Graphische Interpretation des Differentialquotienten. Differentialquotient
 Differenzenquotient Sei f : R R eine Funktion. Der Quotient Kapitel 7 Differentialrechnung f = f 0 + f 0 = f 0 0 heißt Differenzenquotient an der Stelle 0., Sekante 0, f 0 f 0 Josef Leydold Auffrischungskurs
Differenzenquotient Sei f : R R eine Funktion. Der Quotient Kapitel 7 Differentialrechnung f = f 0 + f 0 = f 0 0 heißt Differenzenquotient an der Stelle 0., Sekante 0, f 0 f 0 Josef Leydold Auffrischungskurs
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Wirtschaftsmathematik
 Wirtschatsmathematik ür die Betriebswirtschatslehre (B.Sc.) Sommersemester 017 Dr. rer. nat. habil. E-mail: adam-georg.balogh@h-da.de 1 Kurvendiskussion / Analyse von Funktionen Anwendung der Dierentialrechnung
Wirtschatsmathematik ür die Betriebswirtschatslehre (B.Sc.) Sommersemester 017 Dr. rer. nat. habil. E-mail: adam-georg.balogh@h-da.de 1 Kurvendiskussion / Analyse von Funktionen Anwendung der Dierentialrechnung
bestimmt werden. Allein die Regel (5.4) würde wegen g(x) = 2, folglich erhalten wir den korrekten lim
 bestimmt werden. Allein die Regel (5.4) würde wegen f (x) lim x g (x) = lim 2e 2x = lim x e x x 2ex = 0 dengrenzwert0für(5.5)liefern.dasistaberfalsch,dennwegen lim 0 ist lim x g(x) = 2, folglich erhalten
bestimmt werden. Allein die Regel (5.4) würde wegen f (x) lim x g (x) = lim 2e 2x = lim x e x x 2ex = 0 dengrenzwert0für(5.5)liefern.dasistaberfalsch,dennwegen lim 0 ist lim x g(x) = 2, folglich erhalten
13. Übungsblatt zur Mathematik I für Maschinenbau
 Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 3. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 00/ 07.0.-.0. Aufgabe G Stetigkeit) a) Gegeben
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 3. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 00/ 07.0.-.0. Aufgabe G Stetigkeit) a) Gegeben
Funktionen untersuchen
 Funktionen untersuchen Mögliche Fragestellungen Definition: lokale und globale Extrema Monotonie und Extrema Notwendige Bedingung für Extrema Hinreichende Kriterien, Vergleich Krümmungsverhalten Neumann/Rodner
Funktionen untersuchen Mögliche Fragestellungen Definition: lokale und globale Extrema Monotonie und Extrema Notwendige Bedingung für Extrema Hinreichende Kriterien, Vergleich Krümmungsverhalten Neumann/Rodner
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
R. Brinkmann Seite
 R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
Gegeben: Die beiden Funktionen (a x) 2, 0 x < 1
 SoSe 216 H-Aufgaben sind weiteres, bunt gemischtes Übungsmaterial, das teilweise auch, wenn die Zeit reicht, in den Tutorien besprochen wird. Im Laufe des Semesters erhalten Sie zu diesen Aufgaben Ergebniskontrollen
SoSe 216 H-Aufgaben sind weiteres, bunt gemischtes Übungsmaterial, das teilweise auch, wenn die Zeit reicht, in den Tutorien besprochen wird. Im Laufe des Semesters erhalten Sie zu diesen Aufgaben Ergebniskontrollen
Differentialrechnung
 Katharina Brazda 5. März 007 Inhaltsverzeichnis Motivation. Das Tangentenproblem................................... Das Problem der Momentangeschwindigkeit.......................3 Differenzenquotient und
Katharina Brazda 5. März 007 Inhaltsverzeichnis Motivation. Das Tangentenproblem................................... Das Problem der Momentangeschwindigkeit.......................3 Differenzenquotient und
Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Vorlesung Mathematik für Ingenieure I (Wintersemester 2007/08)
 1 Vorlesung Mathematik für Ingenieure I (Wintersemester 2007/08) Kapitel 4: Konvergenz und Stetigkeit Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. November 2007) Folgen Eine Folge
1 Vorlesung Mathematik für Ingenieure I (Wintersemester 2007/08) Kapitel 4: Konvergenz und Stetigkeit Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. November 2007) Folgen Eine Folge
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 6. Übung: Woche vom bis
 Übungsaufgaben 6. Übung: Woche vom 17. 11. bis 21. 11. 2014 Heft Ü1: 9.1 (d,n,t); 9.2 (b,h,i); 9.3 (b,e); 9.4 (b,e,f) Übungsverlegung (einmalig!): Gruppe VIW 02 nach Mo., 5. DS; WIL C 204 (für Mittwoch,
Übungsaufgaben 6. Übung: Woche vom 17. 11. bis 21. 11. 2014 Heft Ü1: 9.1 (d,n,t); 9.2 (b,h,i); 9.3 (b,e); 9.4 (b,e,f) Übungsverlegung (einmalig!): Gruppe VIW 02 nach Mo., 5. DS; WIL C 204 (für Mittwoch,
Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften:
 1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
x e x sin(x) lim oder lim bestimmen lassen.
 Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Vorlesungen Analysis von B. Bank
 Vorlesungen Analysis von B. Bank vom 23.4.2002 und 26.4.2002 Zunächst noch zur Stetigkeit von Funktionen f : D(f) C, wobei D(f) C. (Der Text schliesst unmittelbar an die Vorlesung vom 19.4.2002 an.) Auf
Vorlesungen Analysis von B. Bank vom 23.4.2002 und 26.4.2002 Zunächst noch zur Stetigkeit von Funktionen f : D(f) C, wobei D(f) C. (Der Text schliesst unmittelbar an die Vorlesung vom 19.4.2002 an.) Auf
Stetige Funktionen. Definition. Seien (X, d) und (Y, ϱ) metrische Räume und f : X Y eine Abbildung. D(f) X sei der Definitionsbereich von f.
 Stetige Funktionen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume), spielen eine zentrale Rolle in der Mathematik. In der Analysis sind Abbildungen
Stetige Funktionen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume), spielen eine zentrale Rolle in der Mathematik. In der Analysis sind Abbildungen
Kompetenz: Verinnerlichung des Mittelwertsatzes Daraus ergibt sich leicht der wichtige Mittelwertsatz der Differentialrechnung:
 16 Mittelwertsätze und Anwendungen 71 16 Mittelwertsätze und Anwendungen Lernziele: Konzepte: Konvexität und Konkavität Resultate: Mittelwertsätze der Differentialrechnung Methoden: Regeln von de l Hospital
16 Mittelwertsätze und Anwendungen 71 16 Mittelwertsätze und Anwendungen Lernziele: Konzepte: Konvexität und Konkavität Resultate: Mittelwertsätze der Differentialrechnung Methoden: Regeln von de l Hospital
MIA Analysis einer reellen Veränderlichen WS 06/07. Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen
 Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
3.2 Funktionsuntersuchungen mittels Differentialrechnung
 3. Funktionsuntersuchungen mittels Differentialrechnung 46 3. Funktionsuntersuchungen mittels Differentialrechnung In diesem Abschnitt betrachten wir Funktionen f: D, welche je nach Bedarf zumindest ein-
3. Funktionsuntersuchungen mittels Differentialrechnung 46 3. Funktionsuntersuchungen mittels Differentialrechnung In diesem Abschnitt betrachten wir Funktionen f: D, welche je nach Bedarf zumindest ein-
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann
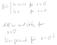 Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Kapitel 5 Differential- und Integralrechnung in einer Variablen
 Kapitel 5 Differential- und Integralrechnung in einer Variablen Inhaltsverzeichnis DIE ABLEITUNG... 3 DEFINITIONEN... 3 EIGENSCHAFTEN UND ABLEITUNGSREGELN... 4 TAYLOR SCHE FORMEL UND MITTELWERTSATZ...
Kapitel 5 Differential- und Integralrechnung in einer Variablen Inhaltsverzeichnis DIE ABLEITUNG... 3 DEFINITIONEN... 3 EIGENSCHAFTEN UND ABLEITUNGSREGELN... 4 TAYLOR SCHE FORMEL UND MITTELWERTSATZ...
Stetigkeit. Definitionen. Beispiele
 Stetigkeit Definitionen Stetigkeit Sei f : D mit D eine Funktion. f heißt stetig in a D, falls für jede Folge x n in D (d.h. x n D für alle n ) mit lim x n a gilt: lim f x n f a. Die Funktion f : D heißt
Stetigkeit Definitionen Stetigkeit Sei f : D mit D eine Funktion. f heißt stetig in a D, falls für jede Folge x n in D (d.h. x n D für alle n ) mit lim x n a gilt: lim f x n f a. Die Funktion f : D heißt
19.2 Mittelwertsatz der Differentialrechnung
 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 19.1 Satz von Rolle 19.2 Mittelwertsatz der Differentialrechnung 19.4 Globaler Wachstumssatz 19.6 Verallgemeinerter Mittelwertsatz der Differentialrechnung
19 Mittelwertsätze der Differentialrechnung mit Anwendungen 19.1 Satz von Rolle 19.2 Mittelwertsatz der Differentialrechnung 19.4 Globaler Wachstumssatz 19.6 Verallgemeinerter Mittelwertsatz der Differentialrechnung
Der Abschluss D ist die Menge, die durch Hinzunahme der Intervallränder entsteht, in den obigen Beispielen also
 Festlegung Definitionsbereich 11.1 Festlegung Definitionsbereich Festlegung: Wir betrachten Funktionen f : D Ñ R, deren Definitionsbereich eine endliche Vereinigung von Intervallen ist, also z.b. D ra,
Festlegung Definitionsbereich 11.1 Festlegung Definitionsbereich Festlegung: Wir betrachten Funktionen f : D Ñ R, deren Definitionsbereich eine endliche Vereinigung von Intervallen ist, also z.b. D ra,
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur 11. Übung
 TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, 06. Dezember 06 Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur. Übung In
TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, 06. Dezember 06 Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur. Übung In
! Die Klausureingrenzung besteht in Aufgabentypen. Die Testaufgaben
 Vorbemerkung zu den Testaufgaben Die klausurrelevanten Aufgabentypen, der Klausurablauf und das Bewertungsschema (Stichwort: Methodenpunkte ) sind im Klausurinfo erläutert.! Die Klausureingrenzung besteht
Vorbemerkung zu den Testaufgaben Die klausurrelevanten Aufgabentypen, der Klausurablauf und das Bewertungsschema (Stichwort: Methodenpunkte ) sind im Klausurinfo erläutert.! Die Klausureingrenzung besteht
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
Wichtige Klassen reeller Funktionen
 0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
differenzierbare Funktionen
 Kapitel IV Differenzierbare Funktionen 18 Differenzierbarkeit und Rechenregeln für differenzierbare Funktionen 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 20 Gleichmäßige Konvergenz von
Kapitel IV Differenzierbare Funktionen 18 Differenzierbarkeit und Rechenregeln für differenzierbare Funktionen 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 20 Gleichmäßige Konvergenz von
Mathe- Multiple-Choice-Test für Wirtschaftsinformatiker
 REELLE FUNKTIONEN 1 Was muss aufgeführt werden, wenn man eine reelle Funktion angibt? a) Ihre Funktionsvorschrift und ihren Wertebereich. Ihre Funktionsvorschrift und ihren Definitionsbereich. c) Den Wertebereich
REELLE FUNKTIONEN 1 Was muss aufgeführt werden, wenn man eine reelle Funktion angibt? a) Ihre Funktionsvorschrift und ihren Wertebereich. Ihre Funktionsvorschrift und ihren Definitionsbereich. c) Den Wertebereich
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
1 Höhere Ableitungen 2. 2 Mittelwertsatz und Monotonie 3. 3 Konvexe und konkave Funktionen 5. 4 Lokale und globale Extremalstellen 7
 Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Kapitel 7 Differentialrechnung
 Kapitel 7 Differentialrechnung 245 Kapitel 7.1 Grundbegriffe 246 Der Differentialquotient und das Integral sind die Kernbegriffe der Analysis. Ableitung und Integralbegriff werden durch gewisse Grenzwerte
Kapitel 7 Differentialrechnung 245 Kapitel 7.1 Grundbegriffe 246 Der Differentialquotient und das Integral sind die Kernbegriffe der Analysis. Ableitung und Integralbegriff werden durch gewisse Grenzwerte
Mathematik 1 Bachelorstudiengang Maschinenbau
 Mathematik 1 Bachelorstudiengang Maschinenbau Prof. Dr. Stefan Etschberger Hochschule Augsburg Sommersemester 2012 7. Differentialrechnung einer Veränderlichen 7.2. Differentialquotient und Ableitung
Mathematik 1 Bachelorstudiengang Maschinenbau Prof. Dr. Stefan Etschberger Hochschule Augsburg Sommersemester 2012 7. Differentialrechnung einer Veränderlichen 7.2. Differentialquotient und Ableitung
Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2012/13 Hochschule Augsburg Aufgabe 98 12.12.2012 Untersuchen Sie die Funktion f W R! R mit f.x/
Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2012/13 Hochschule Augsburg Aufgabe 98 12.12.2012 Untersuchen Sie die Funktion f W R! R mit f.x/
Mathematik für Studierende der Biologie Wintersemester 2018/19. Grundlagentutorium 4 Lösungen
 Mathematik für Studierende der Biologie Wintersemester 2018/19 Grundlagentutorium Lösungen Sebastian Groß Termin Mittwochs 15:5 17:5 Großer Hörsaal Biozentrum (B00.019) E-Mail gross@bio.lmu.de Sprechzeiten
Mathematik für Studierende der Biologie Wintersemester 2018/19 Grundlagentutorium Lösungen Sebastian Groß Termin Mittwochs 15:5 17:5 Großer Hörsaal Biozentrum (B00.019) E-Mail gross@bio.lmu.de Sprechzeiten
Kontrollfragen zur Unterrichtsstunde
 Kontrollfragen zur Unterrichtsstunde Frage 1: Das Newtonverfahren ist eine Methode zur Bestimmung A: der Extremstellen eines C: des Verhalten im Unendlichen. B: der Nullstellen eines D: der Fallzeit eines
Kontrollfragen zur Unterrichtsstunde Frage 1: Das Newtonverfahren ist eine Methode zur Bestimmung A: der Extremstellen eines C: des Verhalten im Unendlichen. B: der Nullstellen eines D: der Fallzeit eines
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Für differenzierbare Funktionen f ist Konvexität gleichbedeutend zu f konvex über [a, b]
![Für differenzierbare Funktionen f ist Konvexität gleichbedeutend zu f konvex über [a, b] Für differenzierbare Funktionen f ist Konvexität gleichbedeutend zu f konvex über [a, b]](/thumbs/92/110918398.jpg) Anwendungen der Differentiation Strikte Monotonie einer Funktion f über einem Intervall [a, b] garantiert die Eistenz der Umkehrfunktion f, die nicht immer formelmäßig (d.h. zusammengesetzt aus Grundfunktionen)
Anwendungen der Differentiation Strikte Monotonie einer Funktion f über einem Intervall [a, b] garantiert die Eistenz der Umkehrfunktion f, die nicht immer formelmäßig (d.h. zusammengesetzt aus Grundfunktionen)
Stetige Funktionen. Definition. Seien (X, d) und (Y, D) metrische Räume und f : X Y eine Abbildung. i) f heißt stetig in x 0 (x 0 D(f)), wenn
 Stetige Funktionen Eine zentrale Rolle in der Analysis spielen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume). Dabei sind i.a. nicht beliebige
Stetige Funktionen Eine zentrale Rolle in der Analysis spielen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume). Dabei sind i.a. nicht beliebige
Univariate Analysis. Analysis und nichtlineare Modelle Sommersemester
 Analysis und nichtlineare Modelle Sommersemester 9 5 Univariate Analysis C. Berechnen Sie ohne Taschenrechner(!). Runden Sie die Ergebnisse auf ganze Zahlen. (a) 7 :, (b) 795 :.. Berechnen Sie ohne Taschenrechner(!):
Analysis und nichtlineare Modelle Sommersemester 9 5 Univariate Analysis C. Berechnen Sie ohne Taschenrechner(!). Runden Sie die Ergebnisse auf ganze Zahlen. (a) 7 :, (b) 795 :.. Berechnen Sie ohne Taschenrechner(!):
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 6. (n+1)!. Daraus folgt, dass e 1/x < (n+
 D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
5. DIFFERENZIEREN UND INTEGRIEREN
 5. DIFFERENZIEREN UND INTEGRIEREN 1 Sei f eine auf R oder auf einer Teilmenge B R definierte Funktion: f : B R Die Funktion heißt differenzierbar in x 0 in B, falls sie in diesem Punkt x 0 lokal linear
5. DIFFERENZIEREN UND INTEGRIEREN 1 Sei f eine auf R oder auf einer Teilmenge B R definierte Funktion: f : B R Die Funktion heißt differenzierbar in x 0 in B, falls sie in diesem Punkt x 0 lokal linear
e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme sin(x+y) = cos(x) sin(y)+sin(x) cos(y). und f. Für eine reelle Zahl x R gilt e ix = 1.
 8. GRENZWERTE UND STETIGKEIT VON FUNKTIONEN 51 e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme cos(x+y) = cos(x) cos(y) sin(x) sin(y) und sin(x+y) = cos(x) sin(y)+sin(x) cos(y). f. Für eine
8. GRENZWERTE UND STETIGKEIT VON FUNKTIONEN 51 e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme cos(x+y) = cos(x) cos(y) sin(x) sin(y) und sin(x+y) = cos(x) sin(y)+sin(x) cos(y). f. Für eine
2.5 Komplexe Wurzeln. Mathematik für Naturwissenschaftler I 2.5
 Mathematik für Naturwissenschaftler I 2.5 Die Periodizität von e z ist der Grund, warum im Komplexen Logarithmen etwas schwieriger zu behandeln sind als im Reellen: Der natürliche Logarithmus ist die Umkehrung
Mathematik für Naturwissenschaftler I 2.5 Die Periodizität von e z ist der Grund, warum im Komplexen Logarithmen etwas schwieriger zu behandeln sind als im Reellen: Der natürliche Logarithmus ist die Umkehrung
streng monoton steigend. streng monoton fallend. Ist f eine in einem Intervall stetige und im Innern des Intervalls differenzierbare Funktion mit
 3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
Wirtschafts- und Finanzmathematik
 Wirtschafts- und Finanzmathematik für Betriebswirtschaft und International Management Wintersemester 2017/18 04.10.2017 Einführung, R, Grundlagen 1 11.10.2017 Grundlagen, Aussagen 2 18.10.2017 Aussagen
Wirtschafts- und Finanzmathematik für Betriebswirtschaft und International Management Wintersemester 2017/18 04.10.2017 Einführung, R, Grundlagen 1 11.10.2017 Grundlagen, Aussagen 2 18.10.2017 Aussagen
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript
 Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Der Differenzenquotient
 Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Mathematik für Sicherheitsingenieure I A
 Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 9.0.08 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+6+4 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH
Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 9.0.08 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+6+4 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH
Zusammenfassung der Kurvendiskussion
 Zusammenfassung der Kurvendiskussion Diskussionspunkte 1 Größtmögliche Definitionsmenge D f 2 Symmetrieeigenschaften des Graphen G f 3 Nullstellen, Polstellen, Schnittpunkte mit der y-achse, Vielfachheit
Zusammenfassung der Kurvendiskussion Diskussionspunkte 1 Größtmögliche Definitionsmenge D f 2 Symmetrieeigenschaften des Graphen G f 3 Nullstellen, Polstellen, Schnittpunkte mit der y-achse, Vielfachheit
Abitur 2010 Mathematik GK Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
