Mathematik ohne Formeln gibt s denn das?
|
|
|
- Dominic Wetzel
- vor 7 Jahren
- Abrufe
Transkript
1 Mathematik ohne Formeln gibt s denn das? Ein Stück Mathematik der anderen Art Daniel Grieser Institut für Mathematik Universität Oldenburg
2 Der Läufer Ein Läufer im Schach kann nur schräg ziehen. Kann er von hier...
3 Der Läufer Ein Läufer im Schach kann nur schräg ziehen. Kann er von hier nach hier... gelangen?
4 Der Läufer Nein!
5 Der Läufer Nein! Warum nicht?
6 Der Läufer Nein! Warum nicht? Der Läufer bleibt immer auf der gleichen Farbe.
7 Domino Kann man das 5x5 Brett mit Dominosteinen überdecken (Überlappungen verboten)?
8 Domino Kann man das 5x5 Brett mit Dominosteinen überdecken (Überlappungen verboten)?
9 Domino Kann man das 5x5 Brett mit Dominosteinen überdecken (Überlappungen verboten)?
10 Domino Kann man das 5x5 Brett mit Dominosteinen überdecken (Überlappungen verboten)?
11 Domino Kann man das 5x5 Brett mit Dominosteinen überdecken (Überlappungen verboten)? Nein.
12 Domino Kann man das 5x5 Brett mit Dominosteinen überdecken (Überlappungen verboten)? Nein. Warum nicht?
13 Domino Kann man das 5x5 Brett mit Dominosteinen überdecken (Überlappungen verboten)? Nein. Warum nicht? Anzahl der Felder ist ungerade.
14 Domino Kann man das 6x6 Brett mit Dominosteinen überdecken?
15 Domino Kann man das 6x6 Brett mit Dominosteinen überdecken? Na klar! Zum Beispiel so.
16 Domino Jetzt schneiden wir zwei Ecken ab. Kann man diese Figur mit Dominosteinen überdecken?
17 Domino Jetzt schneiden wir zwei Ecken ab. Kann man diese Figur mit Dominosteinen überdecken? Anzahl der Felder ist gerade. Könnte also gehen.
18 Domino Versuchen wir s!
19 Domino... und weiter...
20 Domino... und weiter und weiter...
21 Domino... und weiter und weiter Mist!
22 Domino Noch ein Versuch. Wieder nichts!
23 Domino Haben wir nicht genug probiert, oder geht es prinzipiell nicht?
24 Warum es nicht geht Wir färben die Felder schachbrettartig.
25 Warum es nicht geht Jeder Dominostein bedeckt ein weißes und ein schwarzes Feld.
26 Warum es nicht geht Jeder Dominostein bedeckt ein weißes und ein schwarzes Feld. Es werden zwei weiße Felder abgeschnitten.
27 Warum es nicht geht Jeder Dominostein bedeckt ein weißes und ein schwarzes Feld. Es werden zwei weiße Felder abgeschnitten. Also bleiben zwei schwarze Felder übrig!
28 Warum es nicht geht Jeder Dominostein bedeckt ein weißes und ein schwarzes Feld. Es werden zwei weiße Felder abgeschnitten. Also bleiben zwei schwarze Felder übrig! (Egal, wie wir es versuchen.)
29 Zusammenfassung Keine Domino-Überdeckung - obwohl Felderanzahl gerade
30 Zusammenfassung Keine Domino-Überdeckung - obwohl Felderanzahl gerade - erst mittels Schachbrettmuster erkennbar
31 Das 5er Puzzle (Boss puzzle, Jeu de Taquin) er Puzzle
32 Eine Variante
33 Das 5er Puzzle (Boss puzzle, Jeu de Taquin) Erfunden 878 von Sam Loyd 9 0 Löste eine wahre Epidemie aus 4 5 (Sogar im Deutschen Reichstag wurde gepuzzelt)
34 Das 5er Puzzle Problem Sam Loyds 000$-Problem: Löse dieses Puzzle!
35 Das 5er Puzzle Problem Sam Loyds 000$-Problem: Löse dieses Puzzle! Satz: Es geht nicht! Warum nicht?
36 Permutationen (= Anordnungen) Welche Anordnungen der Zahlen,, gibt es?
37 Permutationen Verstellung = Eine größere Zahl kommt vor einer kleineren Permutation Anzahl der Verstellungen 0 gerade ungerade gerade ungerade gerade ungerade
38 Permutationen Verstellung = Eine größere Zahl kommt vor einer kleineren Permutation Anzahl der Verstellungen 0 gerade ungerade gerade ungerade gerade ungerade
39 Permutationen Verstellung = Eine größere Zahl kommt vor einer kleineren Permutation Anzahl der Verstellungen gerade ungerade
40 Permutationen Verstellung = Eine größere Zahl kommt vor einer kleineren Permutation Anzahl der Verstellungen gerade ungerade
41 Vertauschen zweier Zahlen Permutation Anzahl der Verstellungen Zwei benachbarte vertauschen: 5 4 6
42 Vertauschen zweier Zahlen Permutation Anzahl der Verstellungen Zwei benachbarte vertauschen: 5 4 6
43 Vertauschen zweier Zahlen Permutation Anzahl der Verstellungen Zwei beliebige vertauschen: 6 4 5
44 Vertauschen zweier Zahlen Permutation Anzahl der Verstellungen Zwei beliebige vertauschen: Warum muss das ungerade sein?
45 Vertauschen zweier Zahlen Satz: Bei Vertauschen irgendeines Paares geschieht ein Farbwechsel. Beweis: Permutation Anzahl der Verstellungen
46 Das 5er Puzzle Problem Kann man von zu gelangen?
47 Das 5er Puzzle Problem Jede Puzzlestellung entspricht einer Permutation: 4 5 entspricht entspricht = das leere Feld
48 Das 5er Puzzle Problem Ein Zug entspricht einer Vertauschung einer Zahl mit 6. Waagerechter Zug: = das leere Feld
49 Das 5er Puzzle Problem Ein Zug entspricht einer Vertauschung einer Zahl mit 6. Senkrechter Zug: = das leere Feld
50 Das 5er Puzzle Problem Also wechselt die Permutation mit jedem Zug die Farbe
51 Das 5er Puzzle Problem Nun färben wir zusätzlich die Puzzleunterlage schachbrettartig. Das freie Feld wechselt bei jedem Zug die Farbe Die Permutation hat immer dieselbe Farbe wie das freie Feld! (Denn das ist am Anfang so und beide wechseln gemeinsam.)
52 Das 5er Puzzle Problem Satz: Von der Ausgangsstellung sind nur solche Stellungen erreichbar, deren Permutation dieselbe Farbe wie das freie Feld hat. Ausgangsstellung: Preisrätsel-Stellung: Die Preisrätsel-Stellung kann nie erreicht werden!
53 Zurück zum 5er Puzzle 000$-Problem
54 Zurück zum 5er Puzzle 000$-Problem Die Farben sind verschieden Also ist das 000$-Problem nicht lösbar.
55 Andere Stellungen im 5er Puzzle Verstellungen. Nicht lösbar.
56 Andere Stellungen im 5er Puzzle Verstellungen. Lösbar.
57 Die Idee der Invariante Wenn man eine Größe findet, die bei jedem Schritt gleich bleibt, erhält man Unmöglichkeitsbeweise. (Gerade/ungerade, Schachbrettmuster, Färbung von Permutationen,...)
58 Andere Geht nicht -Sätze Knoten: Aus kann man nicht machen.
59 Andere Geht nicht -Sätze Knoten: Aus kann man nicht machen. Kryptographie: Große Zahlen kann man nicht schnell faktorisieren (so hoffen die Banken; bisher nicht bewiesen)
60 Andere Geht nicht -Sätze Knoten: Aus kann man nicht machen. Kryptographie: Große Zahlen kann man nicht schnell faktorisieren (so hoffen die Banken; bisher nicht bewiesen) Alltag: Erklären Sie mal Ihrem Chef, dass es nicht Ihr Fehler ist, wenn etwas nicht klappt!
61 Mathematik ohne Formeln? Ja, die gibt es!
Verflixt, warum geht das nicht? Unmöglichkeitsbeweise in der Mathematik
Verflixt, warum geht das nicht? Unmöglichkeitsbeweise in der Mathematik Daniel Grieser Institut für Mathematik Universität Oldenburg Tag der Mathematik, 5. November 2008 Der Läufer Ein Läufer im Schach
Das Mathematische Duell
Das Mathematische Duell Schachbrettaufgaben vom Mathematischen Duell Bílovec - Chorzów - Graz - Přerov Robert Geretschläger ÖMG Lehrer/innen/fortbildungstagung 2017, Wien am 21. April 2017 Das Mathematische
Beispiel: Aufgaben: T-Stein-Problem Kann ein 10 x 10 Schachbrett mit folgenden T-Steinen ausgelegt werden?
Farben: Beweisen mit Buntstiften Die meisten dieser Probleme stammen aus dem Buch Problem Solving Strategies von A. Engel; Springer-Verlag New York, Inc.. Hintergrund: Viele auf den ersten Blick scheinbar
Das Invarianzprinzip
Das Invarianzprinzip Axel Schüler, Mathematisches Institut, Univ. Leipzig mailto:schueler@mathematik.uni-leipzig.de Juli 2000 Das Invarianzprinzip In vielen Bereichen der Mathematik spielen Invarianten
Färbungsbeweise. 1 Aufgaben
Schweizer Mathematik-Olympiade smo osm Färbungsbeweise Aktualisiert: 1. Dezember 2015 vers. 1.0.0 1 Aufgaben Einstieg 1.1 Kann man überlappungsfrei und ohne Löcher die Figuren auf den Bildern unten mit
Einführung Mathematik Algorithmen Rekorde. Rubik s Cube. Höllinger, Kanzler, Widmoser WS 2016/17
WS 2016/17 1 Einführung -Erfinder -Aufbau -Variationen 2 Mathematik -Permutationen -Singmaster Notation -Gruppentheorie -Zykelschreibweise 3 Algorithmen -Gottes Algorithmus -Thistlethwaite s Algorithmus
Städtewettbewerb Frühjahr 2008
Städtewettbewerb Frühjahr 2008 Lösungsvorschläge Hamburg 5. März 2008 [Version 7. April 2008] M Mittelstufe Aufgabe M.1 (3 P.). Die gegenüberliegenden Seiten eines konvexen Sechsecks ABCDEF seien jeweils
Einführung in das Invarianzprinzip
15.03.2016 Motivation Betrachtet diesen Kreis, der in sechs Sektoren eingeteilt ist. Wir erlauben, die Zahl in je zwei benachbarten Feldern um jeweils 1 zu erhöhen. In welcher Reihenfolge muss man die
Käthe-Kollwitz-Gymnasium, Berlin
Parkettierungen eilnehmer: im Opitz Fabian Balke Phillip Michalski Finn Koepke Laurenz Mädje Niklas Schlüter Gruppenleiter: Stefan Felsner Veit Wiechert Andreas-Oberschule, Berlin Immanuel-Kant-Schule,
Mathematik mit Polyominos - vom Domino zum Pentomino
Mathematik mit Polyominos - vom Domino zum Pentomino Meisterklasse Mathematik - Dresden 2017 Olaf Schimmel (Ulf-Merbold-Gymnasium Greiz) www.mathoid.de, os@mathoid.de Gliederung 1. Was sind Polyominos?
Waben-Sudoku. Günter Aumann und Klaus Spitzmüller. Sudoku ist in. Oder ist es schon wieder langweilig? Es gibt Alternativen.
Waben-Sudoku Günter Aumann und Klaus Spitzmüller Sudoku ist in. Oder ist es schon wieder langweilig? Es gibt Alternativen. Eine Vorüberlegung Reguläre Vierecke und Sechsecke zeichnen sich vor allen anderen
Was ist Diskrete Mathematik und wozu?
Was ist und wozu? Fakultät für Mathematik, Universität Wien Was ist? Was ist? diskret... Was ist? diskret... 1) unauällig, unaufdringlich (Brockhaus) Was ist? diskret... 1) unauällig, unaufdringlich (Brockhaus)
Maturaarbeit. Färbungsbeweise
Maturaarbeit von Markus Sprecher (Jahrgang 86) Klasse 4T Färbungsbeweise Mathematik Betreuende Lehrkraft: Dr. Philipp Schöbi Inhaltsverzeichnis 1 Vorwort 3 2 Was ist ein Färbungsbeweis 4 3 Hauptteil 7
Wie groß ist die Fläche eines Kreises?
Wie groß ist die Fläche eines Kreises? Die Kreiszahl p beschreibt das Längenverhältnis von Umfang (u) und Durchmesser (d) eines Kreises. Mit mathematischen Symbolen ausgedrückt lautet diese Tatsache u/d
Schachbrettaufgaben vom mathematischen Duell
Schachbrettaufgaben vom mathematischen Duell ROBERT GERETSCHLÄGER (GRAZ) Seit einem viertel Jahrhundert gibt es nun schon das Mathematische Duell, einen mathematischen Wettbewerb von Schulen aus Österreich,
Schach für Anfänger. Hier möchte ich für Anfänger das Schachspiel näher bringen.
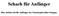Schach für Anfänger Hier möchte ich für Anfänger das Schachspiel näher bringen. Bild 1 Die Grundstellung Das Schachbrett sollte man immer so legen, daß rechts unten ein weißes Feld ist (Bild1: rotes Feld).
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik - WS 11/12. Klausurvorbereitung
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik - WS 11/12 Prof. Dr. A. Taraz, Dr. O. Cooley, Klausurvorbereitung Die Klausur zum Propädeutikum Diskrete Mathematik findet
Jedes zweite ist schwarz Analyse und Spielereien um die Formulierung jedes zweite. Es zeigen sich Paritätsprobleme.
Hans Walser, [20111120b] Jedes zweite ist schwarz Analyse und Spielereien um die Formulierung jedes zweite. Es zeigen sich Paritätsprobleme. 1 Schachbrett Im Schachbrett (Abb. 1) ist jedes zweite Feld
Vorlesung. Vollständige Induktion 1
WS 015/16 Vorlesung Vollständige Induktion 1 1 Einführung Bei der vollständigen Induktion handelt es sich um ein wichtiges mathematisches Beweisverfahren, mit dem man Aussagen, die für alle natürlichen
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik. Weihnachtsblatt
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Hamiltonsche Graphen (2. Teil)
Hamiltonsche Graphen (2. Teil) Themen des Vortrages Für Schachspieler Hamiltons Spiel Sitzordnungen Eine billige Rundreise Ein vielleicht unlösbares Problem Bäcker mit Kenntnissen in Graphentheorie Fazit
L a L b L c
55. Mathematik-Olympiade 2. Stufe (Regionalrunde) Olympiadeklasse 10 Lösungen c 2015 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 551021 Lösung
Beispiellösungen zu Blatt 77
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 77 Die Zahl 9 ist sowohl als Summe der drei aufeinanderfolgenden Quadratzahlen,
Puzzle-Mathematik. Martin Kreuzer. Universität Passau
Puzzle-Mathematik Martin Kreuzer Universität Passau martin.kreuzer@uni-passau.de Lehrerfortbildung Unterhaltungsmathematik Universität Passau, 18.12.2013 1 Inhaltsübersicht 2 Inhaltsübersicht 1. Licht
Übersicht 2. Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben. Martin Oellrich. wer das Problem löste 4
Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht 5. April 009 5. April 009 Martin Oellrich 1 vom Problem zur Theorie die Idee weiter denken 3 MathematikerIn werden? Gibt
typische Beweismuster Allgemeine Hilfe Beweistechniken WS2014/ Januar 2015 R. Düffel Beweistechniken
Beweistechniken Ronja Düffel WS2014/15 13. Januar 2015 Warum ist Beweisen so schwierig? unsere natürliche Sprache ist oft mehrdeutig wir sind in unserem Alltag von logischen Fehlschlüssen umgeben Logik
Vorkurs Beweisen
Vorkurs -- 4. Beweisen.0.05 Aussageformen Aussagen können auch Parameter enthalten (z.b. x) Wahr oder falsch hängt dann vom Parameter x ab. Können natürlich auch mehrere Parameter sein. Beispiel einer
Lösungen Benjamin 2015, Känguru der Mathematik - Österreich
Lösungen Benjamin 2015, Känguru der Mathematik - Österreich 1. In welcher Figur ist genau die Hälfte grau gefärbt? Lösung: In (A) ist 1/3 gefärbt, in (B) die Hälfte, in (C) ¾, in (D) ¼ und in (E) 2/5.
Derjenige, der die letzte Diagonale einzeichnet, gewinnt.
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Spiele Mit Strategie gewinnen rmblkans opopopop POPOPOPO SNAQJBMR a b c d e f g h Versuche zum Einstieg folgende Knobelaufgabe zu
Übersicht 2. Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben. Martin Oellrich. ein Problem vor der Haustür 3
Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht vom Problem zur Theorie 0. Juni 008 0. Juni 008 Martin Oellrich die Idee weiter denken MathematikerIn werden? Gibt es einen
Zahlenluchs. von Anja Strobach. Spielanleitung
von Anja Strobach Spielanleitung Die Zahlen von 1 bis 25 laden dich zum spannenden Kombinationstraining ein. Noch während du Aufgaben durch ausgeklügelte Rechenkunst löst, jonglieren deine Mitspieler mit
Formale Grundlagen. bis , Lösungen. 1. Beweisen Sie, daß die Summe aller Grade der Knoten stets gerade ist.
Formale Grundlagen 4. Übungsaufgaben bis 2011-06-03, Lösungen 1. Beweisen Sie, daß die Summe aller Grade der Knoten stets gerade ist. 2. Finden Sie einen Eulerschen Weg im Briefumschlag, d.h. in: { ((1,
Plastische Gestaltungsgrundlagen Prof. Ernst Thevis. Stegreif SS15 Architektur Schach
Stegreif SS Architektur Schach Norwegen 15 Jh. 12.Jh. Schottland Mongolei 6.Jh. - Entstehung vermutlich zwischen dem 3. und 6 Jh. in Asien - Ausbreitung in Europa zwischen 9. und 11. Jh. Im Hochmittelalter
Was ändert sich, wenn zu Beginn eine andere Anzahl n an Streichhölzern auf dem Haufen liegt?
NIM Auf dem Tisch liegen mehrere Haufen mit Spielsteinen. Zum Beispiel drei Haufen mit 4, 5 und 6 Steinen. Jeder Spiele nimmt abwechselnd von einem Haufen eine beliebige Anzahl an Steinen. Der Spieler,
Platonische und archimedische Parkettierungen. Meisterklasse Mathematik Dresden 2016 Olaf Schimmel
Platonische und archimedische Parkettierungen Meisterklasse Mathematik Dresden 2016 Olaf Schimmel Inhaltsübersicht 1 Was sind Parkettierungen? 2 Warum Winkel wichtig sind 3 Platonische Parkette 4 Archimedische
Die Komplexität von Domino
Die Komplexität von Domino - oder die Frage nach dem Problem, ob man ein Polygon mit einer Menge von Dominosteinen bedecken kann Referent: Thorsten Reinhardt Freie Universität Berlin / FB Informatik Seminar
KARL-FRANZENS-UNIVERSITÄT GRAZ. Seminar aus Reiner Mathematik. Die Museumswächter. Krupic Mustafa Wintersemester 2013/14
KARL-FRANZENS-UNIVERSITÄT GRAZ Seminar aus Reiner Mathematik Die Museumswächter Krupic Mustafa Wintersemester 2013/14 Inhaltsverzeichnis 2 Inhaltsverzeichnis 1 Einleitung 3 2 Museumswächter-Satz 6 2.1
Eine Anleitung. Zuerst ein paar Worte zur Geschichte. Und jetzt gibt es den Qwürfel! Für die Teilnehmer des Känguru-Wettbewerbs 2019
QWÜRFEL Für die Teilnehmer des Känguru-Wettbewerbs 09 Eine Anleitung Vielleicht hast du ganz vorsichtig gedreht, einmal, zweimal,..., aber auch gleich wieder zurück. Doch plötzlich vielleicht eine Drehung
26. Mathematik Olympiade 1. Stufe (Schulolympiade) Klasse 5 Saison 1986/1987 Aufgaben und Lösungen
. Mathematik Olympiade. Stufe (Schulolympiade) Klasse Saison / Aufgaben und Lösungen OJM. Mathematik-Olympiade. Stufe (Schulolympiade) Klasse Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen
1 Grundlagen. 1.1 Aussagen
1 Grundlagen 1.1 Aussagen In der Mathematik geht es um Aussagen. Eine Aussage ist ein statement, das entweder wahr oder falsch sein kann. Beides geht nicht! Äußerungen, die nicht die Eigenschaft haben,
Übung zur Vorlesung Diskrete Strukturen I
Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
Kapitel 3. Kapitel 3 Graphentheorie
Graphentheorie Inhalt 3.1 3.1 Grundlagen 3.2 3.2 Das Das Königsberger Brückenproblem 3.3 3.3 Bäume 3.4. 3.4. Planare Graphen 3.5 3.5 Färbungen Seite 2 3.1 Grundlagen Definition. Ein Ein Graph besteht aus
Polynome Teil V: Elementarsymmetrische Funktionen.
Die WURZEL Werkstatt Mathematik Polynome Teil V: Elementarsymmetrische Funktionen. Es gibt Gleichungssysteme, die lassen sich mit schulischen Mitteln nicht bzw. nur sehr mühsam knacken. So musste etwa
58. Mathematik Olympiade 2. Runde (Regionalrunde) Lösungen
eolympiadeklass10 58. Mathematik Olympiade 2. Runde (Regionalrunde) Lösungen c 2018 Aufgabenausschuss für die Mathematik-Olympiade in Deutschland www.mathematik-olympiaden.de. Alle Rechte vorbehalten.
Eine kurze Anleitung des Schachs
Eine kurze Anleitung des Schachs In Anschluss an den Artikel der das Schachspiel an sich veranschaulicht schreibe ich hiermit noch eine kurze Anleitung für dieses Spiel. Beim Schach gibt es unendlich viele
Wiederholung aus Diskreter Mathematik I: I: Graphentheorie
Wiederholung aus Diskreter Mathematik I: I: Graphentheorie Inhalt: W.1 Grundlagen W.2 Das Königsberger Brückenproblem W.3 Bäume W.4 Planare Graphen W.5 Färbungen W.1 Grundlagen Ein Ein Graph besteht aus
Schach Spielanleitung
Schach Spielanleitung 1. Schachbrett Untenstehend sieht man ein Schachbrett inklusive Figuren in Grundstellung. Hierbei handelt es sich immer um die Ausgangsposition. Zu beachten ist, dass jedes Feld seinen
Musterlösung Serie 3. ITET Diskrete Mathematik WS 02/03 R. Suter. d) Für beliebige a, b G gilt
ITET Diskrete Mathematik WS 2/3 R. Suter. a) r s = r + )s + ). Assoziativität: Ist erfüllt, denn Musterlösung Serie 3 r s) t = r + )s + ) + ) t + ) = r + )s + )t + ) = r + ) s + )t + ) + ) = r s t) Neutrales
schach-lernen.com Seite 2
Lizenz Dieses Dokument inklusive aller Grafiken stehen unter einer Creative- Commons-Lizenz (Creative Commons Attribution-Noncommercial 3.0 Germany License). Sie dürfen das Dokument vervielfältigen, verbreiten
Meisterklasse Dresden 2014 Olaf Schimmel
Meisterklasse Dresden 2014 Olaf Schimmel 1 Was sind Parkettierungen? 2 Warum Winkel wichtig sind 3 Platonische Parkette 4 Archimedische Parkette 5 Welche Kombination von Vielecken erfüllen die Winkelbedingung?
2015/16 Jahrgangsstufe 9 A. Jahrgangsstufentest im Fach Mathematik am Hanns-Seidel-Gymnasium am
2015/16 Jahrgangsstufe 9 A Jahrgangsstufentest im Fach Mathematik am Hanns-Seidel-Gymnasium am 8.10.2015 Name: Note: Klasse: Punkte: 1 Aufgabe 1 Die Abbildung rechts zeigt zwei Parallelenpaare. a, b, c,
Unmögliches. Denkspiele aus aller Welt (3) Claus Michael Ringel
Unmögliches Denkspiele aus aller Welt (3) Claus Michael Ringel Es gibt eine Vielzahl von Denkspielen, von Gedulds- und Geschicklichkeitsspielen, die einen mathematischen Hintergrund besitzen In diesem
Gleichungen fünften Grades
Gleichungen fünften Grades Teil 1 Marc Pollak 11. Juni 2013 Motivation Was ist uns bisher bekannt? Allgemeine Lösung einer Gleichung zweiten Grades durch die Mitternachtsformel Vor zwei Wochen, Lösung
33. Mathematik Olympiade 1. Stufe (Schulrunde) Klasse 5 Saison 1993/1994 Aufgaben und Lösungen
33. Mathematik Olympiade Saison 1993/1994 Aufgaben und Lösungen 1 OJM 33. Mathematik-Olympiade Aufgaben Hinweis: Der Lösungsweg mit egründungen und Nebenrechnungen soll deutlich erkennbar in logisch und
Beispiel 2 ([1], Ex ) Sei jxj = m, jy j = n. Wieviele Funktionen f : X! Y
![Beispiel 2 ([1], Ex ) Sei jxj = m, jy j = n. Wieviele Funktionen f : X! Y](/thumbs/49/25213753.jpg "Beispiel 2 ([1], Ex ) Sei jxj = m, jy j = n. Wieviele Funktionen f : X! Y")
Kombinatorik Nach [1], Chap.4 (Counting Methods and the Pigeonhole Principle). Multiplikationsprinzip Beispiel 1 Wieviele Wörter der Länge 4 kann man aus den Buchstaben A,B,C,D,E bilden,... 1. wenn Wiederholungen
2.1 Überdeckung des Schachbretts mit Dominosteinen
Färbungsmethoden 2 In der Mathematik werden Probleme oft dadurch gelöst, dass man eine zusätzliche Struktur einführt. Diese Struktur hat in der Regel nur eine Hilfsfunktion, sie kommt weder in der Voraussetzung
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik. Klausurvorbereitung
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl.-Math. S. König, Dipl.-Math. A. Würfl, Klausurvorbereitung Die Klausur zum Propädeutikum Diskrete
Proseminar Graphentheorie Vortrag 3 Matching. Inhalt: 1. Grundlagen 2. Matchings in bipatiten Graphen 3. Matchings in allgemeinen Graphen
Proseminar Graphentheorie Vortrag 3 Matching Inhalt: 1. Grundlagen 2. Matchings in bipatiten Graphen 3. Matchings in allgemeinen Graphen 1. Grundlagen Definition Matching: Eine Menge M von unabhängigen
Kurs 1663 Datenstrukturen" Musterlösungen zur Klausur vom Seite 1. Musterlösungen zur Hauptklausur Kurs 1663 Datenstrukturen 15.
Kurs 1663 Datenstrukturen" Musterlösungen zur Klausur vom 15.08.98 Seite 1 Musterlösungen zur Hauptklausur Kurs 1663 Datenstrukturen 15. August 1998 Kurs 1663 Datenstrukturen" Musterlösungen zur Klausur
TECHNISCHE UNIVERSITÄT MÜNCHEN
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathematik für Informatiker I (Wintersemester 2003/2004) Aufgabenblatt 4
von Heinrich Glumpler und Matthias Schmitt
von Heinrich Glumpler und Matthias Schmitt Schachen spielt sich wie Schach ohne Brett. Die Schachregeln werden dabei geringfügig verändert und ermöglichen neue Strategien, ohne den Kern des Schachspiels
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/18
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/18 26. Oktober 2017 1/35 Abbildungen Boolesche Algebra Summen- und Produktzeichen Definition
2. Grundlagen / der Turm
2. Grundlagen / der Turm Zur Gangart des Turms: Der Turm zieht waagerecht und senkrecht auf den Reihen und Linien. Der Turm kann sich hier entlang der 4. Reihe und E-Linie bewegen Trifft der Turm auf seinem
Abzählen von Färbungen Das Cauchy-Frobeniusoder Burnside-Lemma
Abzählen von Färbungen Das Cauchy-Frobeniusoder Burnside-Lemma Axel Schüler. März 006 Wir wollen hier das Burnside Lemma formulieren und beweisen. Dann wollen wir es anwenden auf das Abzählen von Färbungen
Färbungen von Graphen: Die chromatische Zahl und der Satz von Brooks
Färbungen on Graphen: Die chromatische Zahl und der Satz on Brooks Florian Seerin Heinrich-Heine-Uniersität Düsseldorf Mathe-Akademie 2018 Definition. Ein (endlicher) Graph besteht aus einer (endlichen)
Wie beweise ich etwas? 9. Juli 2012
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Wie beweise ich etwas? 9. Juli 2012 1 Was ist ein Beweis? 1.1 Ein Beispiel Nimm einen Stift und ein Blatt Papier und zeichne fünf
Chromatosaurier Lösungen
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Chromatosaurier Lösungen Aufgabe 1 (Tetrachromatosaurier (nur für die Klassen 7/8) [4 Punkte]). Bei Ausgrabungen wurde der folgende
Spiele in der Informatik
Spiele in der Informatik Martin Lange Lehr- und Forschungseinheit Theoretische Informatik Informatik-Schnupperstudium an der LMU, 29.3.2010 Übersicht Teil 1 Schokoladenessen für Spieltheoretiker ein kleines
Permutationen. ... identische Abbildung
Permutationen n > 0 sei S n {σ : {1, 2,..., n} {1, 2,..., n} : σ ist bijektiv}. Dann ist S n eine Gruppe bzgl. der Verknüpfung von Abbildungen (vgl. früher) und heißt symmetrische Gruppe (vom Index n).
Lösungscode Die markierten Zeilen, jeweils die Einerstelle der zugehörigen Zahl, - für Leerfelder.
1&2. Arukone 5&5 Punkte Verbinden Sie jeweils gleiche Zahlen durch einen Linienzug, der waagerecht und senkrecht von Feldmittelpunkt zu Feldmittelpunkt verläuft. Es müssen nicht alle Felder benutzt werden.
Welche Probleme können Rechner (effizient) lösen? Die P = NP Frage. Ideen der Informatik Kurt Mehlhorn
Welche Probleme können Rechner (effizient) lösen? Die P = NP Frage Ideen der Informatik Kurt Mehlhorn Gliederung Ziele von Theorie Gibt es Probleme, die man prinzipiell nicht mit einem Rechner lösen kann?
Skript und Übungen Teil II
Vorkurs Mathematik Herbst 2009 M. Carl E. Bönecke Skript und Übungen Teil II Das erste Semester wiederholt die Schulmathematik in einer neuen axiomatischen Sprache; es ähnelt damit dem nachträglichen Erlernen
Voransicht. Brüche auf dem Zahlenstrahl. 1 Beschrifte den Zahlenstrahl. 2 Beschrifte den Zahlenstrahl.
Brüche Brüche auf dem Zahlenstrahl Brüche können auf einem Zahlenstrahl dargestellt werden: Beschrifte den Zahlenstrahl. Beschrifte den Zahlenstrahl. Trage die Brüche ein, die durch die Pfeile markiert
Schulbesuch Erich-Kästner Gesamtschule 07. April 2011
Schulbesuch Erich-Kästner Gesamtschule 07. April 0 Bünde Fakultät für Mathematik Universität Bielefeld dotten@math.uni-bielefeld.de Übersicht Was ist ein Sudoku-Rätsel? Die Regeln und das Ziel Zentrale
Kombinatorik. Matthias Bayerlein Matthias Bayerlein Kombinatorik / 34
Kombinatorik Matthias Bayerlein 25.6.2010 Matthias Bayerlein Kombinatorik 25.6.2010 1 / 34 Überblick Grundlagen aus der Schule Spezielle Zahlenfolgen Zusammenfassung Matthias Bayerlein Kombinatorik 25.6.2010
Grundlagen der Mathematik
Universität Hamburg Winter 2016/17 Fachbereich Mathematik Janko Latschev Grundlagen der Mathematik Lösungsskizzen 2 Präsenzaufgaben (P2) Wir betrachten drei Teilmengen der natürlichen Zahlen: - A = {n
Laurins Raumschach: Die Raumschachregel
Laurins Raumschach: Ein Gesamtkunstwerk, welches über einen Entwicklungszeitraum von vier Jahrzehnten entstand, wird jetzt in die Realität umgesetzt. Das Ziel der Schachmetamorphose, also nicht ein weiteres
0 Mengen und Abbildungen, Gruppen und Körper
0 Mengen und Abbildungen, Gruppen und Körper In diesem Paragrafen behandeln wir einige für die Lineare Algebra und für die Analysis wichtige Grundbegriffe. Wir beginnen mit dem Begriff der Menge. Auf Cantor
Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA)
Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2012/13 Hochschule Augsburg Lineare : Einführung Beispiele linearer a) b) c) 2x 1 3x 2 = 1 x 1 +
Vorkurs Mathematik im Sommersemester 2018
Vorkurs Mathematik im Sommersemester 2018 Dr. Regula Krapf Lösungen Übungsblatt 1 Aufgabe 1. Gegeben seien folgende Aussagen: A: Es ist kalt. B: Es schneit. Drücken Sie die nachfolgenden Sätze als aussagenlogische
Musterlösung MafI 1 - Blatt 5
Musterlösung MafI 1 - Blatt 5 Titus Laska Aufgabe 1 (Relationen). Die drei Relationen R, S, T N N sind jeweils auf Reflexivität, Symmetrie und Antisymmetrie zu untersuchen. Lösung. Erinnerung. Sei R A
ein Spielbrett mit 126 sechseckigen Feldern in drei Farben 51 Spielfiguren, davon je 17 in einer Farbe:
Vollständige Spielregeln 1. Inhalt Dreierschach V2.1 Schach für drei Spieler 2004 / 2014 Christian Wahlmann ein Spielbrett mit 126 sechseckigen Feldern in drei Farben 51 Spielfiguren, davon je 17 in einer
IINFORMATION. Keine Angst vor dem Rechner JUMA 1/2000 IM UNTERRICHT. Tetris. 1. Unterrichtsvorschlag: Tetris im Deutschunterricht
JUMA 1/2000 IM UNTERRICHT TIPPS FÜR DIE DEUTSCHSTUNDE MIT DEN JUMA-SEITEN 28 30 IINFORMATION Tetris Tetris ist eines der bekanntesten Computerspiele. Sein Erfinder ist der russische Computer-Spezialist
Abb. 1: Viereck mit aufgesetzten halben Quadraten. Dann sind die beiden roten Strecken gleich lang und orthogonal.
Hans Walser, [20120528] Viereck Es werden einige Spielereien am Viereck untersucht. Daraus ergeben sich interessante Eigenschaften für spezielle Vierecke, die im üblichen Kanon des Hauses der Vierecke
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Lineare : Einführung Beispiele linearer a) b) c) 2x 1 3x 2 = 1 x 1 + x 2 =
4 Färbungen Begriffe Komplexität Greedy-Algorithmus Knotenreihenfolgen Das 4-Farben-Problem...
Inhaltsverzeichnis 4 Färbungen 41 4.1 Begriffe....................... 41 4.2 Komplexität..................... 42 4.3 Greedy-Algorithmus................ 42 4.4 Knotenreihenfolgen................. 43 4.5
Vierter Zirkelbrief: Invarianten. 2 Der Satz von Euler 4 2.1 Kurze Einführung in Graphen... 4 2.2 Der Beweis des Eulerschen Polyedersatzes...
Matheschülerzirkel Universität Augsburg Schuljahr 2014/2015 Vierter Zirkelbrief: Invarianten Inhaltsverzeichnis 1 Erste Beispiele 1 2 Der Satz von Euler 4 2.1 Kurze Einführung in Graphen.........................
Graphentheorie. Perfekte Graphen. Perfekte Graphen. Perfekte Graphen. Rainer Schrader. 22. Januar 2008
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 22. Januar 2008 1 / 47 2 / 47 eine Clique in G ist ein induzierter vollständiger Teilgraph Gliederung α- und χ-perfektheit Replikation
GS1 - Grundelemente Lektion 1
LEKTION 1 DAS SCHACHBRETT Inhalt Einführung Anleitung für den Trainer / Lehrer Ausblick Lösungen Herzlich Willkommen bei der Chess Tigers Universität! In den letzten Jahren strömen immer mehr Grundschüler
Faszination Mathematik
Roland Speicher Universität des Saarlandes Saarbrücken Roland Speicher (U des Saarlandes) Faszination Mathematik 1 / 18 Berufsperspektiven für Mathematiker Section 1 Berufsperspektiven für Mathematiker
1. Einleitung wichtige Begriffe
1. Einleitung wichtige Begriffe Da sich meine besondere Lernleistung mit dem graziösen Färben (bzw. Nummerieren) von Graphen (speziell von Bäumen), einem Teilgebiet der Graphentheorie, beschäftigt, und
Diskrete Mathematik für Informatiker
Universität Siegen Lehrstuhl Theoretische Inormatik Carl Philipp Reh Daniel König Diskrete Mathematik ür Inormatiker WS 2016/2017 Übung 6 1. Beweisen Sie die olgenden Aussagen: a) χ(k n ) = n b) χ(k m,n
Elementare Mengenlehre
Vorkurs Mathematik, PD Dr. K. Halupczok WWU Münster Fachbereich Mathematik und Informatik 5.9.2013 Ÿ2 Elementare Mengenlehre Der grundlegendste Begri, mit dem Objekte und Strukturen der Mathematik (Zahlen,
Vorkurs Mathematik 2016
Vorkurs Mathematik 2016 WWU Münster, Fachbereich Mathematik und Informatik PD Dr. K. Halupczok Skript VK3 vom 15.9.2016 VK3: Elementare Mengenlehre Der grundlegendste Begri, mit dem Objekte und Strukturen
Logik in der Schule. Bildungsplan 2004 (Zitat:) Begründen. Elementare Regeln und Gesetze der Logik kennen und anwenden
1 Nr.2-21.04.2016 Logik in der Schule Bildungsplan 2004 (Zitat:) Begründen Elementare Regeln und Gesetze der Logik kennen und anwenden Begründungstypen und Beweismethoden der Mathematik kennen, gezielt
Technische Universität München Zentrum Mathematik Mathematik 1 (Elektrotechnik) Übungsblatt 1
Technische Universität München Zentrum Mathematik Mathematik 1 (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 1 Hausaufgaben Aufgabe 1.1 Zeigen Sie mit vollständiger Induktion:
6. Einführung 43. gilt. Dann soll also A B x B = b eindeutig lösbar sein, also A B vollen Rang haben, d. h. invertierbar (regulär) sein.
6. Einführung 43 und aus der linearen Unabhängigkeit der (a i ) i I(x) folgt y i = z i auch für i I(x). Insgesamt gilt also y = z, d. h., nach Definition 6.9 ist x eine Ecke von P. Beachte: Der Koordinatenvektor
KV Logik als Arbeitssprache. Christoph Hörtenhuemer LVA-Nummer: LVA-Leiterin: Wolfgang Windsteiger. Agnes Schoßleitner
KV Logik als Arbeitssprache LVA-Nummer: 326.014 LVA-Leiterin: Wolfgang Windsteiger Abgabedatum: 02. 06. 2004 Christoph Hörtenhuemer 0355958 Agnes Schoßleitner 0355468 Inhaltsverzeichnis Kurzbeschreibung...
Leonhard Euler. Ein Mann, mit dem Sie rechnen können. Daniel Steiner Dozent im Fachbereich Mathematik
Leonhard Euler Ein Mann, mit dem Sie rechnen können Daniel Steiner Dozent im Vorstellung Daniel Steiner, 1973, Langenthal verheiratet, drei Kinder 1989-1994: Staatliches Seminar Langenthal 1994-1999: Studium