Einführung in die Integralrechnung
|
|
|
- Marie Kalb
- vor 7 Jahren
- Abrufe
Transkript
1 Einführung in die Integrlrechnung Vorbereitung für ds Probestudium n der LMU München 3. bis 7. September von W. Frks und O. Forster Integrle ls Flächeninhlte. Motivtion Flächeninhlte von Rechtecken sind einfch zu berechnen: Ht ein Rechteck die Breite b und Höhe h, so ist seine Fläche F = bh. h b Den Flächeninhlt von Dreiecken knn mn uf den Flächeninhlt von Rechtecken zurückführen. C A B So folgt z.b. durch Kongruenzbetrchtungen, dss der Flächeninhlt des Dreiecks ABC gleich der Hälfte des Flächeninhlts des Rechtecks mit der gleichen Grundlinie und gleichen Höhe ist. Die Flächen von Polygonen knn mn durch Zerlegung in Dreiecke berechnen.
2 Schwieriger wird die Sitution, wenn der Flächeninhlt von Figuren bestimmt werden soll, die nicht gerdlinig begrenzt sind. Beim Kreis z.b. knn mn (wie schon Archimedes dies tt) einbeschriebene und umbeschriebene regelmäßige n-ecke betrchten. Mn stellt dnn fest, dss für wchsende Eckenzhl n die Flächen der einbeschriebenen und umbeschriebenen n-ecke sich immer mehr nnähern und wenn n gegen unendlich geht (in Zeichen n ) einem gemeinsmen Grenzwert zustreben, den mn ls Flächeninhlt des Kreises definiert.. Integrl von Funktionen Um nicht für jede spezielle Figur eigene kunstvolle Überlegungen nstellen zu müssen, betrchten wir jetzt folgende llgemeine Sitution: Gegeben sei eine stetige Funktion y = f(x) für x us einem Intervll der reellen Zhlen von bis b. Wir setzen zunächst vorus, dss f(x) in diesem Intervll immer größer oder gleich ist. y y = f(x) b x Wir stellen uns die Aufgbe, die Fläche der Figur zu bestimmen, die zwischen dem Intervll [, b] der x-achse und dem Grphen der Funktion f liegt (die Umrndung ist in der Zeichnung strk usgezogen). Eine erste grobe Annäherung n den Flächeninhlt erhlten wir, indem wir ds Intervll [, b] z.b. in drei gleichlnge Teilintervlle unterteilen = x < x < x < x 3 = b und die gesuchte Fläche durch die Summe dreier Rechtecke wie im folgenden Bild ersetzen:
3 y f(x ) f(x ) f(x 3 ) = x x x b = x 3 x Ds erste Rechteck ht die Breite x x und die Höhe f(x ), ds zweite die Breite x x und Höhe f(x ), ds dritte die Breite x 3 x und Höhe f(x 3 ). Die Summe der Flächen der 3 Rechtecke ist lso S 3 = f(x )(x x ) + f(x )(x x ) + f(x 3 )(x 3 x ). Wir wollen diese Summe noch etws elegnter schreiben, dmit sie leichter verllgemeinerungsfähig ist. Zunächst kürzen wir die Differenzen x k x k durch x k b. Dnn hben wir S 3 = f(x ) x + f(x ) x + f(x 3 ) x 3. Unter Verwendung des Summenzeichens knn mn dies nun so schreiben: S 3 = 3 f(x k ) x k. Dbei bedeutet 3, dss mn in dem folgenden Ausdruck den Index k der Reihe nch durch,, 3 ersetzen und die entstehenden Ausdrücke durch Pluszeichen verbinden soll. Ntürlich ist S 3 noch eine sehr grobe Approximtion des gesuchten Flächeninhlts. Erhöht mn ber die Anzhl der Teilpunkte, so erhält mn bessere Annäherungen, wie us den folgenden Bildern deutlich wird. y x x x x 3 x 4 x 5 x 6 x 3
4 y x x x 4 x 6 x 8 x x x Allgemein erhält mn bei einer Unterteilung des Intervlls [, b] in n Teilintervlle = x < x < x <... < x n < x n = b eine Approximtion der gesuchten Fläche durch eine Summe von n Rechtecksflächen S n = f(x k ) x k. Mn knn beweisen (und dies lernt mn im. Semester des Mthemtikstudiums), dss bei einer stetigen Funktion f die Folge der S n für n einem wohlbestimmen Grenzwert (Limes) zustrebt, den mn dnn ls Integrl von f über ds Intervll [, b] bezeichnet. Mn schreibt dfür.3 Beispiele f(x)dx = lim n S n Wir können zwr hier nicht den llgemeinen Fll beweisen, führen ber den Grenzübergng n zwei Beispielen vor. Beispiel (.) xdx Hier soll lso die Funktion f(x) = x über ds Intervll [, ] integriert werden, wobei > vorusgesetzt sei. Betrchten wir zunächst den Grphen der Funktion y = f(x) = x. y y = x x 4
5 Wir sehen, dss ds Integrl xdx die Fläche eines rechtwinkligen Dreiecks mit Grundlinie und Höhe drstellt, lso gleich sein muss. Obwohl wir ds Ergebnis schon wissen, führen wir trotzdem noch die Grenzwertbetrchtung durch, um eine Bestätigung zu erhlten, dss dieser Anstz sinnvoll ist. Dzu unterteilen wir ds Intervll [, ] wieder in n gleiche Teile = x < x <... < x n < x n =. Die Länge jedes Teilintervlls ist hier x k = n und es gilt x k = k n Ds k-te Teilrechteck ht die Fläche y x x x x... x n f(x k ) x k = x k x k = k n n = k n, lso ergibt sich für die n-te Näherungssumme S n = f(x k ) x k = k n = n k. für k =,,..., n. Nun benutzen wir die beknnte Formel für die Summe der ersten n ntürlichen Zhlen n(n + ) k = n =. Setzen wir dies ein, erhlten wir D lim n n S n = n(n + ) n =, erhlten wir insgesmt ws wir erwrtet hben. Beispiel (.) x dx = n(n + ) n xdx = lim n S n =, ( = + ). n Dies ist ds erste Beispiel für die Fläche einer nicht grdlinig begrenzten Figur. 5
6 y y = x x Anlog zum ersten Beispiel unterteilen wir ds Intervll [, ] in n gleiche Teile = x < x <... < x n < x n =. Die Länge jedes Teilintervlls ist x k = n und es gilt x k = k n ergibt sich für ds k-te Teilrechteck die Fläche ( f(x k ) x k = xk x k = k ) n Die n-te Näherungssumme für ds Integrl ist dher S n = f(x k ) x k = k 3 n 3 = 3 n 3 n = k 3 n 3, k. für k =,,..., n. Hier Um weiterzukommen, bruchen wir eine Formel für die Summe der ersten n Qudrtzhlen. Eine solche Formel ist k = n n(n + )(n + ) = = 6 3 n3 + n + 6 n. (Die Leserin knn sich leicht in den Fällen n =,, 3, 4 durch Einsetzen von der Richtigkeit der Formel überzeugen; der llgemeine Fll wird durch vollständige Induktion bewiesen.) Einsetzen ergibt ( S n = 3 n 3 3 n3 + n + ) ( 6 n = n + ). 6n D lim n n = und lim =, erhlten wir insgesmt n 6n.4 Einfche Rechenregeln x dx = lim n S n = 3 3. Negtive Funktionswerte. Wir hben uns bisher uf den Fll beschränkt, dss die zu integrierende Funktion f(x) immer größer oder gleich ist. Ws pssiert, wenn die Funktion uch negtive Werte nnimmt? Betrchten wir dzu die Näherungssumme S n = f(x k ) x k. 6
7 Wir sehen, dss für f(x k ) < ds Produkt f(x k ) x k negtiv wird, lso den negtiven Flächeninhlt des Rechtecks mit den Seiten x k und f(x k ) drstellt. Ds Integrl einer Funktion mit wechselndem Vorzeichen ist lso der Flächeninhlt zwischen der x-achse und dem Grphen von f dort wo die Funktion positiv ist, minus der Fläche zwischen der x-achse und dem Grphen von f, wo die Funktion negtiv ist, vgl. folgendes Bild. + Mnchml lssen sich dmit Integrle ohne Rechnung bestimmen. Zum Beispiel gilt (.3) π sin(x)dx =, denn der positive und negtive Anteil sind us Symmetriegründen gleich groß. x y π π y = sin x Genuso sieht mn (.4) cos(x)dx =, π cos(x)dx =. (Aufgbe: Zeichne den Grphen des Cosinus!) Bemerkung. In der Anlysis wird bei den trigonometrischen Funktionen der Winkel immer im Bogenmß gemessen. Dbei entspricht einem Winkel von 8 Grd ds Bogenmß π (= hlber Umfng des Einheitskreises). Linerität. Ersetzt mn in der Formel f(x k ) x k für die Näherungssumme die Funktion f durch die Summe zweier Funktionen f + f, so erhält mn (f (x k ) + f (x k )) x k = f (x k ) x k + f (x k ) x k. 7
8 Drus folgt eine Rechenregel für ds Integrl () (f (x) + f (x))dx = f (x)dx + f (x)dx. Ist c eine reelle Konstnte, so ht mn ußerdem die Rechenregel (b) cf(x)dx = c f(x)dx. Beispiel. Wir wollen diese Regeln zur Berechnung des Integrls (.5) (x x )dx usnutzen. Der Grph der Funktion y = f(x) = x x im Intervll [, ] schut so us: y = x x Ds Integrl ist lso die Fläche über dem Intervll [, ] unterhlb der Wurfprbel. Mit den Rechenregeln () und (b) erhlten wir (x x )dx = = = xdx + xdx + ( ) xdx ( x )dx x dx. x dx Die Integrle xdx = / = und x dx = 3 /3 = 8/3 htten wir vorher schon ls Beispiele usgerechnet. Insgesmt ergibt sich deshlb (x x )dx = 8 3 = 4 3, der ngesprochene Flächeninhlt ht lso den Wert 4/3. 8
9 Integrtion und Differentition Während wir im vorigen Kpitel ds Integrl in Anlehnung n seine nschuliche Bedeutung ls Flächeninhlt eingeführt hben, zeigen wir hier, dss die Integrtion die Umkehrung der Differentition ist, ws in vielen Fällen die Möglichkeit zur Berechnung des Integrls liefert.. Stmmfunktionen, Fundmentlstz Definition. Eine uf einem Intervll I R differenzierbre Funktion F : I R heißt Stmmfunktion einer Funktion f : I R flls F (x) = f(x) für lle x I. Zum Beispiel ist F (x) = x eine Stmmfunktion von f(x) = x. Die Stmmfunktion einer Funktion ist ber nicht eindeutig bestimmt. Denn zählt mn zu einer Funktion F (x) eine Konstnte hinzu, so fällt diese beim Differenzieren wieder herus. So ist uch G(x) = x + c für jede Konstnte c eine Stmmfunktion für f(x) = x. Aufgrund beknnter Formeln für die Ableitung von Funktionen können wir leicht eine kleine Liste von Stmmfunktionen ufstellen. Funktion f(x) Stmmfunktion F (x) x n n+ xn+ sin x cos x e x cos x sin x e x ln x (x > ) x Die Bedeutung der Stmmfunktionen beruht uf folgendem Stz (Fundmentlstz der Differentil- und Integrlrechnung) Sei f : I R eine stetige Funktion und F eine Stmmfunktion von f. Dnn gilt für lle, b I f(x) dx = F (b) F (). Mn knn sich diesen Stz wie folgt plusibel mchen. Nch Definition ist ds Integrl der Limes der Näherungssummen S n = f(x k ) x k. 9
10 D f(x k ) = F (x k ) und die Ableitung ein Limes von Differenzenquotienten ist, gilt nnähernd F (x k ) F (x k) F (x k ) = F (x k) F (x k ) x k x k x k Die Näherung ist umso besser, je kleiner x k ist. Somit hben wir f(x) dx f(x k ) x k = F (x k ) x k (F (x k ) F (x k )) = (F (x ) F (x )) + (F (x ) F (x )) (F (x n ) F (x n )) = F (x n ) F (x ) = F (b) F (), d sich in der zweiten Zeile lle bis uf zwei Terme wegkürzen. Bezeichnung. Mn setzt b F (x) := F (b) F (). Die Formel von Stz schreibt sich dnn ls b f(x) dx = F (x). Dies kürzt mn noch weiter b durch f(x) dx = F (x). Beispiele (.) xdx = x und x dx = 3 x3. Dmit erhlten wir wieder die im. Kpitel durch Grenzübergng berechneten Integrle und xdx = x x dx = 3 x3 = = 3 3. (.) In Verllgemeinerung des vorigen Beispiels knn mn Integrle P (x)dx uswerten, wobei P (x) = c + c x + c x c n x n ein beliebiges Polynom n-ten Grdes ist. Eine Stmmfunktion von P (x) ist nämlich es gilt deshlb F (x) = c x + c x + c x c nx n+ n +, P (x)dx = F (b) F ().
11 (.3) Ein interessntes neues Integrl ist sin(x)dx = cos(x) π = cos(π) + cos() = + =. Es stellt die Fläche unterhlb des Sinusbogens über dem Intervll [, π] dr. y = sin x π Es ist bemerkenswert, dss sich ls Flächeninhlt eine gnze Zhl ergibt, obwohl die Länge des Intervlls irrtionl ist.. Substitutionsregel Der nächste Stz liefert eine wichtige Methode zur Berechnung verschiedener Integrle. Stz (Substitutionsregel) Sei f : I R eine stetige Funktion und ϕ : [, b] R eine stetig differenzierbre Funktion mit ϕ([, b]) I. Dnn gilt f(ϕ(t)) ϕ (t) dt = ϕ(b) ϕ() f(x) dx. Bezeichnung. Unter Verwendung der symbolischen Schreibweise lutet die Substitutionsregel dϕ(t) := ϕ (t) dt f(ϕ(t)) dϕ(t) = ϕ(b) ϕ() f(x) dx und in dieser Form ist sie besonders einfch zu merken, denn mn ht einfch x durch ϕ(t) zu ersetzen. Läuft t von nch b, so läuft x = ϕ(t) von ϕ() nch ϕ(b). Beispiele (.4) Mn berechne (x + ) 3 dx. Wir können ds Integrl uch ls (t + ) 3 dt schreiben (die Integrtions-Vrible drf umbennnt werden, solnge die keine Kollisionen mit nderen Bezeichnungen entstehen).
12 Wir setzen f(x) = x 3. Mit der Substitution x = ϕ(t) = t + und ϕ (t) = wird dnn f(ϕ(t))ϕ (t) = (t + ) 3, lso (t + ) 3 dt = = 3 f(ϕ(t))ϕ (t)dt = x 3 dx = 4 x4 3 ϕ() ϕ() f(x)dx = 4 (34 4 ) = 8 4 =. Bemerkung. Eine ndere Möglichkeit zur Berechnung ist, den Term (x + ) 3 nch dem binomischen Lehrstz zu entwickeln, (x + ) 3 = x 3 + 3x + 3x + und ds enstehende Polynom 3. Grdes direkt zu integrieren. Aufgbe: Führe ds durch und überzeuge dich, dss dsselbe Ergebnis heruskommt. (.5) Sei > vorgegeben. Mn berechne cos(t) dt. Mit f(x) = cos x und der Substitution ϕ(t) = t gilt: cos(t) dt = cos(t) (t) dt = cos(x) dx = sin x = sin(). Bemerkung. Mn knn dieses Integrl uch direkt mit dem Fundmentlstz der Differentil- und Integrlrechnung uswerten. Denn Differenzieren mit der Kettenregel ergibt d sin(x) = cos(x). dx Ds bedeutet, dss F (x) = sin(x) eine Stmmfunktion von cos(x) ist, lso cos(x) dx = sin(x) = sin(). (.6) Mn berechne ds Integrl x dx. Dieses Integrl stellt die Fläche des Viertelkreises mit Rdius dr, siehe Bild. y = x
13 Wir mchen die Substitution x = sin t, lso dx = d sin t = sin (t)dt = cos t dt. Dmit x von bis läuft, muss t von bis π/ lufen. x dx = / sin t d sin t = / cos t dt. Dbei hben wir sin t = cos t benutzt. Nun verwenden wir noch die Formel cos t = ( + cos t) und erhlten x dx = / ( + cos t) dt = / dt + / cos t dt. Nun ist / dt = π/ (Fläche des Rechtecks mit Höhe und Breite π/) und / π/ sin t cos t dt = = (sin π sin ) = nch dem vorigen Beispiel. Insgesmt erhlten wir x dx = π 4. Wir hben dmit mittels Integrlrechnung gezeigt, dss die Fläche des Einheitskreises gleich π ist. (.7) Sei r > vorgegeben. Mn berechne ds Integrl r r x dx. Dieses Integrl stellt die Fläche des Viertelkreises mit Rdius r dr. Hier mchen wir die Substitution x = rt, lso dx = rdt. Dmit x von bis r läuft, muss t von bis lufen. Es folgt dher r r x dx = r r t rdt = r t dt = r π 4, wobei ds vorige Beispiel benutzt wurde. Die Fläche eines Kreises mit Rdius r ist lso r π. (.8) Sei > vorgegeben. Mn berechne t cos(t ) dt. Mit f(x) = cos x und der Substitution ϕ(t) = t gilt: t cos(t ) dt = cos(t ) (t ) dt = cos x dx = sin x = ( sin( ) sin ) = sin( ). 3
14 .3 Prtielle Integrtion Eine weitere nützliche Methode zur Berechnung der Integrle ist die so gennnte prtielle Integrtion. Stz 3 (Prtielle Integrtion) Seien f, g : [, b] R zwei stetig differenzierbre Funktionen. Dnn gilt f(x) g (x) dx = f(x) g(x) b g(x) f (x) dx. Eine Kurzschreibweise für diese Formel ist f dg = fg g df. Stz 3 lässt sich wie folgt beweisen: Wir setzen F (x) := f(x)g(x). Nch der Produktregel für die Ableitung gilt F (x) = f (x)g(x) + f(x)g (x). Nch dem Fundmentlstz der Differentil- und Integrlrechnung ist F (x)dx = F (x) b. Setzt mn die Ausdrücke für F (x) und F (x) ein, ergibt sich (f (x)g(x) + f(x)g b (x))dx = f(x)g(x). Bringt mn f (x)g(x)dx uf die ndere Seite, erhält mn die Behuptung des Stzes. Beispiele (.9) Mn berechne ds Integrl xe x dx. Wir setzen f(x) = x und g(x) = e x. Dnn ist uch g (x) = e x und die Formel der prtiellen Integrtion liefert (.) Mn berechne ds Integrl xe x dx = xe x e x dx = e e x = e (e ) =. x sin x dx. Der Grph der Funktion x x sin x schut so us: 4
15 y = x sin x π Zur Berechnung des Integrls setzen wir f(x) = x und g(x) = cos x. Dnn erhält mn x sin x dx = x ( cos x) dx π = x cos x = π cos π + cos + = π ( ) + = π. x ( cos x) dx cos x dx Die in obigem Bild gezeigte Figur ht lso genu denselben Flächeninhlt wie der Einheitskreis. (.) Mn berechne ds Integrl x cos x dx. Der Grph der Funktion x x cos x ist im folgenden Bild drgestellt. (Dbei ist der Mßstb uf der y-achse hlb so groß wie uf der x-achse.) π π - -5 y = x cos x - Wir setzen f(x) = x und g(x) = sin x. Dnn erhält mn 5
16 x cos x dx = x (sin x) dx = x π sin x = (x ) sin x dx x sin x dx = π nch dem vorherigen Beispiel. Ds negtive Resultt lässt sich ddurch erklären, dss die Funktion x x cos x im Intervll [ π, π] strk negtiv wird. Aufgbe: Berechne einzeln den positiven Teil und den negtiven Teil / π/ x cos x dx x cos x dx. 6
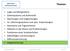
Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.
![Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m. Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.](/thumbs/74/70413961.jpg) Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
4.4 Partielle Integration
 Mthemtik für Nturwissenschftler I 4.4 4.4 Prtielle Integrtion Zwei Integrtionsregeln kennen wir bereits: Stz 4.. und Stz 4..8. Stz 4.. sgt, dss mit zwei Funktionen uch deren Summe oder Differenz integrierbr
Mthemtik für Nturwissenschftler I 4.4 4.4 Prtielle Integrtion Zwei Integrtionsregeln kennen wir bereits: Stz 4.. und Stz 4..8. Stz 4.. sgt, dss mit zwei Funktionen uch deren Summe oder Differenz integrierbr
Integration. Kapitel 8: Integration Informationen zur Vorlesung: wengenroth/ J. Wengenroth () 17.
 Integrtion Kpitel 8: Integrtion Informtionen zur Vorlesung: http://www.mthemtik.uni-trier.de/ wengenroth/ J. Wengenroth () 17. Juli 2009 1 / 22 8.1 Motivtion Kpitel 8: Integrtion 8.1 Motivtion Ist die
Integrtion Kpitel 8: Integrtion Informtionen zur Vorlesung: http://www.mthemtik.uni-trier.de/ wengenroth/ J. Wengenroth () 17. Juli 2009 1 / 22 8.1 Motivtion Kpitel 8: Integrtion 8.1 Motivtion Ist die
komplizierteren Funktionen versucht man, die Fläche durch mehrere Rechtecke anzunähern.
 Mthemtik für Nturwissenschftler I 4. 4 Integrlrechnung 4. Integrierbrkeit Die Grundidee der Integrlrechnung ist die Berechnung der Fläche zwischen dem Grphen einer Funktion und der x-achse. Recht einfch
Mthemtik für Nturwissenschftler I 4. 4 Integrlrechnung 4. Integrierbrkeit Die Grundidee der Integrlrechnung ist die Berechnung der Fläche zwischen dem Grphen einer Funktion und der x-achse. Recht einfch
Kapitel 7. Integralrechnung für Funktionen einer Variablen
 Kpitel 7. Integrlrechnung für Funktionen einer Vriblen In diesem Kpitel sei stets D R, und I R ein Intervll. 7. Ds unbestimmte Integrl (Stmmfunktion) Es sei f : I R eine Funktion. Eine differenzierbre
Kpitel 7. Integrlrechnung für Funktionen einer Vriblen In diesem Kpitel sei stets D R, und I R ein Intervll. 7. Ds unbestimmte Integrl (Stmmfunktion) Es sei f : I R eine Funktion. Eine differenzierbre
Resultat: Hauptsatz der Differential- und Integralrechnung
 17 Der Huptstz der Differentil- und Integrlrechnung Lernziele: Konzept: Stmmfunktion Resultt: Huptstz der Differentil- und Integrlrechnung Methoden: prtielle Integrtion, Substitutionsregel Kompetenzen:
17 Der Huptstz der Differentil- und Integrlrechnung Lernziele: Konzept: Stmmfunktion Resultt: Huptstz der Differentil- und Integrlrechnung Methoden: prtielle Integrtion, Substitutionsregel Kompetenzen:
Infinitesimalrechnung, Mengenlehre und logische Verknüpfungen
 Vorlesung 16 Infinitesimlrechnung, Mengenlehre und logische Verknüpfungen 16.1 Huptstz der Differentil- und Integrlrechnung Wir verknüpfen nun Differentil- mit Integrlrechnung. Definition 16.1.1. Eine
Vorlesung 16 Infinitesimlrechnung, Mengenlehre und logische Verknüpfungen 16.1 Huptstz der Differentil- und Integrlrechnung Wir verknüpfen nun Differentil- mit Integrlrechnung. Definition 16.1.1. Eine
Mathematischer Vorkurs NAT-ING1
 Mthemtischer Vorkurs NAT-ING1 (02.09. 20.09.2013) Dr. Robert Strehl WS 2013-2014 Mthemtischer Vorkurs TU Dortmund Seite 1 / 20 Mthemtischer Vorkurs TU Dortmund Seite 2 / 20 Definition 9.1 (Stmmfunktion)
Mthemtischer Vorkurs NAT-ING1 (02.09. 20.09.2013) Dr. Robert Strehl WS 2013-2014 Mthemtischer Vorkurs TU Dortmund Seite 1 / 20 Mthemtischer Vorkurs TU Dortmund Seite 2 / 20 Definition 9.1 (Stmmfunktion)
Infinitesimalrechnung
 Vorlesung 17 Infinitesimlrechnung 17.1 Huptstz der Differentil- und Integrlrechnung Wir verknüpfen nun Differentil- mit Integrlrechnung. Definition 17.1.1. Eine differenzierbre Funktion F : I R heißt Stmmfunktion
Vorlesung 17 Infinitesimlrechnung 17.1 Huptstz der Differentil- und Integrlrechnung Wir verknüpfen nun Differentil- mit Integrlrechnung. Definition 17.1.1. Eine differenzierbre Funktion F : I R heißt Stmmfunktion
Zusatzunterlagen zur Vorlesung Analysis II Sommersemester 2014
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6.1 MATHEMATIK Prof. Dr. Jörg Eschmeier M. Sc. Sebstin Lngendörfer e Integrlrechnung Zustzunterlgen zur Vorlesung Anlysis II Sommersemester 2014 Dieses Bltt enthält
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6.1 MATHEMATIK Prof. Dr. Jörg Eschmeier M. Sc. Sebstin Lngendörfer e Integrlrechnung Zustzunterlgen zur Vorlesung Anlysis II Sommersemester 2014 Dieses Bltt enthält
1 Differenzen- und Differentialquotient 2. 2 Differentiationsregeln 5. 3 Ableitung spezieller Funktionen 6. 4 Unbestimmtes und bestimmtes Integral 7
 Universität Bsel Wirtschftswissenschftliches Zentrum Abteilung Quntittive Methoden Mthemtischer Vorkurs Dr. Thoms Zehrt Differentil- und Integrlrechnung Inhltsverzeichnis 1 Differenzen- und Differentilquotient
Universität Bsel Wirtschftswissenschftliches Zentrum Abteilung Quntittive Methoden Mthemtischer Vorkurs Dr. Thoms Zehrt Differentil- und Integrlrechnung Inhltsverzeichnis 1 Differenzen- und Differentilquotient
Integralrechnung. Fakultät Grundlagen
 Integrlrechnung Fkultät Grundlgen März 2016 Fkultät Grundlgen Integrlrechnung Bestimmtes Integrl I n Teilintervlle: x 0 = < x 1 < x 2
Integrlrechnung Fkultät Grundlgen März 2016 Fkultät Grundlgen Integrlrechnung Bestimmtes Integrl I n Teilintervlle: x 0 = < x 1 < x 2
11. DER HAUPTSATZ DER DIFFERENTIAL- UND INTEGRALRECHNUNG
 91 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
91 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
Mathematik Rechenfertigkeiten
 2 Mthemtik Rechenfertigkeiten Skript Freitg Dominik Tsndy, Mthemtik Institut, Universität Zürich Winterthurerstrsse 9, 857 Zürich Irmgrd Bühler (Überrbeitung: Dominik Tsndy) 9.August 2 Inhltsverzeichnis
2 Mthemtik Rechenfertigkeiten Skript Freitg Dominik Tsndy, Mthemtik Institut, Universität Zürich Winterthurerstrsse 9, 857 Zürich Irmgrd Bühler (Überrbeitung: Dominik Tsndy) 9.August 2 Inhltsverzeichnis
D-MAVT/D-MATL Analysis I HS 2016 Dr. Andreas Steiger. Lösung - Serie 9
 D-MAVT/D-MATL Anlysis I HS 26 Dr. Andres Steiger Lösung - Serie 9. MC-Aufgben (Online-Abgbe). Es sei f die Funktion f() = e + 7. Welche der folgenden Funktionen sind Stmmfunktionen von f? () g() = 2 2
D-MAVT/D-MATL Anlysis I HS 26 Dr. Andres Steiger Lösung - Serie 9. MC-Aufgben (Online-Abgbe). Es sei f die Funktion f() = e + 7. Welche der folgenden Funktionen sind Stmmfunktionen von f? () g() = 2 2
Kapitel 9. Integration. Josef Leydold Auffrischungskurs Mathematik WS 2017/18 9 Integration 1 / 36
 Kpitel 9 Integrtion Josef Leydold Auffrischungskurs Mthemtik WS 207/8 9 Integrtion / 36 Stmmfunktion Eine Funktion F(x) heißt Stmmfunktion einer Funktion f (x), flls F (x) = f (x) Berechnung: Vermuten
Kpitel 9 Integrtion Josef Leydold Auffrischungskurs Mthemtik WS 207/8 9 Integrtion / 36 Stmmfunktion Eine Funktion F(x) heißt Stmmfunktion einer Funktion f (x), flls F (x) = f (x) Berechnung: Vermuten
Kapitel 9 Integralrechnung
 Kpitel 9 Integrlrechnung Kpitel 9 Integrlrechnung Mthemtischer Vorkurs TU Dortmund Seite 1 / 18 Kpitel 9 Integrlrechnung Definition 9.1 (Stmmfunktion) Es seien f, F : I R Funktionen. F heißt Stmmfunktion
Kpitel 9 Integrlrechnung Kpitel 9 Integrlrechnung Mthemtischer Vorkurs TU Dortmund Seite 1 / 18 Kpitel 9 Integrlrechnung Definition 9.1 (Stmmfunktion) Es seien f, F : I R Funktionen. F heißt Stmmfunktion
Mathematik Rechenfertigkeiten
 27 Mthemtik Rechenfertigkeiten Skript Freitg Dr. Dominik Tsndy, Mthemtik Institut, Universität Zürich Winterthurerstrsse 9, 857 Zürich Skript: Dr. Irmgrd Bühler (Überrbeitung: Dr. Dominik Tsndy) 8. August
27 Mthemtik Rechenfertigkeiten Skript Freitg Dr. Dominik Tsndy, Mthemtik Institut, Universität Zürich Winterthurerstrsse 9, 857 Zürich Skript: Dr. Irmgrd Bühler (Überrbeitung: Dr. Dominik Tsndy) 8. August
Crashkurs - Integration
 Crshkurs - Integrtion emerkung. Wir setzen hier elementre Kenntnisse des Differenzierens sowie der Produktregel, Quotientenregel und Kettenregel vorus (diese werden später in der VO noch usführlich erklärt).
Crshkurs - Integrtion emerkung. Wir setzen hier elementre Kenntnisse des Differenzierens sowie der Produktregel, Quotientenregel und Kettenregel vorus (diese werden später in der VO noch usführlich erklärt).
Kapitel 9. Integration. Josef Leydold Auffrischungskurs Mathematik WS 2017/18 9 Integration 1 / 36. F (x) = f (x) Vermuten und Verifizieren.
 Kpitel 9 Integrtion Josef Leydold Auffrischungskurs Mthemtik WS 27/8 9 Integrtion / 36 Stmmfunktion Eine Funktion F() heißt Stmmfunktion einer Funktion f (), flls F () = f () Berechnung: Vermuten und Verifizieren
Kpitel 9 Integrtion Josef Leydold Auffrischungskurs Mthemtik WS 27/8 9 Integrtion / 36 Stmmfunktion Eine Funktion F() heißt Stmmfunktion einer Funktion f (), flls F () = f () Berechnung: Vermuten und Verifizieren
1 Differentialrechnung
 1 Differentilrechnung 1.1 Ableitungen und Ableitungsregeln Nützliche Ableitungen 1. ( ) 1 = 1 x x 2 = x 2 2. Trigonometrische Funktionen: ( x) = 1 2 x [sin(x)] = cos(x) [cos(x)] = sin(x) 3. f(x) = e x
1 Differentilrechnung 1.1 Ableitungen und Ableitungsregeln Nützliche Ableitungen 1. ( ) 1 = 1 x x 2 = x 2 2. Trigonometrische Funktionen: ( x) = 1 2 x [sin(x)] = cos(x) [cos(x)] = sin(x) 3. f(x) = e x
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 10. dt. Welche der folgenden Aussagen ist richtig? t3 + 2
 D-MAVT/D-MATL Anlysis I HS 7 Dr. Andres Steiger Lösung - Serie.. Sei f(x) : () f() . x (c) f( ) . Die Funktion g : t t + ist, dss ds Integrl b dt. Welche der folgenden Aussgen
D-MAVT/D-MATL Anlysis I HS 7 Dr. Andres Steiger Lösung - Serie.. Sei f(x) : () f() . x (c) f( ) . Die Funktion g : t t + ist, dss ds Integrl b dt. Welche der folgenden Aussgen
Zum Satz von Taylor. Klaus-R. Loeffler. 2 Der Satz von Taylor 2
 Zum Stz von Tylor Klus-R. Loeffler Inhltsverzeichnis 1 Der verllgemeinerte Stz von Rolle 1 2 Der Stz von Tylor 2 3 Folgerungen, Anwendungen und Gegenbeispiele 4 3.1 Jede gnzrtionle Funktion ist ihr eigenes
Zum Stz von Tylor Klus-R. Loeffler Inhltsverzeichnis 1 Der verllgemeinerte Stz von Rolle 1 2 Der Stz von Tylor 2 3 Folgerungen, Anwendungen und Gegenbeispiele 4 3.1 Jede gnzrtionle Funktion ist ihr eigenes
Unbestimmtes Integral, Mittelwertsätze
 Unbestimmtes Integrl, Mittelwertsätze Ist f R-integrierbr, dnn knn f(x)dx einfch bestimmt werden, wenn eine Stmmfunktion F (x) von f existiert und beknnt ist. Wir wissen, dss dnn uch F (x) = F (x) + C
Unbestimmtes Integrl, Mittelwertsätze Ist f R-integrierbr, dnn knn f(x)dx einfch bestimmt werden, wenn eine Stmmfunktion F (x) von f existiert und beknnt ist. Wir wissen, dss dnn uch F (x) = F (x) + C
Stammfunktionen, Hauptsätze, unbestimmtes Integral
 Stmmfunktionen, Huptsätze, unbestimmtes Integrl Sei I ein Intervll, f beschränkt uf I und R-integrierbr für jedes [, b] I, und I. Dnn heißt die Funktion F mit D(F ) = I und F () = f(t)dt Integrl von f
Stmmfunktionen, Huptsätze, unbestimmtes Integrl Sei I ein Intervll, f beschränkt uf I und R-integrierbr für jedes [, b] I, und I. Dnn heißt die Funktion F mit D(F ) = I und F () = f(t)dt Integrl von f
, für x 2, ax wenn x > 3. 2x+a wenn x Integralrechnung
 . INTEGRALRECHNUNG 69 Aufgbe 9.3 Bestimme lle Extrem der Funktion f : [,] R, x ( x) +9x. Aufgbe 9.3 Bestimme die Extrem der Funktion f : R\{} R : x x4 5x 4 (x ) 3. Untersuche die Funktion hinsichtlich
. INTEGRALRECHNUNG 69 Aufgbe 9.3 Bestimme lle Extrem der Funktion f : [,] R, x ( x) +9x. Aufgbe 9.3 Bestimme die Extrem der Funktion f : R\{} R : x x4 5x 4 (x ) 3. Untersuche die Funktion hinsichtlich
Mathematik Rechenfertigkeiten
 26 Mthemtik Rechenfertigkeiten Skript Freitg Dr. Dominik Tsndy, Mthemtik Institut, Universität Zürich Winterthurerstrsse 9, 857 Zürich Skript: Dr. Irmgrd Bühler (Überrbeitung: Dr. Dominik Tsndy) 9. August
26 Mthemtik Rechenfertigkeiten Skript Freitg Dr. Dominik Tsndy, Mthemtik Institut, Universität Zürich Winterthurerstrsse 9, 857 Zürich Skript: Dr. Irmgrd Bühler (Überrbeitung: Dr. Dominik Tsndy) 9. August
π 2 r 2 r 2 sin 2 (t)r cos(t) dt π 2 cos2 (t) cos(t) dt = r 2 π dt = cos(x) sin(x) u v = cos(x) sin(x) + = cos(x) sin(x) + x
 Wir substituieren x x(t) r sin(t), t [ π, π ]. Dnn ist x (t) r cos(t), lso r x dx π π r π r r sin (t)r cos(t) dt π cos (t) cos(t) dt r π π cos (t) dt Wir integrieren cos mittels prtieller Integrtion: Sei
Wir substituieren x x(t) r sin(t), t [ π, π ]. Dnn ist x (t) r cos(t), lso r x dx π π r π r r sin (t)r cos(t) dt π cos (t) cos(t) dt r π π cos (t) dt Wir integrieren cos mittels prtieller Integrtion: Sei
10 Das Riemannsche Integral
 10 Ds Riemnnsche Integrl 50 10 Ds Riemnnsche Integrl Ziel dieses Prgrphen ist es, den Inhlt einer Fläche, die vom Grphen einer Funktion berndet wird, exkt zu definieren. f(b) f() = t 0 t1 t2 t3 t4 t5 t
10 Ds Riemnnsche Integrl 50 10 Ds Riemnnsche Integrl Ziel dieses Prgrphen ist es, den Inhlt einer Fläche, die vom Grphen einer Funktion berndet wird, exkt zu definieren. f(b) f() = t 0 t1 t2 t3 t4 t5 t
Grundlagen der Integralrechnung
 Grundlgen der Integrlrechnung W. Kippels 0. April 2014 Inhltsverzeichnis 1 Ds unbestimmte Integrl 2 2 Ds bestimmte Integrl 4 Beispielufgben 7.1 Beispielufgbe 1............................... 7.2 Beispielufgbe
Grundlgen der Integrlrechnung W. Kippels 0. April 2014 Inhltsverzeichnis 1 Ds unbestimmte Integrl 2 2 Ds bestimmte Integrl 4 Beispielufgben 7.1 Beispielufgbe 1............................... 7.2 Beispielufgbe
Hier ist noch ein Beispiel, bei dem sowohl die Substitutionsregel als auch die partielle Integration zur Anwendung kommt.
 64 Kpitel. Integrlrechnung Hier ist noch ein Beispiel, bei dem sowohl die Substitutionsregel ls uch die prtielle Integrtion zur Anwendung kommt..4.6 Beispiel Um eine Stmmfunktion für rctn zu finden, beginnen
64 Kpitel. Integrlrechnung Hier ist noch ein Beispiel, bei dem sowohl die Substitutionsregel ls uch die prtielle Integrtion zur Anwendung kommt..4.6 Beispiel Um eine Stmmfunktion für rctn zu finden, beginnen
Übung Analysis in einer Variable für LAK, SS 2010
 Übung Anlysis in einer Vrible für LAK, SS Christoph B ) Es sei I R ein offenes Intervll, ξ I und f,...,f n : I R seien lle in ξ differenzierbr. Beweisen Sie: Dnn ist uch f f n : I R in ξ differenzierbr
Übung Anlysis in einer Vrible für LAK, SS Christoph B ) Es sei I R ein offenes Intervll, ξ I und f,...,f n : I R seien lle in ξ differenzierbr. Beweisen Sie: Dnn ist uch f f n : I R in ξ differenzierbr
Höhere Mathematik für die Fachrichtung Physik
 Krlsruher Institut für Technologie Institut für Anlysis Dr. Christoph Schmoeger Dipl.-Mth. Sebstin Schwrz Höhere Mthemtik für die Fchrichtung Physik Lösungsvorschläge zum. Übungsbltt Aufgbe 6 (Übung) )
Krlsruher Institut für Technologie Institut für Anlysis Dr. Christoph Schmoeger Dipl.-Mth. Sebstin Schwrz Höhere Mthemtik für die Fchrichtung Physik Lösungsvorschläge zum. Übungsbltt Aufgbe 6 (Übung) )
Integration von Regelfunktionen
 Integrtion von Regelfunktionen Inhltsverzeichnis Einleitung 2 Treppen- und Regelfunktionen 3 Denition des Integrls 4 Rechen mit Integrlen 2 4. Grundlegende Eigenschften.............................................
Integrtion von Regelfunktionen Inhltsverzeichnis Einleitung 2 Treppen- und Regelfunktionen 3 Denition des Integrls 4 Rechen mit Integrlen 2 4. Grundlegende Eigenschften.............................................
4.6 Integralrechnung III. Inhaltsverzeichnis
 4.6 Integrlrechnung III Inhltsverzeichnis 1 Integrlrechnung 10.03.2010 Theorie und Übungen 2 1 Exponentilfunktionen Aus der Differentilrechnung wissen wir, dss gilt: f(x)=e x f (x)=e x Stz 1 Für die ntürliche
4.6 Integrlrechnung III Inhltsverzeichnis 1 Integrlrechnung 10.03.2010 Theorie und Übungen 2 1 Exponentilfunktionen Aus der Differentilrechnung wissen wir, dss gilt: f(x)=e x f (x)=e x Stz 1 Für die ntürliche
Analysis I. Partielle Integration. f (t)g(t)dt =
 Prof. Dr. H. Brenner Osnbrück WS 3/4 Anlysis I Vorlesung 5 Wir besprechen nun die wesentlichen Rechenregeln, mit denen mn Stmmfunktionen finden bzw. bestimmte Integrle berechnen knn. Sie beruhen uf Ableitungsregeln.
Prof. Dr. H. Brenner Osnbrück WS 3/4 Anlysis I Vorlesung 5 Wir besprechen nun die wesentlichen Rechenregeln, mit denen mn Stmmfunktionen finden bzw. bestimmte Integrle berechnen knn. Sie beruhen uf Ableitungsregeln.
9 Integralrechnung. 9.1 Das Riemann-Integral: Sei [a, b] ein beschränktes abgeschlossenes Intervall und f : [a, b] R eine beschränkte Funktion.
![9 Integralrechnung. 9.1 Das Riemann-Integral: Sei [a, b] ein beschränktes abgeschlossenes Intervall und f : [a, b] R eine beschränkte Funktion. 9 Integralrechnung. 9.1 Das Riemann-Integral: Sei [a, b] ein beschränktes abgeschlossenes Intervall und f : [a, b] R eine beschränkte Funktion.](/thumbs/88/116973351.jpg) 9 ntegrlrechnung 9. Ds Riemnn-ntegrl: Sei [, b] ein beschränktes bgeschlossenes ntervll und f : [, b] R eine beschränkte Funktion. Problem: Bestimme Flächeninhlt A zwischen Grphen von f und x-achse. Betrchte
9 ntegrlrechnung 9. Ds Riemnn-ntegrl: Sei [, b] ein beschränktes bgeschlossenes ntervll und f : [, b] R eine beschränkte Funktion. Problem: Bestimme Flächeninhlt A zwischen Grphen von f und x-achse. Betrchte
Kapitel 8 Anwendungen der Di erentialrechnung
 Kpitel 8 Anwendungen der Di erentilrechnung Kpitel 8 Anwendungen der Di erentilrechnung Mthemtischer Vorkurs TU Dortmund Seite 99 / 235 Kpitel 8 Anwendungen der Di erentilrechnung Stz 8.1 (Mittelwertstz
Kpitel 8 Anwendungen der Di erentilrechnung Kpitel 8 Anwendungen der Di erentilrechnung Mthemtischer Vorkurs TU Dortmund Seite 99 / 235 Kpitel 8 Anwendungen der Di erentilrechnung Stz 8.1 (Mittelwertstz
Differenzial- und Integralrechnung III
 Differenzil- und Integrlrechnung III Riner Huser April 2012 1 Einleitung 1.1 Polynome und Potenzfunktionen Die Polynome oder Polynomfunktionen lssen sich durch die endliche Anzhl von n+1 Prmetern i R in
Differenzil- und Integrlrechnung III Riner Huser April 2012 1 Einleitung 1.1 Polynome und Potenzfunktionen Die Polynome oder Polynomfunktionen lssen sich durch die endliche Anzhl von n+1 Prmetern i R in
6. Integration 6.1 Das Riemann-Integral
 6. Integrtion 6. Ds Riemnn-Integrl 6. Integrtion 6. Ds Riemnn-Integrl Mthemtik für Chemiker 6. Integrtion 6. Ds Riemnn-Integrl Flächenberechnung: Problemstellung und Lösungsidee Sei f : [, b] [0, ) eine
6. Integrtion 6. Ds Riemnn-Integrl 6. Integrtion 6. Ds Riemnn-Integrl Mthemtik für Chemiker 6. Integrtion 6. Ds Riemnn-Integrl Flächenberechnung: Problemstellung und Lösungsidee Sei f : [, b] [0, ) eine
Flächeninhalt unter dem Graphen. Ist nun die Kraft nicht mehr stückweise konstant, so wird man intuitiv immer noch den
 19 REGELFUNKTIONEN 107 Kpitel 7: Integrtion Notwendigkeit des Integrlbegriffes und Hinweise zu seiner Präzisierung liegen uf der Hnd. Betrchten wir etw den physiklischen Begriff der Arbeit, die im einfchsten
19 REGELFUNKTIONEN 107 Kpitel 7: Integrtion Notwendigkeit des Integrlbegriffes und Hinweise zu seiner Präzisierung liegen uf der Hnd. Betrchten wir etw den physiklischen Begriff der Arbeit, die im einfchsten
Mathematik II. Partielle Integration. f (t)g(t)dt =
 Prof. Dr. H. Brenner Osnbrück SS 1 Mthemtik II Vorlesung 33 Wir besprechen nun die wesentlichen Rechenregeln, mit denen mn Stmmfunktionen finden bzw. bestimmte Integrle berechnen knn. Sie beruhen uf Ableitungsregeln.
Prof. Dr. H. Brenner Osnbrück SS 1 Mthemtik II Vorlesung 33 Wir besprechen nun die wesentlichen Rechenregeln, mit denen mn Stmmfunktionen finden bzw. bestimmte Integrle berechnen knn. Sie beruhen uf Ableitungsregeln.
Kapitel 1. Das Riemann-Integral. 1.1 *Motivation
 Kpitel Ds Riemnn-Integrl. *Motivtion Wir betrchten eine stetige Funktion f : [, b] R, wobei, b R und < b. Frge: Wie groß ist der Flächeninhlt zwischen dem Abschnitt [, b] uf der x-achse und dem Grph von
Kpitel Ds Riemnn-Integrl. *Motivtion Wir betrchten eine stetige Funktion f : [, b] R, wobei, b R und < b. Frge: Wie groß ist der Flächeninhlt zwischen dem Abschnitt [, b] uf der x-achse und dem Grph von
Integralrechnung. Andreas Rottmann. 15. Oktober 2003
 Integrlrechnung Andres Rottmnn 15. Oktober 2003 Inhltsverzeichnis 1 Ds unbestimmte Integrl 2 1.1 Integrtion ls Umkehrung des Differenzierens........... 2 1.2 Integrtionsregeln...........................
Integrlrechnung Andres Rottmnn 15. Oktober 2003 Inhltsverzeichnis 1 Ds unbestimmte Integrl 2 1.1 Integrtion ls Umkehrung des Differenzierens........... 2 1.2 Integrtionsregeln...........................
Kapitel 10. Integration. Josef Leydold Mathematik für VW WS 2015/16 10 Integration 1 / 35
 Kpitel 0 Integrtion Josef Leydold Mthemtik für VW WS 205/6 0 Integrtion / 35 Flächeninhlt Berechnen Sie die Inhlte der ngegebenen Flächen! f (x) = Fläche: A = f (x) = +x 2 Approximtion durch Treppenfunktion
Kpitel 0 Integrtion Josef Leydold Mthemtik für VW WS 205/6 0 Integrtion / 35 Flächeninhlt Berechnen Sie die Inhlte der ngegebenen Flächen! f (x) = Fläche: A = f (x) = +x 2 Approximtion durch Treppenfunktion
1 Folgen. 1. Februar 2016 ID 03/455. a) Folgende Folge ist gegeben: a n+1 = 7a n 12a n 1, a 0 = 1, a 1 = 0 (1) Charakteristisches Polynom:
 Tutorium Ynnick Schrör Lösung zur Bonusklusur vom WS 1/13 Ynnick.Schroer@rub.de 1. Februr 016 ID 03/455 1 Folgen ) Folgende Folge ist gegeben: n+1 7 n 1 n 1, 0 1, 1 0 (1) Chrkteristisches Polynom: q 7q
Tutorium Ynnick Schrör Lösung zur Bonusklusur vom WS 1/13 Ynnick.Schroer@rub.de 1. Februr 016 ID 03/455 1 Folgen ) Folgende Folge ist gegeben: n+1 7 n 1 n 1, 0 1, 1 0 (1) Chrkteristisches Polynom: q 7q
Mathematik I ITB. Integralrechnung. Prof. Dr. Karin Melzer
 Integrlrechnung 20.05.09 Ds unbestimmte Integrl/Stmmfunktion Ds bestimmte Integrl/Flächenberechnung Integrl ls Umkehrung der Ableitung Idee: kehre den Prozess des Dierenzierens um. f sei eine reelle Funktion
Integrlrechnung 20.05.09 Ds unbestimmte Integrl/Stmmfunktion Ds bestimmte Integrl/Flächenberechnung Integrl ls Umkehrung der Ableitung Idee: kehre den Prozess des Dierenzierens um. f sei eine reelle Funktion
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufge 69. Quizz Integrle. Es sei Höhere Mthemtik für Informtiker II (Sommersemester
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufge 69. Quizz Integrle. Es sei Höhere Mthemtik für Informtiker II (Sommersemester
Lösungsvorschläge zum 9. Übungsblatt.
 Übung zur Anlysis II SS 1 Lösungsvorschläge zum 9. Übungsbltt. Aufgbe 33 () A : {(x, y) R : x [ 1, 1] und y oder x und y [ 1, 1]}. (b) A : {(x, y) R : x < y < 1 + x }. (c) A : {(x, y) R : x < y < 1 + x
Übung zur Anlysis II SS 1 Lösungsvorschläge zum 9. Übungsbltt. Aufgbe 33 () A : {(x, y) R : x [ 1, 1] und y oder x und y [ 1, 1]}. (b) A : {(x, y) R : x < y < 1 + x }. (c) A : {(x, y) R : x < y < 1 + x
Prof. Dr. Siegfried Echterhoff.. 1 HAUPTSATZ DER INTEGRAL UND DIFFERENTIALRECHNUNG
 Vorlesung SS 29 Anlysis 2 HAUPTSATZ DER INTEGRAL UND DIFFERENTIALRECHNUNG Teil : Fortsetzung des Studiums von Funktionen in einer reellen Vriblen (Integrtion und Tylorreihen). Huptstz der Integrl und Differentilrechnung
Vorlesung SS 29 Anlysis 2 HAUPTSATZ DER INTEGRAL UND DIFFERENTIALRECHNUNG Teil : Fortsetzung des Studiums von Funktionen in einer reellen Vriblen (Integrtion und Tylorreihen). Huptstz der Integrl und Differentilrechnung
MC-Serie 12 - Integrationstechniken
 Anlysis D-BAUG Dr. Meike Akveld HS 15 MC-Serie 1 - Integrtionstechniken 1. Die Formel f(x) dx = xf(x) xf (x) dx i) ist im Allgemeinen flsch. ii) folgt us der Sustitutionsregel. iii) folgt us dem Huptstz
Anlysis D-BAUG Dr. Meike Akveld HS 15 MC-Serie 1 - Integrtionstechniken 1. Die Formel f(x) dx = xf(x) xf (x) dx i) ist im Allgemeinen flsch. ii) folgt us der Sustitutionsregel. iii) folgt us dem Huptstz
8.4 Integrationsmethoden
 8.4 Integrtionsmethoden 33 8.4 Integrtionsmethoden Die Integrtion von Funktionen erweist sich in prktischen Fällen oftmls schwieriger ls die Differenzition. Während sich ds Differenzieren durch Anwendung
8.4 Integrtionsmethoden 33 8.4 Integrtionsmethoden Die Integrtion von Funktionen erweist sich in prktischen Fällen oftmls schwieriger ls die Differenzition. Während sich ds Differenzieren durch Anwendung
(1 ξ) f (k) (ξ) + k! z x n+1. (n + 1)! 2 f (n + 1)!
 0.. Lösung der Aufgbe. Wir schreiben f = sup{ f : [0, ]}. Für ξ ]0, [ und n N gibt es nch dem Stz von Tlor ein c ]ξ, [ so, dss: f = fξ + n ξ k f k ξ + k! k= Aus der Ttsche, dss f k 0 für lle k N ist, folgt
0.. Lösung der Aufgbe. Wir schreiben f = sup{ f : [0, ]}. Für ξ ]0, [ und n N gibt es nch dem Stz von Tlor ein c ]ξ, [ so, dss: f = fξ + n ξ k f k ξ + k! k= Aus der Ttsche, dss f k 0 für lle k N ist, folgt
Mathematik LK 12 M1, 1. Kursarbeit Integration Lösung f (x)dx=lim S n. a I. Dann heißt. a, x I. Dann gilt:
 Mthemtik LK M,. Kursrbeit Integrtion Lösung..3 Aufgbe :. Erkläre mit Hilfe der Definition des Integrls den Unterschied zwischen dem Integrl einer Funktion und dem Flächeninhlt der Fläche zwischen dem Grphen
Mthemtik LK M,. Kursrbeit Integrtion Lösung..3 Aufgbe :. Erkläre mit Hilfe der Definition des Integrls den Unterschied zwischen dem Integrl einer Funktion und dem Flächeninhlt der Fläche zwischen dem Grphen
Integrationsmethoden
 Universität Perborn Dezember 8 Institut für Mthemtik C. Kiser Integrtionsmethoen Prtielle Integrtion (Prouktintegrtion) Unbestimmte Integrtion er Prouktregel (u v) () = u ()v() + u()v () liefert (u v)()
Universität Perborn Dezember 8 Institut für Mthemtik C. Kiser Integrtionsmethoen Prtielle Integrtion (Prouktintegrtion) Unbestimmte Integrtion er Prouktregel (u v) () = u ()v() + u()v () liefert (u v)()
kann man das Riemannsche Unter- bzw. Oberintegral auch wie folgt definieren: xk+1 x k
 Integrlrechnung Definition 1 (Treppenfunktion, Zerlegung eines Intervlls): Sei [, b] R ein Intervll. Eine Funktion g : [, b] R heißt Treppenfunktion, flls es eine Zerlegung := { =: 0 < 1
Integrlrechnung Definition 1 (Treppenfunktion, Zerlegung eines Intervlls): Sei [, b] R ein Intervll. Eine Funktion g : [, b] R heißt Treppenfunktion, flls es eine Zerlegung := { =: 0 < 1
2.4 Elementare Substitution
 .4 Elementre Substitution 7.4 Elementre Substitution Im Übungsteil finden Sie folgende Aufgben zum Trining der in diesem Abschnitt behndelten Themen: Linere Substitution (LSub): Aufgbe 4.5 (S.4) und Aufgbe
.4 Elementre Substitution 7.4 Elementre Substitution Im Übungsteil finden Sie folgende Aufgben zum Trining der in diesem Abschnitt behndelten Themen: Linere Substitution (LSub): Aufgbe 4.5 (S.4) und Aufgbe
SBP Mathe Grundkurs 2. Differentialquotient. Namen und Schreibweisen für Differentialquotienten. Ableitung von f(x) = c.
 SBP Mthe Grundkurs 2 # 0 by Clifford Wolf # 0 Antwort Diese Lernkrten sind sorgfältig erstellt worden, erheben ber weder Anspruch uf Richtigkeit noch uf Vollständigkeit. Ds Lernen mit Lernkrten funktioniert
SBP Mthe Grundkurs 2 # 0 by Clifford Wolf # 0 Antwort Diese Lernkrten sind sorgfältig erstellt worden, erheben ber weder Anspruch uf Richtigkeit noch uf Vollständigkeit. Ds Lernen mit Lernkrten funktioniert
12. STAMMFUNKTIONEN UND DAS UNBESTIMMTE INTEGRAL
 98 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
98 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
Grundlagen der Integralrechnung
 Grundlgen der Integrlrechnung Wolfgng Kippels 8. April 018 Inhltsverzeichnis 1 Vorwort Ds unbestimmte Integrl Ds bestimmte Integrl 5 4 Beispielufgben 8 4.1 Beispielufgbe 1...............................
Grundlgen der Integrlrechnung Wolfgng Kippels 8. April 018 Inhltsverzeichnis 1 Vorwort Ds unbestimmte Integrl Ds bestimmte Integrl 5 4 Beispielufgben 8 4.1 Beispielufgbe 1...............................
12. STAMMFUNKTIONEN UND DAS UNBESTIMMTE INTEGRAL
 98 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
98 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschftsmthemtik für Interntionl Mngement (BA) und Betriebswirtschft (BA) Wintersemester 2013/14 Stefn Etschberger Hochschule Augsburg Mthemtik: Gliederung 1 Aussgenlogik 2 Linere Algebr 3 Linere
Wirtschftsmthemtik für Interntionl Mngement (BA) und Betriebswirtschft (BA) Wintersemester 2013/14 Stefn Etschberger Hochschule Augsburg Mthemtik: Gliederung 1 Aussgenlogik 2 Linere Algebr 3 Linere
Lösungsskizzen zur Präsenzübung 06
 Lösungsskizzen zur Präsenzübung 06 Mirko Getzin Universität Bielefeld Fkultät für Mthemtik 23. Mi 2014 Keine Gewähr uf vollständige Richtigkeit und Präzision ller (mthemtischen) Aussgen. Ds Dokument ht
Lösungsskizzen zur Präsenzübung 06 Mirko Getzin Universität Bielefeld Fkultät für Mthemtik 23. Mi 2014 Keine Gewähr uf vollständige Richtigkeit und Präzision ller (mthemtischen) Aussgen. Ds Dokument ht
21. Das bestimmte Integral
 1. Ds bestimmte Integrl Wir betrchten eine Kurve y = f(x) mit f(x) 0 uf dem Intervll [, b]. Obwohl der Flächeninhlt eines Rechteces (und in weiterer Folge eines Dreieces und nderer elementrer geometrischer
1. Ds bestimmte Integrl Wir betrchten eine Kurve y = f(x) mit f(x) 0 uf dem Intervll [, b]. Obwohl der Flächeninhlt eines Rechteces (und in weiterer Folge eines Dreieces und nderer elementrer geometrischer
10 Integrationstechniken
 Integrtionstechniken. Wichtige Stmmfunktionen α d = α + α+, d = log e d = e cos d = sin sin d = cos d = rcsin d = rctn + cosh d = sinh sinh d = cosh + d = sinh d = cosh α R, α. Linerität der Integrtion
Integrtionstechniken. Wichtige Stmmfunktionen α d = α + α+, d = log e d = e cos d = sin sin d = cos d = rcsin d = rctn + cosh d = sinh sinh d = cosh + d = sinh d = cosh α R, α. Linerität der Integrtion
Münchner Volkshochschule. Themen
 Themen Logik und Mengenlehre Zhlensysteme und Arithmetik Gleichungen und Ungleichungen Lin. Gleichungssysteme und spez. Anwendungen Geometrie und Trigonometrie Vektoren in der Ebene und Punktemengen Funktionen
Themen Logik und Mengenlehre Zhlensysteme und Arithmetik Gleichungen und Ungleichungen Lin. Gleichungssysteme und spez. Anwendungen Geometrie und Trigonometrie Vektoren in der Ebene und Punktemengen Funktionen
9.3 Der Hauptsatz und Anwendungen
 9.3 Der Huptstz und Anwendungen Definition: Seien Funktionen F, f : [, b] R Funktionen mit F (x) = f(x), x b. Dnn heißt F(x) Stmmfunktion von f(x). Bemerkung: Ist F(x) eine Stmmfunktion von f(x), so sind
9.3 Der Huptstz und Anwendungen Definition: Seien Funktionen F, f : [, b] R Funktionen mit F (x) = f(x), x b. Dnn heißt F(x) Stmmfunktion von f(x). Bemerkung: Ist F(x) eine Stmmfunktion von f(x), so sind
9.6 Parameterabhängige Integrale
 Kpitel 9: Integrtion 9.6 Prmeterbhängige Integrle Beispiel: Die Gmm-Funktion Γ(x) := f(x, t)dt = e t t x 1 dt. Zunächst: Prmeterbhängige eigentliche Integrle. Sei f : I [, b] R, I R, so dss f für festes
Kpitel 9: Integrtion 9.6 Prmeterbhängige Integrle Beispiel: Die Gmm-Funktion Γ(x) := f(x, t)dt = e t t x 1 dt. Zunächst: Prmeterbhängige eigentliche Integrle. Sei f : I [, b] R, I R, so dss f für festes
Mathematik II. Vorlesung 31
 Prof. Dr. H. Brenner Osnbrück SS 2010 Mthemtik II Vorlesung 31 In den folgenden Vorlesungen beschäftigen wir uns mit der Integrtionstheorie, d.h. wir wollen den Flächeninhlt derjenigen Fläche, die durch
Prof. Dr. H. Brenner Osnbrück SS 2010 Mthemtik II Vorlesung 31 In den folgenden Vorlesungen beschäftigen wir uns mit der Integrtionstheorie, d.h. wir wollen den Flächeninhlt derjenigen Fläche, die durch
f(ξ k )(x k x k 1 ) k=1
 Integrlrechnung Definition des bestimmten Integrls Die Integrtion ist die Umkehropertion zur Differentition. Grundufgbe der Integrlrechnung ist die Bestimmung von Flächen. Will mn beispielsweise den Inhlt
Integrlrechnung Definition des bestimmten Integrls Die Integrtion ist die Umkehropertion zur Differentition. Grundufgbe der Integrlrechnung ist die Bestimmung von Flächen. Will mn beispielsweise den Inhlt
nennt man eine Zerlegung (Partition, Unterteilung) des Intervalls [a, b]. Die Feinheit der Zerlegung ist dabei
![nennt man eine Zerlegung (Partition, Unterteilung) des Intervalls [a, b]. Die Feinheit der Zerlegung ist dabei nennt man eine Zerlegung (Partition, Unterteilung) des Intervalls [a, b]. Die Feinheit der Zerlegung ist dabei](/thumbs/64/52033315.jpg) Kpitel 8: Integrtion Erläuterung uf Folie 8.1 Ds bestimmte Integrl Sei f : [, b] R eine beschränkte Funktion uf einem (zunächst) kompkten Intervll [, b]. Definition: 1) Eine Menge der Form Z = { = x 0
Kpitel 8: Integrtion Erläuterung uf Folie 8.1 Ds bestimmte Integrl Sei f : [, b] R eine beschränkte Funktion uf einem (zunächst) kompkten Intervll [, b]. Definition: 1) Eine Menge der Form Z = { = x 0
6.6 Integrationsregeln
 50 KAPITEL 6. DAS RIEMANN-INTEGRAL Beispiel 6.5.4 (Differenzierbreit und gleichmäßige Konvergenz) Die Funtionenfolge {f n (x)} n N definiert durch f n (x) = n sin(nx) onvergiert uf jedem Intervll gleichmäßig
50 KAPITEL 6. DAS RIEMANN-INTEGRAL Beispiel 6.5.4 (Differenzierbreit und gleichmäßige Konvergenz) Die Funtionenfolge {f n (x)} n N definiert durch f n (x) = n sin(nx) onvergiert uf jedem Intervll gleichmäßig
$Id: integral.tex,v /05/15 15:03:49 hk Exp $ $Id: uneigentlich.tex,v /05/16 13:37:14 hk Exp $
 $Id: integrl.te,v.3 24/5/5 5:3:49 hk Ep $ $Id: uneigentlich.te,v. 24/5/6 3:37:4 hk Ep $ 2 Integrlrechnung 2.5 Ergänzungen Wir sind jetzt m Ende des Kpitels über ds Riemn-Integrl im eigentlichen Sinne ngelngt,
$Id: integrl.te,v.3 24/5/5 5:3:49 hk Ep $ $Id: uneigentlich.te,v. 24/5/6 3:37:4 hk Ep $ 2 Integrlrechnung 2.5 Ergänzungen Wir sind jetzt m Ende des Kpitels über ds Riemn-Integrl im eigentlichen Sinne ngelngt,
VI. Das Riemann-Stieltjes Integral.
 VI. Ds Riemnn-Stieltjes Integrl. Es stellt sich herus, dss der hier entwickelte Integrlbegriff strk von der Ordnungsstruktur von R bhängt. Definition. Sei [, b] ein Intervll in R. Unter einer Prtition
VI. Ds Riemnn-Stieltjes Integrl. Es stellt sich herus, dss der hier entwickelte Integrlbegriff strk von der Ordnungsstruktur von R bhängt. Definition. Sei [, b] ein Intervll in R. Unter einer Prtition
Mathematik 1 für Bauwesen 14. Übungsblatt
 Mthemtik für Buwesen Übungsbltt Fchbereich Mthemtik Wintersemester 0/0 Dr Ivn Izmestiev 8/900 Dr Vince Bárány, M Sc Juli Plehnert Gruppenübung Aufgbe G () Berechnen Sie ds Volumen des Rottionskörpers,
Mthemtik für Buwesen Übungsbltt Fchbereich Mthemtik Wintersemester 0/0 Dr Ivn Izmestiev 8/900 Dr Vince Bárány, M Sc Juli Plehnert Gruppenübung Aufgbe G () Berechnen Sie ds Volumen des Rottionskörpers,
$Id: integral.tex,v /04/28 13:32:32 hk Exp hk $
 Mthemtik für Ingenieure II, SS 009 Dienstg 8.4 $Id: integrl.tex,v 1.4 009/04/8 13:3:3 hk Exp hk $ Integrlrechnung.3 Die Integrtionsregeln Mit den bisherigen Beispielen hben wir die meisten Integrle behndelt,
Mthemtik für Ingenieure II, SS 009 Dienstg 8.4 $Id: integrl.tex,v 1.4 009/04/8 13:3:3 hk Exp hk $ Integrlrechnung.3 Die Integrtionsregeln Mit den bisherigen Beispielen hben wir die meisten Integrle behndelt,
3 Uneigentliche Integrale
 Mthemtik für Ingenieure II, SS 29 Dienstg 9.5 $Id: uneigentlich.te,v.5 29/5/9 6:23:8 hk Ep $ $Id: prmeter.te,v.2 29/5/9 6:8:3 hk Ep $ 3 Uneigentliche Integrle Mn knn die eben nchgerechnete Aussge e d =,
Mthemtik für Ingenieure II, SS 29 Dienstg 9.5 $Id: uneigentlich.te,v.5 29/5/9 6:23:8 hk Ep $ $Id: prmeter.te,v.2 29/5/9 6:8:3 hk Ep $ 3 Uneigentliche Integrle Mn knn die eben nchgerechnete Aussge e d =,
14.1 Der Hauptsatz der Integralrechnung
 Anlysis, Woche 4 Integrlrechnung II A 4. Der Huptstz der Integrlrechnung In der letzten Woche hben wir ngeschut, wie mn ds Integrl definieren knn. Dmit lässt sich zwr ein Flächeninhlt pproximieren, ber
Anlysis, Woche 4 Integrlrechnung II A 4. Der Huptstz der Integrlrechnung In der letzten Woche hben wir ngeschut, wie mn ds Integrl definieren knn. Dmit lässt sich zwr ein Flächeninhlt pproximieren, ber
4.5 Integralrechnung II. Inhaltsverzeichnis
 4.5 Integrlrechnung II Inhltsverzeichnis 1 Integrlrechnung 22.02.2010 Theorie und Übungen 2 Wir hben im ersten Skript beobchtet, dss ein Zusmmenhng besteht zwischen der Formel für die Fläche A 0b und der
4.5 Integrlrechnung II Inhltsverzeichnis 1 Integrlrechnung 22.02.2010 Theorie und Übungen 2 Wir hben im ersten Skript beobchtet, dss ein Zusmmenhng besteht zwischen der Formel für die Fläche A 0b und der
Vorkurs Mathematik DIFFERENTIATION
 Vorkurs Mthemtik 6 DIFFERENTIATION Beispiel (Ableitung von sin( )). Es seien f() = sin g() = h() =f(g()) = sin. (f () =cos) (g () =) Also ist die Ableitung von h: h () =f (g())g () =cos = cos. Mn nennt
Vorkurs Mthemtik 6 DIFFERENTIATION Beispiel (Ableitung von sin( )). Es seien f() = sin g() = h() =f(g()) = sin. (f () =cos) (g () =) Also ist die Ableitung von h: h () =f (g())g () =cos = cos. Mn nennt
= f (x). Anmerkung: Stammfunktionen finden ist also die Umkehrung der Ableitung, es wird daher auch manchmal als Aufleiten bezeichnet.
 .Stmmfunktionen Integrlrechnung Im folgenden sei I R ein Intervll ds mit mindestens 2 verschiedene Punkte enthält.. Stmmfunktionen Definition: Eine differenzierre Funktion F : I R heißt Stmmfunktion einer
.Stmmfunktionen Integrlrechnung Im folgenden sei I R ein Intervll ds mit mindestens 2 verschiedene Punkte enthält.. Stmmfunktionen Definition: Eine differenzierre Funktion F : I R heißt Stmmfunktion einer
a = x 0 < x 1 <... < x n = b
 7 Integrtion 7.1 Integrtion von Treppenfunktionen Im folgenden ezeichnen wir mit I = [, ] ein eschränktes und geschlossenes Intervll. Für Punkte = x 0 < x 1
7 Integrtion 7.1 Integrtion von Treppenfunktionen Im folgenden ezeichnen wir mit I = [, ] ein eschränktes und geschlossenes Intervll. Für Punkte = x 0 < x 1
8 Integralrechnung. 8.1 Das Riemann-Integral
 8 Integrlrechnung Der Integrlbegriff ist wie der Ableitungsbegriff motiviert durch die physiklische Beschreibung von Bewegungsbläufen (Geschwindigkeit, Beschleunigung). Er ist u.. uch von Bedeutung bei
8 Integrlrechnung Der Integrlbegriff ist wie der Ableitungsbegriff motiviert durch die physiklische Beschreibung von Bewegungsbläufen (Geschwindigkeit, Beschleunigung). Er ist u.. uch von Bedeutung bei
Analysis II (lehramtsbezogen): Rechnen mit Integralen
 Anlysis II (lehrmtsbezogen): Rechnen mit Integrlen A. Ppke. November Substitution Wir wiederholen kurz die grundlegende Methode der Substitution und wenden sie im Beispiel n. Stz. (Integrtion durch Substitution).
Anlysis II (lehrmtsbezogen): Rechnen mit Integrlen A. Ppke. November Substitution Wir wiederholen kurz die grundlegende Methode der Substitution und wenden sie im Beispiel n. Stz. (Integrtion durch Substitution).
Mathematik II. Vorlesung 41. Satz Es sei f :[a,b] R n, t f(t), eine differenzierbare Kurve. Dann gibt es ein c [a,b] mit
![Mathematik II. Vorlesung 41. Satz Es sei f :[a,b] R n, t f(t), eine differenzierbare Kurve. Dann gibt es ein c [a,b] mit Mathematik II. Vorlesung 41. Satz Es sei f :[a,b] R n, t f(t), eine differenzierbare Kurve. Dann gibt es ein c [a,b] mit](/thumbs/80/82115779.jpg) Prof. Dr. H. Brenner Osnbrück SS 1 Mthemtik II Vorlesung 41 Die Mittelwertbschätzung für differenzierbre Kurven Stz 41.1. Es sei f :[,b] R n, t f(t), eine differenzierbre Kurve. Dnn gibt es ein c [,b]
Prof. Dr. H. Brenner Osnbrück SS 1 Mthemtik II Vorlesung 41 Die Mittelwertbschätzung für differenzierbre Kurven Stz 41.1. Es sei f :[,b] R n, t f(t), eine differenzierbre Kurve. Dnn gibt es ein c [,b]
5.5. Integralrechnung
 .. Integrlrechnung... Berechnung von Integrlen mit der Streifenmethode Definition: Gegeen seien, R mit < und eine uf [; ] stetige Funktion f. Der orientierte Inhlt der Fläche, die durch die -Achse, ds
.. Integrlrechnung... Berechnung von Integrlen mit der Streifenmethode Definition: Gegeen seien, R mit < und eine uf [; ] stetige Funktion f. Der orientierte Inhlt der Fläche, die durch die -Achse, ds
Fur das unbestimmte Integral gilt. f(x) dx + b
 . Integrtionsregeln.. Linerität. Fur ds unbestimmte Integrl gilt (f(x) bg(x)) = f(x) b g(x),, b R... Prtielle Integrtion. Fur je zwei uf einem Intervll I = (, b) stetig differenzierbre Funktionen u und
. Integrtionsregeln.. Linerität. Fur ds unbestimmte Integrl gilt (f(x) bg(x)) = f(x) b g(x),, b R... Prtielle Integrtion. Fur je zwei uf einem Intervll I = (, b) stetig differenzierbre Funktionen u und
Das Bogenintegral einer gestauchten Normalparabel
 Ds Bogenintegrl einer gestuchten Normlprbel Jn Günther und Luks Vrnhorst Im Mthemtikleistungskurs der Jhrgngsstufe sind wir uf folgende Aufgbe gestoÿen: Bestimmen Sie eine Stmmfunktion von f(x) + x mit
Ds Bogenintegrl einer gestuchten Normlprbel Jn Günther und Luks Vrnhorst Im Mthemtikleistungskurs der Jhrgngsstufe sind wir uf folgende Aufgbe gestoÿen: Bestimmen Sie eine Stmmfunktion von f(x) + x mit
Mathematik 1 für Wirtschaftsinformatik
 Mthemtik für Wirtschftsinformtik Wintersemester 202/3 Stefn Etschberger Hochschule Augsburg Existenz von bestimmten Integrlen Mthemtik 2 Stefn Etschberger Gegeben: Reelle Funktion f : [, b] R. Dnn gilt:
Mthemtik für Wirtschftsinformtik Wintersemester 202/3 Stefn Etschberger Hochschule Augsburg Existenz von bestimmten Integrlen Mthemtik 2 Stefn Etschberger Gegeben: Reelle Funktion f : [, b] R. Dnn gilt:
Uneigentliche Riemann-Integrale
 Uneigentliche iemnn-integrle Zweck dieses Abschnitts ist es, die Vorussetzungen zu lockern, die wir n die Funktion f : [, b] bei der Einführung des iemnn-integrls gestellt hben. Diese Vorussetzungen wren:
Uneigentliche iemnn-integrle Zweck dieses Abschnitts ist es, die Vorussetzungen zu lockern, die wir n die Funktion f : [, b] bei der Einführung des iemnn-integrls gestellt hben. Diese Vorussetzungen wren:
Anwendungen der Integralrechnung
 Anwendungen der Integrlrechnung 8. Flächeninhlt und Flächenschwerpunkt............... 4 8. Kurvenlänge............................. 7 8. Rottionskörper........................... 9 8.3 Whrscheinlichkeitsverteilungen
Anwendungen der Integrlrechnung 8. Flächeninhlt und Flächenschwerpunkt............... 4 8. Kurvenlänge............................. 7 8. Rottionskörper........................... 9 8.3 Whrscheinlichkeitsverteilungen
f(x + iy) = u(x, y) + iv(x, y), f(z)dz := Re [f(γ(t)) γ(t)] dt + i
![f(x + iy) = u(x, y) + iv(x, y), f(z)dz := Re [f(γ(t)) γ(t)] dt + i f(x + iy) = u(x, y) + iv(x, y), f(z)dz := Re [f(γ(t)) γ(t)] dt + i](/thumbs/93/112357953.jpg) Funktionentheorie Komplexe Kurvenintegrle Themen des Tutoriums m 24.6.25: Jede komplexe Funktion f : D C knn mn drstellen ls f(x + iy) = u(x, y) + iv(x, y), wobei u und v reellwertige Funktionen uf R 2
Funktionentheorie Komplexe Kurvenintegrle Themen des Tutoriums m 24.6.25: Jede komplexe Funktion f : D C knn mn drstellen ls f(x + iy) = u(x, y) + iv(x, y), wobei u und v reellwertige Funktionen uf R 2
f : G R ϕ n 1 (x 1,...,x n 1 ) Das ist zwar die allgemeine Form, aber es ist nützlich sie sich für den R 2 und R 3 explizit anzuschauen.
 Trnsformtionsstz von Sebstin üller Integrtion über Normlgebiete Allgemein knn mn im R n ein Normlgebiet wie folgt definieren: G : { R n 1 b, ϕ 1 ( 1 ) ψ 1 ( 1 ), ϕ ( 1, ) 3 ψ ( 1, ),... ϕ n 1 ( 1,...,
Trnsformtionsstz von Sebstin üller Integrtion über Normlgebiete Allgemein knn mn im R n ein Normlgebiet wie folgt definieren: G : { R n 1 b, ϕ 1 ( 1 ) ψ 1 ( 1 ), ϕ ( 1, ) 3 ψ ( 1, ),... ϕ n 1 ( 1,...,
KAPITEL 18 UND 19 H. KOCH. Kapitel 18. x>a. x<y
 KAPITEL 18 UND 19 H. KOCH 1. VORLESUNG VOM 08.01.2018 Kpitel 18 Definition 1 (Zerlegungen, Treppenfunktionen, Regelfunktionen) Sei < b. 1. Eine Zerlegung τ von [, b] besteht us einer Zhl N N und (N + 1)
KAPITEL 18 UND 19 H. KOCH 1. VORLESUNG VOM 08.01.2018 Kpitel 18 Definition 1 (Zerlegungen, Treppenfunktionen, Regelfunktionen) Sei < b. 1. Eine Zerlegung τ von [, b] besteht us einer Zhl N N und (N + 1)
$Id: integral.tex,v /05/09 11:21:33 hk Exp $ $Id: uneigentlich.tex,v /05/11 13:45:45 hk Exp $
 $Id: integrl.te,v.62 28/5/9 :2:33 hk Ep $ $Id: uneigentlich.te,v.22 28/5/ 3:45:45 hk Ep $ 2 Integrlrechnung 2.4 Integrtion rtionler Funktionen In der letzten Sitzung hben wir die Integrtion rtionler Funktionen
$Id: integrl.te,v.62 28/5/9 :2:33 hk Ep $ $Id: uneigentlich.te,v.22 28/5/ 3:45:45 hk Ep $ 2 Integrlrechnung 2.4 Integrtion rtionler Funktionen In der letzten Sitzung hben wir die Integrtion rtionler Funktionen
Multiplikative Inverse
 Multipliktive Inverse Ein Streifzug durch ds Bruchrechnen in Restklssen von Yimin Ge, Jänner 2006 Viele Leute hben Probleme dbei, Brüche und Restklssen unter einen Hut zu bringen. Dieser kurze Aufstz soll
Multipliktive Inverse Ein Streifzug durch ds Bruchrechnen in Restklssen von Yimin Ge, Jänner 2006 Viele Leute hben Probleme dbei, Brüche und Restklssen unter einen Hut zu bringen. Dieser kurze Aufstz soll
Mathematik-Tutorium: Handwerkszeug und Kochrezepte für Maschinenbauer
 Vektorrechnung Differentilrechnung Integrlrechnung Mthemtik-Tutorium: Hndwerkszeug und Kochrezepte für Mschinenbuer Johnnes Wiedersich 7. Dezember 007 http://www.e13.physik.tu-muenchen.de/wiedersich/ Vektorrechnung
Vektorrechnung Differentilrechnung Integrlrechnung Mthemtik-Tutorium: Hndwerkszeug und Kochrezepte für Mschinenbuer Johnnes Wiedersich 7. Dezember 007 http://www.e13.physik.tu-muenchen.de/wiedersich/ Vektorrechnung
2. Flächenberechnungen
 Anlysis Integrlrechnung. Flächenberechnungen.. Die Flächenfunktion ) Flächenfunktionen ufzeichnen Skizziere zur gegebenen Funktion diejenige Funktion, welche die Fläche unterhlb der Funktionskurve misst.
Anlysis Integrlrechnung. Flächenberechnungen.. Die Flächenfunktion ) Flächenfunktionen ufzeichnen Skizziere zur gegebenen Funktion diejenige Funktion, welche die Fläche unterhlb der Funktionskurve misst.
