Differentiation der Exponential- und Logarithmusfunktion. Mag. Mone Denninger 23. Oktober 2004
|
|
|
- Edmund Sauer
- vor 7 Jahren
- Abrufe
Transkript
1 Differentiation der Exponential- und Logarithmusfunktion Mag. Mone Denninger 23. Oktober
2 INHALTSVERZEICHNIS 8. Klasse Inhaltsverzeichnis 1 Differentiation der Exponentialfunktion 3 2 Differentiation der Logarithmusfunktion Herleitung der Ableitung von ln x Implizit Differentieren Logarithmische Differentiation Kurvendiskussion 11 4 Anwendungen der Exponentialfunktion Wachstums- und Zerfallsprozesse diffexplog 2
3 1 DIFFERENTIATION DER EXPONENTIALFUNKTION 8. Klasse 1 Differentiation der Exponentialfunktion Unter der Exponentialfunktion zur Basis e versteht man die Funktion D=R, W=R + f(x) = e x f(x) = e x f (x) = e x Beweis siehe Seite 1 im Buch! Beispiel 1. Differenziere die Funktion f(x) = 2 x! f(x) = 2 x f (x) = 2 x Beispiel 2. Differenziere die Funktion f(x) = 1 2 ex! f(x) = 1 2 ex f (x) = 1 2 ex Sofern der Exponent von e eine Funktion ist, muss die Kettenregel angewandt werden: [ e f(x) ] = e f(x) f (x) Beispiel 3. Differenziere die Funktion f(x) = e 2x f(x) = e 2x f (x) = e 2x 2 diffexplog 3
4 1 DIFFERENTIATION DER EXPONENTIALFUNKTION 8. Klasse Beispiel 4. Differenziere die Funktion f(x) = e 3x2 4x! f(x) = e 3x2 4x f (x) = (6x 4) e 3x2 4x Beispiel 5. Differenziere die Funktion f(x) = x 3 e x2! f(x) = x 3 e x2 Produktregel! (u v) = u v + uv f (x) = 3x 2 e x2 + x 3 2x e x2 = = 3x 2 e x2 + 2x 4 e x2 = = e x2 (3x 2 + 2x 4) Beispiel 6 (6b). Es ist f (x 0 ) der durch die Funktionsgleichung f(x) = e x (sin x cos x) gegebenen Funktion für x 0 = π 2 zu berechnen! f(x) = e x (sin x cos x) x 0 = π 2 f (x) = e x (sin x cos x) + e x (cos x + sin x) = = e x (sin x cos x + cos x + sin x) = = 2 sin x e x f ( π 2 ) = 2 sin π e π 2 9, }{{ 2} 1 (RAD!) f ( π ) 9, ac diffexplog 4
5 2 DIFFERENTIATION DER LOGARITHMUSFUNKTION 8. Klasse 2 Differentiation der Logarithmusfunktion Jede Zahl x R, für die a x = b (a R + \{1}, b R + ) gilt, heißt Logarithmus von b zur Basis a: a x = b x = a log b Unter der Logarithmusfunktion zur Basis e versteht man die Funktion D=R +, W=R f(x) = ln x (ln x) = 1 x diffexplog 5
6 2 DIFFERENTIATION DER LOGARITHMUSFUNKTION 8. Klasse 2.1 Herleitung der Ableitung von ln x f(x) = ln x y = ln x e y = x e ln x = x ges. f (x) wie leiten beide Seiten ab: ( e ln x ) = (x) e ln x (ln x) = 1 nach (ln x) umformen: (ln x) = 1 e ln x da e ln x = x : (ln x) = 1 x Beispiel 7. Differenziere die Funktion f(x) = 3 ln x! f(x) = 3 ln x f (x) = 3 x Beispiel 8. Bilde die erste Ableitung von f(x) = ln x 2! Wir benötigen wiederum die Kettenregel: [ln f(x)] = 1 f(x) f (x) f (x) = 1 x 2 2x = 2 x diffexplog 6
7 2 DIFFERENTIATION DER LOGARITHMUSFUNKTION 8. Klasse Beispiel 9. Differenziere die Funktion f(x) = ln ( ) 3x 2 2! 2 ( ) 2 3x 2 f(x) = ln 2 ( ) f 1 3x 2 (x) = ) ( 3x 2 2 = 3 3x 2 2 = 6 3x = ( ) Beispiel 10 (9a). Es ist f x (x 0 ) der Funnktion f(x) = ln 2 1+x mit x 2 0 = 3 zu berechnen! ( ) x 2 ( u ) u v uv f(x) = ln = 1 + x 2 v v 2 f (x) = 1 2x(1 + x2 ) x2 (2x) = x 2 (1 + x 2 ) 2 1+x 2 = (1 + x2 ) x [ 2 + 2x 2 2x 2] = x 2 (1 + x 2 ) 2 2 = x(1 + x 2 ) 7 8 x 0 = 3 f 2 ( 3) = ( 3)(1 + ( 3) 2 ) = 2 30 = 1 ( 0, 07) 15 9bc diffexplog 7
8 2 DIFFERENTIATION DER LOGARITHMUSFUNKTION 8. Klasse 2.2 Implizit Differentieren Beispiel 11 (15a). Sofern die Funktionsgleichung zweier Variablen x und y nach keiner der Variablen gelöst ist (z.b. 5x y = 3), spricht man von einer sogenannten impliziten Funktion. Durch Lösen der Gleichung nach y (y = 5x 3) erhält man die Gleichung der expliziten Funktion. (1) Die Relation 2x 2 + xy 3y 2 = 0 ist nach y zu lösen und zu differenzieren. (2) Weiters ist die erste Ableitung durch implizite Differentiation zu bilden! (1) umformen: 3y 2 xy 2x 2 = 0 mit der ABC-Formel nach y auflösen: y 1,2 = b ± b 2 4ac 2a y 1,2 = x ± x x = x ± 25x 2 6 y 1 = x y 2 = 2 3 x = x ± 5x 6 = y 1 = 1 y 2 = 2 3 (2) implizite Differentiation: nach y umformen: 4x + y + xy }{{} Produktregel ( 2x 2 + xy 3y 2 = 0) 6yy }{{} = 0 Kettenregel 4x + y = y (6y x) y = 4x + y 6y x (würde man hier nun für y x bzw. 2 3x einsetzen, kommt man wieder auf die Ergebnisse 1 und 2 3 ) 15bc diffexplog 8
9 2 DIFFERENTIATION DER LOGARITHMUSFUNKTION 8. Klasse Beispiel 12 (16a). Es ist der Anstieg der Kurve x 2 +y 2 = 25 (Mittelpunktskreis mit r = 5) im Punkt P(3 y) zu berechnen! P (3 y) y 2 = 25 x 2 y = ± 25 x 2 = ± ( 25 x 2) 1 2 y = ± 1 ( ) 25 x 2 12 ( 2x) = 2 x = 25 x 2 x 0 = 3 y 3 = = 3 = diffexplog 9
10 2 DIFFERENTIATION DER LOGARITHMUSFUNKTION 8. Klasse 2.3 Logarithmische Differentiation Beispiel 13 (17a). Sofern y = f(x) positiv ist, können wir beide Seiten der Gleichung zur Basis e logarithmieren: ln y = ln f(x). Differenziert man die Linke und die Rechte Gleichungsseite nach x, ergibt sich unter beachtung der Kettenregel 1 y y = 1 f(x) f (x). Aus dem letzten Ausdruck lässt sich y berechnen; das Verfahren nennt man logarithmische Differentiation. Die logarithmische Differentiation ist manchmal vorteilhafter als der übliche Weg zur Berechnung der Ableitung. Vor allem bei Problemstellungen, die die Veränderliche sowohl in der Basis, als auch im Exponenten enthalten, ist dies der Fall. Bei der folgenden Aufgabe ist die logarithmische Differentiation anzuwenden: f(x) = x x, f (3)=? f(x) = x x ln ln f(x) = x ln x 1 f(x) f (x) = x 1 x + 1 ln x }{{} Produktregel f (x) = f(x) [1 + ln x] = = x x (1 + ln x) f (3) = 3 3 (1 + ln 3) f (3) 56, bc Beispiel 14 (31b). Berechne die erste Ableitung mittels logarithmischer Differentiation! f(x) = (e x ) x ln ln f(x) = x ln e x 1 f(x) f (x) = ln e x + x 1 e ( xex ) f (x) = (e x ) x ln }{{} e x +x x f (x) = (e x ) x 2x f (x) = 2x e x2 31ag diffexplog 10
11 3 KURVENDISKUSSION 8. Klasse 3 Kurvendiskussion Beispiel 15 (33). Die Funktion mit der Gleichung (a) f(x) = x ln x (b) f(x) = x (ln x) 2 (c) f(x) = x + ln x 1 (d) f(x) = 2 ln(x 2 1) (e) f(x) = x e x (f) f(x) = 2xe x (g) f(x) = (x 2 1)e x (h) f(x) = 0.5 e x 1+x ist zu diskutieren! (a) f(x) = x ln x Hü f(x) = x ln x f (x) = 1 ln x + x 1 x = ln x + 1 f (x) = 1 x = x 1 f (x) = x 2 = 1 x 2 (1) D = R + (2) Nullstelle: f(x) = 0 x ln x = 0 x = 0 oder ln x = 0 e... x = e 0 = 1 x = 1 N 1 (0 0) N 2 (1 0) diffexplog 11
12 3 KURVENDISKUSSION 8. Klasse (3) Extremwerte: f (x) = 0 ln x + 1 = 0 ln x = 1 e... x = e 1 x = 1 e f ( 1 e ) = e > 0 T (1 e 1 e ) (4) Wendepunkte: (5) Monotonie: 0 < x < 1 e f (x) = 0 1 x = 0 x 1 = 0 f.a. kein Wendepunkt 1 e 1 e < x < f (x) < 0 0 > 0 f(x) str. mo. fa. T str. mo. st. (6) Krümmungsverhalten: 0 < x < f (x) > 0 f(x) pos. gekr. links gekr. (7) Graph: diffexplog 12
13 3 KURVENDISKUSSION 8. Klasse (b) f(x) = x (ln x) 2 Hü diffexplog 13
14 3 KURVENDISKUSSION 8. Klasse (c) f(x) = x + ln x 1 Sü diffexplog 14
15 3 KURVENDISKUSSION 8. Klasse (d) f(x) = 2 ln(x 2 1) diffexplog 15
16 3 KURVENDISKUSSION 8. Klasse (e) f(x) = x e x diffexplog 16
17 3 KURVENDISKUSSION 8. Klasse (f) f(x) = 2xe x diffexplog 17
18 3 KURVENDISKUSSION 8. Klasse (g) f(x) = (x 2 1)e x diffexplog 18
19 3 KURVENDISKUSSION 8. Klasse (h) f(x) = 0.5 e x 1+x diffexplog 19
20 4 ANWENDUNGEN DER EXPONENTIALFUNKTION 8. Klasse 4 Anwendungen der Exponentialfunktion 4.1 Wachstums- und Zerfallsprozesse Viele Wachstums- und Zerfallsprozesse können durch Exponentialfunktionen beschrieben werden. Mit Hilfe der Ableitung können momentane Wachstumsgeschwindigkeit bzw. Zerfallsgeschwindigkeit beschrieben werden. Für diese Wachstums- bzw. Zerfallsfunktionen gilt N(t) = N 0 e λt bzw. N(t) = N 0 a t Dabei ist N 0 der Bestand zur Zeit 0 und λ die Wachstumskonstante bzw. Zerfallskonstante. Für Wachstumsprozesse gilt λ > 0, für Zerfallsprozesse gilt λ < 0. diffexplog 20
21 4 ANWENDUNGEN DER EXPONENTIALFUNKTION 8. Klasse Die C 14 -Methode (eigentlich: 14 C) Um das Alter von Gesteinen oder anderen Materialien zu bestimmen, verwendet man Isotope bestimmter Elemente. Isotop ist die Bezeichnung für die Nuklide eines chemischen Elements. Isotope sind also Nuklide gleicher Kernladungs- und Ordnungszahl (Protonenzahl), aber unterschiedlicher Anzahl der im Kern enthaltenen Neutronen und damit unterschiedlicher Massenzahl (Nukleonenzahl). Vom Stickstoff zum Beispiel gibt es zwei stabile Isotope: N 14 (also 14 Neutronen) und N 15 (15 Neutronen). Daneben gibt es vom Stickstoff allerdings auch noch sechs instabile Isotope, d.h. sie zerfallen nach einer bestimmten Zeit. Gemessen wird dabei die sogenannte Halbwertszeit, also die Zeitspanne, in der die Hälfte eines Ausgangsmaterials zerfallen bzw. umgewandelt ist. Im Falle der instabilen Stickstoff-Isotope liegt sie zwischen 11ms (N 12 ) und 9.96min (N 13 ). Aus den Halbwertszeiten der in extraterrestrischem Material nachgewiesenen Elemente lassen sich gegebenenfalls Rückschlüsse auf das Alter des Sonnensystems bzw. der Sterne ziehen. Da die Isotope eines Elements die gleiche Anzahl an Protonen im Kern aufweisen, haben sie auch die gleiche Anzahl an Elektronen in der Hülle. Sie verhalten sich somit chemisch gleichartig. Viele Radioisotope (Bezeichnung für die radioaktiven Isotope eines best. Elements) lassen sich anhand ihrer charakteristischen Strahlung leicht nachweisen. Sie werden deshalb in vielfältiger Weise benutzt, um das Verhalten der reinen Elemente oder deren Verbindungen in der belebten und unbelebten Natur zu erforschen. Die Isotope des Kohlenstoff werden normalerweise nur benutzt, um junge Materialien im Boden zu datieren. Mit C 14 -Atomen markierte Verbindungen finden Verwendung als Radioindikatoren. In einer Altersbestimmungsmethode spielt das Mengenverhältnis C 14 :C 12 in organischen Resten eine Rolle. Man nennt diese Altersbestimmungsmethode Radiocarbon-Methode oder C 14 -Datierung. Dies ist die Bezeichnung für eine von LIBBY seit 1947 entwickelten physikalischen Methode, die eine Alterbestimmung von ehemals belebten Materialien (z.b. Holz, Knochen, Zähne, Torf) oder von Carbonaten (z.b. Muschelschalen) enthaltenden Gegenstände mit einem verhältnismäßig hohen Genauigkeitsgrad ermöglicht. Die C 14 -Datierung beruht darauf, dass durch die Primär-Teilchen der kosmischen Strahlung in der Atmosphäre Neutronen gebildet werden, die aus dem Stickstoff der Luft nach N 14 (n,p) C 14 radioaktiven Kohlenstoff bilden, der mit einer Halbwertszeit von 5730 Jahren unter Aussendung von β-strahlen geringer Energie wieder im N 14 übergeht. Die frisch gebildeten C 14 -Atome werden in der Atmosphäre rasch zu Kohlenstoffdioxid oxidiert, das sich gleichmäßig mit dem atmosphärischen CO 2 vermischt und zusammen mit diesem in den Kohlenstoff-Kreislauf eingeht. Nach dem Tod hört der Stoffwechsel jedoch auf, und da von einem toten Organismus somit kein radioaktives C 14 mehr aufgenommen werden kann, zerfällt der zum Zeitpunkt des Todes vorhandene C 14 -Anteil. Bei etwa Jahre alten Leichen ist der Gehalt an radioaktivem Kohlenstoff auf 1 8 des zu Lebzeiten vorhandenen Betrages abgesunken. Die C 14-Datierung ermöglicht plausible Altersbestimmungen für Zeiträume von bis Jahren; eine Ausdehnung bis zu Jahren erscheint möglich, denn neuerdings bestimmt man das C 14 /C 12 -Verhältnis direkt durch Massenspektroskopie. Da die radioaktive Zerfallsgeschwindigkeit durch äußere Bedingungen wie Druck und Temperatur nicht beeinflussbar ist und auch davon unabhängig ist, in welcher chemischen Verbindung ein radioaktives Nuklid vorliegt, kann der radioaktive Zerfall als geologische Uhr verwendet werden. diffexplog 21
22 4 ANWENDUNGEN DER EXPONENTIALFUNKTION 8. Klasse Beispiel 16 (Die C 14 -Methode). C 14 hat eine Halbwertszeit von 5600 Jahren. (a) Berechne die Zerfallskonstante λ und gib das Zerfallsgesetz an! Berechne die prozentuelle Abnahme pro Jahr! (b) Bestimme das Alter des Materials dessen C 14 -Gehalt auf 7% des ursprünglichen Wertes abgesunken ist. (c) Wie viel Gramm C 14 sind nach 4000 Jahren von einer Ausgangsmenge von 100g noch übrig? (d) Mit welcher Geschwindigkeit zerfällt ein Ausgangsmaterial von 200g C 14 nach Jahren? (e) Skizziere diesen Zerfall für N 0 =100g. (f) Wie viel % der ursprünglichen Menge sind nach 1000 Jahren zerfallen? diffexplog 22
23 4 ANWENDUNGEN DER EXPONENTIALFUNKTION 8. Klasse Beispiel 17 (Die C 14 -Methode). Siehe c14methode.tex: Handout und Angabe! C 14 hat eine Halbwertszeit von 5600 Jahren. (a) Berechne die Zerfallskonstante λ und gib das Zerfallsgesetz an! Berechne die prozentuelle Abnahme pro Jahr! N(t) = N 0 e λt ges. λ nach 5600J. N(5600) = N 0 2 N 0 2 = N 0 e λ 5600 : N = e λ 5600 ln ln 1 2 ln = λ = λ 5600 λ = 0, N(t) = N 0 e 0, t : ( 5600) Prozentuelle Abnahme pro Jahr: N(t) = N 0 a t a = e 0, N(t) = N 0 0, 9999 t 1 0, 9999 = 0, % Abnahme/Jahr (b) Bestimme das Alter des Materials dessen C 14 -Gehalt auf 7% des ursprünglichen Wertes abgesunken ist. N 0 0, 07 = N 0 e 0, t ln 0, 07 = 0, t t = 21484, 4 Jahre (c) Wie viel Gramm C 14 sind nach 4000 Jahren von einer Ausgangsmenge von 100g noch übrig? N(4000) = 100 e 0, N(4000) 60, 95g diffexplog 23
24 4 ANWENDUNGEN DER EXPONENTIALFUNKTION 8. Klasse (d) Mit welcher Geschwindigkeit zerfällt ein Ausgangsmaterial von 200g C 14 nach Jahren? N(t) = N 0 e 0, t N (t) = N 0 e 0, t ( 0, ) Zerfallsgeschwindigkeit N (10000) = 0, e 0, N (10000) = 0, 00718g/Jahr (e) Skizziere diesen Zerfall für N 0 =100g: (f) Wie viel % der ursprünglichen Menge sind nach 1000 Jahren zerfallen? N(1000) = N 0 e 0, N(1000) = N 0 0, , = 0, , 64% Abnahme diffexplog 24
Potenz- & Exponentialfunktionen
 Potenz- & Exponentialfunktionen 4. Kapitel aus meinem Lehrgang ANALYSIS Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch e-mail: theorie@ronaldbalestra.ch 8. Februar 2009 Überblick über die bisherigen
Potenz- & Exponentialfunktionen 4. Kapitel aus meinem Lehrgang ANALYSIS Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch e-mail: theorie@ronaldbalestra.ch 8. Februar 2009 Überblick über die bisherigen
Potenz- & Exponentialfunktionen
 Potenz- & Exponentialfunktionen ANALYSIS Kapitel 4 Sprachprofil - Oberstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch 17. Januar 2012 Überblick über die bisherigen ANALYSIS - Themen:
Potenz- & Exponentialfunktionen ANALYSIS Kapitel 4 Sprachprofil - Oberstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch 17. Januar 2012 Überblick über die bisherigen ANALYSIS - Themen:
Planungsblatt Mathematik für die 7A
 Planungsblatt Mathematik für die 7A Woche 24 (von 29.02 bis 04.03) Hausaufgaben 1 Donnerstag 03.03: Lerne die Grundkompetenzen zu Exponentielfunktionen FA 5.1 bis FA 5.6. Lerne/Erledige das kleine Arbeitsblatt
Planungsblatt Mathematik für die 7A Woche 24 (von 29.02 bis 04.03) Hausaufgaben 1 Donnerstag 03.03: Lerne die Grundkompetenzen zu Exponentielfunktionen FA 5.1 bis FA 5.6. Lerne/Erledige das kleine Arbeitsblatt
Mathematikaufgaben zur Vorbereitung auf das Studium
 Hochschule für Technik und Wirtschaft Dresden (FH) Fachbereich Informatik/Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Allgemeiner Maschinenbau Fahrzeugtechnik Dresden 2002
Hochschule für Technik und Wirtschaft Dresden (FH) Fachbereich Informatik/Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Allgemeiner Maschinenbau Fahrzeugtechnik Dresden 2002
Einstiegsvoraussetzungen für das 3. Semester Angewandte Mathematik AM
 Einstiegsvoraussetzungen für das 3. Semester Angewandte Mathematik AM 1. Siehe: Einstiegsvoraussetzungen für das 1. Semester 2. Bereich: Zahlen und Maße 2.1. Fehlerrechnung (Begriffe absoluter und relativer
Einstiegsvoraussetzungen für das 3. Semester Angewandte Mathematik AM 1. Siehe: Einstiegsvoraussetzungen für das 1. Semester 2. Bereich: Zahlen und Maße 2.1. Fehlerrechnung (Begriffe absoluter und relativer
Einführung in die Algebra
 1 Einführung in die Algebra 1.1 Wichtige Formeln Formel Symbol Definition Wert Bedingungen n Fakultät n! k = 1 2 3 n n N Binomialkoeffizient Binomische Formeln Binomischer Lehrsatz Potenzen ( ) n k Definition
1 Einführung in die Algebra 1.1 Wichtige Formeln Formel Symbol Definition Wert Bedingungen n Fakultät n! k = 1 2 3 n n N Binomialkoeffizient Binomische Formeln Binomischer Lehrsatz Potenzen ( ) n k Definition
Mathematikaufgaben zur Vorbereitung auf das Studium
 Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik / Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Betriebswirtschaft International Business Dresden 05 . Mengen
Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik / Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Betriebswirtschaft International Business Dresden 05 . Mengen
Gruppe 1. Lies den folgenden Text aus einem Biologiebuch.
 Gruppe Lies den folgenden Text aus einem Biologiebuch.. Notiere das Wachstum der Salmonellen übersichtlich in einer Tabelle. Am Anfang soll eine Salmonelle vorhanden sein. Verwende dabei auch Potenzen..
Gruppe Lies den folgenden Text aus einem Biologiebuch.. Notiere das Wachstum der Salmonellen übersichtlich in einer Tabelle. Am Anfang soll eine Salmonelle vorhanden sein. Verwende dabei auch Potenzen..
- 1 - Eine Funktion f(x) heißt differenzierbar an der Stelle x 0, wenn der Grenzwert (siehe Kap. 3)
 - 1-4 Differentialrechnung 4.1 Ableitung einer Funktion Eine Funktion f() ist in einer Umgebung definiert. Abb.: Differenzenquotient Man kann immer einen Quotienten bilden, ( + ) f ( + h) f ( ) f h f +
- 1-4 Differentialrechnung 4.1 Ableitung einer Funktion Eine Funktion f() ist in einer Umgebung definiert. Abb.: Differenzenquotient Man kann immer einen Quotienten bilden, ( + ) f ( + h) f ( ) f h f +
Prof. Dr. Rolf Linn
 Prof. Dr. Rolf Linn 6.4.5 Übungsaufgaben zu Mathematik Analysis. Einführung. Gegeben seien die Punkte P=(;) und Q=(5;5). a) Berechnen Sie den Anstieg m der Verbindungsgeraden von P und Q. b) Berechnen
Prof. Dr. Rolf Linn 6.4.5 Übungsaufgaben zu Mathematik Analysis. Einführung. Gegeben seien die Punkte P=(;) und Q=(5;5). a) Berechnen Sie den Anstieg m der Verbindungsgeraden von P und Q. b) Berechnen
Mathematikaufgaben zur Vorbereitung auf das Studium
 Hochschule für Technik und Wirtschaft Dresden (FH) Fachbereich Informatik/Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengang Bauingenieurwesen Dresden 2005 . Mengen Kenntnisse
Hochschule für Technik und Wirtschaft Dresden (FH) Fachbereich Informatik/Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengang Bauingenieurwesen Dresden 2005 . Mengen Kenntnisse
Physik am Samstagmorgen 19. November Radioaktivität. Ein unbestechlicher Zeitzeuge. Christiane Rhodius
 Physik am Samstagmorgen 19. November 2005 Radioaktivität Ein unbestechlicher Zeitzeuge Christiane Rhodius Archäochronometrie Warum und wie datieren wir? Ereignisse innerhalb der menschlichen Kulturentwicklung
Physik am Samstagmorgen 19. November 2005 Radioaktivität Ein unbestechlicher Zeitzeuge Christiane Rhodius Archäochronometrie Warum und wie datieren wir? Ereignisse innerhalb der menschlichen Kulturentwicklung
Examensaufgaben RADIOAKTIVITÄT
 Examensaufgaben RADIOAKTIVITÄT Aufgabe 1 (September 2007) a) Stellen Sie das Grundgesetz des radioaktiven Zerfalls auf und leiten sie aus diesem Gesetz den Zusammenhang zwischen der Halbwertszeit und der
Examensaufgaben RADIOAKTIVITÄT Aufgabe 1 (September 2007) a) Stellen Sie das Grundgesetz des radioaktiven Zerfalls auf und leiten sie aus diesem Gesetz den Zusammenhang zwischen der Halbwertszeit und der
Exponentielles Wachstum:
 Exponentielles Wachstum: Bsp.: Ein Wald hat zum Zeitpunkt t = 0 einen Holzbestand von N 0 = N(0) = 20 000 m 3. Nach 0 Jahren ist der Holzbestand auf 25 000 m 3 angewachsen. a) Nimm an, dass die Zunahme
Exponentielles Wachstum: Bsp.: Ein Wald hat zum Zeitpunkt t = 0 einen Holzbestand von N 0 = N(0) = 20 000 m 3. Nach 0 Jahren ist der Holzbestand auf 25 000 m 3 angewachsen. a) Nimm an, dass die Zunahme
Röntgenstrahlen. Röntgenröhre von Wilhelm Konrad Röntgen. Foto: Deutsches Museum München.
 Röntgenstrahlen 1 Wilhelm Konrad Röntgen Foto: Deutsches Museum München. Röntgenröhre von 1896 2 1 ev = 1 Elektronenvolt = Energie die ein Elektron nach Durchlaufen der Potentialdifferenz 1V hat (1.6 10-19
Röntgenstrahlen 1 Wilhelm Konrad Röntgen Foto: Deutsches Museum München. Röntgenröhre von 1896 2 1 ev = 1 Elektronenvolt = Energie die ein Elektron nach Durchlaufen der Potentialdifferenz 1V hat (1.6 10-19
Energie wird normalerweise in Joule gemessen. Ein Joule (J) einspricht einem Newtonmeter
 Maße wie Gammastrahlen abgeschwächt werden. Im Gegensatz zu den Gammastrahlen sind die Neutronenstrahlen auch Teilchenstrahlen wie Alpha- und Betastrahlen. Die Reichweiten von Strahlen mit einer Energie
Maße wie Gammastrahlen abgeschwächt werden. Im Gegensatz zu den Gammastrahlen sind die Neutronenstrahlen auch Teilchenstrahlen wie Alpha- und Betastrahlen. Die Reichweiten von Strahlen mit einer Energie
Der Funktionsbegri und elementare Kurvendiskussion
 Der Funktionsbegri und elementare Kurvendiskussion Christoph Jansen Institut für Statistik, LMU München Formalisierungspropädeutikum 6. Oktober 2017 1 / 25 Allgemeiner Funktionsbegri Eine Funktion f ist
Der Funktionsbegri und elementare Kurvendiskussion Christoph Jansen Institut für Statistik, LMU München Formalisierungspropädeutikum 6. Oktober 2017 1 / 25 Allgemeiner Funktionsbegri Eine Funktion f ist
Einstiegsvoraussetzungen 3. Semester
 Einstiegsvoraussetzungen 3. Semester Wiederholung vom VL Bereich: Zahlen und Maße Fehlerrechnung kennen Fehler in der Darstellung von Zahlen und können Ergebnisse auf sinnvolle Art runden. verstehen die
Einstiegsvoraussetzungen 3. Semester Wiederholung vom VL Bereich: Zahlen und Maße Fehlerrechnung kennen Fehler in der Darstellung von Zahlen und können Ergebnisse auf sinnvolle Art runden. verstehen die
Formelsammlung für das Niveau II
 PH Bern, Vorbereitungskurs MATHEMATIK, Niveau II Formelsammlung 1 Formelsammlung für das Niveau II Binomische Formeln (a + b) = a + ab + b (a b) = a ab + b Potenzregeln a b = (a b)(a + b) a m a n = a m+n
PH Bern, Vorbereitungskurs MATHEMATIK, Niveau II Formelsammlung 1 Formelsammlung für das Niveau II Binomische Formeln (a + b) = a + ab + b (a b) = a ab + b Potenzregeln a b = (a b)(a + b) a m a n = a m+n
ALGEBRA UND GEOMETRIE. 5. und 6. Klasse
 ü ALGEBRA UND GEOMETRIE 5. und 6. Klasse 1. VERKAUFSPREIS Für einen Laufmeter Stoff betragen die Selbstkosten S Euro, der Verkaufspreis ohne Mehrwertsteuer N Euro. a) Gib eine Formel für den Gewinn G in
ü ALGEBRA UND GEOMETRIE 5. und 6. Klasse 1. VERKAUFSPREIS Für einen Laufmeter Stoff betragen die Selbstkosten S Euro, der Verkaufspreis ohne Mehrwertsteuer N Euro. a) Gib eine Formel für den Gewinn G in
die Wachstumsrate ist proportional zur Anzahl der vorhandenen Individuen.
 Exponentielles Wachstum und Zerfall Angenommen, man möchte ein Modell des Wachstums oder Zerfalls einer Population erarbeiten, dann ist ein Gedanke naheliegend: die Wachstumsrate ist proportional zur Anzahl
Exponentielles Wachstum und Zerfall Angenommen, man möchte ein Modell des Wachstums oder Zerfalls einer Population erarbeiten, dann ist ein Gedanke naheliegend: die Wachstumsrate ist proportional zur Anzahl
Nach der Halbwertszeit τ ist nur noch die Hälfte der Atomkerne vorhanden. Durch diese Angabe ist b bestimmt.
 1 9. Exponentieller Zerfall Von einer radioaktiven Substanz sind zu Beginn (0) Atome vorhanden. () ist die Anzahl der radioaktiven Atomkerne im Zeitpunkt t. () nimmt exponentiell ab, d.h. es gilt ()=(0)
1 9. Exponentieller Zerfall Von einer radioaktiven Substanz sind zu Beginn (0) Atome vorhanden. () ist die Anzahl der radioaktiven Atomkerne im Zeitpunkt t. () nimmt exponentiell ab, d.h. es gilt ()=(0)
Mathematikaufgaben zur Vorbereitung auf das Studium
 Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik / Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Kartographie/Geoinformatik Vermessung/Geoinformatik Dresden
Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik / Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Kartographie/Geoinformatik Vermessung/Geoinformatik Dresden
Technologie/Informatik Kernaufbau und Kernzerfälle. Dipl.-Phys. Michael Conzelmann, StR Staatliche FOS und BOS Bad Neustadt a. d.
 Technologie/Informatik Kernaufbau und Kernzerfälle Dipl.-Phys. Michael Conzelmann, StR Staatliche FOS und BOS Bad Neustadt a. d. Saale Übersicht Kernaufbau Rutherford-Experiment, Nukleonen Schreibweise,
Technologie/Informatik Kernaufbau und Kernzerfälle Dipl.-Phys. Michael Conzelmann, StR Staatliche FOS und BOS Bad Neustadt a. d. Saale Übersicht Kernaufbau Rutherford-Experiment, Nukleonen Schreibweise,
Übungsarbeit zum Thema: Exponentialfunktion und. Logarithmusfunktion
 Übungsarbeit zum Thema: Exponentialfunktion und Logarithmusfunktion a) Bestimme die Exponentialfunktion f (x) a x mit a R +, deren Graph durch den Punkt P (3 / 0,343) verläuft. b) Bestimme die Exponentialfunktion
Übungsarbeit zum Thema: Exponentialfunktion und Logarithmusfunktion a) Bestimme die Exponentialfunktion f (x) a x mit a R +, deren Graph durch den Punkt P (3 / 0,343) verläuft. b) Bestimme die Exponentialfunktion
Der Funktionsbegri und elementare Kurvendiskussion
 Der Funktionsbegri und elementare Kurvendiskussion Christoph Jansen Institut für Statistik, LMU München Formalisierungspropädeutikum 5. Oktober 2016 1 / 24 Allgemeiner Funktionsbegri Eine Funktion f ist
Der Funktionsbegri und elementare Kurvendiskussion Christoph Jansen Institut für Statistik, LMU München Formalisierungspropädeutikum 5. Oktober 2016 1 / 24 Allgemeiner Funktionsbegri Eine Funktion f ist
Natürliche Radioaktivität
 Natürliche Radioaktivität Definition Natürliche Radioaktivität Die Eigenschaft von Atomkernen sich spontan in andere umzuwandeln, wobei Energie in Form von Teilchen oder Strahlung frei wird, nennt man
Natürliche Radioaktivität Definition Natürliche Radioaktivität Die Eigenschaft von Atomkernen sich spontan in andere umzuwandeln, wobei Energie in Form von Teilchen oder Strahlung frei wird, nennt man
A5 Exponentialfunktion und Logarithmusfunktion
 A5 Exponentialfunktion und Logarithmusfunktion A5 Exponentialfunktion und Logarithmusfunktion Wachstums- und Zerfallsprozesse. Beispiel: Bakterien können sich sehr schnell vermehren. Eine bestimmte Bakterienart
A5 Exponentialfunktion und Logarithmusfunktion A5 Exponentialfunktion und Logarithmusfunktion Wachstums- und Zerfallsprozesse. Beispiel: Bakterien können sich sehr schnell vermehren. Eine bestimmte Bakterienart
Lösungen der Aufgaben zu Kapitel 10
 Lösungen der Aufgaben zu Kapitel 10 Abschnitt 10.2 Aufgabe 1 (a) Die beiden Funktionen f(x) = 1 und g(y) = y sind auf R definiert und stetig. 1 + x2 Der Definitionsbereich der Differentialgleichung ist
Lösungen der Aufgaben zu Kapitel 10 Abschnitt 10.2 Aufgabe 1 (a) Die beiden Funktionen f(x) = 1 und g(y) = y sind auf R definiert und stetig. 1 + x2 Der Definitionsbereich der Differentialgleichung ist
Wir gehen in dieser Vorlesung mit folgenden Zahlbereichen um: zweier ganzer Zahlen p und q schreiben kann.
 1 Grundlagen 1.1 Das Rechnen mit Zahlen Wir gehen in dieser Vorlesung mit folgenden Zahlbereichen um: N: natürliche Zahlen 1, 2, 3, 4, 5,... Z: ganze Zahlen..., 3, 2, 1, 0, 1, 2, 3,... Q: rationale Zahlen:
1 Grundlagen 1.1 Das Rechnen mit Zahlen Wir gehen in dieser Vorlesung mit folgenden Zahlbereichen um: N: natürliche Zahlen 1, 2, 3, 4, 5,... Z: ganze Zahlen..., 3, 2, 1, 0, 1, 2, 3,... Q: rationale Zahlen:
Exponential- u. Logarithmusfunktionen. Funktionen. Exponentialfunktion u. Logarithmusfunktionen. Los geht s Klick auf mich!
 Exponential- u. Logarithmusfunktionen Los geht s Klick auf mich! Melanie Gräbner Inhalt Exponentialfunktion Euler sche Zahl Formel für Wachstum/Zerfallsfunktionen Logarithmen Logarithmusfunktionen Exponentialgleichung
Exponential- u. Logarithmusfunktionen Los geht s Klick auf mich! Melanie Gräbner Inhalt Exponentialfunktion Euler sche Zahl Formel für Wachstum/Zerfallsfunktionen Logarithmen Logarithmusfunktionen Exponentialgleichung
Radioaktivität. den 7 Oktober Dr. Emőke Bódis
 Radioaktivität den 7 Oktober 2016 Dr. Emőke Bódis Prüfungsfrage Die Eigenschaften und Entstehung der radioaktiver Strahlungen: Alpha- Beta- und Gamma- Strahlungen. Aktivität. Zerfallgesetz. Halbwertzeit.
Radioaktivität den 7 Oktober 2016 Dr. Emőke Bódis Prüfungsfrage Die Eigenschaften und Entstehung der radioaktiver Strahlungen: Alpha- Beta- und Gamma- Strahlungen. Aktivität. Zerfallgesetz. Halbwertzeit.
Partielle Ableitungen
 Partielle Ableitungen 7-E Partielle Ableitungen einer Funktion von n Variablen Bei einer Funktion y f x1, x,..., xn von n unabhängigen Variablen x1, x,..., x n lassen sich insgesamt n partielle Ableitungen
Partielle Ableitungen 7-E Partielle Ableitungen einer Funktion von n Variablen Bei einer Funktion y f x1, x,..., xn von n unabhängigen Variablen x1, x,..., x n lassen sich insgesamt n partielle Ableitungen
(in)stabile Kerne & Radioaktivität
 Übersicht (in)stabile Kerne & Radioaktivität Zerfallsgesetz Natürliche und künstliche Radioaktivität Einteilung der natürlichen Radionuklide Zerfallsreihen Zerfallsarten Untersuchung der Strahlungsarten
Übersicht (in)stabile Kerne & Radioaktivität Zerfallsgesetz Natürliche und künstliche Radioaktivität Einteilung der natürlichen Radionuklide Zerfallsreihen Zerfallsarten Untersuchung der Strahlungsarten
allgemeine Informationen
 allgemeine Informationen Für das Zerfallsgesetz gilt der Zusammenhang N t =N 0 e t, wobei t die Zeit, N t die Anzahl der Kerne zum Zeitpunkt t, N 0 die Anzahl der Kerne zum Zeitpunkt t=0 (also zu Beginn
allgemeine Informationen Für das Zerfallsgesetz gilt der Zusammenhang N t =N 0 e t, wobei t die Zeit, N t die Anzahl der Kerne zum Zeitpunkt t, N 0 die Anzahl der Kerne zum Zeitpunkt t=0 (also zu Beginn
Projekt Standardisierte schriftliche Reifeprüfung in Mathematik. T e s t h e f t. Vorname:
 Projekt Standardisierte schriftliche Reifeprüfung in Mathematik T e s t h e f t 2 Schüler(in) Nachname:. Vorname:. Projekt Standardisierte schriftliche Reifeprüfung in Mathematik B211 Quadratische Funktionen
Projekt Standardisierte schriftliche Reifeprüfung in Mathematik T e s t h e f t 2 Schüler(in) Nachname:. Vorname:. Projekt Standardisierte schriftliche Reifeprüfung in Mathematik B211 Quadratische Funktionen
Logarithmische Skalen
 Logarithmische Skalen Arbeitsblatt Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 1
Logarithmische Skalen Arbeitsblatt Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 1
Wachstumsprozesse. Natürliches Wachstum Größenbeschränktes Wachstum Logistisches Wachstum Differenzialgleichungen
 Wachstumsprozesse Natürliches Wachstum Größenbeschränktes Wachstum Logistisches Wachstum Differenzialgleichungen klaus_messner@web.de www.elearning-freiburg.de Natürliches/exponentielles Wachstum Natürliches
Wachstumsprozesse Natürliches Wachstum Größenbeschränktes Wachstum Logistisches Wachstum Differenzialgleichungen klaus_messner@web.de www.elearning-freiburg.de Natürliches/exponentielles Wachstum Natürliches
1 Grundlagen 8 Funktionen 8 Differenzenquotient und Änderungsrate 9 Ableitung 11
 Inhalt A Differenzialrechnung 8 Grundlagen 8 Funktionen 8 Differenzenquotient und Änderungsrate 9 Ableitung 2 Ableitungsregeln 2 Potenzregel 2 Konstantenregel 3 Summenregel 4 Produktregel 4 Quotientenregel
Inhalt A Differenzialrechnung 8 Grundlagen 8 Funktionen 8 Differenzenquotient und Änderungsrate 9 Ableitung 2 Ableitungsregeln 2 Potenzregel 2 Konstantenregel 3 Summenregel 4 Produktregel 4 Quotientenregel
Examensaufgaben RADIOAKTIVITÄT
 Examensaufgaben RADIOAKTIVITÄT Aufgabe 1 (September 2007) a) Stellen Sie das Grundgesetz des radioaktiven Zerfalls auf und leiten sie aus diesem Gesetz den Zusammenhang zwischen der Halbwertszeit und der
Examensaufgaben RADIOAKTIVITÄT Aufgabe 1 (September 2007) a) Stellen Sie das Grundgesetz des radioaktiven Zerfalls auf und leiten sie aus diesem Gesetz den Zusammenhang zwischen der Halbwertszeit und der
Dritte Schularbeit Mathematik Klasse 7A G am
 Dritte Schularbeit Mathematik Klasse 7A G am 31.03.2016 Wiederholung für Abwesende SCHÜLERNAME: Punkte im Basisteil: / 24 Punkte im Vertiefungsteil: /24 Davon Kompensationspunkte: /4 Note: Notenschlüssel:
Dritte Schularbeit Mathematik Klasse 7A G am 31.03.2016 Wiederholung für Abwesende SCHÜLERNAME: Punkte im Basisteil: / 24 Punkte im Vertiefungsteil: /24 Davon Kompensationspunkte: /4 Note: Notenschlüssel:
Gewöhnliche Differentialgleichungen Aufgaben, Teil 1
 Gewöhnliche Differentialgleichungen Aufgaben, Teil 1 4-E1 4-E2 4-E3 Gewöhnliche Differentialgleichung: Aufgaben Bestimmen Sie allgemeine und spezielle Lösungen der folgenden Differentialgleichungen Aufgabe
Gewöhnliche Differentialgleichungen Aufgaben, Teil 1 4-E1 4-E2 4-E3 Gewöhnliche Differentialgleichung: Aufgaben Bestimmen Sie allgemeine und spezielle Lösungen der folgenden Differentialgleichungen Aufgabe
Radioaktiver Zerfall
 11.3.2 Radioaktiver Zerfall Betrachtet man einen einzelnen instabilen Atomkern, so kann nicht vorhergesagt werden zu welchem Zeitpunkt der Atomkern zerfällt. So könnte der Atomkern im nächsten Moment,
11.3.2 Radioaktiver Zerfall Betrachtet man einen einzelnen instabilen Atomkern, so kann nicht vorhergesagt werden zu welchem Zeitpunkt der Atomkern zerfällt. So könnte der Atomkern im nächsten Moment,
MATHEMATIK K1. Gesamtpunktzahl /30 Notenpunkte
 MATHEMATIK K1 21.11.2013 Aufgabe 1 2 3 4 5 6 7 Punkte (max) 6 3 4 4 2 10 1 Punkte Gesamtpunktzahl /30 Notenpunkte Der GTR ist nur für die Lösung der Textaufgabe (und zur Kontrolle der andern) zugelassen.
MATHEMATIK K1 21.11.2013 Aufgabe 1 2 3 4 5 6 7 Punkte (max) 6 3 4 4 2 10 1 Punkte Gesamtpunktzahl /30 Notenpunkte Der GTR ist nur für die Lösung der Textaufgabe (und zur Kontrolle der andern) zugelassen.
Mathematik I Herbstsemester 2018 Kapitel 3: Differentialrechnung
 Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 39 3. Differentialrechnung Einführung Ableitung elementarer Funktionen Ableitungsregeln Kettenregel Ableitung
Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 39 3. Differentialrechnung Einführung Ableitung elementarer Funktionen Ableitungsregeln Kettenregel Ableitung
Mathematik I für MB und ME
 Mathematik I für MB und ME Übungsaufgaben Serie 5: Folgen Funktionen Dierentialrechnung Fachbereich Grundlagenwissenschaften Prof Dr Viola Weiÿ Wintersemester 206/207 Bestimmen Sie die Grenzwerte der nachstehenden
Mathematik I für MB und ME Übungsaufgaben Serie 5: Folgen Funktionen Dierentialrechnung Fachbereich Grundlagenwissenschaften Prof Dr Viola Weiÿ Wintersemester 206/207 Bestimmen Sie die Grenzwerte der nachstehenden
Thema heute: Aufbau der Materie: Kernumwandlungen, Spaltung von Atomkernen
 Wiederholung der letzten Vorlesungsstunde: Experiment von Rutherford, Atombau, atomare Masseneinheit u, 118 bekannte Elemente, Isotope, Mischisotope, Massenspektroskopie, Massenverlust 4H 4 He, Einstein:
Wiederholung der letzten Vorlesungsstunde: Experiment von Rutherford, Atombau, atomare Masseneinheit u, 118 bekannte Elemente, Isotope, Mischisotope, Massenspektroskopie, Massenverlust 4H 4 He, Einstein:
Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION
 Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION Fassung vom 3 Dezember 2005 Mathematik für Humanbiologen und Biologen 39 3 Exponentialfunktion 3 Exponentialfunktion Wir betrachten als einführendes Beispiel
Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION Fassung vom 3 Dezember 2005 Mathematik für Humanbiologen und Biologen 39 3 Exponentialfunktion 3 Exponentialfunktion Wir betrachten als einführendes Beispiel
Mathematik für Naturwissenschaftler I WS 2009/2010
 Mathematik für Naturwissenschaftler I WS 2009/2010 Lektion 16 18. Dezember 2009 Differenzierbarkeit der Exponentialfunktion Zerfall, Halbwertszeit Die wichtige Exponentialfunktion exp ist definiert durch
Mathematik für Naturwissenschaftler I WS 2009/2010 Lektion 16 18. Dezember 2009 Differenzierbarkeit der Exponentialfunktion Zerfall, Halbwertszeit Die wichtige Exponentialfunktion exp ist definiert durch
Lösung zur Übung 19 SS 2012
 Lösung zur Übung 19 SS 01 69) Beim radioaktiven Zerfall ist die Anzahl der pro Zeiteinheit zerfallenden Kerne dn/dt direkt proportional zur momentanen Anzahl der Kerne N(t). a) Formulieren Sie dazu die
Lösung zur Übung 19 SS 01 69) Beim radioaktiven Zerfall ist die Anzahl der pro Zeiteinheit zerfallenden Kerne dn/dt direkt proportional zur momentanen Anzahl der Kerne N(t). a) Formulieren Sie dazu die
Beispiel: Bestimmung des Werts 3 2 ( 2 1, 4142) Es gilt 3 1,41 = 3 141/100 = , 707. Es gilt 3 1,42 = 3 142/100 = , 759.
 (4) Exponential- und Logarithmusfunktionen Satz Für jedes b > 1 gibt es eine eindeutig bestimmte Funktion exp b : R R + mit folgenden Eigenschaften. exp b (r) = b r für alle r Q Die Funktion exp b ist
(4) Exponential- und Logarithmusfunktionen Satz Für jedes b > 1 gibt es eine eindeutig bestimmte Funktion exp b : R R + mit folgenden Eigenschaften. exp b (r) = b r für alle r Q Die Funktion exp b ist
f : x 2 x f : x 1 Exponentialfunktion zur Basis a. Für alle Exponentialfunktionen gelten die Gleichungen (1) a x a y = a x+y (2) ax a y = ax y
 5. Die natürliche Exponentialfunktion und natürliche Logarithmusfunktion ================================================================== 5.1 Die natürliche Exponentialfunktion f : x 2 x f : x 1 2 x
5. Die natürliche Exponentialfunktion und natürliche Logarithmusfunktion ================================================================== 5.1 Die natürliche Exponentialfunktion f : x 2 x f : x 1 2 x
Abiturprüfung Physik, Grundkurs. Induktionsspannungen an einer im Magnetfeld schwingenden Leiterschaukel
 Seite 1 von 8 Abiturprüfung 2009 Physik, Grundkurs Aufgabenstellung: Aufgabe 1: Induktionsspannungen an einer im Magnetfeld schwingenden Leiterschaukel Ein Kupferstab der Länge L = 14 cm hängt wie in Abbildung
Seite 1 von 8 Abiturprüfung 2009 Physik, Grundkurs Aufgabenstellung: Aufgabe 1: Induktionsspannungen an einer im Magnetfeld schwingenden Leiterschaukel Ein Kupferstab der Länge L = 14 cm hängt wie in Abbildung
Musterlösung Übung 4
 Musterlösung Übung 4 Aufgabe 1: Radon im Keller a) 222 86Rn hat 86 Protonen, 86 Elektronen und 136 Neutronen. Der Kern hat demnach eine gerade Anzahl Protonen und eine gerade Anzahl Neutronen und gehört
Musterlösung Übung 4 Aufgabe 1: Radon im Keller a) 222 86Rn hat 86 Protonen, 86 Elektronen und 136 Neutronen. Der Kern hat demnach eine gerade Anzahl Protonen und eine gerade Anzahl Neutronen und gehört
(3) Wurzelfunktionen. Definition Sei f : D R eine Funktion. Eine Funktion g : D R heißt Umkehrfunktion von f, wenn für alle (x, y) R 2 die Äquivalenz
 (3) Wurzelfunktionen Definition Sei f : D R eine Funktion. Eine Funktion g : D R heißt Umkehrfunktion von f, wenn für alle (x, y) R 2 die Äquivalenz Definition y = f (x) g(y) = x gilt. Für jedes k N ist
(3) Wurzelfunktionen Definition Sei f : D R eine Funktion. Eine Funktion g : D R heißt Umkehrfunktion von f, wenn für alle (x, y) R 2 die Äquivalenz Definition y = f (x) g(y) = x gilt. Für jedes k N ist
Aufgabenblock : Lösen Sie folgenden Ausdruck nach x auf: 5x : Vereinfachen Sie folgenden Ausdruck: x + x2 (δ + a) x x x5 (δ + a) x 6
 Aufgabenblock 1 1.1: Lösen Sie folgenden Ausdruck nach x auf: 5x 5 2π ω = ω δ 1.2: Vereinfachen Sie folgenden Ausdruck: δ + a x + x2 (δ + a) x 3 + 1 x x5 (δ + a) x 6 1.3: Lösen Sie folgende Gleichung nach
Aufgabenblock 1 1.1: Lösen Sie folgenden Ausdruck nach x auf: 5x 5 2π ω = ω δ 1.2: Vereinfachen Sie folgenden Ausdruck: δ + a x + x2 (δ + a) x 3 + 1 x x5 (δ + a) x 6 1.3: Lösen Sie folgende Gleichung nach
a) Geben Sie eine Formel an, mit deren Hilfe man ermitteln kann, wie viel Wasser der Teich nach x regenlosen Tagen enthält!
 1) Wasserstand Der Wasserstand eines Gartenteichs wird durch Verdunstung und Niederschlag reguliert. Im Sommer kann mit einer täglichen Verdunstung von 4 % des am Morgen vorhandenen Wassers gerechnet werden.
1) Wasserstand Der Wasserstand eines Gartenteichs wird durch Verdunstung und Niederschlag reguliert. Im Sommer kann mit einer täglichen Verdunstung von 4 % des am Morgen vorhandenen Wassers gerechnet werden.
Exponential- & Logarithmusfunktionen
 Exponential- & Logarithmusfunktionen Referenten: Paul Schmelz & Wadim Krapp Fachlehrer: Herr Wettlaufer Fach: Mathematik Thema: Exponential- & Logarithmusfunktionen Inhaltsverzeichnis file:///d /Refs/_To%20Do/zips/ExponentialLogarithmusfunktionen.html
Exponential- & Logarithmusfunktionen Referenten: Paul Schmelz & Wadim Krapp Fachlehrer: Herr Wettlaufer Fach: Mathematik Thema: Exponential- & Logarithmusfunktionen Inhaltsverzeichnis file:///d /Refs/_To%20Do/zips/ExponentialLogarithmusfunktionen.html
1. Physikalische Grundlagen
 1.2. Kernumwandlung und Radioaktivität - Entdeckung Antoine Henri Becquerel Entdeckte Radioaktivität 1896 Ehepaar Marie und Pierre Curie Nobelpreise 1903 und 1911 Liese Meitner, Otto Hahn 1. Kernspaltung
1.2. Kernumwandlung und Radioaktivität - Entdeckung Antoine Henri Becquerel Entdeckte Radioaktivität 1896 Ehepaar Marie und Pierre Curie Nobelpreise 1903 und 1911 Liese Meitner, Otto Hahn 1. Kernspaltung
Aufbau des Atomkerns a) Gib an, aus wie vielen Protonen und Neutronen die
 Aufbau des Atomkerns a) Gib an, aus wie vielen Protonen und Neutronen die Atomkerne von Cl bestehen. b) Erkläre, was man unter Isotopen versteht. Gib ein Beispiel an. 3, Cl c) Im Periodensystem wird die
Aufbau des Atomkerns a) Gib an, aus wie vielen Protonen und Neutronen die Atomkerne von Cl bestehen. b) Erkläre, was man unter Isotopen versteht. Gib ein Beispiel an. 3, Cl c) Im Periodensystem wird die
6.7 Zerfallsgesetz, Halbwertszeit, Aktivität; Gegenüberstellen von induktivem und deduktivem
 6.7 Zerfallsgesetz, Halbwertszeit, Aktivität; Gegenüberstellen von induktivem und deduktivem Vorgehen Das Zerfallsgesetz Im Allgemeinen ist es nicht möglich, den Zerfall eines Elements getrennt vom Zerfall
6.7 Zerfallsgesetz, Halbwertszeit, Aktivität; Gegenüberstellen von induktivem und deduktivem Vorgehen Das Zerfallsgesetz Im Allgemeinen ist es nicht möglich, den Zerfall eines Elements getrennt vom Zerfall
Crashkurs sin 2 x + 5 cos 2 x = sin 2 x 2 sin x = 3
 Crashkurs. Funktion mit Parameter/Ortskurve - Wahlteil Analysis.. Gegeben sei für t > die Funktion f t durch f t (x) = 4 x 4t x 2 ; x R\{}. a) Welche Scharkurve geht durch den Punkt Q( 4)? b) Bestimme
Crashkurs. Funktion mit Parameter/Ortskurve - Wahlteil Analysis.. Gegeben sei für t > die Funktion f t durch f t (x) = 4 x 4t x 2 ; x R\{}. a) Welche Scharkurve geht durch den Punkt Q( 4)? b) Bestimme
C. Eicher Analysis Study Center ETH Zürich HS Extremwerte
 C. Eicher Analysis Study Center ETH Zürich HS 05 Extremwerte Gelöste Aufgabenbeispiele:. Bestimme die lokalen und globalen Extrema der Funktion f(x) = x x + x auf dem Intervall [ 4, ]. a. Bestimmung der
C. Eicher Analysis Study Center ETH Zürich HS 05 Extremwerte Gelöste Aufgabenbeispiele:. Bestimme die lokalen und globalen Extrema der Funktion f(x) = x x + x auf dem Intervall [ 4, ]. a. Bestimmung der
x A, x / A x ist (nicht) Element von A. A B, A B A ist (nicht) Teilmenge von B. A B, A B A ist (nicht) echte Teilmenge von B.
 SBP Mathe Grundkurs 1 # 0 by Clifford Wolf # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das Lernen mit Lernkarten
SBP Mathe Grundkurs 1 # 0 by Clifford Wolf # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das Lernen mit Lernkarten
SBP Mathe Grundkurs 1 # 0 by Clifford Wolf. SBP Mathe Grundkurs 1
 SBP Mathe Grundkurs 1 # 0 by Clifford Wolf SBP Mathe Grundkurs 1 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
SBP Mathe Grundkurs 1 # 0 by Clifford Wolf SBP Mathe Grundkurs 1 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
Thema heute: Aufbau der Materie, Atommodelle Teil 2
 Wiederholung der letzten Vorlesungsstunde: Atomistischer Aufbau der Materie, historische Entwicklung des Atombegriffes Atome Thema heute: Aufbau der Materie, Atommodelle Teil 2 Vorlesung Allgemeine Chemie,
Wiederholung der letzten Vorlesungsstunde: Atomistischer Aufbau der Materie, historische Entwicklung des Atombegriffes Atome Thema heute: Aufbau der Materie, Atommodelle Teil 2 Vorlesung Allgemeine Chemie,
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Mathematik 3 für Informatik
 Gunter Ochs Sommersemester 0 Mathematik 3 für Informatik Hausaufgabenblatt Lösungshinweise ohne Garantie auf Fehlerfeiheit). Seien f ) = { {, falls, falls und f ) =. ln, falls a) Skizzieren
Gunter Ochs Sommersemester 0 Mathematik 3 für Informatik Hausaufgabenblatt Lösungshinweise ohne Garantie auf Fehlerfeiheit). Seien f ) = { {, falls, falls und f ) =. ln, falls a) Skizzieren
HAW Hamburg Fachbereich HWI Hamburg, Prof. Dr. Badura B. Hamraz, O. Zarenko, M. Behrens. Chemie Testat 2. Name: Vorname: Matrikelnummer:
 Chemie Testat 2 Name: Vorname: Matrikelnummer: Bearbeitungszeit: 1 Stunde Zugelassene Hilfsmittel: Stifte, unbeschriebenes Papier, ein nichtprogrammierbarer Taschenrechner und ein Periodensystem Bitte
Chemie Testat 2 Name: Vorname: Matrikelnummer: Bearbeitungszeit: 1 Stunde Zugelassene Hilfsmittel: Stifte, unbeschriebenes Papier, ein nichtprogrammierbarer Taschenrechner und ein Periodensystem Bitte
5 Differenzialrechnung für Funktionen einer Variablen
 5 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
5 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
Serie 4: Gradient und Linearisierung
 D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 4: Gradient und Linearisierung Bemerkungen: Die Aufgaben der Serie 4 bilden den Fokus der Übungsgruppen vom 7./9. März.. Wir betrachten die
D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 4: Gradient und Linearisierung Bemerkungen: Die Aufgaben der Serie 4 bilden den Fokus der Übungsgruppen vom 7./9. März.. Wir betrachten die
Differenzialrechnung
 Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
R. Brinkmann Seite Anwendungen der Exponentialfunktion
 R. Brinkmann http://brinkmann-du.de Seite 6..2 Aufstellen der Funktionsgleichung : Anwendungen der Eponentialfunktion Coli Bakterien verrichten ihre Arbeit im menschlichen Darm. Sie vermehren sich durch
R. Brinkmann http://brinkmann-du.de Seite 6..2 Aufstellen der Funktionsgleichung : Anwendungen der Eponentialfunktion Coli Bakterien verrichten ihre Arbeit im menschlichen Darm. Sie vermehren sich durch
Bezeichnung von Funktionen x := y:=
 Bezeichnung von Funktionen x := y:= Bezeichnung von Funktionen x := y:= Analytische Darstellung (Funktionsgleichung) Explizit: (aufgelöst nach y) Analytische Darstellung (Funktionsgleichung) Explizit:
Bezeichnung von Funktionen x := y:= Bezeichnung von Funktionen x := y:= Analytische Darstellung (Funktionsgleichung) Explizit: (aufgelöst nach y) Analytische Darstellung (Funktionsgleichung) Explizit:
Funktionen mehrerer Variabler
 Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
41. Kerne. 34. Lektion. Kernzerfälle
 41. Kerne 34. Lektion Kernzerfälle Lernziel: Stabilität von Kernen ist an das Verhältnis von Protonen zu Neutronen geknüpft. Zu viele oder zu wenige Neutronen führen zum spontanen Zerfall. Begriffe Stabilität
41. Kerne 34. Lektion Kernzerfälle Lernziel: Stabilität von Kernen ist an das Verhältnis von Protonen zu Neutronen geknüpft. Zu viele oder zu wenige Neutronen führen zum spontanen Zerfall. Begriffe Stabilität
Kreuze nur die zutreffenden Eigenschaften für die folgenden Funktionen im richtigen Feld an!
 Teil : Grundkompetenzen ( Punkte) Beispiel : ( Punkt) Die nebenstehende Graphik stellt ein eponentielles Wachstum der Form f() = a b (a, b R + ) dar. Bestimme aus dem Graphen die Werte der Konstanten a
Teil : Grundkompetenzen ( Punkte) Beispiel : ( Punkt) Die nebenstehende Graphik stellt ein eponentielles Wachstum der Form f() = a b (a, b R + ) dar. Bestimme aus dem Graphen die Werte der Konstanten a
Mathematik 6A 2. Schularbeit, 21. Dezember 2018 Gruppe A Note. von 48 P Befriedigend. Aufgabe 1 Funktionen 2 P.
 Mathematik 6A 2. Schularbeit, 21. Dezember 2018 Gruppe A Name: Erreicht Note von 48 P. Notenschlüssel 0 23 Nicht genügend 24-29 Genügend 30-36 Befriedigend 37-42 Gut 43-48 Sehr gut Aufgabe 1 Funktionen
Mathematik 6A 2. Schularbeit, 21. Dezember 2018 Gruppe A Name: Erreicht Note von 48 P. Notenschlüssel 0 23 Nicht genügend 24-29 Genügend 30-36 Befriedigend 37-42 Gut 43-48 Sehr gut Aufgabe 1 Funktionen
Höhere Mathematik II für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung
 TU Bergakademie Freiberg Sommersemester Dr. Gunter Semmler Dr. Anja Kohl Höhere Mathematik II für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung Differentialrechnung für Funktionen
TU Bergakademie Freiberg Sommersemester Dr. Gunter Semmler Dr. Anja Kohl Höhere Mathematik II für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung Differentialrechnung für Funktionen
3.2 Exponentialfunktion und Wachstum/Zerfall
 3.2 Exponentialfunktion und Wachstum/Zerfall Inhaltsverzeichnis 1 Die Exponentialfunktion 2 2 Exponentielles Wachtum und exponentieller Zerfall 3 1 Exp.-funktion,Wachstum,Zerfall 27.08.2008 Theorie und
3.2 Exponentialfunktion und Wachstum/Zerfall Inhaltsverzeichnis 1 Die Exponentialfunktion 2 2 Exponentielles Wachtum und exponentieller Zerfall 3 1 Exp.-funktion,Wachstum,Zerfall 27.08.2008 Theorie und
Die Umkehrung des Potenzierens ist das Logarithmieren.
 Die Umkehrung des Potenzierens ist das Logarithmieren. Gilt a x = b, a,b > 0, a 1, so heißt x der Logarithmus von b zur Basis a. Bezeichnung: x = log a (b). Manchmal lassen wir die Angabe der Basis auch
Die Umkehrung des Potenzierens ist das Logarithmieren. Gilt a x = b, a,b > 0, a 1, so heißt x der Logarithmus von b zur Basis a. Bezeichnung: x = log a (b). Manchmal lassen wir die Angabe der Basis auch
42. Radioaktivität. 35. Lektion Radioaktivität
 42. Radioaktivität 35. Lektion Radioaktivität Lernziel: Unstabile Kerne zerfallen unter Emission von α, β, oder γ Strahlung Begriffe Begriffe Radioaktiver Zerfall ktivität Natürliche Radioaktivität Künstliche
42. Radioaktivität 35. Lektion Radioaktivität Lernziel: Unstabile Kerne zerfallen unter Emission von α, β, oder γ Strahlung Begriffe Begriffe Radioaktiver Zerfall ktivität Natürliche Radioaktivität Künstliche
Funktionen mehrerer Variabler
 Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Damit hat man die Potenzfunktion mit rationalem Exponenten definiert:
 Mathematik 1, Übungen Nr. 9 Joachim Schneider 11. Dezember 2006 Funktionen Teil 2 Die Potenzfunktion mit rationalem Exponenten Sei x R. Dann definieren wir für natürliches n x n := x} x {{ x} n Faktoren
Mathematik 1, Übungen Nr. 9 Joachim Schneider 11. Dezember 2006 Funktionen Teil 2 Die Potenzfunktion mit rationalem Exponenten Sei x R. Dann definieren wir für natürliches n x n := x} x {{ x} n Faktoren
Implizite Differentiation
 Implizite Differentiation -E -E Implizite Darstellung Eine Funktion ist in impliziter Form gegeben, wenn ie Funktionsgleichung nach keiner er beien Variablen x un y aufgelöst ist. Beispielsweise x y =
Implizite Differentiation -E -E Implizite Darstellung Eine Funktion ist in impliziter Form gegeben, wenn ie Funktionsgleichung nach keiner er beien Variablen x un y aufgelöst ist. Beispielsweise x y =
Tutorium: Analysis und lineare Algebra. Differentialrechnung. Steven Köhler. mathe.stevenkoehler.de Steven Köhler
 Tutorium: Analysis und lineare Algebra Differentialrechnung Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Differenzenquotient Der Di erenzenquotient ist de niert als f(x) x f(x) f(x 0)
Tutorium: Analysis und lineare Algebra Differentialrechnung Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Differenzenquotient Der Di erenzenquotient ist de niert als f(x) x f(x) f(x 0)
2) Kernstabilität und radioaktive Strahlung (2)
 2) Kernstabilität und radioaktive Strahlung (2) Periodensystem der Elemente vs. Nuklidkarte ca. 115 unterschiedliche chemische Elemente Periodensystem der Elemente 7 2) Kernstabilität und radioaktive Strahlung
2) Kernstabilität und radioaktive Strahlung (2) Periodensystem der Elemente vs. Nuklidkarte ca. 115 unterschiedliche chemische Elemente Periodensystem der Elemente 7 2) Kernstabilität und radioaktive Strahlung
Die elementaren Funktionen (Überblick)
 Die elementaren Funktionen (Überblick) Zu den elementaren Funktionen zählen wir die Potenz- und die Exponentialfunktion, den Logarithmus, sowie die hyperbolischen und die trigonometrischen Funktionen und
Die elementaren Funktionen (Überblick) Zu den elementaren Funktionen zählen wir die Potenz- und die Exponentialfunktion, den Logarithmus, sowie die hyperbolischen und die trigonometrischen Funktionen und
Elementare Funktionen. Analysis I November 28, / 101
 Elementare Funktionen Analysis I November 28, 2017 76 / 101 Exponentialfunktion Buch Kap. 2.3 Exponentialfunktionen f(x) = a x, a > 0, D = R. Ist a = e (Eulerzahl e = 2, 71828...), sprechen wir von der
Elementare Funktionen Analysis I November 28, 2017 76 / 101 Exponentialfunktion Buch Kap. 2.3 Exponentialfunktionen f(x) = a x, a > 0, D = R. Ist a = e (Eulerzahl e = 2, 71828...), sprechen wir von der
Absolute Datierungsmethoden. Dr. Gnoyke, Bi-GK 13.1 Methoden zur Altersbestimmung von Fossilfunden
 Absolute Datierungsmethoden Dr. Gnoyke, Bi-GK 13.1 Methoden zur Altersbestimmung von Fossilfunden Datierungsmethoden Datierungsmethoden relative Datierungsmethoden Absolute Datierungsmethoden z. B. Stratigrafie
Absolute Datierungsmethoden Dr. Gnoyke, Bi-GK 13.1 Methoden zur Altersbestimmung von Fossilfunden Datierungsmethoden Datierungsmethoden relative Datierungsmethoden Absolute Datierungsmethoden z. B. Stratigrafie
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann
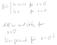 Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
FH Gießen-Friedberg, FB 06 (MNI) Lösungen zu Übungsblatt 8 Einführung in die höhere Mathematik 6. Dezember 2006 Prof. Dr. H.-R.
 FH Gießen-Friedberg, FB 06 (MNI) Lösungen zu Übungsblatt 8 Einführung in die höhere Mathematik 6. Dezember 006 Prof. Dr. H.-R. Metz Aufgabe 1 Skizzieren Sie die Funktionen e x, ln(x) = log e (x) und e
FH Gießen-Friedberg, FB 06 (MNI) Lösungen zu Übungsblatt 8 Einführung in die höhere Mathematik 6. Dezember 006 Prof. Dr. H.-R. Metz Aufgabe 1 Skizzieren Sie die Funktionen e x, ln(x) = log e (x) und e
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Übungen zur Klausur über das Propädeutikum Dr. Daniel Bick 08. November 2013 Daniel Bick Physik für Biologen und Zahnmediziner 08. November 2013 1 / 27 Information
Physik für Biologen und Zahnmediziner Übungen zur Klausur über das Propädeutikum Dr. Daniel Bick 08. November 2013 Daniel Bick Physik für Biologen und Zahnmediziner 08. November 2013 1 / 27 Information
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Standardisierte kompetenzorientierte schriftliche Reifeprüfung AHS. 28. September Mathematik. Teil-2-Aufgaben. Korrekturheft
 Standardisierte kompetenzorientierte schriftliche Reifeprüfung AHS 28. September 2017 Mathematik Teil-2-Aufgaben Korrekturheft Aufgabe 1 Aktivität und Altersbestimmung a) Lösungserwartung: A(t) = N (t)
Standardisierte kompetenzorientierte schriftliche Reifeprüfung AHS 28. September 2017 Mathematik Teil-2-Aufgaben Korrekturheft Aufgabe 1 Aktivität und Altersbestimmung a) Lösungserwartung: A(t) = N (t)
