LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Gliederung Lineare Mdelle zur Klassifikatin und Regressin 1 Lineare
|
|
|
- Miriam Hauer
- vor 6 Jahren
- Abrufe
Transkript
1 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Lineare Mdelle zur Klassifikatin und Regressin Vrlesung Maschinelles Lernen Klassifikatin und Regressin: Lineare Mdelle Katharina Mrik LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund vn 39
2 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Gliederung Lineare Mdelle zur Klassifikatin und Regressin 1 Lineare Mdelle zur Klassifikatin und Regressin Klassifikatin und Regressin Lineare Mdelle Gemetrie linearer Mdelle: Hyperebenen 2 Exkurs:Erwartungswert Bias und Varianz bei linearen Mdellen 2 vn 39
3 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Grundlagen Lineare Mdelle zur Klassifikatin und Regressin Sei X = {X 1,..., X p } eine Menge vn Zufallsvariablen und Y eine Menge. Ein Beispiel (der Bebachtung) x ist ein knkreter p-dimensinaler Vektr über diesen Zufallsvariablen. Eine Menge vn n Beispielen X = { x 1,..., x N } können wir dann als (N p)-matrix auffassen: x 1,1 x 1,2... x 1,p. X = x.. 2, x N,1 x N,2... x N,p Dabei entspricht jede Zeile x i der Matrix X einem Beispiel. 3 vn 39
4 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Klassifikatin und Regressin Lineare Mdelle zur Klassifikatin und Regressin Beim überwachten Lernen (darum geht es hier), ist zusätzlich zu jeder Bebachtung x ein Label (Klasse) y gegeben, d.h. wir haben Bebachtungen ( x, y) X Y. Y kann swhl eine qualitative, als auch eine quantitative Beschreibung vn x sein. Für den quantitativen Fall ist z.b. Y = R und wir versuchen für unbekanntes x den Wert y vrherzusagen Regressin. Im Falle qualitativer Beschreibungen ist Y eine diskrete Menge und wir nutzen f zur Klassifikatin. 4 vn 39
5 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Lernen auf Trainingsdaten Lineare Mdelle zur Klassifikatin und Regressin Wvn gehen wir als aus? Was ist unser Ziel? Wir suchen die wahre Funktin f : X Y mit f( x) =y ( x, y) X Y Wir haben jedch nur eine Teilmenge der Bebachtungen gegeben (Trainingsdaten) 5 vn 39
6 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Klassifikatin und Regressin Lineare Mdelle zur Klassifikatin und Regressin Auf Grundlage der Trainingsdaten suchen wir eine möglichst gute Annäherung ˆf an die wahre Funktin f. Die Funktin ˆf bezeichnen wir auch als das gelernte Mdell. Haben wir ein Mdell ˆf gelernt, s liefert uns dieses Mdell mit ŷ = ˆf ( x) für neue Daten x X eine Vrhersage ŷ Y. 6 vn 39
7 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Klassifikatin und Regressin Lineare Mdelle zur Klassifikatin und Regressin Im Falle der Regressin läßt sich s für zuvr unbekannte x X der Wert ŷ = ˆf ( x) mit ŷ R vrhersagen. Dieses Mdell ˆf läßt sich auch für die Klassifikatin nutzen, bei der z.b. ŷ { 1, +1} vrhergesagt werden sllen: { +1, falls ˆf ( x) θ ŷ = 1, snst Hier ist θ ein vrgegebener Schwellwert. 7 vn 39
8 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Beispiel Lineare Mdelle zur Klassifikatin und Regressin Gegeben seien Gewicht (X 1 ) und Größe (X 2 ) einiger Persnen und ein Label y {m, w}: X 1 X 2 Y x m x w x w. Die Tabelle enthält die zur Verfügung stehenden Trainingsdaten, als X = vn 39
9 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Beispiel Lineare Mdelle zur Klassifikatin und Regressin Es wird nun eine Funktin ˆf gesucht, die für neue Daten x das Attribut Y (Geschlecht) vraussagt, als { m, falls ˆf(x) >θ ŷ = w, snst 9 vn 39
10 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Beispiel Lineare Mdelle zur Klassifikatin und Regressin Es wird nun eine Funktin ˆf gesucht, die für neue Daten x das Attribut Y (Geschlecht) vraussagt, als { m, falls ˆf(x) >θ ŷ = w, snst 200 Klasse m Klasse w 190 Größe (in cm) vn 39
11 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Lineare Mdelle Lineare Mdelle zur Klassifikatin und Regressin Welche Art vn Funktinen sind denkbar? Lineare Funktinen als einfachste Funktinenklasse: y = f(x) =mx + b Gerade im R 2 Allerdings betrachten wir als Beispielraum den R p, d.h. wir brauchen eine verallgemeinerte Frm: y = f ( x) = p β i x i + β 0 mit β 0 R, x, β R p (1) i=1 Die Funktin f wird als durch β und β 0 festgelegt und sagt uns für ein gegebenes x das entsprechende y vraus 10 vn 39
12 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Ntatin, Vereinbarungen Lineare Mdelle zur Klassifikatin und Regressin Bei genauerer Betrachtung vn Frmel (1) läßt sich p i=1 β ix i als Matrizenmultiplikatin schreiben, als y = p β i x i + β 0 = x T β + β0 i=1 Zur einfacheren Darstellung vn f, wird β 0 in den Vektr β cdiert, indem jedes Beispiel x =(x 1,..., x p ) aufgefasst wird als (p + 1)-dimensinaler Vektr (x 1,..., x p ) (1,x 1,..., x p ) Dies ermöglicht die Darstellung vn f als: y = f ( x) = p β i x i = x T β i=0 11 vn 39
13 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Was haben wir nun gemacht? Lineare Mdelle zur Klassifikatin und Regressin Wir haben (bei der Beschränkung auf lineare Mdelle) nun eine Darstellung für das, was wir lernen wllen: y = ˆf( x) = x T β Wir haben die Zielfunktin ˆf in Abhängigkeit vn β geschrieben und müssen nur nch das passende β finden. 12 vn 39
14 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Veranschaulichung Lineare Mdelle zur Klassifikatin und Regressin Bevr wir uns an die Wahl des passenden β machen, zunächst einige Vrüberlegungen. Betrachten wir dazu die binäre Klassifikatin (Y = { 1, +1}): Was passiert dabei eigentlich anschaulich? Wie klassifiziert unser ˆf die Daten? Wie wirkt sich die Wahl vn β aus? 13 vn 39
15 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Zur Erinnerung: Hyperebene Lineare Mdelle zur Klassifikatin und Regressin Sei V = R p ein Vektrraum, dann ist eine Hyperebene H ein (p 1)-dimensinaler affiner Untervektrraum. H lässt sich über einen Stützvektr a und einen Nrmalenvektr β schreiben als { H = x R p β( x } a) =0 Hesse Nrmalfrm Die Ebenengleichung β( x a) = 0 ist in Hesse Nrmalfrm, falls β =1. 14 vn 39
16 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Zur Erinnerung: Hyperebene Lineare Mdelle zur Klassifikatin und Regressin Sei V = R p ein Vektrraum, dann ist eine Hyperebene H ein (p 1)-dimensinaler affiner Untervektrraum. H lässt sich über einen Stützvektr a und einen Nrmalenvektr β schreiben als { H = x R p β( x } a) =0 Hesse Nrmalfrm Die Ebenengleichung β( x a) = 0 ist in Hesse Nrmalfrm, falls β =1. 14 vn 39
17 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Beispiel Lineare Mdelle zur Klassifikatin und Regressin (Hyper-) Ebene im R 3 mit Nrmalenvektr β und Stützvektr a. 15 vn 39
18 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Beispiel Lineare Mdelle zur Klassifikatin und Regressin 16 vn 39
19 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Beispiel: Ein mögliches β 200 Lineare Mdelle zur Klassifikatin und Regressin Klasse m Klasse w f(x) 190 Größe (in cm) Gewicht (in kg) f( x) = x T ˆ β mit ˆ β = β 0 β 1 β 2 = vn 39
20 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Es ist nicht garantiert, dass β immer paßt! Lineare Mdelle zur Klassifikatin und Regressin 200 Klasse m Klasse w 190 Größe (in cm) Gewicht (in kg) 18 vn 39
21 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Mdell-Anpassung Lineare Mdelle zur Klassifikatin und Regressin Unsere linearen Mdelle sind durch β parametrisiert, das Lernen eines Mdells haben wir als auf die Wahl eines β abgewälzt. Das wirft eine Reihe vn Fragen auf: Was ist ein gutes β? Gibt es ein ptimales β? Welche Möglichkeiten haben wir, unser Mdell zu beurteilen? 19 vn 39
22 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Mdell-Anpassung Lineare Mdelle zur Klassifikatin und Regressin Unsere linearen Mdelle sind durch β parametrisiert, das Lernen eines Mdells haben wir als auf die Wahl eines β abgewälzt. Das wirft eine Reihe vn Fragen auf: Was ist ein gutes β? Gibt es ein ptimales β? Welche Möglichkeiten haben wir, unser Mdell zu beurteilen? Eine Möglichkeit: Berechne den Trainingsfehler Err( β)= N y i ˆf( x i ) = i=1 N y i x T i β i=1 19 vn 39
23 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Mdell-Anpassung Lineare Mdelle zur Klassifikatin und Regressin Häufig wird als Fehlerfunktin die quadratische Fehlersumme (RSS) verwendet: RSS( β) = N T (y i x i β) 2 i=1 = ( y X β) T ( y X β) Wir wählen jetzt β derart, dass der Fehler minimiert wird: min RSS( β) β R p Knvexes Minimierungsprblem! 20 vn 39
24 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Minimierung vn RSS( β) Lineare Mdelle zur Klassifikatin und Regressin Um RSS( β) zu minimieren, bilden wir die partielle Ableitung nach β: RSS( β) β = X T (y X β) Ntwendige Bedingung für die Existenz eines (lkalen) Minimums vn RSS ist RSS( β) β = X T (y X β) = 0 Ist X T X regulär, s erhalten wir ˆ β =(X T X) 1 X T y 21 vn 39
25 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Optimales ˆ β? Lineare Mdelle zur Klassifikatin und Regressin Mit Hilfe der Minimierung der (quadratischen) Fehlerfunktin RSS auf unseren Trainingsdaten haben wir ein (bzgl. RSS) ptimales ˆ β gefunden. Damit liefert unser Mdell Vraussagen ŷ für x X: ŷ = ˆf( x) =x T ˆ β 22 vn 39
26 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Sind wir schn fertig? Lineare Mdelle zur Klassifikatin und Regressin Schön wär s! Aber drei Gründe sprechen für weitere Arbeit: 1 Es ist nicht immer s einfach, z.b. dann nicht, wenn wir viele Dimensinen haben (Fluch der hhen Dimensin). 2 Vielleicht lassen sich die Beispiele nicht linear trennen! 3 Nur den Fehler zu minimieren reicht nicht aus, wir suchen nch nach weiteren Beschränkungen, die zu besseren Lösungen führen. Als schauen wir uns den Fehler nch einmal genauer an, stßen auf Bias und Varianz und merken, dass wir nch keine perfekte Lösung haben. 23 vn 39
27 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Fehler Lineare Mdelle zur Klassifikatin und Regressin Bisher haben wir mit RSS die Fehler einfach summiert. Wir wllen aber einbeziehen, wie wahrscheinlich der Fehler ist vielleicht ist er ja ganz unwahrscheinlich! Wann können wir denn einen Fehler erwarten? 24 vn 39
28 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Zur Erinnerung: Erwartungswert Lineare Mdelle zur Klassifikatin und Regressin Erwartungswert Sei X eine diskrete Zufallsvariable, mit Werten x 1,..., x n und p i die Wahrscheinlichkeit für x i. Der Erwartungswert vn X ist E(X) = i x i p i = i x i P (X = x i ) Ist X eine stetige Zufallsvariable und f die zugehörige Wahrscheinlichkeitsdichtefunktin, s ist der Erwartungswert vn X E(X) = xf(x)dx 25 vn 39
29 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Erwartungswert (Eigenschaften) Lineare Mdelle zur Klassifikatin und Regressin Eigenschaften Seien X, Y und X 1,..., X n Zufallsvariablen, dann gilt: Der Erwartungswert ist additiv, d.h. es gilt ( n ) n E X i = E(X i ) (2) i=1 i=1 Ist Y = kx + d, s gilt für den Erwartungswert E(Y )=E(kX + d) =ke(x)+d Sind die Zufallsvariablen X i stchastisch unabhängig, gilt ( n ) n E X i = E(X i ) i=1 i=1 26 vn 39
30 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Varianz und Standardabweichung Lineare Mdelle zur Klassifikatin und Regressin Über den Erwartungswert einer Zufallsvariablen X sind mehrere Eigenschaften vn X definiert, die helfen, X zu charakterisieren: Varianz Sei X eine Zufallsvariable mit µ = E(X). Die Varianz V ar(x) ist definiert als V ar(x) := E ( (X µ) 2). Standardabweichung Die Standardabweichung σ einer Zufallsvariable X ist definiert als σ := V ar(x) 27 vn 39
31 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Varianz und Standardabweichung Lineare Mdelle zur Klassifikatin und Regressin Über den Erwartungswert einer Zufallsvariablen X sind mehrere Eigenschaften vn X definiert, die helfen, X zu charakterisieren: Varianz Sei X eine Zufallsvariable mit µ = E(X). Die Varianz V ar(x) ist definiert als V ar(x) := E ( (X µ) 2). Standardabweichung Die Standardabweichung σ einer Zufallsvariable X ist definiert als σ := V ar(x) Die Varianz wird häufig auch mit σ 2 bezeichnet. 27 vn 39
32 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Varianz und Standardabweichung Lineare Mdelle zur Klassifikatin und Regressin Verschiebungssatz Sei X eine Zufallsvariable, für die Varianz gilt V ar(x) =E(X E(X)) 2 = E(X 2 ) (E(X)) 2 (3) Eine weitere Charakteristik, die häufig zur Beschreibung vn erwarteten Fehlern verwendet wird, ist die Verzerrung: Verzerrung (Bias) Sei X eine Zufallsvariable, dann ist die Verzerrung definiert als der erwartete Schätzfehler für X Bias(ˆx) =E(X ˆx) (4) 28 vn 39
33 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Erwartungswert des Fehlers einer Regressin Lineare Mdelle zur Klassifikatin und Regressin Erwarteter quadratischer Fehler: Gelernte Funktin ˆf : X Y, der Erwartungswert ihres Fehlers ist: EP E(f) =E(Y ˆf(X)) 2 (5) Optimierungsprblem: Wähle ˆf s, dass der erwartete Fehler minimiert wird! ˆf(x) =argmin c E Y X ((Y c) 2 X = x) Lösung (Regressinsfunktin): f(x) = E(Y X = x) 29 vn 39
34 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Bias und Varianz Lineare Mdelle zur Klassifikatin und Regressin Zwei Aspekte machen den erwarteten Fehler aus, die Verzerrung (Bias) und die Varianz. Wir wllen den Fehler an einem Testpunkt x 0 =0angeben und mitteln über allen Trainingsmengen T. Wie das? MSE( x 0 ) = E T [y 0 ŷ 0 ] 2 = E T [ŷ 0 E T (ŷ 0 )] 2 +[E T (ŷ 0 y 0 )] 2 = E T [y 2 0] E T [2y 0 ŷ 0 ]+E T [ŷ 2 0] = V ar T (ŷ 0 )+Bias 2 (ŷ 0 ) 30 vn 39
35 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Herleitung der Varianz in MSE Lineare Mdelle zur Klassifikatin und Regressin Nach dem Verschiebungssatz (3) gilt V ar T (y 0 )=E T [ŷ 2 0] (E T [ŷ 0 ]) 2 E T [ŷ 2 0]=V ar T (y 0 )+(E T [ŷ 0 ]) 2 (6) Damit flgt MSE( x 0 ) = E T [y 0 ŷ 0 ] 2 [ = E T y 2 0 2y 0 ŷ 0 +ŷ0 2 ] (2) = E T [y 2 0] E T [2yŷ 0 ]+E T [ŷ 2 0] (6) = E T [y 2 0] E T [2y 0 ŷ 0 ]+V ar T (ŷ 0 )+(E T [ŷ 0 ]) 2 = E T [y 2 0 2yŷ 0 +ŷ 2 0]+V ar T (ŷ 0 ) = E T [y 0 ŷ 0 ] 2 + V ar T (ŷ 0 ) (4) = Bias 2 (ŷ 0 )+V ar T (ŷ 0 ) 31 vn 39
36 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Herleitung des Bias in MSE Lineare Mdelle zur Klassifikatin und Regressin Smit gilt MSE( x 0 )=V ar T (ŷ 0 )+Bias 2 (ŷ 0 ) Die Dekmpsitin des MSE in Bias und Varianz abstrahiert s, dass wir besser über Mdelle nachdenken können. Frage: Wie wirken sich Bias und Varianz nun auf unsere linearen Mdelle aus? 32 vn 39
37 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Lineare Mdelle zur Klassifikatin und Regressin Erwartungswert des Fehlers bei linearen Mdellen Unter der Annahme, dass unsere Beispiele Messfehler enhalten, aber X und Y wirklich linear vneinander abhängen (Bias=0), passen wir das Mdell Y = X T β + ɛ durch Minimieren des quadratischen Fehlers an. Der erwartete Fehler der ŷ-vrhersage für ein beliebiges x 0 ist: EP E( x 0 ) = E y0 x 0 E T (y 0 ŷ 0 ) 2 = V ar(y 0 x 0 )+E T (ŷ 0 E T (y 0 )) 2 +(E T (ŷ 0 ) E T (y 0 )) 2 = V ar(y 0 x 0 )+V ar T (ŷ 0 )+Bias 2 (ŷ 0 ) = σ 2 + E T ( x 0 T (X T X) 1 x 0 σ 2 )+0 2 Die zusätzliche Varianz kmmt durch das Rauschen. 33 vn 39
38 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Lineare Mdelle zur Klassifikatin und Regressin Zusammenhang zwischen Anzahl der Beispiele, der Attribute und erwartetem Fehler Beziehen wir den Erwartungswert vn x ein, erhalten wir E x EP E( x) =σ 2 (p/n)+σ 2 Bei kleinem σ 2 und grßem N klappt alles auch bei grßem p, wenn das lineare Mdell perfekt passt, d.h. die Beispiele sind linear trennbar. 34 vn 39
39 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Lineare Mdelle zur Klassifikatin und Regressin Fluch der hhen Dimensin bei linearen Mdellen Leider mussten wir annehmen, dass das Mdell genau passt, um den erwarteten Fehler klein zu halten. Wir wissen aber nicht, welche Art vn Funktin gut zu unseren Daten passt! Mdellselektin ist schwierig! Das Mdell muss immer kmplizierter werden, je mehr Dimensinen es gibt. Bei linearen Mdellen entspricht die Kmplexität des Mdells direkt p, denn β hat s viele Kmpnenten wie p bzw. p vn 39
40 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Bias und Varianz bei linearen Mdellen Lineare Mdelle zur Klassifikatin und Regressin Das lineare Mdell wird an die Daten angepasst durch ˆf p ( x) = ˆβ T x Der Fehler ist dann für ein beliebiges x: Err( x) = E[(Y ˆf p ( x)) 2 X = x] (7) = σɛ 2 + V ar( ˆf [ p ( x)+ f( x) E ˆf 2 p ( x)] (8) Im Mittel über allen x i ist V ar( ˆf p ) = (p/n)σ 2. Mdellkmplexität und Varianz hängen bei linearen Mdellen direkt zusammen. Der Trainingsfehler linearer Mdelle ist: 1 N N Err(x i )=σɛ 2 + p 1 N σ2 ɛ N i=1 N i=1 [ f( x i ) E ˆf( x i )] 2 (9) 36 vn 39
41 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Lineare Mdelle zur Klassifikatin und Regressin Lineare Mdelle Die grünen und rten Datenpunkte werden durch eine Ebene getrennt. Linear Regressin f 0/1 Respnse Figure 2.1: A classificatin example in tw dimensins. The classes are cded as a binary variable GREEN = 0, RED = 1 and then fit by linear regressin. The line is the decisin bundary defined by x T ˆβ = vn 39
42 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Was wissen Sie jetzt? Lineare Mdelle zur Klassifikatin und Regressin Sie haben theretisch lineare Mdelle für Klassifikatin und Regressin kennengelernt. Sie kennen das Optimierungsprblem der kleinsten Quadrate RSS für lineare Mdelle (Gleichung 9). Sie kennen den erwarteten Fehler EPE bei linearen Mdellen. Sie kennen den Fluch der hhen Dimensin bei linearen Mdellen: Kmplexität und Varianz hängen an der Dimensin! Der Bias kann sehr hch sein, wenn die Beispiele tatsächlich nicht linear separierbar sind. 38 vn 39
43 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Bis zum nächsten Mal... Lineare Mdelle zur Klassifikatin und Regressin Gehen Sie alle Flien nch einmal in Ruhe durch. Vertiefen Sie sich nch einmal in die Ebenengleichung! Die lineare Algebra wird immer wieder vrkmmen. Sie können auch die partiellen Ableitungen für RSS mit der Nrmalengleichung vrnehmen. Rechnen Sie mal ein Beispiel durch mit Gleichung (9), (9)... Diskutieren Sie, warum Bias und Varianz s wichtig sind! Prbieren Sie lineare Regressin in RapidMiner aus! 39 vn 39
Vorlesung Wissensentdeckung in Datenbanken
 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Cmputergestützte Statistik Technische Universität Drtmund Lineare Mdelle zur Klassifikatin und Regressin Bias-Varianz knn zur Klassifikatin, Regressin
LS 8 Künstliche Intelligenz Fakultät für Infrmatik Cmputergestützte Statistik Technische Universität Drtmund Lineare Mdelle zur Klassifikatin und Regressin Bias-Varianz knn zur Klassifikatin, Regressin
Maschinelles Lernen. Skript zur Vorlesung. Katharina Morik. September 17, 2013
 Maschinelles Lernen Skript zur Vrlesung Katharina Mrik September 17, 2013 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Inhaltsverzeichnis 1 Einführung 1 1.1 Anwendungen........................................
Maschinelles Lernen Skript zur Vrlesung Katharina Mrik September 17, 2013 LS 8 Künstliche Intelligenz Fakultät für Infrmatik Technische Universität Drtmund Inhaltsverzeichnis 1 Einführung 1 1.1 Anwendungen........................................
Teil III: Wissensrepräsentation und Inferenz. Nachtrag zu Kap.5: Neuronale Netze. w i,neu = w i,alt + x i * (Output soll - Output ist ) Delta-Regel
 Einfaches Perzeptrn Delta-Regel Vrlesung Künstliche Intelligenz Wintersemester 2006/07 Teil III: Wissensrepräsentatin und Inferenz Nachtrag zu Kap.5: Neurnale Netze Beim Training werden die Beispiele dem
Einfaches Perzeptrn Delta-Regel Vrlesung Künstliche Intelligenz Wintersemester 2006/07 Teil III: Wissensrepräsentatin und Inferenz Nachtrag zu Kap.5: Neurnale Netze Beim Training werden die Beispiele dem
Statistik, Datenanalyse und Simulation
 Dr. Michael O. Distler distler@kph.uni-mainz.de Mainz, 31. Mai 2011 4. Methode der kleinsten Quadrate Geschichte: Von Legendre, Gauß und Laplace zu Beginn des 19. Jahrhunderts eingeführt. Die Methode der
Dr. Michael O. Distler distler@kph.uni-mainz.de Mainz, 31. Mai 2011 4. Methode der kleinsten Quadrate Geschichte: Von Legendre, Gauß und Laplace zu Beginn des 19. Jahrhunderts eingeführt. Die Methode der
Dr. Maike M. Burda. Welchen Einfluss hat die Körperhöhe auf das Körpergewicht? Eine Regressionsanalyse. HU Berlin, Econ Bootcamp
 Dr. Maike M. Burda Welchen Einfluss hat die Körperhöhe auf das Körpergewicht? Eine Regressionsanalyse. HU Berlin, Econ Bootcamp 8.-10. Januar 2010 BOOTDATA.GDT: 250 Beobachtungen für die Variablen... cm:
Dr. Maike M. Burda Welchen Einfluss hat die Körperhöhe auf das Körpergewicht? Eine Regressionsanalyse. HU Berlin, Econ Bootcamp 8.-10. Januar 2010 BOOTDATA.GDT: 250 Beobachtungen für die Variablen... cm:
Wichtige Definitionen und Aussagen
 Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Mathematik für Naturwissenschaften, Teil 2
 Lösungsvorschläge für die Aufgaben zur Vorlesung Mathematik für Naturwissenschaften, Teil Zusatzblatt SS 09 Dr. J. Schürmann keine Abgabe Aufgabe : Eine Familie habe fünf Kinder. Wir nehmen an, dass die
Lösungsvorschläge für die Aufgaben zur Vorlesung Mathematik für Naturwissenschaften, Teil Zusatzblatt SS 09 Dr. J. Schürmann keine Abgabe Aufgabe : Eine Familie habe fünf Kinder. Wir nehmen an, dass die
Veranstaltung: Statistik für das Lehramt Dozent: Martin Tautenhahn Referenten: Belinda Höher, Thomas Holub, Maria Böhm.
 Veranstaltung: Statistik für das Lehramt 16.12.2016 Dozent: Martin Tautenhahn Referenten: Belinda Höher, Thomas Holub, Maria Böhm Erwartungswert Varianz Standardabweichung Die Wahrscheinlichkeitsverteilung
Veranstaltung: Statistik für das Lehramt 16.12.2016 Dozent: Martin Tautenhahn Referenten: Belinda Höher, Thomas Holub, Maria Böhm Erwartungswert Varianz Standardabweichung Die Wahrscheinlichkeitsverteilung
Lineare Regression. Volker Tresp
 Lineare Regression Volker Tresp 1 Die Lernmaschine: Das lineare Modell / ADALINE Wie beim Perzeptron wird zunächst die Aktivierungsfunktion gewichtete Summe der Eingangsgrößen x i berechnet zu h i = M
Lineare Regression Volker Tresp 1 Die Lernmaschine: Das lineare Modell / ADALINE Wie beim Perzeptron wird zunächst die Aktivierungsfunktion gewichtete Summe der Eingangsgrößen x i berechnet zu h i = M
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
Mathematik 2 Probeprüfung 1
 WWZ Wirtschaftswissenschaftliche Fakultät der Universität Basel Dr. Thomas Zehrt Bitte in Druckbuchstaben ausfüllen: Name Vorname Mathematik 2 Probeprüfung 1 Zeit: 90 Minuten, Maximale Punktzahl: 72 Zur
WWZ Wirtschaftswissenschaftliche Fakultät der Universität Basel Dr. Thomas Zehrt Bitte in Druckbuchstaben ausfüllen: Name Vorname Mathematik 2 Probeprüfung 1 Zeit: 90 Minuten, Maximale Punktzahl: 72 Zur
Vorlesung 8a. Kovarianz und Korrelation
 Vorlesung 8a Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X, Y ] := E [ (X EX)(Y EY ) ] Insbesondere
Vorlesung 8a Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X, Y ] := E [ (X EX)(Y EY ) ] Insbesondere
Dr. Maike M. Burda. Welchen Einfluss hat die Körperhöhe auf das Körpergewicht? Eine Regressionsanalyse. HU Berlin, Econ Bootcamp 7.-9.
 Dr. Maike M. Burda Welchen Einfluss hat die Körperhöhe auf das Körpergewicht? Eine Regressionsanalyse. HU Berlin, Econ Bootcamp 7.-9. Januar 2011 BOOTDATA11.GDT: 250 Beobachtungen für die Variablen...
Dr. Maike M. Burda Welchen Einfluss hat die Körperhöhe auf das Körpergewicht? Eine Regressionsanalyse. HU Berlin, Econ Bootcamp 7.-9. Januar 2011 BOOTDATA11.GDT: 250 Beobachtungen für die Variablen...
Eine zweidimensionale Stichprobe
 Eine zweidimensionale Stichprobe liegt vor, wenn zwei qualitative Merkmale gleichzeitig betrachtet werden. Eine Urliste besteht dann aus Wertepaaren (x i, y i ) R 2 und hat die Form (x 1, y 1 ), (x 2,
Eine zweidimensionale Stichprobe liegt vor, wenn zwei qualitative Merkmale gleichzeitig betrachtet werden. Eine Urliste besteht dann aus Wertepaaren (x i, y i ) R 2 und hat die Form (x 1, y 1 ), (x 2,
3.4 Asymptotische Evaluierung von Sch atzer Konsistenz Konsistenz Definition 3.4.1: konsistente Folge von Sch atzer
 3.4 Asymptotische Evaluierung von Schätzer 3.4.1 Konsistenz Bis jetzt haben wir Kriterien basierend auf endlichen Stichproben betrachtet. Konsistenz ist ein asymptotisches Kriterium (n ) und bezieht sich
3.4 Asymptotische Evaluierung von Schätzer 3.4.1 Konsistenz Bis jetzt haben wir Kriterien basierend auf endlichen Stichproben betrachtet. Konsistenz ist ein asymptotisches Kriterium (n ) und bezieht sich
70 Wichtige kontinuierliche Verteilungen
 70 Wichtige kontinuierliche Verteilungen 70. Motivation Zufallsvariablen sind nicht immer diskret, sie können oft auch jede beliebige reelle Zahl in einem Intervall [c, d] einnehmen. Beispiele für solche
70 Wichtige kontinuierliche Verteilungen 70. Motivation Zufallsvariablen sind nicht immer diskret, sie können oft auch jede beliebige reelle Zahl in einem Intervall [c, d] einnehmen. Beispiele für solche
Didaktisches Seminar über Stochastik. Themen: ffl Korrelation von zwei Zufallsvariablen
 Didaktisches Seminar über Stochastik Themen: ffl Gemeinsame Verteilung von zwei Zufallsvariablen ffl Lineare Regression ffl Korrelation von zwei Zufallsvariablen Michael Ralph Pape Mai 1998 1 1 GEMEINSAME
Didaktisches Seminar über Stochastik Themen: ffl Gemeinsame Verteilung von zwei Zufallsvariablen ffl Lineare Regression ffl Korrelation von zwei Zufallsvariablen Michael Ralph Pape Mai 1998 1 1 GEMEINSAME
Aufgabe 1 (8= Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten:
 Aufgabe 1 (8=2+2+2+2 Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten: Die Zufallsvariable X bezeichne die Note. 1443533523253. a) Wie groß ist h(x 5)? Kreuzen
Aufgabe 1 (8=2+2+2+2 Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten: Die Zufallsvariable X bezeichne die Note. 1443533523253. a) Wie groß ist h(x 5)? Kreuzen
Reelle Zufallsvariablen
 Kapitel 3 eelle Zufallsvariablen 3. Verteilungsfunktionen esultat aus der Maßtheorie: Zwischen der Menge aller W-Maße auf B, nennen wir sie W B ), und der Menge aller Verteilungsfunktionen auf, nennen
Kapitel 3 eelle Zufallsvariablen 3. Verteilungsfunktionen esultat aus der Maßtheorie: Zwischen der Menge aller W-Maße auf B, nennen wir sie W B ), und der Menge aller Verteilungsfunktionen auf, nennen
5. Spezielle stetige Verteilungen
 5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
2 Zufallsvariable und Verteilungsfunktionen
 8 2 Zufallsvariable und Verteilungsfunktionen Häufig ist es so, dass den Ausgängen eines Zufallexperiments, d.h. den Elementen der Ereignisalgebra, eine Zahl zugeordnet wird. Das wollen wir etwas mathematischer
8 2 Zufallsvariable und Verteilungsfunktionen Häufig ist es so, dass den Ausgängen eines Zufallexperiments, d.h. den Elementen der Ereignisalgebra, eine Zahl zugeordnet wird. Das wollen wir etwas mathematischer
1.5 Erwartungswert und Varianz
 Ziel: Charakterisiere Verteilungen von Zufallsvariablen durch Kenngrößen (in Analogie zu Lage- und Streuungsmaßen der deskriptiven Statistik). Insbesondere: a) durchschnittlicher Wert Erwartungswert, z.b.
Ziel: Charakterisiere Verteilungen von Zufallsvariablen durch Kenngrößen (in Analogie zu Lage- und Streuungsmaßen der deskriptiven Statistik). Insbesondere: a) durchschnittlicher Wert Erwartungswert, z.b.
5 Erwartungswerte, Varianzen und Kovarianzen
 47 5 Erwartungswerte, Varianzen und Kovarianzen Zur Charakterisierung von Verteilungen unterscheidet man Lageparameter, wie z. B. Erwartungswert ( mittlerer Wert ) Modus (Maximum der Wahrscheinlichkeitsfunktion,
47 5 Erwartungswerte, Varianzen und Kovarianzen Zur Charakterisierung von Verteilungen unterscheidet man Lageparameter, wie z. B. Erwartungswert ( mittlerer Wert ) Modus (Maximum der Wahrscheinlichkeitsfunktion,
Universität Basel Wirtschaftswissenschaftliches Zentrum. Zufallsvariablen. Dr. Thomas Zehrt
 Universität Basel Wirtschaftswissenschaftliches Zentrum Zufallsvariablen Dr. Thomas Zehrt Inhalt: 1. Einführung 2. Zufallsvariablen 3. Diskrete Zufallsvariablen 4. Stetige Zufallsvariablen 5. Erwartungswert
Universität Basel Wirtschaftswissenschaftliches Zentrum Zufallsvariablen Dr. Thomas Zehrt Inhalt: 1. Einführung 2. Zufallsvariablen 3. Diskrete Zufallsvariablen 4. Stetige Zufallsvariablen 5. Erwartungswert
Forschungsstatistik I
 Prof. Dr. G. Meinhardt 2. Stock, Nordflügel R. 02-429 (Persike) R. 02-431 (Meinhardt) Sprechstunde jederzeit nach Vereinbarung Forschungsstatistik I Dr. Malte Persike persike@uni-mainz.de http://psymet03.sowi.uni-mainz.de/
Prof. Dr. G. Meinhardt 2. Stock, Nordflügel R. 02-429 (Persike) R. 02-431 (Meinhardt) Sprechstunde jederzeit nach Vereinbarung Forschungsstatistik I Dr. Malte Persike persike@uni-mainz.de http://psymet03.sowi.uni-mainz.de/
1 Beispiel zur Methode der kleinsten Quadrate
 1 Beispiel zur Methode der kleinsten Quadrate 1.1 Daten des Beispiels t x y x*y x 2 ŷ ˆɛ ˆɛ 2 1 1 3 3 1 2 1 1 2 2 3 6 4 3.5-0.5 0.25 3 3 4 12 9 5-1 1 4 4 6 24 16 6.5-0.5 0.25 5 5 9 45 25 8 1 1 Σ 15 25
1 Beispiel zur Methode der kleinsten Quadrate 1.1 Daten des Beispiels t x y x*y x 2 ŷ ˆɛ ˆɛ 2 1 1 3 3 1 2 1 1 2 2 3 6 4 3.5-0.5 0.25 3 3 4 12 9 5-1 1 4 4 6 24 16 6.5-0.5 0.25 5 5 9 45 25 8 1 1 Σ 15 25
Kapitel 8. Parameter multivariater Verteilungen. 8.1 Erwartungswerte
 Kapitel 8 Parameter multivariater Verteilungen 8.1 Erwartungswerte Wir können auch bei mehrdimensionalen Zufallsvariablen den Erwartungswert betrachten. Dieser ist nichts anderes als der vektor der Erwartungswerte
Kapitel 8 Parameter multivariater Verteilungen 8.1 Erwartungswerte Wir können auch bei mehrdimensionalen Zufallsvariablen den Erwartungswert betrachten. Dieser ist nichts anderes als der vektor der Erwartungswerte
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen
 Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.)
 Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.) 1 Zusammenfassung Bedingte Verteilung: P (y x) = P (x, y) P (x) mit P (x) > 0 Produktsatz P (x, y) = P (x y)p (y) = P (y x)p (x) Kettenregel
Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.) 1 Zusammenfassung Bedingte Verteilung: P (y x) = P (x, y) P (x) mit P (x) > 0 Produktsatz P (x, y) = P (x y)p (y) = P (y x)p (x) Kettenregel
Probeklausur zu Mathematik 3 für Informatik Lösungshinweise (ohne Garantie auf Fehlefreiheit)
 Gunter Ochs 9. Juni 05 Probeklausur zu Mathematik für Informatik Lösungshinweise ohne Garantie auf Fehlefreiheit. Sei fx x x. a Bestimmen Sie den Grenzwert lim x fx. Da an der Stelle x Zähler Nenner Null
Gunter Ochs 9. Juni 05 Probeklausur zu Mathematik für Informatik Lösungshinweise ohne Garantie auf Fehlefreiheit. Sei fx x x. a Bestimmen Sie den Grenzwert lim x fx. Da an der Stelle x Zähler Nenner Null
0 für t < für 1 t < für 2 t < für 3 t < für 4 t < 5 1 für t 5
 4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
Ausgleichsproblem. Definition (1.0.3)
 Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Wahrscheinlichkeitstheorie und Statistik vom
 INSTITUT FÜR STOCHASTIK SS 2007 UNIVERSITÄT KARLSRUHE Priv.-Doz. Dr. D. Kadelka Dipl.-Math. oec. W. Lao Klausur (Maschineningenieure) Wahrscheinlichkeitstheorie und Statistik vom 2.9.2007 Musterlösungen
INSTITUT FÜR STOCHASTIK SS 2007 UNIVERSITÄT KARLSRUHE Priv.-Doz. Dr. D. Kadelka Dipl.-Math. oec. W. Lao Klausur (Maschineningenieure) Wahrscheinlichkeitstheorie und Statistik vom 2.9.2007 Musterlösungen
1.5 Erwartungswert und Varianz
 Ziel: Charakterisiere Verteilungen von Zufallsvariablen (Bildbereich also reelle Zahlen, metrische Skala) durch Kenngrößen (in Analogie zu Lage- und Streuungsmaßen der deskriptiven Statistik). Insbesondere:
Ziel: Charakterisiere Verteilungen von Zufallsvariablen (Bildbereich also reelle Zahlen, metrische Skala) durch Kenngrößen (in Analogie zu Lage- und Streuungsmaßen der deskriptiven Statistik). Insbesondere:
Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management
 Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management Sommersemester 2013 Hochschule Augsburg Lageparameter: Erwartungswert d) Erwartungswert
Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management Sommersemester 2013 Hochschule Augsburg Lageparameter: Erwartungswert d) Erwartungswert
Modellanpassung und Parameterschätzung. A: Übungsaufgaben
 7 Modellanpassung und Parameterschätzung 1 Kapitel 7: Modellanpassung und Parameterschätzung A: Übungsaufgaben [ 1 ] Bei n unabhängigen Wiederholungen eines Bernoulli-Experiments sei π die Wahrscheinlichkeit
7 Modellanpassung und Parameterschätzung 1 Kapitel 7: Modellanpassung und Parameterschätzung A: Übungsaufgaben [ 1 ] Bei n unabhängigen Wiederholungen eines Bernoulli-Experiments sei π die Wahrscheinlichkeit
6. Schätzverfahren für Parameter
 6. Schätzverfahren für Parameter Ausgangssituation: Ein interessierender Zufallsvorgang werde durch die ZV X repräsentiert X habe eine unbekannte Verteilungsfunktion F X (x) Wir interessieren uns für einen
6. Schätzverfahren für Parameter Ausgangssituation: Ein interessierender Zufallsvorgang werde durch die ZV X repräsentiert X habe eine unbekannte Verteilungsfunktion F X (x) Wir interessieren uns für einen
Vorlesung Wissensentdeckung
 Gliederung Vorlesung Wissensentdeckung Additive Modelle Katharina Morik, Weihs 1 Merkmalsauswahl Gütemaße und Fehlerabschätzung.6.015 1 von 33 von 33 Ausgangspunkt: Funktionsapproximation Aufteilen der
Gliederung Vorlesung Wissensentdeckung Additive Modelle Katharina Morik, Weihs 1 Merkmalsauswahl Gütemaße und Fehlerabschätzung.6.015 1 von 33 von 33 Ausgangspunkt: Funktionsapproximation Aufteilen der
Theorie Parameterschätzung Ausblick. Schätzung. Raimar Sandner. Studentenseminar "Statistische Methoden in der Physik"
 Studentenseminar "Statistische Methoden in der Physik" Gliederung 1 2 3 Worum geht es hier? Gliederung 1 2 3 Stichproben Gegeben eine Beobachtungsreihe x = (x 1, x 2,..., x n ): Realisierung der n-dimensionalen
Studentenseminar "Statistische Methoden in der Physik" Gliederung 1 2 3 Worum geht es hier? Gliederung 1 2 3 Stichproben Gegeben eine Beobachtungsreihe x = (x 1, x 2,..., x n ): Realisierung der n-dimensionalen
Regression ein kleiner Rückblick. Methodenseminar Dozent: Uwe Altmann Alexandra Kuhn, Melanie Spate
 Regression ein kleiner Rückblick Methodenseminar Dozent: Uwe Altmann Alexandra Kuhn, Melanie Spate 05.11.2009 Gliederung 1. Stochastische Abhängigkeit 2. Definition Zufallsvariable 3. Kennwerte 3.1 für
Regression ein kleiner Rückblick Methodenseminar Dozent: Uwe Altmann Alexandra Kuhn, Melanie Spate 05.11.2009 Gliederung 1. Stochastische Abhängigkeit 2. Definition Zufallsvariable 3. Kennwerte 3.1 für
Übung Teil 1: Einkommen, Lorenzkurven und Equity
 Vrlesung: Infrmatinsgesellschaft u. Glbalisierung I Dzent: Prf. Dr. Dr. F.-J. Radermacher Übung Teil 1: Einkmmen, Lrenzkurven und Equity Allgemeine Infrmatinen Die Übungen finden in 14-tägigem Rhythmus
Vrlesung: Infrmatinsgesellschaft u. Glbalisierung I Dzent: Prf. Dr. Dr. F.-J. Radermacher Übung Teil 1: Einkmmen, Lrenzkurven und Equity Allgemeine Infrmatinen Die Übungen finden in 14-tägigem Rhythmus
Übung zur Empirischen Wirtschaftsforschung V. Das Lineare Regressionsmodell
 Universität Ulm 89069 Ulm Germany Dipl.-WiWi Christian Peukert Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2010
Universität Ulm 89069 Ulm Germany Dipl.-WiWi Christian Peukert Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2010
Statistik. Sommersemester Prof. Dr. Stefan Etschberger HSA. für Betriebswirtschaft und International Management
 Statistik für Betriebswirtschaft und International Management Sommersemester 2014 Prof. Dr. Stefan Etschberger HSA Streuungsparameter Varianz Var(X) bzw. σ 2 : [x i E(X)] 2 f(x i ), wenn X diskret Var(X)
Statistik für Betriebswirtschaft und International Management Sommersemester 2014 Prof. Dr. Stefan Etschberger HSA Streuungsparameter Varianz Var(X) bzw. σ 2 : [x i E(X)] 2 f(x i ), wenn X diskret Var(X)
Taylorreihen. Kapitel 9. Lernziele. Taylorreihe. (x x 0 ) + f (x 0 ) 2! (x x 0 ) f (n) (x 0 ) (x x 0 ) n. Taylorreihe und MacLaurinreihe
 Kapitel 9 Taylorreihen Josef Leydold c 2006 Mathematische Methoden IX Taylorreihen 1 / 25 Lernziele Taylorreihe und MacLaurinreihe Beispiele Alternative Schreibweisen Approimation der Veränderung einer
Kapitel 9 Taylorreihen Josef Leydold c 2006 Mathematische Methoden IX Taylorreihen 1 / 25 Lernziele Taylorreihe und MacLaurinreihe Beispiele Alternative Schreibweisen Approimation der Veränderung einer
Statistik II. II. Univariates lineares Regressionsmodell. Martin Huber 1 / 20
 Statistik II II. Univariates lineares Regressionsmodell Martin Huber 1 / 20 Übersicht Definitionen (Wooldridge 2.1) Schätzmethode - Kleinste Quadrate Schätzer / Ordinary Least Squares (Wooldridge 2.2)
Statistik II II. Univariates lineares Regressionsmodell Martin Huber 1 / 20 Übersicht Definitionen (Wooldridge 2.1) Schätzmethode - Kleinste Quadrate Schätzer / Ordinary Least Squares (Wooldridge 2.2)
Beweis: Mit Hilfe des Satzes von der totalen Wahrscheinlichkeit folgt, dass
 Beweis: Mit Hilfe des Satzes von der totalen Wahrscheinlichkeit folgt, dass f Z (z) = Pr[Z = z] = x W X Pr[X + Y = z X = x] Pr[X = x] = x W X Pr[Y = z x] Pr[X = x] = x W X f X (x) f Y (z x). Den Ausdruck
Beweis: Mit Hilfe des Satzes von der totalen Wahrscheinlichkeit folgt, dass f Z (z) = Pr[Z = z] = x W X Pr[X + Y = z X = x] Pr[X = x] = x W X Pr[Y = z x] Pr[X = x] = x W X f X (x) f Y (z x). Den Ausdruck
Der metrische Raum (X, d) ist gegeben. Zeigen Sie, dass auch
 TECHNISCHE UNIVERSITÄT BERLIN SS 07 Institut für Mathematik Stand: 3. Juli 007 Ferus / Garcke Lösungsskizzen zur Klausur vom 6.07.07 Analysis II. Aufgabe (5 Punkte Der metrische Raum (X, d ist gegeben.
TECHNISCHE UNIVERSITÄT BERLIN SS 07 Institut für Mathematik Stand: 3. Juli 007 Ferus / Garcke Lösungsskizzen zur Klausur vom 6.07.07 Analysis II. Aufgabe (5 Punkte Der metrische Raum (X, d ist gegeben.
Zufallsvariable: Verteilungen & Kennzahlen
 Mathematik II für Biologen 12. Juni 2015 Zufallsvariable Kennzahlen: Erwartungswert Kennzahlen: Varianz Kennzahlen: Erwartungstreue Verteilungsfunktion Beispiel: Exponentialverteilung Kennzahlen: Erwartungswert
Mathematik II für Biologen 12. Juni 2015 Zufallsvariable Kennzahlen: Erwartungswert Kennzahlen: Varianz Kennzahlen: Erwartungstreue Verteilungsfunktion Beispiel: Exponentialverteilung Kennzahlen: Erwartungswert
15.5 Stetige Zufallsvariablen
 5.5 Stetige Zufallsvariablen Es gibt auch Zufallsvariable, bei denen jedes Elementarereignis die Wahrscheinlich keit hat. Beispiel: Lebensdauer eines radioaktiven Atoms Die Lebensdauer eines radioaktiven
5.5 Stetige Zufallsvariablen Es gibt auch Zufallsvariable, bei denen jedes Elementarereignis die Wahrscheinlich keit hat. Beispiel: Lebensdauer eines radioaktiven Atoms Die Lebensdauer eines radioaktiven
Numerische Methoden und Algorithmen in der Physik
 Numerische Methoden und Algorithmen in der Physik Hartmut Stadie, Christian Autermann 15.01.2009 Numerische Methoden und Algorithmen in der Physik Christian Autermann 1/ 47 Methode der kleinsten Quadrate
Numerische Methoden und Algorithmen in der Physik Hartmut Stadie, Christian Autermann 15.01.2009 Numerische Methoden und Algorithmen in der Physik Christian Autermann 1/ 47 Methode der kleinsten Quadrate
Sabrina Kallus, Eva Lotte Reinartz, André Salé
 Sabrina Kallus, Eva Lotte Reinartz, André Salé } Wiederholung (Zufallsvariable) } Erwartungswert Was ist das? } Erwartungswert: diskrete endliche Räume } Erwartungswert: Räume mit Dichten } Eigenschaften
Sabrina Kallus, Eva Lotte Reinartz, André Salé } Wiederholung (Zufallsvariable) } Erwartungswert Was ist das? } Erwartungswert: diskrete endliche Räume } Erwartungswert: Räume mit Dichten } Eigenschaften
Anpassungsrechnungen mit kleinsten Quadraten und Maximum Likelihood
 Anpassungsrechnungen mit kleinsten Quadraten und Maximum Likelihood Hauptseminar - Methoden der experimentellen Teilchenphysik WS 2011/2012 Fabian Hoffmann 2. Dezember 2011 Inhaltsverzeichnis 1 Einleitung
Anpassungsrechnungen mit kleinsten Quadraten und Maximum Likelihood Hauptseminar - Methoden der experimentellen Teilchenphysik WS 2011/2012 Fabian Hoffmann 2. Dezember 2011 Inhaltsverzeichnis 1 Einleitung
Bestimmte Zufallsvariablen sind von Natur aus normalverteilt. - naturwissenschaftliche Variablen: originär z.b. Intelligenz, Körpergröße, Messfehler
 6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
Nachklausur zur Vorlesung. Statistik für Studierende der Biologie
 Institut für Mathematische Stochastik WS 1999/2000 Universität Karlsruhe 11. Mai 2000 Dr. Bernhard Klar Nachklausur zur Vorlesung Statistik für Studierende der Biologie Bearbeitungszeit: 90 Minuten Name:
Institut für Mathematische Stochastik WS 1999/2000 Universität Karlsruhe 11. Mai 2000 Dr. Bernhard Klar Nachklausur zur Vorlesung Statistik für Studierende der Biologie Bearbeitungszeit: 90 Minuten Name:
18.2 Implizit definierte Funktionen
 18.2 Implizit definierte Funktionen Ziel: Untersuche Lösungsmengen von nichtlinearen Gleichungssystemen g(x) = 0 mit g : D R m, D R n, d.h. betrachte m Gleichungen für n Unbekannte mit m < n, d.h. wir
18.2 Implizit definierte Funktionen Ziel: Untersuche Lösungsmengen von nichtlinearen Gleichungssystemen g(x) = 0 mit g : D R m, D R n, d.h. betrachte m Gleichungen für n Unbekannte mit m < n, d.h. wir
Kapitel 3 Schließende Statistik
 Motivation Grundgesamtheit mit unbekannter Verteilung F Stichprobe X 1,...,X n mit Verteilung F Realisation x 1,...,x n der Stichprobe Rückschluss auf F Dr. Karsten Webel 160 Motivation (Fortsetzung) Kapitel
Motivation Grundgesamtheit mit unbekannter Verteilung F Stichprobe X 1,...,X n mit Verteilung F Realisation x 1,...,x n der Stichprobe Rückschluss auf F Dr. Karsten Webel 160 Motivation (Fortsetzung) Kapitel
Statistisches Testen
 Statistisches Testen Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Differenzen Anteilswert Chi-Quadrat Tests Gleichheit von Varianzen Prinzip des Statistischen Tests Konfidenzintervall
Statistisches Testen Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Differenzen Anteilswert Chi-Quadrat Tests Gleichheit von Varianzen Prinzip des Statistischen Tests Konfidenzintervall
Übung V Lineares Regressionsmodell
 Universität Ulm 89069 Ulm Germany Dipl.-WiWi Michael Alpert Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2007 Übung
Universität Ulm 89069 Ulm Germany Dipl.-WiWi Michael Alpert Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2007 Übung
Überbestimmte lineare Gleichungssysteme
 Überbestimmte lineare Gleichungssysteme Fakultät Grundlagen September 2009 Fakultät Grundlagen Überbestimmte lineare Gleichungssysteme Übersicht 1 2 Fakultät Grundlagen Überbestimmte lineare Gleichungssysteme
Überbestimmte lineare Gleichungssysteme Fakultät Grundlagen September 2009 Fakultät Grundlagen Überbestimmte lineare Gleichungssysteme Übersicht 1 2 Fakultät Grundlagen Überbestimmte lineare Gleichungssysteme
Zufallsvariablen [random variable]
![Zufallsvariablen [random variable] Zufallsvariablen [random variable]](/thumbs/52/29710821.jpg) Zufallsvariablen [random variable] Eine Zufallsvariable (Zufallsgröße) X beschreibt (kodiert) die Versuchsausgänge ω Ω mit Hilfe von Zahlen, d.h. X ist eine Funktion X : Ω R ω X(ω) Zufallsvariablen werden
Zufallsvariablen [random variable] Eine Zufallsvariable (Zufallsgröße) X beschreibt (kodiert) die Versuchsausgänge ω Ω mit Hilfe von Zahlen, d.h. X ist eine Funktion X : Ω R ω X(ω) Zufallsvariablen werden
7.5 Erwartungswert, Varianz
 7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
Erwartungswert und Varianz von Zufallsvariablen
 Kapitel 7 Erwartungswert und Varianz von Zufallsvariablen Im Folgenden sei (Ω, A, P ) ein Wahrscheinlichkeitsraum. Der Erwartungswert von X ist ein Lebesgue-Integral (allerdings allgemeiner als in Analysis
Kapitel 7 Erwartungswert und Varianz von Zufallsvariablen Im Folgenden sei (Ω, A, P ) ein Wahrscheinlichkeitsraum. Der Erwartungswert von X ist ein Lebesgue-Integral (allerdings allgemeiner als in Analysis
67 Zufallsvariable, Erwartungswert, Varianz
 67 Zufallsvariable, Erwartungswert, Varianz 67.1 Motivation Oft möchte man dem Resultat eines Zufallsexperiments eine reelle Zahl zuordnen. Der Gewinn bei einem Glücksspiel ist ein Beispiel hierfür. In
67 Zufallsvariable, Erwartungswert, Varianz 67.1 Motivation Oft möchte man dem Resultat eines Zufallsexperiments eine reelle Zahl zuordnen. Der Gewinn bei einem Glücksspiel ist ein Beispiel hierfür. In
Lernzettel Nr Definition eines Zufallsversuchs und die Begriffe rund um diesen
 - Definitin eines Zufallsversuchs und die Begriffe rund um diesen Begriff Bedeutung / Beispiel / Frmel Stichprbe Zufällige entnahme einer kleinen Menge aus einer grßen Menge (Klasse) Merkmal Ist charakteristisches
- Definitin eines Zufallsversuchs und die Begriffe rund um diesen Begriff Bedeutung / Beispiel / Frmel Stichprbe Zufällige entnahme einer kleinen Menge aus einer grßen Menge (Klasse) Merkmal Ist charakteristisches
Kapitel 6. Verteilungsparameter. 6.1 Der Erwartungswert Diskrete Zufallsvariablen
 Kapitel 6 Verteilungsparameter Wie bei einem Merkmal wollen wir nun die Lage und die Streuung der Verteilung einer diskreten Zufallsvariablen durch geeignete Maßzahlen beschreiben. Beginnen wir mit Maßzahlen
Kapitel 6 Verteilungsparameter Wie bei einem Merkmal wollen wir nun die Lage und die Streuung der Verteilung einer diskreten Zufallsvariablen durch geeignete Maßzahlen beschreiben. Beginnen wir mit Maßzahlen
Textmining Klassifikation von Texten Teil 2: Im Vektorraummodell
 Textmining Klassifikation von Texten Teil 2: Im Vektorraummodell Dept. Informatik 8 (Künstliche Intelligenz) Friedrich-Alexander-Universität Erlangen-Nürnberg (Informatik 8) Klassifikation von Texten Teil
Textmining Klassifikation von Texten Teil 2: Im Vektorraummodell Dept. Informatik 8 (Künstliche Intelligenz) Friedrich-Alexander-Universität Erlangen-Nürnberg (Informatik 8) Klassifikation von Texten Teil
Musterlösung. Modulklausur Multivariate Verfahren
 Musterlösung Modulklausur 31821 Multivariate Verfahren 25. September 2015 Aufgabe 1 (15 Punkte) Kennzeichnen Sie die folgenden Aussagen zur Regressionsanalyse mit R für richtig oder F für falsch. F Wenn
Musterlösung Modulklausur 31821 Multivariate Verfahren 25. September 2015 Aufgabe 1 (15 Punkte) Kennzeichnen Sie die folgenden Aussagen zur Regressionsanalyse mit R für richtig oder F für falsch. F Wenn
Lösungen zur Klausur GRUNDLAGEN DER WAHRSCHEINLICHKEITSTHEORIE UND STATISTIK
 Institut für Stochastik Dr. Steffen Winter Lösungen zur Klausur GRUNDLAGEN DER WAHRSCHEINLICHKEITSTHEORIE UND STATISTIK für Studierende der INFORMATIK vom 17. Juli 01 (Dauer: 90 Minuten) Übersicht über
Institut für Stochastik Dr. Steffen Winter Lösungen zur Klausur GRUNDLAGEN DER WAHRSCHEINLICHKEITSTHEORIE UND STATISTIK für Studierende der INFORMATIK vom 17. Juli 01 (Dauer: 90 Minuten) Übersicht über
Klassifikation von Daten Einleitung
 Klassifikation von Daten Einleitung Lehrstuhl für Künstliche Intelligenz Institut für Informatik Friedrich-Alexander-Universität Erlangen-Nürnberg (Lehrstuhl Informatik 8) Klassifikation von Daten Einleitung
Klassifikation von Daten Einleitung Lehrstuhl für Künstliche Intelligenz Institut für Informatik Friedrich-Alexander-Universität Erlangen-Nürnberg (Lehrstuhl Informatik 8) Klassifikation von Daten Einleitung
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 11. November 2010 1 Erwartungswert und Varianz Erwartungswert Varianz und Streuung Rechenregeln Binomialverteilung
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 11. November 2010 1 Erwartungswert und Varianz Erwartungswert Varianz und Streuung Rechenregeln Binomialverteilung
Varianz und Kovarianz
 KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik. PD Dr. U. Ludwig. Vorlesung 7 1 / 19
 Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik PD Dr. U. Ludwig Vorlesung 7 1 / 19 2.2 Erwartungswert, Varianz und Standardabweichung (Fortsetzung) 2 / 19 Bedingter Erwartungswert
Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik PD Dr. U. Ludwig Vorlesung 7 1 / 19 2.2 Erwartungswert, Varianz und Standardabweichung (Fortsetzung) 2 / 19 Bedingter Erwartungswert
Rückblick auf die letzte Vorlesung. Bemerkung
 Bemerkung 1) Die Bedingung grad f (x 0 ) = 0 T definiert gewöhnlich ein nichtlineares Gleichungssystem zur Berechnung von x = x 0, wobei n Gleichungen für n Unbekannte gegeben sind. 2) Die Punkte x 0 D
Bemerkung 1) Die Bedingung grad f (x 0 ) = 0 T definiert gewöhnlich ein nichtlineares Gleichungssystem zur Berechnung von x = x 0, wobei n Gleichungen für n Unbekannte gegeben sind. 2) Die Punkte x 0 D
4. Verteilungen von Funktionen von Zufallsvariablen
 4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
Finanzmathematische Modelle und Simulation
 Finanzmathematische Modelle und Simulation WS 9/1 Rebecca Henkelmann In meiner Ausarbeitung Grundbegriffe der Stochastik I, geht es darum die folgenden Begriffe für die nächsten Kapitel einzuführen. Auf
Finanzmathematische Modelle und Simulation WS 9/1 Rebecca Henkelmann In meiner Ausarbeitung Grundbegriffe der Stochastik I, geht es darum die folgenden Begriffe für die nächsten Kapitel einzuführen. Auf
1 Multivariate Zufallsvariablen
 1 Multivariate Zufallsvariablen 1.1 Multivariate Verteilungen Definition 1.1. Zufallsvariable, Zufallsvektor (ZV) Sei Ω die Ergebnismenge eines Zufallsexperiments. Eine (univariate oder eindimensionale)
1 Multivariate Zufallsvariablen 1.1 Multivariate Verteilungen Definition 1.1. Zufallsvariable, Zufallsvektor (ZV) Sei Ω die Ergebnismenge eines Zufallsexperiments. Eine (univariate oder eindimensionale)
2 Zufallsvariable, Verteilungen, Erwartungswert
 2 Zufallsvariable, Verteilungen, Erwartungswert Bisher: Zufallsexperimente beschrieben durch W-Räume (Ω, A, P) Häufig interessiert nur eine zufällige Größe X = X(ω), die vom Ergebnis ω des Zufallsexperiments
2 Zufallsvariable, Verteilungen, Erwartungswert Bisher: Zufallsexperimente beschrieben durch W-Räume (Ω, A, P) Häufig interessiert nur eine zufällige Größe X = X(ω), die vom Ergebnis ω des Zufallsexperiments
Übungsblatt 9 (25. bis 29. Juni)
 Statistik 2 Dr. Andrea Beccarini Dipl.-Vw. Dipl.-Kffr. Heike Bornewasser-Hermes Sommersemester 2012 Übungsblatt 9 (25. bis 29. Juni) Stetiges Verteilungsmodell und Gemeinsame Verteilung Stetiges Verteilungsmodell
Statistik 2 Dr. Andrea Beccarini Dipl.-Vw. Dipl.-Kffr. Heike Bornewasser-Hermes Sommersemester 2012 Übungsblatt 9 (25. bis 29. Juni) Stetiges Verteilungsmodell und Gemeinsame Verteilung Stetiges Verteilungsmodell
Einführung in die Maximum Likelihood Methodik
 in die Maximum Likelihood Methodik Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Gliederung 1 2 3 4 2 / 31 Maximum Likelihood
in die Maximum Likelihood Methodik Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Gliederung 1 2 3 4 2 / 31 Maximum Likelihood
DWT 2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen 330/467 Ernst W. Mayr
 2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen Wir betrachten nun ein Verfahren zur Konstruktion von Schätzvariablen für Parameter von Verteilungen. Sei X = (X 1,..., X n ). Bei X
2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen Wir betrachten nun ein Verfahren zur Konstruktion von Schätzvariablen für Parameter von Verteilungen. Sei X = (X 1,..., X n ). Bei X
Deskription, Statistische Testverfahren und Regression. Seminar: Planung und Auswertung klinischer und experimenteller Studien
 Deskription, Statistische Testverfahren und Regression Seminar: Planung und Auswertung klinischer und experimenteller Studien Deskriptive Statistik Deskriptive Statistik: beschreibende Statistik, empirische
Deskription, Statistische Testverfahren und Regression Seminar: Planung und Auswertung klinischer und experimenteller Studien Deskriptive Statistik Deskriptive Statistik: beschreibende Statistik, empirische
4.1. Verteilungsannahmen des Fehlers. 4. Statistik im multiplen Regressionsmodell Verteilungsannahmen des Fehlers
 4. Statistik im multiplen Regressionsmodell In diesem Kapitel wird im Abschnitt 4.1 zusätzlich zu den schon bekannten Standardannahmen noch die Annahme von normalverteilten Residuen hinzugefügt. Auf Basis
4. Statistik im multiplen Regressionsmodell In diesem Kapitel wird im Abschnitt 4.1 zusätzlich zu den schon bekannten Standardannahmen noch die Annahme von normalverteilten Residuen hinzugefügt. Auf Basis
Eindimensionale Zufallsvariablen
 Eindimensionale Grundbegriffe Verteilungstypen Diskrete Stetige Spezielle Maßzahlen für eindimensionale Erwartungswert Varianz Standardabweichung Schwankungsintervalle Bibliografie Bleymüller / Gehlert
Eindimensionale Grundbegriffe Verteilungstypen Diskrete Stetige Spezielle Maßzahlen für eindimensionale Erwartungswert Varianz Standardabweichung Schwankungsintervalle Bibliografie Bleymüller / Gehlert
Statistik II. II. Univariates lineares Regressionsmodell. Martin Huber 1 / 27
 Statistik II II. Univariates lineares Regressionsmodell Martin Huber 1 / 27 Übersicht Definitionen (Wooldridge 2.1) Schätzmethode - Kleinste Quadrate Schätzer / Ordinary Least Squares (Wooldridge 2.2)
Statistik II II. Univariates lineares Regressionsmodell Martin Huber 1 / 27 Übersicht Definitionen (Wooldridge 2.1) Schätzmethode - Kleinste Quadrate Schätzer / Ordinary Least Squares (Wooldridge 2.2)
Die Familie der χ 2 (n)-verteilungen
 Die Familie der χ (n)-verteilungen Sind Z 1,..., Z m für m 1 unabhängig identisch standardnormalverteilte Zufallsvariablen, so genügt die Summe der quadrierten Zufallsvariablen χ := m Z i = Z 1 +... +
Die Familie der χ (n)-verteilungen Sind Z 1,..., Z m für m 1 unabhängig identisch standardnormalverteilte Zufallsvariablen, so genügt die Summe der quadrierten Zufallsvariablen χ := m Z i = Z 1 +... +
7.2 Moment und Varianz
 7.2 Moment und Varianz Def. 21 Es sei X eine zufällige Variable. Falls der Erwartungswert E( X p ) existiert, heißt der Erwartungswert EX p p tes Moment der zufälligen Variablen X. Es gilt dann: + x p
7.2 Moment und Varianz Def. 21 Es sei X eine zufällige Variable. Falls der Erwartungswert E( X p ) existiert, heißt der Erwartungswert EX p p tes Moment der zufälligen Variablen X. Es gilt dann: + x p
Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 2016
 Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 1 M. Sperber (matthias.sperber@kit.edu) S. Nguyen (thai.nguyen@kit.edu) Übungsblatt 3 Maschinelles Lernen und Klassifikation Abgabe online
Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 1 M. Sperber (matthias.sperber@kit.edu) S. Nguyen (thai.nguyen@kit.edu) Übungsblatt 3 Maschinelles Lernen und Klassifikation Abgabe online
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert
 Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Die Funktion f X;Y (x; y) := Pr[X = x; Y = y] heit gemeinsame Dichte der Zufallsvariablen X und Y. Aus der gemeinsamen Dichte f X;Y kann man ableiten
![Die Funktion f X;Y (x; y) := Pr[X = x; Y = y] heit gemeinsame Dichte der Zufallsvariablen X und Y. Aus der gemeinsamen Dichte f X;Y kann man ableiten Die Funktion f X;Y (x; y) := Pr[X = x; Y = y] heit gemeinsame Dichte der Zufallsvariablen X und Y. Aus der gemeinsamen Dichte f X;Y kann man ableiten](/thumbs/71/64227736.jpg) Die Funktion f ;Y (x; y) := Pr[ = x; Y = y] heit gemeinsame Dichte der Zufallsvariablen und Y. Aus der gemeinsamen Dichte f ;Y kann man ableiten f (x) = y2w Y f ;Y (x; y) bzw. f Y (y) = Die Funktionen
Die Funktion f ;Y (x; y) := Pr[ = x; Y = y] heit gemeinsame Dichte der Zufallsvariablen und Y. Aus der gemeinsamen Dichte f ;Y kann man ableiten f (x) = y2w Y f ;Y (x; y) bzw. f Y (y) = Die Funktionen
Support Vector Machines (SVM)
 Universität Ulm 12. Juni 2007 Inhalt 1 2 3 Grundlegende Idee Der Kern-Trick 4 5 Multi-Klassen-Einteilung Vor- und Nachteile der SVM 1 2 3 Grundlegende Idee Der Kern-Trick 4 5 Multi-Klassen-Einteilung Vor-
Universität Ulm 12. Juni 2007 Inhalt 1 2 3 Grundlegende Idee Der Kern-Trick 4 5 Multi-Klassen-Einteilung Vor- und Nachteile der SVM 1 2 3 Grundlegende Idee Der Kern-Trick 4 5 Multi-Klassen-Einteilung Vor-
Analysis II 14. Übungsblatt
 Jun.-Prof. PD Dr. D. Mugnolo Wintersemester 01/13 F. Stoffers 04. Februar 013 Analysis II 14. Übungsblatt 1. Aufgabe (8 Punkte Man beweise: Die Gleichung z 3 + z + xy = 1 besitzt für jedes (x, y R genau
Jun.-Prof. PD Dr. D. Mugnolo Wintersemester 01/13 F. Stoffers 04. Februar 013 Analysis II 14. Übungsblatt 1. Aufgabe (8 Punkte Man beweise: Die Gleichung z 3 + z + xy = 1 besitzt für jedes (x, y R genau
Korrelation und Regression
 FB 1 W. Ludwig-Mayerhofer und 1 und FB 1 W. Ludwig-Mayerhofer und 2 Mit s- und sanalyse werden Zusammenhänge zwischen zwei metrischen Variablen analysiert. Wenn man nur einen Zusammenhang quantifizieren
FB 1 W. Ludwig-Mayerhofer und 1 und FB 1 W. Ludwig-Mayerhofer und 2 Mit s- und sanalyse werden Zusammenhänge zwischen zwei metrischen Variablen analysiert. Wenn man nur einen Zusammenhang quantifizieren
Statistik III. Walter Zucchini Fred Böker Andreas Stadie
 Statistik III Walter Zucchini Fred Böker Andreas Stadie Inhaltsverzeichnis 1 Zufallsvariablen und ihre Verteilung 1 1.1 Diskrete Zufallsvariablen........................... 1 1.2 Stetige Zufallsvariablen............................
Statistik III Walter Zucchini Fred Böker Andreas Stadie Inhaltsverzeichnis 1 Zufallsvariablen und ihre Verteilung 1 1.1 Diskrete Zufallsvariablen........................... 1 1.2 Stetige Zufallsvariablen............................
Einfache lineare Modelle mit Statistik-Software R Beispiel (Ausgaben in Abhängigkeit vom Einkommen)
 3 Einfache lineare Regression Einfache lineare Modelle mit R 36 Einfache lineare Modelle mit Statistik-Software R Beispiel (Ausgaben in Abhängigkeit vom Einkommen) > summary(lm(y~x)) Call: lm(formula =
3 Einfache lineare Regression Einfache lineare Modelle mit R 36 Einfache lineare Modelle mit Statistik-Software R Beispiel (Ausgaben in Abhängigkeit vom Einkommen) > summary(lm(y~x)) Call: lm(formula =
Die folgende Grafik zeigt eine Übergangsmatrix mit zugehörigem Graph: Geben Sie analog zu den folgenden Graphen jeweils eine Transitionsmatrix an.
 Stephan Peter Wirtschaftsingenieurwesen SS 2017 Mathematik II Serie 2 Matrizen II Aufgabe 1 Die flgende Grafik zeigt eine Übergangsmatrix mit zugehörigem Graph: a) Geben Sie analg zu den flgenden Graphen
Stephan Peter Wirtschaftsingenieurwesen SS 2017 Mathematik II Serie 2 Matrizen II Aufgabe 1 Die flgende Grafik zeigt eine Übergangsmatrix mit zugehörigem Graph: a) Geben Sie analg zu den flgenden Graphen
Softwaretechnik. Prof. Dr. Rainer Koschke. Fachbereich Mathematik und Informatik Arbeitsgruppe Softwaretechnik Universität Bremen
 Softwaretechnik Prof. Dr. Rainer Koschke Fachbereich Mathematik und Informatik Arbeitsgruppe Softwaretechnik Universität Bremen Wintersemester 2010/11 Überblick I Statistik bei kontrollierten Experimenten
Softwaretechnik Prof. Dr. Rainer Koschke Fachbereich Mathematik und Informatik Arbeitsgruppe Softwaretechnik Universität Bremen Wintersemester 2010/11 Überblick I Statistik bei kontrollierten Experimenten
1 Diskriminanzanalyse
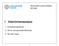 Multivariate Lineare Modelle SS 2008 1 Diskriminanzanalyse 1. Entscheidungstheorie 2. DA für normalverteilte Merkmale 3. DA nach Fisher 1 Problemstellungen Jedes Subjekt kann einer von g Gruppen angehören
Multivariate Lineare Modelle SS 2008 1 Diskriminanzanalyse 1. Entscheidungstheorie 2. DA für normalverteilte Merkmale 3. DA nach Fisher 1 Problemstellungen Jedes Subjekt kann einer von g Gruppen angehören
Wahrscheinlichkeitstheorie und Statistik für Studierende des Maschinenbaus vom
 Institut für Stochastik WS 009/10 Karlsruher Institut für Technologie (KIT) Dr. B. Klar Klausur Wahrscheinlichkeitstheorie und Statistik für Studierende des Maschinenbaus vom 08.0.010 Musterlösungen Aufgabe
Institut für Stochastik WS 009/10 Karlsruher Institut für Technologie (KIT) Dr. B. Klar Klausur Wahrscheinlichkeitstheorie und Statistik für Studierende des Maschinenbaus vom 08.0.010 Musterlösungen Aufgabe
2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung
 2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung Die einfachste Verteilung ist die Gleichverteilung, bei der P(X = x i ) = 1/N gilt, wenn N die Anzahl möglicher Realisierungen von
2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung Die einfachste Verteilung ist die Gleichverteilung, bei der P(X = x i ) = 1/N gilt, wenn N die Anzahl möglicher Realisierungen von
Klausur zur Mathematik für Biologen
 Mathematisches Institut der Heinrich-Heine-Universität DÜSSELDORF WS 2002/2003 12.02.2003 (1) Prof. Dr. A. Janssen / Dr. H. Weisshaupt Klausur zur Mathematik für Biologen Bitte füllen Sie das Deckblatt
Mathematisches Institut der Heinrich-Heine-Universität DÜSSELDORF WS 2002/2003 12.02.2003 (1) Prof. Dr. A. Janssen / Dr. H. Weisshaupt Klausur zur Mathematik für Biologen Bitte füllen Sie das Deckblatt
