Darstellungsarten für 3D-Körper. Boundary Representation (BRep):
|
|
|
- Renate Christin Franke
- vor 6 Jahren
- Abrufe
Transkript
1 Darstellungsarten für 3D-Körper Boundary Representation (BRep): Darstellung eines (verallgemeinerten) Polyeders durch das System seiner Ecken, Kanten und Facetten Abspeichern durch (Teilgraphen des) vef-graphen (siehe vorangegangener Abschnitt) verschiedene Varianten möglich oft durch Eckenindex-Listen (vgl. VRML IndexedFaceSet-Knoten) Orientierung der Facetten wichtig fürs Rendering!
2 Zellmodelle 1. Nomzellen-Aufzählungsschema 2. Zellzerlegungsschema 3. Oktalbäume (Quadtrees und Octrees) 4. BSP-Trees Normzellen-Aufzählungsschema (auch: Voxel-Modelle; SOE = spatial occupancy enumeration) Ein Körper wird durch eine Menge von gleichgroßen dreidimensionalen Zellen dargestellt (meist Würfel der Kantenlänge h). Eine Zelle wird dabei durch die Koordinaten ihres Mittelpunktes repräsentiert. Voxel = volume pixel ("3D-Pixel"). Kriterium: Liegt der Mittelpunkt einer Zelle im Körper oder nicht? Alle Zellen, deren Mittelpunkt im Körper liegen, ergeben eine Liste von Zellen bzw. eine Bit-Matrix. Genauigkeit: abhängig von der Kantenlänge h, dem zur Verfügung stehenden Speicherplatzressourcen, der Beschaffenheit der Begrenzungsflächen des Körpers (eben oder gekrümmt). bei sehr hohem Speicherplatzbedarf Methoden der Lauflängencodierung für die Bit-Matrix verwendet. Vorteil: die einzelnen Voxel können mit zusätzlichen Parametern (Temperatur, Stoffkonzentrationen usw.) versehen und entsprechend eingefärbt werden. Anwendung u.a. in der medizinischen Visualisierung.
3 Zellzerlegungsschema: Hier erfolgt die Modellierung eines Körpers aus (parametrisierten) Grundobjekten mittels Vereinigung ("Klebeoperationen"). Grundkörper: quaderförmig, eben berandet, aber auch gekrümmte Kanten/Flächen. Für einen gegebenen Körper sind verschiedene Repräsentationen möglich (keine Eindeutigkeit): Oktalbäume (Octrees): Anwendung eines hierarchischen und rekursiven Oktalbaumschemas 1. ein den ganzen Körper umschließender Würfel wird gewählt 2. rekursiv wird dieser Würfel in Teilwürfel halber Kantenlänge geteilt, bis ein Teilwürfel entweder ganz im Körper oder ganz außerhalb des Körpers liegt. Abbruch, wenn alle Teilwürfel im oder außerhalb des Körpers liegen oder die vorgegebene kleinste Kantenlänge erreicht ist. Beispiel: Quadtree (= 2D-Version der Datenstruktur) der Tiefe 3 für ein einfaches Objekt
4 weitere Beispiele:
5
6 Boolesche Operationen mit Quadtrees: Oktalbäume sind im Speicherplatzbedarf oft eine Ordnung effizienter als Normzellen- Aufzählungsschemen. Sie liefern einen eindeutigen Repräsentanten des vorgegebenen Körpers.
7 Zusammenfassung: Zellmodelle oft bei Finite Elemente-Methoden benutzt Nachteilig ist, dass nur Körper sehr genau beschrieben werden können, deren Oberflächen parallel zu den Würfeln (Voxel) liegen. Binary Space Partitioning - Bäume (BSP Trees): Statt in Octrees zu zerlegen, wird eine binäre Raumaufteilung gewählt, dabei werden die Baumknoten nicht in acht Oktanten, sondern in zwei Hälften aufgeteilt. Das kann sukzessive in x,y,z-richtung erfolgen. Eine Ebene mit beliebiger Richtung, Orientierung und Lage wird zur Trennung in Teilbäume benutzt. Jeder Knoten besitzt dann eine Flächengleichung und zwei Zeiger auf die beiden Halbräume H1 und H2. Der Normalenvektor der Ebene zeigt dabei meist auf das Äußere des H2- Halbraumes. Wird der Knoten nicht mehr unterteilt, entsteht ein Blatt, das einen Teil repräsentiert, der entweder ganz innen oder ganz außen zum Objekt liegt.
8
9
10 CSG (Constructive Solid Geometry) - Modelle Modellierung entspricht der Vorgehensweise beim Konstruieren von Körpern Körper werden durch regularisierte Mengenoperationen aus vorgegebenen Grundkörpern gebildet Definition für regularisierte Mengenoperationen: A op* B = abgeschlossene Hülle (Inneres (A op B ))
11 Die Darstellung erfolgt als Binärbaum: Primitive = Blätter Operatoren = Knoten Für die geeigneten Grundkörper gilt als Eignungskriterium: Mengenberechnungen müssen schnell und effizient erfolgen können (Würfel, Zylinder, Halbraummodelle, Boundary- Modelle) Bei CSG- Bäumen können verschiedene Bäume den gleichen Körper repräsentieren Beisp.: Bildung eines Werkstückes aus Quadern und Zylindern weiteres Beisp.:
12 Nicht-Eindeutigkeit der CSG-Darstellung:
13 In einem CSG-Baum wird die Geometrie von Kanten und Flächen nicht im Baum abgespeichert! Sie muss erst aus dem Baum ermittelt werden. Klassifikation einer Menge M bezogen auf ein CSG-Objekt Q: M: M in Q oder M auf Q oder M aus Q Menge von Menge von Menge von Punkten, Punkten, die in Q Punkten, die auf die außerhalb von Q liegen dem Rand von Q liegen liegen Das muss auf der Ebene der Primitive berechnet werden, da nur sie die Geometriewerte enthalten. Dazu wird der Baum rekursiv bis zu den Primitiven durchlaufen, dann dort die Berechnung für ein Primitiv durchgeführt. Das Teilergebnis wird mit Hilfe der Operatoren (Knoten im Baum) wieder sukzessive zusammengesetzt, bis das Ergebnis für das Gesamtobjekt vorliegt. Genau diese aufwändige Operation begrenzt die Einsatzgebiete. Bei direkten Displayalgorithmen wird daher oft keine vollständige Konvertierung eines CSG- Baumes in eine Boundary -Repräsentation durchgeführt. Hybridmodelle: Grundidee: Jedes Modell ist nur für bestimmte Einsatzzwecke gut, für andere wiederum nicht. Konstruktion: CSG-Darstellung gut wegen Boolescher Operationen. schnelle Visualisierung : Boundary- Repräsentationen (BRep) besser, da keine Neuauswertungen des CSG Baumes nach affinen Transformationen nötig sind.
14 Konvertierungsalgorithmen : CSG----- > BRep-Modellierer von nach----- > CSG BOUNDARY ZELLMODELLE CSG X gelöst einfach/approximativ BOUNDARY nicht gelöst X einfach/approximativ ZELL nicht gelöst nicht gelöst X Beachte: Rückkonvertierungen bei approximativen Konvertierungen sind nicht sinnvoll! Oft ist es schwierig, dabei die Konsistenz zwischen den verschiedenen Repräsentationen zu erhalten oft nur für bestimmte Objekte und nicht in allen Phasen gewährleistet!
15 weitere Modellierungs-Ansätze: Sweep-Körper (Extrusion) Es werden Körper durch eine Fläche (Grundfläche) und eine Transformationsvorschrift (Erzeugende) beschrieben. Aus einem Kreis als Grundfläche und einer erzeugenden senkrechten Linie im Mittelpunkt des Kreises entsteht durch Translation in Richtung der Linie ein Zylinder.
16 Kombination mit Skalierungsoperationen (entlang der Sweep- Kurve) und mit Rotationen möglich (vgl. Extrusion-Knoten in VRML). Flächeninterpolation lineare Interpolation zwischen zwei Flächenstücken.
12. Modelle für 3D-Objekte und -Szenen
 12. Modelle für 3D-Objekte und -Szenen Modell: Abbild der Realität, welches bestimmte Aspekte der Realität repräsentiert (und andere ausblendet) mathematische Modelle symbolische Modelle Datenmodelle Experimentalmodelle
12. Modelle für 3D-Objekte und -Szenen Modell: Abbild der Realität, welches bestimmte Aspekte der Realität repräsentiert (und andere ausblendet) mathematische Modelle symbolische Modelle Datenmodelle Experimentalmodelle
Geometrierepräsentation
 Geometrierepräsentation Forderungen an Repräsentationsform: 1. mächtig (eine sinnvolle Menge von Objekten modellierbar) 2. eindeutig (es muß klar sein, was repräsentiert wird) H E D A F G C B Punkte, Linien,
Geometrierepräsentation Forderungen an Repräsentationsform: 1. mächtig (eine sinnvolle Menge von Objekten modellierbar) 2. eindeutig (es muß klar sein, was repräsentiert wird) H E D A F G C B Punkte, Linien,
3D - Modellierung. Arne Theß. Proseminar Computergraphik TU Dresden
 3D - Modellierung Arne Theß Proseminar Computergraphik TU Dresden Gliederung Darstellungsschemata direkte Constructive Solid Geometry (CSG) Generative Modellierung Voxelgitter indirekte Drahtgittermodell
3D - Modellierung Arne Theß Proseminar Computergraphik TU Dresden Gliederung Darstellungsschemata direkte Constructive Solid Geometry (CSG) Generative Modellierung Voxelgitter indirekte Drahtgittermodell
Geometrische Modellierung mittels Oktalbäumen und Visualisierung von Simulationsdaten aus der Strömungsmechanik. Klaus Daubner
 Geometrische Modellierung mittels Oktalbäumen und Visualisierung von Simulationsdaten aus der Strömungsmechanik Klaus Daubner 1 / 22 Übersicht Motivation Geometriemodelle Oberflächenmodelle Volumenmodelle
Geometrische Modellierung mittels Oktalbäumen und Visualisierung von Simulationsdaten aus der Strömungsmechanik Klaus Daubner 1 / 22 Übersicht Motivation Geometriemodelle Oberflächenmodelle Volumenmodelle
Modellierungsmethoden
 Modellierungsmethoden Definition (smethoden) smethoden fassen verschiedene Beschreibungsmittel, insbesondere Datenstrukturen und Operationen, für geometrische Objekte zusammen. Äquivalente Begriffe: Geometrische
Modellierungsmethoden Definition (smethoden) smethoden fassen verschiedene Beschreibungsmittel, insbesondere Datenstrukturen und Operationen, für geometrische Objekte zusammen. Äquivalente Begriffe: Geometrische
CSG (constructive solid geometry) mit mengentheoretischer Verknüpfung von Elementarobjekten.
 Kapitel 16 3D-Repräsentation Für 3-dimensionale Objekte gibt es mehrere Möglichkeiten der Repräsentation (d.h. Definition des Objekts) und der Darstellung (d.h. Projektion des Objekts auf den Bildschirm
Kapitel 16 3D-Repräsentation Für 3-dimensionale Objekte gibt es mehrere Möglichkeiten der Repräsentation (d.h. Definition des Objekts) und der Darstellung (d.h. Projektion des Objekts auf den Bildschirm
Algorithmen und Datenstrukturen Bereichsbäume
 Algorithmen und Datenstrukturen Bereichsbäume Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Überblick Einführung k-d Baum BSP Baum R Baum Motivation
Algorithmen und Datenstrukturen Bereichsbäume Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Überblick Einführung k-d Baum BSP Baum R Baum Motivation
8. Modelle für feste Körper
 8. Modelle für feste Körper Modell: Abbild der Realität, welches bestimmte Aspekte der Realität repräsentiert (und andere ausblendet) mathematische Modelle symbolische Modelle Datenmodelle Experimentalmodelle
8. Modelle für feste Körper Modell: Abbild der Realität, welches bestimmte Aspekte der Realität repräsentiert (und andere ausblendet) mathematische Modelle symbolische Modelle Datenmodelle Experimentalmodelle
Boolesche Operationen und lokale Manipulationen
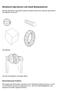 1 Boolesche Operationen und lokale Manipulationen Mit Hilfe Boolescher Operatoren werden komplexe Körper aus Instanzen generischer Grundkörper konstruiert.. Grundkörper Aus den Grundkörpern erzeugter Körper
1 Boolesche Operationen und lokale Manipulationen Mit Hilfe Boolescher Operatoren werden komplexe Körper aus Instanzen generischer Grundkörper konstruiert.. Grundkörper Aus den Grundkörpern erzeugter Körper
Seminar Computerspiele Räumliche Datenstrukturen. Ralf Pramberger
 Seminar Computerspiele Räumliche Datenstrukturen Ralf Pramberger Themen 2 1. Grundlagen Szene Sichtbarkeit (Raytracing) Culling 2. Räumliche Datenstrukturen Bounding Volume Hierarchie Quadtree/Octree BSP-Tree
Seminar Computerspiele Räumliche Datenstrukturen Ralf Pramberger Themen 2 1. Grundlagen Szene Sichtbarkeit (Raytracing) Culling 2. Räumliche Datenstrukturen Bounding Volume Hierarchie Quadtree/Octree BSP-Tree
Featurebasierte 3D Modellierung
 1 Featurebasierte 3D Modellierung Moderne 3D arbeiten häufig mit einer Feature Modellierung. Hierbei gibt es eine Reihe von vordefinierten Konstruktionen, die der Reihe nach angewandt werden. Diese Basis
1 Featurebasierte 3D Modellierung Moderne 3D arbeiten häufig mit einer Feature Modellierung. Hierbei gibt es eine Reihe von vordefinierten Konstruktionen, die der Reihe nach angewandt werden. Diese Basis
146
 145 netpbm PBM Portable Bitmap PGM Portable Greymap PPM Portable Pixmap PNM Portable Anymap Konvertierungsroutinen: anytopnm, asciitopgm, bmptoppm, giftopnm, pbmtopgm, pgmtopbm, pgmtoppm, ppmtopgm, pstopnm,
145 netpbm PBM Portable Bitmap PGM Portable Greymap PPM Portable Pixmap PNM Portable Anymap Konvertierungsroutinen: anytopnm, asciitopgm, bmptoppm, giftopnm, pbmtopgm, pgmtopbm, pgmtoppm, ppmtopgm, pstopnm,
Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle. zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"):
 Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"): 1 Erzeugung des Voronoi-Diagramms (siehe Vorlesung "Algorithmische
Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"): 1 Erzeugung des Voronoi-Diagramms (siehe Vorlesung "Algorithmische
{0,1} rekursive Aufteilung des Datenraums in die Quadranten NW, NE, SW und SE feste Auflösung des Datenraums in 2 p 2 p Gitterzellen
 4.4 MX-Quadtrees (I) MatriX Quadtree Verwaltung 2-dimensionaler Punkte Punkte als 1-Elemente in einer quadratischen Matrix mit Wertebereich {0,1} rekursive Aufteilung des Datenraums in die Quadranten NW,
4.4 MX-Quadtrees (I) MatriX Quadtree Verwaltung 2-dimensionaler Punkte Punkte als 1-Elemente in einer quadratischen Matrix mit Wertebereich {0,1} rekursive Aufteilung des Datenraums in die Quadranten NW,
Kollisionserkennung
 1 Kollisionserkennung von Jens Schedel, Christoph Forman und Philipp Baumgärtel 2 1. Einleitung Wozu wird Kollisionserkennung benötigt? 3 - für Computergraphik 4 - für Simulationen 5 - für Wegeplanung
1 Kollisionserkennung von Jens Schedel, Christoph Forman und Philipp Baumgärtel 2 1. Einleitung Wozu wird Kollisionserkennung benötigt? 3 - für Computergraphik 4 - für Simulationen 5 - für Wegeplanung
Aufgaben für den Mathematikunterricht. Inhaltsbereich 1: Raum und Form. 1.2 elementare geometrische Figuren kennen und herstellen
 Nr. 1 Geometrische Körper und ihre Eigenschaften Fülle die Tabelle aus. Würfel Quader Pyramide Zylinder Kegel Kugel Ecken Kanten Flächen Nr. 1 Geometrische Körper und ihre Eigenschaften Fülle die Tabelle
Nr. 1 Geometrische Körper und ihre Eigenschaften Fülle die Tabelle aus. Würfel Quader Pyramide Zylinder Kegel Kugel Ecken Kanten Flächen Nr. 1 Geometrische Körper und ihre Eigenschaften Fülle die Tabelle
Conservative Volumetric Visibility with Occluder Fusion
 Conservative Volumetric Visibility with Occluder Fusion Worum geht es? Ausgangspunkt komplexe Szene, wie Städte, Straßenzüge, etc. Ziel effiziente Berechnung von nicht sichtbaren Regionen Begriffe / Definitionen
Conservative Volumetric Visibility with Occluder Fusion Worum geht es? Ausgangspunkt komplexe Szene, wie Städte, Straßenzüge, etc. Ziel effiziente Berechnung von nicht sichtbaren Regionen Begriffe / Definitionen
Proseminar Computergraphik. 3D - Modellierung
 TECHNISCHE UNIVERSITÄT DRESDEN FAKULTÄT INFORMATIK INSTITUT FÜR SOFTWARE- UND MULTIMEDIATECHNIK PROFESSUR FÜR COMPUTERGRAPHIK UND VISUALISIERUNG PROF. DR. STEFAN GUMHOLD Proseminar Computergraphik 3D -
TECHNISCHE UNIVERSITÄT DRESDEN FAKULTÄT INFORMATIK INSTITUT FÜR SOFTWARE- UND MULTIMEDIATECHNIK PROFESSUR FÜR COMPUTERGRAPHIK UND VISUALISIERUNG PROF. DR. STEFAN GUMHOLD Proseminar Computergraphik 3D -
Einführung in die Robotik. Jianwei Zhang
 - Jianwei Zhang zhang@informatik.uni-hamburg.de Fakultät für Mathematik, Informatik und Naturwissenschaften Technische Aspekte Multimodaler Systeme 26. Juni 2012 J. Zhang 296 Programmierung auf Aufgabenebene
- Jianwei Zhang zhang@informatik.uni-hamburg.de Fakultät für Mathematik, Informatik und Naturwissenschaften Technische Aspekte Multimodaler Systeme 26. Juni 2012 J. Zhang 296 Programmierung auf Aufgabenebene
Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen
 Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen Sommersemester 2012 Matthias Fischer mafi@upb.de Vorlesung 12 26.6.2012 Matthias Fischer 374 Übersicht Motivation Modell der Sichtbarkeit Eigenschaft
Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen Sommersemester 2012 Matthias Fischer mafi@upb.de Vorlesung 12 26.6.2012 Matthias Fischer 374 Übersicht Motivation Modell der Sichtbarkeit Eigenschaft
Was bisher geschah. 1. Zerlegung in monotone Polygone 2. Triangulierung der monotonen Teilpolygone
 Was bisher geschah Motivation, Beispiele geometrische Objekte im R 2 : Punkt, Gerade, Halbebene, Strecke, Polygon, ebene Zerlegung in Regionen (planare Graphen) maschinelle Repräsentation geometrischer
Was bisher geschah Motivation, Beispiele geometrische Objekte im R 2 : Punkt, Gerade, Halbebene, Strecke, Polygon, ebene Zerlegung in Regionen (planare Graphen) maschinelle Repräsentation geometrischer
Körperberechnung. Würfel - Einheitswürfel. Pyramide. - Oberfläche - Volumen. - Oberfläche. - Volumen. Kegel. Quader. - Oberfläche - Volumen
 Körperberechnung Würfel - Einheitswürfel - Oberfläche - Volumen Quader - Oberfläche - Volumen - zusammengesetzte Körper Prisma - Oberfläche Zylinder - Oberfläche Pyramide - Oberfläche - Volumen Kegel -
Körperberechnung Würfel - Einheitswürfel - Oberfläche - Volumen Quader - Oberfläche - Volumen - zusammengesetzte Körper Prisma - Oberfläche Zylinder - Oberfläche Pyramide - Oberfläche - Volumen Kegel -
Oberfläche von Körpern
 Definition Die Summe der Flächeninhalte der Flächen eines Körpers nennt man Oberflächeninhalt. Quader Der Oberflächeninhalt eines Quaders setzt sich folgendermaßen zusammen: O Q =2 h b+2 h l+2 l b=2 (h
Definition Die Summe der Flächeninhalte der Flächen eines Körpers nennt man Oberflächeninhalt. Quader Der Oberflächeninhalt eines Quaders setzt sich folgendermaßen zusammen: O Q =2 h b+2 h l+2 l b=2 (h
Abitur 2013 Mathematik Geometrie V
 Seite 1 http://www.abiturloesung.de/ Seite Abitur 1 Mathematik Geometrie V Teilaufgabe b ( BE) Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massiven Beton, der die
Seite 1 http://www.abiturloesung.de/ Seite Abitur 1 Mathematik Geometrie V Teilaufgabe b ( BE) Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massiven Beton, der die
(1) Geometrie. Vorlesung Computergraphik 3 S. Müller U N I V E R S I T Ä T KOBLENZ LANDAU
 (1) Geometrie Vorlesung Computergraphik 3 S. Müller KOBLENZ LANDAU KOBLENZ LANDAU Organisatorisches Vorlesung CG 2+3 Die Veranstaltung besteht aus 2 Teilen, wobei in der Mitte und am Ende eine Klausur
(1) Geometrie Vorlesung Computergraphik 3 S. Müller KOBLENZ LANDAU KOBLENZ LANDAU Organisatorisches Vorlesung CG 2+3 Die Veranstaltung besteht aus 2 Teilen, wobei in der Mitte und am Ende eine Klausur
Grundlagen von Rasterdaten
 LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS DATABASE Kapitel 7: Grundlagen von Rasterdaten Skript zur Vorlesung Geo-Informationssysteme Wintersemester 2014/15 Ludwig-Maximilians-Universität
LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS DATABASE Kapitel 7: Grundlagen von Rasterdaten Skript zur Vorlesung Geo-Informationssysteme Wintersemester 2014/15 Ludwig-Maximilians-Universität
Binary Decision Diagrams
 Hauptseminar Model Checking Binary Decision Diagrams Kristofer Treutwein 23.4.22 Grundlagen Normalformen Als kanonische Darstellungsform für boolesche Terme gibt es verschiedene Normalformen, u.a. die
Hauptseminar Model Checking Binary Decision Diagrams Kristofer Treutwein 23.4.22 Grundlagen Normalformen Als kanonische Darstellungsform für boolesche Terme gibt es verschiedene Normalformen, u.a. die
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Kopiervorlagen Geometrie (3) - Stereometrie
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Kopiervorlagen Geometrie (3) - Stereometrie Das komplette Material finden Sie hier: School-Scout.de Inhaltsverzeichnis Stereometrie
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Kopiervorlagen Geometrie (3) - Stereometrie Das komplette Material finden Sie hier: School-Scout.de Inhaltsverzeichnis Stereometrie
5. Gitter, Gradienten, Interpolation Gitter. (Rezk-Salama, o.j.)
 5. Gitter, Gradienten, Interpolation 5.1. Gitter (Rezk-Salama, o.j.) Gitterklassifikation: (Bartz 2005) (Rezk-Salama, o.j.) (Bartz 2005) (Rezk-Salama, o.j.) Allgemeine Gitterstrukturen: (Rezk-Salama, o.j.)
5. Gitter, Gradienten, Interpolation 5.1. Gitter (Rezk-Salama, o.j.) Gitterklassifikation: (Bartz 2005) (Rezk-Salama, o.j.) (Bartz 2005) (Rezk-Salama, o.j.) Allgemeine Gitterstrukturen: (Rezk-Salama, o.j.)
Klasse räumlicher Indexstrukturen, die den Datenraum rekursiv in 4 gleich große Zellen unterteilen (Quadranten NW, NE, SW, SE)
 4.4 Quadtrees Überblick Klasse räumlicher Indexstrukturen, die den Datenraum rekursiv in 4 gleich große Zellen unterteilen (Quadranten NW, NE, SW, SE) Verwaltung von Punkten, Kurven, Flächen usw., häufig
4.4 Quadtrees Überblick Klasse räumlicher Indexstrukturen, die den Datenraum rekursiv in 4 gleich große Zellen unterteilen (Quadranten NW, NE, SW, SE) Verwaltung von Punkten, Kurven, Flächen usw., häufig
Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume)
 WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
Mathematische Grundlagen für die Vorlesung. Differentialgeometrie
 Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Flächeninhalt, Volumen und Integral
 Flächeninhalt, Volumen und Integral Prof. Herbert Koch Mathematisches Institut - Universität Bonn Schülerwoche 211 Hausdorff Center for Mathematics Donnerstag, der 8. September 211 Inhaltsverzeichnis 1
Flächeninhalt, Volumen und Integral Prof. Herbert Koch Mathematisches Institut - Universität Bonn Schülerwoche 211 Hausdorff Center for Mathematics Donnerstag, der 8. September 211 Inhaltsverzeichnis 1
5 BINÄRE ENTSCHEIDUNGS- DIAGRAMME (BDDS)
 5 BINÄRE ENTSCHEIDUNGS- DIAGRAMME (BDDS) Sommersemester 2009 Dr. Carsten Sinz, Universität Karlsruhe Datenstruktur BDD 2 1986 von R. Bryant vorgeschlagen zur Darstellung von aussagenlogischen Formeln (genauer:
5 BINÄRE ENTSCHEIDUNGS- DIAGRAMME (BDDS) Sommersemester 2009 Dr. Carsten Sinz, Universität Karlsruhe Datenstruktur BDD 2 1986 von R. Bryant vorgeschlagen zur Darstellung von aussagenlogischen Formeln (genauer:
Relationen und Graphentheorie
 Seite Graphentheorie- Relationen und Graphentheorie Grundbegriffe. Relationen- und Graphentheorie gehören zu den wichtigsten Hilfsmitteln der Informatik, die aus der diskretenmathematik stammen. Ein Graph
Seite Graphentheorie- Relationen und Graphentheorie Grundbegriffe. Relationen- und Graphentheorie gehören zu den wichtigsten Hilfsmitteln der Informatik, die aus der diskretenmathematik stammen. Ein Graph
Binary Space Partitioning Trees Grundlagen und Verfahren zur Erzeugung von BSP-Trees
 Binary Space Partitioning Trees Grundlagen und Verfahren zur Erzeugung von BSP-Trees Vortrag im Rahmen des Seminars "Geometrische Modellierung" (Wintersemester 2008/09) Timm Linder Universität Duisburg-Essen,
Binary Space Partitioning Trees Grundlagen und Verfahren zur Erzeugung von BSP-Trees Vortrag im Rahmen des Seminars "Geometrische Modellierung" (Wintersemester 2008/09) Timm Linder Universität Duisburg-Essen,
Lernmodul 7 Algorithmus von Dijkstra
 Folie 1 von 30 Lernmodul 7 Algorithmus von Dijkstra Quelle: http://www.map24.de Folie 2 von 30 Algorithmus von Dijkstra Übersicht Kürzester Weg von A nach B in einem Graphen Problemstellung: Suche einer
Folie 1 von 30 Lernmodul 7 Algorithmus von Dijkstra Quelle: http://www.map24.de Folie 2 von 30 Algorithmus von Dijkstra Übersicht Kürzester Weg von A nach B in einem Graphen Problemstellung: Suche einer
Mathematische Probleme, SS 2016 Freitag $Id: convex.tex,v /05/13 14:42:55 hk Exp $
 $Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
$Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
Darstellung dreidimensionaler Figuren in der Ebene. Schrägbild
 Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
4.4 Quadtrees. Literatur
 4.4 Quadtrees Überblick Klasse räumlicher Indexstrukturen, die den Datenraum rekursiv in 4 gleich große Zellen unterteilen (Quadranten NW, NE, SW, SE) Verwaltung von Punkten, Kurven, Flächen usw., häufig
4.4 Quadtrees Überblick Klasse räumlicher Indexstrukturen, die den Datenraum rekursiv in 4 gleich große Zellen unterteilen (Quadranten NW, NE, SW, SE) Verwaltung von Punkten, Kurven, Flächen usw., häufig
3D-Objektmodellierung
 3D-Objektmodellierung Beschränkung auf echte dreidimensionale Strukturen: keine isolierten Punkte, Kanten oder Flächen keine baumelnden Kanten oder Flächen Computergrafik: Modellierung dreidimensionaler
3D-Objektmodellierung Beschränkung auf echte dreidimensionale Strukturen: keine isolierten Punkte, Kanten oder Flächen keine baumelnden Kanten oder Flächen Computergrafik: Modellierung dreidimensionaler
Computergrafik 1 Transformationen
 Computergrafik 1 Transformationen Kai Köchy Sommersemester 2010 Beuth Hochschule für Technik Berlin Überblick Repräsentationen, Primitiven Transformationen in 2D Skalierung Translation Rotation Scherung
Computergrafik 1 Transformationen Kai Köchy Sommersemester 2010 Beuth Hochschule für Technik Berlin Überblick Repräsentationen, Primitiven Transformationen in 2D Skalierung Translation Rotation Scherung
1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie
 Gliederung 1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie 4/3, Folie 1 2010 Prof. Steffen Lange - HDa/FbI
Gliederung 1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie 4/3, Folie 1 2010 Prof. Steffen Lange - HDa/FbI
Mathematischer Vorkurs für Physiker WS 2012/13 Vorlesung 8
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 212/1 Vorlesung 8 Integration über ebene Bereiche Wir betrachten einen regulären Bereich in der x-y Ebene, der einfach zusammenhängend ist.
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 212/1 Vorlesung 8 Integration über ebene Bereiche Wir betrachten einen regulären Bereich in der x-y Ebene, der einfach zusammenhängend ist.
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Binärbaum Suchbaum Dr. Frank Seifert Vorlesung Datenstrukturen - Sommersemester 2016 Folie 356 Datenstruktur Binärbaum Strukturrepräsentation des mathematischen Konzepts Binärbaum
Vorlesung Datenstrukturen Binärbaum Suchbaum Dr. Frank Seifert Vorlesung Datenstrukturen - Sommersemester 2016 Folie 356 Datenstruktur Binärbaum Strukturrepräsentation des mathematischen Konzepts Binärbaum
Triangulierungen von Punktmengen und Polyedern
 Triangulierungen von Punktmengen und Polyedern Vorlesung im Sommersemester 2 Technische Universität Berlin Jörg Rambau 2.4.2 Motivation und Beispiele Wir wollen hier den Begriff der Triangulierungen von
Triangulierungen von Punktmengen und Polyedern Vorlesung im Sommersemester 2 Technische Universität Berlin Jörg Rambau 2.4.2 Motivation und Beispiele Wir wollen hier den Begriff der Triangulierungen von
Das Modellieren von 2D- und 3D-Objekten
 Das Modellieren von 2D- und 3D-Objekten 1 VTK-Format Florian Buchegger, Michael Haberleitner December 11, 2015 Eine VTK-Datei besteht aus einem Header und einem Body. Während im Header lediglich wichtige
Das Modellieren von 2D- und 3D-Objekten 1 VTK-Format Florian Buchegger, Michael Haberleitner December 11, 2015 Eine VTK-Datei besteht aus einem Header und einem Body. Während im Header lediglich wichtige
Aufgaben zu Merkmalen und Eigenschaften von Körpern 1. 1 Allgemeine Merkmale vergleichen und beschreiben
 Aufgaben zu Merkmalen und Eigenschaften von Körpern 1 Sicheres Wissen und Können am Ende der Klasse 6 1 Allgemeine Merkmale vergleichen und beschreiben 1. Die folgenden Zeichnungen zeigen Körper. Fülle
Aufgaben zu Merkmalen und Eigenschaften von Körpern 1 Sicheres Wissen und Können am Ende der Klasse 6 1 Allgemeine Merkmale vergleichen und beschreiben 1. Die folgenden Zeichnungen zeigen Körper. Fülle
Europäisches Patentamt European Patent Office Office europeen des brevets (11) EP A2
 (19) (12) Europäisches Patentamt 1 1 1 1 European Patent Office Office europeen des brevets (11) EP 0 788 071 A2 EUROPÄISCHE PATENTANMELDUNG (43) Veröffentlichungstag: igstag: (51) Int. Cl.6: G06T 7/60
(19) (12) Europäisches Patentamt 1 1 1 1 European Patent Office Office europeen des brevets (11) EP 0 788 071 A2 EUROPÄISCHE PATENTANMELDUNG (43) Veröffentlichungstag: igstag: (51) Int. Cl.6: G06T 7/60
D-MAVT Lineare Algebra I HS 2017 Prof. Dr. N. Hungerbühler. Lösungen Serie 10
 D-MAVT Lineare Algebra I HS 2017 Prof. Dr. N. Hungerbühler Lösungen Serie 10 1. Für a 1 : 1 1 0, a 2 : 1 1, a 3 : 1 1 1, b : 2 2 2 1 und A : (a 1, a 2, a 3 ) gelten welche der folgenden Aussagen? (a) det(a)
D-MAVT Lineare Algebra I HS 2017 Prof. Dr. N. Hungerbühler Lösungen Serie 10 1. Für a 1 : 1 1 0, a 2 : 1 1, a 3 : 1 1 1, b : 2 2 2 1 und A : (a 1, a 2, a 3 ) gelten welche der folgenden Aussagen? (a) det(a)
Natürliche Bäume. (Algorithmen und Datenstrukturen I) Prof. Dr. Oliver Braun. Letzte Änderung: :16. Natürliche Bäume 1/16
 Natürliche Bäume (Algorithmen und Datenstrukturen I) Prof. Dr. Oliver Braun Letzte Änderung: 18.03.2018 18:16 Natürliche Bäume 1/16 Bäume Begriffe (1/2) Bäume sind verallgemeinerte Listenstrukturen ein
Natürliche Bäume (Algorithmen und Datenstrukturen I) Prof. Dr. Oliver Braun Letzte Änderung: 18.03.2018 18:16 Natürliche Bäume 1/16 Bäume Begriffe (1/2) Bäume sind verallgemeinerte Listenstrukturen ein
Datenstrukturen Teil 2. Bäume. Definition. Definition. Definition. Bäume sind verallgemeinerte Listen. Sie sind weiter spezielle Graphen
 Bäume sind verallgemeinerte Listen Datenstrukturen Teil 2 Bäume Jeder Knoten kann mehrere Nachfolger haben Sie sind weiter spezielle Graphen Graphen bestehen aus Knoten und Kanten Kanten können gerichtet
Bäume sind verallgemeinerte Listen Datenstrukturen Teil 2 Bäume Jeder Knoten kann mehrere Nachfolger haben Sie sind weiter spezielle Graphen Graphen bestehen aus Knoten und Kanten Kanten können gerichtet
3 Planare Graphen die Eulersche Polyederformel
 3 Planare Graphen die Eulersche Polyederformel Planare Graphen sind solche Graphen, die sich ohne Überkreuzungen von Kanten in eine Ebene zeichnen lassen. Wir nehmen hierbei an, dass die Knoten als Punkte
3 Planare Graphen die Eulersche Polyederformel Planare Graphen sind solche Graphen, die sich ohne Überkreuzungen von Kanten in eine Ebene zeichnen lassen. Wir nehmen hierbei an, dass die Knoten als Punkte
Bachelor Thesis. Fachgebiet für Computergestützte Modellierung und Simulation Prof. Dr.-Ing. André Borrmann
 Bachelor Thesis Fachgebiet für Computergestützte Modellierung und Simulation Prof. Dr.-Ing. André Borrmann 1 Technische Universität München Fakultät für Bauingenieur- und Vermessungswesen Fachgebiet für
Bachelor Thesis Fachgebiet für Computergestützte Modellierung und Simulation Prof. Dr.-Ing. André Borrmann 1 Technische Universität München Fakultät für Bauingenieur- und Vermessungswesen Fachgebiet für
Kapitel D : Flächen- und Volumenberechnungen
 Kapitel D : Flächen- und Volumenberechnungen Berechnung einfacher Flächen Bei Flächenberechnungen werden die Masse folgendermassen bezeichnet: = Fläche in m 2, dm 2, cm 2, mm 2, etc a, b, c, d = Bezeichnung
Kapitel D : Flächen- und Volumenberechnungen Berechnung einfacher Flächen Bei Flächenberechnungen werden die Masse folgendermassen bezeichnet: = Fläche in m 2, dm 2, cm 2, mm 2, etc a, b, c, d = Bezeichnung
8.1 Vorstellen im Raum
 äumliche Geometrie 1 8 äumliche Geometrie 8.1 Vorstellen im aum 1. Alle dargestellten Körper sind aus elf Würfeln zusammengesetzt. a) Welche der Körper sind deckungsgleich zueinander? b) Welche der Körper
äumliche Geometrie 1 8 äumliche Geometrie 8.1 Vorstellen im aum 1. Alle dargestellten Körper sind aus elf Würfeln zusammengesetzt. a) Welche der Körper sind deckungsgleich zueinander? b) Welche der Körper
Technische Universität München. Vorlesungsgrobstruktur: wo stehen wir, wie geht s weiter
 Vorlesungsgrobstruktur: wo stehen wir, wie geht s weiter Kapitel 7 Fortgeschrittene Datenstrukturen Motivation: Lineare Liste: Suchen eines Elements ist schnell O(log n) Einfügen eines Elements ist langsam
Vorlesungsgrobstruktur: wo stehen wir, wie geht s weiter Kapitel 7 Fortgeschrittene Datenstrukturen Motivation: Lineare Liste: Suchen eines Elements ist schnell O(log n) Einfügen eines Elements ist langsam
9 Minimum Spanning Trees
 Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
Mathematische Probleme, SS 2013 Montag $Id: convex.tex,v /10/22 15:58:28 hk Exp $
 $Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
$Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
Grundlagen der 3D-Modellierung
 April 28, 2009 Inhaltsverzeichnis 1 Einführung 2 Direkte Darstellungsschemata 3 Indirekte Darstellungsschemata 4 Parametrische Kurven und Freiformflächen 5 Abschluss Motivation Vom physikalischen Körper
April 28, 2009 Inhaltsverzeichnis 1 Einführung 2 Direkte Darstellungsschemata 3 Indirekte Darstellungsschemata 4 Parametrische Kurven und Freiformflächen 5 Abschluss Motivation Vom physikalischen Körper
Bildbasierte CSG. Techniken zur Darstellung solider Objekte in Echtzeit
 Techniken zur Darstellung solider Objekte in Echtzeit Vortrag im Seminar Computergrafik am Hasso-Plattner-Institut gehalten von Stephan Brumme am 12.Juni 2002 Gliederung 2 I. Einführung II. III. IV. V.
Techniken zur Darstellung solider Objekte in Echtzeit Vortrag im Seminar Computergrafik am Hasso-Plattner-Institut gehalten von Stephan Brumme am 12.Juni 2002 Gliederung 2 I. Einführung II. III. IV. V.
1 Grundwissen Pyramide
 1 Grundwissen Pyramide 1 Definition und Volumen der Pyramide Eine Pyramide ist ein geradlinig begrenzter Körper im R 3. Dabei wird ein Punkt S außerhalb der Ebene eines Polygons (Vieleck) mit den Ecken
1 Grundwissen Pyramide 1 Definition und Volumen der Pyramide Eine Pyramide ist ein geradlinig begrenzter Körper im R 3. Dabei wird ein Punkt S außerhalb der Ebene eines Polygons (Vieleck) mit den Ecken
Quadtrees. Christian Höner zu Siederdissen
 Quadtrees Christian Höner zu Siederdissen Quadtrees Zum Verständnis benötigt... Was sind Quadtrees Datenstruktur Wofür Quadtrees Operationen auf dem Baum Vor- und Nachteile (spezialisierte Formen) Zum
Quadtrees Christian Höner zu Siederdissen Quadtrees Zum Verständnis benötigt... Was sind Quadtrees Datenstruktur Wofür Quadtrees Operationen auf dem Baum Vor- und Nachteile (spezialisierte Formen) Zum
WER WIRD MATHESTAR? Raum und Form. Mathematisch argumentieren. Gruppenspiel oder Einzelarbeit. 45 Minuten
 WER WIRD MATHESTAR? Lehrplaneinheit Berufsrelevantes Rechnen - Leitidee Kompetenzen Sozialform, Methode Ziel, Erwartungshorizont Zeitlicher Umfang Didaktische Hinweise Raum und Form Mathematisch argumentieren
WER WIRD MATHESTAR? Lehrplaneinheit Berufsrelevantes Rechnen - Leitidee Kompetenzen Sozialform, Methode Ziel, Erwartungshorizont Zeitlicher Umfang Didaktische Hinweise Raum und Form Mathematisch argumentieren
Teil 1: Modellierung. Einleitung. 3D Szene Inhalt. Objekte und ihre Beschreibung
 Objekte und ihre Beschreibung Einleitung Computergraphik: 3D sehr wichtig photo-realistic rendering Computer-Animation, Modellierung Visualisierung, Virtual Reality Ansatz: per rendering wird eine 3D-Szene
Objekte und ihre Beschreibung Einleitung Computergraphik: 3D sehr wichtig photo-realistic rendering Computer-Animation, Modellierung Visualisierung, Virtual Reality Ansatz: per rendering wird eine 3D-Szene
Indizierung von Geodaten - Raumbezogene Indexstrukturen. Seminar mobile Geoinformationssystem Vortrag von Markus Steger
 Indizierung von Geodaten - Raumbezogene Indexstrukturen Seminar mobile Geoinformationssystem Vortrag von Markus Steger Index wozu ist er gut? Index allgemein Effizienter Zugriff auf Daten, i.d.r. mit B-Baum
Indizierung von Geodaten - Raumbezogene Indexstrukturen Seminar mobile Geoinformationssystem Vortrag von Markus Steger Index wozu ist er gut? Index allgemein Effizienter Zugriff auf Daten, i.d.r. mit B-Baum
Aufgaben aus den Vergleichenden Arbeiten im Fach Mathematik Verschiedenes Verschiedenes
 2012 A 1e) Verschiedenes Schreiben Sie die Namen der drei Vierecke auf. 2011 A 1e) Verschiedenes Wie heißen diese geometrischen Objekte? Lösungen: Aufgabe Lösungsskizze BE 2012 A 1e) Rechteck Parallelogramm
2012 A 1e) Verschiedenes Schreiben Sie die Namen der drei Vierecke auf. 2011 A 1e) Verschiedenes Wie heißen diese geometrischen Objekte? Lösungen: Aufgabe Lösungsskizze BE 2012 A 1e) Rechteck Parallelogramm
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A Bremen. Die Kursübersicht für das Fach Mathematik
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
1 Pyramide, Kegel und Kugel
 1 Pyramide, Kegel und Kugel Pyramide und Kegel sind beides Körper, die - anders als Prismen und Zylinder - spitz zulaufen. Während das Volumen von Prismen mit V = G h k berechnet wird, wobei G die Grundfläche
1 Pyramide, Kegel und Kugel Pyramide und Kegel sind beides Körper, die - anders als Prismen und Zylinder - spitz zulaufen. Während das Volumen von Prismen mit V = G h k berechnet wird, wobei G die Grundfläche
4. Segmentierung von Objekten Video - Inhaltsanalyse
 4. Segmentierung von Objekten Video - Inhaltsanalyse Stephan Kopf Inhalt Vorgehensweise Berechnung der Kamerabewegungen zwischen beliebigen Bildern Transformation eines Bildes Hintergrundbilder / Panoramabilder
4. Segmentierung von Objekten Video - Inhaltsanalyse Stephan Kopf Inhalt Vorgehensweise Berechnung der Kamerabewegungen zwischen beliebigen Bildern Transformation eines Bildes Hintergrundbilder / Panoramabilder
Kurs 1663 Datenstrukturen" Musterlösungen zur Klausur vom Seite 1. Musterlösungen zur Hauptklausur Kurs 1663 Datenstrukturen 15.
 Kurs 1663 Datenstrukturen" Musterlösungen zur Klausur vom 15.08.98 Seite 1 Musterlösungen zur Hauptklausur Kurs 1663 Datenstrukturen 15. August 1998 Kurs 1663 Datenstrukturen" Musterlösungen zur Klausur
Kurs 1663 Datenstrukturen" Musterlösungen zur Klausur vom 15.08.98 Seite 1 Musterlösungen zur Hauptklausur Kurs 1663 Datenstrukturen 15. August 1998 Kurs 1663 Datenstrukturen" Musterlösungen zur Klausur
Szenengraphen. Codruţa Cosma. Universität Ulm Sommersemester 2005
 Szenengraphen Codruţa Cosma Universität Ulm Sommersemester 2005 Übersicht Einführung VRML OpenSceneGraph Java3D vs. VRML OpenGL vs. Java3D und VRML Zusammenfassung 2/26 Was sind Szenengraphen? Datenstruktur
Szenengraphen Codruţa Cosma Universität Ulm Sommersemester 2005 Übersicht Einführung VRML OpenSceneGraph Java3D vs. VRML OpenGL vs. Java3D und VRML Zusammenfassung 2/26 Was sind Szenengraphen? Datenstruktur
Oberflächenrepräsentationen Kontinuierliche Kurven Bezier-Kurven. Freiformflächen. Diskret
 Oberflächenrepräsentationen Kontinuierliche Kurven Bezier-Kurven Thomas Jung Freiformflächen NURBS Die Modellierung von Objekten erfordert die geeignete Repräsentation der Oberfläche Je nach Anforderung
Oberflächenrepräsentationen Kontinuierliche Kurven Bezier-Kurven Thomas Jung Freiformflächen NURBS Die Modellierung von Objekten erfordert die geeignete Repräsentation der Oberfläche Je nach Anforderung
Marching Cubes - Erstellung von Polygonmodellen aus Voxelgittern
 Marching Cubes - Erstellung von Polygonmodellen aus Voxelgittern Matthias Kirschner Advanced Topics in Computer Graphics - WS06/07 Marching Cubes - Erstellung von Polygonmodellen aus Voxelgittern Matthias
Marching Cubes - Erstellung von Polygonmodellen aus Voxelgittern Matthias Kirschner Advanced Topics in Computer Graphics - WS06/07 Marching Cubes - Erstellung von Polygonmodellen aus Voxelgittern Matthias
M. Pester 29. Ein konvexes d-polytop ist eine begrenzte d-dimensionale polyedrale Menge. (d = 3 Polyeder, d = 2 Polygon)
 M. Pester 29 6 Konvexe Hülle 6.1 Begriffe Per Definition ist die konvexe Hülle für eine Menge S von lich vielen Punkten die kleinste konvexe Menge, die S enthölt (z.b. in der Ebene durch ein umspannes
M. Pester 29 6 Konvexe Hülle 6.1 Begriffe Per Definition ist die konvexe Hülle für eine Menge S von lich vielen Punkten die kleinste konvexe Menge, die S enthölt (z.b. in der Ebene durch ein umspannes
13. Bäume: effektives Suchen und Sortieren
 Schwerpunkte Aufgabe und Vorteile von Bäumen 13. Bäume: effektives Suchen und Sortieren Java-Beispiele: Baum.java Traverse.java TraverseTest.java Sortieren mit Bäumen Ausgabealgorithmen: - Preorder - Postorder
Schwerpunkte Aufgabe und Vorteile von Bäumen 13. Bäume: effektives Suchen und Sortieren Java-Beispiele: Baum.java Traverse.java TraverseTest.java Sortieren mit Bäumen Ausgabealgorithmen: - Preorder - Postorder
Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen
 Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen Sommersemester 2012 Matthias Fischer mafi@upb.de Vorlesung 2 10.4.2012 Matthias Fischer 59 Übersicht = Binary Space Partitions Motivation Idee Anwendungsbeispiel:
Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen Sommersemester 2012 Matthias Fischer mafi@upb.de Vorlesung 2 10.4.2012 Matthias Fischer 59 Übersicht = Binary Space Partitions Motivation Idee Anwendungsbeispiel:
Einführung in die Informatik I
 Einführung in die Informatik I Graphen und Bäume Prof. Dr. Nikolaus Wulff Weitere Datentypen Als wichtige abstrakte Datentypen (ADT) kennen wir bis lang die Liste, den Stapel und die Warteschlange. Diese
Einführung in die Informatik I Graphen und Bäume Prof. Dr. Nikolaus Wulff Weitere Datentypen Als wichtige abstrakte Datentypen (ADT) kennen wir bis lang die Liste, den Stapel und die Warteschlange. Diese
A Simple and Practical Method for Interactive Ray Tracing of Dynamic Scenes
 A Simple and Practical Method for Interactive Ray Tracing of Dynamic Scenes Ingo Wald Carsten Benthin Philipp Slusallek Marco Lang Bisher Ray Tracing erstmals von Appel benutzt dutzende Algorithmen vor
A Simple and Practical Method for Interactive Ray Tracing of Dynamic Scenes Ingo Wald Carsten Benthin Philipp Slusallek Marco Lang Bisher Ray Tracing erstmals von Appel benutzt dutzende Algorithmen vor
Lösungen. Christian Haas. Durchdringungen. Ausbildungseinheit für Anlagen- und Apparatebauer/innen. Reform Lernziele:
 Durchdringungen Ausbildungseinheit für Anlagen- und Apparatebauer/innen EFZ Reform 2013 13 Lösungen Lernziele: Durchdringungen im Zusammenhang mit den Abwicklungen konstruieren Christian Haas Zeichnungstechnik
Durchdringungen Ausbildungseinheit für Anlagen- und Apparatebauer/innen EFZ Reform 2013 13 Lösungen Lernziele: Durchdringungen im Zusammenhang mit den Abwicklungen konstruieren Christian Haas Zeichnungstechnik
Körper erkennen und beschreiben
 Vertiefen 1 Körper erkennen und beschreiben zu Aufgabe 6 Schulbuch, Seite 47 6 Passt, passt nicht Nenne zu jeder Aussage alle Formen, auf die die Aussage zutrifft. a) Die Form hat keine Ecken. b) Die Form
Vertiefen 1 Körper erkennen und beschreiben zu Aufgabe 6 Schulbuch, Seite 47 6 Passt, passt nicht Nenne zu jeder Aussage alle Formen, auf die die Aussage zutrifft. a) Die Form hat keine Ecken. b) Die Form
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Graphdarstellungen Maike Buchin 0.6.017 Graphen Motivation: Graphen treten häufig als Abstraktion von Objekten (Knoten) und ihren Beziehungen (Kanten) auf. Beispiele: soziale
Vorlesung Datenstrukturen Graphdarstellungen Maike Buchin 0.6.017 Graphen Motivation: Graphen treten häufig als Abstraktion von Objekten (Knoten) und ihren Beziehungen (Kanten) auf. Beispiele: soziale
Quad-trees. Benjamin Niedermann Übung Algorithmische Geometrie
 Übung Algorithmische Geometrie Quad-trees LEHRSTUHL FÜR ALGORITHMIK I INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Benjamin Niedermann 02.07.2014 Übersicht Übungsblatt 11 - Quadtrees Motivation:
Übung Algorithmische Geometrie Quad-trees LEHRSTUHL FÜR ALGORITHMIK I INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Benjamin Niedermann 02.07.2014 Übersicht Übungsblatt 11 - Quadtrees Motivation:
Digraphen, DAGs und Wurzelbäume
 Digraphen (gerichtete Graphen) Slide 1 Digraphen, DAGs und Wurzelbäume Digraphen (gerichtete Graphen) Slide 2 Eingangs- und Ausgangsgrad Bei einer gerichteten Kante e = (u,v) E heißt u Startknoten von
Digraphen (gerichtete Graphen) Slide 1 Digraphen, DAGs und Wurzelbäume Digraphen (gerichtete Graphen) Slide 2 Eingangs- und Ausgangsgrad Bei einer gerichteten Kante e = (u,v) E heißt u Startknoten von
Computergrafik. Michael Bender, Manfred Brill. Ein anwendungsorientiertes Lehrbuch ISBN Inhaltsverzeichnis
 Computergrafik Michael Bender, Manfred Brill Ein anwendungsorientiertes Lehrbuch ISBN 3-446-40434-1 Inhaltsverzeichnis Weitere Informationen oder Bestellungen unter http://www.hanser.de/3-446-40434-1 sowie
Computergrafik Michael Bender, Manfred Brill Ein anwendungsorientiertes Lehrbuch ISBN 3-446-40434-1 Inhaltsverzeichnis Weitere Informationen oder Bestellungen unter http://www.hanser.de/3-446-40434-1 sowie
4.1 Bäume, Datenstrukturen und Algorithmen. Zunächst führen wir Graphen ein. Die einfachste Vorstellung ist, dass ein Graph gegeben ist als
 Kapitel 4 Bäume 4.1 Bäume, Datenstrukturen und Algorithmen Zunächst führen wir Graphen ein. Die einfachste Vorstellung ist, dass ein Graph gegeben ist als eine Menge von Knoten und eine Menge von zugehörigen
Kapitel 4 Bäume 4.1 Bäume, Datenstrukturen und Algorithmen Zunächst führen wir Graphen ein. Die einfachste Vorstellung ist, dass ein Graph gegeben ist als eine Menge von Knoten und eine Menge von zugehörigen
Clausthal C G C C G C. Informatik II Bäume. G. Zachmann Clausthal University, Germany Beispiele.
 lausthal Informatik II Bäume. Zachmann lausthal University, ermany zach@in.tu-clausthal.de Beispiele Stammbaum. Zachmann Informatik 2 - SS 06 Bäume 2 Stammbaum Parse tree, Rekursionsbaum Unix file hierarchy
lausthal Informatik II Bäume. Zachmann lausthal University, ermany zach@in.tu-clausthal.de Beispiele Stammbaum. Zachmann Informatik 2 - SS 06 Bäume 2 Stammbaum Parse tree, Rekursionsbaum Unix file hierarchy
Oberflächenrekonstruktion aus Punktwolken
 Oberflächenrekonstruktion aus Punktwolken Betreuer: Dominik Fritz Seminar Medizinische Simulationssysteme SS 2005 Gliederung 1 2 Der - 3 Der von Hoppe 4 Der - Gliederung 1 2 Der - 3 Der von Hoppe 4 Der
Oberflächenrekonstruktion aus Punktwolken Betreuer: Dominik Fritz Seminar Medizinische Simulationssysteme SS 2005 Gliederung 1 2 Der - 3 Der von Hoppe 4 Der - Gliederung 1 2 Der - 3 Der von Hoppe 4 Der
Grundzüge der Vektoranalysis
 KAPITEL 7 Grundzüge der Vektoranalysis 7. Satz von Green................................... 2 7.2 Satz von Stokes................................... 22 7.2. Zirkulation und Wirbelstärke..........................
KAPITEL 7 Grundzüge der Vektoranalysis 7. Satz von Green................................... 2 7.2 Satz von Stokes................................... 22 7.2. Zirkulation und Wirbelstärke..........................
Quader und Würfel. 1. Kreuze jene Wörter oder Bilder an, die Körper bezeichnen. Mathematische Bildung von der Schulstufe
 Geometrische Körper Diagnoseblatt 5. Schulstufe Quader und Würfel 1. Kreuze jene Wörter oder Bilder an, die Körper bezeichnen Kreis Schuhschachtel Eistüte Fahrkarte Kugel Seite 1 2. Kannst du Quader und
Geometrische Körper Diagnoseblatt 5. Schulstufe Quader und Würfel 1. Kreuze jene Wörter oder Bilder an, die Körper bezeichnen Kreis Schuhschachtel Eistüte Fahrkarte Kugel Seite 1 2. Kannst du Quader und
Einführung (1/3) Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (1) Vorlesungen zur Komplexitätstheorie.
 Einführung (1/3) 3 Wir verfolgen nun das Ziel, Komplexitätsklassen mit Hilfe von charakteristischen Problemen zu beschreiben und zu strukturieren Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit
Einführung (1/3) 3 Wir verfolgen nun das Ziel, Komplexitätsklassen mit Hilfe von charakteristischen Problemen zu beschreiben und zu strukturieren Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit
Datenstrukturen & Algorithmen
 Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Binäre Suchbäume. Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps
 Binäre Suchbäume Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps Mengen n Ziel: Aufrechterhalten einer Menge (hier: ganzer Zahlen) unter folgenden Operationen: Mengen n Ziel: Aufrechterhalten einer
Binäre Suchbäume Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps Mengen n Ziel: Aufrechterhalten einer Menge (hier: ganzer Zahlen) unter folgenden Operationen: Mengen n Ziel: Aufrechterhalten einer
2.4A. Reguläre Polyeder (Platonische Körper)
 .A. Reguläre Polyeder (Platonische Körper) Wie schon in der Antike bekannt war, gibt es genau fünf konvexe reguläre Polyeder, d.h. solche, die von lauter kongruenten regelmäßigen Vielecken begrenzt sind:
.A. Reguläre Polyeder (Platonische Körper) Wie schon in der Antike bekannt war, gibt es genau fünf konvexe reguläre Polyeder, d.h. solche, die von lauter kongruenten regelmäßigen Vielecken begrenzt sind:
Übung zur Vorlesung Algorithmische Geometrie
 Übung zur Vorlesung Algorithmische Geometrie Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 8. Mai 2012 B. Rieck (CoVis)
Übung zur Vorlesung Algorithmische Geometrie Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 8. Mai 2012 B. Rieck (CoVis)
(a, b)-bäume / 1. Datenmenge ist so groß, dass sie auf der Festplatte abgespeichert werden muss.
 (a, b)-bäume / 1. Szenario: Datenmenge ist so groß, dass sie auf der Festplatte abgespeichert werden muss. Konsequenz: Kommunikation zwischen Hauptspeicher und Festplatte - geschieht nicht Byte für Byte,
(a, b)-bäume / 1. Szenario: Datenmenge ist so groß, dass sie auf der Festplatte abgespeichert werden muss. Konsequenz: Kommunikation zwischen Hauptspeicher und Festplatte - geschieht nicht Byte für Byte,
Polyeder und Platonische Körper
 Polyeder und Platonische Körper Ausarbeitung zum 30.11.2016 Linus Leopold Boes Matrikelnummer: 2446248 Algorithmen für planare Graphen Institut für Informatik HHU Düsseldorf Inhaltsverzeichnis 1 Einleitung
Polyeder und Platonische Körper Ausarbeitung zum 30.11.2016 Linus Leopold Boes Matrikelnummer: 2446248 Algorithmen für planare Graphen Institut für Informatik HHU Düsseldorf Inhaltsverzeichnis 1 Einleitung
3. Die Datenstruktur Graph
 3. Die Datenstruktur Graph 3.1 Einleitung: Das Königsberger Brückenproblem Das Königsberger Brückenproblem ist eine mathematische Fragestellung des frühen 18. Jahrhunderts, die anhand von sieben Brücken
3. Die Datenstruktur Graph 3.1 Einleitung: Das Königsberger Brückenproblem Das Königsberger Brückenproblem ist eine mathematische Fragestellung des frühen 18. Jahrhunderts, die anhand von sieben Brücken
Graphentheorie. Eulersche Graphen. Eulersche Graphen. Eulersche Graphen. Rainer Schrader. 14. November Gliederung.
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
