Das Universum als RaumZeit
|
|
|
- Elizabeth Weiß
- vor 6 Jahren
- Abrufe
Transkript
1 Das Universum als RaumZeit Max Camenzind Würzburg
2 Das ist eine der ältesten Aufnahmen von Andromeda "nebula, photographiert am Yerkes Observatorium um Für unsere modernen Augen ist dies wirklich eine Galaxie. Damals wurde das Objekt als a mass of glowing gas bezeichnet.
3 1925 bestimmte Hubble zum ersten Mal die Distanz d = 1 Mio. LJ
4 Spektren von Galaxien rot verschoben l emitted
5 Galaxien haben verschiedene Rotverschiebung. Jeder Punkt in diesem Slice am Himmel ist eine Galaxie. Galaxien füllen den Raum aus sie sind die Bausteine des Universums. [Credit:Michael Blanton and SDSS collaboration ]
6 In der Folge wuchs und wuchs das Universum heute bis 13,8 Mrd. LJ 1925 Teleskope erforschen das Universum Zeit nach heute Mrd. Mrd. Mio. Mio. Mio. Big Bang Jahre Jahre Jahre Jahre Jahre
7 Wie also das Universum mathematisch erfassen?
8 Übersicht: Universum als RaumZeit Das Universum muss ein metrischer Raum sein. Hermann Minkowski interpretiert 1908 Einsteins Relativität als 4D RaumZeit = 4D metrischer Raum. Raum und Zeit verlieren ihre Eigenständigkeit. Wie beschreibe ich das Universum als RaumZeit? RaumZeit als Blätterung von 3-Räumen. Ich muss im Universum messen können! Also ist das Universum ein 4D metrischer Raum Welche Räume sind möglich? Jede Expansion des Universums Rotverschiebung z und Hubble-Gesetz.
9 Universum metrischer Raum Das Universum ist um uns herum sphärisch symmetrisch. Um Distanzen messen zu können, muss das Universum ein metrischer Raum sein. Damit existiert ein Maß d(g1,g2) > 0 für zwei Galaxien G1 und G2.
10 Universum Schachtelung von S² Das Universum ist eine Schachtelung von 2-Sphären. Die kosmische Photosphäre stellt einen Beobachtungsrand im Universum dar. Photonen dahinter können nicht bis zu uns propagieren Die Photosphäre ist ganze 13,8 Mrd. LJ von uns entfernt.
11 Ein metrischer Raum Unter einem metrischen Raum versteht man in der Mathematik eine Menge, auf der eine Metrik definiert ist. Eine Metrik (auch Abstandsfunktion) ist eine Funktion, die je zwei Elementen des Raums einen nicht negativen reellen Wert zuordnet, der als Abstand der beiden Elemente voneinander aufgefasst werden kann.
12 Euklidischer Raum metrischer Raum Newton wählte Universum als Euklidischen Raum Es gab damals mathematisch keine andere Möglichkeit! z Dreiecksungleichung x y
13 Der Abstand zwischen 2 Punkten Der Euklidische Raum ist ein Vektorraum, in dem Distanzen auf alt bekannte Art ermittelt werden können. Es gilt die Geometrie des Euklid. Das Universum ist kein Vektorraum, Distanzen müssen auf andere Art berechnet werden.
14 Das Universum nach Isaac Newton Wir leben in einer dreidimensionalen Welt, gedacht als feste Bühne. Der Raum hat Höhe, Breite und Tiefe. In der Physik wird der Raum mathematisch durch Koordinatensysteme beschrieben. Diese Methode geht auf René Descartes (lateinisch Cartesius, ) zurück. Ihm zu ehren nennt man die gebräuchlichste Form eines Koordinatensystems kartesisches Koordinatensystem. Im kartesischen Koordinatensystem wird der Ort eines Punktes durch drei Koordinaten angegeben. Meist nennt man diese x, y und z. Sie sind voneinander unabhängig, die Richtungen der x-, y- und z-achse stehen in rechten Winkeln aufeinander. Es gibt aber auch andere Koordinatensysteme: So kann man die Position eines Punktes auch durch einen Abstand von einem beliebig gewählten Mittelpunkt und zwei Winkeln angeben. Damit erhält man Kugelkoordinaten. Im Grunde können Koordinaten durch ein beliebig kompliziert verzerrtes Netz von Gitterlinien erzeugt werden. Es müssen nur jedem Punkt eindeutig drei Werte als Koordinaten zugeordnet werden. Diese dürfen sogar Zeitabhängig sein. So kann man rotierende Koordinatensysteme definieren, die sich zum Beispiel mit der Erde mitdrehen.
15 Der Raum ist eine leere Bühne Newton stellte sich den Raum als leere Bühne vor: Newton sah im Raum den Rahmen für alles, was im Kosmos vorgeht. Er war das Theater für das Drama des Universums. Newtons Bühne war passiv, absolut, ewig und unveränderlich. Das Schauspiel hatte keinen Einfluss auf die Bühne, und umgekehrt.
16 Newton alles in dieser Bühne beschreiben
17 Gauß: es gibt allgemeinere Räume
18 Kugeloberfläche S² metrischer Raum Ameise stellt fest: Die Welt ist 2D, jedoch gekrümmt Wie kann sie feststellen, dass S² nicht-euklidisch ist?
19 durch Vermessen der Winkelsumme! a + b + g = 180 a + b + g > 180 Grafik: Wikipedia
20 Wie bestimmt man Abstand zwischen zwei Punkten auf dem Globus? Geodäten sind die Kurven minimaler Länge auf gekrümmten Flächen. Im euklidischen Raum sind Geodäten Geraden. Großkreise sind die Geodäten der Kugeloberfläche.
21 Kugeloberfläche metrischer Raum
22 Wie kann ich die Krümmung feststellen? Sphäre Pos. Krümmung Hyperboloid Neg. Krümmung
23 Flächen konstanter Krümmung positive Krümmung Krümmung null negative Krümmung
24 Hypersphäre S³ ist metrischer Raum Die Hypersphäre S³ kann als Fläche im 4D Euklidischen Raum aller Punkte {x 1,x 2,x 3,x 4 } generiert werden mit der Bedingung: S³: Jeder Punkt auf dem Kreis besteht aus Sphäre S²
25 Längenelement auf der Hypersphäre I
26 Längenelement auf der Hypersphäre II
27 Oberflächen von Hypersphären S 1 S² S³ S 4
28 Distanzmessung auf gekrümmten 3-Flächen Euklidischer 3-Raum kartesisch: ds² = dx² + dy² + dz² Euklidischer Raum als 2-Sphären S²: 2 Winkel ds² = dr² + r² (dq² + sin²q df²) Hypersphäre S³: 3 Winkel ds² = R 0 ²[dc² + sin²c (dq² + sin²q df²)] 3-Hyperboloid H³: 3 Winkel ds² = R 0 ²[dc² + sinh²c (dq² + sin²q df²)]
29 S², S³ & H 3 sind Mannigfaltigkeiten M Wesentlich Der Raum ist lokal flach Jede Mannigfaltigkeit kannn durch abzählbar viele Karten eines Atlas überdeckt werden.
30 Kugeloberfläche S² lokal Euklidisch! Der Atlas ist in der Kartografie eine Sammlung thematisch, inhaltlich oder regional zusammenhängender flacher Landkarten der ganzen Erdoberfläche.
31 In jedem Punkt ein Tangentenraum, der Euklidisch (Minkowski) ist
32 Tangentenräume längs einer Kurve
33 Der Tangentenraum der Sphäre
34 Die Tangentenräume der Sphäre sind zunächst unkorreliert
35 Wie Vektoren entlang Kurve transportieren?
36 Krümmung einer Fläche nach Gauß Gauß Krümmung: K = k 1 k 2 Theorema Egregium: Die Gaußsche Krümmung K einer Fläche S R³ ist nur eine Größe der inneren Geometrie von S.
37 Die Krümmung Mannigfaltigkeiten Dieser intrinsische Krümmungsbegriff von Gauß lässt sich verallgemeinern auf Mannigfaltigkeiten beliebiger Dimension mit einer Metrik ds². Auf solchen Mannigfaltigkeiten ist der Paralleltransport längs Kurven erklärt und die Krümmungsgrößen (Riemann-Tensor) geben an, wie groß die Richtungsänderung von Vektoren beim Paralleltransport längs geschlossener Kurven nach einem Umlauf ist.
38 Zeit als vierte Dimension Zusätzlich zu den drei Raumdimensionen braucht man im Universum eine Angabe der Zeit. In der Newtonschen Physik, die seit der Renaissance bis 1905 für uneingeschränkt gültig gehalten wurde, stellte man sich die Zeit von allen physikalischen Prozessen unabhängig vor. Die Zeit sollte sozusagen den Takt vorgeben, nach dem sich alle physikalischen Prozesse richten, ohne selbst auf die Zeit zurückzuwirken. Schon vor der Relativitätstheorie war es nicht unüblich, sich die Zeit als eine vierte Dimension vorzustellen. Fasst man die Zeit als eine vierte Dimension auf, so wird jedes Objekt nicht nur durch sein Volumen im Raum, also Länge, Höhe und Breite, sondern zusätzlich durch seine Ausdehnung in der Zeit beschrieben. Das ist seine Dauer. Man kann sich also die ganze Entwicklung eines Menschen vom Säugling bis zum Greis als ein Objekt in einer vierdimensionalen Raumzeit aus Raum- und Zeitkoordinaten vorstellen. Ein bestimmter Zeitpunkt im Leben dieses Menschen ist dann ein Schnitt durch diese Raumzeit bei einer bestimmten Zeitkoordinate.
39 Die Universalität Lichtgeschwindigkeit Albert Einstein 1905: c hängt nicht von Bewegung ab Aus der Universalität der Lichtgeschwindigkeit folgt direkt, dass die Lichtgeschwindigkeit die maximal erreichbare Geschwindigkeit ist. Es ist nicht möglich einen Körper auf Lichtgeschwindigkeit oder darüber hinaus zu beschleunigen. Anschaulich kann man das damit begründen, dass sich Licht aus der Sicht jedes Objektes mit der konstanten Geschwindigkeit von über einer Milliarde Kilometern in der Stunde bewegt. Jedes Objekt ist also stets gleich weit von der Lichtgeschwindigkeit entfernt. Für den äußeren Beobachter macht sich diese Tatsache dadurch bemerkbar, dass man immer mehr Energie braucht um einen Körper zu beschleunigen je näher er der Lichtgeschwindigkeit kommt. Es hat den Anschein, als würde der Körper immer träger werden, als würde seine Masse zunehmen. Wenn es eine maximale Geschwindigkeit gibt, die für jede Form von Bewegung gilt, dann hat das Konsequenzen auf den Begriff der Gleichzeitigkeit: Ereignisse, die nacheinander geschehen aber räumlich weit voneinander getrennt sind, können einander ebenso wenig beeinflussen wie gleichzeitige Ereignisse.
40 Raum und Zeit müssen zusammenarbeiten
41 Hermann Minkowski interpretiert 1908 Einstein RaumZeit Weltpunkt oder Ereignis: (ct,x,y,z) Abstand zwischen 2 Ereignissen: ds² = c²dt² - dx² - dy² - dz² Von Stund an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken, und nur noch eine Union der beiden soll Selbständigkeit bewahren. Minkowski generiert den Begriff der RaumZeit = {(ct,x,y,z)}.
42 Hermann Minkowski interpretiert Einsteins Relativität als 4D RaumZeit = {Ereignisse} = {ct,x,y,z}
43 Teilchen beschreibt Weltlinie RaumZeit
44 History der Objekte im Universum
45 Minkowski RaumZeit = Vektorraum V µ = (V 0,V 1,V 2,V 3 ) V² = h µn V µ V n Grafik: Camenzind
46 Die kausale Struktur der RaumZeit Jedes Ereignis innerhalb des oberen Teils des Lichtkegels von B kann Informationen bzw. Nachrichten von B erhalten. Ereignis innerhalb des oberen Teils des Lichtkegels von B kann von B kausal beeinflusst werden. Das Innere des unteren Teils des Lichtkegels vom Beobachter hat eine ähnliche Bedeutung wie der obere. In ihm sind alle Ereignisse enthalten, die B kausal beeinflussen können. Alle Ereignisse außerhalb des unteren Teils des Lichtkegels von B können B nicht kausal beeinflussen.
47 1915: Wie Gravitation einbauen? Verallgemeinerung von Minkowski: Die RaumZeit ist nur noch lokal Minkowski: RaumZeit ist eine Mannigfaltigkeit mit Metrik ds² = g µn dx µ dx n. Mit Materie ist die RaumZeit nicht mehr flach. Das Universum ist eine RaumZeit
48 Das Geheimnis der Gravitation ist die RaumZeit selbst Raum ist krümm- und dehnbar!
49 Materie & Energie krümmt den Raum Gravitation ist die Form der RaumZeit
50 Raum ist real, denn er verdreht Kreisel im Gravity Probe B Experiment
51 Postulate der Einsteinschen Gravitation
52 Vakuum: Der Raum ist aber nicht leer!
Gravitation und Krümmung der Raum-Zeit - Teil 1
 Gravitation und Krümmung der Raum-Zeit - Teil 1 Gauß hat gezeigt, daß es Möglichkeiten gibt, die Krümmung von Flächen durch inhärente Messungen auf der Fläche selbst zu bestimmen Gauß sches Krümmungsmaß
Gravitation und Krümmung der Raum-Zeit - Teil 1 Gauß hat gezeigt, daß es Möglichkeiten gibt, die Krümmung von Flächen durch inhärente Messungen auf der Fläche selbst zu bestimmen Gauß sches Krümmungsmaß
Die Geometrie des Universums. Max Camenzind Akademie Heidelberg November 2014
 Die Geometrie des Universums Max Camenzind Akademie Heidelberg November 2014 Komet 67P Komet 67P: Perihel: 1,2432 AE Aphel: 5,689 AE a = 3,463 AE e = 0,6412 P = 6,44 a i = 7,04 P Rot = 12,4 h 67P Kometenbahn
Die Geometrie des Universums Max Camenzind Akademie Heidelberg November 2014 Komet 67P Komet 67P: Perihel: 1,2432 AE Aphel: 5,689 AE a = 3,463 AE e = 0,6412 P = 6,44 a i = 7,04 P Rot = 12,4 h 67P Kometenbahn
Das Konzept der Raumzeit-Krümmung
 Das Konzept der Raumzeit-Krümmung Franz Embacher Fakultät für Physik der Universität Wien Vortrag auf der Jahrestagung der Wiener Arbeitsgemeinschaft für Astronomie Wien, 14. November 2015 Das Konzept
Das Konzept der Raumzeit-Krümmung Franz Embacher Fakultät für Physik der Universität Wien Vortrag auf der Jahrestagung der Wiener Arbeitsgemeinschaft für Astronomie Wien, 14. November 2015 Das Konzept
Raum, Zeit, Universum Die Rätsel des Beginns. Bild : pmmagazin
 Raum, Zeit, Universum Die Rätsel des Beginns Bild : pmmagazin Der Urknall Wie unser Universum aus fast Nichts entstand Inflationäres Universum Überall fast Nichts nur Fluktuationen Explosionsartige Expansion
Raum, Zeit, Universum Die Rätsel des Beginns Bild : pmmagazin Der Urknall Wie unser Universum aus fast Nichts entstand Inflationäres Universum Überall fast Nichts nur Fluktuationen Explosionsartige Expansion
Allgemeine Relativitätstheorie, was ist das?
 , was ist das? 1905 stellte Albert Einstein die Spezielle Relativitätstheorie auf Beim Versuch die Gravitation im Rahmen der Speziellen Relativitätstheorie zu beschreiben stieß er allerdings schnell auf
, was ist das? 1905 stellte Albert Einstein die Spezielle Relativitätstheorie auf Beim Versuch die Gravitation im Rahmen der Speziellen Relativitätstheorie zu beschreiben stieß er allerdings schnell auf
Krümmung in der Mathematik und Physik. Relativitätstheorie im Alltag
 Krümmung in der Mathematik und Physik Relativitätstheorie im Alltag Justus-Liebig-Universität Giessen Dr. Frank Morherr Was ist Krümmung? Gerade soll Krümmung Null haben. Prototyp Kreis - großer Radius,
Krümmung in der Mathematik und Physik Relativitätstheorie im Alltag Justus-Liebig-Universität Giessen Dr. Frank Morherr Was ist Krümmung? Gerade soll Krümmung Null haben. Prototyp Kreis - großer Radius,
Kapitel 3. Minkowski-Raum. 3.1 Raumzeitlicher Abstand
 Kapitel 3 Minkowski-Raum Die Galilei-Transformation lässt zeitliche Abstände und Längen unverändert. Als Länge wird dabei der räumliche Abstand zwischen zwei gleichzeitigen Ereignissen verstanden. Solche
Kapitel 3 Minkowski-Raum Die Galilei-Transformation lässt zeitliche Abstände und Längen unverändert. Als Länge wird dabei der räumliche Abstand zwischen zwei gleichzeitigen Ereignissen verstanden. Solche
Die Geometrie. des Universums. Max Camenzind APCOSMO SS2012
 Die Geometrie des Universums Max Camenzind APCOSMO TUDA @ SS01 Das Universum Expandiert Der Raum wird gestreckt Hubble: Das Universum der Galaxien expandiert! Das Universum ist jedoch ein Kontinuum aus
Die Geometrie des Universums Max Camenzind APCOSMO TUDA @ SS01 Das Universum Expandiert Der Raum wird gestreckt Hubble: Das Universum der Galaxien expandiert! Das Universum ist jedoch ein Kontinuum aus
Die Geometrie des Universums. Max Camenzind Senioren Uni
 Die Geometrie des Universums Max Camenzind Senioren Uni Würzburg @WS2012 Mike Turner 2009 Wie stellen Sie sich unser Universum vor? Wie groß? Wie alt? Struktur? Antike Vorstellung Van Gogh 1889 Einstein
Die Geometrie des Universums Max Camenzind Senioren Uni Würzburg @WS2012 Mike Turner 2009 Wie stellen Sie sich unser Universum vor? Wie groß? Wie alt? Struktur? Antike Vorstellung Van Gogh 1889 Einstein
Grundideen der allgemeinen Relativitätstheorie
 Grundideen der allgemeinen Relativitätstheorie David Moch La Villa 2006 Inhalt Newtons Physik und ihr Versagen Einsteins Lösung von Raum und Zeit: Die spezielle Relativitätstheorie Minkowskis Vereinigung
Grundideen der allgemeinen Relativitätstheorie David Moch La Villa 2006 Inhalt Newtons Physik und ihr Versagen Einsteins Lösung von Raum und Zeit: Die spezielle Relativitätstheorie Minkowskis Vereinigung
Allgemeine Relativitätstheorie
 Allgemeine Relativitätstheorie Ein konzeptioneller Einblick Von Jan Kaprolat Gliederung Einleitung Übergang SRT -> ART Grundlegende Fragestellungen der ART Kurzer Einblick: Tensoralgebra Einsteinsche Feldgleichungen
Allgemeine Relativitätstheorie Ein konzeptioneller Einblick Von Jan Kaprolat Gliederung Einleitung Übergang SRT -> ART Grundlegende Fragestellungen der ART Kurzer Einblick: Tensoralgebra Einsteinsche Feldgleichungen
Minkowski-Geometrie in der Schule. Michael Bürker
 Minkowski-Geometrie in der Schule Michael Bürker buerker@online.de Gliederung Weg-Zeit-Diagramme Grundprinzipien der speziellen Relativitätstheorie Drei Symmetrieprinzipien Der relativistische Faktor Lorentz-Kontraktion
Minkowski-Geometrie in der Schule Michael Bürker buerker@online.de Gliederung Weg-Zeit-Diagramme Grundprinzipien der speziellen Relativitätstheorie Drei Symmetrieprinzipien Der relativistische Faktor Lorentz-Kontraktion
24 Minkowskis vierdimensionale Raumzeit
 24 Minkowskis vierdimensionale Raumzeit Der deutsche Mathematiker Hermann Minkowski (1864 1909) erkannte, daß sich die von Albert Einstein 1905 entwickelte spezielle Relativitätstheorie am elegantesten
24 Minkowskis vierdimensionale Raumzeit Der deutsche Mathematiker Hermann Minkowski (1864 1909) erkannte, daß sich die von Albert Einstein 1905 entwickelte spezielle Relativitätstheorie am elegantesten
Nichteuklidische Geometrien und gekrümmte Räume
 Nichteuklidische Geometrien und gekrümmte Räume Es begann mit dem Problem der Landvermessung... Carl Friedrich Gauß (1777-1855): Theorie gekrümmter Flächen Landesvermessung des Königreichs Hannover Entdeckung
Nichteuklidische Geometrien und gekrümmte Räume Es begann mit dem Problem der Landvermessung... Carl Friedrich Gauß (1777-1855): Theorie gekrümmter Flächen Landesvermessung des Königreichs Hannover Entdeckung
Die Expansion des Kosmos
 Die Expansion des Kosmos Mythos und Wirklichkeit Dr. Wolfgang Steinicke MNU-Tagung Freiburg 2012 Eine Auswahl populärer Mythen und Probleme der Kosmologie Der Urknall vor 13,7 Mrd. Jahren war eine Explosion
Die Expansion des Kosmos Mythos und Wirklichkeit Dr. Wolfgang Steinicke MNU-Tagung Freiburg 2012 Eine Auswahl populärer Mythen und Probleme der Kosmologie Der Urknall vor 13,7 Mrd. Jahren war eine Explosion
Allgemeine Relativitätstheorie
 Allgemeine Relativitätstheorie Eine anschauliche Einführung in die Grundlagen Wegelemente euklidischer Raum: Minkowski-Raum: y c t ds dy ds 2 =dx 2 dy 2 ds c d t ds 2 =c 2 dt 2 dx 2 dx x invariant bei
Allgemeine Relativitätstheorie Eine anschauliche Einführung in die Grundlagen Wegelemente euklidischer Raum: Minkowski-Raum: y c t ds dy ds 2 =dx 2 dy 2 ds c d t ds 2 =c 2 dt 2 dx 2 dx x invariant bei
Gravitation und Raumzeitkrümmung
 Roland Steinbauer Fakultät für Mathematik, Universität Wien ÖAW, Gravitation 2015, Oktober 2015 1 / 36 Die Einsteingleichungen (1) November 1915 Albert Einstein, Zur allgemeinen Relativitätstheorie Die
Roland Steinbauer Fakultät für Mathematik, Universität Wien ÖAW, Gravitation 2015, Oktober 2015 1 / 36 Die Einsteingleichungen (1) November 1915 Albert Einstein, Zur allgemeinen Relativitätstheorie Die
Allgemeine Relativitätstheorie
 Kontrollfragen Allgemeine Relativitätstheorie Stephan Mertens Wintersemester 2009 UE R ICKE UNI VERSITÄT MAG G N VO D O TT O EBURG 1 Einführung und Motivation 1. Warum kann das Newton sche Gravitationsgesetz
Kontrollfragen Allgemeine Relativitätstheorie Stephan Mertens Wintersemester 2009 UE R ICKE UNI VERSITÄT MAG G N VO D O TT O EBURG 1 Einführung und Motivation 1. Warum kann das Newton sche Gravitationsgesetz
Triangulierungen und Kartographie
 Triangulierungen und Kartographie Ein Einblick in geometrische und topologische Methoden Stefan Krauss, Clara Löh Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg 23. Juli 2014 Was verraten
Triangulierungen und Kartographie Ein Einblick in geometrische und topologische Methoden Stefan Krauss, Clara Löh Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg 23. Juli 2014 Was verraten
Vorlesung: Klassische Theoretische Physik I
 Vorlesung: Klassische Theoretische Physik I M. Zirnbauer Institut für Theoretische Physik Universität zu Köln Sommersemester 2015 Contents 1 Newtonsche Mechanik 3 1.1 Affine und Euklidische Räume.............................
Vorlesung: Klassische Theoretische Physik I M. Zirnbauer Institut für Theoretische Physik Universität zu Köln Sommersemester 2015 Contents 1 Newtonsche Mechanik 3 1.1 Affine und Euklidische Räume.............................
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Kosmologie. der Allgemeinen Relativitätstheorie. Das expandierende Universum
 Kosmologie der Allgemeinen Relativitätstheorie Das expandierende Universum Historie der Theorie Albert Einstein 1916 Es gibt keinen absoluten Raum im Newtonschen Sinne. Massen bestimmen die Geometrie des
Kosmologie der Allgemeinen Relativitätstheorie Das expandierende Universum Historie der Theorie Albert Einstein 1916 Es gibt keinen absoluten Raum im Newtonschen Sinne. Massen bestimmen die Geometrie des
Relativität und Realität
 Max Drömmer Relativität und Realität Zur Physik und Philosophie der allgemeinen und der speziellen Relativitätstheorie mentis PADERBORN Inhaltsverzeichnis Vorwort... 15 Einleitung... 17 Kapitel 1 Allgemeine
Max Drömmer Relativität und Realität Zur Physik und Philosophie der allgemeinen und der speziellen Relativitätstheorie mentis PADERBORN Inhaltsverzeichnis Vorwort... 15 Einleitung... 17 Kapitel 1 Allgemeine
Gravitation und Krümmung der Raum-Zeit - Teil 2
 Gravitation und Krümmung der Raum-Zeit - Teil 2 Einsteinsche Gravitationsfeldgleichungen Krümmung der Raumzeit = universelle Konstante x Energie- und Impulsdichte Die Raumzeit wirkt auf die Masse (Energie),
Gravitation und Krümmung der Raum-Zeit - Teil 2 Einsteinsche Gravitationsfeldgleichungen Krümmung der Raumzeit = universelle Konstante x Energie- und Impulsdichte Die Raumzeit wirkt auf die Masse (Energie),
Was ist Trägheit und Gravitation wirklich! Thermal-Time-Theorie
 Was ist Trägheit und Gravitation wirklich! Thermal-Time-Theorie Hypothese Nach der Thermal-Time-Theorie (ttt) ist die Gravitation keine Kraft zwischen zwei Massen, sondern eine Beschleunigung bzw. Kraft,
Was ist Trägheit und Gravitation wirklich! Thermal-Time-Theorie Hypothese Nach der Thermal-Time-Theorie (ttt) ist die Gravitation keine Kraft zwischen zwei Massen, sondern eine Beschleunigung bzw. Kraft,
Der Big Bang Was sagt die Relativitätstheorie über den Anfang unseres Universums?
 Der Big Bang Was sagt die Relativitätstheorie über den Anfang unseres Universums? Wir leben in einem Universum, das den Gesetzen der von Einstein gegründeten Relativitätstheorie gehorcht. Im letzten Jahrhundert
Der Big Bang Was sagt die Relativitätstheorie über den Anfang unseres Universums? Wir leben in einem Universum, das den Gesetzen der von Einstein gegründeten Relativitätstheorie gehorcht. Im letzten Jahrhundert
Rotverschiebung & Hubble-Gesetz
 Rotverschiebung z Rotverschiebung & Hubble-Gesetz Rückblickzeit in Mrd. Jahren Max Camenzind Akademie Heidelberg Dezember 2014 Universum = 4D RaumZeit Beispiel EdS (k=0): a(t) = (t/t 0 ) 2/3 a 0, t 0 Koordinaten
Rotverschiebung z Rotverschiebung & Hubble-Gesetz Rückblickzeit in Mrd. Jahren Max Camenzind Akademie Heidelberg Dezember 2014 Universum = 4D RaumZeit Beispiel EdS (k=0): a(t) = (t/t 0 ) 2/3 a 0, t 0 Koordinaten
Seminar Einführung in die Kunst mathematischer Ungleichungen
 Seminar Einführung in die Kunst mathematischer Ungleichungen Geometrie und die Summe von Quadraten Clara Brünn 25. April 2016 Inhaltsverzeichnis 1 Einleitung 2 1.1 Geometrie allgemein.................................
Seminar Einführung in die Kunst mathematischer Ungleichungen Geometrie und die Summe von Quadraten Clara Brünn 25. April 2016 Inhaltsverzeichnis 1 Einleitung 2 1.1 Geometrie allgemein.................................
Euklidischer Raum Kartesisches Koordinatensystem. 1 E Ma 1 Lubov Vassilevskaya
 Euklidischer Raum Kartesisches Koordinatensystem 1 E Ma 1 Lubov Vassilevskaya Algebra und Geometrie Man zerlegt die Mathematik in Teildisziplinen: Arithmetik, Algebra, Geometrie und so weiter, doch diese
Euklidischer Raum Kartesisches Koordinatensystem 1 E Ma 1 Lubov Vassilevskaya Algebra und Geometrie Man zerlegt die Mathematik in Teildisziplinen: Arithmetik, Algebra, Geometrie und so weiter, doch diese
Kosmologische Entfernungen Samstag, 07. März Das heißt, dass sich
 Reiner Guse Astro-Stammtisch Peine Kosmologische Entfernungen Samstag, 07. März 2015 Amateurastronomie in 360 Planetarium Wolfsburg 1. Die Expansion des Universums und ihre Folgen Hubble stellte 1929 fest,
Reiner Guse Astro-Stammtisch Peine Kosmologische Entfernungen Samstag, 07. März 2015 Amateurastronomie in 360 Planetarium Wolfsburg 1. Die Expansion des Universums und ihre Folgen Hubble stellte 1929 fest,
Proseminar Kosmologie und Astroteilchen: Das kosmologische Standardmodell
 Proseminar Kosmologie und Astroteilchen: Das kosmologische Standardmodell Tobias Behrendt 24.11.2011 Inhaltsverzeichnis 1 Das kosmologische Prinzip 4 2 Erinnerung: ART und Metriken 5 2.1 Gauss sche Koordinaten............................
Proseminar Kosmologie und Astroteilchen: Das kosmologische Standardmodell Tobias Behrendt 24.11.2011 Inhaltsverzeichnis 1 Das kosmologische Prinzip 4 2 Erinnerung: ART und Metriken 5 2.1 Gauss sche Koordinaten............................
Grundlagen ART: Koordinaten und
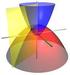 Grundlagen ART: Koordinaten und gekrümmte Flächen Vom Schwarzen Loch bis zum Urknall: Einsteins Astrophysik für Nicht-Physiker Haus der Astronomie/Institut für Theoretische Astrophysik 22.10.2015 Zunächst
Grundlagen ART: Koordinaten und gekrümmte Flächen Vom Schwarzen Loch bis zum Urknall: Einsteins Astrophysik für Nicht-Physiker Haus der Astronomie/Institut für Theoretische Astrophysik 22.10.2015 Zunächst
Urknall und. Entwicklung des Universums. Grundlegende Beobachtungen Das Big-Bang Modell Die Entwicklung des Universums 1.1
 Urknall und Entwicklung des Universums Thomas Hebbeker RWTH Aachen Dies Academicus 08.06.2005 Grundlegende Beobachtungen Das Big-Bang Modell Die Entwicklung des Universums 1.1 Blick ins Universum: Sterne
Urknall und Entwicklung des Universums Thomas Hebbeker RWTH Aachen Dies Academicus 08.06.2005 Grundlegende Beobachtungen Das Big-Bang Modell Die Entwicklung des Universums 1.1 Blick ins Universum: Sterne
Ist das Universum ein 3-Torus?
 1 / 20 Ist das Universum ein 3-Torus? RHO-Sommercamp, Waren Martin Haufschild 19. August 2009 2 / 20 Krümmung Kosmologische Räume werden gewöhnlich nach ihrer (Gaußschen) Krümmung K unterschieden: positive
1 / 20 Ist das Universum ein 3-Torus? RHO-Sommercamp, Waren Martin Haufschild 19. August 2009 2 / 20 Krümmung Kosmologische Räume werden gewöhnlich nach ihrer (Gaußschen) Krümmung K unterschieden: positive
v = z c (1) m M = 5 log
 Hubble-Gesetz Das Hubble-Gesetz ist eines der wichtigsten Gesetze der Kosmologie. Gefunden wurde es 1929 von dem amerikanischen Astronom Edwin Hubble. Hubble maß zunächst die Rotverschiebung z naher Galaxien
Hubble-Gesetz Das Hubble-Gesetz ist eines der wichtigsten Gesetze der Kosmologie. Gefunden wurde es 1929 von dem amerikanischen Astronom Edwin Hubble. Hubble maß zunächst die Rotverschiebung z naher Galaxien
Theoretische Physik 1, Mechanik
 Theoretische Physik 1, Mechanik Harald Friedrich, Technische Universität München Sommersemester 2009 Mathematische Ergänzungen Vektoren und Tensoren Partielle Ableitungen, Nabla-Operator Physikalische
Theoretische Physik 1, Mechanik Harald Friedrich, Technische Universität München Sommersemester 2009 Mathematische Ergänzungen Vektoren und Tensoren Partielle Ableitungen, Nabla-Operator Physikalische
Urknall und Entwicklung des Universums
 Urknall und Entwicklung des Universums Thomas Hebbeker RWTH Aachen University Dies Academicus 11.06.2008 Grundlegende Beobachtungen Das Big-Bang Modell Die Entwicklung des Universums 1.0 Blick ins Universum:
Urknall und Entwicklung des Universums Thomas Hebbeker RWTH Aachen University Dies Academicus 11.06.2008 Grundlegende Beobachtungen Das Big-Bang Modell Die Entwicklung des Universums 1.0 Blick ins Universum:
Mathematisierung der Gravitation: Die Schwarzschildlösung der Einsteingleichungen als Grundmodell vieler Phänomene der Gravitation
 Gerhard Huisken Mathematisierung der Gravitation: Die Schwarzschildlösung der Einsteingleichungen als Grundmodell vieler Phänomene der Gravitation Als Beispiel für ein mathematisches Modell in der theoretischen
Gerhard Huisken Mathematisierung der Gravitation: Die Schwarzschildlösung der Einsteingleichungen als Grundmodell vieler Phänomene der Gravitation Als Beispiel für ein mathematisches Modell in der theoretischen
1 Einleitung. 1.1 Motivation. 6 Differentialgeometrie: Grundlagen Vorlesung 1
 6 Differentialgeometrie: Grundlagen Vorlesung Einleitung. Motivation.. Name of the game Geometer bezeichnet klassisch einen Landvermesser (heute ist eher Geodät gebräuchlich. Die klassische Differentialgeometrie
6 Differentialgeometrie: Grundlagen Vorlesung Einleitung. Motivation.. Name of the game Geometer bezeichnet klassisch einen Landvermesser (heute ist eher Geodät gebräuchlich. Die klassische Differentialgeometrie
RIEMANNSCHE GEOMETRIE UND TENSORANALYSIS
 P. K. RASCHEWSKI RIEMANNSCHE GEOMETRIE UND TENSORANALYSIS 2. unveränderte Auflage mit 32 Abbildungen VERLAG HARRI DEUTSCH INHALTSVERZEICHNIS L Tensoren im dreidimensionalen euklidischen Baum 1. Einstufige
P. K. RASCHEWSKI RIEMANNSCHE GEOMETRIE UND TENSORANALYSIS 2. unveränderte Auflage mit 32 Abbildungen VERLAG HARRI DEUTSCH INHALTSVERZEICHNIS L Tensoren im dreidimensionalen euklidischen Baum 1. Einstufige
Die Entwicklung der Urknalltheorie. Manuel Erdin Gymnasium Liestal, 2012
 Die Entwicklung der Urknalltheorie Manuel Erdin Gymnasium Liestal, 2012 William Herschel (1738 1822) Das statische Universum mit einer Galaxie Das Weltbild Herschels Die Position unseres Sonnensystems
Die Entwicklung der Urknalltheorie Manuel Erdin Gymnasium Liestal, 2012 William Herschel (1738 1822) Das statische Universum mit einer Galaxie Das Weltbild Herschels Die Position unseres Sonnensystems
4. Veranstaltung. 16. November 2012
 4. Veranstaltung 16. November 2012 Heute Wiederholung Beschreibung von Bewegung Ursache von Bewegung Prinzip von Elektromotor und Generator Motor Generator Elektrischer Strom Elektrischer Strom Magnetkraft
4. Veranstaltung 16. November 2012 Heute Wiederholung Beschreibung von Bewegung Ursache von Bewegung Prinzip von Elektromotor und Generator Motor Generator Elektrischer Strom Elektrischer Strom Magnetkraft
Formelsammlung. Lagrange-Gleichungen: q k. Zur Koordinate q k konjugierter Impuls: p k = L. Hamilton-Funktion: p k. Hamiltonsche Gleichungen: q k = H
 Formelsammlung Lagrange-Gleichungen: ( ) d L dt q k L q k = 0 mit k = 1,..., n. (1) Zur Koordinate q k konjugierter Impuls: p k = L q k. (2) Hamilton-Funktion: n H(q 1,..., q n, p 1,..., p n, t) = p k
Formelsammlung Lagrange-Gleichungen: ( ) d L dt q k L q k = 0 mit k = 1,..., n. (1) Zur Koordinate q k konjugierter Impuls: p k = L q k. (2) Hamilton-Funktion: n H(q 1,..., q n, p 1,..., p n, t) = p k
Vektoren. Jörn Loviscach. Versionsstand: 11. April 2009, 23:42
 Vektoren Jörn Loviscach Versionsstand:. April 29, 23:42 Rechnen mit Pfeilen Bei den komplexen Zahlen haben wir das Rechnen mit Pfeilen schon kennen gelernt. Addition und Subtraktion klappen in drei wie
Vektoren Jörn Loviscach Versionsstand:. April 29, 23:42 Rechnen mit Pfeilen Bei den komplexen Zahlen haben wir das Rechnen mit Pfeilen schon kennen gelernt. Addition und Subtraktion klappen in drei wie
Die allgemeine Relativitätstheorie
 Die allgemeine Relativitätstheorie Manuel Hohmann Universität Hamburg 20. Juni 2006 Inhaltsverzeichnis 1 Was ist die ART? 3 2 Wie löst die ART alte Probleme? 9 3 Welche neuen Vorhersagen macht die ART?
Die allgemeine Relativitätstheorie Manuel Hohmann Universität Hamburg 20. Juni 2006 Inhaltsverzeichnis 1 Was ist die ART? 3 2 Wie löst die ART alte Probleme? 9 3 Welche neuen Vorhersagen macht die ART?
Mathematik für das Ingenieurstudium
 Mathematik für das Ingenieurstudium von Martin Stämpfle, Jürgen Koch 2., aktual. Aufl. Hanser München 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 43232 1 Zu Inhaltsverzeichnis schnell
Mathematik für das Ingenieurstudium von Martin Stämpfle, Jürgen Koch 2., aktual. Aufl. Hanser München 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 43232 1 Zu Inhaltsverzeichnis schnell
Moderne Kosmologie. Michael H Soffel. Lohrmann Observatorium TU Dresden
 Moderne Kosmologie Michael H Soffel Lohrmann Observatorium TU Dresden Die Expansion des Weltalls NGC 1300 1 Nanometer = 1 Millionstel mm ; 10 Å = 1 nm Fraunhofer Spektrum Klar erkennbare Absorptionslinien
Moderne Kosmologie Michael H Soffel Lohrmann Observatorium TU Dresden Die Expansion des Weltalls NGC 1300 1 Nanometer = 1 Millionstel mm ; 10 Å = 1 nm Fraunhofer Spektrum Klar erkennbare Absorptionslinien
Albert Einsteins Relativitätstheorie und die moderne Kosmologie In welchem Universum leben wir?
 Albert Einsteins Relativitätstheorie und die moderne Kosmologie In welchem Universum leben wir? Günter Wunner Institut für Theoretische Physik Universität Stuttgart Einsteins Wunderjahr 1905 09.06.1905
Albert Einsteins Relativitätstheorie und die moderne Kosmologie In welchem Universum leben wir? Günter Wunner Institut für Theoretische Physik Universität Stuttgart Einsteins Wunderjahr 1905 09.06.1905
2.3 Gekrümmte Oberflächen
 2.3 Gekrümmte Oberflächen Jede Fläche im R 3 besitzt eine zweidimensionale Parameterdarstellung, so dass die Punkte der Fläche durch r(u, u 2 ) = x(u, u 2 )ê x + y(u, u 2 )ê y + z(u, u 2 )ê z beschrieben
2.3 Gekrümmte Oberflächen Jede Fläche im R 3 besitzt eine zweidimensionale Parameterdarstellung, so dass die Punkte der Fläche durch r(u, u 2 ) = x(u, u 2 )ê x + y(u, u 2 )ê y + z(u, u 2 )ê z beschrieben
Brückenkurs Mathematik. Mittwoch Freitag
 Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Die nummerierten Felder bitte mithilfe der Videos ausfüllen:
 5 Koordinatensysteme Zoltán Zomotor Versionsstand: 6. August 2015, 21:43 Die nummerierten Felder bitte mithilfe der Videos ausfüllen: http://www.z5z6.de This work is based on the works of Jörn Loviscach
5 Koordinatensysteme Zoltán Zomotor Versionsstand: 6. August 2015, 21:43 Die nummerierten Felder bitte mithilfe der Videos ausfüllen: http://www.z5z6.de This work is based on the works of Jörn Loviscach
Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3 Differenziation und Integration von Vektorfunktionen Der Ortsvektor: Man kann einen Punkt P im Raum eindeutig durch die
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3 Differenziation und Integration von Vektorfunktionen Der Ortsvektor: Man kann einen Punkt P im Raum eindeutig durch die
IX Relativistische Mechanik
 IX Relativistische Mechanik 34 Relativitätsprinzip Die bisher behandelte Newtonsche Mechanik gilt nur für Geschwindigkeiten, die klein gegenüber der Lichtgeschwindigkeit sind. Im Teil IX stellen wir die
IX Relativistische Mechanik 34 Relativitätsprinzip Die bisher behandelte Newtonsche Mechanik gilt nur für Geschwindigkeiten, die klein gegenüber der Lichtgeschwindigkeit sind. Im Teil IX stellen wir die
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Hyperbolische Geometrie
 Hyperbolische Geometrie von Sebastian Kalinka und Alexander Thomaso nach dem Buch Elementare Differentialgeometrie von Christian Bär Wiederholung Für κ R setzt man ˆM κ := {(x, y, z) R 3 x 2 + κ(y 2 +
Hyperbolische Geometrie von Sebastian Kalinka und Alexander Thomaso nach dem Buch Elementare Differentialgeometrie von Christian Bär Wiederholung Für κ R setzt man ˆM κ := {(x, y, z) R 3 x 2 + κ(y 2 +
Kosmologie. der Allgemeinen Relativitätstheorie. Das Standard-Modell der. Kosmologie
 Kosmologie der Allgemeinen Relativitätstheorie Das Standard-Modell der Kosmologie Unbeantwortete Fragen der Kosmologie (Stand 1980) Warum beobachtet man keine magnetischen Monopole? Flachheitsproblem:
Kosmologie der Allgemeinen Relativitätstheorie Das Standard-Modell der Kosmologie Unbeantwortete Fragen der Kosmologie (Stand 1980) Warum beobachtet man keine magnetischen Monopole? Flachheitsproblem:
Raum und Zeit Nobelpreisträger Max von Laue spricht über die Relativitätstheorien
 2 Raum und Zeit Nobelpreisträger Max von Laue spricht über die Relativitätstheorien Seit 1951 treffen sich jedes Jahr für eine ganze Woche eine große Anzahl von Nobelpreisträgern aus Medizin, Physik, Chemie
2 Raum und Zeit Nobelpreisträger Max von Laue spricht über die Relativitätstheorien Seit 1951 treffen sich jedes Jahr für eine ganze Woche eine große Anzahl von Nobelpreisträgern aus Medizin, Physik, Chemie
WARUM FINDET MEIN SMARTPHONE OHNE EINSTEIN SEINEN WEG NICHT?
 WARUM FINDET MEIN SMARTPHONE OHNE EINSTEIN SEINEN WEG NICHT? Jürgen R. Reuter, DESY Science Café, DESY 28.11.2012 ALLTAG: (GPS-)NAVIGATION MIT IPHONE Smartphone enthält GPS- Empfänger Positionsbestimmung
WARUM FINDET MEIN SMARTPHONE OHNE EINSTEIN SEINEN WEG NICHT? Jürgen R. Reuter, DESY Science Café, DESY 28.11.2012 ALLTAG: (GPS-)NAVIGATION MIT IPHONE Smartphone enthält GPS- Empfänger Positionsbestimmung
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Analytische Geometrie, Vektorund Matrixrechnung
 Kapitel 1 Analytische Geometrie, Vektorund Matrixrechnung 11 Koordinatensysteme Eine Gerade, eine Ebene oder den Anschauungsraum beschreibt man durch Koordinatensysteme 111 Was sind Koordinatensysteme?
Kapitel 1 Analytische Geometrie, Vektorund Matrixrechnung 11 Koordinatensysteme Eine Gerade, eine Ebene oder den Anschauungsraum beschreibt man durch Koordinatensysteme 111 Was sind Koordinatensysteme?
Mittwochsakademie WS 15/16 Claus Grupen
 Hatte Gott bei der Erschaffung der Welt eine Wahl? Mittwochsakademie WS 15/16 Claus Grupen Am Anfang schuf Gott Himmel Am Anfang schuf Gott und Erde Himmel und Erde. und die Erde war wüst und leer, Und
Hatte Gott bei der Erschaffung der Welt eine Wahl? Mittwochsakademie WS 15/16 Claus Grupen Am Anfang schuf Gott Himmel Am Anfang schuf Gott und Erde Himmel und Erde. und die Erde war wüst und leer, Und
Riemann Geometrie. Basis für die allgemeine Relativitätstheorie. Huber Stefan Rathgeb Christian Walkner Stefan
 Basis für die allgemeine Huber Stefan Rathgeb Christian Walkner Stefan Universität Salzburg Angewandte Informatik 10. Jänner 2005 Inhalt 1 2 Euklidische Geometrie Nichteuklidische Geometrie Krümmung und
Basis für die allgemeine Huber Stefan Rathgeb Christian Walkner Stefan Universität Salzburg Angewandte Informatik 10. Jänner 2005 Inhalt 1 2 Euklidische Geometrie Nichteuklidische Geometrie Krümmung und
Kosmologie I. Thorben Kröger. Juni 2008
 Kosmologie I Thorben Kröger Juni 2008 1 / 48 1 Einführung 2 Robertson-Walker-Metrik 3 Friedmann Gleichungen 4 Einfache Universen 2 / 48 1 Einführung 2 Robertson-Walker-Metrik 3 Friedmann Gleichungen 4
Kosmologie I Thorben Kröger Juni 2008 1 / 48 1 Einführung 2 Robertson-Walker-Metrik 3 Friedmann Gleichungen 4 Einfache Universen 2 / 48 1 Einführung 2 Robertson-Walker-Metrik 3 Friedmann Gleichungen 4
Die Expansion des Universums. Und sein Schicksaal
 Die Expansion des Universums Und sein Schicksaal Was ist das Universum eigentlich? Statisches, unveränderliches, räumlich gekrümmtes Universum von ewiger Dauer mit endlicher Größe? Die größte Eselei Einsteins
Die Expansion des Universums Und sein Schicksaal Was ist das Universum eigentlich? Statisches, unveränderliches, räumlich gekrümmtes Universum von ewiger Dauer mit endlicher Größe? Die größte Eselei Einsteins
entspricht der Länge des Vektorpfeils. Im R 2 : x =
 Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Kosmische Evolution: der Ursprung unseres Universums
 Marsilius Vorlesung Heidelberg 2012 Kosmische Evolution: der Ursprung unseres Universums Simon White Max Planck Institute for Astrophysics Sternkarte des ganzen Himmels bis 10,000 Lichtjahre IR-karte
Marsilius Vorlesung Heidelberg 2012 Kosmische Evolution: der Ursprung unseres Universums Simon White Max Planck Institute for Astrophysics Sternkarte des ganzen Himmels bis 10,000 Lichtjahre IR-karte
Vektoren, Vektorräume
 Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Mathematische Methoden
 Institut für Theoretische Physik der Universität zu Köln http://www.thp.uni-koeln.de/~berg/so/ http://www.thp.uni-koeln.de/~af/ Johannes Berg Andrej Fischer Abgabe: Montag,. Juni Mathematische Methoden.
Institut für Theoretische Physik der Universität zu Köln http://www.thp.uni-koeln.de/~berg/so/ http://www.thp.uni-koeln.de/~af/ Johannes Berg Andrej Fischer Abgabe: Montag,. Juni Mathematische Methoden.
RELATIVITÄTSTHEORIE. (Albert Einstein ) spezielle Relativitätstheorie - allgemeine Relativitätstheorie. Spezielle Relativitätstheorie
 RELATIVITÄTSTHEORIE (Albert Einstein 1879-1955) spezielle Relativitätstheorie - allgemeine Relativitätstheorie Spezielle Relativitätstheorie (Albert Einstein 1905) Zeitdilatation - Längenkontraktion =
RELATIVITÄTSTHEORIE (Albert Einstein 1879-1955) spezielle Relativitätstheorie - allgemeine Relativitätstheorie Spezielle Relativitätstheorie (Albert Einstein 1905) Zeitdilatation - Längenkontraktion =
Aus was besteht unser Universum?
 Aus was besteht unser Universum? Inhalt der Vorlesung Moderne Kosmologie. 1. Von Aristoteles zu Kopernikus 2. Die beobachtbaren Fakten: Kosmologisches Prinzip; Hintergrundstrahlung; Rotverschiebung; dunkle
Aus was besteht unser Universum? Inhalt der Vorlesung Moderne Kosmologie. 1. Von Aristoteles zu Kopernikus 2. Die beobachtbaren Fakten: Kosmologisches Prinzip; Hintergrundstrahlung; Rotverschiebung; dunkle
Outline. 1 Vektoren im Raum. 2 Komponenten und Koordinaten. 3 Skalarprodukt. 4 Vektorprodukt. 5 Analytische Geometrie. 6 Lineare Räume, Gruppentheorie
 Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
2. Vorlesung Wintersemester
 2. Vorlesung Wintersemester 1 Mechanik von Punktteilchen Ein Punktteilchen ist eine Abstraktion. In der Natur gibt es zwar Elementarteilchen (Elektronen, Neutrinos, usw.), von denen bisher keine Ausdehnung
2. Vorlesung Wintersemester 1 Mechanik von Punktteilchen Ein Punktteilchen ist eine Abstraktion. In der Natur gibt es zwar Elementarteilchen (Elektronen, Neutrinos, usw.), von denen bisher keine Ausdehnung
Vorträge gehalten im Rahmen der L2 Vorlesung von Prof. R.A. Bertlmann Jänner Philipp Köhler
 Vorträge gehalten im Rahmen der L2 Vorlesung von Prof. R.A. Bertlmann Jänner 2012 Philipp Köhler Übersicht Newton sche Mechanik und Galileitransformation Elektrodynamik Äther und das Michelson Morley Experiment
Vorträge gehalten im Rahmen der L2 Vorlesung von Prof. R.A. Bertlmann Jänner 2012 Philipp Köhler Übersicht Newton sche Mechanik und Galileitransformation Elektrodynamik Äther und das Michelson Morley Experiment
Lineare Algebra I Vorlesung - Prof. Dr. Daniel Roggenkamp & Falko Gauß
 Lineare Algebra I - 26. Vorlesung - Prof. Dr. Daniel Roggenkamp & Falko Gauß Donnerstag 8.12.: 8:30 Uhr - Vorlesung 10:15 Uhr - große Übung / Fragestunde Klausur: Mittwoch, 14.12. 14:15 Uhr, A3 001 Cauchy-Schwarz
Lineare Algebra I - 26. Vorlesung - Prof. Dr. Daniel Roggenkamp & Falko Gauß Donnerstag 8.12.: 8:30 Uhr - Vorlesung 10:15 Uhr - große Übung / Fragestunde Klausur: Mittwoch, 14.12. 14:15 Uhr, A3 001 Cauchy-Schwarz
Das gravitomagnetische Feld der Erde
 Das gravitomagnetische Feld der Erde von T. Fließbach 1. Einführung magnetisch gravitomagnetisch 2. Bezugssysteme Bevorzugte Inertialsysteme 3. Newton und Mach Absoluter Raum? 4. Drehung eines Foucault-Pendels
Das gravitomagnetische Feld der Erde von T. Fließbach 1. Einführung magnetisch gravitomagnetisch 2. Bezugssysteme Bevorzugte Inertialsysteme 3. Newton und Mach Absoluter Raum? 4. Drehung eines Foucault-Pendels
Friedmann-Robertson-Walker-Metrik und Friedmann-Gleichung
 Friedmann-Robertson-Walker-Metrik und Friedmann-Gleichung Anja Teuber Münster, 29. Oktober 2008 Inhaltsverzeichnis 1 Einleitung 2 2 Allgemeine Relativitätstheorie und die Einstein schen Feldgleichungen
Friedmann-Robertson-Walker-Metrik und Friedmann-Gleichung Anja Teuber Münster, 29. Oktober 2008 Inhaltsverzeichnis 1 Einleitung 2 2 Allgemeine Relativitätstheorie und die Einstein schen Feldgleichungen
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
Mathematischer Vorkurs für Physiker WS 2012/13 Vorlesung 8
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 212/1 Vorlesung 8 Integration über ebene Bereiche Wir betrachten einen regulären Bereich in der x-y Ebene, der einfach zusammenhängend ist.
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 212/1 Vorlesung 8 Integration über ebene Bereiche Wir betrachten einen regulären Bereich in der x-y Ebene, der einfach zusammenhängend ist.
Geometrische Objekte im 3-dimensionalen affinen Raum oder,... wie nützlich ist ein zugehöriger Vektorraum der Verschiebungen
 Geometrische Objekte im -dimensionalen affinen Raum Bekanntlich versteht man unter geometrischen Objekten Punktmengen, auf die man die üblichen Mengenoperationen wie z.b.: Schnittmenge bilden: - aussagenlogisch:
Geometrische Objekte im -dimensionalen affinen Raum Bekanntlich versteht man unter geometrischen Objekten Punktmengen, auf die man die üblichen Mengenoperationen wie z.b.: Schnittmenge bilden: - aussagenlogisch:
Über die Vergangenheit und Zukunft des Universums
 Über die Vergangenheit und Zukunft des Universums Jutta Kunz CvO Universität Oldenburg CvO Universität Oldenburg Physics in the City, 10. Dezember 2009 Jutta Kunz (Universität Oldenburg) Vergangenheit
Über die Vergangenheit und Zukunft des Universums Jutta Kunz CvO Universität Oldenburg CvO Universität Oldenburg Physics in the City, 10. Dezember 2009 Jutta Kunz (Universität Oldenburg) Vergangenheit
Definition von R n. Parallelverschiebungen in R n. Definition 8.1 Unter dem Raum R n (n N) versteht man das kartesische Produkt R R... R (n-mal), d.h.
 8 Elemente der linearen Algebra 81 Der euklidische Raum R n Definition von R n Definition 81 Unter dem Raum R n (n N) versteht man das kartesische Produkt R R R (n-mal), dh R n = {(x 1, x 2,, x n ) : x
8 Elemente der linearen Algebra 81 Der euklidische Raum R n Definition von R n Definition 81 Unter dem Raum R n (n N) versteht man das kartesische Produkt R R R (n-mal), dh R n = {(x 1, x 2,, x n ) : x
1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat.
 1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat. übliche Beispiele: Ort r = r( x; y; z; t ) Kraft F Geschwindigkeit
1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat. übliche Beispiele: Ort r = r( x; y; z; t ) Kraft F Geschwindigkeit
Lorentz-Transformation
 Lorentz-Transformation Aus Sicht von Alice fliegt Bob nach rechts. Aus Sicht von Bob fliegt Alice nach links. Für t = t' = 0 sei also x(0) = x'(0) = Lichtblitz starte bei t = t' = 0 in und erreiche etwas
Lorentz-Transformation Aus Sicht von Alice fliegt Bob nach rechts. Aus Sicht von Bob fliegt Alice nach links. Für t = t' = 0 sei also x(0) = x'(0) = Lichtblitz starte bei t = t' = 0 in und erreiche etwas
Schwarze Löcher Staubsauger oder Stargate? Kai Zuber Inst. f. Kern- und Teilchenphysik TU Dresden
 Schwarze Löcher Staubsauger oder Stargate? Kai Zuber Inst. f. Kern- und Teilchenphysik TU Dresden 4.12.2010 Das Leben des Albert E. - Relativitätstheorie Das Leben der Sterne Schwarze Löcher Wurmlöcher
Schwarze Löcher Staubsauger oder Stargate? Kai Zuber Inst. f. Kern- und Teilchenphysik TU Dresden 4.12.2010 Das Leben des Albert E. - Relativitätstheorie Das Leben der Sterne Schwarze Löcher Wurmlöcher
2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n
![2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n 2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n](/thumbs/49/25862272.jpg) 2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n f ist in dem Fall ein Weg in R n. Das Bild f(t) des Weges wird als Kurve
2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n f ist in dem Fall ein Weg in R n. Das Bild f(t) des Weges wird als Kurve
11. Vorlesung Wintersemester
 11. Vorlesung Wintersemester 1 Ableitungen vektorieller Felder Mit Resultat Skalar: die Divergenz diva = A = A + A y y + A z z (1) Mit Resultat Vektor: die Rotation (engl. curl): ( rota = A Az = y A y
11. Vorlesung Wintersemester 1 Ableitungen vektorieller Felder Mit Resultat Skalar: die Divergenz diva = A = A + A y y + A z z (1) Mit Resultat Vektor: die Rotation (engl. curl): ( rota = A Az = y A y
Lernmaterialblatt Mathematik. Vektorrechnung eine Einführung. Anwendung Mathematik I. Einleitung:
 Vektorrechnung eine Einführung Einleitung: Um beispielsweise das Dreieck ABC in der Abbildung an die Position A'B'C' zu verschieben, muss jeder Punkt um sieben Einheiten nach rechts und drei nach oben
Vektorrechnung eine Einführung Einleitung: Um beispielsweise das Dreieck ABC in der Abbildung an die Position A'B'C' zu verschieben, muss jeder Punkt um sieben Einheiten nach rechts und drei nach oben
Analytische Geometrie des Raumes
 Analytische Geometrie des Raumes Als Begründer der analytischen Geometrie gilt René Descartes (Discours de la méthode). Seine grundliegende Idee bestand darin, geometrische Gebilde (Gerade, Kreis, Ellipse
Analytische Geometrie des Raumes Als Begründer der analytischen Geometrie gilt René Descartes (Discours de la méthode). Seine grundliegende Idee bestand darin, geometrische Gebilde (Gerade, Kreis, Ellipse
Standardmodell der Kosmologie
 ! "# $! "# # % & Standardmodell der Kosmologie Urknall und Entwicklung des Universums Inhalt Einleitung Experimentelle Hinweise auf einen Urknall Rotverschiebung der Galaxien kosmische Hintergrundstrahlung
! "# $! "# # % & Standardmodell der Kosmologie Urknall und Entwicklung des Universums Inhalt Einleitung Experimentelle Hinweise auf einen Urknall Rotverschiebung der Galaxien kosmische Hintergrundstrahlung
Neues aus Kosmologie und Astrophysik 1.0
 Neues aus Kosmologie und Astrophysik 1.0 Unser Universum Sterne und Galaxien Hintergrundstrahlung Elemententstehung Das Big-Bang-Modell Prozesse im frühen Universum Fragen und Antworten (?) Dunkle Materie
Neues aus Kosmologie und Astrophysik 1.0 Unser Universum Sterne und Galaxien Hintergrundstrahlung Elemententstehung Das Big-Bang-Modell Prozesse im frühen Universum Fragen und Antworten (?) Dunkle Materie
Allgemeine Relativitätstheorie und Kosmologie
 Allgemeine Relativitätstheorie und Kosmologie Franz Embacher Fakultät für Physik der Universität Wien Seminar an der PH Oberösterreich Linz, 3. Dezember 2014 Allgemeine Relativitätstheorie + Kosmologie
Allgemeine Relativitätstheorie und Kosmologie Franz Embacher Fakultät für Physik der Universität Wien Seminar an der PH Oberösterreich Linz, 3. Dezember 2014 Allgemeine Relativitätstheorie + Kosmologie
String Theorie - Die Suche nach der großen Vereinheitlichung
 String Theorie - Die Suche nach der großen Vereinheitlichung Ralph Blumenhagen Max-Planck-Institut für Physik String Theorie - Die Suche nach der großen Vereinheitlichung p.1 Das Ziel der Theoretischen
String Theorie - Die Suche nach der großen Vereinheitlichung Ralph Blumenhagen Max-Planck-Institut für Physik String Theorie - Die Suche nach der großen Vereinheitlichung p.1 Das Ziel der Theoretischen
Abbildung 10.1: Das Bild zu Beispiel 10.1
 Analysis 3, Woche Mannigfaltigkeiten I. Definition einer Mannigfaltigkeit Die Definition einer Mannigfaltigkeit braucht den Begriff Diffeomorphismus, den wir in Definition 9.5 festgelegt haben. Seien U,
Analysis 3, Woche Mannigfaltigkeiten I. Definition einer Mannigfaltigkeit Die Definition einer Mannigfaltigkeit braucht den Begriff Diffeomorphismus, den wir in Definition 9.5 festgelegt haben. Seien U,
Wie Einstein seine Feldgleichungen fand
 Wie Einstein seine Feldgleichungen fand Johannes Neidhart 5. November 2009 Inhaltsverzeichnis 1 Einleitung 1 2 Die ersten Schritte 2 3 Die Entwurf Arbeit 2 4 Die Abkehr von der allgemeinen Kovarianz 4
Wie Einstein seine Feldgleichungen fand Johannes Neidhart 5. November 2009 Inhaltsverzeichnis 1 Einleitung 1 2 Die ersten Schritte 2 3 Die Entwurf Arbeit 2 4 Die Abkehr von der allgemeinen Kovarianz 4
Frühes Universum in Newton scher Kosmologie. Tobias Lautenschlager 27. Juni 2007
 Frühes Universum in Newton scher Kosmologie Tobias Lautenschlager 7. Juni 7 Inhaltsverzeichnis 1 Annahmen 1.1 Das kosmologische Prinzip...................... 1. Die Bewegung von Galaxien.....................
Frühes Universum in Newton scher Kosmologie Tobias Lautenschlager 7. Juni 7 Inhaltsverzeichnis 1 Annahmen 1.1 Das kosmologische Prinzip...................... 1. Die Bewegung von Galaxien.....................
beschrieben wird. B' sei ein IS das derjenigen Weltlinie folgt, die P und Q in gleichförmiger Bewegung verbindet. Aus Sicht von A folgt B' Bahn mit
 Minkowski-Wegelement und Eigenzeit Invariantes Wegelement entlang einer Bahnkurve einesteilchens im IS A: immer "Instantan mitlaufendes" Inertialsystem B' sei so gewählt, dass es zum Zeitpunkt t dieselbe
Minkowski-Wegelement und Eigenzeit Invariantes Wegelement entlang einer Bahnkurve einesteilchens im IS A: immer "Instantan mitlaufendes" Inertialsystem B' sei so gewählt, dass es zum Zeitpunkt t dieselbe
Spezielle Relativitätstheorie
 Die SRT behandelt Ereignisse, die von einem Inertialsystem (IS) beobachtet werden und gemessen werden. Dabei handelt es sich um Bezugssyteme, in denen das erste Newton sche Axiom gilt. Die Erde ist strenggenommen
Die SRT behandelt Ereignisse, die von einem Inertialsystem (IS) beobachtet werden und gemessen werden. Dabei handelt es sich um Bezugssyteme, in denen das erste Newton sche Axiom gilt. Die Erde ist strenggenommen
ein geeignetes Koordinatensystem zu verwenden.
 1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
LHC: Beschleuniger, Experimente, physikalische Ziele. Peter Mättig Bergische Universität Wuppertal
 LHC: Beschleuniger, Experimente, physikalische Ziele Peter Mättig Bergische Universität Wuppertal Das (?) größte Wissenschaftsprojekt LHC Beschleuniger: 26 km Umfang Experimente groß wie 5 Stockwerke 10000
LHC: Beschleuniger, Experimente, physikalische Ziele Peter Mättig Bergische Universität Wuppertal Das (?) größte Wissenschaftsprojekt LHC Beschleuniger: 26 km Umfang Experimente groß wie 5 Stockwerke 10000
