BERÜHMTE KURVEN Logarithmische Spirale. Die Logarithmische Spirale wird durch eine Gleichung in Polarkoordinaten angegeben: r(φ)=a*e k φ
|
|
|
- Caroline Hase
- vor 6 Jahren
- Abrufe
Transkript
1 BERÜHMTE KURVEN Gruppenleiter: Jürgen Appell, Kristina Appell, Anna Martellotti Hilfskräfte: Alison Cross, Ruth Smith Teilnehmer(innen): Ann-Christin Gerstner, Matthias Geuder, Michael Kierstein, Lukas Lürzel, Julian Schary, Tina Wagner, Stefanie Wellert, Florian Wisheckel 1. Spiralen. Auf der Suche nach berühmten Kurven sind wir als erstes auf Spiralen gestoßen. Wir fanden folgende interessante Varianten von jenen, die wir während der Projekttage genauer untersucht und auch mit groooooooooooooooooooooooooooooßem Aufwand selbst konstruiert haben. Diese haben wir ausgesucht, weil sie anschauliche und einfache Beispiele für berühmte Kurven sind Logarithmische Spirale. Die Logarithmische Spirale wird durch eine Gleichung in Polarkoordinaten angegeben: r(φ)=a*e k φ Wie man an der unteren Grafik sieht, wächst der Radius exponentiell mit dem Polarwinkel. Umgekehrt hängt der Polarwinkel logarithmisch vom Radius ab und man spricht daher von einer logarithmischen Spirale. Der Windungsabstand nimmt dabei mit wachsender Entfernung zum Zentrum zu. Besonders an der logarithmischen Spirale ist, dass alle durch den Pol gehenden Geraden die Kurve also ihre Tangenten unter dem gleichen Tangentenwinkel schneiden. Außerdem ist der Ursprung ein asymptotischer Punkt, d.h. die Spirale umkreist den Ursprung unendlich oft, ohne ihn zu erreichen. Beispiel in der Natur: Das Schneckenhaus
2 1.2. Archimedische Spirale. Auch die archimedische Spirale wird durch Polarkoordinaten bestimmt: r(φ)=a* φ mit a >0 Im Gegensatz zur logarithmischen Spirale wächst hier der Radius direkt proportional zum Drehwinkel φ. Beispiele in der Technik: Plattenspieler Beispiele in der Natur: Die Lakritzschnecke 2. Fraktale. Den Schwerpunkt unseres Projektes haben wir auf das Thema Fraktale gesetzt, da wir diese besonders interessant fanden. Zum einen wegen der ästhetischen Form, zum anderen auch weil sie oft in der Natur vorkommen Historischer Hintergrund. Der französische Mathematiker polnischer Herkunft Benoît Mandelbrot beschäftigte sich als einer der ersten sehr ausführlich mit dem Thema fraktale Geometrie. Er stieß darauf, als er aus unterschiedlichen Quellen abweichende Angaben zur Küstenlänge Großbritanniens entnahm.
3 Das kommt daher, dass die Küstenlänge je nach Maßstab unterschiedlich genau gemessen werden kann. Je detaillierter die Karte ist, desto länger ist die Küste. Nach Mandelbrot wurde auch die Mandelbrot-Menge, die wir später näher erklären, benannt Definition. Fraktal = aus dem Lat.: fractus, in Teile gebrochen (B. Mandelbrot, 1975) Fraktale besitzen beliebig kleine Teilbereiche (engl.: fractions ), die bei Vergrößerung immer wieder gleichermaßen komplizierte Strukturen aufweisen und oft selbstähnlich sind. Ein weiteres Merkmal von Fraktalen ist, dass sie keine ganzzahlige Dimension haben. 2.. Erstes Beispiel: Die Kochsche Schneeflocke Gestartet wird mit einem gleichseitigen Dreieck. Nun wird jede Seite gedrittelt und die mittlere durch zwei Strecken gleicher Länge ersetzt. (Ergebnis des ersten Schrittes: Davidstern) So fährt man nun immer weiter fort und erhält ein Fraktal, dessen Länge unendlich ist. Die eingegrenzte Fläche ist jedoch endlich Zweites Beispiel: Der Cantor-Staub. Der Cantor-Staub entsteht folgendermaßen: Aus dem Intervall [0,1] wird das mittlere Drittel entfernt. Im nächsten Schritt wird aus den beiden verbliebenen Strecken das mittlere Drittel entfernt usw.
4 n= n 1 2 = 1 n n = 1 n + 1 Der Cantor-Staub kann also wie folgt definiert werden: C = I n Ν C n Eine Besonderheit des Cantor-Staubs ist, dass die Länge der entfernten Teile 1 beträgt und dass dennoch unendlich viele Punkte übrig bleiben. An diesem Beispiel haben wir uns die Berechnung der Dimension eines Fraktals erarbeitet Berechnung der Dimension eines Fraktals log( AnzahlMselbstähnlicherMTeile) Dim = log( Verkleinerungsfaktor) Beim Cantor-Staub ergibt sich also: log 2 Dim ( C) = 0,58 log Der Cantor-Staub ist also eher eine eindimensionale Strecke als ein nulldimensionaler Punkt, da 0,58 näher an 1 als an 0 liegt. Auch für die Koch sche Schneeflocke können wir die Dimension errechnen: log 4 Dim ( K) = 1,26 log
5 Die Koch sche Schneeflocke ist also eher eine eindimensionale Strecke als eine zweidimensionale Fläche Drittes Beispiel: Das Sierpinski-Dreieck Man startet mit einer ausgefüllten schwarzen Fläche in Dreiecksform. Nun bestimmt man den Mittelpunkt jeder Seite und verbindet diese Punkte. Das so entstandene mittlere Teildreieck wird ausgeschnitten. Mit den übrigen Dreiecken verfährt man immer wieder genauso. log Dim ( S) = 1,585 log 2 Beim Sierpinski-Dreieck hat man also eher eine zweidimensionale Fläche als eine eindimensionale Strecke. Am Sierpinski-Dreieck konnten wir auch die Selbstähnlichkeit gut beobachten. Zoomt man immer weiter in das Dreieck hinein, so erscheinen immer wieder die selben Strukturen Viertes Beispiel: Die Mandelbrot-Menge Nachdem wir uns mit den obigen relativ anschaulichen Beispielen beschäftigt haben, fanden wir mit der Mandelbrot-Menge ein sehr ästhetisches, aber auch mathematisch äußerst kompliziertes Fraktal. Wir fanden im Internet ein gut veranschaulichendes Beispiel ( Das Flohbeispiel ) für die Entstehung einer solchen Menge. Da die Erklärung der Mandelbrot-Menge den Rahmen sprengen würde, wollen wir stattdessen berichten, wie wir uns mit der Mandelbrot-Menge beschäftigt haben. Wir fanden im Internet das Programm Ultra Fractal 5, mit dem wir eigene Fraktale und besonders Mandelbrot-Mengen erstellt und animiert haben. Dabei kamen immer neue faszinierende Formen zum Vorschein.
Fraktale. Mathe Fans an die Uni. Sommersemester 2009
 Fraktale Mathe Fans an die Uni Ein Fraktal ist ein Muster, das einen hohen Grad Selbstähnlichkeit aufweist. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst
Fraktale Mathe Fans an die Uni Ein Fraktal ist ein Muster, das einen hohen Grad Selbstähnlichkeit aufweist. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst
Kunst und Wissenschaft
 Kunst und Wissenschaft HS 8 Visualisierung von Newton-Fraktalen Inhalt 1. Ist Schönheit Harmonie? Mathematik in Musik und Malerei 2. Warum heissen Fraktale Fraktale? oder: was ist hier zerbrochen? 3. Was
Kunst und Wissenschaft HS 8 Visualisierung von Newton-Fraktalen Inhalt 1. Ist Schönheit Harmonie? Mathematik in Musik und Malerei 2. Warum heissen Fraktale Fraktale? oder: was ist hier zerbrochen? 3. Was
2. Fraktale Geometrie
 2. Fraktale Geometrie Komplexe Systeme ohne charakteristische Längenskala z.b. Risse in festen Materialien, Küstenlinien, Flussläufe und anderes.. Skaleninvariante Systeme Gebrochene Dimensionen Fraktale
2. Fraktale Geometrie Komplexe Systeme ohne charakteristische Längenskala z.b. Risse in festen Materialien, Küstenlinien, Flussläufe und anderes.. Skaleninvariante Systeme Gebrochene Dimensionen Fraktale
9 Fraktale. Dabei hängt das Ergebnis vom Maßstab der Karte und von der eingestellten Weite des Stechzirkels
 79 9 Fraktale Problemstellung Im Jahr 1967 veröffentlichte der Mathematiker Benoit Mandelbrot 3 eine Arbeit mit dem Titel How long is the coast of Britain? Statistical self-similarity and fractional dimension.
79 9 Fraktale Problemstellung Im Jahr 1967 veröffentlichte der Mathematiker Benoit Mandelbrot 3 eine Arbeit mit dem Titel How long is the coast of Britain? Statistical self-similarity and fractional dimension.
Zufällige Fraktale. Klaus Scheufele. 16. Januar 2007
 16. Januar 2007 1 Beispiele von zufälligen Fraktalen Zufällige Koch Kurve Zufällige Cantor Menge 2 3 4 Theorem 3 Zufällige Koch Kurve Zufällige Koch Kurve Zufällige Cantor Menge Zufällige Cantor Menge
16. Januar 2007 1 Beispiele von zufälligen Fraktalen Zufällige Koch Kurve Zufällige Cantor Menge 2 3 4 Theorem 3 Zufällige Koch Kurve Zufällige Koch Kurve Zufällige Cantor Menge Zufällige Cantor Menge
Vorlesung Modelle in Biophysik/Biochemie 4. Fraktale
 Vorlesung Modelle in Biophysik/Biochemie 4. Fraktale c Priv.-Doz. Dr. Adelhard Köhler May 19, 2005 1 Gebrochene (fraktale) Dimension Fraktale haben eine gebrochene Dimension. Unterschiedliche Dimensionsbegriffe
Vorlesung Modelle in Biophysik/Biochemie 4. Fraktale c Priv.-Doz. Dr. Adelhard Köhler May 19, 2005 1 Gebrochene (fraktale) Dimension Fraktale haben eine gebrochene Dimension. Unterschiedliche Dimensionsbegriffe
Martin-Anderson-Nexö-Gymnasium, Dresden
 Fraktale Wechselspiel zwischen Chaos und Ordnung Teilnehmer: David Burgschweiger Tim Gabriel Welf Garkisch Anne Kell Leonard König Erik Lorenz Sofie Martins Niklas Schelten Heinrich-Hertz-Oberschule, Berlin
Fraktale Wechselspiel zwischen Chaos und Ordnung Teilnehmer: David Burgschweiger Tim Gabriel Welf Garkisch Anne Kell Leonard König Erik Lorenz Sofie Martins Niklas Schelten Heinrich-Hertz-Oberschule, Berlin
Zufällige Fraktale. Klaus Scheufele. February 27, 2007
 Zufällige Fraktale Klaus Scheufele February 27, 2007 1 Einleitung Why is geometry often discribed as cold and dry? One reason lies in its inability to describe the shape of a cloud, a mountain, a coastline,
Zufällige Fraktale Klaus Scheufele February 27, 2007 1 Einleitung Why is geometry often discribed as cold and dry? One reason lies in its inability to describe the shape of a cloud, a mountain, a coastline,
Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale?
 Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale? Klaus Kusche Frühjahr 2019 Inhalt Unser Ziel Was ist ein Fraktal? Von linearen geometrischen Abbildungen zu iterierten
Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale? Klaus Kusche Frühjahr 2019 Inhalt Unser Ziel Was ist ein Fraktal? Von linearen geometrischen Abbildungen zu iterierten
Die Archimedische und logarithmische Spirale
 Aus dem Seminar Ausgewählte höhere Kurven- WS 2016/17 Die Archimedische und logarithmische Spirale Estefani Rodriguez Diaz Bei Prof. Dr. Duco van Straten Contents 1 Definition 2 2 Polarkoordinaten 3 3
Aus dem Seminar Ausgewählte höhere Kurven- WS 2016/17 Die Archimedische und logarithmische Spirale Estefani Rodriguez Diaz Bei Prof. Dr. Duco van Straten Contents 1 Definition 2 2 Polarkoordinaten 3 3
Wie lang ist die Küste Großbritanniens?
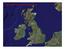 Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Archimedische Spiralen
 Hauptseminar: Spiralen WS 05/06 Dozent: Prof. Dr. Deißler Datum: 31.01.2006 Vorgelegt von Sascha Bürgin Archimedische Spiralen Man kann sich auf zwei Arten zeichnerisch den archimedischen Spiralen annähern.
Hauptseminar: Spiralen WS 05/06 Dozent: Prof. Dr. Deißler Datum: 31.01.2006 Vorgelegt von Sascha Bürgin Archimedische Spiralen Man kann sich auf zwei Arten zeichnerisch den archimedischen Spiralen annähern.
Fraktale und Chaos. Wir beschftigten uns mit Fraktalen, die aus dem Studium komplexer dynamischer
 Fraktale und Chaos Teilnehmer: Markus Auricht (Heinrich-Hertz-Oberschule) Martin Czudra (Andreas-Oberschule) Robert Foellmer (Heinrich-Hertz-Oberschule) Aser Hage-Ali (Heinrich-Hertz-Oberschule) Alexej
Fraktale und Chaos Teilnehmer: Markus Auricht (Heinrich-Hertz-Oberschule) Martin Czudra (Andreas-Oberschule) Robert Foellmer (Heinrich-Hertz-Oberschule) Aser Hage-Ali (Heinrich-Hertz-Oberschule) Alexej
Mathematik für die Sekundarstufe 1
 Hans Walser Mathematik für die Sekundarstufe 1 Modul 406 Fraktale Lernumgebung Hans Walser: Modul 406, Fraktale. Lernumgebung ii Inhalt 1 Die Kochsche Schneeflocke... 1 2 Weißt du wie viel Würfel stehen?...
Hans Walser Mathematik für die Sekundarstufe 1 Modul 406 Fraktale Lernumgebung Hans Walser: Modul 406, Fraktale. Lernumgebung ii Inhalt 1 Die Kochsche Schneeflocke... 1 2 Weißt du wie viel Würfel stehen?...
1. Einleitung ggf. Vorwissen abgreifen. 2. Space Filling Curves. - Cantors Erstes Diagonalargument. - Gosper-Curve - Sierpiński-Curve - Moore-Curve
 1. Einleitung ggf. Vorwissen abgreifen - Cantors Erstes Diagonalargument 2. Space Filling Curves - Allgemeiner Ansatz - Z-Curve (Morton Order, Z-Order) - Hilbert-Curve - Peano-Curve - Gosper-Curve - Sierpiński-Curve
1. Einleitung ggf. Vorwissen abgreifen - Cantors Erstes Diagonalargument 2. Space Filling Curves - Allgemeiner Ansatz - Z-Curve (Morton Order, Z-Order) - Hilbert-Curve - Peano-Curve - Gosper-Curve - Sierpiński-Curve
Musterbildung. Vom Kleinen zum Großen. 4. Lange Nacht der Mathematik. Thomas Westermann. Formen u. Muster. Differenzialgleichungen.
 bildung Vom Kleinen zum Großen Thomas Westermann 4. Lange Nacht der Mathematik HS Karlsruhe 12. Mai 2006 Formen und Formen und Formen und Formen und A R U B L R L UB = UR + UL U B U = RI() t + LI'() t
bildung Vom Kleinen zum Großen Thomas Westermann 4. Lange Nacht der Mathematik HS Karlsruhe 12. Mai 2006 Formen und Formen und Formen und Formen und A R U B L R L UB = UR + UL U B U = RI() t + LI'() t
10.3. Krümmung ebener Kurven
 0.3. Krümmung ebener Kurven Jeder der einmal beim Durchfahren einer Kurve bremsen oder beschleunigen mußte hat im wahrsten Sinne des Wortes erfahren daß die lokale Krümmung einen ganz wesentlichen Einfluß
0.3. Krümmung ebener Kurven Jeder der einmal beim Durchfahren einer Kurve bremsen oder beschleunigen mußte hat im wahrsten Sinne des Wortes erfahren daß die lokale Krümmung einen ganz wesentlichen Einfluß
2 Selbstähnlichkeit, Selbstähnlichkeitsdimension
 9 2 Selbstähnlichkeit, Selbstähnlichkeitsdimension und Fraktale 2.1 Selbstähnlichkeit Bei den Betrachtungen zur Dimension in Kapitel 1 haben wir ähnliche (im geometrischen Sinn) Figuren miteinander verglichen.
9 2 Selbstähnlichkeit, Selbstähnlichkeitsdimension und Fraktale 2.1 Selbstähnlichkeit Bei den Betrachtungen zur Dimension in Kapitel 1 haben wir ähnliche (im geometrischen Sinn) Figuren miteinander verglichen.
Iteriertes Funktionensystem. Martin Aigner Rainer Brodinger Martin Rieger
 Iteriertes Funktionensystem Martin Aigner Rainer Brodinger Martin Rieger Agenda Einleitendes Beispiel Definition und Beschreibung Einsatzgebiete / Anwendungen weitere Beispiele Sierpinski-Dreieck "Das
Iteriertes Funktionensystem Martin Aigner Rainer Brodinger Martin Rieger Agenda Einleitendes Beispiel Definition und Beschreibung Einsatzgebiete / Anwendungen weitere Beispiele Sierpinski-Dreieck "Das
Hauptseminar Fraktale: Andere Begriffe der Dimension
 Hauptseminar Fraktale: Andere Begriffe der Dimension 21. November 2006 Überblick 1 Einleitung 2 Fraktale Dimension Begriffsklärung Gewünschte Eigenschaften Beispiel: Teilerdimension 3 Boxdimension Definition
Hauptseminar Fraktale: Andere Begriffe der Dimension 21. November 2006 Überblick 1 Einleitung 2 Fraktale Dimension Begriffsklärung Gewünschte Eigenschaften Beispiel: Teilerdimension 3 Boxdimension Definition
Übungen mit dem Applet Kurven in Polarkoordinaten
 Kurven in Polarkoordinaten 1 Übungen mit dem Applet Kurven in Polarkoordinaten 1 Ziele des Applets...2 2 Wie entsteht eine Kurve in Polarkoordinaten?...3 3 Kurvenverlauf für ausgewählte r(ϕ)...4 3.1 r
Kurven in Polarkoordinaten 1 Übungen mit dem Applet Kurven in Polarkoordinaten 1 Ziele des Applets...2 2 Wie entsteht eine Kurve in Polarkoordinaten?...3 3 Kurvenverlauf für ausgewählte r(ϕ)...4 3.1 r
Die Chaostheorie und Fraktale in der Natur
 Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
MATHE-BRIEF. Juni 2017 Nr. 80. Die Mandelbrotmenge
 MATHE-BRIEF Juni 2017 Nr. 80 Herausgegeben von der Österreichischen Mathematischen Gesellschaft http: // www.oemg.ac.at / Mathe Brief mathe brief@oemg.ac.at Die Mandelbrotmenge Komplexe Zahlen werden im
MATHE-BRIEF Juni 2017 Nr. 80 Herausgegeben von der Österreichischen Mathematischen Gesellschaft http: // www.oemg.ac.at / Mathe Brief mathe brief@oemg.ac.at Die Mandelbrotmenge Komplexe Zahlen werden im
Fraktale und Julia-Mengen
 Uutner, J. Roser, A. Unseld, F. Fraktale und Julia-Mengen mit 77 Abbildungen Verlag Harri Deutsch Inhalt I Klassische Fraktale l 1 Cantor-Menge 2 1.1 Konstruktion und Eigenschaften 2 1.2 Triadische Darstellung
Uutner, J. Roser, A. Unseld, F. Fraktale und Julia-Mengen mit 77 Abbildungen Verlag Harri Deutsch Inhalt I Klassische Fraktale l 1 Cantor-Menge 2 1.1 Konstruktion und Eigenschaften 2 1.2 Triadische Darstellung
Das Modellieren von 2D- und 3D-Objekten
 Das Modellieren von 2D- und 3D-Objekten 1 VTK-Format Florian Buchegger, Michael Haberleitner December 11, 2015 Eine VTK-Datei besteht aus einem Header und einem Body. Während im Header lediglich wichtige
Das Modellieren von 2D- und 3D-Objekten 1 VTK-Format Florian Buchegger, Michael Haberleitner December 11, 2015 Eine VTK-Datei besteht aus einem Header und einem Body. Während im Header lediglich wichtige
Kenneth J. Falconer. Fraktale Geometrie. Mathematische Grundlagen und Anwendungen. Aus dem Englischen von Jens Meyer. Mit 98 Abbildungen
 Kenneth J. Falconer Fraktale Geometrie Mathematische Grundlagen und Anwendungen Aus dem Englischen von Jens Meyer Mit 98 Abbildungen Spektrum Akademischer Verlag Heidelberg Berlin Oxford Inhalt Vorwort
Kenneth J. Falconer Fraktale Geometrie Mathematische Grundlagen und Anwendungen Aus dem Englischen von Jens Meyer Mit 98 Abbildungen Spektrum Akademischer Verlag Heidelberg Berlin Oxford Inhalt Vorwort
Mathematik für die Sekundarstufe 1
 Hans Walser Mathematik für die Sekundarstufe 1 Modul 05 Schnecken und Spiralen Lernumgebung Hans Walser: Modul 05, Schnecken und Spiralen. Lernumgebung ii Inhalt 1 Spiralen in der Umwelt... 1 Archimedische
Hans Walser Mathematik für die Sekundarstufe 1 Modul 05 Schnecken und Spiralen Lernumgebung Hans Walser: Modul 05, Schnecken und Spiralen. Lernumgebung ii Inhalt 1 Spiralen in der Umwelt... 1 Archimedische
Junge. Wissenschaft. Klimaneutral Autofahren. Young Researcher. Zukunftsprojekt: Jugend forscht in Natur und Technik. Das Magazin
 Junge 9,50 EUR // Ausgabe Nr. 96 // 28. Jahrgang // 2013 Wissenschaft Jugend forscht in Natur und Technik Young Researcher The European Journal of Science and Technology Medienpartner des Wissenschaftsjahres
Junge 9,50 EUR // Ausgabe Nr. 96 // 28. Jahrgang // 2013 Wissenschaft Jugend forscht in Natur und Technik Young Researcher The European Journal of Science and Technology Medienpartner des Wissenschaftsjahres
Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen.
 10.1. Ebene Kurven Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen. Parameterdarstellungen einer Kurve sind stetige
10.1. Ebene Kurven Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen. Parameterdarstellungen einer Kurve sind stetige
K A N T O N S S C H U L E I M L E E MATHEMATIK. Grafiktaschenrechner ohne CAS, beliebige Formelsammlung
 K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 06 Klasse: 4g Profil: MN Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 06 Klasse: 4g Profil: MN Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
Fraktale und Beispiele aus der Physik
 Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 3 Folie 1 /18 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 3. Zahlenfolgen und Grenzwerte
A. Filler Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 3 Folie 1 /18 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 3. Zahlenfolgen und Grenzwerte
Beispiele. Strecke A R 1 (genauso für R d ):
 Definition 6.1.1 (fraktale Dimension). Sei A R d beschränkt und für ε > 0 sei N A (ε) die minimale Anzahl der d-dimensionalen Kugeln vom Radius ε, mit denen A überdeckt werden kann. Die fraktale Dimension
Definition 6.1.1 (fraktale Dimension). Sei A R d beschränkt und für ε > 0 sei N A (ε) die minimale Anzahl der d-dimensionalen Kugeln vom Radius ε, mit denen A überdeckt werden kann. Die fraktale Dimension
Mathematische Modellierung Lösungen zum 10. Übungsblatt
 Mathematische Modellierung Lösungen zum Klaus G. Blümel Lars Hoegen 30. Januar 2006 Aufgabe 1 Die Figur (a) zeigt bei einem Skalierungsfaktor s 3 eine selbstähnliche Vielfachheit von N 5 auf, sie hat demnach
Mathematische Modellierung Lösungen zum Klaus G. Blümel Lars Hoegen 30. Januar 2006 Aufgabe 1 Die Figur (a) zeigt bei einem Skalierungsfaktor s 3 eine selbstähnliche Vielfachheit von N 5 auf, sie hat demnach
MATHEMATISCHE MONSTER - ALGORITHMEN der FRAKTALEN GEOMETRIE II
 MATHEMATISCHE MONSTER - ALGORITHMEN der FRAKTALEN GEOMETRIE II Wolf Bayer. Februar 00 Zusammenfassung Viele Formen der Natur lassen sich nicht mit der klassischen, auf Euklid basierenden Mathematik beschreiben.
MATHEMATISCHE MONSTER - ALGORITHMEN der FRAKTALEN GEOMETRIE II Wolf Bayer. Februar 00 Zusammenfassung Viele Formen der Natur lassen sich nicht mit der klassischen, auf Euklid basierenden Mathematik beschreiben.
Euklid ( v. Chr.) Markus Wurster
 Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Punkte und Linien Zwei Linien Markus Wurster Markus Wurster Geometrische Grundbegriffe Winkel Euklid
Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Punkte und Linien Zwei Linien Markus Wurster Markus Wurster Geometrische Grundbegriffe Winkel Euklid
Mathematik für das Ingenieurstudium
 Mathematik für das Ingenieurstudium von Martin Stämpfle, Jürgen Koch 2., aktual. Aufl. Hanser München 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 43232 1 Zu Inhaltsverzeichnis schnell
Mathematik für das Ingenieurstudium von Martin Stämpfle, Jürgen Koch 2., aktual. Aufl. Hanser München 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 43232 1 Zu Inhaltsverzeichnis schnell
2.3 Chaos und Lyapunov-Exponent. d dx f(x) λ = lim n n . (1) Programm. k=0. PROGRAM lyapunov ...
 2.3 Chaos und Lyapunov-Exponent... PROGRAM lyapunov REAL*8 1 λ = lim n n :: a,x,fly n k=0 ln d dx f(x). (1) x=xk DO it=1,itmax+ivor! Schleife Iterationen x=a*x*(1.-x)! log. Abbildung IF(it.GT.ivor.and.ABS(x-.5).GT.1.E-30)
2.3 Chaos und Lyapunov-Exponent... PROGRAM lyapunov REAL*8 1 λ = lim n n :: a,x,fly n k=0 ln d dx f(x). (1) x=xk DO it=1,itmax+ivor! Schleife Iterationen x=a*x*(1.-x)! log. Abbildung IF(it.GT.ivor.and.ABS(x-.5).GT.1.E-30)
Geometrie Jahrgangsstufe 5
 Geometrie Jahrgangsstufe 5 Im Rahmen der Kooperation der Kollegen, die im Schuljahr 1997/98 in der fünften Jahrgangstufe Mathematik unterrichteten, wurde in Gemeinschaftsarbeit unter Federführung von Frau
Geometrie Jahrgangsstufe 5 Im Rahmen der Kooperation der Kollegen, die im Schuljahr 1997/98 in der fünften Jahrgangstufe Mathematik unterrichteten, wurde in Gemeinschaftsarbeit unter Federführung von Frau
1 Die Mandelbrotmenge
 1 Die Mandelbrotmenge In diesem Abschnitt wollen wir mathematische Aspekte der sogenannten Mandelbrotmenge beleuchten, die wir im Folgenden mit M bezeichnen wollen. 1 Ihr Name ist ihrem Entdecker Benoît
1 Die Mandelbrotmenge In diesem Abschnitt wollen wir mathematische Aspekte der sogenannten Mandelbrotmenge beleuchten, die wir im Folgenden mit M bezeichnen wollen. 1 Ihr Name ist ihrem Entdecker Benoît
Thema: Visualisierung mit MAPLE
 Ostervortrag zum Linux-Stammtisch am 07.04.2017 Thema: Visualisierung mit MAPLE Sybille Handrock 1 Computeralgebrasysteme Computeralgebra beschäftigt sich mit Methoden zum Lösen mathematischer Probleme
Ostervortrag zum Linux-Stammtisch am 07.04.2017 Thema: Visualisierung mit MAPLE Sybille Handrock 1 Computeralgebrasysteme Computeralgebra beschäftigt sich mit Methoden zum Lösen mathematischer Probleme
Die Barth-Sextik ein ewiger Weltrekord. 3D-Skulptur von Oliver Labs
 Die Barth-Sextik ein ewiger Weltrekord 3D-Skulptur von Oliver Labs Auch in der Mathematik gibt es Weltrekorde und die Barth-Sextik, entdeckt um 1996 vom Erlanger Professor Wolf Barth, stellt einen solchen
Die Barth-Sextik ein ewiger Weltrekord 3D-Skulptur von Oliver Labs Auch in der Mathematik gibt es Weltrekorde und die Barth-Sextik, entdeckt um 1996 vom Erlanger Professor Wolf Barth, stellt einen solchen
Fraktale und Lindenmayer-Systeme Zusammenfassung des Vortrages
 Proseminar Grundlagen der theoretischen Informatik Dozent: Prof. Helmut Alt Fraktale und Lindenmayer-Systeme Zusammenfassung des Vortrages Richard Wilhelm Wintersemester 2007 Fraktale Vorgestellt wurden
Proseminar Grundlagen der theoretischen Informatik Dozent: Prof. Helmut Alt Fraktale und Lindenmayer-Systeme Zusammenfassung des Vortrages Richard Wilhelm Wintersemester 2007 Fraktale Vorgestellt wurden
Grenzwerte und Stetigkeit
 Grenzwerte und Stetigkeit Gegeben sei eine Funktion z = f(,) von zwei Variablen. Außerdem sei ( 0, 0 ) eine vorgegebene Stelle der -Ebene. Wir interessieren uns für das Verhalten der Funktion bzw. der
Grenzwerte und Stetigkeit Gegeben sei eine Funktion z = f(,) von zwei Variablen. Außerdem sei ( 0, 0 ) eine vorgegebene Stelle der -Ebene. Wir interessieren uns für das Verhalten der Funktion bzw. der
Fraktale: Eine Einführung
 Fraktale: Eine Einführung Fraktale Geometrie und ihre Anwendungen Seminar im WS 06/07 Florian Daikeler Übersicht: I. Einführung: Die Cantor-Drittelmenge II. Fraktale in 2D: Selbstähnlichkeit III. Beispiele:
Fraktale: Eine Einführung Fraktale Geometrie und ihre Anwendungen Seminar im WS 06/07 Florian Daikeler Übersicht: I. Einführung: Die Cantor-Drittelmenge II. Fraktale in 2D: Selbstähnlichkeit III. Beispiele:
Seminarvortrag Schnitte von Fraktalen
 Seminarvortrag Schnitte von Fraktalen Matthias Schmid matthias.schmid@uni-ulm.de Universität Ulm 9. Februar 2007 Inhaltsverzeichnis 1 Einleitung 2 1.1 Einordnung................................... 2 1.2
Seminarvortrag Schnitte von Fraktalen Matthias Schmid matthias.schmid@uni-ulm.de Universität Ulm 9. Februar 2007 Inhaltsverzeichnis 1 Einleitung 2 1.1 Einordnung................................... 2 1.2
Fraktale. 1. Fortgesetzte Bifurkationen der gleichen Art
 Fraktale 1. Fortgesetzte Bifurkationen der gleichen Art Bisher wurden nur Selbstorganisationsphänomena betrachtet, die durch einzelne Bifurkationen beschrieben werden können. Viele reale Prozesse bestehen
Fraktale 1. Fortgesetzte Bifurkationen der gleichen Art Bisher wurden nur Selbstorganisationsphänomena betrachtet, die durch einzelne Bifurkationen beschrieben werden können. Viele reale Prozesse bestehen
Gedanken zur Unendlichkeit
 Gedanken zur Unendlichkeit Was erwartet Sie heute abend? Theologie ist eine besondere Wissenschaft Theologie ist mehr als bloße Bibel- Wissenschaft Theologie ist anschlussfähig an andere Wissenschaften
Gedanken zur Unendlichkeit Was erwartet Sie heute abend? Theologie ist eine besondere Wissenschaft Theologie ist mehr als bloße Bibel- Wissenschaft Theologie ist anschlussfähig an andere Wissenschaften
Projektive Räume und Unterräume
 Projektive Räume und Unterräume Erik Slawski Proseminar Analytische Geometrie bei Prof. Dr. Werner Seiler und Marcus Hausdorf Wintersemester 2007/2008 Fachbereich 17 Mathematik Universität Kassel Inhaltsverzeichnis
Projektive Räume und Unterräume Erik Slawski Proseminar Analytische Geometrie bei Prof. Dr. Werner Seiler und Marcus Hausdorf Wintersemester 2007/2008 Fachbereich 17 Mathematik Universität Kassel Inhaltsverzeichnis
Kapitel 4 TRIGONOMETRISCHE FUNKTIONEN
 Kapitel 4 TRIGONOMETRISCHE FUNKTIONEN Fassung vom 9. Dezember 005 Mathematik für Humanbiologen und Biologen 53 4. Periodische Vorgänge 4. Periodische Vorgänge Neben den Wachstumsprozessen spielen die periodischen
Kapitel 4 TRIGONOMETRISCHE FUNKTIONEN Fassung vom 9. Dezember 005 Mathematik für Humanbiologen und Biologen 53 4. Periodische Vorgänge 4. Periodische Vorgänge Neben den Wachstumsprozessen spielen die periodischen
Demo-Text für Inversion (Spiegelung am Kreis) Ein Spezialthema INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 Inversion (Spiegelung am Kreis) Ein Spezialthema Teil 1 Grundlagen Text Nr. 1400 Stand: 4. Februar 016 FIEDICH W. BUCKEL INTENETBIBLIOTHEK FÜ SCHULMATHEMATIK 1400 Inversion 1 Vorwort Die Inversion, die
Inversion (Spiegelung am Kreis) Ein Spezialthema Teil 1 Grundlagen Text Nr. 1400 Stand: 4. Februar 016 FIEDICH W. BUCKEL INTENETBIBLIOTHEK FÜ SCHULMATHEMATIK 1400 Inversion 1 Vorwort Die Inversion, die
Modulabschlussklausur
 Sommersemester 2010 Dr. Reimund Albers Modul EM1: Mathematisches Denken in Arithmetik und Geometrie Modulabschlussklausur Name: Mat.Nr.: Schulschwerpunkt: Grund- oder Sekundarbitte ankreuzen Aufgabe 1
Sommersemester 2010 Dr. Reimund Albers Modul EM1: Mathematisches Denken in Arithmetik und Geometrie Modulabschlussklausur Name: Mat.Nr.: Schulschwerpunkt: Grund- oder Sekundarbitte ankreuzen Aufgabe 1
Tag der Mathematik 2018
 Gruppenwettbewerb Einzelwettbewerb Mathematische Hürden Aufgaben mit en Aufgabe G mit Aufgabe G Stein Für reelle Zahlen ist die Relation... ist kleiner als... transitiv, d.h. aus a < b und b < c folgt
Gruppenwettbewerb Einzelwettbewerb Mathematische Hürden Aufgaben mit en Aufgabe G mit Aufgabe G Stein Für reelle Zahlen ist die Relation... ist kleiner als... transitiv, d.h. aus a < b und b < c folgt
Kurven. Modul 4 Fraktale Kurvenmonster
 Modul 4 Fraktale Kurvenmonster Wie lang ist die Küste Großbritanniens? Die Antwort auf diese Frage scheint klar zu sein. Allerdings findet man in jedem Nachschlagewerk einen (nicht nur geringfügig) anderen
Modul 4 Fraktale Kurvenmonster Wie lang ist die Küste Großbritanniens? Die Antwort auf diese Frage scheint klar zu sein. Allerdings findet man in jedem Nachschlagewerk einen (nicht nur geringfügig) anderen
Anlage des Spiels. Forschungsgruppe. Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern
 Anlage des Spiels Forschungsgruppe Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern Ziel Die SuS erkennen, dass auf drei verschiedenen Wegen drei ähnliche Erkenntnisse
Anlage des Spiels Forschungsgruppe Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern Ziel Die SuS erkennen, dass auf drei verschiedenen Wegen drei ähnliche Erkenntnisse
Anlage des Spiels. Forschungsgruppe. Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern
 Anlage des Spiels Forschungsgruppe Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern Ziel Die SuS erkennen, dass auf drei verschiedenen Wegen drei ähnliche Erkenntnisse
Anlage des Spiels Forschungsgruppe Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern Ziel Die SuS erkennen, dass auf drei verschiedenen Wegen drei ähnliche Erkenntnisse
Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle. zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"):
 Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"): 1 Erzeugung des Voronoi-Diagramms (siehe Vorlesung "Algorithmische
Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"): 1 Erzeugung des Voronoi-Diagramms (siehe Vorlesung "Algorithmische
Zentrum für Mathematik
 Fakultät: Mathematik und Naturwissenschaften, Fachrichtung: Mathematik, Professur für Didaktik der Mathematik Bilder und Perlen der Mathematik Tag der Mathematik 2017 Dr. rer. nat. Frank Morherr Marburg,
Fakultät: Mathematik und Naturwissenschaften, Fachrichtung: Mathematik, Professur für Didaktik der Mathematik Bilder und Perlen der Mathematik Tag der Mathematik 2017 Dr. rer. nat. Frank Morherr Marburg,
Lösung: Mathematisches Denken in Arithmetik und Geometrie1 Funktionen und Abbildungen mit GeoGebra
 Hinweis: Alle Grafiken dieser Lösung finden Sie auch als GeoGebra-Dateien zum Ausprobieren. 1. Verschiebung: Zeichnen Sie einen beliebigen Vektor zwischen 2 Punkten. a) Verschieben Sie den Graphen von
Hinweis: Alle Grafiken dieser Lösung finden Sie auch als GeoGebra-Dateien zum Ausprobieren. 1. Verschiebung: Zeichnen Sie einen beliebigen Vektor zwischen 2 Punkten. a) Verschieben Sie den Graphen von
Darstellung von Kurven und Flächen
 Darstellung von Kurven und Flächen Proseminar Computergraphik, 10. Juni 2008 Christoph Dähne Seite 1 Inhalt Polygonnetze 3 Knotenliste 3 Kantenliste 3 Parametrisierte kubische Kurven 4 Definition 4 Stetigkeit
Darstellung von Kurven und Flächen Proseminar Computergraphik, 10. Juni 2008 Christoph Dähne Seite 1 Inhalt Polygonnetze 3 Knotenliste 3 Kantenliste 3 Parametrisierte kubische Kurven 4 Definition 4 Stetigkeit
Mathematik für die Sekundarstufe 1
 Hans Walser Mathematik für die Sekundarstufe 1 Modul 406 Fraktale Hans Walser: Modul 406, Fraktale ii Inhalt 1 Was ist ein Fraktal?... 1 2 Fragen... 2 2.1 Wie viele Kurven hat die Gotthardstraße?... 2
Hans Walser Mathematik für die Sekundarstufe 1 Modul 406 Fraktale Hans Walser: Modul 406, Fraktale ii Inhalt 1 Was ist ein Fraktal?... 1 2 Fragen... 2 2.1 Wie viele Kurven hat die Gotthardstraße?... 2
FRAKTALE. Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier
 FRAKTALE Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier I. Fraktale allgemein a. Mathematischer Algorithmus i. Komplexe Zahlen b. Konvergieren und Divergieren i. Bei Mandelbrotmengen
FRAKTALE Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier I. Fraktale allgemein a. Mathematischer Algorithmus i. Komplexe Zahlen b. Konvergieren und Divergieren i. Bei Mandelbrotmengen
D-ERDW, D-HEST, D-USYS Mathematik II FS 16 Dr. Ana Cannas. MC-Serie 3. Kurven in der Ebene Einsendeschluss: 18. März 2016, 16 Uhr (MEZ)
 D-ERDW, D-HEST, D-USYS Mathematik II FS 16 Dr. Ana Cannas MC-Serie 3 Kurven in der Ebene Einsendeschluss: 18. März 216, 16 Uhr (MEZ) Bei allen Aufgaben ist genau eine Antwort richtig. Sie dürfen während
D-ERDW, D-HEST, D-USYS Mathematik II FS 16 Dr. Ana Cannas MC-Serie 3 Kurven in der Ebene Einsendeschluss: 18. März 216, 16 Uhr (MEZ) Bei allen Aufgaben ist genau eine Antwort richtig. Sie dürfen während
Juliamengen und Mandelbrotmenge
 Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
7.8. Die Regel von l'hospital
 7.8. Die Regel von l'hospital Der Marquis de l'hospital (sprich: lopital) war der erste Autor eines Buches über Infinitesimalrechnung (696) - allerdings basierte dieses Werk wesentlich auf den Ausführungen
7.8. Die Regel von l'hospital Der Marquis de l'hospital (sprich: lopital) war der erste Autor eines Buches über Infinitesimalrechnung (696) - allerdings basierte dieses Werk wesentlich auf den Ausführungen
1.4. Funktionen, Kurven und Parameterdarstellungen
 .4. Funktionen, Kurven und Parameterdarstellungen Reellwertige Funktionen Eine reelle Relation ist eine beliebige Teilmenge F der Ebene (also eine ebene "Fläche"). Von einer reellen Funktion spricht man,
.4. Funktionen, Kurven und Parameterdarstellungen Reellwertige Funktionen Eine reelle Relation ist eine beliebige Teilmenge F der Ebene (also eine ebene "Fläche"). Von einer reellen Funktion spricht man,
4 Die Fibonacci-Zahlen
 4 Die Fibonacci-Zahlen 4.1 Fibonacci-Zahlen und goldener Schnitt Die Fibonacci-Zahlen F n sind definiert durch die Anfangsvorgaben F 0 = 0, F 1 = 1, sowie durch die Rekursion F n+1 = F n + F n 1 für alle
4 Die Fibonacci-Zahlen 4.1 Fibonacci-Zahlen und goldener Schnitt Die Fibonacci-Zahlen F n sind definiert durch die Anfangsvorgaben F 0 = 0, F 1 = 1, sowie durch die Rekursion F n+1 = F n + F n 1 für alle
3.2. Polarkoordinaten
 3.2. Polarkoordinaten Die geometrische Bedeutung der komplexen Multiplikation versteht man besser durch die Einführung von Polarkoordinaten. Der Betrag einer komplexen Zahl z x + i y ist r: z x 2 + y 2.
3.2. Polarkoordinaten Die geometrische Bedeutung der komplexen Multiplikation versteht man besser durch die Einführung von Polarkoordinaten. Der Betrag einer komplexen Zahl z x + i y ist r: z x 2 + y 2.
1 Der Goldene Schnitt
 Goldener Schnitt 1 Der Goldene Schnitt 1 1.1 Das regelmäßige Zehneck 1 1. Ein anderer Name für den Goldenen Schnitt 4 1.3 Der Goldene Schnitt in Zahlen 6 1.4 Die Potenzen von und 8 1.5 Drei Beispiele 10
Goldener Schnitt 1 Der Goldene Schnitt 1 1.1 Das regelmäßige Zehneck 1 1. Ein anderer Name für den Goldenen Schnitt 4 1.3 Der Goldene Schnitt in Zahlen 6 1.4 Die Potenzen von und 8 1.5 Drei Beispiele 10
Rückblick. Dynamische Systeme. Reiner Lauterbach. Fakultät für Mathematik, Informatik und Naturwissenschaften Universität Hamburg
 Fakultät für Mathematik, Informatik und Naturwissenschaften Universität Hamburg 5. Vorlesung Ergänzungen 14.05.2012 Satz. Die C [0, 1] ist gegeben durch C = c [0, 1] c = c j 3 j, c j {0, 2}. j=1 Beweis.
Fakultät für Mathematik, Informatik und Naturwissenschaften Universität Hamburg 5. Vorlesung Ergänzungen 14.05.2012 Satz. Die C [0, 1] ist gegeben durch C = c [0, 1] c = c j 3 j, c j {0, 2}. j=1 Beweis.
K A N T O N S S C H U L E I M L E E MATHEMATIK. Grafiktaschenrechner ohne CAS, beliebige Formelsammlung
 K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 017 Klasse: g Profil: MN / M Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 017 Klasse: g Profil: MN / M Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
Prof. Dr. H. Garcke, D. Depner WS 2009/10 NWF I - Mathematik Universität Regensburg. Analysis III
 Prof. Dr. H. Garcke, D. Depner WS 2009/10 NWF I - Mathematik 18.11.2009 Universität Regensburg Analysis III Verbesserung der Zusatzaufgabe von Übungsblatt 4 Zusatzaufgabe Wir definieren die Cantormenge
Prof. Dr. H. Garcke, D. Depner WS 2009/10 NWF I - Mathematik 18.11.2009 Universität Regensburg Analysis III Verbesserung der Zusatzaufgabe von Übungsblatt 4 Zusatzaufgabe Wir definieren die Cantormenge
Die Dreiecks Ungleichung: I x + y I I x I + I y I
 Die Dreiecks Ungleichung: I x + y I I x I + I y I In dieser Proseminar-Arbeit geht es um die sog. Dreiecks-Ungleichung (Δ-Ungl.). Wir werden unter anderen sehen, wie man die Δ-Ungl. beweisen kann, welche
Die Dreiecks Ungleichung: I x + y I I x I + I y I In dieser Proseminar-Arbeit geht es um die sog. Dreiecks-Ungleichung (Δ-Ungl.). Wir werden unter anderen sehen, wie man die Δ-Ungl. beweisen kann, welche
Die Aktivitäten des vierten Tages der ersten Autonomie-Woche
 Die Aktivitäten des vierten Tages der ersten Autonomie-Woche 7 A / 7 B: Drogenpräventionskurs mit Sonia Parra Im Kurs haben wir die emotionalen Bedürfnisse und Defizite behandelt, die dazu führen, dass
Die Aktivitäten des vierten Tages der ersten Autonomie-Woche 7 A / 7 B: Drogenpräventionskurs mit Sonia Parra Im Kurs haben wir die emotionalen Bedürfnisse und Defizite behandelt, die dazu führen, dass
FC3 - Duffing Oszillator
 FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
Mathematik verstehen 7 Lösungsblatt Aufgabe 6.67
 Aufgabenstellung: Berechne die Schnittpunkte der e k1 und k mit den Mittelpunkten M1 bzw. M und den Radien r1 bzw. r a. k1: M1 3, 4, P 5, 3 k 1, k geht durch A 0 und B 4 0 r 5 M liegt im 1. Quadranten
Aufgabenstellung: Berechne die Schnittpunkte der e k1 und k mit den Mittelpunkten M1 bzw. M und den Radien r1 bzw. r a. k1: M1 3, 4, P 5, 3 k 1, k geht durch A 0 und B 4 0 r 5 M liegt im 1. Quadranten
Strophoiden. Eckart Schmidt
 Strophoiden Eckart Schmidt Strophoiden sind als anallagmatische Kurven invariant gegenüber einer Kreisspiegelung; sie sind weiterhin das Inverse einer gleichseitigen Hyperbel, die Fußpunktkurve einer Parabel
Strophoiden Eckart Schmidt Strophoiden sind als anallagmatische Kurven invariant gegenüber einer Kreisspiegelung; sie sind weiterhin das Inverse einer gleichseitigen Hyperbel, die Fußpunktkurve einer Parabel
Prof. U. Stephan Wi-Ing 1.2
 Seite 1 von 5 Prof. U. Stephan Wi-Ing 1. inweis: Dateien Starmath.ttf und Starbats.ttf im Verzeichnis C:\WINDOWS\FONTS erforderlich Ich vermisse im Vorspann "Was man weiß, was man wissen sollte" die trigonometrischen
Seite 1 von 5 Prof. U. Stephan Wi-Ing 1. inweis: Dateien Starmath.ttf und Starbats.ttf im Verzeichnis C:\WINDOWS\FONTS erforderlich Ich vermisse im Vorspann "Was man weiß, was man wissen sollte" die trigonometrischen
DIOPHANTISCHE GLEICHUNGEN
 DIOPHANTISCHE GLEICHUNGEN Teilnehmer: Inka Eschke (Andreas-Oberschule) Klaus Gülzow (Heinrich-Hertz-Oberschule) Lena Kalleske (Heinrich-Hertz-Oberschule) Thomas Lindner (Heinrich-Hertz-Oberschule) Valentin
DIOPHANTISCHE GLEICHUNGEN Teilnehmer: Inka Eschke (Andreas-Oberschule) Klaus Gülzow (Heinrich-Hertz-Oberschule) Lena Kalleske (Heinrich-Hertz-Oberschule) Thomas Lindner (Heinrich-Hertz-Oberschule) Valentin
Übungsaufgaben Geometrie und lineare Algebra - Serie 1
 Übungsaufgaben Geometrie und lineare Algebra - Serie. Bei einer geraden Pyramide mit einer quadratischen Grundfläche von 00 cm beträgt die Seitenkante 3 cm. a) Welche Höhe hat die Pyramide? b) Wie groß
Übungsaufgaben Geometrie und lineare Algebra - Serie. Bei einer geraden Pyramide mit einer quadratischen Grundfläche von 00 cm beträgt die Seitenkante 3 cm. a) Welche Höhe hat die Pyramide? b) Wie groß
Erfüllt eine Funktion f für eine feste positive Zahl p und sämtliche Werte t des Definitionsbereichs die Gleichung
 34 Schwingungen Im Zusammenhang mit Polardarstellungen trifft man häufig auf Funktionen, die Schwingungen beschreiben und deshalb für den Ingenieur von besonderer Wichtigkeit sind Fast alle in der Praxis
34 Schwingungen Im Zusammenhang mit Polardarstellungen trifft man häufig auf Funktionen, die Schwingungen beschreiben und deshalb für den Ingenieur von besonderer Wichtigkeit sind Fast alle in der Praxis
BENOÎT MANDELBROT ( )
 BENOÎT MANDELBROT (1924 2010) Erfinder der Fraktale wird er genannt und Vater des Apfelmännchens sowie der nach ihm benannten Mandelbrot-Menge M: Benoît Mandelbrot Mathematiker, Physiker, Informatiker,
BENOÎT MANDELBROT (1924 2010) Erfinder der Fraktale wird er genannt und Vater des Apfelmännchens sowie der nach ihm benannten Mandelbrot-Menge M: Benoît Mandelbrot Mathematiker, Physiker, Informatiker,
Abitur allg. bildendes Gymnasium Wahlteil Analysis 2012 BW
 Aufgabe A1.1 Die Abbildung zeigt den Verlauf einer Umgehungsstraße zur Entlastung der Ortsdurchfahrt einer Gemeinde. Das Gemeindegebiet ist kreisförmig mit dem Mittelpunkt und dem Radius 1,5. Die Umgehungsstraße
Aufgabe A1.1 Die Abbildung zeigt den Verlauf einer Umgehungsstraße zur Entlastung der Ortsdurchfahrt einer Gemeinde. Das Gemeindegebiet ist kreisförmig mit dem Mittelpunkt und dem Radius 1,5. Die Umgehungsstraße
Prof. Dr. Dörte Haftendorn, Leuphana Universität Lüneburg, 2013
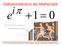 Selbstverständnis der Mathematik i 1 Selbstverständnis der Mathematik Komplexe Zahlen Geometrie i Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 Selbstverständnis der Mathematik : = Menge der Menschen,
Selbstverständnis der Mathematik i 1 Selbstverständnis der Mathematik Komplexe Zahlen Geometrie i Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 Selbstverständnis der Mathematik : = Menge der Menschen,
Gleichung nach Diophantos von Alexandria (etwa n. Chr.), dessen Buch Arithmetica Gleichungen dieser Art behandelt.
 Faszinierende Bilder 2 Die Mathematik, richtig betrachtet, besitzt nicht nur Wahrheit, sondern auch überragende Schönheit eine kalte und nüchterne Schönheit wie die der Bildhauerei, ohne Reiz für irgendeinen
Faszinierende Bilder 2 Die Mathematik, richtig betrachtet, besitzt nicht nur Wahrheit, sondern auch überragende Schönheit eine kalte und nüchterne Schönheit wie die der Bildhauerei, ohne Reiz für irgendeinen
Binomischer Satz. 1-E Vorkurs, Mathematik
 Binomischer Satz 1-E Vorkurs, Mathematik Terme Einer der zentralen Begriffe der Algebra ist der Term. Definition: Eine sinnvoll verknüpfte mathematische Zeichenreihe bezeichnet man als Term. Auch eine
Binomischer Satz 1-E Vorkurs, Mathematik Terme Einer der zentralen Begriffe der Algebra ist der Term. Definition: Eine sinnvoll verknüpfte mathematische Zeichenreihe bezeichnet man als Term. Auch eine
Brückenkurs Mathematik. Jörn Steuding (Uni Würzburg), 25. November 2017
 Brückenkurs Mathematik Jörn Steuding (Uni Würzburg), 25. November 2017 unser Programm 11. November: 1. Zahlen und einfache Gleichungen Zahlen, Rechengesetze, lineare u. quadratische Gleichungen, Dezimalbrüche,
Brückenkurs Mathematik Jörn Steuding (Uni Würzburg), 25. November 2017 unser Programm 11. November: 1. Zahlen und einfache Gleichungen Zahlen, Rechengesetze, lineare u. quadratische Gleichungen, Dezimalbrüche,
SCHRIFTLICHE ABITURPRÜFUNG 2009 Mathematik (Leistungskursniveau) Arbeitszeit: 300 Minuten
 Mathematik (Leistungskursniveau) Arbeitszeit: 300 Minuten Es sind die drei Pflichtaufgaben und eine Wahlpflichtaufgabe zu lösen. Der Prüfling entscheidet sich für eine Wahlpflichtaufgabe. Die zur Bewertung
Mathematik (Leistungskursniveau) Arbeitszeit: 300 Minuten Es sind die drei Pflichtaufgaben und eine Wahlpflichtaufgabe zu lösen. Der Prüfling entscheidet sich für eine Wahlpflichtaufgabe. Die zur Bewertung
Seminar: Ausgewählte höhere Kurven
 Seminar: Ausgewählte höhere Kurven Janine Scholtes 6. März 2017 Die Pascalsche Schnecke und die Kartesische Ovale 1 Pascalsche Schnecke 1.1 Etienne Pascal Etienne Pascal war ein französischer Mathematiker
Seminar: Ausgewählte höhere Kurven Janine Scholtes 6. März 2017 Die Pascalsche Schnecke und die Kartesische Ovale 1 Pascalsche Schnecke 1.1 Etienne Pascal Etienne Pascal war ein französischer Mathematiker
Zahlen. Vorlesung Mathematische Strukturen. Sommersemester Zahlen. Zahlen
 Vorlesung Mathematische Strukturen Sommersemester 2016 Prof. Barbara König Übungsleitung: Christine Mika & Dennis Nolte Division mit Rest Seien a, b Z zwei ganze mit a 0. Dann gibt es eindeutig bestimmte
Vorlesung Mathematische Strukturen Sommersemester 2016 Prof. Barbara König Übungsleitung: Christine Mika & Dennis Nolte Division mit Rest Seien a, b Z zwei ganze mit a 0. Dann gibt es eindeutig bestimmte
Tag der Mathematik 2018
 Tag der Mathematik 08 Gruppenwettbewerb Einzelwettbewerb Mathematische Hürden Aufgaben mit en und Punkteverteilung Tag der Mathematik 08 Hinweise für Korrektoren Generell gilt: Zielführende Zwischenschritte
Tag der Mathematik 08 Gruppenwettbewerb Einzelwettbewerb Mathematische Hürden Aufgaben mit en und Punkteverteilung Tag der Mathematik 08 Hinweise für Korrektoren Generell gilt: Zielführende Zwischenschritte
Hausdorff-Maß und Hausdorff-Dimension. Jens Krüger
 Hausdorff-Maß und Hausdorff-Dimension Jens Krüger Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen aus der Maßtheorie 3 3 Die Konstruktion des Hausdorff-Maßes 4 4 Eigenschaften des Hausdorff-Maßes und Hausdorff-Dimension
Hausdorff-Maß und Hausdorff-Dimension Jens Krüger Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen aus der Maßtheorie 3 3 Die Konstruktion des Hausdorff-Maßes 4 4 Eigenschaften des Hausdorff-Maßes und Hausdorff-Dimension
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 13 EBENE KOORDINATENGEOMETRIE DER ORTSVEKTOR
 ARBEITSBLATT 13 EBENE KOORDINATENGEOMETRIE DER ORTSVEKTOR Bei sehr vielen mathematischen Aufgabenstellungen ist nicht nur die Länge von bestimmten Strecken oder der Umfang interessant, sondern auch die
ARBEITSBLATT 13 EBENE KOORDINATENGEOMETRIE DER ORTSVEKTOR Bei sehr vielen mathematischen Aufgabenstellungen ist nicht nur die Länge von bestimmten Strecken oder der Umfang interessant, sondern auch die
Zum Einstieg. Mittelsenkrechte
 Zum Einstieg Mittelsenkrechte 1. Zeichne einen Kreis um A mit einem Radius r, der größer ist, als die Länge der halben Strecke AB. 2. Zeichne einen Kreis um B mit dem gleichen Radius. 3. Die Gerade durch
Zum Einstieg Mittelsenkrechte 1. Zeichne einen Kreis um A mit einem Radius r, der größer ist, als die Länge der halben Strecke AB. 2. Zeichne einen Kreis um B mit dem gleichen Radius. 3. Die Gerade durch
Differentialgeometrie I (Kurventheorie) SS 2013
 Differentialgeometrie I (Kurventheorie) SS 2013 Lektion 1 18. April 2013 c Daria Apushkinskaya 2013 () Kurventheorie: Lektion 1 18. April 2013 1 / 23 Organisatorisches Allgemeines Dozentin: Dr. Darya Apushkinskaya
Differentialgeometrie I (Kurventheorie) SS 2013 Lektion 1 18. April 2013 c Daria Apushkinskaya 2013 () Kurventheorie: Lektion 1 18. April 2013 1 / 23 Organisatorisches Allgemeines Dozentin: Dr. Darya Apushkinskaya
Geraden in R 2 Lösungsblatt Aufgabe 17.16
 Aufgabenstellung: Berechne den Umkreismittelpunkt und den Umkreisradius des Dreiecks ABC. a. A 2 1, B 8 3, C 5 6 b. A 1 3, B 9 3, C 11 19 c. A 2 3, B 3 3, C 4 5 d. A 5 3, B 7 9, C 1 15 Lösung der Aufgabe:
Aufgabenstellung: Berechne den Umkreismittelpunkt und den Umkreisradius des Dreiecks ABC. a. A 2 1, B 8 3, C 5 6 b. A 1 3, B 9 3, C 11 19 c. A 2 3, B 3 3, C 4 5 d. A 5 3, B 7 9, C 1 15 Lösung der Aufgabe:
Das Geheimnis der Zahl 5
 Das Geheimnis der Zahl 5 Ingo Blechschmidt iblech@speicherleck.de Pizzaseminar in Mathematik Universität Augsburg 2. Oktober 206 Gewidmet an Prof. Dr. Jost-Hinrich Eschenburg. Pizzaseminar in Mathematik
Das Geheimnis der Zahl 5 Ingo Blechschmidt iblech@speicherleck.de Pizzaseminar in Mathematik Universität Augsburg 2. Oktober 206 Gewidmet an Prof. Dr. Jost-Hinrich Eschenburg. Pizzaseminar in Mathematik
