Bernd Döring. Wege, Plätten, Färben. Vom Problem zur Theorie der Graphen
|
|
|
- Alke Weiss
- vor 6 Jahren
- Abrufe
Transkript
1 Bernd Döring Wege, Plätten, Färben Vom Problem zur Theorie der Graphen
2 Bernd Döring, Bernd Döring Johannes-Althusius-Gymnasium Früchteburger Weg Emden - 2 -
3 Inhaltsverzeichnis 0. Einleitung 1. Probleme 1.1. Vier Probleme und ihre Geschichte 2. Graphen 3. Eulersche Graphen 4. Hamiltonsche Graphen 5. Planare Graphen 6. Der Vierfarbensatz 7. Literatur 7.1. Literatur 7.2. Internet-Seiten - 3 -
4 0. Einleitung Leonhard Euler, einer der genialsten Mathematiker aller Zeiten, veröffentlichte 1736 die erste Arbeit über Graphentheorie. Darin löste er die seitdem als Königsberger Brückenproblem bekannte Aufgabe, zu entscheiden, ob es möglich sei, einen Rundweg über alle Brücken der Stadt zu gehen. Graphentheorie hat mit den bekannteren Funktionsgraphen der Analysis nichts zu tun. Mathematiker beschäftigen sich dort vielmehr mit zunächst recht einfach aussehenden Strukturen, die aus Punkten (in der Fachsprache Ecken genannt) und Verbindungslinien zwischen ihnen (Kanten genannt) bestehen. Besonders reizvoll an der Graphentheorie ist, dass fast alle Begriffe und Sätze in enger Beziehung zu Problemen stehen, von denen sich viele allgemein verständlich formulieren lassen. Trotzdem hat es bei einigen über einhundert Jahre gedauert, bis eine Lösung bewiesen wurde. Hier wird ein kleiner aber grundlegender Teil der Graphentheorie dargestellt. Dabei liegt der in jedem Kapitel entwickelten Mathematik ein Problem zu Grunde, zu dessen Lösung Definitionen und Sätze entwickelt werden. Dadurch kann der Leser leichter als in anderen Gebieten der Mathematik miterleben, warum und wie Theorie (von Menschen) gemacht wird
5 1. Vier Probleme 1.1. Probleme... Problem 1 Problem 2 Abbildung 1.1 Gibt es einen Rundweg, der jede Brücke genau einmal überquert? Woran erkennt man, ob es solch einen Weg gibt? Problem 3 Abbildung 1.2 Gibt es einen Rundweg um den Dodekaeder, der jeden Eckpunkt genau einmal durchläuft? Woran erkennt man, ob es solch einen Weg gibt? Problem 4 Abbildung 1.3 Kann man jedes Haus direkt mit jedem Werk verbinden und die Leitungen so legen, dass keine Kreuzungen entstehen? Woran erkennt man, ob kreuzungsfreie Verbindungen möglich sind? Abbildung 1.4 Wie viele Farben benötigt man mindestens, wenn aneinander grenzende Länder verschiedene Farben haben?
6 und ihre Geschichte Problem 1: Das Königsberger Brückenproblem In seiner Arbeit solutio problematis ad geometriam situs pertinentis, die Leonhard Euler 1736 in lateinischer Sprache veröffentlichte, lieferte er eine Lösung für die allgemeine Problemstellung von Rundwegen. Problem 2: Around the World 1859 kam in London das Spiel The Icosian Game auf den Markt, in dem auf einem Dodekaeder alle Eckpunkte genau einmal durchlaufen werden sollten. Autor des Spiels war der Mathematiker Sir William Rowan Hamilton. Ein finanzieller Erfolg war das Spiel nicht. Problem 3: Kreuzungsfreie Verbindungen Abbildung veröffentlichte H. E. Dudeney in Amusements in Mathematics unter dem Titel water, gas, and electricity das Rätsel, die drei Werke jeweils mit den drei Häusern ohne Kreuzungen zu verbinden. Angeblich ist das Rätsel noch viel älter. Problem 4: Das Vierfarbenproblem In der Mitte des 19. Jahrhunderts vermutete Francis Guthrie, man könne jede Landkarte mit nur vier Farben so kolorieren, dass aneinandergrenzende Länder verschieden gefärbt sind. Sein Bruder Frederick teilte dem Mathematik-Professor Augustus De Morgan diese Vermutung mit, die erstmals 1852 in einem Brief erwähnt wurde veröffentlichte Alfred Bray Kempe einen (allseits akzeptierten) Beweis und wurde daraufhin Fellow of the Royal Society. Doch der Beweis enthielt einen Fehler, der erst 1890 von Percy John Heawood aufgedeckt wurde
7 2. Graphen Bei den Problemen 2 und 3 lag offensichtlich eine Struktur aus Punkten und Verbindungslinien zwischen diesen Punkten zu Grunde. Dies lässt sich auch bei den Problemen 1 und 4 wiederfinden. Problem 1 Problem 4 Abbildung 2.1 Auch Problem 2 lässt sich auch in der Ebene zeichnen. Für Problem 3 gibt es eine naheliegende Veranschaulichung, die leider nicht die geforderte Kreuzungsfreiheit besitzt. Problem 2 Problem 3 Abbildung 2.3 Abbildung 2.4 Diese Struktur wird als Graph definiert. Die Punkte werden Ecken genannt, die Verbindungslinien Kanten. Dabei kann eine Kante zwei Ecken verbinden, oder von einer Ecke zur selben Ecke führen. Dann wird die Kante Schlinge genannt. Verbinden zwei Kanten die selben Ecken, spricht man von Mehrfachkanten
8 Definition 2.1 Seien E und K endliche Mengen, E, a: K P(E) (1) eine Abbildung, die jedem k K eine ein- oder zweielementige Teilmenge von E zuordnet. G = (E, K, a) heißt Graph, die Elemente von E Ecken, die Elemente von K Kanten. Eine Ecke e E und eine Kante k K heißen benachbart, wenn e a(k). Zwei Ecken e 1, e 2 E heißen benachbart, wenn es ein k K mit a(k) = {e 1, e 2 } gibt. Zwei Kanten k 1, k 2 K heißen benachbart, wenn es ein e E mit e a(k 1 ) und e a(k 2 ) gibt. Eine Ecke, die zu keiner anderen Ecke benachbart ist, heißt isoliert. Ist a(k) eine einelementige Teilmenge von E, heißt k Schlinge. Gibt es keine zwei verschiedenen k 1, k 2 K mit a(k 1 ) = a(k 2 ), so ist der Graph ohne Mehrfachkanten. Beispiel 2.1 E = {e 1, e 2, e 3, e 4 }, K = {k 1, k 2, k 3, k 4, k 5 }, a: K P(E) mit a(k 1 ) = {e 1 }, a(k 2 ) = {e 1, e 2 }, a(k 3 ) = {e 2, e 3 }, a(k 4 ) = {e 1, e 3 }, a(k 5 ) = {e 1, e 3 }. Dann ist G = (E, K, a) ein Graph, der so veranschaulicht werden kann. Abbildung 2.5 Dabei ist k 1 eine Schlinge, e 4 ist eine isolierte Ecke. Wegen k 4 und k 5 enthält der Graph Mehrfachkanten. Bei den Problemen 1 und 2 war es wichtig, wie viele Kanten zu einer Ecke benachbart sind. Definition 2.2 Sei G = (E, K, a) ein Graph. Der Grad einer Ecke e E ist die Anzahl der Kanten k K, für die gilt: e a(k), wobei Schlingen doppelt zählen. Im Beispiel 2.1 ist der Grad von e 1 5, von e 2 2, von e 3 3 und von e 4 0. (1) P(E) ist die Menge aller Teilmengen von E
9 Satz 2.1 Die Summe aller Eckengrade ist eine gerade Zahl. Beweis: Jede Kante wird genau zweimal gezählt, was auch für Schlingen gilt. Also ist die Summe aller Eckengrade gleich 2 K (2) und damit eine gerade Zahl. Satz 2.2 In jedem Graphen ist die Anzahl der Ecken mit ungeradem Grad gerade. Beweis: Siehe Aufgabe 4. Definition 2.3 Seien n, m ln, G = (E, K, a) ein Graph. (i) G heißt vollständig, wenn es keine Schlingen und keine Mehrfachkanten gibt und jede Ecke zu jeder anderen Ecke benachbart ist. Ein vollständiger Graph mit n Ecken wird mit K n bezeichnet. (ii) G heißt paar, wenn sich die Eckenmenge E in zwei Teilmengen zerlegen lässt: E 1, E 2 E, E 1 E 2 =, E 1 E 2 = E, so dass keine zwei Ecken aus einer dieser Teilmengen zueinander benachbart sind, aber jede Ecke einer Teilmenge zu jeder Ecke der anderen Teilmenge. Ein paarer Graph mit E 1 =n und E 2 =m wird mit K m,n bezeichnet. Die Bezeichnungen K n und K m,n erinnern an Kazimir Kuratowski. Zwei dieser Graphen spielen die Hauptrolle im Kapitel über planare Graphen. Bei Beispiel 3 geht es darum, die Kanten geschickt in die Ebene zu zeichnen. Vielleicht erreicht man sein Ziel auch durch eine Veränderung der Lage der Ecken. Daher ist es sinnvoll, Graphen zu identifizieren, die sich nicht wesentlich unterscheiden, in denen also die benachbart -Beziehung gleich ist. Definition 2.4 Zwei Graphen G 1 = (E 1, K 1, a 1 ) und G 2 = (E 2, K 2, a 2 ) heißen isomorph, wenn es bijektive Abbildungen (3) i E : E 1 E 2 und i K : K 1 K 2 gibt, mit e a 1 (k) i E (e) a 2 (i K (k)) für alle e E 1 und k K. (2) K ist die Anzahl der Elemente der Menge K (3) Eine Abbildung f : M N heißt bijektiv, wenn es zu jedem n N genau ein m M mit f(m)=n gibt
10 Bei isomorphen Graphen sind die Bilder benachbarter Ecken und Kanten benachbart. Ferner sind die Bilder je zwei benachbarte Ecken benachbart sowie die Bilder je zwei benachbarter Kanten benachbart. Aufgaben 1. Gib alle Graphen ohne Mehrfachkanten mit E =1 und E =2 an. 2. Beweise, dass es genau 4 nicht isomorphe Graphen ohne Schlingen und Mehrfachkanten mit drei Ecken gibt und genau 11 Graphen mit 4 Ecken. 3. Gib die Graphen K 5, K 6 und K 7 an. Gib die Graphen K 1,3, K 1,4, K 2,3, K 2,4, K 3,3 an. 4. Beweise Satz Sind die Graphen isomorph? Abbildung Beweise, dass der Graph in Abbildung 2.3 isomorph zum Dodekaeder in Abbildung 1.2 ist. 7. Sind die Graphen isomorph? Abbildung
11 3. Eulersche Graphen Das Königsberger Brückenproblem lässt sich zu der Frage verallgemeinern, woran ein Graph erkennbar ist, in dem es einen Rundweg aus benachbarten Kanten gibt, der jede Kante genau einmal enthält. Definition 3.1 Seien G = (E, K, a) ein Graph, n ln, e 1, e n E zwei Ecken. Eine endliche Folge (e 1, k 1, e 2, k 2,... k n-1, e n ) aus nicht notwendig verschiedenen Ecken e 1, e 2,... e n E und nicht notwendig verschiedenen Kanten k 1, k 2,... k n-1 K heißt Weg zwischen e 1 und e n, wenn gilt: a(k i ) = {e i, e i+1 } für alle i = 1, 2,... n-1. Ist e 1 = e n, heißt der Weg Rundweg. Definition 3.2 Sei G = (E, K, a) ein Graph. G heißt zusammenhängend, wenn es für je zwei beliebige Ecken e, f E, e f, einen Weg zwischen e und f gibt. Definition 3.3 Sei G = (E, K, a) ein Graph. Ein Weg heißt Eulerscher Weg, wenn in ihm jede Kante des Graphen genau einmal auftritt. Ein Rundweg heißt Eulerscher Rundweg, wenn in ihm jede Kante des Graphen genau einmal auftritt. Satz 3.1 (Euler, 1736) Sei G = (E, K, a) ein zusammenhängender Graph mit mindestens zwei Ecken. (i) G enthält genau dann einen Eulerschen Rundweg, wenn der Grad aller Ecken gerade ist. (ii) G enthält genau dann einen Eulerschen Weg, wenn keine oder genau zwei Ecken einen ungeraden Grad haben. Beweis: (i) Jede Ecke in dem Rundweg ist zu der in der Folge vorangehenden und der nachfolgenden Kante benachbart. Da die erste und die letzte Ecke gleich sind, ist diese Ecke zur ersten und zur letzten Kante der Folge benachbart. Da in einem Eulerschen Rundweg jede Kante genau einmal auftritt, ist der Grad jeder Ecke die doppelte Anzahl des Auftretens der Ecke in der Folge, wobei
12 (ii) die erste und die letzte Ecke nur einmal gezählt werden. Also ist der Grad jeder Ecke eine gerade Zahl. Da der Graph zusammenhängend ist und zwei Ecken enthält, haben alle Ecken mindestens den Grad 2. In einer beliebigen Ecke wird ein Weg begonnen und solange über noch nicht benutzte Kanten fortgesetzt, bis man eine bereits durchlaufene Ecke erreicht oder der Weg nicht weiter fortgeführt werden kann. In beiden Fällen enthält der Weg einen Rundweg. Hat man eine bereits durchlaufene Ecke erreicht, so ist dies unmittelbar klar. Ist der Weg nicht mehr fortsetzbar, so hat man die letzte Ecke auf einer Kante erreicht und es findet sich keine noch nicht benutzte Kante, um die Ecke zu verlassen. Da der Grad der Ecke mindestens 2 ist, ist die Ecke in dem Weg bereits durchlaufen worden und der Weg enthält einen Rundweg. Wenn der Rundweg nicht alle Kanten des Graphen enthält, entfernt man die Kanten des Rundweges aus dem Graphen erhält man einen möglicherweise nicht zusammenhängenden Graphen, in dem erneut jede Ecke einen geraden Grad hat. Von einer Ecke mit Grad größer 0 beginnt man erneut einen beliebigen Weg über noch nicht benutzte Kanten, bis man eine bereits durchlaufene Ecke erreicht oder der Weg nicht weiter fortgeführt werden kann. Auch dieser Weg enthält einen Rundweg, der aus dem Graphen entfernt wird. Da der Grad aller Ecken gerade bleibt, kann man solange Rundwege konstruieren, die in keiner Kante übereinstimmen, bis alle Ecken den Grad 0 haben, also jede Kante in genau einem dieser Rundwege auftritt. Da der Graph zusammenhängend ist, kann man die Rundwege nacheinander vereinen, so dass jeweils ein längerer Rundweg entsteht. Zum Schluss erhält man einen Rundweg, der jede Kante genau einmal enthält. Ist der Eulersche Weg ein Rundweg, folgt die Behauptung aus (i). Ist der Eulersche Weg kein Rundweg, fügt man eine Kante zwischen der ersten und der letzten Ecke des Weges ein und erhält so einen Eulerschen Rundweg in einem um eine Kante erweiterten Graphen. Nach (i) ist in diesem Graphen der Grad jeder Ecke gerade. Wird die neue Kante wieder entfernt, haben genau die beiden mit ihr benachbarten Ecken einen ungeraden Grad. Ist der Grad jeder Ecke gerade folgt die Behauptung aus (i). Haben genau
13 zwei Ecken einen ungeraden Grad, so fügt man zwischen ihnen eine zusätzliche Kante ein. Der neue Graph enthält nach (i) einen Eulerschen Rundweg, der auch so angeordnet werden kann, dass die neue Kante die letzte Kante im Rundweg ist. Entfernt man die neue Kante und die letzte Ecke aus dem Rundweg, so erhält man einen Eulerschen Weg im ursprünglichen Graphen. Definition 3.4 Ein Graph, der einen Eulerschen Rundweg enthält, heißt Eulerscher Graph. Damit ist das Problem der Rundwege, die jede Kante eines Graphen genau einmal enthalten, gelöst. Mit einem einfach zu überprüfenden Kriterium lässt sich entscheiden, ob es einen solchen Rundweg gibt. Der Beweis des Satzes liefert sogar einen Algorithmus, zur Konstruktion eines Rundweges. Aufgaben 1. Erschwerte Überfahrt Ein Fährmann soll einen Wolf, eine Ziege und einen Kohlkopf über einen Fluss bringen. Das zur Verfügung stehende Boot fasst außer dem Fährmann nur einen weiteren Passagier. Aus leicht ersichtlichen Gründen darf in Abwesenheit des Fährmanns weder der Wolf mit der Ziege noch die Ziege mit dem Kohlkopf zusammen sein. Löse das Problem durch Angabe eines Weges in einem Graphen. 2. Krieger und Gefangene Drei Krieger wollen mit drei Gefangenen einen Fluss in einem Boot überqueren, in dem nur zwei Personen Platz finden. Die Gefangenen rebellieren, sobald sie in der Überzahl sind, fliehen aber nicht, auch wenn sie alleine gelassen werden. 3. Missionare und Kannibalen Drei Missionare wollten mit drei Kannibalen einen Fluss überqueren. Das Boot konnte nur zwei Personen aufnehmen. Nur die Missionare und einer der Kannibalen waren in der Lage zu rudern. Da ihre Bemühungen um das
14 Seelenheil der Eingeboren nicht sehr erfolgreich war, durften die Missionare nie in Unterzahl sein. 4. Kann man das Haus des Nikolaus in einem Zug zeichnen? Falls dies möglich ist, auf wie viele Arten? 5. Für welche natürliche Zahlen m und n sind die vollständigen Graphen K n und die paaren Graphen K m,n Eulersche Graphen? 6. Kann ein Springer auf einem 8x8-Schachbrett so umherziehen, dass jeder mögliche Zug genau einmal ausgeführt wird? Ist dies auf einem 7x7-Schachbrett möglich? 7. Enthält der Dodekaeder-Graph einen Eulerschen Rundweg?
15 4. Hamiltonsche Graphen Das im Spiel The Icosian Game gestellte Problem lässt sich zu der Frage verallgemeinern, woran ein Graph erkennbar ist, in dem es einen Rundweg gibt, der jede Ecke genau einmal enthält. Definition 4.1 Sei G = (E, K, a) ein Graph. Ein Weg heißt Hamiltonscher Weg, wenn in ihm jede Ecke des Graphen genau einmal auftritt. Ein Rundweg heißt Hamiltonscher Rundweg, wenn in ihm jede Ecke des Graphen genau einmal auftritt, mit Ausnahme der Anfangsecke, die der Endecke entspricht. Dieses Problem ist weitaus schwieriger als das der Eulerschen Rundwege. So gibt es keinen Satz, der Graphen mit Hamiltonschen Rundwegen charakterisiert, also eine Äquivalenz-Beschreibung liefert. Hier wird ein Satz bewiesen, der lediglich eine hinreichende Bedingung (aus der folgt, dass ein Hamiltonscher Rundweg existiert) enthält. Leicht überlegt man sich, dass es Graphen mit Hamiltonschen Rundwegen gibt, die diese Bedingung nicht erfüllen. Weiter enthält der Beweis keinen Algorithmus zur Konstruktion eines Hamiltonschen Rundwegs. Jeder Graph lässt sich durch Hinzufügen von Ecken, die mit jeder ursprünglich vorhandenen Ecke durch eine ebenfalls hinzugefügte Kante verbunden sind, so ergänzen, dass er einen Hamiltonschen Rundweg enthält. Maximal benötigt man zusätzlich so viele Ecken wie der Graph ursprünglich enthält Satz 4.1 Sei G = (E, K, a) ein Graph. Dann enthält der Graph G = (E E, K K, a ) mit E = E, K enthält zu jeder Ecke aus E genau eine Kante zu jeder Ecke aus E, einen Hamiltonschen Rundweg. Beweis: Durchläuft man beliebig jeweils abwechselnd noch nicht benutzte Ecken aus E und aus E und benutzt nur Kanten aus K und wird als letzte Ecke die Anfangsecke in den Weg eingebaut, so hat man einen Hamiltonschen Rundweg erhalten
16 Satz 4.2 (Dirac, 1952) Sei G = (E, K, a) ein Graph ohne Schlingen und Mehrfachkanten mit E 3. Wenn der Grad jeder Ecke größer oder gleich 1 E ist, dann existiert ein Hamiltonscher Rundweg. Beweis: (indirekt 1 ) In den Graphen wird eine minimale Anzahl von Ecken eingefügt, die mit jeder Ecke aus E durch eine Kante verbunden sind, so dass der neue Graph G einen Hamiltonschen Rundweg enthält. Wenn G keinen Hamiltonschen Rundweg enthält, ist die Anzahl n der minimal eingefügten Ecken größer als 0. In dem Hamiltonschen Rundweg tritt also mindestens eine hinzugefügte Ecke p (mit zwei hinzugefügten Kanten k 1 und k 2 ) zwischen zwei Ecken e, f E auf, wobei der Rundweg bei e beginne: (e, k 1, p, k 2, f,..., e). Zwischen e und f kann es keine Kante geben, da sonst p nicht erforderlich wäre und man auch mit n-1 neuen Ecken auskäme. Auch kann in dem Hamiltonschen Rundweg keine zu f benachbarte Ecke f direkt nach einer zu e benachbarte Ecke e in der Folge stehen: man könnte sonst ebenfalls auf p verzichten, indem man den Abschnitt von f zu e umgekehrt durchläuft und erhielte statt (e, k 1, p, k 2, f,..., e, k, f,..., e) den Rundweg (e, k e, e,..., f, k f, f,..., e), wobei k e eine Kante zwischen e und e, k f eine Kante zwischen f und f ist. Also folgt in dem Hamiltonschen Rundweg auf jede zu e benachbarte Ecke eine nicht zu f benachbarte Ecke. Da es mindestens 1 E +n zu e benachbarte Ecken gibt, gibt es auch mindestens 1 E +n nicht zu f benachbarte Ecken. Da die Anzahl der zu f benachbarten Ecken mindestens 1 E +n ist, gibt es insgesamt mindestens 2 (1 E + n) = E + 2n Ecken. Da zu E jedoch nur n Ecken hinzugefügt wurden, haben wir aus der Annahme, G enthalte keinen Hamiltonschen Kreis, einen Widerspruch gefolgert. Also ist die Behauptung, G enthalte einen Hamiltonschen Kreis, wahr. Definition 4.2 Ein Graph, der einen Hamiltonschen Rundweg enthält heißt Hamiltonscher Graph. 1 In einem indirekten Beweis wird aus der Annahme der Nichtgültigkeit der Behauptung ein Widerspruch abgeleitet. Da die Mathematik solche Widersprüche nicht enthalten darf, ist die Nichtgültigkeit der Behauptung falsch, also die Behauptung wahr
17 Aufgaben 1. Für welche natürlichen Zahlen n und m gibt es in den Graphen a) K m,n b) K n einen Hamiltonschen Rundweg? 2. Kann ein Springer auf einem 8x8 (7x7) Schachbrett so umherziehen, dass er jedes Feld genau einmal besucht und zum Ausgangsfeld zurückkehrt? 3. Gib einen Graphen an, der a) einen Eulerschen Rundweg aber keinen Hamiltonschen Rundweg b) keinen Eulerschen Rundweg aber einen Hamiltonschen Rundweg c) einen Eulerschen und einen Hamiltonschen Rundweg besitzt
18 5. Planare Graphen Definition 5.1 Ein Graph G = (E, K, a) heißt eben, wenn alle Ecken Punkte der Ebene sind, jede Kante k K eine Kurve zwischen den Ecken aus a(k) ist und sich zwei Kanten höchstens in den zu ihnen benachbarten Ecken schneiden. Ein Graph heißt planar, wenn er zu einem ebenen Graphen isomorph ist. Definition 5.2 Sei G ein ebener Graph. Eine Menge, die alle Punkte der Ebene enthält, die durch Kurven, die weder eine Kante von G schneiden noch eine Ecke von G enthalten, verbunden werden können, heißt ein Gebiet von G. Satz 5.1 (Eulersche Polyederformel, 1752) Sei G ein zusammenhängender ebener Graph mit n Ecken, m Kanten und f Gebieten, n, m, f IN. Dann gilt: n + f = m + 2. Beweis: Der Beweis wird durch vollständige Induktion 2 nach der Anzahl der Kanten des Graphen geführt. Ist m = 0, so besitzt der Graph keine Kante. Da er zusammenhängend ist und E, gibt es genau eine Ecke und damit genau ein Gebiet. Also ist n = 1 und f = 1 und die Behauptung gilt: = Die Behauptung gelte für alle Graphen mit m Kanten. Aus einem zusammenhängenden ebenen Graphen G mit m+1 Kanten wird eine beliebige Kante und gegebenenfalls eine dann isolierte Ecke so entfernt, dass der entstehende Graph G zusammenhängend ist. Er ist ebenfalls eben. Da er m Kanten hat, gilt die Gleichung: n + f = m + 2. Wird in den Graphen G die entfernte Kante und gegebenenfalls die entfernte Ecke eingefügt, so erhält man erneut den Graphen G. Die eingefügte Kante kann a) eine Schlinge an einer vorhandenen Ecke sein, 2 Man kann eine Aussage für alle natürlichen Zahlen beweisen, indem man zeigt, dass sie für die erste natürliche Zahl (0 oder 1 je nach Definition) gilt, und beweist, dass wenn die Aussage für eine natürliche Zahl n gilt, sie auch für die nachfolgende Zahl n+1 gilt. Da die natürlichen Zahlen so definiert sind, dass es eine erste Zahl (0 oder 1) gibt und jede Zahl n genau eine Nachfolgezahl (n+1) besitzt, ist auf diese Art gezeigt, dass die Aussage für alle natürlichen Zahlen gilt
19 b) zwei vorhandene Ecken verbinden oder c) eine vorhandene Ecke mit einer entfernten und nun ebenfalls eingefügten Ecke verbinden. Da der Graph G zusammenhängend ist, kann die neue Kante nicht zwei neu eingefügte Ecken verbinden und auch keine Schlinge an einer neu eingefügten Ecke sein. In den Fällen a) und b) erhöht sich die Anzahl der Gebiete um 1 und die Anzahl der Ecken bleibt unverändert, im Fall c) erhöht sich die Anzahl der Ecken um 1 und die Anzahl der Gebiete verändert sich nicht. Da sich in allen drei Fällen die Anzahl der Kanten um 1 erhöht, gilt die Gleichung auch für m+1 Kanten. In den Fällen a) und b): n + f = m + 2 n + f+1 = m+1 + 2, im Fall c): n + f = m + 2 n+1 + f = m Satz 5.2 Sei G ein planarer zusammenhängender Graph ohne Schlingen und Mehrfachkanten mit n Ecken und m Kanten, n, m IN, n 3. Dann gilt: m 3n 6. Beweis: G ist isomorph zu einem ebenen Graphen G. G hat ebenfalls n Ecken und m Kanten. Die Anzahl der Gebiete in G sei f, f IN. In G wird jedes Gebiet durch mindestens 3 Kanten begrenzt, da es keine Schlingen und keine Mehrfachkanten gibt. Jede Kante liegt zwischen genau 2 Gebieten. Also ist 3f 2m und somit f Bm. Nach Satz 5.1 ist: n + f = m + 2 m = n + f 2 m n + Bm 2 2m n 2 m 3n 6. Satz 5.3 Die Graphen K 5 und K 3,3 sind nicht planar. Beweis: Der K 5 hat 5 Ecken und 10 Kanten. Wäre er planar, so wäre nach Satz 5.2: = 9. Widerspruch. Der K 3,3 hat 6 Ecken und 9 Kanten. Also wäre nach Satz 5.1: f = m n + 2 = = 5. Wäre er planar, so wäre in einem isomorphen ebenen Graphen jedes Gebiet von mindestens 4 Kanten begrenzt, also wäre 4f 2m. Dann wäre 20 = = 18. Widerspruch
16. Flächenfärbungen
 Chr.Nelius: Graphentheorie (WS 2015/16) 57 16. Flächenfärbungen In der Mitte des 19. Jahrhunderts tauchte eine Vermutung auf, die erst 125 Jahre später bewiesen werden sollte und die eine der bekanntesten
Chr.Nelius: Graphentheorie (WS 2015/16) 57 16. Flächenfärbungen In der Mitte des 19. Jahrhunderts tauchte eine Vermutung auf, die erst 125 Jahre später bewiesen werden sollte und die eine der bekanntesten
1. Einleitung wichtige Begriffe
 1. Einleitung wichtige Begriffe Da sich meine besondere Lernleistung mit dem graziösen Färben (bzw. Nummerieren) von Graphen (speziell von Bäumen), einem Teilgebiet der Graphentheorie, beschäftigt, und
1. Einleitung wichtige Begriffe Da sich meine besondere Lernleistung mit dem graziösen Färben (bzw. Nummerieren) von Graphen (speziell von Bäumen), einem Teilgebiet der Graphentheorie, beschäftigt, und
Westfählische Wilhelms-Universität. Eulersche Graphen. Autor: Jan-Hendrik Hoffeld
 Westfählische Wilhelms-Universität Eulersche Graphen Autor: 21. Mai 2015 Inhaltsverzeichnis 1 Das Königsberger Brückenproblem 1 2 Eulertouren und Eulersche Graphen 2 3 Auffinden eines eulerschen Zyklus
Westfählische Wilhelms-Universität Eulersche Graphen Autor: 21. Mai 2015 Inhaltsverzeichnis 1 Das Königsberger Brückenproblem 1 2 Eulertouren und Eulersche Graphen 2 3 Auffinden eines eulerschen Zyklus
Diskrete Mathematik. Sebastian Iwanowski FH Wedel. Kap. 6: Graphentheorie
 Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Vier-Farbenproblem. (c) Ein etwas schwereres Beispiel...
 Vier-Farbenproblem Kann man jede Landkarte mit vier Farben färben, sodass keine aneindander angrenzenden Länder die gleiche Farbe haben? Versuchen Sie die Karte Deutschlands oder eines der anderen Bilder
Vier-Farbenproblem Kann man jede Landkarte mit vier Farben färben, sodass keine aneindander angrenzenden Länder die gleiche Farbe haben? Versuchen Sie die Karte Deutschlands oder eines der anderen Bilder
Liegt eine Kante k auf einem Zyklus Z, so liegt k auf dem Rand genau zweier
 4 Planare Graphen Bisher wurden Graphen abstrakt durch Mengen E und K und eine Abbildung ψ : K P(E) definiert. In diesem Kapitel beschäftigen wir uns mit einem Abschnitt der sogenannten topologischen Graphentheorie.
4 Planare Graphen Bisher wurden Graphen abstrakt durch Mengen E und K und eine Abbildung ψ : K P(E) definiert. In diesem Kapitel beschäftigen wir uns mit einem Abschnitt der sogenannten topologischen Graphentheorie.
5 Graphen und Polyeder
 5 Graphen und Polyeder 5.1 Graphen und Eulersche Polyederformel Ein Graph besteht aus einer Knotenmenge V (engl. vertex) und einer Kantenmenge E (engl. edge). Anschaulich verbindet eine Kante zwei Knoten,
5 Graphen und Polyeder 5.1 Graphen und Eulersche Polyederformel Ein Graph besteht aus einer Knotenmenge V (engl. vertex) und einer Kantenmenge E (engl. edge). Anschaulich verbindet eine Kante zwei Knoten,
Elementargeometrie. Prof. Dr. Andreas Meister SS digital von: Frank Lieberknecht
 Prof. Dr. Andreas Meister SS 2004 digital von: Frank Lieberknecht Geplanter Vorlesungsverlauf...1 Graphentheorie...1 Beispiel 1.1: (Königsberger Brückenproblem)... 1 Beispiel 1.2: (GEW - Problem)... 2
Prof. Dr. Andreas Meister SS 2004 digital von: Frank Lieberknecht Geplanter Vorlesungsverlauf...1 Graphentheorie...1 Beispiel 1.1: (Königsberger Brückenproblem)... 1 Beispiel 1.2: (GEW - Problem)... 2
Übersicht 2. Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben. Martin Oellrich. wer das Problem löste 4
 Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht 5. April 009 5. April 009 Martin Oellrich 1 vom Problem zur Theorie die Idee weiter denken 3 MathematikerIn werden? Gibt
Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht 5. April 009 5. April 009 Martin Oellrich 1 vom Problem zur Theorie die Idee weiter denken 3 MathematikerIn werden? Gibt
Gibt es in Königsberg einen Spaziergang, bei dem man jede der. Pregelbrücken. überquert?
 Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? 1 Königsberger Brückenproblem Im Jahre 1736 Leonhard Euler löste das Problem allgemein
Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? 1 Königsberger Brückenproblem Im Jahre 1736 Leonhard Euler löste das Problem allgemein
Der Fünffarbensatz. Ausarbeitung des Seminarvortrags vom
 Philipps-Universität Marburg Fachbereich 12: Mathematik und Informatik PS Über klassische Probleme der Mathematik Leitung: Prof. Harald Upmeier, Benjamin Schwarz Referentin: Sabrina Klöpfel Wintersemester
Philipps-Universität Marburg Fachbereich 12: Mathematik und Informatik PS Über klassische Probleme der Mathematik Leitung: Prof. Harald Upmeier, Benjamin Schwarz Referentin: Sabrina Klöpfel Wintersemester
Daniel Platt Einführung in die Graphentheorie
 Einführung in die Für die Mathematische Schülergesellschaft Leonhard Euler Humboldt Universität zu Berlin, Institut für Mathematik Das vorliegende Skript beschäftigt sich mit dem Thema. Das Skript entsteht
Einführung in die Für die Mathematische Schülergesellschaft Leonhard Euler Humboldt Universität zu Berlin, Institut für Mathematik Das vorliegende Skript beschäftigt sich mit dem Thema. Das Skript entsteht
2 Eulersche Polyederformel und reguläre Polyeder
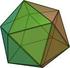 6 2 Eulersche Polyederformel und reguläre Polyeder 2.1 Eulersche Polyederformel Formal besteht ein Graph aus einer Knotenmenge X und einer Kantenmenge U. Jede Kante u U ist eine zweielementige Teilmenge
6 2 Eulersche Polyederformel und reguläre Polyeder 2.1 Eulersche Polyederformel Formal besteht ein Graph aus einer Knotenmenge X und einer Kantenmenge U. Jede Kante u U ist eine zweielementige Teilmenge
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik. Weihnachtsblatt
 Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Minimal spannender Baum
 Minimal spannender Baum 16 1 2 21 5 11 19 6 6 3 14 33 10 5 4 18 Die Kreise zeigen die vorgesehenen Standorte neu zu errichtender Filialen einer Bank. Entlang der bestehenden Straßen sollen Telefonleitungen
Minimal spannender Baum 16 1 2 21 5 11 19 6 6 3 14 33 10 5 4 18 Die Kreise zeigen die vorgesehenen Standorte neu zu errichtender Filialen einer Bank. Entlang der bestehenden Straßen sollen Telefonleitungen
Vier Farben reichen! Von farbigen Landkarten und kniffeligen Beweisen. Martin Oellrich. Warum eine Karte? 3. Warum stetige Grenzen?
 Vier Farben reichen! Von farbigen Landkarten und kniffeligen Beweisen Problemstellung Deutsche Bundesländer in vier Farben 4. April 06 Martin Oellrich Warum geht das immer? Gegeben: Karte eines Gebietes
Vier Farben reichen! Von farbigen Landkarten und kniffeligen Beweisen Problemstellung Deutsche Bundesländer in vier Farben 4. April 06 Martin Oellrich Warum geht das immer? Gegeben: Karte eines Gebietes
Der Vier-Farben-Satz
 , Samuel Hetterich, Felicia Raßmann Goethe-Universität Frankfurt, Institut für Mathematik 21.Juni 2013 Wieviele Farben braucht man zum Färben einer Landkarte? Spielregeln Länder mit einer gemeinsamen Grenze
, Samuel Hetterich, Felicia Raßmann Goethe-Universität Frankfurt, Institut für Mathematik 21.Juni 2013 Wieviele Farben braucht man zum Färben einer Landkarte? Spielregeln Länder mit einer gemeinsamen Grenze
6. Übung zur Linearen Optimierung SS08
 6 Übung zur Linearen Optimierung SS08 1 Sei G = (V, E) ein schlichter ungerichteter Graph mit n Ecken und m Kanten Für eine Ecke v V heißt die Zahl der Kanten (u, v) E Grad der Ecke (a) Ist die Anzahl
6 Übung zur Linearen Optimierung SS08 1 Sei G = (V, E) ein schlichter ungerichteter Graph mit n Ecken und m Kanten Für eine Ecke v V heißt die Zahl der Kanten (u, v) E Grad der Ecke (a) Ist die Anzahl
Donnerstag, 11. Dezember 03 Satz 2.2 Der Name Unterraum ist gerechtfertigt, denn jeder Unterraum U von V ist bzgl.
 Unterräume und Lineare Hülle 59 3. Unterräume und Lineare Hülle Definition.1 Eine Teilmenge U eines R-Vektorraums V heißt von V, wenn gilt: Unterraum (U 1) 0 U. (U ) U + U U, d.h. x, y U x + y U. (U )
Unterräume und Lineare Hülle 59 3. Unterräume und Lineare Hülle Definition.1 Eine Teilmenge U eines R-Vektorraums V heißt von V, wenn gilt: Unterraum (U 1) 0 U. (U ) U + U U, d.h. x, y U x + y U. (U )
Graphentheorie Mathe-Club Klasse 5/6
 Graphentheorie Mathe-Club Klasse 5/6 Thomas Krakow Rostock, den 26. April 2006 Inhaltsverzeichnis 1 Einleitung 3 2 Grundbegriffe und einfache Sätze über Graphen 5 2.1 Der Knotengrad.................................
Graphentheorie Mathe-Club Klasse 5/6 Thomas Krakow Rostock, den 26. April 2006 Inhaltsverzeichnis 1 Einleitung 3 2 Grundbegriffe und einfache Sätze über Graphen 5 2.1 Der Knotengrad.................................
Vorlesungen vom 5.Januar 2005
 Vorlesungen vom 5.Januar 2005 5 Planare Graphen 5.1 Beispiel: Gas, Wasser, Elektrik Drei eingeschworene Feinde, die im Wald leben, planen Trassen zu den Versorgungswerken für die drei Grundgüter Gas, Wasser
Vorlesungen vom 5.Januar 2005 5 Planare Graphen 5.1 Beispiel: Gas, Wasser, Elektrik Drei eingeschworene Feinde, die im Wald leben, planen Trassen zu den Versorgungswerken für die drei Grundgüter Gas, Wasser
Ausarbeitung zum Modulabschluss. Graphentheorie. spannende Bäume, bewertete Graphen, optimale Bäume, Verbindungsprobleme
 Universität Hamburg Fachbereich Mathematik Seminar: Proseminar Graphentheorie Dozentin: Haibo Ruan Sommersemester 2011 Ausarbeitung zum Modulabschluss Graphentheorie spannende Bäume, bewertete Graphen,
Universität Hamburg Fachbereich Mathematik Seminar: Proseminar Graphentheorie Dozentin: Haibo Ruan Sommersemester 2011 Ausarbeitung zum Modulabschluss Graphentheorie spannende Bäume, bewertete Graphen,
Das Briefträgerproblem
 Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
1. Übung Graphentheorie WS2016/17
 1. Übung Graphentheorie WS2016/17 1. Schreiben Sie für jede Ecke der folgenden 7 Graphen den Grad auf! Welche der Graphen sind regulär? G 1 G 2 G 5 G 3 2. Bestimmen Sie alle paarweise nicht-isomorphen
1. Übung Graphentheorie WS2016/17 1. Schreiben Sie für jede Ecke der folgenden 7 Graphen den Grad auf! Welche der Graphen sind regulär? G 1 G 2 G 5 G 3 2. Bestimmen Sie alle paarweise nicht-isomorphen
Brückenkurs. Beweise. Anja Haußen Brückenkurs, Seite 1/23
 Brückenkurs Beweise Anja Haußen 30.09.2016 Brückenkurs, 30.09.2016 Seite 1/23 Inhalt 1 Einführung 2 Sätze 3 Beweise 4 direkter Beweis Brückenkurs, 30.09.2016 Seite 2/23 Einführung Die höchste Form des
Brückenkurs Beweise Anja Haußen 30.09.2016 Brückenkurs, 30.09.2016 Seite 1/23 Inhalt 1 Einführung 2 Sätze 3 Beweise 4 direkter Beweis Brückenkurs, 30.09.2016 Seite 2/23 Einführung Die höchste Form des
M. Anderegg, E. Müller Graphentheorie
 Graphentheorie In den nächsten zwei Doppellektion lernen Sie ein Gebiet der Mathematik kennen, dass sich komplett von allem bisher Gehörten unterscheidet: Die Graphentheorie. Sie wurde vom Schweizer Mathematiker
Graphentheorie In den nächsten zwei Doppellektion lernen Sie ein Gebiet der Mathematik kennen, dass sich komplett von allem bisher Gehörten unterscheidet: Die Graphentheorie. Sie wurde vom Schweizer Mathematiker
Aufgaben und Lösungen zum Vorkurs Mathematik: Beweismethoden Für Mittwoch den
 Fachbereich Mathematik Aufgaben und Lösungen zum Vorkurs Mathematik: Beweismethoden Für Mittwoch den 8.9.011 Vorkurs Mathematik WS 011/1 Die mit * gekennzeichneten Aufgaben sind etwas schwerer. Dort braucht
Fachbereich Mathematik Aufgaben und Lösungen zum Vorkurs Mathematik: Beweismethoden Für Mittwoch den 8.9.011 Vorkurs Mathematik WS 011/1 Die mit * gekennzeichneten Aufgaben sind etwas schwerer. Dort braucht
Vollständige Induktion
 Schweizer Mathematik-Olympiade smo osm Vollständige Induktion Aktualisiert: 1 Dezember 01 vers 100 Eine der wichtigsten Beweistechniken der Mathematik überhaupt ist die (vollständige) Induktion Wir nehmen
Schweizer Mathematik-Olympiade smo osm Vollständige Induktion Aktualisiert: 1 Dezember 01 vers 100 Eine der wichtigsten Beweistechniken der Mathematik überhaupt ist die (vollständige) Induktion Wir nehmen
Vervollständigung Lateinischer Quadrate
 Vervollständigung Lateinischer Quadrate Elisabeth Schmidhofer 01.12.2013 Inhaltsverzeichnis 1 Vorwort 3 2 Einleitung 4 2.1 Beispele.............................................. 4 3 Lateinische Quadrate
Vervollständigung Lateinischer Quadrate Elisabeth Schmidhofer 01.12.2013 Inhaltsverzeichnis 1 Vorwort 3 2 Einleitung 4 2.1 Beispele.............................................. 4 3 Lateinische Quadrate
Vorlesung. Vollständige Induktion 1
 WS 015/16 Vorlesung Vollständige Induktion 1 1 Einführung Bei der vollständigen Induktion handelt es sich um ein wichtiges mathematisches Beweisverfahren, mit dem man Aussagen, die für alle natürlichen
WS 015/16 Vorlesung Vollständige Induktion 1 1 Einführung Bei der vollständigen Induktion handelt es sich um ein wichtiges mathematisches Beweisverfahren, mit dem man Aussagen, die für alle natürlichen
Aufgaben und Lösungen zum Vorkurs Mathematik: Beweismethoden Für Donnerstag den x > 1 3x > 3 3x + 3 > 6 6x + 3 > 3x + 6.
 Fachbereich Mathematik Aufgaben und Lösungen zum Vorkurs Mathematik: Beweismethoden Für Donnerstag den 7.9.01 Vorkurs Mathematik WS 01/13 Die mit * gekennzeichneten Aufgaben sind etwas schwerer. Dort braucht
Fachbereich Mathematik Aufgaben und Lösungen zum Vorkurs Mathematik: Beweismethoden Für Donnerstag den 7.9.01 Vorkurs Mathematik WS 01/13 Die mit * gekennzeichneten Aufgaben sind etwas schwerer. Dort braucht
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph.
 Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Elementare Beweismethoden
 Elementare Beweismethoden Christian Hensel 404015 Inhaltsverzeichnis Vortrag zum Thema Elementare Beweismethoden im Rahmen des Proseminars Mathematisches Problemlösen 1 Einführung und wichtige Begriffe
Elementare Beweismethoden Christian Hensel 404015 Inhaltsverzeichnis Vortrag zum Thema Elementare Beweismethoden im Rahmen des Proseminars Mathematisches Problemlösen 1 Einführung und wichtige Begriffe
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Große Übung #2 Phillip Keldenich, Arne Schmidt 10.11.2016 Organisatorisches Fragen? Checkliste: Anmeldung kleine Übungen Anmeldung Mailingliste Dies ersetzt nicht die Prüfungsanmeldung!
Algorithmen und Datenstrukturen Große Übung #2 Phillip Keldenich, Arne Schmidt 10.11.2016 Organisatorisches Fragen? Checkliste: Anmeldung kleine Übungen Anmeldung Mailingliste Dies ersetzt nicht die Prüfungsanmeldung!
Wozu ist Mathematik gut? M. Hinze
 Wozu ist Mathematik gut? M. Hinze Technische Universität Dresden Institut für Numerische Mathematik hinze@math.tu-dresden.de www.math.tu-dresden.de/ hinze Technische Universität Dresden Institut für Numerische
Wozu ist Mathematik gut? M. Hinze Technische Universität Dresden Institut für Numerische Mathematik hinze@math.tu-dresden.de www.math.tu-dresden.de/ hinze Technische Universität Dresden Institut für Numerische
Vier-Farben-Vermutung (1)
 Vier-Farben-Vermutung (1) Landkarten möchte man so färben, dass keine benachbarten Länder die gleiche Farbe erhalten. Wie viele Farben braucht man zur Färbung einer Landkarte? Vier-Farben-Vermutung: Jede
Vier-Farben-Vermutung (1) Landkarten möchte man so färben, dass keine benachbarten Länder die gleiche Farbe erhalten. Wie viele Farben braucht man zur Färbung einer Landkarte? Vier-Farben-Vermutung: Jede
1 Axiomatische Charakterisierung der reellen. 3 Die natürlichen, die ganzen und die rationalen. 4 Das Vollständigkeitsaxiom und irrationale
 Kapitel I Reelle Zahlen 1 Axiomatische Charakterisierung der reellen Zahlen R 2 Angeordnete Körper 3 Die natürlichen, die ganzen und die rationalen Zahlen 4 Das Vollständigkeitsaxiom und irrationale Zahlen
Kapitel I Reelle Zahlen 1 Axiomatische Charakterisierung der reellen Zahlen R 2 Angeordnete Körper 3 Die natürlichen, die ganzen und die rationalen Zahlen 4 Das Vollständigkeitsaxiom und irrationale Zahlen
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 15: Graphen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Grundbegriffe der Informatik Kapitel 15: Graphen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
9. Algorithmus der Woche Die Eulertour Wie Leonhard Euler das Haus vom Nikolaus zeichnet
 9. Algorithmus der Woche Die Eulertour Wie Leonhard Euler das Haus vom Nikolaus zeichnet Autoren Michael Behrisch, Humboldt-Universität zu Berlin Amin Coja-Oghlan, Humboldt-Universität zu Berlin, Humboldt-Universität
9. Algorithmus der Woche Die Eulertour Wie Leonhard Euler das Haus vom Nikolaus zeichnet Autoren Michael Behrisch, Humboldt-Universität zu Berlin Amin Coja-Oghlan, Humboldt-Universität zu Berlin, Humboldt-Universität
11. Folgen und Reihen.
 - Funktionen Folgen und Reihen Folgen Eine Folge reeller Zahlen ist eine Abbildung a: N R Statt a(n) für n N schreibt man meist a n ; es handelt sich also bei einer Folge um die Angabe der Zahlen a, a
- Funktionen Folgen und Reihen Folgen Eine Folge reeller Zahlen ist eine Abbildung a: N R Statt a(n) für n N schreibt man meist a n ; es handelt sich also bei einer Folge um die Angabe der Zahlen a, a
mathe plus Aussagenlogik Seite 1
 mathe plus Aussagenlogik Seite 1 1 Aussagenlogik 1.1 Grundbegriffe Def 1 Aussage Eine Aussage ist ein beschriebener Sachverhalt, dem eindeutig einer der Wahrheitswerte entweder wahr oder falsch zugeordnet
mathe plus Aussagenlogik Seite 1 1 Aussagenlogik 1.1 Grundbegriffe Def 1 Aussage Eine Aussage ist ein beschriebener Sachverhalt, dem eindeutig einer der Wahrheitswerte entweder wahr oder falsch zugeordnet
Graph Paar (V,E) V: nichtleere Menge von Knoten (vertex) E: Menge von Kanten (edges): Relation (Verbindung) zwischen den Knoten
 Graphentheorie Graph Paar (V,E) V: nichtleere Menge von Knoten (vertex) E: Menge von Kanten (edges): Relation (Verbindung) zwischen den Knoten gerichteter Graph (DiGraph (directed graph) E: Teilmenge E
Graphentheorie Graph Paar (V,E) V: nichtleere Menge von Knoten (vertex) E: Menge von Kanten (edges): Relation (Verbindung) zwischen den Knoten gerichteter Graph (DiGraph (directed graph) E: Teilmenge E
Polyeder, Konvexität, Platonische und archimedische Körper
 Unter einem Polyeder verstehen wir einen zusammenhängenden Teil des dreidimensionalen Raumes der durch Polygone begrenzt wird. Seine Oberfläche besteht also aus Punkten (Ecken genannt), Strecken (Kanten
Unter einem Polyeder verstehen wir einen zusammenhängenden Teil des dreidimensionalen Raumes der durch Polygone begrenzt wird. Seine Oberfläche besteht also aus Punkten (Ecken genannt), Strecken (Kanten
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Graphen. Leonhard Euler ( )
 Graphen Leonhard Euler (1707-1783) 2 Graph Ein Graph besteht aus Knoten (nodes, vertices) die durch Kanten (edges) miteinander verbunden sind. 3 Nachbarschaftsbeziehungen Zwei Knoten heissen adjazent (adjacent),
Graphen Leonhard Euler (1707-1783) 2 Graph Ein Graph besteht aus Knoten (nodes, vertices) die durch Kanten (edges) miteinander verbunden sind. 3 Nachbarschaftsbeziehungen Zwei Knoten heissen adjazent (adjacent),
Übersicht 2. Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben. Martin Oellrich. ein Problem vor der Haustür 3
 Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht vom Problem zur Theorie 0. Juni 008 0. Juni 008 Martin Oellrich die Idee weiter denken MathematikerIn werden? Gibt es einen
Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht vom Problem zur Theorie 0. Juni 008 0. Juni 008 Martin Oellrich die Idee weiter denken MathematikerIn werden? Gibt es einen
Beispiellösungen zu Blatt 7
 µathematischer κorrespondenz- zirkel Mathematisches Institut Georg August Universität Göttingen Aufgabe Beispiellösungen zu Blatt 7 Die handelsüblichen Papierformate DIN A0, DIN A usw. haben folgende praktische
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg August Universität Göttingen Aufgabe Beispiellösungen zu Blatt 7 Die handelsüblichen Papierformate DIN A0, DIN A usw. haben folgende praktische
Vorkurs Mathematik Abbildungen
 Vorkurs Mathematik Abbildungen Philip Bell 19. September 2016 Diese Arbeit beruht im Wesentlichen auf dem Vortrag Relationen, Partitionen und Abbildungen von Fabian Grünig aus den vorangehenden Jahren.
Vorkurs Mathematik Abbildungen Philip Bell 19. September 2016 Diese Arbeit beruht im Wesentlichen auf dem Vortrag Relationen, Partitionen und Abbildungen von Fabian Grünig aus den vorangehenden Jahren.
Anmerkungen zur Übergangsprüfung
 DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
3 Vom Zählen zur Induktion
 7 3 Vom Zählen zur Induktion 3.1 Natürliche Zahlen und Induktions-Prinzip Seit unserer Kindheit kennen wir die Zahlen 1,, 3, 4, usw. Diese Zahlen gebrauchen wir zum Zählen, und sie sind uns so vertraut,
7 3 Vom Zählen zur Induktion 3.1 Natürliche Zahlen und Induktions-Prinzip Seit unserer Kindheit kennen wir die Zahlen 1,, 3, 4, usw. Diese Zahlen gebrauchen wir zum Zählen, und sie sind uns so vertraut,
Einführung Grundbegriffe
 Einführung Grundbegriffe 1.1 Der Modellbegriff Broy: Informatik 1, Springer 1998 (2) Die Modellbildung der Informatik zielt auf die Darstellung der unter dem Gesichtspunkt einer gegebenen Aufgabenstellung
Einführung Grundbegriffe 1.1 Der Modellbegriff Broy: Informatik 1, Springer 1998 (2) Die Modellbildung der Informatik zielt auf die Darstellung der unter dem Gesichtspunkt einer gegebenen Aufgabenstellung
Reihen/Partialsummenfolgen und vollständige Induktion. Robert Klinzmann
 Reihen/Partialsummenfolgen und vollständige Induktion Robert Klinzmann 3. Mai 00 Reihen / Partialsummen 1 Inhaltsverzeichnis 1 Vorwort Das Prinzip der vollständigen Induktion 3 3 Herleitung der Gauß schen
Reihen/Partialsummenfolgen und vollständige Induktion Robert Klinzmann 3. Mai 00 Reihen / Partialsummen 1 Inhaltsverzeichnis 1 Vorwort Das Prinzip der vollständigen Induktion 3 3 Herleitung der Gauß schen
24 KAPITEL 2. REELLE UND KOMPLEXE ZAHLEN
 24 KAPITEL 2. REELLE UND KOMPLEXE ZAHLEN x 2 = 0+x 2 = ( a+a)+x 2 = a+(a+x 2 ) = a+(a+x 1 ) = ( a+a)+x 1 = x 1. Daraus folgt dann, wegen x 1 = x 2 die Eindeutigkeit. Im zweiten Fall kann man für a 0 schreiben
24 KAPITEL 2. REELLE UND KOMPLEXE ZAHLEN x 2 = 0+x 2 = ( a+a)+x 2 = a+(a+x 2 ) = a+(a+x 1 ) = ( a+a)+x 1 = x 1. Daraus folgt dann, wegen x 1 = x 2 die Eindeutigkeit. Im zweiten Fall kann man für a 0 schreiben
Technische Universität München Zentrum Mathematik Mathematik 1 (Elektrotechnik) Übungsblatt 1
 Technische Universität München Zentrum Mathematik Mathematik 1 (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 1 Hausaufgaben Aufgabe 1.1 Zeigen Sie mit vollständiger Induktion:
Technische Universität München Zentrum Mathematik Mathematik 1 (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 1 Hausaufgaben Aufgabe 1.1 Zeigen Sie mit vollständiger Induktion:
Kapitel 3. Natürliche Zahlen und vollständige Induktion
 Kapitel 3 Natürliche Zahlen und vollständige Induktion In Kapitel 1 haben wir den direkten Beweis, den modus ponens, kennen gelernt, der durch die Tautologie ( A (A = B) ) = B gegeben ist Dabei war B eine
Kapitel 3 Natürliche Zahlen und vollständige Induktion In Kapitel 1 haben wir den direkten Beweis, den modus ponens, kennen gelernt, der durch die Tautologie ( A (A = B) ) = B gegeben ist Dabei war B eine
1 Vorbereitung: Potenzen 2. 2 Einstieg und typische Probleme 3
 Das vorliegende Skript beschäftigt sich mit dem Thema Rechnen mit Kongruenzen. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft (MSG) im Jahr 2013. Die vorliegende
Das vorliegende Skript beschäftigt sich mit dem Thema Rechnen mit Kongruenzen. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft (MSG) im Jahr 2013. Die vorliegende
Graphentheorie 1. Diskrete Strukturen. Sommersemester Uta Priss ZeLL, Ostfalia. Hausaufgaben Graph-Äquivalenz SetlX
 Graphentheorie 1 Diskrete Strukturen Uta Priss ZeLL, Ostfalia Sommersemester 2016 Diskrete Strukturen Graphentheorie 1 Slide 1/19 Agenda Hausaufgaben Graph-Äquivalenz SetlX Diskrete Strukturen Graphentheorie
Graphentheorie 1 Diskrete Strukturen Uta Priss ZeLL, Ostfalia Sommersemester 2016 Diskrete Strukturen Graphentheorie 1 Slide 1/19 Agenda Hausaufgaben Graph-Äquivalenz SetlX Diskrete Strukturen Graphentheorie
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein
 Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
Analysis II (FS 2015): ZUSAMMENHÄNGENDE METRISCHE RÄUME
 Analysis II (FS 2015): ZUSAMMENHÄNGENDE METRISCHE RÄUME Dietmar A. Salamon ETH-Zürich 23. Februar 2015 1 Topologische Grundbegriffe Sei (X, d) ein metrischer Raum, d.h. X ist eine Menge und d : X X R ist
Analysis II (FS 2015): ZUSAMMENHÄNGENDE METRISCHE RÄUME Dietmar A. Salamon ETH-Zürich 23. Februar 2015 1 Topologische Grundbegriffe Sei (X, d) ein metrischer Raum, d.h. X ist eine Menge und d : X X R ist
Minimal spannende Bäume
 Minimal spannende Bäume Ronny Harbich 4. Mai 006 (geändert 19. August 006) Vorwort Ich danke Patrick Bahr und meinem Bruder Steffen Harbich für die Unterstützung bei dieser Arbeit. Sie haben sowohl zu
Minimal spannende Bäume Ronny Harbich 4. Mai 006 (geändert 19. August 006) Vorwort Ich danke Patrick Bahr und meinem Bruder Steffen Harbich für die Unterstützung bei dieser Arbeit. Sie haben sowohl zu
Mengen und Abbildungen
 Mengen und Abbildungen Der Mengenbegriff Durchschnitt, Vereinigung, Differenzmenge Kartesisches Produkt Abbildungen Prinzip der kleinsten natürlichen Zahl Vollständige Induktion Mengen und Abbildungen
Mengen und Abbildungen Der Mengenbegriff Durchschnitt, Vereinigung, Differenzmenge Kartesisches Produkt Abbildungen Prinzip der kleinsten natürlichen Zahl Vollständige Induktion Mengen und Abbildungen
3 Vollständige Induktion
 3.1 Natürliche Zahlen In den vorherigen Kapiteln haben wir die Menge der natürlichen Zahlen schon mehrfach als Beispiel benutzt. Das Konzept der natürlichen Zahlen erscheint uns einfach, da wir es schon
3.1 Natürliche Zahlen In den vorherigen Kapiteln haben wir die Menge der natürlichen Zahlen schon mehrfach als Beispiel benutzt. Das Konzept der natürlichen Zahlen erscheint uns einfach, da wir es schon
Freie Universität Berlin. Diskrete Mathematik. Ralf Borndörfer, Stephan Schwartz. Freie Universität. 08. April 2013
 Diskrete Mathematik Ralf Borndörfer, Stephan Schwartz 08. April 2013 FUB VL Diskrete Mathematik SS 2013 1 Leonhard Euler (1707-1783) e i sin cos f(x) FUB VL Diskrete Mathematik SS 2013 2 Das Königsberger
Diskrete Mathematik Ralf Borndörfer, Stephan Schwartz 08. April 2013 FUB VL Diskrete Mathematik SS 2013 1 Leonhard Euler (1707-1783) e i sin cos f(x) FUB VL Diskrete Mathematik SS 2013 2 Das Königsberger
Lernmodul 2 Graphen. Lernmodul 2: Geoobjekte und ihre Modellierung - Graphen
 Folie 1 von 20 Lernmodul 2 Graphen Folie 2 von 20 Graphen Übersicht Motivation Ungerichteter Graph Gerichteter Graph Inzidenz, Adjazenz, Grad Pfad, Zyklus Zusammenhang, Trennende Kante, Trennender Knoten
Folie 1 von 20 Lernmodul 2 Graphen Folie 2 von 20 Graphen Übersicht Motivation Ungerichteter Graph Gerichteter Graph Inzidenz, Adjazenz, Grad Pfad, Zyklus Zusammenhang, Trennende Kante, Trennender Knoten
Seminarvortrag aus Reiner Mathematik Existenz von Primitivwurzeln
 Seminarvortrag aus Reiner Mathematik Existenz von Primitivwurzeln Michael Kniely November 2009 1 Vorbemerkungen Definition. Sei n N +, ϕ(n) := {d [0, n 1] ggt (d, n) = 1}. Die Abbildung ϕ : N + N + heißt
Seminarvortrag aus Reiner Mathematik Existenz von Primitivwurzeln Michael Kniely November 2009 1 Vorbemerkungen Definition. Sei n N +, ϕ(n) := {d [0, n 1] ggt (d, n) = 1}. Die Abbildung ϕ : N + N + heißt
Einführung in die Graphentheorie. Modellierung mit Graphen. Aufgabe
 Einführung in die Graphentheorie Modellierung mit Graphen Aufgabe Motivation Ungerichtete Graphen Gerichtete Graphen Credits: D. Jungnickel: Graphen, Netzwerke und Algorithmen, BI 99 G. Goos: Vorlesungen
Einführung in die Graphentheorie Modellierung mit Graphen Aufgabe Motivation Ungerichtete Graphen Gerichtete Graphen Credits: D. Jungnickel: Graphen, Netzwerke und Algorithmen, BI 99 G. Goos: Vorlesungen
2. Vorlesung. Die Theorie der schwarz-weissen Ketten.
 2. Vorlesung. Die Theorie der schwarz-weissen Ketten. Die Theorie der schwarzen Steinchen haben wir jetzt halbwegs vertanden. Statt mit schwarzen Steinen wie die Griechen, wollen wir jetzt mit schwarzen
2. Vorlesung. Die Theorie der schwarz-weissen Ketten. Die Theorie der schwarzen Steinchen haben wir jetzt halbwegs vertanden. Statt mit schwarzen Steinen wie die Griechen, wollen wir jetzt mit schwarzen
Die Menge C der komplexen Zahlen wird im Kapitel Weitere Themen behandelt.
 1 1 Funktionen 1.1 Grundlegende Zahlenmengen Georg Cantor (1845-1918) hat den Begriff der Menge eingeführt. Man versteht darunter die Zusammenfassung einzelner Dinge, welche Elemente genannt werden, zu
1 1 Funktionen 1.1 Grundlegende Zahlenmengen Georg Cantor (1845-1918) hat den Begriff der Menge eingeführt. Man versteht darunter die Zusammenfassung einzelner Dinge, welche Elemente genannt werden, zu
7 KONVERGENTE FOLGEN 35. inf M = Infimum von M. bezeichnet haben. Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt.
 7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
Lineare Algebra I. Auswahlaxiom befragen. (Wer schon im Internet danach sucht, sollte das auch mal mit dem Begriff
 Universität Konstanz Wintersemester 2009/2010 Fachbereich Mathematik und Statistik Lösungsblatt 2 Prof. Dr. Markus Schweighofer 11.11.2009 Aaron Kunert / Sven Wagner Lineare Algebra I Lösung 2.1: Behauptung:
Universität Konstanz Wintersemester 2009/2010 Fachbereich Mathematik und Statistik Lösungsblatt 2 Prof. Dr. Markus Schweighofer 11.11.2009 Aaron Kunert / Sven Wagner Lineare Algebra I Lösung 2.1: Behauptung:
Wie beweise ich etwas? 9. Juli 2012
 Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Wie beweise ich etwas? 9. Juli 2012 1 Was ist ein Beweis? 1.1 Ein Beispiel Nimm einen Stift und ein Blatt Papier und zeichne fünf
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Wie beweise ich etwas? 9. Juli 2012 1 Was ist ein Beweis? 1.1 Ein Beispiel Nimm einen Stift und ein Blatt Papier und zeichne fünf
Lösungen 1 zum Mathematik-Brückenkurs für alle, die sich für Mathematik interessieren
 Lösungen 1 zum Mathematik-Brückenkurs für alle, die sich für Mathematik interessieren µfsr, TU Dresden Version vom 11. Oktober 2016, Fehler, Ideen, Anmerkungen und Verbesserungsvorschläge bitte an benedikt.bartsch@myfsr.de
Lösungen 1 zum Mathematik-Brückenkurs für alle, die sich für Mathematik interessieren µfsr, TU Dresden Version vom 11. Oktober 2016, Fehler, Ideen, Anmerkungen und Verbesserungsvorschläge bitte an benedikt.bartsch@myfsr.de
1 Das Prinzip der vollständigen Induktion
 1 1 Das Prinzip der vollständigen Induktion 1.1 Etwas Logik Wir nennen eine Formel oder einen Satz der Alltagssprache eine Aussage, wenn sie wahr oder falsch sein kann. Die Formeln 2 = 3, 2 4, 5 5 sind
1 1 Das Prinzip der vollständigen Induktion 1.1 Etwas Logik Wir nennen eine Formel oder einen Satz der Alltagssprache eine Aussage, wenn sie wahr oder falsch sein kann. Die Formeln 2 = 3, 2 4, 5 5 sind
Analysis I. Vorlesung 4. Angeordnete Körper
 Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 4 Angeordnete Körper Zwei reelle Zahlen kann man ihrer Größe nach vergleichen, d.h. die eine ist größer als die andere oder es handelt sich
Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 4 Angeordnete Körper Zwei reelle Zahlen kann man ihrer Größe nach vergleichen, d.h. die eine ist größer als die andere oder es handelt sich
Institut für Mathematik Geometrie und Lineare Algebra J. Schönenberger-Deuel. Aufgabe 1. Wir geben nur zwei von sehr vielen möglichen Strategien.
 Lösungen Übung 13 Aufgabe 1. Wir geben nur zwei von sehr vielen möglichen Strategien. a) Strategie 1 (nächster Nachbar): Jedes Mal reist der Reisende vom Punkt, wo er gerade ist, zur nächstgelegenen Stadt,
Lösungen Übung 13 Aufgabe 1. Wir geben nur zwei von sehr vielen möglichen Strategien. a) Strategie 1 (nächster Nachbar): Jedes Mal reist der Reisende vom Punkt, wo er gerade ist, zur nächstgelegenen Stadt,
Beispiel einer Zerlegung in vier Schritten (Zerlegungszahl n = 51)
 Fachbereich Mathematik Tag der Mathematik 9. November 2013 Klassenstufen 9, 10 Beispiel einer Zerlegung in vier Schritten (Zerlegungszahl n = 51) Aufgabe 1 (6+4+4+3+3 Punkte). In dieser Aufgabe geht es
Fachbereich Mathematik Tag der Mathematik 9. November 2013 Klassenstufen 9, 10 Beispiel einer Zerlegung in vier Schritten (Zerlegungszahl n = 51) Aufgabe 1 (6+4+4+3+3 Punkte). In dieser Aufgabe geht es
5.1 Drei wichtige Beweistechniken... 55 5.2 Erklärungen zu den Beweistechniken... 56
 5 Beweistechniken Übersicht 5.1 Drei wichtige Beweistechniken................................. 55 5. Erklärungen zu den Beweistechniken............................ 56 Dieses Kapitel ist den drei wichtigsten
5 Beweistechniken Übersicht 5.1 Drei wichtige Beweistechniken................................. 55 5. Erklärungen zu den Beweistechniken............................ 56 Dieses Kapitel ist den drei wichtigsten
(x, x + y 2, x y 2 + z 3. = e x sin y. sin y. Nach dem Umkehrsatz besitzt f dann genau auf der Menge
 ÜBUNGSBLATT 0 LÖSUNGEN MAT/MAT3 ANALYSIS II FRÜHJAHRSSEMESTER 0 PROF DR CAMILLO DE LELLIS Aufgabe Finden Sie für folgende Funktionen jene Punkte im Bildraum, in welchen sie sich lokal umkehren lassen,
ÜBUNGSBLATT 0 LÖSUNGEN MAT/MAT3 ANALYSIS II FRÜHJAHRSSEMESTER 0 PROF DR CAMILLO DE LELLIS Aufgabe Finden Sie für folgende Funktionen jene Punkte im Bildraum, in welchen sie sich lokal umkehren lassen,
Topologische Räume und stetige Abbildungen Teil 2
 TU Dortmund Mathematik Fakultät Proseminar zur Linearen Algebra Ausarbeitung zum Thema Topologische Räume und stetige Abbildungen Teil 2 Anna Kwasniok Dozent: Prof. Dr. L. Schwachhöfer Vorstellung des
TU Dortmund Mathematik Fakultät Proseminar zur Linearen Algebra Ausarbeitung zum Thema Topologische Räume und stetige Abbildungen Teil 2 Anna Kwasniok Dozent: Prof. Dr. L. Schwachhöfer Vorstellung des
Brückenkurs Mathematik
 Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 1 Logik,, Doris Bohnet Universität Hamburg - Department Mathematik Mo 6.10.2008 Zeitplan Tagesablauf: 9:15-11:45 Vorlesung Audimax I 13:00-14:30 Übung Übungsräume
Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 1 Logik,, Doris Bohnet Universität Hamburg - Department Mathematik Mo 6.10.2008 Zeitplan Tagesablauf: 9:15-11:45 Vorlesung Audimax I 13:00-14:30 Übung Übungsräume
Untersuchen Sie, inwiefern sich die folgenden Funktionen für die Verwendung als Hashfunktion eignen. Begründen Sie Ihre Antwort.
 Prof. aa Dr. Ir. Joost-Pieter Katoen Christian Dehnert, Friedrich Gretz, Benjamin Kaminski, Thomas Ströder Tutoraufgabe 1 (Güte von Hashfunktionen): Untersuchen Sie, inwiefern sich die folgenden Funktionen
Prof. aa Dr. Ir. Joost-Pieter Katoen Christian Dehnert, Friedrich Gretz, Benjamin Kaminski, Thomas Ströder Tutoraufgabe 1 (Güte von Hashfunktionen): Untersuchen Sie, inwiefern sich die folgenden Funktionen
16. Platonische Körper kombinatorisch
 16. Platonische Körper kombinatorisch Ein Würfel zeigt uns, daß es Polyeder gibt, wo in jeder Ecke gleich viele Kanten zusammenlaufen, und jede Fläche von gleich vielen Kanten berandet wird. Das Tetraeder
16. Platonische Körper kombinatorisch Ein Würfel zeigt uns, daß es Polyeder gibt, wo in jeder Ecke gleich viele Kanten zusammenlaufen, und jede Fläche von gleich vielen Kanten berandet wird. Das Tetraeder
Kapitel 2 MENGENLEHRE
 Kapitel 2 MENGENLEHRE In diesem Kapitel geben wir eine kurze Einführung in die Mengenlehre, mit der man die ganze Mathematik begründen kann. Wir werden sehen, daßjedes mathematische Objekt eine Menge ist.
Kapitel 2 MENGENLEHRE In diesem Kapitel geben wir eine kurze Einführung in die Mengenlehre, mit der man die ganze Mathematik begründen kann. Wir werden sehen, daßjedes mathematische Objekt eine Menge ist.
Algorithmen und Datenstrukturen (WS 2007/08) 63
 Kapitel 6 Graphen Beziehungen zwischen Objekten werden sehr oft durch binäre Relationen modelliert. Wir beschäftigen uns in diesem Kapitel mit speziellen binären Relationen, die nicht nur nur besonders
Kapitel 6 Graphen Beziehungen zwischen Objekten werden sehr oft durch binäre Relationen modelliert. Wir beschäftigen uns in diesem Kapitel mit speziellen binären Relationen, die nicht nur nur besonders
Das Vierfarbenproblem und verwandte Fragestellungen
 Eichstätter Kolloquium zur Februar 010 Didaktik der Mathematik Das Vierfarbenproblem und verwandte Fragestellungen Cornelia Minette Busch 1 Das Vierfarbenproblem Wenn Schüler eine politische Landkarte
Eichstätter Kolloquium zur Februar 010 Didaktik der Mathematik Das Vierfarbenproblem und verwandte Fragestellungen Cornelia Minette Busch 1 Das Vierfarbenproblem Wenn Schüler eine politische Landkarte
1.4 Äquivalenzrelationen
 8 1.4 Äquivalenzrelationen achdem nun die axiomatische Grundlage gelegt ist, können wir uns bis zur Einführung der Kategorien das Leben dadurch erleichtern, daß wir bis dorthin, also bis auf weiteres,
8 1.4 Äquivalenzrelationen achdem nun die axiomatische Grundlage gelegt ist, können wir uns bis zur Einführung der Kategorien das Leben dadurch erleichtern, daß wir bis dorthin, also bis auf weiteres,
Graphentheorie. Organisatorisches. Organisatorisches. Organisatorisches. Rainer Schrader. 23. Oktober 2007
 Graphentheorie Rainer Schrader Organisatorisches Zentrum für Angewandte Informatik Köln 23. Oktober 2007 1 / 79 2 / 79 Organisatorisches Organisatorisches Dozent: Prof. Dr. Rainer Schrader Weyertal 80
Graphentheorie Rainer Schrader Organisatorisches Zentrum für Angewandte Informatik Köln 23. Oktober 2007 1 / 79 2 / 79 Organisatorisches Organisatorisches Dozent: Prof. Dr. Rainer Schrader Weyertal 80
Kapitel 5: Minimale spannende Bäume Gliederung der Vorlesung
 Gliederung der Vorlesung 1. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman Problem. Flüsse in Netzwerken
Gliederung der Vorlesung 1. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman Problem. Flüsse in Netzwerken
Schnupperkurs: Ausgewählte Methoden zur Aufgabenlösung
 Mathematisches Institut II.06.004 Universität Karlsruhe Priv.-Doz. Dr. N. Grinberg SS 05 Schnupperkurs: Ausgewählte Methoden zur Aufgabenlösung Vorlesung 3: Elementare Beweismethoden: Direkter Beweis,
Mathematisches Institut II.06.004 Universität Karlsruhe Priv.-Doz. Dr. N. Grinberg SS 05 Schnupperkurs: Ausgewählte Methoden zur Aufgabenlösung Vorlesung 3: Elementare Beweismethoden: Direkter Beweis,
Topologische Begriffe
 Kapitel 3 Topologische Begriffe 3.1 Inneres, Rand und Abschluss von Mengen Definition (innerer Punkt und Inneres). Sei (V, ) ein normierter Raum über K, und sei M V eine Menge. Ein Vektor v M heißt innerer
Kapitel 3 Topologische Begriffe 3.1 Inneres, Rand und Abschluss von Mengen Definition (innerer Punkt und Inneres). Sei (V, ) ein normierter Raum über K, und sei M V eine Menge. Ein Vektor v M heißt innerer
Primitiv? Primzahlen und Primfaktoren schätzen lernen. Dr. Heinrich Schneider, Wien. M 1 Grundlegende Zahlenmengen wiederhole dein Wissen!
 S 1 Primitiv? Primzahlen und Primfaktoren schätzen lernen Dr. Heinrich Schneider, Wien M 1 Grundlegende Zahlenmengen wiederhole dein Wissen! Die natürlichen Zahlen n 1, 2, 3, 4, 5, heißen natürliche Zahlen.
S 1 Primitiv? Primzahlen und Primfaktoren schätzen lernen Dr. Heinrich Schneider, Wien M 1 Grundlegende Zahlenmengen wiederhole dein Wissen! Die natürlichen Zahlen n 1, 2, 3, 4, 5, heißen natürliche Zahlen.
Eine kurze Tabelle soll uns erste Einsichten erleichtern. Der Strich heißt, dass es eine solche Darstellung nicht gibt.
 Summen von Quadraten 1 Physikalische Motivation Eine schwingende Saite hat eine Grundfrequenz F, die von Länge, Dicke, Beschaffenheit der Saite und so fort abhängt Neben dieser Grundfrequenz gibt es auch
Summen von Quadraten 1 Physikalische Motivation Eine schwingende Saite hat eine Grundfrequenz F, die von Länge, Dicke, Beschaffenheit der Saite und so fort abhängt Neben dieser Grundfrequenz gibt es auch
1. Mathematik Olympiade 1. Stufe (Schulolympiade) Klasse 8 Saison 1961/1962 Aufgaben und Lösungen
 . Mathematik Olympiade. Stufe (Schulolympiade) Saison 96/96 Aufgaben und Lösungen OJM. Mathematik-Olympiade. Stufe (Schulolympiade) Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen
. Mathematik Olympiade. Stufe (Schulolympiade) Saison 96/96 Aufgaben und Lösungen OJM. Mathematik-Olympiade. Stufe (Schulolympiade) Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen
Lösungen zur Vorrundenprüfung 2004
 Lösungen zur Vorrundenprüfung 2004 Zuerst einige Bemerkungen zum Punkteschema. Eine vollständige und korrekte Lösung einer Aufgabe ist jeweils 7 Punkte wert. Für komplette Lösungen mit kleineren Fehlern
Lösungen zur Vorrundenprüfung 2004 Zuerst einige Bemerkungen zum Punkteschema. Eine vollständige und korrekte Lösung einer Aufgabe ist jeweils 7 Punkte wert. Für komplette Lösungen mit kleineren Fehlern
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Lösungen Wintersemester 2016/17 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler Wintersemester 2016/17 Kapitel I: Mengen Aufgabe
Vorkurs: Mathematik für Informatiker Lösungen Wintersemester 2016/17 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler Wintersemester 2016/17 Kapitel I: Mengen Aufgabe
Mengen, Funktionen und Logik
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Mengen, Funktionen und Logik Literatur Referenz: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen,
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Mengen, Funktionen und Logik Literatur Referenz: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen,
Stetige Funktionen, Binomischer Lehrsatz
 Vorlesung 13 Stetige Funktionen, Binomischer Lehrsatz 13.1 Funktionenfolgen Wir verbinden nun den Grenzwertbegriff mit dem Funktionsbegriff. Es seien (a n ) n N eine reelle Folge und f : R R eine Funktion.
Vorlesung 13 Stetige Funktionen, Binomischer Lehrsatz 13.1 Funktionenfolgen Wir verbinden nun den Grenzwertbegriff mit dem Funktionsbegriff. Es seien (a n ) n N eine reelle Folge und f : R R eine Funktion.
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume?
 Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
2. Symmetrische Gruppen
 14 Andreas Gathmann 2 Symmetrische Gruppen Im letzten Kapitel haben wir Gruppen eingeführt und ihre elementaren Eigenschaften untersucht Wir wollen nun eine neue wichtige Klasse von Beispielen von Gruppen
14 Andreas Gathmann 2 Symmetrische Gruppen Im letzten Kapitel haben wir Gruppen eingeführt und ihre elementaren Eigenschaften untersucht Wir wollen nun eine neue wichtige Klasse von Beispielen von Gruppen
