13 3. a) Uhrzeit Wasseranstieg (in cm pro Stunde)
|
|
|
- Tobias Holtzer
- vor 6 Jahren
- Abrufe
Transkript
1 1 Funktionen als mathematische Modelle Noch it in Dierenzialrechnung? 1 1. a) Höhenänderung zwischen 0 m und 1 00 m (in der Horizontalen): ca. 800 m 600 m = 00 m durchschnittliche Änderungsrate im Intervall [0; 1 00]: _ 00 m 1 00 m = 6 b) Um die lokale Änderungsrate an einer Stelle zu ermitteln, müssen wir die Steigung der Tangente an dieser Stelle ermitteln. Im Bereich zwischen x = 00 und x = 00 verläut das Höhenproil nahezu geradlinig. Somit ist die lokale Änderungsrate nach 300 m ca. 850 m 770 m 00 m 300 m = _ 80 m 100 m = 0,8. An der Stelle x = 500 hat das Höhenproil einen Hochpunkt, die lokale Änderungsrate beträgt 0. An der Stelle x = 700 ermitteln wir näherungsweise _ 10 m 100 m = 1,. An der Stelle x = hat das Höhenproil einen Sattelpunkt, die lokale Änderungsrate beträgt 0.. a) (x) = 3 x c) (x) = 9 x e) (x) = cos (x) b) (x) = 8 x 3 d) (x) = 3_ x ) (x) = 1 x 3 cos (x) a) Uhrzeit Wasseranstieg (in cm pro Stunde) Also steigt das Wasser von 9 Uhr bis 10 Uhr mit 0 cm am schnellsten an. h b) Wir wissen, dass die durchschnittliche Geschwindigkeit von 7 Uhr bis 9 Uhr 15 cm beträgt und zwischen 9 Uhr und 10 Uhr 0 cm. Die momentane Geschwindigkeit, mit der h h sich der Wasserstand um 9 Uhr ändert, liegt zwischen diesen Werten. Als ungeähren Wert könnte man berechnen: ( 0 cm_ h + 15 cm_ h ) : = 7,5 cm_ h. Um die momentane Geschwindigkeit zum Zeitpunkt 9 Uhr exakter zu bestimmen, müsste man wissen, wie hoch der Wasserstand um kurz vor und um kurz nach 9 Uhr war. Damit könnte man eine Durchschnittsgeschwindigkeit bestimmen, die hinreichend nah an der momentanen Geschwindigkeit liegt.. 0 m m: positive Steigung m 000 m: negative Steigung 000 m 500 m: positive Steigung 500 m m: negative Steigung m m: positive Steigung m 500 m: negative Steigung 500 m m: positive Steigung m m: negative Steigung Die Steigung ist null an den Stellen 1 500, 000, 500, 3 000, 3 750, 500, An diesen Stellen besitzt der Graph der Funktion eine waagerechte Tangente.
2 5 13 Stelle (in m) geschätzte Steigung an der Stelle _ = _ ,036 3,6 % Geälle _ = 0_ 0,0, % Steigung _ = _ ,033 3,3 % Geälle 5. a) b) (1) h (5) = 3 5 = 75 Die Rakete ist also nach 5 s in 75 m Höhe. () h (10) h (0) = = 300 Das bedeutet, dass die Rakete in den ersten 10 s um 300 m gestiegen ist. (3) h (10) h (0) _ 10 0 = _ 10 0 = 30 Das bedeutet, dass die Rakete in den ersten 10 s eine durchschnittliche Geschwindigkeit von 30 m_ s hatte. () h (x) = 6 x h (5) = 6 5 = 30 Das bedeutet, dass die Rakete nach 5 s eine Geschwindigkeit von 30 m_ s erreicht hat. h (t) h (10) (5) lim _ 3 t t 10 = lim t 10 t 10 _ t 10 = lim t 10 3 (10 + t) = 3 0 = 60 Das bedeutet, dass die Rakete nach 10 s eine Geschwindigkeit von 60 m_ s erreicht hat Die Ableitung gibt Auskünte darüber, wie schnell die Temperatur gestiegen bzw. gesunken ist. Ihre Einheit wäre C_ h.
3 a) (A) () bzw. (5) (B) () bzw. (5) (C) (1) (D) (3) (E) () b) (A): x x (A) = () = (5): x x (B): x x 1 (B) = () = (5): x x (C): x x (C) = (1): x x (D): x (x 1) (D) = (3): x (x 1) (E): x x3 (E) = (): x 3_ x 8. a) (x) = 7 x 6 c) (x) = x 3 + x e) (x) = 0 x 3 x b) (x) = x 7 d) (x) = 6 x ) (x) = cos (x) + 9. a) (x) = x 9 + c, c R b) (x) = x 3 x + c, c R c) (x) = 3 cos (x) + x + c, c R 10. a) (x) = 3 x ; () = 1 b) (x) = _ 3 x3 15 x ; (0) = 0 c) (x) = 1 + cos (x); (π) = 1 + cos (π) = 1 + ( 1) = (a) = a 3 Änderungsrate: (a) = lim _ (a + h) (a) = lim _(a + h) 3 a 3 = 3 a h 0 h h 0 h Das Volumen wächst kubisch, seine lokale Änderungsrate dagegen quadratisch. Geometrisch ist die lokale Änderungsrate 3 a die Hälte des Oberlächeninhalts 6 a des Quadrats. 1. a) (x) = x; (x) = 1, also x = 1 x = b) (x) = x 3 ; (x) = 1, also x 3 = 1 x = 3 c) (x) = 3 x + 1; (x) = 1, also 3 x + 1 = 1 x = 0 d) (x) = cos (x); (x) = 1, also cos (x) = 1 x = k π, k Z (3) (1) 13. a) _ 3 1 = _ 9 a a = a = a = 8 b) (x) = a x; (1) = a = a = c) Die Steigung einer Geraden, die die x-achse unter einem Winkel von 5 schneidet, beträgt 1. () = a = 1 a =
4 7 Noch it in Funktionsuntersuchungen? ist streng monoton wachsend, wenn > 0 ist. Deshalb ist die Funktion ür 1 < x < streng monoton wachsend. ist streng monoton allend, wenn < 0 ist. Deshalb ist die Funktion ür x < 1 und x > streng monoton allend. Die Extrempunkte liegen bei x = 1 und x =. Dort liegen die Nullstellen des Graphen der Ableitung. Möglicher Graph:. (x) = 3 x3 x Graph (3): Die Funktion enthält nur ungerade Exponenten, also ist ihr Graph punktsmmetrisch zum Ursprung. g (x) = x x + 3 Graph (1): -Achsenabschnitt: 3; nur gerade Exponenten, also achsensmmetrisch zur Achse. h (x) = 5 x5 3_ x Graph (): Der Graph von h ist weder achsensmmetrisch zur -Achse noch punktsmmetrisch zu O (0 0), weil h (x) sowohl gerade als auch ungerade Exponenten besitzt. ( Außerdem gilt ür h (x) = x 3 x 3 : h (0) = 0 und h (x) > 0 ür x < 0 und h (x) < 0 ür x > 0 (und x < 3), also Hochpunkt bei (0 0). ) a) x : (x), x : (x) b) x : (x), x : (x) c) x : (x), x : (x) d) x : (x), x : (x) e) x : (x), x : (x) ) x : (x), x : (x). a) punktsmmetrisch zum Ursprung b) smmetrisch zur -Achse c) keine Smmetrie zur -Achse bzw. zum Ursprung d) punktsmmetrisch zum Ursprung e) keine Smmetrie zur -Achse bzw. zum Ursprung ( aber punktsmmetrisch zu P (0 1) ). ) smmetrisch zur -Achse
5 a) x 1 = 0; x = ; x 3 = ; x = b) x 1 = 0 oder x + 1,5 x 1 = 0, also x 1 = 0; x = ; x 3 = 0,5 c) x 1 = 0 oder x + x + = 0 (keine Lösung), also x 1 = 1 d) x (x + x 6) = 0, x = 0 oder x + x 6 = 0, also x 1 = 0; x = 3; x 3 = e) x 3 (x ) = 0, x 3 = 0 oder x = 0, also x 1 = 0; x = ; x 3 = ) 8 x + 6 x 5 = 0, Substitution x = u 8 u + 6 u 5 = 0 hat die Lösungen u 1 = 3; u = 9_ Rücksubstitution: x = 3 keine Lösung; x = 9_, also x 1 = 3_ ; x = 3_ 6. a) (x) = x + 1 b) (x) = a (x + ) (x 1) (x ), a 0 c) (x) = a (x + ) (x 5) (x c), a 0, c und c 5 7. a) Es gilt: (x) = ( x + ) (x + b x + c) = x 3 + b x + x + b_ x + c x + c_ = x3 + ( b + ) x + ( b_ + c ) x + c_ Vergleich mit (x) = x 3 x x + ergibt (1) b + = 1 () b_ + c = (3) c_ = also b = 3_, c = Damit gilt: (x) = ( x + ) ( x 3_ x + ) Nullstellen x 1 = ; x = ; x 3 = 1 b) Der Graph von ist achsensmmetrisch zur -Achse, also hat die Nullstellen x 1 = 3; x = ; x 3 = ; x = 3 Weitere Nullstellen kann es nicht geben (1) Wir lesen am Graphen die Nullstellen 3, 0 und 3 sowie (1) = 8 ab. (x) = a (x + 3) x (x 3) Aus (1) = 8 erhält man a = 1 Also (x) = x (x 9) = x x () hat die doppelte Nullstelle x 1 = sowie die einachen Nullstellen x = 0 und x 3 = 3. Außerdem gilt: () = 8 Also (x) = a (x + ) (x 3) x Aus () = 8 erhält man a = Also (x) = x (x + ) (x 3) = x + x3 x 3 x (3) hat die einachen Nullstellen x 1 = und x = 3 sowie die dreiache Nullstelle x 3 = 0. Außerdem können wir näherungsweise (1) 5 ablesen. Also (x) = a x 3 (x + ) (x 3) Aus (1) = 5 erhält man a = 5_ 6. Ein möglicher Funktionsterm könnte (x) = 5_ 6 x3 (x + ) (x 3) sein.
6 a) b) c)
7 10 18 d) 10. a) (x) = 6 ( x + 5_ ) x ( x _ 3) Der Graph hat einache Nullstellen bei x = 5_, x = 0 und x = _ 3. b) (x) = x (x 3) (x 1) Der Graph hat einache Nullstellen bei x = 0, x = 3 und eine doppelte Nullstelle bei x = 1. c) (x) = (x ) (x 1) (x + 3) hat eine einache Nullstelle bei x = 1 sowie je eine doppelte Nullstelle bei x = und x = 3. d) (x) = (x ) 3 x (x + 1) Der Graph hat doppelte Nullstellen bei x = 0 und x = 1 und eine dreiache Nullstelle bei x =. 11. (1) Graph (3) -Achsenabschnitt 90, smmetrisch zur -Achse. Der Graph zeigt nur einen Teil des Verlaus in der Mitte, denn ür x ± gilt: (x) +. () Graph (1) -Achsenabschnitt 0, punktsmmetrisch zum Ursprung. Der Graph zeigt nicht den wesentlichen Verlau, denn ür x gilt: (x). (3) Graph () -Achsenabschnitt 9, keine Smmetrie zur -Achse bzw. zum Ursprung. Der Graph zeigt den wesentlichen Verlau: Alle 3 Nullstellen sind zu sehen. 1. a) streng monoton steigend: ] ; 3[, ] 1; [, ]; [ streng monoton allend: ] 3; 1[ b) Maximum bei x = 3 Minimum bei x = 1 Sattelpunkt bei x = Wendestellen bei x =,5 und x = 0,5
8 11 18 c) 13. a) 8 6 Q P 6 x c) 8 6 Q P 6 x e) 6 Q P 6 x b) 8 Q d) 8 Q P P 6 x 6 x (1) Richtig, denn in dem Intervall gilt: Für x 1 < x (x 1 ) < (x ). () Falsch, denn ( ) = 0 und ür < x < 0 ist (x) < 0. (3) Die korrekte Formulierung lautet: Der Grad der Funktion ist mindestens 3, denn hat drei Nullstellen und zwei Extrema. () Richtig, denn hat bei x = 3 ein Extremum. (5) Falsch, denn die Steigung (und somit die Ableitung) von ist in diesem Intervall größer null.
9 a) Ja, es sind alle Punkte mit waagerechter Tangente zu sehen. Bei einer Funktion vierten Grades hat die Ableitung den Grad 3, also 3 Nullstellen. Da beim Graphen ein Sattelpunkt (doppelte Nullstelle der Ableitung) und ein Minimum (einache Nullstelle) zu sehen sind, sind im Graphen alle Punkte sichtbar. b) Zu sehen ist eine Funktion 3. Grades mit einer doppelten Nullstelle bei 1 und einer einachen Nullstelle bei. 16. a) (x) = 3 x 9_ x 3 hat die einachen Nullstellen x 1 = ; x = jeweils mit einem VZW. Es gilt: (x) = ( x + ) (x ) (x) > 0 ür x < oder ür x > (x) < 0 ür < x < Damit gilt: streng monoton wachsend ür x < oder ür x > streng monoton allend ür < x < an der Stelle x = hat der Graph von einen Hochpunkt, da an dieser Stelle eine Nullstelle mit einem VZW von + nach hat. an der Stelle x = hat der Graph von einen Tiepunkt, da an dieser Stelle eine Nullstelle mit einem VZW von nach + hat. b) Nullstellen von : x ( x 9_ x 3 ) = 0, also x = 0 oder x 9_ x 3 = 0 Also: x 1 = 0; 9 x = _ ,9; 9 + x 3 = _ , x
10 a) hat die beiden einachen Nullstellen x 1 = 1; x = 3 jeweils mit einem VZW. Es gilt: (x) = (x + 1) (x 3) An der Stelle x 1 = 1 hat einen VZW von nach +, also hat der Graph von an dieser Stelle einen Tiepunkt. An der Stelle x = 3 hat einen VZW von + nach, also hat der Graph von an dieser Stelle einen Hochpunkt. b) (x) = 6 x3 + x + 3_ x + c Aus (0) = erhält man c =, also (x) = 6 x3 + x + 3_ x. x 18. a) (x) = 5 x 8 x = x (5 x 3 8) Nullstellen von : x 1 = 0; x = _ 3, jeweils mit VZW 5 An der Stelle x = 0 liegt ein Hochpunkt des Graphen, da einen VZW von + nach hat: H (0 0) An der Stelle x = _ 3 1,17 liegt ein Tiepunkt des Graphen, da einen VZW von 5 nach + hat: T (1,17 3,8) b) (x) = x + x + hat keine Nullstellen, d. h. der Graph von hat keine Extrempunkte. c) (x) = 3 x 1 Nullstellen von : x 1 = 3 ; x = jeweils mit VZW 3 (x) > 0 ür x < 3 oder x > 3 (x) < 0 ür 3 < x < 3 An der Stelle x = 3 liegt ein Hochpunkt, an der Stelle x = liegt ein Tiepunkt a) (x) = x x 3 Nullstellen von : x 1 = ; x = 3 Punkte mit waagerechter Tangente: P 1 ( 1_ 3 ), P ( 3 3_ ) b) () = 1_ 3 m 1 = () = 1 _ 3 = + c 1, also c 1 = _ 3 t: = x _ 3 c) m = 1_ 3 = + c c = 17_ 3 n: = x 17_ 3
11 a) x 68 b) (6) = _ 5 7, Am 6. Tag sind ca. 7 Personen erkrankt. c) (5) = 0 Nach 5 Tagen sind keine Personen mehr erkrankt. d) (x) = 3_ 5 x + x = x ( 3_ 5 x + ) Nullstellen von : x 1 = 0; x = 50_ 3 16,7 an der Stelle x 1 = 0 VZW von von nach + an der Stelle x = 50_ 3 VZW von von + nach ( 50_ 3 ) 9,6 Am 17. Tag ist mit ca. 93 Personen der Höchststand der Krankheitswelle erreicht. e) Am Graphen von lesen wir ein Maximum bei x 8,3 ab. Dort ist die Zunahme am größten. Die Zunahme hat an der Stelle x = _ 50 3 den Wert 0, danach nimmt die Zahl der Erkrankten ab. ) Schnitt des Graphen von mit der Geraden = 7 Schnittstellen: x 1 = 5; x 11,7 Am 5. sowie am 1. Tag betrug die Erkrankungsrate 7 Personen am Tag.
Abb lokales Maximum und Minimum
 .13 Lokale Extrema, Monotonie und Konvexität Wir kommen nun zu den ersten Anwendungen der Dierentialrechnung. Zwischen den Eigenschaten einer Funktion, dem Verlau des zugehörigen Graphen und den Ableitungen
.13 Lokale Extrema, Monotonie und Konvexität Wir kommen nun zu den ersten Anwendungen der Dierentialrechnung. Zwischen den Eigenschaten einer Funktion, dem Verlau des zugehörigen Graphen und den Ableitungen
5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation
 5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation Aufgabe : Verschiebung und Streckung trigonometrischer Funktionen (5) a) Bestimmen Sie die Periode p sowie die Nullstellen der Funktion
5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation Aufgabe : Verschiebung und Streckung trigonometrischer Funktionen (5) a) Bestimmen Sie die Periode p sowie die Nullstellen der Funktion
Förderaufgaben EF Arbeitsblatt 1 Abgabe Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung.
 Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
GF MA Differentialrechnung A2
 Kurvendiskussion Nullstellen: Für die Nullstellen x i ( i! ) einer Funktion f gilt: Steigen bzw. Fallen: f ( x i ) = 0 f '( x) > 0 im Intervall I f ist streng monoton wachsend in I f '( x) < 0 im Intervall
Kurvendiskussion Nullstellen: Für die Nullstellen x i ( i! ) einer Funktion f gilt: Steigen bzw. Fallen: f ( x i ) = 0 f '( x) > 0 im Intervall I f ist streng monoton wachsend in I f '( x) < 0 im Intervall
Ableitungsfunktion einer linearen Funktion
 Ableitungsfunktion einer linearen Funktion Aufgabennummer: 1_009 Prüfungsteil: Typ 1! Typ 2 " Aufgabenformat: Konstruktionsformat Grundkompetenz: AN 3.1! keine Hilfsmittel! gewohnte Hilfsmittel möglich
Ableitungsfunktion einer linearen Funktion Aufgabennummer: 1_009 Prüfungsteil: Typ 1! Typ 2 " Aufgabenformat: Konstruktionsformat Grundkompetenz: AN 3.1! keine Hilfsmittel! gewohnte Hilfsmittel möglich
1 Die zweite Ableitung
 Schülerbuchseite 5 Lösungen vorläuig und deren Graphen Die zweite Ableitung S. Um den Graphen der Ableitung zu skizzieren, sucht man zuerst die Punkte mit waagrechten Tangenten. so erhält man die Nullstellen
Schülerbuchseite 5 Lösungen vorläuig und deren Graphen Die zweite Ableitung S. Um den Graphen der Ableitung zu skizzieren, sucht man zuerst die Punkte mit waagrechten Tangenten. so erhält man die Nullstellen
Hinweis: Dieses Aufgabeblatt enthält auch Teilaufgaben zum grafischen Integrieren. Tipp: NEW-Regel anwenden für alle Aufgaben.
 Dokument mit 33 Aufgaben Hinweis: Dieses Aufgabeblatt enthält auch Teilaufgaben zum grafischen Integrieren. Tipp: NEW-Regel anwenden für alle Aufgaben. Aufgabe A1 gegründet Stellung. (1) besitzt im Intervall
Dokument mit 33 Aufgaben Hinweis: Dieses Aufgabeblatt enthält auch Teilaufgaben zum grafischen Integrieren. Tipp: NEW-Regel anwenden für alle Aufgaben. Aufgabe A1 gegründet Stellung. (1) besitzt im Intervall
4 x x kleinste6 Funktionswert für alle x aus einer Umgebung von x 1 ist.
 Differenzialrechnung 51 1.2.2 Etrempunkte Die Funktion f mit f () = 1 12 3 7 4 2 + 10 + 17 3 beschreibt näherungsweise die wöch entlichen Verkaufszahlen von Rasenmähern. Dabei ist die Zeit in Wochen nach
Differenzialrechnung 51 1.2.2 Etrempunkte Die Funktion f mit f () = 1 12 3 7 4 2 + 10 + 17 3 beschreibt näherungsweise die wöch entlichen Verkaufszahlen von Rasenmähern. Dabei ist die Zeit in Wochen nach
Aufgaben zum Aufstellen von Funktionen aus gegebenen Bedingungen
 Augaben zum Austellen von Funktionen aus gegebenen Bedingungen 1. Die Parabel Gp ist der Graph der quadratischen Funktion p(. Diese Parabel schneidet die x-achse im Punkt N(6/0). Ihr Scheitelpunkt S(/yS)
Augaben zum Austellen von Funktionen aus gegebenen Bedingungen 1. Die Parabel Gp ist der Graph der quadratischen Funktion p(. Diese Parabel schneidet die x-achse im Punkt N(6/0). Ihr Scheitelpunkt S(/yS)
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Lösungen zu den Vermischten Aufgaben Kapitel 5
 Band 10 - Einführungsphase NRW Lösungen zu den Vermischten Aufgaben Kapitel 5 1. Qualitative Skizzen der Füllgraphen (oben) und der zugehörigen Geschwindigkeitsgraphen (unten). a) b) c) d). a) IV) b) II)
Band 10 - Einführungsphase NRW Lösungen zu den Vermischten Aufgaben Kapitel 5 1. Qualitative Skizzen der Füllgraphen (oben) und der zugehörigen Geschwindigkeitsgraphen (unten). a) b) c) d). a) IV) b) II)
9 Funktionen und ihre Graphen
 57 9 Funktionen und ihre Graphen Funktionsbegriff Eine Funktion ordnet jedem Element aus einer Menge D f genau ein Element aus einer Menge W f zu. mit = f(), D f Die Menge aller Funktionswerte nennt man
57 9 Funktionen und ihre Graphen Funktionsbegriff Eine Funktion ordnet jedem Element aus einer Menge D f genau ein Element aus einer Menge W f zu. mit = f(), D f Die Menge aller Funktionswerte nennt man
2 Wiederholung der Ableitungsregeln und höhere Ableitungen
 2 Wiederholung der Ableitungsregeln und höhere Ableitungen In der Abbildung sehen Sie die Graphen der Funktionen f und g mit f (x) = x 2 und g (x) = _ 1 x 2 4 sowie die Graphen der Ableitungsfunktionen
2 Wiederholung der Ableitungsregeln und höhere Ableitungen In der Abbildung sehen Sie die Graphen der Funktionen f und g mit f (x) = x 2 und g (x) = _ 1 x 2 4 sowie die Graphen der Ableitungsfunktionen
3.3 Linkskurve, Rechtskurve Wendepunkte
 166 FUNKTIONSUNTERSUCHUNGEN 3.3 Linkskurve, Rechtskurve Wendepunkte Einführung (1) Anschauliche Erklärung des Begriffs Wendepunkt Bei Motorradrennen lässt sich beobachten, wie sich die Motorradfahrer beim
166 FUNKTIONSUNTERSUCHUNGEN 3.3 Linkskurve, Rechtskurve Wendepunkte Einführung (1) Anschauliche Erklärung des Begriffs Wendepunkt Bei Motorradrennen lässt sich beobachten, wie sich die Motorradfahrer beim
1 Ableitungen. Hinweise und Lösungen:
 Hinweise und Lösungen: http://mathemathemathe.de/analsis/analsis-grundagen Ableitungen Übung.: Einfache Ableitungen - Bestimme die ersten Ableitungen a) f() = 7 + + 8 b) f() = a + a a K(t) = t t + 0 Übung.:
Hinweise und Lösungen: http://mathemathemathe.de/analsis/analsis-grundagen Ableitungen Übung.: Einfache Ableitungen - Bestimme die ersten Ableitungen a) f() = 7 + + 8 b) f() = a + a a K(t) = t t + 0 Übung.:
Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 2011 Mathematik
 ZK M A (ohne CAS) Seite 1 von 10 Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 011 Mathematik 1. Aufgabenart Analysis. Aufgabenstellung Aufgabe 1: Hochwasser am Rhein Aufgabe
ZK M A (ohne CAS) Seite 1 von 10 Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 011 Mathematik 1. Aufgabenart Analysis. Aufgabenstellung Aufgabe 1: Hochwasser am Rhein Aufgabe
Tiefpunkt = relatives Minimum hinreichende Bedingung:
 R. Brinkmann http://brinkmann-du.de Seite 1 0.0.01 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
R. Brinkmann http://brinkmann-du.de Seite 1 0.0.01 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
Pflichtteilaufgaben zu Funktionenkompetenz. Baden-Württemberg
 Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Trigonometrische Funktionen
 Trigonometrische Funktionen. Gegeben ist die Funktion f() = (sin( π )) Ihr Graph sei K. a) Skizzieren Sie K im Intervall [0,]. Geben Sie die Periode von f an. Geben Sie alle Hoch- und Tiefpunkte von K
Trigonometrische Funktionen. Gegeben ist die Funktion f() = (sin( π )) Ihr Graph sei K. a) Skizzieren Sie K im Intervall [0,]. Geben Sie die Periode von f an. Geben Sie alle Hoch- und Tiefpunkte von K
( 0 ( x) d) Die Funktionsgleichung der Funktion 1 lautet: f( Für x 2 = 0 : Wähle die Werte -1 und 1. Überprüfe x1 = 1,
 Differentialrechnung IV (Wendepunkte) (Kap 7) (Haben Sie Probleme bei der Bearbeitung dieser Aufgaben versuchen Sie diese in Ihrer Kleingruppe mit Hilfe des Arbeitsbuchs Mathematik zu klären Führt dies
Differentialrechnung IV (Wendepunkte) (Kap 7) (Haben Sie Probleme bei der Bearbeitung dieser Aufgaben versuchen Sie diese in Ihrer Kleingruppe mit Hilfe des Arbeitsbuchs Mathematik zu klären Führt dies
Funktionen untersuchen
 Funktionen untersuchen Mögliche Fragestellungen Definition: lokale und globale Extrema Monotonie und Extrema Notwendige Bedingung für Extrema Hinreichende Kriterien, Vergleich Krümmungsverhalten Neumann/Rodner
Funktionen untersuchen Mögliche Fragestellungen Definition: lokale und globale Extrema Monotonie und Extrema Notwendige Bedingung für Extrema Hinreichende Kriterien, Vergleich Krümmungsverhalten Neumann/Rodner
Hauptprüfung Fachhochschulreife Baden-Württemberg
 Hauptprüung Fachhochschulreie 204 Baden-Württemberg Augabe 2 Analysis Hilsmittel: graikähiger Taschenrechner Beruskolleg Alexander Schwarz www.mathe-augaben.com September 204 Gegeben ist die Funktion mit
Hauptprüung Fachhochschulreie 204 Baden-Württemberg Augabe 2 Analysis Hilsmittel: graikähiger Taschenrechner Beruskolleg Alexander Schwarz www.mathe-augaben.com September 204 Gegeben ist die Funktion mit
Mathematik im Berufskolleg II
 Bohner Ott Deusch Mathematik im Berufskolleg II Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 6 ISBN 978--8-- Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung
Bohner Ott Deusch Mathematik im Berufskolleg II Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 6 ISBN 978--8-- Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung
Beispielklausur für zentrale Klausuren Mathematik Unterlagen für die Lehrkraft - Modelllösungen
 ZK M A (mit CAS) Seite von 5 Nr. Beispielklausur für zentrale Klausuren Mathematik Unterlagen für die Lehrkraft - Modelllösungen Punkte a Nullstellen von f: f ( = 0 x = x = x = + Lokale Extrempunkte:,7
ZK M A (mit CAS) Seite von 5 Nr. Beispielklausur für zentrale Klausuren Mathematik Unterlagen für die Lehrkraft - Modelllösungen Punkte a Nullstellen von f: f ( = 0 x = x = x = + Lokale Extrempunkte:,7
Kurvendiskussion. Mag. Mone Denninger 10. Oktober Extremwerte (=Lokale Extrema) 2. 5 Monotonieverhalten 3. 6 Krümmungsverhalten 4
 Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
von Prof. Dr. Ing. Dirk Rabe Hochschule Emden/Leer
 von Prof. Dr. Ing. Dirk Rabe Hochschule Emden/Leer Überblick Tangentensteigung einer Funktion Extremstellen Sattelstellen Extremstellen: notwendige und hinreichende Bedingung lokale bzw. relative und absolute
von Prof. Dr. Ing. Dirk Rabe Hochschule Emden/Leer Überblick Tangentensteigung einer Funktion Extremstellen Sattelstellen Extremstellen: notwendige und hinreichende Bedingung lokale bzw. relative und absolute
Analysis: Klausur Analysis
 Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
assume(type::real) //Definiert die Definitionsmenge über die reele a) f:=x->1/2*x^3-4*x^2+8*x // Definition einer Funktion mit der Variable "x".
 Wochenplan zu Wendestellen; Kurvendiskussion und Tangenten reset() //Entleert sämtliche Speicher! A1 assume(type::real) //Definiert die Definitionsmenge über die reele R a) f:=x->1/*x^-*x^+8*x // Definition
Wochenplan zu Wendestellen; Kurvendiskussion und Tangenten reset() //Entleert sämtliche Speicher! A1 assume(type::real) //Definiert die Definitionsmenge über die reele R a) f:=x->1/*x^-*x^+8*x // Definition
Mathematik GK 11 m3, AB 08 Kurvendisk./Textaufgaben Lösung lim x. f ' 1 =0. Skizzen: a) b) f(x)
 Aufgabe 1: Führe eine vollständige Funktionsuntersuchung für die folgenden Funktionen durch: a) f =3 4 8 3 6 2 b) f =0,1 3 0,3 2 0,9 0,5 1. Ableitung f =12 3 24 2 12 f ' =0,3 2 0,6 0,9 =0,3 2 2 3 2. Ableitung
Aufgabe 1: Führe eine vollständige Funktionsuntersuchung für die folgenden Funktionen durch: a) f =3 4 8 3 6 2 b) f =0,1 3 0,3 2 0,9 0,5 1. Ableitung f =12 3 24 2 12 f ' =0,3 2 0,6 0,9 =0,3 2 2 3 2. Ableitung
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Mathemathik-Prüfungen
 M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
Bestimmung ganzrationaler Funktionen, Steckbriefaufgaben
 Bestimmung ganzrationaler Funktionen, Steckbriefaufgaben 30 0 0-50 -40-30 -0-0 0 0 30 40 50 x. Eine Brücke ist 30 m hoch und hat eine Spannweite von 00 m. Welche Parabel beschreibt die Krümmung des Stützbogens?
Bestimmung ganzrationaler Funktionen, Steckbriefaufgaben 30 0 0-50 -40-30 -0-0 0 0 30 40 50 x. Eine Brücke ist 30 m hoch und hat eine Spannweite von 00 m. Welche Parabel beschreibt die Krümmung des Stützbogens?
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
1 Die natürliche Exponentialfunktion und ihre Ableitung
 Schülerbuchseite 5 5 Lösungen vorläuig VI Natürliche Eponential- und Logarithmusunktion Die natürliche Eponentialunktion und ihre Ableitung S. 5 Durch Ausprobieren erkennt man, dass < a
Schülerbuchseite 5 5 Lösungen vorläuig VI Natürliche Eponential- und Logarithmusunktion Die natürliche Eponentialunktion und ihre Ableitung S. 5 Durch Ausprobieren erkennt man, dass < a
und geben Sie die Gleichungen und Art aller Asymptoten an. an, bestimmen Sie die Koordinaten der Achsenschnittpunkte von G f auflösen x x 2 2 ( 2/ 0)
 Abiturprüfung Berufliche Oberschule Mathematik Nichttechnik - A II - Lösung Teilaufgabe. x Gegeben ist die Funktion f( x) ( x ) in ihrer maximalen Definitionsmenge D f IR. Der zugehörige Graph heißt. Teilaufgabe.
Abiturprüfung Berufliche Oberschule Mathematik Nichttechnik - A II - Lösung Teilaufgabe. x Gegeben ist die Funktion f( x) ( x ) in ihrer maximalen Definitionsmenge D f IR. Der zugehörige Graph heißt. Teilaufgabe.
Beispielklausur für zentrale Klausuren
 Seite von 5 Beispielklausur für zentrale Klausuren Mathematik Aufgabenstellung Gegeben ist die Funktion f mit f ( = 0,5 x 4,5 x + x 9. Die Abbildung zeigt den zu f gehörigen Graphen. Abbildung a) Ermitteln
Seite von 5 Beispielklausur für zentrale Klausuren Mathematik Aufgabenstellung Gegeben ist die Funktion f mit f ( = 0,5 x 4,5 x + x 9. Die Abbildung zeigt den zu f gehörigen Graphen. Abbildung a) Ermitteln
Analysis II. Abitur Mathematik Bayern 2012 Musterlösung. Bayern Teil 1. Aufgabe 1. Aufgabe 2. Abitur Mathematik: Musterlösung.
 Abitur Mathematik: Musterlösung Bayern 2012 Teil 1 Aufgabe 1 2x + 3 f(x) = x² + 4x + 3 DEFINITIONSMGE Nullstellen des Nenners:! x² + 4x + 3=0 Lösungen x 1,2 = 4 ± 16 12 2 = 2 ± 1, d.h. x 1 = 3 und x 2
Abitur Mathematik: Musterlösung Bayern 2012 Teil 1 Aufgabe 1 2x + 3 f(x) = x² + 4x + 3 DEFINITIONSMGE Nullstellen des Nenners:! x² + 4x + 3=0 Lösungen x 1,2 = 4 ± 16 12 2 = 2 ± 1, d.h. x 1 = 3 und x 2
Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 2011 Mathematik
 ZK M A1 (mit CAS) Seite 1 von 5 Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 011 Mathematik 1. Aufgabenart Analysis. Aufgabenstellung siehe Prüfungsaufgabe. Materialgrundlage
ZK M A1 (mit CAS) Seite 1 von 5 Unterlagen für die Lehrkraft Zentrale Klausur am Ende der Einführungsphase 011 Mathematik 1. Aufgabenart Analysis. Aufgabenstellung siehe Prüfungsaufgabe. Materialgrundlage
Differenzial- und Integralrechnung II
 Differenzial- und Integralrechnung II Rainer Hauser Dezember 011 1 Einleitung 1.1 Ableitung Die Ableitung einer Funktion f: R R, x f(x) ist definiert als f (x) = df(x) dx = d f(x + h) f(x) f(x) = lim dx
Differenzial- und Integralrechnung II Rainer Hauser Dezember 011 1 Einleitung 1.1 Ableitung Die Ableitung einer Funktion f: R R, x f(x) ist definiert als f (x) = df(x) dx = d f(x + h) f(x) f(x) = lim dx
Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
e-funktionen f(x) = e x2
 e-funktionen f(x) = e x. Smmetrie: Der Graph ist achsensmmetrisch, da f( x) = f(x).. Nullstellen: Bed.: f(x) = 0 Es sind keine Nullstellen vorhanden, da e x stets positiv ist. 3. Extrema: notw. Bed.: f
e-funktionen f(x) = e x. Smmetrie: Der Graph ist achsensmmetrisch, da f( x) = f(x).. Nullstellen: Bed.: f(x) = 0 Es sind keine Nullstellen vorhanden, da e x stets positiv ist. 3. Extrema: notw. Bed.: f
(Unvollständige) Zusammenfassung Analysis Grundkurs
 (Unvollständige) Zusammenfassung Analysis Grundkurs. Ableitungs und Integrationsregeln (Folgende 0 Funktionen sind alles Funktionen aus dem Zentralabitur Grundkurs.) a) f(t) = 0,0t e 0,t b) f(t) = t 3
(Unvollständige) Zusammenfassung Analysis Grundkurs. Ableitungs und Integrationsregeln (Folgende 0 Funktionen sind alles Funktionen aus dem Zentralabitur Grundkurs.) a) f(t) = 0,0t e 0,t b) f(t) = t 3
Analysis. A1 Funktionen/Funktionsklassen. 1 Grundbegriffe. 2 Grundfunktionen
 A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
M I N I S T E R I U M F Ü R K U L T U S, J U G E N D U N D S P O R T. Berufsoberschule (BOS) SO/TO/WO. 2 2x
 Mathematik (43) Musteraufgabe Gruppe I: Analysis ohne Hilfsmittel ab 07 Seite /3 Gegeben ist die Funktion f mit 4 3 f(x) x x 3x 4x ; xir. 6 Bestimmen Sie den Bereich, in dem das Schaubild von f rechtsgekrümmt
Mathematik (43) Musteraufgabe Gruppe I: Analysis ohne Hilfsmittel ab 07 Seite /3 Gegeben ist die Funktion f mit 4 3 f(x) x x 3x 4x ; xir. 6 Bestimmen Sie den Bereich, in dem das Schaubild von f rechtsgekrümmt
Lösungen Kapitel A: Funktionen
 Lösungen Kapitel A: Funktionen Arbeitsblatt 01: Abhängigkeiten entstehen a) Zu Beginn des Tages befinden sich 10 Besucher am Strand. Bis um 4 Uhr nachts haben alle den Strand verlassen. Um 6 Uhr sind bereits
Lösungen Kapitel A: Funktionen Arbeitsblatt 01: Abhängigkeiten entstehen a) Zu Beginn des Tages befinden sich 10 Besucher am Strand. Bis um 4 Uhr nachts haben alle den Strand verlassen. Um 6 Uhr sind bereits
Kurvendiskussion Ganzrationale Funktion Aufgaben und Lösungen
 Kurvendiskussion Ganzrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Ganzrationale Funktion Quadratische Funktionen f x) = ax + bx + c 8. Aufgaben...................................................
Kurvendiskussion Ganzrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Ganzrationale Funktion Quadratische Funktionen f x) = ax + bx + c 8. Aufgaben...................................................
Lösungserwartung und Lösungsschlüssel zur prototypischen Schularbeit für die 7. Klasse (Autor: Gottfried Gurtner)
 Lösungserwartung und Lösungsschlüssel zur prototypischen Schularbeit für die 7. Klasse (Autor: Gottfried Gurtner) Teil : Mathematische Grundkompetenzen ) Es muss (ausschließlich) die richtige Antwortmöglichkeit
Lösungserwartung und Lösungsschlüssel zur prototypischen Schularbeit für die 7. Klasse (Autor: Gottfried Gurtner) Teil : Mathematische Grundkompetenzen ) Es muss (ausschließlich) die richtige Antwortmöglichkeit
Analysis: Klausur Analysis
 Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Matura2016-Lösung. Problemstellung 1
 Matura-Lösung Problemstellung. Die Funktion f( = + 9k + müsste bei = den Wert annehmen, also gilt + 9k + = k =. Wir betrachten den Bereich mit positiven Werten. Dann gilt: f ( = 8 + 8 = = ; = Bei liegt
Matura-Lösung Problemstellung. Die Funktion f( = + 9k + müsste bei = den Wert annehmen, also gilt + 9k + = k =. Wir betrachten den Bereich mit positiven Werten. Dann gilt: f ( = 8 + 8 = = ; = Bei liegt
Bestimmung ganzrationaler Funktionen
 Bestimmung ganzrationaler Funktionen 30 0 0-50 -40-30 -0-0 0 0 30 40 50 x. Eine Brücke ist 30 m hoch und hat eine Spannweite von 00 m. Welche Parabel beschreibt die Krümmung des Stützbogens? Wir führen
Bestimmung ganzrationaler Funktionen 30 0 0-50 -40-30 -0-0 0 0 30 40 50 x. Eine Brücke ist 30 m hoch und hat eine Spannweite von 00 m. Welche Parabel beschreibt die Krümmung des Stützbogens? Wir führen
Lösung Abiturprüfung 1992 Leistungskurs (Baden-Württemberg)
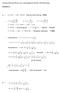 Lösung Abiturprüfung 199 Leistungskurs (Baden-Württemberg) Analysis I.1. a) f x= x= f = K geht durch denursprung U / f ' x= x x x 1 f ' ' x= x x 1 4 f ' x= x x = x 1 = ; x = f ' ' ' x= 6x x 1 5 f ' ' =
Lösung Abiturprüfung 199 Leistungskurs (Baden-Württemberg) Analysis I.1. a) f x= x= f = K geht durch denursprung U / f ' x= x x x 1 f ' ' x= x x 1 4 f ' x= x x = x 1 = ; x = f ' ' ' x= 6x x 1 5 f ' ' =
a) Im Berührungspunkt müssen die y-werte und die Steigungen übereinstimmen:
 . ANALYSIS Gegeben ist die kubische Parabel f: y = x 3 6x + 8x + a) Die Gerade g: y = k x + berührt die Parabel an der Stelle x = x 0 > 0. Bestimmen Sie den Parameter k. b) Berechnen Sie den Inhalt der
. ANALYSIS Gegeben ist die kubische Parabel f: y = x 3 6x + 8x + a) Die Gerade g: y = k x + berührt die Parabel an der Stelle x = x 0 > 0. Bestimmen Sie den Parameter k. b) Berechnen Sie den Inhalt der
7.4 Bestimmung von Funktionsgleichungen aus vorgegebenen Eigenschaften
 195 7.4 Bestimmung von Funktionsgleichungen aus vorgegebenen Eigenschaften In der Kurvenuntersuchung werden von einer gegebenen Funktionsgleichung ausgehend die Graphen von Funktionen auf ganz bestimmte
195 7.4 Bestimmung von Funktionsgleichungen aus vorgegebenen Eigenschaften In der Kurvenuntersuchung werden von einer gegebenen Funktionsgleichung ausgehend die Graphen von Funktionen auf ganz bestimmte
5.5. Abituraufgaben zu ganzrationalen Funktionen
 .. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
.. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
Natürliche Exponential- und Logarithmusfunktion. Kapitel 5
 Natürliche Eponential- und Logarithmusfunktion Kapitel . Die natürliche Eponentialfunktion und ihre Ableitung 48 Arbeitsaufträge. Individuelle Lösungen Jahr 908 90 90 930 90 960 970 990 000 00 in Sekunden
Natürliche Eponential- und Logarithmusfunktion Kapitel . Die natürliche Eponentialfunktion und ihre Ableitung 48 Arbeitsaufträge. Individuelle Lösungen Jahr 908 90 90 930 90 960 970 990 000 00 in Sekunden
Zentrale schriftliche Abiturprüfungen im Fach Mathematik
 Zentrale schritliche Abiturprüungen im Fach Mathematik Augabe : Schibau Au einer Hamburger Wert wird eine Hochgeschwindigkeitsähre als Doppelrumpschi (Katamaran) geplant. Der mittlere Teil des Schisrumpes
Zentrale schritliche Abiturprüungen im Fach Mathematik Augabe : Schibau Au einer Hamburger Wert wird eine Hochgeschwindigkeitsähre als Doppelrumpschi (Katamaran) geplant. Der mittlere Teil des Schisrumpes
I. Verfahren mit gebrochen rationalen Funktionen:
 I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
Pflichtteilaufgaben zu Elemente der Kurvendiskussion. Baden-Württemberg
 Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
1 2 x x. 1 2 x 4
 S. Potenzfunktionen mit rationalen Exponenten und ihre Ableitung Zuordung f(x) = x g(x) = x h(x) = x k(x) = x p(x) = x 0, q(x) = x r(x) = x s(x) = x, 6 7 Wurzelfunktionen a) f(x) = x + D = [ ; [ f '(x)
S. Potenzfunktionen mit rationalen Exponenten und ihre Ableitung Zuordung f(x) = x g(x) = x h(x) = x k(x) = x p(x) = x 0, q(x) = x r(x) = x s(x) = x, 6 7 Wurzelfunktionen a) f(x) = x + D = [ ; [ f '(x)
Linearisierung einer Funktion Tangente, Normale
 Linearisierung einer Funktion Tangente, Normale 1 E Linearisierung einer Funktion Abb. 1 1: Die Gerade T ist die Tangente der Funktion y = f (x) im Punkt P Eine im Punkt x = a differenzierbare Funktion
Linearisierung einer Funktion Tangente, Normale 1 E Linearisierung einer Funktion Abb. 1 1: Die Gerade T ist die Tangente der Funktion y = f (x) im Punkt P Eine im Punkt x = a differenzierbare Funktion
1 /40. dargestellt werden.
 Abschlussprüfung Fachoberschule 0 () Aufgabenvorschlag B /40 Auf der Berliner Stadtautobahn A00 / Autobahndreieck Charlottenburg wurde über einen bestimmten Zeitraum die Staulänge l in Abhängigkeit von
Abschlussprüfung Fachoberschule 0 () Aufgabenvorschlag B /40 Auf der Berliner Stadtautobahn A00 / Autobahndreieck Charlottenburg wurde über einen bestimmten Zeitraum die Staulänge l in Abhängigkeit von
Differentialquotient. Aufgabe 1. o Gegeben: Das Bild zeigt den Graphen der Funktion f mit f(x) = 0,5x 3 1,5x²
 Differentialquotient Aufgabe 1 Das Bild zeigt den Graphen der Funktion f mit f(x) = 0,5x 3 1,5x² a) Bestimmen Sie die Nullstellen der Funktion. Berechnen Sie in diesen Nullstellen die Steigung des Graphen
Differentialquotient Aufgabe 1 Das Bild zeigt den Graphen der Funktion f mit f(x) = 0,5x 3 1,5x² a) Bestimmen Sie die Nullstellen der Funktion. Berechnen Sie in diesen Nullstellen die Steigung des Graphen
Analysis: Trigonometr. Funktionen Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben
 Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben Gymnasium Oberstufe J oder J Alexander Schwarz www.mathe-aufgaben.com Dezember 0 Pflichtteilaufgaben (ohne GTR): Aufgabe : Leite die folgenden
Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben Gymnasium Oberstufe J oder J Alexander Schwarz www.mathe-aufgaben.com Dezember 0 Pflichtteilaufgaben (ohne GTR): Aufgabe : Leite die folgenden
4.4. Aufgaben zu Potenzfunktionen
 .. Aufgaben zu Potenzfunktionen Definition: Eine Funktion der Form f() = c z mit z Z\{;} heißt Potenzfunktion. Aufgabe : Potenzfunktionen mit positiven Eponenten (Parabeln). Ergänze: 9 8 7 6 - - - - -
.. Aufgaben zu Potenzfunktionen Definition: Eine Funktion der Form f() = c z mit z Z\{;} heißt Potenzfunktion. Aufgabe : Potenzfunktionen mit positiven Eponenten (Parabeln). Ergänze: 9 8 7 6 - - - - -
2. Symmetrie f(x) hat sowohl gerade als auch ungerade Exponenten, daher besitzt er weder eine Punktnoch eine Achsensymmetrie.
 Mathematik Stufe 11, Boll, Fischer Eichendorffschule 05/009 Lösungen zu den Wochenplanaufgaben Tangenten zu Wendestellen, Kurvendiskussion und 1. Führe eine vollständige Funktionsuntersuchung ( Kurvendiskussion)
Mathematik Stufe 11, Boll, Fischer Eichendorffschule 05/009 Lösungen zu den Wochenplanaufgaben Tangenten zu Wendestellen, Kurvendiskussion und 1. Führe eine vollständige Funktionsuntersuchung ( Kurvendiskussion)
1 Kurvenuntersuchung /40
 00 Herbst, (Mathematik) Aufgabenvorschlag B Kurvenuntersuchung /40 Die Tragflächen des berühmten Flugzeuges Junkers Ju-5 können an der Nahtstelle zum Flugzeugrumpf mithilfe der Funktionen f und g mit 8
00 Herbst, (Mathematik) Aufgabenvorschlag B Kurvenuntersuchung /40 Die Tragflächen des berühmten Flugzeuges Junkers Ju-5 können an der Nahtstelle zum Flugzeugrumpf mithilfe der Funktionen f und g mit 8
Gebrochen rationale Funktion f(x) = x2 +1
 Gebrochen rationale Funktion f() = +. Der Graph der Funktion f ist punktsmmetrisch, es gilt: f( ) = ( ) + f() = f( ) = + = + = f(). An der Stelle = 0 ist f nicht definiert, an dieser Stelle liegt ein Pol
Gebrochen rationale Funktion f() = +. Der Graph der Funktion f ist punktsmmetrisch, es gilt: f( ) = ( ) + f() = f( ) = + = + = f(). An der Stelle = 0 ist f nicht definiert, an dieser Stelle liegt ein Pol
1. Mathematikklausur NAME:
 Themen: Ganzrationale Funktionen: Skizzieren, untersuchen bestimmen. 1. Mathematikklausur NAME: Schreiben Sie die Lösung mit dem Lösungsweg auf ein kariertes Doppelblatt. Lassen Sie auf jeder Seite einen
Themen: Ganzrationale Funktionen: Skizzieren, untersuchen bestimmen. 1. Mathematikklausur NAME: Schreiben Sie die Lösung mit dem Lösungsweg auf ein kariertes Doppelblatt. Lassen Sie auf jeder Seite einen
Typ-1-Aufgaben für Schularbeiten
 Potenz-, Wurzel- und Polynomunktionen Typ-1-Augaben ür Schularbeiten 1 Gegeben ist eine Potenzunktion mit = a r mit a R und r ist eine durch Zwei teilbare Zahl kleiner als Null. Kreuze die beiden zutreenden
Potenz-, Wurzel- und Polynomunktionen Typ-1-Augaben ür Schularbeiten 1 Gegeben ist eine Potenzunktion mit = a r mit a R und r ist eine durch Zwei teilbare Zahl kleiner als Null. Kreuze die beiden zutreenden
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Beispielklausur für zentrale Klausuren
 ZK M A (mit CAS) Seite von 5 Beispielklausur für zentrale Klausuren Aufgabenstellung Mathematik Die Titanwurz ist die Pflanze, die die größte Blüte der Welt hervorbringt. Für ein Referat hat ein Schüler
ZK M A (mit CAS) Seite von 5 Beispielklausur für zentrale Klausuren Aufgabenstellung Mathematik Die Titanwurz ist die Pflanze, die die größte Blüte der Welt hervorbringt. Für ein Referat hat ein Schüler
Funktionen ) W(t) = 105 l 15 l. 3) 7 Minuten; Werte von 0 bis 7 Minuten; Definitionsmenge 4) Werte von 0 bis 105 l 6) Der Graph ist eine Gerade.
 Funktionen. ) W(t) = l l min t ) W l ) t min W(t) l 9 ) Minuten; Werte von bis Minuten; Definitionsmenge ) Werte von bis l ) Der Graph ist eine Gerade. t min. a) ) ) ) - - - - - - - - - Funktion. Die Funktions-
Funktionen. ) W(t) = l l min t ) W l ) t min W(t) l 9 ) Minuten; Werte von bis Minuten; Definitionsmenge ) Werte von bis l ) Der Graph ist eine Gerade. t min. a) ) ) ) - - - - - - - - - Funktion. Die Funktions-
Kurvendiskussion. Gesetzmäßigkeiten. Lineare Funktionen. Funktionsgleichung
 Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
( 8) ( 1) LÖSUNGEN. Aufgabe 1. Aufgabe 1. 3x eine vollständige. Führen Sie für die Funktion f aus a) mit. Kurvendiskussion durch. 1.
 Schuljahr 7/ Kurs Mathematik AHR Schuljahr 7/ Kurs Mathematik AHR Aufgabe Übungsaufgaben zur Klausur Nr Kurvendiskussion und Anwendungen Führen Sie für die Funktion f mit f ( + + eine vollständige Kurvendiskussion
Schuljahr 7/ Kurs Mathematik AHR Schuljahr 7/ Kurs Mathematik AHR Aufgabe Übungsaufgaben zur Klausur Nr Kurvendiskussion und Anwendungen Führen Sie für die Funktion f mit f ( + + eine vollständige Kurvendiskussion
Basistext Kurvendiskussion
 Basistext Kurvendiskussion In einer Kurvendiskussion sollen zu einer vorgegebenen Funktion (bzw. Funktionsschar) Aussagen über ihrem Verlauf gemacht werden. Im Nachfolgenden werden die einzelnen Untersuchungspunkte
Basistext Kurvendiskussion In einer Kurvendiskussion sollen zu einer vorgegebenen Funktion (bzw. Funktionsschar) Aussagen über ihrem Verlauf gemacht werden. Im Nachfolgenden werden die einzelnen Untersuchungspunkte
Abiturprüfung Mathematik 2005 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
e-funktionen Aufgaben
 e-funktionen Aufgaben Die Fichte ist in Nordeuropa und den Gebirgen Mitteleuropas beheimatet. Durch Aufforsten wurde sie jedoch auch im übrigen Europa weit verbreitet. Fichten können je nach Standort Höhen
e-funktionen Aufgaben Die Fichte ist in Nordeuropa und den Gebirgen Mitteleuropas beheimatet. Durch Aufforsten wurde sie jedoch auch im übrigen Europa weit verbreitet. Fichten können je nach Standort Höhen
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
MATHEMATIK K1. Gesamtpunktzahl /30 Notenpunkte
 MATHEMATIK K1 21.11.2013 Aufgabe 1 2 3 4 5 6 7 Punkte (max) 6 3 4 4 2 10 1 Punkte Gesamtpunktzahl /30 Notenpunkte Der GTR ist nur für die Lösung der Textaufgabe (und zur Kontrolle der andern) zugelassen.
MATHEMATIK K1 21.11.2013 Aufgabe 1 2 3 4 5 6 7 Punkte (max) 6 3 4 4 2 10 1 Punkte Gesamtpunktzahl /30 Notenpunkte Der GTR ist nur für die Lösung der Textaufgabe (und zur Kontrolle der andern) zugelassen.
KOMPETENZHEFT ZUM DIFFERENZIEREN, II. d) s(x) = 5 x x e) k(x) = 2 x 3. f) q(x) = 4 x 3 6 x 2 24 x + 31
 KOMPETENZHEFT ZUM DIFFERENZIEREN, II 1. Aufgabenstellungen Aufgabe 1.1. Berechne die Punkte, an denen die Funktion eine waagrechte Tangente besitzt, sowie das globale Minimum bzw. Maximum der Funktion
KOMPETENZHEFT ZUM DIFFERENZIEREN, II 1. Aufgabenstellungen Aufgabe 1.1. Berechne die Punkte, an denen die Funktion eine waagrechte Tangente besitzt, sowie das globale Minimum bzw. Maximum der Funktion
Sommerschule Änderungsrate Ableiten Aufgaben im Umfeld der Tangente
 Sommerschule 2013 Änderungsrate Ableiten Aufgaben im Umfeld der Tangente Arbeiten in der Kursstufe Wisst ihr noch?????? Durchschnittsgeschwindigkeit s (t)=v(t) Ableitungsfunktion Tangentensteigung Mittlere
Sommerschule 2013 Änderungsrate Ableiten Aufgaben im Umfeld der Tangente Arbeiten in der Kursstufe Wisst ihr noch?????? Durchschnittsgeschwindigkeit s (t)=v(t) Ableitungsfunktion Tangentensteigung Mittlere
Serie 4: Flächeninhalt und Integration
 D-ERDW, D-HEST, D-USYS Mathematik I HS 5 Dr. Ana Cannas Serie 4: Flächeninhalt und Integration Bemerkung: Die Aufgaben dieser Serie bilden den Fokus der Übungsgruppen vom. und 4. Oktober.. Das Bild zeigt
D-ERDW, D-HEST, D-USYS Mathematik I HS 5 Dr. Ana Cannas Serie 4: Flächeninhalt und Integration Bemerkung: Die Aufgaben dieser Serie bilden den Fokus der Übungsgruppen vom. und 4. Oktober.. Das Bild zeigt
Übungsaufgaben II zur Klausur 1
 Übungsaufgaben II zur Klausur. Ableitungen 0. Führen Sie für g mit f ( +,9 8 eine vollständige Kurvendiskussion (siehe S. 9f durch. Markieren Sie alle von Ihnen bestimmten Punkte in der abschließenden
Übungsaufgaben II zur Klausur. Ableitungen 0. Führen Sie für g mit f ( +,9 8 eine vollständige Kurvendiskussion (siehe S. 9f durch. Markieren Sie alle von Ihnen bestimmten Punkte in der abschließenden
A Abituraufgaben. 1 Analysis. Aufgabe 1
 A Abituraufgaben 1 Analsis Aufgabe 1 Dem menschlichen Körper können Medikamente durch einen Tropf kontinuierlich zugeführt werden. Zu Beginn weist der Körper keine Medikamentenmenge auf, nach In- Gang-Setzen
A Abituraufgaben 1 Analsis Aufgabe 1 Dem menschlichen Körper können Medikamente durch einen Tropf kontinuierlich zugeführt werden. Zu Beginn weist der Körper keine Medikamentenmenge auf, nach In- Gang-Setzen
Bestimmen Sie jeweils die Lösungsmenge der Gleichung: 1. Bestimmen Sie jeweils die Lösungsmenge der Gleichung:
 Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
1.2 Berechne den Inhalt der Fläche, die das Schaubild von mit 5P der -Achse einschließt.
 Diese Aufgaben sind zu bearbeiten. Sie können nicht abgewählt werden. Aufgabe A1 1. Gegeben ist die Funktion mit 2 3; 1.1 Eine der folgenden Abbildung zeigt das Schaubild. 6P Untersuche für jede der Abbildungen,
Diese Aufgaben sind zu bearbeiten. Sie können nicht abgewählt werden. Aufgabe A1 1. Gegeben ist die Funktion mit 2 3; 1.1 Eine der folgenden Abbildung zeigt das Schaubild. 6P Untersuche für jede der Abbildungen,
Beispielklausur für zentrale Klausuren
 ZK M A (ohne CAS) Seite von 4 Beispielklausur für zentrale Klausuren Mathematik Aufgabenstellung Die Titanwurz ist die Pflanze, die die größte Blüte der Welt hervorbringt. Für ein Referat hat ein Schüler
ZK M A (ohne CAS) Seite von 4 Beispielklausur für zentrale Klausuren Mathematik Aufgabenstellung Die Titanwurz ist die Pflanze, die die größte Blüte der Welt hervorbringt. Für ein Referat hat ein Schüler
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Demo: Mathe-CD. Prüfungsaufgaben Mündliches Abitur. Analysis. Teilbereich 1: Ganzrationale Funktionen 1. März 2002
 Prüfungsaufgaben Mündliches Abitur Analysis Teilbereich : Ganzrationale Funktionen Hier nur Aufgaben als Demo Datei Nr. 9 März 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Vorwort Die in dieser Reihe von
Prüfungsaufgaben Mündliches Abitur Analysis Teilbereich : Ganzrationale Funktionen Hier nur Aufgaben als Demo Datei Nr. 9 März 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Vorwort Die in dieser Reihe von
Differenzialrechnung
 Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Analysis1-Klausuren in den ET-Studiengängen (Ba) ab 2007
 Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
ANALYSIS. 3. Extremwertaufgaben (folgt)
 ANALYSIS 1. Untersuchung ganzrationaler Funktionen 1.1 Symmetrie 2 1.2 Ableitung 2 1.3 Berechnung der Nullstellen 3 1.4 Funktionsuntersuchung I 4 1.5 Funktionsuntersuchung II 6 2. Bestimmung ganzrationaler
ANALYSIS 1. Untersuchung ganzrationaler Funktionen 1.1 Symmetrie 2 1.2 Ableitung 2 1.3 Berechnung der Nullstellen 3 1.4 Funktionsuntersuchung I 4 1.5 Funktionsuntersuchung II 6 2. Bestimmung ganzrationaler
Höhere Mathematik 1 Übung 9
 Aufgaben, die in der Präsenzübung nicht besprochen wurden, können in der darauf folgenden übung beim jeweiligen übungsleiter bzw. bei der jeweiligen übungsleiterin abgegeben werden. Diese Abgabe ist freiwillig
Aufgaben, die in der Präsenzübung nicht besprochen wurden, können in der darauf folgenden übung beim jeweiligen übungsleiter bzw. bei der jeweiligen übungsleiterin abgegeben werden. Diese Abgabe ist freiwillig
Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg Wahlteil Analysis A1 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 2017 1 Aufgabe
Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg Wahlteil Analysis A1 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 2017 1 Aufgabe
4.4. Potenzfunktionen
 .. Potenzfunktionen Definition: Eine Funktion der Form f() = c z mit z \{; } heißt Potenzfunktion.... Potenzfunktionen mit positiven Eponenten (Parabeln) Schaubilder und Wertetabelle: = = - - - - - - -
.. Potenzfunktionen Definition: Eine Funktion der Form f() = c z mit z \{; } heißt Potenzfunktion.... Potenzfunktionen mit positiven Eponenten (Parabeln) Schaubilder und Wertetabelle: = = - - - - - - -
Zusammenfassung Abitursstoff Mathematik
 Zusammenfassung Abitursstoff Mathematik T. Schneider, J. Wirtz, M. Blessing 2015 Inhaltsverzeichnis 1 Analysis 2 1.1 Monotonie............................................ 2 1.2 Globaler Verlauf........................................
Zusammenfassung Abitursstoff Mathematik T. Schneider, J. Wirtz, M. Blessing 2015 Inhaltsverzeichnis 1 Analysis 2 1.1 Monotonie............................................ 2 1.2 Globaler Verlauf........................................
Funktionenlehre. Grundwissenskatalog G8-Lehrplanstandard
 GRUNDWISSEN MATHEMATIK Funktionenlehre Grundwissenskatalog G8-Lehrplanstandard Basierend auf den Grundwissenskatalogen des Rhöngmnasiums Bad Neustadt und des Kurt-Huber-Gmnasiums Gräfelfing J O H A N N
GRUNDWISSEN MATHEMATIK Funktionenlehre Grundwissenskatalog G8-Lehrplanstandard Basierend auf den Grundwissenskatalogen des Rhöngmnasiums Bad Neustadt und des Kurt-Huber-Gmnasiums Gräfelfing J O H A N N
