Kapitel IV Minimale Spannbäume
|
|
|
- Edith Baumgartner
- vor 5 Jahren
- Abrufe
Transkript
1 Kapitel IV Minimale Spannbäume 1. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten. Die Anzahl der Knoten bezeichnen wir mit n ( V = n), die Anzahl der Kanten mit m ( E = m). Eine gerichtete Kante mit den Endknoten u und v wird mit (u, v), eine ungerichtete mit {u, v} notiert. Eine Kante (v, v) E (bzw. {v, v}) heißt Schlinge. Falls E eine Multimenge ist, spricht man von Mehrfachkanten. Kanten (u, v) und (v, u) heißen antiparallel. Graphen ohne Schlingen und Mehrfachkanten heißen einfache Graphen (engl. simple). Für einfache ungerichtete Graphen gilt daher: ( ) V E := {X V, X = } EADS 1 Grundlagen 414/530
2 Graphische Darstellung: v 4 K 5 v 5 v 3 v v 1 K 3,3 v 3 v 6 v v 5 v 1 v 4 EADS 1 Grundlagen 415/530
3 Ist E V V, dann heißt G gerichteter Graph (engl. digraph). u v Der zu G gehörige ungerichtete Graph ist G = (V, E ). E erhält man, indem man in E die Richtungen weglässt und Mehrfachkanten beseitigt. Sei v V. Unter der Nachbarschaft N(v) := {w; (v, w) oder (w, v) E} eines Knotens v versteht man die Menge der direkten Nachbarn von v. Der Grad eines Knotens ist definiert als: { N(v) ; falls G ungerichtet und deg(v) = indeg(v) + outdeg(v) ; falls G gerichtet. Dabei ist indeg(v) die Anzahl aller Kanten, die v als Endknoten, und outdeg(v) die Anzahl aller Kanten, die v als Anfangsknoten haben. EADS 1 Grundlagen 416/530
4 Beobachtung: Für einfache (gerichtete oder ungerichtete) Graphen gilt deg(v) = E. v V Korollar 94 In jedem (einfachen) Graphen ist die Anzahl der Knoten mit ungeradem Grad eine gerade Zahl. EADS 1 Grundlagen 417/530
5 Das Komplement Ḡ = (V, ( V ) \ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E. Ein Graph H = (V, E ) heißt Teilgraph (aka. Subgraph) von G = (V, E), falls V V und E E. H heißt (knoten-) induzierter Teilgraph, falls H Teilgraph von G ist und ( ) V E = E. EADS 1 Grundlagen 41/530
6 Ein Kantenzug (oder Pfad) ist eine Folge e 1 := {v 0, v 1 },..., e l := {v l 1, v l }. v 0 und v l sind die Endknoten, l ist die Länge des Kantenzuges. Sind bei einem Pfad alle v i (und damit erst recht alle e i ) verschieden, so sprechen wir von einem einfachen Pfad. Ein Kantenzug mit v l = v 0 heißt Zykel oder Kreis. Ein Kreis, in dem alle v i verschieden sind, heißt einfacher Kreis. Ein (ungerichteter) Graph G heißt zusammenhängend, wenn es für alle u, v V einen Pfad gibt, der u und v verbindet. Ein (knoten-)maximaler induzierter zusammenhängender Teilgraph heißt (Zusammenhangs-)Komponente. EADS 1 Grundlagen 419/530
7 K K 3 K 1 K 4 Ein Graph G heißt azyklisch, wenn er keinen Kreis enthält. Wir bezeichnen einen solchen ungerichteten Graphen dann als Wald. Ist dieser auch zusammenhängend, so sprechen wir von einem Baum. Ist der Teilgraph T = (V, E ) G = (V, E) ein Baum, dann heißt T ein Spannbaum von G. EADS 1 Grundlagen 40/530
8 Satz 95 Ist T = (V, E) ein Baum, dann ist E = V 1. Beweis: Induktion über die Anzahl n der Knoten: n = 0, 1: klar. n n + 1: Sei V = n + 1. Da T zusammenhängend ist, ist deg(v) 1 für alle v V. T muss einen Knoten v mit deg(v) = 1 enthalten, denn ansonsten würde, wie wiederum eine einfache Induktion zeigt, T einen Kreis enthalten. Wende nun die Induktionsannahme auf den durch V {v} induzierten Teilgraphen an. Korollar 96 Ein (ungerichteter) Graph G ist zusammenhängend, gdw G einen Spannbaum hat. EADS 1 Grundlagen 41/530
9 . Traversierung von Graphen Sei G = (V, E) ein ungerichteter Graph. Anhand eines Beipiels betrachten wir die zwei Algorithmen DFS (Tiefensuche) und BFS (Breitensuche). EADS Traversierung von Graphen 4/530
10 .1 DFS-Algorithmus while unvisited v do r := pick (random) unvisited node push r onto stack while stack do v := pop top element if v unvisited then mark v visited push all neighbours of v onto stack perform operations DFS Ops(v) fi od od EADS.1 DFS-Algorithmus 43/530
11 Beispiel EADS.1 DFS-Algorithmus 44/530
12 Beobachtung: Die markierten Kanten bilden einen Spannbaum: Rückwärtskante EADS.1 DFS-Algorithmus 45/530
13 Folge der Stackzustände visited visited Stack: : oberstes Stackelement : schon besuchte Knoten : Nachbarn Zustand: a) b) c) d) e) f) g) h) i) j) EADS.1 DFS-Algorithmus 46/530
14 Wir betrachten den Stackzustand: Im Zustand g) sind die Elemente, 3 und 5 als visited markiert (siehe Zustände b), c) und e)). Deswegen werden sie aus dem Stack entfernt, und das Element wird zum obersten Stackelement. Im Zustand j) sind alle Elemente markiert, so dass eins nach dem anderen aus dem Stack entfernt wird. EADS.1 DFS-Algorithmus 47/530
15 . BFS-Algorithmus while unvisited v do r := pick (random) unvisited node push r into (end of) queue while queue do v := remove front element of queue if v unvisited then mark v visited append all neighbours of v to end of queue perform operations BFS Ops(v) fi od od EADS. BFS-Algorithmus 4/530
16 Beispiel EADS. BFS-Algorithmus 49/530
17 Beobachtung: Die markierten Kanten bilden einen Spannbaum: Rückwärtskanten EADS. BFS-Algorithmus 430/530
18 Folge der Queuezustände Queue: 1 Zustand: (a 7 (b (c (d visited (e (f visited visited visited visited (g (h (i (j EADS. BFS-Algorithmus 431/530
19 Wir betrachten die Folge der Queuezustände. Wiederum bedeutet die Notation: : vorderstes Queue-Element : schon besuchte Knoten : Nachbarn Im Zustand e) sind die Elemente 1 und als visited markiert (siehe Zustände a) und c)). Deswegen werden sie aus der Queue entfernt, und so wird das Element 9 das vorderste Queueelement. Das gleiche passiert in den Zuständen g), h) und i). Im Zustand j) sind alle Elemente markiert, so dass sie eins nach dem anderen aus der Queue entfernt werden. EADS. BFS-Algorithmus 43/530
20 3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e), T = (V, E ) ein Teilgraph von G: w(t ) = w(e ). Definition 99 T heißt minimaler Spannbaum (MSB, MST) von G, falls T Spannbaum von G ist und gilt: w(t ) w(t ) für alle Spannbäume T von G. EADS 3.0 BFS-Algorithmus 433/530
21 Beispiel minimaler 1 4 Spannbaum 5 3 Anwendungen: Telekom: Verbindungen der Telefonvermittlungen Leiterplatinen EADS 3.0 BFS-Algorithmus 434/530
22 3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel EADS 3.1 Konstruktion von minimalen Spannbäumen 435/530
23 Satz 101 Sei G = (V, E) ein zusammenhängender ungerichteter Graph, w : E R eine Gewichtsfunktion, C = (V 1, V ) ein Schnitt (d.h. V = V 1 V, V 1 V =, V 1 V ). Sei weiter E C = E (V 1 V ) die Menge der Kanten über den Schnitt hinweg. Dann gilt: ( blaue Regel) 1 Ist e E C die einzige Kante minimalen Gewichts (über alle Kanten in E C ), dann ist e in jedem minimalen Spannbaum für (G,w) enthalten. Hat e E C minimales Gewicht (über alle Kanten in E C ), dann gibt es einen minimalen Spannbaum von (G,w), der e enthält. EADS 3.1 Konstruktion von minimalen Spannbäumen 436/530
24 Beweis: [durch Widerspruch] 1 Sei T ein minimaler Spannbaum von (G, w), sei e E C die minimale Kante. Annahme: e / T. Da T Spannbaum T E C. Sei T E C = {e 1, e,..., e k }, k 1. Dann enthält T {e} einen eindeutig bestimmten Kreis (den sogenannten durch e bzgl. T bestimmten Fundamentalkreis). Dieser Kreis muss mindestens eine Kante E C T enthalten, da die beiden Endpunkte von e auf verschiedenen Seiten des Schnitts C liegen. EADS 3.1 Konstruktion von minimalen Spannbäumen 437/530
25 Beweis (Forts.): T e e e e V 1 V Sei e E C T. Dann gilt nach Voraussetzung w(e ) > w(e). Also ist T := T {e } {e} ein Spannbaum von G, der echt kleineres Gewicht als T hat, Widerspruch zu T ist minimaler Spannbaum. EADS 3.1 Konstruktion von minimalen Spannbäumen 43/530
26 Beweis (Forts.): Sei e E C minimal. Annahme: e kommt in keinem minimalen Spannbaum vor. Sei T ein beliebiger minimaler Spannbaum von (G, w). e e / T E c V 1 V e / T E C. Sei e E C T eine Kante auf dem durch e bezüglich T erzeugten Fundamentalkreis. Dann ist T = T {e } {e} wieder ein Spannbaum von G, und es ist w(t ) w(t ). Also ist T minimaler Spannbaum und e T. EADS 3.1 Konstruktion von minimalen Spannbäumen 439/530
27 Satz 10 Sei G = (V, E) ein ungerichteter, gewichteter, zusammenhängender Graph mit Gewichtsfunktion w : E R. Dann gilt: ( rote Regel) 1 Gibt es zu e E einen Kreis C in G, der e enthält und w(e) > w(e ) für alle e C \ {e} erfüllt, dann kommt e in keinem minimalen Spannbaum vor. Ist C 1 = e 1,..., e k ein Kreis in G und w(e i ) = max{w(e j ); 1 j k}, dann gibt es einen minimalen Spannbaum, der e i nicht enthält. EADS 3.1 Konstruktion von minimalen Spannbäumen 440/530
28 Beweis: 1 Nehmen wir an, dass es einen minimalen Spannbaum T gibt, der e = {v 1, v } enthält. Wenn wir e aus T entfernen, so zerfällt T in zwei nicht zusammenhängende Teilbäume T 1 und T mit v i T i, i = 1,. Da aber e auf einem Kreis in G liegt, muss es einen Weg von v 1 nach v geben, der e nicht benützt. Mithin gibt es eine Kante ê e auf diesem Weg, die einen Knoten in T 1 mit T verbindet. Verbinden wir T 1 und T entlang ê, so erhalten wir einen von T verschiedenen Spannbaum ˆT. Wegen w(ê) < w(e) folgt w( ˆT ) < w(t ), im Widerspruch zur Minimalität von T. EADS 3.1 Konstruktion von minimalen Spannbäumen 441/530
29 Beweis (Forts.): Wir nehmen an, e i liege in jedem minimalen Spannbaum (MSB) von G, und zeigen die Behauptung durch Widerspruch. Sei T ein beliebiger MSB von G. Entfernen wir e i aus T, so zerfällt T in zwei nicht zusammenhängende Teilbäume T 1 und T. Da e i auf einem Kreis C 1 = e 1,..., e k in G liegt, können wir wie zuvor e i durch eine Kante e j des Kreises C 1 ersetzen, die T 1 und T verbindet. Dadurch erhalten wir einen von T verschiedenen Spannbaum T, der e i nicht enthält. Da nach Voraussetzung w(e j ) w(e i ) gilt, folgt w( T ) w(t ) (und sogar w( T ) = w(t ), da T nach Annahme ein MSB ist). Also ist T ein MSB von G, der e i nicht enthält, im Widerspruch zur Annahme, e i liege in jedem MSB von G. EADS 3.1 Konstruktion von minimalen Spannbäumen 44/530
30 Literatur Robert E. Tarjan: Data Structures and Network Algorithms SIAM CBMS-NSF Regional Conference Series in Applied Mathematics Bd. 44 (193) EADS 3.1 Konstruktion von minimalen Spannbäumen 443/530
\ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E.
 Das Komplement Ḡ = (V, ( V ) \ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E. Ein Graph H = (V, E )
Das Komplement Ḡ = (V, ( V ) \ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E. Ein Graph H = (V, E )
Kapitel IV Minimale Spannbäume
 Kapitel IV Minimale Spannbäume. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten.
Kapitel IV Minimale Spannbäume. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten.
Quicksort ist ein Divide-and-Conquer-Verfahren.
 . Quicksort Wie bei vielen anderen Sortierverfahren (Bubblesort, Mergesort, usw.) ist auch bei Quicksort die Aufgabe, die Elemente eines Array a[..n] zu sortieren. Quicksort ist ein Divide-and-Conquer-Verfahren.
. Quicksort Wie bei vielen anderen Sortierverfahren (Bubblesort, Mergesort, usw.) ist auch bei Quicksort die Aufgabe, die Elemente eines Array a[..n] zu sortieren. Quicksort ist ein Divide-and-Conquer-Verfahren.
3. Minimale Spannbäume. Definition 99 T heißt minimaler Spannbaum (MSB, MST) von G, falls T Spannbaum von G ist und gilt:
 3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e),
3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e),
3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel
 3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel EADS 3.1 Konstruktion von minimalen Spannbäumen 16/36
3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel EADS 3.1 Konstruktion von minimalen Spannbäumen 16/36
Seien u, v V, u v. Da G zusammenhängend ist, muss mindestens ein Pfad zwischen u und v existieren.
 Beweis: 1. 2. Seien u, v V, u v. Da G zusammenhängend ist, muss mindestens ein Pfad zwischen u und v existieren. Widerspruchsannahme: Es gibt zwei verschiedene Pfade zwischen u und v. Dann gibt es einen
Beweis: 1. 2. Seien u, v V, u v. Da G zusammenhängend ist, muss mindestens ein Pfad zwischen u und v existieren. Widerspruchsannahme: Es gibt zwei verschiedene Pfade zwischen u und v. Dann gibt es einen
3.2 Generischer minimaler Spannbaum-Algorithmus
 3.2 Generischer minimaler Spannbaum-Algorithmus Initialisiere Wald F von Bäumen, jeder Baum ist ein singulärer Knoten (jedes v V bildet einen Baum) while Wald F mehr als einen Baum enthält do wähle einen
3.2 Generischer minimaler Spannbaum-Algorithmus Initialisiere Wald F von Bäumen, jeder Baum ist ein singulärer Knoten (jedes v V bildet einen Baum) while Wald F mehr als einen Baum enthält do wähle einen
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 1: Grundlagen der algorithmischen Graphentheorie
 Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 1: Grundlagen der algorithmischen Graphentheorie Dipl-Math. Wolfgang Kinzner 2.4.2012 Kapitel 1: Grundlagen der algorithmischen Graphgentheorie
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 1: Grundlagen der algorithmischen Graphentheorie Dipl-Math. Wolfgang Kinzner 2.4.2012 Kapitel 1: Grundlagen der algorithmischen Graphgentheorie
Definition Gerichteter Pfad. gerichteter Pfad, wenn. Ein gerichteter Pfad heißt einfach, falls alle u i paarweise verschieden sind.
 3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
Diskrete Strukturen WS 2005/06. Ernst W. Mayr. 27. Januar Fakultät für Informatik TU München
 WS 2005/06 Ernst W. Mayr Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2005ws/ds/ 27. Januar 2006 Ernst W. Mayr 2.16 Inzidenzmatrix 3. Definitionen für gerichtete Graphen 3.1 Digraph
WS 2005/06 Ernst W. Mayr Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2005ws/ds/ 27. Januar 2006 Ernst W. Mayr 2.16 Inzidenzmatrix 3. Definitionen für gerichtete Graphen 3.1 Digraph
Algorithmen und Datenstrukturen 2-1. Seminar -
 Algorithmen und Datenstrukturen 2-1. Seminar - Dominic Rose Bioinformatics Group, University of Leipzig Sommersemster 2010 Outline 1. Übungsserie: 3 Aufgaben, insgesamt 30 28 Punkte A1 Spannbäume (10 8
Algorithmen und Datenstrukturen 2-1. Seminar - Dominic Rose Bioinformatics Group, University of Leipzig Sommersemster 2010 Outline 1. Übungsserie: 3 Aufgaben, insgesamt 30 28 Punkte A1 Spannbäume (10 8
Nachbarschaft, Grad, regulär, Inzidenz
 Nachbarschaft, Grad, regulär, Inzidenz Definition Eigenschaften von Graphen Sei G = (V, E) ein ungerichteter Graph. 1 Die Nachbarschaftschaft Γ(u) eines Knoten u V ist Γ(u) := {v V {u, v} E}. 2 Der Grad
Nachbarschaft, Grad, regulär, Inzidenz Definition Eigenschaften von Graphen Sei G = (V, E) ein ungerichteter Graph. 1 Die Nachbarschaftschaft Γ(u) eines Knoten u V ist Γ(u) := {v V {u, v} E}. 2 Der Grad
Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od
 Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od Diskrete Strukturen 3.7 dag 473/556 3.8 Zusammenhang Definition
Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od Diskrete Strukturen 3.7 dag 473/556 3.8 Zusammenhang Definition
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph.
 Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 16 (2.7.2014) Graphtraversierung II, Minimale Spannbäume I Algorithmen und Komplexität Tiefensuche: Pseusocode DFS Traversal: for all u in
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 16 (2.7.2014) Graphtraversierung II, Minimale Spannbäume I Algorithmen und Komplexität Tiefensuche: Pseusocode DFS Traversal: for all u in
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 4: Suchstrategien Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 14. April 2017 HALBORDNUNG TOPOLOGISCHE ORDNUNG TOPOLOGISCHES
Algorithmische Graphentheorie Vorlesung 4: Suchstrategien Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 14. April 2017 HALBORDNUNG TOPOLOGISCHE ORDNUNG TOPOLOGISCHES
Breitensuche BFS (Breadth First Search)
 Breitensuche BFS (Breadth First Search) Algorithmus BREITENSUCHE EINGABE: G = (V, E) als Adjazenzliste, Startknoten s V 1 Für alle v V 1 If (v = s) then d[v] 0 else d[v] ; 2 pred[v] nil; 2 Q new Queue;
Breitensuche BFS (Breadth First Search) Algorithmus BREITENSUCHE EINGABE: G = (V, E) als Adjazenzliste, Startknoten s V 1 Für alle v V 1 If (v = s) then d[v] 0 else d[v] ; 2 pred[v] nil; 2 Q new Queue;
Das Heiratsproblem. Definition Matching
 Das Heiratsproblem Szenario: Gegeben: n Frauen und m > n Männer. Bekanntschaftsbeziehungen zwischen allen Männern und Frauen. Fragestellung: Wann gibt es für jede der Frauen einen Heiratspartner? Modellierung
Das Heiratsproblem Szenario: Gegeben: n Frauen und m > n Männer. Bekanntschaftsbeziehungen zwischen allen Männern und Frauen. Fragestellung: Wann gibt es für jede der Frauen einen Heiratspartner? Modellierung
Graphentheorie. Eulersche Graphen. Eulersche Graphen. Eulersche Graphen. Rainer Schrader. 14. November Gliederung.
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Programm heute. Algorithmen und Datenstrukturen (für ET/IT) Übersicht: Graphen. Definition: Ungerichteter Graph. Definition: Ungerichteter Graph
 Programm heute Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 07 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München 7 Fortgeschrittene Datenstrukturen Graphen
Programm heute Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 07 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München 7 Fortgeschrittene Datenstrukturen Graphen
Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume)
 WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
Betriebswirtschaftliche Optimierung
 Institut für Statistik und OR Uni Graz 1 Approximationsalgorithmen auf metrischen Instanzen Minimum Spanning Tree Definition (Spannbaum) Ein Spannbaum in einem Graphen G = (V,E) ist ein kreisfreier Teilgraph
Institut für Statistik und OR Uni Graz 1 Approximationsalgorithmen auf metrischen Instanzen Minimum Spanning Tree Definition (Spannbaum) Ein Spannbaum in einem Graphen G = (V,E) ist ein kreisfreier Teilgraph
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 6 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 16. Mai 2018 [Letzte Aktualisierung: 18/05/2018,
ADS: Algorithmen und Datenstrukturen 2 Teil 6 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 16. Mai 2018 [Letzte Aktualisierung: 18/05/2018,
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Betriebliche Optimierung
 Betriebliche Optimierung Joachim Schauer Institut für Statistik und OR Uni Graz Joachim Schauer ( Institut für Statistik und OR Uni Graz Betriebliche ) Optimierung 1 / 21 1 Approximationsalgorithmen auf
Betriebliche Optimierung Joachim Schauer Institut für Statistik und OR Uni Graz Joachim Schauer ( Institut für Statistik und OR Uni Graz Betriebliche ) Optimierung 1 / 21 1 Approximationsalgorithmen auf
Informatik II, SS 2018
 Informatik II - SS 2018 (Algorithmen & Datenstrukturen) Vorlesung 13 (6.6.2018) Graphenalgorithmen II Yannic Maus Algorithmen und Komplexität Repräsentation von Graphen Zwei klassische Arten, einen Graphen
Informatik II - SS 2018 (Algorithmen & Datenstrukturen) Vorlesung 13 (6.6.2018) Graphenalgorithmen II Yannic Maus Algorithmen und Komplexität Repräsentation von Graphen Zwei klassische Arten, einen Graphen
5 Graphen. Repräsentationen endlicher Graphen. 5.1 Gerichtete Graphen. 5.2 Ungerichtete Graphen. Ordnung von Graphen
 Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 5 Graphen 5.1 Gerichtete Graphen Definition 5.1 (V, E) heißt gerichteter Graph (Digraph), wenn V Menge von Knoten
Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 5 Graphen 5.1 Gerichtete Graphen Definition 5.1 (V, E) heißt gerichteter Graph (Digraph), wenn V Menge von Knoten
4.2 Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition 4.2.1
 Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
Definition Ein gerichteter Graph G = (V, E) ist ein Graph von geordneten Paaren (u, v) mit u V und v V.
 Kapitel 4 Graphenalgorithmen 4.1 Definitionen Definition 4.1.1. Der Graph G = (V, E) ist über die beiden Mengen V und E definiert, wobei V die Menge der Knoten und E die Menge der Kanten in dem Graph ist.
Kapitel 4 Graphenalgorithmen 4.1 Definitionen Definition 4.1.1. Der Graph G = (V, E) ist über die beiden Mengen V und E definiert, wobei V die Menge der Knoten und E die Menge der Kanten in dem Graph ist.
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 018/19 1. Vorlesung Minimale Spannbäume Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Motivation ) Kantengewichte w : E R >0 ) w(e ) := e E w(e)
1 Algorithmen und Datenstrukturen Wintersemester 018/19 1. Vorlesung Minimale Spannbäume Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Motivation ) Kantengewichte w : E R >0 ) w(e ) := e E w(e)
12. Graphen. Notation, Repräsentation, Traversieren (DFS, BFS), Topologisches Sortieren, Ottman/Widmayer, Kap ,Cormen et al, Kap.
 254 12. Graphen Notation, Repräsentation, Traversieren (DFS, BFS), Topologisches Sortieren, Ottman/Widmayer, Kap. 9.1-9.4,Cormen et al, Kap. 22 Königsberg 1736 255 Königsberg 1736 255 Königsberg 1736 255
254 12. Graphen Notation, Repräsentation, Traversieren (DFS, BFS), Topologisches Sortieren, Ottman/Widmayer, Kap. 9.1-9.4,Cormen et al, Kap. 22 Königsberg 1736 255 Königsberg 1736 255 Königsberg 1736 255
Diskrete Strukturen. Hausaufgabe 1 (5 Punkte) Hausaufgabe 2 (5 Punkte) Wintersemester 2007/08 Lösungsblatt Januar 2008
 Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
= n (n 1) 2 dies beruht auf der Auswahl einer zweielementigen Teilmenge aus V = n. Als Folge ergibt sich, dass ein einfacher Graph maximal ( n E = 2
 1 Graphen Definition: Ein Graph G = (V,E) setzt sich aus einer Knotenmenge V und einer (Multi)Menge E V V, die als Kantenmenge bezeichnet wird, zusammen. Falls E symmetrisch ist, d.h.( u,v V)[(u,v) E (v,u)
1 Graphen Definition: Ein Graph G = (V,E) setzt sich aus einer Knotenmenge V und einer (Multi)Menge E V V, die als Kantenmenge bezeichnet wird, zusammen. Falls E symmetrisch ist, d.h.( u,v V)[(u,v) E (v,u)
Algo&Komp. - Wichtige Begriffe Mattia Bergomi Woche 6 7
 1 Kürzeste Pfade Woche 6 7 Hier arbeiten wir mit gewichteten Graphen, d.h. Graphen, deren Kanten mit einer Zahl gewichtet werden. Wir bezeichnen die Gewichtsfunktion mit l : E R. Wir wollen einen kürzesten
1 Kürzeste Pfade Woche 6 7 Hier arbeiten wir mit gewichteten Graphen, d.h. Graphen, deren Kanten mit einer Zahl gewichtet werden. Wir bezeichnen die Gewichtsfunktion mit l : E R. Wir wollen einen kürzesten
Bemerkung: Der vollständige Graph K n hat n(n 1)
 Bemerkung: Der vollständige Graph K n hat n(n 1) 2 Kanten. Bew: Abzählen! Definition 111. Graphen mit n paarweise zyklisch verbundenen Kanten heißen Kreise (vom Grad n) und werden mit C n bezeichnet. Beispiel
Bemerkung: Der vollständige Graph K n hat n(n 1) 2 Kanten. Bew: Abzählen! Definition 111. Graphen mit n paarweise zyklisch verbundenen Kanten heißen Kreise (vom Grad n) und werden mit C n bezeichnet. Beispiel
Übung zur Vorlesung Diskrete Mathematik (MAT.107) Blatt Beispiellösungen Abgabefrist:
 Svenja Hüning, Michael Kerber, Hannah Schreiber WS 2016/2017 Übung zur Vorlesung Diskrete Mathematik (MAT.107) Blatt Beispiellösungen Abgabefrist: Hinweise: Dieses Blatt präsentiert Beispiellösungen zu
Svenja Hüning, Michael Kerber, Hannah Schreiber WS 2016/2017 Übung zur Vorlesung Diskrete Mathematik (MAT.107) Blatt Beispiellösungen Abgabefrist: Hinweise: Dieses Blatt präsentiert Beispiellösungen zu
3 Klassifikation wichtiger Optimierungsprobleme
 3 Klassifikation wichtiger Optimierungsprobleme 3.1 Das MIN- -TSP Wir kehren nochmal zurück zum Handlungsreisendenproblem für Inputs (w {i,j} ) 1 i
3 Klassifikation wichtiger Optimierungsprobleme 3.1 Das MIN- -TSP Wir kehren nochmal zurück zum Handlungsreisendenproblem für Inputs (w {i,j} ) 1 i
Formale Grundlagen. Graphentheorie 2008W. Vorlesung im 2008S
 Minimale Formale Grundlagen Graphentheorie Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Minimale Inhalt Minimale
Minimale Formale Grundlagen Graphentheorie Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Minimale Inhalt Minimale
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 24. April 2019 [Letzte Aktualisierung: 24/04/2019,
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 24. April 2019 [Letzte Aktualisierung: 24/04/2019,
Bäume und Wälder. Definition 1
 Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen)
 WS 2015/16 Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
WS 2015/16 Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
Informatik II, SS 2016
 Informatik II - SS 208 (Algorithmen & Datenstrukturen) Vorlesung 4 (..208) Graphenalgorithmen III Algorithmen und Komplexität Bäume Gegeben: Zusammenhängender, ungerichteter Graph G = V, E Baum: Zusammenhängender,
Informatik II - SS 208 (Algorithmen & Datenstrukturen) Vorlesung 4 (..208) Graphenalgorithmen III Algorithmen und Komplexität Bäume Gegeben: Zusammenhängender, ungerichteter Graph G = V, E Baum: Zusammenhängender,
Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo?
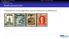 Briefmarkensammeln (Folie 413, Seite 80 im Skript) Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo? Welche Briefmarken für einen 20 fen Brief? Der Greedy-Algorithmus führt nicht
Briefmarkensammeln (Folie 413, Seite 80 im Skript) Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo? Welche Briefmarken für einen 20 fen Brief? Der Greedy-Algorithmus führt nicht
Bäume und Wälder. Definition 1
 Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Graphdurchmusterung, Breiten- und Tiefensuche
 Prof. Thomas Richter 18. Mai 2017 Institut für Analysis und Numerik Otto-von-Guericke-Universität Magdeburg thomas.richter@ovgu.de Material zur Vorlesung Algorithmische Mathematik II am 18.05.2017 Graphdurchmusterung,
Prof. Thomas Richter 18. Mai 2017 Institut für Analysis und Numerik Otto-von-Guericke-Universität Magdeburg thomas.richter@ovgu.de Material zur Vorlesung Algorithmische Mathematik II am 18.05.2017 Graphdurchmusterung,
Algorithmen für Planare Graphen
 Algorithmen für Planare Graphen 12. Juni 2018, Übung 4 Lars Gottesbüren, Michael Hamann INSTITUT FÜR THEORETISCHE INFORMATIK KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Prüfungstermine
Algorithmen für Planare Graphen 12. Juni 2018, Übung 4 Lars Gottesbüren, Michael Hamann INSTITUT FÜR THEORETISCHE INFORMATIK KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Prüfungstermine
Lösungen zu Kapitel 5
 Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
Graphen KAPITEL 3. Dieses Problem wird durch folgenden Graph modelliert:
 KAPITEL 3 Graphen Man kann als Ursprung der Graphentheorie ein Problem sehen, welches Euler 1736 von Studenten aus Königsberg gestellt bekam. Der Fluss Pregel wird von 7 Brücken überquert, und die Frage
KAPITEL 3 Graphen Man kann als Ursprung der Graphentheorie ein Problem sehen, welches Euler 1736 von Studenten aus Königsberg gestellt bekam. Der Fluss Pregel wird von 7 Brücken überquert, und die Frage
Übersicht. Bielefeld Hannover. Kamen Paderborn. Unna Wünnenberg Kassel. Ziffer wählen. abheben. auflegen. Gespräch führen
 Übersicht Graphen beschreiben Objekte und Beziehungen zwischen ihnen geeignet für Modellierung verschiedener Aufgaben betrachten endliche, ungerichtete und endliche, gerichtete Graphen Graphen bestehen
Übersicht Graphen beschreiben Objekte und Beziehungen zwischen ihnen geeignet für Modellierung verschiedener Aufgaben betrachten endliche, ungerichtete und endliche, gerichtete Graphen Graphen bestehen
Wir betrachten einen einfachen Algorithmus, der den Zusammenhang eines Graphen testen soll.
 Kapitel 2 Zusammenhang 2.1 Zusammenhängende Graphen Wir betrachten einen einfachen Algorithmus, der den Zusammenhang eines Graphen testen soll. (1) Setze E = E, F =. (2) Wähle e E und setze F = F {e},
Kapitel 2 Zusammenhang 2.1 Zusammenhängende Graphen Wir betrachten einen einfachen Algorithmus, der den Zusammenhang eines Graphen testen soll. (1) Setze E = E, F =. (2) Wähle e E und setze F = F {e},
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Prof. Martin Lercher Institut für Informatik Heinrich-Heine-Universität Düsseldorf Teil 10 Suche in Graphen Version vom 13. Dezember 2016 1 / 2 Vorlesung 2016 / 2017 2 /
Algorithmen und Datenstrukturen Prof. Martin Lercher Institut für Informatik Heinrich-Heine-Universität Düsseldorf Teil 10 Suche in Graphen Version vom 13. Dezember 2016 1 / 2 Vorlesung 2016 / 2017 2 /
Graphentheorie. Zusammenhang. Zusammenhang. Zusammenhang. Rainer Schrader. 13. November 2007
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 13. November 2007 1 / 84 2 / 84 Gliederung stest und Schnittkanten älder und Bäume minimal aufspannende Bäume Der Satz von Menger 2-zusammenhängende
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 13. November 2007 1 / 84 2 / 84 Gliederung stest und Schnittkanten älder und Bäume minimal aufspannende Bäume Der Satz von Menger 2-zusammenhängende
2. Entsprechende Listen P i von Vorgängern von i 3. for i := 1 to n do. (ii) S i = Knoten 2 + 1}
 1. Berechne für jeden Knoten i in BFS-Art eine Liste S i von von i aus erreichbaren Knoten, so dass (i) oder (ii) gilt: (i) S i < n 2 + 1 und Si enthält alle von i aus erreichbaren Knoten (ii) S i = n
1. Berechne für jeden Knoten i in BFS-Art eine Liste S i von von i aus erreichbaren Knoten, so dass (i) oder (ii) gilt: (i) S i < n 2 + 1 und Si enthält alle von i aus erreichbaren Knoten (ii) S i = n
Vollständiger Graph. Definition 1.5. Sei G =(V,E) ein Graph. Gilt {v, w} E für alle v, w V,v w, dann heißt G vollständig (complete).
 Vollständiger Graph Definition 1.5. Sei G =(V,E) ein Graph. Gilt {v, w} E für alle v, w V,v w, dann heißt G vollständig (complete). Mit K n wird der vollständige Graph mit n Knoten bezeichnet. Bemerkung
Vollständiger Graph Definition 1.5. Sei G =(V,E) ein Graph. Gilt {v, w} E für alle v, w V,v w, dann heißt G vollständig (complete). Mit K n wird der vollständige Graph mit n Knoten bezeichnet. Bemerkung
11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME
 Algorithmen und Datenstrukturen 11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME Algorithmen und Datenstrukturen - Ma5hias Thimm (thimm@uni-koblenz.de) 1 Algorithmen und Datenstrukturen 11.1. BERECHNUNG MAXIMALER FLÜSSE
Algorithmen und Datenstrukturen 11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME Algorithmen und Datenstrukturen - Ma5hias Thimm (thimm@uni-koblenz.de) 1 Algorithmen und Datenstrukturen 11.1. BERECHNUNG MAXIMALER FLÜSSE
Richtig oder falsch? Richtig oder falsch? Richtig oder falsch? Mit dynamischer Programmierung ist das Knapsack- Problem in Polynomialzeit lösbar.
 Gegeben sei ein Netzwerk N = (V, A, c, s, t) wie in der Vorlesung. Ein maximaler s-t-fluss kann immer mit Hilfe einer Folge von höchstens A Augmentationsschritten gefunden werden. Wendet man den Dijkstra-Algorithmus
Gegeben sei ein Netzwerk N = (V, A, c, s, t) wie in der Vorlesung. Ein maximaler s-t-fluss kann immer mit Hilfe einer Folge von höchstens A Augmentationsschritten gefunden werden. Wendet man den Dijkstra-Algorithmus
Algorithmentechnik - U bung 3 4. Sitzung Tanja Hartmann 03. Dezember 2009
 Algorithmentechnik - U bung 3 4. Sitzung Tanja Hartmann 03. Dezember 2009 I NSTITUT F U R T HEORETISCHE I NFORMATIK, P ROF. D R. D OROTHEA WAGNER KIT Universita t des Landes Baden-Wu rttemberg und nationales
Algorithmentechnik - U bung 3 4. Sitzung Tanja Hartmann 03. Dezember 2009 I NSTITUT F U R T HEORETISCHE I NFORMATIK, P ROF. D R. D OROTHEA WAGNER KIT Universita t des Landes Baden-Wu rttemberg und nationales
Satz 324 Sei M wie oben. Dann gibt es für ein geeignetes k Konstanten c i > 0 und Permutationsmatrizen P i, i = 1,...
 Satz 324 Sei M wie oben. Dann gibt es für ein geeignetes k Konstanten c i > 0 und Permutationsmatrizen P i, i = 1,..., k, so dass gilt M = k c i P i i=1 k c i = r. i=1 Diskrete Strukturen 7.1 Matchings
Satz 324 Sei M wie oben. Dann gibt es für ein geeignetes k Konstanten c i > 0 und Permutationsmatrizen P i, i = 1,..., k, so dass gilt M = k c i P i i=1 k c i = r. i=1 Diskrete Strukturen 7.1 Matchings
Übungsblatt 2 - Lösung
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 2 - Lösung Vorlesung Algorithmentechnik im WS 08/09 Ausgabe 04. November 2008 Abgabe 8. November, 5:0 Uhr (im Kasten vor Zimmer
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 2 - Lösung Vorlesung Algorithmentechnik im WS 08/09 Ausgabe 04. November 2008 Abgabe 8. November, 5:0 Uhr (im Kasten vor Zimmer
1 DFS-Bäume in ungerichteten Graphen
 Praktikum Algorithmen-Entwurf (Teil 3) 06.11.2006 1 1 DFS-Bäume in ungerichteten Graphen Sei ein ungerichteter, zusammenhängender Graph G = (V, E) gegeben. Sei ferner ein Startknoten s V ausgewählt. Startet
Praktikum Algorithmen-Entwurf (Teil 3) 06.11.2006 1 1 DFS-Bäume in ungerichteten Graphen Sei ein ungerichteter, zusammenhängender Graph G = (V, E) gegeben. Sei ferner ein Startknoten s V ausgewählt. Startet
1 DFS-Bäume in ungerichteten Graphen
 Praktikum Algorithmen-Entwurf (Teil 3) 31.10.2005 1 1 DFS-Bäume in ungerichteten Graphen Sei ein ungerichteter, zusammenhängender Graph G = (V, E) gegeben. Sei ferner ein Startknoten s V ausgewählt. Startet
Praktikum Algorithmen-Entwurf (Teil 3) 31.10.2005 1 1 DFS-Bäume in ungerichteten Graphen Sei ein ungerichteter, zusammenhängender Graph G = (V, E) gegeben. Sei ferner ein Startknoten s V ausgewählt. Startet
Graphentheorie. Formale Grundlagen (WIN) 2008S, F. Binder. Vorlesung im 2008S
 Minimale Graphentheorie Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Minimale Inhalt
Minimale Graphentheorie Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Minimale Inhalt
Was bisher geschah. gerichtete / ungerichtete Graphen G = (V, E) Darstellungen von Graphen
 Was bisher geschah gerichtete / ungerichtete Graphen G = (V, E) Darstellungen von Graphen Spezielle Graphen: I n, K n, P n, C n, K m,n, K 1,n, K n1,...,n m Beziehungen zwischen Graphen: Isomorphie, Teilgraph,
Was bisher geschah gerichtete / ungerichtete Graphen G = (V, E) Darstellungen von Graphen Spezielle Graphen: I n, K n, P n, C n, K m,n, K 1,n, K n1,...,n m Beziehungen zwischen Graphen: Isomorphie, Teilgraph,
12. Graphen. Königsberg Zyklen. [Multi]Graph
![12. Graphen. Königsberg Zyklen. [Multi]Graph 12. Graphen. Königsberg Zyklen. [Multi]Graph](/thumbs/94/119271554.jpg) Königsberg 76. Graphen, Repräsentation, Traversieren (DFS, BFS), Topologisches Sortieren, Ottman/Widmayer, Kap. 9. - 9.,Cormen et al, Kap. [Multi]Graph Zyklen C Kante Gibt es einen Rundweg durch die Stadt
Königsberg 76. Graphen, Repräsentation, Traversieren (DFS, BFS), Topologisches Sortieren, Ottman/Widmayer, Kap. 9. - 9.,Cormen et al, Kap. [Multi]Graph Zyklen C Kante Gibt es einen Rundweg durch die Stadt
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 3: Einführung in die Graphentheorie - Teil 3 Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 2. März 2018 1/72 ZUSAMMENHANG
Algorithmische Graphentheorie Vorlesung 3: Einführung in die Graphentheorie - Teil 3 Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 2. März 2018 1/72 ZUSAMMENHANG
Programmiertechnik II
 Graph-Algorithmen Anwendungsgebiete "Verbundene Dinge" oft Teilproblem/Abstraktion einer Aufgabenstellung Karten: Wie ist der kürzeste Weg von Sanssouci nach Kunnersdorf? Hypertext: Welche Seiten sind
Graph-Algorithmen Anwendungsgebiete "Verbundene Dinge" oft Teilproblem/Abstraktion einer Aufgabenstellung Karten: Wie ist der kürzeste Weg von Sanssouci nach Kunnersdorf? Hypertext: Welche Seiten sind
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 17 (8.7.2014) Minimale Spannbäume II Union Find, Prioritätswarteschlangen Algorithmen und Komplexität Minimaler Spannbaum Gegeben: Zus. hängender,
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 17 (8.7.2014) Minimale Spannbäume II Union Find, Prioritätswarteschlangen Algorithmen und Komplexität Minimaler Spannbaum Gegeben: Zus. hängender,
Programmiertechnik II
 Graph-Algorithmen Anwendungsgebiete "Verbundene Dinge" oft Teilproblem/Abstraktion einer Aufgabenstellung Karten: Wie ist der kürzeste Weg von Sanssouci nach Kunnersdorf? Hypertext: Welche Seiten sind
Graph-Algorithmen Anwendungsgebiete "Verbundene Dinge" oft Teilproblem/Abstraktion einer Aufgabenstellung Karten: Wie ist der kürzeste Weg von Sanssouci nach Kunnersdorf? Hypertext: Welche Seiten sind
15. Elementare Graphalgorithmen
 Graphen sind eine der wichtigste Modellierungskonzepte der Informatik Graphalgorithmen bilden die Grundlage vieler Algorithmen in der Praxis Zunächst kurze Wiederholung von Graphen. Dann Darstellungen
Graphen sind eine der wichtigste Modellierungskonzepte der Informatik Graphalgorithmen bilden die Grundlage vieler Algorithmen in der Praxis Zunächst kurze Wiederholung von Graphen. Dann Darstellungen
3. Musterlösung. Problem 1: Boruvka MST
 Universität Karlsruhe Algorithmentechnik Fakultät für Informatik WS 06/07 ITI Wagner. Musterlösung Problem : Boruvka MST pt (a) Beweis durch Widerspruch. Sei T MST von G, e die lokal minimale Kante eines
Universität Karlsruhe Algorithmentechnik Fakultät für Informatik WS 06/07 ITI Wagner. Musterlösung Problem : Boruvka MST pt (a) Beweis durch Widerspruch. Sei T MST von G, e die lokal minimale Kante eines
10. Übungsblatt zu Algorithmen I im SS 2010
 Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter Sanders G.V. Batz, C. Schulz, J. Speck 0. Übungsblatt zu Algorithmen I im SS 00 http//algo.iti.kit.edu/algorithmeni.php
Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter Sanders G.V. Batz, C. Schulz, J. Speck 0. Übungsblatt zu Algorithmen I im SS 00 http//algo.iti.kit.edu/algorithmeni.php
Wege, Pfade und Kreise
 Wege, Pfade und Kreise ef.: in Weg ist eine olge von Knoten (v 1, v2,..., vk), so dass {vi,vi+1} für alle 1 i
Wege, Pfade und Kreise ef.: in Weg ist eine olge von Knoten (v 1, v2,..., vk), so dass {vi,vi+1} für alle 1 i
Graphenalgorithmen I. Geschickt Programmieren für den ICPC- Wettbewerb. Felix Weissenberger
 Graphenalgorithmen I Geschickt Programmieren für den ICPC- Wettbewerb Felix Weissenberger Inhalt Grundlagen zu Graphen Begriffe Darstellung von Graphen Graphenalgorithmen Breitensuche Tiefensuche Topologisches
Graphenalgorithmen I Geschickt Programmieren für den ICPC- Wettbewerb Felix Weissenberger Inhalt Grundlagen zu Graphen Begriffe Darstellung von Graphen Graphenalgorithmen Breitensuche Tiefensuche Topologisches
Matchings in Graphen. Praktikum Diskrete Optimierung (Teil 5)
 Praktikum Diskrete Optimierung (Teil 5) 6.05.009 Matchings in Graphen Es sei ein ungerichteter Graph G = (V, E) gegeben. Ein Matching in G ist eine Teilmenge M E, so dass keine zwei Kanten aus M einen
Praktikum Diskrete Optimierung (Teil 5) 6.05.009 Matchings in Graphen Es sei ein ungerichteter Graph G = (V, E) gegeben. Ein Matching in G ist eine Teilmenge M E, so dass keine zwei Kanten aus M einen
Wiederholung zu Flüssen
 Universität Konstanz Methoden der Netzwerkanalyse Fachbereich Informatik & Informationswissenschaft SS 2008 Prof. Dr. Ulrik Brandes / Melanie Badent Wiederholung zu Flüssen Wir untersuchen Flüsse in Netzwerken:
Universität Konstanz Methoden der Netzwerkanalyse Fachbereich Informatik & Informationswissenschaft SS 2008 Prof. Dr. Ulrik Brandes / Melanie Badent Wiederholung zu Flüssen Wir untersuchen Flüsse in Netzwerken:
Wie wird ein Graph dargestellt?
 Wie wird ein Graph dargestellt? Für einen Graphen G = (V, E), ob gerichtet oder ungerichtet, verwende eine Adjazenzliste A G : A G [i] zeigt auf eine Liste aller Nachbarn von Knoten i, wenn G ungerichtet
Wie wird ein Graph dargestellt? Für einen Graphen G = (V, E), ob gerichtet oder ungerichtet, verwende eine Adjazenzliste A G : A G [i] zeigt auf eine Liste aller Nachbarn von Knoten i, wenn G ungerichtet
Grundzüge von Algorithmen und Datenstrukturen, WS 15/16: Lösungshinweise zum 13. Übungsblatt
 U N S A R I V E R S A V I E I T A S N I S S Grundzüge von Algorithmen und Datenstrukturen, WS /6: Lösungshinweise zum 3. Übungsblatt Christian Hoffmann, Fabian Bendun Aufgabe 3. (a) Sei j i + = n die Größe
U N S A R I V E R S A V I E I T A S N I S S Grundzüge von Algorithmen und Datenstrukturen, WS /6: Lösungshinweise zum 3. Übungsblatt Christian Hoffmann, Fabian Bendun Aufgabe 3. (a) Sei j i + = n die Größe
Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Esparza)
 WS 2013/14 Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Esparza) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2013ws/ds/uebung/ 22. Januar 2014 ZÜ DS ZÜ XIII
WS 2013/14 Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Esparza) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2013ws/ds/uebung/ 22. Januar 2014 ZÜ DS ZÜ XIII
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
KAPITEL 3 MATCHINGS IN BIPARTITEN GRAPHEN
 KAPITEL 3 MATCHINGS IN BIPARTITEN GRAPHEN F. VALLENTIN, A. GUNDERT 1. Definitionen Notation 1.1. Ähnlich wie im vorangegangenen Kapitel zunächst etwas Notation. Wir beschäftigen uns jetzt mit ungerichteten
KAPITEL 3 MATCHINGS IN BIPARTITEN GRAPHEN F. VALLENTIN, A. GUNDERT 1. Definitionen Notation 1.1. Ähnlich wie im vorangegangenen Kapitel zunächst etwas Notation. Wir beschäftigen uns jetzt mit ungerichteten
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen 13. Übung minimale Spannbäume, topologische Sortierung, AVL-Bäume Clemens Lang Übungen zu AuD 4. Februar 2010 Clemens Lang (Übungen zu AuD) Algorithmen und Datenstrukturen
Algorithmen und Datenstrukturen 13. Übung minimale Spannbäume, topologische Sortierung, AVL-Bäume Clemens Lang Übungen zu AuD 4. Februar 2010 Clemens Lang (Übungen zu AuD) Algorithmen und Datenstrukturen
Bemerkung: Es gibt Algorithmen für minimale Spannbäume der Komplexität O(m + n log n) und, für dünnbesetzte Graphen, der Komplexität O(m log n), wobei
 Bemerkung: Es gibt Algorithmen für minimale Spannbäume der Komplexität O(m + n log n) und, für dünnbesetzte Graphen, der Komplexität O(m log n), wobei { log x = min n N n: log (log ( log(x) )) } {{ } n
Bemerkung: Es gibt Algorithmen für minimale Spannbäume der Komplexität O(m + n log n) und, für dünnbesetzte Graphen, der Komplexität O(m log n), wobei { log x = min n N n: log (log ( log(x) )) } {{ } n
Kap. 6.5: Minimale Spannbäume
 Kap. 6.5: Minimale Spannbäume Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 19./20. VO DAP2 SS 2009 30.6./2.7.2009 1 Anmeldung zur Klausur 31.07.2009 um 10:15
Kap. 6.5: Minimale Spannbäume Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 19./20. VO DAP2 SS 2009 30.6./2.7.2009 1 Anmeldung zur Klausur 31.07.2009 um 10:15
Graphentheorie. Yichuan Shen. 10. Oktober 2013
 Graphentheorie Yichuan Shen 0. Oktober 203 Was ist ein Graph? Ein Graph ist eine kombinatorische Struktur, die bei der Modellierung zahlreicher Probleme Verwendung findet. Er besteht ganz allgemein aus
Graphentheorie Yichuan Shen 0. Oktober 203 Was ist ein Graph? Ein Graph ist eine kombinatorische Struktur, die bei der Modellierung zahlreicher Probleme Verwendung findet. Er besteht ganz allgemein aus
Diskrete Mathematik Graphentheorie (Übersicht)
 Diskrete Mathematik Graphentheorie (Übersicht) Dr. C. Löh 2. Februar 2010 0 Graphentheorie Grundlagen Definition (Graph, gerichteter Graph). Ein Graph ist ein Paar G = (V, E), wobei V eine Menge ist (die
Diskrete Mathematik Graphentheorie (Übersicht) Dr. C. Löh 2. Februar 2010 0 Graphentheorie Grundlagen Definition (Graph, gerichteter Graph). Ein Graph ist ein Paar G = (V, E), wobei V eine Menge ist (die
Programmierkurs Python
 Programmierkurs Python Stefan Thater Michaela Regneri 2010-0-29 Heute Ein wenig Graph-Theorie (in aller Kürze) Datenstrukturen für Graphen Tiefen- und Breitensuche Nächste Woche: mehr Algorithmen 2 Was
Programmierkurs Python Stefan Thater Michaela Regneri 2010-0-29 Heute Ein wenig Graph-Theorie (in aller Kürze) Datenstrukturen für Graphen Tiefen- und Breitensuche Nächste Woche: mehr Algorithmen 2 Was
Tutoraufgabe 1 (Suchen in Graphen):
 Prof. aa Dr. E. Ábrahám Datenstrukturen und Algorithmen SS14 F. Corzilius, S. Schupp, T. Ströder Tutoraufgabe 1 (Suchen in Graphen): a) Geben Sie die Reihenfolge an, in der die Knoten besucht werden, wenn
Prof. aa Dr. E. Ábrahám Datenstrukturen und Algorithmen SS14 F. Corzilius, S. Schupp, T. Ströder Tutoraufgabe 1 (Suchen in Graphen): a) Geben Sie die Reihenfolge an, in der die Knoten besucht werden, wenn
Programmierkurs Python II
 Programmierkurs Python II Stefan Thater & Michaela Regneri FR.7 Allgemeine Linguistik (Computerlinguistik) Universität des Saarlandes Sommersemester 011 Heute Ein wenig Graph-Theorie (in aller Kürze) Datenstrukturen
Programmierkurs Python II Stefan Thater & Michaela Regneri FR.7 Allgemeine Linguistik (Computerlinguistik) Universität des Saarlandes Sommersemester 011 Heute Ein wenig Graph-Theorie (in aller Kürze) Datenstrukturen
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 02. Mai 2017 [Letzte Aktualisierung: 10/07/2018,
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 02. Mai 2017 [Letzte Aktualisierung: 10/07/2018,
Graphen und Bäume. A.1 Graphen
 Algorithmen und Datenstrukturen 96 A Graphen und Bäume A.1 Graphen Ein gerichteter Graph (auch Digraph) G ist ein Paar (V, E), wobei V eine endliche Menge und E eine Relation auf V ist, d.h. E V V. V heißt
Algorithmen und Datenstrukturen 96 A Graphen und Bäume A.1 Graphen Ein gerichteter Graph (auch Digraph) G ist ein Paar (V, E), wobei V eine endliche Menge und E eine Relation auf V ist, d.h. E V V. V heißt
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 5 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
ADS: Algorithmen und Datenstrukturen 2 Teil 5 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 2014/15 17. Vorlesung Graphen: Repräsentation und Durchlaufstrategien Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Vorlesungsumfrage Nutzen Sie
1 Algorithmen und Datenstrukturen Wintersemester 2014/15 17. Vorlesung Graphen: Repräsentation und Durchlaufstrategien Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Vorlesungsumfrage Nutzen Sie
Übung zur Vorlesung Diskrete Strukturen I
 Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 7 und 8: Euler- und Hamilton-Graphen Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 17. April 2018 1/96 WIEDERHOLUNG Eulersche
Algorithmische Graphentheorie Vorlesung 7 und 8: Euler- und Hamilton-Graphen Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 17. April 2018 1/96 WIEDERHOLUNG Eulersche
11. Übungsblatt zu Algorithmen I im SS 2010
 Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter Sanders G.V. Batz, C. Schulz, J. Speck 11. Übungsblatt zu Algorithmen I im SS 2010 http://algo2.iti.kit.edu/algorithmeni.php
Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter Sanders G.V. Batz, C. Schulz, J. Speck 11. Übungsblatt zu Algorithmen I im SS 2010 http://algo2.iti.kit.edu/algorithmeni.php
Graphenalgorithmen I
 Graphenalgorithmen I Vortrag im Seminar Hallo Welt! für Fortgeschrittene 7. Juni 211 Graphenalgorithmen I 1/33 Motivation Problem Wie komme ich am schnellsten ins Kanapee? Problem Wie kommt ein Datenpaket
Graphenalgorithmen I Vortrag im Seminar Hallo Welt! für Fortgeschrittene 7. Juni 211 Graphenalgorithmen I 1/33 Motivation Problem Wie komme ich am schnellsten ins Kanapee? Problem Wie kommt ein Datenpaket
Dieser Graph hat 3 Zusammenhangskomponenten
 Vl 2, Informatik B, 19. 04. 02 1.1.3 Definitionen und wichtige Graphen Sei im folgenden G =(V;E) ein schlichter ungerichteter Graph. Definition: Der Grad eines Knoten v in einem ungerichteten Graphen ist
Vl 2, Informatik B, 19. 04. 02 1.1.3 Definitionen und wichtige Graphen Sei im folgenden G =(V;E) ein schlichter ungerichteter Graph. Definition: Der Grad eines Knoten v in einem ungerichteten Graphen ist
