mathematik und informatik
|
|
|
- Josef Breiner
- vor 6 Jahren
- Abrufe
Transkript
1 Prof. Dr. Delio Mugnolo, Dr. Hafida Laasri, Dr. Joachim Kerner Kurs Funktionalanalysis I LESEPROBE mathematik und informatik
2 Das Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere das Recht der Vervielfältigung und Verbreitung sowie der Übersetzung und des Nachdrucks bleiben, auch bei nur auszugsweiser Verwertung, vorbehalten. Kein Teil des Werkes darf in irgendeiner Form (Druck, Fotokopie, Mikrofilm oder ein anderes Verfahren) ohne schriftliche Genehmigung der FernUniversität reproduziert oder unter Verwendung elektronischer Systeme verarbeitet, vervielfältigt oder verbreitet werden.
3 i Liebe Studentin, lieber Student, wir freuen uns über Ihr Interesse für den Kurs Funktionalanalysis und wünschen Ihnen Erfolg bei der Bearbeitung und Vergnügen beim Lernen. Funktionalanalysis was soll das sein? Schließlich haben Sie das gesamte bisherige Studium hindurch reichlich viele Funktionen getroffen, ohne dass man auf die Idee kommen würde, ihnen einen ganzen Kurs zu widmen. Nein, die Funktionalanalysis hat wenig mit allgemeinen Funktionen zu tun, vielmehr ist sie die Lehre von den Funktionale beziehungsweise ist sie als solche entstanden. Funktionale sind wiederum auch keine allzu geheimnisvollen Objekte: Sie sind nichts anderes als Abbildungen von R n nach R, beziehungsweise ihre natürlichen Verallgemeinerungen auf unendlichdimensionale Vektorräume. Fordert man darüber hinaus, dass sie eine geeignete Linearitätsbedingung erfüllen, so werden Funktionale zu hoch interessanten mathematischen Objekten mit erstaunlich vielen Anwendungen sowie bemerkenswerten subtilen Problematiken lineare Funktionale auf unendlichdimensionalen Vektorräumen müssen zum Beispiel nicht stetig sein, so lang man bereit ist, das gängige axiomatische System um das Auswahlaxiom zu ergänzen! Erstmals untersucht wurden Funktionale zu Beginn des 20. Jahrhunderts. Die Welt der Mathematik war damals ein interessanter, widerspruchsreicher Ort: Viele Forscher (und leider nur sehr wenige Forscherinnen) kämpften um die korrekte Gestaltung der Fundamente obwohl oder gerade weil? sie gleichzeitig immer wieder auch viele Probleme instinktiv lösten, die erst viel später akkurat untersucht, ja sogar genau formuliert werden konnten. Dies springt besonders ins Auge wenn man bedenkt, dass viele Gruppen etwa die Göttinger Schule um David Hilbert tiefe Resultate in der Analyse von Integralgleichungen erzielten, ohne jedoch über den Begriff von unendlichdimensionalem Vektorraum oder von Norm zu verfügen. Funktionalanalysis also als Fokussierung der klassischen Analysis auf lineare Abbildungen. Gleichzeitig lässt sich die Funktionalanalysis aber auch als Disziplin beschreiben, in der die analytischen Eigenschaften der klassischen Objekte der linearen Algebra untersucht werden. Was nämlich die Analysis von der linearen Algebra im Kern unterscheidet, ist die Möglichkeit die in allgemeinen Vektorräumen nicht gegeben ist, Grenzwerte zu bilden und Stetigkeit zu definieren. Somit bilden normierte Räume das Thema unserer Kurseinheit 2 gewissermaßen die denkbar elementarsten Objekte, die aus einer Hybridisierung von Analysis und linearer Algebra entstehen können. Normierte Räume wurden somit schnell zu einem der beliebtesten Spielplätze der klassischen Funktionalanalysis und sind in diesem Kurs allgegenwärtig. Die stürmischen Entwicklungen der Jahre zeigten deutlich, wie wichtig und vielversprechend ein abstrakterer, ja von der linearen Algebra inspirierter Zugang zur Analysis sein konnte. 100 Jahre alte Probleme der Fourier-Analyse konnten in einem neuen algebraischen Rahmen aufgefasst und gelöst, die Struktur zahlreicher Gegenbeispiele erläutert, die Approximierbarkeit stetiger Funktionen durch Polynome oder trigonometrische Reihen strukturell untersucht werden. In diesen Jahren wurden vor allem in Deutschland und Frankreich, aber auch in Österreich-Ungarn und Italien, etwa Funktionen- und Folgenräume, Lebesguesche Integrationstheorie, Konvergenz in allgemeinen topologischen Räumen eingeführt. Sie blieben jedoch für eine Weile weitgehend getrennte Gebiete. Die Strukturierung und die Systematisierung dieser und weiterer Theorien ist vor allem einer Gruppe polnischer Mathematiker um Stefan Banach und Hugo Steinhaus in Lwów (bis 1918: Lemberg, Österreich-Ungarn; heute Lwiw, Ukraine) zu verdanken, von denen bis 1945 viele starben oder emigrierten. Die goldenen Jahre der klassischen Funktionalanalysis umfassen die Zeit zwischen der Promotion von Stefan Banach im Jahr 1922 und dem Einmarsch der Wehrmacht in Lwów im Jahr Somit ist sie auch, stärker und offensichtlicher als wohl die meisten anderen mathematischen Bereiche, ein Spiegel der europäischen Geschichte im 20. Jahrhundert; kaum ein anderes Gebiet wurde so
4 ii stark von Diktaturen, Kriegen, antisemitischen Verfolgungen, Verschiebungen von Grenzen und Flucht beeinflusst; eine sehr gute und informierte Quelle über die Wechselwirkung von Politik und Funktionalanalysis ist [?]. Die Anfänge der Funktionalanalysis wurden von Frankreich und Deutschland besonders geprägt, den beiden Staaten, die an an der Jahrhundertwende de facto das Monopol der Analysis weltweit innehatten; die ersten Versuche im Bereich der Funktionalanalysis waren vor allem darauf gerichtet, alte analytische Probleme mit neuen Methoden zu behandeln. In der Zeit zwischen den Weltkriegen entwickelte sich die Funktionalanalysis vor allem unter dem Impuls der Mitglieder der bereits erwähnten Lemberger Mathematikerschule, deren Interessen eher abstrakt waren und sich von der Wechselwirkung von Topologie und linearer Algebra ableiteten. Nach dem zweitem Weltkrieg nahmen auch die USA und die Sowjetunion, die mittlerweile auch mathematische Mächte geworden waren, selber an der Entwicklung des Gebietes maßgeblich teil, was wieder zu einer Verschiebung der Schwerpunkte führte: Funktionalanalysis wurde nun vor allem als Werkzeug für Numerik, Approximationstheorie, Differenzialgleichungen, Stochastik und vor allem mathematische Physik verstanden. Denn es ist ein großes Wunder der Natur, dass die Funktionalanalysis und ihre Tochterdisziplinen die Sprache der Quantenmechanik sind. Wenig, was nach 1950 in der Funktionalanalysis passiert ist, wird aber in diesem Kurs abgebildet. Und nun zur Struktur dieses Kurses: Er besteht aus sieben Einheiten über Metrische Räume Normierte Räume Lineare Operatoren Funktionale und schwache Konvergenz Lebesgue- und Sobolevräume Hilberträume Spektraltheorie Wir empfehlen Ihnen, die Kapitel in dieser Reihenfolge durchzuarbeiten, da sie meistens aufeinander aufbauen. Die Kapitel werden getaktet durch das Abwechseln von lockereren Texten mit formalisierten Inhalten. Zum einem haben wir versucht, die historischen Entwicklungen zu schildern, die dazu geführt haben, dass einige Begrifflichkeiten oder sogar ganze Forschungsrichtungen sich herauskristallisiert haben; zum anderen präsentieren wir die wichtigsten Sätzen der Funktionalanalysis zusammen mit ihren Beweisen, welche oft ihre ganz eigenen interessanten Geschichten aufweisen. Darüber hinaus werden Sie im Text zahlreiche Übungsaufgaben finden: Sie selbständig zu lösen wird Ihnen helfen, die Begriffe und die Beweismethoden im Lernstoff besser zu verinnerlichen. (Die zugehörigen Lösungsvorschläge finden Sie dann am Ende der jeweiligen Kapitel.) Ebenfalls am Ende jedes Kapitels finden sie einen kurzen Abschnitt über Anmerkungen und Empfehlungen fürs weitere Lernen: Sie sind eine Auswahl jener Themen, die aus Platzmangel nicht in den Haupttext aufgenommen wurden und trotzdem interessant sind ob wegen der eleganten Beweise und der Verschärfung von Resultaten im Haupttext oder aufgrund der unerwarteten Einblicke in benachbarte Gebiete, die sie erlauben. Sie bieten durchaus mögliche Themen für ein Seminar oder für eine Abschlussarbeit. Nachdem die wichtigsten Inhalte dieses Kurses zusammengefasst wurden, sollte nicht unerwähnt bleiben, was in diesem Kurs nicht behandelt wird, darunter:
5 iii Unbeschränkte Operatoren: Im Text werden ausschließlich Resultate über beschränkte lineare Operatoren präsentiert. Dabei haben unbeschränkte Operatoren seit den 1930er Jahren sehr viel Aufmerksamkeit bekommen, auch angesichts ihrer Rolle in der Quantenmechanik. Der Kurs 1347 Lineare Operatoren im Hilbertraum ist vor allem der Spektraltheorie dieser Operatoren so wie ihrer Anwendung gewidmet. Nichtlineare Funktionalanalysis: Einige der Resultate, die Sie in diesem Skript finden, gelten nicht nur für lineare Operatoren. Die meisten Methoden topologischer Natur können tatsächlich den nichtlinearen Kontexten erweitert werden, außerdem kann man manchmal die Linearität eines Funktionals durch die schwächere Bedingung der Konvexität ersetzen. Bei genügendem Interesse könnte gerne ein Seminar über nichtlineare Funktionalanalysis gerne angeboten werden. Anwendungen in der Theorie der linearen Differenzialgleichungen: Funktionalanalytische Methoden für die Untersuchung von partiellen Differenzialgleichungen gehören seit Jahrzehnten zur Grundausstattung der angewandten Mathematik. Außerdem sind sie interessant, weil sie eine Wechselwirkung von Hilbertraummethoden, Sobolevräumen und Ad-hoc-Argumenten, die von der relevanten Klasse von Differenzialgleichungen abhängen, erfordern. Viele dieser Themen werden in den kommenden Jahren im Skript zum Kurs 1380 Partielle Differenzialgleichungen Eingang finden. Eine letzte, wichtige Anmerkung zum Schluss: Wie Sie schon im Modulhandbuch gelesen haben, ist dieses Skript in englischer Sprache verfasst. Es gibt verschiedene Gründe für unsere Entscheidung, einen Kurs an einer deutschen Universität von einem Lehrtext auf Englisch begleiten zu lassen: Zum einen gehört seit vielen Jahrzehnten die Fähigkeit, mathematische Texte in englischer Sprache zu verstehen, zu den Kernexpertisen jeder Mathematikerin und jedes Mathematikers; zum anderen wird die Erfahrung mit mathematischem Englisch ihre erste Phase bei einer Abschlussarbeit deutlich vereinfachen, da seit längerer Zeit praktisch alle Forschungsartikel, die Sie dafür lesen können müssen, eben in englischer Sprache verfasst sind. Sie sollten auch nicht vergessen, dass bereits jetzt die meisten Seminarreferate auf Fachliteratur in englischer Sprache beruhen. Wir haben versucht, Ihren Einstieg ins mathematische Englisch möglichst zu vereinfachen: Am Anfang jedes Kapitels finden sie eine kurze Zusammenfassung der relevanten Resultate und Lernziele auf Deutsch; darüber hinaus wird allen (englischen) Einträgen im Glossar eine deutsche Übersetzung beigefügt. Selbstverständlich werden Klausur und mündliche Prüfungen zu diesem Kurs auf Deutsch formuliert beziehungsweise abgenommen. In diesem Sinne: have fun! DR. JOACHIM KERNER DR. HAFIDA LAASRI PROF. DR. DELIO MUGNOLO Wir bedanken uns ganz herzlich bei Dr. Waed Dada für ihre wichtige Mitarbeit bei der Fertigstellung des Skriptes.
6 iv
7 Contents Studierhinweise zu Kurseinheit Metric spaces Definition Exercises Topological concepts Exercises Sequences in metric spaces Convergence Cauchy sequences and complete metric spaces Subsequences and cluster points Exercises Continuous functions Exercises Extension by density of continuous functions Separable metric spaces Exercises The Banach fixed-point theorem Exercises Compact metric spaces Heine-Borel property The Bolzano-Weierstrass characterization of compact metric spaces Continuous functions in compact metric space Exercises Notes and suggestions for further learning Solutions v
8 vi CONTENTS
9 Studierhinweise zu Kurseinheit 1 In dieser Kurseinheit befassen wir uns mit einem zentralen Aspekt der Funktionalanalysis, den metrischen Räumen. Das sind Mengen, auf denen ein gewissen Axiomen genügender Abstandsbegriff gegeben ist. Wir werden topologische Grundbegriffe wie den der offenen Menge, abgeschlossenen Menge, Umgebung eines Punktes einführen, die dann für die weiteren Kurseinheiten grundlegend sind. Einige Definitionen und Begriffe sind Ihnen bereits aus der reellen Analysis bekannt. In dieser Kurseinheit werden diese aber entsprechend verallgemeinert. Ferner werden vollständige und kompakte metrische Räumen ausführlich diskutiert. Wir setzen etwas Vertrautheit mit den Begriffen Grenzwert einer Folge, Stetigkeit einer Funktion sowie Isomorphismus, Kontraktion u.a. voraus. Besonders zentrale Aussagen dieser Kurseinheit sind der Satz von Bolzano-Weierstrass und der Banachsche Fixpunktsatz. Lernziele: Abschnitt 1.1: Definition und Beispiele (Definition and examples) Nach der Lektüre dieses Paragraphen sollten Sie in der Lage sein, den Begriff der Metrik und des metrischen Raumes definieren und an Beispielen erläutern zu können. Wichtig sind vor allem Beispiele, die über den R n hinausgehen. Abschnitte 1.2: Topologische Begriffe (Topological concepts) In diesem Abschnitt wird die topologische Struktur metrischer Räume diskutiert. Nach der Bearbeitung dieses Paragraphen sollten Sie die Begriffe: offene (abgeschlossener) Kugel (Menge), Umgebung, Abschluss einer Menge verstanden haben und erklären können. wissen, dass eine Metrik eine topologische Struktur induziert. wissen, wie das System der offenen Mengen mit dem System der abgeschlossenen Mengen bzw. dem des Umgebungssystems zusammenhängt. Abschnitte 1.3: Folgen in metrischen Rämen (Sequences in metric spaces) In diesem Abschnitt werden wir lernen, dass eine Metrik nicht nur eine topologische Struktur, sondern auch eine uniforme Struktur induziert. Nach Durcharbeiten dieses Abschnitts sollten Sie mit den Begriffen: konvergente Folge, Teilfolge, Cauchy-Folge, vollständiger metrischer Raum umgehen und an Beispielen erläutern können. 1
10 wissen, wie abgeschlossene Mengen mittels der Konvergenz von Folgen charakterisiert werden. die Beziehung zwischen konvergente Folgen, konvergente Teilfolgen und Cauchy-Folgen aufzeigen können; in der Lage sein, ein Beispiel einer Cauchy-Folge, die nicht konvergiert, angeben zu können. wissen, wann ein Teilraum eines vollständigen metrischen Raumes selbst vollständig ist. in der Lage sein nachzuweisen, dass verschiedene Metriken auf einer Menge zwar dieselbe Topologie, aber unterschiedliche uniforme Strukturen erzeugen können. Abschnitte 1.4: Stetige Abbildungen (Continuous functions) In diesem Abschnitt werden wir uns mit verschiedenen Begiffen der Stetigkeit einer Abbildung befassen. Nach dem Durcharbeiten dieses Abschnitts sollten Sie in der Lage sein, die Definition der Stetigkeit, der gleichmäßigen Stetigkeit und der Lipschitz- Stetigkeit einer Abbildung anzugeben. Desweiteren sollten Sie Kriterien für Stetigkeit angeben und diese anwenden können. wissen, dass Stetigkeit und Folgenstetigkeit einer Abbildung in metrischen Räumen äquivalente Konzepte sind. Abschnitt 1.5: Fortsetzung von stetigen Funktionen (Extension by density of continuous functions) Nach dem Durcharbeiten dieses Abschnittes sollte Ihnen klar geworden sein, dass man sich gleichmässig stetige Abbildungen, die auf einem dichten Teilraum definiert sind, eindeutig auf den ganzen Raum fortsetzen lassen. Abschnitt 1.6: Separable metrische Räume (Separable metric spaces) Nach dem Durcharbeiten dieses Abschnitts sollten Sie wissen, was man unter einem separablen metrischen Raum versteht und Kriterien für Separabilität formulieren können. Abschnitt 1.7: Kontraktionsprinzip (Banach fixed-point theorem) In diesem Abschnitt werden Existenz- und Eindeutigkeitssätze von Fixpunkten einer Abbildung behandelt. Nach der Lektüre dieses Abschnitts sollten Sie in der Lage sein, den Banachschen Fixpunktsätz formulieren, beweisen und anwenden zu können. Abschnitt 1.8: Kompakte metrische Räume (Compact metric spaces) Ein weiteres zentrales Konzept der Funktionalanalysis, welches wir in diesem letzten Abschnitt betrachten, ist das der Kompaktheit. Nachdem Sie diesen Abschnitt durchgearbeitet haben, sollten Sie wissen, was man unter einem kompakten Raum und was unter einer kompakten bzw. relativkompakten Teilmenge versteht. die Eigenschaften kompakter Räume (Teilmengen) aufzählen und diese nachweisen können. Darüber hinaus sollten Sie nachweisen können, 2
11 dass in einem metrischen Raum kompakte Mengen abgeschlossen und beschränkt sind und die Umkehrung (im Gegensatz zum R n ) im Allgemeinen nicht gilt. dass stetige Funktionen auf kompakten Mengen gleichmäßig stetig sind und dass, im reellwertigegen Fall, das Supremum sowie das Infimum angenommen werden. 3
12 4 CONTENTS
13 Chapter 1 Metric spaces In this chapter we will introduce the important concept of metric spaces and give several examples thereof. If functional analysis is a hybrid of linear algebra and analysis, then metric spaces may look out of place: no sums or further operations are in general defined, only distances can be measured. This is enough to discuss limiting processes and more general topological issues, but not to allow for composition of vectors or to introduce the notion of linearity. Nevertheless, we will present in this chapter a manifold of objects and also prove several results that will play an important role in all later chapters. This introduction will also allow us to follow the earliest historical developments of functional analysis and to meet some of its pioneers, like Maurice Fréchet and Stefan Banach. Introduced in 1906 in Paris by Maurice René Fréchet, metric spaces are sets on which a (meaningful) distance can be defined. The most well-known example of a metric space is the Euclidean space R n where by the Pythagorean theorem the distance d 2 (x, y) of two points x, y R n can be calculated via ( n d 2 (x, y) = x j y j 2) 1 2. j=1 This particular distance is meaningful since it is positive and equals zero only if and only if the two points x and y are identical. Furthermore, it fulfills some minimizing property in the sense that d 2 (x, y) is the least distance one has to walk to get from x to y. In other words, if z R n is any additional point one has d 2 (x, y) d 2 (x, z) + d 2 (z, y). Also, as you have already learned in earlier courses, concepts like convergence and continuity of functions f : R n R can be defined in terms of the metric d 2. For example, a function f : R R is continuous at x 0 R if for any ε > 0 there exists a δ > 0 such that, d 2 (x, x 0 ) < δ implies d 2 (f(x), f(x 0 )) < ε for all x X. The crucial insight in defining a distance on more general sets is then to realize that the explicit form of the distance function d is not that important. As we will see, only a few requirements are necessary to determine a good metric d which then allows to transfer important concepts such as the two mentioned above from Euclidean to more general spaces. In addition to that, we know that the topology of Euclidean space is also determined by the metric d 2. Namely, a subset A R n is called open whenever for each point x A there exists r > 0 such that B R n(x, r) := {y R n : d 2 (x, y) < r} 5
14 6 CHAPTER 1. METRIC SPACES is contained in A. However, this construction can be made for all metric spaces and we hence see that a metric d on any set X also defines a topology in a very natural way. 1.1 Definition In the following K will denote either the real field R or the complex field C and X shall always be a non-empty set. Definition A metric or distance d on X is a mapping d : X X R (x, y) d(x, y) such that for all x, y, z in X, the following conditions are satisfied: (M1) d(x, y) = 0 if and only if x = y, (M2) d(x, y) = d(y, x), (M3) d(x, z) d(x, y) + d(y, z). A pair (X, d) of a set X and a metric d on X is called a metric space. We call d(x, y) the distance between x and y (with respect to the metric d). One usually refers to properties (M1), (M2), (M3) by saying that a distance mapping is positive definite, symmetric and satisfies the triangle inequality, respectively. Remark If (X, d) is a metric space, then d is necessarily a non-negative mapping, i.e., d(x, y) 0 for all x, y X. This is an easy consequence of the axioms (M1), (M2), (M3). In fact, for all x, y X we have Furthermore, the inequalities 0 = d(x, x) d(x, y) + d(y, x) = 2d(x, y). d(x, z) d(y, z) d(x, y) for all x, y, z X, (1.1) and d(x, y) d(u, v) d(x, u) + d(y, v) for all x, y, u, v X (1.2) hold. Let us emphasize that different metrics on the same set X can exist, cf. Example However, sometimes there is no confusion about what metric is considered and one simply writes X referring to a metric space without specifying d (the most prominent example here is Euclidean space R n ). We now want to give several standard examples of metric spaces some of which will appear repeatedly in later chapters.
15 1.1. DEFINITION 7 Example ) The Euclidean metric d2 : Rn Rn R on Rn is given by!1/2 n X d2 (x, y) := xi yi 2 i=1 with x = (x1, x2,..., xn ) and y = (y1, y2,..., yn ) in Rn. For n = 1, the Euclidean metric reduces to the usual absolute-value distance d(x, y) = x y on the real line. Also the mappings d1 (x, y) := n X xi yi and i=1 d (x, y) := max xi yi 1 i n define metrics on Rn. They are called the Manhattan metric and the maximum metric on Rn, respectively. Can you imagine why d1 is called so? If not, try to compute the distance between, say, (0, 0) and (12, 3) with respect to d1, and then take a look at a map of Manhattan (or downtown Mannheim, for that matters) and then think of how distant two junctions are. More generally,!1/p n X dp (x, y) := xi yi p i=1 defines a metric on Rn for all p > 0. Figure 1.1: A map of Manhattan in ) On Rn the mapping ( d2 (x, y) if x = κy for some κ R d(x, y) := d2 (x, 0) + d2 (y, 0) otherwise (1.3)
16 8 CHAPTER 1. METRIC SPACES Figure 1.2: A finite graph with 10 vertices and 15 edges Figure 1.3: An infinite graph defines a metric on R n where d 2 is the Euclidean metric. The metric d is called SNCF metric because in the French railway system (managed by France s national railway company SNCF), the fastest connection between two cities x and y (e.g., from Bordeaux to Lyon) usually goes through the origin (Paris of course) unless y = κx, i.e., they already lie on the same TGV line (e.g., Lyon and Marseille). 3) A rather trivial example of a metric on an arbitrary non-empty set X is given by the discrete metric defined by { 1 if x y d(x, y) := x, y X. (1.4) 0 if x = y In particular, any non-empty set X is metrizable, i.e, there exists a mapping d : X X R that turns X into a metric space (X, d). 4) Let us consider the set X := Z of integer numbers and the mapping d Z defined by d Z (n, m) := n m for all n, m Z. Then (Z, d Z ) is a metric space. 5) A (simple, undirected) graph is a pair G = (V, E) composed of a finite or countable set V, whose elements are called vertices, and another set E {{v, w} : v, w V, v w}, whose elements are called edges): if e = {v, w} is an element of E, then the vertices v, w are said to be adjacent (by means of e). A path of length m from v to w is a sequence v 0, e 1, v 1, e 2,, e m, v m of vertices v := v 0, v 1,, v m =: w V and edges e 1, e 2,, e m E such that v i and v i+1 are adjacent by means of e i+1. The graph is called connected if any two vertices are joined by at least one path. If G is connected, then the function d G : V V N defined by d G (v, w) := inf{length of P : P is a path from v to w} turns V into a metric space (V, d G ); d G is called the shortest-path metric. We emphasize that this construction strictly generalizes two already considered notions. Indeed, if (X, d) is a discrete metric space, i.e., d is the discrete metric, then we can turn it into a graph with vertex set V := X and such that any two vertices are adjacent, so that d G (v, w) = 1 if and only if v w. Then d G = d and thus (X, d) coincides with (V, d G ).
17 1.1. DEFINITION 9 Furthermore, we can look at Z as a graph, letting V := Z and regarding two numbers/vertices n, m as adjacent if n m = 1, i.e., if n, m are subsequent numbers. Then, the metric spaces (Z, d Z ) and (V, d G ) agree. 6) It is known that a matrix M M n,m (R) has rank 0 if and only if M = 0. Using this, one sees that the mapping defines a metric on M n,m (R). d(m, N) := rank (M N), M, N M n,m (R), 7) Let C(K, K), or simply C(K), denote the set of continuous function f : K K where K R is compact. For example we could take K to be the closed bounded interval [a, b]. Then both (f, g) f(x) g(x) dx and (f, g) sup f(x) g(x). x K are metrics on C(K). 8) Let (X, d) be a metric space. Then K d 1 (x, y) := d(x, y) 1 + d(x, y) and d 2 (x, y) := min{d(x, y), 1} are also metrics on X. More generally, if d is a metric then ϕ d is also a metric provided that ϕ : R + R + is a non-decreasing mapping such that ϕ(0) = 0 and ϕ(s) > 0 for s > 0. ϕ(s + r) ϕ(s) + ϕ(r), 9) Let (X, d) be a metric space and let A be a subset of X. The restriction d A of d to A A, that is d A (x, y) := d(x, y), x, y A, defines a metric on A, called induced metric. Whenever a metric space (X, d) is given and we wish to generate a metric space structure on a subset A X, we will always canonically endow A with the relative metric d A, unless otherwise stated Exercises E Show that the inequalities (1.1) and (1.2) hold. E Let X be the extended real line R {± } and set d X (x, y) := arctan x arctan y, x, y X, where arctan(± ) := lim x ± arctan(x) = ±π 2. Show that (X, d X ) is a metric space.
18 10 CHAPTER 1. METRIC SPACES E Let l (N) := {(x n ) n N R : sup x n < } n N be the space of bounded real sequences. For check if (l, d ) is a metric space. E Consider the set d (x, y) := sup x n y n, n N c 00 (N) := {(x n ) n N l (N) : n 0 such that x n = 0 n n 0 } of all eventually vanishing sequences of real numbers, which is clearly a subspace of l (N). Prove that d H (x, y) := #{n N x n y n } defines a metric on c 00 (N) but not on l (N). (This function d H is referred to as Hamming distance, after the early computer scientist Richard Wesley Hamming: if x, y are two pieces of binary code, d H (x, y) says how close they are by measuring at how many entries they differ, possibly up to equalizing their lengths by extending the shorter one by 0.) E Check if the following maps define a metric on R : i) d 1 (x, y) := x 2 y 2, ii) d 2 (x, y) := x 3 y 3, iii) d 3 (x, y) := e 1 x y. E Show that the space C(K) of continuous functions on a compact interval K with d from Example is, in fact, a metric space. (The same assertion also holds for C(K) whenever K is merely a compact metric space, a notion that generalizes compact intervals which we will meet later on.) 1.2 Topological concepts When you first met continuous functions in the courses 1141 and 1144, they were (more or less explicitly) defined by means of an ε δ criterion, but an equivalent definition of continuity is based on the notion of open set: A function f : R n R m is continuous if and only if the pre-image f 1 (O) of each open set O R m is an open subset of R n. This has a major advantage: it allows for an abstract introduction of the notion of continuity independently of the specific structure of the Euclidean spaces. This sounds good, since the extension of analytical notions and results to sets as general as possible is among the leading ideas of functional analysis. Because open sets were defined by means of neighborhoods, everything boils down to replacing the classical Euclidean distance by more general mappings: this has been done in the previous section. For a metric space, we will see that open sets can be constructed from a particular important subclass of open sets, the so called open balls. More precisely, the set B(x, r) = {y X : d(x, y) < r} is called the open ball of radius r and center x. For example, the open ball in R of radius r centered at x is the open interval (x r, x + r). Note that, in the mathematical literature it is also customary to write B r (x) instead of B(x, r).
19 1.2. TOPOLOGICAL CONCEPTS 11 Definition A set U X is called neighborhood of a point x X if there exists r > 0 such that B(x, r) U. The following theorem shows that each metric space is a Hausdorff space, i.e., a space in which any two distinct elements admit a pair of disjoint neighborhoods. Theorem Let (X, d) be a metric space. Then for every pair of distinct points x, y X, there exist neighborhoods U and V of x and y, respectively, such that U V =. Proof. Let x, y be two distinct points of X and let r := d(x, y) > 0. Define U := B(x, r 2 ) and V := B(y, r 2 ). Thus U and V are disjoint: if there existed a z U V then, using the triangle inequality, r = d(x, y) d(x, z) + d(z, y) < r 2 + r 2 = r. This is absurd, hence U V =. Definition Let (X, d) be a metric space. A set O X is called open if for all x O there exists r > 0 such that B(x, r) O. It is always important to specify the relevant metric space! The set [0, 1) is e.g. an open set in the metric space [0, 1] (with the induced metric of R), since [0, 1) = ( 1, 1) [0, 1]. However, [0, 1) is not open in R. Remark Clearly, in a metric space a set is open if and only if it is a neighborhood of each of its elements. A first example of an open set is given by the open ball B(x 0, r) for some x 0 X and r > 0. In fact, consider y 0 B(x 0, r) and choose r > 0 such that 0 < r < r d(x 0, y 0 ). For every y B(y 0, r ) d(y, x 0 ) d(y, y 0 ) + d(y 0, x ) r + d(y 0, x 0 ) < r. This implies y B(x 0, r) and hence B(y 0, r ) B(x 0, r). As a consequence, B(x 0, r) is open. Theorem Let (X, d) be a metric space. Then the following assertions hold. 1) and X are open. 2) If O 1 X and O 2 X are two open sets, then O 1 O 2 is open. 3) If (O i ) i I is an arbitrary family of open sets of X, then the union i I O i is open. Proof. 1) is clear. 2) Let x O 1 O 2. Then there exists r 1 > 0 and r 2 > 0 such that B(x, r 1 ) O 1 and B(x, r 2 ) O 2. For r := min{r 1, r 2 } > 0 we have B(x, r) O 1 O 2. This proves that O 1 O 2 is open. The assertion follows from (a) if O 1 and O 2 are disjoint. 3) Let x i I O i. Then there exists j I with x O j. Since O j is open there exists r j > 0 such that B(x, r j ) O j i I O i. Remark It follows from assertion 2) in Theorem that finite intersections of open sets are also open. However, this is not true anymore for an infinite number of intersections. For example, in R with the absolute-value metric, the intervals ( 1 n, n ) with n > 0 are open but the intersection ( 1 n, ) = [0, 1] n is not open. n=1
20 12 CHAPTER 1. METRIC SPACES Definition A set F X is called closed if its complement F := X \ F is open. The closed ball with center x and radius r > 0 is the set B(x, r) := {y X : d(x, y) r}. Each closed ball is a closed set in X, since its complement is open. Indeed, let x 0 B(x, r) and set r 1 := d(x, x 0 ) r > 0. Then for each y B(x 0, r 1 ) we have by the triangle inequality and therefore d(x, x 0 ) d(x, y) + d(y, x 0 ) d(x, y) d(x, x 0 ) d(x 0, y) > r 1 + r r 1 = r. This implies that B(x 0, r 1 ) B(x, r) and we conclude that B(x 0, r) is in fact open. Starting from Definition we can immediately establish an analog of Theorem for closed sets. Theorem Let (X, d) be a metric space. Then the following assertions hold. 1) and X are closed sets. 2) If F 1 X and F 2 X are two closed sets, then F 1 F 2 is closed. 3) If (F i ) i I is an arbitrary family of closed sets of X, then the intersection i I F i is closed. Note that and X are example of sets that are both open and closed. Furthermore, if a set is not open, this, in general, does not mean that it is closed. For instance, the half-open interval [0, 1) is neither open nor closed in R. Definition Let (X, d) be a metric space and let A X. 1) The set Å := {x X : r > 0 such that B(x, r) A} is called the interior of A. The elements of Å are called interior points of A. 2) The set A := {x X : r > 0 B(x, r) A } is called the closure of A. 3) The set A := A A is called the boundary of A. 4) A subset A X is said to be dense in X (or simply dense, if no confusion is possible) if A = X. Proposition Let (X, d) be a metric space X and let A X. Then the following assertions hold. 1) The interior Å of a set A is the largest open set which is contained in A. 2) The closure A of a set A X is the smallest closed set which contains A. Proof. 1) Let O X be an open set with A O. Following Definition we can find, for any x O, a r > 0 such that B(x, r) O. Hence x A and therefore O A. 2) The assertion follows from 1) by passing to the complement. Proposition Let (X, d) be a metric space and let A X. Then the following assertions hold.
21 1.2. TOPOLOGICAL CONCEPTS 13 1) A = (A ) and (A ) = A. 2) A = A and Å = Å. 3) A is open if and only if A = Å. 4) A is closed if and only if A = A. 5) A = (A ). 6) Let additionally A X. If A is dense, it is not closed. If A is closed, it is not dense. Example On a metric space (X, d) every singleton {x}, x X, is closed, see Exercise Example A topology is called discrete if every subset is open, or equivalently closed (since its complement is open). If a non-empty set X is endowed with the discrete metric introduced in Example 1.1.3, then every subset of X is both open and closed. The same holds in general for any metric space in which neighborhoods of a point x cannot become arbitrarily small without reducing to the singleton {x}: this is for instance also the case for the metric space (V, d G ) where V is the set of vertices of a graph G = (V, E) and d G the shortest-path metric (see again Example 1.1.3), and more generally for all metric spaces (X, d) whose metric d can only attain finitely many values. For this reason, in the following we generally call discrete metric spaces all metric spaces (X, d) with the property that the set of all values of d is a subset of R + without cluster points. Things are however less trivial if G is turned into a weighted graph G µ = (V, E) by associating a weight µ(e) > 0 with each e E: then the length of a path between two nodes is defined as the sum of the weights of the edges that appear in the path and the distance between two nodes is modified accordingly. Hence, if inf µ(e) = 0, then (V, d G µ ) is not a discrete metric space any e E more. Remark A closed ball B(x, r) always contains the closure of the open ball B(x, r), but they do not coincide in general. For instance, let X be a set which contains more than one point equipped with the discrete metric d. For x X, B(x, 1) = {x}, B(x, 1) = X and since the set {x} is closed, {x} = {x} B(x, 1). Definition A subset A of a metric space X is called bounded if it is non-empty and there exist x 0 X and 0 R < such that d(x 0, y) R for all y A. (1.5) We readily see that A X is bounded if and only if there exists r > 0 such that A B(x 0, r). This definition is independent of x 0 since, due to the triangle inequality, one has B(x 0, r) B(x, r ) for all x X where r = r + d(x 0, x). The diameter of a set A is defined by diam(a) := sup{d(x, y) x, y A}. Then A is bounded if and only if diam(a) <.
22 14 CHAPTER 1. METRIC SPACES Remark The notion of boundedness depends on the metric which is considered. For any given metric space (X, d), every subset A X is bounded with respect to the new metric (x, y) d(x, y) 1 + d(x, y). Definition Let (X, d) be a metric space. For two subsets A, B X the distance from A to B is the number d(a, B) := inf inf d(x, y). x A y B If A = {x} then d(x, B) := d({x}, B) is the distance from x to the set B. Remark ) Let A be a non-empty subset of a metric space X. We have seen in Section 1.1 that (A, d A ) is a metric space, where d A is the induced metric. Let B(x, ε) be an open ball in X and let B A (x, ε) the open ball in A with radius ε > 0 and center x X, i.e., B A (x, ε) = {y A : d(x, y) < ε}, we see that B A (x, ε) = B(x, ε) A. A similar relation holds for closed and open sets in A. A subset O A is open in A (i.e., with respect to d A ) if and only if O = A U where U is a open set in X. Similarly, a subset B A is closed in A if and only if B = A F where F is a closed set in X. 2) Observe that if (X, d) is a metric space, then X may or may not be bounded in its own right: think of the intervals (0, 1) and (0, ) with respect to the canonical distance. If the metric space is bounded, then so are all its subsets; more generally, subsets of bounded sets are clearly bounded. 3) The closure of a bounded set is bounded (try to prove it!) and hence, in particular, bounded sets always have bounded boundary the converse is obviously wrong for any unbounded metric space: think of the example of the unbounded set R n \ B(x, r), for any given x R n and r > 0, whose boundary is the sphere S(0, 1) := {y R n : d(x, y) = r}. 4) Let A, B be two subsets of a metric space (X, d). If A B, then d(a, B) = 0. The converse is in general not true. Take for instance X = R with the absolute-value metric and the sets A = (0, 1) and B = (1, 2) Exercises E Let X be a metric space and let x X. Prove that the set {x} is closed. E Let (X, d X ) be a metric space. a) For d X being the discrete metric, show that X is the only dense set. b) Show that A X is dense if and only if A B r for all open balls B r (x), x X. E Let (X, d) be a metric space and let A be a non-empty subset of it. Prove that: i) If x A then d(x, A) = 0.
23 1.3. SEQUENCES IN METRIC SPACES 15 ii) If d(x, A) = 0 then x A. Conclude that d(x, A) = 0 if and only if x A. E Prove that the union of two bounded subsets A and B of a metric space (X, d) is bounded. E Let (X, d) be a metric space. Let A, B be two non-empty subsets of X. Show that i) diam(a) = diam(a). ii) Assume that A B. Then d(a, B) = 0. iii) diam(a B) diam(a) + d(a, B) + diam(b). E A metric d on a vector space X is called an ultrametric if for all x, y and z X d(x, z) max{d(x, y), d(y, z)}, and we say that (X, d) is an ultrametric space. The discrete metric is for example an ultrametric (but general discrete metric spaces are not necessarily ultrametric spaces!). Let (X, d) be a ultrametric space. 1. Show that for each x, y, z X with d(x, y) d(y, z) we have d(x, z) = max{d(x, y), d(y, z)}. 2. Show that each open ball B(x, r) is closed and open. Moreover, B(y, r) = B(x, r) for all y B(x, r). 3. Show that each closed ball B(x, r) is closed and open and moreover, B(y, r) = B(x, r) for all y B(x, r). 1.3 Sequences in metric spaces A sequence in a set X is a mapping N n x n X, usually denoted by (x n ) n N. As soon as the set X carries suitable structures of topological nature, we may inquire convergence of sequences Convergence Definition We say that a sequence (x n ) n N X converges to some element x X and we write lim x n = x, x n x as n, or simply x n x if for every ε > 0 there exists n n 0 N such that for every n n 0 one has d(x n, x) ε. If x n x then we call x the limit of (x n ) n N. Observe that this agrees with the classical definition of sequence convergence in normed space (and, in particular, in R) which you have learned in the course Remark Let (X, d) be a metric space. 1) A sequence (x n ) n N X converges to some x X if and only if the sequence of real numbers (d(x n, x)) n N converges to 0 as n. Equivalently, x n x if and only if for every neighborhood U of x there exists n 0 N such that for every n n 0 one has x n U.
24 16 CHAPTER 1. METRIC SPACES 2) Each convergent sequence on X has a unique limit. This is, if (x n ) n N X is a sequence and x, y X such that x n x and x n y as n, then x = y. This is due to the fact that each metric space is a Hausdorff space. Example Consider the metric space (C([0, 1]), d ), see Example Then a sequence (f n ) n N C[0, 1] converges to f C[0, 1] if and only if the sequence (f n ) n N converges uniformly to f in the sense that you have learned in the course Example Let X be a non-empty set and d be the discrete metric upon it. If a sequence (x n ) n N X converges to x with respect to d, then there exists n 0 N such that for all n n 0 on has d(x n, x) 1 2. Since d is the discrete metric this means that d(x n, x) = 0 and thus x n = x for all n n 0 : we have thus observed that every convergent sequence with respect to the discrete metric is eventually constant. This result clearly holds in the context of general discrete metric spaces. Conversely, every eventually constant function is convergent with respect to any metric. Since every metric defines a topology in a natural way, metric spaces form a subclass of the topological spaces. In general topological spaces it might be difficult to characterize the closure or the boundary of a given subset A X. For metric spaces, however, it is always possible to characterize closed sets of X in terms of convergent sequences as follows. Theorem Let A be a subset of a metric space X. Then the following assertions are equivalent. a) x 0 A. b) There exists a sequence (x n ) n N X such that x n x 0. Proof. In order to show that a) b), let x 0 A. Then for every n N one has B(x 0, 1 n ) A. Thus for every n N we can find x n A such that d(x 0, x n ) 1 n. This implies that the sequence x n x 0. Conversely, assume that b) holds and let (x n ) n N X which converges to some x 0 X. Let ε > 0. From the convergence there exists n 0 N such that d(x n, x 0 ) ε for all n n 0. This implies that B(x 0, 1 n ) A. Because ε is arbitrary, we conclude that x 0 A. We thus deduce the following characterizations. Corollary A subset A of a metric space X is closed if and only if for every sequence (x n ) n N A converging to some x 0 X, one has x A. Corollary Let A be a subset of a metric space X. Then the following assertions are equivalent. a) A is dense in X. b) For each x 0 X there exists (x n ) n N A such that x n x 0. c) A O for any open subset O X Cauchy sequences and complete metric spaces Let (X, d) be a metric space. A sequence (x n ) n N X is a Cauchy sequence if for all ε > 0 there exists n 0 N such that d(x n, x m ) ε for all n, m n 0.
25 1.3. SEQUENCES IN METRIC SPACES 17 By the triangle inequality, each convergent sequence in a metric space X is a Cauchy sequence. The converse is however not true. For instance, consider (0, 1) with the absolute-value metric and the sequence x n := 1 1 n (0, 1). Since (x n) n N converges in R to 1, (x n ) n N is a Cauchy sequence (in R and then) in (0, 1) but (x n ) n N has no limit in (0, 1). Definition We say that a metric space (X, d) is complete if every Cauchy sequence is convergent. For complete metric spaces, like the Euclidean spaces R n, the definition of Cauchy sequences is thus a convergence criterion. This criterion does not involve the limit of the sequence, hence it gives us a tool to prove that a sequence is convergent without knowing its limit. Example ) (R n, d 2 ) and (C[0, 1], d ) are complete metric spaces 2) Every set endowed with the discrete metric is complete. In fact, let (x n ) n N X be a Cauchy sequence. Then there exists n 0 N such that for all n, m n 0 on has d(x n, x m ) 1 2 and therefore x n = x m, thus (x n ) n N is eventually constant and hence convergent. The same proof shows that also general discrete metric spaces are complete. Theorem Let (X, d) be a metric space. Then the following assertions hold. 1) If (X, d) is complete, then also every closed subset F X is complete with respect to the induced metric. 2) If A X is complete, then A is closed. Proof. 1) Let (x n ) n N F be a Cauchy sequence. Then (x n ) n N converges to some element x X and since F is closed, x F. Thus F is complete. 2) Let (x n ) n N A converging to x 0 X. Thus is a Cauchy sequence in A and then in X. Since A is complete, (x n ) n N converges to a an element y belonging to A. By uniqueness of the limit, x 0 = y and thus x 0 F. By Corollary this implies that F is closed. Let ([a n, b n ]) n N be a sequence of closed intervals such that the sequences (a n ) n N and (b n ) n N are adjacent, i.e., (a n ) n N is increasing and (b n ) n N decreasing with (b n a n ) 0. Then it is known that n N [a n, b n ] = {l} with l := lim a n = lim b n. For a complete metric n n space (X, d) a similar result holds. Proposition Let (F n ) n N be a decreasing sequence of closed subset of a complete metric space (X, d) such that diam(f n ) 0 as n. Then n N F n = {x} for some x X. Proof. Since diam(f n ) 0 the intersection F := n N F n contains at most one element. Regarding existence, we choose x n F n for each n N. Since d(x n, x m ) diam(f N ) for all n, m N the sequence (x n ) n N is a Cauchy sequence and thus converges to some element x X. For every k N, we have x n F n F k for n k. Since F k are closed, the limit x of (x n ) n N belongs to F k. Thus F is not empty Subsequences and cluster points As introduced above, a sequence (x n ) n N on a metric space (X, d) is a mapping n x n from N to X. A subsequence of (x n ) n N is a mapping k x nk from N to X where k n k : N N is strictly increasing. For example, (x n+1 ) n N is a subsequence of (x n ) n N because n n + 1 is strictly increasing from N into N.
26 18 CHAPTER 1. METRIC SPACES Remark Bijectivity of k n k is a necessary but not sufficient condition for (x nk ) k N to be a subsequence of (x n ) n N : e.g., is not a subsequence of (x n ) n N. x 1, x 4, x 2, x 5, x 6, x 7,... Proposition If a sequence (x n ) n N X converges to some x X, then every subsequence converges to the same limit x. Proof. Let ε > 0. Since (x n ) n N converges to x, there exists n 0 N such that d(x, x n ) ε if n n 0. Taking k 0 N such that n k0 n 0 we obtain that d(x, x nk ) ε. Note that the converse of the statement of Proposition is also true since (x n ) n N is always a subsequence of itself. Definition We say that x X is a cluster point or accumulation point of the sequence (x n ) n N if there exists a subsequence (x nk ) k N converging to x. For example the real sequence { 1 x n := n if n = 2k, k N, 1 otherwise, has two cluster points. Indeed, the subsequences (x 2n ) n N and (x 2n+1 ) n N converges to 0 and 1 respectively. Clearly, if x is the limit of a convergent sequence (x n ) n N, then x is the unique cluster point of (x n ) n N. Proposition Let (x n ) n N be a sequence in a metric space (X, d). Then the following assertions are equivalent. a) x is a cluster point of (x n ) n N. b) For all ε > 0 and n N there exists m > n such that d(x m, x) ε. c) For each p N, x {x n, n p}. Proof. The implication a) b) is clear. Indeed, let ε > 0 and n N be fixed. Since there exists k(ε) N such that d(x nk, x) ε for each k k(ε), it suffices to take m = n k for k (ε) with n k n. The implication b) c) is left as an exercise. Assume now that c) holds. For every k, n N there exists n(k) N such that d(x, x n(k) ) 1/k. We can then define a subsequence (x nk ) k N such that x nk is the smallest integer with x nk 1 < x nk and d(x, x nk ) 1/k. This subsequence converges to x, which shows that a) holds. Remark Let (X, d) be a metric space. Then x is a cluster point of a sequence (x n ) n N X if and only if every open ball B(x, ε) contains x n for infinitely many n N. In the previous section we have seen that, in general metric spaces, not every Cauchy sequence converges. It turns out that convergent Cauchy sequences can indeed be characterized in terms of cluster points.
27 1.4. CONTINUOUS FUNCTIONS 19 Proposition If a Cauchy sequence (x n ) n N has a cluster point x, then (x n ) n N converges and x is its limit. Proof. Let ε > 0. Since x is a cluster point there exists k 0 N such that d(x, x nk ) ε/2 for k k 0. Since (x n ) n N is a Cauchy sequence there exists n 0 N such that d(x n, x m ) ε/2 for n, m n 0. By taking n 1 := max(n 0, n k0 ) and k k 0 such that n k n 0 we obtain for all m n 1. Thus x n x. d(x, x m ) d(x, x nk ) + d(x nk, x m ) ε/2 + ε/2 = ε Exercises E Show that each convergent sequence on a metric space X has a unique limit. E Let X be a metric space and let x X. Using Corollary show that the set {x} is closed. E Let (X, d) be a metric space and let (x n ) n N be a sequence of elements of X. Then (x n ) is a Cauchy sequence if and only if lim n diam (A n) = 0 where A n := {x n, x n+1,...}. E Let (X, d) be a metric space. Show that X consists of only one element if and only if every bounded sequence is convergent. E Consider the vector space l 1 (N) := {(x n ) n N : x n < } of all absolutely convergent series of real numbers and the vector space c 00 introduced in Exercise Clearly c 00 (N) l 1 (N) and we can define on both l 1 (N) l 1 (N) and c 00 (N) c 00 (N) the mapping d(x, y) := x n y n. Show that 1. (l 1 (N), d) is a complete metric space. n=1 2. c 00 (N) is dense in l 1 (N), i.e., c 00 = l 1 (N). n=0 1.4 Continuous functions The purpose of this paragraph is to introduce a general concept of continuous functions on metric spaces. For this let (X, d X ) and (Y, d Y ) be two metric spaces. Definition A function f : X Y is said to be continuous at x 0 X if for all ε > 0 there exists δ = δ(x 0, ε) such that d X (x 0, x) δ d Y (f(x 0 ), f(y)) ε. The function f is continuous on X if it is continuous at every point x X.
Übungsblatt 6. Analysis 1, HS14
 Übungsblatt 6 Analysis, HS4 Ausgabe Donnerstag, 6. Oktober. Abgabe Donnerstag, 23. Oktober. Bitte Lösungen bis spätestens 7 Uhr in den Briefkasten des jeweiligen Übungsleiters am J- oder K-Geschoss von
Übungsblatt 6 Analysis, HS4 Ausgabe Donnerstag, 6. Oktober. Abgabe Donnerstag, 23. Oktober. Bitte Lösungen bis spätestens 7 Uhr in den Briefkasten des jeweiligen Übungsleiters am J- oder K-Geschoss von
Unit 4. The Extension Principle. Fuzzy Logic I 123
 Unit 4 The Extension Principle Fuzzy Logic I 123 Images and Preimages of Functions Let f : X Y be a function and A be a subset of X. Then the image of A w.r.t. f is defined as follows: f(a) = {y Y there
Unit 4 The Extension Principle Fuzzy Logic I 123 Images and Preimages of Functions Let f : X Y be a function and A be a subset of X. Then the image of A w.r.t. f is defined as follows: f(a) = {y Y there
Magic Figures. We note that in the example magic square the numbers 1 9 are used. All three rows (columns) have equal sum, called the magic number.
 Magic Figures Introduction: This lesson builds on ideas from Magic Squares. Students are introduced to a wider collection of Magic Figures and consider constraints on the Magic Number associated with such
Magic Figures Introduction: This lesson builds on ideas from Magic Squares. Students are introduced to a wider collection of Magic Figures and consider constraints on the Magic Number associated with such
Übungen zur Analysis 2
 Mathematisches Institut der Universität München Prof. Dr. Franz Merkl Sommersemester 013 Blatt 3 03.04.013 Übungen zur Analysis 3.1 Abstraktion des Beweises der Minkowskiungleichung. Es seien V ein K-Vektorraum
Mathematisches Institut der Universität München Prof. Dr. Franz Merkl Sommersemester 013 Blatt 3 03.04.013 Übungen zur Analysis 3.1 Abstraktion des Beweises der Minkowskiungleichung. Es seien V ein K-Vektorraum
A Classification of Partial Boolean Clones
 A Classification of Partial Boolean Clones DIETLINDE LAU, KARSTEN SCHÖLZEL Universität Rostock, Institut für Mathematik 25th May 2010 c 2010 UNIVERSITÄT ROSTOCK MATHEMATISCH-NATURWISSENSCHAFTLICHE FAKULTÄT,
A Classification of Partial Boolean Clones DIETLINDE LAU, KARSTEN SCHÖLZEL Universität Rostock, Institut für Mathematik 25th May 2010 c 2010 UNIVERSITÄT ROSTOCK MATHEMATISCH-NATURWISSENSCHAFTLICHE FAKULTÄT,
Functional Analysis Final Test, Funktionalanalysis Endklausur,
 Spring term 2012 / Sommersemester 2012 Functional Analysis Final Test, 16.07.2012 Funktionalanalysis Endklausur, 16.07.2012 Name:/Name: Matriculation number:/matrikelnr.: Semester:/Fachsemester: Degree
Spring term 2012 / Sommersemester 2012 Functional Analysis Final Test, 16.07.2012 Funktionalanalysis Endklausur, 16.07.2012 Name:/Name: Matriculation number:/matrikelnr.: Semester:/Fachsemester: Degree
Functional Analysis Exam [MA3001]
![Functional Analysis Exam [MA3001] Functional Analysis Exam [MA3001]](/thumbs/63/48868020.jpg) Functional Analysis Exam [MA3001] Technische Universität München Prof Dr Michael Wolf 04042016, 10:30-12:00 0002001, MI HS 1, Friedrich L Bauer Hörsaal (5602EG001) Score Signature (marker) Please fill
Functional Analysis Exam [MA3001] Technische Universität München Prof Dr Michael Wolf 04042016, 10:30-12:00 0002001, MI HS 1, Friedrich L Bauer Hörsaal (5602EG001) Score Signature (marker) Please fill
Unit 1. Motivation and Basics of Classical Logic. Fuzzy Logic I 6
 Unit 1 Motivation and Basics of Classical Logic Fuzzy Logic I 6 Motivation In our everyday life, we use vague, qualitative, imprecise linguistic terms like small, hot, around two o clock Even very complex
Unit 1 Motivation and Basics of Classical Logic Fuzzy Logic I 6 Motivation In our everyday life, we use vague, qualitative, imprecise linguistic terms like small, hot, around two o clock Even very complex
Musterlösung 3. D-MATH Algebra I HS 2015 Prof. Richard Pink. Faktorielle Ringe, Grösster gemeinsamer Teiler, Ideale, Faktorringe
 D-MATH Algebra I HS 2015 Prof. Richard Pink Musterlösung 3 Faktorielle Ringe, Grösster gemeinsamer Teiler, Ideale, Faktorringe 1. Sei K ein Körper. Zeige, dass K[X 2, X 3 ] K[X] ein Integritätsbereich,
D-MATH Algebra I HS 2015 Prof. Richard Pink Musterlösung 3 Faktorielle Ringe, Grösster gemeinsamer Teiler, Ideale, Faktorringe 1. Sei K ein Körper. Zeige, dass K[X 2, X 3 ] K[X] ein Integritätsbereich,
Mitschrift zur Vorlesung Analysis III
 Mitschrift zur Vorlesung Analysis III Prof. Dr. M. Röckner Universität Bielefeld Wintersemester 1996/97 ii Inhaltsverzeichnis I Measure Theory and Integration 1 1 Introduction 3 2 Systems of sets, measures
Mitschrift zur Vorlesung Analysis III Prof. Dr. M. Röckner Universität Bielefeld Wintersemester 1996/97 ii Inhaltsverzeichnis I Measure Theory and Integration 1 1 Introduction 3 2 Systems of sets, measures
Number of Maximal Partial Clones
 Number of Maximal Partial Clones KARSTEN SCHÖLZEL Universität Rostoc, Institut für Mathemati 26th May 2010 c 2010 UNIVERSITÄT ROSTOCK MATHEMATISCH-NATURWISSENSCHAFTLICHE FAKULTÄT, INSTITUT FÜR MATHEMATIK
Number of Maximal Partial Clones KARSTEN SCHÖLZEL Universität Rostoc, Institut für Mathemati 26th May 2010 c 2010 UNIVERSITÄT ROSTOCK MATHEMATISCH-NATURWISSENSCHAFTLICHE FAKULTÄT, INSTITUT FÜR MATHEMATIK
Analysis III Serie 13 Musterlösung
 Ana-3 Hs 22 Analysis III Serie 3 Musterlösung Abgabe: Freitag, 2.2.22, Uhr, in der Vorlesung * Aufgabe Welche der folgenden Aussagen sind wahr und welche sind falsch? (Mit Begründung) (i) Sei A R 3 3 eine
Ana-3 Hs 22 Analysis III Serie 3 Musterlösung Abgabe: Freitag, 2.2.22, Uhr, in der Vorlesung * Aufgabe Welche der folgenden Aussagen sind wahr und welche sind falsch? (Mit Begründung) (i) Sei A R 3 3 eine
Wie man heute die Liebe fürs Leben findet
 Wie man heute die Liebe fürs Leben findet Sherrie Schneider Ellen Fein Click here if your download doesn"t start automatically Wie man heute die Liebe fürs Leben findet Sherrie Schneider Ellen Fein Wie
Wie man heute die Liebe fürs Leben findet Sherrie Schneider Ellen Fein Click here if your download doesn"t start automatically Wie man heute die Liebe fürs Leben findet Sherrie Schneider Ellen Fein Wie
Seeking for n! Derivatives
 Seeking for n! Derivatives $,000$ Reward A remarkable determinant (,0) (,) (0,0) (0,) (,0) (,0) (,) (,) (0,0) (0,) (0,) General definition Δ μ (X, Y ) = det x p i j yq i n j i,j= As a starter... n! dim
Seeking for n! Derivatives $,000$ Reward A remarkable determinant (,0) (,) (0,0) (0,) (,0) (,0) (,) (,) (0,0) (0,) (0,) General definition Δ μ (X, Y ) = det x p i j yq i n j i,j= As a starter... n! dim
Introduction FEM, 1D-Example
 Introduction FEM, 1D-Example home/lehre/vl-mhs-1-e/folien/vorlesung/3_fem_intro/cover_sheet.tex page 1 of 25. p.1/25 Table of contents 1D Example - Finite Element Method 1. 1D Setup Geometry 2. Governing
Introduction FEM, 1D-Example home/lehre/vl-mhs-1-e/folien/vorlesung/3_fem_intro/cover_sheet.tex page 1 of 25. p.1/25 Table of contents 1D Example - Finite Element Method 1. 1D Setup Geometry 2. Governing
Final Exam. Friday June 4, 2008, 12:30, Magnus-HS
 Stochastic Processes Summer Semester 2008 Final Exam Friday June 4, 2008, 12:30, Magnus-HS Name: Matrikelnummer: Vorname: Studienrichtung: Whenever appropriate give short arguments for your results. In
Stochastic Processes Summer Semester 2008 Final Exam Friday June 4, 2008, 12:30, Magnus-HS Name: Matrikelnummer: Vorname: Studienrichtung: Whenever appropriate give short arguments for your results. In
Topologie. Proposition 0.1 Let M be a countable (abzählbar) set. Then the set of all finite sequences of elements of M is countable.
 Topologie Lecture Oct. 15, 2013 Proposition 0.1 Let M be a countable (abzählbar) set. Then the set of all finite sequences of elements of M is countable. Then the power set (Potenz- Proposition 0.2 Let
Topologie Lecture Oct. 15, 2013 Proposition 0.1 Let M be a countable (abzählbar) set. Then the set of all finite sequences of elements of M is countable. Then the power set (Potenz- Proposition 0.2 Let
DYNAMISCHE GEOMETRIE
 DYNAMISCHE GEOMETRIE ÄHNLICHKEITSGEOMETRIE & MODELLIERUNG PAUL LIBBRECHT PH WEINGARTEN WS 2014-2015 CC-BY VON STAUDT KONSTRUKTIONEN Menü Erinnerung: Strahlensatz Längen, Frame Zielartikel Addition, Subtraktion
DYNAMISCHE GEOMETRIE ÄHNLICHKEITSGEOMETRIE & MODELLIERUNG PAUL LIBBRECHT PH WEINGARTEN WS 2014-2015 CC-BY VON STAUDT KONSTRUKTIONEN Menü Erinnerung: Strahlensatz Längen, Frame Zielartikel Addition, Subtraktion
Application: Tree-packing
 Application: Tree-packing Application: Tree-packing Reminder of finite tree-packing theorem: Theorem 2.4.1. (Nash-Williams 1961; Tutte 1961) The following are equivalent for all finite multigraphs G and
Application: Tree-packing Application: Tree-packing Reminder of finite tree-packing theorem: Theorem 2.4.1. (Nash-Williams 1961; Tutte 1961) The following are equivalent for all finite multigraphs G and
Ein Stern in dunkler Nacht Die schoensten Weihnachtsgeschichten. Click here if your download doesn"t start automatically
 Ein Stern in dunkler Nacht Die schoensten Weihnachtsgeschichten Click here if your download doesn"t start automatically Ein Stern in dunkler Nacht Die schoensten Weihnachtsgeschichten Ein Stern in dunkler
Ein Stern in dunkler Nacht Die schoensten Weihnachtsgeschichten Click here if your download doesn"t start automatically Ein Stern in dunkler Nacht Die schoensten Weihnachtsgeschichten Ein Stern in dunkler
3. The proof of Theorem
 3. The proof of Theorem Objekttyp: Chapter Zeitschrift: L'Enseignement Mathématique Band (Jahr): 31 (195) Heft 1-2: L'ENSEIGNEMENT MATHÉMATIQUE PDF erstellt am: 19.9.217 Nutzungsbedingungen Die ETH-Bibliothek
3. The proof of Theorem Objekttyp: Chapter Zeitschrift: L'Enseignement Mathématique Band (Jahr): 31 (195) Heft 1-2: L'ENSEIGNEMENT MATHÉMATIQUE PDF erstellt am: 19.9.217 Nutzungsbedingungen Die ETH-Bibliothek
Topologies on the set of Banach space representations
 Research Collection Doctoral Thesis Topologies on the set of Banach space representations Author(s): Koller, Michael Dominik Fabian Publication Date: 1993 Permanent Link: https://doi.org/10.3929/ethz-a-000888466
Research Collection Doctoral Thesis Topologies on the set of Banach space representations Author(s): Koller, Michael Dominik Fabian Publication Date: 1993 Permanent Link: https://doi.org/10.3929/ethz-a-000888466
Introduction FEM, 1D-Example
 Introduction FEM, D-Example /home/lehre/vl-mhs-/inhalt/cover_sheet.tex. p./22 Table of contents D Example - Finite Element Method. D Setup Geometry 2. Governing equation 3. General Derivation of Finite
Introduction FEM, D-Example /home/lehre/vl-mhs-/inhalt/cover_sheet.tex. p./22 Table of contents D Example - Finite Element Method. D Setup Geometry 2. Governing equation 3. General Derivation of Finite
On Euler s attempt to compute logarithms by interpolation
 Euler p. 1/1 On Euler s attempt to compute logarithms by interpolation Walter Gautschi wxg@cs.purdue.edu Purdue University Leonhard Euler 1707 1783 Euler p. 2/1 Euler p. 3/1 From Euler s letter to Daniel
Euler p. 1/1 On Euler s attempt to compute logarithms by interpolation Walter Gautschi wxg@cs.purdue.edu Purdue University Leonhard Euler 1707 1783 Euler p. 2/1 Euler p. 3/1 From Euler s letter to Daniel
Bayesian Networks. Syntax Semantics Parametrized Distributions Inference in Bayesian Networks. Exact Inference. Approximate Inference
 Syntax Semantics Parametrized Distributions Inference in Exact Inference Approximate Inference enumeration variable elimination stochastic simulation Markov Chain Monte Carlo (MCMC) 1 Includes many slides
Syntax Semantics Parametrized Distributions Inference in Exact Inference Approximate Inference enumeration variable elimination stochastic simulation Markov Chain Monte Carlo (MCMC) 1 Includes many slides
Englisch-Grundwortschatz
 Englisch-Grundwortschatz Die 100 am häufigsten verwendeten Wörter also auch so so in in even sogar on an / bei / in like wie / mögen their with but first only and time find you get more its those because
Englisch-Grundwortschatz Die 100 am häufigsten verwendeten Wörter also auch so so in in even sogar on an / bei / in like wie / mögen their with but first only and time find you get more its those because
aus Doktorarbeiten Anna Lena Birkmeyer Oktober 2016
 aus Doktorarbeiten Anna Lena Birkmeyer Fachbereich Mathematik TU Kaiserslautern Oktober 2016 In der der Arbeit: The mathematical modeling and optimization of... is a wide field of research [4,15,19,35,61,62,66,76,86]
aus Doktorarbeiten Anna Lena Birkmeyer Fachbereich Mathematik TU Kaiserslautern Oktober 2016 In der der Arbeit: The mathematical modeling and optimization of... is a wide field of research [4,15,19,35,61,62,66,76,86]
Jägersprache, Wildkunde und Begriffe aus der Jagd: Schwerpunkt Jägerprüfung Rotwild, Rehwild, Gamswild, Steinwild, Muffelwild (German Edition)
 Jägersprache, Wildkunde und Begriffe aus der Jagd: Schwerpunkt Jägerprüfung Rotwild, Rehwild, Gamswild, Steinwild, Muffelwild (German Edition) Ernst Jäger Click here if your download doesn"t start automatically
Jägersprache, Wildkunde und Begriffe aus der Jagd: Schwerpunkt Jägerprüfung Rotwild, Rehwild, Gamswild, Steinwild, Muffelwild (German Edition) Ernst Jäger Click here if your download doesn"t start automatically
FEM Isoparametric Concept
 FEM Isoparametric Concept home/lehre/vl-mhs--e/folien/vorlesung/4_fem_isopara/cover_sheet.tex page of 25. p./25 Table of contents. Interpolation Functions for the Finite Elements 2. Finite Element Types
FEM Isoparametric Concept home/lehre/vl-mhs--e/folien/vorlesung/4_fem_isopara/cover_sheet.tex page of 25. p./25 Table of contents. Interpolation Functions for the Finite Elements 2. Finite Element Types
Finite Difference Method (FDM)
 Finite Difference Method (FDM) home/lehre/vl-mhs-1-e/folien/vorlesung/2a_fdm/cover_sheet.tex page 1 of 15. p.1/15 Table of contents 1. Problem 2. Governing Equation 3. Finite Difference-Approximation 4.
Finite Difference Method (FDM) home/lehre/vl-mhs-1-e/folien/vorlesung/2a_fdm/cover_sheet.tex page 1 of 15. p.1/15 Table of contents 1. Problem 2. Governing Equation 3. Finite Difference-Approximation 4.
Computational Models
 - University of Applied Sciences - Computational Models - CSCI 331 - Friedhelm Seutter Institut für Angewandte Informatik Part I Automata and Languages 0. Introduction, Alphabets, Strings, and Languages
- University of Applied Sciences - Computational Models - CSCI 331 - Friedhelm Seutter Institut für Angewandte Informatik Part I Automata and Languages 0. Introduction, Alphabets, Strings, and Languages
Algebra. Übungsblatt 2 (Lösungen)
 Fakultät für Mathematik Sommersemester 2017 JProf. Dr. Christian Lehn Dr. Alberto Castaño Domínguez Algebra Übungsblatt 2 (Lösungen) Aufgabe 1. Es sei n 3. Zeigen Sie, dass S n von (1 2) und (1... n) erzeugt
Fakultät für Mathematik Sommersemester 2017 JProf. Dr. Christian Lehn Dr. Alberto Castaño Domínguez Algebra Übungsblatt 2 (Lösungen) Aufgabe 1. Es sei n 3. Zeigen Sie, dass S n von (1 2) und (1... n) erzeugt
Funktion der Mindestreserve im Bezug auf die Schlüsselzinssätze der EZB (German Edition)
 Funktion der Mindestreserve im Bezug auf die Schlüsselzinssätze der EZB (German Edition) Philipp Heckele Click here if your download doesn"t start automatically Download and Read Free Online Funktion
Funktion der Mindestreserve im Bezug auf die Schlüsselzinssätze der EZB (German Edition) Philipp Heckele Click here if your download doesn"t start automatically Download and Read Free Online Funktion
Algorithmic Bioinformatics III Graphs, Networks, and Systems SS2008 Ralf Zimmer
 Algorithmic Bioinformatics III Graphs, Networks, and Systems SS2008 Ralf Zimmer Graph Theory Introduction Ralf Zimmer, LMU Institut für Informatik, Lehrstuhl für Praktische Informatik und Bioinformatik,
Algorithmic Bioinformatics III Graphs, Networks, and Systems SS2008 Ralf Zimmer Graph Theory Introduction Ralf Zimmer, LMU Institut für Informatik, Lehrstuhl für Praktische Informatik und Bioinformatik,
Weather forecast in Accra
 Weather forecast in Accra Thursday Friday Saturday Sunday 30 C 31 C 29 C 28 C f = 9 5 c + 32 Temperature in Fahrenheit Temperature in Celsius 2 Converting Celsius to Fahrenheit f = 9 5 c + 32 tempc = 21
Weather forecast in Accra Thursday Friday Saturday Sunday 30 C 31 C 29 C 28 C f = 9 5 c + 32 Temperature in Fahrenheit Temperature in Celsius 2 Converting Celsius to Fahrenheit f = 9 5 c + 32 tempc = 21
Unit 5. Mathematical Morphology. Knowledge-Based Methods in Image Processing and Pattern Recognition; Ulrich Bodenhofer 85
 Unit 5 Mathematical Morphology Knowledge-Based Methods in Image Processing and Pattern Recognition; Ulrich Bodenhofer 85 Introduction to Mathematical Morphology Use of algebraic analysis for detecting
Unit 5 Mathematical Morphology Knowledge-Based Methods in Image Processing and Pattern Recognition; Ulrich Bodenhofer 85 Introduction to Mathematical Morphology Use of algebraic analysis for detecting
Geometrie und Bedeutung: Kap 5
 : Kap 5 21. November 2011 Übersicht Der Begriff des Vektors Ähnlichkeits Distanzfunktionen für Vektoren Skalarprodukt Eukidische Distanz im R n What are vectors I Domininic: Maryl: Dollar Po Euro Yen 6
: Kap 5 21. November 2011 Übersicht Der Begriff des Vektors Ähnlichkeits Distanzfunktionen für Vektoren Skalarprodukt Eukidische Distanz im R n What are vectors I Domininic: Maryl: Dollar Po Euro Yen 6
3. A NEIGHBORHOOD OF THE UNIT CIRCLE
 3. A NEIGHBORHOOD OF THE UNIT CIRCLE Objekttyp: Chapter Zeitschrift: L'Enseignement Mathématique Band (Jahr): 39 (1993) Heft 3-4: L'ENSEIGNEMENT MATHÉMATIQUE PDF erstellt am: 26.11.2017 Nutzungsbedingungen
3. A NEIGHBORHOOD OF THE UNIT CIRCLE Objekttyp: Chapter Zeitschrift: L'Enseignement Mathématique Band (Jahr): 39 (1993) Heft 3-4: L'ENSEIGNEMENT MATHÉMATIQUE PDF erstellt am: 26.11.2017 Nutzungsbedingungen
Was heißt Denken?: Vorlesung Wintersemester 1951/52. [Was bedeutet das alles?] (Reclams Universal-Bibliothek) (German Edition)
![Was heißt Denken?: Vorlesung Wintersemester 1951/52. [Was bedeutet das alles?] (Reclams Universal-Bibliothek) (German Edition) Was heißt Denken?: Vorlesung Wintersemester 1951/52. [Was bedeutet das alles?] (Reclams Universal-Bibliothek) (German Edition)](/thumbs/68/59244907.jpg) Was heißt Denken?: Vorlesung Wintersemester 1951/52. [Was bedeutet das alles?] (Reclams Universal-Bibliothek) (German Edition) Martin Heidegger Click here if your download doesn"t start automatically Was
Was heißt Denken?: Vorlesung Wintersemester 1951/52. [Was bedeutet das alles?] (Reclams Universal-Bibliothek) (German Edition) Martin Heidegger Click here if your download doesn"t start automatically Was
FACHKUNDE FüR KAUFLEUTE IM GESUNDHEITSWESEN FROM THIEME GEORG VERLAG
 FACHKUNDE FüR KAUFLEUTE IM GESUNDHEITSWESEN FROM THIEME GEORG VERLAG DOWNLOAD EBOOK : FACHKUNDE FüR KAUFLEUTE IM GESUNDHEITSWESEN Click link bellow and free register to download ebook: FACHKUNDE FüR KAUFLEUTE
FACHKUNDE FüR KAUFLEUTE IM GESUNDHEITSWESEN FROM THIEME GEORG VERLAG DOWNLOAD EBOOK : FACHKUNDE FüR KAUFLEUTE IM GESUNDHEITSWESEN Click link bellow and free register to download ebook: FACHKUNDE FüR KAUFLEUTE
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Reguläre Ausdrücke und reguläre Grammatiken Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 20 Regular expressions (1) Let Σ be an alphabet. The
Einführung in die Computerlinguistik Reguläre Ausdrücke und reguläre Grammatiken Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 20 Regular expressions (1) Let Σ be an alphabet. The
In 1900, David Hilbert outlined 23 mathematical problems to the International Congress of Mathematicians in Paris. Here is the first:
 1 Introduction In 1900, David Hilbert outlined 23 mathematical problems to the International Congress of Mathematicians in Paris. Here is the first: 1. Cantors Problem von der Mächtigkeit des Continuums
1 Introduction In 1900, David Hilbert outlined 23 mathematical problems to the International Congress of Mathematicians in Paris. Here is the first: 1. Cantors Problem von der Mächtigkeit des Continuums
Algorithmische Bioinformatik II WS2004/05 Ralf Zimmer Part III Probabilistic Modeling IV Bayesian Modeling: Algorithms, EM and MC Methods HMMs
 Algorithmische Bioinformatik II WS2004/05 Ralf Zimmer Part III Probabilistic Modeling IV Bayesian Modeling: Algorithms, EM and MC Methods HMMs Ralf Zimmer, LMU Institut für Informatik, Lehrstuhl für Praktische
Algorithmische Bioinformatik II WS2004/05 Ralf Zimmer Part III Probabilistic Modeling IV Bayesian Modeling: Algorithms, EM and MC Methods HMMs Ralf Zimmer, LMU Institut für Informatik, Lehrstuhl für Praktische
Duell auf offener Straße: Wenn sich Hunde an der Leine aggressiv verhalten (Cadmos Hundebuch) (German Edition)
 Duell auf offener Straße: Wenn sich Hunde an der Leine aggressiv verhalten (Cadmos Hundebuch) (German Edition) Nadine Matthews Click here if your download doesn"t start automatically Duell auf offener
Duell auf offener Straße: Wenn sich Hunde an der Leine aggressiv verhalten (Cadmos Hundebuch) (German Edition) Nadine Matthews Click here if your download doesn"t start automatically Duell auf offener
Martin Luther. Click here if your download doesn"t start automatically
 Die schönsten Kirchenlieder von Luther (Vollständige Ausgabe): Gesammelte Gedichte: Ach Gott, vom Himmel sieh darein + Nun bitten wir den Heiligen Geist... der Unweisen Mund... (German Edition) Martin
Die schönsten Kirchenlieder von Luther (Vollständige Ausgabe): Gesammelte Gedichte: Ach Gott, vom Himmel sieh darein + Nun bitten wir den Heiligen Geist... der Unweisen Mund... (German Edition) Martin
Attention: Give your answers to problem 1 and problem 2 directly below the questions in the exam question sheet. ,and C = [ ].
![Attention: Give your answers to problem 1 and problem 2 directly below the questions in the exam question sheet. ,and C = [ ]. Attention: Give your answers to problem 1 and problem 2 directly below the questions in the exam question sheet. ,and C = [ ].](/thumbs/72/66904987.jpg) Page 1 LAST NAME FIRST NAME MATRIKEL-NO. Attention: Give your answers to problem 1 and problem 2 directly below the questions in the exam question sheet. Problem 1 (15 points) a) (1 point) A system description
Page 1 LAST NAME FIRST NAME MATRIKEL-NO. Attention: Give your answers to problem 1 and problem 2 directly below the questions in the exam question sheet. Problem 1 (15 points) a) (1 point) A system description
EVANGELISCHES GESANGBUCH: AUSGABE FUR DIE EVANGELISCH-LUTHERISCHE LANDESKIRCHE SACHSEN. BLAU (GERMAN EDITION) FROM EVANGELISCHE VERLAGSAN
 EVANGELISCHES GESANGBUCH: AUSGABE FUR DIE EVANGELISCH-LUTHERISCHE LANDESKIRCHE SACHSEN. BLAU (GERMAN EDITION) FROM EVANGELISCHE VERLAGSAN DOWNLOAD EBOOK : EVANGELISCHES GESANGBUCH: AUSGABE FUR DIE EVANGELISCH-LUTHERISCHE
EVANGELISCHES GESANGBUCH: AUSGABE FUR DIE EVANGELISCH-LUTHERISCHE LANDESKIRCHE SACHSEN. BLAU (GERMAN EDITION) FROM EVANGELISCHE VERLAGSAN DOWNLOAD EBOOK : EVANGELISCHES GESANGBUCH: AUSGABE FUR DIE EVANGELISCH-LUTHERISCHE
Reparaturen kompakt - Küche + Bad: Waschbecken, Fliesen, Spüle, Armaturen, Dunstabzugshaube... (German Edition)
 Reparaturen kompakt - Küche + Bad: Waschbecken, Fliesen, Spüle, Armaturen, Dunstabzugshaube... (German Edition) Peter Birkholz, Michael Bruns, Karl-Gerhard Haas, Hans-Jürgen Reinbold Click here if your
Reparaturen kompakt - Küche + Bad: Waschbecken, Fliesen, Spüle, Armaturen, Dunstabzugshaube... (German Edition) Peter Birkholz, Michael Bruns, Karl-Gerhard Haas, Hans-Jürgen Reinbold Click here if your
Fachübersetzen - Ein Lehrbuch für Theorie und Praxis
 Fachübersetzen - Ein Lehrbuch für Theorie und Praxis Radegundis Stolze Click here if your download doesn"t start automatically Fachübersetzen - Ein Lehrbuch für Theorie und Praxis Radegundis Stolze Fachübersetzen
Fachübersetzen - Ein Lehrbuch für Theorie und Praxis Radegundis Stolze Click here if your download doesn"t start automatically Fachübersetzen - Ein Lehrbuch für Theorie und Praxis Radegundis Stolze Fachübersetzen
Teil 2.2: Lernen formaler Sprachen: Hypothesenräume
 Theorie des Algorithmischen Lernens Sommersemester 2006 Teil 2.2: Lernen formaler Sprachen: Hypothesenräume Version 1.1 Gliederung der LV Teil 1: Motivation 1. Was ist Lernen 2. Das Szenario der Induktiven
Theorie des Algorithmischen Lernens Sommersemester 2006 Teil 2.2: Lernen formaler Sprachen: Hypothesenräume Version 1.1 Gliederung der LV Teil 1: Motivation 1. Was ist Lernen 2. Das Szenario der Induktiven
Algebra. 1. Geben Sie alle abelschen Gruppen mit 8 und 12 Elementen an. (Ohne Nachweis).
 1 Wiederholungsblatt zur Gruppentheorie 18.12.2002 Wiederholen Sie für die Klausur: Algebra WS 2002/03 Dr. Elsholtz Alle Hausaufgaben. Aufgaben, die vor Wochen schwer waren, sind hoffentlich mit Abstand,
1 Wiederholungsblatt zur Gruppentheorie 18.12.2002 Wiederholen Sie für die Klausur: Algebra WS 2002/03 Dr. Elsholtz Alle Hausaufgaben. Aufgaben, die vor Wochen schwer waren, sind hoffentlich mit Abstand,
FEM Isoparametric Concept
 FEM Isoparametric Concept home/lehre/vl-mhs--e/cover_sheet.tex. p./26 Table of contents. Interpolation Functions for the Finite Elements 2. Finite Element Types 3. Geometry 4. Interpolation Approach Function
FEM Isoparametric Concept home/lehre/vl-mhs--e/cover_sheet.tex. p./26 Table of contents. Interpolation Functions for the Finite Elements 2. Finite Element Types 3. Geometry 4. Interpolation Approach Function
Handbuch der therapeutischen Seelsorge: Die Seelsorge-Praxis / Gesprächsführung in der Seelsorge (German Edition)
 Handbuch der therapeutischen Seelsorge: Die Seelsorge-Praxis / Gesprächsführung in der Seelsorge (German Edition) Reinhold Ruthe Click here if your download doesn"t start automatically Handbuch der therapeutischen
Handbuch der therapeutischen Seelsorge: Die Seelsorge-Praxis / Gesprächsführung in der Seelsorge (German Edition) Reinhold Ruthe Click here if your download doesn"t start automatically Handbuch der therapeutischen
Im Zeichen der Sonne: Schamanische Heilrituale (German Edition)
 Im Zeichen der Sonne: Schamanische Heilrituale (German Edition) Click here if your download doesn"t start automatically Im Zeichen der Sonne: Schamanische Heilrituale (German Edition) Im Zeichen der Sonne:
Im Zeichen der Sonne: Schamanische Heilrituale (German Edition) Click here if your download doesn"t start automatically Im Zeichen der Sonne: Schamanische Heilrituale (German Edition) Im Zeichen der Sonne:
ist ein n-dimensionaler, reeller Vektorraum (vgl. Lineare Algebra). Wir definieren auf diesem VR ein Skalarprodukt durch i y i i=1
 24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
Zariski-Van Kampen Method
 Zariski-Van Kampen Method Purpose: Obtain a presentation for the fundamental group of the complement of a plane projective curve in P 2. We will put together several ingredients, among which, the Van Kampen
Zariski-Van Kampen Method Purpose: Obtain a presentation for the fundamental group of the complement of a plane projective curve in P 2. We will put together several ingredients, among which, the Van Kampen
D-MATH Algebra I HS 2015 Prof. Richard Pink. Musterlösung 1. Ringe, Polynome, Potenzreihen. x(y z) = x(y + ( z)) = xy + x( z) = xy + ( xz) = xy xz.
 D-MATH Algebra I HS 20 Prof. Richard Pink Musterlösung Ringe, Polynome, Potenzreihen. Zeige, dass in jedem Ring R die Distributivregel gilt. Lösung: Für alle x, y, z R gilt x, y, z R : x(y z = xy xz x(y
D-MATH Algebra I HS 20 Prof. Richard Pink Musterlösung Ringe, Polynome, Potenzreihen. Zeige, dass in jedem Ring R die Distributivregel gilt. Lösung: Für alle x, y, z R gilt x, y, z R : x(y z = xy xz x(y
Im Fluss der Zeit: Gedanken beim Älterwerden (HERDER spektrum) (German Edition)
 Im Fluss der Zeit: Gedanken beim Älterwerden (HERDER spektrum) (German Edition) Ulrich Schaffer Click here if your download doesn"t start automatically Im Fluss der Zeit: Gedanken beim Älterwerden (HERDER
Im Fluss der Zeit: Gedanken beim Älterwerden (HERDER spektrum) (German Edition) Ulrich Schaffer Click here if your download doesn"t start automatically Im Fluss der Zeit: Gedanken beim Älterwerden (HERDER
Accelerating Information Technology Innovation
 Accelerating Information Technology Innovation http://aiti.mit.edu Ghana Summer 2011 Lecture 05 Functions Weather forecast in Accra Thursday Friday Saturday Sunday 30 C 31 C 29 C 28 C f = 9 5 c + 32 Temperature
Accelerating Information Technology Innovation http://aiti.mit.edu Ghana Summer 2011 Lecture 05 Functions Weather forecast in Accra Thursday Friday Saturday Sunday 30 C 31 C 29 C 28 C f = 9 5 c + 32 Temperature
Zu + Infinitiv Constructions
 Zu + Infinitiv Constructions You have probably noticed that in many German sentences, infinitives appear with a "zu" before them. These "zu + infinitive" structures are called infinitive clauses, and they're
Zu + Infinitiv Constructions You have probably noticed that in many German sentences, infinitives appear with a "zu" before them. These "zu + infinitive" structures are called infinitive clauses, and they're
Kursbuch Naturheilverfahren: Curriculum der Weiterbildung zur Erlangung der Zusatzbezeichnung Naturheilverfahren (German Edition)
 Kursbuch Naturheilverfahren: Curriculum der Weiterbildung zur Erlangung der Zusatzbezeichnung Naturheilverfahren (German Edition) Click here if your download doesn"t start automatically Kursbuch Naturheilverfahren:
Kursbuch Naturheilverfahren: Curriculum der Weiterbildung zur Erlangung der Zusatzbezeichnung Naturheilverfahren (German Edition) Click here if your download doesn"t start automatically Kursbuch Naturheilverfahren:
Killy Literaturlexikon: Autoren Und Werke Des Deutschsprachigen Kulturraumes 2., Vollstandig Uberarbeitete Auflage (German Edition)
 Killy Literaturlexikon: Autoren Und Werke Des Deutschsprachigen Kulturraumes 2., Vollstandig Uberarbeitete Auflage (German Edition) Walther Killy Click here if your download doesn"t start automatically
Killy Literaturlexikon: Autoren Und Werke Des Deutschsprachigen Kulturraumes 2., Vollstandig Uberarbeitete Auflage (German Edition) Walther Killy Click here if your download doesn"t start automatically
Note: With respect to the basis consisting of the e i e j, ordered lexicographically on the indexes (i.e. e i e j e k e l
 Übungen zur Vorlesung Lineare Algebra II (SS ) 7.7. Prof. Dr. Martin Ziegler Dr. Juan Diego Caycedo Blatt Keine Abgabe. Dieses Blatt wird nicht korrigiert oder bewertet. Aufgabe. {e, e, e 3 } bzw. {e,
Übungen zur Vorlesung Lineare Algebra II (SS ) 7.7. Prof. Dr. Martin Ziegler Dr. Juan Diego Caycedo Blatt Keine Abgabe. Dieses Blatt wird nicht korrigiert oder bewertet. Aufgabe. {e, e, e 3 } bzw. {e,
Level 2 German, 2015
 91126 911260 2SUPERVISOR S Level 2 German, 2015 91126 Demonstrate understanding of a variety of written and / or visual German text(s) on familiar matters 2.00 p.m. Friday 4 December 2015 Credits: Five
91126 911260 2SUPERVISOR S Level 2 German, 2015 91126 Demonstrate understanding of a variety of written and / or visual German text(s) on familiar matters 2.00 p.m. Friday 4 December 2015 Credits: Five
Zusammenfassung Analysis 2
 Zusammenfassung Analysis 2 1.2 Metrische Räume Die Grundlage metrischer Räume bildet der Begriff des Abstandes (Metrik). Definition 1.1 Ein metrischer Raum ist ein Paar (X, d), bestehend aus einer Menge
Zusammenfassung Analysis 2 1.2 Metrische Räume Die Grundlage metrischer Räume bildet der Begriff des Abstandes (Metrik). Definition 1.1 Ein metrischer Raum ist ein Paar (X, d), bestehend aus einer Menge
Tschernobyl: Auswirkungen des Reaktorunfalls auf die Bundesrepublik Deutschland und die DDR (German Edition)
 Tschernobyl: Auswirkungen des Reaktorunfalls auf die Bundesrepublik Deutschland und die DDR (German Edition) Melanie Arndt Click here if your download doesn"t start automatically Tschernobyl: Auswirkungen
Tschernobyl: Auswirkungen des Reaktorunfalls auf die Bundesrepublik Deutschland und die DDR (German Edition) Melanie Arndt Click here if your download doesn"t start automatically Tschernobyl: Auswirkungen
PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB
 Read Online and Download Ebook PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB DOWNLOAD EBOOK : PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: Click link bellow
Read Online and Download Ebook PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB DOWNLOAD EBOOK : PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: Click link bellow
PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB
 Read Online and Download Ebook PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB DOWNLOAD EBOOK : PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: Click link bellow
Read Online and Download Ebook PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB DOWNLOAD EBOOK : PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: Click link bellow
Die Bedeutung neurowissenschaftlicher Erkenntnisse für die Werbung (German Edition)
 Die Bedeutung neurowissenschaftlicher Erkenntnisse für die Werbung (German Edition) Lisa Johann Click here if your download doesn"t start automatically Download and Read Free Online Die Bedeutung neurowissenschaftlicher
Die Bedeutung neurowissenschaftlicher Erkenntnisse für die Werbung (German Edition) Lisa Johann Click here if your download doesn"t start automatically Download and Read Free Online Die Bedeutung neurowissenschaftlicher
Benjamin Whorf, Die Sumerer Und Der Einfluss Der Sprache Auf Das Denken (Philippika) (German Edition)
 Benjamin Whorf, Die Sumerer Und Der Einfluss Der Sprache Auf Das Denken (Philippika) (German Edition) Sebastian Fink Click here if your download doesn"t start automatically Benjamin Whorf, Die Sumerer
Benjamin Whorf, Die Sumerer Und Der Einfluss Der Sprache Auf Das Denken (Philippika) (German Edition) Sebastian Fink Click here if your download doesn"t start automatically Benjamin Whorf, Die Sumerer
VGM. VGM information. HAMBURG SÜD VGM WEB PORTAL USER GUIDE June 2016
 Overview The Hamburg Süd VGM Web portal is an application that enables you to submit VGM information directly to Hamburg Süd via our e-portal Web page. You can choose to enter VGM information directly,
Overview The Hamburg Süd VGM Web portal is an application that enables you to submit VGM information directly to Hamburg Süd via our e-portal Web page. You can choose to enter VGM information directly,
Ewald s Sphere/Problem 3.7
 Ewald s Sphere/Problem 3.7 Studentproject/Molecular and Solid-State Physics Lisa Marx 831292 15.1.211, Graz Ewald s Sphere/Problem 3.7 Lisa Marx 831292 Inhaltsverzeichnis 1 General Information 3 1.1 Ewald
Ewald s Sphere/Problem 3.7 Studentproject/Molecular and Solid-State Physics Lisa Marx 831292 15.1.211, Graz Ewald s Sphere/Problem 3.7 Lisa Marx 831292 Inhaltsverzeichnis 1 General Information 3 1.1 Ewald
Sagen und Geschichten aus dem oberen Flöhatal im Erzgebirge: Pfaffroda - Neuhausen - Olbernhau - Seiffen (German Edition)
 Sagen und Geschichten aus dem oberen Flöhatal im Erzgebirge: Pfaffroda - Neuhausen - Olbernhau - Seiffen (German Edition) Dr. Frank Löser Click here if your download doesn"t start automatically Sagen und
Sagen und Geschichten aus dem oberen Flöhatal im Erzgebirge: Pfaffroda - Neuhausen - Olbernhau - Seiffen (German Edition) Dr. Frank Löser Click here if your download doesn"t start automatically Sagen und
Konkret - der Ratgeber: Die besten Tipps zu Internet, Handy und Co. (German Edition)
 Konkret - der Ratgeber: Die besten Tipps zu Internet, Handy und Co. (German Edition) Kenny Lang, Marvin Wolf, Elke Weiss Click here if your download doesn"t start automatically Konkret - der Ratgeber:
Konkret - der Ratgeber: Die besten Tipps zu Internet, Handy und Co. (German Edition) Kenny Lang, Marvin Wolf, Elke Weiss Click here if your download doesn"t start automatically Konkret - der Ratgeber:
Einführung in die Finite Element Methode Projekt 2
 Einführung in die Finite Element Methode Projekt 2 Juri Schmelzer und Fred Brockstedt 17.7.2014 Juri Schmelzer und Fred Brockstedt Einführung in die Finite Element Methode Projekt 2 17.7.2014 1 / 29 Project
Einführung in die Finite Element Methode Projekt 2 Juri Schmelzer und Fred Brockstedt 17.7.2014 Juri Schmelzer und Fred Brockstedt Einführung in die Finite Element Methode Projekt 2 17.7.2014 1 / 29 Project
Integer Convex Minimization in Low Dimensions
 DISS. ETH NO. 22288 Integer Convex Minimization in Low Dimensions A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZURICH (Dr. sc. ETH Zurich) presented by TIMM OERTEL Diplom-Mathematiker,
DISS. ETH NO. 22288 Integer Convex Minimization in Low Dimensions A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZURICH (Dr. sc. ETH Zurich) presented by TIMM OERTEL Diplom-Mathematiker,
Research Collection. Backward stochastic differential equations with super-quadratic growth. Doctoral Thesis. ETH Library. Author(s): Bao, Xiaobo
 Research Collection Doctoral Thesis Backward stochastic differential equations with super-quadratic growth Author(s): Bao, Xiaobo Publication Date: 2009 Permanent Link: https://doi.org/10.3929/ethz-a-005955736
Research Collection Doctoral Thesis Backward stochastic differential equations with super-quadratic growth Author(s): Bao, Xiaobo Publication Date: 2009 Permanent Link: https://doi.org/10.3929/ethz-a-005955736
Vollständigkeit. Andreas Schmitt. Ausarbeitung zum Proseminar zur Topologie im WS 2012/13
 Vollständigkeit Andreas Schmitt Ausarbeitung zum Proseminar zur Topologie im WS 2012/13 1 Einleitung Bei der Konvergenz von Folgen im Raum der reellen Zahlen R trifft man schnell auf den Begriff der Cauchy-Folge.
Vollständigkeit Andreas Schmitt Ausarbeitung zum Proseminar zur Topologie im WS 2012/13 1 Einleitung Bei der Konvergenz von Folgen im Raum der reellen Zahlen R trifft man schnell auf den Begriff der Cauchy-Folge.
Die einfachste Diät der Welt: Das Plus-Minus- Prinzip (GU Reihe Einzeltitel)
 Die einfachste Diät der Welt: Das Plus-Minus- Prinzip (GU Reihe Einzeltitel) Stefan Frà drich Click here if your download doesn"t start automatically Die einfachste Diät der Welt: Das Plus-Minus-Prinzip
Die einfachste Diät der Welt: Das Plus-Minus- Prinzip (GU Reihe Einzeltitel) Stefan Frà drich Click here if your download doesn"t start automatically Die einfachste Diät der Welt: Das Plus-Minus-Prinzip
Diabetes zu heilen natürlich: German Edition( Best Seller)
 Diabetes zu heilen natürlich: German Edition( Best Seller) Dr Maria John Click here if your download doesn"t start automatically Diabetes zu heilen natürlich: German Edition( Best Seller) Dr Maria John
Diabetes zu heilen natürlich: German Edition( Best Seller) Dr Maria John Click here if your download doesn"t start automatically Diabetes zu heilen natürlich: German Edition( Best Seller) Dr Maria John
8.1. DER RAUM R N ALS BANACHRAUM 17
 8.1. DER RAUM R N ALS BANACHRAUM 17 Beweis. Natürlich ist d 0 und d(x, y) = 0 genau dann, wenn x = y. Wegen (N2) ist x = x und damit d(x, y) = d(y, x). Die letzte Eigenschaft einer Metrik schließt man
8.1. DER RAUM R N ALS BANACHRAUM 17 Beweis. Natürlich ist d 0 und d(x, y) = 0 genau dann, wenn x = y. Wegen (N2) ist x = x und damit d(x, y) = d(y, x). Die letzte Eigenschaft einer Metrik schließt man
Max und Moritz: Eine Bubengeschichte in Sieben Streichen (German Edition)
 Max und Moritz: Eine Bubengeschichte in Sieben Streichen (German Edition) Wilhelm Busch Click here if your download doesn"t start automatically Max und Moritz: Eine Bubengeschichte in Sieben Streichen
Max und Moritz: Eine Bubengeschichte in Sieben Streichen (German Edition) Wilhelm Busch Click here if your download doesn"t start automatically Max und Moritz: Eine Bubengeschichte in Sieben Streichen
Level 2 German, 2013
 91126 911260 2SUPERVISOR S Level 2 German, 2013 91126 Demonstrate understanding of a variety of written and / or visual German text(s) on familiar matters 9.30 am Monday 11 November 2013 Credits: Five
91126 911260 2SUPERVISOR S Level 2 German, 2013 91126 Demonstrate understanding of a variety of written and / or visual German text(s) on familiar matters 9.30 am Monday 11 November 2013 Credits: Five
Mock Exam Behavioral Finance
 Mock Exam Behavioral Finance For the following 4 questions you have 60 minutes. You may receive up to 60 points, i.e. on average you should spend about 1 minute per point. Please note: You may use a pocket
Mock Exam Behavioral Finance For the following 4 questions you have 60 minutes. You may receive up to 60 points, i.e. on average you should spend about 1 minute per point. Please note: You may use a pocket
Selbstbild vs. Fremdbild. Selbst- und Fremdwahrnehmung des Individuums (German Edition)
 Selbstbild vs. Fremdbild. Selbst- und Fremdwahrnehmung des Individuums (German Edition) Jasmin Nowak Click here if your download doesn"t start automatically Selbstbild vs. Fremdbild. Selbst- und Fremdwahrnehmung
Selbstbild vs. Fremdbild. Selbst- und Fremdwahrnehmung des Individuums (German Edition) Jasmin Nowak Click here if your download doesn"t start automatically Selbstbild vs. Fremdbild. Selbst- und Fremdwahrnehmung
PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB
 Read Online and Download Ebook PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB DOWNLOAD EBOOK : PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: Click link bellow
Read Online and Download Ebook PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB DOWNLOAD EBOOK : PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: Click link bellow
Mercedes OM 636: Handbuch und Ersatzteilkatalog (German Edition)
 Mercedes OM 636: Handbuch und Ersatzteilkatalog (German Edition) Mercedes-Benz Click here if your download doesn"t start automatically Mercedes OM 636: Handbuch und Ersatzteilkatalog (German Edition) Mercedes-Benz
Mercedes OM 636: Handbuch und Ersatzteilkatalog (German Edition) Mercedes-Benz Click here if your download doesn"t start automatically Mercedes OM 636: Handbuch und Ersatzteilkatalog (German Edition) Mercedes-Benz
Die UN-Kinderrechtskonvention. Darstellung der Bedeutung (German Edition)
 Die UN-Kinderrechtskonvention. Darstellung der Bedeutung (German Edition) Daniela Friedrich Click here if your download doesn"t start automatically Die UN-Kinderrechtskonvention. Darstellung der Bedeutung
Die UN-Kinderrechtskonvention. Darstellung der Bedeutung (German Edition) Daniela Friedrich Click here if your download doesn"t start automatically Die UN-Kinderrechtskonvention. Darstellung der Bedeutung
arxiv: v1 [math.ho] 23 Mar 2015
![arxiv: v1 [math.ho] 23 Mar 2015 arxiv: v1 [math.ho] 23 Mar 2015](/thumbs/79/79279752.jpg) About Cantor Works on Trigonometric Series arxiv:1503.06845v1 [math.ho] 23 Mar 2015 Abstract Muhammad-Ali A rabi a,c, Farnaz Irani b,c a m aerabi@mehr.sharif.ir b f.irani@modares.ac.ir c Shahid Beheshti
About Cantor Works on Trigonometric Series arxiv:1503.06845v1 [math.ho] 23 Mar 2015 Abstract Muhammad-Ali A rabi a,c, Farnaz Irani b,c a m aerabi@mehr.sharif.ir b f.irani@modares.ac.ir c Shahid Beheshti
Die besten Chuck Norris Witze: Alle Fakten über den härtesten Mann der Welt (German Edition)
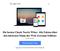 Die besten Chuck Norris Witze: Alle Fakten über den härtesten Mann der Welt (German Edition) Click here if your download doesn"t start automatically Die besten Chuck Norris Witze: Alle Fakten über den
Die besten Chuck Norris Witze: Alle Fakten über den härtesten Mann der Welt (German Edition) Click here if your download doesn"t start automatically Die besten Chuck Norris Witze: Alle Fakten über den
Wer bin ich - und wenn ja wie viele?: Eine philosophische Reise. Click here if your download doesn"t start automatically
 Wer bin ich - und wenn ja wie viele?: Eine philosophische Reise Click here if your download doesn"t start automatically Wer bin ich - und wenn ja wie viele?: Eine philosophische Reise Wer bin ich - und
Wer bin ich - und wenn ja wie viele?: Eine philosophische Reise Click here if your download doesn"t start automatically Wer bin ich - und wenn ja wie viele?: Eine philosophische Reise Wer bin ich - und
VGM. VGM information. HAMBURG SÜD VGM WEB PORTAL - USER GUIDE June 2016
 Overview The Hamburg Süd VGM-Portal is an application which enables to submit VGM information directly to Hamburg Süd via our e-portal web page. You can choose to insert VGM information directly, or download
Overview The Hamburg Süd VGM-Portal is an application which enables to submit VGM information directly to Hamburg Süd via our e-portal web page. You can choose to insert VGM information directly, or download
Flow - der Weg zum Glück: Der Entdecker des Flow-Prinzips erklärt seine Lebensphilosophie (HERDER spektrum) (German Edition)
 Flow - der Weg zum Glück: Der Entdecker des Flow-Prinzips erklärt seine Lebensphilosophie (HERDER spektrum) (German Edition) Mihaly Csikszentmihalyi Click here if your download doesn"t start automatically
Flow - der Weg zum Glück: Der Entdecker des Flow-Prinzips erklärt seine Lebensphilosophie (HERDER spektrum) (German Edition) Mihaly Csikszentmihalyi Click here if your download doesn"t start automatically
Wirtschaftskrise ohne Ende?: US-Immobilienkrise Globale Finanzkrise Europäische Schuldenkrise (German Edition)
 Wirtschaftskrise ohne Ende?: US-Immobilienkrise Globale Finanzkrise Europäische Schuldenkrise (German Edition) Aymo Brunetti Click here if your download doesn"t start automatically Wirtschaftskrise ohne
Wirtschaftskrise ohne Ende?: US-Immobilienkrise Globale Finanzkrise Europäische Schuldenkrise (German Edition) Aymo Brunetti Click here if your download doesn"t start automatically Wirtschaftskrise ohne
Final Exam. Friday June 4, 2008, 12:30, Magnus-HS
 Stochastic Processes Summer Semester 008 Final Exam Friday June 4, 008, 1:30, Magnus-HS Name: Matrikelnummer: Vorname: Studienrichtung: Whenever appropriate give short arguments for your results. In each
Stochastic Processes Summer Semester 008 Final Exam Friday June 4, 008, 1:30, Magnus-HS Name: Matrikelnummer: Vorname: Studienrichtung: Whenever appropriate give short arguments for your results. In each
Star Trek: die Serien, die Filme, die Darsteller: Interessante Infod, zusammengestellt aus Wikipedia-Seiten (German Edition)
 Star Trek: die Serien, die Filme, die Darsteller: Interessante Infod, zusammengestellt aus Wikipedia-Seiten (German Edition) Doktor Googelberg Click here if your download doesn"t start automatically Star
Star Trek: die Serien, die Filme, die Darsteller: Interessante Infod, zusammengestellt aus Wikipedia-Seiten (German Edition) Doktor Googelberg Click here if your download doesn"t start automatically Star
Josh Engwer (TTU) Line Integrals 11 November / 25
 Line Integrals alculus III Josh Engwer TTU 11 November 2014 Josh Engwer (TTU) Line Integrals 11 November 2014 1 / 25 PART I PART I: LINE INTEGRALS OF SALAR FIELDS Josh Engwer (TTU) Line Integrals 11 November
Line Integrals alculus III Josh Engwer TTU 11 November 2014 Josh Engwer (TTU) Line Integrals 11 November 2014 1 / 25 PART I PART I: LINE INTEGRALS OF SALAR FIELDS Josh Engwer (TTU) Line Integrals 11 November
Harry gefangen in der Zeit Begleitmaterialien
 Episode 011 Grammar 1. Plural forms of nouns Most nouns can be either singular or plural. The plural indicates that you're talking about several units of the same thing. Ist das Bett zu hart? Sind die
Episode 011 Grammar 1. Plural forms of nouns Most nouns can be either singular or plural. The plural indicates that you're talking about several units of the same thing. Ist das Bett zu hart? Sind die
Willkommen zur Vorlesung Komplexitätstheorie
 Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V11, 16.1.2012 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V11, 16.1.2012 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Logik für Informatiker Logic for computer scientists
 Logik für Informatiker Logic for computer scientists Till Mossakowski WiSe 2007/08 2 Rooms Monday 13:00-15:00 GW2 B1410 Thursday 13:00-15:00 GW2 B1410 Exercises (bring your Laptops with you!) either Monday
Logik für Informatiker Logic for computer scientists Till Mossakowski WiSe 2007/08 2 Rooms Monday 13:00-15:00 GW2 B1410 Thursday 13:00-15:00 GW2 B1410 Exercises (bring your Laptops with you!) either Monday
