Übung zur Vorlesung Sicherheit Übungsblatt 4. Björn Kaidel 1 / 70
|
|
|
- Arthur Bauer
- vor 5 Jahren
- Abrufe
Transkript
1 Übung zur Vorlesung Sicherheit Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu 1 / 70
2 RSA: Warnung! Mehrere Nachfragen nach der letzten Übung: Wir wollen zu e ein d berechnen mit e d = 1 mod ϕ(n) Idee: Verwende nicht EEA, sondern folgendes Vorgehen: Beobachtung: Gesucht ist d mit e d = k ϕ(n) + 1 Berechne dieses k! Beginne mit k = 1. Erhöhe k, bis k ϕ(n) + 1 teilbar durch e (in Z). Dann ist d = (k ϕ(n) + 1)/e) mod ϕ(n) (Teile in Z, rechne dann Modulo) Gute Nachricht: Funktioniert! Schlechte Nachricht: Exponentielle Laufzeit! 2 / 70
3 RSA: Warnung! Also: In Praxis eine schlechte Idee! Aber... Kann per Hand gut gehen muss aber nicht! Laufzeit vom EEA ist polynomiell. EEA sieht schwieriger aus, als er ist und geht auf jeden Fall recht gut von Hand! :) Hinweis: EEA jetzt detailliert im Skript erklärt! 3 / 70
4 Kummerkasten In der VL wird von TLS < 1.2 abgeraten, warum kann euer Server nur TLS 1.0? Wofür machen wir die Aufgaben? 4 / 70
5 Wofür machen wir die Aufgaben? Von euch angesprochene Probleme: Aufgaben ziemlich theoretisch Praxisrelevanz nur bedingt ersichtlich 5 / 70
6 Wofür machen wir die Aufgaben? Argument 1: Forschung Krypto ist Teilmenge der theoretischen Informatik Wie Algorithmen, Komplexitätstheorie, etc. Forschung reicht aber von sehr praxisnah bis sehr theoretisch Ziel von vertiefenden VLs ist auch Vorbereitung auf Forschung! 6 / 70
7 Wofür machen wir die Aufgaben? Argument 2: Was ist überhaupt Sicherheit? Wir wollen weg von ad-hoc-sicherheit/security through Obscurity Ziel: Nachvollziehbare, möglichst beweisbare Sicherheit Also: Sicherheitsdenitionen Aber: Was kann so eine Sicherheitsdenition eigentlich? IND-CPA, Kollres., EUF-CMA etc. wirken sehr stark aber sind sie das auch?... was liefern sie mir? Bsp.: ÜB2 A2; ÜB3 A1, A3; ÜB4 A2, A3, A4 7 / 70
8 Wofür machen wir die Aufgaben? Argument 3: Umgang mit Kryptographie lernen Kritik 1: Gegenbeispiele bei Beweisen unrealistisch Viele praktische Angrie nutzen aber sowas aus! Schadcode wird kaum das komplette System ändern können Ziel: Gibt es Kleinigkeiten die ich ändern kann? Führen zu eben solchen Abwandlung des Verfahrens... Bsp: Bug-Using, Fault-Induction, CRIME... 8 / 70
9 Wofür machen wir die Aufgaben? Argument 3: Umgang mit Kryptographie lernen Kritik 1: Gegenbeispiele bei Beweisen unrealistisch Implementierungsfehler, Optimierungen z.b. ÜB3 A3: Einuss der Nachrichtenlänge in Merkle-Damgård wirkt unwichtig weglassen macht aber das ganze System unsicher! CRIME: Nachrichten komprimieren scheint sinnvoll, gefährdet aber die Sicherheit! (siehe ÜB5 A4) Es gibt unsichere laufzeitoptimierte Impl. von RSA Lösung dieser Probleme durch Hotxes(siehe ÜB4 A3) nicht zielführend Fazit: Kryptoprotokolle nicht einfach ändern! 9 / 70
10 Wofür machen wir die Aufgaben? Argument 3: Umgang mit Kryptographie lernen Kritik 2: Transformationen Schema X zu Schema Y praxisfern... Unsere Beispiele sind einfach..... aber Transformationen sind Standard Zahlreiche Beispiele theoretischer & praktischer Natur (z.b. TLS!) Theorie: klärt Zusammenhänge, was ist möglich... Praxis: Spart Implementierung, Wiederverwendbarkeit,... Fazit: Lernen, wie man sowas richtig verwendet (nur müssen wir halt klein anfangen) 10 / 70
11 Wofür machen wir die Aufgaben? Wir werden versuchen das ab jetzt klarer darzustellen! 11 / 70
12 Sicherheit Übungsblatt 4 Aufgabe 1 ElGamal-Verschlüsselungsverfahren Gruppe G := Z 59 Erzeuger g := 27 g erzeugt Untergruppe (UG) der Quadrate, nicht G! Gruppenoperation: Multiplikation modulo 59 Z 59 ist Einheitengruppe von Z 59 d.h. alle invertierbaren Elemente hier: Z = Z \ {0}, da 59 prim {x 2 mod 59: x Z 59} ist UG der Quadrate und hat Ordnung / 70
13 Sicherheit Übungsblatt 4 Aufgabe 1 Tricks zum Rechnen: (i) Finden von Äquivalenzklassen, z.b.: 51 2 mod 59 = (59 8) 2 mod 59 = ( 8) 2 mod 59 = 64 mod 59 = 5 mod / 70
14 Sicherheit Übungsblatt 4 Aufgabe 1 Tricks zum Rechnen: (ii) Reduzierung des Exponenten modulo der Gruppenordnung, z.b.: 3 60 mod 59 = 3 60 mod 58 mod 59 = 3 2 mod 59 = 9 mod 59 Hintergrund: Satz von Euler bzw. Kleiner Satz von Fermat Ordnung von G ist ϕ(59) = 58. Für Primzahlen p: ϕ(p) = p 1. Ordnung der UG der Quadrate ist / 70
15 Sicherheit Übungsblatt 4 Aufgabe 1 (a) Berechnen Sie zum geheimen Schlüssel sk := 20 den öentlichen Schlüssel pk. pk = g sk mod N = mod 59 = (3 3 ) 20 mod 59 = 3 60 mod 58 mod 59 = 3 2 mod 59 = 9 mod / 70
16 Sicherheit Übungsblatt 4 Aufgabe 1 (b) Verschlüsseln Sie m := 22 unter dem in (a) berechneten Schlüssel (mit dem Zufall r := 12). Erinnerung: Enc(pk, M) = (g r, pk r M) C 1 = g r mod N = mod 59 = 3 36 mod 59 ( ) = mod 29 mod 59 = 3 7 mod 59 = mod 59 = mod 59 =... (*): 3 ist ein Quadrat! 11 2 mod 59 = 3 mod / 70
17 Sicherheit Übungsblatt 4 Aufgabe 1 (b) Verschlüsseln Sie m := 22 unter dem in (a) berechneten Schlüssel (mit dem Zufall r := 12). C 1 =... = mod 59 = mod 59 = mod 59 = 7 9 mod 59 = 63 mod 59 = 4 mod / 70
18 Sicherheit Übungsblatt 4 Aufgabe 1 (b) Verschlüsseln Sie m := 22 unter dem in (a) berechneten Schlüssel (mit dem Zufall r := 12). C 2 = pk r m mod N = mod 59 = 9 12 ( ) mod 59 = mod 59 = mod 59 = 3 28 mod 59 = 3 1 mod 59 = 20 mod / 70
19 Sicherheit Übungsblatt 4 Aufgabe 1 (b) Verschlüsseln Sie m := 22 unter dem in (a) berechneten Schlüssel (mit dem Zufall r := 12). Insgesamt ergibt sich: C = (C 1, C 2 ) = (4, 20) 19 / 70
20 Sicherheit Übungsblatt 4 Aufgabe 1 (c) Entschlüsseln Sie C := (51, 8) unter dem Schlüssel aus (a). Erinnerung: Dec(sk, (C 1, C 2 )) = C 2 C sk 1 Wir berechnen zuerst: C sk 1 = mod 59 = ( 8) 20 mod 59 = ( 2) 60 mod 59 = ( 2) 2 mod 59 = 4 mod 59 Invertieren ergibt: C sk 1 = 4 1 mod 59 = 15 mod 59 (Berechnung durch erw. euklid. Alg. oder Scharfes Hinsehen) 20 / 70
21 Sicherheit Übungsblatt 4 Aufgabe 1 (c) Entschlüsseln Sie C := (51, 8) unter dem Schlüssel aus (a). C 2 C sk 1 = 8 15 mod 59 = 120 mod 59 = 2 mod / 70
22 Sicherheit Übungsblatt 4 Aufgabe 1 Frage: Warum eigentlich UG der Quadrate? Antwort: ElGamal in Z p nicht sicher Es existiert ein ezienter Angri Angri verwendet Legendre-Symbol Legendre-Symbol entscheidet, ob geg. x ein quad. Rest mod p Angri funktioniert in der UG der quad. Reste nicht mehr In der UG kein anderer Angri bekannt (auÿer ineziente DLog-Algorithmen etc.) 22 / 70
23 Sicherheit Übungsblatt 4 Aufgabe 1 Fazit: ElGamal ist praxistauglich Wichtiger, grundlegender Baustein für komplexere Krypto Rechnen üben 23 / 70
24 Wdh.: EUF-CMA Herausforderer C führt (pk, sk) Gen(1 k ) aus. C stellt Sign(sk, )-Orakel für A bereit. C A Orakel pk M σ = Sign(sk, M i ) M, σ (Poly. viele Anfragen erlaubt!) Ver(pk, M, σ ) = 1? M / {M 1,..., M n }? 24 / 70
25 Sicherheit Übungsblatt 4 Aufgabe 2 Es sei Σ = (Gen, Sign, Ver) ein EUF-CMA-sicheres Signaturverfahren. Wir konstruieren daraus zwei neue Verfahren. 25 / 70
26 Sicherheit Übungsblatt 4 Aufgabe 2 (1) Betrachte Σ mit: Gen (1 k ) := Gen(1 k ), Sign (sk, M) := (Sign(sk, M r), r) = (σ 1, σ 2 ) (r {0, 1} M ), Ver (pk, M, σ) := Ver(pk, M σ 2, σ 1 ). (a) Korrektheit: Ver (pk, M, σ) = Ver(pk, M r, σ 1 ) = Ver(pk, M r, Sign(sk, M r)) = 1. (folgt aus Korrektheit von Σ) 26 / 70
27 Sicherheit Übungsblatt 4 Aufgabe 2 (1) Betrachte Σ mit: Gen (1 k ) := Gen(1 k ), Sign (sk, M) := (Sign(sk, M r), r) = (σ 1, σ 2 ) (r {0, 1} M ), Ver (pk, M, σ) := Ver(pk, M σ 2, σ 1 ). (b) Zeigen Sie: Σ ist nicht EUF-CMA-sicher. A schickt bel. M und erhält Signatur σ = (σ 1, r).... wählt bel. M M.... setzt r = M M r... setzt σ = (σ 1, r). 27 / 70
28 Sicherheit Übungsblatt 4 Aufgabe 2 (1) σ = (σ 1, r ) = (σ 1, M M r) ist gültige Fälschung für M, denn: Ver (pk, M, σ ) = Ver (pk, M, (σ 1, r )) = Ver(pk, M r, σ 1 ) = Ver(pk, M (M M r), σ 1 ) = Ver(pk, M r, σ 1 ) = Ver (pk, M, (σ 1, r)) = Ver (pk, M, σ) = 1. Polynomielle Laufzeit, Erfolgswkt. ist 1 Σ nicht EUF-CMAsicher. 28 / 70
29 Sicherheit Übungsblatt 4 Aufgabe 2 (2) Betrachte Σ mit: Gen (1 k ) := Gen(1 k ), Sign (sk, M) := Sign(sk, M) (M bitw. Inverse von M), Ver (pk, M, σ) = Ver(pk, M, σ) (a) Korrektheit: Ver (pk, M, σ) = Ver(pk, M, σ) = Ver(pk, M, Sign(sk, M)) = 1. (folgt aus Korrektheit von Σ) 29 / 70
30 Sicherheit Übungsblatt 4 Aufgabe 2 (2) Betrachte Σ mit: Gen (1 k ) := Gen(1 k ), Sign (sk, M) := Sign(sk, M) (M bitw. Inverse von M), Ver (pk, M, σ) = Ver(pk, M, σ) (b) Zeigen Sie: Σ ist EUF-CMA-sicher. Widerspruchsbeweis/Reduktion: Annahme: Σ nicht EUF-CMA-sicher. D.h. es existiert PPT A mit nicht-vernachl. Erfolgswkt. Konstruiere Angreifer B gegen Σ mit nicht-vernachl. Erfolgswkt. Widerspruch zur EUF-CMA-Sicherheit von Σ. D.h. Σ ist EUF-CMA-sicher. 30 / 70
31 σ = Sign(sk, M) σ Sicherheit Übungsblatt 4 Aufgabe 2 (2) Simulation des Orakels: B hat Zugri auf Σ-Sign-Orakel. A braucht Zugri auf Σ -Sign -Orakel. B muss Σ -Sign -Orakel simulieren. Zur Erinnerung: Sign (sk, M) := Sign(sk, M) Sign(sk, )-Orakel M B M A 31 / 70
32 Sicherheit Übungsblatt 4 Aufgabe 2 (2) Verwendung der Fälschung: A schickt Fälschung M, σ. C M, σ B M, σ A Ist M, σ eine gültige Fälschung für Σ so gilt: Ver(pk, M, σ ) = Ver (pk, M, σ ) = 1 Wenn M nie von A ans Orakel geschickt, so schickt B nie M an sein Orakel d.h. M ist frisch (Wichtig!) 32 / 70
33 Sicherheit Übungsblatt 4 Aufgabe 2 (2) Beweisende: B simuliert das EUF-CMA-Spiel für A perfekt. Gibt A eine gültige Fälschung aus, so auch B. B gewinnt A gewinnt. Also: Pr[B gewinnt] nicht vernachlässigbar. Widerspruch zur EUF-CMA-Sicherheit von Σ. Σ muss ebenfalls EUF-CMA-sicher sein. 33 / 70
34 Sicherheit Übungsblatt 4 Aufgabe 2 Fazit: Was kann EUF-CMA? Theoretischen Umgang mit Signaturen üben Transformationen wie diese im Signaturumfeld sehr wichtig! 34 / 70
35 Unterbrechung... Übungsevaluation Bitte nur die Übung evaluieren obwohl wir auch VL gemacht haben, dass bitte in der VL Textantworten am Hilfreichsten :) bitte schreibt dazu, auf wen (Alex, Björn oder beide) ihr euch bezieht Vorlesungsevaluation nächsten Montag 35 / 70
36 Sicherheit Übungsblatt 4 Aufgabe 3 Authentizierter Kanal zwischen A(lice) und B(ob) Vereinfachung: Nur Nachrichten von A nach B Realisierung mit MAC MAC = (Gen, Sign, Ver) EUF-CMA-sicher Unterschied MAC/Digitale Signaturen MACs haben nur einen (geheimen) Schlüssel Angreifer hat bei EUF-CMA Zugri auf Sign-Orakel,... aber nicht auf Ver-Orakel! 36 / 70
37 Sicherheit Übungsblatt 4 Aufgabe 3 Sicherheitsdenition von authentiziertem Kanal: Setup: A Exp bereitet Schlüssel etc. vor. Exp K Gen(1 k ) c A := 0, c B := 0 L A :=, L B := 37 / 70
38 Sicherheit Übungsblatt 4 Aufgabe 3 Sicherheitsdenition von authentiziertem Kanal: Ablauf: A darf Nachrichten von A an B schicken: Alice(M) A Alice(M) (c A, M), σ Exp σ Sign(K, (c A, M)) c A := c A + 1 L A := L A {(c A, M)} 38 / 70
39 Sicherheit Übungsblatt 4 Aufgabe 3 A kann Bob ein Zähler/Nachrichten-Paar und eine Signatur empfangen lassen: Bob((c, M), σ) A Bob((c, M), σ) Exp wenn Ver(K, (c, M), σ) = 1 und c = c B, dann: L B := L B {(c, M)} c B := c B + 1 sonst: gib 0 aus (A verliert!) 39 / 70
40 Sicherheit Übungsblatt 4 Aufgabe 3 Sicherheitsdenition von authentiziertem Kanal: Ende: Exp überprüft, ob L B L A wenn ja: sonst: gebe 0 aus (A verliert) gebe 1 aus (A gewinnt) Wkt. das A gewinnt soll vernachlässigbar sein. 40 / 70
41 Sicherheit Übungsblatt 4 Aufgabe 3 Sicherheitsdenition von authentiziertem Kanal: Ende Intuition: Ziel von A: an Bob mind. eine Nachricht schicken, die... Bob akzeptiert, die aber nicht von Alice geschickt wurde! L B L A heiÿt, dass Bob nur Nachrichten akzeptiert hat, die von Alice kamen! 41 / 70
42 Sicherheit Übungsblatt 4 Aufgabe 3 Zeige: Existiert ein PPT-Angreifer A, der das Sicherheitsspiel gegen den auth. Kanal gewinnt (mit nicht-vernachlässigbarer Wahrscheinlichkeit!), dann existiert ein PPT-Angreifer B, der... dass EUF-CMA-Spiel gegen MAC gewinnt (mit nicht-vernachlässigbarer Wahrscheinlichkeit!). (d.h. MAC EUF-CMA-sicher Kanal sicher nach dieser Def.) 42 / 70
43 Sicherheit Übungsblatt 4 Aufgabe 3 B verwendet A. B spielt das EUF-CMA-Spiel mit MAC B hat Zugri auf ein Sign(K, )-Orakel B kennt K nicht! B initialisiert den Kanal und berechnet: ca := 0, c B := 0 B startet A LA := (L B wird zur Sim. nicht gebraucht) 43 / 70
44 Sicherheit Übungsblatt 4 Aufgabe 3 Beantwortung von Alice(M): Sign(K, ) (c A, M) B Alice(M) A σ c A := c A + 1 L A := L A {(c A, M)} (c A, M), σ Anfragen werden richtig beantwortet! 44 / 70
45 Sicherheit Übungsblatt 4 Aufgabe 3 Beantwortung von Bob((c A, M), σ): Schwierig, da B kein Ver-Orakel hat... B kann Gültigkeit von σ nicht überprüfen Entscheidung nur anhand von (c, M)? L A 45 / 70
46 Sicherheit Übungsblatt 4 Aufgabe 3 (c, M) L A : B prüft, ob c = c B. Wenn ja: c B := c B + 1 Sonst: Abbruch σ gültig: Alles okay! σ nicht gültig: A hätte nun eigentlich verloren... Simulation läuft trotzdem weiter Also: Simulation falsch! Es können jetzt keine Aussagen über A mehr getroen werden 46 / 70
47 Sicherheit Übungsblatt 4 Aufgabe 3 (c, M) / L A : Gebe (c, M), σ als Fälschung aus. σ gültig: Fälschung gefunden Da (c, M) / L A ist Nachricht frisch. Gewinnt A, so tritt dieser Fall ein! σ nicht gültig: Dann zwar keine gültige Fälschung aber Spiel würde dann eh abgebrochen (A hat verloren) 47 / 70
48 Sicherheit Übungsblatt 4 Aufgabe 3 Gewinnt A, so gibt B eine gültige Fälschung aus! Laufzeit von B Laufzeit von A Erfolgswkt. von B = Erfolgswkt. von A Also: Aus A einen erfolgreichen MAC-Angreifer B konstruiert 48 / 70
49 Sicherheit Übungsblatt 4 Aufgabe 3 Welchen Zweck erfüllen die Zähler c A und c B? Verhinderung von Replay-Angrien Replay-Angri: Passiver Angri Nachrichten abhören und später einfach nochmal senden Problematisch z.b. bei Fahrzeugelektronik Herzschrittmacher Türschloss / 70
50 Sicherheit Übungsblatt 4 Aufgabe 3 Fazit: Auth. Kanal realisierbar durch MACs & Zähler Unterschiedliche Sicherheitsforderungen, lassen sich aber ineinander überführen Ähnliche Implementierung bei TLS 50 / 70
51 Sicherheit Übungsblatt 4 Aufgabe 4 Doktor Meta Aufgabe (Story siehe Blatt) Betrachte folgendes Wahlverfahren: Ja/Nein-Wahl n N Wähler (polynomiell im Sicherheitsparam.) G zyklische Gruppe Ordnung p von G ist prim, p < n g sei Erzeuger, e G das neutrale Element von G Es gibt eine Wahlautorität (Organisiert die Wahl) Verwendet ElGamal-Verschlüsselung 3 Phasen: Setup, Abstimmung, Auszählung 51 / 70
52 Sicherheit Übungsblatt 4 Aufgabe 4 Setup: Wahlautorität berechnet pk = (G, g, g x ) sk = (G, g, x) mit x Z p Wahlautorität gibt pk öentlich bekannt. (also im Prinzip nichts anderes als ElGamal-Schlüsselerzeugung) 52 / 70
53 Sicherheit Übungsblatt 4 Aufgabe 4 Abstimmung: Ja-Stimme: Verschlüssele g C := Enc(pk, g) = (g y, g xy g), y Z p Nein-Stimme: Verschlüssele e G C := Enc(pk, g) = (g y, g xy e G ), y Z p Schicke C an die Wahlautorität 53 / 70
54 Sicherheit Übungsblatt 4 Aufgabe 4 Auszählung: Wahlautorität hat Chirate C 1 = (C 1,1, C 1,2 ),..., C n = (C n,1, C n,2 ) Auszählung wie folgt: 1. Berechne C = (Π n i=1 C i,1, Π n i=1 C i,2) 2. Berechne Dec(sk, C) =: M 3. Berechne DLog i von M zur Basis g (d.h. g i = M) 4. Ergebnis: i Ja-Stimmen, n i Nein-Stimmen 54 / 70
55 Sicherheit Übungsblatt 4 Aufgabe 4 (1.) (1.) Zeigen Sie, dass das Wahlverfahren das korrekte Ergebnis berechnet, wenn sich alle Parteien an das Verfahren halten. 55 / 70
56 Sicherheit Übungsblatt 4 Aufgabe 4 (1.) Sei v N 0, v < n die Anzahl der Ja-Stimmen OBdA C 1,..., C v Chirate der Ja-Stimmen, C v+1,..., C n die der Nein-Stimmen Dann gilt: 1 < i v : C i = (C i,1, C i,2 ) = (g y i, g xy i g) (mit y i Z p ) v < i n : C i = (C i,1, C i,2 ) = (g y i, g xy i e G ) (mit y i Z p ) 56 / 70
57 Sicherheit Übungsblatt 4 Aufgabe 4 (1.) Im ersten Schritt wird C = ( n i=1 C i,1, n i=1 C i,2) berechnet: n C i,1 = i=1 n C i,2 = i=1 n g y i = g y 1+ +y n, i=1 v g xy i g i=1 i=v+1 n g xy i e G = g x(y 1+ +y n) g v. C ist also Chirat von g v Somit Dec(sk, C) = g v =: M DLog g von M ist v = Anzahl Ja-Stimmen 57 / 70
58 Sicherheit Übungsblatt 4 Aufgabe 4 (2.) (2.) Wie kann der diskrete Logarithmus von M ezient berechnet werden, obwohl er in G schwierig zu berechnen sein muss? (weiterhin halten sich alle Parteien an das Verfahren) 58 / 70
59 Sicherheit Übungsblatt 4 Aufgabe 4 (2.) Anzahl Wähler n ist festgelegt... und polynomiell im Sicherheitsparameter! D.h. Brute-Force hier okay: Probiere für alle 0 i n Überprüfe, ob g i = M erfüllt Sobald erfüllt, gebe i aus i ist eindeutig und wird gefunden Laufzeit ist polynomiell, da n poly. im Sicherheitsparam. (daraus folgt: G = p exponentiell im Sicherheitsparam., damit DLog schwierig) 59 / 70
60 Sicherheit Übungsblatt 4 Aufgabe 4 (3.) (3.) Vorteil gegenüber trivialen Lösungen, z.b. Abstimmung per unverschlüsselter ? Eigentlich nur die verschlüsselte Übertragung der Stimme... Schützt (in beschränktem Maÿe) das Wahlgeheimnis (mehr dazu später) 60 / 70
61 Sicherheit Übungsblatt 4 Aufgabe 4 (4.) (4.) Wie kann man das Wahlergebnis manipulieren? Verfahren sichert weder Integrität noch Authentizität der gesendeten Stimmee Man-in-the-Middle-Angri möglich... Chirate abfangen, selbstgewählte Chirate senden; Chirate manipulieren (Homomorphie!) Unmögliche Stimmen senden: z.b. g 50 verschlüsseln = 50 Ja-Stimmen oder g 1 = -1 Ja-Stimme 61 / 70
62 Sicherheit Übungsblatt 4 Aufgabe 4 (5.) (5.) Nachteile des Verfahrens? Sehr viele / 70
63 Sicherheit Übungsblatt 4 Aufgabe 4 (5.) Manipulierbarkeit: Siehe vorherige Aufgabe 63 / 70
64 Sicherheit Übungsblatt 4 Aufgabe 4 (5.) Wahlgeheimnis: Verschlüsselung sichert Wahlgeheimnis gegenüber Dritten Wahlautorität kann aber jedes Chirat einzelne entschlüsseln und eindeutig den einzelnen Wählern zuordnen! Stimmen zwar nicht signiert o.ä., aber Wahlautorität kann sich einfach merken, wer was schickt Also: Stimmeneinsammlung muss irgendwie anonymisiert werden 64 / 70
65 Sicherheit Übungsblatt 4 Aufgabe 4 (5.) Erpressungsfreiheit: Grobe Def: Erpressung der Form Wähle Option X, sonst passiert Y soll nicht möglich sein. Hier nicht gegeben, z.b.: Wahlautorität kann Wahlgeheimnis brechen. Also: Wahlautorität kann überprüfen, wer für welche Option stimmt und dadurch Wähler erpressen. Erpressungsfreiheit ist nicht trivial! 65 / 70
66 Sicherheit Übungsblatt 4 Aufgabe 4 (5.) Nachvollziehbarkeit: Niemand kann nachvollziehen, ob die eigene Stimme tatsächlich gezählt wurde oder ob die Auszählung überhaupt korrekt ausgeführt wurde. Man möchte, dass das möglich ist Viele Verfahren geben Wähler eine Art Quittung Quittung ermöglicht Überprüfung Auch nicht einfach zu realisieren! Quittung evtl. problematisch bzgl. Erpressungsfreiheit / 70
67 Sicherheit Übungsblatt 4 Aufgabe 4 (5.) Ehrlicher Ablauf: Unehrliches Verhalten fällt nicht unbedingt auf bzw. wird nicht verhindert Insbesondere kleine Abweichungen werden kaum auallen Schicke g 1, g 2 etc. Wenn es auällt, dann erst zu spät (nach Auszählung) Mögliche (schlechte) Lösung hier: Wahlautorität entschlüsselt und überprüft alle Stimmen einzeln Aber: Problematisch bzgl. Wahlgeheimnis / 70
68 Sicherheit Übungsblatt 4 Aufgabe 4 Fazit: Wahlverfahren als Beispiel für komplexe Krypto-Protokolle Realisierung nicht trivial Wie immer: Wie deniert man überhaupt Sicherheit? Krypto. Verfahren (hier Verschlüsselung) nicht unbedingt so mächtig, wie man denkt Weitere Beispiele: Datenbankauslagerung, Cloud Computing, Mehrparteienberechnungen, Smart Meter / 70
69 Sicherheit Übungsblatt 4 Aufgabe 4 (6.) Bonusfrage: Warum muss der DLog schwierig sein, damit El- Gamal sicher sein kann? Schlüssel: pk = g x, sk = x Wäre Dlog einfach, könnte man also DLog von g x ziehen und würde den geheimen Schlüssel bekommen. 69 / 70
70 Sicherheit Übungsblatt 5 A1: RSA-Signaturen, DSA EUF-CMA Rechnen in Gruppen üben A2: Die-Hellman Schlüsselaustausch Rechnen in Gruppen üben A3: Schlüsselaustausch Formal betrachtet A4: Doktor Meta TLS bzw. CRIME Formal und Praktisch! Formal: IND-CPA Praktisch: CRIME (vereinfacht) implementieren 70 / 70
https://b.socrative.com/login/student/
 Übung zur Vorlesung Sicherheit 23.06.2016 Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 62 Feedback: Kummerkasten/Feedback
Übung zur Vorlesung Sicherheit 23.06.2016 Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 62 Feedback: Kummerkasten/Feedback
https://b.socrative.com/login/student/
 Übung zur Vorlesung Sicherheit 23.06.2016 Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 62 Feedback: Kummerkasten/Feedback
Übung zur Vorlesung Sicherheit 23.06.2016 Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 62 Feedback: Kummerkasten/Feedback
Übung zur Vorlesung Sicherheit Übungsblatt 3. Björn Kaidel 1 / 52
 Übung zur Vorlesung Sicherheit 21.05.2014 Übungsblatt 3 Björn Kaidel bjoern.kaidel@kit.edu 1 / 52 Kummerkasten Bitte helleren Laserpointer verwenden. Sind die Skriptlinks vertauscht? Nein! Wegen allgemeiner
Übung zur Vorlesung Sicherheit 21.05.2014 Übungsblatt 3 Björn Kaidel bjoern.kaidel@kit.edu 1 / 52 Kummerkasten Bitte helleren Laserpointer verwenden. Sind die Skriptlinks vertauscht? Nein! Wegen allgemeiner
Institut für Theoretische Informatik Prof. Dr. Dennis Hofheinz Übungsleiter: Thomas Agrikola. Stammvorlesung Sicherheit im Sommersemester 2017
 Institut für Theoretische Informatik Prof. Dr. Dennis Hofheinz Übungsleiter: Thomas Agrikola Stammvorlesung Sicherheit im Sommersemester 2017 Übungsblatt 4 Aufgabe 1. Wir instanziieren das ElGamal-Verschlüsselungsverfahren
Institut für Theoretische Informatik Prof. Dr. Dennis Hofheinz Übungsleiter: Thomas Agrikola Stammvorlesung Sicherheit im Sommersemester 2017 Übungsblatt 4 Aufgabe 1. Wir instanziieren das ElGamal-Verschlüsselungsverfahren
Übungsblatt 4. Stammvorlesung Sicherheit im Sommersemester Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Übungsblatt 4 Aufgabe 1. Wir instanziieren das ElGamal-Verschlüsselungsverfahren aus der
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Übungsblatt 4 Aufgabe 1. Wir instanziieren das ElGamal-Verschlüsselungsverfahren aus der
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Klausur Hinweise
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Klausur 21.07.2015 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Klausur 21.07.2015 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Übung zur Vorlesung. Sicherheit Übungsblatt 5 Björn Kaidel
 Übung zur Vorlesung Sicherheit 30.06.2016 Übungsblatt 5 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 55 Evaluation (siehe Evaluations-PDF)
Übung zur Vorlesung Sicherheit 30.06.2016 Übungsblatt 5 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 55 Evaluation (siehe Evaluations-PDF)
Vorlesung Sicherheit
 Vorlesung Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 23.05.2016 1 / 32 Überblick 1 Symmetrische Authentifikation von Nachrichten Ziel Konstruktionen MACs
Vorlesung Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 23.05.2016 1 / 32 Überblick 1 Symmetrische Authentifikation von Nachrichten Ziel Konstruktionen MACs
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz. Übungsblatt 4
 Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Übungsblatt 4 Hinweis: Übungsblätter können freiwillig bei Florian Böhl, Raum 255, Geb.
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Übungsblatt 4 Hinweis: Übungsblätter können freiwillig bei Florian Böhl, Raum 255, Geb.
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Nachklausur Hinweise
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2016 Nachklausur 12.10.2016 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2016 Nachklausur 12.10.2016 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Nachklausur. Lösung Hinweise
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2016 Nachklausur Lösung 12.10.2016 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2016 Nachklausur Lösung 12.10.2016 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Einmalsignaturen Björn Kaidel (Vertretung für Prof. Müller-Quade) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-02-01 B. Kaidel Asymmetrische
Asymmetrische Verschlüsselungsverfahren Einmalsignaturen Björn Kaidel (Vertretung für Prof. Müller-Quade) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-02-01 B. Kaidel Asymmetrische
Digitale Signaturen. Einmalsignaturen Gunnar Hartung, Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-04 B. Kaidel Digitale Signaturen: Einmalsignaturen KIT Die Forschungsuniversität
Digitale Signaturen Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-04 B. Kaidel Digitale Signaturen: Einmalsignaturen KIT Die Forschungsuniversität
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Nachklausur. Lösungsvorschlag Hinweise
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Nachklausur Lösungsvorschlag 29.09.2015 Vorname: Nachname: Matrikelnummer: Hinweise - Für
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Nachklausur Lösungsvorschlag 29.09.2015 Vorname: Nachname: Matrikelnummer: Hinweise - Für
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Vorlesung 4 Alexander Koch (Vertretung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT 2015-11-12 Universität desalexander Landes Baden-Württemberg
Asymmetrische Verschlüsselungsverfahren Vorlesung 4 Alexander Koch (Vertretung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT 2015-11-12 Universität desalexander Landes Baden-Württemberg
Vorlesung Digitale Signaturen im Wintersemester 2017/-18. Socrative-Fragen aus der Vorlesung vom
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2017/-18 Socrative-Fragen aus der Vorlesung vom 17.11.2017 1 Quiz 1:
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2017/-18 Socrative-Fragen aus der Vorlesung vom 17.11.2017 1 Quiz 1:
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz. Klausur Hinweise
 Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Klausur 22.07.2014 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Klausur 22.07.2014 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Digitale Signaturen. Sicherheitsdefinitionen Gunnar Hartung, Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Sicherheitsdefinitionen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-10-28 B. Kaidel Digitale Signaturen: Sicherheitsdefinitionen
Digitale Signaturen Sicherheitsdefinitionen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-10-28 B. Kaidel Digitale Signaturen: Sicherheitsdefinitionen
Digitale Signaturen. GHR-und Chamäleon-Signaturen Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen GHR-und Chamäleon-Signaturen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-12-15 B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen KIT
Digitale Signaturen GHR-und Chamäleon-Signaturen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-12-15 B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen KIT
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Vorlesung 4 Alexander Koch (Vertretung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-10 Alexander Koch Asymmetrische Verschlüsselungsverfahren
Asymmetrische Verschlüsselungsverfahren Vorlesung 4 Alexander Koch (Vertretung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-10 Alexander Koch Asymmetrische Verschlüsselungsverfahren
Übung zur Vorlesung Sicherheit Übungsblatt 2. Alexander Koch Björn Kaidel
 Übung zur Vorlesung Sicherheit 07.05.2014 Übungsblatt 2 Alexander Koch alexander.koch@kit.edu Björn Kaidel bjoern.kaidel@kit.edu 1 / 32 Kummerkasten In der Übung lauter und deutlicher sprechen: Wir geben
Übung zur Vorlesung Sicherheit 07.05.2014 Übungsblatt 2 Alexander Koch alexander.koch@kit.edu Björn Kaidel bjoern.kaidel@kit.edu 1 / 32 Kummerkasten In der Übung lauter und deutlicher sprechen: Wir geben
Übungsblatt 3. Stammvorlesung Sicherheit im Sommersemester Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Übungsblatt 3 Aufgabe 1. Beurteilen Sie für die folgenden Konstruktionen jeweils, ob es sich
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Übungsblatt 3 Aufgabe 1. Beurteilen Sie für die folgenden Konstruktionen jeweils, ob es sich
Übung zur Vorlesung Sicherheit Übungsblatt 2. Alexander Koch Björn Kaidel
 Übung zur Vorlesung Sicherheit 07.05.2014 Übungsblatt 2 Alexander Koch alexander.koch@kit.edu Björn Kaidel bjoern.kaidel@kit.edu 1 / 32 Kummerkasten In der Übung lauter und deutlicher sprechen: Wir geben
Übung zur Vorlesung Sicherheit 07.05.2014 Übungsblatt 2 Alexander Koch alexander.koch@kit.edu Björn Kaidel bjoern.kaidel@kit.edu 1 / 32 Kummerkasten In der Übung lauter und deutlicher sprechen: Wir geben
Digitale Signaturen. RSA-FDH & das Random Oracle Model Jiaxin Pan (Slides from Björn Kaidel and Gunnar Hartung)
 Digitale Signaturen RSA-FDH & das Random Oracle Model Jiaxin Pan (Slides from Björn Kaidel and Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-10-26 B. Kaidel Digitale
Digitale Signaturen RSA-FDH & das Random Oracle Model Jiaxin Pan (Slides from Björn Kaidel and Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-10-26 B. Kaidel Digitale
Digitale Signaturen. RSA-FDH & das Random Oracle Model Björn Kaidel (mit Folien von Gunnar Hartung)
 Digitale Signaturen RSA-FDH & das Random Oracle Model Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-12-01 B. Kaidel Digitale Signaturen:
Digitale Signaturen RSA-FDH & das Random Oracle Model Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-12-01 B. Kaidel Digitale Signaturen:
Homomorphe Verschlüsselung
 Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Institut für Theoretische Informatik Prof. Dr. D. Hofheinz. Stammvorlesung Sicherheit im Sommersemester Klausur. Lösung
 Institut für Theoretische Informatik Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2017 Klausur Lösung 02.08.2017 Vorname: Nachname: Matrikelnummer: Klausur-ID: Hinweise - Schreiben
Institut für Theoretische Informatik Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2017 Klausur Lösung 02.08.2017 Vorname: Nachname: Matrikelnummer: Klausur-ID: Hinweise - Schreiben
Digitale Signaturen. Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel.
 Digitale Signaturen Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-18 G. Hartung Digitale Signaturen: Anwendung von
Digitale Signaturen Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-18 G. Hartung Digitale Signaturen: Anwendung von
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz. Klausur Hinweise
 Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Klausur 22.07.2014 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Klausur 22.07.2014 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz. Übungsblatt 5. pk = (g, y) und sk = (g, x). ? = y H(t m) t. g s
 Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Übungsblatt 5 Hinweis: Übungsblätter können freiwillig bei Jessica Koch, Raum 256, Geb.
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Übungsblatt 5 Hinweis: Übungsblätter können freiwillig bei Jessica Koch, Raum 256, Geb.
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 15.05.2017 1 / 25 Überblick 1 Hashfunktionen Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel: RSA
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 15.05.2017 1 / 25 Überblick 1 Hashfunktionen Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel: RSA
Vorlesung Digitale Signaturen im Wintersemester 2016/-17. Socrative-Fragen aus der Vorlesung vom
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Gunnar Hartung, Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2016/-17 Socrative-Fragen aus der Vorlesung vom 25.11.2016
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Gunnar Hartung, Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2016/-17 Socrative-Fragen aus der Vorlesung vom 25.11.2016
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Digitale Signaturen Prof. Jörn Müller-Quade mit Folien von G. Hartung und B. Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-01-25 J.
Asymmetrische Verschlüsselungsverfahren Digitale Signaturen Prof. Jörn Müller-Quade mit Folien von G. Hartung und B. Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-01-25 J.
Digitale Signaturen. GHR-und Chamäleon-Signaturen Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen GHR-und Chamäleon-Signaturen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-12 B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen KIT
Digitale Signaturen GHR-und Chamäleon-Signaturen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-12 B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen KIT
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 12.05.2014 1 / 26 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 12.05.2014 1 / 26 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
Digitale Signaturen. seuf-cma & Pairings Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen seuf-cma & Pairings Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-01-19 B. Kaidel Digitale Signaturen: seuf-cma & Pairings KIT Die Forschungsuniversität
Digitale Signaturen seuf-cma & Pairings Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-01-19 B. Kaidel Digitale Signaturen: seuf-cma & Pairings KIT Die Forschungsuniversität
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Digitale Signaturen Björn Kaidel - Vertretung für Prof. Müller-Quade FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-19 B. Kaidel Asymmetrische
Asymmetrische Verschlüsselungsverfahren Digitale Signaturen Björn Kaidel - Vertretung für Prof. Müller-Quade FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-19 B. Kaidel Asymmetrische
Socrative-Fragen aus der Übung vom
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Übungsleiter: Björn Kaidel, Alexander Koch Stammvorlesung Sicherheit im Sommersemester 2016 Socrative-Fragen aus der Übung vom 28.04.2016
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Übungsleiter: Björn Kaidel, Alexander Koch Stammvorlesung Sicherheit im Sommersemester 2016 Socrative-Fragen aus der Übung vom 28.04.2016
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 5 Kryptosysteme auf der Basis diskreter Logarithmen 1. Diffie Hellman Schlüsselaustausch 2. El Gamal Systeme 3. Angriffe auf Diskrete Logarithmen 4. Elliptische Kurven
Kryptographie und Komplexität Einheit 5 Kryptosysteme auf der Basis diskreter Logarithmen 1. Diffie Hellman Schlüsselaustausch 2. El Gamal Systeme 3. Angriffe auf Diskrete Logarithmen 4. Elliptische Kurven
Digitale Signaturen. Sicherheitsdefinitionen Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Sicherheitsdefinitionen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-10-27 B. Kaidel Digitale Signaturen: Sicherheitsdefinitionen KIT Die Forschungsuniversität
Digitale Signaturen Sicherheitsdefinitionen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-10-27 B. Kaidel Digitale Signaturen: Sicherheitsdefinitionen KIT Die Forschungsuniversität
Ziel: Zertifiziere Pfad von Wurzel zu m mittels Signaturen. Signieren Public-Keys auf Pfad inklusive der Nachbarknoten.
 Merkle-Baum Idee: Konstruktion von Merkle-Bäumen Ersetze Signaturkette durch Baum (sogenannter Merkle-Baum). Verwenden Baum der Tiefe n für Nachrichten der Länge n. Die Wurzel erhält Label ɛ. Die Kinder
Merkle-Baum Idee: Konstruktion von Merkle-Bäumen Ersetze Signaturkette durch Baum (sogenannter Merkle-Baum). Verwenden Baum der Tiefe n für Nachrichten der Länge n. Die Wurzel erhält Label ɛ. Die Kinder
Vorlesung Sicherheit
 Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 04.05.2015 1 / 20 Kummerkasten Vorlesungsfolien bitte einen Tag vorher hochladen : Sollte
Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 04.05.2015 1 / 20 Kummerkasten Vorlesungsfolien bitte einen Tag vorher hochladen : Sollte
Vorlesung Sicherheit
 Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 18.05.2015 1 / 30 Überblick 1 Asymmetrische Authentifikation von Nachrichten Erinnerung
Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 18.05.2015 1 / 30 Überblick 1 Asymmetrische Authentifikation von Nachrichten Erinnerung
Kryptographische Protokolle
 Kryptographische Protokolle Lerneinheit 4: Schlüsselvereinbarung Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2017 8.5.2017 Einleitung Einleitung In dieser Lerneinheit
Kryptographische Protokolle Lerneinheit 4: Schlüsselvereinbarung Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2017 8.5.2017 Einleitung Einleitung In dieser Lerneinheit
6: Public-Key Kryptographie (Grundidee)
 6: Public-Key Kryptographie (Grundidee) Ein Teil des Schlüssels ist nur dem Empfänger bekannt. Der auch dem Sender bekannte Teil kann sogar veröffentlicht werden. Man spricht dann von einem Schlüsselpaar.
6: Public-Key Kryptographie (Grundidee) Ein Teil des Schlüssels ist nur dem Empfänger bekannt. Der auch dem Sender bekannte Teil kann sogar veröffentlicht werden. Man spricht dann von einem Schlüsselpaar.
Digitale Signaturen. seuf-cma & Pairings Gunnar Hartung, Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen seuf-cma & Pairings Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-20 B. Kaidel Digitale Signaturen: seuf-cma & Pairings KIT Die
Digitale Signaturen seuf-cma & Pairings Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-20 B. Kaidel Digitale Signaturen: seuf-cma & Pairings KIT Die
Voll homomorpe Verschlüsselung
 Voll homomorpe Verschlüsselung Definition Voll homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : R R für Ringe R, R. Π heißt voll homomorph, falls 1 Enc(m 1 ) + Enc(m 2 ) eine gültige
Voll homomorpe Verschlüsselung Definition Voll homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : R R für Ringe R, R. Π heißt voll homomorph, falls 1 Enc(m 1 ) + Enc(m 2 ) eine gültige
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz IKS, KIT 06.05.2013 1 / 25 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
Vorlesung Sicherheit Dennis Hofheinz IKS, KIT 06.05.2013 1 / 25 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
VI.4 Elgamal. - vorgestellt 1985 von Taher Elgamal. - nach RSA das wichtigste Public-Key Verfahren
 VI.4 Elgamal - vorgestellt 1985 von Taher Elgamal - nach RSA das wichtigste Public-Key Verfahren - besitzt viele unterschiedliche Varianten, abhängig von zugrunde liegender zyklischer Gruppe - Elgamal
VI.4 Elgamal - vorgestellt 1985 von Taher Elgamal - nach RSA das wichtigste Public-Key Verfahren - besitzt viele unterschiedliche Varianten, abhängig von zugrunde liegender zyklischer Gruppe - Elgamal
Digitale Signaturen. Einführung Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Einführung Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-10-20 B. Kaidel Digitale Signaturen: Einführung KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft
Digitale Signaturen Einführung Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-10-20 B. Kaidel Digitale Signaturen: Einführung KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft
Blinde Signaturen, geheime Abstimmungen und digitale Münzen
 Blinde Signaturen, geheime Abstimmungen und digitale Münzen Claus Diem Im Wintersemester 2017 / 18 Crypto 1982 Geheime Abstimmungen Eine geheime Abstimmung Problem. Eine Gruppe von Personen will per Brief
Blinde Signaturen, geheime Abstimmungen und digitale Münzen Claus Diem Im Wintersemester 2017 / 18 Crypto 1982 Geheime Abstimmungen Eine geheime Abstimmung Problem. Eine Gruppe von Personen will per Brief
Digitale Signaturen. Einführung Gunnar Hartung, Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Einführung Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-10-21 G. Hartung, B. Kaidel Digitale Signaturen: Einführung KIT Die Forschungsuniversität
Digitale Signaturen Einführung Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-10-21 G. Hartung, B. Kaidel Digitale Signaturen: Einführung KIT Die Forschungsuniversität
Sicherheit von Merkle Signaturen
 Sicherheit von Merkle Signaturen Algorithmus Angreifer A für die Einwegsignatur EINGABE: pk, Zugriff auf eine Anfrage an Orakel Sign sk ( ) 1 Berechne (pk (i), sk (i) ) Gen(1 n ) für i = 1,...,l. Wähle
Sicherheit von Merkle Signaturen Algorithmus Angreifer A für die Einwegsignatur EINGABE: pk, Zugriff auf eine Anfrage an Orakel Sign sk ( ) 1 Berechne (pk (i), sk (i) ) Gen(1 n ) für i = 1,...,l. Wähle
Kryptograhie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik
 Kryptograhie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik Übersicht Zwecke der Krytographie Techniken Symmetrische Verschlüsselung( One-time Pad,
Kryptograhie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik Übersicht Zwecke der Krytographie Techniken Symmetrische Verschlüsselung( One-time Pad,
Satz von Euler. Satz von Euler. Korollar 1. Korollar 2 Kleiner Fermat. Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G.
 Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Satz von Euler. Satz von Euler. Korollar 1. Korollar 2 Kleiner Fermat. Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G.
 Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 23.06.2014 1 / 26 Überblick 1 Zero-Knowledge-Protokolle Erinnerung Beispiel für Zero-Knowledge-Protokoll Analyse des Beispiel-Zero-Knowledge-Protokolls Proof-of-Knowledge-Eigenschaft
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 23.06.2014 1 / 26 Überblick 1 Zero-Knowledge-Protokolle Erinnerung Beispiel für Zero-Knowledge-Protokoll Analyse des Beispiel-Zero-Knowledge-Protokolls Proof-of-Knowledge-Eigenschaft
Definition Message Authentication Code (MAC) Ein Message Authentication Code (MAC) bzgl. des Nachrichtenraumen M besteht aus den ppt Alg.
 Message Authentication Code (MAC) Szenario: Integrität und Authentizität mittels MACs. Alice und Bob besitzen gemeinsamen Schlüssel k. Alice berechnet für m einen MAC-Tag t als Funktion von m und k. Alice
Message Authentication Code (MAC) Szenario: Integrität und Authentizität mittels MACs. Alice und Bob besitzen gemeinsamen Schlüssel k. Alice berechnet für m einen MAC-Tag t als Funktion von m und k. Alice
Public-Key-Verschlüsselung und Diskrete Logarithmen
 Public-Key-Verschlüsselung und Diskrete Logarithmen Carsten Baum Institut für Informatik Universität Potsdam 10. Juni 2009 1 / 30 Inhaltsverzeichnis 1 Mathematische Grundlagen Gruppen, Ordnung, Primitivwurzeln
Public-Key-Verschlüsselung und Diskrete Logarithmen Carsten Baum Institut für Informatik Universität Potsdam 10. Juni 2009 1 / 30 Inhaltsverzeichnis 1 Mathematische Grundlagen Gruppen, Ordnung, Primitivwurzeln
Hybride Verschlüsselungsverfahren
 Hybride Verschlüsselungsverfahren Ziel: Flexibilität von asym. Verfahren und Effizienz von sym. Verfahren. Szenario: Sei Π = (Gen, Enc, Dec) ein PK-Verschlüsselungsverfahren und Π = (Gen, Enc, Dec ) ein
Hybride Verschlüsselungsverfahren Ziel: Flexibilität von asym. Verfahren und Effizienz von sym. Verfahren. Szenario: Sei Π = (Gen, Enc, Dec) ein PK-Verschlüsselungsverfahren und Π = (Gen, Enc, Dec ) ein
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz. Nachklausur Hinweise
 Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Nachklausur 29.09.2014 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Nachklausur 29.09.2014 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Vorlesung Sicherheit
 Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 08.06.2015 1 / 34 Überblick 1 Schlüsselaustauschprotokolle Erinnerung Weitere Schlüsselaustauschtypen
Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 08.06.2015 1 / 34 Überblick 1 Schlüsselaustauschprotokolle Erinnerung Weitere Schlüsselaustauschtypen
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 5.2 ElGamal Systeme 1. Verschlüsselungsverfahren 2. Korrektheit und Komplexität 3. Sicherheitsaspekte Das ElGamal Verschlüsselungsverfahren Public-Key Verfahren von
Kryptographie und Komplexität Einheit 5.2 ElGamal Systeme 1. Verschlüsselungsverfahren 2. Korrektheit und Komplexität 3. Sicherheitsaspekte Das ElGamal Verschlüsselungsverfahren Public-Key Verfahren von
4 Kryptologie. Übersicht
 4 Kryptologie Übersicht 4.1 Der erweiterte euklidische Algorithmus................................ 38 4.2 Rechnen mit Restklassen modulo p................................... 39 4.3 Der kleine Satz von
4 Kryptologie Übersicht 4.1 Der erweiterte euklidische Algorithmus................................ 38 4.2 Rechnen mit Restklassen modulo p................................... 39 4.3 Der kleine Satz von
Digitale Unterschriften mit ElGamal
 Digitale Unterschriften mit ElGamal Seminar Kryptographie und Datensicherheit Institut für Informatik Andreas Havenstein Inhalt Einführung RSA Angriffe auf Signaturen und Verschlüsselung ElGamal Ausblick
Digitale Unterschriften mit ElGamal Seminar Kryptographie und Datensicherheit Institut für Informatik Andreas Havenstein Inhalt Einführung RSA Angriffe auf Signaturen und Verschlüsselung ElGamal Ausblick
Kryptologie. Bernd Borchert. Univ. Tübingen SS Vorlesung. Teil 10. Signaturen, Diffie-Hellman
 Kryptologie Bernd Borchert Univ. Tübingen SS 2017 Vorlesung Teil 10 Signaturen, Diffie-Hellman Signatur Signatur s(m) einer Nachricht m Alice m, s(m) Bob K priv K pub K pub Signatur Signatur (Thema Integrity
Kryptologie Bernd Borchert Univ. Tübingen SS 2017 Vorlesung Teil 10 Signaturen, Diffie-Hellman Signatur Signatur s(m) einer Nachricht m Alice m, s(m) Bob K priv K pub K pub Signatur Signatur (Thema Integrity
Digitale Signaturen. Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel.
 Digitale Signaturen Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-15 G. Hartung Digitale Signaturen: Anwendung von
Digitale Signaturen Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-15 G. Hartung Digitale Signaturen: Anwendung von
Aufgabe der Kryptografie
 Aufgabe der Kryptografie Eve möchte die Unterhaltung mithören und/oder ausgetauschte Informationen ändern. Alice & Bob kommunzieren über einen unsicheren Kanal. Alice & Bob nutzen Verschlüsselung und digitale
Aufgabe der Kryptografie Eve möchte die Unterhaltung mithören und/oder ausgetauschte Informationen ändern. Alice & Bob kommunzieren über einen unsicheren Kanal. Alice & Bob nutzen Verschlüsselung und digitale
VIII. Digitale Signaturen
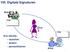 VIII. Digitale Signaturen Bob Eve Eve möchte - lauschen - ändern - personifizieren Alice 1 Aufgaben - Vertraulichkeit - Lauschen - Authentizität - Tauschen des Datenursprungs - Integrität - Änderung der
VIII. Digitale Signaturen Bob Eve Eve möchte - lauschen - ändern - personifizieren Alice 1 Aufgaben - Vertraulichkeit - Lauschen - Authentizität - Tauschen des Datenursprungs - Integrität - Änderung der
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
3 Public-Key-Kryptosysteme
 Stand: 05.11.2013 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 3 Public-Key-Kryptosysteme 3.1 Verschlüsselung von Nachrichten Wir betrachten ganz einfache Kommunikationsszenarien.
Stand: 05.11.2013 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 3 Public-Key-Kryptosysteme 3.1 Verschlüsselung von Nachrichten Wir betrachten ganz einfache Kommunikationsszenarien.
Björn Kaidel Alexander Koch
 Übung zur Vorlesung Sicherheit Übung 1 Björn Kaidel Bjoern.Kaidel@kit.edu Alexander Koch Alexander.Koch@kit.edu 23.04.2015 1 / 31 Sicherheit Literatur zur Vorlesung Jonathan Katz, Yehuda Lindell. Introduction
Übung zur Vorlesung Sicherheit Übung 1 Björn Kaidel Bjoern.Kaidel@kit.edu Alexander Koch Alexander.Koch@kit.edu 23.04.2015 1 / 31 Sicherheit Literatur zur Vorlesung Jonathan Katz, Yehuda Lindell. Introduction
Public Key Kryptographie
 3. Juni 2006 1 Algorithmen für Langzahlen 1 RSA 1 Das Rabin-Kryptosystem 1 Diskrete Logarithmen Grundlagen der PK Kryptographie Bisher: Ein Schlüssel für Sender und Empfänger ( Secret-Key oder symmetrische
3. Juni 2006 1 Algorithmen für Langzahlen 1 RSA 1 Das Rabin-Kryptosystem 1 Diskrete Logarithmen Grundlagen der PK Kryptographie Bisher: Ein Schlüssel für Sender und Empfänger ( Secret-Key oder symmetrische
Homomorphe Verschlüsselung
 Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Kurzskript MfI:AGS WS 2018/19 Teil II: Gruppen / Teil III: Ringe 34
 Kurzskript MfI:AGS WS 2018/19 Teil II: Gruppen / Teil III: Ringe 34 Satz 4.2.11 (Chinesischer Restsatz, Ring-Version) Sind N teilerfremd (d.h. ggt( ) =1), so ist die Abbildung ein Ring-Isomorphismus. :
Kurzskript MfI:AGS WS 2018/19 Teil II: Gruppen / Teil III: Ringe 34 Satz 4.2.11 (Chinesischer Restsatz, Ring-Version) Sind N teilerfremd (d.h. ggt( ) =1), so ist die Abbildung ein Ring-Isomorphismus. :
7: Grundlagen der Public-Key-Kryptographie
 7: Grundlagen der Public-Key-Kryptographie 214 7: Public-Key-Kryptographie 7: Grundlagen der Public-Key-Kryptographie Wiederholung: Symmetrische Kryptographie 1 Schlüssel für Sender und Empfänger Benötigt
7: Grundlagen der Public-Key-Kryptographie 214 7: Public-Key-Kryptographie 7: Grundlagen der Public-Key-Kryptographie Wiederholung: Symmetrische Kryptographie 1 Schlüssel für Sender und Empfänger Benötigt
El Gamal Verschlüsselung und seine Anwendungen
 El Gamal Verschlüsselung und seine Anwendungen Andrés Guevara July 11, 2005 1 Kurze Einführung in die Kryptographie Situation: Absender will Empfänger eine Nachricht schicken. Einige Ziele der Kryptographie
El Gamal Verschlüsselung und seine Anwendungen Andrés Guevara July 11, 2005 1 Kurze Einführung in die Kryptographie Situation: Absender will Empfänger eine Nachricht schicken. Einige Ziele der Kryptographie
Kryptographie II Asymmetrische Kryptographie
 Kryptographie II Asymmetrische Kryptographie Christopher Wolf Fakultät für Mathematik Ruhr-Universität Bochum Sommersemester 2010 Krypto II - Vorlesung 01-14.04.2010 () Schlüsselverteil-Center, Diffie-Hellman
Kryptographie II Asymmetrische Kryptographie Christopher Wolf Fakultät für Mathematik Ruhr-Universität Bochum Sommersemester 2010 Krypto II - Vorlesung 01-14.04.2010 () Schlüsselverteil-Center, Diffie-Hellman
Diskrete Strukturen Kapitel 5: Algebraische Strukturen (RSA-Verfahren)
 WS 2016/17 Diskrete Strukturen Kapitel 5: Algebraische Strukturen (RSA-Verfahren) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 5: Algebraische Strukturen (RSA-Verfahren) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz IKS, KIT 13.05.2013 1 / 16 Überblick 1 Asymmetrische Verschlüsselung Erinnerung Andere Verfahren Demonstration Zusammenfassung 2 Symmetrische Authentifikation von Nachrichten
Vorlesung Sicherheit Dennis Hofheinz IKS, KIT 13.05.2013 1 / 16 Überblick 1 Asymmetrische Verschlüsselung Erinnerung Andere Verfahren Demonstration Zusammenfassung 2 Symmetrische Authentifikation von Nachrichten
3: Zahlentheorie / Primzahlen
 Stefan Lucks Diskrete Strukturen (WS 2009/10) 96 3: Zahlentheorie / Primzahlen 3: Zahlentheorie / Primzahlen Stefan Lucks Diskrete Strukturen (WS 2009/10) 97 Definition 37 (Teiler, Vielfache, Primzahlen,
Stefan Lucks Diskrete Strukturen (WS 2009/10) 96 3: Zahlentheorie / Primzahlen 3: Zahlentheorie / Primzahlen Stefan Lucks Diskrete Strukturen (WS 2009/10) 97 Definition 37 (Teiler, Vielfache, Primzahlen,
3: Primzahlen. 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen
 3: Primzahlen 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen Definition 40 (Teiler, Vielfache, Primzahlen, zusammengesetzte Zahlen) Seien a, b N. a ist ein Teiler von b ( a b ), falls es ein k N gibt
3: Primzahlen 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen Definition 40 (Teiler, Vielfache, Primzahlen, zusammengesetzte Zahlen) Seien a, b N. a ist ein Teiler von b ( a b ), falls es ein k N gibt
Digitale Signaturen. Anwendung von Einmalsignaturen Björn Kaidel (mit Folien von Gunnar Hartung)
 Digitale Signaturen Anwendung von Einmalsignaturen Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-11-24 B. Kaidel Digitale Signaturen:
Digitale Signaturen Anwendung von Einmalsignaturen Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-11-24 B. Kaidel Digitale Signaturen:
Digitale Signaturen. Andreas Spillner. Kryptografie, SS 2018
 Digitale Signaturen Andreas Spillner Kryptografie, SS 2018 Ausgangspunkt Digitale Signaturen bieten unter anderem das, was man auch mit einer eigenhändigen Unterschrift auf einem Dokument bezweckt. Beispiel:
Digitale Signaturen Andreas Spillner Kryptografie, SS 2018 Ausgangspunkt Digitale Signaturen bieten unter anderem das, was man auch mit einer eigenhändigen Unterschrift auf einem Dokument bezweckt. Beispiel:
Vorlesung Diskrete Strukturen Gruppe und Ring
 Vorlesung Diskrete Strukturen Gruppe und Ring Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul Einführung in
Vorlesung Diskrete Strukturen Gruppe und Ring Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul Einführung in
Kryptographie. Nachricht
 Kryptographie Kryptographie Sender Nachricht Angreifer Empfänger Ziele: Vertraulichkeit Angreifer kann die Nachricht nicht lesen (Flüstern). Integrität Angreifer kann die Nachricht nicht ändern ohne dass
Kryptographie Kryptographie Sender Nachricht Angreifer Empfänger Ziele: Vertraulichkeit Angreifer kann die Nachricht nicht lesen (Flüstern). Integrität Angreifer kann die Nachricht nicht ändern ohne dass
Proseminar Bakkalaureat TM 2008/2009 Datensicherheit und Versicherungsmathematik Public-Key-Kryptosystem
 Proseminar Bakkalaureat TM 2008/2009 Datensicherheit und Versicherungsmathematik Technische Universität Graz 29. Dezember 2008 Überblick Unterschied zwischen symmetrischen und asymmetrischen Verschlüsselungsverfahren
Proseminar Bakkalaureat TM 2008/2009 Datensicherheit und Versicherungsmathematik Technische Universität Graz 29. Dezember 2008 Überblick Unterschied zwischen symmetrischen und asymmetrischen Verschlüsselungsverfahren
Der kleine Satz von Fermat
 Der kleine Satz von Fermat Luisa-Marie Hartmann 5. Mai 2017 Inhaltsverzeichnis 1 Einleitung 3 2 Hauptteil 4 2.1 Prime Restklassengruppen............................ 4 2.2 Ordnung von Gruppenelementen........................
Der kleine Satz von Fermat Luisa-Marie Hartmann 5. Mai 2017 Inhaltsverzeichnis 1 Einleitung 3 2 Hauptteil 4 2.1 Prime Restklassengruppen............................ 4 2.2 Ordnung von Gruppenelementen........................
Übung GSS Blatt 6. SVS Sicherheit in Verteilten Systemen
 Übung GSS Blatt 6 SVS Sicherheit in Verteilten Systemen 1 Einladung zum SVS-Sommerfest SVS-Sommerfest am 12.07.16 ab 17 Uhr Ihr seid eingeladen! :-) Es gibt Thüringer Bratwürste im Brötchen oder Grillkäse
Übung GSS Blatt 6 SVS Sicherheit in Verteilten Systemen 1 Einladung zum SVS-Sommerfest SVS-Sommerfest am 12.07.16 ab 17 Uhr Ihr seid eingeladen! :-) Es gibt Thüringer Bratwürste im Brötchen oder Grillkäse
CPA-Sicherheit ist ungenügend
 CPA-Sicherheit ist ungenügend Definition CCA CCA (=Chosen Ciphertext Attack) ist ein Angriff, bei dem der Angreifer sich Chiffretext seiner Wahl entschlüsseln lassen kann. Beispiele in denen CPA nicht
CPA-Sicherheit ist ungenügend Definition CCA CCA (=Chosen Ciphertext Attack) ist ein Angriff, bei dem der Angreifer sich Chiffretext seiner Wahl entschlüsseln lassen kann. Beispiele in denen CPA nicht
Übung zur Vorlesung Sicherheit Übungsblatt 2. Alexander Koch Björn Kaidel
 Übung zur Vorlesung Sicherheit 07.05.2014 Übungsblatt 2 Alexander Koch alexander.koch@kit.edu Björn Kaidel bjoern.kaidel@kit.edu 1 / 39 Werbung: KASTEL-Zertifikat Nachweis für Spezialisierung in IT-Sicherheit
Übung zur Vorlesung Sicherheit 07.05.2014 Übungsblatt 2 Alexander Koch alexander.koch@kit.edu Björn Kaidel bjoern.kaidel@kit.edu 1 / 39 Werbung: KASTEL-Zertifikat Nachweis für Spezialisierung in IT-Sicherheit
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Übungsblatt 5
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Übungsblatt 5 Aufgabe 1. (1.) In der Vorlesung wurde gezeigt, dass Lehrbuch-RSA-Signaturen
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Übungsblatt 5 Aufgabe 1. (1.) In der Vorlesung wurde gezeigt, dass Lehrbuch-RSA-Signaturen
4 Der diskrete Logarithmus mit Anwendungen
 4 Der diskrete Logarithmus mit Anwendungen 62 4.1 Der diskrete Logarithmus Für eine ganze Zahl a Z mit ggt(a, n) = 1 hat die Exponentialfunktion mod n zur Basis a exp a : Z M n, x a x mod n, die Periode
4 Der diskrete Logarithmus mit Anwendungen 62 4.1 Der diskrete Logarithmus Für eine ganze Zahl a Z mit ggt(a, n) = 1 hat die Exponentialfunktion mod n zur Basis a exp a : Z M n, x a x mod n, die Periode
Wiederholung. Symmetrische Verfahren: klassische Verfahren / grundlegende Prinzipien: Substitution, Transposition, One-Time-Pad DES AES
 Wiederholung Symmetrische Verfahren: klassische Verfahren / grundlegende Prinzipien: Substitution, Transposition, One-Time-Pad DES AES Mathematische Grundlagen: algebraische Strukturen: Halbgruppe, Monoid,
Wiederholung Symmetrische Verfahren: klassische Verfahren / grundlegende Prinzipien: Substitution, Transposition, One-Time-Pad DES AES Mathematische Grundlagen: algebraische Strukturen: Halbgruppe, Monoid,
Beliebige Anzahl von Signaturen
 Beliebige Anzahl von Signaturen Algorithmus Signaturketten Sei Π = (Gen, Sign, Vrfy) ein Einwegsignaturverfahren. 1 Gen : (pk 1, sk 1 ) Gen(1 n ) 2 Sign : Signieren der Nachricht m i. Verwende gemerkten
Beliebige Anzahl von Signaturen Algorithmus Signaturketten Sei Π = (Gen, Sign, Vrfy) ein Einwegsignaturverfahren. 1 Gen : (pk 1, sk 1 ) Gen(1 n ) 2 Sign : Signieren der Nachricht m i. Verwende gemerkten
Ununterscheidbarkeit von Chiffretexten
 Ununterscheidbarkeit von Chiffretexten Spiel Ununterscheidbarkeit von Chiffretexten PrivK eav A,Π (n) Sei Π ein Verschlüsselungsverfahren und A ein Angreifer. 1 (m 0, m 1 ) A. 2 k Gen(1 n ). 3 Wähle b
Ununterscheidbarkeit von Chiffretexten Spiel Ununterscheidbarkeit von Chiffretexten PrivK eav A,Π (n) Sei Π ein Verschlüsselungsverfahren und A ein Angreifer. 1 (m 0, m 1 ) A. 2 k Gen(1 n ). 3 Wähle b
Diffie-Hellman, ElGamal und DSS. Vortrag von David Gümbel am 28.05.2002
 Diffie-Hellman, ElGamal und DSS Vortrag von David Gümbel am 28.05.2002 Übersicht Prinzipielle Probleme der sicheren Nachrichtenübermittlung 'Diskreter Logarithmus'-Problem Diffie-Hellman ElGamal DSS /
Diffie-Hellman, ElGamal und DSS Vortrag von David Gümbel am 28.05.2002 Übersicht Prinzipielle Probleme der sicheren Nachrichtenübermittlung 'Diskreter Logarithmus'-Problem Diffie-Hellman ElGamal DSS /
Digitale Signaturen. Parameterwahl & RSA-PSS Björn Kaidel (mit Folien von Gunnar Hartung)
 Digitale Signaturen Parameterwahl & RSA-PSS Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-15 B. Kaidel Digitale Signaturen: RSA-PSS
Digitale Signaturen Parameterwahl & RSA-PSS Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-15 B. Kaidel Digitale Signaturen: RSA-PSS
Das Rucksackproblem. Definition Sprache Rucksack. Satz
 Das Rucksackproblem Definition Sprache Rucksack Gegeben sind n Gegenstände mit Gewichten W = {w 1,...,w n } N und Profiten P = {p 1,...,p n } N. Seien ferner b, k N. RUCKSACK:= {(W, P, b, k) I [n] : i
Das Rucksackproblem Definition Sprache Rucksack Gegeben sind n Gegenstände mit Gewichten W = {w 1,...,w n } N und Profiten P = {p 1,...,p n } N. Seien ferner b, k N. RUCKSACK:= {(W, P, b, k) I [n] : i
6. Übung - Kanalkodierung/Datensicherheit
 6. Übung - Kanalkodierung/Datensicherheit Informatik I für Verkehrsingenieure Aufgaben inkl. Beispiellösungen 1. Aufgabe: Kanalkodierung a) Bestimmen Sie die Kodeparameter (n, l, d min ) des zyklischen
6. Übung - Kanalkodierung/Datensicherheit Informatik I für Verkehrsingenieure Aufgaben inkl. Beispiellösungen 1. Aufgabe: Kanalkodierung a) Bestimmen Sie die Kodeparameter (n, l, d min ) des zyklischen
