Structure-Acoustic Coupling
|
|
|
- Damian Rosenberg
- vor 5 Jahren
- Abrufe
Transkript
1 Eingereicht von Lukas Burgholzer Angefertigt am Institut für Numerische Mathematik Betreuer Dipl.-Ing. Dr. Martin Neumüller November 2016 Structure-Acoustic Coupling Bachelorarbeit zur Erlangung des akademischen Grades Bachelor of Science im Bachelorstudium Technische Mathematik JOHANNES KEPLER UNIVERSITÄT LINZ Altenbergerstraße Linz, Österreich DVR
2 Abstract The goal of this bachelor thesis is the coupling of the defining equations for mechanics and acoustics to form a so-called structure-acoustic coupling problem. In the first chapter we will therefore develop a model for the mechanical structure by in a first step deriving the three fundamental equations for mechanics (the equilibrium equation, the strain-displacement-relation and the constitutive equation). We will then combine these to arrive at the Navier- Lamé equation for isotropic, homogeneous, elastic materials. At the end of the first chapter we consider two special cases (the plane strain state and the plain stress state). The second chapter deals with a model for acoustics where we derive the corresponding fundamental equations (the continuity equation, the Euler equation and the state equation). We then consider linear versions of these equations and combine them to form the linear acoustic wave equation. Then we have a look at two special cases (plane waves and spherical waves) and at the end of the chapter we derive a non-linear acoustic wave equation, also called Kuznetsov equation. In the third chapter we will then consider the coupling of both linear models. For this we examine a solid immersed in an acoustic field and find coupling conditions which have to hold at the solid-fluid interface. Then we transform the Navier-Lamé equation and the linear acoustic wave equation into their weak formulation and finally combine them to one system of coupled equations. The last chapter provides some conclusions and gives an outlook on possible further work.
3 Zusammenfassung Das Ziel dieser Bachelorarbeit ist die Kopplung der beschreibenden Gleichungen der Mechanik und der Akustik, die dann ein sogennantes Fluid-Struktur Kopplungsproblem bilden. Im ersten Kapitel entwickeln wir daher ein Modell für die Mechanik, angefangen von der Herleitung der drei fundamentalen Gleichungen der Mechanik (die Gleichgewichtsgleichung, die Verzerrungs- Verschiebungs-Relation und die Zustandsgleichung). Diese werden wir dann kombinieren um zur Navier-Lamé Gleichung für isotrope, homogene, elastische Materialen zu kommen. Am Ende des ersten Kapitels betrachten wir zwei Spezialfälle (den ebenen Verzerrungszustand und den ebenen Spannungszustand). Das zweite Kapitel beschäftigt sich mit einem Model für die Akustik, wo wir die entsprechenden beschreibenden Gleichungen herleiten (die Kontinuitätsgleichung, die Bewegungsgleichung und die Zustandsgleichung der Akustik). Wir betrachten dann lineare Versionen dieser Gleichungen und kombinieren sie zur linearen akustischen Wellengleichung. Dann folgen zwei Spezialfälle (Ebene Wellen und Kugelwellen) und am Ende des Kapitels leiten wir eine nichtlineare akustische Wellengleichung, auch Kuznetsov Gleichung genannt, her. Im dritten Kapitel betrachten wir dann die Kopplung beider linearen Modelle. Dafür analysieren wir einen von einem akustischen Feld umgebenen Festkörper und finden Kopplungsbedingungen, welche an der Schnittstelle zwischen Festkörper und Fluid gelten müssen. Dann führen wir die Navier-Lamé Gleichung und die lineare akustische Wellengleichung in ihre schwache Formulierung über und kombinieren sie zu einem einzigen gekoppelten System von Gleichungen. Im letzten Kapitel finden sich einige Schlussbemerkungen und ein Ausblick auf Möglichkeiten der Weiterarbeit. ii
4 Notation R v e (i) n set of real numbers vector i-th Cartesian unit vector unit normal vector Σ 1 set of unit vectors, i.e. Σ 1 := {v R 3 : v = 1} Ω Ω div curl / x / n d/dx u i,j dx Ω Γ ds x boundary of Ω closure of Ω divergence gradient curl Laplace operator partial derivative normal derivative material/total derivative u i x j volume integral surface integral Euclidean norm, Euclidean inner product A : B 3 i,j=1 A ijb ij iii
5 Contents 1 Derivation of a model for the mechanical structure Stress State - Kinetic Cauchy Stress Tensor Equilibrium of Forces and Moments Strain State - Kinematic Green-St.Venant Strain Tensor Chauchy s Strain Tensor Constitutive Equation - Hook s Law Navier - Lamé s Equation Static Case Dynamic Case Special Cases Plane Strain State Plane Stress State Derivation of a model for the acoustic field Introduction to Acoustics Mass Conservation - Continuity Equation Conservation of Momentum - Euler s Equation Pressure-Density-Relation - State Equation Ideal gases Liquids Linear Acoustic Wave Equation Acoustic Quantities Special Cases Plane Waves Spherical Waves Non-linear Acoustic Wave Equation Non-linear Euler s Equation Non-linear State Equation Combination of Equations Coupling of the two models Solid-Fluid Interface iv
6 3.2 Coupled formulation Mechanical field Acoustic field Coupled System Conclusions 27 Bibliography 28 v
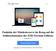
7 Chapter 1 Derivation of a model for the mechanical structure In this chapter we will develop a model for the mechanical field. Therefore we will derive the three defining equations the equilibrium equation, the strain-displacement-relation, the constitutive equation, and combine them to arrive at the Navier-Lamé equation. We will then have a look at two special cases, see Section Stress State - Kinetic t (n) Ω f B Γ = Ω n B Figure 1.1.1: Mechanical Field Let us consider a solid body, which occupies the region Ω R 3 with sufficiently smooth boundary Γ = Ω (see Figure 1.1.1). A bounded sub-region of Ω with sufficiently smooth boundary is called a part. We distinguish two kinds of forces acting on Ω: 1
8 volume forces: act on all particles of Ω, e.g. gravity or electromagnetic forces. surface tractions: describe the interaction of two adjacent parts of the body across the separating surface. Surface forces only act on the surface of a body or part of it and do not only depend on the position x Ω, but also on the normal vector n on the surface. For example the pressure acting on a solid immersed in water. It is assumed as an axiom, that a density f (volume force density), depending only on the position x, for the total amount of volume forces F V (B) acting on a part B Ω exists, i.e. F V (B) = f(x) dx. Moreover, it is postulated that for all parts B of Ω there exists a density t (surface traction density), depending on the position x B and the normal vector n(x), for the sum of all surface tractions F S (B) acting on B, i.e. F S (B) = t (n) (x) ds x. B If B Ω we can imagine this as internal surface tractions. Then t (n) (x) describes the force density at which the parts of the body at location x press against each other in direction n (see Figure 1.1.1). Thus, we have that the sum of all forces acting on a part B Ω is given by F (B) = F V (B) + F S (B). For a point x Ω we define the stress state by B {t (n) (x): n Σ 1 } Cauchy Stress Tensor If we now fix a point x Ω and consider the surface force density t with respect to the Cartesian coordinate unit vectors {e (1), e (2), e (3) } as directions, we obtain the so called Cauchy stress tensor t (e(1)) (x) =: (σ 11 (x), σ 12 (x), σ 13 (x)), t (e(2)) (x) =: (σ 21 (x), σ 22 (x), σ 23 (x)), t (e(3)) (x) =: (σ 31 (x), σ 32 (x), σ 33 (x)) σ = σ(x) = [σ ij ] 3 i,j=1, where the (i, j)-th component denotes the j-th component of the force acting on a cutting plane orthogonal to the x i axis. We call (σ 11, σ 22, σ 33 ) normal stresses and (σ 12, σ 13, σ 21, σ 23, σ 31, σ 32 ) shear stresses. 2
9 Cauchy s stress theorem Cauchy s stress theorem tells us that it is sufficient to know the Cauchy stress tensor to describe the whole stress state in a point x. It states t (n) i (x) = 3 σ ji (x)n j (x) = (σ n) i for n = (n 1, n 2, n 3 ) Σ 1. j=1 The theorem can be proven by considering a body with an oblique cutting face and investigating on the equilibrium of the forces acting on it. For a detailed proof, see [1, p. 52] Equilibrium of Forces and Moments We know from Newton s second law of motion that the sum of all forces acting on a body is equal to the mass of the body times its acceleration, which is called inertia. It also states that the sum of all moments is equal to the moment of inertia. Static Case In the static case, i.e. a body at rest, there is no acceleration, which means that the sum of all forces acting on all parts of the body has to be zero. This is expressed as F (Ω ) = F V (Ω ) + F S (Ω ) = f(x) dx + Ω t (n) (x) ds x = 0 Ω for all Ω Ω with Ω sufficiently smooth. Using Cauchy s stress theorem and Gauß s theorem (see [4, p. 729]) we obtain Ω [f(x) + div(σ)] dx = 0. We now utilize the so-called Euler trick to get rid of the integral. Theorem 1.1. (Euler trick) Let f C(Ω). If f(x) dx = 0 for arbitrary V Ω, then V f(x) = 0 x Ω. 3
10 Proof. Assume f(x) 0 for some x Ω. Since f is continuous, it is also non-zero in a neighborhood U x of x. However, choosing V = U x yields U x f(x) dx > 0, which leads to a contradiction. So f(x) = 0 for all x Ω. Since Ω was chosen arbitrary we may use Theorem 1.1 to drop the integral and arrive at the equilibrium equation for a body at rest div(σ) = f. (1.1) Now we consider the sum of all moments, which should be zero, as for the equilibrium of forces x f(x) dx + Ω x t (n) (x) ds x = 0. Ω (1.2) From this it follows that the stress tensor σ is symmetric. Proof. To keep the proof short we define σ ji,j := 3 j=1 σ ji x j for i = 1, 2, 3. Then, by using partial integration, it holds that x 2 σ j3,j x 3 σ j2,j x divσ dx = x 3 σ j1,j x 1 σ j3,j dx Ω Ω x 1 σ j2,j x 2 σ j1,j σ 23 σ 32 = σ 31 σ 13 dx + x σ }{{} n ds x. Ω σ 12 σ Ω 21 =t (n) (x) Substituting this into the equilibrium of moments (1.2) and using (1.1) we get σ 23 σ 32 x [f + divσ] σ 31 σ 13 dx = 0. Ω }{{} Ω σ 12 σ 21 =0 Since Ω was chosen arbitrary, there must hold σ = σ. If we specify a given surface traction g acting on the boundary Γ of Ω this corresponds to the boundary condition t (n) = σ n = g. 4
11 Dynamic Case In the dynamic case we consider a time frame (0, T ) and a body Ω with density ρ(x). Let u(x, t) denote the displacement of the body and a(x, t) = 2 u(x, t) its acceleration. Then we obtain the equation for the equilibrium of t 2 forces f(x, t) dx + t (n) (x, t) ds x = a(x, t)ρ(x) dx Ω Ω Ω for all Ω Ω and all t (0, T ), which leads to the equilibrium equation for a body in motion ρa div(σ) = f (1.3) by applying the same procedure as in the static case. For the equilibrium of moments we get x f(x, t) dx + Ω x t (n) (x, t) ds x = Ω x a(x, t)ρ(x) dx Ω from which it follows in a similar manner as for (1.2) that the stress tensor is symmetric. 1.2 Strain State - Kinematic Green-St.Venant Strain Tensor Under the influence of external forces a material point x of a deformable body Ω moves in a new position x + u(x) with the displacement vector u 1 (x) u(x) = u 2 (x) for x Ω R 3. u 3 (x) The distance ds between the point x and a neighboring point x+dx changes through deformation to ds, i.e. ds = dx and ds = dx + du where du = u(x + dx) u(x). We have (ds ) 2 = dx + du, dx + du = (ds) dx, du + du 2. Since we are interested in the case dx 0, the following relation is reasonable du ( u)dx. We will now calculate the change in length (ds ) 2 (ds) 2 (ds ) 2 (ds) 2 = 2 dx, du + du 2 = 2 dx, ( u)dx + ( u)dx, ( u)dx = 2 ( u) dx, dx + ( u) ( u)dx, dx. 5
12 Since 2 ( u) dx, dx = ( u) dx, dx + ( u)dx, dx we arrive at (ds ) 2 (ds) 2 = ( u + u + u u)dx, dx = 2 e(u)dx, dx where e = e(u) = 1 2 ( u + u + u u) (1.4) denotes the Green-St.Venant strain tensor. The component e kk describes the relative change in length of a line element ds parallel to the x k axis for k = 1, 2, 3. Whereas e kl for l k describes the angular change between two line elements dx k and dx l Chauchy s Strain Tensor If we assume that ( u) kl 1 for k = 1, 2, 3, we can neglect the quadratic terms of the Green-St.Venant strain tensor and arrive at the Cauchy strain tensor ε e(u) ε(u) := 1 2 ( u + u ). (1.5) 1.3 Constitutive Equation - Hook s Law For linear elastic material we assume that a linear stress-strain-relation between σ and ε is given by σ ij = 3 D ijkl ε kl i, j = 1, 2, 3 (Hook s Law) k,l=1 with the elastic coefficients D ijkl for i, j, k, l = 1, 2, 3. We call the material homogeneous if the elastic coefficients do not depend on x and in-homogeneous otherwise. From the symmetry of the stress and the strain tensor it follows that the elastic coefficients fulfill D ijkl = D klji and D ijkl = D jikl = D jilk. From this it follows that we can associate this fourth-order tensor D, indexed by (i, j, k, l), with a second-order tensor D, indexed by (I, K), in the following 6
13 way ij/kl I/K and D is symmetric. Thus only 21 of the 81 coefficients of D can be chosen independently. Materials which have no preferred direction, i.e. one can arbitrarily rotate the object and the output of the deformation stays the same, are called isotropic. One can show, that for isotropic materials only 2 coefficients can be chosen independently and that for linear elastic isotropic material Hook s law then reads σ = λ tr(ε(u))i + 2µ ε(u) (1.6) with the so-called Lamé parameters λ and µ. For details see [3]. Instead of the Lamé parameters one can use the elasticity modulus E and the Poisson ratio ν which are given by E = µ(3λ + 2µ) λ + µ, ν = 1 λ 2 λ + µ with the inverse relation λ = Eν (1 + ν)(1 2ν), µ = E 2(1 + ν). The parameters E and ν can be determined experimentally. 1.4 Navier - Lamé s Equation Static Case From The kinetic - equilibrium equation (1.1) divσ = f The kinematic - strain-displacement-relation (1.5): ε = 1( u + 2 u ) The constitutive equation - Hook s law (1.6): σ = λ tr(ε(u))i+2µ ε(u) 7
14 we can now derive the Lamé Equation for isotropic and homogeneous elastic materials in the static case: f (1.1) = divσ (1.6) = div(λtr(ε)i + 2µε) (1.5) = λ div(tr( u))i µ div( u) µ div( u ) = µ u (λ + µ) (div u). So the Lamé equation now reads Dynamic Case µ u (λ + µ) (div u) = f. (1.7) For the dynamic case we derived the equilibrium equations (1.3): ρ 2 u divσ = f. t2 Following the same procedure as above we arrive at the Navier-Lamé equation for isotropic and homogeneous elastic materials in the dynamic case: 1.5 Special Cases Plane Strain State ρ 2 u µ u (λ + µ) (div u) = f. (1.8) t2 Assume a body K R 3 with constant cross-section Ω R 2, which is much longer in one dimension than in the other two: K = {x R 3 : (x 1, x 2 ) Ω, L < x 3 < L} with L diam(ω). The volume forces f and surface tractions t act on the plane which is orthogonal to the x 3 -axis and are independent of x 3, i.e. f 1 (x 1, x 2 ) t 1 (x 1, x 2 ) f(x) = f 2 (x 1, x 2 ), t(x) = t 2 (x 1, x 2 ) x and we assume ε 3i = ε i3 = 0 for i = 1, 2, 3. 8
15 Then the displacement field u has the following form u 1 (x 1, x 2 ) u(x) = u 2 (x 1, x 2 ), 0 since 0 = ε 33 = u 3 x 3 and 0 = u i x 3 = u 3 x i for i = 1, 2 and therefore u 3 is constant. W.l.o.g. we can set this constant to 0. It follows from the assumptions that σ 13 = σ 31 = σ 23 = σ 32 = 0 and that σ 33 can be expressed by σ 11 and σ 22, because σ 33 = λ(ε 11 + ε 22 ) = λ 2(λ + µ) (σ 11 + σ 22 ). It can therefore be eliminated and the Lamé equation now simplifies from a 3D equation to a 2D equation: ( ) ( ) µ ũ (λ + µ) (div ũ) = f u1 (x with ũ = 1, x 2 ), u 2 (x 1, x 2 ) f f1 (x = 1, x 2 ). f 2 (x 1, x 2 ) Plane Stress State Consider a deformation problem for a plate K = {x R 3 : (x 1, x 2 ) Ω, h < x 3 < h} with h diam(ω). under the influence of x 3 -independent volume forces and surface tractions f 1 (x 1, x 2 ) t 1 (x 1, x 2 ) f(x) = f 2 (x 1, x 2 ), (x 1, x 2 ) Ω, t(x) = t 2 (x 1, x 2 ), (x 1, x 2 ) Γ t 0 0 and It is then assumed that t(x 1, x 2, +h) = t(x 1, x 2, h) = 0, (x 1, x 2 ) Ω. σ ij (x 1, x 2, x 3 ) = σ ij (x 1, x 2 ) for i, j = 1, 2 σ 3i = σ i3 = 0 for i = 1, 2, 3. From which it follows that ε 33 can be expressed by ε 11 and ε 22 as ε 33 = λ(ε 11 + ε 22 ) λ + 2µ. 9
16 This leads to ( ) σ11 σ σ = 12 σ 21 σ 22 with σ ij = 2λµ λ + 2µ (ε 11 + ε 22 )δ ij + 2µε ij for i, j = 1, 2 and therefore, we arrive arrive at the same equations as for the plane strain state, but with λ = 2λµ λ+2µ. 10
17 Chapter 2 Derivation of a model for the acoustic field In this chapter we will develop a model for the acoustic field. Therefore we will derive the three defining equations the continuity equation, Euler s equation, the state equation, and combine them to arrive at the linear acoustic wave equation. We will then consider some acoustic quantities and two special cases and end the chapter with a section on the nonlinear acoustic wave theory. 2.1 Introduction to Acoustics We will limit ourselves to wave propagation in fluids like air and water, so called non-viscous media. Sound (waves) can be described as small pressure fluctuations in the media. Therefore we introduce the following quantities, which one can compose into their mean part, denoted by a subscript 0, and their alternating part, denoted by a prime: the density ρ = ρ 0 + ρ, the pressure p = p 0 + p, the velocity v = v 0 + v, where ρ is called acoustic density, p the acoustic pressure and v the acoustic particle velocity. In the linear theory we assume small fluctuations, i.e. that the alternating parts are much smaller then the mean quantities. We will now derive the three defining equations for the acoustic field. 11
18 2.2 Mass Conservation - Continuity Equation Γ = Ω n Ω Figure 2.2.1: Acoustic Field Consider a volume Ω with boundary Γ and given density ρ(x, t) (see Figure 2.2.1). Then the mass m at time t is given by m(t) = ρ(x, t) dx. Ω If we now consider a time step t, a reduction of mass has to be balanced by a mass flow through the surface Γ, which can be stated as ρ v n t ds x = (ρ(x, t + t) ρ(x, t)) dx. Γ Ω Now we multiply the above equation by 1, take the limit t 0 and apply t Gauß s theorem (see [4, p. 729]) to obtain Ω div(vρ) dx = Ω ρ t dx. And since Ω was chosen arbitrary we may use Theorem 1.1 and drop the integral to obtain the continuity equation div(vρ) = ρ t. (2.1) 2.3 Conservation of Momentum - Euler s Equation As for the mechanical field we now consider the equilibrium of moments. Newton s first law of motion tells us that force is equal to mass times acceleration. We consider a point x = (x 1, x 2, x 3 ) Ω and a small cube x around x, i.e. x = (x 1 x 1 2, x 1 + x 1 2 ) (x 2 x 2 2, x 2 + x 2 2 ) (x 3 x 3 2, x 3 + x 3 2 ), 12
19 x x 3 x 2 x 1 Figure 2.3.1: Cube x around x Ω with x i R + for i = 1, 2, 3, see Figure The cube s mass is then given by m = ρ x 1 x 2 x 3. Let a denote the acceleration, which is given by the material derivative (see [1, p. 142]) of the velocity v, i.e. a = dv dt = v + v v, (2.2) t since the position of particles is time dependent. Then Newton s law tells us that f = a m. In our case the force f is the pressure change in the media which is characterized as ( pn) where n denotes the outer normal vector. So we have and since f 1 = ( p(x 1 + x 1 2, x 2, x 3 ) p(x 1 x 1 2, x 2, x 3 ) ) x 2 x 3, f 2 = ( p(x 1, x 2 + x 2 2, x 3) p(x 1, x 2 x 2 2, x 3) ) x 1 x 3, f 3 = ( p(x 1, x 2, x 3 + x 3 2 ) p(x 1, x 2, x 3 x 3 2 )) x 1 x 2, ( p(x1 + x 1 2, x 2, x 3 ) p(x 1 x 1 2, x 2, x 3 ) ) p x 1, x 1 ( p(x1, x 2 + x 2 2, x 3) p(x 1, x 2 x 2 2, x 3) ) p x 2, x 2 ( p(x1, x 2, x 3 + x 3 2 ) p(x 1, x 2, x 3 x 3 2 )) p x 3, x 3 13
20 we obtain f = p x 1 x 2 x 3. (2.3) Combining (2.2) and (2.3) we now arrive at Euler s equation ( ) v ρ t + v v = p. (2.4) 2.4 Pressure-Density-Relation - State Equation We now want to derive a relation between the pressure p and the density ρ. Therefore we consider a fluid in rest, occupying the volume Ω 0 with pressure p 0 and density ρ 0, and a fluid where an acoustic wave propagates, characterized by a volume Ω, pressure p and density ρ. If we now assume no thermal exchange between fluid particles it holds that ( Ω0 Ω ) κ = p p 0, where κ denotes the so called adiabatic exponent, for details see [1, p. 143]. If we further assume constant mass, i.e. we get that m 0 = ρ 0 Ω 0 = ρω, ( ρ ρ 0 We now consider two types of fluids: Ideal gases ) κ = p p 0. (2.5) Let us consider an ideal gas, let T denote the temperature and R the specific gas constant, then we have the relation p = ρrt and the speed of sound c can be written as c = κrt, see [6, p. 16]. Since we consider the linear acoustic theory we may approximate ( ) κ ( ) ρ ρ0 + ρ κ = 1 + κ ρ ρ 0 and arrive at the linear state equation for acoustic waves ρ 0 ρ 0 p ρ = κ p 0 ρ 0 = c 2. (2.6) 14
21 2.4.2 Liquids For liquids we view the pressure p as a quantity depending on the density ρ and the specific entropy s, which is related to heat transfer (see [1, p. 143]). The main pressure density relation is then given by p(ρ, s) ρ = K s ρ, where K s denotes the adiabatic bulk modulus, see [6, p. 16]. Additionally the speed of sound c can now be expressed as K s c = ρ, see [6, p. 17]. 2.5 Linear Acoustic Wave Equation In this section we want to combine the three derived equations (2.1), (2.4) and (2.6) to arrive at the linear acoustic wave equation. Since we only consider linear theory for now, we can assume that v ρ ρ divv ρ 0 divv and v v v t. Therefore Euler s equation simplifies to and the continuity equation to v t = 1 ρ 0 p (2.7) divv = 1 ρ 0 ρ t. (2.8) Now we may replace the total physical quantities (v, p, ρ) with the acoustic quantities (v, p, ρ ), since all derivatives of the mean quantities (v 0, p 0, ρ 0 ) are zero. By differentiating the linear continuity equation (2.8) with respect to t, we get t divv = 1 2 ρ ρ 0 t, 2 and by switching the order of differentiation the equation becomes div( v t ) = 1 ρ 0 2 ρ t 2. 15
22 Using the linear Euler equation (2.7) yields div( 1 ρ 0 p ) = 1 ρ 0 2 ρ t 2. (2.9) Now we combine (2.9) with the linear state equation (2.6) ρ = p /c 2 to arrive at the linear acoustic wave equation for p p = 1 c 2 2 p t 2. (2.10) One can show that for the acoustic particle velocity v it holds that curl(v ) = 0, i.e. v is irrotational, see [1, p. 145], and therefore we can write v as the gradient of a scalar function ψ, which is then called the acoustic velocity potential v = ψ. (2.11) It follows from substituting the acoustic velocity potential into (2.7), that the relation between p and ψ is given by p = ρ 0 ψ t. (2.12) Thus, we can state the wave equation for the acoustic velocity potential 2.6 Acoustic Quantities ψ = 1 c 2 2 ψ t 2. (2.13) In this section we want to state some important acoustic quantities, namely the acoustic energy density, the acoustic energy flux and acoustic impedance. Starting from the linear Euler equation (2.7), taking the dot product with v and combining this with the linear continuity equation (2.8) and the linear state equation (2.6) yields the following equation with the acoustic energy flux and the total acoustic energy density w a = w kin a w a t + divi a = 0 (2.14) I a = v p + w pot a with w kin a = 1 2 ρ 0 v 2 and w pot a = (p ) 2 2ρ 0 c 2, 16
23 which consists of the acoustic kinetic energy wa kin and the acoustic potential energy density wa pot. Let us now consider an acoustic source with constant angular frequency ω = 2πf. Then we can write p (t) = ˆp cos(ωt) and v (t) = ˆv cos(ωt + φ). In doing so we can calculate the time averaged acoustic energy density wa av and intensity I av a (for details see [1, p. 147]) and get w av a = 1 4 ρ 0 ˆv 2 and I av a = ˆpˆv 2 cos φ. Replacing the acoustic quantities with their time averaged ones in (2.14) results in divi av a = 0 which implies divi av a dx = I av a n ds x = 0. Ω Γ This only holds if the volume under consideration does not contain any acoustic sources. For the case of a volume which encloses an acoustic source, the result of the integral is the average acoustic power radiated by all enclosed sources Pa av Γ I av a n ds x = P av a. Another important quantity by which we characterize acoustic media (see Section 2.7) is the acoustic impedance Z a 2.7 Special Cases Z a = p v. There are two special cases we will treat in this section. First we will look at so-called plane waves and then we will have a look at so-called spherical waves Plane Waves A wave is called plane wave if it shows the same behavior in the plane orthogonal to the direction of propagation (see Figure 2.7.1). This allows us, to write the pressure p as a one-dimensional function in space and the velocity proportional to e (1), i.e. p = p(x, t) and v = v (x, t)e (1). 17
24 p = p (x, t) Figure 2.7.1: Plane Wave By substituting this ansatz into the linear wave equation (2.10), we get which could also be written as ( x 1 c 2 p x 1 2 p 2 c t = 0, 2 t )( x + 1 c By introducing the new variables ξ and η as t )p = 0. ξ = t x c and η = t + x c, and expressing space and time derivatives by the new variables t = ξ + η the wave equation becomes and 1 4c 2 ξ η p = 0. x = 1 c ( η ), (2.15) ξ This means that the unknown p can be written as the sum of one function depending only on η and one only depending on ξ, i.e. p = f(η) + g(ξ) = f(t x c ) + g(t + x c ), which describes a wave moving with the speed of sound in direction +x and x. To obtain a relation between p and v we utilize the linear state equation (2.6) and use (2.15) in the linear, 1D version of the equations for momentum (2.7) and mass (2.8) conservation, which leads to ξ (p ρ 0 cv )+ η (p +ρ 0 cv ) = 0 and ξ (ρ 0cv p )+ η (ρ 0cv +p ) = 0. 18
25 Adding these two equations yields η (p + ρ 0 cv ) = 0 which means, that (p + ρ 0 cv ) is a function of ξ, while subtracting the two equations tells us that ξ (ρ 0cv p ) = 0 which means that (ρ 0 cv p ) is a function of η. Thus we have that v = 1 ρ 0 c (f(t x c ) + g(t + x p )) = c ρ 0 c. So for plane waves we have that the ratio p v the specific acoustic impedance is constant. This is then called Z 0 = p v = ρ 0 c. If we further look at the acoustic energy density w a, which simplifies to w a = ρ 0(v ) (p ) 2 2ρ 0 c 2 = (p ) 2 ρ 0 c 2, we see that for a plane wave the acoustic kinetic energy and the acoustic potential energy are equal. Considering the acoustic energy intensity I a we get I a = (p ) 2 ρ 0 c e 1 = cw a e 1 which can be interpreted as the acoustic energy moving with the speed of sound Spherical Waves For a spherical wave we assume a point source at the origin and that all quantities involved are independent of the angle φ. We now switch to spherical coordinates and rewrite the linear wave equation (2.10). For this we need the laplacian of p = p (r, t), which is given by p (r, t) = 2 p So the wave equation becomes r r p r = 1 2 (rp ). r r (rp ) 1 2 p = 0. (2.16) r r 2 c 2 t2 19
26 If we now express 2 p t = 1 2 (rp ) 2 r t 2 and multiply (2.16) with r, we arrive at the same result as for a plane wave, but with rp as the unknown function. From Section we know that the solution is then given by p (r, t) = 1 r (f(t r c ) + g(t + r c ) ), which implies that the pressure amplitude decreases with the distance from the origin. Furthermore the averaged acoustic energy intensity now only depends on the radius and is given by I av r := I av a n = P av 4πr 2. This is also called the spherical spreading law and describes that the acoustic intensity decreases with the squared distance. The last thing we want to have is again the relation between p and v = v (r, t)e r. After some computation (see [1, p. 151]) one obtains that lim r v (r, t) = p ρ 0 c, so that we asymptotically have the same behavior as for plane waves. 2.8 Non-linear Acoustic Wave Equation In this last section we want to deal with non-linear wave propagation. We will first find non-linear versions of the three defining equations (2.1), (2.4) and (2.6) and then proceed as before by combining these into one equation, the so called Kuznetsov s equation. For this we only consider lossy and compressible fluids and further assume that v = v. The first thing to note is, that the continuity equation (2.1) still holds in the non-linear case. So we just have to replace the Euler equation (2.4) and the state equation (2.6) Non-linear Euler s Equation In the non-linear case the equation for momentum conservation is the Navier- Stokes equation for compressible fluids (see [1, p. 156]) ρ( v t + (v v)) + p = µ v + (µ 3 + ζ) (divv), 20
27 where ζ denotes the bulk viscosity and µ the shear viscosity. Using some vector identities (which assume our domain of interest to be convex) and the assumption v = v the equation can be rewritten as ρ v t + ρ 2 ( v 2 )+ p = ( 4µ 3 +ζ) v ( µ 3 +ζ)curl (curl(v ))+ρv curlv. We may still assume that v is irrotational, i.e curlv = 0, so the last two terms, which are related to acoustic streaming, drop and we arrive at our non-linear Euler equation ρ 0 v t + ρ v t + ρ 0 2 ( v 2 ) + p = ( 4µ 3 + ζ) v. (2.17) Non-linear State Equation According to [1, p. 157] a non-linear relation between pressure and density is given by ρ = p c 1 B 2 ρ 0 c 4 2A (p ) 2 κ ρ 0 c ( 1 1 ) p 4 c Ω c p t, (2.18) where B is the non-linearity parameter, κ the adiabatic exponent, c A Ω and c p the specific heat capacitance at constant volume respectively constant pressure Combination of Equations To combine the equations we approximate every physical quantity in a second order term by it s linear version which we obtained in the previous sections. So we will utilize ρ p (2.6), p v ρ c 2 0 t (2.7) and divv 1 ρ 0 ρ Starting from the continuity equation (2.1) in the form these approximations yield ρ t + ρ 0divv = ρ divv v ρ ρ t + ρ 0divv = 1 (p ) 2 + ρ 0 v 2. 2ρ 0 c 4 t 2c 2 t By using the non-linear state equation (2.18) this becomes 1 p c 2 t 1 B (p ) 2 κ ρ 0 c 4 2A t ρ 0 c ( 1 1 ) 2 p 4 c Ω c p t + ρ 0divv 2 t (2.8). = 1 (p ) 2 + ρ 0 v 2. (2.19) 2ρ 0 c 4 t 2c 2 t 21
28 If we now use a similar procedure for the non-linear Euler equation (see [1, p. 158]) we get ρ 0 v t + p = 1 2ρ 0 c 2 (p ) 2 ρ 0 2 v 2 1 ρ 0 c 2 (4µ 3 + ζ) p t. (2.20) Just as in the linear theory (Section 2.5) we differentiate (2.19) with respect to t and apply the divergence operator to (2.20). Then we subtract the resulting equations, interchange the order of differentiation and use the linear relations between space and time derivatives p = 1 c 2 2 p t 2 and v = 1 c 2 2 v t 2, to finally arrive at the non-linear wave equation for p p 1 c 2 2 p t = b p 2 c 2 t 1 B 2 p ρ 0 c 4 2A t ρ 0 2 v 2, 2 c 2 t 2 where b = 1 ρ 0 ( 4µ 3 + ζ) + κ ρ 0 ( 1 c Ω 1 c p ) denotes the diffusivity of sound. As in the linear theory, we can still express v and p by the vector potential ψ as v = ψ and p = ρ 0 ψ t. Using this ansatz we have finally derived the so-called Kuznetsov equation for non-linear acoustics c 2 ψ 2 ψ t = ( b ψ + 1 ) B 2 t c 2 2A ( ψ t )2 + ψ 2. 22
29 Chapter 3 Coupling of the two models In the final chapter we consider a solid immersed in an acoustic field, e.g. a loudspeaker and the air surrounding it. Mechanical vibrations in the solid cause acoustic waves in the surrounding which act as surface tractions on the vibrating structure. We will derive the weak formulation of both PDE s and incorporate coupling conditions. When talking about solid fluid interaction there are two scenarios: 1. Strong coupling: Here we need to solve both equations and their coupling conditions simultaneously, e.g. a piezoelectric ultrasound array immersed in water. 2. Weak coupling: If the pressure of the fluid on the solid can be neglected, we may compute the solutions sequentially, i.e we first calculate the mechanical vibrations and then use them as input for the acoustic field. For example the acoustic noise of an electric transformer. 3.1 Solid-Fluid Interface To ensure that the velocity field is continuous, we need that at the interface between solid and fluid the normal components of both velocity fields coincide. Let u be the displacement of the mechanical field and denote by v the mechanical velocity, defined as v = u/ t. Furthermore, let v be the acoustic particle velocity, which we expressed by the acoustic scalar potential ψ as v = ψ, see (2.11). Then we must have that n (v v ) = 0 which means that n u t = n ψ = ψ n. (3.1) 23
30 Additionally we have to take in account that the fluid acts as a surface traction on the solid, which can be stated as t (n) = np = (2.12) nρ 0 ψ t, (3.2) where p denotes the acoustic pressure and ρ 0 the mean density of the fluid. 3.2 Coupled formulation Γ f Ω f Γ I n f n Ω s Figure 3.2.1: Coupled Field We now want to derive the coupled system of equations in its weak formulation. Let Ω s be the domain for the mechanical field, Ω f the domain for the acoustic field, Γ I the interface between these two with normal vector n facing from solid to fluid, and Γ f the boundary of the fluid, with outer normal vector n f (see Figure 3.2.1) Mechanical field Starting from the equilibrium equation for the dynamic case (1.3) ρ 2 u t 2 divσ = f we multiply with a test function ϕ and integrate over Ω s ρ 2 u Ω s t ϕ dx divσ ϕ dx = f ϕ dx. 2 Ω s Ω s Using integration by parts on the divergence term we obtain ρ 2 u Ω s t ϕ dx + σ : ϕ dx (σn) ϕ ds 2 x = f ϕ dx. Ω s Γ I }{{} Ω s t (n) 24
31 Since σ = σ we have σ : ϕ = 1 2 (σ : ϕ) (σ : ϕ) = σ : }{{} σ : ( ϕ) From the constitutive law (1.6) we get that σ = λ tr(ε(u)) I + 2µε(u) }{{} tr( u)=divu σ : ε(ϕ) = (2µε(u) + λ(divu)i): ε(ϕ) 1 2 ( ϕ + ϕ ) = σ : ε(ϕ). = 2µ(ε(u): ε(ϕ)) + λ(divu) (I : ε(ϕ)) }{{} tr(ε(ϕ))=divϕ = 2µ(ε(u): ε(ϕ)) + λ(divu)(divϕ). So the weak formulation is given by ρ 2 u Ω s t ϕ dx + 2µ(ε(u): ε(ϕ)) + λ(divu)(divϕ) dx 2 Ω s t (n) ϕ ds x = f ϕ dx. (3.3) Γ I Ω s Acoustic field For the acoustic field we start with the wave equation for the acoustic velocity potential (2.13) ψ = 1 2 ψ c 2 t, 2 multiply it with a test function w and integrate over Ω f 1 2 ψ ψ w dx + w dx = 0. Ω f Ω f c 2 t2 Using partial integration on the Laplace term we obtain the weak formulation for the acoustic field 1 2 ψ ψ w dx w n f ψ ds x + w n ψ ds x + w dx = 0, Ω f Γ f Γ I Ω f c 2 t2 (3.4) where the plus sign in front of the interface surface integral comes from the choice of the normal vector n. 25
32 3.2.3 Coupled System Now we incorporate the coupling conditions, i.e. t (n) ϕ ds x = (3.2) p ψ n ϕ ds x = ρ 0 Γ I Γ I Γ I t n ϕ ds x. For simplicity we assume ψ/ n = 0 on Γ f so we just have to deal with w n ψ ds x = w ψ Γ I Γ I n ds x = (3.1) w n u Γ I t ds x. So the final coupled system of equations is given by ρ 2 u Ω s t ϕ dx + 2µ(ε(u): ε(ϕ)) + λ(divu)(divϕ) dx 2 Ω s ψ + ρ 0 Γ I t n ϕ ds x = f ϕ dx Ω s 1 2 ψ Ω f c 2 t w dx + ψ w dx w n u 2 Ω f Γ I t ds x = 0. 26
33 Chapter 4 Conclusions In the course of this thesis we managed to derive all the necessary tools to model a structure-acoustic coupling problem. For the mechanical model we started with the equilibrium equation (1.3), derived a linear relation between the displacement and the strain in (1.5) and combined both of them with Hook s law for isotropic, elastic materials (1.6) to arrive at the Navier- Lamé equation (1.8). For the acoustic model we first derived the continuity equation (2.1) and the Euler equation (2.4). Additionally we used the linear state equation (2.6) and linear versions of the Euler (2.7) and the continuity equation (2.8), to arrive at the linear acoustic wave equation (2.10). For the coupled system we derived coupling conditions, (3.1) and (3.2), and deduced the weak formulations for the mechanical (3.3) and the acoustic field (3.4). By incorporating the coupling conditions we reached our final system of coupled equations: ρ 2 u Ω s t ϕ dx + 2 Ω f 1 c 2 2 ψ t 2 w dx + 2µ(ε(u): ε(ϕ)) + λ(divu)(divϕ) dx Ω s ψ + ρ 0 Γ I t n ϕ ds x = f ϕ dx Ω s ψ w dx w n u Ω f Γ I t ds x = 0. From this one can start to think about numerical computations. One way is to apply the finite element method to the coupled system of equations, see for example [1]. Other methods have been proposed, see for example [7] or [8]. For a further study in acoustics and structure-acoustic coupling one may refer to [9]. 27
34 Bibliography [1] M. Kaltenbacher. Numerical Simulation of Mechatronic Sensors and Actuators. 2. Auflage, Springer, [2] U. Langer. Skriptum zur Vorlesung Mathematische Modelle in der Technik. Johannes Kepler Universität Linz, [3] S. Kindermann. An introduction to mathematical methods for continuum mechanics. Johannes Kepler Universität Linz, [4] I. N. Bronstein, K. A. Semendjajew, G. Musiol, H. Mühlig. Taschenbuch der Mathematik. 7. Auflage, Harri Deutsch, [5] M. Jung, U. Langer. Methode der finiten Elemente für Ingenieure. 2. Auflage, Springer, 2013 [6] S.W. Rienstra, A. Hirschberg. An Introduction to Acoustics. Eindhoven University of Technology, [7] M. Fischer, L. Gaul. Fast BEM FEM mortar coupling for acoustic structure interaction. Institut A für Mechanik, Universität Stuttgart, [8] G. Hou, J. Wang and A. Layton. Numerical Methods for Fluid-Structure Interaction A Review. Communications in Computational Physics, 12(2), pp , [9] F. Dunn, et al. Springer Handbook of Acoustics. Springer,
35 Eidesstattliche Erklärung Ich, Lukas Burgholzer, erkläre an Eides statt, dass ich die vorliegende Bachelorarbeit selbständig und ohne fremde Hilfe verfasst, andere als die angegebenen Quellen und Hilfsmittel nicht benutzt bzw. die wörtlich oder sinngemäß entnommenen Stellen als solche kenntlich gemacht habe. Linz, November 2016 Lukas Burgholzer
36 Curriculum Vitae Name: Lukas Burgholzer Nationality: Austria Date of Birth: 22 January, 1994 Place of Birth: Linz, Austria Education: Volksschule (elementary school) Kremsdorf in Haid bei Ansfelden Akademisches Gymnasium (secondary comprehensive school) Linz Studies in Technical Mathematics, Johannes Kepler University Linz
Introduction FEM, 1D-Example
 Introduction FEM, 1D-Example home/lehre/vl-mhs-1-e/folien/vorlesung/3_fem_intro/cover_sheet.tex page 1 of 25. p.1/25 Table of contents 1D Example - Finite Element Method 1. 1D Setup Geometry 2. Governing
Introduction FEM, 1D-Example home/lehre/vl-mhs-1-e/folien/vorlesung/3_fem_intro/cover_sheet.tex page 1 of 25. p.1/25 Table of contents 1D Example - Finite Element Method 1. 1D Setup Geometry 2. Governing
Introduction FEM, 1D-Example
 Introduction FEM, D-Example /home/lehre/vl-mhs-/inhalt/cover_sheet.tex. p./22 Table of contents D Example - Finite Element Method. D Setup Geometry 2. Governing equation 3. General Derivation of Finite
Introduction FEM, D-Example /home/lehre/vl-mhs-/inhalt/cover_sheet.tex. p./22 Table of contents D Example - Finite Element Method. D Setup Geometry 2. Governing equation 3. General Derivation of Finite
Finite Difference Method (FDM)
 Finite Difference Method (FDM) home/lehre/vl-mhs-1-e/folien/vorlesung/2a_fdm/cover_sheet.tex page 1 of 15. p.1/15 Table of contents 1. Problem 2. Governing Equation 3. Finite Difference-Approximation 4.
Finite Difference Method (FDM) home/lehre/vl-mhs-1-e/folien/vorlesung/2a_fdm/cover_sheet.tex page 1 of 15. p.1/15 Table of contents 1. Problem 2. Governing Equation 3. Finite Difference-Approximation 4.
FEM Isoparametric Concept
 FEM Isoparametric Concept home/lehre/vl-mhs--e/folien/vorlesung/4_fem_isopara/cover_sheet.tex page of 25. p./25 Table of contents. Interpolation Functions for the Finite Elements 2. Finite Element Types
FEM Isoparametric Concept home/lehre/vl-mhs--e/folien/vorlesung/4_fem_isopara/cover_sheet.tex page of 25. p./25 Table of contents. Interpolation Functions for the Finite Elements 2. Finite Element Types
Allgemeine Mechanik Musterlösung 11.
 Allgemeine Mechanik Musterlösung 11. HS 2014 Prof. Thomas Gehrmann Übung 1. Poisson-Klammern 1 Zeigen Sie mithilfe der Poisson-Klammern, dass folgendes gilt: a Für das Potential V ( r = α r 1+ε ist der
Allgemeine Mechanik Musterlösung 11. HS 2014 Prof. Thomas Gehrmann Übung 1. Poisson-Klammern 1 Zeigen Sie mithilfe der Poisson-Klammern, dass folgendes gilt: a Für das Potential V ( r = α r 1+ε ist der
1D-Example - Finite Difference Method (FDM)
 D-Example - Finite Difference Method (FDM) h left. Geometry A = m 2 = m ents 4m q right x 2. Permeability k f = 5 m/s 3. Boundary Conditions q right = 4 m/s y m 2 3 4 5 h left = 5 m x x x x home/baumann/d_beispiel/folie.tex.
D-Example - Finite Difference Method (FDM) h left. Geometry A = m 2 = m ents 4m q right x 2. Permeability k f = 5 m/s 3. Boundary Conditions q right = 4 m/s y m 2 3 4 5 h left = 5 m x x x x home/baumann/d_beispiel/folie.tex.
FEM Isoparametric Concept
 FEM Isoparametric Concept home/lehre/vl-mhs--e/cover_sheet.tex. p./26 Table of contents. Interpolation Functions for the Finite Elements 2. Finite Element Types 3. Geometry 4. Interpolation Approach Function
FEM Isoparametric Concept home/lehre/vl-mhs--e/cover_sheet.tex. p./26 Table of contents. Interpolation Functions for the Finite Elements 2. Finite Element Types 3. Geometry 4. Interpolation Approach Function
A Classification of Partial Boolean Clones
 A Classification of Partial Boolean Clones DIETLINDE LAU, KARSTEN SCHÖLZEL Universität Rostock, Institut für Mathematik 25th May 2010 c 2010 UNIVERSITÄT ROSTOCK MATHEMATISCH-NATURWISSENSCHAFTLICHE FAKULTÄT,
A Classification of Partial Boolean Clones DIETLINDE LAU, KARSTEN SCHÖLZEL Universität Rostock, Institut für Mathematik 25th May 2010 c 2010 UNIVERSITÄT ROSTOCK MATHEMATISCH-NATURWISSENSCHAFTLICHE FAKULTÄT,
Hydroinformatik II: Grundlagen der Kontinuumsmechanik V3
 Hydroinformatik II: Grundlagen der Kontinuumsmechanik V3 1 Helmholtz Centre for Environmental Research UFZ, Leipzig 2 Technische Universität Dresden TUD, Dresden Dresden, 21. April / 05. Mai 2017 1/18
Hydroinformatik II: Grundlagen der Kontinuumsmechanik V3 1 Helmholtz Centre for Environmental Research UFZ, Leipzig 2 Technische Universität Dresden TUD, Dresden Dresden, 21. April / 05. Mai 2017 1/18
Allgemeine Mechanik Musterlösung 7.
 Allgemeine Mechanik Musterlösung 7. HS 204 Prof. Thomas Gehrmann Übung. Lagrange-Funktion eines geladenen Teilchens Die Lagrange-Funktion für ein Teilchen der Ladung q in elektrischen und magnetischen
Allgemeine Mechanik Musterlösung 7. HS 204 Prof. Thomas Gehrmann Übung. Lagrange-Funktion eines geladenen Teilchens Die Lagrange-Funktion für ein Teilchen der Ladung q in elektrischen und magnetischen
Unit 4. The Extension Principle. Fuzzy Logic I 123
 Unit 4 The Extension Principle Fuzzy Logic I 123 Images and Preimages of Functions Let f : X Y be a function and A be a subset of X. Then the image of A w.r.t. f is defined as follows: f(a) = {y Y there
Unit 4 The Extension Principle Fuzzy Logic I 123 Images and Preimages of Functions Let f : X Y be a function and A be a subset of X. Then the image of A w.r.t. f is defined as follows: f(a) = {y Y there
Übungsblatt 6. Analysis 1, HS14
 Übungsblatt 6 Analysis, HS4 Ausgabe Donnerstag, 6. Oktober. Abgabe Donnerstag, 23. Oktober. Bitte Lösungen bis spätestens 7 Uhr in den Briefkasten des jeweiligen Übungsleiters am J- oder K-Geschoss von
Übungsblatt 6 Analysis, HS4 Ausgabe Donnerstag, 6. Oktober. Abgabe Donnerstag, 23. Oktober. Bitte Lösungen bis spätestens 7 Uhr in den Briefkasten des jeweiligen Übungsleiters am J- oder K-Geschoss von
a) Name and draw three typical input signals used in control technique.
 12 minutes Page 1 LAST NAME FIRST NAME MATRIKEL-NO. Problem 1 (2 points each) a) Name and draw three typical input signals used in control technique. b) What is a weight function? c) Define the eigen value
12 minutes Page 1 LAST NAME FIRST NAME MATRIKEL-NO. Problem 1 (2 points each) a) Name and draw three typical input signals used in control technique. b) What is a weight function? c) Define the eigen value
Transport Equation. Institut für Wasserbau, Lehrstuhl für Hydromechanik und Hydrosystemmodellierung
 Transport Equation home/lehre/vl-mhs--e/folien/vorlesung/8_transport/cover_sheet.tex page of 22. p./22 Table of contents. Introduction 2. Transport Equation 3. Analytical Solution 4. Discretization of
Transport Equation home/lehre/vl-mhs--e/folien/vorlesung/8_transport/cover_sheet.tex page of 22. p./22 Table of contents. Introduction 2. Transport Equation 3. Analytical Solution 4. Discretization of
Josh Engwer (TTU) Line Integrals 11 November / 25
 Line Integrals alculus III Josh Engwer TTU 11 November 2014 Josh Engwer (TTU) Line Integrals 11 November 2014 1 / 25 PART I PART I: LINE INTEGRALS OF SALAR FIELDS Josh Engwer (TTU) Line Integrals 11 November
Line Integrals alculus III Josh Engwer TTU 11 November 2014 Josh Engwer (TTU) Line Integrals 11 November 2014 1 / 25 PART I PART I: LINE INTEGRALS OF SALAR FIELDS Josh Engwer (TTU) Line Integrals 11 November
Seeking for n! Derivatives
 Seeking for n! Derivatives $,000$ Reward A remarkable determinant (,0) (,) (0,0) (0,) (,0) (,0) (,) (,) (0,0) (0,) (0,) General definition Δ μ (X, Y ) = det x p i j yq i n j i,j= As a starter... n! dim
Seeking for n! Derivatives $,000$ Reward A remarkable determinant (,0) (,) (0,0) (0,) (,0) (,0) (,) (,) (0,0) (0,) (0,) General definition Δ μ (X, Y ) = det x p i j yq i n j i,j= As a starter... n! dim
Number of Maximal Partial Clones
 Number of Maximal Partial Clones KARSTEN SCHÖLZEL Universität Rostoc, Institut für Mathemati 26th May 2010 c 2010 UNIVERSITÄT ROSTOCK MATHEMATISCH-NATURWISSENSCHAFTLICHE FAKULTÄT, INSTITUT FÜR MATHEMATIK
Number of Maximal Partial Clones KARSTEN SCHÖLZEL Universität Rostoc, Institut für Mathemati 26th May 2010 c 2010 UNIVERSITÄT ROSTOCK MATHEMATISCH-NATURWISSENSCHAFTLICHE FAKULTÄT, INSTITUT FÜR MATHEMATIK
Dekohärenz und die Entstehung klassischer Eigenschaften aus der Quantenmechanik
 Dekohärenz und die Entstehung klassischer Eigenschaften aus der Quantenmechanik G. Mahler Spezialvorlesung SS 006 7. 4. 006 Einführung und Übersicht Warum und in welchem Sinn ist Kohärenz»untypisch«? 04.
Dekohärenz und die Entstehung klassischer Eigenschaften aus der Quantenmechanik G. Mahler Spezialvorlesung SS 006 7. 4. 006 Einführung und Übersicht Warum und in welchem Sinn ist Kohärenz»untypisch«? 04.
Finite Difference Method (FDM) Integral Finite Difference Method (IFDM)
 Finite Difference Method (FDM) Integral Finite Difference Method (IFDM) home/lehre/vl-mhs-1-e/cover sheet.tex. p.1/29 Table of contents 1. Finite Difference Method (FDM) 1D-Example (a) Problem and Governing
Finite Difference Method (FDM) Integral Finite Difference Method (IFDM) home/lehre/vl-mhs-1-e/cover sheet.tex. p.1/29 Table of contents 1. Finite Difference Method (FDM) 1D-Example (a) Problem and Governing
Transport Equation. Institut für Wasserbau, Lehrstuhl für Hydromechanik und Hydrosystemmodellierung. . p.1/21. home/lehre/vl-mhs-1-e/cover_sheet.
 Transport Equation home/lehre/vl-mhs-1-e/cover_sheet.tex. p.1/21 Table of contents 1. Introduction 2. Transport Equation 3. Analytical Solution 4. Discretization of the transport equation 5. Explicit schemes
Transport Equation home/lehre/vl-mhs-1-e/cover_sheet.tex. p.1/21 Table of contents 1. Introduction 2. Transport Equation 3. Analytical Solution 4. Discretization of the transport equation 5. Explicit schemes
Inverse Problems In Medical Imaging
 Inverse Problems In Medical Imaging 07.05.18 Simon Krug physics654: Seminar Medical Imaging University of Bonn Inverse Problems Problem solving Inverse problems Noise Object and Image Radon transform Silent
Inverse Problems In Medical Imaging 07.05.18 Simon Krug physics654: Seminar Medical Imaging University of Bonn Inverse Problems Problem solving Inverse problems Noise Object and Image Radon transform Silent
Musterlösung 3. D-MATH Algebra I HS 2015 Prof. Richard Pink. Faktorielle Ringe, Grösster gemeinsamer Teiler, Ideale, Faktorringe
 D-MATH Algebra I HS 2015 Prof. Richard Pink Musterlösung 3 Faktorielle Ringe, Grösster gemeinsamer Teiler, Ideale, Faktorringe 1. Sei K ein Körper. Zeige, dass K[X 2, X 3 ] K[X] ein Integritätsbereich,
D-MATH Algebra I HS 2015 Prof. Richard Pink Musterlösung 3 Faktorielle Ringe, Grösster gemeinsamer Teiler, Ideale, Faktorringe 1. Sei K ein Körper. Zeige, dass K[X 2, X 3 ] K[X] ein Integritätsbereich,
Weather forecast in Accra
 Weather forecast in Accra Thursday Friday Saturday Sunday 30 C 31 C 29 C 28 C f = 9 5 c + 32 Temperature in Fahrenheit Temperature in Celsius 2 Converting Celsius to Fahrenheit f = 9 5 c + 32 tempc = 21
Weather forecast in Accra Thursday Friday Saturday Sunday 30 C 31 C 29 C 28 C f = 9 5 c + 32 Temperature in Fahrenheit Temperature in Celsius 2 Converting Celsius to Fahrenheit f = 9 5 c + 32 tempc = 21
Field-Circuit Coupling for Mechatronic Systems: Some Trends and Techniques
 Field-Circuit Coupling for Mechatronic Systems: Some Trends and Techniques Stefan Kurz Robert Bosch GmbH, Stuttgart Now with the University of the German Federal Armed Forces, Hamburg stefan.kurz@unibw-hamburg.de
Field-Circuit Coupling for Mechatronic Systems: Some Trends and Techniques Stefan Kurz Robert Bosch GmbH, Stuttgart Now with the University of the German Federal Armed Forces, Hamburg stefan.kurz@unibw-hamburg.de
Ewald s Sphere/Problem 3.7
 Ewald s Sphere/Problem 3.7 Studentproject/Molecular and Solid-State Physics Lisa Marx 831292 15.1.211, Graz Ewald s Sphere/Problem 3.7 Lisa Marx 831292 Inhaltsverzeichnis 1 General Information 3 1.1 Ewald
Ewald s Sphere/Problem 3.7 Studentproject/Molecular and Solid-State Physics Lisa Marx 831292 15.1.211, Graz Ewald s Sphere/Problem 3.7 Lisa Marx 831292 Inhaltsverzeichnis 1 General Information 3 1.1 Ewald
DYNAMISCHE GEOMETRIE
 DYNAMISCHE GEOMETRIE ÄHNLICHKEITSGEOMETRIE & MODELLIERUNG PAUL LIBBRECHT PH WEINGARTEN WS 2014-2015 CC-BY VON STAUDT KONSTRUKTIONEN Menü Erinnerung: Strahlensatz Längen, Frame Zielartikel Addition, Subtraktion
DYNAMISCHE GEOMETRIE ÄHNLICHKEITSGEOMETRIE & MODELLIERUNG PAUL LIBBRECHT PH WEINGARTEN WS 2014-2015 CC-BY VON STAUDT KONSTRUKTIONEN Menü Erinnerung: Strahlensatz Längen, Frame Zielartikel Addition, Subtraktion
Magic Figures. We note that in the example magic square the numbers 1 9 are used. All three rows (columns) have equal sum, called the magic number.
 Magic Figures Introduction: This lesson builds on ideas from Magic Squares. Students are introduced to a wider collection of Magic Figures and consider constraints on the Magic Number associated with such
Magic Figures Introduction: This lesson builds on ideas from Magic Squares. Students are introduced to a wider collection of Magic Figures and consider constraints on the Magic Number associated with such
Computational Models
 - University of Applied Sciences - Computational Models - CSCI 331 - Friedhelm Seutter Institut für Angewandte Informatik Part I Automata and Languages 0. Introduction, Alphabets, Strings, and Languages
- University of Applied Sciences - Computational Models - CSCI 331 - Friedhelm Seutter Institut für Angewandte Informatik Part I Automata and Languages 0. Introduction, Alphabets, Strings, and Languages
Interpolation Functions for the Finite Elements
 Interpolation Functions for the Finite Elements For the finite elements method, the following is valid: The global function of a sought function consists of a sum of local functions: GALERKIN method: the
Interpolation Functions for the Finite Elements For the finite elements method, the following is valid: The global function of a sought function consists of a sum of local functions: GALERKIN method: the
Fakultät III Univ.-Prof. Dr. Jan Franke-Viebach
 1 Universität Siegen Fakultät III Univ.-Prof. Dr. Jan Franke-Viebach Klausur Monetäre Außenwirtschaftstheorie und politik / International Macro Wintersemester 2011-12 (2. Prüfungstermin) Bearbeitungszeit:
1 Universität Siegen Fakultät III Univ.-Prof. Dr. Jan Franke-Viebach Klausur Monetäre Außenwirtschaftstheorie und politik / International Macro Wintersemester 2011-12 (2. Prüfungstermin) Bearbeitungszeit:
Accelerating Information Technology Innovation
 Accelerating Information Technology Innovation http://aiti.mit.edu Ghana Summer 2011 Lecture 05 Functions Weather forecast in Accra Thursday Friday Saturday Sunday 30 C 31 C 29 C 28 C f = 9 5 c + 32 Temperature
Accelerating Information Technology Innovation http://aiti.mit.edu Ghana Summer 2011 Lecture 05 Functions Weather forecast in Accra Thursday Friday Saturday Sunday 30 C 31 C 29 C 28 C f = 9 5 c + 32 Temperature
2. Basic concepts of computations in engineering sciences
 asic concepts of computations in engineering sciences 1 Introduction alculating technical or natural systems requires the following steps for the setup of the model Idealisation of the system to a form
asic concepts of computations in engineering sciences 1 Introduction alculating technical or natural systems requires the following steps for the setup of the model Idealisation of the system to a form
Allgemeine Mechanik Musterlösung 5.
 Allgemeine Mechanik Musterlösung 5. HS 014 Prof. Thomas Gehrmann Übung 1. Rotierende Masse. Eine Punktmasse m rotiere reibungslos auf einem Tisch (siehe Abb. 1). Dabei ist sie durch einen Faden der Länge
Allgemeine Mechanik Musterlösung 5. HS 014 Prof. Thomas Gehrmann Übung 1. Rotierende Masse. Eine Punktmasse m rotiere reibungslos auf einem Tisch (siehe Abb. 1). Dabei ist sie durch einen Faden der Länge
Attention: Give your answers to problem 1 and problem 2 directly below the questions in the exam question sheet. ,and C = [ ].
![Attention: Give your answers to problem 1 and problem 2 directly below the questions in the exam question sheet. ,and C = [ ]. Attention: Give your answers to problem 1 and problem 2 directly below the questions in the exam question sheet. ,and C = [ ].](/thumbs/72/66904987.jpg) Page 1 LAST NAME FIRST NAME MATRIKEL-NO. Attention: Give your answers to problem 1 and problem 2 directly below the questions in the exam question sheet. Problem 1 (15 points) a) (1 point) A system description
Page 1 LAST NAME FIRST NAME MATRIKEL-NO. Attention: Give your answers to problem 1 and problem 2 directly below the questions in the exam question sheet. Problem 1 (15 points) a) (1 point) A system description
Functional Analysis Final Test, Funktionalanalysis Endklausur,
 Spring term 2012 / Sommersemester 2012 Functional Analysis Final Test, 16.07.2012 Funktionalanalysis Endklausur, 16.07.2012 Name:/Name: Matriculation number:/matrikelnr.: Semester:/Fachsemester: Degree
Spring term 2012 / Sommersemester 2012 Functional Analysis Final Test, 16.07.2012 Funktionalanalysis Endklausur, 16.07.2012 Name:/Name: Matriculation number:/matrikelnr.: Semester:/Fachsemester: Degree
Algebra. Übungsblatt 2 (Lösungen)
 Fakultät für Mathematik Sommersemester 2017 JProf. Dr. Christian Lehn Dr. Alberto Castaño Domínguez Algebra Übungsblatt 2 (Lösungen) Aufgabe 1. Es sei n 3. Zeigen Sie, dass S n von (1 2) und (1... n) erzeugt
Fakultät für Mathematik Sommersemester 2017 JProf. Dr. Christian Lehn Dr. Alberto Castaño Domínguez Algebra Übungsblatt 2 (Lösungen) Aufgabe 1. Es sei n 3. Zeigen Sie, dass S n von (1 2) und (1... n) erzeugt
Aufgabe 1 (12 Punkte)
 Aufgabe ( Punkte) Ein Medikament wirkt in drei Organen O, O, O 3. Seine Menge zur Zeit t im Organ O k wird mit x k (t) bezeichnet, und die Wechselwirkung wird durch folgendes System von Differentialgleichungen
Aufgabe ( Punkte) Ein Medikament wirkt in drei Organen O, O, O 3. Seine Menge zur Zeit t im Organ O k wird mit x k (t) bezeichnet, und die Wechselwirkung wird durch folgendes System von Differentialgleichungen
Unit 1. Motivation and Basics of Classical Logic. Fuzzy Logic I 6
 Unit 1 Motivation and Basics of Classical Logic Fuzzy Logic I 6 Motivation In our everyday life, we use vague, qualitative, imprecise linguistic terms like small, hot, around two o clock Even very complex
Unit 1 Motivation and Basics of Classical Logic Fuzzy Logic I 6 Motivation In our everyday life, we use vague, qualitative, imprecise linguistic terms like small, hot, around two o clock Even very complex
TEHL Simulation of Gear Contacts
 Thomas Lohner, Andreas Ziegltrum, Karsten Stahl COMSOL Conference 216 12-14 October 216 Munich, Germany 671-1-46 1 Outline Introduction Problem Description Model Implementation Exemplarily Results Conclusion
Thomas Lohner, Andreas Ziegltrum, Karsten Stahl COMSOL Conference 216 12-14 October 216 Munich, Germany 671-1-46 1 Outline Introduction Problem Description Model Implementation Exemplarily Results Conclusion
Englisch-Grundwortschatz
 Englisch-Grundwortschatz Die 100 am häufigsten verwendeten Wörter also auch so so in in even sogar on an / bei / in like wie / mögen their with but first only and time find you get more its those because
Englisch-Grundwortschatz Die 100 am häufigsten verwendeten Wörter also auch so so in in even sogar on an / bei / in like wie / mögen their with but first only and time find you get more its those because
DICO Dimension Coupling
 DICO Dimension Coupling 3D!" 1D and phase transition (liquid vapor) Jonathan Jung, Martina Friedrich, Claus-Dieter Munz, Jean-Marc Hérard, Philippe Helluy MAC days, Paris University of Stuttgart Institut
DICO Dimension Coupling 3D!" 1D and phase transition (liquid vapor) Jonathan Jung, Martina Friedrich, Claus-Dieter Munz, Jean-Marc Hérard, Philippe Helluy MAC days, Paris University of Stuttgart Institut
The Navier-Stokes equations on polygonal domains with mixed boundary conditions theory and approximation
 Research Collection Doctoral Thesis The Navier-Stokes equations on polygonal domains with mixed boundary conditions theory and approximation Author(s): Brun, Markus Publication Date: 2002 Permanent Link:
Research Collection Doctoral Thesis The Navier-Stokes equations on polygonal domains with mixed boundary conditions theory and approximation Author(s): Brun, Markus Publication Date: 2002 Permanent Link:
4. Bayes Spiele. S i = Strategiemenge für Spieler i, S = S 1... S n. T i = Typmenge für Spieler i, T = T 1... T n
 4. Bayes Spiele Definition eines Bayes Spiels G B (n, S 1,..., S n, T 1,..., T n, p, u 1,..., u n ) n Spieler 1,..., n S i Strategiemenge für Spieler i, S S 1... S n T i Typmenge für Spieler i, T T 1...
4. Bayes Spiele Definition eines Bayes Spiels G B (n, S 1,..., S n, T 1,..., T n, p, u 1,..., u n ) n Spieler 1,..., n S i Strategiemenge für Spieler i, S S 1... S n T i Typmenge für Spieler i, T T 1...
Priorities (time independent and time dependent) Different service times of different classes at Type-1 nodes -
 E.6 Approximate Analysis of Non-product-Form Queueing Networks Non exponentially distributed service times Priorities (time independent and time dependent) Different service times of different classes
E.6 Approximate Analysis of Non-product-Form Queueing Networks Non exponentially distributed service times Priorities (time independent and time dependent) Different service times of different classes
Algebra. 1. Geben Sie alle abelschen Gruppen mit 8 und 12 Elementen an. (Ohne Nachweis).
 1 Wiederholungsblatt zur Gruppentheorie 18.12.2002 Wiederholen Sie für die Klausur: Algebra WS 2002/03 Dr. Elsholtz Alle Hausaufgaben. Aufgaben, die vor Wochen schwer waren, sind hoffentlich mit Abstand,
1 Wiederholungsblatt zur Gruppentheorie 18.12.2002 Wiederholen Sie für die Klausur: Algebra WS 2002/03 Dr. Elsholtz Alle Hausaufgaben. Aufgaben, die vor Wochen schwer waren, sind hoffentlich mit Abstand,
Lattice Boltzmann Study of the Drag Correlation in Dilute and Moderately Dense Fluid-Particle Systems
 Lattice Boltzmann Study of the Drag Correlation in Dilute and Moderately Dense Fluid-Particle Systems Simon Bogner, Swati Mohanty1 and Ulrich Rüde Chair for System Simulation (LSS), University of Erlangen-Nürnberg,
Lattice Boltzmann Study of the Drag Correlation in Dilute and Moderately Dense Fluid-Particle Systems Simon Bogner, Swati Mohanty1 and Ulrich Rüde Chair for System Simulation (LSS), University of Erlangen-Nürnberg,
Wie man heute die Liebe fürs Leben findet
 Wie man heute die Liebe fürs Leben findet Sherrie Schneider Ellen Fein Click here if your download doesn"t start automatically Wie man heute die Liebe fürs Leben findet Sherrie Schneider Ellen Fein Wie
Wie man heute die Liebe fürs Leben findet Sherrie Schneider Ellen Fein Click here if your download doesn"t start automatically Wie man heute die Liebe fürs Leben findet Sherrie Schneider Ellen Fein Wie
Air-Sea Gas Transfer: Schmidt Number Dependency and Intermittency
 Air-Sea Gas Transfer: Schmidt Number Dependency and Intermittency Bernd Jähne, Reinhard Nielsen, Christopher Pop, Uwe Schimpf, and Christoph Garbe Interdisziplinäres Zentrum für Wissenschaftliches Rechnen
Air-Sea Gas Transfer: Schmidt Number Dependency and Intermittency Bernd Jähne, Reinhard Nielsen, Christopher Pop, Uwe Schimpf, and Christoph Garbe Interdisziplinäres Zentrum für Wissenschaftliches Rechnen
Algorithm Theory 3 Fast Fourier Transformation Christian Schindelhauer
 Algorithm Theory 3 Fast Fourier Transformation Institut für Informatik Wintersemester 2007/08 Chapter 3 Fast Fourier Transformation 2 Polynomials Polynomials p over real numbers with a variable x p(x)
Algorithm Theory 3 Fast Fourier Transformation Institut für Informatik Wintersemester 2007/08 Chapter 3 Fast Fourier Transformation 2 Polynomials Polynomials p over real numbers with a variable x p(x)
Analysis III Serie 13 Musterlösung
 Ana-3 Hs 22 Analysis III Serie 3 Musterlösung Abgabe: Freitag, 2.2.22, Uhr, in der Vorlesung * Aufgabe Welche der folgenden Aussagen sind wahr und welche sind falsch? (Mit Begründung) (i) Sei A R 3 3 eine
Ana-3 Hs 22 Analysis III Serie 3 Musterlösung Abgabe: Freitag, 2.2.22, Uhr, in der Vorlesung * Aufgabe Welche der folgenden Aussagen sind wahr und welche sind falsch? (Mit Begründung) (i) Sei A R 3 3 eine
Level 1 German, 2014
 90886 908860 1SUPERVISOR S Level 1 German, 2014 90886 Demonstrate understanding of a variety of German texts on areas of most immediate relevance 9.30 am Wednesday 26 November 2014 Credits: Five Achievement
90886 908860 1SUPERVISOR S Level 1 German, 2014 90886 Demonstrate understanding of a variety of German texts on areas of most immediate relevance 9.30 am Wednesday 26 November 2014 Credits: Five Achievement
On Euler s attempt to compute logarithms by interpolation
 Euler p. 1/1 On Euler s attempt to compute logarithms by interpolation Walter Gautschi wxg@cs.purdue.edu Purdue University Leonhard Euler 1707 1783 Euler p. 2/1 Euler p. 3/1 From Euler s letter to Daniel
Euler p. 1/1 On Euler s attempt to compute logarithms by interpolation Walter Gautschi wxg@cs.purdue.edu Purdue University Leonhard Euler 1707 1783 Euler p. 2/1 Euler p. 3/1 From Euler s letter to Daniel
aus Doktorarbeiten Anna Lena Birkmeyer Oktober 2016
 aus Doktorarbeiten Anna Lena Birkmeyer Fachbereich Mathematik TU Kaiserslautern Oktober 2016 In der der Arbeit: The mathematical modeling and optimization of... is a wide field of research [4,15,19,35,61,62,66,76,86]
aus Doktorarbeiten Anna Lena Birkmeyer Fachbereich Mathematik TU Kaiserslautern Oktober 2016 In der der Arbeit: The mathematical modeling and optimization of... is a wide field of research [4,15,19,35,61,62,66,76,86]
Mathematics (M4) (English version) ORIENTIERUNGSARBEIT (OA 11) Gymnasium. Code-Nr.:
 Gymnasium 2. Klassen MAR Code-Nr.: Schuljahr 2005/2006 Datum der Durchführung Donnerstag, 6.4.2006 ORIENTIERUNGSARBEIT (OA 11) Gymnasium Mathematics (M4) (English version) Lesen Sie zuerst Anleitung und
Gymnasium 2. Klassen MAR Code-Nr.: Schuljahr 2005/2006 Datum der Durchführung Donnerstag, 6.4.2006 ORIENTIERUNGSARBEIT (OA 11) Gymnasium Mathematics (M4) (English version) Lesen Sie zuerst Anleitung und
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Reguläre Ausdrücke und reguläre Grammatiken Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 20 Regular expressions (1) Let Σ be an alphabet. The
Einführung in die Computerlinguistik Reguläre Ausdrücke und reguläre Grammatiken Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 20 Regular expressions (1) Let Σ be an alphabet. The
Geometrie und Bedeutung: Kap 5
 : Kap 5 21. November 2011 Übersicht Der Begriff des Vektors Ähnlichkeits Distanzfunktionen für Vektoren Skalarprodukt Eukidische Distanz im R n What are vectors I Domininic: Maryl: Dollar Po Euro Yen 6
: Kap 5 21. November 2011 Übersicht Der Begriff des Vektors Ähnlichkeits Distanzfunktionen für Vektoren Skalarprodukt Eukidische Distanz im R n What are vectors I Domininic: Maryl: Dollar Po Euro Yen 6
Level 2 German, 2013
 91126 911260 2SUPERVISOR S Level 2 German, 2013 91126 Demonstrate understanding of a variety of written and / or visual German text(s) on familiar matters 9.30 am Monday 11 November 2013 Credits: Five
91126 911260 2SUPERVISOR S Level 2 German, 2013 91126 Demonstrate understanding of a variety of written and / or visual German text(s) on familiar matters 9.30 am Monday 11 November 2013 Credits: Five
VGM. VGM information. HAMBURG SÜD VGM WEB PORTAL USER GUIDE June 2016
 Overview The Hamburg Süd VGM Web portal is an application that enables you to submit VGM information directly to Hamburg Süd via our e-portal Web page. You can choose to enter VGM information directly,
Overview The Hamburg Süd VGM Web portal is an application that enables you to submit VGM information directly to Hamburg Süd via our e-portal Web page. You can choose to enter VGM information directly,
Fakultät III Univ.-Prof. Dr. Jan Franke-Viebach
 1 Universität Siegen Fakultät III Univ.-Prof. Dr. Jan Franke-Viebach Klausur Monetäre Außenwirtschaftstheorie und politik / International Macro Wintersemester 2011-12 (1. Prüfungstermin) Bearbeitungszeit:
1 Universität Siegen Fakultät III Univ.-Prof. Dr. Jan Franke-Viebach Klausur Monetäre Außenwirtschaftstheorie und politik / International Macro Wintersemester 2011-12 (1. Prüfungstermin) Bearbeitungszeit:
Asynchronous Generators
 Asynchronous Generators Source: ABB 1/21 2. Asynchronous Generators 1. Induction generator with squirrel cage rotor 2. Induction generator with woed rotor Source: electricaleasy.com 2/21 2.1. Induction
Asynchronous Generators Source: ABB 1/21 2. Asynchronous Generators 1. Induction generator with squirrel cage rotor 2. Induction generator with woed rotor Source: electricaleasy.com 2/21 2.1. Induction
Teil 2.2: Lernen formaler Sprachen: Hypothesenräume
 Theorie des Algorithmischen Lernens Sommersemester 2006 Teil 2.2: Lernen formaler Sprachen: Hypothesenräume Version 1.1 Gliederung der LV Teil 1: Motivation 1. Was ist Lernen 2. Das Szenario der Induktiven
Theorie des Algorithmischen Lernens Sommersemester 2006 Teil 2.2: Lernen formaler Sprachen: Hypothesenräume Version 1.1 Gliederung der LV Teil 1: Motivation 1. Was ist Lernen 2. Das Szenario der Induktiven
Snap-in switch for switches PSE, MSM and MCS 30
 Product manual Snap-in switch for switches PSE, MSM and MCS 30 CONTENTS 1. PRODUCT DESCRIPTION 2. DATA AND DIMENSIONAL DRAWINGS 2.1. Technical Data 2.2. Dimensions of PSE with a Mounting Diameter 19 mm
Product manual Snap-in switch for switches PSE, MSM and MCS 30 CONTENTS 1. PRODUCT DESCRIPTION 2. DATA AND DIMENSIONAL DRAWINGS 2.1. Technical Data 2.2. Dimensions of PSE with a Mounting Diameter 19 mm
Monotony based imaging in EIT
 Monotony based imaging in EIT Bastian von Harrach harrach@ma.tum.de Department of Mathematics - M, Technische Universität München, Germany Joint work with Marcel Ullrich, Universität Mainz, Germany ICNAAM
Monotony based imaging in EIT Bastian von Harrach harrach@ma.tum.de Department of Mathematics - M, Technische Universität München, Germany Joint work with Marcel Ullrich, Universität Mainz, Germany ICNAAM
Statistics, Data Analysis, and Simulation SS 2015
 Mainz, June 11, 2015 Statistics, Data Analysis, and Simulation SS 2015 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Dr. Michael O. Distler
Mainz, June 11, 2015 Statistics, Data Analysis, and Simulation SS 2015 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Dr. Michael O. Distler
Molecular dynamics simulation of confined multiphasic systems
 VI. International Conference on Computational Fluid Dynamics Molecular dynamics simulation of confined multiphasic systems St. Petersburg, July 15, 2010 G. C. Lehmann, C. Dan, J. Harting, M. Heitzig, M.
VI. International Conference on Computational Fluid Dynamics Molecular dynamics simulation of confined multiphasic systems St. Petersburg, July 15, 2010 G. C. Lehmann, C. Dan, J. Harting, M. Heitzig, M.
Ein Stern in dunkler Nacht Die schoensten Weihnachtsgeschichten. Click here if your download doesn"t start automatically
 Ein Stern in dunkler Nacht Die schoensten Weihnachtsgeschichten Click here if your download doesn"t start automatically Ein Stern in dunkler Nacht Die schoensten Weihnachtsgeschichten Ein Stern in dunkler
Ein Stern in dunkler Nacht Die schoensten Weihnachtsgeschichten Click here if your download doesn"t start automatically Ein Stern in dunkler Nacht Die schoensten Weihnachtsgeschichten Ein Stern in dunkler
Newest Generation of the BS2 Corrosion/Warning and Measurement System
 Newest Generation of the BS2 Corrosion/Warning and Measurement System BS2 System Description: BS2 CorroDec 2G is a cable and energyless system module range for detecting corrosion, humidity and prevailing
Newest Generation of the BS2 Corrosion/Warning and Measurement System BS2 System Description: BS2 CorroDec 2G is a cable and energyless system module range for detecting corrosion, humidity and prevailing
Level 2 German, 2015
 91126 911260 2SUPERVISOR S Level 2 German, 2015 91126 Demonstrate understanding of a variety of written and / or visual German text(s) on familiar matters 2.00 p.m. Friday 4 December 2015 Credits: Five
91126 911260 2SUPERVISOR S Level 2 German, 2015 91126 Demonstrate understanding of a variety of written and / or visual German text(s) on familiar matters 2.00 p.m. Friday 4 December 2015 Credits: Five
Where are we now? The administration building M 3. Voransicht
 Let me show you around 9 von 26 Where are we now? The administration building M 3 12 von 26 Let me show you around Presenting your company 2 I M 5 Prepositions of place and movement There are many prepositions
Let me show you around 9 von 26 Where are we now? The administration building M 3 12 von 26 Let me show you around Presenting your company 2 I M 5 Prepositions of place and movement There are many prepositions
Technische Universität Kaiserslautern Lehrstuhl für Virtuelle Produktentwicklung
 functions in SysML 2.0 La Jolla, 22.05.2014 12/10/2015 Technische Universität Kaiserslautern Lehrstuhl für Virtuelle Produktentwicklung Dipl. Wirtsch.-Ing. Christian Muggeo Dipl. Wirtsch.-Ing. Michael
functions in SysML 2.0 La Jolla, 22.05.2014 12/10/2015 Technische Universität Kaiserslautern Lehrstuhl für Virtuelle Produktentwicklung Dipl. Wirtsch.-Ing. Christian Muggeo Dipl. Wirtsch.-Ing. Michael
Übungen zur Analysis 2
 Mathematisches Institut der Universität München Prof. Dr. Franz Merkl Sommersemester 013 Blatt 3 03.04.013 Übungen zur Analysis 3.1 Abstraktion des Beweises der Minkowskiungleichung. Es seien V ein K-Vektorraum
Mathematisches Institut der Universität München Prof. Dr. Franz Merkl Sommersemester 013 Blatt 3 03.04.013 Übungen zur Analysis 3.1 Abstraktion des Beweises der Minkowskiungleichung. Es seien V ein K-Vektorraum
Simulating the Idle: A New Load Case for Vehicle Thermal Management
 Simulating the Idle: A New Load Case for Vehicle Thermal Management Jan Eller FKFS / IVK University of Stuttgart Thomas Binner and Heinrich Reister Daimler AG Nils Widdecke and Jochen Wiedemann FKFS /
Simulating the Idle: A New Load Case for Vehicle Thermal Management Jan Eller FKFS / IVK University of Stuttgart Thomas Binner and Heinrich Reister Daimler AG Nils Widdecke and Jochen Wiedemann FKFS /
Grade 12: Qualifikationsphase. My Abitur
 Grade 12: Qualifikationsphase My Abitur Qualifikationsphase Note 1 Punkte Prozente Note 1 15 14 13 85 % 100 % Note 2 12 11 10 70 % 84 % Note 3 9 8 7 55 % 69 % Note 4 6 5 4 40 % 54 % Note 5 3 2 1 20 % 39
Grade 12: Qualifikationsphase My Abitur Qualifikationsphase Note 1 Punkte Prozente Note 1 15 14 13 85 % 100 % Note 2 12 11 10 70 % 84 % Note 3 9 8 7 55 % 69 % Note 4 6 5 4 40 % 54 % Note 5 3 2 1 20 % 39
Zariski-Van Kampen Method
 Zariski-Van Kampen Method Purpose: Obtain a presentation for the fundamental group of the complement of a plane projective curve in P 2. We will put together several ingredients, among which, the Van Kampen
Zariski-Van Kampen Method Purpose: Obtain a presentation for the fundamental group of the complement of a plane projective curve in P 2. We will put together several ingredients, among which, the Van Kampen
Worksheet 2. Problem 4. (a) 1 x x 2 2. dx 4 x2 + b ( x2. x 2 + 3c ] dx 4 + 3b ) (b) Since the points. f(x i, y i )
![Worksheet 2. Problem 4. (a) 1 x x 2 2. dx 4 x2 + b ( x2. x 2 + 3c ] dx 4 + 3b ) (b) Since the points. f(x i, y i ) Worksheet 2. Problem 4. (a) 1 x x 2 2. dx 4 x2 + b ( x2. x 2 + 3c ] dx 4 + 3b ) (b) Since the points. f(x i, y i )](/thumbs/87/95517929.jpg) Worksheet Problem 4 a 4 + x dy ax + by x 4 4 4 4 4 axy + b y+ x y y x 4 a 4 x + b { + x a 4 x + b x + 6 x a 4 + b x + b 4 x x } 4 6a + 8b. b Since the points P, P and P are distributed within the triangle
Worksheet Problem 4 a 4 + x dy ax + by x 4 4 4 4 4 axy + b y+ x y y x 4 a 4 x + b { + x a 4 x + b x + 6 x a 4 + b x + b 4 x x } 4 6a + 8b. b Since the points P, P and P are distributed within the triangle
Martin Luther. Click here if your download doesn"t start automatically
 Die schönsten Kirchenlieder von Luther (Vollständige Ausgabe): Gesammelte Gedichte: Ach Gott, vom Himmel sieh darein + Nun bitten wir den Heiligen Geist... der Unweisen Mund... (German Edition) Martin
Die schönsten Kirchenlieder von Luther (Vollständige Ausgabe): Gesammelte Gedichte: Ach Gott, vom Himmel sieh darein + Nun bitten wir den Heiligen Geist... der Unweisen Mund... (German Edition) Martin
Unit 6. Fuzzy Inference. Fuzzy Logic I 159
 Unit 6 Fuzzy Inference Fuzzy Logic I 159 Motivation Our ultimate goal is to be able to proceed IF-THEN rules involving vague linguistic expressions which are modeled by fuzzy sets. Question: What is still
Unit 6 Fuzzy Inference Fuzzy Logic I 159 Motivation Our ultimate goal is to be able to proceed IF-THEN rules involving vague linguistic expressions which are modeled by fuzzy sets. Question: What is still
Funktion der Mindestreserve im Bezug auf die Schlüsselzinssätze der EZB (German Edition)
 Funktion der Mindestreserve im Bezug auf die Schlüsselzinssätze der EZB (German Edition) Philipp Heckele Click here if your download doesn"t start automatically Download and Read Free Online Funktion
Funktion der Mindestreserve im Bezug auf die Schlüsselzinssätze der EZB (German Edition) Philipp Heckele Click here if your download doesn"t start automatically Download and Read Free Online Funktion
v+s Output Quelle: Schotter, Microeconomics, , S. 412f
 The marginal cost function for a capacity-constrained firm At output levels that are lower than the firm s installed capacity of K, the marginal cost is merely the variable marginal cost of v. At higher
The marginal cost function for a capacity-constrained firm At output levels that are lower than the firm s installed capacity of K, the marginal cost is merely the variable marginal cost of v. At higher
Numerical Analysis of a Radiant Syngas Cooler
 Numerical Analysis of a Radiant Syngas Cooler Folie 2, Dr.-Ing. Gerd Oeljeklaus, Universität Duisburg-Essen Universität Duisburg-Essen Prof. Dr.-Ing., Universität Duisburg-Essen - Ulrich Günther Siemens
Numerical Analysis of a Radiant Syngas Cooler Folie 2, Dr.-Ing. Gerd Oeljeklaus, Universität Duisburg-Essen Universität Duisburg-Essen Prof. Dr.-Ing., Universität Duisburg-Essen - Ulrich Günther Siemens
Einführung in die Finite Element Methode Projekt 2
 Einführung in die Finite Element Methode Projekt 2 Juri Schmelzer und Fred Brockstedt 17.7.2014 Juri Schmelzer und Fred Brockstedt Einführung in die Finite Element Methode Projekt 2 17.7.2014 1 / 29 Project
Einführung in die Finite Element Methode Projekt 2 Juri Schmelzer und Fred Brockstedt 17.7.2014 Juri Schmelzer und Fred Brockstedt Einführung in die Finite Element Methode Projekt 2 17.7.2014 1 / 29 Project
Lukas Hydraulik GmbH Weinstraße 39 D Erlangen. Mr. Sauerbier. Lukas Hydraulik GmbH Weinstraße 39 D Erlangen
 Technical Report No. 028-71 30 95685-350 of 22.02.2017 Client: Lukas Hydraulik GmbH Weinstraße 39 D-91058 Erlangen Mr. Sauerbier Manufacturing location: Lukas Hydraulik GmbH Weinstraße 39 D-91058 Erlangen
Technical Report No. 028-71 30 95685-350 of 22.02.2017 Client: Lukas Hydraulik GmbH Weinstraße 39 D-91058 Erlangen Mr. Sauerbier Manufacturing location: Lukas Hydraulik GmbH Weinstraße 39 D-91058 Erlangen
FACHKUNDE FüR KAUFLEUTE IM GESUNDHEITSWESEN FROM THIEME GEORG VERLAG
 FACHKUNDE FüR KAUFLEUTE IM GESUNDHEITSWESEN FROM THIEME GEORG VERLAG DOWNLOAD EBOOK : FACHKUNDE FüR KAUFLEUTE IM GESUNDHEITSWESEN Click link bellow and free register to download ebook: FACHKUNDE FüR KAUFLEUTE
FACHKUNDE FüR KAUFLEUTE IM GESUNDHEITSWESEN FROM THIEME GEORG VERLAG DOWNLOAD EBOOK : FACHKUNDE FüR KAUFLEUTE IM GESUNDHEITSWESEN Click link bellow and free register to download ebook: FACHKUNDE FüR KAUFLEUTE
There are 10 weeks this summer vacation the weeks beginning: June 23, June 30, July 7, July 14, July 21, Jul 28, Aug 4, Aug 11, Aug 18, Aug 25
 Name: AP Deutsch Sommerpaket 2014 The AP German exam is designed to test your language proficiency your ability to use the German language to speak, listen, read and write. All the grammar concepts and
Name: AP Deutsch Sommerpaket 2014 The AP German exam is designed to test your language proficiency your ability to use the German language to speak, listen, read and write. All the grammar concepts and
Rev. Proc Information
 Rev. Proc. 2006-32 Information 2006, CPAs 1 Table 1-Total loss of the home Table 2- Near total loss is water to the roofline. Completely gut the home from floor to rafters - wiring, plumbing, electrical
Rev. Proc. 2006-32 Information 2006, CPAs 1 Table 1-Total loss of the home Table 2- Near total loss is water to the roofline. Completely gut the home from floor to rafters - wiring, plumbing, electrical
Level 2 German, 2016
 91126 911260 2SUPERVISOR S Level 2 German, 2016 91126 Demonstrate understanding of a variety of written and / or visual German texts on familiar matters 2.00 p.m. Tuesday 29 November 2016 Credits: Five
91126 911260 2SUPERVISOR S Level 2 German, 2016 91126 Demonstrate understanding of a variety of written and / or visual German texts on familiar matters 2.00 p.m. Tuesday 29 November 2016 Credits: Five
Zu + Infinitiv Constructions
 Zu + Infinitiv Constructions You have probably noticed that in many German sentences, infinitives appear with a "zu" before them. These "zu + infinitive" structures are called infinitive clauses, and they're
Zu + Infinitiv Constructions You have probably noticed that in many German sentences, infinitives appear with a "zu" before them. These "zu + infinitive" structures are called infinitive clauses, and they're
Die Bedeutung neurowissenschaftlicher Erkenntnisse für die Werbung (German Edition)
 Die Bedeutung neurowissenschaftlicher Erkenntnisse für die Werbung (German Edition) Lisa Johann Click here if your download doesn"t start automatically Download and Read Free Online Die Bedeutung neurowissenschaftlicher
Die Bedeutung neurowissenschaftlicher Erkenntnisse für die Werbung (German Edition) Lisa Johann Click here if your download doesn"t start automatically Download and Read Free Online Die Bedeutung neurowissenschaftlicher
https://cuvillier.de/de/shop/publications/6886
 Kristofer Leach (Autor) Modelling Force Transfer in Boundary Layers of Moving Walls for Compressible and Incompressible Turbulent Flows Across Multiple Scales https://cuvillier.de/de/shop/publications/6886
Kristofer Leach (Autor) Modelling Force Transfer in Boundary Layers of Moving Walls for Compressible and Incompressible Turbulent Flows Across Multiple Scales https://cuvillier.de/de/shop/publications/6886
Übung 3: VHDL Darstellungen (Blockdiagramme)
 Übung 3: VHDL Darstellungen (Blockdiagramme) Aufgabe 1 Multiplexer in VHDL. (a) Analysieren Sie den VHDL Code und zeichnen Sie den entsprechenden Schaltplan (mit Multiplexer). (b) Beschreiben Sie zwei
Übung 3: VHDL Darstellungen (Blockdiagramme) Aufgabe 1 Multiplexer in VHDL. (a) Analysieren Sie den VHDL Code und zeichnen Sie den entsprechenden Schaltplan (mit Multiplexer). (b) Beschreiben Sie zwei
PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB
 Read Online and Download Ebook PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB DOWNLOAD EBOOK : PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: Click link bellow
Read Online and Download Ebook PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB DOWNLOAD EBOOK : PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: Click link bellow
Geostatistics for modeling of soil spatial variability in Adapazari, Turkey
 1 Geostatistics for modeling of soil spatial variability in Adapazari, Turkey Jack W. Baker Michael H. Faber (IBK) ETH - Zürich 2 Practical evaluation of liquefaction occurrence Obtained from empirical
1 Geostatistics for modeling of soil spatial variability in Adapazari, Turkey Jack W. Baker Michael H. Faber (IBK) ETH - Zürich 2 Practical evaluation of liquefaction occurrence Obtained from empirical
Electrical tests on Bosch unit injectors
 Valid for Bosch unit injectors with order numbers 0 414 700 / 0 414 701 / 0 414 702 Parts Kit Magnet*: - F00H.N37.925 - F00H.N37.933 - F00H.N37.934 * For allocation to the 10-place Bosch order number,
Valid for Bosch unit injectors with order numbers 0 414 700 / 0 414 701 / 0 414 702 Parts Kit Magnet*: - F00H.N37.925 - F00H.N37.933 - F00H.N37.934 * For allocation to the 10-place Bosch order number,
ENCYCLOPEDIA OF PHYSICS
 ENCYCLOPEDIA OF PHYSICS EDITED BY S. FLOGGE VOLUME 111/1 PRINCIPLES OF CLASSICAL MECHANICS AND FIELD THEORY WITH 106 FIGURES SPRINGER-VERLAG BERLIN HEIDELBERG GMBH 1960 HANDBUCH DER PHYSIK HERAUSGEGEBEN
ENCYCLOPEDIA OF PHYSICS EDITED BY S. FLOGGE VOLUME 111/1 PRINCIPLES OF CLASSICAL MECHANICS AND FIELD THEORY WITH 106 FIGURES SPRINGER-VERLAG BERLIN HEIDELBERG GMBH 1960 HANDBUCH DER PHYSIK HERAUSGEGEBEN
Unit 5. Mathematical Morphology. Knowledge-Based Methods in Image Processing and Pattern Recognition; Ulrich Bodenhofer 85
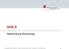 Unit 5 Mathematical Morphology Knowledge-Based Methods in Image Processing and Pattern Recognition; Ulrich Bodenhofer 85 Introduction to Mathematical Morphology Use of algebraic analysis for detecting
Unit 5 Mathematical Morphology Knowledge-Based Methods in Image Processing and Pattern Recognition; Ulrich Bodenhofer 85 Introduction to Mathematical Morphology Use of algebraic analysis for detecting
Integer Convex Minimization in Low Dimensions
 DISS. ETH NO. 22288 Integer Convex Minimization in Low Dimensions A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZURICH (Dr. sc. ETH Zurich) presented by TIMM OERTEL Diplom-Mathematiker,
DISS. ETH NO. 22288 Integer Convex Minimization in Low Dimensions A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZURICH (Dr. sc. ETH Zurich) presented by TIMM OERTEL Diplom-Mathematiker,
[[ [ [ [[ Natur, Technik, Systeme. Test, Dezember Erstes Semester WI10. PV Panel und Kondensator
 Natur, Technik, Systeme Test, Dezember 00 Erstes Semester WI0 Erlaubte Hilfsmittel: Bücher und persönlich verfasste Zusammenfassung. Rechen- und Schreibzeugs. Antworten müssen begründet und nachvollziehbar
Natur, Technik, Systeme Test, Dezember 00 Erstes Semester WI0 Erlaubte Hilfsmittel: Bücher und persönlich verfasste Zusammenfassung. Rechen- und Schreibzeugs. Antworten müssen begründet und nachvollziehbar
PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB
 Read Online and Download Ebook PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB DOWNLOAD EBOOK : PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: Click link bellow
Read Online and Download Ebook PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: ENGLISCH LERNEN MIT JUSTUS, PETER UND BOB DOWNLOAD EBOOK : PONS DIE DREI??? FRAGEZEICHEN, ARCTIC ADVENTURE: Click link bellow
Titelmasterformat Object Generator durch Klicken bearbeiten
 Titelmasterformat Object Generator durch Klicken bearbeiten How to model 82 screws in 2 minutes By Pierre-Louis Ruffieux 17.11.2014 1 Object Generator The object generator is usefull tool to replicate
Titelmasterformat Object Generator durch Klicken bearbeiten How to model 82 screws in 2 minutes By Pierre-Louis Ruffieux 17.11.2014 1 Object Generator The object generator is usefull tool to replicate
Quantenmechanik II Musterlösung 7.
 Quantenmechanik II Musterlösung 7. FS 07 Prof. Thomas Gehrmann Übung. [Auswahlregeln] Beweise die Drehimpulsauswahlregeln m = 0, ± und l = ± für Dipolübergänge in wasserstoffähnlichen Atomen unter Verwendung
Quantenmechanik II Musterlösung 7. FS 07 Prof. Thomas Gehrmann Übung. [Auswahlregeln] Beweise die Drehimpulsauswahlregeln m = 0, ± und l = ± für Dipolübergänge in wasserstoffähnlichen Atomen unter Verwendung
