ADS: Algorithmen und Datenstrukturen 2
|
|
|
- Viktoria Acker
- vor 9 Jahren
- Abrufe
Transkript
1 ADS: Algorithmen und Datenstrukturen 2 Teil 5 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität Leipzig 4. Mai 2016 [Letzte Aktualisierung: 06/05/2016, 15:00] 1 / 17
2 Aus gegebenem Anlaß Computergesetzte Übungsabgaben sind nur zulässig, wenn sie nicht in gleichartigen Kopien/Ausdrucken von mehreren Studierenden abgegeben werden Es gilt das Highlander Prinzip: Es kann nur eine geben. Für elektronische Plagiate gibt es KEINE Punkte. die Abgaben hinreichende Information an Zwischenschritten enthalten, um die Lösungswege zu dokumentieren. Es ist nicht statthaft UND nicht Sinn der Übung, dass Sie den Algorithmus implementieren und dann den Output abgeben. Bedenken Sie, dass Sie bei der Klausur keinerlei elektronische Hilfsmittel verwenden dürfen und Algorithmen daher in ihrem Gehirn ausführen können müssen. P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
3 Greedy-Algorithmen Annahme: Gewichtsfunktion w misst Güte einer Lösung (oder Teillösung). Ziel: konstruiere Lösung mit maximalen Gewicht (w). 1 Starte mit leerer Lösung 2 In jedem Schritt: Erweitere die bisher konstruierte Teillösung. Unter k möglichen Erweiterungen, die zu Teillösungen L 1,..., L k führen, wähle L i, so dass w(l i ) maximal. (greedy = gierig) Also bedeutet greedy : Nimm immer das größte Stück. Oft wird die Greedy-Strategie im Sinne einer Heuristik verwendet. (Heuristik bedeutet dabei: i.d.r. wird eine brauchbar gute Lösung erzeugt) Es gibt aber auch Probleme, für die das Greedy-Prinzip optimal ist, d.h. tatsächlich immer zu einer optimalen Lösung führt. P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
4 Unabhängigkeitssystem Sei E eine endliche Menge und M eine Menge von Teilmengen von E, also M P(E). Dann heißt (E, M) Mengensystem. Ein Mengensystem (E, M) heißt Unabhängigkeitssystem, wenn M und zu jeder Menge in M auch alle Teilmengen enthalten sind, also gilt: Aus A M und B A folgt B M. Ein Unabhängigkeitssystem ist somit abgeschlossen unter Bildung von Teilmengen. Man kann eine in M gefundene Menge kleiner machen und bleibt in M. Idee: für jede Menge A in M gelten die Elemente von A als unabhänigig voneinander (vergleichbar mit linear unabhängigen Vektoren). P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
5 Gewichtsfunktion und Optimierungsproblem Sei (E, M) ein Mengensystem Sei w eine Funktion w : E R +, genannt Gewichtsfunktion Erweitere Notation (Gewicht eine Menge A M): w(a) := w(e) e A Optimierungsproblem: Finde A M, das die Gewichtssumme maximiert. Für alle A M soll also gelten: w(a ) w(a). P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
6 Kanonischer Greedy-Algorithmus... für Unabhängigkeitssystem (E, M) und Gewichtsfunktion w : E R + : A ; for e E in Reihenfolge absteigender Gewichte w(e) do if A {e} M then A A {e} end end return A Liefert der Algorithmus Greedy immer die optimale Lösung? (immer ˆ= für beliebige Mengensysteme und Gewichte) P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
7 Beispiel: Greedy nicht immer optimal E = {a, b, c} M = {, {a}, {b}, {c}, {b, c} } w(a) = 3, w(b) = w(c) = 2 Dazu liefert der kanonische Greedy-Algorithmus die Lösung {a} mit Gewichtssume w(a) = 3 Die optimale Lösung ist {b, c} mit Gewichtssumme w(b) + w(c) = 4. Gesucht: Kriterium wann ist Greedy optimal? P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
8 Matroid Definition (Matroid) Ein Unabhängigkeitssystem (E, M) heißt Matroid, wenn für alle A, B M die folgende Austauscheigenschaft gilt: Ist A > B, dann gibt es x A \ B, so dass B {x} M. Definition (Basis) Sei (E, M) ein Matroid und B M ein maximales Element, also für alle x E \ B: B {x} / M. B heisst Basis des Matroids (E, M). Beobachtung: Alle Basen eines Matroids sind gleich gross. Also: sind B und C Basen des Matroids (E, M), dann B = C. P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
9 Exkurs: Bezug zur Linearen Algebra Matroide sind eine Abstraktion von linearer Unabhängigkeit und Basen. E ˆ= Vektorraum M ˆ= Menge aller Teilmengen von E mit linear unabhängigen Elementen Austauscheigenschaft ˆ= vgl. Basisergänzungssatz und Austauschlemma aus der linearen Algebra. Basis ˆ= maximale Menge linear unabhängiger Elemente; d.h. jede Obermenge ist linear abhängig. P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
10 Matroid garantiert Greedy-Optimalität Satz (Greedy-Optimalität): Sei (E, M) ein Unabhängigkeitssystem Für jede beliebige Gewichtsfunktion w : E R + berechnet der kanonische Greedy-Algorithmus eine optimale Lösung (E, M) ist ein Matroid. Beweis: Tafel P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
11 Auftragsplanung Gegeben: Menge E von n Aufträgen mit jeweils gleichem Zeitbedarf (ein Tag) Zu jedem Auftrag x E: Gewinn w(x) > 0 (Gewichtsfunktion). Anzahl Tage d(x), bis zu der Auftrag x abgeschlossen sein muss Gesucht: Menge L E von Aufträgen, so dass a) der Gesamtgewinn x L w(x) maximal ist, und b) L sich so sortieren lässt, dass jeder Auftrag vor seinem Abschlusstermin erledigt wird. Menge M zulässiger Auftragsmengen ist also gegeben durch A M s N : {y A : d(y) s} s P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
12 Auftragsplanung: Beispiel Auftragsmenge E = {a, b, c, d, e} Auftrag x Wert w(x) Termin d(x) a 13 2 b 7 1 c 9 1 d 3 2 e 5 1 Lösung Gewinn 0 {a} 13 {b} 7 {c} 9 {d} 3 {e} 5 {a, b} 20 {a, c} 22 {a, d} 16 {a, e} 18 {b, d} 10 {c, d} 12 {d, e} 8 P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
13 Auftragsplanung: Lösung Ordne Aufträge in E absteigend nach Gewinn Jetzt der kanonische Greedy-Algorithmus wie folgt: A ; for e E in Reihenfolge absteigenden Gewinns w(e) do if A {e} M then A A {e} end end return A In A seien die Aufträge nach ihrem Abschlusstermin geordnet: d 1 d 2... d i Die Lösung ist genau dann zulässig, wenn gilt: d 1 1, d 2 2,..., d i i. P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
14 ... und noch mal der Kruskal-Algorithmus Kruskal-Algorithmus (1956) für minimalen Spannbaum auf ungerichtetem zusammenhängendem Graph (V, E) mit Kantengewicht w(e) für e E 1 Erzeuge Liste Q mit der Kantenmenge E aufsteigend sortiert nach Gewicht (kleinstes zuerst). Initialisiere F als leere Menge. 2 Entferne vorderste Kante e = {u, v} (mit kleinstem Gewicht) aus Q 3 Falls (V, F ) keinen Pfad zwischen u und v enthält: 4 Falls Q nicht leer, zurück zu 2. 5 Ausgabe F. F := F {e} Greedy-Algorithmus zur Minimierung der Summe der Kantengewichte P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
15 Beispiel-Lauf: Kruskal-Algorithmus Q = [{2, 3}, {4, 5}, {1, 3}, {1, 2}, {3, 5}, {2, 4}, {2, 5}, {3, 4}] F = {} P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
16 Beispiel-Lauf: Kruskal-Algorithmus Q = [{4, 5}, {1, 3}, {1, 2}, {3, 5}, {2, 4}, {2, 5}, {3, 4}] F = {{2, 3}} 5 P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
17 Beispiel-Lauf: Kruskal-Algorithmus Q = [{1, 3}, {1, 2}, {3, 5}, {2, 4}, {2, 5}, {3, 4}] F = {{2, 3}}, {4, 5}} P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
18 Beispiel-Lauf: Kruskal-Algorithmus Q = [{1, 2}, {3, 5}, {2, 4}, {2, 5}, {3, 4}] F = {{2, 3}}, {4, 5}, {1, 3}} P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
19 Beispiel-Lauf: Kruskal-Algorithmus Q = [{3, 5}, {2, 4}, {2, 5}, {3, 4}] F = {{2, 3}}, {4, 5}, {1, 3}} P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
20 Beispiel-Lauf: Kruskal-Algorithmus Q = [{2, 4}, {2, 5}, {3, 4}] F = {{2, 3}}, {4, 5}, {1, 3}, {3, 5}} P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
21 Beispiel-Lauf: Kruskal-Algorithmus Q = [] F = {{2, 3}}, {4, 5}, {1, 3}, {3, 5}} P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
22 Kruskal: Korrektheit (1) E = Kantenmenge Gewichtsfunktion w : E R = Kantengewichte M enthält F E genau dann wenn (V, F ) azyklisch (Wald) ist. Wende Satz über Greedy-Optimalität an: Kruskal findet optimale Lösung für beliebige Kantengewichte (E, M) ist ein Matroid. Der Kruskal minimiert, während der kanonische Greedy-Algorithmus maximiert. Der Algorithmus ist direkt anwendbar nach Transformation der Kantengewichte w (e) = c w(e). Die Konstante c ist so groß zu wählen, dass alle w (e) positiv werden. P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
23 Kruskal: Korrektheit (2) Behauptung: (E, M) ist ein Matroid. Beweis(skizze): (E, M) ist Unabhängigkeitssystem, denn Teilgraphen von azyklischen Graphen sind azyklisch. Austauscheigenschaft: Seien A, B M mit A > B, also (V, A) azyklisch und (V, B) azyklisch. (V, A) ist disjunkte Vereinigung von V A Bäumen, (V, B) ist disjunkte Vereinigung von V B Bäumen. Somit besteht (V, B) aus mehr Bäumen als (V, A), und es gibt Knoten u, v V, die in demselben Baum von (V, A) liegen, aber nicht innerhalb eines Baums von (V, B). Insbesondere können u und v so gewählt werden, dass die Kante {u, v} := e in A liegt aber nicht in B. Ausserdem ist (V, B {e}) azyklisch nach Wahl von u und v aus verschiedenen Bäumen von (V, B). Also e A \ B und B {e} M, q.e.d. (E, M) heißt graphisches Matroid. P.F. Stadler & C. Höner (Bioinf, Uni LE) ADS 2, V5 4. Mai / 17
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2007 11. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik [email protected] Das Rucksack-Problem Ein Dieb, der einen Safe
Algorithmen und Datenstrukturen 2 Sommersemester 2007 11. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik [email protected] Das Rucksack-Problem Ein Dieb, der einen Safe
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2009 11. Vorlesung Uwe Quasthoff Universität Leipzig Institut für Informatik [email protected] Das Rucksack-Problem Ein Dieb, der einen
Algorithmen und Datenstrukturen 2 Sommersemester 2009 11. Vorlesung Uwe Quasthoff Universität Leipzig Institut für Informatik [email protected] Das Rucksack-Problem Ein Dieb, der einen
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl. Beispiele für optimale Greedy-Lösungen
 Wiederholung Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl unabhängig von Subproblemen Optimalität der Subprobleme Beispiele für optimale Greedy-Lösungen Scheduling Problem
Wiederholung Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl unabhängig von Subproblemen Optimalität der Subprobleme Beispiele für optimale Greedy-Lösungen Scheduling Problem
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 3 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
ADS: Algorithmen und Datenstrukturen 2 Teil 3 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide
 Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide Dipl-Math. Wolfgang Kinzner 3.4.2012 Kapitel 3: Minimal aufspannende Bäume und Matroide Minimal aufspannende
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide Dipl-Math. Wolfgang Kinzner 3.4.2012 Kapitel 3: Minimal aufspannende Bäume und Matroide Minimal aufspannende
Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo?
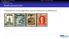 Briefmarkensammeln (Folie 413, Seite 80 im Skript) Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo? Welche Briefmarken für einen 20 fen Brief? Der Greedy-Algorithmus führt nicht
Briefmarkensammeln (Folie 413, Seite 80 im Skript) Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo? Welche Briefmarken für einen 20 fen Brief? Der Greedy-Algorithmus führt nicht
1 Matroide. 1.1 Definitionen und Beispiele. Seminar zur ganzzahligen Optimierung Thema: Durchschnitt von Matroiden - Satz von Edmonds von Dany Sattler
 Seminar zur ganzzahligen Optimierung Thema: Durchschnitt von Matroiden - Satz von Edmonds von Dany Sattler 1 Matroide 1.1 Definitionen und Beispiele 1. Definition (Unabhängigkeitssystem): Ein Mengensystem
Seminar zur ganzzahligen Optimierung Thema: Durchschnitt von Matroiden - Satz von Edmonds von Dany Sattler 1 Matroide 1.1 Definitionen und Beispiele 1. Definition (Unabhängigkeitssystem): Ein Mengensystem
Durchschnitt von Matroiden
 Durchschnitt von Matroiden Satz von Edmonds Dany Sattler 18. Januar 2007/ Seminar zur ganzzahligen Optimierung / Wallenfels Definition: Unabhängigkeitssystem Definition: Ein Mengensystem (S, J ) nennt
Durchschnitt von Matroiden Satz von Edmonds Dany Sattler 18. Januar 2007/ Seminar zur ganzzahligen Optimierung / Wallenfels Definition: Unabhängigkeitssystem Definition: Ein Mengensystem (S, J ) nennt
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 02. Mai 2017 [Letzte Aktualisierung: 10/07/2018,
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 02. Mai 2017 [Letzte Aktualisierung: 10/07/2018,
Datenstrukturen und Algorithmen (SS 2013)
 Datenstrukturen und Algorithmen (SS 2013) Übungsblatt 10 Abgabe: Montag, 08.07.2013, 14:00 Uhr Die Übungen sollen in Gruppen von zwei bis drei Personen bearbeitet werden. Schreiben Sie die Namen jedes
Datenstrukturen und Algorithmen (SS 2013) Übungsblatt 10 Abgabe: Montag, 08.07.2013, 14:00 Uhr Die Übungen sollen in Gruppen von zwei bis drei Personen bearbeitet werden. Schreiben Sie die Namen jedes
Definition Gerichteter Pfad. gerichteter Pfad, wenn. Ein gerichteter Pfad heißt einfach, falls alle u i paarweise verschieden sind.
 3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph.
 Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
3. Minimale Spannbäume. Definition 99 T heißt minimaler Spannbaum (MSB, MST) von G, falls T Spannbaum von G ist und gilt:
 3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e),
3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e),
3.2 Generischer minimaler Spannbaum-Algorithmus
 3.2 Generischer minimaler Spannbaum-Algorithmus Initialisiere Wald F von Bäumen, jeder Baum ist ein singulärer Knoten (jedes v V bildet einen Baum) while Wald F mehr als einen Baum enthält do wähle einen
3.2 Generischer minimaler Spannbaum-Algorithmus Initialisiere Wald F von Bäumen, jeder Baum ist ein singulärer Knoten (jedes v V bildet einen Baum) while Wald F mehr als einen Baum enthält do wähle einen
Graphalgorithmen Netzwerkalgorithmen. Laufzeit
 Netzwerkalgorithmen Laufzeit (Folie 390, Seite 78 im Skript) Finden eines Matchings maximaler Kardinalität dauert nur O( E min{ V, V 2 }) mit der Ford Fulkerson Methode. Der Fluß ist höchstens f = min{
Netzwerkalgorithmen Laufzeit (Folie 390, Seite 78 im Skript) Finden eines Matchings maximaler Kardinalität dauert nur O( E min{ V, V 2 }) mit der Ford Fulkerson Methode. Der Fluß ist höchstens f = min{
9 Minimum Spanning Trees
 Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
\ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E.
 Das Komplement Ḡ = (V, ( V ) \ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E. Ein Graph H = (V, E )
Das Komplement Ḡ = (V, ( V ) \ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E. Ein Graph H = (V, E )
Theoretische Informatik 1
 Theoretische Informatik 1 Approximierbarkeit David Kappel Institut für Grundlagen der Informationsverarbeitung Technische Universität Graz 02.07.2015 Übersicht Das Problem des Handelsreisenden TSP EUCLIDEAN-TSP
Theoretische Informatik 1 Approximierbarkeit David Kappel Institut für Grundlagen der Informationsverarbeitung Technische Universität Graz 02.07.2015 Übersicht Das Problem des Handelsreisenden TSP EUCLIDEAN-TSP
Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od
 Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od Diskrete Strukturen 3.7 dag 473/556 3.8 Zusammenhang Definition
Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od Diskrete Strukturen 3.7 dag 473/556 3.8 Zusammenhang Definition
Rückblick: Starke Zusammenhangskomponenten
 Rückblick: Starke Zusammenhangskomponenten Der Algorithmus von Kosaraju bestimmt die starken Zusammenhangskomponenten eines gerichteten Graphen wie folgt: Schritt 1: Bestimme den transponierten Graphen
Rückblick: Starke Zusammenhangskomponenten Der Algorithmus von Kosaraju bestimmt die starken Zusammenhangskomponenten eines gerichteten Graphen wie folgt: Schritt 1: Bestimme den transponierten Graphen
Theoretische Informatik 1
 Theoretische Informatik 1 Approximierbarkeit David Kappel Institut für Grundlagen der Informationsverarbeitung Technische Universität Graz 10.06.2016 Übersicht Das Problem des Handelsreisenden TSP EUCLIDEAN-TSP
Theoretische Informatik 1 Approximierbarkeit David Kappel Institut für Grundlagen der Informationsverarbeitung Technische Universität Graz 10.06.2016 Übersicht Das Problem des Handelsreisenden TSP EUCLIDEAN-TSP
Berechnung minimaler Spannbäume. Beispiel
 Minimale Spannbäume Definition Sei G pv, Eq ein ungerichteter Graph und sei w : E Ñ R eine Funktion, die jeder Kante ein Gewicht zuordnet. Ein Teilgraph T pv 1, E 1 q von G heißt Spannbaum von G genau
Minimale Spannbäume Definition Sei G pv, Eq ein ungerichteter Graph und sei w : E Ñ R eine Funktion, die jeder Kante ein Gewicht zuordnet. Ein Teilgraph T pv 1, E 1 q von G heißt Spannbaum von G genau
Kapitel IV Minimale Spannbäume
 Kapitel IV Minimale Spannbäume 1. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten.
Kapitel IV Minimale Spannbäume 1. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten.
Algorithmen und Komplexität Lösungsvorschlag zu Übungsblatt 8
 ETH Zürich Institut für Theoretische Informatik Prof. Dr. Angelika Steger Florian Meier, Ralph Keusch HS 2017 Algorithmen und Komplexität Lösungsvorschlag zu Übungsblatt 8 Lösungsvorschlag zu Aufgabe 1
ETH Zürich Institut für Theoretische Informatik Prof. Dr. Angelika Steger Florian Meier, Ralph Keusch HS 2017 Algorithmen und Komplexität Lösungsvorschlag zu Übungsblatt 8 Lösungsvorschlag zu Aufgabe 1
5. Bäume und Minimalgerüste
 5. Bäume und Minimalgerüste Charakterisierung von Minimalgerüsten 5. Bäume und Minimalgerüste Definition 5.1. Es ein G = (V, E) ein zusammenhängender Graph. H = (V,E ) heißt Gerüst von G gdw. wenn H ein
5. Bäume und Minimalgerüste Charakterisierung von Minimalgerüsten 5. Bäume und Minimalgerüste Definition 5.1. Es ein G = (V, E) ein zusammenhängender Graph. H = (V,E ) heißt Gerüst von G gdw. wenn H ein
Datenstrukturen und Algorithmen SS07
 Datenstrukturen und Algorithmen SS0 Datum:.6.200 Michael Belfrage [email protected] belfrage.net/eth Programm von Heute Minimaler Spannbaum (MST) Challenge der Woche Fibonacci Heap Minimaler Spannbaum
Datenstrukturen und Algorithmen SS0 Datum:.6.200 Michael Belfrage [email protected] belfrage.net/eth Programm von Heute Minimaler Spannbaum (MST) Challenge der Woche Fibonacci Heap Minimaler Spannbaum
4.2 Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition 4.2.1
 Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Lerneinheit 3: Greedy Algorithmen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2016 10.5.2016 Einleitung Einleitung Diese Lerneinheit
Algorithmen und Datenstrukturen 2 Lerneinheit 3: Greedy Algorithmen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2016 10.5.2016 Einleitung Einleitung Diese Lerneinheit
Algo&Komp. - Wichtige Begriffe Mattia Bergomi Woche 6 7
 1 Kürzeste Pfade Woche 6 7 Hier arbeiten wir mit gewichteten Graphen, d.h. Graphen, deren Kanten mit einer Zahl gewichtet werden. Wir bezeichnen die Gewichtsfunktion mit l : E R. Wir wollen einen kürzesten
1 Kürzeste Pfade Woche 6 7 Hier arbeiten wir mit gewichteten Graphen, d.h. Graphen, deren Kanten mit einer Zahl gewichtet werden. Wir bezeichnen die Gewichtsfunktion mit l : E R. Wir wollen einen kürzesten
Übungsblatt 2 - Lösung
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 2 - Lösung Vorlesung Algorithmentechnik im WS 08/09 Ausgabe 04. November 2008 Abgabe 8. November, 5:0 Uhr (im Kasten vor Zimmer
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 2 - Lösung Vorlesung Algorithmentechnik im WS 08/09 Ausgabe 04. November 2008 Abgabe 8. November, 5:0 Uhr (im Kasten vor Zimmer
Algorithmen und Datenstrukturen Tafelübung 14. Jens Wetzl 8. Februar 2012
 Algorithmen und Datenstrukturen Tafelübung 14 Jens Wetzl 8. Februar 2012 Folien Keine Garantie für Vollständigkeit und/oder Richtigkeit Keine offizielle Informationsquelle LS2-Webseite Abrufbar unter:
Algorithmen und Datenstrukturen Tafelübung 14 Jens Wetzl 8. Februar 2012 Folien Keine Garantie für Vollständigkeit und/oder Richtigkeit Keine offizielle Informationsquelle LS2-Webseite Abrufbar unter:
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 4: Suchstrategien Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca [email protected] 14. April 2017 HALBORDNUNG TOPOLOGISCHE ORDNUNG TOPOLOGISCHES
Algorithmische Graphentheorie Vorlesung 4: Suchstrategien Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca [email protected] 14. April 2017 HALBORDNUNG TOPOLOGISCHE ORDNUNG TOPOLOGISCHES
Datenstrukturen und Algorithmen
 Prof. Dr. Erika Ábrahám Datenstrukturen und Algorithmen 1/1 Datenstrukturen und Algorithmen Vorlesung 14: Prof. Dr. Erika Ábrahám Theorie Hybrider Systeme Informatik 2 http://ths.rwth-aachen.de/teaching/ss-14/
Prof. Dr. Erika Ábrahám Datenstrukturen und Algorithmen 1/1 Datenstrukturen und Algorithmen Vorlesung 14: Prof. Dr. Erika Ábrahám Theorie Hybrider Systeme Informatik 2 http://ths.rwth-aachen.de/teaching/ss-14/
3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel
 3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel EADS 3.1 Konstruktion von minimalen Spannbäumen 16/36
3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel EADS 3.1 Konstruktion von minimalen Spannbäumen 16/36
Algorithmen und Datenstrukturen 2-1. Seminar -
 Algorithmen und Datenstrukturen 2-1. Seminar - Dominic Rose Bioinformatics Group, University of Leipzig Sommersemster 2010 Outline 1. Übungsserie: 3 Aufgaben, insgesamt 30 28 Punkte A1 Spannbäume (10 8
Algorithmen und Datenstrukturen 2-1. Seminar - Dominic Rose Bioinformatics Group, University of Leipzig Sommersemster 2010 Outline 1. Übungsserie: 3 Aufgaben, insgesamt 30 28 Punkte A1 Spannbäume (10 8
1. Klausur zur Vorlesung Algorithmentechnik Wintersemester 2008/2009
 . Klausur zur Vorlesung Algorithmentechnik Wintersemester 008/009 Hier Aufkleber mit Name und Matrikelnummer anbringen Vorname: Nachname: Matrikelnummer: Beachten Sie: Bringen Sie den Aufkleber mit Ihrem
. Klausur zur Vorlesung Algorithmentechnik Wintersemester 008/009 Hier Aufkleber mit Name und Matrikelnummer anbringen Vorname: Nachname: Matrikelnummer: Beachten Sie: Bringen Sie den Aufkleber mit Ihrem
21. Greedy Algorithmen. Aktivitätenauswahl, Fractional Knapsack Problem, Huffman Coding Cormen et al, Kap. 16.1, 16.3
 581 21. Greedy Algorithmen Aktivitätenauswahl, Fractional Knapsack Problem, Huffman Coding Cormen et al, Kap. 16.1, 16.3 Aktivitäten Auswahl 582 Koordination von Aktivitäten, die gemeinsame Resource exklusiv
581 21. Greedy Algorithmen Aktivitätenauswahl, Fractional Knapsack Problem, Huffman Coding Cormen et al, Kap. 16.1, 16.3 Aktivitäten Auswahl 582 Koordination von Aktivitäten, die gemeinsame Resource exklusiv
Kombinatorische Optimierung
 Juniorprof. Dr. Henning Meyerhenke 1 Henning Meyerhenke: KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Vorlesung 16 Programm: Einführung
Juniorprof. Dr. Henning Meyerhenke 1 Henning Meyerhenke: KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Vorlesung 16 Programm: Einführung
S=[n] Menge von Veranstaltungen J S kompatibel mit maximaler Größe J
![S=[n] Menge von Veranstaltungen J S kompatibel mit maximaler Größe J S=[n] Menge von Veranstaltungen J S kompatibel mit maximaler Größe J](/thumbs/26/8373971.jpg) Greedy-Strategie Definition Paradigma Greedy Der Greedy-Ansatz verwendet die Strategie 1 Top-down Auswahl: Bestimme in jedem Schritt eine lokal optimale Lösung, so dass man eine global optimale Lösung
Greedy-Strategie Definition Paradigma Greedy Der Greedy-Ansatz verwendet die Strategie 1 Top-down Auswahl: Bestimme in jedem Schritt eine lokal optimale Lösung, so dass man eine global optimale Lösung
3. Musterlösung. Problem 1: Heapsort
 Universität Karlsruhe Algorithmentechnik Fakultät für Informatik WS 05/06 ITI Wagner 3. Musterlösung Problem : Heapsort ** 2 3 4 5 Algorithmus : Heapsort (A) Eingabe : Array A der Länge n Ausgabe : Aufsteigend
Universität Karlsruhe Algorithmentechnik Fakultät für Informatik WS 05/06 ITI Wagner 3. Musterlösung Problem : Heapsort ** 2 3 4 5 Algorithmus : Heapsort (A) Eingabe : Array A der Länge n Ausgabe : Aufsteigend
Das Problem des minimalen Steiner-Baumes
 Das Problem des minimalen Steiner-Baumes Ein polynomieller Approximationsalgorithmus Benedikt Wagner 4.05.208 INSTITUT FU R THEORETISCHE INFORMATIK, LEHRSTUHL ALGORITHMIK KIT Die Forschungsuniversita t
Das Problem des minimalen Steiner-Baumes Ein polynomieller Approximationsalgorithmus Benedikt Wagner 4.05.208 INSTITUT FU R THEORETISCHE INFORMATIK, LEHRSTUHL ALGORITHMIK KIT Die Forschungsuniversita t
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2006 5. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik [email protected] Wdhlg.: Dijkstra-Algorithmus I Bestimmung der
Algorithmen und Datenstrukturen 2 Sommersemester 2006 5. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik [email protected] Wdhlg.: Dijkstra-Algorithmus I Bestimmung der
Grundlagen: Algorithmen und Datenstrukturen
 Grundlagen: Algorithmen und Datenstrukturen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Sommersemester 00
Grundlagen: Algorithmen und Datenstrukturen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Sommersemester 00
Übungsblatt 5 Lösungsvorschläge
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 5 Lösungsvorschläge Vorlesung Algorithmentechnik im WS 09/10 Problem 1: Lineare Weihnachtsalgebra Kreisbasen [vgl. Kapitel
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 5 Lösungsvorschläge Vorlesung Algorithmentechnik im WS 09/10 Problem 1: Lineare Weihnachtsalgebra Kreisbasen [vgl. Kapitel
Fortgeschrittene Netzwerk- und Graph-Algorithmen
 Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Algorithmen II Vorlesung am 15.11.2012
 Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
1. Klausur zur Vorlesung Algorithmentechnik Wintersemester 2008/2009
 . Klausur zur Vorlesung Algorithmentechnik Wintersemester 8/9 Lösung! Beachten Sie: Bringen Sie den Aufkleber mit Ihrem Namen und Matrikelnummer auf diesem Deckblatt an und beschriften Sie jedes Aufgabenblatt
. Klausur zur Vorlesung Algorithmentechnik Wintersemester 8/9 Lösung! Beachten Sie: Bringen Sie den Aufkleber mit Ihrem Namen und Matrikelnummer auf diesem Deckblatt an und beschriften Sie jedes Aufgabenblatt
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 11 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
ADS: Algorithmen und Datenstrukturen 2 Teil 11 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
f h c 7 a 1 b 1 g 2 2 d
 ) Man bestimme mit Hilfe des Dijkstra-Algorithmus einen kürzesten Weg von a nach h: c 7 a b f 5 h 3 4 5 i e 6 g 2 2 d Beim Dijkstra-Algorithmus wird in jedem Schritt von den noch unmarkierten Knoten jener
) Man bestimme mit Hilfe des Dijkstra-Algorithmus einen kürzesten Weg von a nach h: c 7 a b f 5 h 3 4 5 i e 6 g 2 2 d Beim Dijkstra-Algorithmus wird in jedem Schritt von den noch unmarkierten Knoten jener
Theoretische Informatik. Exkurs: Komplexität von Optimierungsproblemen. Optimierungsprobleme. Optimierungsprobleme. Exkurs Optimierungsprobleme
 Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
Graphalgorithmen 2. Dominik Paulus Dominik Paulus Graphalgorithmen / 47
 Graphalgorithmen Dominik Paulus.0.01 Dominik Paulus Graphalgorithmen.0.01 1 / 7 1 Spannbäume Kruskal Prim Edmonds/Chu-Liu Datenstrukturen Fibonacci-Heap Union/Find Kürzeste Pfade Dijkstra Bellman-Ford
Graphalgorithmen Dominik Paulus.0.01 Dominik Paulus Graphalgorithmen.0.01 1 / 7 1 Spannbäume Kruskal Prim Edmonds/Chu-Liu Datenstrukturen Fibonacci-Heap Union/Find Kürzeste Pfade Dijkstra Bellman-Ford
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein
 Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
Matching. Organisatorisches. VL-18: Matching. (Datenstrukturen und Algorithmen, SS 2017) Gerhard Woeginger. Tanzabend
 Organisatorisches VL-18: Matching (Datenstrukturen und Algorithmen, SS 2017) Gerhard Woeginger Vorlesung: Gerhard Woeginger (Zimmer 4024 im E1) Sprechstunde: Mittwoch 11:15 12:00 Übungen: Tim Hartmann,
Organisatorisches VL-18: Matching (Datenstrukturen und Algorithmen, SS 2017) Gerhard Woeginger Vorlesung: Gerhard Woeginger (Zimmer 4024 im E1) Sprechstunde: Mittwoch 11:15 12:00 Übungen: Tim Hartmann,
Algorithmen & Komplexität
 Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik [email protected] Kürzeste Pfade Problem Gegeben Netzwerk: Graph G = (V, E), Gewichtsfunktion w: E N Zwei Knoten: s, t Kantenzug/Weg
Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik [email protected] Kürzeste Pfade Problem Gegeben Netzwerk: Graph G = (V, E), Gewichtsfunktion w: E N Zwei Knoten: s, t Kantenzug/Weg
Algorithmen und Datenstrukturen 2. Stefan Florian Palkovits, BSc Juni 2016
 Algorithmen und Datenstrukturen 2 Übung 1 Stefan Florian Palkovits, BSc 0926364 [email protected] 12. Juni 2016 Aufgabe 1: Es existiert eine Reduktion von Problem A auf Problem B in O(n 3 +
Algorithmen und Datenstrukturen 2 Übung 1 Stefan Florian Palkovits, BSc 0926364 [email protected] 12. Juni 2016 Aufgabe 1: Es existiert eine Reduktion von Problem A auf Problem B in O(n 3 +
Lösungen zu Kapitel 5
 Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
Wie wird ein Graph dargestellt?
 Wie wird ein Graph dargestellt? Für einen Graphen G = (V, E), ob gerichtet oder ungerichtet, verwende eine Adjazenzliste A G : A G [i] zeigt auf eine Liste aller Nachbarn von Knoten i, wenn G ungerichtet
Wie wird ein Graph dargestellt? Für einen Graphen G = (V, E), ob gerichtet oder ungerichtet, verwende eine Adjazenzliste A G : A G [i] zeigt auf eine Liste aller Nachbarn von Knoten i, wenn G ungerichtet
Kap. 6.5: Minimale Spannbäume
 Kap. 6.5: Minimale Spannbäume Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 19./20. VO DAP2 SS 2009 30.6./2.7.2009 1 Anmeldung zur Klausur 31.07.2009 um 10:15
Kap. 6.5: Minimale Spannbäume Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 19./20. VO DAP2 SS 2009 30.6./2.7.2009 1 Anmeldung zur Klausur 31.07.2009 um 10:15
Algorithmen für Planare Graphen
 Algorithmen für Planare Graphen 12. Juni 2018, Übung 4 Lars Gottesbüren, Michael Hamann INSTITUT FÜR THEORETISCHE INFORMATIK KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Prüfungstermine
Algorithmen für Planare Graphen 12. Juni 2018, Übung 4 Lars Gottesbüren, Michael Hamann INSTITUT FÜR THEORETISCHE INFORMATIK KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Prüfungstermine
Quicksort ist ein Divide-and-Conquer-Verfahren.
 . Quicksort Wie bei vielen anderen Sortierverfahren (Bubblesort, Mergesort, usw.) ist auch bei Quicksort die Aufgabe, die Elemente eines Array a[..n] zu sortieren. Quicksort ist ein Divide-and-Conquer-Verfahren.
. Quicksort Wie bei vielen anderen Sortierverfahren (Bubblesort, Mergesort, usw.) ist auch bei Quicksort die Aufgabe, die Elemente eines Array a[..n] zu sortieren. Quicksort ist ein Divide-and-Conquer-Verfahren.
Datenstrukturen und Algorithmen. Christian Sohler FG Algorithmen & Komplexität
 Datenstrukturen und Algorithmen Christian Sohler FG Algorithmen & Komplexität 1 Klausur Wichtige Hinweise: 2.7.07, Beginn 9 Uhr Bitte spätestens 8:4 Uhr vor Ort sein Sporthalle + Audimax Informationen
Datenstrukturen und Algorithmen Christian Sohler FG Algorithmen & Komplexität 1 Klausur Wichtige Hinweise: 2.7.07, Beginn 9 Uhr Bitte spätestens 8:4 Uhr vor Ort sein Sporthalle + Audimax Informationen
Definition Ein gerichteter Graph G = (V, E) ist ein Graph von geordneten Paaren (u, v) mit u V und v V.
 Kapitel 4 Graphenalgorithmen 4.1 Definitionen Definition 4.1.1. Der Graph G = (V, E) ist über die beiden Mengen V und E definiert, wobei V die Menge der Knoten und E die Menge der Kanten in dem Graph ist.
Kapitel 4 Graphenalgorithmen 4.1 Definitionen Definition 4.1.1. Der Graph G = (V, E) ist über die beiden Mengen V und E definiert, wobei V die Menge der Knoten und E die Menge der Kanten in dem Graph ist.
Graphen. Definitionen
 Graphen Graphen werden häufig als Modell für das Lösen eines Problems aus der Praxis verwendet, wie wir im Kapitel 1 gesehen haben. Der Schweizer Mathematiker Euler hat als erster Graphen verwendet, um
Graphen Graphen werden häufig als Modell für das Lösen eines Problems aus der Praxis verwendet, wie wir im Kapitel 1 gesehen haben. Der Schweizer Mathematiker Euler hat als erster Graphen verwendet, um
Algorithmen und Datenstrukturen Kapitel 9. und
 Algorithmen und Datenstrukturen Kapitel 9 und Kürzeste Pfade Frank Heitmann [email protected] 9. Dezember 0 Frank Heitmann [email protected] / Problemstellung Definition
Algorithmen und Datenstrukturen Kapitel 9 und Kürzeste Pfade Frank Heitmann [email protected] 9. Dezember 0 Frank Heitmann [email protected] / Problemstellung Definition
11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME
 Algorithmen und Datenstrukturen 11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME Algorithmen und Datenstrukturen - Ma5hias Thimm ([email protected]) 1 Algorithmen und Datenstrukturen 11.1. BERECHNUNG MAXIMALER FLÜSSE
Algorithmen und Datenstrukturen 11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME Algorithmen und Datenstrukturen - Ma5hias Thimm ([email protected]) 1 Algorithmen und Datenstrukturen 11.1. BERECHNUNG MAXIMALER FLÜSSE
Tutoraufgabe 1 (Suchen in Graphen):
 Prof. aa Dr. E. Ábrahám Datenstrukturen und Algorithmen SS14 F. Corzilius, S. Schupp, T. Ströder Tutoraufgabe 1 (Suchen in Graphen): a) Geben Sie die Reihenfolge an, in der die Knoten besucht werden, wenn
Prof. aa Dr. E. Ábrahám Datenstrukturen und Algorithmen SS14 F. Corzilius, S. Schupp, T. Ströder Tutoraufgabe 1 (Suchen in Graphen): a) Geben Sie die Reihenfolge an, in der die Knoten besucht werden, wenn
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen 13. Übung minimale Spannbäume, topologische Sortierung, AVL-Bäume Clemens Lang Übungen zu AuD 4. Februar 2010 Clemens Lang (Übungen zu AuD) Algorithmen und Datenstrukturen
Algorithmen und Datenstrukturen 13. Übung minimale Spannbäume, topologische Sortierung, AVL-Bäume Clemens Lang Übungen zu AuD 4. Februar 2010 Clemens Lang (Übungen zu AuD) Algorithmen und Datenstrukturen
Betriebswirtschaftliche Optimierung
 Institut für Statistik und OR Uni Graz 1 Approximationsalgorithmen auf metrischen Instanzen Minimum Spanning Tree Definition (Spannbaum) Ein Spannbaum in einem Graphen G = (V,E) ist ein kreisfreier Teilgraph
Institut für Statistik und OR Uni Graz 1 Approximationsalgorithmen auf metrischen Instanzen Minimum Spanning Tree Definition (Spannbaum) Ein Spannbaum in einem Graphen G = (V,E) ist ein kreisfreier Teilgraph
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Wintersemester 2012/13 25. Vorlesung Dynamisches Programmieren Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Klausurvorbereitung Tipp: Schreiben Sie sich alle Fragen
Algorithmen und Datenstrukturen Wintersemester 2012/13 25. Vorlesung Dynamisches Programmieren Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Klausurvorbereitung Tipp: Schreiben Sie sich alle Fragen
Grundzüge von Algorithmen und Datenstrukturen, WS 15/16: Lösungshinweise zum 13. Übungsblatt
 U N S A R I V E R S A V I E I T A S N I S S Grundzüge von Algorithmen und Datenstrukturen, WS /6: Lösungshinweise zum 3. Übungsblatt Christian Hoffmann, Fabian Bendun Aufgabe 3. (a) Sei j i + = n die Größe
U N S A R I V E R S A V I E I T A S N I S S Grundzüge von Algorithmen und Datenstrukturen, WS /6: Lösungshinweise zum 3. Übungsblatt Christian Hoffmann, Fabian Bendun Aufgabe 3. (a) Sei j i + = n die Größe
Minimal spannender Baum
 Minimal spannender Baum 16 1 2 21 5 11 19 6 6 3 14 33 10 5 4 18 Die Kreise zeigen die vorgesehenen Standorte neu zu errichtender Filialen einer Bank. Entlang der bestehenden Straßen sollen Telefonleitungen
Minimal spannender Baum 16 1 2 21 5 11 19 6 6 3 14 33 10 5 4 18 Die Kreise zeigen die vorgesehenen Standorte neu zu errichtender Filialen einer Bank. Entlang der bestehenden Straßen sollen Telefonleitungen
Kapitel 8 Graphenalgorithmen. Minimaler Spannbaum Union-find-Problem Kürzeste Wege
 Kapitel 8 Graphenalgorithmen Minimaler Spannbaum Union-find-Problem Kürzeste Wege Rückblick Graphen Modelle für Objekte und Beziehungen untereinander Personen - Bekanntschaften Ereignisse - Abhängigkeiten
Kapitel 8 Graphenalgorithmen Minimaler Spannbaum Union-find-Problem Kürzeste Wege Rückblick Graphen Modelle für Objekte und Beziehungen untereinander Personen - Bekanntschaften Ereignisse - Abhängigkeiten
