Erinnerung Blockchiffre
|
|
|
- Rainer Schulz
- vor 8 Jahren
- Abrufe
Transkript
1 Erinnerung Blockchiffre Definition schlüsselabhängige Permutation Seien F, F 1 pt Algorithmen. F heißt schlüsselabhängige Permutation auf l Bits falls 1 F berechnet eine Funktion {0, 1} n {0, 1} l {0, 1} l, so dass für alle k {0, 1} n die Funktion F k ( ) eine Bijektion ist. 2 F 1 k ( ) berechnet die Umkehrfunktion von F k ( ). Definition Starke Pseudozufallspermutation (Blockchiffre) Sei F eine schlüsselabhängige Permutation auf l Bits. Wir bezeichnen F als starke Pseudozufallspermutation (Blockchiffre), falls für alle ppt D gilt Ws[D F k ( ),F 1 k ( ) (1 n ) = 1] Ws[D f ( ),f 1 ( ) (1 n ) = 1] negl(n), mit k R {0, 1} n und f R Perm l. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 165 / 180
2 Angriffe auf Blockchiffren Angriffe: in aufsteigender Stärke 1 Ciphertext-only: A erhält F k (x i ) für unbekannte x i. 2 Known plaintext: A erhält Paare (x i, F k (x i )) 3 Chosen plaintext: A wählt x i und erhält F k (x i ). 4 Chosen ciphertext: A wählt x i, y i und erhält F k (x i ), F 1 k (y i ). Sicherheit: Jede Pseudozufallspermutation F ist CPA-sicher. Jede starke Pseudozufallspermutation F ist CCA-sicher. Warnung: Blockchiffren selbst sind kein sicheres Verschlüsselungsschema. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 166 / 180
3 Design Prinzip: Konfusion und Diffusion Ziel: Kleine Eingabedifferenzen erzeugen pseudozufällige Ausgaben. Paradigma Konfusion und Diffusion Rundeniterierte Vorgehensweise zur Konstruktion einer Blockchiffre 1 Konfusion: Permutiere kleine Bitblöcke schlüsselabhängig. 2 Diffusion: Permutiere alle Bits. Bsp: F soll Blocklänge 128 Bits besitzen. Konfusion: Definiere schlüsselabhängige Permutation S 1,..., S 16 auf 8 Bits. Sei x = x 1... x 16 ({0, 1} 8 ) 16. Definiere F k (x) = S 1 (x 1 )... S 16 (x 16 ). Diffusion: Permutiere die Bits von F k (x). Iteriere die obigen beiden Schritte hinreichend oft, damit kleine Eingabedifferenzen sich auf alle Ausgabebits auswirken. Beschreibungslänge von S i : Bits, F : = 2 15 Bits. Länge einer echten Zufallspermutation: = Bits. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 167 / 180
4 Substitutions-Permutations Netzwerk (SPN) Szenario: Verwende einen Masterschlüssel k. Berechne aus dem Masterschlüssel k Rundenschlüssel k 1,... k r mittels eines sogenannten Keyschedule-Algorithmus. Die Permutationsfunktionen S 1,..., S m werden fest und schlüsselunabhängig gewählt (sogenannte S-Boxen). Beschreibung Substitutions-Permutations Netzwerk (SPN) EINGABE: S 1,..., S m, k {0, 1} n, x, l, r 1 Berechne k 1,..., k r {0, 1} l aus k. y x. 2 For i 1 to r 1 Schlüsseladdition: y y k i. Schreibe y = y 1... y m. 2 Substitution per S-Boxen: y S 1 (y 1 )..., S m (y m ) 3 Permutation: y Permutation der Bits von y. AUSGABE: F k (x) := y Beobachtung: F ist invertierbar, da jeder Schritt invertierbar ist. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 168 / 180
5 Lawineneffekt Ziel: Veränderung in Eingabebit wirkt sich auf alle Ausgabebits aus. Beobachtung Notwendige Eigenschaften für Lawineneffekt 1 S-Box: Ändern eines Eingabebits verändert 2 Ausgabebits. 2 Permutation: Ausgabebits einer S-Box werden zu Eingabebits verschiedener S-Boxen. Beobachtung: Lawineneffekt Betrachten ein SPN mit 4 Bit S-Boxen und Blocklänge 128 Bit. 1-Bit Eingabedifferenz erzeugt mindestens eine 2-Bit Differenz. Eine 2-Bit Differenz resultiert in zwei 1-Bit Differenzen an verschiedenen S-Boxen in der nächsten Runde. Diese sorgen für mindestens 4-Bit Differenz, usw. D.h. jede Runde verdoppelt potentiell die beeinträchtigten Bits. Nach 7 Runden sind alle 2 7 = 128 Bits von der Veränderung eines Eingabebits beeinträchtigt. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 169 / 180
6 Angriff auf eine Runde eines SPN Algorithmus Angriff auf eine Runde eines SPN EINGABE: x, y = F k (x) 1 y := Invertiere auf y die Permutation und die S-Boxen. 2 Berechne k := x y. AUSGABE: k Anmerkungen: Die Invertierung in Schritt 1 ist möglich, da sowohl die Permutation als auch die S-Boxen öffentlich sind. Nach Invertierung erhält man den Wert x k. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 170 / 180
7 Distinguisher für 2 Runden Bsp: Distinguisher für 2 Runden Wir betrachten Blocklänge 80 Bit und 4 Bit S-Boxen. Wähle x i, die sich nur im ersten 4-Bit Block unterscheiden. Nach 1. Runde: Ausgaben unterscheiden sich in 4 Blöcken. Nach 2. Runde: Ausgaben unterscheiden sich in 16 Blöcken. D.h. nicht alle der 20 Ausgabeblöcke werden verändert. Können SPN leicht von Pseudozufallspermutation entscheiden. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 171 / 180
8 DES - Data Encryption Standard Beschreibung von DES: Entwickelt 1973 von IBM, standardisiert DES besitzt Schlüssellänge 56 Bit und Blocklänge 64 Bit. Besteht aus Feistelnetzwerk (siehe Vorlesung 8) mit 16 Runden. Aus Bits von k werden 48-Bit Schlüssel k 1,..., k 16 ausgewählt. Rundenfunktionen f i sind SPNs mit nicht invertierbaren S-Boxen. Algorithmus Rundenfunktion f i EINGABE: k i, R i 1 {0, 1} 32 1 y := Erweitere R i 1 auf 48 Bit durch Verdopplung von 16 Bits. 2 y := y k i 3 y := Splitte y in 6-Bit Blöcke y 1... y 8 auf. Wende auf jedes y i eine S-Box S i : {0, 1} 6 {0, 1} 4 an. Permutiere das Ergebnis. AUSGABE: f i (R i 1 ) := y Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 172 / 180
9 Die DES S-Boxen DES S-Boxen: Alle 8 S-Boxen realisieren verschiedene Abb. {0, 1} 6 {0, 1} 4. Jede S-Box ist eine 4:1-Abbildung. D.h. jede S-Box sendet genau 4 Eingaben auf eine Ausgabe. Wechsel eines Eingabebits ändert mindestens zwei Ausgabebits. Lawineneffekt bei DES: Wähle (L 0, R 0 ) und (L 0, R 0) mit 1-Bit Differenz in L 0, L 0. (L 1, R 1 ) und (L 1, R 1 ) besitzen 1-Bit Differenz in R 1, R 1. Durch f 2 erhält man mindestens eine 2-Bit Differenz in R 2, R 2. D.h. (L 2, R 2 ) und (L 2, R 2 ) besitzen mind. eine 3-Bit Differenz. f 3 angewendet auf R 2, R 2 liefert mind. eine 4-Bit Differenz, usw. Nach 8 Runden erreicht man volle Diffusion auf alle Ausgabebits. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 173 / 180
10 Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997 DESCHALL, Internet 96 Tage 1998 distributed.net, Internet 41 Tage 1998 Deep Crack, Dollar Maschine 2 Tage 2008 COPACOBANA, Euro FPGAs 1 Tag Das Design von DES ist gut, nur die Schlüssellänge ist zu kurz. Die Blocklänge von 64 Bits von DES gilt als zu kurz. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 174 / 180
11 Doppelte Verschlüsselung bringt wenig Szenario: doppelte Verschlüsselung Sei F eine Blockchiffre mit Schlüssellänge n wie z.b. DES. Dann besitzt F k 1,k 2 (x) = F k2 (F k1 (x)) Schlüssellänge 2n. Leider liefert F kein Sicherheitsniveau von 2 2n. Algorithmus Meet-in-the-Middle Angriff auf doppelte Verschl. EINGABE: (x 1, y 1 ), (x 2, y 2 ) 1 Für alle k 1 {0, 1} n, berechne z := F k1 (x 1 ). Speichere (z, k 1 ) in einer nach der ersten Komponente sortierten Liste L 1. 2 Für alle k 2 {0, 1} n, berechne z := F 1 k 2 (y 1 ). Speichere (z, k 2 ) in einer nach der ersten Komponente sortierten Liste L 2. 3 Für alle z mit (z, k 1 ) L 1 und (z, k 2 ) L 2, speichere (k 1, k 2 ) in S. 4 Für alle (k 1, k 2 ) S: Verifiziere Korrektheit mittels (x 2, y 2 ). AUSGABE: k = (k 1, k 2 ) Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 175 / 180
12 Doppelte Verschlüsselung bringt wenig Korrektheit: Für korrektes (k 1, k 2 ) gilt F k2 (F k1 (x)) = y, d.h. F k1 (x) = F 1 k 2 (y). Ein falsches (k 1, k 2 ) erfüllt diese Identität mit Ws etwa 2 n. D.h. wir erwarten 2 2n 2 n = 2 n Elemente in der Menge S. Verifizieren mit (x 2, y 2 ) liefert erwartet den korrekten Schlüssel. Laufzeit: Operationen auf einzelnen Schlüsseln zählen Zeit O(1). Schritt 1 und 2: jeweils Zeit und Platz O(n 2 n ). Schritt 3: Laufzeit O(2 n ) und Platz O(n 2 n ). Schritt 4 lässt sich in Laufzeit O(2 n ) realisieren. D.h. wir erhalten insgesamt Laufzeit und Platz O(n 2 n ). Damit erhöht sich die Laufzeit gegenüber einem Brute-Force Angriff bei einfacher Verschlüsselung nicht wesentlich. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 176 / 180
13 Dreifache Verschlüsselung Szenario: dreifache Verschlüsselung 1 Variante 1: F k 1,k 2,k 3 (x) := F k3 (F 1 k 2 (F k1 (x))) 2 Variante 2: F k 1,k 2 (x) := F k1 (F 1 k 2 (F k1 (x))) Grund des Alternierens von F, F 1, F: Für die Wahl von k 1 = k 2 = k 3 erhalten wir eine einfache Anwendung von F k1 (x). Sicherheit der 1. Variante: Meet-in-the-Middle Angriff wie zuvor in Zeit und Platz O(n 2 2n ). Sicherheit der 2. Variante: Bekannter CPA-Angriff mit O(2 n ) gewählten Paaren. Zeitkomplexität beträgt ebenfalls O(2 n ). Triple-DES: Beide Varianten von Triple-DES finden in der Praxis Verwendung. Löste 1999 DES als Standard ab. Trotz Standardisierung von AES im Jahr 2002 ist Triple-DES auch heute noch weitverbreitet. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 177 / 180
14 AES - Advanced Encryption Standard NIST Wettbewerb: (National Institute of Standard and Technology) Jan 1997: Aufruf zum Konstruktions-Wettbewerb einer Blockchiffre Ursprünglich 15 Kandidaten eingereicht. Aug 1999: Auswahl von fünf AES-Finalisten MARS, RC6, Rijndael, Serpent und Twofish. Okt 2000: Auswahl von Rijndael der Autoren Rijmen und Daemen. Struktur von AES (Rijndael): AES ist ein SPN und besitzt Blocklänge 128. Schlüssel mit 128, 192 und 256 Bit können verwendet werden. Eingaben x {0, 1} 128 werden rundenweise in einer 4 4-Byte Matrix, der sogenannten Zustandsmatrix, modifiziert. Anzahl Runden: 10 für 128-Bit k, 12 für 192-Bit und 14 für 256-Bit. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 178 / 180
15 Die vier Rundenoperationen von AES Operation 1: AddRoundKey Leite aus k einen Rundenschlüssel k i {0, 1} 128 ab. XOR der Zustandsmatrix mit k i. Operation 2: SubByte Interpretiere jedes Byte der Zustandsmatrix als Element x F 8. Ersetze x durch x 1 in F 8 und 0 8 durch 0 8. Wende eine affine Transformation auf die Zustandsbytes an. Man beachte: Dieselbe S-Box wird für alle Bytes verwendet. Operation 3: ShiftRow Verschiebe die 4 Zeilen der 4 4-Zustandsmatrix zyklisch. Lasse die 1. Zeile unverändert. Verschiebe die 2. Zeile um eine Position nach links, die 3. Zeile um 2 nach links und die 3. Zeile um 3 Positionen nach links. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 179 / 180
16 Die vier Rundenoperationen von AES Operation 4: MixColumn Sei a 0,j, a 1,j, a 2,j, a 3,j eine Spalte der Zustandsmatrix. Betrachte die Spalte als Element aus F 8 /(x 4 + 1), d.h. a 0,j + a 1,j x + a 2,j x 2 + a 3,j x 3 mit a i,j F 8. Multipliziere mit c(x) = 2 + x + x 2 + 3x 3 F 8 /(x 4 + 1). Kodieren a F 2 8 = F 2 [y]/π, π irreduzibel mit Grad 8, wie folgt: Sei z.b. a = y 5 + y + 1. Wir schreiben a = ( ) = 35. MixColumn entspricht Multiplikation mit einer Matrix C F D.h. eine Spalte x wird mittels x Cx linear abgebildet. Menge aller (x, Cx) definiert einen linearen Code mit Distanz 5. D.h. unterscheiden sich zwei Spalten x, x in nur einer Position, so unterscheiden sie sich nach MixColumn in allen 4 Positionen. Diese Eigenschaft führt zu einer schnellen Diffusion bei AES. Krypto I - Vorlesung () Substitution-Permutations- und Feistelnetzwerk, Data Encryption Standard 180 / 180
Erinnerung Blockchiffre
 Erinnerung Blockchiffre Definition schlüsselabhängige Permutation Seien F, F 1 pt Algorithmen. F heißt schlüsselabhängige Permutation auf l Bits falls 1 F berechnet eine Funktion {0, 1} n {0, 1} l {0,
Erinnerung Blockchiffre Definition schlüsselabhängige Permutation Seien F, F 1 pt Algorithmen. F heißt schlüsselabhängige Permutation auf l Bits falls 1 F berechnet eine Funktion {0, 1} n {0, 1} l {0,
Erinnerung Blockchiffre
 Erinnerung Blockchiffre Definition schlüsselabhängige Permutation Seien F, F 1 pt Algorithmen. F heißt schlüsselabhängige Permutation auf l Bits falls 1 F berechnet eine Funktion {0, 1} n {0, 1} l {0,
Erinnerung Blockchiffre Definition schlüsselabhängige Permutation Seien F, F 1 pt Algorithmen. F heißt schlüsselabhängige Permutation auf l Bits falls 1 F berechnet eine Funktion {0, 1} n {0, 1} l {0,
Die (Un-)Sicherheit von DES
 Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997
Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997
Die (Un-)Sicherheit von DES
 Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997
Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997
Pseudozufallsfunktionen (PRF) Kapitel 3
 Pseudozufallsfunktionen (PRF) Kapitel 3 Motivation Verschlüsselung eines Dateisystems durch PRG: PRG G(x) Entschlüsselung: berechne aus x entsprechende Generator-Ausgabe Aber: Entschlüsselung der letzten
Pseudozufallsfunktionen (PRF) Kapitel 3 Motivation Verschlüsselung eines Dateisystems durch PRG: PRG G(x) Entschlüsselung: berechne aus x entsprechende Generator-Ausgabe Aber: Entschlüsselung der letzten
4: Blockchiffren. Klartexte (n bit) Chiffretexte. VERschlüsseln. ENTschlüsseln. Stefan Lucks Kryptographie und Mediensicherheit (2017)
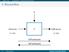 96 4: Blockchiffren 4: Blockchiffren K Klartexte (n bit) E Chiffretexte (n bit) VERschlüsseln ENTschlüsseln 97 4: Blockchiffren 4.1: Abstrakte Blockchiffren 4.1: Abstrakte Blockchiffren Familie von Paaren
96 4: Blockchiffren 4: Blockchiffren K Klartexte (n bit) E Chiffretexte (n bit) VERschlüsseln ENTschlüsseln 97 4: Blockchiffren 4.1: Abstrakte Blockchiffren 4.1: Abstrakte Blockchiffren Familie von Paaren
6 Der Advanced Encryption Standard (AES)
 Stand: 9..25 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger Dieser Abschnitt lehnt sich an die Beschreibung im Buch Kryptographische Systeme von Baumann, Franz und Ptzmann an. 6 Der
Stand: 9..25 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger Dieser Abschnitt lehnt sich an die Beschreibung im Buch Kryptographische Systeme von Baumann, Franz und Ptzmann an. 6 Der
Data Encryption Standard
 Sommersemester 2008 1 Blockchiffren 2 Der DES 3 Differentielle Kryptanalyse 4 Lineare Kryptanalyse 5 Triple DES Blockchiffren Klartext Arbeits richtung Schlüssel Chiffretext Wichtige Parameter: Blockgröße,
Sommersemester 2008 1 Blockchiffren 2 Der DES 3 Differentielle Kryptanalyse 4 Lineare Kryptanalyse 5 Triple DES Blockchiffren Klartext Arbeits richtung Schlüssel Chiffretext Wichtige Parameter: Blockgröße,
Vorlesung IT-Sicherheit FH Frankfurt Sommersemester 2007
 Vorlesung IT-Sicherheit FH Frankfurt Sommersemester 2007 Dr. Volker Scheidemann Standards für symmetrische Verschlüsselung DES, 3DES, AES DES Seite: 3 DES Data Encryption Standard 1974 von IBM unter Beteiligung
Vorlesung IT-Sicherheit FH Frankfurt Sommersemester 2007 Dr. Volker Scheidemann Standards für symmetrische Verschlüsselung DES, 3DES, AES DES Seite: 3 DES Data Encryption Standard 1974 von IBM unter Beteiligung
Designziele in Blockchiffren
 Designziele in Blockchiffren Konstruiere Verschlüsselungsfunktion die sich wie eine zufällige Funktion verhalten soll. Konfusion: Verschleiern des Zusammenhangs zwischen Klartext und Chiffretext. Diffusion:
Designziele in Blockchiffren Konstruiere Verschlüsselungsfunktion die sich wie eine zufällige Funktion verhalten soll. Konfusion: Verschleiern des Zusammenhangs zwischen Klartext und Chiffretext. Diffusion:
AES. Jens Kubieziel [email protected]. 07. Dezember 2009. Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik
 Angriffe gegen Jens Kubieziel [email protected] Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik 07. Dezember 2009 Angriffe gegen Outline 1 Zur Geschichte 2 3 Angriffe gegen
Angriffe gegen Jens Kubieziel [email protected] Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik 07. Dezember 2009 Angriffe gegen Outline 1 Zur Geschichte 2 3 Angriffe gegen
Hashfunktionen und Kollisionen
 Hashfunktionen und Kollisionen Definition Hashfunktion Eine Hashfunktion ist ein Paar (Gen, H) von pt Algorithmen mit 1 Gen: s Gen(1 n ). Gen ist probabilistisch. 2 H: H s berechnet Funktion {0, 1} {0,
Hashfunktionen und Kollisionen Definition Hashfunktion Eine Hashfunktion ist ein Paar (Gen, H) von pt Algorithmen mit 1 Gen: s Gen(1 n ). Gen ist probabilistisch. 2 H: H s berechnet Funktion {0, 1} {0,
Stefan Lucks Krypto und Mediensicherheit (2009) 5: Blockchiffren. 5: Blockchiffren. (n bit) (n bit) VERschlüsseln ENTschlüsseln
 5: Blockchiffren Klartexte 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 Chiffretexte (n bit) (n bit) VERschlüsseln ENTschlüsseln 74 5.1: Abstrakte Blockchiffren Familie
5: Blockchiffren Klartexte 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 Chiffretexte (n bit) (n bit) VERschlüsseln ENTschlüsseln 74 5.1: Abstrakte Blockchiffren Familie
Der Advanced Encryption Standard (AES)
 Der Advanced Encryption Standard (AES) Prof. Dr. Rüdiger Weis TFH Berlin Sommersemester 2008 Geschichte des AES Die Struktur des AES Angriffe auf den AES Aktuelle Ergebnisse DerAdvanced Encryption Standard
Der Advanced Encryption Standard (AES) Prof. Dr. Rüdiger Weis TFH Berlin Sommersemester 2008 Geschichte des AES Die Struktur des AES Angriffe auf den AES Aktuelle Ergebnisse DerAdvanced Encryption Standard
Kryptographie. Vorlesung 7: Der AES Algorithmus. Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca
 Kryptographie Vorlesung 7: Der AES Algorithmus Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca [email protected] 1/48 KONSTRUKTION ENDLICHER KÖRPER Wir beschreiben, wie man zu jeder
Kryptographie Vorlesung 7: Der AES Algorithmus Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca [email protected] 1/48 KONSTRUKTION ENDLICHER KÖRPER Wir beschreiben, wie man zu jeder
Alice (A) und Bob (B) wollen sicher kommunizieren (vgl. Schutzziele) Oskar (O) versucht, die Schutzziele zu durchbrechen
 Vorlesung am 21.04.2015 3 Symmetrische Verschlüsselung Alice (A) und Bob (B) wollen sicher kommunizieren (vgl. Schutzziele) Oskar (O) versucht, die Schutzziele zu durchbrechen Passiver Angri : Abhören
Vorlesung am 21.04.2015 3 Symmetrische Verschlüsselung Alice (A) und Bob (B) wollen sicher kommunizieren (vgl. Schutzziele) Oskar (O) versucht, die Schutzziele zu durchbrechen Passiver Angri : Abhören
Kryptographie I Symmetrische Kryptographie
 Kryptographie I Symmetrische Kryptographie Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2009/10 Krypto I - Vorlesung 01-12.10.2009 Verschlüsselung, Kerckhoffs, Angreifer,
Kryptographie I Symmetrische Kryptographie Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2009/10 Krypto I - Vorlesung 01-12.10.2009 Verschlüsselung, Kerckhoffs, Angreifer,
Homomorphe Verschlüsselung
 Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
6. Lösungsblatt
 TECHNISCHE UNIVERSITÄT DARMSTADT FACHGEBIET THEORETISCHE INFORMATIK PROF. JOHANNES BUCHMANN DR. JULIANE KRÄMER Einführung in die Kryptographie WS 205/ 206 6. Lösungsblatt 9..205 Ankündigung Es besteht
TECHNISCHE UNIVERSITÄT DARMSTADT FACHGEBIET THEORETISCHE INFORMATIK PROF. JOHANNES BUCHMANN DR. JULIANE KRÄMER Einführung in die Kryptographie WS 205/ 206 6. Lösungsblatt 9..205 Ankündigung Es besteht
Definition Message Authentication Code (MAC) Ein Message Authentication Code (MAC) bzgl. des Nachrichtenraumen M besteht aus den ppt Alg.
 Message Authentication Code (MAC) Szenario: Integrität und Authentizität mittels MACs. Alice und Bob besitzen gemeinsamen Schlüssel k. Alice berechnet für m einen MAC-Tag t als Funktion von m und k. Alice
Message Authentication Code (MAC) Szenario: Integrität und Authentizität mittels MACs. Alice und Bob besitzen gemeinsamen Schlüssel k. Alice berechnet für m einen MAC-Tag t als Funktion von m und k. Alice
Wiederholung. Symmetrische Verschlüsselung klassische Verfahren: moderne Verfahren: DES (Feistel-Chiffre) mehrfache Wiederholung einer Kombination aus
 Wiederholung Symmetrische Verschlüsselung klassische Verfahren: Substitutionschiffren Transpositionschiffren Vigenère-Chiffre One-Time-Pad moderne Verfahren: DES (Feistel-Chiffre) mehrfache Wiederholung
Wiederholung Symmetrische Verschlüsselung klassische Verfahren: Substitutionschiffren Transpositionschiffren Vigenère-Chiffre One-Time-Pad moderne Verfahren: DES (Feistel-Chiffre) mehrfache Wiederholung
AES und Public-Key-Kryptographie
 Jens Kubieziel [email protected] Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik 22. Juni 2009 Beschreibung des Algorithmus Angriffe gegen AES Wichtige Algorithmen im 20. Jahrhundert
Jens Kubieziel [email protected] Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik 22. Juni 2009 Beschreibung des Algorithmus Angriffe gegen AES Wichtige Algorithmen im 20. Jahrhundert
Praktikum IT-Sicherheit
 IT-Sicherheit Praktikum IT-Sicherheit - Versuchshandbuch - Aufgaben Kryptografie II In diesem zweiten Versuch zur Kryptografie gehen wir etwas genauer auf die Art und Weise der Verschlüsselung mit der
IT-Sicherheit Praktikum IT-Sicherheit - Versuchshandbuch - Aufgaben Kryptografie II In diesem zweiten Versuch zur Kryptografie gehen wir etwas genauer auf die Art und Weise der Verschlüsselung mit der
4.6.1 Mathematische Grundlagen
 4.6.1 Mathematische Grundlagen Die Basiseinheit für Berechnungen im AES stellt das Byte dar, daher sind viele Operationen im AES im GF(2 8 ) definiert. Um den Wert eines Byte darzustellen benutzen wir
4.6.1 Mathematische Grundlagen Die Basiseinheit für Berechnungen im AES stellt das Byte dar, daher sind viele Operationen im AES im GF(2 8 ) definiert. Um den Wert eines Byte darzustellen benutzen wir
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 3 Praktisch sichere Blockchiffren 1. Substitutions-Permutations Netzwerke 2. Feistel-Chiffren und der DES 3. Der Advanced Encryption Standard AES Sichere und effiziente
Kryptographie und Komplexität Einheit 3 Praktisch sichere Blockchiffren 1. Substitutions-Permutations Netzwerke 2. Feistel-Chiffren und der DES 3. Der Advanced Encryption Standard AES Sichere und effiziente
Folie 1. Kryptographie
 Folie 1 Kryptographie Klassische Verfahren Etwas Theorie Folie 2 Übersicht Moderne symmetrische Chiffren AES-Entscheidung Die Kunst der Anwendung Fazit Folie 3 Klassische Verfahren Skytala: Vor rund 2.500
Folie 1 Kryptographie Klassische Verfahren Etwas Theorie Folie 2 Übersicht Moderne symmetrische Chiffren AES-Entscheidung Die Kunst der Anwendung Fazit Folie 3 Klassische Verfahren Skytala: Vor rund 2.500
Kryptographie I Symmetrische Kryptographie
 Kryptographie I Symmetrische Kryptographie Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2012/13 Krypto I - Vorlesung 01-08.10.2012 Verschlüsselung, Kerckhoffs, Angreifer,
Kryptographie I Symmetrische Kryptographie Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2012/13 Krypto I - Vorlesung 01-08.10.2012 Verschlüsselung, Kerckhoffs, Angreifer,
Blockverschlüsselung und AES
 Blockverschlüsselung und AES Proseminar/Seminar Kryptographie und Datensicherheit SoSe 2009 Universität Potsdam ein Vortrag von Linda Tschepe Übersicht Allgemeines SPNs (Substitutions- Permutations- Netzwerke)
Blockverschlüsselung und AES Proseminar/Seminar Kryptographie und Datensicherheit SoSe 2009 Universität Potsdam ein Vortrag von Linda Tschepe Übersicht Allgemeines SPNs (Substitutions- Permutations- Netzwerke)
Merkle-Damgard Transformation
 Merkle-Damgard Transformation Ziel: Konstruiere H : {0, 1} {0, 1} l aus h : {0, 1} 2l {0, 1} l. Algorithmus Merkle-Damgard Konstruktion Sei (Gen, h) eine kollisionsresistente Hashfunktion mit h : {0, 1}
Merkle-Damgard Transformation Ziel: Konstruiere H : {0, 1} {0, 1} l aus h : {0, 1} 2l {0, 1} l. Algorithmus Merkle-Damgard Konstruktion Sei (Gen, h) eine kollisionsresistente Hashfunktion mit h : {0, 1}
Kryptographie I WS 2005/2006
 Kryptographie I WS 2005/2006 G. Leander T. Brecher, M. Goldack, O. Grieb, S. Hoerder, S. Spitz, C. Wachsmann 21. Februar 2006 ii Inhaltsverzeichnis 1 Block Ciphers 1 1.1 DES - Data Encryption Standard................
Kryptographie I WS 2005/2006 G. Leander T. Brecher, M. Goldack, O. Grieb, S. Hoerder, S. Spitz, C. Wachsmann 21. Februar 2006 ii Inhaltsverzeichnis 1 Block Ciphers 1 1.1 DES - Data Encryption Standard................
Prinzipien der modernen Kryptographie Sicherheit
 Prinzipien der modernen Kryptographie Sicherheit Prinzip 1 Sicherheitsziel Die Sicherheitsziele müssen präzise definiert werden. Beispiele für ungenügende Definitionen von Sicherheit Kein Angreifer kann
Prinzipien der modernen Kryptographie Sicherheit Prinzip 1 Sicherheitsziel Die Sicherheitsziele müssen präzise definiert werden. Beispiele für ungenügende Definitionen von Sicherheit Kein Angreifer kann
Betriebssysteme und Sicherheit Sicherheit. Florian Kerschbaum TU Dresden Wintersemester 2011/12
 Betriebssysteme und Sicherheit Sicherheit Florian Kerschbaum TU Dresden Wintersemester 2011/12 Begriffe Kryptographie: Geheimschrift Nachrichten schreiben ohne das sie von einem Anderen gelesen (verändert)
Betriebssysteme und Sicherheit Sicherheit Florian Kerschbaum TU Dresden Wintersemester 2011/12 Begriffe Kryptographie: Geheimschrift Nachrichten schreiben ohne das sie von einem Anderen gelesen (verändert)
Hybride Verschlüsselungsverfahren
 Hybride Verschlüsselungsverfahren Ziel: Flexibilität von asym. Verfahren und Effizienz von sym. Verfahren. Szenario: Sei Π = (Gen, Enc, Dec) ein PK-Verschlüsselungsverfahren und Π = (Gen, Enc, Dec ) ein
Hybride Verschlüsselungsverfahren Ziel: Flexibilität von asym. Verfahren und Effizienz von sym. Verfahren. Szenario: Sei Π = (Gen, Enc, Dec) ein PK-Verschlüsselungsverfahren und Π = (Gen, Enc, Dec ) ein
Das Generalized Birthday Problem
 Das Generalized Birthday Problem Problem Birthday Gegeben: L 1, L 2 Listen mit Elementen aus {0, 1} n Gesucht: x 1 L 1 und x 2 L 2 mit x 1 x 2 = 0. Anwendungen: Meet-in-the-Middle Angriffe (z.b. für RSA,
Das Generalized Birthday Problem Problem Birthday Gegeben: L 1, L 2 Listen mit Elementen aus {0, 1} n Gesucht: x 1 L 1 und x 2 L 2 mit x 1 x 2 = 0. Anwendungen: Meet-in-the-Middle Angriffe (z.b. für RSA,
Kryptographie I Symmetrische Kryptographie
 Kryptographie I Symmetrische Kryptographie Eike Kiltz 1 Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2011/12 1 Basierend auf Folien von Alexander May. Krypto I - Vorlesung 01-10.10.2011
Kryptographie I Symmetrische Kryptographie Eike Kiltz 1 Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2011/12 1 Basierend auf Folien von Alexander May. Krypto I - Vorlesung 01-10.10.2011
Ununterscheidbarkeit von Chiffretexten
 Ununterscheidbarkeit von Chiffretexten Spiel Ununterscheidbarkeit von Chiffretexten PrivK eav A,Π (n) Sei Π ein Verschlüsselungsverfahren und A ein Angreifer. 1 (m 0, m 1 ) A. 2 k Gen(1 n ). 3 Wähle b
Ununterscheidbarkeit von Chiffretexten Spiel Ununterscheidbarkeit von Chiffretexten PrivK eav A,Π (n) Sei Π ein Verschlüsselungsverfahren und A ein Angreifer. 1 (m 0, m 1 ) A. 2 k Gen(1 n ). 3 Wähle b
Stromchiffre. Algorithmus Stromchiffre
 Stromchiffre Algorithmus Stromchiffre Sei G ein Pseudozufallsgenerator mit Expansionsfaktor l(n). Wir definieren Π s = (Gen, Enc, Dec) mit Sicherheitsparameter n für Nachrichten der Länge l(n). 1 Gen:
Stromchiffre Algorithmus Stromchiffre Sei G ein Pseudozufallsgenerator mit Expansionsfaktor l(n). Wir definieren Π s = (Gen, Enc, Dec) mit Sicherheitsparameter n für Nachrichten der Länge l(n). 1 Gen:
Prinzipien der modernen Kryptographie Sicherheit
 Prinzipien der modernen Kryptographie Sicherheit Prinzip 1 Sicherheitsmodell Das Sicherheitsmodell (Berechnungsmodell, Angriffstypen, Sicherheitsziele) muss präzise definiert werden. Berechnungsmodell:
Prinzipien der modernen Kryptographie Sicherheit Prinzip 1 Sicherheitsmodell Das Sicherheitsmodell (Berechnungsmodell, Angriffstypen, Sicherheitsziele) muss präzise definiert werden. Berechnungsmodell:
CPA-Sicherheit ist ungenügend
 CPA-Sicherheit ist ungenügend Definition CCA CCA (=Chosen Ciphertext Attack) ist ein Angriff, bei dem der Angreifer sich Chiffretext seiner Wahl entschlüsseln lassen kann. Beispiele in denen CPA nicht
CPA-Sicherheit ist ungenügend Definition CCA CCA (=Chosen Ciphertext Attack) ist ein Angriff, bei dem der Angreifer sich Chiffretext seiner Wahl entschlüsseln lassen kann. Beispiele in denen CPA nicht
Socrative-Fragen aus der Übung vom
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Übungsleiter: Björn Kaidel, Alexander Koch Stammvorlesung Sicherheit im Sommersemester 2016 Socrative-Fragen aus der Übung vom 28.04.2016
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Übungsleiter: Björn Kaidel, Alexander Koch Stammvorlesung Sicherheit im Sommersemester 2016 Socrative-Fragen aus der Übung vom 28.04.2016
Analyse Kryptographischer Algorithmen: KRYPTON & TWOFISH
 Analyse Kryptographischer Algorithmen: KRYPTON & TWOFISH Martin Lötzsch [email protected] Einleitung. Das Seminar Analyse Kryptographischer Algorithmen beschäftigte sich mit interessanten,
Analyse Kryptographischer Algorithmen: KRYPTON & TWOFISH Martin Lötzsch [email protected] Einleitung. Das Seminar Analyse Kryptographischer Algorithmen beschäftigte sich mit interessanten,
74 5 DES und AES. 5.1 Der Data Encryption Standard (DES)
 74 5 DES und AES 5 DES und AES 5.1 Der Data Encryption Standard (DES) Der DES wurde von IBM im Zuge einer im Mai 1973 veröffentlichten Ausschreibung des NBS (National Bureau of Standards; heute National
74 5 DES und AES 5 DES und AES 5.1 Der Data Encryption Standard (DES) Der DES wurde von IBM im Zuge einer im Mai 1973 veröffentlichten Ausschreibung des NBS (National Bureau of Standards; heute National
Stromchiffre. Algorithmus Stromchiffre
 Stromchiffre Algorithmus Stromchiffre Sei G ein Pseudozufallsgenerator mit Expansionsfaktor l(n). Wir definieren Π s = (Gen, Enc, Dec) mit Sicherheitsparameter n für Nachrichten der Länge l(n). 1 Gen:
Stromchiffre Algorithmus Stromchiffre Sei G ein Pseudozufallsgenerator mit Expansionsfaktor l(n). Wir definieren Π s = (Gen, Enc, Dec) mit Sicherheitsparameter n für Nachrichten der Länge l(n). 1 Gen:
9.5 Blockverschlüsselung
 9.5 Blockverschlüsselung Verschlüsselung im Rechner: Stromverschlüsselung (stream cipher): kleine Klartexteinheiten (Bytes, Bits) werden polyalphabetisch verschlüsselt Blockverschlüsselung (block cipher):
9.5 Blockverschlüsselung Verschlüsselung im Rechner: Stromverschlüsselung (stream cipher): kleine Klartexteinheiten (Bytes, Bits) werden polyalphabetisch verschlüsselt Blockverschlüsselung (block cipher):
Rabin Verschlüsselung 1979
 Rabin Verschlüsselung 1979 Idee: Rabin Verschlüsselung Beobachtung: Berechnen von Wurzeln in Z p ist effizient möglich. Ziehen von Quadratwurzeln in Z N ist äquivalent zum Faktorisieren. Vorteil: CPA-Sicherheit
Rabin Verschlüsselung 1979 Idee: Rabin Verschlüsselung Beobachtung: Berechnen von Wurzeln in Z p ist effizient möglich. Ziehen von Quadratwurzeln in Z N ist äquivalent zum Faktorisieren. Vorteil: CPA-Sicherheit
AES und DES. Maria Eichlseder. 20. November 2007
 AES und DES Maria Eichlseder 20. November 2007 Im Folgenden wird ein Überblick über Funktionsweise und Eigenschaften der beiden kryptographischen Standards DES und AES gegeben. Der erste Abschnitt erklärt
AES und DES Maria Eichlseder 20. November 2007 Im Folgenden wird ein Überblick über Funktionsweise und Eigenschaften der beiden kryptographischen Standards DES und AES gegeben. Der erste Abschnitt erklärt
Kryptographie I Symmetrische Kryptographie
 Kryptographie I Symmetrische Kryptographie Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2010/11 Krypto I - Vorlesung 01-11.10.2010 Verschlüsselung, Kerckhoffs, Angreifer,
Kryptographie I Symmetrische Kryptographie Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2010/11 Krypto I - Vorlesung 01-11.10.2010 Verschlüsselung, Kerckhoffs, Angreifer,
Sicherheit von ElGamal
 Sicherheit von ElGamal Satz CPA-Sicherheit ElGamal ElGamal Π ist CPA-sicher unter der DDH-Annahme. Beweis: Sei A ein Angreifer auf ElGamal Π mit Erfolgsws ɛ(n) := Ws[PubK cpa A,Π (n) = 1]. Wir konstruieren
Sicherheit von ElGamal Satz CPA-Sicherheit ElGamal ElGamal Π ist CPA-sicher unter der DDH-Annahme. Beweis: Sei A ein Angreifer auf ElGamal Π mit Erfolgsws ɛ(n) := Ws[PubK cpa A,Π (n) = 1]. Wir konstruieren
Hardcore-Prädikat. Definition Hardcore-Prädikat. Ziel: Destilliere Komplexität des Invertierens auf ein Bit.
 Hardcore-Prädikat Ziel: Destilliere Komplexität des Invertierens auf ein Bit. Definition Hardcore-Prädikat Sei Π f eine Einwegfunktion. Sei hc ein deterministischer pt Alg mit Ausgabe eines Bits hc(x)
Hardcore-Prädikat Ziel: Destilliere Komplexität des Invertierens auf ein Bit. Definition Hardcore-Prädikat Sei Π f eine Einwegfunktion. Sei hc ein deterministischer pt Alg mit Ausgabe eines Bits hc(x)
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 17.04.2014 1 / 26 Logistisches Überschneidungsfreiheit Vorlesung: nachfragen Übungsblatt nicht vergessen Frage: Wie viele würden korrigiertes Übungsblatt nutzen?
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 17.04.2014 1 / 26 Logistisches Überschneidungsfreiheit Vorlesung: nachfragen Übungsblatt nicht vergessen Frage: Wie viele würden korrigiertes Übungsblatt nutzen?
Advanced Encryption Standard. Copyright Stefan Dahler 20. Februar 2010 Version 2.0
 Advanced Encryption Standard Copyright Stefan Dahler 20. Februar 2010 Version 2.0 Vorwort Diese Präsentation erläutert den Algorithmus AES auf einfachste Art. Mit Hilfe des Wissenschaftlichen Rechners
Advanced Encryption Standard Copyright Stefan Dahler 20. Februar 2010 Version 2.0 Vorwort Diese Präsentation erläutert den Algorithmus AES auf einfachste Art. Mit Hilfe des Wissenschaftlichen Rechners
Existenz von Einwegfunktionen
 Existenz von Einwegfunktionen Satz Einweg-Eigenschaft von f FO Unter der Faktorisierungsannahme ist f FO eine Einwegfunktion. Beweis: f FO ist mittels FACTOR-ONEWAY effizient berechenbar. z.z.: Invertierer
Existenz von Einwegfunktionen Satz Einweg-Eigenschaft von f FO Unter der Faktorisierungsannahme ist f FO eine Einwegfunktion. Beweis: f FO ist mittels FACTOR-ONEWAY effizient berechenbar. z.z.: Invertierer
Kryptographie I Symmetrische Kryptographie
 Kryptographie I Symmetrische Kryptographie Eike Kiltz 1 Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2014/15 1 Basierend auf Folien von Alexander May. Krypto - Vorlesung 01-6.10.2014
Kryptographie I Symmetrische Kryptographie Eike Kiltz 1 Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2014/15 1 Basierend auf Folien von Alexander May. Krypto - Vorlesung 01-6.10.2014
9 Rechnergestütze Blockchiffren
 9 Rechnergestütze n 9.1 ata Encryption Standard (ES) 1977 von National Bureau of Standards (heute National Institute of Standards and Technology) genormt arbeitet auf bit-blöcken Schlüssel 5 bit + 8 bit
9 Rechnergestütze n 9.1 ata Encryption Standard (ES) 1977 von National Bureau of Standards (heute National Institute of Standards and Technology) genormt arbeitet auf bit-blöcken Schlüssel 5 bit + 8 bit
Inhaltsverzeichnis. Wolfgang Ertel. Angewandte Kryptographie. ISBN (Buch): ISBN (E-Book):
 Inhaltsverzeichnis Wolfgang Ertel Angewandte Kryptographie ISBN (Buch): 978-3-446-42756-3 ISBN (E-Book): 978-3-446-43196-6 Weitere Informationen oder Bestellungen unter http://www.hanser-fachbuch.de/978-3-446-42756-3
Inhaltsverzeichnis Wolfgang Ertel Angewandte Kryptographie ISBN (Buch): 978-3-446-42756-3 ISBN (E-Book): 978-3-446-43196-6 Weitere Informationen oder Bestellungen unter http://www.hanser-fachbuch.de/978-3-446-42756-3
Algorithmische Anwendungen Prof. Dr. Heinrich Klocke
 Algorithmische Anwendungen Prof. Dr. Heinrich Klocke Algorithmisches Projekt im Wintersemester 2005/06 Advanced Encryption Standard (AES) Rijndael Algorithmus Gruppe: C_gelb Thomas Boddenberg 11032925
Algorithmische Anwendungen Prof. Dr. Heinrich Klocke Algorithmisches Projekt im Wintersemester 2005/06 Advanced Encryption Standard (AES) Rijndael Algorithmus Gruppe: C_gelb Thomas Boddenberg 11032925
Kapitel 7: Symmetrische Kryptosysteme. Prof. Dr. Helmut Reiser, LRZ, WS 2017/18 IT-Sicherheit
 Kapitel 7: Symmetrische Kryptosysteme Prof. Dr. Helmut Reiser, LRZ, WS 2017/18 IT-Sicherheit 1 Frauen MINT-Award BA und MA zu den Themen, dürfen 1,5 Jahre zurückliegen Preisgeld: 3.000 Euro Info: https://www.frauen-mint-award.de/#info
Kapitel 7: Symmetrische Kryptosysteme Prof. Dr. Helmut Reiser, LRZ, WS 2017/18 IT-Sicherheit 1 Frauen MINT-Award BA und MA zu den Themen, dürfen 1,5 Jahre zurückliegen Preisgeld: 3.000 Euro Info: https://www.frauen-mint-award.de/#info
Kryptologie. K l a u s u r WS 2006/2007, Prof. Dr. Harald Baier
 Kryptologie K l a u s u r WS 2006/2007, 2007-02-01 Prof. Dr. Harald Baier Name, Vorname: Matrikelnummer: Hinweise: (a) Als Hilfsmittel ist nur der Taschenrechner TI-30 zugelassen. Weitere Hilfsmittel sind
Kryptologie K l a u s u r WS 2006/2007, 2007-02-01 Prof. Dr. Harald Baier Name, Vorname: Matrikelnummer: Hinweise: (a) Als Hilfsmittel ist nur der Taschenrechner TI-30 zugelassen. Weitere Hilfsmittel sind
Sicherer MAC für Nachrichten beliebiger Länge
 Sicherer MAC für Nachrichten beliebiger Länge Korollar Sicherer MAC für Nachrichten beliebiger Länge Sei F eine Pseudozufallsfunktion. Dann ist Π MAC2 für Π = Π MAC sicher. Nachteile: Für m ({0, 1} n 4
Sicherer MAC für Nachrichten beliebiger Länge Korollar Sicherer MAC für Nachrichten beliebiger Länge Sei F eine Pseudozufallsfunktion. Dann ist Π MAC2 für Π = Π MAC sicher. Nachteile: Für m ({0, 1} n 4
Netzwerktechnologien 3 VO
 Netzwerktechnologien 3 VO Univ.-Prof. Dr. Helmut Hlavacs [email protected] Dr. Ivan Gojmerac [email protected] Bachelorstudium Medieninformatik SS 2012 Kapitel 8 - Netzwerksicherheit 8.1 Was ist
Netzwerktechnologien 3 VO Univ.-Prof. Dr. Helmut Hlavacs [email protected] Dr. Ivan Gojmerac [email protected] Bachelorstudium Medieninformatik SS 2012 Kapitel 8 - Netzwerksicherheit 8.1 Was ist
Die Größe A(n, d) und optimale Codes
 Die Größe A(n, d) und optimale Codes Definition Optimaler Code Wir definieren A(n, d) = max{m binärer (n, M, d) Code} Ein (n, M, d)-code heißt optimal, falls M = A(n, d). Bestimmung von A(n, d) ist offenes
Die Größe A(n, d) und optimale Codes Definition Optimaler Code Wir definieren A(n, d) = max{m binärer (n, M, d) Code} Ein (n, M, d)-code heißt optimal, falls M = A(n, d). Bestimmung von A(n, d) ist offenes
DES der vergangene Standard für Bitblock-Chiffren
 DES der vergangene Standard für Bitblock-Chiffren Klaus Pommerening Fachbereich Mathematik der Johannes-Gutenberg-Universität Saarstraße 1 D-55099 Mainz Vorlesung Kryptologie 1. März 1991, letzte Änderung:
DES der vergangene Standard für Bitblock-Chiffren Klaus Pommerening Fachbereich Mathematik der Johannes-Gutenberg-Universität Saarstraße 1 D-55099 Mainz Vorlesung Kryptologie 1. März 1991, letzte Änderung:
Kryptologie und Kodierungstheorie
 Kryptologie und Kodierungstheorie Alexander May Horst Görtz Institut für IT-Sicherheit Ruhr-Universität Bochum Lehrerfortbildung 17.01.2012 Kryptologie Verschlüsselung, Substitution, Permutation 1 / 18
Kryptologie und Kodierungstheorie Alexander May Horst Görtz Institut für IT-Sicherheit Ruhr-Universität Bochum Lehrerfortbildung 17.01.2012 Kryptologie Verschlüsselung, Substitution, Permutation 1 / 18
Kryptograhie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik
 Kryptograhie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik Übersicht Zwecke der Krytographie Techniken Symmetrische Verschlüsselung( One-time Pad,
Kryptograhie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik Übersicht Zwecke der Krytographie Techniken Symmetrische Verschlüsselung( One-time Pad,
Isomorphismus. Definition Gruppen-Isomorphismus. Seien (G, +) und (G, ) Gruppen. Die Abbildung f : G G heißt Gruppen-Isomorphismus, falls gilt
 Isomorphismus Definition Gruppen-Isomorphismus Seien (G, +) und (G, ) Gruppen. Die Abbildung f : G G heißt Gruppen-Isomorphismus, falls gilt 1 f ist bijektiv f (u + v) = f (u) f (v) für alle u, v G, die
Isomorphismus Definition Gruppen-Isomorphismus Seien (G, +) und (G, ) Gruppen. Die Abbildung f : G G heißt Gruppen-Isomorphismus, falls gilt 1 f ist bijektiv f (u + v) = f (u) f (v) für alle u, v G, die
Algorithmische Anwendungen
 Algorithmische Anwendungen Projekt: Data Encryption Standard Team: Adil Sbiyou El Moussaid Tawfik Inhalt Projekt DES 2. Geschichte des DES 3. Eigenschaften 4. Funktionsweise im Detail 5. Sicherheit des
Algorithmische Anwendungen Projekt: Data Encryption Standard Team: Adil Sbiyou El Moussaid Tawfik Inhalt Projekt DES 2. Geschichte des DES 3. Eigenschaften 4. Funktionsweise im Detail 5. Sicherheit des
ElGamal Verschlüsselungsverfahren (1984)
 ElGamal Verschlüsselungsverfahren (1984) Definition ElGamal Verschlüsselungsverfahren Sei n ein Sicherheitsparameter. 1 Gen : (q, g) G(1 n ), wobei g eine Gruppe G der Ordnung q generiert. Wähle x R Z
ElGamal Verschlüsselungsverfahren (1984) Definition ElGamal Verschlüsselungsverfahren Sei n ein Sicherheitsparameter. 1 Gen : (q, g) G(1 n ), wobei g eine Gruppe G der Ordnung q generiert. Wähle x R Z
Sicherheit: Fragen und Lösungsansätze
 Vorlesung (WS 2014/15) Sicherheit: Fragen und Lösungsansätze Dr. Thomas P. Ruhroth TU Dortmund, Fakultät Informatik, Lehrstuhl XIV 1 Kryptographie I [mit freundlicher Genehmigung basierend auf einem Foliensatz
Vorlesung (WS 2014/15) Sicherheit: Fragen und Lösungsansätze Dr. Thomas P. Ruhroth TU Dortmund, Fakultät Informatik, Lehrstuhl XIV 1 Kryptographie I [mit freundlicher Genehmigung basierend auf einem Foliensatz
DES (Data Encryption Standard)
 Juli 2012 LB 3 Kryptographie F. Kaden 1/19 1973 von IBM im Auftrag der NSA (National Security Agency) entwickelt Ziel: sicheres Verschlüsselungsverfahren für mindestens 10-15 Jahre für den sensiblen, aber
Juli 2012 LB 3 Kryptographie F. Kaden 1/19 1973 von IBM im Auftrag der NSA (National Security Agency) entwickelt Ziel: sicheres Verschlüsselungsverfahren für mindestens 10-15 Jahre für den sensiblen, aber
Seminar Kryptographie und Datensicherheit
 Seminar Kryptographie und Datensicherheit Einfache Kryptosysteme und ihre Analyse Christoph Kreitz 1. Grundlagen von Kryptosystemen 2. Buchstabenorientierte Systeme 3. Blockbasierte Verschlüsselung 4.
Seminar Kryptographie und Datensicherheit Einfache Kryptosysteme und ihre Analyse Christoph Kreitz 1. Grundlagen von Kryptosystemen 2. Buchstabenorientierte Systeme 3. Blockbasierte Verschlüsselung 4.
IT-Sicherheit - Sicherheit vernetzter Systeme -
 IT-Sicherheit - Sicherheit vernetzter Systeme - Kapitel 5: Symmetrische Kryptosysteme Helmut Reiser, LRZ, WS 09/10 IT-Sicherheit 1 Inhalt Symmetrische Kryptosysteme Data Encryption Standard (DES) Advanced
IT-Sicherheit - Sicherheit vernetzter Systeme - Kapitel 5: Symmetrische Kryptosysteme Helmut Reiser, LRZ, WS 09/10 IT-Sicherheit 1 Inhalt Symmetrische Kryptosysteme Data Encryption Standard (DES) Advanced
Name:... Vorname:... Matrikel-Nr.:... Studienfach:...
 Stefan Lucks Medien Bauhaus-Univ. Weimar Probeklausur Name:.............................. Vorname:........................... Matrikel-Nr.:....................... Studienfach:........................ Wichtige
Stefan Lucks Medien Bauhaus-Univ. Weimar Probeklausur Name:.............................. Vorname:........................... Matrikel-Nr.:....................... Studienfach:........................ Wichtige
Hintergründe zur Kryptographie
 3. Januar 2009 Creative Commons by 3.0 http://creativecommons.org/licenses/by/3.0/ CAESAR-Chiffre Vigenère CAESAR-Chiffre Vigenère Einfache Verschiebung des Alphabets Schlüsselraum: 26 Schlüssel Einfaches
3. Januar 2009 Creative Commons by 3.0 http://creativecommons.org/licenses/by/3.0/ CAESAR-Chiffre Vigenère CAESAR-Chiffre Vigenère Einfache Verschiebung des Alphabets Schlüsselraum: 26 Schlüssel Einfaches
Effizienten MAC-Konstruktion aus der Praxis: NMAC Idee von NMAC:
 Effizienten MAC-Konstruktion aus der Praxis: NMAC Idee von NMAC: Hashe m {0, 1} auf einen Hashwert in {0, 1} n. Verwende Π MAC3 für Nachrichten fixer Länge auf dem Hashwert. Wir konstruieren Π MAC3 mittels
Effizienten MAC-Konstruktion aus der Praxis: NMAC Idee von NMAC: Hashe m {0, 1} auf einen Hashwert in {0, 1} n. Verwende Π MAC3 für Nachrichten fixer Länge auf dem Hashwert. Wir konstruieren Π MAC3 mittels
Voll homomorpe Verschlüsselung
 Voll homomorpe Verschlüsselung Definition Voll homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : R R für Ringe R, R. Π heißt voll homomorph, falls 1 Enc(m 1 ) + Enc(m 2 ) eine gültige
Voll homomorpe Verschlüsselung Definition Voll homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : R R für Ringe R, R. Π heißt voll homomorph, falls 1 Enc(m 1 ) + Enc(m 2 ) eine gültige
Grundlagen der Verschlüsselung und Authentifizierung (1)
 Grundlagen der Verschlüsselung und Authentifizierung (1) Proseminar im SS 2010 Friedrich-Alexander-Universität Erlangen-Nürnberg 18.05.2010 1 Motivation
Grundlagen der Verschlüsselung und Authentifizierung (1) Proseminar im SS 2010 Friedrich-Alexander-Universität Erlangen-Nürnberg 18.05.2010 1 Motivation
3. Lösungsblatt
 TECHNISCHE UNIVERSITÄT DARMSTADT FACHGEBIET THEORETISCHE INFORMATIK PROF JOHANNES BUCHMANN NABIL ALKEILANI ALKADRI Einführung in die Kryptographie WS 7/ 8 3 Lösungsblatt 67 P Matrizen und Determinanten
TECHNISCHE UNIVERSITÄT DARMSTADT FACHGEBIET THEORETISCHE INFORMATIK PROF JOHANNES BUCHMANN NABIL ALKEILANI ALKADRI Einführung in die Kryptographie WS 7/ 8 3 Lösungsblatt 67 P Matrizen und Determinanten
Was heißt Kryptographie I? Understanding Cryptography Christof Paar und Jan Pelzl
 Was heißt Kryptographie I? Understanding Cryptography Christof Paar und Jan Pelzl Die Autoren Dr.-Ing. Jan Pelzl Prof. Dr.-Ing. Christof Paar Gliederung Historischer Überblick Begrifflichkeiten Symmetrische
Was heißt Kryptographie I? Understanding Cryptography Christof Paar und Jan Pelzl Die Autoren Dr.-Ing. Jan Pelzl Prof. Dr.-Ing. Christof Paar Gliederung Historischer Überblick Begrifflichkeiten Symmetrische
Wann sind Codes eindeutig entschlüsselbar?
 Wann sind Codes eindeutig entschlüsselbar? Definition Suffix Sei C ein Code. Ein Folge s {0, 1} heißt Suffix in C falls 1 c i, c j C : c i = c j s oder 2 c C und einen Suffix s in C: s = cs oder 3 c C
Wann sind Codes eindeutig entschlüsselbar? Definition Suffix Sei C ein Code. Ein Folge s {0, 1} heißt Suffix in C falls 1 c i, c j C : c i = c j s oder 2 c C und einen Suffix s in C: s = cs oder 3 c C
Homomorphe Verschlüsselung
 Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Einführung in die. Kryptographie WS 2016/ Lösungsblatt
 Technische Universität Darmstadt Fachgebiet Theoretische Informatik Prof. Johannes Buchmann Thomas Wunderer Einführung in die Kryptographie WS 6/ 7. Lösungsblatt 8..6 Ankündigungen Arithmetik modulo n
Technische Universität Darmstadt Fachgebiet Theoretische Informatik Prof. Johannes Buchmann Thomas Wunderer Einführung in die Kryptographie WS 6/ 7. Lösungsblatt 8..6 Ankündigungen Arithmetik modulo n
Kryptographische Verfahren. zur Datenübertragung im Internet. Patrick Schmid, Martin Sommer, Elvis Corbo
 Kryptographische Verfahren zur Datenübertragung im Internet Patrick Schmid, Martin Sommer, Elvis Corbo 1. Einführung Übersicht Grundlagen Verschlüsselungsarten Symmetrisch DES, AES Asymmetrisch RSA Hybrid
Kryptographische Verfahren zur Datenübertragung im Internet Patrick Schmid, Martin Sommer, Elvis Corbo 1. Einführung Übersicht Grundlagen Verschlüsselungsarten Symmetrisch DES, AES Asymmetrisch RSA Hybrid
Kryptografische Algorithmen
 Kryptografische Algorithmen Lerneinheit 5: Weitere symmetrische Kryptosysteme Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2015/2016 21.9.2015 Einleitung Einleitung Diese
Kryptografische Algorithmen Lerneinheit 5: Weitere symmetrische Kryptosysteme Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2015/2016 21.9.2015 Einleitung Einleitung Diese
Urbild Angriff auf Inkrementelle Hashfunktionen
 Urbild Angriff auf Inkrementelle Hashfunktionen AdHash Konstruktion: (Bellare, Micciancio 1997) Hashe Nachricht x = (x 1,..., x k ) als H(x) = k i=1 h(i, x i) mod M. Inkrementell: Block x i kann leicht
Urbild Angriff auf Inkrementelle Hashfunktionen AdHash Konstruktion: (Bellare, Micciancio 1997) Hashe Nachricht x = (x 1,..., x k ) als H(x) = k i=1 h(i, x i) mod M. Inkrementell: Block x i kann leicht
Vorlesung Datensicherheit. Sommersemester 2010
 Vorlesung Datensicherheit Sommersemester 2010 Harald Baier Kapitel 2: Kryptographische Begriffe und symmetrische Verschlüsselungsverfahren Inhalt Kryptographische Begriffe Historische Verschlüsselungsverfahren
Vorlesung Datensicherheit Sommersemester 2010 Harald Baier Kapitel 2: Kryptographische Begriffe und symmetrische Verschlüsselungsverfahren Inhalt Kryptographische Begriffe Historische Verschlüsselungsverfahren
Sommersemester 2002 Konzepte von Betriebssystem-Komponenten: Schwerpunkt Sicherheit (KVBK)
 Sommersemester 2002 Konzepte von Betriebssystem-Komponenten: Schwerpunkt Sicherheit (KVBK) Vortrag zum Thema: Symmetrische Verschlüsselung (DES, 3DES, AES) und Schlüsselaustausch (Diffie-Hellman) Referent:
Sommersemester 2002 Konzepte von Betriebssystem-Komponenten: Schwerpunkt Sicherheit (KVBK) Vortrag zum Thema: Symmetrische Verschlüsselung (DES, 3DES, AES) und Schlüsselaustausch (Diffie-Hellman) Referent:
2. Entsprechende Listen P i von Vorgängern von i 3. for i := 1 to n do. (ii) S i = Knoten 2 + 1}
 1. Berechne für jeden Knoten i in BFS-Art eine Liste S i von von i aus erreichbaren Knoten, so dass (i) oder (ii) gilt: (i) S i < n 2 + 1 und Si enthält alle von i aus erreichbaren Knoten (ii) S i = n
1. Berechne für jeden Knoten i in BFS-Art eine Liste S i von von i aus erreichbaren Knoten, so dass (i) oder (ii) gilt: (i) S i < n 2 + 1 und Si enthält alle von i aus erreichbaren Knoten (ii) S i = n
