How To Understand The Algebraic Structure Of A Program In Python (For Beginners)
|
|
|
- Karlheinz Bader
- vor 5 Jahren
- Abrufe
Transkript
1 Algorithmen und Programmierung Kapitel 8 Abstrakte Datentypen 1 Überblick Abstrakte Datentypen Signaturen und Algebren Spezifikation von ADTs Umsetzung von ADTs 2
2 Einführung Motivation: Wiederverwendbarkeit und Strukturierung von Software Ziel: Beschreibung von Datenstrukturen unabhängig von ihrer späteren Implementierung in einer konkreten Programmiersprache Abstrakter Datentyp (ADT) 3 Formen von Datentypen Konkrete Datentypen: Konstruiert aus Basisdatentypen bzw. Java-Klassen Abstrakte Datentypen: Spezifikation der Schnittstelle nach außen Operationen und ihre Funktionalität 4
3 Prinzipien von Abstrakten Datentypen ADT = Software-Modul Kapselung: darf nur über Schnittstelle benutzt werden Geheimnisprinzip: die interne Realisierung ist verborgen... somit sind abstrakte Datentypen eine Grundlage des Prinzips der objektorientierten Programmierung! 5 Signatur Eine Signatur ist definiert als = (S, Ω) wobei Folgendes gilt: S ist eine Menge von Sorten. Ω = { f S*, S } definiert die Funktionssymbole für Funktionen f : s 1 s n s mit Parametersorten s 1,..., s n und Ergebnissorte s. Funktionen ohne Parameter heißen Konstanten 6
4 Algebra zu einer Signatur Eine Algebra A zu einer Signatur ist definiert als A = (A S, A Ω ) wobei Folgendes gilt: A S sind die Trägermengen der Sorten in S. A Ω = { A f : A s1 A sn A s } sind Funktionen auf diesen Trägermengen. Eine Algebra heißt partiell definiert, wenn mindestens eine der Funktionen eine partielle Funktion ist. 7 Algebraische Spezifikation Gleichungsspezifikation Die Angabe der Signatur legt die Namen der Typen sowie die Funktionssignaturen fest. Gleichungen dienen als Axiome zur Einschränkung möglicher Algebren als Modelle. Zusätzlich erfolgt evtl. ein Import anderer Spezifikationen. 8
5 Algebraische Spezifikation: Beispiel type Nat operators 0: Nat suc: Nat Nat add: Nat Nat Nat axioms i,j : Nat add (i, 0) = i add (i, suc (j)) = suc (add (i, j)) 9 Spezifikationen und Modelle Algebra der Wahrheitswerte type Bool operators true: Bool false: Bool Modelle für diese Spezifikation? 10
6 Modelle für Bool 1. Gewünschte Algebra: A Bool = { T, F } ; A true := T; A false := F 2. Wahrheitswerte über Zahlen realisiert: A Bool = N ; A true := 1; A false := 0 Akzeptabel, aber die Trägermenge ist eigentlich zu groß 3. Algebra mit einem Element: A Bool = { 1 } ; A true := 1; A false := 1 Diese Algebra ist sicherlich als Modell nicht erwünscht! 11 Standardmodelle Wie komme ich zu einem kanonischen Standardmodell (also genau einer Algebra, die die Axiome respektiert) für eine gegebene Spezifikation? Weder zu wenige noch zu viele Elemente No confusion, no junk Wir gehen dazu in zwei Schritten vor: In einem ersten Schritt konstruieren wir eine Algebra, die keine unnützen, also keine nicht durch Funktionsberechnung konstruierbaren Werte enthält. Im zweiten Schritt setzen wir dann die Werte gleich, die mittels der Gleichungen als gleich charakterisiert werden (und nicht mehr!). 12
7 Termalgebra Die Termalgebra zu einer gegebenen Spezifikation ist definiert durch: Die Trägermenge, bestehend aus allen korrekt gebildeten Termen der Signatur. Der Funktionsanwendung als Konstruktion des zugehörigen Terms. 13 Beispiel Termalgebra für Nat Vorüberlegung: A nat induktiv definiert: 0 A nat x, y A nat suc(x) A nat und add(x,y) A nat A nat = { 0,suc(0),suc(suc(0)),add(0,suc(0)), } A 0 = 0 A suc (x) = suc(x) A add (x,y) = add(x,y) 14
8 Quotiententermalgebra QTA Die Quotiententermalgebra QTA ist wie folgt definiert: Die Trägermenge besteht aus den Äquivalenzklassen auf den Termen gemäß der durch die Axiome induzierten Gleichheit =. Die Operationen auf den Äquivalenzklassen nehmen jeweils (Repräsentanten der) Äquivalenzklassen und haben als Ergebnis die (Repräsentanten der) Äquivalenzklasse des Ergebnisterms über den Repräsentanten. 15 Beispiel QTA für Nat Vorüberlegung: Äquivalenzklassen und ihre Repräsentanten 0 repräsentiert { 0, add(0,0), add(add(0,0),0),... } suc(0) repräsentiert { suc(0), add(0,suc(0)), add(add(0,suc(0)),0),... } suc(suc(0))... A nat = { 0,suc(0),suc(suc(0)),suc 3 (0),suc 4 (0), } A 0 = 0 A suc (x) = suc(x) A add (suc n (0),suc m (0)) = suc n+m (0) 16
9 Initiale Semantik QTA als Muster für Standardsemantik Semantik eines ADT: Klasse aller Algebren die äquivalent zur QTA sind Äquivalenz basiert auf bijektiven Morphismen Initialität: Prinzip der maximalen Ungleichheit Zwei Werte sind nur dann gleich wenn dies aufgrund der Gleichungen bewiesen werden kann Symmetrisches Gegenstück ist Terminalität: Prinzip der maximalen Gleichheit Zwei Werte sind nur dann ungleich wenn dies bewiesen werden kann. Erfordert Spezifikation von Ungleichheit! 17 Probleme mit initialer Semantik type Set[Item] operators create: Set is_empty: Set Bool insert: Set Item Set is_in: Set Item Bool axioms s : Set, i : Item is_empty (create) = true is_empty (insert (s, i)) = false is_in (create, i) = false is_in (insert (s, i), j) = if i=j then true else is_in (s, j) 18
10 Probleme mit initialer Semantik II Mengensemantik: insert(insert(s,i),j) = insert(insert(s,j),i) insert(insert(s,i),i) = insert(s,i) Gilt auch in Beispielspezifikation: Eine Menge kann man nur mit is_empty und is_in beobachten, und deren Gleichungen respektieren diese Regeln. Diese Regeln können aber nicht mit den Gleichungen bewiesen werden: insert(insert(s,i),i) und insert(s,i) sind unterschiedliche Elemente in der QTA! 19 Spezifikation und Beispiele Konsequenzen aus der Theorie für Spezifikation Oft initiale Semantik für Konstruktorfunktionen Bei terminaler Semantik muss Ungleichheit auf importierten Datentypen erhalten bleiben Hier Theorie nur oberflächlich diskutiert Ab jetzt konkrete Spezifikationen! 20
11 Spezifikation von Abstrakten Datentypen 1. Type: Name des neuen Typs zusammen mit eventuellen Parametern 2. Functions: Signaturen der auf dem ADT definierten Funktionen: für jede Funktion der Name, Typen und Reihenfolge der Parameter, Ausgabetyp sowie ggf. ob die Funktion total ( ) oder partiell ( ) ist 3. Axioms: beschreiben Eigenschaften der eingeführten Funktionen als prädikatenlogische Formeln (zumeist Gleichungen) 4. Preconditions: für jede partielle Funktion kann eine Vorbedingung angegeben werden, die angibt, wann sie definiert ist 21 Klassifikation der Funktionen Konstruktorfunktionen: Funktionen zum Aufbauen von Elementen des ADT Selektorfunktionen: die Inversen der Konstruktorfunktionen; zerlegen ein Element des Datentyps in seine Einzelteile sonstige Funktionen 22
12 Beispiel für Abstrakten Datentyp ADT für natürliche Zahlen type Nat operators 0: Nat suc: Nat Nat add: Nat Nat Nat axioms i,j : Nat add (i, 0) = i add (i, suc (j)) = suc (add (i, j)) 23 Beispiel: Liste type List(T) import Nat operators [] : List _ : _ : T List List head : List T tail : List List length : List Nat axioms l : List, x : T head (x : l) = x tail (x : l) = l length ([]) = 0 length (x : l) = suc(length(l)) 24
13 Liste: Erläuterungen _ : _ ist Notation für Infix-Operatoren (wie + in artithmetischen Ausdrücken) import importiert bereits definierten Datentypen mögliche Werte für Listen über Zahlen sind nun: [] 1 : [] 5 : ( 6 : ( 7 : [] ) ) 1 : ( 1 : [] ) 25 Kellerspeicher (Stack): Prinzip LIFO-Prinzip: Last-In-First-Out-Speicher push pop top
14 Stack: Definition des ADT type Stack(T) import Bool operators empty : Stack push : Stack T Stack pop : Stack Stack top : Stack T is_empty : Stack Bool axioms s : Stack, x : T pop (push (s, x)) = s top (push (s, x)) = x is_empty (empty) = true is_empty (push (s, x)) = false 27 Keller implementiert über Liste empty == [] push(l,x) == x:l pop(x:l) == l top(x:l) == x is_empty([]) == true is_empty(x:l) == false 28
15 Beispiel für Keller-Nutzung Auswertung einfacher arithmetischer Ausdrücke analysierte Sprache: A ::= B = B ::= Int (B+B) (B*B) Beispiel: ((3 + (4 5)) (6 + 7)) = 29 Bearbeitungsregeln value(t ) = eval t, empty (1) eval (t, S = eval t, (S (2) eval t, S = eval t, S (3) eval +t, S = eval t, +S (4) eval )t, yxs = eval )t, x y S (5) eval )t, y+xs = eval )t, x + y S (6) eval )t, x(s = eval t, xs (7) eval =, x empty = x (8) eval xt, S = eval t, x S (9) 30
16 Auswertungsbeispiel (1) bearbeiteter Term t Stack Regel ((3+(45))(6+7))= ] (2) (3+(45))(6+7)) = ( ] (2) 3+(45))(6+7)) = (( ] (9) +(45))(6+7)) = 3 (( ] (4) (45))(6+7)) = +3 (( ] (2) 45))(6+7)) = (+3 (( ] (9) 5))(6+7)) = 4(+3 (( ] (3) 5))(6+7)) = 4(+3 (( ] (9) ))(6+7)) = 54(+3 (( ] (5) ))(6+7)) = 20 (+3 (( ] (7) )(6+7)) = 20+3 (( ] (6) 31 Auswertungsbeispiel (2) bearbeiteter Term t Stack Regel )(6+7)) = 20+3 (( ] (6) )(6+7)) = 23(( ] (7) (6+7)) = 23 ( ] (3) (6+7)) = 23 ( ] (2) 6+7)) = (23 ( ] (9) +7)) = 6 (23 ( ] (4) 7)) = +6 (23 ( ] (9) )) = 7+6 (23 ( ] (6) )) = 13 (23 ( ] (7) ) = ( ] (5) ) = 299 ( ] (7) = 299 ] (8) 32
17 Komplexere Terme A ::= B = B ::= Int B+B B*B (B) Arithmetische Ausdrücke ohne vollständige Klammerung Interpreter muss die unterschiedlichen Prioritäten der Operatoren berücksichtigen Lösungsansatz zwei Stacks: einen für die Operatoren, den zweiten für die Operanden 33 Komplexere Terme: Regeln value(t ) = eval t, empty, empty (10) eval (t, S 1, S 2 = eval t, (S 1, S 2 (11) eval t, S 1, S 2 = eval t, S 1, S 2 (12) eval +t, S 1, yxs 2 = eval +t, S 1, x y S 2 (13) eval +t, S 1, S 2 = eval t, +S 1, S 2 (14) eval )t, +S 1, yxs 2 = eval )t, S 1, x + y S 2 (15) eval )t, S 1, yxs 2 = eval )t, S 1, x y S 2 (16) eval )t, (S 1, S 2 = eval t, S 1, S 2 (17) eval =, +S 1, yxs 2 = eval =, S 1, x + y S 2 (18) eval =, S 1, yxs 2 = eval =, S 1, x y S 2 (19) eval =, empty, x empty = x (20) eval xt, S 1, S 2 = eval t, S 1, x S 2 (21) 34
18 Komplexere Terme: Abarbeitung (1) bearbeiteter Term t Stack S 1 Stack S 2 Regel (45+3) (6+7) = ] ] (11) 45+3) (6+7) = ( ] ] (21) 5+3) (6+7) = ( ] 4 ] (12) 5+3) (6+7) = ( ] 4 ] (21) +3) (6+7) = ( ] 5 4 ] (13) +3) (6+7) = ( ] 20 ] (14) 3) (6+7) = + ( ] 20 ] (21) ) (6+7) = + ( ] 3 20 ] (15) ) (6+7) = ( ] 23 ] (17) 35 Komplexere Terme: Abarbeitung (2) bearbeiteter Term t Stack S 1 Stack S 2 Regel ) (6+7) = ( ] 23 ] (17) (6+7) = ] 23 ] (12) (6+7) = ] 23 ] (11) 6+7) = ( ] 23 ] (21) +7) = ( ] 6 23 ] (14) 7) = + ( ] 6 23 ] (21) ) = + ( ] ] (15) ) = ( ] ] (17) = ] ] (19) = ] 299 ] (20) 36
19 Warteschlange (Queue) FIFO-Prinzip: First in, first out enter leave front 37 Warteschlange (Queue) type Queue(T) import Bool operators empty : Queue enter : Queue T Queue leave : Queue Queue front : Queue T is_empty : Queue Bool axioms q : Queue, x, y : T leave (enter (empty, x)) = empty leave (enter (enter(q, x), y)) = enter (leave (enter(q, x)), y) front (enter (empty, x)) = x front (enter (enter(q, x), y)) = front (enter (q, x)) is_empty (empty) = true is_empty (enter(q, x)) = false 38
20 Entwurf von ADT Wie komme ich zu den Gleichungen? Wann habe ich genug Gleichungen? Wann fehlt mir ein Axiom? leider keine einfache Antworten zu erwarten 39 Systematische Vorgehensweise 1. Festlegung der Konstruktoren Bei Stack: empty und push 2. Eventuell: Axiome zur Gleichsetzung von Konstruktortermen Siehe Beispiel Set : mehrfaches Einfügen und Reihenfolge der Einfügeoperationen ist unerheblich 3. Definition geeigneter Selektoren Selektoren erlauben den lesenden Zugriff auf konstruierte Werte und liefern meist importierte Datentypen zurück Die Auswertung von Selektoren kann auf ausschließlich mit Konstruktoren konstruierten Termen erfolgen Bei Stack: is_empty, top 4. Weitere Operationen ( Manipulatoren ) festlegen Bei Stack: pop 5. Fehlersituationen abfangen 40
21 Festlegung weiterer Operationen Wenn möglich: direkt auf Konstruktoren und Selektoren zurückführen Regeln von links nach rechts als Ersetzungsregeln aufbauen Rechte Seite einfacher als linke Seite Bei Rekursion: Argumente einfacher (echt monoton schrumpfend) Abbruch garantiert? (Vorsicht! wird oft vergessen) Oft: Vorgehen analog zu applikativen Algorithmen Vollständige Fallunterscheidung: Jeder Konstruktor muss bei den Parametern berücksichtigt werden 41 Umsetzung von ADTs ADT in Programmiersprachen Konzept der Kapselung Verbergen der internen Repräsentation Gleiche Verwendung trotz unterschiedlicher Implementierung Vorteile: Stabilität gegenüber Änderungen, Auswahl einer geeigneten Implementierungsvariante ADT in Java (objektorientiert!) Typen Klassen Funktionen Methoden Klassen als konkrete Implementierung Das nächste Kapitel führt daher in die objektorientierte Programmierung mit Java ein. 42
22 Zusammenfassung Abstrakte Datentypen Kapselung & Geheimnisprinzip Implementierungsunabhängige Definition Literatur: Saake/Sattler: Algorithmen und Datenstrukturen, Kapitel
Algorithmen und Programmierung
 Algorithmen und Programmierung Kapitel 8 Abstrakte Datentypen A&P (WS 14/15): 08 Abstrakte Datentypen 1 Überblick Abstrakte Datentypen Signaturen und Algebren Spezifikation von ADTs Umsetzung von ADTs
Algorithmen und Programmierung Kapitel 8 Abstrakte Datentypen A&P (WS 14/15): 08 Abstrakte Datentypen 1 Überblick Abstrakte Datentypen Signaturen und Algebren Spezifikation von ADTs Umsetzung von ADTs
2.3 Spezifikation von Abstrakten Datentypen
 Abstrakte Datentypen (ADT) 2.3 Spezifikation von Abstrakten Datentypen Sichtbare Schnittstelle: Typbezeichner Signaturen der Operationen Spezifikation der Operationen Abstraktionsbarriere Implementierung
Abstrakte Datentypen (ADT) 2.3 Spezifikation von Abstrakten Datentypen Sichtbare Schnittstelle: Typbezeichner Signaturen der Operationen Spezifikation der Operationen Abstraktionsbarriere Implementierung
Geheimnisprinzip: (information hiding principle, Parnas 1972)
 2. Abstrakte Datentypen 2.0 Begriffe Geheimnisprinzip: (information hiding principle, Parnas 1972) Zugriffe auf Teile einer Programmeinheit, die für die reguläre Benutzung nicht erforderlich sind, sollten
2. Abstrakte Datentypen 2.0 Begriffe Geheimnisprinzip: (information hiding principle, Parnas 1972) Zugriffe auf Teile einer Programmeinheit, die für die reguläre Benutzung nicht erforderlich sind, sollten
Algebraische Spezifikation. André Kießling
 Algebraische Spezifikation André Kießling Das Problem Software nach wie vor sehr Fehlerhaft Fehler oft schon in Spezifikation Ursachen u.a.: - Beschreibung zu schwammig - Kunde und Entwickler meinen nicht
Algebraische Spezifikation André Kießling Das Problem Software nach wie vor sehr Fehlerhaft Fehler oft schon in Spezifikation Ursachen u.a.: - Beschreibung zu schwammig - Kunde und Entwickler meinen nicht
Mehrsortige Strukturen
 Was bisher geschah Modellierung von Daten durch Mengen (Individuenbereiche), häufig zusammengesetzt durch Mengenoperationen, Zusammenhängen zwischen Individuen durch Relationen (auch Eigenschaften) Funktionen
Was bisher geschah Modellierung von Daten durch Mengen (Individuenbereiche), häufig zusammengesetzt durch Mengenoperationen, Zusammenhängen zwischen Individuen durch Relationen (auch Eigenschaften) Funktionen
Abstrakte Datentypen und deren Implementierung in Python
 Kapitel 15: Abstrakte Datentypen und deren Implementierung in Python Einführung in die Informatik Wintersemester 007/08 Prof. Bernhard Jung Übersicht Abstrakte Datentypen ADT Stack Python-Implementierung(en)
Kapitel 15: Abstrakte Datentypen und deren Implementierung in Python Einführung in die Informatik Wintersemester 007/08 Prof. Bernhard Jung Übersicht Abstrakte Datentypen ADT Stack Python-Implementierung(en)
Algebraische Spezifikation. Teil 2. André Kießling
 Algebraische Spezifikation Teil 2 André Kießling Zur Erinnerung: Signaturen Spezifikation Signatur Σ-BOOL Sorten BOOL Operatoren TRUE: BOOL FALSE: BOOL : BOOL BOOL : BOOL x BOOL BOOL Umsetzung Algebra
Algebraische Spezifikation Teil 2 André Kießling Zur Erinnerung: Signaturen Spezifikation Signatur Σ-BOOL Sorten BOOL Operatoren TRUE: BOOL FALSE: BOOL : BOOL BOOL : BOOL x BOOL BOOL Umsetzung Algebra
Programmierung im Grossen
 1 Letzte Aktualisierung: 16. April 2004 Programmierung im Grossen Bertrand Meyer 2 Vorlesung 4: Abstrakte Daten-Typen Übungen 3 Passe die vorhergehende Spezifikation von Stacks (LIFO, Last-In First-Out
1 Letzte Aktualisierung: 16. April 2004 Programmierung im Grossen Bertrand Meyer 2 Vorlesung 4: Abstrakte Daten-Typen Übungen 3 Passe die vorhergehende Spezifikation von Stacks (LIFO, Last-In First-Out
Wiederholung: Zusammenfassung Felder. Algorithmen und Datenstrukturen (für ET/IT) Definition Abstrakter Datentyp. Programm heute
 Wiederholung: Zusammenfassung Felder Algorithmen und Datenstrukturen (für ET/IT) Wintersemester / Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Ein Feld A kann repräsentiert
Wiederholung: Zusammenfassung Felder Algorithmen und Datenstrukturen (für ET/IT) Wintersemester / Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Ein Feld A kann repräsentiert
1.1 Abstrakte Datentypen 1.2 Lineare Strukturen 1.3 Bäume 1.4 Prioritätsschlangen 1.5 Graphen
 1 Datenstrukturen 1.1 Abstrakte Datentypen 1.2 Lineare Strukturen 1.3 Bäume 1.4 Prioritätsschlangen 1.5 Graphen 1 Abstrakte Datentypen Spezifizieren Form und Funktionalität der zu verarbeitenden Daten
1 Datenstrukturen 1.1 Abstrakte Datentypen 1.2 Lineare Strukturen 1.3 Bäume 1.4 Prioritätsschlangen 1.5 Graphen 1 Abstrakte Datentypen Spezifizieren Form und Funktionalität der zu verarbeitenden Daten
B2.1 Abstrakte Datentypen
 Algorithmen und Datenstrukturen 21. März 2018 B2. Abstrakte Datentypen Algorithmen und Datenstrukturen B2. Abstrakte Datentypen B2.1 Abstrakte Datentypen Marcel Lüthi and Gabriele Röger B2.2 Multimengen,
Algorithmen und Datenstrukturen 21. März 2018 B2. Abstrakte Datentypen Algorithmen und Datenstrukturen B2. Abstrakte Datentypen B2.1 Abstrakte Datentypen Marcel Lüthi and Gabriele Röger B2.2 Multimengen,
13 Abstrakte Datentypen
 13 Abstrakte Datentypen Bisher: Konkrete Datentypen Menge von Elementen Operationen auf den Elementen (Konstruktoren, Selektoren, Typprädikate) Eigenschaften abgeleitet Jetzt: Abstrakte Datentypen (ADT)
13 Abstrakte Datentypen Bisher: Konkrete Datentypen Menge von Elementen Operationen auf den Elementen (Konstruktoren, Selektoren, Typprädikate) Eigenschaften abgeleitet Jetzt: Abstrakte Datentypen (ADT)
Σ = (z; c : z, f : z z) Σ = (z; c : z, f : z z) ( ; 17, x -x) ( ; 17, pred) ( ; true, neg) ( ; 0, suc) ({a,b} + ; a, xa xb und xb xa)
 METHODEN UND MODELLE DES SYSTEMENTWURFS 3. Algebraische Spezifikation mit CASL 3.1 Spezifikationen 3.2 CASL 3.1 SPEZIFIKATIONEN JAN SÜRMELI u.hu-berlin.de/mms-13 ZUR ERINNERUNG 2 DAS ZIEL 3 Signatur charakterisiert
METHODEN UND MODELLE DES SYSTEMENTWURFS 3. Algebraische Spezifikation mit CASL 3.1 Spezifikationen 3.2 CASL 3.1 SPEZIFIKATIONEN JAN SÜRMELI u.hu-berlin.de/mms-13 ZUR ERINNERUNG 2 DAS ZIEL 3 Signatur charakterisiert
10 Abstrakte Datentypen
 10 Abstrakte Datentypen abstrakte Datentypen generische Implementierung datengesteuerte Programmierung Operationstabelle 10.1 Abstrakte Datentypen Bisher: Konkrete Datentypen Menge von Elementen Operationen
10 Abstrakte Datentypen abstrakte Datentypen generische Implementierung datengesteuerte Programmierung Operationstabelle 10.1 Abstrakte Datentypen Bisher: Konkrete Datentypen Menge von Elementen Operationen
Counting - Sort [ [ ] [ [ ] 1. SS 2008 Datenstrukturen und Algorithmen Sortieren in linearer Zeit
![Counting - Sort [ [ ] [ [ ] 1. SS 2008 Datenstrukturen und Algorithmen Sortieren in linearer Zeit Counting - Sort [ [ ] [ [ ] 1. SS 2008 Datenstrukturen und Algorithmen Sortieren in linearer Zeit](/thumbs/60/44575606.jpg) Counting-Sort Counting - Sort ( A,B,k ). for i to k. do C[ i]. for j to length[ A]. do C[ A[ j ] C[ A[ j ] +. > C[ i] enthält Anzahl der Elemente in 6. for i to k. do C[ i] C[ i] + C[ i ]. > C[ i] enthält
Counting-Sort Counting - Sort ( A,B,k ). for i to k. do C[ i]. for j to length[ A]. do C[ A[ j ] C[ A[ j ] +. > C[ i] enthält Anzahl der Elemente in 6. for i to k. do C[ i] C[ i] + C[ i ]. > C[ i] enthält
Stacks, Queues & Bags. Datenstrukturen. Pushdown/Popup Stack. Ferd van Odenhoven. 19. September 2012
 , Queues & Ferd van Odenhoven Fontys Hogeschool voor Techniek en Logistiek Venlo Software Engineering 19. September 2012 ODE/FHTBM, Queues & 19. September 2012 1/42 Datenstrukturen Elementare Datenstrukturen
, Queues & Ferd van Odenhoven Fontys Hogeschool voor Techniek en Logistiek Venlo Software Engineering 19. September 2012 ODE/FHTBM, Queues & 19. September 2012 1/42 Datenstrukturen Elementare Datenstrukturen
5. Januar Universität Bielefeld AG Praktische Informatik. Programmieren in Haskell. Stefan Janssen. Abstrakte Datentypen.
 Universität Bielefeld AG Praktische Informatik 5. Januar 2015 Themen-Vorschau Module In der Software-Entwicklung unterscheidet zwei Arten von : konkrete beziehen sich auf eine konkrete Repräsentation in
Universität Bielefeld AG Praktische Informatik 5. Januar 2015 Themen-Vorschau Module In der Software-Entwicklung unterscheidet zwei Arten von : konkrete beziehen sich auf eine konkrete Repräsentation in
Was bisher geschah Modellierung von Daten durch Mengen Beziehungen (Zusammenhänge und Eigenschaften) durch Relationen, Graphen und Funktionen
 Was bisher geschah Modellierung von Daten durch Mengen Beziehungen (Zusammenhänge und Eigenschaften) durch Relationen, Graphen und Funktionen Anforderungen durch Logiken Modellierung zusammenhängender
Was bisher geschah Modellierung von Daten durch Mengen Beziehungen (Zusammenhänge und Eigenschaften) durch Relationen, Graphen und Funktionen Anforderungen durch Logiken Modellierung zusammenhängender
1 Abstrakte Datentypen
 1 Abstrakte Datentypen Spezifiziere nur die Operationen! Verberge Details der Datenstruktur; der Implementierung der Operationen. == Information Hiding 1 Sinn: Verhindern illegaler Zugriffe auf die Datenstruktur;
1 Abstrakte Datentypen Spezifiziere nur die Operationen! Verberge Details der Datenstruktur; der Implementierung der Operationen. == Information Hiding 1 Sinn: Verhindern illegaler Zugriffe auf die Datenstruktur;
Einfügen immer nur am Kopf der Liste Löschen auch nur an einem Ende (2 Möglichkeiten!)
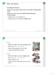 Stack und Queue Grundlegender Datentyp Menge von Operationen (add, remove, test if empty) auf generischen Daten Ähnlich wie Listen, aber mit zusätzlichen Einschränkungen / Vereinfachungen: Einfügen immer
Stack und Queue Grundlegender Datentyp Menge von Operationen (add, remove, test if empty) auf generischen Daten Ähnlich wie Listen, aber mit zusätzlichen Einschränkungen / Vereinfachungen: Einfügen immer
16. Dynamische Datenstrukturen
 Datenstrukturen 6. Dynamische Datenstrukturen Eine Datenstruktur organisiert Daten so in einem Computer, dass man sie effizient nutzen kann. Verkettete Listen, Abstrakte Datentypen Stapel, Warteschlange
Datenstrukturen 6. Dynamische Datenstrukturen Eine Datenstruktur organisiert Daten so in einem Computer, dass man sie effizient nutzen kann. Verkettete Listen, Abstrakte Datentypen Stapel, Warteschlange
Abstrakte Datentypen und Datenstrukturen
 Abstrakte Datentypen und Datenstrukturen Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 3. VO DAP2 SS 2008 15. April 2008 1 Überblick ADT Sequence ADT Stack
Abstrakte Datentypen und Datenstrukturen Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 3. VO DAP2 SS 2008 15. April 2008 1 Überblick ADT Sequence ADT Stack
Übungsblatt 10. Thema: Abstrakte Datentypen, Datenstrukturen in Java
 Informatik I WS 05/06 Prof. Dr. W. May Dipl.-Inform. Oliver Fritzen Dipl.-Inform. Christian Kubczak Übungsblatt 10 Ausgegeben am: Abgabe bis: 13.01.2006 24.1.2006 (Theorie) 27.1.2006 (Praktisch) Thema:
Informatik I WS 05/06 Prof. Dr. W. May Dipl.-Inform. Oliver Fritzen Dipl.-Inform. Christian Kubczak Übungsblatt 10 Ausgegeben am: Abgabe bis: 13.01.2006 24.1.2006 (Theorie) 27.1.2006 (Praktisch) Thema:
Abstract Data Type and the Development of Data Structures
 Abstract Data Type and the Development of Data Structures John Guttag, 1976 2. Mai 2006 Inhalt 1 Motivation 2 3 4 Motivation - Komplexe Probleme lösen Dekomposition Problem Abstraktion Komplexität reduzieren
Abstract Data Type and the Development of Data Structures John Guttag, 1976 2. Mai 2006 Inhalt 1 Motivation 2 3 4 Motivation - Komplexe Probleme lösen Dekomposition Problem Abstraktion Komplexität reduzieren
Stack. Queue. pop() liefert zuletzt auf den Stack gelegtes Element und löscht es push( X ) legt ein Element X auf den Stack
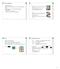 Stack und Queue Grundlegender Datentyp Menge von Operationen (add, remove, test if empty) auf generischen Daten Ähnlich wie Listen, aber mit zusätzlichen Einschränkungen / Vereinfachungen: Einfügen immer
Stack und Queue Grundlegender Datentyp Menge von Operationen (add, remove, test if empty) auf generischen Daten Ähnlich wie Listen, aber mit zusätzlichen Einschränkungen / Vereinfachungen: Einfügen immer
11. Elementare Datenstrukturen
 11. Elementare Datenstrukturen Definition 11.1: Eine dynamische Menge ist gegeben durch eine oder mehrer Mengen von Objekten sowie Operationen auf diesen Mengen und den Objekten der Mengen. Dynamische
11. Elementare Datenstrukturen Definition 11.1: Eine dynamische Menge ist gegeben durch eine oder mehrer Mengen von Objekten sowie Operationen auf diesen Mengen und den Objekten der Mengen. Dynamische
Programmieren in Haskell Abstrakte Datentypen
 Programmieren in Haskell Abstrakte Datentypen Peter Steffen Universität Bielefeld Technische Fakultät 09.01.2009 1 Programmieren in Haskell Einführung Man unterscheidet zwei Arten von Datentypen: konkrete
Programmieren in Haskell Abstrakte Datentypen Peter Steffen Universität Bielefeld Technische Fakultät 09.01.2009 1 Programmieren in Haskell Einführung Man unterscheidet zwei Arten von Datentypen: konkrete
Übungsblatt 6: Softwareentwicklung I (WS 2006/07)
 Prof. Dr. A. Poetzsch-Heffter Dipl.-Inform. J.O. Blech Dipl.-Inform. M.J. Gawkowski Dipl.-Inform. N. Rauch Technische Universität Kaiserslautern Fachbereich Informatik AG Softwaretechnik Übungsblatt 6:
Prof. Dr. A. Poetzsch-Heffter Dipl.-Inform. J.O. Blech Dipl.-Inform. M.J. Gawkowski Dipl.-Inform. N. Rauch Technische Universität Kaiserslautern Fachbereich Informatik AG Softwaretechnik Übungsblatt 6:
- Welche konkreten Invarianten müssen gelten? Berücksichtigen: Invarianten aus Modell und Implem.
 234 Implementierung von Abstrakten Datentypen und Korrektheitskriterien Ziel: Zusammenhang zwischen Spezifikation (Modell!) und Implementierung(en) herstellen Spezifikation Implementierung abstraktes Modell?
234 Implementierung von Abstrakten Datentypen und Korrektheitskriterien Ziel: Zusammenhang zwischen Spezifikation (Modell!) und Implementierung(en) herstellen Spezifikation Implementierung abstraktes Modell?
Algorithmen und Datenstrukturen (für ET/IT)
 Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2016 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Programm heute 1 Einführung 2 Grundlagen von Algorithmen
Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2016 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Programm heute 1 Einführung 2 Grundlagen von Algorithmen
Grundlagen der Informatik
 Grundlagen der Informatik Musterklausur 1. Dynamische Datenstrukturen und objektorientierte Programmierung Zur Verwaltung einer digitalen Fotogalerie sollen Techniken der objektorientierten Programmierung
Grundlagen der Informatik Musterklausur 1. Dynamische Datenstrukturen und objektorientierte Programmierung Zur Verwaltung einer digitalen Fotogalerie sollen Techniken der objektorientierten Programmierung
Daten mit Typetikett Abstrakter Datentyp (ADT) 4-Stufen-Modell Generische Operationen Datengesteuerte Programmierung.
 Datenabstraktion Prof. Dr. Christian Wagenknecht Prof. Dr. Christian Wagenknecht Datenabstraktion 1 von 36 Daten mit Typetikett Programmiersprachen mit Deklarationszwang von Variablen Schlüsselworte, wie
Datenabstraktion Prof. Dr. Christian Wagenknecht Prof. Dr. Christian Wagenknecht Datenabstraktion 1 von 36 Daten mit Typetikett Programmiersprachen mit Deklarationszwang von Variablen Schlüsselworte, wie
Stand der Vorlesung. Vergleich verkettete Liste und sequentielle Liste
 Stand der Vorlesung Kapitel 5 Elementare Datenstrukturen Felder: Folge gleichartiger Elemente Repräsentiert als statische Liste, sequentiell verwaltete Elemente Feste Länge, statische Struktur Direkter
Stand der Vorlesung Kapitel 5 Elementare Datenstrukturen Felder: Folge gleichartiger Elemente Repräsentiert als statische Liste, sequentiell verwaltete Elemente Feste Länge, statische Struktur Direkter
ALP II Dynamische Datenmengen Datenabstraktion
 ALP II Dynamische Datenmengen Datenabstraktion O1 O2 O3 O4 SS 2012 Prof Dr Margarita Esponda M Esponda-Argüero 1 Dynamische Datenmengen Dynamische Datenmengen können durch verschiedene Datenstrukturen
ALP II Dynamische Datenmengen Datenabstraktion O1 O2 O3 O4 SS 2012 Prof Dr Margarita Esponda M Esponda-Argüero 1 Dynamische Datenmengen Dynamische Datenmengen können durch verschiedene Datenstrukturen
Teil IV : Abstrakte Datentypen (ADT)
 Teil IV : Abstrakte Datentypen (ADT) Abstraktion ADT in Modula-2 K. Murmann, H. Neumann, Fakultät für Informatik, Universität Ulm, 2001 1. Abstraktion Rekapitulation Realisation eines Stacks Idee für ADT-Konzept
Teil IV : Abstrakte Datentypen (ADT) Abstraktion ADT in Modula-2 K. Murmann, H. Neumann, Fakultät für Informatik, Universität Ulm, 2001 1. Abstraktion Rekapitulation Realisation eines Stacks Idee für ADT-Konzept
Stapel (Stack, Keller)
 Stapel (Stack, Keller) Eine wichtige Datenstruktur ist der Stapel. Das Prinzip, dass das zuletzt eingefügte Element als erstes wieder entfernt werden muss, bezeichnet man als LIFO-Prinzip (last-in, first-out).
Stapel (Stack, Keller) Eine wichtige Datenstruktur ist der Stapel. Das Prinzip, dass das zuletzt eingefügte Element als erstes wieder entfernt werden muss, bezeichnet man als LIFO-Prinzip (last-in, first-out).
13. Dynamische Datenstrukturen
 Motivation: Stapel. Dynamische Datenstrukturen Verkettete Listen, Abstrakte Datentypen Stapel, Warteschlange, Sortierte Liste 40 40 Motivation: Stapel ( push, pop, top, empty ) Wir brauchen einen neuen
Motivation: Stapel. Dynamische Datenstrukturen Verkettete Listen, Abstrakte Datentypen Stapel, Warteschlange, Sortierte Liste 40 40 Motivation: Stapel ( push, pop, top, empty ) Wir brauchen einen neuen
Grundlagen der Programmierung 2. Operationale Semantik
 Grundlagen der Programmierung 2 Operationale Semantik Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 29. April 2009 Semantik von Programmiersprachen Semantik = Bedeutung
Grundlagen der Programmierung 2 Operationale Semantik Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 29. April 2009 Semantik von Programmiersprachen Semantik = Bedeutung
12. Dynamische Datenstrukturen
 Motivation: Stapel. Dynamische Datenstrukturen Verkettete Listen, Abstrakte Datentypen Stapel, Warteschlange, Implementationsvarianten der verketteten Liste 0 04 Motivation: Stapel ( push, pop, top, empty
Motivation: Stapel. Dynamische Datenstrukturen Verkettete Listen, Abstrakte Datentypen Stapel, Warteschlange, Implementationsvarianten der verketteten Liste 0 04 Motivation: Stapel ( push, pop, top, empty
mathematik und informatik
 Prof. Dr. Martin Erwig Kurs 01852 Fortgeschrittene Konzepte funktionaler Programmierung LESEPROBE mathematik und informatik Das Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere
Prof. Dr. Martin Erwig Kurs 01852 Fortgeschrittene Konzepte funktionaler Programmierung LESEPROBE mathematik und informatik Das Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere
Tutoraufgabe 1 (Implementierung eines ADTs):
 Prof. aa Dr. E. Ábrahám Datenstrukturen und Algorithmen SS Tutoriumslösung - Übung (Abgabe.05.0) F. Corzilius, S. Schupp, T. Ströder Tutoraufgabe (Implementierung eines ADTs): Wir spezifizieren den ADT
Prof. aa Dr. E. Ábrahám Datenstrukturen und Algorithmen SS Tutoriumslösung - Übung (Abgabe.05.0) F. Corzilius, S. Schupp, T. Ströder Tutoraufgabe (Implementierung eines ADTs): Wir spezifizieren den ADT
1. Die rekursive Datenstruktur Liste
 1. Die rekursive Datenstruktur Liste 1.6 Die Datenstruktur Stapel Ein Stack, auch Stapel oder Keller genannt, ist eine Datenstruktur, bei der die Elemente nur an einem Ende der Folge eingefügt bzw. gelöscht
1. Die rekursive Datenstruktur Liste 1.6 Die Datenstruktur Stapel Ein Stack, auch Stapel oder Keller genannt, ist eine Datenstruktur, bei der die Elemente nur an einem Ende der Folge eingefügt bzw. gelöscht
5.3 Doppelt verkettete Listen
 5.3 Doppelt verkettete Listen Einfach verkettete Listen unterstützen das Einfügen und Löschen am Anfang in konstanter Zeit; für das Einfügen und Löschen am Ende benötigen sie jedoch lineare Laufzeit Doppelt
5.3 Doppelt verkettete Listen Einfach verkettete Listen unterstützen das Einfügen und Löschen am Anfang in konstanter Zeit; für das Einfügen und Löschen am Ende benötigen sie jedoch lineare Laufzeit Doppelt
Algorithmen und Datenstrukturen (für ET/IT)
 Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2014 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München 2 Programm heute 1 Einführung 2 Grundlagen von Algorithmen
Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2014 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München 2 Programm heute 1 Einführung 2 Grundlagen von Algorithmen
Beispiele: Funktionsabstraktion (3) Funktionsdeklaration. Funktionsdeklaration (2) Funktionsdeklaration (3) 3. Abstraktion über Funktionsbezeichner:
 Beispiele: Funktionsabstraktion (3) Funktionsdeklaration 3. Abstraktion über Funktionsbezeichner: Ausdruck: f (f x) Abstraktion: \ f x -> f (f x) Mit Bezeichnervereinbarung: twice = \ f x -> f (f x) erg
Beispiele: Funktionsabstraktion (3) Funktionsdeklaration 3. Abstraktion über Funktionsbezeichner: Ausdruck: f (f x) Abstraktion: \ f x -> f (f x) Mit Bezeichnervereinbarung: twice = \ f x -> f (f x) erg
Gliederung. n Teil I: Einleitung und Grundbegriffe. n Teil II: Imperative und objektorientierte Programmierung
 Gliederung n Teil I: Einleitung und Grundbegriffe l 1. Organisatorisches l 2. Grundlagen von Programmiersprachen n Teil II: Imperative und objektorientierte Programmierung l 1. Grundelemente der Programmierung
Gliederung n Teil I: Einleitung und Grundbegriffe l 1. Organisatorisches l 2. Grundlagen von Programmiersprachen n Teil II: Imperative und objektorientierte Programmierung l 1. Grundelemente der Programmierung
4.3 Keller und Warteschlangen
 .3 Keller und Warteschlangen Wir werden zuerst die weitverbreitete Datenstruktur Keller (auch stack, pushdown) kennenlernen. Auch in Python selbst wird sie z.b. bei der Auswertung arithmetischer Ausdrücke
.3 Keller und Warteschlangen Wir werden zuerst die weitverbreitete Datenstruktur Keller (auch stack, pushdown) kennenlernen. Auch in Python selbst wird sie z.b. bei der Auswertung arithmetischer Ausdrücke
Abschnitt 10: Datenstrukturen
 Abschnitt 10: Datenstrukturen 10. Datenstrukturen 10.1Einleitung 10.2 Peer Kröger (LMU München) Einführung in die Programmierung WS 16/17 829 / 867 Einleitung Überblick 10. Datenstrukturen 10.1Einleitung
Abschnitt 10: Datenstrukturen 10. Datenstrukturen 10.1Einleitung 10.2 Peer Kröger (LMU München) Einführung in die Programmierung WS 16/17 829 / 867 Einleitung Überblick 10. Datenstrukturen 10.1Einleitung
Datenstrukturen und Algorithmen (SS 2013)
 Datenstrukturen und Algorithmen (SS 2013) Präsenzübung Musterlösung Dienstag, 28.05.2013 Aufgabe 1 (Allgemeine Fragen [20 Punkte]) 1. Tragen Sie in der folgenden Tabelle die Best-, Average- und Worst-Case-
Datenstrukturen und Algorithmen (SS 2013) Präsenzübung Musterlösung Dienstag, 28.05.2013 Aufgabe 1 (Allgemeine Fragen [20 Punkte]) 1. Tragen Sie in der folgenden Tabelle die Best-, Average- und Worst-Case-
Programmierung 1 (Wintersemester 2015/16) Wiederholungstutorium Lösungsblatt 15 (Linearer Speicher, Listen, Bäume)
 Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2015/16) Wiederholungstutorium Lösungsblatt 15 (Linearer Speicher, Listen,
Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2015/16) Wiederholungstutorium Lösungsblatt 15 (Linearer Speicher, Listen,
Programmieren in Haskell. Abstrakte Datentypen
 Programmieren in Haskell Abstrakte Datentypen Einführung Man unterscheidet zwei Arten von Datentypen: konkrete Datentypen: beziehen sich auf eine konkrete Repräsentation in der Sprache. Beispiele: Listen,
Programmieren in Haskell Abstrakte Datentypen Einführung Man unterscheidet zwei Arten von Datentypen: konkrete Datentypen: beziehen sich auf eine konkrete Repräsentation in der Sprache. Beispiele: Listen,
Einführung in die Informatik: Programmierung und Software-Entwicklung, WS 12/13. Kapitel 3. Grunddatentypen, Ausdrücke und Variable
 1 Kapitel 3 Grunddatentypen, Ausdrücke und Variable 2 Eine Datenstruktur besteht aus Grunddatentypen in Java einer Menge von Daten (Werten) charakteristischen Operationen Datenstrukturen werden mit einem
1 Kapitel 3 Grunddatentypen, Ausdrücke und Variable 2 Eine Datenstruktur besteht aus Grunddatentypen in Java einer Menge von Daten (Werten) charakteristischen Operationen Datenstrukturen werden mit einem
Übung Algorithmen und Datenstrukturen
 Übung Algorithmen und Datenstrukturen Sommersemester 2017 Marc Bux, Humboldt-Universität zu Berlin Agenda 1. (Sortierte) Listen 2. Stacks & Queues 3. Datenstrukturen 4. Rekursion und vollständige Induktion
Übung Algorithmen und Datenstrukturen Sommersemester 2017 Marc Bux, Humboldt-Universität zu Berlin Agenda 1. (Sortierte) Listen 2. Stacks & Queues 3. Datenstrukturen 4. Rekursion und vollständige Induktion
Gliederung. 5. Compiler. 6. Sortieren und Suchen. 7. Graphen
 Gliederung 5. Compiler 1. Struktur eines Compilers 2. Syntaxanalyse durch rekursiven Abstieg 3. Ausnahmebehandlung 4. Arrays und Strings 6. Sortieren und Suchen 1. Grundlegende Datenstrukturen 2. Bäume
Gliederung 5. Compiler 1. Struktur eines Compilers 2. Syntaxanalyse durch rekursiven Abstieg 3. Ausnahmebehandlung 4. Arrays und Strings 6. Sortieren und Suchen 1. Grundlegende Datenstrukturen 2. Bäume
Abstrakte Datentypen und Datenstrukturen
 Abstrakte Datentypen und Datenstrukturen Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 3. VO DAP2 SS 2009 21. April 2009 1 Praktikum zu DAP 2 Beginn: Mittwoch
Abstrakte Datentypen und Datenstrukturen Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 3. VO DAP2 SS 2009 21. April 2009 1 Praktikum zu DAP 2 Beginn: Mittwoch
Kapitel 11: Wiederholung und Zusammenfassung
 Wiederholung und Zusammenfassung 1: Begriff und Grundprobleme der Informatik Begriff Informatik Computer als universelle Rechenmaschine Grenzen der Berechenbarkeit Digitalisierung Problem der Komplexität
Wiederholung und Zusammenfassung 1: Begriff und Grundprobleme der Informatik Begriff Informatik Computer als universelle Rechenmaschine Grenzen der Berechenbarkeit Digitalisierung Problem der Komplexität
Zum Buch Hinweise Handhabung des Buchs Website In eigener Sache... 19
 Vorwort 13 Zum Buch.................................................... 15 Hinweise..................................................... 17 Handhabung des Buchs.........................................
Vorwort 13 Zum Buch.................................................... 15 Hinweise..................................................... 17 Handhabung des Buchs.........................................
Was ist ein Problem? Ein Problem im Sinne der Programmierung ist durch Computer lösbar. Programmieren Entwurf/ Implementierung
 VOM PROBLEM ZUM PROGRAMM Was ist ein Problem? Ein Problem im Sinne der Programmierung ist durch Computer lösbar. Aspekte -> es läßt sich hinreichend genau spezifizieren (z. B. als Funktion Eingabewerte
VOM PROBLEM ZUM PROGRAMM Was ist ein Problem? Ein Problem im Sinne der Programmierung ist durch Computer lösbar. Aspekte -> es läßt sich hinreichend genau spezifizieren (z. B. als Funktion Eingabewerte
Einführung in die funktionale Programmierung
 Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 26. Oktober 2006 Haskell - Einführung Syntax Typen Auswertung Programmierung
Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 26. Oktober 2006 Haskell - Einführung Syntax Typen Auswertung Programmierung
Formale Methoden in der Informatik Wiederholung klassische Logik Konkrete Datentypen (algebraische Strukturen) Abstrakte Datentypen
 Was bisher geschah Formale Methoden in der Informatik Wiederholung klassische Logik Konkrete Datentypen (algebraische Strukturen) Abstrakte Datentypen Syntax: Signatur Semantik: Axiome (FOL-Formeln, meist
Was bisher geschah Formale Methoden in der Informatik Wiederholung klassische Logik Konkrete Datentypen (algebraische Strukturen) Abstrakte Datentypen Syntax: Signatur Semantik: Axiome (FOL-Formeln, meist
Abstrakte Datentypen I
 6 Abstrakte Datentypen I Ein Datentyp heißt abstrakt, wenn seine Eigenschaften allein durch die für ihn definierten Operationen festgelegt sind, während die Repräsentation seiner Werte dem Benutzer verborgen
6 Abstrakte Datentypen I Ein Datentyp heißt abstrakt, wenn seine Eigenschaften allein durch die für ihn definierten Operationen festgelegt sind, während die Repräsentation seiner Werte dem Benutzer verborgen
Abstrakter Datentyp (ADT): Besteht aus einer Menge von Objekten, sowie Operationen, die auf diesen Objekten wirken.
 Abstrakte Datentypen und Datenstrukturen/ Einfache Beispiele Abstrakter Datentyp (ADT): Besteht aus einer Menge von Objekten, sowie Operationen, die auf diesen Objekten wirken. Datenstruktur (DS): Realisierung
Abstrakte Datentypen und Datenstrukturen/ Einfache Beispiele Abstrakter Datentyp (ADT): Besteht aus einer Menge von Objekten, sowie Operationen, die auf diesen Objekten wirken. Datenstruktur (DS): Realisierung
Kapitel 4. Kontrollstrukturen
 Kapitel 4 Kontrollstrukturen Kontrollstrukturen 1 Ziele Kontrollstrukturen in imperativen Programmen kennenlernen und verstehen. Realisierung der Kontrollstrukturen in Java. Kontrollstrukturen 2 Anweisungen
Kapitel 4 Kontrollstrukturen Kontrollstrukturen 1 Ziele Kontrollstrukturen in imperativen Programmen kennenlernen und verstehen. Realisierung der Kontrollstrukturen in Java. Kontrollstrukturen 2 Anweisungen
