Abstrakte Datentypen I
|
|
|
- Katarina Grosser
- vor 8 Jahren
- Abrufe
Transkript
1 6 Abstrakte Datentypen I Ein Datentyp heißt abstrakt, wenn seine Eigenschaften allein durch die für ihn definierten Operationen festgelegt sind, während die Repräsentation seiner Werte dem Benutzer verborgen bleibt. Zur Realisierung abstrakter Datentypen aber nicht nur dafür braucht man Konzepte zur Kapselung, die Vereinbarungen zusammenfassen, und einige davon verbergen können, um so das Prinzip des information hiding zu realisieren. In diesem Kapitel werden zunächst anhand des Beispiels der geordneten Bäume entwickeln, wie ein Datentyp in einem Modul gekapselt werden kann, wie durch Exportschnittstellen seine Hilfsdefinitionen nach außen verborgen bleiben, und wie endlich ein abstrakter Datentyp für Mengen entsteht, wenn auch die Realisierung des Datentypen verborgen wird. Dann betrachten wir die Realisierungen einiger klassische abstrakter Datentypen in Haskell: Stapel (Stack) und Warteschlangen (Queue). 6.1 Konkrete und abstrakte Datentypen Ein konkreter Datentyp besteht aus der Definition eines Datentypen D und einer Menge von Operationen auf D. D heißt konkret, weil die Darstellung seiner Werte vorgegeben ist in einer funktionalen Sprache geschieht dass das durch die Definition der Wertkonstruktoren für D. Beispiel 6.1 (Rationale Zahlen). Die rationalen Zahlen Q sind Brüche n d von ganzahligen Zählern n und granzzahligen Nennern d (engl. nominator und denominator). Die arithmetischen Operationen auf rationalen Zahlen sind wie folgt definiert: n d + n d = nd + n d dd n d n d = nd n d dd Die Vergleichsoperationen sind definiert als n n d d = nn dd n d /n d = nd dn
2 84 6. Abstrakte Datentypen I n d n d = nd dn für {<,,, =,, >} In einer funktionalen Sprache könnte man dies leicht hinschreiben: type Rat = Rat Integer Integer plus, minus, times, by :: Rat Rat Rat (Rat n d) plus (Rat n d ) = Rat (n d + n d) (d d ) (Rat n d) minus (Rat n d ) = Rat (n d - n d) (d d ) (Rat n d) times (Rat n d ) = Rat (n n ) (d d ) (Rat n d) by (Rat n d ) = Rat (n d ) (d n ) lt, le, ne, eq, ge, gt :: Rat Rat Rat (Rat n d) lt (Rat n d ) = n d < n d (Rat n d) le (Rat n d ) = n d n d (Rat n d) ne (Rat n d ) = n d /= n d (Rat n d) eq (Rat n d ) = n d == n d (Rat n d) ge (Rat n d ) = n d n d (Rat n d) gt (Rat n d ) = n d > n d Diese Implementierung macht jedoch einige Probleme, denn Rat hat eine andere Wertemenge als Q: 1. Einige Werte von Rat repräsentieren überhaupt keine rationale Zahl: Der Nenner einer rationalen Zahl muss immer ungleich Null sein. 2. Rat enthält (unendlich viele Werte, die jeweils die gleiche rationale Zahl repräsentieren: n d = m n m d für beliebige ganze Zahlen m. Bei äquivalenten Werte nach 2. haben Nenner und Zähler einen gemeinsamen Teiler m. Für die Darstellung rationaler Zahlen reichen die Brüche n d aus, wo n und d teilerfremd sind, also nicht mehr gekürzt werden können, und wo der Nenner nicht negativ ist. Da der Nenner auch nicht Null sein darf, reichen für eine nicht redundante Darstellung von rationalen Zahlen also folgende Brüche aus: { n } Q = d n, d Z, d > 0, gcd n d = 1 Diese Wertemenge lässt sich aber mit den gängigen Tykkonstruktoren nicht definieren. wegen der Bedingung der Teilerfremdheit. Wenn wir mit allgemeinen Paaren von ganzen Zahlen rechnen, müssen wir also vor jeder Operation überprüfen, dass keiner der Nenner Null ist, und nach jeder Operation sicherstellen, dass Zähler und Nenner teilerfremd sind. 1 Das kann man mit der Funktion reduce erreichen: 1 Eigentlich ist das für die Endergebnisse nötig, denn die Definitionen der Operationen funktionieren auch so höchstens etwas langsamer.
3 6.1. Konkrete und abstrakte Datentypen 85 reduce :: Integer Integer Rat reduce _ 0 = error "reduce: zero denominator" reduce n d = Rat (n div g) (d div g) where g = gcd n d Trotzdem bleibt das Arbeiten mit rationalen Zahlen unbequem. Eigentlich sollten sich die Benutzer von rationalen Zahlen nicht mit solchen Details iher konkreten Darstellung herumschlagen müssen. Wünschenswert wäre eine Implementierung, die die Invarianten für die Elemente von Q schon bei der Konstruktion automatisch sicherstellt, so dass sie danach bei den Operationen nicht immer überprüft werden müssen. So eine Funktion könnte leicht implementiert werden; hier definieren wir die Selektoren (von Zähler und Nenner einer Zahl) gleich mit: infixl 7 % (%) :: Integer Integer Rat x % y = reduce (x signum y) (abs y) numerator, denominator :: (Integral a) Ratio a a numerator (Rat x _) = x denominator (Rat _ y) = y Das hilft wenig, weil mit dem Wertkonstruktor Rat immer noch Zahlen wie Rat 12 (-4) und Rat 1 0 konstruiert werden können. Wir müssen die Definition des Datentyps kapseln, d.h. in einen Modul stecken und erreichen, dass alle Benuzter des Moduls rationale Zahlen nur noch mit der Operation (%), nicht aber mehr mit Rat konstruieren können. In Haskell können die Definitionen so in ein Modul gepackt werden: module Rat (Rat, (%), nominator, denominator, plus, minus, times, by, lt, le, ne, eq, ge, gt) where hier kommen die Definitionen Die Namen in der Klammer werden vom Modul exportiert. Alle anderen bleiben nach außen verborgen z.b. reduce. Vom Datentyp Rat wird nur desen Name, nicht aber dessen Wertkonstruktor gleichen Namens exportiert. In einem Modul, der Rat importiert, können nur diese Operationen benutzt werden. Inbesondere kann der Wertkonstruktor nicht benuztzt werden, und also bei der Definition von neuen Funktionen auch keine Muster des Typ Rat gebildet werden. So ähnlich wie hier vorgestellt sind die rationalen Zahlen in Haskell auch im Modul Ratio vordefiniert. Folgende Unterschiede sind zu beachten:
4 86 6. Abstrakte Datentypen I Der Typ heißt Rational und ist ein Synonym für Ratio Integer. Es können also auch rationale Zahlen über Int (den ganzen Zahlen, die die Hardware unterstützt) gebildet werden auch wenn das wenig Sinn macht. Ratio und damit Rational instanziieren die Klassen Eq, Ord, Num, Real, Fractional, RealFrac, Enum, Read und Show so dass die arithmetischen Operationen und Vergleichsprädikate mit ihren vertrauten Symbolen (+), (-), ( ), ( ), (<), ( ), (==), (/=), ( ) und (>) bneutzt werden können. Zusätzlich sind noch einige Konversionen mit ganzen und Fließpunktzahlen definiert. Details finden sich in der Bibliothel Ratio. 6.2 Kapselung Im vorigen Kapitel haben wir geordnete Bäume mit den passenden Operationen darauf implementiert (vgl. Beispiel 5.8). Es könnte sich lohnen, dies als ein wiederverwendbares Stück Software in einem Modul zu kapseln. In Haskell dienen Module nicht nur zur Kapselung, sondern definieren auch Übersetzungs-Einheiten. Ein Modul wird also getrennt übersetzt. Beispiel 6.2 (Gekapselte geordnete Bäume). Die Operationen insert und delete können zusammen mit dem Datentyp Tree in einen Modul geschrieben und in einer Datei OrderedTree.hs abgespeichert werden. module OrderedTree where data Ord a Tree a = Null Node (Tree a) a (Tree a) deriving (Eq, Read, Show) insert :: Ord a Tree a a Tree a insert Null a = Node Null a Null insert (Node l a r) b b < a = Node (insert l b) a r b == a = Node l a r b > a = Node l a (insert r b) delete :: Ord a Tree a a Tree a delete Null x = Null delete (Node l y r) x x < y = Node (delete l x) y r x == y = join l r x > y = Node l y (delete r x) join :: Ord a Tree a Tree a Tree a join xt Null = xt join xt yt = Node xt u nu
5 6.2. Kapselung 87 where (u, nu) = splittree yt splittree :: Ord a Tree a (a, Tree a) splittree (Node Null a t) = (a, t) splittree (Node lt a rt) = (u, Node nu a rt) where (u, nu) = splittree lt Diesen Modul können wir in einem anderen Modul importieren: module Use where import OrderedTree... Danach können wir die Definitionen des Moduls benutzen, als stünden sie in Use selber. Oft werden wir nicht alle Definitionen eines Moduls exportieren wollen: Die Operation join ist z. B. eine Hilfsfunktion, die nur lokal benutzt werden sollte. Wollen wir sie im Modul OrderedTree verbergen, müssen wir in seinem Kopf angeben, welche Definitionen exportiert werden sollen. Ändern wir also den Modulkopf wie folgt: module Orderedtree (Tree(..), -- a type with constructors -- Null :: Tree a -- Node :: Tree a -> a -> Tree a -> Tree a member, -- Ord a=> Tree a -> a-> Bool insert, -- Ord a=> Tree a -> a-> Tree a delete -- Ord a=> Tree a -> a-> Tree a ) where Dann werden alle Definitionen bis auf das ausgelassene join exportiert. (In der Exportliste dürfen nur die Namen der exportierten Definitionen stehen; deshalb schreiben wir ihre Typen dahinter, damit im Kopf des Moduls alle wesentlichen Informationen für seine Benutzung beisammen stehen. Die Zeichen (..) hinter dem Typnamen Tree bedeuten, dass seine Wertkonstruktoren Null und Node zusammen mit dem Typnamen exportiert werden sollen. Das kann dazu führen, das im Modul Use mithilfe der Konstruktoren ungeordnete Bäume wie t = Node (Node Null 4 Null) 3 (Node Null 2 Null) konstruiert werden. Dann funktionieren Aufrufe wie delete t 4 oder insert t 2 nicht richtig, weil die Invariante für geordnete Bäume verletzt ist. Dies kann man verhindern, indem man die Konstruktoren Null und Node verbirgt und Tree zu einem abstrakten Datentyp macht, der nur durch die expliziten Operationen definiert ist. Dies kann man durch Weglassen von (..) nach Tree in der Export-Schnittstelle erreichen. Leider stellt sich dann das nächste (kleine) Problem: Wie können die Werte des Typs ohne die Wertkonstruktoren aufgebaut werden? Die Funktion insert fügt zwar ein Element in einen Baum ein, aber es gibt keine Möglichkeit, einen leeren Baum (Null)
6 88 6. Abstrakte Datentypen I zu erzeugen. Wir definieren dafür eine Konstante empty und exportieren sie. Gleichzeitig führen wir auch noch eine weitere Operation enumeration ein, die alle Einträge eines geordneten Baumes aufzählt, sowie ein Prädikat contains, das feststellt, ob ein Element in einem Baum bereits vorhanden ist. module OrderedTree (Tree, -- an abstract type empty, -- Tree a isempty, -- Tree a -> Bool insert, -- Ord a => Tree a -> a-> Tree a delete, -- Ord a => Tree a -> a-> Tree a contains, -- Ord a => Tree a -> a-> Bool enumeration -- Ord a => Tree a -> [a] ) where -- Definition von insert und delete empty :: Tree a empty = Null isempty :: Tree a Bool isempty Null = True isempty _ = False contains :: Ord a Tree a a Bool contains Null _ = False contains (Node l a r) b = (b < a && contains l b) b == a ( b > a && contains r b) enumeration :: Ord a Tree a [a] enumeration Null = [] enumeration (Node l a r) = (enumeration l) ++ [a] ++ (enumeration r)... Nun definiert OrderedTree einen abstrakten Datentyp, denn jedes Modul, das diesen Typ importiert, kennt von Tree nur den Namen und die exportierten Operationen, weiß aber nichts über die Darstellung seiner Werte. Das hat einerseits den kleinen Nachteil, dass in einem importiernden Modul weitere Funktionen auf Tree nur als Kombination der exportierten Operationen definiert werden können und nicht durch primitive Rekursion über den (dort nicht bekannten) Wertkonstruktoren. Andererseits hat es den großen Vorteil, dass jeder importierende Modul nur noch geordnete Bäume konstruieren kann (mit empty und insert), so dass die Operationieren immer funktionieren. Außerdem kann die Implementierung
7 6.3. Klassische abstrakte Datentypen 89 von OrderedTree geändert werden, ohne dass dies in den importierenden Modulen bemerkt wird, solange die Operationen das Gleiche tun. Dies ist eine wesentliche Voraussetzung für Programmentwicklung im Großen. 6.3 Klassische abstrakte Datentypen In den folgenden Unterabschnitten werden wir zwei bekannte abstrakte Datentypen in Haskell definieren Speicher In diesem Abschnitt betrachten wir ein sehr einfaches Beispiel für einen abstrakten Datentyp, bei dem die Schnittstelle auf verschiedene Arten realisiert werden kann. Beispiel 6.3 (Speicher). Ein Speicher ist ein Datentyp Store a b, der parametrisiert ist über einem Indextyp a (der vergleichbar oder besser noch total geordnet sein sollte) und mit einem Wertetyp b. Der Speicher hat drei Operationen: Die Konstruktor-Operation initial ::Store a b schafft einen leeren Speicher. Die Selektor-Operation value ::Store a b a Maybe b liest den unter einem Index abgelegten Wert. Ihr Ergebnistyp ist Maybe b, weil der Wert undefiniert sein könnte. Die Operation update ::Store a b a b Store a b setzt den Wert für einen Index. Wir schreiben den abstrakten Datentyp als einen Modul Store in eine Datei Store.hs und versehen den Modul mit folgender Export-Schnittstelle: module Store(Store, -- an abstract type initial, -- Store a b value, -- Eq a => Store a b-> a-> Maybe b update, -- Store a b-> a-> b-> Store a b ) where Die semantischen Eigenschaften, die wir von einem Speicher erwarten, sind damit noch nicht beschrieben. Informell könnten wir sie so angeben: 1. Die Funktion value liefert just denjenigen Wert zurück, der für einen Index x zuletzt mit update abgespeichert wurde. 2. Wurde bisher kein Wert für x abgespeichert, ist dies ein Fehler. Formal könnten wir den Zusammenhang der Operationen durch algebraische Gleichungen etwa so beschreiben
8 90 6. Abstrakte Datentypen I value initial = Nothing (6.1) { Just b wenn x = a value(update s a b) x = (6.2) value s x sonst update(update s a b) a b = update s a b (6.3) Das geht aber nicht in Haskell, oder allenfalls als Kommentar. Mindestens eine informelle Beschreibung der Eigenschaften gehört aber zu jeder Schnittstelle dazu, damit ein abstrakter Datentyp korrekt benutzt werden kann, ohne die Implementierung zu kennen. Die Schnittstelle kann nun implementiert werden, und zwar im Verborgenen. Insbesondere können wir verschiedene Implementierungen entwickeln und eine durch die andere ersetzen, ohne das die Benutzer des abstrakten Datentypen es bemerken. Die erste Implementierung stellt den Speicher als Paarliste dar. (Der Typ muss als Datentyp mit als data oder newtype definiert werden, wenn seine Konstuktoren verborgen werden sollen, nicht mit type.) data Store a b = St [(a, b)] deriving Show Der leere Speicher wird als leere Liste dargestellt. Die Funktion update hängt ein neues Index-Werte-Paar vorne an die Liste an, und value sucht nach dem ersten Paar mit passenden Index. (Deshalb ist es unwichtig, ob update ein schon abgespeichertes Paar oder ein neues einträgt.) initial = St [] value (St [] ) x = Nothing value (St ((a,b):st)) x a == x = Just b otherwise = value (St st) x update (St ls) a b = St ((a, b): ls) Andere Implementierungen des Speichers sind denkbar: Geordnete Listen, Bäume oder sogar Funktionen aber dass Funktionen auch Daten sein können, werden wir erst im nächsten Kapitel sehen. Eine Schnittstelle kann also auf verschiedene Arten implementiert werden, ohne dass dies für den Benutzer relevant ist, weil er den Datentyp nur über die Operationen in der Schnittstelle benutzt. Wenn wir den Modul Store in einem Modul Main benutzen wollen, müssen wir schreiben module Main where import Store Im Rumpf von Main können wir nun die exportierten Namen von Store benutzen, um Werte vom Typ Store a b anzulegen und zu bearbeiten. Außer
9 6.3. Klassische abstrakte Datentypen 91 diesen Namen wissen wir nichts über die Repräsentation des Speichers, insbesondere kennen wir seinen Wertkonstruktor und seinen Komponententyp nicht und können damit auch kein pattern matching benutzen, um weitere Funktionen auf dem Speicher zu definieren. Dazu können wir nur die exportierten Funktionen benutzen. Deshalb ist es wichtig, für jeden abstrakten Datentyp einen vollständigen Satz von Operationen zu definieren: Konstruktoren wie initial und update, die Werte aufbauen. Selektoren wie value, die auf Komponenenten des Datentyps zugreifen. Ggf. Prädikate, die Eigenschaften des Datentyps bestimmen. Für den Speicher hätte man beispielsweise eine Funktion isstored vorsehen können, die ermittelt, ob für einen Index ein Wert abgespeichert ist. In der vorliegenden Schnittstelle kann man diese Funktion jedoch aus der Funktion value ableiten: isstored :: Eq a Store a b a Bool isstored st x = value st x /= Nothing Stapel und Warteschlangen Stapel (oder Keller, engl. stacks) und Warteschlangen (queues) sind die abstrakten Datentypen schlechthin. Wir stellen die Schnittstellen in einer Tabelle einander gegenüber: Bestandteil Stack Queue Typ St a Qu a Initialwert empty ::St a empty :: Qu a Wert eintragen push ::St a a St a enq :: Qu a a Qu a Wert lesen top :: St a a first ::Qu a a Wert löschen pop :: St a St a deq :: Qu a Qu a Leerheitstest isempty ::St a Bool isempty ::Qu a Bool Während ihre Signaturen annähernd gleich sind, haben Stapel und Schlange eine unterschiedliche Semantik: Der erste realisiert das Prinzip last in, first out, die zweite das Prinzip first in, first out. Dementsprechend unterscheiden sich auch ihre Implementierungen. Beispiel 6.4 (Implementation eines Stapels als Liste). Dies ist sehr einfach, weil sich die Strukturen von Listen und Stapeln eins zu eins entsprechen: Der Konstruktor empty ist die leere Liste [], der Konstruktor push ist der Listenkonstruktor(:), die Selektoren top und pop entsprechen den Listenselektoren head und tail und das Prädikat isempty entspricht dem Leerheits-Prädikat null.
10 92 6. Abstrakte Datentypen I module Stack (St, empty, push, pop, top, isempty) where data St a= St [a] deriving (Show, Eq) empty :: St a empty = St [] push :: St a a St a push (St s) a = St (a:s) top :: St a a top (St []) = error "Stack: top on empty stack" top (St s) = head s pop :: St a St a pop (St []) = error "Stack: pop on empty stack" pop (St s) = St (tail s) isempty :: St a Bool isempty (St s)= null s Beispiel 6.5 (Implementation von Queue). Die einfachste Darstellung einer Schlange ist ebenfalls eine Liste. Weil neue Elemente immer hinten angefügt werden müssen, hätte dann enq linearen Aufwand. Deshalb repräsentieren wir die Schlange als ein Paar von Listen: Die erste Liste enthält die zu entnehmenden Elemente. Die zweite Liste enthält die hinzugefügten Elemente in umgekehrter Reihenfolge. Die Schlange ist leer, wenn beide Listen leer sind. Bei den selektierenden Operationen first und deq wird überprüft, ob die erste Liste leer ist; nötigenfalls wird dann die zweite Liste umgekehrt in die erste Liste gesteckt. Damit sieht der Modul so aus: module Queue(Qu, empty, isempty, enq, first, deq) where data Qu a = Qu [a] [a] empty :: Qu a empty = Qu [] [] isempty :: Qu a Bool isempty (Qu xs ys) = null xs && null ys
11 6.4. Haskells Eck 93 enq :: Qu a a Qu a enq (Qu xs ys) x = Qu xs (x:ys) first :: Qu a a first (Qu (x:_) _ ) = x first (Qu [] ys) = first (Qu (reverse ys) []) first (Qu [] []) = error "Qu: first of empty Q" deq :: Qu a Qu a deq (Qu (_:xs) ys) = Qu xs ys deq (Qu [] ys) = deq (Qu (reverse ys) []) deq (Qu [] []) = error "Qu: deq of empty Q" Betrachten wir eine Sequenz von Operationen, die damit definierte Schlange und die Repräsentation mit zwei Listen: Operation Queue Darstellung empty Qu [], [] enq 9 9 Qu [9], [] enq Qu [9], [4] deq 4 Qu [4], [] enq Qu [4], [7] enq Qu [4], [5, 7] deq 7 5 Qu [7, 5], [] deq 7 Qu [5], [] deq Qu [], [] Immer wenn die erste Liste leer ist, füllt deq sie wieder mit hinzugefügten Elementen auf. 6.4 Haskells Eck Module Module im Allgemeinen können zu nicht nur zur Definition von abstrakten Datentypen benutzt werden. Module bilden die Übersetzungseinheiten eines Haskell-Programms, in dem Teile des Programms als Datei abgespeichert und von einem Haskell- System wie hugs übersetzt werden können. Jeder Modul kapselt eine Menge von Typen, Funktionen und Klassen. Ein Modul kann in einer Exportschnittstelle die Klassen, Typen und Funktionen nennen, die beim Import des Moduls sichtbar sind. Er kann andere Module ganz oder teilweise importieren. Ein Modul in der Datei Name.hs (oder Name.lhs) ist so aufgebaut: module Name [(exportierte Bezeichner)] where Importe RumpfDefinitionen
12 94 6. Abstrakte Datentypen I Wenn die geklammerte Liste der exportierten Bezeichner fehlt, werden alle Definitionen des Modulrumpfes exportiert; bei Typdefinitionen einschließlich ihrer Konstruktoren. Wenn ein mit newtype oder data definierter Typkonstruktor T in der Liste der exportierten Definitionen auftaucht, wird nur der Name von T exportiert. Sollen auch die Wertkonstruktoren des Typs exportiert werden, muss man dies mit T(..) angeben; ein anderer Modul, der T importiert, kennt dann die Repräsentation von T und kann Funktionen über T mit Mustervergleich (pattern matching) definieren. Die Repräsentation von mit mit type definierten Typsynonymen ist immer sichtbar. Importe von Modulen haben die Form import Modulname [as Modulname] [qualified] [hiding] (Bezeichner) Ohne die geklammerte Liste (Bezeichner) wird alles importiert. Mit as wird der Modulname innerhalb des importierenden Moduls umbenannt. Wird qualified angegeben, muss jeder importierte Name n im importierenden Modul qualifiziert werden, also in der Form Modulname.n benutzt werden.mit hiding wird erreicht, dass die in Klammern genannten Bezeichner versteckt werden: import Prelude hiding (foldr) foldr f e ls =... Mit qualified und hiding kann man also Namenskonflikte zwischen den Namen von Modulen auflösen. (Dies ist Fassung von 8. Dezember 2009.)
Programmieren in Haskell. Abstrakte Datentypen
 Programmieren in Haskell Abstrakte Datentypen Einführung Man unterscheidet zwei Arten von Datentypen: konkrete Datentypen: beziehen sich auf eine konkrete Repräsentation in der Sprache. Beispiele: Listen,
Programmieren in Haskell Abstrakte Datentypen Einführung Man unterscheidet zwei Arten von Datentypen: konkrete Datentypen: beziehen sich auf eine konkrete Repräsentation in der Sprache. Beispiele: Listen,
Programmieren in Haskell Programmiermethodik
 Programmieren in Haskell Programmiermethodik Peter Steffen Universität Bielefeld Technische Fakultät 12.01.2011 1 Programmieren in Haskell Bisherige Themen Was soll wiederholt werden? Bedienung von hugs
Programmieren in Haskell Programmiermethodik Peter Steffen Universität Bielefeld Technische Fakultät 12.01.2011 1 Programmieren in Haskell Bisherige Themen Was soll wiederholt werden? Bedienung von hugs
Programmieren in Haskell
 Programmieren in Haskell Wir steigen ein... Programmieren in Haskell 1 Was wir heute machen Umfrage: Wer hat den Hugs ausprobiert? Ausdrücke und Werte Datentypen Funktionen Aufgabe für s Wochenende Programmieren
Programmieren in Haskell Wir steigen ein... Programmieren in Haskell 1 Was wir heute machen Umfrage: Wer hat den Hugs ausprobiert? Ausdrücke und Werte Datentypen Funktionen Aufgabe für s Wochenende Programmieren
Programmieren in Haskell
 Programmieren in Haskell Wir steigen ein... Programmieren in Haskell 1 Was wir heute machen Umfrage: Wer hat den Hugs ausprobiert? Ausdrücke und Werte Datentypen Funktionen Aufgabe für diese Woche Programmieren
Programmieren in Haskell Wir steigen ein... Programmieren in Haskell 1 Was wir heute machen Umfrage: Wer hat den Hugs ausprobiert? Ausdrücke und Werte Datentypen Funktionen Aufgabe für diese Woche Programmieren
Grundlagen der Informatik. Prof. Dr. Stefan Enderle NTA Isny
 Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 2 Datenstrukturen 2.1 Einführung Syntax: Definition einer formalen Grammatik, um Regeln einer formalen Sprache (Programmiersprache) festzulegen.
Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 2 Datenstrukturen 2.1 Einführung Syntax: Definition einer formalen Grammatik, um Regeln einer formalen Sprache (Programmiersprache) festzulegen.
Programmieren in Haskell Einstieg in Haskell
 Programmieren in Haskell Einstieg in Haskell Peter Steffen Universität Bielefeld Technische Fakultät 24.10.2008 1 Programmieren in Haskell Was wir heute machen Umfrage: Wer hat den Hugs ausprobiert? Ausdrücke
Programmieren in Haskell Einstieg in Haskell Peter Steffen Universität Bielefeld Technische Fakultät 24.10.2008 1 Programmieren in Haskell Was wir heute machen Umfrage: Wer hat den Hugs ausprobiert? Ausdrücke
Algebraische Datentypen
 5 Algebraische Datentypen Wir haben in früheren Kapiteln schon gesehen, dass in einer funktionalen Sprache alle zusammengesetzten Datentypen wie Tupel, Listen und Bäume algebraische Datentypen sind. In
5 Algebraische Datentypen Wir haben in früheren Kapiteln schon gesehen, dass in einer funktionalen Sprache alle zusammengesetzten Datentypen wie Tupel, Listen und Bäume algebraische Datentypen sind. In
Programmieren in Haskell
 Programmieren in Haskell Syntax und Semantik von Haskell Programmieren in Haskell 1 Was wir heute (und nächstes mal) machen Datentypdefinitionen Wertdefinitionen, Variablenbindungen Musterbindungen Funktionsbindungen
Programmieren in Haskell Syntax und Semantik von Haskell Programmieren in Haskell 1 Was wir heute (und nächstes mal) machen Datentypdefinitionen Wertdefinitionen, Variablenbindungen Musterbindungen Funktionsbindungen
Zahlen in Haskell Kapitel 3
 Einführung in die Funktionale Programmiersprache Haskell Zahlen in Haskell Kapitel 3 FH Wedel IT-Seminar: WS 2003/04 Dozent: Prof. Dr. Schmidt Autor: Timo Wlecke (wi3309) Vortrag am: 04.11.2003 - Kapitel
Einführung in die Funktionale Programmiersprache Haskell Zahlen in Haskell Kapitel 3 FH Wedel IT-Seminar: WS 2003/04 Dozent: Prof. Dr. Schmidt Autor: Timo Wlecke (wi3309) Vortrag am: 04.11.2003 - Kapitel
Beispiele: (Funktionen auf Listen) (3) Bemerkungen: Die Datenstrukturen der Paare (2) Die Datenstrukturen der Paare
 Beispiele: (Funktionen auf Listen) (3) Bemerkungen: 5. Zusammenhängen der Elemente einer Liste von Listen: concat :: [[a]] -> [a] concat xl = if null xl then [] else append (head xl) ( concat (tail xl))
Beispiele: (Funktionen auf Listen) (3) Bemerkungen: 5. Zusammenhängen der Elemente einer Liste von Listen: concat :: [[a]] -> [a] concat xl = if null xl then [] else append (head xl) ( concat (tail xl))
Programmieren in Haskell
 Programmieren in Haskell Felder (Arrays) Programmieren in Haskell 1 Was wir heute machen Motivationsbeispiel Die Typklasse Ix Felder in Haskell Funktionstabellierung Binäre Suche Pascalsches Dreieck Ein
Programmieren in Haskell Felder (Arrays) Programmieren in Haskell 1 Was wir heute machen Motivationsbeispiel Die Typklasse Ix Felder in Haskell Funktionstabellierung Binäre Suche Pascalsches Dreieck Ein
Programmieren in Haskell
 Programmieren in Haskell Felder (Arrays) Programmieren in Haskell 1 Was wir heute machen Motivationsbeispiel Die Typklasse Ix Felder in Haskell Funktionstabellierung Binäre Suche Pascalsches Dreieck Hashing
Programmieren in Haskell Felder (Arrays) Programmieren in Haskell 1 Was wir heute machen Motivationsbeispiel Die Typklasse Ix Felder in Haskell Funktionstabellierung Binäre Suche Pascalsches Dreieck Hashing
expr :: Expr expr = Mul (Add (Const 3) (Const 4)) (Div (Sub (Const 73) (Const 37)) (Const 6))
 1 - Korrektur 2 - Abstrakte Datentypen für arithmetische Ausdrücke Der Datentyp Wir beginnen zunächst mit dem algebraischen Datentyp für Ausdrücke. Hierfür definieren wir einen Konstruktor Number für Zahlen,
1 - Korrektur 2 - Abstrakte Datentypen für arithmetische Ausdrücke Der Datentyp Wir beginnen zunächst mit dem algebraischen Datentyp für Ausdrücke. Hierfür definieren wir einen Konstruktor Number für Zahlen,
Einführung in die Funktionale Programmierung mit Haskell
 Einführung in die Funktionale Programmierung mit Haskell Typklassen und Polymorphie LFE Theoretische Informatik, Institut für Informatik, Ludwig-Maximilians Universität, München 23. Mai 2013 Planung Freitag:
Einführung in die Funktionale Programmierung mit Haskell Typklassen und Polymorphie LFE Theoretische Informatik, Institut für Informatik, Ludwig-Maximilians Universität, München 23. Mai 2013 Planung Freitag:
Was bisher geschah. deklarative Programmierung. funktionale Programmierung (Haskell):
 Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
Algorithmen und Datenstrukturen (für ET/IT)
 Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2016 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Programm heute 1 Einführung 2 Grundlagen von Algorithmen
Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2016 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Programm heute 1 Einführung 2 Grundlagen von Algorithmen
Counting - Sort [ [ ] [ [ ] 1. SS 2008 Datenstrukturen und Algorithmen Sortieren in linearer Zeit
![Counting - Sort [ [ ] [ [ ] 1. SS 2008 Datenstrukturen und Algorithmen Sortieren in linearer Zeit Counting - Sort [ [ ] [ [ ] 1. SS 2008 Datenstrukturen und Algorithmen Sortieren in linearer Zeit](/thumbs/60/44575606.jpg) Counting-Sort Counting - Sort ( A,B,k ). for i to k. do C[ i]. for j to length[ A]. do C[ A[ j ] C[ A[ j ] +. > C[ i] enthält Anzahl der Elemente in 6. for i to k. do C[ i] C[ i] + C[ i ]. > C[ i] enthält
Counting-Sort Counting - Sort ( A,B,k ). for i to k. do C[ i]. for j to length[ A]. do C[ A[ j ] C[ A[ j ] +. > C[ i] enthält Anzahl der Elemente in 6. for i to k. do C[ i] C[ i] + C[ i ]. > C[ i] enthält
Agenda. 1 Einleitung. 2 Binäre Bäume. 3 Binäre Suchbäume. 4 Rose Trees. 5 Zusammenfassung & Ausblick. Haskell Bäume. Einleitung.
 Vortrag: Bäume in Haskell Bäume in Haskell Vortrag Christoph Forster Thomas Kresalek Fachhochschule Wedel University of Applied Sciences 27. November 2009 Christoph Forster, Thomas Kresalek 1/53 Vortrag
Vortrag: Bäume in Haskell Bäume in Haskell Vortrag Christoph Forster Thomas Kresalek Fachhochschule Wedel University of Applied Sciences 27. November 2009 Christoph Forster, Thomas Kresalek 1/53 Vortrag
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Tag 7. Pattern Matching und eigene Datentypen
 Tag 7 Pattern Matching und eigene Datentypen Heute werden wir eine Technik kennenlernen, die dafür sorgt, daß wir sehr viel übersichtlichere und kürzere Programme schreiben können. Als Überleitung auf
Tag 7 Pattern Matching und eigene Datentypen Heute werden wir eine Technik kennenlernen, die dafür sorgt, daß wir sehr viel übersichtlichere und kürzere Programme schreiben können. Als Überleitung auf
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Binärbaum Suchbaum Dr. Frank Seifert Vorlesung Datenstrukturen - Sommersemester 2016 Folie 356 Datenstruktur Binärbaum Strukturrepräsentation des mathematischen Konzepts Binärbaum
Vorlesung Datenstrukturen Binärbaum Suchbaum Dr. Frank Seifert Vorlesung Datenstrukturen - Sommersemester 2016 Folie 356 Datenstruktur Binärbaum Strukturrepräsentation des mathematischen Konzepts Binärbaum
Advanced Programming in C
 Advanced Programming in C Pointer und Listen Institut für Numerische Simulation Rheinische Friedrich-Wilhelms-Universität Bonn Oktober 2013 Überblick 1 Variablen vs. Pointer - Statischer und dynamischer
Advanced Programming in C Pointer und Listen Institut für Numerische Simulation Rheinische Friedrich-Wilhelms-Universität Bonn Oktober 2013 Überblick 1 Variablen vs. Pointer - Statischer und dynamischer
Theoretische Informatik 1 WS 2007/2008. Prof. Dr. Rainer Lütticke
 Theoretische Informatik 1 WS 2007/2008 Prof. Dr. Rainer Lütticke Inhalt der Vorlesung Grundlagen - Mengen, Relationen, Abbildungen/Funktionen - Datenstrukturen - Aussagenlogik Automatentheorie Formale
Theoretische Informatik 1 WS 2007/2008 Prof. Dr. Rainer Lütticke Inhalt der Vorlesung Grundlagen - Mengen, Relationen, Abbildungen/Funktionen - Datenstrukturen - Aussagenlogik Automatentheorie Formale
Programmieren in Haskell. Stefan Janssen. Strukturelle Rekursion. Universität Bielefeld AG Praktische Informatik. 10.
 Universität Bielefeld AG Praktische Informatik 10. Dezember 2014 Wiederholung: Schema: f :: [σ] -> τ f [] = e 1 f (a : as) = e 2 where s = f as wobei e 1 und e 2 Ausdrücke vom Typ τ sind und e 2 die Variablen
Universität Bielefeld AG Praktische Informatik 10. Dezember 2014 Wiederholung: Schema: f :: [σ] -> τ f [] = e 1 f (a : as) = e 2 where s = f as wobei e 1 und e 2 Ausdrücke vom Typ τ sind und e 2 die Variablen
October 29, Universität Bielefeld AG Praktische Informatik. Programmieren in Haskell. Stefan Janssen. Typ-Synonyme. Algebraische Datentypen
 Universität Bielefeld AG Praktische Informatik October 29, 2014 Typsynonyme Neue Typnamen durch Typsynonyme: 1 type Pair a b = (a,b) 2 type Triple a b c = (a,b,c) 3 type OrdList a = [ a] definiert neue
Universität Bielefeld AG Praktische Informatik October 29, 2014 Typsynonyme Neue Typnamen durch Typsynonyme: 1 type Pair a b = (a,b) 2 type Triple a b c = (a,b,c) 3 type OrdList a = [ a] definiert neue
26 Hierarchisch strukturierte Daten
 Algorithmik II Peter Wilke Sommersemester 2005 Teil III Funktionale Programmierung 26 Hierarchisch strukturierte Daten Peter Wilke Algorithmik II Sommersemester 2005 1 Peter Wilke Algorithmik II Sommersemester
Algorithmik II Peter Wilke Sommersemester 2005 Teil III Funktionale Programmierung 26 Hierarchisch strukturierte Daten Peter Wilke Algorithmik II Sommersemester 2005 1 Peter Wilke Algorithmik II Sommersemester
11. Elementare Datenstrukturen
 11. Elementare Datenstrukturen Definition 11.1: Eine dynamische Menge ist gegeben durch eine oder mehrer Mengen von Objekten sowie Operationen auf diesen Mengen und den Objekten der Mengen. Dynamische
11. Elementare Datenstrukturen Definition 11.1: Eine dynamische Menge ist gegeben durch eine oder mehrer Mengen von Objekten sowie Operationen auf diesen Mengen und den Objekten der Mengen. Dynamische
Schwerpunkte. Verkettete Listen. Verkettete Listen: 7. Verkettete Strukturen: Listen. Überblick und Grundprinzip. Vergleich: Arrays verkettete Listen
 Schwerpunkte 7. Verkettete Strukturen: Listen Java-Beispiele: IntList.java List.java Stack1.java Vergleich: Arrays verkettete Listen Listenarten Implementation: - Pascal (C, C++): über Datenstrukturen
Schwerpunkte 7. Verkettete Strukturen: Listen Java-Beispiele: IntList.java List.java Stack1.java Vergleich: Arrays verkettete Listen Listenarten Implementation: - Pascal (C, C++): über Datenstrukturen
Funktionale Programmiersprachen
 Funktionale Programmiersprachen An den Beispielen Haskell und Erlang Übersicht Programmiersprachen λ-kalkül Syntax, Definitionen Besonderheiten von funktionalen Programmiersprache, bzw. Haskell Objektorientierte
Funktionale Programmiersprachen An den Beispielen Haskell und Erlang Übersicht Programmiersprachen λ-kalkül Syntax, Definitionen Besonderheiten von funktionalen Programmiersprache, bzw. Haskell Objektorientierte
Beispiele elementarer Datentypen Ganze Zahlen (integer) Unterbereiche Gleitkommazahlen Festkommazahlen
 Beispiele elementarer Datentypen Ganze Zahlen (integer) - Werte sind ganze Zahlen in vorgegebenen Bereich (z. B. -2 31 bis 2 31-1) - Übliche Operationen: Arithmetik (z. B. +,-,*, Division mit Rest, Rest
Beispiele elementarer Datentypen Ganze Zahlen (integer) - Werte sind ganze Zahlen in vorgegebenen Bereich (z. B. -2 31 bis 2 31-1) - Übliche Operationen: Arithmetik (z. B. +,-,*, Division mit Rest, Rest
Teil IV : Abstrakte Datentypen (ADT)
 Teil IV : Abstrakte Datentypen (ADT) Abstraktion ADT in Modula-2 K. Murmann, H. Neumann, Fakultät für Informatik, Universität Ulm, 2001 1. Abstraktion Rekapitulation Realisation eines Stacks Idee für ADT-Konzept
Teil IV : Abstrakte Datentypen (ADT) Abstraktion ADT in Modula-2 K. Murmann, H. Neumann, Fakultät für Informatik, Universität Ulm, 2001 1. Abstraktion Rekapitulation Realisation eines Stacks Idee für ADT-Konzept
Wiederholung ADT Menge Ziel: Verwaltung (Finden, Einfügen, Entfernen) einer Menge von Elementen
 Was bisher geschah abstrakter Datentyp : Signatur Σ und Axiome Φ z.b. ADT Menge zur Verwaltung (Finden, Einfügen, Entfernen) mehrerer Elemente desselben Typs Spezifikation einer Schnittstelle Konkreter
Was bisher geschah abstrakter Datentyp : Signatur Σ und Axiome Φ z.b. ADT Menge zur Verwaltung (Finden, Einfügen, Entfernen) mehrerer Elemente desselben Typs Spezifikation einer Schnittstelle Konkreter
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 7 (21.5.2014) Binäre Suche, Hashtabellen I Algorithmen und Komplexität Abstrakte Datentypen : Dictionary Dictionary: (auch: Maps, assoziative
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 7 (21.5.2014) Binäre Suche, Hashtabellen I Algorithmen und Komplexität Abstrakte Datentypen : Dictionary Dictionary: (auch: Maps, assoziative
Funktionale Programmierung ALP I. Funktionen höherer Ordnung. Teil 2 SS 2013. Prof. Dr. Margarita Esponda. Prof. Dr.
 ALP I Funktionen höherer Ordnung Teil 2 SS 2013 Funktionen höherer Ordnung Nehmen wir an, wir möchten alle Zahlen innerhalb einer Liste miteinander addieren addall:: (Num a) => [a -> a addall [ = 0 addall
ALP I Funktionen höherer Ordnung Teil 2 SS 2013 Funktionen höherer Ordnung Nehmen wir an, wir möchten alle Zahlen innerhalb einer Liste miteinander addieren addall:: (Num a) => [a -> a addall [ = 0 addall
Haskell, Typen, und Typberechnung. Grundlagen der Programmierung 3 A. Einige andere Programmiersprachen. Typisierung in Haskell
 Haskell, Typen, und Typberechnung Grundlagen der Programmierung 3 A Typen, Typberechnung und Typcheck Prof. Dr. Manfred Schmidt-Schauß Ziele: Haskells Typisierung Typisierungs-Regeln Typ-Berechnung Milners
Haskell, Typen, und Typberechnung Grundlagen der Programmierung 3 A Typen, Typberechnung und Typcheck Prof. Dr. Manfred Schmidt-Schauß Ziele: Haskells Typisierung Typisierungs-Regeln Typ-Berechnung Milners
Crashkurs Haskell Mentoring WiSe 2016/17. Anja Wolffgramm Freie Universität Berlin
 Crashkurs Haskell Mentoring WiSe 2016/17 Anja Wolffgramm Freie Universität Berlin 02/11/2016 , Inhalt Kommandozeile Haskell installieren & starten Ein 1. Haskell-Programm Funktionsdefinition Primitive
Crashkurs Haskell Mentoring WiSe 2016/17 Anja Wolffgramm Freie Universität Berlin 02/11/2016 , Inhalt Kommandozeile Haskell installieren & starten Ein 1. Haskell-Programm Funktionsdefinition Primitive
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Prof. Dr. Hans J. Schneider Lehrstuhl für Programmiersprachen und Programmiermethodik Friedrich-Alexander-Universität Erlangen-Nürnberg Sommersemester 2011 I. Die
Funktionale Programmierung mit Haskell Prof. Dr. Hans J. Schneider Lehrstuhl für Programmiersprachen und Programmiermethodik Friedrich-Alexander-Universität Erlangen-Nürnberg Sommersemester 2011 I. Die
ALP II Dynamische Datenmengen Datenabstraktion (Teil 2)
 ALP II Dynamische Datenmengen Datenabstraktion (Teil 2) O1 O2 O3 O4 SS 2012 Prof. Dr. Margarita Esponda 49 Einfach verkettete Listen O1 O2 O3 50 Einführung Einfach verkettete Listen sind die einfachsten
ALP II Dynamische Datenmengen Datenabstraktion (Teil 2) O1 O2 O3 O4 SS 2012 Prof. Dr. Margarita Esponda 49 Einfach verkettete Listen O1 O2 O3 50 Einführung Einfach verkettete Listen sind die einfachsten
[10] Software Transactional Memory in Haskell, Tortenwurf und Aufgabenblatt 7
![[10] Software Transactional Memory in Haskell, Tortenwurf und Aufgabenblatt 7 [10] Software Transactional Memory in Haskell, Tortenwurf und Aufgabenblatt 7](/thumbs/27/11687557.jpg) Haskell Live [10 Software Transactional Memory in Haskell, Tortenwurf und Aufgabenblatt 7 Bong Min Kim [email protected] Christoph Spörk [email protected] Bernhard Urban [email protected]
Haskell Live [10 Software Transactional Memory in Haskell, Tortenwurf und Aufgabenblatt 7 Bong Min Kim [email protected] Christoph Spörk [email protected] Bernhard Urban [email protected]
Einstieg in die Informatik mit Java
 1 / 34 Einstieg in die Informatik mit Java Klassen mit Instanzmethoden Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 34 1 Definition von Klassen 2 Methoden 3 Methoden
1 / 34 Einstieg in die Informatik mit Java Klassen mit Instanzmethoden Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 34 1 Definition von Klassen 2 Methoden 3 Methoden
WS 2011/2012. Georg Sauthoff 1. October 18, 2011
 in in WS 2011/2012 Georg 1 AG Praktische Informatik October 18, 2011 1 [email protected] Neue Übungsgruppen in neue Übungsgruppen neue Tutoren Sprechstunden in GZI-Arbeitsraum (V2-240)
in in WS 2011/2012 Georg 1 AG Praktische Informatik October 18, 2011 1 [email protected] Neue Übungsgruppen in neue Übungsgruppen neue Tutoren Sprechstunden in GZI-Arbeitsraum (V2-240)
2.5 Listen. Kurzschreibweise: [42; 0; 16] Listen werden mithilfe von [] und :: konstruiert.
![2.5 Listen. Kurzschreibweise: [42; 0; 16] Listen werden mithilfe von [] und :: konstruiert. 2.5 Listen. Kurzschreibweise: [42; 0; 16] Listen werden mithilfe von [] und :: konstruiert.](/thumbs/55/37072779.jpg) 2.5 Listen Listen werden mithilfe von [] und :: konstruiert. Kurzschreibweise: [42; 0; 16] # let mt = [];; val mt : a list = [] # let l1 = 1::mt;; val l1 : int list = [1] # let l = [1;2;3];; val l : int
2.5 Listen Listen werden mithilfe von [] und :: konstruiert. Kurzschreibweise: [42; 0; 16] # let mt = [];; val mt : a list = [] # let l1 = 1::mt;; val l1 : int list = [1] # let l = [1;2;3];; val l : int
Typdeklarationen. Es gibt in Haskell bereits primitive Typen:
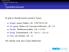 Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
11. Übungsblatt. x y(top(push(x, y)) = y)
 Logik, Berechenbarkeit und Komplexität Sommersemester 2012 Hochschule RheinMain Prof. Dr. Steffen Reith 11. Übungsblatt 1. Ein Keller (engl. stack) ist eine bekannte Datenstruktur. Sei die Signatur S =
Logik, Berechenbarkeit und Komplexität Sommersemester 2012 Hochschule RheinMain Prof. Dr. Steffen Reith 11. Übungsblatt 1. Ein Keller (engl. stack) ist eine bekannte Datenstruktur. Sei die Signatur S =
Assoziative Container in C++ Christian Poulter
 Assoziative Container in C++ Christian Poulter Seminar: Die Sprache C++ Mat-Nr.: 53 03 129 EMail: [email protected] Christian Poulter Assoziative Container in C++ Seite 1/10 Inhalt 1. Einleitung: Container...
Assoziative Container in C++ Christian Poulter Seminar: Die Sprache C++ Mat-Nr.: 53 03 129 EMail: [email protected] Christian Poulter Assoziative Container in C++ Seite 1/10 Inhalt 1. Einleitung: Container...
4. Objektrelationales Typsystem Kollektionstypen. Nested Table
 Nested Table Bei einer Nested Table handelt es sich um eine Tabelle als Attributwert. Im Gegensatz zu Varray gibt es keine Beschränkung bei der Größe. Definition erfolgt auf einem Basistyp, als Basistypen
Nested Table Bei einer Nested Table handelt es sich um eine Tabelle als Attributwert. Im Gegensatz zu Varray gibt es keine Beschränkung bei der Größe. Definition erfolgt auf einem Basistyp, als Basistypen
Verschlüsseln eines Bildes. Visuelle Kryptographie. Verschlüsseln eines Bildes. Verschlüsseln eines Bildes
 Verschlüsseln eines Bildes Visuelle Kryptographie Anwendung von Zufallszahlen Wir wollen ein Bild an Alice und Bob schicken, so dass Alice allein keine Information über das Bild bekommt Bob allein keine
Verschlüsseln eines Bildes Visuelle Kryptographie Anwendung von Zufallszahlen Wir wollen ein Bild an Alice und Bob schicken, so dass Alice allein keine Information über das Bild bekommt Bob allein keine
Programmierung im Grossen
 1 Letzte Aktualisierung: 16. April 2004 Programmierung im Grossen Bertrand Meyer 2 Vorlesung 4: Abstrakte Daten-Typen Übungen 3 Passe die vorhergehende Spezifikation von Stacks (LIFO, Last-In First-Out
1 Letzte Aktualisierung: 16. April 2004 Programmierung im Grossen Bertrand Meyer 2 Vorlesung 4: Abstrakte Daten-Typen Übungen 3 Passe die vorhergehende Spezifikation von Stacks (LIFO, Last-In First-Out
3. Auflage. O Reillys Taschenbibliothek. C# 5.0 kurz & gut. Joseph Albahari & Ben Albahari O REILLY. Aktualisierung von Lars Schulten
 O Reillys Taschenbibliothek 3. Auflage C# 5.0 kurz & gut O REILLY Joseph Albahari & Ben Albahari Aktualisierung von Lars Schulten Inhalt C# 5.0 kurz & gut... 1 Ein erstes C#-Programm... 2 Syntax... 5 Typgrundlagen...
O Reillys Taschenbibliothek 3. Auflage C# 5.0 kurz & gut O REILLY Joseph Albahari & Ben Albahari Aktualisierung von Lars Schulten Inhalt C# 5.0 kurz & gut... 1 Ein erstes C#-Programm... 2 Syntax... 5 Typgrundlagen...
Folge 18 - Vererbung
 Workshop Folge 18 - Vererbung 18.1 Ein einfacher Fall der Vererbung Schritt 1 - Vorbereitungen Besorgen Sie sich - vielleicht aus einer der Übungen der Folge 17 - ein fertiges und lauffähiges Listenprojekt,
Workshop Folge 18 - Vererbung 18.1 Ein einfacher Fall der Vererbung Schritt 1 - Vorbereitungen Besorgen Sie sich - vielleicht aus einer der Übungen der Folge 17 - ein fertiges und lauffähiges Listenprojekt,
Programmieren in Haskell
 Programmieren in Haskell Programmieren mit Listen Programmieren in Haskell 1 Was wir heute machen Eigener Listen-Datentyp Eine Sortierfunktion Nützliche Listenfunktionen Programmieren in Haskell 2 Ein
Programmieren in Haskell Programmieren mit Listen Programmieren in Haskell 1 Was wir heute machen Eigener Listen-Datentyp Eine Sortierfunktion Nützliche Listenfunktionen Programmieren in Haskell 2 Ein
Programmierung und Modellierung
 Programmierung und Modellierung Terme, Suchbäume und Pattern Matching Martin Wirsing in Zusammenarbeit mit Moritz Hammer SS 2009 2 Inhalt Kap. 7 Benutzerdefinierte Datentypen 7. Binärer Suchbaum 8. Anwendung:
Programmierung und Modellierung Terme, Suchbäume und Pattern Matching Martin Wirsing in Zusammenarbeit mit Moritz Hammer SS 2009 2 Inhalt Kap. 7 Benutzerdefinierte Datentypen 7. Binärer Suchbaum 8. Anwendung:
Übungsblatt Programmierung und Software-Entwicklung Generizität, Interfaces, Listen, Sortieralgorithmen & JUnit
 Übungsblatt Programmierung und Software-Entwicklung Generizität, Interfaces, Listen, Sortieralgorithmen & JUnit Aufgabe : Die allgemeine Object-Liste Gegeben sei folgendes UML-Klassendiagramm: MyObjectList
Übungsblatt Programmierung und Software-Entwicklung Generizität, Interfaces, Listen, Sortieralgorithmen & JUnit Aufgabe : Die allgemeine Object-Liste Gegeben sei folgendes UML-Klassendiagramm: MyObjectList
Programmieren in Haskell
 Programmieren in Haskell Programmieren mit Listen Programmieren in Haskell 1 Was wir heute machen Eigener Listen-Datentyp Eine Sortierfunktion Nützliche Listenfunktionen Programmieren in Haskell 2 Ein
Programmieren in Haskell Programmieren mit Listen Programmieren in Haskell 1 Was wir heute machen Eigener Listen-Datentyp Eine Sortierfunktion Nützliche Listenfunktionen Programmieren in Haskell 2 Ein
Übungsaufgaben: 1. Objektorientierte Programmierung - Teil 1
 Übungsaufgaben: 1. Objektorientierte Programmierung - Teil 1 1. Das Objekt Bruch mit einem Standardkonstruktor (initialisieren mit 0), einem allgemeinen Konstruktor (Zähler und Nenner können beliebig vorgegeben
Übungsaufgaben: 1. Objektorientierte Programmierung - Teil 1 1. Das Objekt Bruch mit einem Standardkonstruktor (initialisieren mit 0), einem allgemeinen Konstruktor (Zähler und Nenner können beliebig vorgegeben
Programmieren in Haskell Felder (Arrays)
 Programmieren in Haskell Felder (Arrays) Peter Steffen Universität Bielefeld Technische Fakultät 05.12.2008 1 Programmieren in Haskell Quadratzahlen 0 1 2 3 n 0 1 4 9 n 2 squareslist :: Integral a => [a]
Programmieren in Haskell Felder (Arrays) Peter Steffen Universität Bielefeld Technische Fakultät 05.12.2008 1 Programmieren in Haskell Quadratzahlen 0 1 2 3 n 0 1 4 9 n 2 squareslist :: Integral a => [a]
Haskell in der Schule - (K)ein Thema? Ralf Dorn - Dennis Buchmann - Felix Last - Carl Ambroselli
 Haskell in der Schule - (K)ein Thema? Haskell in der Schule Otto-Nagel-Gymnasium in Berlin-Biesdorf Hochbegabtenförderung und MacBook-Schule Leistungskurse seit 2005 Rahmenplanvorgaben Berlin:... deklarative
Haskell in der Schule - (K)ein Thema? Haskell in der Schule Otto-Nagel-Gymnasium in Berlin-Biesdorf Hochbegabtenförderung und MacBook-Schule Leistungskurse seit 2005 Rahmenplanvorgaben Berlin:... deklarative
Einführung in die Informatik: Programmierung und Software-Entwicklung, WS 12/13. Kapitel 3. Grunddatentypen, Ausdrücke und Variable
 1 Kapitel 3 Grunddatentypen, Ausdrücke und Variable 2 Eine Datenstruktur besteht aus Grunddatentypen in Java einer Menge von Daten (Werten) charakteristischen Operationen Datenstrukturen werden mit einem
1 Kapitel 3 Grunddatentypen, Ausdrücke und Variable 2 Eine Datenstruktur besteht aus Grunddatentypen in Java einer Menge von Daten (Werten) charakteristischen Operationen Datenstrukturen werden mit einem
Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T:
 Binäre Bäume Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T: BinTree [T: TYPE]: DATATYPE empty: empty? node (key: T, left:bibtree, right:bibtree):
Binäre Bäume Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T: BinTree [T: TYPE]: DATATYPE empty: empty? node (key: T, left:bibtree, right:bibtree):
Strukturelle Rekursion und Induktion
 Kapitel 2 Strukturelle Rekursion und Induktion Rekursion ist eine konstruktive Technik für die Beschreibung unendlicher Mengen (und damit insbesondere für die Beschreibung unendliche Funktionen). Induktion
Kapitel 2 Strukturelle Rekursion und Induktion Rekursion ist eine konstruktive Technik für die Beschreibung unendlicher Mengen (und damit insbesondere für die Beschreibung unendliche Funktionen). Induktion
Was bisher geschah Funktionale Programmierung in Haskell: Algebraische Datentypen Pattern Matching Polymorphie Typklassen Rekursive Datentypen:
 Was bisher geschah Funktionale Programmierung in Haskell: Algebraische Datentypen Pattern Matching Polymorphie Typklassen Rekursive Datentypen: Peano-Zahlen, Listen, Bäume Rekursive Funktionen strukturelle
Was bisher geschah Funktionale Programmierung in Haskell: Algebraische Datentypen Pattern Matching Polymorphie Typklassen Rekursive Datentypen: Peano-Zahlen, Listen, Bäume Rekursive Funktionen strukturelle
7down Zusatzaufgaben. Mathias Ziebarth und Joachim Breitner. 13. März 2008
 7down Zusatzaufgaben Mathias Ziebarth und Joachim Breitner 13. März 2008 1 Problem 1 Unser Programm hat folgende Lösungen berechnet: Testfall 1 153131 141441 973493 330529 869017 876927 Testfall 2 279841
7down Zusatzaufgaben Mathias Ziebarth und Joachim Breitner 13. März 2008 1 Problem 1 Unser Programm hat folgende Lösungen berechnet: Testfall 1 153131 141441 973493 330529 869017 876927 Testfall 2 279841
Standard.lib. Inhalt. WAGO-I/O-PRO 32 Bibliothek
 Anhang A Weitere Bibliotheken WAGO-I/O-PRO 32 Bibliothek Standard.lib Inhalt ASCIIBYTE_TO_STRING...3 REAL_STATE...4 STANDARD_VERSION...6 STRING_COMPARE...7 STRING_TO_ASCIIBYTE...8 WAGO-I/O-PRO 32 Standard.lib
Anhang A Weitere Bibliotheken WAGO-I/O-PRO 32 Bibliothek Standard.lib Inhalt ASCIIBYTE_TO_STRING...3 REAL_STATE...4 STANDARD_VERSION...6 STRING_COMPARE...7 STRING_TO_ASCIIBYTE...8 WAGO-I/O-PRO 32 Standard.lib
C++ Teil 5. Sven Groß. 13. Mai Sven Groß (IGPM, RWTH Aachen) C++ Teil Mai / 18
 C++ Teil 5 Sven Groß 13. Mai 2016 Sven Groß (IGPM, RWTH Aachen) C++ Teil 5 13. Mai 2016 1 / 18 Themen der letzten Vorlesung Funktionen Funktionsüberladung, Signatur Rekursion const-deklaration Referenzen
C++ Teil 5 Sven Groß 13. Mai 2016 Sven Groß (IGPM, RWTH Aachen) C++ Teil 5 13. Mai 2016 1 / 18 Themen der letzten Vorlesung Funktionen Funktionsüberladung, Signatur Rekursion const-deklaration Referenzen
Nachname: Vorname: Matr.-Nr.: Punkte: 1. Aufgabe: ( / 25 Pkt.) Gegeben ist das folgende Struktogramm zur Berechnung von sin(x) mit Hilfe einer Reihe.
 Hiermit bestätige ich, dass ich die Übungsleistungen als Voraussetzung für diese Klausur in folgender Übung erfüllt habe. Jahr: Übungsleiter: Unterschrift: 1. Aufgabe: ( / 25 Pkt.) Gegeben ist das folgende
Hiermit bestätige ich, dass ich die Übungsleistungen als Voraussetzung für diese Klausur in folgender Übung erfüllt habe. Jahr: Übungsleiter: Unterschrift: 1. Aufgabe: ( / 25 Pkt.) Gegeben ist das folgende
Funktionale Programmierung
 Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
C# - Einführung in die Programmiersprache Arrays, Enumeration und Collections. Leibniz Universität IT Services Anja Aue
 C# - Einführung in die Programmiersprache Arrays, Enumeration und Collections Leibniz Universität IT Services Anja Aue Arrays... speichern mehrere Werte vom gleichen Datentyp. fassen zusammenhängende Werte
C# - Einführung in die Programmiersprache Arrays, Enumeration und Collections Leibniz Universität IT Services Anja Aue Arrays... speichern mehrere Werte vom gleichen Datentyp. fassen zusammenhängende Werte
Übung: Algorithmen und Datenstrukturen SS 2007
 Übung: Algorithmen und Datenstrukturen SS 2007 Prof. Lengauer Sven Apel, Michael Claÿen, Christoph Zengler, Christof König Blatt 4 Votierung in der Woche vom 21.05.0725.05.07 Aufgabe 9 Waggons rangieren
Übung: Algorithmen und Datenstrukturen SS 2007 Prof. Lengauer Sven Apel, Michael Claÿen, Christoph Zengler, Christof König Blatt 4 Votierung in der Woche vom 21.05.0725.05.07 Aufgabe 9 Waggons rangieren
Praktische Informatik 3: Funktionale Programmierung Vorlesung 3 vom : Algebraische Datentypen
 16:01:59 2017-01-17 1 [35] Praktische Informatik 3: Funktionale Programmierung Vorlesung 3 vom 01.11.2016: Algebraische Datentypen Christoph Lüth Universität Bremen Wintersemester 2016/17 PI3 WS 16/17
16:01:59 2017-01-17 1 [35] Praktische Informatik 3: Funktionale Programmierung Vorlesung 3 vom 01.11.2016: Algebraische Datentypen Christoph Lüth Universität Bremen Wintersemester 2016/17 PI3 WS 16/17
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2009 5. April 2009 Vorteile bei der Verwendung höherer Programmiersprachen Vorteile bei der Verwendung höherer Programmiersprachen 1. Einfache Notation
Programmiersprachen und Übersetzer Sommersemester 2009 5. April 2009 Vorteile bei der Verwendung höherer Programmiersprachen Vorteile bei der Verwendung höherer Programmiersprachen 1. Einfache Notation
Einführung in die Informatik: Programmierung und Software-Entwicklung, WS 11/12 1. Kapitel 11. Listen. Listen
 Einführung in die Informatik: Programmierung und Software-Entwicklung, WS 11/12 1 Kapitel 11 Einführung in die Informatik: Programmierung und Software-Entwicklung, WS 11/12 2 Ziele Implementierungen für
Einführung in die Informatik: Programmierung und Software-Entwicklung, WS 11/12 1 Kapitel 11 Einführung in die Informatik: Programmierung und Software-Entwicklung, WS 11/12 2 Ziele Implementierungen für
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens [email protected] Überblick Grundlagen Definitionen Eigene Entwicklungen Datenstrukturen Elementare Datentypen Abstrakte Datentypen Elementare
Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens [email protected] Überblick Grundlagen Definitionen Eigene Entwicklungen Datenstrukturen Elementare Datentypen Abstrakte Datentypen Elementare
Funktionale Programmierung. ALP I Lambda-Kalkül. Teil IVb WS 2012/2013. Prof. Dr. Margarita Esponda. Prof. Dr. Margarita Esponda
 ALP I Lambda-Kalkül Teil IVb WS 2012/2013 λ-kalkül-parser Hilfsfunktionen: Die break-funktion ist eine Funktion höherer Ordnung, die eine Liste beim ersten Vorkommen einer Bedingung in zwei Listen spaltet.
ALP I Lambda-Kalkül Teil IVb WS 2012/2013 λ-kalkül-parser Hilfsfunktionen: Die break-funktion ist eine Funktion höherer Ordnung, die eine Liste beim ersten Vorkommen einer Bedingung in zwei Listen spaltet.
Kapitel 3: Variablen
 Kapitel 3: Variablen Thema: Programmieren Seite: 1 Kapitel 3: Variablen Im letzten Kapitel haben wir gelernt, bestimmte Ereignisse zu wiederholen solange eine Bedingung erfüllt ist. Nun möchten wir aber
Kapitel 3: Variablen Thema: Programmieren Seite: 1 Kapitel 3: Variablen Im letzten Kapitel haben wir gelernt, bestimmte Ereignisse zu wiederholen solange eine Bedingung erfüllt ist. Nun möchten wir aber
Praktische Informatik 3: Einführung in die Funktionale Programmierung Vorlesung vom 10.11.2010: Rekursive Datentypen
 Rev. 1152 1 [23] Praktische Informatik 3: Einführung in die Funktionale Programmierung Vorlesung vom 10.11.2010: Rekursive Datentypen Christoph Lüth & Dennis Walter Universität Bremen Wintersemester 2010/11
Rev. 1152 1 [23] Praktische Informatik 3: Einführung in die Funktionale Programmierung Vorlesung vom 10.11.2010: Rekursive Datentypen Christoph Lüth & Dennis Walter Universität Bremen Wintersemester 2010/11
Informatik 11 Kapitel 2 - Rekursive Datenstrukturen
 Fachschaft Informatik Informatik 11 Kapitel 2 - Rekursive Datenstrukturen Michael Steinhuber König-Karlmann-Gymnasium Altötting 15. Januar 2016 Folie 1/77 Inhaltsverzeichnis I 1 Datenstruktur Schlange
Fachschaft Informatik Informatik 11 Kapitel 2 - Rekursive Datenstrukturen Michael Steinhuber König-Karlmann-Gymnasium Altötting 15. Januar 2016 Folie 1/77 Inhaltsverzeichnis I 1 Datenstruktur Schlange
BTree.dll - Balancierte und verkettete Bäume. Ecofor. BTree.dll. Realisiert mit Microsoft Visual Studio 16.04.2015 1/9
 BTree.dll Realisiert mit Microsoft Visual Studio 16.04.2015 1/9 INHALT 1. Allgemein... 3 2. Class BTree1 (balanciert)... 3 3. Class BTree2 (balanciert und verkettet)... 4 4. Beschreibung BTree1 und BTree2...
BTree.dll Realisiert mit Microsoft Visual Studio 16.04.2015 1/9 INHALT 1. Allgemein... 3 2. Class BTree1 (balanciert)... 3 3. Class BTree2 (balanciert und verkettet)... 4 4. Beschreibung BTree1 und BTree2...
Binärbäume: Beispiel
 Binärbäume Als Beispiel für eine interessantere dynamische Datenstruktur sehen wir uns jetzt Binärbäume an Ein Binärbaum wird rekursiv definiert: Er ist leer oder besteht aus einem Knoten (die Wurzel des
Binärbäume Als Beispiel für eine interessantere dynamische Datenstruktur sehen wir uns jetzt Binärbäume an Ein Binärbaum wird rekursiv definiert: Er ist leer oder besteht aus einem Knoten (die Wurzel des
1 Abstrakte Klassen, finale Klassen und Interfaces
 1 Abstrakte Klassen, finale Klassen und Interfaces Eine abstrakte Objekt-Methode ist eine Methode, für die keine Implementierung bereit gestellt wird. Eine Klasse, die abstrakte Objekt-Methoden enthält,
1 Abstrakte Klassen, finale Klassen und Interfaces Eine abstrakte Objekt-Methode ist eine Methode, für die keine Implementierung bereit gestellt wird. Eine Klasse, die abstrakte Objekt-Methoden enthält,
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 22: Mima-X Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Grundbegriffe der Informatik Kapitel 22: Mima-X Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
CGI Programmierung mit Ha. Markus Schwarz
 CGI Programmierung mit Ha Markus Schwarz Überblick Was ist funktionale Programmierung Einführung in Haskell CGI-Programmierung mit Haskell Ein etwas größeres Beispiel Was ist funktionale Programm Ein Programm
CGI Programmierung mit Ha Markus Schwarz Überblick Was ist funktionale Programmierung Einführung in Haskell CGI-Programmierung mit Haskell Ein etwas größeres Beispiel Was ist funktionale Programm Ein Programm
Schnittstellen, Stack und Queue
 Schnittstellen, Stack und Queue Schnittstelle Stack Realisierungen des Stacks Anwendungen von Stacks Schnittstelle Queue Realisierungen der Queue Anwendungen von Queues Hinweise zum Üben Anmerkung: In
Schnittstellen, Stack und Queue Schnittstelle Stack Realisierungen des Stacks Anwendungen von Stacks Schnittstelle Queue Realisierungen der Queue Anwendungen von Queues Hinweise zum Üben Anmerkung: In
1. Typen und Literale (6 Punkte) 2. Zuweisungen (6 = Punkte)
 Praktische Informatik (Software) Vorlesung Softwareentwicklung 1 Prof. Dr. A. Ferscha Hauptklausur am 01. 02. 2001 Zuname Vorname Matr. Nr. Stud. Kennz. Sitzplatz HS / / / Punkte Note korr. Fügen Sie fehlende
Praktische Informatik (Software) Vorlesung Softwareentwicklung 1 Prof. Dr. A. Ferscha Hauptklausur am 01. 02. 2001 Zuname Vorname Matr. Nr. Stud. Kennz. Sitzplatz HS / / / Punkte Note korr. Fügen Sie fehlende
ALP I. Funktionale Programmierung
 ALP I Funktionale Programmierung Sortieren und Suchen (Teil 1) WS 2012/2013 Suchen 8 False unsortiert 21 4 16 7 19 11 12 7 1 5 27 3 8 False sortiert 2 4 6 7 9 11 12 18 21 24 27 36 Suchen in unsortierten
ALP I Funktionale Programmierung Sortieren und Suchen (Teil 1) WS 2012/2013 Suchen 8 False unsortiert 21 4 16 7 19 11 12 7 1 5 27 3 8 False sortiert 2 4 6 7 9 11 12 18 21 24 27 36 Suchen in unsortierten
Generische Record-Kombinatoren mit statischer Typprüfung
 System Generische mit statischer Typprüfung Brandenburgische Technische Universität Cottbus Lehrstuhl Programmiersprachen und Compilerbau Lehrstuhlkolloquium am 13. Januar 2010 Überblick System System
System Generische mit statischer Typprüfung Brandenburgische Technische Universität Cottbus Lehrstuhl Programmiersprachen und Compilerbau Lehrstuhlkolloquium am 13. Januar 2010 Überblick System System
Vererbung & Schnittstellen in C#
 Vererbung & Schnittstellen in C# Inhaltsübersicht - Vorüberlegung - Vererbung - Schnittstellenklassen - Zusammenfassung 1 Vorüberlegung Wozu benötigt man Vererbung überhaubt? 1.Um Zeit zu sparen! Verwendung
Vererbung & Schnittstellen in C# Inhaltsübersicht - Vorüberlegung - Vererbung - Schnittstellenklassen - Zusammenfassung 1 Vorüberlegung Wozu benötigt man Vererbung überhaubt? 1.Um Zeit zu sparen! Verwendung
Inhaltsverzeichnis. Einführende Bemerkungen 11. Das Fach Informatik 11 Zielsetzung der Vorlesung Grundbegriffe
 Inhaltsverzeichnis Einführende Bemerkungen 11 Das Fach Informatik 11 Zielsetzung der Vorlesung 12 1. Grundbegriffe 1 3 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Information und Nachricht 1.1.1 Information 1.1.2 Nachricht
Inhaltsverzeichnis Einführende Bemerkungen 11 Das Fach Informatik 11 Zielsetzung der Vorlesung 12 1. Grundbegriffe 1 3 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Information und Nachricht 1.1.1 Information 1.1.2 Nachricht
Funktionale Programmierung mit Haskell. Jan Hermanns
 Funktionale Programmierung mit Haskell Jan Hermanns 1 Programmiersprachen imperativ deklarativ konventionell OO logisch funktional Fortran Smalltalk Prolog Lisp C Eiffel ML Pascal Java Haskell 2 von Neumann
Funktionale Programmierung mit Haskell Jan Hermanns 1 Programmiersprachen imperativ deklarativ konventionell OO logisch funktional Fortran Smalltalk Prolog Lisp C Eiffel ML Pascal Java Haskell 2 von Neumann
Einstieg in die Informatik mit Java
 1 / 25 Einstieg in die Informatik mit Java Objektorientierte Programmierung und Klassen Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 25 1 Die Philosophie 2 Definition
1 / 25 Einstieg in die Informatik mit Java Objektorientierte Programmierung und Klassen Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 25 1 Die Philosophie 2 Definition
Einstieg in die Informatik mit Java
 1 / 22 Einstieg in die Informatik mit Java Generics Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 22 1 Überblick Generics 2 Generische Klassen 3 Generische Methoden 4
1 / 22 Einstieg in die Informatik mit Java Generics Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 22 1 Überblick Generics 2 Generische Klassen 3 Generische Methoden 4
Tutoraufgabe 1 (Datenstrukturen in Haskell):
 Prof. aa Dr. J. Giesl Programmierung WS12/13 M. Brockschmidt, F. Emmes, C. Otto, T. Ströder Allgemeine Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus der gleichen Kleingruppenübung (Tutorium)
Prof. aa Dr. J. Giesl Programmierung WS12/13 M. Brockschmidt, F. Emmes, C. Otto, T. Ströder Allgemeine Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus der gleichen Kleingruppenübung (Tutorium)
Verkettete Datenstrukturen: Bäume
 Verkettete Datenstrukturen: Bäume 1 Graphen Gerichteter Graph: Menge von Knoten (= Elementen) + Menge von Kanten. Kante: Verbindung zwischen zwei Knoten k 1 k 2 = Paar von Knoten (k 1, k 2 ). Menge aller
Verkettete Datenstrukturen: Bäume 1 Graphen Gerichteter Graph: Menge von Knoten (= Elementen) + Menge von Kanten. Kante: Verbindung zwischen zwei Knoten k 1 k 2 = Paar von Knoten (k 1, k 2 ). Menge aller
