Funktionale Programmierung mit Haskell
|
|
|
- Angela Kaufer
- vor 10 Jahren
- Abrufe
Transkript
1 Funktionale Programmierung mit Haskell Prof. Dr. Hans J. Schneider Lehrstuhl für Programmiersprachen und Programmiermethodik Friedrich-Alexander-Universität Erlangen-Nürnberg Sommersemester 2011 I. Die Sprache Haskell II. Fallstudien 8. Suchbäume und beliebige Graphen 9. Lambda-Interpretierer 10. Syntaxanalyse 11. Algebraische Spezifikation 12. Semantik operationeller Sprachen 13. Kategorien in Haskell 14. Compilieren funktionaler Programme c Hans J. Schneider 2011
2 Chomsky-Grammatik Definition: Eine Chomsky-Grammatik ist ein Quadrupel G = (T, N, P, S) mit T, N (endliche, disjunkte) Alphabete terminale und nichtterminale Symbole S N Startsymbol P endliche Teilmenge von V NV V, wobei V = T N ist. Produktionen Definition: Eine kontextfreie Grammatik ist eine Chomsky-Grammatik mit P N V Beispiel (BNF-Schreibweise) E ::= E + T E T T T ::= T F T/F F F ::= v n ( E ) Funktionale Programmierung mit Haskell 10.1
3 Direkte Ableitbarkeit Sei p = (u, v) P x p y : ( w, z V )(x = wuz y = wvz) Sei G = (T, N, P, S) x y : ( p P )(x G p y) Wenn keine Verwechslung möglich: x y statt x G y Beispiel: E E + T T + T T + T F v + T F... E E + T E + T F T + T F v + T F... Funktionale Programmierung mit Haskell 10.2
4 Ableitbarkeit Definition der Ableitbarkeit: x y : ( n 0)( w 0, w 1,..., w n V ) (w 0 = x ( 1 i n)(w i 1 w i ) w n = y) Andere Schreibweisen: Feste Anzahl von Schritten: In der Literatur auch: = n Menge der erzeugten Zeichenreihen: L(G) := {w S G w w T } Funktionale Programmierung mit Haskell 10.3
5 Ableitungsbaum Ableitungsbaum = Graphische Darstellung einer Ableitung bei kontextfreien Grammatiken E E + T T T F p 1 p 3 p 4 p 6 p 6 p 7 F F v p 7 p 8 v n Zusammenhang: Wurzel = Startsymbol Innere Knoten = Nichtterminale Symbole Blätter = Terminale Symbole Verkettung der Blätter = abgeleitete Zeichenreihe Funktionale Programmierung mit Haskell 10.4
6 Kontextfreie Grammatik in Haskell: Symbole Wir unterscheiden die terminalen und die nichtterminalen Symbole: data Symbol a b = T a N b deriving (Eq,Ord,Read) Wir können unterschiedliche Symbolvorräte wählen: Symbol Char Char verwendet sowohl für terminale als auch für nichtterminale Symbole Einzelzeichen. Symbol Char String verwendet für nichtterminale Symbole Zeichenketten. Bei der Ausgabe sollen die Konstruktoren entfallen: instance (Show a, Show b) => Show (Symbol a b) where show (T x) = show x show (N x) = show x Abfrage: nonterm :: Symbol a b -> Bool nonterm (T _) = False nonterm _ = True Funktionale Programmierung mit Haskell 10.5
7 Kontextfreie Produktionen in Haskell Produktionen: data Prod a b = Prod (Symbol a b) [Symbol a b] deriving Eq Aufteilung in linke und rechte Seite: lhs :: Prod a b -> (Symbol a b) lhs (Prod x ys) = x rhs :: Prod a b -> [Symbol a b] rhs (Prod x ys) = ys Drucken von Produktionen: instance (Show a, Show b) => Show (Prod a b) where show (Prod y zs) = show y ++ " ==> " ++ show zs Beispiel: Grammar> rhs prod1 ["expr", +,"expr"] Grammar> prod1 "expr" ==> "expr" + "expr" Funktionale Programmierung mit Haskell 10.6
8 Kontextfreie Grammatik in Haskell Man kann Grammatiken auf unterschiedliche Weise implementieren. Also ist es sinnvoll, eine Typklasse zu definieren: class Grammar grammar where startsymbol :: grammar a b -> Symbol a b prettyprintgrammar :: (Show a, Show b) => grammar a b -> IO () Einfache Implementierung: Grammatik als Liste von Produktionen: data ProdList a b = ProdList [Prod a b] Vereinfachung: Startsymbol = linke Seite der ersten Produktion instance Grammar ProdList where startsymbol (ProdList[]) = error "empty grammar" startsymbol (ProdList (r:rs)) = lhs r prettyprintgrammar g = putstr (prtgram g) where prtgram (ProdList []) = "" prtgram (ProdList (r:rs)) = (show r) ++ "\n" ++ (prtgram (ProdList rs)) Funktionale Programmierung mit Haskell 10.7
9 Kontextfreie Grammatik: Beispiel Einfaches Beispiel: grammar2 :: ProdList Char String grammar2 = ProdList [ Prod (N "expr") [N "expr", T +, N "term"], Prod (N "expr") [N "term"], Prod (N "term") [N "term", T *, N "fact"], Prod (N "term") [N "fact"], Prod (N "fact") [T n ], Prod (N "fact") [T v ], Prod (N "fact") [T (, N "expr", T ) ] ] Funktionale Programmierung mit Haskell 10.8
10 Bottom-Up-Aufbau von Bäumen Beispiel: T F = T T F F v F v n n Zusammenfassen von Bäumen mittels einer Produktion: reduce :: (Eq a, Eq b) => (Prod a b, [h (Symbol a b)]) -> h (Symbol a b) reduce((prod lhs rhs), subtrees) = if map root subtrees == rhs then ArbNode(lhs, subtrees) else error "production not applicable" StandArbTree wird Instanz von DerivTree. Funktionale Programmierung mit Haskell 10.9
11 Top-Down-Entwicklung von Bäumen Beispiel: E T E + T E T E + T T F Welches T ist gemäß der Produktion T T F zu ersetzen? Dewey-Indizierung: [] [1] [2] [1, 1] [3] [3, 1] [3, 2] [3, 3] Funktionale Programmierung mit Haskell 10.10
12 Expandieren an einer bestimmten Stelle Typdefinition: type DeweyIndex = [Int] expand :: (Eq a, Eq b) => (h (Symbol a b), DeweyIndex, Prod a b) -> h (Symbol a b) Implementieren der Expandierung: expand(t, [], (Prod lhs rhs)) = if (root t) == lhs then ArbNode(lhs, map newleaf rhs) else error "Production not applicable" expand(t, i:d, p) = if i > length (successors t) i < 1 then error "Wrong Dewey index" else ArbNode(root t, replace (successors t, i, p)) where replace(ti:r, 1, p) = expand(ti, d, p) : r replace(f:r, i, p) = f: replace(r, i-1, p) Funktionale Programmierung mit Haskell 10.11
13 Finden eines bestimmten Blattes findleftmost :: (Eq a, Eq b) => Symbol a b -> h (Symbol a b) -> DeweyIndex findleftmost x t = if found then d else error "Element not found" where (found, d) = find(x, t) find(x, t) = if (height t ) == 0 then (False, []) {- 2. Komponente ohne Bedeutung -} else if (height t ) == 1 then if (root t) == x then (True, []) else (False, []) else helper(x, successors t, 1) helper(x, [], i) = (False, []) helper(x, f:st, i) = if foundinthis then (True, i:d ) else helper(x, st, i+1) where (foundinthis, d ) = find(x, f) Funktionale Programmierung mit Haskell 10.12
14 Erzeugen einer Linksableitung Setze die Produktion soweit links wie möglich ein: expandleftmost(t, p) = expand(t, findleftmost x t, p) where x = lhs p Beispiele: t0 = starttree grammar2 t1 = expandleftmost(t0, Prod (N "expr") [N "expr", T +, N "term"]) Grammar> t0 ("expr") Grammar> t1 ("expr" ("expr") ( + ) ("term")) Grammar> expandleftmost(t1, Prod (N "expr") [N "expr", T +, N "term"]) ("expr" ("expr" ("expr") ( + ) ("term")) ( + ) ("term")) Funktionale Programmierung mit Haskell 10.13
15 Klasse der Ableitungsbäume class (Tree h) => DerivTree h where starttree :: Grammar a b -> h (Symbol a b) termnode :: Symbol a b -> h (Symbol a b) reduce :: (Eq a, Eq b) => (Prod a b, [h (Symbol a b)]) -> h (Symbol a b) expand :: (Eq a, Eq b) => (h (Symbol a b), DeweyIndex, Prod a b) -> h (Symbol a b) findleftmost :: (Eq a, Eq b) => Symbol a b -> h (Symbol a b) -> DeweyIndex expandleftmost :: (Eq a, Eq b) => (h (Symbol a b), Prod a b) -> h (Symbol a b) instance DerivTree StandArbTree where starttree g = ArbNode(startSymbol g, []) termnode (T c) = ArbNode(T c, []) termnode (N _) = error "termnode needs terminal symbol"... Funktionale Programmierung mit Haskell 10.14
16 Cocke-Kasami-Younger: Definitionen Chomsky-Normalform: Alle Produktionen sind von der Form: A ::= B C a Syntaxanalyse nach Cocke, Kasami und Younger: Gegeben: w = t 1 t 2... t n Zentrale Datenstruktur: Matrix m ij ( 0 i < j n)(m ij = {A A N A t i+1... t j }) w L(G) S m 0n Effektive Konstruktion der m ij : m i,i+1 := {A A ::= t i+1 } m ij := {A ( i < k < j)( B m ik )( C m kj )(A ::= BC)} Funktionale Programmierung mit Haskell 10.15
17 Cocke-Kasami-Younger: Rechenschema t 1 t 2 t n 0 1 m 0n n Funktionale Programmierung mit Haskell 10.16
18 Beispielgrammatik Übliche Formulierung (BNF): S ::= AB BB A ::= CC AB a B ::= BB CA b C ::= BA AA b Beispiel eines Wortes mit mehreren Ableitungen: A a S B B B A A S B B b b b a b Funktionale Programmierung mit Haskell 10.17
19 Beispielgrammatik in Haskell Wir speichern zur Vereinfachung die Grammatik als Liste der Produktionen: data Prod a b = Prod (Symbol a b) [Symbol a b] deriving Eq Haskell-Formulierung des Beispiels: g2 = ProdList [ Prod (N S ) [N A, N B ], Prod (N S ) [N B, N B ], Prod (N A ) [N C, N C ], Prod (N A ) [N A, N B ], Prod (N A ) [T a ], Prod (N B ) [N B, N B ], Prod (N B ) [N C, N A ], Prod (N B ) [T b ], Prod (N C ) [N B, N A ], Prod (N C ) [N A, N A ], Prod (N C ) [T b ] ] Funktionale Programmierung mit Haskell 10.18
20 Kern des CKY-Algorithmus Effektive Konstruktion der m ij : m i,i+1 := {A A ::= t i+1 } m ij := {A ( i < k < j)( B m ik )( C m kj )(A ::= BC)} Implementierung der effektiven Konstruktion: cky(i,j) = if j == i+1 then [a (Prod a [T b]) <- listofprods, b == word!! i ] else concat [ [a (Prod a [b,c]) <- listofprods, elem b (cky(i,k)) && elem c (cky(k,j)) ] k <- [i+1.. j-1] ] where (ProdList listofprods) = grammar Ein Feld kann ein Element mehrfach enthalten. Funktionale Programmierung mit Haskell 10.19
21 CKY-Algorithmus in Haskell Top-Level-Funktion im Modul CKYParsing: ckyisword grammar word = elem (startsymbol grammar) (cky(0, length word)) where cky(i,j) =... Beispiel: CKYParsing> ckyisword g2 "abb" True Kann man den CKY-Kern so ändern, dass alle Bäume ausgegeben werden? Funktionale Programmierung mit Haskell 10.20
22 CKY mit Bäumen Wir speichern in jedem Feld der Matrix alle Teilbäume mit der Eigenschaft ( 0 i < j n)(m ij = {A A N A t i+1... t j }) cky(i,j) = if j == i+1 then [ArbNode(a, [termnode (T b)]) (Prod a [T b]) <- listofprods, b == word!! i ] else concat [ [reduce (Prod a [b,c], [t1, t2]) t1 <- cky(i,k), t2 <- cky(k,j), (Prod a [b,c]) <- listofprods, b == root t1 && c == root t2 ] k <- [i+1.. j-1] ] where (ProdList listofprods) = grammar Funktionale Programmierung mit Haskell 10.21
23 CKY mit Bäumen (II) Die Analysefunktion muss die Bäume aus m 0n heraussuchen, die mit dem Startsymbol beginnen. ckytrees grammar word = if length(result) == 0 then error "Word not derivable" else result where result = validtrees (cky(0, length(word))) Bemerkungen: validtrees [] = [] validtrees (h:t) = if (root h) == (startsymbol grammar) then h : (validtrees t) else validtrees t cky(i,j) =... cky ist lokal definiert und kann daher in beiden Algorithmen verwandt werden. Benutze bei validtrees die filter-funktion! Die Lösung ist sehr ineffizient. Funktionale Programmierung mit Haskell 10.22
24 Ausdrucken aller Ableitungsbäume Erzeugung von Leerzeilen zwischen den Bäumen: printckytrees grammar word = putstr(printdertrees (ckytrees grammar word)) where -- printdertrees :: [StandArbTree Char] -> String printdertrees [] = "\n" printdertrees [t] = show t ++ "\n" printdertrees (t1:rest) = (show t1) ++ "\n\n" ++ (printdertrees rest) Beispiel einer (mehrdeutigen) Analyse: CKYParsing> printckytrees g2 "abb" ( S ( A ( a )) ( B ( B ( b )) ( B ( b )))) ( S ( A ( A ( a )) ( B ( b ))) ( B ( b ))) Funktionale Programmierung mit Haskell 10.23
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
2.11 Kontextfreie Grammatiken und Parsebäume
 2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Prof. Dr. Hans J. Schneider Lehrstuhl für Programmiersprachen und Programmiermethodik Friedrich-Alexander-Universität Erlangen-Nürnberg Sommersemester 2011 I. Die
Funktionale Programmierung mit Haskell Prof. Dr. Hans J. Schneider Lehrstuhl für Programmiersprachen und Programmiermethodik Friedrich-Alexander-Universität Erlangen-Nürnberg Sommersemester 2011 I. Die
Kapitel 2: Formale Sprachen Kontextfreie Sprachen. reguläre Grammatiken/Sprachen. kontextfreie Grammatiken/Sprachen
 reguläre Grammatiken/prachen Beschreibung für Bezeichner in Programmiersprachen Beschreibung für wild cards in kriptsprachen (/* reguläre Ausdrücke */)?; [a-z]; * kontextfreie Grammatiken/prachen Beschreibung
reguläre Grammatiken/prachen Beschreibung für Bezeichner in Programmiersprachen Beschreibung für wild cards in kriptsprachen (/* reguläre Ausdrücke */)?; [a-z]; * kontextfreie Grammatiken/prachen Beschreibung
Theorie der Informatik
 Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theoretische Informatik I
 Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen 19
 Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Formale Sprachen und Grammatiken
 Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
t r Lineare Codierung von Binärbbäumen (Wörter über dem Alphabet {, }) Beispiel code( ) = code(, t l, t r ) = code(t l ) code(t r )
 Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
1. Formale Sprachen 1.2 Grammatiken formaler Sprachen
 1. Formale Sprachen 1.2 Grammatiken formaler Sprachen Die Regeln zur Bildung korrekter Wörter einer Sprache kann man in einer natürlichen Sprache formulieren. Da dies jedoch wieder Mehrdeutigkeiten mit
1. Formale Sprachen 1.2 Grammatiken formaler Sprachen Die Regeln zur Bildung korrekter Wörter einer Sprache kann man in einer natürlichen Sprache formulieren. Da dies jedoch wieder Mehrdeutigkeiten mit
Objektorientierte Programmierung
 Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann [email protected]
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann [email protected]
Formale Sprachen. Der Unterschied zwischen Grammatiken und Sprachen. Rudolf Freund, Marian Kogler
 Formale Sprachen Der Unterschied zwischen Grammatiken und Sprachen Rudolf Freund, Marian Kogler Es gibt reguläre Sprachen, die nicht von einer nichtregulären kontextfreien Grammatik erzeugt werden können.
Formale Sprachen Der Unterschied zwischen Grammatiken und Sprachen Rudolf Freund, Marian Kogler Es gibt reguläre Sprachen, die nicht von einer nichtregulären kontextfreien Grammatik erzeugt werden können.
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Kapitel MK:IV. IV. Modellieren mit Constraints
 Kapitel MK:IV IV. Modellieren mit Constraints Einführung und frühe Systeme Konsistenz I Binarization Generate-and-Test Backtracking-basierte Verfahren Konsistenz II Konsistenzanalyse Weitere Analyseverfahren
Kapitel MK:IV IV. Modellieren mit Constraints Einführung und frühe Systeme Konsistenz I Binarization Generate-and-Test Backtracking-basierte Verfahren Konsistenz II Konsistenzanalyse Weitere Analyseverfahren
IT-Basics 2. DI Gerhard Fließ
 IT-Basics 2 DI Gerhard Fließ Wer bin ich? DI Gerhard Fließ Telematik Studium an der TU Graz Softwareentwickler XiTrust www.xitrust.com www.tugraz.at Worum geht es? Objektorientierte Programmierung Konzepte
IT-Basics 2 DI Gerhard Fließ Wer bin ich? DI Gerhard Fließ Telematik Studium an der TU Graz Softwareentwickler XiTrust www.xitrust.com www.tugraz.at Worum geht es? Objektorientierte Programmierung Konzepte
Programmieren in Haskell Einführung
 Programmieren in Haskell Einführung Peter Steffen Universität Bielefeld Technische Fakultät 16.10.2009 1 Programmieren in Haskell Veranstalter Dr. Peter Steffen Raum: M3-124 Tel.: 0521/106-2906 Email:
Programmieren in Haskell Einführung Peter Steffen Universität Bielefeld Technische Fakultät 16.10.2009 1 Programmieren in Haskell Veranstalter Dr. Peter Steffen Raum: M3-124 Tel.: 0521/106-2906 Email:
Grundlagen der Programmierung Prof. H. Mössenböck. 14. Schrittweise Verfeinerung
 Grundlagen der Programmierung Prof. H. Mössenböck 14. Schrittweise Verfeinerung Entwurfsmethode für Algorithmen Wie kommt man von der Aufgabenstellung zum Programm? Beispiel geg.: Text aus Wörtern ges.:
Grundlagen der Programmierung Prof. H. Mössenböck 14. Schrittweise Verfeinerung Entwurfsmethode für Algorithmen Wie kommt man von der Aufgabenstellung zum Programm? Beispiel geg.: Text aus Wörtern ges.:
Erwin Grüner 09.02.2006
 FB Psychologie Uni Marburg 09.02.2006 Themenübersicht Folgende Befehle stehen in R zur Verfügung: {}: Anweisungsblock if: Bedingte Anweisung switch: Fallunterscheidung repeat-schleife while-schleife for-schleife
FB Psychologie Uni Marburg 09.02.2006 Themenübersicht Folgende Befehle stehen in R zur Verfügung: {}: Anweisungsblock if: Bedingte Anweisung switch: Fallunterscheidung repeat-schleife while-schleife for-schleife
Einführung in die Programmierung
 Technische Universität München WS 2003/2004 Institut für Informatik Prof. Dr. Christoph Zenger Testklausur Einführung in die Programmierung Probeklausur Java (Lösungsvorschlag) 1 Die Klasse ArrayList In
Technische Universität München WS 2003/2004 Institut für Informatik Prof. Dr. Christoph Zenger Testklausur Einführung in die Programmierung Probeklausur Java (Lösungsvorschlag) 1 Die Klasse ArrayList In
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Einführung in die Programmierung
 : Inhalt Einführung in die Programmierung Wintersemester 2008/09 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering Fakultät für Informatik TU Dortmund - mit / ohne Parameter - mit / ohne Rückgabewerte
: Inhalt Einführung in die Programmierung Wintersemester 2008/09 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering Fakultät für Informatik TU Dortmund - mit / ohne Parameter - mit / ohne Rückgabewerte
Computeranwendung und Programmierung (CuP)
 Computeranwendung und Programmierung (CuP) VO: Peter Auer (Informationstechnologie) UE: Norbert Seifter (Angewandet Mathematik) Organisatorisches (Vorlesung) Vorlesungszeiten Montag 11:15 12:45 Freitag
Computeranwendung und Programmierung (CuP) VO: Peter Auer (Informationstechnologie) UE: Norbert Seifter (Angewandet Mathematik) Organisatorisches (Vorlesung) Vorlesungszeiten Montag 11:15 12:45 Freitag
Theoretische Informatik I
 Theoretische nformatik inheit 3 Kontextfreie Sprachen 1. Kontextfreie Grammatiken 2. Pushdown Automaten 3. igenschaften kontextfreier Sprachen Theoretische nformatik inheit 3.1 Kontextfreie Grammatiken
Theoretische nformatik inheit 3 Kontextfreie Sprachen 1. Kontextfreie Grammatiken 2. Pushdown Automaten 3. igenschaften kontextfreier Sprachen Theoretische nformatik inheit 3.1 Kontextfreie Grammatiken
Formale Sprachen, reguläre und kontextfreie Grammatiken
 Formale Sprachen, reguläre und kontextfreie Grammatiken Alphabet A: endliche Menge von Zeichen Wort über A: endliche Folge von Zeichen aus A A : volle Sprache über A: Menge der A-Worte formale Sprache
Formale Sprachen, reguläre und kontextfreie Grammatiken Alphabet A: endliche Menge von Zeichen Wort über A: endliche Folge von Zeichen aus A A : volle Sprache über A: Menge der A-Worte formale Sprache
Grundlagen der Informatik II. Teil I: Formale Modelle der Informatik
 Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Mathematische Grundlagen der Informatik 2
 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss [email protected] 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss [email protected] 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Algorithmen II Vorlesung am 15.11.2012
 Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2006 3. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik [email protected] Algorithmen für Graphen Fragestellungen: Suche
Algorithmen und Datenstrukturen 2 Sommersemester 2006 3. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik [email protected] Algorithmen für Graphen Fragestellungen: Suche
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit
 Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Zusammenfassung. 1 Wir betrachten die folgende Signatur F = {+,,, 0, 1} sodass. 3 Wir betrachten die Gleichungen E. 4 Dann gilt E 1 + x 1
 Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Was bisher geschah. deklarative Programmierung. funktionale Programmierung (Haskell):
 Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
Grundlagen der Programmierung Prof. H. Mössenböck. 3. Verzweigungen
 Grundlagen der Programmierung Prof. H. Mössenböck 3. Verzweigungen If-Anweisung n > 0? j n if (n > 0) x = x / n; ohne else-zweig x x / n j max x x > y? n max y if (x > y) max = x; else max = y; mit else-zweig
Grundlagen der Programmierung Prof. H. Mössenböck 3. Verzweigungen If-Anweisung n > 0? j n if (n > 0) x = x / n; ohne else-zweig x x / n j max x x > y? n max y if (x > y) max = x; else max = y; mit else-zweig
Typdeklarationen. Es gibt in Haskell bereits primitive Typen:
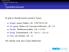 Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Einführung in die Programmierung (EPR)
 Goethe-Center for Scientific Computing (G-CSC) Goethe-Universität Frankfurt am Main Einführung in die Programmierung (EPR) (Übung, Wintersemester 2014/2015) Dr. S. Reiter, M. Rupp, Dr. A. Vogel, Dr. K.
Goethe-Center for Scientific Computing (G-CSC) Goethe-Universität Frankfurt am Main Einführung in die Programmierung (EPR) (Übung, Wintersemester 2014/2015) Dr. S. Reiter, M. Rupp, Dr. A. Vogel, Dr. K.
public class SternchenRechteckGefuellt {
 Java programmieren: Musterlösungen Konsolen-Aufgaben Aufgabe 1: Gefüllte Rechtecke zeichnen Schreiben Sie ein Programm, das ein durch Sternchen gefülltes Rechteck zeichnet. Der Benutzer soll Breite und
Java programmieren: Musterlösungen Konsolen-Aufgaben Aufgabe 1: Gefüllte Rechtecke zeichnen Schreiben Sie ein Programm, das ein durch Sternchen gefülltes Rechteck zeichnet. Der Benutzer soll Breite und
ALP I. Funktionale Programmierung
 ALP I Funktionale Programmierung Sortieren und Suchen (Teil 1) WS 2012/2013 Suchen 8 False unsortiert 21 4 16 7 19 11 12 7 1 5 27 3 8 False sortiert 2 4 6 7 9 11 12 18 21 24 27 36 Suchen in unsortierten
ALP I Funktionale Programmierung Sortieren und Suchen (Teil 1) WS 2012/2013 Suchen 8 False unsortiert 21 4 16 7 19 11 12 7 1 5 27 3 8 False sortiert 2 4 6 7 9 11 12 18 21 24 27 36 Suchen in unsortierten
Scala kann auch faul sein
 Scala kann auch faul sein Kapitel 19 des Buches 1 Faulheit Faulheit ( lazy evaluation ) ist auch in C oder Java nicht unbekannt int x=0; if(x!=0 && 10/x>3){ System.out.println("In if"); } Nutzen der Faulheit?
Scala kann auch faul sein Kapitel 19 des Buches 1 Faulheit Faulheit ( lazy evaluation ) ist auch in C oder Java nicht unbekannt int x=0; if(x!=0 && 10/x>3){ System.out.println("In if"); } Nutzen der Faulheit?
Grundlagen der Programmierung 2. Bäume
 Grundlagen der Programmierung 2 Bäume Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 24. Mai 2006 Graphen Graph: Menge von Knoten undzugehörige (gerichtete oder ungerichtete)
Grundlagen der Programmierung 2 Bäume Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 24. Mai 2006 Graphen Graph: Menge von Knoten undzugehörige (gerichtete oder ungerichtete)
Wortproblem für kontextfreie Grammatiken
 Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung: Lösungsvorschlag
 Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 9 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 9 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Objektorientierte Programmierung. Kapitel 3: Syntaxdiagramme und Grammatikregeln
 Stefan Brass: OOP (Java), 3. Syntaxdiagramme und Grammatikregeln 1/32 Objektorientierte Programmierung Kapitel 3: Syntaxdiagramme und Grammatikregeln Stefan Brass Martin-Luther-Universität Halle-Wittenberg
Stefan Brass: OOP (Java), 3. Syntaxdiagramme und Grammatikregeln 1/32 Objektorientierte Programmierung Kapitel 3: Syntaxdiagramme und Grammatikregeln Stefan Brass Martin-Luther-Universität Halle-Wittenberg
Funktionale Programmierung
 Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
Konzepte der Informatik
 Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Programmieren in C. Macros, Funktionen und modulare Programmstruktur. Prof. Dr. Nikolaus Wulff
 Programmieren in C Macros, Funktionen und modulare Programmstruktur Prof. Dr. Nikolaus Wulff Der C Präprozessor Vor einem Compile Lauf werden alle Präprozessor Kommandos/Makros ausgewertet. Diese sind
Programmieren in C Macros, Funktionen und modulare Programmstruktur Prof. Dr. Nikolaus Wulff Der C Präprozessor Vor einem Compile Lauf werden alle Präprozessor Kommandos/Makros ausgewertet. Diese sind
Grammatiken. Einführung
 Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Lernziele: Ausgleichstechniken für binäre Bäume verstehen und einsetzen können.
 6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
Diana Lange. Generative Gestaltung Operatoren
 Diana Lange Generative Gestaltung Operatoren Begriffserklärung Verknüpfungsvorschrift im Rahmen logischer Kalküle. Quelle: google Operatoren sind Zeichen, die mit einer bestimmten Bedeutung versehen sind.
Diana Lange Generative Gestaltung Operatoren Begriffserklärung Verknüpfungsvorschrift im Rahmen logischer Kalküle. Quelle: google Operatoren sind Zeichen, die mit einer bestimmten Bedeutung versehen sind.
Grammatiken in Prolog
 12. Grammatiken in Prolog 12-1 Grammatiken in Prolog Allgemeines: Gedacht zur Verarbeitung natürlicher Sprache. Dort braucht man kompliziertere Grammatiken als etwa im Compilerbau, andererseits sind die
12. Grammatiken in Prolog 12-1 Grammatiken in Prolog Allgemeines: Gedacht zur Verarbeitung natürlicher Sprache. Dort braucht man kompliziertere Grammatiken als etwa im Compilerbau, andererseits sind die
Grundlagen der Künstlichen Intelligenz
 Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie [email protected]
 Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie [email protected] Interpreter für funktionale Sprache
Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie [email protected] Interpreter für funktionale Sprache
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
7. Formale Sprachen und Grammatiken
 7. Formale Sprachen und Grammatiken Computer verwenden zur Verarbeitung von Daten und Informationen künstliche, formale Sprachen (Maschinenspr., Assemblerspachen, Programmierspr., Datenbankspr., Wissensrepräsentationsspr.,...)
7. Formale Sprachen und Grammatiken Computer verwenden zur Verarbeitung von Daten und Informationen künstliche, formale Sprachen (Maschinenspr., Assemblerspachen, Programmierspr., Datenbankspr., Wissensrepräsentationsspr.,...)
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Beispiele: (Funktionen auf Listen) (3) Bemerkungen: Die Datenstrukturen der Paare (2) Die Datenstrukturen der Paare
 Beispiele: (Funktionen auf Listen) (3) Bemerkungen: 5. Zusammenhängen der Elemente einer Liste von Listen: concat :: [[a]] -> [a] concat xl = if null xl then [] else append (head xl) ( concat (tail xl))
Beispiele: (Funktionen auf Listen) (3) Bemerkungen: 5. Zusammenhängen der Elemente einer Liste von Listen: concat :: [[a]] -> [a] concat xl = if null xl then [] else append (head xl) ( concat (tail xl))
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
VBA-Programmierung: Zusammenfassung
 VBA-Programmierung: Zusammenfassung Programmiersprachen (Definition, Einordnung VBA) Softwareentwicklung-Phasen: 1. Spezifikation 2. Entwurf 3. Implementierung Datentypen (einfach, zusammengesetzt) Programmablaufsteuerung
VBA-Programmierung: Zusammenfassung Programmiersprachen (Definition, Einordnung VBA) Softwareentwicklung-Phasen: 1. Spezifikation 2. Entwurf 3. Implementierung Datentypen (einfach, zusammengesetzt) Programmablaufsteuerung
Algorithmische Mathematik
 Algorithmische Mathematik Wintersemester 2013 Prof. Dr. Marc Alexander Schweitzer und Dr. Einar Smith Patrick Diehl und Daniel Wissel Übungsblatt 6. Abgabe am 02.12.2013. Aufgabe 1. (Netzwerke und Definitionen)
Algorithmische Mathematik Wintersemester 2013 Prof. Dr. Marc Alexander Schweitzer und Dr. Einar Smith Patrick Diehl und Daniel Wissel Übungsblatt 6. Abgabe am 02.12.2013. Aufgabe 1. (Netzwerke und Definitionen)
Reihungen. Martin Wirsing. in Zusammenarbeit mit Matthias Hölzl und Nora Koch 11/03
 Reihungen Martin Wirsing in Zusammenarbeit mit Matthias Hölzl und Nora Koch 11/03 2 Ziele Die Datenstruktur der Reihungen verstehen: mathematisch und im Speicher Grundlegende Algorithmen auf Reihungen
Reihungen Martin Wirsing in Zusammenarbeit mit Matthias Hölzl und Nora Koch 11/03 2 Ziele Die Datenstruktur der Reihungen verstehen: mathematisch und im Speicher Grundlegende Algorithmen auf Reihungen
Idee: Wenn wir beim Kopfknoten zwei Referenzen verfolgen können, sind die Teillisten kürzer. kopf Eine Datenstruktur mit Schlüsselwerten 1 bis 10
 Binäre Bäume Bäume gehören zu den wichtigsten Datenstrukturen in der Informatik. Sie repräsentieren z.b. die Struktur eines arithmetischen Terms oder die Struktur eines Buchs. Bäume beschreiben Organisationshierarchien
Binäre Bäume Bäume gehören zu den wichtigsten Datenstrukturen in der Informatik. Sie repräsentieren z.b. die Struktur eines arithmetischen Terms oder die Struktur eines Buchs. Bäume beschreiben Organisationshierarchien
Suchmaschinen. Universität Augsburg, Institut für Informatik SS 2014 Prof. Dr. W. Kießling 23. Mai 2014 Dr. M. Endres, F. Wenzel Lösungsblatt 6
 Universität Augsburg, Institut für Informatik SS 2014 Prof. Dr. W. Kießling 23. Mai 2014 Dr. M. Endres, F. Wenzel Lösungsblatt 6 Aufgabe 1: Pareto mit SV-Semantik Suchmaschinen Pareto Definition: x < P
Universität Augsburg, Institut für Informatik SS 2014 Prof. Dr. W. Kießling 23. Mai 2014 Dr. M. Endres, F. Wenzel Lösungsblatt 6 Aufgabe 1: Pareto mit SV-Semantik Suchmaschinen Pareto Definition: x < P
Programmieren in Haskell
 Programmieren in Haskell Felder (Arrays) Programmieren in Haskell 1 Was wir heute machen Motivationsbeispiel Die Typklasse Ix Felder in Haskell Funktionstabellierung Binäre Suche Pascalsches Dreieck Ein
Programmieren in Haskell Felder (Arrays) Programmieren in Haskell 1 Was wir heute machen Motivationsbeispiel Die Typklasse Ix Felder in Haskell Funktionstabellierung Binäre Suche Pascalsches Dreieck Ein
Studentische Lösung zum Übungsblatt Nr. 7
 Studentische Lösung zum Übungsblatt Nr. 7 Aufgabe 1) Dynamische Warteschlange public class UltimateOrderQueue private Order[] inhalt; private int hinten; // zeigt auf erstes freies Element private int
Studentische Lösung zum Übungsblatt Nr. 7 Aufgabe 1) Dynamische Warteschlange public class UltimateOrderQueue private Order[] inhalt; private int hinten; // zeigt auf erstes freies Element private int
4. 4. Algorithmen und Datenstrukturen in deskriptiven Programmiersprachen
 Kapitel Kapitel 4 Deskriptive Programmierung SS 2008 4. 4. Algorithmen und Datenstrukturen in in deskriptiven Programmiersprachen Deskriptive Programmierung 1 Sprachverarbeitung in in Prolog Prolog Prolog
Kapitel Kapitel 4 Deskriptive Programmierung SS 2008 4. 4. Algorithmen und Datenstrukturen in in deskriptiven Programmiersprachen Deskriptive Programmierung 1 Sprachverarbeitung in in Prolog Prolog Prolog
Graphic Coding. Klausur. 9. Februar 2007. Kurs A
 Graphic Coding Klausur 9. Februar 2007 Kurs A Name: Matrikelnummer: Hinweise - Es sind keine Hilfsmaterialien erlaubt. (Keine Bücher, Taschenrechner, Handys) - Sie haben zwei Stunden Zeit. - Insgesamt
Graphic Coding Klausur 9. Februar 2007 Kurs A Name: Matrikelnummer: Hinweise - Es sind keine Hilfsmaterialien erlaubt. (Keine Bücher, Taschenrechner, Handys) - Sie haben zwei Stunden Zeit. - Insgesamt
Matrizennorm. Definition 1. Sei A M r,s (R). Dann heißt A := sup die Matrixnorm. Wir wissen zunächst nicht, ob A eine reelle Zahl ist.
 Matrizennorm Es seien r,s N Mit M r,s (R bezeichnen wir die Menge der reellen r s- Matrizen (also der linearen Abbildungen R s R r, und setze M s (R := M s,s (R (also die Menge der linearen Abbildungen
Matrizennorm Es seien r,s N Mit M r,s (R bezeichnen wir die Menge der reellen r s- Matrizen (also der linearen Abbildungen R s R r, und setze M s (R := M s,s (R (also die Menge der linearen Abbildungen
Logische Folgerung. Definition 2.11
 Logische Folgerung Definition 2.11 Sei 2A eine aussagenlogische Formel und F eine endliche Menge aussagenlogischer Formeln aus A. heißt logische Folgerung von F genau dann, wenn I ( ) =1für jedes Modell
Logische Folgerung Definition 2.11 Sei 2A eine aussagenlogische Formel und F eine endliche Menge aussagenlogischer Formeln aus A. heißt logische Folgerung von F genau dann, wenn I ( ) =1für jedes Modell
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Sortieralgorithmen. Inhalt: InsertionSort BubbleSort QuickSort. Marco Block
 Inhalt: InsertionSort BubbleSort QuickSort Block M.: "Java-Intensivkurs - In 14 Tagen lernen Projekte erfolgreich zu realisieren", Springer-Verlag 2007 InsertionSort I Das Problem unsortierte Daten in
Inhalt: InsertionSort BubbleSort QuickSort Block M.: "Java-Intensivkurs - In 14 Tagen lernen Projekte erfolgreich zu realisieren", Springer-Verlag 2007 InsertionSort I Das Problem unsortierte Daten in
Compiler, Übersetzer. Allgemeine Erklärung / Definition
 Compiler, Übersetzer Allgemeine Erklärung / Definition Ein Übersetzer ist ein Programm, das ein S 1 -Wort den Quelltext in ein S 2 -Wort umwandelt den Zieltext wobei die Semantik erhalten bleibt. Frage:
Compiler, Übersetzer Allgemeine Erklärung / Definition Ein Übersetzer ist ein Programm, das ein S 1 -Wort den Quelltext in ein S 2 -Wort umwandelt den Zieltext wobei die Semantik erhalten bleibt. Frage:
Datenbanken Microsoft Access 2010
 Datenbanken Microsoft Access 2010 Abfragen Mithilfe von Abfragen kann ich bestimmte Informationen aus einer/mehrerer Tabellen auswählen und nur diese anzeigen lassen die Daten einer/mehrerer Tabellen sortieren
Datenbanken Microsoft Access 2010 Abfragen Mithilfe von Abfragen kann ich bestimmte Informationen aus einer/mehrerer Tabellen auswählen und nur diese anzeigen lassen die Daten einer/mehrerer Tabellen sortieren
Vorkurs C++ Programmierung
 Vorkurs C++ Programmierung Klassen Letzte Stunde Speicherverwaltung automatische Speicherverwaltung auf dem Stack dynamische Speicherverwaltung auf dem Heap new/new[] und delete/delete[] Speicherklassen:
Vorkurs C++ Programmierung Klassen Letzte Stunde Speicherverwaltung automatische Speicherverwaltung auf dem Stack dynamische Speicherverwaltung auf dem Heap new/new[] und delete/delete[] Speicherklassen:
Datentypen. Agenda für heute, 4. März, 2010. Pascal ist eine streng typisierte Programmiersprache
 Agenda für heute, 4. März, 2010 Zusammengesetzte if-then-else-anweisungen Datentypen Pascal ist eine streng typisierte Programmiersprache Für jeden Speicherplatz muss ein Datentyp t (Datenformat) t) definiert
Agenda für heute, 4. März, 2010 Zusammengesetzte if-then-else-anweisungen Datentypen Pascal ist eine streng typisierte Programmiersprache Für jeden Speicherplatz muss ein Datentyp t (Datenformat) t) definiert
R ist freie Software und kann von der Website. www.r-project.org
 R R ist freie Software und kann von der Website heruntergeladen werden. www.r-project.org Nach dem Herunterladen und der Installation von R kann man R durch Doppelklicken auf das R-Symbol starten. R wird
R R ist freie Software und kann von der Website heruntergeladen werden. www.r-project.org Nach dem Herunterladen und der Installation von R kann man R durch Doppelklicken auf das R-Symbol starten. R wird
Einführung in. Logische Schaltungen
 Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Typklassen. Natascha Widder
 Typklassen Natascha Widder 19.11.2007 Motivation Typklassen fassen Typen mit ähnlichen Operatoren zusammen ermöglichen überladenen Funktionen Definition Typklassen Deklarationsschema class Name Platzhalter
Typklassen Natascha Widder 19.11.2007 Motivation Typklassen fassen Typen mit ähnlichen Operatoren zusammen ermöglichen überladenen Funktionen Definition Typklassen Deklarationsschema class Name Platzhalter
Informatik 11 Kapitel 2 - Rekursive Datenstrukturen
 Fachschaft Informatik Informatik 11 Kapitel 2 - Rekursive Datenstrukturen Michael Steinhuber König-Karlmann-Gymnasium Altötting 15. Januar 2016 Folie 1/77 Inhaltsverzeichnis I 1 Datenstruktur Schlange
Fachschaft Informatik Informatik 11 Kapitel 2 - Rekursive Datenstrukturen Michael Steinhuber König-Karlmann-Gymnasium Altötting 15. Januar 2016 Folie 1/77 Inhaltsverzeichnis I 1 Datenstruktur Schlange
Objektorientierte Programmierung für Anfänger am Beispiel PHP
 Objektorientierte Programmierung für Anfänger am Beispiel PHP Johannes Mittendorfer http://jmittendorfer.hostingsociety.com 19. August 2012 Abstract Dieses Dokument soll die Vorteile der objektorientierten
Objektorientierte Programmierung für Anfänger am Beispiel PHP Johannes Mittendorfer http://jmittendorfer.hostingsociety.com 19. August 2012 Abstract Dieses Dokument soll die Vorteile der objektorientierten
CGI Programmierung mit Ha. Markus Schwarz
 CGI Programmierung mit Ha Markus Schwarz Überblick Was ist funktionale Programmierung Einführung in Haskell CGI-Programmierung mit Haskell Ein etwas größeres Beispiel Was ist funktionale Programm Ein Programm
CGI Programmierung mit Ha Markus Schwarz Überblick Was ist funktionale Programmierung Einführung in Haskell CGI-Programmierung mit Haskell Ein etwas größeres Beispiel Was ist funktionale Programm Ein Programm
Das Typsystem von Scala. L. Piepmeyer: Funktionale Programmierung - Das Typsystem von Scala
 Das Typsystem von Scala 1 Eigenschaften Das Typsystem von Scala ist statisch, implizit und sicher 2 Nichts Primitives Alles ist ein Objekt, es gibt keine primitiven Datentypen scala> 42.hashCode() res0:
Das Typsystem von Scala 1 Eigenschaften Das Typsystem von Scala ist statisch, implizit und sicher 2 Nichts Primitives Alles ist ein Objekt, es gibt keine primitiven Datentypen scala> 42.hashCode() res0:
Wiederholung ADT Menge Ziel: Verwaltung (Finden, Einfügen, Entfernen) einer Menge von Elementen
 Was bisher geschah abstrakter Datentyp : Signatur Σ und Axiome Φ z.b. ADT Menge zur Verwaltung (Finden, Einfügen, Entfernen) mehrerer Elemente desselben Typs Spezifikation einer Schnittstelle Konkreter
Was bisher geschah abstrakter Datentyp : Signatur Σ und Axiome Φ z.b. ADT Menge zur Verwaltung (Finden, Einfügen, Entfernen) mehrerer Elemente desselben Typs Spezifikation einer Schnittstelle Konkreter
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Die Java Stream API. Funktionale Programmierung mit der Stream API des JDK 1.8. Prof. Dr. Nikolaus Wulff
 Die Java Stream API Funktionale Programmierung mit der Stream API des JDK 1.8 Prof. Dr. Nikolaus Wulff Funktionale Programmierung Neben der Collection API mit default Methoden ist als weitere Neuerung
Die Java Stream API Funktionale Programmierung mit der Stream API des JDK 1.8 Prof. Dr. Nikolaus Wulff Funktionale Programmierung Neben der Collection API mit default Methoden ist als weitere Neuerung
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
1 Syntax von Programmiersprachen
 1 Syntax von Programmiersprachen Syntax ( Lehre vom Satzbau ): formale Beschreibung des Aufbaus der Worte und Sätze, die zu einer Sprache gehören; im Falle einer Programmier-Sprache Festlegung, wie Programme
1 Syntax von Programmiersprachen Syntax ( Lehre vom Satzbau ): formale Beschreibung des Aufbaus der Worte und Sätze, die zu einer Sprache gehören; im Falle einer Programmier-Sprache Festlegung, wie Programme
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume?
 Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden [email protected] WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden [email protected] WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Modellierung und Programmierung 1
 Modellierung und Programmierung 1 Prof. Dr. Sonja Prohaska Computational EvoDevo Group Institut für Informatik Universität Leipzig 19. November 2015 Gültigkeitsbereich (Scope) von Variablen { int m; {
Modellierung und Programmierung 1 Prof. Dr. Sonja Prohaska Computational EvoDevo Group Institut für Informatik Universität Leipzig 19. November 2015 Gültigkeitsbereich (Scope) von Variablen { int m; {
Folge 19 - Bäume. 19.1 Binärbäume - Allgemeines. Grundlagen: Ulrich Helmich: Informatik 2 mit BlueJ - Ein Kurs für die Stufe 12
 Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Einführung in die Java- Programmierung
 Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger [email protected] WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger [email protected] WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
368 4 Algorithmen und Datenstrukturen
 Kap04.fm Seite 368 Dienstag, 7. September 2010 1:51 13 368 4 Algorithmen und Datenstrukturen Java-Klassen Die ist die Klasse Object, ein Pfeil von Klasse A nach Klasse B bedeutet Bextends A, d.h. B ist
Kap04.fm Seite 368 Dienstag, 7. September 2010 1:51 13 368 4 Algorithmen und Datenstrukturen Java-Klassen Die ist die Klasse Object, ein Pfeil von Klasse A nach Klasse B bedeutet Bextends A, d.h. B ist
Künstliche Intelligenz Maschinelles Lernen
 Künstliche Intelligenz Maschinelles Lernen Stephan Schwiebert Sommersemester 2009 Sprachliche Informationsverarbeitung Institut für Linguistik Universität zu Köln Maschinelles Lernen Überwachtes Lernen
Künstliche Intelligenz Maschinelles Lernen Stephan Schwiebert Sommersemester 2009 Sprachliche Informationsverarbeitung Institut für Linguistik Universität zu Köln Maschinelles Lernen Überwachtes Lernen
