Gitterbasierte Kryptosysteme
|
|
|
- Kirsten Fürst
- vor 5 Jahren
- Abrufe
Transkript
1 Gitterbasierte Kryptosysteme SVP, CVP und SBP Die Abkürzungen stehen für Shortest Vector, Closest Vector Problem und Smallest Basis Problem. Hierbei handelt es sich um folgende algorithmische Probleme. 1 Definition. Sei Λ Z n ein Gitter. Das SVP besteht darin, aus einer Basis von Λ einen Vektor v Λ\{0} mit v minimal auszurechnen. 2 Definition. Sei Λ Z n ein Gitter. Das CVP besteht darin, aus einer Basis von Λ und einem w Z n einen Vektor v Λ mit v w minimal auszurechnen. 3 Definition. Sei Λ Z n ein Gitter. Das SBP besteht darin, aus einer Basis von Λ eine Basis von Λ zu berechnen, so daß das Produkt über die Längen der Basisvektoren minimal wird. Man kann anstelle des Produkts auch das Maximum der Längen der Basisvektoren betrachten. Vom SVP und CVP gibt es auch Approximations- beziehungsweise Entscheidungsvarianten, ebenso für das SBP. Ist zusätzlich d Z gegeben, so kann man im SVP nach v Λ\{0} mit v d und im CVP nach v Λ mit v w d fragen. Der Quotient der Größe d und des jeweiligen möglichen Minimalwerts für v beziehungsweise v w heißt dann Approximationsfaktor. Interessiert man sich nur für die Existenz geeigneter v, so handelt es sich um Entscheidungsprobleme. Das SVP und CVP kann darüber hinaus auch für andere Normen betrachtet werden. Das CVP ist NP hart und das SVP NP hart unter randomisierten Reduktionen. Das SBP ist ebenfalls NP hart (evtl. unter randomisierten Reduktionen). Es ist daher naheliegend, zu fragen, ob diese Probleme für kryptographische Zwecke verwendet werden können. NP und NP hart Wir wollen kurz informell auf die Begriffe NP und NP hart eingehen. 1
2 2 Unter einem Problem verstehen wir die Aufgabe, zu einer Relation {0, 1} {0, 1} und Eingabedaten x mögliche Ausgabedaten y mit x y zu berechnen. Ist x, gegeben, so spricht man von einer Instanz des Problems. Bei einem Entscheidungsproblem handelt es sich bei der Relation um eine Funktion nach {0, 1}. Für Entscheidungsprobleme kann man L = {x x 1} definieren. Dann nennt man L eine Sprache und das Entscheidungsproblem für x besteht darin, x L oder nicht zu entscheiden. Es stellt sich die Frage, ob und in welcher Zeit Probleme durch Algorithmen (Turingmaschinen) gelöst werden können. P steht für polynomial time. Es handelt sich hierbei um die Klasse der Entscheidungsprobleme, welche durch eine deterministische Turingmaschine in Polynomzeit in der Länge der Eingabedaten des Problems gelöst werden können. Eine solche Maschine ist im wesentlichen ein Programm, welches in jedem Schritt genau eine mögliche Ausführung hat. NP steht für non-deterministic polynomial time. Es handelt sich hierbei um die Klasse der Entscheidungsprobleme, welche durch eine nicht-deterministische Turingmaschine in Polynomzeit in der Länge der Eingabedaten des Problems gelöst werden können. Eine solche Maschine ist im wesentlichen ein Programm, welches in jedem Schritt mehrere Möglichkeiten der Ausführung hat. Dies liefert (theoretisch) einen Ausführungsbaum, und man fordert, daß die Entscheidung durch einen Weg durch den Baum in polynomiell vielen Schritten berechnet werden kann. Alternativ kann man auch eine deterministische Turingmaschine verwenden, welche mit Hilfe einer zusätzlichen polynomiell großen Eingabe die Entscheidung in Polynomzeit berechnen kann. Diese zusätzliche Eingabe wird Zeuge genannt und spezifiziert sozusagen den Weg durch den Ausführungsbaum der nicht-deterministischen Turingmaschine. Eine der großen Vermutungen ist P NP. Dies führt manchmal zu dem Irrtum, NP stünde für non-polynomial time. Unter einer Reduktion eines Problems A auf ein Problem B versteht man im allgemeinen ein Verfahren, welches eine Lösung einer Instanz von A mit Hilfe von Lösungen von Instanzen von B berechnen kann. Die jeweils zulässigen Verfahren werden anhand der üblichen Eigenschaften (deterministisch, probabilistisch, Laufzeit, wann und wie oft wird eine Lösung einer Instanz von B benötigt, etc.) eingeteilt. Sind A und B Entscheidungsprobleme und gibt es eine Abbildung f : {0, 1} {0, 1} mit x L A f(x) L B, welche mit einer deterministischen Turingmaschine in Polynomzeit berechnet werden kann, spricht man von Karp Reduktion. Insbesondere wird hier keine Instanz von B gelöst. Allgemeiner spricht man von Cook Reduktion, wenn das Verfahren eine deterministische Turingmaschine ist, welche in Polynomzeit läuft und Instanzen von B per Orakel löst. Meist wird wohl Karp Reduktion verwendet.
3 Man kann P und NP auch für allgemeinere Probleme als Entscheidungsprobleme definieren. Bei den Reduktionen muß man dann auch Verfahren für die Ausgaben berücksichtigen. Solche allgemeineren NP Probleme können häufig in Polynomzeit auf NP Entscheidungsprobleme reduziert werden (zum Beispiel binäre Suche nach dem kürzesten Gittervektor). NP harte Entscheidungsprobleme sind Probleme, auf die sich jedes Entscheidungsproblem in NP Karp reduzieren läßt. Liegt ein NP hartes Problem in NP, so heißt es NP vollständig. Diese sind die schwersten Probleme in NP. 3 GGH Kryptosystem Die Abkürzung GGH steht für die Erfinder Goldreich, Goldwasser und Halevi. Wir wählen n Z 1, unabhängige, kurze Vektoren b 1,...,b n Z n und setzen Λ = Zb Zb n. Außerdem werden Parameter p,q Z gewählt. Der geheime Schlüssel ist B = (b 1,...,b n ). Der öffentliche Schlüssel ist V = (v 1,...,v n ) mit einer Basis v i von Λ, welche durch ausreichend viele, zufällige unimodulare Transformationen aus den b i entsteht. Eine andere Wahl für die v i besteht in der Hermite Normalform von B. Verschlüsseln: Die Nachricht wird geeignet in einen Vektor m Z n [ q,...,q] abgebildet. Ein geeignetes, kleines e Z n [ p,p] wird gewählt. Der Chiffretext ist c = V m + e. Entschlüsseln: Die Idee ist, den zu c nächsten Vektor in Λ zu bestimmen. Wenn e klein genug ist, sollte aufgrund der Diskretheit von Λ der Vektor V m herauskommen, und man kann nach m auflösen. Zur Berechnung des CVP verwendet man als Hintertür die Basis B wie folgt. Man stellt c in der Basis B dar, rundet die Koordinaten und hofft, so den zu c nächsten Vektor zu finden, welcher V m sein sollte. Man berechnet also m = B 1 V V 1 c als entschlüsselte Nachricht. Es läßt sich zeigen, daß bei geeigneter Wahl der Parameter, insbesondere p, die Wahrscheinlichkeit für m = m ausreichend gut ist. Typische Parameter sind beispielsweise n = 300, q = 127 und p = 3. Das GGH Kryptosystem kann mit der ElGamal Verschlüsselung wie folgt verglichen werden. Ein Chiffretext in ElGamal ist c = (g r,my r ), wobei y = g x der öffentliche und x der geheime Schlüssel ist. Die Nachricht m wird mit einem Fehler y r perturbiert. Um diesen Fehler wieder wegrechnen zu können, schickt man noch g r mit. Allerdings kann nach Annahme nur der Besitzer von x aus g r auch (g r ) x = y r ausrechnen. Demgegenüber wird g r im GGH System nicht benötigt. Die Nachricht m wird wieder durch einen Fehler e perturbiert. Durch das CVP kann man
4 4 allein aus c den Fehler wieder wegrechnen, allerdings nach Annahme nur, wenn man im Besitz des privaten Schlüssels B ist. Die Analogie zwischen ElGamal und GGH wird noch auffälliger, wenn man die Nachricht nach e und den Fehler nach m bringt, so daß der Chiffretext c = V m + e ist. Sicherheit Die Sicherheit des Verfahrens beruht auf zwei unterliegenden Problemen. Zum einen, daß man nicht B aus V berechnen kann. Dies entspricht im wesentlichen einer Instanz vom SBP. Zum anderen, daß man nicht V m aus c = V m + e ausrechnen kann. Dies entspricht im wesentlichen einer Instanz des CVP. Aufgrund der speziell erforderlichen Parameterwahlen konnte gezeigt werden, daß man n 400 benötigt, um nicht eines dieser Probleme mit dem LLL Algorithmus und Varianten davon lösen zu können. Für solche n ist das Verfahren aber nicht mehr praktikabel. GGH Signaturverfahren Die Funktion (m,e) V m + e verhält sich wie eine Einwegfunktion mit Falltür. Ähnlich wie bei RSA kann man daraus auch ein Signaturverfahren erhalten. Öffentlicher und geheimer Schlüssel sind wie beim Kryptosystem. Die Parameter werden teilweise anders gewählt. Signieren: Die Nachricht wird in einen geeigneten Vektor m Z n abgebildet. Mithilfe der geheimen Basis wird ein naheliegender Gitterpunkt σ Λ als Linearkombination der öffentlichen Basis bestimmt. Dies ist die Unterschrift. Verifizieren: Es wird überprüft, ob σ Λ gilt und σ m klein genug ist. Sicherheit Dieses Verfahren ist ebenfalls nicht sicher, denn ein adaptiver chosen-message Angriff ist möglich. Durch eine Anzahl von Signaturanfragen kann der Angreifer ein Teilgitter von Λ definieren und mit dem Teilgitter Unterschriften fälschen. Warum gitterbasierte Kryptographie? Im wesentlichen basiert die Kryptographie mit öffentlichem Schlüssel auf der Schwierigkeit des DLP und der Faktorisierung. Zur Absicherung wäre
5 es wünschenswert, auch auf andere schwierige Probleme zurückgreifen zu können. Die beiden ersten Probleme können auf einem Quantencomputer beispielsweise in Polynomzeit gelöst werden, wohingegen dies für SVP und CVP bisher nicht bekannt ist. Ein weiterer Grund ergibt sich aus der Effizienz. Für den Sicherheitsparameter n ergibt sich folgende Tabelle. Die Sicherheit in der Tabelle ist natürlich System Schlüsselgröße Laufzeit Sicherheit RSA O(n) O(n 3 ) L n (1/3) DLP endl. Körper O(n) O(n 3 ) L n (1/3) DLP ell. Kurve O(n) O(n 3 ) L n (1) GGH O(n 2 ) O(n 2 ) L n (1)? NTRU O(n) O(n 2 ) L n (1)? 5 in keinem Fall bewiesen. Jedoch erscheinen die Abschätzungen für RSA und DLP eher sicher als die für GGH und NTRU, da diese Probleme schon länger untersucht werden und sich auch nicht soviele böse Überraschungen eingestellt haben. In gewisser Weise hat sich die gitterbasierte Kryptographie (siehe auch Merkle-Hellmann) als sehr instabil bezüglich der erforderlichen Parameterwahl gezeigt und ist auch sehr von statistischen Zusammenhängen abhängig. Auf der anderen Seite sieht es so aus, aus würden Gittermethoden häufig zu sehr effizienten Verfahren führen, wenn sie denn sicher wären. Die Schlüsselgröße bei GGH ist allerdings in besonderem Maß dafür verantwortlich, daß GGH nicht praktikabel ist (Challenge mit n = 400 liefert 1.8MB Schlüssel). NTRU NTRU steht (inoffiziell) für Number Theorists are Us, da die Erfinder und Firmengründer Pipher, Hoffstein und J. Silverman Zahlentheoretiker sind (J. Silverman ist insbesondere Experte für elliptische Kurven). Bei NTRU handelt es sich um das wohl einzige zur Zeit sichere und dabei sehr effiziente Kryptosystem basierend auf speziellen Gittern. Entwicklungsversuche für ein Signaturverfahren basierend auf diesen speziellen NTRU Gittern sind bisher fehlgeschlagen, jede Version wurde in relativ kurzer Zeit gebrochen. Im Vergleich zum GGH Kryptosystem kann man folgendes festhalten. Die Verschlüsselung erfolgt ähnlich wie beim GGH Kryptosystem, eine Nachricht wird mit einem Fehlerterm perturbiert. Die Entschlüsselung basiert jedoch nicht auf dem Lösen eines CVP mittels einer kurzen, geheimen Basis als
6 6 Falltür, sondern auf gewissen modulo q und modulo p Rechnungen unter Verwendung eines sehr kurzen, geheimen Vektors des NTRU Gitters als Falltür. Die Sicherheit des Verfahrens hängt daher (mindestens) von der Schwierigkeit des SVP im NTRU Gitter ab. Die Schlüssel (die öffentliche und geheime Gitterbasen) im GGH Kryptosystem sind sehr speicheraufwendig. Im NTRU Gitter benötigt man jedoch aufgrund der speziellen rotationssymmetrischen Gestalt des Gitters nur je einen einzigen Vektor, um eine vollständige Basis (öffentlich und geheim) zu beschreiben. Daraus ergeben sich besonders speichereffiziente öffentliche und geheime Schlüssel. Weitere Details des NTRU Verfahrens und Gitters werden in der Übung besprochen. Ajtai-Dwork Kryptosystem Dieses Kryptosystem ist nicht praktikabel (z.b. bitweise Verschlüsselung), ist aber von theoretischem Interesse, da es auf einer worst-case/average-case Verbindung von SVP Varianten beruht. In der Kryptographie benötigt man Probleme (mit Falltür), deren zufällige Instanzen nur schwer zu lösen sind, also Probleme, die im Durchschnitt bzw. average-case schwer zu lösen sind. Im Gegensatz dazu weiß man von vielen Problemen wie SVP nur, daß es Instanzen gibt, welche schwer zu lösen sind. Dies sind also Probleme, welche im worst-case nur schwer zu lösen sind. Eine worst-case/average-case Reduktion von worst-case Instanzen eines schwierigen Problems A auf average-case Instanzen eines Problems B ist daher von großem Interesse. Mit einer solchen Reduktion könnte man worstcase Instanzen von A lösen, wenn man nur zufällige Instanzen von B lösen kann. Da A schwierig im worst-case ist, muß B schwierig im average-case sein. Eine solche Reduktion wurde 1996 erstmalig von Ajtai gefunden. Beim average-case Problem B handelt es sich hier um ein approximiertes SVP in einer besonderen Klasse von Gittern (das NTRU Gitter weist gewisse Ähnlichkeiten zu diesem Gitter auf). Das worst-case Problem A ist eines der drei folgenden Probleme. A1 Das SVP mit in der Dimension polynomiellem Approximationsfaktor, A2 Eine Variante vom SBP in Dimension n, wo max n i=1 b i mit in n polynomiellen Approximationsfaktor zu minimieren ist, A3 Das SVP in Gittern Λ der Dimension n mit λ 2 (Λ) n c λ 1 (Λ) und c eine ausreichend große, von n unabhängige Konstante.
7 Das Ajtai-Dwork Kryptosystem zeichnet sich durch die Eigenschaft aus: Wenn eine Verschlüsselung von 0 von einer Verschlüsselung von 1 in einer zufälligen Instanz des Systems mit von 1/2 signifikant abweichender Wahrscheinlichkeit unterschieden werden kann, dann läßt sich Problem A3 effizient lösen. Es gibt also im wesentlichen keine unsicheren Instanzen bzw. unsicheren Schlüssel dieses Kryptosystems. Das Problem, einen Chiffretext zu entschlüsseln, ist aber vermutlich nicht NP hart. Aus praktischer Sicht gilt die Aussage über die unsicheren Schlüssel auch für RSA und DLP basierte Systeme. Aussagen über das SVP und CVP Hier sind ein paar Aussagen über die worst-case Schwierigkeit des SVP und CVP. Das SVP ist NP hart bezüglich randomisierter Reduktionen und konstantem Approximationsfaktor. Das CVP in Dimension n ist NP hart bezüglich subpolynomiellem Approximationsfaktor n c/ log(log(n)) für eine absolute Konstante c > 0. Das SVP läßt sich effizient auf das CVP in der gleichen Dimension und bezüglich des gleichen, beliebigen Approximationsfaktors reduzieren. Das SVP und CVP in der Dimension n mit Approximationsfaktor n 1/2 ist wahrscheinlich nicht NP hart. Das SVP und CVP können mit exponentiellem Approximationsfaktor (1 + ε) n für festes ε > 0 in Polynomzeit in n gelöst werden (Schnorr s LLL Variante). Häufig sind die erreichten Approximationsfaktoren deutlich besser als exponentiell. Für andere Normen sind weitere Aussagen bekannt, das CVP ist beispielsweise für jede p-norm p NP hart. Das SVP scheint theoretisch etwas unzugänglicher als das CVP zu sein. 7
NTRU: Effiziente gitterbasierte Kryptographie
 NTRU: Effiziente gitterbasierte Kryptographie Christoph Ludwig 8. April 2002 TECHNISCHE UNIVERSITÄT DARMSTADT Institut für Theoretische Informatik TU Darmstadt; Institut für Theoretische Informatik 1 Übersicht
NTRU: Effiziente gitterbasierte Kryptographie Christoph Ludwig 8. April 2002 TECHNISCHE UNIVERSITÄT DARMSTADT Institut für Theoretische Informatik TU Darmstadt; Institut für Theoretische Informatik 1 Übersicht
Technische Universität. Fakultät für Informatik
 Technische Universität München Fakultät für Informatik Forschungs- und Lehreinheit Informatik VII Lattice-based Cryptography Kryptographie in Gittern Masterseminar Sebastian Rettenberger Betreuer: Dr.
Technische Universität München Fakultät für Informatik Forschungs- und Lehreinheit Informatik VII Lattice-based Cryptography Kryptographie in Gittern Masterseminar Sebastian Rettenberger Betreuer: Dr.
RSA Äquivalenz der Parameter
 RSA Kryptosystem Wurde 1977 von Rivest, Shamir und Adleman erfunden. Genaue Beschreibung im PKCS #1. De-facto Standard für asymmetrische Kryptosysteme. Schlüsselerzeugung: Seien p, q zwei verschiedene,
RSA Kryptosystem Wurde 1977 von Rivest, Shamir und Adleman erfunden. Genaue Beschreibung im PKCS #1. De-facto Standard für asymmetrische Kryptosysteme. Schlüsselerzeugung: Seien p, q zwei verschiedene,
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 16.11.2010 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Vorlesung am 16.11.2010 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 4.4 Semantische Sicherheit 1. Sicherheit partieller Informationen 2. Das Verfahren von Rabin 3. Sicherheit durch Randomisierung Semantische Sicherheit Mehr als nur
Kryptographie und Komplexität Einheit 4.4 Semantische Sicherheit 1. Sicherheit partieller Informationen 2. Das Verfahren von Rabin 3. Sicherheit durch Randomisierung Semantische Sicherheit Mehr als nur
Hybride Verschlüsselungsverfahren
 Hybride Verschlüsselungsverfahren Ziel: Flexibilität von asym. Verfahren und Effizienz von sym. Verfahren. Szenario: Sei Π = (Gen, Enc, Dec) ein PK-Verschlüsselungsverfahren und Π = (Gen, Enc, Dec ) ein
Hybride Verschlüsselungsverfahren Ziel: Flexibilität von asym. Verfahren und Effizienz von sym. Verfahren. Szenario: Sei Π = (Gen, Enc, Dec) ein PK-Verschlüsselungsverfahren und Π = (Gen, Enc, Dec ) ein
Vorlesung Digitale Signaturen im Wintersemester 2017/-18. Socrative-Fragen aus der Vorlesung vom
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2017/-18 Socrative-Fragen aus der Vorlesung vom 17.11.2017 1 Quiz 1:
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2017/-18 Socrative-Fragen aus der Vorlesung vom 17.11.2017 1 Quiz 1:
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 20. November 2014 INSTITUT FÜR THEORETISCHE 0 KIT 20.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 20. November 2014 INSTITUT FÜR THEORETISCHE 0 KIT 20.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Gruppenbasierte Kryptographie. ElGamal Sicherheit. Drei Probleme. ElGamal Verschlüsselung. Benutzt zyklische Gruppen von (fast) Primzahlordnung:
 Gruppenbasierte Kryptographie Benutzt zyklische Gruppen von (fast) Primzahlordnung: G = g und #G = l = cl 0 mit c klein und l 0 prim. b G : x Z : b = g x. Das Element x heißt diskreter Logarithmus von
Gruppenbasierte Kryptographie Benutzt zyklische Gruppen von (fast) Primzahlordnung: G = g und #G = l = cl 0 mit c klein und l 0 prim. b G : x Z : b = g x. Das Element x heißt diskreter Logarithmus von
P, NP und NP -Vollständigkeit
 P, NP und NP -Vollständigkeit Mit der Turing-Maschine haben wir einen Formalismus kennengelernt, um über das Berechenbare nachdenken und argumentieren zu können. Wie unsere bisherigen Automatenmodelle
P, NP und NP -Vollständigkeit Mit der Turing-Maschine haben wir einen Formalismus kennengelernt, um über das Berechenbare nachdenken und argumentieren zu können. Wie unsere bisherigen Automatenmodelle
Public-Key-Verschlüsselung und Diskrete Logarithmen
 Public-Key-Verschlüsselung und Diskrete Logarithmen Carsten Baum Institut für Informatik Universität Potsdam 10. Juni 2009 1 / 30 Inhaltsverzeichnis 1 Mathematische Grundlagen Gruppen, Ordnung, Primitivwurzeln
Public-Key-Verschlüsselung und Diskrete Logarithmen Carsten Baum Institut für Informatik Universität Potsdam 10. Juni 2009 1 / 30 Inhaltsverzeichnis 1 Mathematische Grundlagen Gruppen, Ordnung, Primitivwurzeln
13. Woche: NP-Vollständigkeit Satz von Cook-Levin Anwendungen in der Kryptographie
 13 Woche: NP-Vollständigkeit Satz von Cook-Levin Anwendungen in der Kryptographie 13 Woche: NP-Vollständigkeit, Satz von Cook-Levin, Anwendungen 276/ 333 N P-Vollständigkeit Ḋefinition NP-vollständig Sei
13 Woche: NP-Vollständigkeit Satz von Cook-Levin Anwendungen in der Kryptographie 13 Woche: NP-Vollständigkeit, Satz von Cook-Levin, Anwendungen 276/ 333 N P-Vollständigkeit Ḋefinition NP-vollständig Sei
Kryptographie I Symmetrische Kryptographie
 Kryptographie I Symmetrische Kryptographie Eike Kiltz 1 Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2011/12 1 Basierend auf Folien von Alexander May. Krypto I - Vorlesung 01-10.10.2011
Kryptographie I Symmetrische Kryptographie Eike Kiltz 1 Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2011/12 1 Basierend auf Folien von Alexander May. Krypto I - Vorlesung 01-10.10.2011
Digitale Unterschriften. Angriffe und Sicherheitsmodelle. Bemerkungen. Angriffe und Sicherheitsmodelle
 Digitale Unterschriften Auch digitale Signaturen genannt. Nachrichten aus Nachrichtenraum: M M. Signaturen aus Signaturenraum: σ S. Schlüssel sind aus Schlüsselräumen: d K 1, e K 2. SignierungsverfahrenS
Digitale Unterschriften Auch digitale Signaturen genannt. Nachrichten aus Nachrichtenraum: M M. Signaturen aus Signaturenraum: σ S. Schlüssel sind aus Schlüsselräumen: d K 1, e K 2. SignierungsverfahrenS
Vorlesung Theoretische Informatik (Info III)
 1 Vorlesung Theoretische Informatik (Info III) Prof. Dr. Dorothea Wagner Dipl.-Math. Martin Holzer 20. Dezember 2007 Einleitung Motivation 2 Thema heute Relative Approximation (Forts.) Approximationsschemata
1 Vorlesung Theoretische Informatik (Info III) Prof. Dr. Dorothea Wagner Dipl.-Math. Martin Holzer 20. Dezember 2007 Einleitung Motivation 2 Thema heute Relative Approximation (Forts.) Approximationsschemata
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 5. Dezember 2017 INSTITUT FÜR THEORETISCHE 0 05.12.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 5. Dezember 2017 INSTITUT FÜR THEORETISCHE 0 05.12.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Bemerkungen. Orientierung. Digitale Unterschriften. Angriffe und Sicherheitsmodelle
 Orientierung Haben bisher im Public-Key Bereich nur Verschlüsselung betrachtet. Haben dafür geeignete mathematische Strukturen und ihre Eigenschaften diskutiert. RSA, Rabin: Restklassenringe modulo n,
Orientierung Haben bisher im Public-Key Bereich nur Verschlüsselung betrachtet. Haben dafür geeignete mathematische Strukturen und ihre Eigenschaften diskutiert. RSA, Rabin: Restklassenringe modulo n,
3: Primzahlen. 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen
 3: Primzahlen 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen Definition 40 (Teiler, Vielfache, Primzahlen, zusammengesetzte Zahlen) Seien a, b N. a ist ein Teiler von b ( a b ), falls es ein k N gibt
3: Primzahlen 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen Definition 40 (Teiler, Vielfache, Primzahlen, zusammengesetzte Zahlen) Seien a, b N. a ist ein Teiler von b ( a b ), falls es ein k N gibt
6: Public-Key Kryptographie (Grundidee)
 6: Public-Key Kryptographie (Grundidee) Ein Teil des Schlüssels ist nur dem Empfänger bekannt. Der auch dem Sender bekannte Teil kann sogar veröffentlicht werden. Man spricht dann von einem Schlüsselpaar.
6: Public-Key Kryptographie (Grundidee) Ein Teil des Schlüssels ist nur dem Empfänger bekannt. Der auch dem Sender bekannte Teil kann sogar veröffentlicht werden. Man spricht dann von einem Schlüsselpaar.
3: Zahlentheorie / Primzahlen
 Stefan Lucks Diskrete Strukturen (WS 2009/10) 96 3: Zahlentheorie / Primzahlen 3: Zahlentheorie / Primzahlen Stefan Lucks Diskrete Strukturen (WS 2009/10) 97 Definition 37 (Teiler, Vielfache, Primzahlen,
Stefan Lucks Diskrete Strukturen (WS 2009/10) 96 3: Zahlentheorie / Primzahlen 3: Zahlentheorie / Primzahlen Stefan Lucks Diskrete Strukturen (WS 2009/10) 97 Definition 37 (Teiler, Vielfache, Primzahlen,
EINIGE GRUNDLAGEN DER KRYPTOGRAPHIE
 EINIGE GRUNDLAGEN DER KRYPTOGRAPHIE Steffen Reith reith@thi.uni-hannover.de 22. April 2005 Download: http://www.thi.uni-hannover.de/lehre/ss05/kry/folien/einleitung.pdf WAS IST KRYPTOGRAPHIE? Kryptographie
EINIGE GRUNDLAGEN DER KRYPTOGRAPHIE Steffen Reith reith@thi.uni-hannover.de 22. April 2005 Download: http://www.thi.uni-hannover.de/lehre/ss05/kry/folien/einleitung.pdf WAS IST KRYPTOGRAPHIE? Kryptographie
VI.4 Elgamal. - vorgestellt 1985 von Taher Elgamal. - nach RSA das wichtigste Public-Key Verfahren
 VI.4 Elgamal - vorgestellt 1985 von Taher Elgamal - nach RSA das wichtigste Public-Key Verfahren - besitzt viele unterschiedliche Varianten, abhängig von zugrunde liegender zyklischer Gruppe - Elgamal
VI.4 Elgamal - vorgestellt 1985 von Taher Elgamal - nach RSA das wichtigste Public-Key Verfahren - besitzt viele unterschiedliche Varianten, abhängig von zugrunde liegender zyklischer Gruppe - Elgamal
Der komplexitätstheoretische Zugang zur Kryptographie
 Der komplexitätstheoretische Zugang zur Kryptographie Claus Diem Im Wintersemester 2017 / 18 Literatur Oded Goldreich: Foundations of Cryptography Jonathan Katz & Yeduda Lindell: Intoduction to Modern
Der komplexitätstheoretische Zugang zur Kryptographie Claus Diem Im Wintersemester 2017 / 18 Literatur Oded Goldreich: Foundations of Cryptography Jonathan Katz & Yeduda Lindell: Intoduction to Modern
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 06. Dezember 2011 INSTITUT FÜR THEORETISCHE 0 KIT 06.12.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 06. Dezember 2011 INSTITUT FÜR THEORETISCHE 0 KIT 06.12.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Kryptographie I Symmetrische Kryptographie
 Kryptographie I Symmetrische Kryptographie Eike Kiltz 1 Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2014/15 1 Basierend auf Folien von Alexander May. Krypto - Vorlesung 01-6.10.2014
Kryptographie I Symmetrische Kryptographie Eike Kiltz 1 Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2014/15 1 Basierend auf Folien von Alexander May. Krypto - Vorlesung 01-6.10.2014
Kryptographie I Symmetrische Kryptographie
 Kryptographie I Symmetrische Kryptographie Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2012/13 Krypto I - Vorlesung 01-08.10.2012 Verschlüsselung, Kerckhoffs, Angreifer,
Kryptographie I Symmetrische Kryptographie Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2012/13 Krypto I - Vorlesung 01-08.10.2012 Verschlüsselung, Kerckhoffs, Angreifer,
Homomorphe Verschlüsselung
 Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Kryptographie I Symmetrische Kryptographie
 Kryptographie I Symmetrische Kryptographie Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2009/10 Krypto I - Vorlesung 01-12.10.2009 Verschlüsselung, Kerckhoffs, Angreifer,
Kryptographie I Symmetrische Kryptographie Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Wintersemester 2009/10 Krypto I - Vorlesung 01-12.10.2009 Verschlüsselung, Kerckhoffs, Angreifer,
Digitale Signaturen. Einführung und das Schnorr Signatur Schema. 1 Digitale Signaturen Einführung & das Schnorr Signatur Schema.
 Digitale Signaturen Einführung und das Schnorr Signatur Schema 1 Übersicht 1. Prinzip der digitalen Signatur 2. Grundlagen Hash Funktionen Diskreter Logarithmus 3. ElGamal Signatur Schema 4. Schnorr Signatur
Digitale Signaturen Einführung und das Schnorr Signatur Schema 1 Übersicht 1. Prinzip der digitalen Signatur 2. Grundlagen Hash Funktionen Diskreter Logarithmus 3. ElGamal Signatur Schema 4. Schnorr Signatur
Post-quantum cryptography
 Post-quantum cryptography Post-quantum cryptography 1. Komplexität & Quantencomputer 2. Kryptografie in Gittern 3. FHE Eine Revolution im Datenschutz? WIESO? KOMPLEXITÄT Public-Key-Kryptografie Grafiken:
Post-quantum cryptography Post-quantum cryptography 1. Komplexität & Quantencomputer 2. Kryptografie in Gittern 3. FHE Eine Revolution im Datenschutz? WIESO? KOMPLEXITÄT Public-Key-Kryptografie Grafiken:
CPA-Sicherheit ist ungenügend
 CPA-Sicherheit ist ungenügend Definition CCA CCA (=Chosen Ciphertext Attack) ist ein Angriff, bei dem der Angreifer sich Chiffretext seiner Wahl entschlüsseln lassen kann. Beispiele in denen CPA nicht
CPA-Sicherheit ist ungenügend Definition CCA CCA (=Chosen Ciphertext Attack) ist ein Angriff, bei dem der Angreifer sich Chiffretext seiner Wahl entschlüsseln lassen kann. Beispiele in denen CPA nicht
Vorlesung Digitale Signaturen im Wintersemester 2016/-17. Socrative-Fragen aus der Vorlesung vom
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Gunnar Hartung, Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2016/-17 Socrative-Fragen aus der Vorlesung vom 25.11.2016
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Gunnar Hartung, Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2016/-17 Socrative-Fragen aus der Vorlesung vom 25.11.2016
Rabin Verschlüsselung 1979
 Rabin Verschlüsselung 1979 Idee: Rabin Verschlüsselung Beobachtung: Berechnen von Wurzeln in Z p ist effizient möglich. Ziehen von Quadratwurzeln in Z N ist äquivalent zum Faktorisieren. Vorteil: CPA-Sicherheit
Rabin Verschlüsselung 1979 Idee: Rabin Verschlüsselung Beobachtung: Berechnen von Wurzeln in Z p ist effizient möglich. Ziehen von Quadratwurzeln in Z N ist äquivalent zum Faktorisieren. Vorteil: CPA-Sicherheit
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 5 Kryptosysteme auf der Basis diskreter Logarithmen 1. Diffie Hellman Schlüsselaustausch 2. El Gamal Systeme 3. Angriffe auf Diskrete Logarithmen 4. Elliptische Kurven
Kryptographie und Komplexität Einheit 5 Kryptosysteme auf der Basis diskreter Logarithmen 1. Diffie Hellman Schlüsselaustausch 2. El Gamal Systeme 3. Angriffe auf Diskrete Logarithmen 4. Elliptische Kurven
Socrative-Fragen aus der Übung vom
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Übungsleiter: Björn Kaidel, Alexander Koch Stammvorlesung Sicherheit im Sommersemester 2016 Socrative-Fragen aus der Übung vom 28.04.2016
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Übungsleiter: Björn Kaidel, Alexander Koch Stammvorlesung Sicherheit im Sommersemester 2016 Socrative-Fragen aus der Übung vom 28.04.2016
Algorithmentheorie Randomisierung
 Algorithmentheorie 03 - Randomisierung Prof. Dr. S. Albers Randomisierung Klassen von randomisierten Algorithmen Randomisierter Quicksort Randomisierter Primzahltest Kryptographie 2 1. Klassen von randomisierten
Algorithmentheorie 03 - Randomisierung Prof. Dr. S. Albers Randomisierung Klassen von randomisierten Algorithmen Randomisierter Quicksort Randomisierter Primzahltest Kryptographie 2 1. Klassen von randomisierten
Attacken auf RSA und Das Rabin Kryptosystem
 Attacken auf RSA und Das Rabin Kryptosystem Institut für Informatik Universität Potsdam 4. Januar 2005 Überblick Wiederholung: RSA Das RSA Kryptosystem Attacken auf RSA RSA-FACTOR Wieners Algorithmus Das
Attacken auf RSA und Das Rabin Kryptosystem Institut für Informatik Universität Potsdam 4. Januar 2005 Überblick Wiederholung: RSA Das RSA Kryptosystem Attacken auf RSA RSA-FACTOR Wieners Algorithmus Das
Public Key Kryptographie
 3. Juni 2006 1 Algorithmen für Langzahlen 1 RSA 1 Das Rabin-Kryptosystem 1 Diskrete Logarithmen Grundlagen der PK Kryptographie Bisher: Ein Schlüssel für Sender und Empfänger ( Secret-Key oder symmetrische
3. Juni 2006 1 Algorithmen für Langzahlen 1 RSA 1 Das Rabin-Kryptosystem 1 Diskrete Logarithmen Grundlagen der PK Kryptographie Bisher: Ein Schlüssel für Sender und Empfänger ( Secret-Key oder symmetrische
Quantenalgorithmus für die Faktorisierung ganzer Zahlen
 Quantenalgorithmus für die Faktorisierung ganzer Zahlen Ausgehend von dem allgemeinen Algorithmus für das Hidden Subgroup Problem behandlen wir in diesem Abschnitt den Quantenalgorithmus für die Faktorisierung
Quantenalgorithmus für die Faktorisierung ganzer Zahlen Ausgehend von dem allgemeinen Algorithmus für das Hidden Subgroup Problem behandlen wir in diesem Abschnitt den Quantenalgorithmus für die Faktorisierung
Das Rucksackproblem: schwache NP-Härte und Approximation
 Das Rucksackproblem: schwache NP-Härte und Approximation Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1. Februar 2010 Berthold Vöcking, Informatik 1 () Vorlesung
Das Rucksackproblem: schwache NP-Härte und Approximation Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1. Februar 2010 Berthold Vöcking, Informatik 1 () Vorlesung
Der LLL-Algorithmus. Konrad Schade. January 19, 2007
 January 19, 2007 Gliederung Allgemeines Ziel Vor- und Nachteil des LLL-Algorithmuses Gliederung Allgemeines Ziel Vor- und Nachteil des LLL-Algorithmuses enthaelt in seinem Namen auch die Namen seiner Erfinder,
January 19, 2007 Gliederung Allgemeines Ziel Vor- und Nachteil des LLL-Algorithmuses Gliederung Allgemeines Ziel Vor- und Nachteil des LLL-Algorithmuses enthaelt in seinem Namen auch die Namen seiner Erfinder,
Kryptographie - eine mathematische Einführung
 Kryptographie - eine mathematische Einführung Rosa Freund 28. Dezember 2004 Überblick Grundlegende Fragestellungen Symmetrische Verschlüsselung: Blockchiffren, Hashfunktionen
Kryptographie - eine mathematische Einführung Rosa Freund 28. Dezember 2004 Überblick Grundlegende Fragestellungen Symmetrische Verschlüsselung: Blockchiffren, Hashfunktionen
Lösungsblatt zur Vorlesung. Kryptanalyse WS 2009/2010. Blatt 6 / 23. Dezember 2009 / Abgabe bis spätestens 20. Januar 2010, 10 Uhr (vor der Übung)
 Ruhr-Universität Bochum Lehrstuhl für Kryptologie und IT-Sicherheit Prof. Dr. Alexander May Mathias Herrmann, Alexander Meurer Lösungsblatt zur Vorlesung Kryptanalyse WS 2009/2010 Blatt 6 / 23. Dezember
Ruhr-Universität Bochum Lehrstuhl für Kryptologie und IT-Sicherheit Prof. Dr. Alexander May Mathias Herrmann, Alexander Meurer Lösungsblatt zur Vorlesung Kryptanalyse WS 2009/2010 Blatt 6 / 23. Dezember
Miller-Rabin Test. Primzahl- und Zerlegbarkeitstests. Zeugen für die Zerlegbarkeit ganzer Zahlen
 Miller-Rabin Test Primzahl- und Zerlegbarkeitstests Sei N eine positive ganze Zahl. Wie kann man möglichst effizient feststellen, ob N eine Primzahl oder zerlegbar ist? Dies ist die Aufgabe von Primzahlund
Miller-Rabin Test Primzahl- und Zerlegbarkeitstests Sei N eine positive ganze Zahl. Wie kann man möglichst effizient feststellen, ob N eine Primzahl oder zerlegbar ist? Dies ist die Aufgabe von Primzahlund
Ziel: Zertifiziere Pfad von Wurzel zu m mittels Signaturen. Signieren Public-Keys auf Pfad inklusive der Nachbarknoten.
 Merkle-Baum Idee: Konstruktion von Merkle-Bäumen Ersetze Signaturkette durch Baum (sogenannter Merkle-Baum). Verwenden Baum der Tiefe n für Nachrichten der Länge n. Die Wurzel erhält Label ɛ. Die Kinder
Merkle-Baum Idee: Konstruktion von Merkle-Bäumen Ersetze Signaturkette durch Baum (sogenannter Merkle-Baum). Verwenden Baum der Tiefe n für Nachrichten der Länge n. Die Wurzel erhält Label ɛ. Die Kinder
Lösungen zur Vorlesung Berechenbarkeit und Komplexität
 Lehrstuhl für Informatik 1 WS 009/10 Prof. Dr. Berthold Vöcking 0.0.010 Alexander Skopalik Thomas Kesselheim Lösungen zur Vorlesung Berechenbarkeit und Komplexität. Zulassungsklausur Aufgabe 1: (a) Worin
Lehrstuhl für Informatik 1 WS 009/10 Prof. Dr. Berthold Vöcking 0.0.010 Alexander Skopalik Thomas Kesselheim Lösungen zur Vorlesung Berechenbarkeit und Komplexität. Zulassungsklausur Aufgabe 1: (a) Worin
Einführung in die asymmetrische Kryptographie
 !"#$$% Einführung in die asymmetrische Kryptographie Dipl.-Inform. Mel Wahl Prof. Dr. Christoph Ruland Universität Siegen Institut für digitale Kommunikationssysteme Grundlagen Verschlüsselung Digitale
!"#$$% Einführung in die asymmetrische Kryptographie Dipl.-Inform. Mel Wahl Prof. Dr. Christoph Ruland Universität Siegen Institut für digitale Kommunikationssysteme Grundlagen Verschlüsselung Digitale
VI.3 RSA. - RSA benannt nach seinen Erfindern R. Rivest, A. Shamir und L. Adleman. - vorgestellt erstes Public-Key Verschlüsselungsverfahren
 VI.3 RSA - RSA benannt nach seinen Erfindern R. Rivest, A. Shamir und L. Adleman - vorgestellt 1977 - erstes Public-Key Verschlüsselungsverfahren - auch heute noch das wichtigste Public-Key Verfahren 1
VI.3 RSA - RSA benannt nach seinen Erfindern R. Rivest, A. Shamir und L. Adleman - vorgestellt 1977 - erstes Public-Key Verschlüsselungsverfahren - auch heute noch das wichtigste Public-Key Verfahren 1
Vortrag 20: Kurze Vektoren in Gittern
 Seminar: Wie genau ist ungefähr Vortrag 20: Kurze Vektoren in Gittern Kerstin Bauer Sommerakademie Görlitz, 2007 Definition und Problembeschreibung Definition: Gitter Seien b 1,,b k Q n. Dann heißt die
Seminar: Wie genau ist ungefähr Vortrag 20: Kurze Vektoren in Gittern Kerstin Bauer Sommerakademie Görlitz, 2007 Definition und Problembeschreibung Definition: Gitter Seien b 1,,b k Q n. Dann heißt die
Theorie der Informatik. Theorie der Informatik P und NP Polynomielle Reduktionen NP-Härte und NP-Vollständigkeit
 Theorie der Informatik 13. Mai 2015 20. P, NP und polynomielle Reduktionen Theorie der Informatik 20. P, NP und polynomielle Reduktionen 20.1 P und NP Malte Helmert Gabriele Röger 20.2 Polynomielle Reduktionen
Theorie der Informatik 13. Mai 2015 20. P, NP und polynomielle Reduktionen Theorie der Informatik 20. P, NP und polynomielle Reduktionen 20.1 P und NP Malte Helmert Gabriele Röger 20.2 Polynomielle Reduktionen
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Klausur Hinweise
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Klausur 21.07.2015 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Klausur 21.07.2015 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Sicherheit von Merkle Signaturen
 Sicherheit von Merkle Signaturen Algorithmus Angreifer A für die Einwegsignatur EINGABE: pk, Zugriff auf eine Anfrage an Orakel Sign sk ( ) 1 Berechne (pk (i), sk (i) ) Gen(1 n ) für i = 1,...,l. Wähle
Sicherheit von Merkle Signaturen Algorithmus Angreifer A für die Einwegsignatur EINGABE: pk, Zugriff auf eine Anfrage an Orakel Sign sk ( ) 1 Berechne (pk (i), sk (i) ) Gen(1 n ) für i = 1,...,l. Wähle
Quantenkryptographie
 Quantenkryptographie Tobias Mühlbauer Technische Universität München Hauptseminar Kryptographische Protokolle 2009 Outline 1 Motivation Klassische Kryptographie Alternativen zur klassischen Kryptographie
Quantenkryptographie Tobias Mühlbauer Technische Universität München Hauptseminar Kryptographische Protokolle 2009 Outline 1 Motivation Klassische Kryptographie Alternativen zur klassischen Kryptographie
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 5.2 ElGamal Systeme 1. Verschlüsselungsverfahren 2. Korrektheit und Komplexität 3. Sicherheitsaspekte Das ElGamal Verschlüsselungsverfahren Public-Key Verfahren von
Kryptographie und Komplexität Einheit 5.2 ElGamal Systeme 1. Verschlüsselungsverfahren 2. Korrektheit und Komplexität 3. Sicherheitsaspekte Das ElGamal Verschlüsselungsverfahren Public-Key Verfahren von
3 Probabilistische Komplexitätsklassen
 3 Probabilistische Komplexitätsklassen 3.1 Probabilistische Turingmaschinen 3.1 Wir gehen davon aus, dass die Konzepte deterministischer und nichtdeterministischer Turingmaschinen im wesentlichen bekannt
3 Probabilistische Komplexitätsklassen 3.1 Probabilistische Turingmaschinen 3.1 Wir gehen davon aus, dass die Konzepte deterministischer und nichtdeterministischer Turingmaschinen im wesentlichen bekannt
Abschnitt 5: Kryptographie. j (p j 1). 1 (p 1 1)p α 2
 Abschnitt 5: Kryptographie. Zunächst wollen wir die Struktur von (Z/mZ) untersuchen. 5.1 Definition: Die Eulersche ϕ-funktion: ϕ : N N; ϕ(m) := (Z/mZ) 5.2 Bemerkung: (Z/mZ) {a {1,..., m 1} ggt(a, m) =
Abschnitt 5: Kryptographie. Zunächst wollen wir die Struktur von (Z/mZ) untersuchen. 5.1 Definition: Die Eulersche ϕ-funktion: ϕ : N N; ϕ(m) := (Z/mZ) 5.2 Bemerkung: (Z/mZ) {a {1,..., m 1} ggt(a, m) =
1. Welche Eigenschaften sollte ein Pseudo-Random Generator haben?
 Die Themen 1. Welche Eigenschaften sollte ein Pseudo-Random Generator haben? Er sollte von wirklichen Zufallsgeneratoren nicht unterscheidbar sein?! Eine viel zu starke Forderung: Stattdessen sollte ein
Die Themen 1. Welche Eigenschaften sollte ein Pseudo-Random Generator haben? Er sollte von wirklichen Zufallsgeneratoren nicht unterscheidbar sein?! Eine viel zu starke Forderung: Stattdessen sollte ein
Prinzipien der modernen Kryptographie Sicherheit
 Prinzipien der modernen Kryptographie Sicherheit Prinzip 1 Sicherheitsmodell Das Sicherheitsmodell (Berechnungsmodell, Angriffstypen, Sicherheitsziele) muss präzise definiert werden. Berechnungsmodell:
Prinzipien der modernen Kryptographie Sicherheit Prinzip 1 Sicherheitsmodell Das Sicherheitsmodell (Berechnungsmodell, Angriffstypen, Sicherheitsziele) muss präzise definiert werden. Berechnungsmodell:
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 23.06.2014 1 / 26 Überblick 1 Zero-Knowledge-Protokolle Erinnerung Beispiel für Zero-Knowledge-Protokoll Analyse des Beispiel-Zero-Knowledge-Protokolls Proof-of-Knowledge-Eigenschaft
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 23.06.2014 1 / 26 Überblick 1 Zero-Knowledge-Protokolle Erinnerung Beispiel für Zero-Knowledge-Protokoll Analyse des Beispiel-Zero-Knowledge-Protokolls Proof-of-Knowledge-Eigenschaft
Volker Kaatz. Faktorisierung. Faktorisierung. Problem und Algorithmen. Relevanz in der Kryptographie
 Faktorisierung Problem und Algorithmen Relevanz in der Kryptographie Inhalt Begriff Faktorisierung Algorithmen (Übersicht) Strategie und Komplexität Pollard p-1 Algorithmus Pseudocode, mathematische Basis,
Faktorisierung Problem und Algorithmen Relevanz in der Kryptographie Inhalt Begriff Faktorisierung Algorithmen (Übersicht) Strategie und Komplexität Pollard p-1 Algorithmus Pseudocode, mathematische Basis,
Digitale Signaturen. GHR-und Chamäleon-Signaturen Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen GHR-und Chamäleon-Signaturen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-12-15 B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen KIT
Digitale Signaturen GHR-und Chamäleon-Signaturen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-12-15 B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen KIT
Elliptische Kurven und ihre Anwendung in der Kryptographie
 Elliptische Kurven und ihre Anwendung in der Kryptographie Carsten Baum Institut für Informatik Universität Potsdam 17. Juni 2009 1 / 29 Inhaltsverzeichnis 1 Mathematische Grundlagen Charakteristik eines
Elliptische Kurven und ihre Anwendung in der Kryptographie Carsten Baum Institut für Informatik Universität Potsdam 17. Juni 2009 1 / 29 Inhaltsverzeichnis 1 Mathematische Grundlagen Charakteristik eines
Vorlesung Sicherheit
 Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 18.05.2015 1 / 30 Überblick 1 Asymmetrische Authentifikation von Nachrichten Erinnerung
Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 18.05.2015 1 / 30 Überblick 1 Asymmetrische Authentifikation von Nachrichten Erinnerung
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Nachklausur Hinweise
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2016 Nachklausur 12.10.2016 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2016 Nachklausur 12.10.2016 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 6.2 Digitale Signaturen 1. Sicherheitsanforderungen 2. RSA Signaturen 3. ElGamal Signaturen Wozu Unterschriften? Verbindliche Urheberschaft von Dokumenten Unterschrift
Kryptographie und Komplexität Einheit 6.2 Digitale Signaturen 1. Sicherheitsanforderungen 2. RSA Signaturen 3. ElGamal Signaturen Wozu Unterschriften? Verbindliche Urheberschaft von Dokumenten Unterschrift
Herausforderungen an den Datenschutz und die Sicherheit nutzerbezogener Verbrauchsdaten. -Datenschutzfragen zum Messsystem-
 Herausforderungen an den Datenschutz und die Sicherheit nutzerbezogener Verbrauchsdaten -Datenschutzfragen zum Messsystem- Umsetzung Ziel Datenschutz und -Sicherheit Die schutzwürdigen Interessen der Betroffenen
Herausforderungen an den Datenschutz und die Sicherheit nutzerbezogener Verbrauchsdaten -Datenschutzfragen zum Messsystem- Umsetzung Ziel Datenschutz und -Sicherheit Die schutzwürdigen Interessen der Betroffenen
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Proseminar Schlüsselaustausch (Diffie - Hellman)
 Proseminar Schlüsselaustausch (Diffie - Hellman) Schlüsselaustausch Mathematische Grundlagen Das DH Protokoll Sicherheit Anwendung 23.06.2009 Proseminar Kryptographische Protokolle SS 2009 : Diffie Hellman
Proseminar Schlüsselaustausch (Diffie - Hellman) Schlüsselaustausch Mathematische Grundlagen Das DH Protokoll Sicherheit Anwendung 23.06.2009 Proseminar Kryptographische Protokolle SS 2009 : Diffie Hellman
Miller-Rabin Test. Primzahl- und Zerlegbarkeitstests. Zeugen für die Zerlegbarkeit ganzer Zahlen
 Miller-Rabin Test Primzahl- und Zerlegbarkeitstests Sei N eine positive ganze Zahl. Wie kann man möglichst effizient feststellen, ob N eine Primzahl oder zerlegbar ist? Dies ist die Aufgabe von Primzahlund
Miller-Rabin Test Primzahl- und Zerlegbarkeitstests Sei N eine positive ganze Zahl. Wie kann man möglichst effizient feststellen, ob N eine Primzahl oder zerlegbar ist? Dies ist die Aufgabe von Primzahlund
Theoretische Informatik II
 Theoretische Informatik II Einheit 5.2 Das P N P Problem 1. Nichtdeterministische Lösbarkeit 2. Sind N P-Probleme handhabbar? 3. N P-Vollständigkeit Bei vielen schweren Problemen ist Erfolg leicht zu testen
Theoretische Informatik II Einheit 5.2 Das P N P Problem 1. Nichtdeterministische Lösbarkeit 2. Sind N P-Probleme handhabbar? 3. N P-Vollständigkeit Bei vielen schweren Problemen ist Erfolg leicht zu testen
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Public-Key-Kryptographie
 Kapitel 2 Public-Key-Kryptographie In diesem Kapitel soll eine kurze Einführung in die Kryptographie des 20. Jahrhunderts und die damit verbundene Entstehung von Public-Key Verfahren gegeben werden. Es
Kapitel 2 Public-Key-Kryptographie In diesem Kapitel soll eine kurze Einführung in die Kryptographie des 20. Jahrhunderts und die damit verbundene Entstehung von Public-Key Verfahren gegeben werden. Es
Theoretische Informatik. Exkurs: Komplexität von Optimierungsproblemen. Optimierungsprobleme. Optimierungsprobleme. Exkurs Optimierungsprobleme
 Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
Einwegfunktionen. Problemseminar. Komplexitätstheorie und Kryptographie. Martin Huschenbett. 30. Oktober 2008
 Problemseminar Komplexitätstheorie und Kryptographie Martin Huschenbett Student am Institut für Informatik an der Universität Leipzig 30. Oktober 2008 1 / 33 Gliederung 1 Randomisierte Algorithmen und
Problemseminar Komplexitätstheorie und Kryptographie Martin Huschenbett Student am Institut für Informatik an der Universität Leipzig 30. Oktober 2008 1 / 33 Gliederung 1 Randomisierte Algorithmen und
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 12.05.2014 1 / 26 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 12.05.2014 1 / 26 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
2 Komplexitätstheorie
 2 Komplexitätstheorie Bemerkung: Einige der im Folgenden verwendeten Begriffe werden nicht präzise definiert, da dies den Rahmen dieser Veranstaltung sprengen würde. Wer die exakten Termini nachlesen möchte,
2 Komplexitätstheorie Bemerkung: Einige der im Folgenden verwendeten Begriffe werden nicht präzise definiert, da dies den Rahmen dieser Veranstaltung sprengen würde. Wer die exakten Termini nachlesen möchte,
Beliebige Anzahl von Signaturen
 Beliebige Anzahl von Signaturen Algorithmus Signaturketten Sei Π = (Gen, Sign, Vrfy) ein Einwegsignaturverfahren. 1 Gen : (pk 1, sk 1 ) Gen(1 n ) 2 Sign : Signieren der Nachricht m i. Verwende gemerkten
Beliebige Anzahl von Signaturen Algorithmus Signaturketten Sei Π = (Gen, Sign, Vrfy) ein Einwegsignaturverfahren. 1 Gen : (pk 1, sk 1 ) Gen(1 n ) 2 Sign : Signieren der Nachricht m i. Verwende gemerkten
Lösung zur Klausur zu Krypographie Sommersemester 2005
 Lösung zur Klausur zu Krypographie Sommersemester 2005 1. Bestimmen Sie die zwei letzten Ziffern der Dezimaldarstellung von 12 34 Es gilt: 12 34 = 12 32+2 = 12 32 12 2 = 12 (25) 12 2 = ((((12 2 ) 2 ) 2
Lösung zur Klausur zu Krypographie Sommersemester 2005 1. Bestimmen Sie die zwei letzten Ziffern der Dezimaldarstellung von 12 34 Es gilt: 12 34 = 12 32+2 = 12 32 12 2 = 12 (25) 12 2 = ((((12 2 ) 2 ) 2
Digitale Signaturen. Einführung Gunnar Hartung, Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Einführung Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-10-21 G. Hartung, B. Kaidel Digitale Signaturen: Einführung KIT Die Forschungsuniversität
Digitale Signaturen Einführung Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-10-21 G. Hartung, B. Kaidel Digitale Signaturen: Einführung KIT Die Forschungsuniversität
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Vorlesung 4 Alexander Koch (Vertretung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT 2015-11-12 Universität desalexander Landes Baden-Württemberg
Asymmetrische Verschlüsselungsverfahren Vorlesung 4 Alexander Koch (Vertretung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT 2015-11-12 Universität desalexander Landes Baden-Württemberg
Polynomialzeit- Approximationsschema
 Polynomialzeit- Approximationsschema 27.01.2012 Elisabeth Sommerauer, Nicholas Höllermeier Inhalt 1.NP-Vollständigkeit Was ist NP-Vollständigkeit? Die Klassen P und NP Entscheidungsproblem vs. Optimierungsproblem
Polynomialzeit- Approximationsschema 27.01.2012 Elisabeth Sommerauer, Nicholas Höllermeier Inhalt 1.NP-Vollständigkeit Was ist NP-Vollständigkeit? Die Klassen P und NP Entscheidungsproblem vs. Optimierungsproblem
Kurzskript MfI:AGS WS 2018/19 Teil II: Gruppen / Teil III: Ringe 34
 Kurzskript MfI:AGS WS 2018/19 Teil II: Gruppen / Teil III: Ringe 34 Satz 4.2.11 (Chinesischer Restsatz, Ring-Version) Sind N teilerfremd (d.h. ggt( ) =1), so ist die Abbildung ein Ring-Isomorphismus. :
Kurzskript MfI:AGS WS 2018/19 Teil II: Gruppen / Teil III: Ringe 34 Satz 4.2.11 (Chinesischer Restsatz, Ring-Version) Sind N teilerfremd (d.h. ggt( ) =1), so ist die Abbildung ein Ring-Isomorphismus. :
Teil III. Komplexitätstheorie
 Teil III Komplexitätstheorie 125 / 160 Übersicht Die Klassen P und NP Die Klasse P Die Klassen NP NP-Vollständigkeit NP-Vollständige Probleme Weitere NP-vollständige Probleme 127 / 160 Die Klasse P Ein
Teil III Komplexitätstheorie 125 / 160 Übersicht Die Klassen P und NP Die Klasse P Die Klassen NP NP-Vollständigkeit NP-Vollständige Probleme Weitere NP-vollständige Probleme 127 / 160 Die Klasse P Ein
subexponentielle Algorithmen (d.h. Laufzeiten wie z. B. 2 n oder
 Wie schwer ist SAT? Ziel: Nachweis, dass SAT eines der schwersten Probleme in NP ist: SAT ist das erste bekannte Beispiel eines NP-vollständigen Problems. Demnach kann SAT mit bisher bekannten Techniken
Wie schwer ist SAT? Ziel: Nachweis, dass SAT eines der schwersten Probleme in NP ist: SAT ist das erste bekannte Beispiel eines NP-vollständigen Problems. Demnach kann SAT mit bisher bekannten Techniken
Gitter in der Kryptographie
 Gitter in der Kryptographie Diplomarbeit Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Fakultät II Institut für Informatik eingereicht von: Betreuer: Kay Schönberger Prof. Dr. Johannes
Gitter in der Kryptographie Diplomarbeit Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Fakultät II Institut für Informatik eingereicht von: Betreuer: Kay Schönberger Prof. Dr. Johannes
Nichtdeterministische Platzklassen
 Sommerakademie 2010 Rot an der Rot AG 1: Wieviel Platz brauchen Algorithmen wirklich? Nichtdeterministische Platzklassen Ulf Kulau August 23, 2010 1 Contents 1 Einführung 3 2 Nichtdeterminismus allgemein
Sommerakademie 2010 Rot an der Rot AG 1: Wieviel Platz brauchen Algorithmen wirklich? Nichtdeterministische Platzklassen Ulf Kulau August 23, 2010 1 Contents 1 Einführung 3 2 Nichtdeterminismus allgemein
IT-Sicherheit Kapitel 4 Public Key Algorithmen
 IT-Sicherheit Kapitel 4 Public Key Algorithmen Dr. Christian Rathgeb Sommersemester 2014 1 Einführung Der private Schlüssel kann nicht effizient aus dem öffentlichen Schlüssel bestimmt werden bzw. die
IT-Sicherheit Kapitel 4 Public Key Algorithmen Dr. Christian Rathgeb Sommersemester 2014 1 Einführung Der private Schlüssel kann nicht effizient aus dem öffentlichen Schlüssel bestimmt werden bzw. die
Satz von Euler. Satz von Euler. Korollar 1. Korollar 2 Kleiner Fermat. Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G.
 Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Satz von Euler. Satz von Euler. Korollar 1. Korollar 2 Kleiner Fermat. Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G.
 Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
VIII. Digitale Signaturen
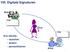 VIII. Digitale Signaturen Bob Eve Eve möchte - lauschen - ändern - personifizieren Alice 1 Aufgaben - Vertraulichkeit - Lauschen - Authentizität - Tauschen des Datenursprungs - Integrität - Änderung der
VIII. Digitale Signaturen Bob Eve Eve möchte - lauschen - ändern - personifizieren Alice 1 Aufgaben - Vertraulichkeit - Lauschen - Authentizität - Tauschen des Datenursprungs - Integrität - Änderung der
Aufgabe Mögliche Punkte Erreichte Punkte a b c d Σ a b c d Σ x1 13
 Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 2003/04 ILKD Prof. Dr. D. Wagner 14. April 2004 2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004 Hier Aufkleber
Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 2003/04 ILKD Prof. Dr. D. Wagner 14. April 2004 2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004 Hier Aufkleber
Das RSA-Verfahren. Proseminar Kryptographische Protokolle SS Armin Litzel
 in der Praxis Proseminar Kryptographische Protokolle SS 2009 5.5.2009 in der Praxis Gliederung 1 Grundlegendes über RSA 2 in der Praxis Allgemeine Vorgehensweise zur Verschlüsselung Signieren mit RSA 3
in der Praxis Proseminar Kryptographische Protokolle SS 2009 5.5.2009 in der Praxis Gliederung 1 Grundlegendes über RSA 2 in der Praxis Allgemeine Vorgehensweise zur Verschlüsselung Signieren mit RSA 3
Prinzipien der modernen Kryptographie Sicherheit
 Prinzipien der modernen Kryptographie Sicherheit Prinzip 1 Sicherheitsziel Die Sicherheitsziele müssen präzise definiert werden. Beispiele für ungenügende Definitionen von Sicherheit Kein Angreifer kann
Prinzipien der modernen Kryptographie Sicherheit Prinzip 1 Sicherheitsziel Die Sicherheitsziele müssen präzise definiert werden. Beispiele für ungenügende Definitionen von Sicherheit Kein Angreifer kann
Informatik III - WS07/08
 Informatik III - WS07/08 Kapitel 4 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 4 : Komplexitätsklassen Informatik III - WS07/08 Kapitel 4 2 Sprachen, Probleme, Zeitkomplexität
Informatik III - WS07/08 Kapitel 4 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 4 : Komplexitätsklassen Informatik III - WS07/08 Kapitel 4 2 Sprachen, Probleme, Zeitkomplexität
Die Komplexitätsklassen P und NP
 Die Komplexitätsklassen P und NP Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Die Komplexitätsklassen P und NP Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 23. November 2017 INSTITUT FÜR THEORETISCHE 0 23.11.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 23. November 2017 INSTITUT FÜR THEORETISCHE 0 23.11.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 08.05.2017 1 / 32 Überblick 1 Blockchiffren Erinnerung Varianten von DES Beispiel: AES Angriffe auf Blockchiffren 2 Formalisierung von Sicherheit (symmetrischer
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 08.05.2017 1 / 32 Überblick 1 Blockchiffren Erinnerung Varianten von DES Beispiel: AES Angriffe auf Blockchiffren 2 Formalisierung von Sicherheit (symmetrischer
