Probabilistische Algorithmen
|
|
|
- Eike Weber
- vor 7 Jahren
- Abrufe
Transkript
1 Proseminar Theoretische Informatik Diane Hanke, Alexander Korzec Probabilistische Algorithmen Wolfgang Mulzer 1 Einführung 1.1 Probabilistischer Algorithmus Definition 1. [Probabilistischer Algorithmus]: Ein probabilistischer Algorithmus ist ein Algorithmus, der zufallsbasiert arbeitet. Entscheidungen werden per Zufall getroffen. Ihre Arbeitsweise lässt sich interpretieren als Münzwurf mit fairer Münze, wobei das Ergebnis des Münzwurfes das Verhalten des probabilistischen Algorithmus beeinflusst. 1.2 Probabilistische Turingmaschine Definition 2. [Probabilistische Turingmaschine]: Eine probabilistische Turingmaschine (PTM) ist ein Typ einer nichtdeterministischen Turingmaschine mit genau zwei Übergangsfunktionen δ 1 und δ 2. In jedem Berechnungsschritt einer PTM M wird mittels Zufall eine der beiden Übergangsfunktionen für den nächsten Schritt gewählt. Es wird jeweils mit einer Wahrscheinlichkeit von 1 2 die Übergangsfunktion δ 1 oder δ 2 gewählt. Diese Wahl ist unabhängig von den vorausgegangenen Wahlen. Eine PTM kann am Ende einer Berechnung entweder eine Eingabe akzeptieren oder verwerfen. Mit M(x) beschreiben wir eine Zufallsvariable, die den Wert von einer PTM M am Ende einer Berechnung angibt. Sei T : N N eine Funktion. Wir sagen, dass M in T(n) Zeit läuft, wenn M für alle Eingaben x Σ in T ( x ) Zeit hält, unabhängig von den zufälligen Entscheidungen von der Übergangsfunktion δ 1 und δ 2 in jedem Berechnungsschritt PTM als Berechnungsbaum Wir können uns die Berechnungen einer nichtdeterministischen TM N als einen Berechnungsbaum vorstellen. Die nichtdeterministischen Wahlen von N können wir als Münzwürfe interpretieren. Wenn b ein Knoten in einem solchen Berechnungsbaum ist, dann ist die Wahrscheinlichkeit zum Erreichen von b wie folgt definiert: P r[b] = 2 k Dabei ist k die Anzahl der Übergänge in diesem Berechnungsbaum bis zum Knoten b. Die Wahrscheinlichkeit, dass eine PTM M ein Wort w Σ als Eingabe akzeptiert sei definiert als: 1
2 P r[m akzeptiert w] = P r[b] b = akz. Knoten Entsprechend ergibt sich für die Wahrscheinlichkeit, dass M eine Eingabe w verwirft: P r[m verwirft w] = 1 P r[m akzeptiert w] 2 Die Komplexitätsklasse BPP Wir wollen nun eine neue Komplexitätsklasse einführen, um Probleme untersuchen zu können. Dazu wollen wir zunächst definieren, was wir unter Fehlerwahrscheinlichkeit verstehen. 2.1 Fehlerwahrscheinlichkeit Definition 3. [Fehlerwahrscheinlichkeit]: Wenn eine PTM M eine Sprache L Σ akzeptiert, dann sei die Fehlerwahrscheinlichkeit ɛ, für 0 ɛ < 1 2 definiert durch: w L P r[m akzeptiert w] 1 ɛ w / L P r[m verwirft w] 1 ɛ Wir suchen nach probabilistischen Algorithmen, die effizient arbeiten in Bezug auf Zeit und Platz. Wir messen die Komplexität bei probabilistischen Turingmaschinen, wie auch bei nichtdeterministischen Turingmaschinen, durch die Betrachtung des worst-case Pfades für jede Eingabe w Σ ( = längster Berechnungspfad). Wir definieren eine neue Komplexitätsklasse BPP, welche die Klasse von Sprachen beinhaltet, die von probabilistischen Turingmaschinen in polynomieller Zeit mit einer bestimmten Fehlerwahrscheinlichkeit erkannt werden. 2.2 BPTIME und BPP Definition 4. [BPTIME und BPP]: Sei T: N N eine Funktion und L Σ ein Entscheidungsproblem. Eine PTM M entscheidet eine Sprache L in T (n) Zeit, wenn für alle x Σ die PTM M in T ( x ) Zeit hält, unabhängig von den zufälligen Wahlen der Berechnungsschritte mit einer Fehlerwahrscheinlichkeit von ɛ, wobei 0 < ɛ < 1 2 Wir definieren BPTIME(T(n)) als die Menge aller Sprachen, welche sich durch eine PTM in O(T (n)) Zeit entscheiden lassen: BP T IME(T (n)) := {L Σ L ist von einer PTM in O(T (n)) Zeit entscheidbar } Wir wollen BPP wie folgt definieren: BPP := BP T IME(n c ) c N 2
3 Das Erstaunliche ist, dass wir ɛ beliebig aus dem vorgegebenen Intervall auswählen können. Das bedeutet, wenn wir BPP mit jeweils ɛ 1 = 1/3 und ɛ 2 = 4/129 wählen, dann erhalten wir die gleiche Komplexitätsklasse. Daher kann man BPP auch folgendermaßen definieren: Definition 5. [Alternative Definition von BPP]: BPP sei definiert als die Klasse von Sprachen, die von einer probabilistischen TM in polynomieller Zeit mit einer Fehlerwahrscheinlichkeit von ɛ = 1 3 erkannt werden. Das beide Definitionen äquivalent sind, rechtfertigt das amplification lemma. Lemma 6. [Amplification lemma für BPP]: Jede konstante Fehlerwahrscheinlichkeit würde eine äquivalente Definition liefern, solange sich die Fehlerwahrscheinlichkeit, die gewählt wird, strikt zwischen 0 und 1 2 liegt. Sei 0 < ɛ < 1/2 fest gewählt. Dann gilt für jedes Polynom poly(n), dass es eine PTM M 1 gibt, die mit einer Fehlerwahrscheinlichkeit von ɛ arbeitet, eine äquivalente PTM M 2 existiert, die mit einer Fehlerwahrscheinlichkeit von 2 poly(n) arbeitet. Beweis. Sei eine TM M 1 gegeben, die eine Sprache mit einer Fehlerwahrscheinlichkeit von ɛ < 1 2 erkennt. Wir konstruieren eine zweite TM M 2, die die gleiche Sprache erkennt mit einer Fehlerwahrscheinlichkeit von 2 poly(n). M 2 = Für eine Eingabe w: 1. Berechne k 2. Führe 2k unabhängige Simulationen von M 1 auf der Eingabe w durch 3. wenn die Mehrheit der Durchläufe von M 1 w akzeptiert, dann akzeptiere die Eingabe, ansonsten verwirf die Eingabe Wir wollen abschätzen, wie hoch die Anzahl der Sequenzen der Länge 2k ist, sodass M 2 die falsche Antwort liefert. Bei jeder Simulation von M 1 ist das Ergebnis entweder falsch oder richtig; sind die meisten Ergebnisse richtig, gibt M 2 die richtige Antwort. Wir nehmen an, dass mindestens die Hälfte der Ergebnisse falsch sind. Sei S die Sequenz von Ergebnissen, die M 2 in Schritt 2 liefert. Sei p S die Wahrscheinlichkeit, dass M 2 die Sequenz S erhält. S hat r richtige Ergebnisse und f falsche Ergebnisse. Dann gilt: r + f = 2k Wenn r f und M 2 S erhält, gibt M 2 ein falsches Ergebnis aus und wir nennen eine solche Sequenz bad sequence. Wenn S irgendeine bad sequence ist, dann gilt:. p S ɛ f (1 ɛ) r ɛ k (1 ɛ) k, wegen k f, ɛ < 1 ɛ und ɛ < 1 2 3
4 Die Summe aller p S für jede S ergibt die Wahrscheinlichkeit, dass M 2 ein falsches Ergebnis liefert. Wir haben insgesamt 2 2k Sequenzen und wir nehmen an, dass alle S bad sequences sein können (also auch 2 2k ). Dann gilt: P r[m 2 liefert bei Eingabe w ein falsches Ergebnis] = S ist bad sequence wir haben angenommen: ɛ < 1 2, sodass gilt: 4ɛ(1 ɛ) < 1 p s 2 2k ɛ k (1 ɛ) k = (4ɛ(1 ɛ)) k die Wahrscheinlichkeit dafür, dass wir in M 2 einen Fehler machen, nimmt exponentiell mit der Anzahl an Durchläufen ab um k genau zu berechnen, sodass wir eine Fehlerwahrscheinlichkeit für M 2 von 2 t, für jedes t 1, festlegen können, definieren wir: und wählen α = log(4ɛ(1 ɛ)) k t/α Dann erhalten wir eine Fehlerwahrscheinlichkeit von 2 poly(n) in polynomieller Zeit. 3 Primzahlen In diesem Abschnitt betrachten wir das folgende Problem: PRIMES Gegeben: Eine Zahl n N Frage: Ist n eine Primzahl? Es ist die Frage zu klären, wieso dieses Problem nicht trivial lösbar ist. Betrachten wir folgenden naiven Ansatz: 1. teste für alle a = {2,..., n }, ob ein a ein Teiler von n ist 2. akzeptiere Eingabe, falls kein Test in 1. erfolgreich, sonst verwirf Die Anzahl der Iterationen ist O( n). Das ist leider nur pseudopolynomiell, da man mit n Bits eine Eingabe der Größe O(2 n ) darstellen kann. Daher gilt: P olynomiell ˆ= O(log c n) mit c N Im Folgenden werden wir einen probabilistischen Ansatz entwickeln, der in polynomieller Laufzeit mit einer vernachlässigbaren Fehlerwahrscheinlichkeit bestimmt, ob eine Eingabe n N eine Primzahl ist. Wir benötigen zunächst einige Definitionen: 4
5 Definition 7. [a] n = {a + k n k Z} Definition 8. Z + n = {[a] n 1 a n 1} Definition 9. Z n = {[a] n Z + n ggt (a, n) = 1} Beobachtung 10. Für Primzahlen p gilt Z + p = Z p Satz 11. [Kleiner Satz von Fermat]: Wenn n eine Primzahl ist, dann gilt für alle a Z n a n 1 1 (mod n) Lemma 12. Ist n 3 eine Primzahl und a Z n mit a 2 1 (mod n), dann gilt a ±1 (mod n). Beweis. a 2 1 (mod n) a (mod n) n a 2 1 n (a 1)(a + 1) n (a 1) n (a + 1) x 1 0 (mod n) x (mod n) a 1 (mod n) a 1 (mod n) Bei Algorithmen für zahlentheoretische Probleme verwendet man als Aufwandsmaß die Anzahl der Bitoperationen in den einzelnen Berechnungen. Die Anzahl der Bits einer Eingabe n erhalten wir mit log n. Wir wollen nicht näher drauf eingehen und vereinbaren folgenden Aufwand für die auftretenden elementaren Rechenoperationen: Satz 13. Modulares Potenzieren ist in O(log 3 n) möglich (Zeigen es hier nicht, sondern nehmen an, dass eine Black-Box existiert, die das tut). Außerdem nehmen wir an, dass die Multiplikation und die Modolo-Operation zweier n-stelliger Zahlen in O(log 2 n) möglich ist ( Normale Schulmethode ) 3.1 Ein erster Ansatz Idee: Teste mit Satz 11. Nehme zunächst an, dass eine Eingabe n N prim sei. Versuche anschließend Zeugen für die Zusammengesetztheit von n zu finden. Falls das der Fall sein sollte, dann erhalten wir in Satz 11 eine Implikation der Form 1 0. Aus dem Widerspruch folgt dann, dass n zusammengesetzt sein muss. Fermat Test: Eingabe: n N, k N Anzahl der Iterationen 1. Wiederhole k mal 2. Wähle a {2,..., n 2} zufällig 3. Berechne a n 1 (mod n) 4. Falls einer dieser k Versuche in 3. 1 war, dann verwirf, sonst akzeptiere die Eingabe Problem: Der kleine Satz von Fermat ist keine Äquivalenz! Es existieren sogenannte Carmichael Zahlen, die für alle a Z n a n 1 (mod n) 1 liefern, obwohl sie zusammengesetzt sind. Beispielsweise ist die 561 = eine solche Zahl. Der Fermat Test lässt sich von diesen Eingaben mit hoher Wahrscheinlichkeit austricksen. Wir betrachten deswegen einen verbesserten Ansatz. 5
6 3.2 Miller-Rabin Idee: Erweitere den Fermat-Test mit Test auf Lemma 14 und suche wieder Zeugen für die Zusammengesetztheit von n. Dafür zerlegen wir n 1 in s ungerade und t 1 wie folgt Der Algorithmus: n 1 = s 2 t Eingabe : n N, k N Anzahl der Iterationen Ausgabe : Ist n eine Primzahl? 1 solange noch nicht k mal wiederholt tue 2 wenn n = 2 dann 3 nächster Versuch 4 Ende 5 wenn n 2 dann 6 gebe Zusammengesetzt zurück 7 Ende 8 finde s ungerade und t 1 mit n 1 = s 2 t 9 wähle a {2,..., n 2} zufällig 10 b := a s (mod n) 11 wenn b = 1 oder b = n 1 dann 12 nächster Versuch 13 Ende 14 für jedes i = 1,..., t 1 tue 15 b := b 2 (mod n) 16 wenn b = 1 dann 17 nächster Versuch 18 Ende 19 wenn n = n 1 dann 20 gebe Zusammengesetzt zurück 21 Ende 22 Ende 23 gebe Zusammengesetzt zurück 24 Ende 25 gebe Primzahl zurück Berechne anschließend die Folge X =< s 2 0, s 2 1,..., s 2 t 1, s 2 t > Folgende Fälle sind möglich: Fall 1a: s 2 0 = 1 Fall 1b: s und es existiert ein i t 1 mit s 2 i = n 1 In den Fällen 1a und 1b haben wir keinen Zeugen dafür gefunden, dass die Eingabe n zusammengesetzt sein soll. Fall 2: s 2 t 1 Nach Satz 11 ist n zusammengesetzt. 6
7 s 2 0 s s 2 t 1 s 2 t Fall a n b * *... * * *... * n 1 2 * *... * * *... * * 2 * *... * * *... * * *... * 1 3 Fall 3: s 2 0 1, aber s 2 t = 1 Suche das minimale i 1 mit s 2 i = 1. Es gilt s 2 i 1 ±1 und damit ist n zusammengesetzt nach Lemma 12. Laufzeit: Die interessanten Zeilen, wo wir tatsächlich was berechnen, sind die Zeilen 10 und Zu Zeile 10: Nach Satz 13 haben wir eine Black-Box, die uns in O(log 3 n) modulares Potenzieren ermöglicht. Damit ist die Laufzeit hier O(log 3 n) Zu den Zeilen 14-22: In Zeile 15 führen wir eine Multiplikation und eine Modolo Operation durch. Die Laufzeit dieser Berechnungen ist O(log 2 n) nach Satz 13. Die Schleife in den Zeilen wird O(log n) mal ausgeführt. Damit ist die Laufzeit hier insgesamt: O(log n) O(log 2 n) = O(log 3 n) Die außere Schleife wird insgesamt k-mal ausgeführt. Damit ist die Gesamtlaufzeit O(k log 3 n). k gehört zwar bei unserer Beschreibung vom Algorithmus zur Eingabe, ist aber eher als zusätzlicher fest gewählter Parameter für die Anzahl der Durchläufe gemeint. Wählen wir also k vernünftig, dann ist die Laufzeit vom Miller-Rabin Test polynomiell. Zur Fehlerwahrscheinlichkeit: Wegen Satz 11 und Lemma 12 gilt: Satz 14. Ist die Eingabe n N eine ungeradene Primzahl, dann gilt P r[miller-rabin akzeptiert n] = 1 Das scheint plausibel, weil für Primzahlen n keine Zeugen für die Zusammengesetztheit existieren und der Miller-Rabin Test, damit keinen Grund hat Zusammengesetzt auszugeben. Man kann außerdem zeigen: Lemma 15. Die Anzahl der Zeugen für die Zusammengesetztheit einer ungeradenen zusammengesetzten Zahl n ist n 1 2 Daraus folgt Satz 16. Ist n N eine ungeradene zusammengesetzte Zahl, dann gilt wobei k N die Anzahl der Wiederholungen ist. P r[miller-rabin akzeptiert n] 2 k Durch Lemma 15 reduziert darauf zu bestimmen wie wahrscheinlich es ist in k Versuchen keinen Zeugen a {2,..., n 2} zu ziehen, der die Zusammengesetztheit einer Zahl n belegt. 7
8 4 weitere Komplexitätsklassen Der Miller-Rabin Test macht nur dann einen Fehler, wenn die Eingabe n eine zusammengesetzte Zahl ist. Das bedeutet, wenn n eine Primzahl ist, dann gibt der Miller-Rabin Test garantiert Primzahl aus. Man sagt auch, dass der Miller-Rabin Test nur einen sogenannten einseitigen Fehler macht 4.1 RP Definition 17. [RTIME und RP]: Sei T : N N. In RT IME(T (n)) ist jedes Entscheidungsproblem L Σ enthalten für die eine PTM M existiert, die in T (n)-zeit läuft und für die x L P r[m(x) = 1] 1 2 (1) x L P r[m(x) = 0] = 1 (2) gilt. Darüber hinaus definieren wir RP := RT IME(n c ) c N Wie auch bei BPP kann man zeigen, dass die Konstante 2/3 willkürlich gewählt ist und man mit 1 ɛ mit 0 < ɛ < 1/2 eine äquivalente Beschreibung von RP erhält. Definition 18. [co-rp]: co-rp := {L Σ L RP} Definieren wir COMPOSITES := P RIM ES. Dann haben wir mit unserem Algorithmus COMPOSITES RP gezeigt, weil wir eine Zahl nur dann als zusammengesetzt erkennen, wenn wir einen Zeugen gefunden haben. Da für keine Primzahl ein solcher Zeuge existiert, wird keine Primzahl als zusammengesetzte Zahl erkannt. Daraus folgt PRIMES co-rp. 4.2 ZPP Definition 19. [ZT IME und ZPP]: Sei T : N N. In ZT IME(T (n)) ist jedes Entscheidungsproblem L Σ enthalten für die eine PTM M existiert, die in O(T (n)) erwarteter Laufzeit eine korrekte Antwort liefert oder? ausgibt. Dafür erweitern wir die Menge der Endzustände unserer PTM M um den Zustand weiß nicht. Die Wahrscheinlichkeit für? ist < 1/2. 5 Beziehungen zu bekannten und neuen Komplexitätsklassen Satz 20. P BPP Beweisidee: Simuliere DTM M = (Q, Σ, Γ, q 0, F,, δ) mit PTM M = (Q, Σ, Γ, q 0, F,, δ 1, δ 2 ), indem wir Q := Q, Σ := Σ, Γ := Γ, q 0 := q 0, F := F übernehmen und δ 1 := δ, δ 2 := δ setzen. Da δ 1 = δ 2 werden die zufälligen Münzwürfe egalisiert. Satz 21. BPP PSPACE Beweisidee: Eine PTM ist eine spezielle NTM. Eine DTM kann eine NTM mit polynomiell viel Speicher simulieren. 8
9 Satz 22. RP BPP Beweisidee: Siehe Definitionen. Satz 23. co-rp BPP Beweisidee: Siehe Definitionen. Satz 24. RP N P Beweisidee: Wenn eine NTM M für eine Eingabe w Σ M(w) = 0 ausgibt, dann existiert keine akzeptierende Berechnung. Genauso wie bei einer PTM mit einseitig beschränktem Fehler. Wenn eine NTM M eine Eingabe w Σ akzeptiert, dann existiert mindestens eine akzeptierende Berechnung. M kann auch als PTM mit sehr hoher Fehlerwahrscheinlichkeit interpretiert werden. Satz 25. ZPP = RP co-rp Beweisidee: : Angenommen L ZPP. Immer, wenn die ZPP TM? ausgibt, dann ersetze die? Antwort durch Ja. Daraus folgt L RP. Da ZPP unter Komplement abgeschlossen, gilt L co-rp. : Sei M die RP TM und M die co-rp TM. Wir konstruieren nun eine ZPP TM, indem wir die Eingabe w Σ für M auf M und M ausführen. Wenn M(w) = 0, dann M (w) = 0 und wenn M (w) = 1, dann M (w) = 1. Sonst gebe? aus. M macht keinen Fehler, weil M für zuverlässig für w L(M ) ist und M zuverlässig für w L(M ) ist. Folgerung 26. ZPP BPP Folgt aus Satz 22, Satz 23 und Satz 25 6 Literaturhinweise Sipser, Michael: Introduction to the Theory of Computation. International ed of 2nd revised ed. Boston: Thomson Course Technology, Arora, Sanjeev ; Barak, Boaz: Computational Complexity : A Modern Approach. Cambridge: Cambridge University Press, Goldreich, Oded: Computational Complexity : A Conceptual Perspective. Cambridge: Cambridge University Press, Dietzfelbinger, Martin: Primality Testing in Polynomial Time : From Randomized Algorithms to "PRIMES Is in P". Berlin, Heidelberg: Springer, Papadimitriou, Christos H.: Computational Complexity. New.. Amsterdam: Addison-Wesley, Thomas H Cormen; Charles E Leiserson; Ronald Rivest; Clifford Stein: Introduction to Algorithms. Cambridge: MIT Press,
10 (Letzter Zugriff: :30) (Letzter Zugriff: :31) (Letzter Zugriff: :34) 10
1. Juni Probabilistische Turingmaschinen. Eike Müller. Motivation. Probabilistische Turingmaschinen. Einseitige Fehler und Nullseitige Fehler
 1. Juni 2010 Nullseitige Inhalt 1 2 3 4 5 6 7 8 Nullseitige Primzahltest nach Soloway und Strassen Nullseitige Definition ( Turingmaschine) Eine probabilistische Turingmaschine (PTM) ist eine Turingmaschine
1. Juni 2010 Nullseitige Inhalt 1 2 3 4 5 6 7 8 Nullseitige Primzahltest nach Soloway und Strassen Nullseitige Definition ( Turingmaschine) Eine probabilistische Turingmaschine (PTM) ist eine Turingmaschine
Proseminar Theoretische Informatik. Die Klasse NP. von Marlina Spanel
 Proseminar Theoretische Informatik Die Klasse NP von Marlina Spanel 29.11.2011 1 Gliederung Gliederung Problem des Handlungsreisenden Die Klasse NP Einleitung und Wiederholung Sprachen Nichtdeterministische
Proseminar Theoretische Informatik Die Klasse NP von Marlina Spanel 29.11.2011 1 Gliederung Gliederung Problem des Handlungsreisenden Die Klasse NP Einleitung und Wiederholung Sprachen Nichtdeterministische
Die Komplexitätsklassen P und NP
 Die Komplexitätsklassen P und NP Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Die Komplexitätsklassen P und NP Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Theoretische Informatik. nichtdeterministische Turingmaschinen NDTM. Turingmaschinen. Rainer Schrader. 29. April 2009
 Theoretische Informatik Rainer Schrader nichtdeterministische Turingmaschinen Zentrum für Angewandte Informatik Köln 29. April 2009 1 / 33 2 / 33 Turingmaschinen das Konzept des Nichtdeterminismus nahm
Theoretische Informatik Rainer Schrader nichtdeterministische Turingmaschinen Zentrum für Angewandte Informatik Köln 29. April 2009 1 / 33 2 / 33 Turingmaschinen das Konzept des Nichtdeterminismus nahm
Laufzeit einer DTM, Klasse DTIME
 Laufzeit einer DTM, Klasse DTIME Definition Laufzeit einer DTM Sei M eine DTM mit Eingabealphabet Σ, die bei jeder Eingabe hält. Sei T M (w) die Anzahl der Rechenschritte d.h. Bewegungen des Lesekopfes
Laufzeit einer DTM, Klasse DTIME Definition Laufzeit einer DTM Sei M eine DTM mit Eingabealphabet Σ, die bei jeder Eingabe hält. Sei T M (w) die Anzahl der Rechenschritte d.h. Bewegungen des Lesekopfes
Probabilistische Primzahltests
 23.01.2006 Motivation und Überblick Grundsätzliches Vorgehen Motivation und Überblick Als Primzahltest bezeichnet man ein mathematisches Verfahren, mit dem ermittelt wird, ob eine gegebene Zahl eine Primzahl
23.01.2006 Motivation und Überblick Grundsätzliches Vorgehen Motivation und Überblick Als Primzahltest bezeichnet man ein mathematisches Verfahren, mit dem ermittelt wird, ob eine gegebene Zahl eine Primzahl
Theoretische Informatik 1
 Theoretische Informatik 1 Nichtdeterminismus David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Nichtdeterminismus NTM Nichtdeterministische Turingmaschine Die
Theoretische Informatik 1 Nichtdeterminismus David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Nichtdeterminismus NTM Nichtdeterministische Turingmaschine Die
PRIMES is in P. Ein Vortrag von Holger Szillat.
 PRIMES is in P Ein Vortrag von Holger Szillat [email protected] Übersicht Geschichte Notationen und Definitionen Der Agrawal-Kayal-Saxena-Algorithmus Korrektheit und Aufwand Fazit Geschichte
PRIMES is in P Ein Vortrag von Holger Szillat [email protected] Übersicht Geschichte Notationen und Definitionen Der Agrawal-Kayal-Saxena-Algorithmus Korrektheit und Aufwand Fazit Geschichte
12. Woche: Verifizierer, nicht-deterministische Turingmaschine, Klasse NP
 12 Woche: Verifizierer, nicht-deterministische Turingmaschine, Klasse NP 12 Woche: Verifizierer, nicht-deterministische Turingmaschine, NP 254/ 333 Polynomielle Verifizierer und NP Ḋefinition Polynomieller
12 Woche: Verifizierer, nicht-deterministische Turingmaschine, Klasse NP 12 Woche: Verifizierer, nicht-deterministische Turingmaschine, NP 254/ 333 Polynomielle Verifizierer und NP Ḋefinition Polynomieller
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 4.2 Primzahltests 1. Deterministische Primzahltests 2. Der Primzahltest von Solovay-Strassen 3. Der Milner-Rabin Test Wozu Primzahltests? RSA Schlüssel benötigen sehr
Kryptographie und Komplexität Einheit 4.2 Primzahltests 1. Deterministische Primzahltests 2. Der Primzahltest von Solovay-Strassen 3. Der Milner-Rabin Test Wozu Primzahltests? RSA Schlüssel benötigen sehr
Zeitkomplexität (1) Proseminar Theoretische Informatik. Proseminar Theoretische Informatik: Lisa Dohrmann 1
 Zeitkomplexität (1) Proseminar Theoretische Informatik Proseminar Theoretische Informatik: Lisa Dohrmann 1 Warum Komplexitätsbetrachtung? Ein im Prinzip entscheidbares und berechenbares Problem kann in
Zeitkomplexität (1) Proseminar Theoretische Informatik Proseminar Theoretische Informatik: Lisa Dohrmann 1 Warum Komplexitätsbetrachtung? Ein im Prinzip entscheidbares und berechenbares Problem kann in
Kryptographische Protokolle
 Kryptographische Protokolle Lerneinheit 2: Generierung von Primzahlen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2018/2019 15.11.2018 Einleitung Einleitung Diese Lerneinheit
Kryptographische Protokolle Lerneinheit 2: Generierung von Primzahlen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2018/2019 15.11.2018 Einleitung Einleitung Diese Lerneinheit
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Polynomielle Verifizierer und NP
 Polynomielle Verifizierer und NP Definition Polynomieller Verifizierer Sei L Σ eine Sprache. Eine DTM V heißt Verifizierer für L, falls V für alle Eingaben w Σ hält und folgendes gilt: w L c Σ : V akzeptiert
Polynomielle Verifizierer und NP Definition Polynomieller Verifizierer Sei L Σ eine Sprache. Eine DTM V heißt Verifizierer für L, falls V für alle Eingaben w Σ hält und folgendes gilt: w L c Σ : V akzeptiert
Einwegfunktionen. Problemseminar. Komplexitätstheorie und Kryptographie. Martin Huschenbett. 30. Oktober 2008
 Problemseminar Komplexitätstheorie und Kryptographie Martin Huschenbett Student am Institut für Informatik an der Universität Leipzig 30. Oktober 2008 1 / 33 Gliederung 1 Randomisierte Algorithmen und
Problemseminar Komplexitätstheorie und Kryptographie Martin Huschenbett Student am Institut für Informatik an der Universität Leipzig 30. Oktober 2008 1 / 33 Gliederung 1 Randomisierte Algorithmen und
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 20. November 2014 INSTITUT FÜR THEORETISCHE 0 KIT 20.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 20. November 2014 INSTITUT FÜR THEORETISCHE 0 KIT 20.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Randomisierte Algorithmen Algorithmen, die Zufallsbits benutzen können. Fehlerfreie Algorithmen (Las-Vegas-Alg)
 Wiederholung Randomisierte Algorithmen Algorithmen, die Zufallsbits benutzen können. Fehlerfreie Algorithmen (Las-Vegas-Alg) Komplexitätsklassen: EP=ZPP Algorithmen mit Fehlern (Monte-Carlo-Alg) Zweiseitiger
Wiederholung Randomisierte Algorithmen Algorithmen, die Zufallsbits benutzen können. Fehlerfreie Algorithmen (Las-Vegas-Alg) Komplexitätsklassen: EP=ZPP Algorithmen mit Fehlern (Monte-Carlo-Alg) Zweiseitiger
Einige Grundlagen der Komplexitätstheorie
 Deterministische Polynomialzeit Einige Grundlagen der Komplexitätstheorie Ziel: NP-Vollständigkeit als ressourcenbeschränktes Analagon zur RE-Vollständigkeit. Komplexitätstheorie untersucht den Ressourcenbedarf
Deterministische Polynomialzeit Einige Grundlagen der Komplexitätstheorie Ziel: NP-Vollständigkeit als ressourcenbeschränktes Analagon zur RE-Vollständigkeit. Komplexitätstheorie untersucht den Ressourcenbedarf
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 18. Vorlesung 22.12.2006 1 Komplexitätstheorie - Zeitklassen Komplexitätsmaße Wiederholung: O,o,ω,Θ,Ω Laufzeitanalyse Die Komplexitätsklassen
Informatik III Christian Schindelhauer Wintersemester 2006/07 18. Vorlesung 22.12.2006 1 Komplexitätstheorie - Zeitklassen Komplexitätsmaße Wiederholung: O,o,ω,Θ,Ω Laufzeitanalyse Die Komplexitätsklassen
Willkommen zur Vorlesung Komplexitätstheorie
 Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V5, 21.11.2011 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V5, 21.11.2011 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
13. Woche: NP-Vollständigkeit Satz von Cook-Levin Anwendungen in der Kryptographie
 13 Woche: NP-Vollständigkeit Satz von Cook-Levin Anwendungen in der Kryptographie 13 Woche: NP-Vollständigkeit, Satz von Cook-Levin, Anwendungen 276/ 333 N P-Vollständigkeit Ḋefinition NP-vollständig Sei
13 Woche: NP-Vollständigkeit Satz von Cook-Levin Anwendungen in der Kryptographie 13 Woche: NP-Vollständigkeit, Satz von Cook-Levin, Anwendungen 276/ 333 N P-Vollständigkeit Ḋefinition NP-vollständig Sei
Quanteninformation/ Quantencomputer
 Quanteninformation/ Quantencomputer Jonas Heinze Proseminar SS 2013 Jonas Heinze (University of Bielefeld) Quanteninformation/ Quantencomputer 2013 1 / 20 Übersicht 1 Kurzer Einstieg in die Informatik
Quanteninformation/ Quantencomputer Jonas Heinze Proseminar SS 2013 Jonas Heinze (University of Bielefeld) Quanteninformation/ Quantencomputer 2013 1 / 20 Übersicht 1 Kurzer Einstieg in die Informatik
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 16.11.2010 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Vorlesung am 16.11.2010 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Berechenbarkeitstheorie 19. Vorlesung
 1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Erinnerung:
1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Erinnerung:
Rucksackproblem und Verifizierbarkeit
 Rucksackproblem und Verifizierbarkeit Gegeben: n Gegenstände mit Gewichten G={g 1,g 2,,g n } und Werten W={w 1,w 2,,w n } sowie zulässiges Gesamtgewicht g. Gesucht: Teilmenge S {1,,n} mit i i S unter der
Rucksackproblem und Verifizierbarkeit Gegeben: n Gegenstände mit Gewichten G={g 1,g 2,,g n } und Werten W={w 1,w 2,,w n } sowie zulässiges Gesamtgewicht g. Gesucht: Teilmenge S {1,,n} mit i i S unter der
Nichtdeterministische Platzklassen
 Sommerakademie 2010 Rot an der Rot AG 1: Wieviel Platz brauchen Algorithmen wirklich? Nichtdeterministische Platzklassen Ulf Kulau August 23, 2010 1 Contents 1 Einführung 3 2 Nichtdeterminismus allgemein
Sommerakademie 2010 Rot an der Rot AG 1: Wieviel Platz brauchen Algorithmen wirklich? Nichtdeterministische Platzklassen Ulf Kulau August 23, 2010 1 Contents 1 Einführung 3 2 Nichtdeterminismus allgemein
Diskrete Mathematik 1
 Ruhr-Universität Bochum Lehrstuhl für Kryptologie und IT-Sicherheit Prof. Dr. Alexander May M. Ritzenhofen, M. Mansour Al Sawadi, A. Meurer Lösungsblatt zur Vorlesung Diskrete Mathematik 1 WS 008/09 Blatt
Ruhr-Universität Bochum Lehrstuhl für Kryptologie und IT-Sicherheit Prof. Dr. Alexander May M. Ritzenhofen, M. Mansour Al Sawadi, A. Meurer Lösungsblatt zur Vorlesung Diskrete Mathematik 1 WS 008/09 Blatt
Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie
 Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie Wintersemester 2005/2006 20.12.2005 18. Vorlesung 1 Komplexitätstheorie - Zeitklassen Komplexitätsmaße Wiederholung: O,o,ω,Θ,Ω Laufzeitanalyse
Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie Wintersemester 2005/2006 20.12.2005 18. Vorlesung 1 Komplexitätstheorie - Zeitklassen Komplexitätsmaße Wiederholung: O,o,ω,Θ,Ω Laufzeitanalyse
RSA Parameter öffentlich: N = pq mit p, q prim und e Z RSA Parameter geheim: d Z φ(n)
 RSA Parameter { öffentlich: N = pq mit p, q prim und e Z RSA Parameter φ(n) geheim: d Z φ(n) mit ed = 1 mod φ(n). Satz RSA Parameter Generierung RSA-Parameter (N, e, d) können in Zeit O(log 4 N) generiert
RSA Parameter { öffentlich: N = pq mit p, q prim und e Z RSA Parameter φ(n) geheim: d Z φ(n) mit ed = 1 mod φ(n). Satz RSA Parameter Generierung RSA-Parameter (N, e, d) können in Zeit O(log 4 N) generiert
Bsp: Die kleinsten Carmichael-Zahlen sind 561, 1105, 1729, Es gibt unendlich viele Carmichael-Zahlen (Beweis 1994).
 Primzahltest Wir wollen testen, ob eine gegebene Zahl n eine Primzahl ist Effizienter Algorithmus zum Faktorisieren ist unbekannt Kontraposition des Kleinen Satzes von Fermat liefert: Falls a n 1 1 mod
Primzahltest Wir wollen testen, ob eine gegebene Zahl n eine Primzahl ist Effizienter Algorithmus zum Faktorisieren ist unbekannt Kontraposition des Kleinen Satzes von Fermat liefert: Falls a n 1 1 mod
Proseminar TI: Kellerautomaten. 1 Motivation. 2 Einführung. Vortrag: Von Sebastian Oltmanns und Dorian Wachsmann. Dozent: Wolfgang Mulzer.
 Proseminar TI: Kellerautomaten Vortrag: 10.11.2015 Von Sebastian Oltmanns und Dorian Wachsmann. Dozent: Wolfgang Mulzer. 1 Motivation Wir kennen bereits die Chomsky-Hierarchie. Sie klassiziert formale
Proseminar TI: Kellerautomaten Vortrag: 10.11.2015 Von Sebastian Oltmanns und Dorian Wachsmann. Dozent: Wolfgang Mulzer. 1 Motivation Wir kennen bereits die Chomsky-Hierarchie. Sie klassiziert formale
Semi-Entscheidbarkeit und rekursive Aufzählbarkeit
 Semi-Entscheidbarkeit und rekursive Aufzählbarkeit Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 9. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung
Semi-Entscheidbarkeit und rekursive Aufzählbarkeit Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 9. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung
11. Woche: Turingmaschinen und Komplexität Rekursive Aufzählbarkeit, Entscheidbarkeit Laufzeit, Klassen DTIME und P
 11 Woche: Turingmaschinen und Komplexität Rekursive Aufzählbarkeit, Entscheidbarkeit Laufzeit, Klassen DTIME und P 11 Woche: Turingmaschinen, Entscheidbarkeit, P 239/ 333 Einführung in die NP-Vollständigkeitstheorie
11 Woche: Turingmaschinen und Komplexität Rekursive Aufzählbarkeit, Entscheidbarkeit Laufzeit, Klassen DTIME und P 11 Woche: Turingmaschinen, Entscheidbarkeit, P 239/ 333 Einführung in die NP-Vollständigkeitstheorie
3: Primzahlen. 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen
 3: Primzahlen 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen Definition 40 (Teiler, Vielfache, Primzahlen, zusammengesetzte Zahlen) Seien a, b N. a ist ein Teiler von b ( a b ), falls es ein k N gibt
3: Primzahlen 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen Definition 40 (Teiler, Vielfache, Primzahlen, zusammengesetzte Zahlen) Seien a, b N. a ist ein Teiler von b ( a b ), falls es ein k N gibt
abgeschlossen unter,,,, R,
 Was bisher geschah Turing-Maschinen können Sprachen L X akzeptieren entscheiden Funktionen berechnen f : X X (partiell) Menge aller Turing-akzeptierbaren Sprachen genau die Menge aller Chomsky-Typ-0-Sprachen
Was bisher geschah Turing-Maschinen können Sprachen L X akzeptieren entscheiden Funktionen berechnen f : X X (partiell) Menge aller Turing-akzeptierbaren Sprachen genau die Menge aller Chomsky-Typ-0-Sprachen
Übungsblatt 4. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 4 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 6. Dezember 2017 Abgabe 19. Dezember 2017, 11:00 Uhr
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 4 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 6. Dezember 2017 Abgabe 19. Dezember 2017, 11:00 Uhr
3: Zahlentheorie / Primzahlen
 Stefan Lucks Diskrete Strukturen (WS 2009/10) 96 3: Zahlentheorie / Primzahlen 3: Zahlentheorie / Primzahlen Stefan Lucks Diskrete Strukturen (WS 2009/10) 97 Definition 37 (Teiler, Vielfache, Primzahlen,
Stefan Lucks Diskrete Strukturen (WS 2009/10) 96 3: Zahlentheorie / Primzahlen 3: Zahlentheorie / Primzahlen Stefan Lucks Diskrete Strukturen (WS 2009/10) 97 Definition 37 (Teiler, Vielfache, Primzahlen,
Präsenzübung Berechenbarkeit und Komplexität
 Lehrstuhl für Informatik 1 WS 2013/14 Prof. Dr. Berthold Vöcking 28.01.2014 Kamal Al-Bawani Benjamin Ries Präsenzübung Berechenbarkeit und Komplexität Musterlösung Name:...................................
Lehrstuhl für Informatik 1 WS 2013/14 Prof. Dr. Berthold Vöcking 28.01.2014 Kamal Al-Bawani Benjamin Ries Präsenzübung Berechenbarkeit und Komplexität Musterlösung Name:...................................
Proseminar Komplexitätstheorie P versus NP Wintersemester 2006/07. Nichtdeterministische Turingmaschinen und NP
 Proseminar Komplexitätstheorie P versus NP Wintersemester 2006/07 Vortrag am 17.11.2006 Nichtdeterministische Turingmaschinen und NP Yves Radunz Inhaltsverzeichnis 1 Wiederholung 3 1.1 Allgemeines........................................
Proseminar Komplexitätstheorie P versus NP Wintersemester 2006/07 Vortrag am 17.11.2006 Nichtdeterministische Turingmaschinen und NP Yves Radunz Inhaltsverzeichnis 1 Wiederholung 3 1.1 Allgemeines........................................
1.8 Shift-And-Algorithmus
 .8 Shift-And-Algorithmus nutzt durch Bitoperationen mögliche Parallelisierung Theoretischer Hintergrund: Nichtdeterministischer endlicher Automat Laufzeit: Θ(n), falls die Länge des Suchwortes nicht größer
.8 Shift-And-Algorithmus nutzt durch Bitoperationen mögliche Parallelisierung Theoretischer Hintergrund: Nichtdeterministischer endlicher Automat Laufzeit: Θ(n), falls die Länge des Suchwortes nicht größer
THEORETISCHE INFORMATIK UND LOGIK
 THEORETISCHE INFORMATIK UND LOGIK 9. Vorlesung: NP und NP-Vollständigkeit Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 10. Mai 2017 Rückblick PTime und LogSpace als mathematische Modelle
THEORETISCHE INFORMATIK UND LOGIK 9. Vorlesung: NP und NP-Vollständigkeit Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 10. Mai 2017 Rückblick PTime und LogSpace als mathematische Modelle
Übung zur Vorlesung Berechenbarkeit und Komplexität
 RWTH Aachen Lehrgebiet Theoretische Informatik Reidl Ries Rossmanith Sanchez Tönnis WS 2012/13 Übungsblatt 7 26.11.2012 Übung zur Vorlesung Berechenbarkeit und Komplexität Aufgabe T15 Entwickeln Sie ein
RWTH Aachen Lehrgebiet Theoretische Informatik Reidl Ries Rossmanith Sanchez Tönnis WS 2012/13 Übungsblatt 7 26.11.2012 Übung zur Vorlesung Berechenbarkeit und Komplexität Aufgabe T15 Entwickeln Sie ein
Miller-Rabin Test. Primzahl- und Zerlegbarkeitstests. Zeugen für die Zerlegbarkeit ganzer Zahlen
 Miller-Rabin Test Primzahl- und Zerlegbarkeitstests Sei N eine positive ganze Zahl. Wie kann man möglichst effizient feststellen, ob N eine Primzahl oder zerlegbar ist? Dies ist die Aufgabe von Primzahlund
Miller-Rabin Test Primzahl- und Zerlegbarkeitstests Sei N eine positive ganze Zahl. Wie kann man möglichst effizient feststellen, ob N eine Primzahl oder zerlegbar ist? Dies ist die Aufgabe von Primzahlund
Turing Maschine. Thorsten Timmer. SS 2005 Proseminar Beschreibungskomplexität bei Prof. D. Wotschke. Turing Maschine SS 2005 p.
 Thorsten Timmer SS 2005 Proseminar Beschreibungskomplexität bei Prof. D. Wotschke Turing Maschine SS 2005 p. 1/35 Inhalt Einführung Formale Definition Berechenbare Sprachen und Funktionen Berechnung ganzzahliger
Thorsten Timmer SS 2005 Proseminar Beschreibungskomplexität bei Prof. D. Wotschke Turing Maschine SS 2005 p. 1/35 Inhalt Einführung Formale Definition Berechenbare Sprachen und Funktionen Berechnung ganzzahliger
Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016)
 Technische Universität Berlin, Berlin, 28.07.2016 Name:... Matr.-Nr.:... Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016) Einlesezeit: Bearbeitungszeit: Max.
Technische Universität Berlin, Berlin, 28.07.2016 Name:... Matr.-Nr.:... Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016) Einlesezeit: Bearbeitungszeit: Max.
Programmieren und Problemlösen
 Dennis Komm Programmieren und Problemlösen Komplexität von Algorithmen Frühling 2019 27. Februar 2019 Komplexität von Algorithmen Aufgabe Primzahltest Schreibe ein Programm, das eine ganze Zahl x als Eingabe
Dennis Komm Programmieren und Problemlösen Komplexität von Algorithmen Frühling 2019 27. Februar 2019 Komplexität von Algorithmen Aufgabe Primzahltest Schreibe ein Programm, das eine ganze Zahl x als Eingabe
Klassische Informationstheorie: Berechenbarkeit und Komplexität
 Klassische Informationstheorie: Berechenbarkeit und Komplexität Christian Slupina 1. Institut für Theoretische Physik Datum: 12.Juli 2011 Inhalt Gedankenexperiment: Die Turingmaschine Standard-Turingmaschinen
Klassische Informationstheorie: Berechenbarkeit und Komplexität Christian Slupina 1. Institut für Theoretische Physik Datum: 12.Juli 2011 Inhalt Gedankenexperiment: Die Turingmaschine Standard-Turingmaschinen
Miller-Rabin Test. Primzahl- und Zerlegbarkeitstests. Zeugen für die Zerlegbarkeit ganzer Zahlen
 Miller-Rabin Test Primzahl- und Zerlegbarkeitstests Sei N eine positive ganze Zahl. Wie kann man möglichst effizient feststellen, ob N eine Primzahl oder zerlegbar ist? Dies ist die Aufgabe von Primzahlund
Miller-Rabin Test Primzahl- und Zerlegbarkeitstests Sei N eine positive ganze Zahl. Wie kann man möglichst effizient feststellen, ob N eine Primzahl oder zerlegbar ist? Dies ist die Aufgabe von Primzahlund
Einführung in die Theoretische Informatik Tutorium IX
 Einführung in die Theoretische Informatik Tutorium IX Michael R. Jung 16. & 17. 12. 2014 EThI - Tutorium IX 1 1 Entscheidbarkeit, Semi-Entscheidbarkeit und Unentscheidbarkeit 2 EThI - Tutorium IX 2 Definitionen
Einführung in die Theoretische Informatik Tutorium IX Michael R. Jung 16. & 17. 12. 2014 EThI - Tutorium IX 1 1 Entscheidbarkeit, Semi-Entscheidbarkeit und Unentscheidbarkeit 2 EThI - Tutorium IX 2 Definitionen
Unentscheidbare Probleme bei formalen Sprachen
 Unentscheidbare Probleme bei formalen Sprachen Maximilian Zagler 22.01.2008 Freie Universität Berlin, Institut für Informatik Proseminar Theoretische Informatik WS 07/08 Dozent: Prof. Dr. Helmut Alt 1
Unentscheidbare Probleme bei formalen Sprachen Maximilian Zagler 22.01.2008 Freie Universität Berlin, Institut für Informatik Proseminar Theoretische Informatik WS 07/08 Dozent: Prof. Dr. Helmut Alt 1
Komplexitätsklassen THEORETISCHE INFORMATIK VORGETRAGEN VON: ELIAS DROTLEFF
 Komplexitätsklassen THEORETISCHE INFORMATIK VORGETRAGEN VON: ELIAS DROTLEFF Einflussgrößen bei der Bildung von Komplexitätsklassen Das zugrunde liegende Berechnungsmodell (Turingmaschine, Registermaschine
Komplexitätsklassen THEORETISCHE INFORMATIK VORGETRAGEN VON: ELIAS DROTLEFF Einflussgrößen bei der Bildung von Komplexitätsklassen Das zugrunde liegende Berechnungsmodell (Turingmaschine, Registermaschine
Theorie der Informatik
 Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Wiederholung. Gruppen. Untergruppen. Gruppenisomorphismen. Ordnung: Gruppe, Element Satz von Euler: a ord(g) = 1 Elementordung teilt Gruppenordnung
 Wiederholung Gruppen Ordnung: Gruppe, Element Satz von Euler: a ord(g) = 1 Elementordung teilt Gruppenordnung Untergruppen Satz von Lagrange Untergruppenordnung teilt Gruppenordnung Nebenklassen von Untergruppen
Wiederholung Gruppen Ordnung: Gruppe, Element Satz von Euler: a ord(g) = 1 Elementordung teilt Gruppenordnung Untergruppen Satz von Lagrange Untergruppenordnung teilt Gruppenordnung Nebenklassen von Untergruppen
Deterministische und nichtdeterministische Turing-Maschinen, Typ1- und Typ0-Sprachen
 Dr. Sebastian Bab WiSe 12/13 Theoretische Grundlagen der Informatik für TI Termin: VL 15 + 16 vom 17.12.2012 und 20.12.2012 Deterministische und nichtdeterministische Turing-Maschinen, Typ1- und Typ0-Sprachen
Dr. Sebastian Bab WiSe 12/13 Theoretische Grundlagen der Informatik für TI Termin: VL 15 + 16 vom 17.12.2012 und 20.12.2012 Deterministische und nichtdeterministische Turing-Maschinen, Typ1- und Typ0-Sprachen
19. Nichtdeterministische Turingmaschinen und ihre Komplexität
 19. Nichtdeterministische Turingmaschinen und ihre Komplexität Bei einem Turingmaschinenprogramm P aus bedingten Anweisungen wird durch die Forderung i a b B j i a b B j i a sichergestellt, dass zu jeder
19. Nichtdeterministische Turingmaschinen und ihre Komplexität Bei einem Turingmaschinenprogramm P aus bedingten Anweisungen wird durch die Forderung i a b B j i a b B j i a sichergestellt, dass zu jeder
Die Klasse NP und die polynomielle Reduktion. Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen
 Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 26 Optimierungsprobleme und ihre Entscheidungsvariante Beim Rucksackproblem
Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 26 Optimierungsprobleme und ihre Entscheidungsvariante Beim Rucksackproblem
11.1 Kontextsensitive und allgemeine Grammatiken
 Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Theorie der Informatik
 Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
P, NP und NP -Vollständigkeit
 P, NP und NP -Vollständigkeit Mit der Turing-Maschine haben wir einen Formalismus kennengelernt, um über das Berechenbare nachdenken und argumentieren zu können. Wie unsere bisherigen Automatenmodelle
P, NP und NP -Vollständigkeit Mit der Turing-Maschine haben wir einen Formalismus kennengelernt, um über das Berechenbare nachdenken und argumentieren zu können. Wie unsere bisherigen Automatenmodelle
Diskrete Mathematik. Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom
 Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
Registermaschine. c(1) c(2) c(3) c(4) Speicher. Programm
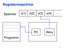 Registermaschine Speicher c(1) c(2) c(3) c(4) PC Akku Programm 1 Befehle einer Registermaschine LOAD i STORE i CLOAD i ILOAD i ISTORE i ADD i SUB i, MUL i, DIV i GOTO i IF (Akku? L) GOTO j END Lade c(i)
Registermaschine Speicher c(1) c(2) c(3) c(4) PC Akku Programm 1 Befehle einer Registermaschine LOAD i STORE i CLOAD i ILOAD i ISTORE i ADD i SUB i, MUL i, DIV i GOTO i IF (Akku? L) GOTO j END Lade c(i)
Die Klasse NP und die polynomielle Reduktion
 Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Dezember 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Dezember 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Hier ist ein einfaches Turingprogramm. Außer dem Leerzeichen ist das Band nur mit. 1 belegt.
 Die Turingmaschine besteht aus der Steuereinheit, die verschiedene Zustände annimmt dem Band, welches unendlich ausgedehnt ist, aber nur auf einem endlichem Bereich mit Zeichen aus einem Alphabet beschrieben
Die Turingmaschine besteht aus der Steuereinheit, die verschiedene Zustände annimmt dem Band, welches unendlich ausgedehnt ist, aber nur auf einem endlichem Bereich mit Zeichen aus einem Alphabet beschrieben
Fortgeschrittene Netzwerk- und Graph-Algorithmen
 Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Willkommen zur Vorlesung Komplexitätstheorie
 Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V11, 16.1.2012 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
Willkommen zur Vorlesung Komplexitätstheorie WS 2011/2012 Friedhelm Meyer auf der Heide V11, 16.1.2012 1 Themen 1. Turingmaschinen Formalisierung der Begriffe berechenbar, entscheidbar, rekursiv aufzählbar
LOOP-Programme: Syntaktische Komponenten
 LOOP-Programme: Syntaktische Komponenten LOOP-Programme bestehen aus folgenden Zeichen (syntaktischen Komponenten): Variablen: x 0 x 1 x 2... Konstanten: 0 1 2... Operationssymbole: + Trennsymbole: ; :=
LOOP-Programme: Syntaktische Komponenten LOOP-Programme bestehen aus folgenden Zeichen (syntaktischen Komponenten): Variablen: x 0 x 1 x 2... Konstanten: 0 1 2... Operationssymbole: + Trennsymbole: ; :=
Musterlösung Informatik-III-Nachklausur
 Musterlösung Informatik-III-Nachklausur Aufgabe 1 (2+2+4+4 Punkte) (a) L = (0 1) 0(0 1) 11(0 1) 0(0 1) (b) Der Automat ist durch folgendes Übergangsdiagramm gegeben: 0, 1 0, 1 0, 1 0, 1 0 s q 1 1 0 0 q
Musterlösung Informatik-III-Nachklausur Aufgabe 1 (2+2+4+4 Punkte) (a) L = (0 1) 0(0 1) 11(0 1) 0(0 1) (b) Der Automat ist durch folgendes Übergangsdiagramm gegeben: 0, 1 0, 1 0, 1 0, 1 0 s q 1 1 0 0 q
Zahlentheorie, Arithmetik und Algebra I
 Zahlentheorie, Arithmetik und Algebra I Ulrich Rabenstein 18.06.2013 Ulrich Rabenstein Zahlentheorie, Arithmetik und Algebra I 18.06.2013 1 / 34 1 Modulare Arithmetik 2 Teiler 3 Primzahlen Ulrich Rabenstein
Zahlentheorie, Arithmetik und Algebra I Ulrich Rabenstein 18.06.2013 Ulrich Rabenstein Zahlentheorie, Arithmetik und Algebra I 18.06.2013 1 / 34 1 Modulare Arithmetik 2 Teiler 3 Primzahlen Ulrich Rabenstein
Der komplexitätstheoretische Zugang zur Kryptographie
 Der komplexitätstheoretische Zugang zur Kryptographie Claus Diem Im Wintersemester 2017 / 18 Literatur Oded Goldreich: Foundations of Cryptography Jonathan Katz & Yeduda Lindell: Intoduction to Modern
Der komplexitätstheoretische Zugang zur Kryptographie Claus Diem Im Wintersemester 2017 / 18 Literatur Oded Goldreich: Foundations of Cryptography Jonathan Katz & Yeduda Lindell: Intoduction to Modern
Berechenbarkeit und Komplexität: Erläuterungen zur Turingmaschine
 Berechenbarkeit und Komplexität: Erläuterungen zur Turingmaschine Prof. Dr. Berthold Vöcking Lehrstuhl Informatik Algorithmen und Komplexität 24. Oktober 26 Programmierung der TM am Beispiel Beispiel:
Berechenbarkeit und Komplexität: Erläuterungen zur Turingmaschine Prof. Dr. Berthold Vöcking Lehrstuhl Informatik Algorithmen und Komplexität 24. Oktober 26 Programmierung der TM am Beispiel Beispiel:
Kryptologie. Bernd Borchert. Univ. Tübingen SS Vorlesung. Teil 11. Primzahltests: Fermat, Miller-Rabin
 Kryptologie Bernd Borchert Univ. Tübingen SS 2017 Vorlesung Teil 11 Primzahltests: Fermat, Miller-Rabin Primzahltests Problem: Gegeben n. Ist n Primzahl? Naive Methoden: Ausprobieren: gehe der Reihe nach
Kryptologie Bernd Borchert Univ. Tübingen SS 2017 Vorlesung Teil 11 Primzahltests: Fermat, Miller-Rabin Primzahltests Problem: Gegeben n. Ist n Primzahl? Naive Methoden: Ausprobieren: gehe der Reihe nach
Das Rucksackproblem: schwache NP-Härte und Approximation
 Das Rucksackproblem: schwache NP-Härte und Approximation Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1. Februar 2010 Berthold Vöcking, Informatik 1 () Vorlesung
Das Rucksackproblem: schwache NP-Härte und Approximation Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1. Februar 2010 Berthold Vöcking, Informatik 1 () Vorlesung
FORMALE SYSTEME. 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten. TU Dresden, 14. November 2016.
 FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
Teil III. Komplexitätstheorie
 Teil III Komplexitätstheorie 125 / 160 Übersicht Die Klassen P und NP Die Klasse P Die Klassen NP NP-Vollständigkeit NP-Vollständige Probleme Weitere NP-vollständige Probleme 127 / 160 Die Klasse P Ein
Teil III Komplexitätstheorie 125 / 160 Übersicht Die Klassen P und NP Die Klasse P Die Klassen NP NP-Vollständigkeit NP-Vollständige Probleme Weitere NP-vollständige Probleme 127 / 160 Die Klasse P Ein
