Prozentrechnen (Aufgaben)
|
|
|
- Sven Fromm
- vor 9 Jahren
- Abrufe
Transkript
1 Gymnasium Pegnitz Wiederholung JS 6 1. Juli 2007 Prozentrechnen (Aufgaben) 1. (a) 30% von 40% von 150 EUR sind... (b) Wenn Tom von seinen 918 EUR mindestens 33 1 % ausgibt, hat er höchstens 3 noch Für die Nasendusche benötigt man eine Salzlösung, in der der Anteil des Salzes 1% beträgt. Da das Abwiegen der kleinen Salzmengen mit einer Küchenwaage sehr ungenau wird, gibt es das Salz in kleinen Tütchen in der Apotheke zu kaufen. In einem Tütchen sind 2,5 g Salz. Wie viel Wasser benötigt man zur Herstellen der Salzlösung? 3. Wenn die Mehrwertsteuer von 16% auf 19% erhöht wird, um wie viel Prozent steigt dann die Mehrwertsteuer? Quelle: G. M. Ziegler, FOCUS 23/ Im,,Jahrhundertsommer 2003 besuchten Personen das Freibad von Nassing. Im Sommer des Jahres 2004 kamen nur noch Besucher. Um wie viel Prozent ist die Besucherzahl gesunken? Quelle: Bayerischer Mathematik - Test für die Jahrgangsstufe 8 der Gymnasien In der Schule soll zum Tag der offenen Tür die Erdgeschichte auf einem 10m langen Papierstreifen maßstäblich dargestellt werden. Dabei soll das linke Ende dem Zeitpunkt Heute, das rechte dem Zeitpunkt der Entstehung der Erde entsprechen. Die Übersicht listet einige Ereignisse auf: Erscheinung des Menschen Erscheinung des Dinosaurier erste Fische erste Pflanzen Entstehung der Erde vor ca. 2 Millionen Jahren vor ca. 200 Millionen Jahren vor ca. 400 Millionen Jahren vor ca. 3 Milliarden Jahren vor ca. 5 Milliarden Jahren (a) In welcher Entfernung vom linken Ende muss das Erscheinen der Dinosaurier markiert werden? (b) Wie viel Prozent der Streifenlänge nimmt die Geschichte der Menschheit ein? 4%, 2%, 0,4%, 0,04%, 0,002% (c) Mit einem Vergrößerungsglas lässt sich ein Punkt, der 0,1 mm vom linken Streifenende entfernt ist, erkennbar machen. Berechne, vor wie vielen Jahren ein dazu passendes Ereignis stattgefunden hat. 1
2 Quelle: Bayerischer Mathematik-Test (a) Der Preis für einen Schokoriegel wurde von 1,40 auf 1,75 erhöht. Um wie viele Prozent ist der Preis gestiegen? (b) Bei einem Waschmittel wurde die Füllmenge um 12 % vergrößert. Es enthält jetzt 0,6kg mehr als vorher. Wie viel ist in der neuen Packung? (c) Ein Platinwürfel mit dem Volumen 8,0 cm 3 wiegt 172g. Die Masse eines gleich großen Goldwürfels ist um 10 % geringer. Welche Masse (auf Gramm genau) hat ein Goldwürfel der Kantenlänge 1,0 cm? (d) Herr K. bekommt für sein Gehalt von 3200 eine Erhöhung um 4 %. i. Welchen Betrag erhält Herr K. nach der Erhöhung? ii. Wie lautet das Ergebnis bei einer Gehaltssenkung um 4 %? (e) Die Aktie der Firma Net kostet zu Jahresbeginn 56. Ihr Kurs ist seitdem um 175 % gestiegen. Was kostet die Aktie nun? (f) Die Einwohnerzahl einer Stadt ist im vergangenen Jahr um 8 % auf gestiegen. Wie viele Einwohner hatte die Stadt vor einem Jahr? (g) Ein Computer kostet laut Preisliste Hinzu kommen noch 16 % Mehrwertsteuer. Bei Barzahlung erhält der Kunde allerdings 3 % Rabatt. Wie hoch ist die Rechung? Literatur: Systematisches Wiederholen und Vernetzen, Staatsinstitut für Schulpädagogik und Bildungsforschung München, Familie Bachschmid will sich einen neuen Videorecorder kaufen. Drei Angebote sind zu vergleichen, um das günstigste herauszufinden: Angebot I: Angebot II: Angebot III: Der Händler verlangt 619 und gibt 3% Skonto. Dieser Händler verlangt 692 und gewährt 15% Rabatt. Im Verbrauchermarkt Maxi wird das Gerät für MWSt angeboten. (a) Welches Angebot ist am günstigsten? (b) Wie groß ist die Ersparnis gegenüber dem teuersten Angebot? (c) Vergleiche mit dem Angebot IV: Der 30km entfernte Großmarkt Giga hat das Gerät mit 589 ausgezeichnet. Um ihn zu erreichen, muss Zeit und Benzin aufgewendet werden. 8. Fred kauft sich ein neues Fahrrad für 760. Er darf vom diesem Betrag 5% Rabatt abziehen. Wie viel muss Fred zahlen? 2
3 9. Ein Fahrradgeschäft macht einen Räumungsverkauf und gewährt 25% Nachlass auf alle Artikel. Franz kauft sich ein Fahrrad und zahlt dafür 255. Wie viel hätte er ohne Preisnachlass gezahlt? 10. Herr Müller bezahlt die Rechnung für seine neue Stereoanlage. Er überweist nach Abzug von 2% Skonto einen Betrag von 1079,96. (a) Wie hoch war der Rechnungsbetrag vor dem Abzug des Skontos? (b) In diesem Rechnungsbetrag sind 16% Mehrwertsteuer enthalten. Wie viel kostet die Stereoanlage ohne Mehrwertsteuer? 11. Cindy kauft sich ein Kleid für 72. Sie erhält einen Preisnachlass und zahlt 61,20. Wie viel Prozent Preisnachlass wurde ihr gewährt? 12. Wie viel Prozent sind 135 mehr als 90? 13. Um wie viel Prozent sind 225km weniger als 300km? 14. Die Länge und die Breite eines Rechteckes werden je um 20% vergrößert. Um wieviel Prozent vergrößert sich die Fläche des Rechteckes? 15. (a) Wieviel Prozent sind: 12 von 16; 6 von 8; 8 von 6; 16 von 12. (b) Wieviel sind 30% von 112 (30% von 121 )? (c) Beim Kauf einer Ware erhält der Käufer 6% Rabatt auf den Listenpreis. Er bezahlt deshalb 75 weniger. Berechne den Brutto- und den Nettopreis der Ware. (d) Ein Glas mit einem Liter einer 5%-igen Salzlösung wird erhitzt. Dabei verdampft 70% des Wassers. Berechne, wieviel prozentig die Lösung jetzt ist. 16. Im Supermarkt hängt ein Werbeplakat für Badeschaum: Die neue 850-ml-Flasche: Jetzt über 20% mehr Inhalt zum Super-Sparspreis von 6,99. (a) Welchen Inhalt hat vermutlich die bisherige Flasche? (b) Im Regal steht auch noch die alte Flaschengröße zum Preis von 5,59. Für welche Flasche entscheidest du dich, wenn du möglichst günstig einkaufen willst? Begründe deine Entscheidung durch eine Rechnung. Quelle: Neue Schwerpunktsetzung in der Aufgabenkultur, ISB
4 17. In einem Hochhaus leben hundert Personen. Fast alle lesen Zeitung: 60% lesen die Zeitung A, 50% lesen die Zeitung B, 45% lesen die Zeitung C 30% lesen die Zeitung A und B, 20% lesen die Zeitung B und C, 30% lesen die Zeitung A und C 10% lesen die Zeitung A, B und C. Wie viele Prozent der Bewohner lesen keine Zeitung? 18. Kuno und Bruno haben je einen quaderförmigen Goldbarren geerbt. Die Kanten von Brunos Barren sind länger als die von Kunos Barren, und zwar die erste um 15 %, die zweite um 20 % und die dritte um 50 %. Um wieviel Prozent ist Brunos Erbschaft mehr wert als die von Kuno? 19. (a) Bei einem Pferderennen hat Phillip verloren, das sind % seines ganzen Vermögens vor dem Rennen. Wie groß war dieses Vermögen? (b) Mit 16 % MWS kostet ein Mountain-Bike Was kostet das Rad, wenn die MWS auf 17 % erhöht wird? 20. Ein Kaufmann verliert 20% seiner Kunden. Um wieviel Prozent muss er die Preise seiner Waren erhöhen, damit seine Gesamteinnahmen gleich bleiben? 21. Professor Snapes Weisheitstrank besteht aus 60% Wasser, 37,5% Mandelöl und 3 g Eulenblut (die Prozentangaben beziehen sich auf die Masse des ganzen Trankes). Wieviele Gramm Wasser beziehungsweise Mandelöl enthält der Trank? 22. (a) Beim Weitsprung schätzt Andi seinen Sprung auf 3,50 m. Mit dem Massband wird die tatsächliche Weite zu 3,35 m gemessen. Berechne den absoluten und den relativen Fehler der Schätzung. (b) Am Jahresbeginn legt Johanna ihr Geld auf der Bank fest an. Sie erhält im ersten Jahr 6% Zinsen. Am Ende des ersten Jahres lässt sie ihr Geld und die Zinsen auf der Bank und bekommt im zweiten Jahr 8% Zinsen. Am Ende des zweiten Jahres werden ihr 4006,80 ausgezahlt. Berechne, wie groß das Anfangskapital war. 23. Ergebnisse der Bürgerschaftswahl in Bremen 4
5 Prozent Mandate Wähler Prozent Mandate Wahlbeteiligung 60, ,6 SPD 42, ,4 37 CDU 37, ,6 37 Grüne 9, ,1 14 DVU 3,0 1 2,5 - AFB 2,4-10,7 12 Sonstige - (a) Fülle die leeren Felder aus. (b) Wie viele Wahlberechtigte waren es 1999? (c) Wie viele Stimmen sind verloren, sei es, weil die Wahlberechtigten nicht zur Wahl gegangen sind, sei es, weil ihre Stimme ungültig war oder weil sie sich für eine Partei entschieden, die nicht in die Bürgerschaft einzieht? (d) Wieviele Prozent der Wahlberechtigten sind dies? (e) Wir nehmen an, dass die Zahl der Wahlberechtigten sich nicht verändert hat. Um wieviel Prozent mehr Wähler stimmten 1999 gegenüber 1995 für die SPD. Quelle: Christoph Hammer, Max-Born-Gymnasium, Germering 24. Messing ist eine Legierung (Mischung) aus 70% Kupfer und 30% Zink. (a) Berechne die Masse eines Messingstückes, in welchem 500 g Zink enthalten sind. (b) Berechne die Masse des im Messingstück enthaltenen Kupfers. 25. Harry Potters neuer Besen, der Magic Rocket, reagiert auf zwei Zauberworte: Bei hig steigt er um 20 % der momentanen Höhe, bei dau sinkt er um 25% der momentanen Höhe. Nach den Kommandos hig hig dau hig dau fliegt Harry in der Höhe 486m. Wie hoch flog er vor den Kommandos? 5
Prozentrechnung. 2. Du bekommst 25% von einer halben Pizza. Welcher Bruchteil ist das? Quelle: Jufo go (Spiel zum Wettbewerb Jugend forscht)
 Prozentrechnung 1. Bei einem Rechteck wird eine Seite um 10% vergrößert, die andere um 10% verkleinert. Wie ändert sich der Flächeninhalt? Quelle: Jufo go (Spiel zum Wettbewerb Jugend forscht) 1% kleiner
Prozentrechnung 1. Bei einem Rechteck wird eine Seite um 10% vergrößert, die andere um 10% verkleinert. Wie ändert sich der Flächeninhalt? Quelle: Jufo go (Spiel zum Wettbewerb Jugend forscht) 1% kleiner
Volumenberechnung (Aufgaben)
 Gymnasium Pegnitz Wiederholung JS 6 1. Juli 2007 Volumenberechnung (Aufgaben) 1. Verwandle in die gemischte Schreibweise: (z.b. 4,51 m = 4 m 5 dm 1 cm): (a) 123,456789 m, 0,000 020 300 401 km, 987 006
Gymnasium Pegnitz Wiederholung JS 6 1. Juli 2007 Volumenberechnung (Aufgaben) 1. Verwandle in die gemischte Schreibweise: (z.b. 4,51 m = 4 m 5 dm 1 cm): (a) 123,456789 m, 0,000 020 300 401 km, 987 006
Übungen M 4. MWS - Nürnberg VIIc
 MWS - Nürnberg VIIc Übungen M 4 1. Butter hat einen Fettgehalt von 82%, Crème Fraiche enthält 30% Fett. Wie viel Gramm Butter enthalten die gleiche Menge Fett wie ein Becher mit 125 g Crème Fraiche? 2.
MWS - Nürnberg VIIc Übungen M 4 1. Butter hat einen Fettgehalt von 82%, Crème Fraiche enthält 30% Fett. Wie viel Gramm Butter enthalten die gleiche Menge Fett wie ein Becher mit 125 g Crème Fraiche? 2.
Brüche und Prozentrechnung (Wiederholung) c) 24 100 9 i) 10. c) 80 400 i) 3200 800. d) 360 900 k) 450 1500. d) 1 4. c) 4 5. k) 23.
 Brüche und Prozentrechnung (Wiederholung) Jg. 10 (G) Prozentrechnung Grundlagen % dezi Zenti milli 10 0 10-1 10-2 10-3 E Zehntel Hundertstel Tausendstel 1. Schreibe als Prozent ( pro Hundert ). a) g) 7
Brüche und Prozentrechnung (Wiederholung) Jg. 10 (G) Prozentrechnung Grundlagen % dezi Zenti milli 10 0 10-1 10-2 10-3 E Zehntel Hundertstel Tausendstel 1. Schreibe als Prozent ( pro Hundert ). a) g) 7
Aufgaben zu Linearen Gleichungssystemen. Gleichsetz-, Einsetz-, Additionsverfahren. 1. y = x + 5 y = -x - 5. 2. x = -4y + 7 x = -6y + 7
 Besuchen Sie auch die Seite http://www.matheaufgaben-loesen.de/ dort gibt es viele Aufgaben zu weiteren Themen und unter Hinweise den Weg zu den Lösungen. Aufgaben zu Linearen Gleichungssystemen Gleichsetz-,
Besuchen Sie auch die Seite http://www.matheaufgaben-loesen.de/ dort gibt es viele Aufgaben zu weiteren Themen und unter Hinweise den Weg zu den Lösungen. Aufgaben zu Linearen Gleichungssystemen Gleichsetz-,
Themenerläuterung. Die wichtigsten benötigten Formeln
 Themenerläuterung Das Thema verlangt von dir die Berechnung von Preisauf- bzw. Preisabschlägen, Mehrwertsteuerberechnungen usw. Vom Prinzip ist dieses Kapitel der Prozentrechnung zuzuordnen. Du musst hierbei
Themenerläuterung Das Thema verlangt von dir die Berechnung von Preisauf- bzw. Preisabschlägen, Mehrwertsteuerberechnungen usw. Vom Prinzip ist dieses Kapitel der Prozentrechnung zuzuordnen. Du musst hierbei
Hauptschulabschlussprüfung 2004
 Hauptschulabschlussprüfung 2004 Pflichtaufgaben 1. Teil Mathematik x+3 45 Die Aufgabenblätter sind Bestandteil der Prüfungsarbeit und müssen mit deinem Namen versehen werden. Du darfst in diesem Teil der
Hauptschulabschlussprüfung 2004 Pflichtaufgaben 1. Teil Mathematik x+3 45 Die Aufgabenblätter sind Bestandteil der Prüfungsarbeit und müssen mit deinem Namen versehen werden. Du darfst in diesem Teil der
Skript Prozentrechnung. Erstellt: 2015/16 Von: www.mathe-in-smarties.de
 Skript Prozentrechnung Erstellt: 2015/16 Von: www.mathe-in-smarties.de Inhaltsverzeichnis Vorwort... 2 1. Einführung... 3 2. Berechnung des Prozentwertes... 5 3. Berechnung des Prozentsatzes... 6 4. Berechnung
Skript Prozentrechnung Erstellt: 2015/16 Von: www.mathe-in-smarties.de Inhaltsverzeichnis Vorwort... 2 1. Einführung... 3 2. Berechnung des Prozentwertes... 5 3. Berechnung des Prozentsatzes... 6 4. Berechnung
Download. Mathematik üben Klasse 8 Prozentrechnung. Differenzierte Materialien für das ganze Schuljahr. Jens Conrad, Hardy Seifert
 Download Jens Conrad, Hardy Seifert Mathematik üben Klasse 8 Prozentrechnung Differenzierte Materialien für das ganze Schuljahr Downloadauszug aus dem Originaltitel: Mathematik üben Klasse 8 Prozentrechnung
Download Jens Conrad, Hardy Seifert Mathematik üben Klasse 8 Prozentrechnung Differenzierte Materialien für das ganze Schuljahr Downloadauszug aus dem Originaltitel: Mathematik üben Klasse 8 Prozentrechnung
Srassensteigung Eine Strasse steigt auf einer Länge von 2,68 km um 215 m. Wie gross ist die Steigung in Prozent und Promille?
 1 RE 8.711 Srassensteigung Eine Strasse steigt auf einer Länge von 2,68 km um 215 m. Wie gross ist die Steigung in Prozent und Promille? 8,02% 80,2 2 Spannungsverbrauch Auf einer mit Gleichspannung betriebenen
1 RE 8.711 Srassensteigung Eine Strasse steigt auf einer Länge von 2,68 km um 215 m. Wie gross ist die Steigung in Prozent und Promille? 8,02% 80,2 2 Spannungsverbrauch Auf einer mit Gleichspannung betriebenen
Proportionale und antiproportionale Zuordnungen
 Proportionale und antiproportionale Zuordnungen Proportionale und antiproportionale Zuordnungen findet man in vielen Bereichen des täglichen Lebens. Zum Beispiel beim Tanken oder beim Einkaufen. Bei proportionalen
Proportionale und antiproportionale Zuordnungen Proportionale und antiproportionale Zuordnungen findet man in vielen Bereichen des täglichen Lebens. Zum Beispiel beim Tanken oder beim Einkaufen. Bei proportionalen
Prozentrechnung (Aufgaben)
 Gymnasium Pegnitz Grundwissen Js. 7 20. Juli 2007 Prozentrechnung (Aufgaben) 07cmr006 07cmr010 1. Butter hat einen Fettgehalt von 82%, Crème Fraiche enthält 30% Fett. Wie viel Gramm Butter enthalten die
Gymnasium Pegnitz Grundwissen Js. 7 20. Juli 2007 Prozentrechnung (Aufgaben) 07cmr006 07cmr010 1. Butter hat einen Fettgehalt von 82%, Crème Fraiche enthält 30% Fett. Wie viel Gramm Butter enthalten die
N & T (R) 1 Stoffeigenschaften 01 Name: Vorname: Datum:
 N & T (R) 1 Stoffeigenschaften 01 Name: Vorname: Datum: Aufgabe 1: Natur und Technik wird aufgeteilt in drei Teilbereiche: diese sind jedoch nicht immer ganz klar abgetrennt: Wasser kann zum Kochen und
N & T (R) 1 Stoffeigenschaften 01 Name: Vorname: Datum: Aufgabe 1: Natur und Technik wird aufgeteilt in drei Teilbereiche: diese sind jedoch nicht immer ganz klar abgetrennt: Wasser kann zum Kochen und
mathbuch 1 LU 15 Arbeitsheft weitere Aufgaben «Zusatzanforderungen»
 A315-3 1 5 21 Wahrscheinlich, unwahrscheinlich oder möglich? Möglich Wahrscheinlich Unwahrscheinlich A Für 1 CHF erhältst du bei der Bank 62 Euro. Für 2 CHF erhältst du daher das Doppelte. B Eine 4-g-Schokoladentafel
A315-3 1 5 21 Wahrscheinlich, unwahrscheinlich oder möglich? Möglich Wahrscheinlich Unwahrscheinlich A Für 1 CHF erhältst du bei der Bank 62 Euro. Für 2 CHF erhältst du daher das Doppelte. B Eine 4-g-Schokoladentafel
mathbuch 1 LU 15 Arbeitsheft weitere Aufgaben «Zusatzanforderungen»
 A315-3 1 5 21 Wahrscheinlich, unwahrscheinlich oder möglich? Möglich Wahrscheinlich Unwahrscheinlich A Für 1 CHF erhältst du bei der Bank 62 Euro. Für 2 CHF erhältst du daher das Doppelte. B Eine 4-g-Schokoladentafel
A315-3 1 5 21 Wahrscheinlich, unwahrscheinlich oder möglich? Möglich Wahrscheinlich Unwahrscheinlich A Für 1 CHF erhältst du bei der Bank 62 Euro. Für 2 CHF erhältst du daher das Doppelte. B Eine 4-g-Schokoladentafel
Mathematik Vergleichsarbeit 2010 Baden-Württemberg Gymnasium Bildungsstandard 6.Klasse
 Mathematik Vergleichsarbeit 2010 Baden-Württemberg Gymnasium Bildungsstandard 6.Klasse Gesamte Bearbeitungszeit: 60 Minuten Diese Aufgaben sind ohne Taschenrechner zu bearbeiten! Aufgabe 1: Berechne 5
Mathematik Vergleichsarbeit 2010 Baden-Württemberg Gymnasium Bildungsstandard 6.Klasse Gesamte Bearbeitungszeit: 60 Minuten Diese Aufgaben sind ohne Taschenrechner zu bearbeiten! Aufgabe 1: Berechne 5
Probeunterricht 2011 an Wirtschaftsschulen in Bayern
 an Wirtschaftsschulen in Bayern Mathematik 6. Jahrgangsstufe - Haupttermin Arbeitszeit Teil I (Zahlenrechnen) Seiten 1 bis 4: Arbeitszeit Teil II (Textrechnen) Seiten 5 bis 7: 45 Minuten 45 Minuten Name:....
an Wirtschaftsschulen in Bayern Mathematik 6. Jahrgangsstufe - Haupttermin Arbeitszeit Teil I (Zahlenrechnen) Seiten 1 bis 4: Arbeitszeit Teil II (Textrechnen) Seiten 5 bis 7: 45 Minuten 45 Minuten Name:....
Kosten berechnen. mathbuch 1 LU 15 Arbeitsheft + weitere Aufgaben «Zusatzanforderungen»
 A5-2 1 9 mathbuch 1 LU Arbeitsheft + weitere Aufgaben «Zusatzanforderungen» 41 Wahrscheinlich, unwahrscheinlich oder möglich? Möglich Wahrscheinlich Unwahrscheinlich A Für 1 CHF erhältst du bei der Bank
A5-2 1 9 mathbuch 1 LU Arbeitsheft + weitere Aufgaben «Zusatzanforderungen» 41 Wahrscheinlich, unwahrscheinlich oder möglich? Möglich Wahrscheinlich Unwahrscheinlich A Für 1 CHF erhältst du bei der Bank
Aufgabe 1 40% G neu : neuer Preis 1. G alt : alter Preis 1. G alt = G neu 100 2. 1. Satz Hier stehen die Mehrheiten beider Seiten.
 Grundkometenzen der Mathematik Bei Christoher Schael Aufgabe 1 40% (a) Benenne die Folgenden Zeichen: /5 G: Grundwert 1 G neu : neuer 1 W: Prozentwert 1 G alt : alter 1 : Prozentsatz oder -Zahl 1 (b) Jedes
Grundkometenzen der Mathematik Bei Christoher Schael Aufgabe 1 40% (a) Benenne die Folgenden Zeichen: /5 G: Grundwert 1 G neu : neuer 1 W: Prozentwert 1 G alt : alter 1 : Prozentsatz oder -Zahl 1 (b) Jedes
Erster Prüfungsteil: Aufgabe 1
 Erster Prüfungsteil: Aufgabe 1 a) Kreuze an, wie viele Minuten du ungefähr seit deiner Geburt gelebt hast.! 80 000 000! 8 000 000! 800 000! 80 000! 8 000 b) Bei einer Durchschnittsgeschwindigkeit von 80
Erster Prüfungsteil: Aufgabe 1 a) Kreuze an, wie viele Minuten du ungefähr seit deiner Geburt gelebt hast.! 80 000 000! 8 000 000! 800 000! 80 000! 8 000 b) Bei einer Durchschnittsgeschwindigkeit von 80
5/27/09. 1.5 Anwendungen der Bruchzahlen. Prozentrechnung. Zwei Möglichkeiten zum Einstieg
 5/27/09 1.5 Anwendungen der Bruchzahlen Sachaufgaben im 6. und 7. Schuljahr a) Prozentrechnung b) Zinsrechnung c) Zinseszinsrechnung Prozentrechnung Zwei Möglichkeiten zum Einstieg I. Man geht von Prozentangaben
5/27/09 1.5 Anwendungen der Bruchzahlen Sachaufgaben im 6. und 7. Schuljahr a) Prozentrechnung b) Zinsrechnung c) Zinseszinsrechnung Prozentrechnung Zwei Möglichkeiten zum Einstieg I. Man geht von Prozentangaben
Prozentrechnung. 1. Von 360 Schülern fahren. b) gehen zu Fuß. 2. Wieviel sind 2 7. von 210? 3. Wieviel sind 3. von 500?
 Prozentrechnung. Von 60 Schülern fahren a) mit dem Fahrrad zur Schule 9 7 b) gehen zu Fuß 8 Wie viele Schüler sind das?. Wieviel sind 7 von 0?. Wieviel sind 00 von 500? 4. Wieviel sind (Typ ) a) 4% von
Prozentrechnung. Von 60 Schülern fahren a) mit dem Fahrrad zur Schule 9 7 b) gehen zu Fuß 8 Wie viele Schüler sind das?. Wieviel sind 7 von 0?. Wieviel sind 00 von 500? 4. Wieviel sind (Typ ) a) 4% von
Wir wiederholen für die Mathematikprüfung
 Wir wiederholen für die Mathematikprüfung A. Kopfrechnen: 4 7 = 7 2 + 4 = 6 + 9 5 = 5 000 200 = 200 4 = 7 7 + 6 = 3 500 2= 2 500 3 = 6 000 4 = 35 000 : 5 = 72 : 9 = 43 + 28 = 42 000 : 6 = 7,2 + 2,6 = 360
Wir wiederholen für die Mathematikprüfung A. Kopfrechnen: 4 7 = 7 2 + 4 = 6 + 9 5 = 5 000 200 = 200 4 = 7 7 + 6 = 3 500 2= 2 500 3 = 6 000 4 = 35 000 : 5 = 72 : 9 = 43 + 28 = 42 000 : 6 = 7,2 + 2,6 = 360
Anwendungsaufgaben. Die folgenden grafischen Darstellungen geben die Höhe h des Wasserstandes in Abhängigkeit von der Füllzeit t an.
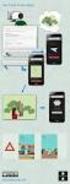 Anwendungsaufgaben 1. Jeder der abgebildeten Behälter wird gleichmäßig mit der gleichen Wassermenge pro Zeiteinheit gefüllt. Die folgenden grafischen Darstellungen geben die Höhe h des Wasserstandes in
Anwendungsaufgaben 1. Jeder der abgebildeten Behälter wird gleichmäßig mit der gleichen Wassermenge pro Zeiteinheit gefüllt. Die folgenden grafischen Darstellungen geben die Höhe h des Wasserstandes in
7 Üben X Prozentsatz P103
 7 Üben X Prozentsatz P103 Berechne (im Kopf) : Wieviel Prozent sind 1) 4 von 40 2) 18 von 40 3) 23 von 40 4) 12 cm von 6 m 5) 12 cm von 6 6) 120 kg von 1 t 7) 110 kg von 200 kg 8) 80 m von 1 km 9) 380
7 Üben X Prozentsatz P103 Berechne (im Kopf) : Wieviel Prozent sind 1) 4 von 40 2) 18 von 40 3) 23 von 40 4) 12 cm von 6 m 5) 12 cm von 6 6) 120 kg von 1 t 7) 110 kg von 200 kg 8) 80 m von 1 km 9) 380
Lösungen zu delta 5 neu
 Lösungen zu delta neu Kann ich das? Lösungen zu Seite 32. Zahl Vorgänger Nachfolger a) 99999 9999 einhundertneunundneunzigtausendneunhundertachtundneunzig 200000 zweihunderttausend b) 2949 294 neunundzwanzigtausendvierhundertachtundachtzig
Lösungen zu delta neu Kann ich das? Lösungen zu Seite 32. Zahl Vorgänger Nachfolger a) 99999 9999 einhundertneunundneunzigtausendneunhundertachtundneunzig 200000 zweihunderttausend b) 2949 294 neunundzwanzigtausendvierhundertachtundachtzig
Prozente. Prozente. 6 Rabatt und Mehrwertsteuer6. 8 Zinsen für mehr als 1 Jahr z% j Jahre Algebra. 3 Berechnung des Prozentsatzes 4 Berechnung des
 Anteile als Darstellung von n Berechnung des Prozentsatzes Berechnung des Rabatt und Mehrwertsteuer Prozentwertes Berechnung des Grundwertes 8 Zinsen mehr als Jahr K K (+ Das magisches Dreieck decke die
Anteile als Darstellung von n Berechnung des Prozentsatzes Berechnung des Rabatt und Mehrwertsteuer Prozentwertes Berechnung des Grundwertes 8 Zinsen mehr als Jahr K K (+ Das magisches Dreieck decke die
BESONDERE LEISTUNGSFESTSTELLUNG MATHEMATIK
 BESONDERE LEISTUNGSFESTSTELLUNG 2004 MATHEMATIK (HAUPTTERMIN) Arbeitszeit: Hilfsmittel: 50 Minuten Taschenrechner (nicht programmierbar, nicht grafikfähig) Tafelwerk Lösen Sie die Pflichtaufgabe und wählen
BESONDERE LEISTUNGSFESTSTELLUNG 2004 MATHEMATIK (HAUPTTERMIN) Arbeitszeit: Hilfsmittel: 50 Minuten Taschenrechner (nicht programmierbar, nicht grafikfähig) Tafelwerk Lösen Sie die Pflichtaufgabe und wählen
Rechnen mit Brüchen (1) 6
 Rechnen mit Brüchen (). Erweitern und Kürzen Der Wert eines Bruches ändert sich nicht, wenn entweder Zähler und Nenner mit derselben natürlichen Zahl multipliziert werden: a a m ( a, b, m ) ERWEITERN,
Rechnen mit Brüchen (). Erweitern und Kürzen Der Wert eines Bruches ändert sich nicht, wenn entweder Zähler und Nenner mit derselben natürlichen Zahl multipliziert werden: a a m ( a, b, m ) ERWEITERN,
Aufgabensammlung für interessierte Bewerber/innen des Berufs. Chemielaborant/in
 Aufgabensammlung für interessierte Bewerber/innen des Berufs Chemielaborant/in Hier die von uns gewünschten Kenntnisse der Mathematik. Bitte keinen Taschenrechner oder andere Hilfsmittel benutzen! Die
Aufgabensammlung für interessierte Bewerber/innen des Berufs Chemielaborant/in Hier die von uns gewünschten Kenntnisse der Mathematik. Bitte keinen Taschenrechner oder andere Hilfsmittel benutzen! Die
Download. Mathematik üben Klasse 8 Körper. Differenzierte Materialien für das ganze Schuljahr. Jens Conrad, Hardy Seifert
 Download Jens Conrad, Hardy Seifert Mathematik üben Klasse 8 Körper Differenzierte Materialien für das ganze Schuljahr Downloadauszug aus dem Originaltitel: Mathematik üben Klasse 8 Körper Differenzierte
Download Jens Conrad, Hardy Seifert Mathematik üben Klasse 8 Körper Differenzierte Materialien für das ganze Schuljahr Downloadauszug aus dem Originaltitel: Mathematik üben Klasse 8 Körper Differenzierte
Mathematik Heft 1 2015 Mittlerer Schulabschluss
 Mathematik Heft 1 2015 Mittlerer Schulabschluss 1 Name Klasse Datum Erstkorrektur Unterschrift Zweitkorrektur Unterschrift Note/Datum Herausgeber Ministerium für Schule und Berufsbildung des Landes Schleswig-Holstein
Mathematik Heft 1 2015 Mittlerer Schulabschluss 1 Name Klasse Datum Erstkorrektur Unterschrift Zweitkorrektur Unterschrift Note/Datum Herausgeber Ministerium für Schule und Berufsbildung des Landes Schleswig-Holstein
Grundwissen Mathematik 6. Jahrgangsstufe Flächen und Prozentrechnung. StR Markus Baur Werdenfels-Gymnasium Garmisch-Partenkirchen 11.
 Flächen und Prozentrechnung StR Markus Baur Werdenfels-Gymnasium Garmisch-Partenkirchen 11. April 2015 1 Inhaltsverzeichnis 1 Der Flächeninhalt von Figuren 3 1.1 Das Parallelogramm...........................
Flächen und Prozentrechnung StR Markus Baur Werdenfels-Gymnasium Garmisch-Partenkirchen 11. April 2015 1 Inhaltsverzeichnis 1 Der Flächeninhalt von Figuren 3 1.1 Das Parallelogramm...........................
Basiswissen Prozentrechnen Seite 1 von 6 0,1= 1 10 = 10
 Basiswissen Prozentrechnen Seite von 6 Nenne die Dezimalzahlen 0,; 0,2; 0,3; bis in der Prozentschreibweise. 0,= 0 = 0 00 =0 00 =0% 0,2=20% ; 0,3=30% ; 0,4=40 % ;0,5=50%; 0,6=60% ; 0,7=70 % ;... 0.9=90%
Basiswissen Prozentrechnen Seite von 6 Nenne die Dezimalzahlen 0,; 0,2; 0,3; bis in der Prozentschreibweise. 0,= 0 = 0 00 =0 00 =0% 0,2=20% ; 0,3=30% ; 0,4=40 % ;0,5=50%; 0,6=60% ; 0,7=70 % ;... 0.9=90%
c) 1 % von kg... b) 100 % = 360 m 1 % =... m 2 % =... m 10 % =... m
 1 Überlege Drei Freunde vergleichen die Höhe des Taschengeldes. Stefan erhält wöchtenlich 5 Euro. Kevin bekommt monatlich 20 Euro und Simon erhält monatlich 1 % vom Lohn seines Vaters. Simons Vater verdient
1 Überlege Drei Freunde vergleichen die Höhe des Taschengeldes. Stefan erhält wöchtenlich 5 Euro. Kevin bekommt monatlich 20 Euro und Simon erhält monatlich 1 % vom Lohn seines Vaters. Simons Vater verdient
Aufgaben zum Basiswissen 7. Klasse
 Aufgaben zum Basiswissen 7. Klasse 1. Achsen- und Punktsymmetrie 1. Aufgabe: Zeichne die Gerade g und alle weiteren Punkte ab und spiegle diese Punkte an der Geraden g und am Zentrum Z. 2. Aufgabe: Zeichne
Aufgaben zum Basiswissen 7. Klasse 1. Achsen- und Punktsymmetrie 1. Aufgabe: Zeichne die Gerade g und alle weiteren Punkte ab und spiegle diese Punkte an der Geraden g und am Zentrum Z. 2. Aufgabe: Zeichne
Abschlussprüfung 11 zur Erlangung der Erweiterten Berufsbildungsreife. Mathematik. Werkschule 2012
 Die Senatorin für Bildung, Wissenschaft und Gesundheit Freie Hansestadt Bremen Abschlussprüfung 11 zur Erlangung der Erweiterten Berufsbildungsreife Mathematik Projekt: Suppentopf Schulzentrum Neustadt
Die Senatorin für Bildung, Wissenschaft und Gesundheit Freie Hansestadt Bremen Abschlussprüfung 11 zur Erlangung der Erweiterten Berufsbildungsreife Mathematik Projekt: Suppentopf Schulzentrum Neustadt
Prozentrechnung Theorie und Aufgaben. Prozentrechnung. Theorie und Aufgaben. von Francesco Grassi. Copyright Francesco Grassi
 Prozentrechnung Theorie und Aufgaben von Francesco Grassi www.educationalapps.ch Inhaltsverzeichnis VORWORT...3 KAP.1 Prozentanteil... 4 KAP.2 Prozentuelle Änderung...23 VORWORT Mit ProzenTutor kann man
Prozentrechnung Theorie und Aufgaben von Francesco Grassi www.educationalapps.ch Inhaltsverzeichnis VORWORT...3 KAP.1 Prozentanteil... 4 KAP.2 Prozentuelle Änderung...23 VORWORT Mit ProzenTutor kann man
Textgleichungen Mischungsrechnung Lösungen
 Textgleichungen Mischungsrechnung Lösungen 1. Eine Firma kauft von der Stuhlsorte A 300 Stück und von der Stuhlsorte B 400 Stück zu einem Gesamtpreis von 68 000. Die Sorte A wird mit einem Aufpreis von
Textgleichungen Mischungsrechnung Lösungen 1. Eine Firma kauft von der Stuhlsorte A 300 Stück und von der Stuhlsorte B 400 Stück zu einem Gesamtpreis von 68 000. Die Sorte A wird mit einem Aufpreis von
BMT8 2013. Bayerischer Mathematik-Test für die Jahrgangsstufe 8 der Gymnasien. Name: Note: Klasse: Bewertungseinheiten: / 21
 BMT8 2013 A Bayerischer Mathematik-Test für die Jahrgangsstufe 8 der Gymnasien Name: Note: Klasse: Bewertungseinheiten: 1 Aufgabe 1 Gib diejenige Zahl an, mit der man 1000 multiplizieren muss, um 250 zu
BMT8 2013 A Bayerischer Mathematik-Test für die Jahrgangsstufe 8 der Gymnasien Name: Note: Klasse: Bewertungseinheiten: 1 Aufgabe 1 Gib diejenige Zahl an, mit der man 1000 multiplizieren muss, um 250 zu
M 7.4 Mathematik im Alltag: Daten, Diagramme und Prozentrechnung
 M 7.4 Mathematik im Alltag: Daten, Diagramme und Prozentrechnung Dieses Kapitel dient vor allem der Wiederholung und Vertiefung bekannter Lerninhalte. Die Schüler haben sich im Rahmen des Lehrplanabschnitts
M 7.4 Mathematik im Alltag: Daten, Diagramme und Prozentrechnung Dieses Kapitel dient vor allem der Wiederholung und Vertiefung bekannter Lerninhalte. Die Schüler haben sich im Rahmen des Lehrplanabschnitts
65 Prozentrechnen Klasse
 65 Prozentrechnen 6. 9. Klasse Inhaltsverzeichnis Vorwort................................................................................................... Seite 1 10 Lerntipps zum Lösen von Sachaufgaben........................................
65 Prozentrechnen 6. 9. Klasse Inhaltsverzeichnis Vorwort................................................................................................... Seite 1 10 Lerntipps zum Lösen von Sachaufgaben........................................
Aufgaben zu quadratischen Gleichungen. a) x² = 169. b) x² = 0,074529. c) x² = 5. d) 19x² = 5 491. a) ax² = b. b) ax² c ----- = --- b d.
 Besuchen Sie auch die Seite http://www.matheaufgaben-loesen.de/ dort gibt es viele Aufgaben zu weiteren Themen und unter Hinweise den Weg zu den Lösungen. Aufgaben zu quadratischen Gleichungen 1. a) x²
Besuchen Sie auch die Seite http://www.matheaufgaben-loesen.de/ dort gibt es viele Aufgaben zu weiteren Themen und unter Hinweise den Weg zu den Lösungen. Aufgaben zu quadratischen Gleichungen 1. a) x²
Reingewinn. Gemeinkosten Nettoerlös. Fr. 280 000.
 34.01 a) Reingewinn Bruttogewinn Fr. 48000. Fr. 328 000. Gemeinkosten Nettoerlös Fr. 280 000. Fr. 528 000. Einstandswert ( Warenkosten) Fr. 200 000. Einstandswert ( Warenkosten) Fr. 200 000. Fr. 480 000.
34.01 a) Reingewinn Bruttogewinn Fr. 48000. Fr. 328 000. Gemeinkosten Nettoerlös Fr. 280 000. Fr. 528 000. Einstandswert ( Warenkosten) Fr. 200 000. Einstandswert ( Warenkosten) Fr. 200 000. Fr. 480 000.
Mathematik 2: Korrekturanleitung (mit Taschenrechner)
 Kanton St.Gallen Bildungsdepartement BMS/FMS/WMS/WMI Aufnahmeprüfung Herbst 2014 Mathematik 2: Korrekturanleitung (mit Taschenrechner) Die Aufgaben sind auf diesen Blättern zu lösen. Der Lösungsweg muss
Kanton St.Gallen Bildungsdepartement BMS/FMS/WMS/WMI Aufnahmeprüfung Herbst 2014 Mathematik 2: Korrekturanleitung (mit Taschenrechner) Die Aufgaben sind auf diesen Blättern zu lösen. Der Lösungsweg muss
I. Lehrplanauszug. Beispielaufgaben. Grundwissen Mathematik 6. Jahrgangsstufe. In der Jahrgangsstufe 6 erwerben die Schüler folgendes Grundwissen:
 Grundwissen Mathematik 6. Jahrgangsstufe I. Lehrplanauszug In der Jahrgangsstufe 6 erwerben die Schüler folgendes Grundwissen: Sie können rationale Zahlen in verschiedenen Schreibweisen darstellen. Sie
Grundwissen Mathematik 6. Jahrgangsstufe I. Lehrplanauszug In der Jahrgangsstufe 6 erwerben die Schüler folgendes Grundwissen: Sie können rationale Zahlen in verschiedenen Schreibweisen darstellen. Sie
Mathematik 22 Prozentrechnen 01 Name: Vorname: Datum:
 Mathematik 22 Prozentrechnen 01 Name: Vorname: Datum: Aufgabe 1: Berechne die jeweils fehlenden Angaben der Tabelle: Nr. Alter Preis in Fr. Rabatt in % Rabatt in Fr. Neuer Preis in Fr. a) 199.00 Fr. 30
Mathematik 22 Prozentrechnen 01 Name: Vorname: Datum: Aufgabe 1: Berechne die jeweils fehlenden Angaben der Tabelle: Nr. Alter Preis in Fr. Rabatt in % Rabatt in Fr. Neuer Preis in Fr. a) 199.00 Fr. 30
AUFGABENPOOL ZUM PROZENTRECHNEN. e) p % von G. f) 25 % von A. g) 20 % von 5 w. h) 200 % von B. e) A von W. f) 3 x von 15 x. g) 12 von B.
 AUFGABENPOOL ZUM PROZENTRECHNEN 1. Grundwert Anteil Prozentsatz 1.1. Berechne jeweils den Anteil bzw. stelle den Anteil jeweils durch einen geeigneten Ausdruck dar: a) 27 % von 200 e) p % von G b) 13 %
AUFGABENPOOL ZUM PROZENTRECHNEN 1. Grundwert Anteil Prozentsatz 1.1. Berechne jeweils den Anteil bzw. stelle den Anteil jeweils durch einen geeigneten Ausdruck dar: a) 27 % von 200 e) p % von G b) 13 %
Name:... Vorname:...
 Zentrale Aufnahmeprüfung 2013 für die Kurzgymnasien des Kantons Zürich Mathematik Neues Lehrmittel Bitte zuerst ausfüllen: Name:... Vorname:... Prüfungsnummer:... Du hast 90 Minuten Zeit. Du musst alle
Zentrale Aufnahmeprüfung 2013 für die Kurzgymnasien des Kantons Zürich Mathematik Neues Lehrmittel Bitte zuerst ausfüllen: Name:... Vorname:... Prüfungsnummer:... Du hast 90 Minuten Zeit. Du musst alle
Streichholzgeschichten von Dieter Ortner.
 Streichholzgeschichten von Dieter Ortner. 1. Streichholzgeschichte Nr. 1 Aus vier n kann man ein Quadrat bilden. Mit diesem Verfahren sollst du nun selber herausfinden, wie viele es braucht, wenn das grosse
Streichholzgeschichten von Dieter Ortner. 1. Streichholzgeschichte Nr. 1 Aus vier n kann man ein Quadrat bilden. Mit diesem Verfahren sollst du nun selber herausfinden, wie viele es braucht, wenn das grosse
Mathematik für die Ferien Seite 1
 Mathematik für die Ferien Seite. Zähle die natürlichen geraden Zahlen auf, die größer als 0 und kleiner oder gleich 0 sind.. Schreib als Zahl: Deutschland hat 8 Millionen Einwohner. China hat Milliarde
Mathematik für die Ferien Seite. Zähle die natürlichen geraden Zahlen auf, die größer als 0 und kleiner oder gleich 0 sind.. Schreib als Zahl: Deutschland hat 8 Millionen Einwohner. China hat Milliarde
Anwendung 1: Rabatt und Skonto
 Anwendung 1: Rabatt und Skonto Herr Gerber kauft sich ein Mountainbike. Dieses kostet gemäss Katalogpreis 2400. Franken. Weil Herr Gerber Stammkunde ist, gewährt ihm der Velohändler 15% Rabatt. Somit muss
Anwendung 1: Rabatt und Skonto Herr Gerber kauft sich ein Mountainbike. Dieses kostet gemäss Katalogpreis 2400. Franken. Weil Herr Gerber Stammkunde ist, gewährt ihm der Velohändler 15% Rabatt. Somit muss
Realschule / Gymnasium. Klassen 9 / 10. - Aufgaben - Am Ende der Aufgabensammlung finden Sie eine Formelübersicht
 Am Ende der Aufgabensammlung finden Sie eine Formelübersicht 1. a) Leite eine Formel her für den Umfang eines Kreises bei gegebener Fläche. b) Wieviel mal größer wird der Umfang eines Kreises, wenn man
Am Ende der Aufgabensammlung finden Sie eine Formelübersicht 1. a) Leite eine Formel her für den Umfang eines Kreises bei gegebener Fläche. b) Wieviel mal größer wird der Umfang eines Kreises, wenn man
Grundwissen und Übungsaufgaben für Industriekeramiker und PTK
 Grundwissen und Übungsaufgaben für Industriekeramiker und PTK 1. Vorzeichenregel bei Addition und Subtraktion a) (+3) + ( 4) (+5) b) (+12) (+11) + (+4) c) ( 13) ( 14) + ( 3) d) (+31) + ( 44) (+12) e) (+7)
Grundwissen und Übungsaufgaben für Industriekeramiker und PTK 1. Vorzeichenregel bei Addition und Subtraktion a) (+3) + ( 4) (+5) b) (+12) (+11) + (+4) c) ( 13) ( 14) + ( 3) d) (+31) + ( 44) (+12) e) (+7)
Der Anteil der Jungen beträgt 68%, der der Mädchen 32%. Der Verbrauch von Auto II liegt um 20% unter dem von Auto I.
 R. Brinkmann http://brinkmann-du.de Seite 1 17.09.2012 Lösungen Prozentrechnung I se: E1 E2 E E4 E5 E6 E7 E8 E9 E10 E11 E12 E1 E14 E15 Der Anteil der Jungen beträgt 68%, der der Mädchen 2%. Der Kaufpreis
R. Brinkmann http://brinkmann-du.de Seite 1 17.09.2012 Lösungen Prozentrechnung I se: E1 E2 E E4 E5 E6 E7 E8 E9 E10 E11 E12 E1 E14 E15 Der Anteil der Jungen beträgt 68%, der der Mädchen 2%. Der Kaufpreis
St.Gallische Kantonsschulen Aufnahmeprüfung 2009 Gymnasium. Kandidatennummer: Geburtsdatum: Note: Aufgabe Punkte
 St.Gallische Kantonsschulen Aufnahmeprüfung 2009 Gymnasium Mathematik 2 mit Taschenrechner Dauer: 90 Minuten Kandidatennummer: Summe: Geburtsdatum: Note: Aufgabe 1 2 3 4 5 6 7 8 9 10 11 12 Punkte Löse
St.Gallische Kantonsschulen Aufnahmeprüfung 2009 Gymnasium Mathematik 2 mit Taschenrechner Dauer: 90 Minuten Kandidatennummer: Summe: Geburtsdatum: Note: Aufgabe 1 2 3 4 5 6 7 8 9 10 11 12 Punkte Löse
Neue Aufgaben, Dezember 2007
 Neue Aufgaben, Dezember 2007 1. Manuelas Zimmer ist 4,00m lang, 3,50m breit und 2,50m hoch. Eine der beiden großen Wandflächen soll einen gelben Farbanstrich erhalten. Von der letzten Renovierung ist noch
Neue Aufgaben, Dezember 2007 1. Manuelas Zimmer ist 4,00m lang, 3,50m breit und 2,50m hoch. Eine der beiden großen Wandflächen soll einen gelben Farbanstrich erhalten. Von der letzten Renovierung ist noch
Teil I (Richtzeit: 30 Minuten)
 Gymnasium Unterstrass Zürich Seite 1 Gymnasium Unterstrass Zürich Aufnahmeprüfung 2011 Kurzgymnasium (Neues Lehrmittel) Mathematik Name: Die Prüfung besteht aus zwei Teilen. Im ersten Teil gilt folgende
Gymnasium Unterstrass Zürich Seite 1 Gymnasium Unterstrass Zürich Aufnahmeprüfung 2011 Kurzgymnasium (Neues Lehrmittel) Mathematik Name: Die Prüfung besteht aus zwei Teilen. Im ersten Teil gilt folgende
Der Maßstab. Methodentraining Maßstab Jgst. 5. Die Karte verkleinert die Wirklichkeit.
 Der Maßstab Die verkleinert die. Der Maßstab gibt an, in welchem Verhältnis die gegenüber der verkleinert wurde. Maßstab Strecke in der 1:25000 (großer Maßstab) 25000 cm = 250 m = 0,250 km 1:50000 50000
Der Maßstab Die verkleinert die. Der Maßstab gibt an, in welchem Verhältnis die gegenüber der verkleinert wurde. Maßstab Strecke in der 1:25000 (großer Maßstab) 25000 cm = 250 m = 0,250 km 1:50000 50000
Flächenberechnung Vierecke 1
 Flächenberechnung Vierecke 1 1.)Stelle für folgendes Deltoid eine Flächenformel auf! 2.) 3.) Rautenförmige Eternitplatten haben Diagonalen in der Länge von 68cm und 42cm. a)welchen Flächeninhalt hat eine
Flächenberechnung Vierecke 1 1.)Stelle für folgendes Deltoid eine Flächenformel auf! 2.) 3.) Rautenförmige Eternitplatten haben Diagonalen in der Länge von 68cm und 42cm. a)welchen Flächeninhalt hat eine
Aufgabe 2: Welche Brüche sind auf dem Zahlenstrahl durch die Pfeile gekennzeichnet? Schreibe die Brüche in die Kästen.
 Grundwissen Klasse 6 - Lösungen I. Bruchzahlen. Sicheres Umgehen mit Bruchzahlen Brüche als Anteil verstehen Brüche am Zahlenstrahl darstellen Brüche erweitern / kürzen können (Mathehelfer: S.6/7) Aufgabe
Grundwissen Klasse 6 - Lösungen I. Bruchzahlen. Sicheres Umgehen mit Bruchzahlen Brüche als Anteil verstehen Brüche am Zahlenstrahl darstellen Brüche erweitern / kürzen können (Mathehelfer: S.6/7) Aufgabe
Prozentrechnung Teste dein Wissen! Station 1 Rechne auf einem Extrablatt und trage nur die Ergebnisse ein!
 Prozentrechnung Teste dein Wissen! Station 1 Rechne auf einem Extrablatt und trage nur die Ergebnisse ein! 1. ib folgende Brüche in Prozent an. a) ¼ = b) 3 20 = 2. Berechne den Prozentsatz: 111,6 km von
Prozentrechnung Teste dein Wissen! Station 1 Rechne auf einem Extrablatt und trage nur die Ergebnisse ein! 1. ib folgende Brüche in Prozent an. a) ¼ = b) 3 20 = 2. Berechne den Prozentsatz: 111,6 km von
Herzlich willkommen zur Demo der mathepower.de Aufgabensammlung
 Herzlich willkommen zur der Um sich schnell innerhalb der ca. 350.000 Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
Herzlich willkommen zur der Um sich schnell innerhalb der ca. 350.000 Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
15/16I 8 a Mathe Übungen 3 Dez. 15
 15/16I 8 a Mathe Übungen 3 Dez. 15 Nr. 1: Übertrage die Tabellen in dein Heft und fülle sie aus: x 4 x - (1 - x ) - 3 x + 4 1-1 - 4 5 a b (3 a - - 9 a + 6 a b 1 3 3-1 - 4 x 4 x - (1 - x ) - 3 x + 4 = x
15/16I 8 a Mathe Übungen 3 Dez. 15 Nr. 1: Übertrage die Tabellen in dein Heft und fülle sie aus: x 4 x - (1 - x ) - 3 x + 4 1-1 - 4 5 a b (3 a - - 9 a + 6 a b 1 3 3-1 - 4 x 4 x - (1 - x ) - 3 x + 4 = x
1. Prozentrechnung. 2. Prozentrechnung Typisches. 3. Prozentsätze veranschaulichen. 7. Übung. 5. Prozentrechnung Zusatztyp. 6. Grundwert (der Bezug)
 . Prozentrechnung 2. Prozentrechnung Typisches 3. Prozentsätze veranschaulichen 4. Übung 5. Prozentrechnung Zusatztyp 6. Grundwert (der Bezug) 7. Übung 8. Aufgaben 9. Bundestagswahl 203 Sitzverteilung
. Prozentrechnung 2. Prozentrechnung Typisches 3. Prozentsätze veranschaulichen 4. Übung 5. Prozentrechnung Zusatztyp 6. Grundwert (der Bezug) 7. Übung 8. Aufgaben 9. Bundestagswahl 203 Sitzverteilung
St.Gallische Kantonsschulen Aufnahmeprüfung 2009 Gymnasium. Kandidatennummer: Geburtsdatum: Note: Aufgabe Punkte
 St.Gallische Kantonsschulen Aufnahmeprüfung 009 Gymnasium Mathematik mit Taschenrechner Dauer: 90 Minuten Kandidatennummer: Summe: Geburtsdatum: Note: Aufgabe 1 3 4 5 6 7 8 9 10 11 1 Punkte Löse die Aufgaben
St.Gallische Kantonsschulen Aufnahmeprüfung 009 Gymnasium Mathematik mit Taschenrechner Dauer: 90 Minuten Kandidatennummer: Summe: Geburtsdatum: Note: Aufgabe 1 3 4 5 6 7 8 9 10 11 1 Punkte Löse die Aufgaben
LERNZIRKEL WIEDERHOLUNG DER FLÄCHEN
 LERNZIRKEL WIEDERHOLUNG DER FLÄCHEN Lehrplaneinheit Methode Sozialform Einsatzmöglichkeit Ziel, Erwartungshorizont Zeitlicher Umfang Didaktische Hinweise Berufsrelevantes Rechnen Einzelarbeit Wiederholung
LERNZIRKEL WIEDERHOLUNG DER FLÄCHEN Lehrplaneinheit Methode Sozialform Einsatzmöglichkeit Ziel, Erwartungshorizont Zeitlicher Umfang Didaktische Hinweise Berufsrelevantes Rechnen Einzelarbeit Wiederholung
7 Prozent- und Zinsrechnung
 45 Lösungen zum Schülerband 7 Prozent- und Zinsrechnung 9 9 400 Zinsen 560 kostet der Kredit bei einer Laufzeit von Monaten (zuzüglich der geliehenen Summe) Summe gesetzlicher Abzüge: 5,7 Netto: 767,6
45 Lösungen zum Schülerband 7 Prozent- und Zinsrechnung 9 9 400 Zinsen 560 kostet der Kredit bei einer Laufzeit von Monaten (zuzüglich der geliehenen Summe) Summe gesetzlicher Abzüge: 5,7 Netto: 767,6
Mathe-Quali Teil B: Aufgaben mit Lösungen
 Mathe-Quali 2016 - Teil B: Aufgaben mit en QA 2016, Teil B - en: Nr. I/1 1. Löse die folgende Gleichung: 3 (1,5x - 2,5) - (3x - 5) + (3,5x + 7) : 0,2 = 12,5 x Angaben ohne Gewähr 3 (1,5x - 2,5) - (3x -
Mathe-Quali 2016 - Teil B: Aufgaben mit en QA 2016, Teil B - en: Nr. I/1 1. Löse die folgende Gleichung: 3 (1,5x - 2,5) - (3x - 5) + (3,5x + 7) : 0,2 = 12,5 x Angaben ohne Gewähr 3 (1,5x - 2,5) - (3x -
QUALIFIZIERENDER HAUPTSCHULABSCHLUSS BESONDERE LEISTUNGSFESTSTELLUNG MATHEMATIK. 27. Juni :30 Uhr 10:20 Uhr. Teil B: 9:10 Uhr 10:20 Uhr.
 QUALIFIZIERENDER HAUPTSCHULABSCHLUSS 2012 BESONDERE LEISTUNGSFESTSTELLUNG MATHEMATIK 27. Juni 2012 8:30 Uhr 10:20 Uhr Teil B: 9:10 Uhr 10:20 Uhr Teil B Jeder Schüler muss die z w e i von der Feststellungskommission
QUALIFIZIERENDER HAUPTSCHULABSCHLUSS 2012 BESONDERE LEISTUNGSFESTSTELLUNG MATHEMATIK 27. Juni 2012 8:30 Uhr 10:20 Uhr Teil B: 9:10 Uhr 10:20 Uhr Teil B Jeder Schüler muss die z w e i von der Feststellungskommission
Materialwirtschaft / Beschaffung
 Die A&S AG ist ein Hersteller von hochwertigen Rollenketten und innovativen Produkten der Antriebstechnik mit Stammsitz in Einbeck. In verschiedenen Abteilungen der funktional aufgebauten Unternehmung
Die A&S AG ist ein Hersteller von hochwertigen Rollenketten und innovativen Produkten der Antriebstechnik mit Stammsitz in Einbeck. In verschiedenen Abteilungen der funktional aufgebauten Unternehmung
Ansgar Schiffler Übungsaufgaben zu Grundlagen der Mathematik Seite 1
 Seite 1 1. Für einen Mietwagen ist eine Grundgebühr in Höhe von 19 zu zahlen und jeder km kostet 0 cent. Du musst 37 bezahlen. Wie viele km bist Du gefahren?. Nachdem der Preis eines Produktes um 40% reduziert
Seite 1 1. Für einen Mietwagen ist eine Grundgebühr in Höhe von 19 zu zahlen und jeder km kostet 0 cent. Du musst 37 bezahlen. Wie viele km bist Du gefahren?. Nachdem der Preis eines Produktes um 40% reduziert
Mathematik 6. Jahrgangsstufe
 M 6 Zahlenrechnen Probeunterricht 2017 an Wirtschaftsschulen in Bayern Mathematik 6. Jahrgangsstufe Punkte- und Notenschlüssel Zahlenrechnen (25 Punkte) und Textrechnen (25 Punkte) = 50 Punkte Punkte Note
M 6 Zahlenrechnen Probeunterricht 2017 an Wirtschaftsschulen in Bayern Mathematik 6. Jahrgangsstufe Punkte- und Notenschlüssel Zahlenrechnen (25 Punkte) und Textrechnen (25 Punkte) = 50 Punkte Punkte Note
Musterprüfung Maturitäts- und Handelsmittelschulen. Name/Vorname: Wohnort:
 Musterprüfung Maturitäts- und Handelsmittelschulen Name/Vorname: Wohnort: Mathematik schriftlich Zeit: 10 Minuten 1 1.) Setze die gegebenen Zahlen in den Term ein und berechne: P. x y z z(x y) + 5 7 4.5
Musterprüfung Maturitäts- und Handelsmittelschulen Name/Vorname: Wohnort: Mathematik schriftlich Zeit: 10 Minuten 1 1.) Setze die gegebenen Zahlen in den Term ein und berechne: P. x y z z(x y) + 5 7 4.5
Bsp. 12% = 100. W- Prozentwert p-prozentsatz G- Grundwert. oder Dreisatz 100% 30 : 100 15% 4,50
 Prozent- und Zinsrechnung Grundgleichung der Prozentrechnung 1 1% = 100 % = 100 12 Bs. 12% = 100 W G W- Prozentwert -Prozentsatz G- Grundwert 1. Berechnung von Prozentwerten W = G Bs. Wie viel sind 15%
Prozent- und Zinsrechnung Grundgleichung der Prozentrechnung 1 1% = 100 % = 100 12 Bs. 12% = 100 W G W- Prozentwert -Prozentsatz G- Grundwert 1. Berechnung von Prozentwerten W = G Bs. Wie viel sind 15%
Matthias Leibold: Gymnasiallehrer für die Fächer Mathematik und Chemie
 Die Autoren: Stephan Dreisbach: Rektor an einer Grundschule in Nordrhein-Westfalen, Entwickler des Lernportals www.mathepirat.de, Lehrerfortbildner zur Arbeit mit neuen Medien im Kompetenzteam NRW Matthias
Die Autoren: Stephan Dreisbach: Rektor an einer Grundschule in Nordrhein-Westfalen, Entwickler des Lernportals www.mathepirat.de, Lehrerfortbildner zur Arbeit mit neuen Medien im Kompetenzteam NRW Matthias
Wie viele Prozent der Flächen sind gefärbt? Schreibe als Prozent, Dezimalbruch und Bruch
 Wie viele Prozent der Flächen sind gefärbt? Schreibe als Prozent, Dezimalbruch und Bruch Station 1 Station 2 Von einem Rechnungsbetrag über 680 werden 3% Skonto abgezogen. Wie viel beträgt der Skonto?
Wie viele Prozent der Flächen sind gefärbt? Schreibe als Prozent, Dezimalbruch und Bruch Station 1 Station 2 Von einem Rechnungsbetrag über 680 werden 3% Skonto abgezogen. Wie viel beträgt der Skonto?
MATHEMATIK-WETTBEWERB 2000/2001 DES LANDES HESSEN
 MTHEMTIK-WETTEWER 2000/2001 ES LNES HESSEN UFGEN ER GRUPPE PFLIHTUFGEN P1. Von 11000 Schülern sind 070 Mitglied in einem Verein. Wie viel Prozent sind das? P2. Ein -Player kostete bisher 80 M. ei einem
MTHEMTIK-WETTEWER 2000/2001 ES LNES HESSEN UFGEN ER GRUPPE PFLIHTUFGEN P1. Von 11000 Schülern sind 070 Mitglied in einem Verein. Wie viel Prozent sind das? P2. Ein -Player kostete bisher 80 M. ei einem
Welches Wachstumsmodell?
 1 Welches Wachstumsmodell? Um ein reales Wachstum näherungsweise richtig beschreiben zu können, benötigt man das richtige mathematische Modell. Wenn man die Art des Wachstums nicht richtig erkennt (modelliert),
1 Welches Wachstumsmodell? Um ein reales Wachstum näherungsweise richtig beschreiben zu können, benötigt man das richtige mathematische Modell. Wenn man die Art des Wachstums nicht richtig erkennt (modelliert),
Känguru der Mathematik 2004 Gruppe Écolier (3. und 4. Schulstufe) 18.3.2004
 Känguru der Mathematik 2004 Gruppe Écolier (3. und 4. Schulstufe) 18.3.2004-3 Punkte Beispiele - 1 1) 21+ 22 + 23 =? A) 56 B) 64 C) 65 D) 66 E) 76 Antwort: D 2) Am Tag der Geburt seiner Schwester war Andreas
Känguru der Mathematik 2004 Gruppe Écolier (3. und 4. Schulstufe) 18.3.2004-3 Punkte Beispiele - 1 1) 21+ 22 + 23 =? A) 56 B) 64 C) 65 D) 66 E) 76 Antwort: D 2) Am Tag der Geburt seiner Schwester war Andreas
Prozentrechnung. Wir können nun eine Formel für die Berechnung des Prozentwertes aufstellen:
 Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Mathematik Klasse 5 Bereich (Kartennummer): Strategie. Gewichte
 Gewichtsmaße Strategie Gewichte Basiswissen Für Gewichte gibt es die Maßeinheiten 1t (Tonne), 1kg (Kilogramm), 1g (Gramm) und 1mg (Milligramm). Wenn zwei Gewichte in verschiedenen Maßeinheiten gegeben
Gewichtsmaße Strategie Gewichte Basiswissen Für Gewichte gibt es die Maßeinheiten 1t (Tonne), 1kg (Kilogramm), 1g (Gramm) und 1mg (Milligramm). Wenn zwei Gewichte in verschiedenen Maßeinheiten gegeben
Prozentrechnen und Diagramme ältere Prüfungsaufgaben. Hinweis: Die in der Aufgabe dargestellten Mehrwertsteuersätze sind nicht mehr aktuell!
 Prozentrechnen Aufgabe 1 (Pflichtbereich 1999) Eine Oberbürgermeisterwahl erbrachte folgendes Ergebnis: Kandidat A: 31.751 Stimmen Kandidat B: 12.964 Stimmen Kandidat C: 8.030 Stimmen Zahl der ungültigen
Prozentrechnen Aufgabe 1 (Pflichtbereich 1999) Eine Oberbürgermeisterwahl erbrachte folgendes Ergebnis: Kandidat A: 31.751 Stimmen Kandidat B: 12.964 Stimmen Kandidat C: 8.030 Stimmen Zahl der ungültigen
Raumgeometrie - Würfel, Quader (Rechtecksäule)
 Hauptschule (Realschule) Raumgeometrie - Würfel, Quader (Rechtecksäule) 1. Gegeben ist ein Würfel mit der Kantenlänge a = 4 cm. a) Zeichne das Netz des Würfels (Abwicklung). b) Zeichne ein Schrägbild des
Hauptschule (Realschule) Raumgeometrie - Würfel, Quader (Rechtecksäule) 1. Gegeben ist ein Würfel mit der Kantenlänge a = 4 cm. a) Zeichne das Netz des Würfels (Abwicklung). b) Zeichne ein Schrägbild des
2)Wenn man zur Zahl a, die um 6 größere Zahl addiert, so erhält man 38. Welche Zahl kann man für a einsetzen? Probe!
 1) Löse die Gleichungen und führe die Probe durch! a) (5x + ) - 1 = (x + 6) b) x + x (x + 1) = 9 + 8x² c) 1 - [ y - 8 - (y + )] = (y - ) d) (5y - )(5y + ) - (5y + )² = 1 e) (a + )² - (a - ) (a - ) = (a
1) Löse die Gleichungen und führe die Probe durch! a) (5x + ) - 1 = (x + 6) b) x + x (x + 1) = 9 + 8x² c) 1 - [ y - 8 - (y + )] = (y - ) d) (5y - )(5y + ) - (5y + )² = 1 e) (a + )² - (a - ) (a - ) = (a
Abitur 2009 Mathematik GK Stochastik Aufgabe C1
 Seite 1 Abiturloesung.de - Abituraufgaben Abitur 009 Mathematik GK Stochastik Aufgabe C1 Auf einem Spielbrett rollt eine Kugel vom Start bis in eines der Fächer F 1 bis F 5. An jeder Verzweigung rollt
Seite 1 Abiturloesung.de - Abituraufgaben Abitur 009 Mathematik GK Stochastik Aufgabe C1 Auf einem Spielbrett rollt eine Kugel vom Start bis in eines der Fächer F 1 bis F 5. An jeder Verzweigung rollt
5. Lernzielkontrolle / Stegreifaufgabe
 Reibung 1. Ein Schlittschuhläufer der Gewichtskraft 0,80 kn muss mit einer Kraft von 12 N gezogen werden damit er seine Geschwindigkeit unverändert beibehält. a) Wie groß ist in diesem Fall die Reibungszahl
Reibung 1. Ein Schlittschuhläufer der Gewichtskraft 0,80 kn muss mit einer Kraft von 12 N gezogen werden damit er seine Geschwindigkeit unverändert beibehält. a) Wie groß ist in diesem Fall die Reibungszahl
Schüler/innen-Arbeitsheft Seite 1
 Schüler/innen-Arbeitsheft Seite 1 M 1 Zum Lesen Mathematische Stenographie In der Mathematik werden die Grundrechenarten häufig benutzt, um Vorgänge (wie das Einzahlen oder Abheben von Geld auf ein Konto)
Schüler/innen-Arbeitsheft Seite 1 M 1 Zum Lesen Mathematische Stenographie In der Mathematik werden die Grundrechenarten häufig benutzt, um Vorgänge (wie das Einzahlen oder Abheben von Geld auf ein Konto)
Name:. Vorname:.. Hinweise: Bei allen Aufgaben muss der Lösungsweg nachvollziehbar sein! Zugelassene Hilfsmittel: keine
 Name:. Vorname:.. Hinweise: Bei allen Aufgaben muss der Lösungsweg nachvollziehbar sein! Zugelassene Hilfsmittel: keine Aufgabe P 1.0 Hans kauft ein neues Auto für 11.500,00. Er zahlt es in jährlichen
Name:. Vorname:.. Hinweise: Bei allen Aufgaben muss der Lösungsweg nachvollziehbar sein! Zugelassene Hilfsmittel: keine Aufgabe P 1.0 Hans kauft ein neues Auto für 11.500,00. Er zahlt es in jährlichen
1) Welcher Bruchteil des nebenstehenden Rechtecks ABCD ist grau gefärbt? e) 12. : 13 k) (2,374. 2,43 7,035). (1
 Gymnasium Stein Wiederholungsaufgaben zum Grundwissenkatalog Mathematik der 6. Jahrgangsstufe ) Welcher Bruchteil des nebenstehenden Rechtecks ABCD ist grau gefärbt? a) b) c) + d) 6 a b c d e f g h e)
Gymnasium Stein Wiederholungsaufgaben zum Grundwissenkatalog Mathematik der 6. Jahrgangsstufe ) Welcher Bruchteil des nebenstehenden Rechtecks ABCD ist grau gefärbt? a) b) c) + d) 6 a b c d e f g h e)
Vergleichsarbeit Mathematik 8. Schuljahrgang 6. März 2007
 Niedersächsisches Kultusministerium Vergleichsarbeit Mathematik 8. Schuljahrgang 6. März 2007 VA TYP 1a Hauptschule Hauptschulzweig der KGS B(G)-Kurs der IGS Hauptschülerinnen und Hauptschüler der Förderschule
Niedersächsisches Kultusministerium Vergleichsarbeit Mathematik 8. Schuljahrgang 6. März 2007 VA TYP 1a Hauptschule Hauptschulzweig der KGS B(G)-Kurs der IGS Hauptschülerinnen und Hauptschüler der Förderschule
Probeunterricht 2009 an Wirtschaftsschulen in Bayern
 an Wirtschaftsschulen in Bayern Mathematik 6. Jahrgangsstufe Arbeitszeit Teil I (Zahlenrechnen): Arbeitszeit Teil II (Textrechnen): 45 Minuten 45 Minuten Name.. Vorname.. Bewertung (Erstkorrektor) Bewertung
an Wirtschaftsschulen in Bayern Mathematik 6. Jahrgangsstufe Arbeitszeit Teil I (Zahlenrechnen): Arbeitszeit Teil II (Textrechnen): 45 Minuten 45 Minuten Name.. Vorname.. Bewertung (Erstkorrektor) Bewertung
Zeit [h] 1 h 12 h 20 h 36 h. Zeit [h] 0,25 0,5 0,75 1 1,5 2 x. Strecke auf der Karte [cm] 1 10 Strecke in Wirklichkeit [km] Karte [cm]
![Zeit [h] 1 h 12 h 20 h 36 h. Zeit [h] 0,25 0,5 0,75 1 1,5 2 x. Strecke auf der Karte [cm] 1 10 Strecke in Wirklichkeit [km] Karte [cm] Zeit [h] 1 h 12 h 20 h 36 h. Zeit [h] 0,25 0,5 0,75 1 1,5 2 x. Strecke auf der Karte [cm] 1 10 Strecke in Wirklichkeit [km] Karte [cm]](/thumbs/41/22501205.jpg) 1 8 Wertetabellen 31 A Höhe von Blattstapeln Anzahl Blätter 2 12 75 2 3 Höhe [cm] 7,5 3 187,5 1 125 4, B Stundenlohn Zeit [h] 1 h 12 h 2 h 36 h Lohn [CHF] 13. 162 27 486 4 2 54 27 13,5 C In 18 min kommt
1 8 Wertetabellen 31 A Höhe von Blattstapeln Anzahl Blätter 2 12 75 2 3 Höhe [cm] 7,5 3 187,5 1 125 4, B Stundenlohn Zeit [h] 1 h 12 h 2 h 36 h Lohn [CHF] 13. 162 27 486 4 2 54 27 13,5 C In 18 min kommt
Mathematik. Aufnahmeprüfung vom 15. Juni
 Berufsmaturität 1 Mathematik Aufnahmeprüfung vom 15. Juni 2016 Kandidaten-Nr.: Name: Vorname:......... Allgemeine Hinweise: Die Prüfungszeit beträgt 60 Minuten. Erlaubte Hilfsmittel: Netzunabhängiger Taschenrechner
Berufsmaturität 1 Mathematik Aufnahmeprüfung vom 15. Juni 2016 Kandidaten-Nr.: Name: Vorname:......... Allgemeine Hinweise: Die Prüfungszeit beträgt 60 Minuten. Erlaubte Hilfsmittel: Netzunabhängiger Taschenrechner
1 1.4 Rechnen mit Größen
 . Rechnen mit Größen Drücke in der angegebenen Einheit aus! a) 0 mm = cm b) km 0 m = m c) 8, cm² = dm² d) 0,9 m² = dm² e) 0, m³ = l f), m³ = dm³ g), hl = dm³ h), kg = dag i) 0, g = kg Die höchsten Berge
. Rechnen mit Größen Drücke in der angegebenen Einheit aus! a) 0 mm = cm b) km 0 m = m c) 8, cm² = dm² d) 0,9 m² = dm² e) 0, m³ = l f), m³ = dm³ g), hl = dm³ h), kg = dag i) 0, g = kg Die höchsten Berge
Aufgaben zu VOLUMEN, MASSE und DICHTE
 Aufgaben zu VOLUMEN, MASSE und DICHTE Aufg. 1: Eine Brauerei füllt Flaschen ab, 0,75l pro Flasche. Wie viel m³ waren im Tank, wenn dessen Inhalt 15000 Flaschen ergab? Aufg. 2: Ein Destillierapparat liefert
Aufgaben zu VOLUMEN, MASSE und DICHTE Aufg. 1: Eine Brauerei füllt Flaschen ab, 0,75l pro Flasche. Wie viel m³ waren im Tank, wenn dessen Inhalt 15000 Flaschen ergab? Aufg. 2: Ein Destillierapparat liefert
