Speicher und Adressraum
|
|
|
- Lioba Wetzel
- vor 7 Jahren
- Abrufe
Transkript
1 Linearer Speicher (Adressraum) Technische Universität München Speicher und Adressraum Freie Speicherhalde (Heap) Freier Speicherstapel (Stack) Globale Variablen Bibliotheksfunktionen Laufzeitsystem Programmcode func2 Programmcode func1 Programmcode main
2 Speicher und Adressraum Die Halde (Heap) ist ein Speicherbereich, aus dem zur Laufzeit eines Programms zusammenhängende Speicherabschnitte angefordert und in beliebiger Reihenfolge wieder freigegeben werden können. Der Stapel (Stack) ist eine Speicherbereich, auf den Elemente nur `oben gespeichert und auch nur von dort wieder gelesen werden. Elemente werden übereinander gestapelt und in umgekehrter Reihenfolge vom Stapel genommen. (siehe später) Dies wird auch Last In First Out Prinzip (LIFO) genannt.
3 Speicher und Adressraum Verwendung der Halde int[][] a; a = new int[100][]; // Feld von 100 Verweisen for (int i = 0; i < 100; i++) // 100 int-felder mit Längen // von 1 bis 100 a[i] = new int[i+1]; Jedes dynamisch allokierte Feld wird auf der Halde angelegt Egal ob die Allokation im Hauptprogramm oder in einer Funktion stattfindet Für den Programmierer erst einmal nicht sichtbar
4 Speicher und Adressraum Verwendung des Stacks Funktionsaufrufe public static void set(int x) { x = 4; return; public static void main(string[] args) { int x = 2; set(x); write(x);
5 Linearer Speicher (Adressraum) Technische Universität München Speicher und Adressraum Frame von set: - Lokale Variablen - Rücksprungaddresse - etc. Freie Speicherhalde (Heap) Freier Speicherstapel (Stack) Globale Variablen Bibliotheksfunktionen Laufzeitsystem Programmcode func2 Programmcode sqr Programmcode main Frame von main: - Lokale Variablen - etc. Situation: main hat set aufgerufen
6 Speicher und Adressraum Verwendung des Stacks Funktionsaufrufe Beim Aufruf von main und den Funktionen/Prozeduren werden die jeweils lokalen Variablen (und evtl. die Rücksprungadresse) als sog. Frames auf den Stack gespeichert Während der Programmausführung ist jeweils nur der oberste Frame `sichtbar, und die als global definierten Variablen Bei der Beendigung einer Funktion/Prozedur (Rücksprung in das Hauptprogramm) wird der zur Funktion/Prozedur gehörende Stack gelöscht
7 Speicher und Adressraum Parameterübergabe an Funktionen in Java public static void set(int x) { x = 4; return; Stack public static void main(string[] args) { int x = 2; set(x); write(x); main()
8 Speicher und Adressraum Parameterübergabe an Funktionen in Java public static void set(int x) { x = 4; return; Stack public static void main(string[] args) { int x = 2; set(x); write(x); x = 2 main()
9 Speicher und Adressraum Parameterübergabe an Funktionen in Java public static void set(int x) { x = 4; return; Stack public static void main(string[] args) { int x = 2; set(x); write(x); Kopieren des Wertes von x nach lokales x in set x = 2; set() x = 2 main()
10 Speicher und Adressraum Parameterübergabe an Funktionen in Java public static void set(int x) { x = 4; return; Stack public static void main(string[] args) { int x = 2; set(x); write(x); x = 4; set() x = 2 main()
11 Speicher und Adressraum Parameterübergabe an Funktionen in Java public static void set(int x) { x = 4; return; Stack public static void main(string[] args) { int x = 2; set(x); write(x); x = 2 main()
12 Speicher und Adressraum Parameterübergabe an Funktionen in Java public static void set(int x) { x = 4; return; Stack public static void main(string[] args) { int x = 2; set(x); write(x); x = 2 main()
13 Speicher und Adressraum Parameterübergabe an Funktionen in Java public static void set(int x) { x = 4; return; Stack public static void main(string[] args) { int x = 2; set(x); write(x); Diese Art der Parameterübergabe nennt man Call-by-Value x = 2 main()
14 Speicher und Adressraum Parameterübergabe mittels Call-by-Reference void set(int &x) { x = 4; return; Stack void main(string[] args) { int x = 2; set(x); write(x); Die Funktion erhält die Adresse (&) von x und nicht dessen Wert main()
15 Speicher und Adressraum Parameterübergabe mittels Call-by-Reference void set(int &x) { x = 4; return; Stack void main(string[] args) { int x = 2; set(x); write(x); Die Funktion erhält die Adresse (&) von x und nicht dessen Wert x = 2 main()
16 Speicher und Adressraum Parameterübergabe mittels Call-by-Reference void set(int &x) { x = 4; return; Stack void main(string[] args) { int x = 2; set(x); write(x); Kopieren der Adresse von x nach lokales x in set (x = 0xA0000) sqr() x = 2 main()
17 Speicher und Adressraum Parameterübergabe mittels Call-by-Reference void set(int &x) { x = 4; return; Stack void main(string[] args) { int x = 2; set(x); write(x); (x = 0xA0000) sqr() x = 4 main()
18 Speicher und Adressraum Parameterübergabe mittels Call-by-Reference void set(int &x) { x = 4; return; Stack void main(string[] args) { int x = 2; set(x); write(x); x = 4 main()
19 Speicher und Adressraum Parameterübergabe mittels Call-by-Reference void set(int &x) { x = 4; return; Stack void main(string[] args) { int x = 2; set(x); write(x); x = 4 main()
20 Speicher und Adressraum Java kennt keinen Adress-Operator & Für primitive Datentypen wird automatisch ein Wertparameter verwendet, der beim Aufruf einer Funktion kopiert wird Call-by-Value Für Objekte (siehe später) wird die Objektreferenz als Wertparameter durch Kopie übergeben Call-by-Reference D.h., dass der Wert des Objektes verändert werden kann
21 Rekursive Funktionen Verwendung des Stacks Rekursion am Beispiel der Fakultätsberechnung public static int fak(int n) { if (n > 0) else return n * fak(n-1); return 1; Definition einer Funktion, die sich selbst aufruft, um den Funktionswert zu berechnen.
22 Fakultätsberechnung 6 fak(3) 3 * fak(2) 2 fak(2) 2 * fak(1) 1 fak(1) 1 * fak(0) public static int fak(int n) { if (n > 0) return n * fak(n-1); else return 1; fak(0) 1 1
23 Rekursive Funktionen Aufbau des Frame-Stacks public static int fak(int n) { if (n > 0) return n * fak(n-1); else return 1; Stack public static void main(string[] args) { int x; x = fak(3); write(x); main(): x = fak(3)
24 Rekursive Funktionen Aufbau des Frame-Stacks public static int fak(int n) { if (n > 0) return n * fak(n-1); else return 1; Stack public static void main(string[] args) { int x; x = fak(3); write(x); n = 3 return n * fak(2) main(): z = fak(3)
25 Rekursive Funktionen Aufbau des Frame-Stacks public static int fak(int n) { if (n > 0) return n * fak(n-1); else return 1; public static void main(string[] args) { int x; x = fak(3); write(x); Stack n = 2 return n * fak(1) n = 3 return n * fak(2) main(): x = fak(3)
26 Rekursive Funktionen Aufbau des Frame-Stacks public static int fak(int n) { if (n > 0) return n * fak(n-1); else return 1; public static void main(string[] args) { int x; x = fak(3); write(x); Stack n = 1 return 1 n = 2 return n * fak(1) n = 3 return n * fak(2) main(): x = fak(3)
27 Rekursive Funktionen Abbau des Frame-Stacks public static int fak(int n) { if (n > 0) return n * fak(n-1); else return 1; public static void main(string[] args) { int x; x = fak(3); write(x); Stack n = 1 return 1 n = 2 return n * fak(1) n = 3 return n * fak(2) main(): x = fak(3) 1
28 Rekursive Funktionen Abbau des Frame-Stacks public static int fak(int n) { if (n > 0) return n * fak(n-1); else return 1; public static void main(string[] args) { int x; x = fak(3); write(x); Stack n = 2 return n * fak(1) n = 3 return n * fak(2) main(): x = fak(3) 2
29 Rekursive Funktionen Abbau des Frame-Stacks public static int fak(int n) { if (n > 0) return n * fak(n-1); else return 1; Stack public static void main(string[] args) { int x; x = fak(3); write(x); n = 3 return n * fak(2) 6 main(): x = fak(3)
30 Rekursive Funktionen Abbau des Frame-Stacks public static int fak(int n) { if (n > 0) return n * fak(n-1); else return 1; Stack public static void main(string[] args) { int x; x = fak(3); write(x); main(): x = 6
31 Rekursion: die Türme von Hanoi Problem: setze alle Scheiben vom Stapel 1 auf den Stapel 2. Es darf nur eine Scheibe pro Zug bewegt werden. Es darf niemals eine größere Scheibe auf einer kleineren sitzen. Stapel #1 Stapel #2 Stapel #3
32 Rekursion: die Türme von Hanoi Rekursionsgleichung für die Türme von Hanoi Sei H n = Anzahl Züge für einen Stapel mit n Scheiben Dann sieht die Zug-Strategie wie folgt aus: Ziehe die obersten n 1 Scheiben auf den Ausweichstapel. (H n 1 Züge) Ziehe die unterste Scheibe. (1 Zug) Ziehe die obersten n 1 Scheiben auf die unterste Scheibe. (H n 1 Züge) Somit ergibt sich: H n = 2H n Die Anzahl Züge wird durch eine Rekursionsgleichung beschrieben.
33 Türme von Hanoi Wie viele Züge muss man machen? H n = 2 H n = 2 (2 H n 2 + 1) + 1 = 2 2 H n = 2 2 (2 H n 3 + 1) = 2 3 H n = 2 n 1 H n = 2 n n (da H 1 = 1) = n 1 i=0 2 i = 2 n 1
34 Rekursion (linear) rekursive Fakultätsberechnung (ein rekursiver Aufruf ) public static int f(int n) { if (n > 0) return n * f(n-1); else return 1; f(4) = 4*f(3) f(3) = 3*f(2) f(2) = 2*f(1) f(3) = 3*2=6 f(2) = 2*1=2 f(4) = 4*6=24 f(1) = 1
35 Rekursion Beobachtung: In der rekursiven Berechnung der Fakultät wird nach der Rekursion noch eine Multiplikation mit dem Argument n berechnet Es müssen Zwischenergebnisse auf dem Stack gespeichert werden und Die Funktion kann am Ende der Rekursion nicht direkt terminieren Eine Rekursion heißt endrekursiv, wenn der Aufruf der Rekursion die letzte Aktion zur Berechnung der rekursiven Funktion ist Endrekursive Funktionen zeigen ein besseres Verhalten hinsichtlich des Speicherbedarfs Wie kann man eine nicht endrekursive Funktion endrekursiv machen?
36 Rekursion Die Endrekursion kann z.b. durch Einführen einer Hilfsfunktion erreicht werden public static int h_f(int n, int fak) { if (n 1) return fak; else return h_f(n-1, fak*n); public static int f(int n) { return h_f(n, 1);
37 Rekursion Ablauf der Fakultätsberechnung mit endrekursiver Hilfsfunktion f(4) = h_f(4,1) = h_f(3,4*1) h_f(3,4) = h_f(2,4*3) h_f(2,12) = h_f(1,12*2) = 24
38 Rekursion Ein Beispiel für eine nichtlineare Rekursion (mehrfache rekursive Aufrufe in einer Funktion) Die Berechnung der Fibonacci Zahlen: 1, 1, 2, 3, 5, 8, 13, 21, 34,... mit der Rekursionsgleichung f n f n 1 + f n 2 mit f 1 f 2 1 Die Aufruffolge zeigt, dass viele Fibonacci Zahlen mehrfach berechnet werden und ~2 n Auswertungen benötigt werden f n f n 1 f n 2 f n 2 f n 3 f n 3 f n 4 f n 4 f n 3
39 Rekursion Hier nun die endrekursive Variante mit ~n Auswertungen public static int h_fib(int n, int fk1, int fk2) { if (n 1) return fk1+fk2; else return h_fib(n-1,fk2+fk1, fk1) public static int fib(int n) { return h_fib(n-1, 1,0);
40 Rekursion Allgemeine Struktur einer Endrekursion f n = g n falls T(n) f(r n ) sonst mit der Abbruchbedingung T(n)
41 Rekursion Iterative Berechnung einer endrekursiven Funktion f n = f r n = f r r n = f r 3 n = = f r k n = g(r k n ) hierbei ist k die kleinste Zahl für die P r k n = true Hieraus folgt die iterative Berechnung while(p(n)==false) n = r(n); return g(n);
42 Rekursion Iteration anstelle von Rekursion Die Endrekursion lässt sich immer durch eine n-fache for-schleife berechnen public static int fib(int n) { int f, fk1 = 1, fk2 = 0; while(--n) { f = fk1 + fk2; fk2 = fk1; fk1 = f; return fk1;
43 Rekursion Allgemeine Struktur einer linearen Rekursion f n = mit der Abbruchbedingung T(n) g n falls T(n) n, f r(n) sonst Expansion der rekursiven Definition ergibt f n = n, f r n = n, r n, f r 2 n = = (n, r n, r 2 n,, r k 1 n, g r k n Achtung: die Sequenz n, r n, r 2 n wird in umgekehrter Reihenfolge benötigt. Wie realisiert man das?
44 Rekursion Weitere Beispiele für rekursive Strukturen - Fraktale Sierpinski- Dreieck Koch- Kurve
45 Rekursion Rekursion in der Natur: die Mandelbrot Menge Rekursive Auswertung der Rekursionsgleichung für initiale Punkte c in der komplexen Zahlenebene (z i = 0) z i+1 = z i 2 + c (Färbung der Punkte zeigt Stärke des Wachstums von z i )
6 Speicherorganisation
 Der Speicher des Programms ist in verschiedene Speicherbereiche untergliedert Speicherbereiche, die den eigentlichen Programmcode und den Code der Laufzeitbibliothek enthalten; einen Speicherbereich für
Der Speicher des Programms ist in verschiedene Speicherbereiche untergliedert Speicherbereiche, die den eigentlichen Programmcode und den Code der Laufzeitbibliothek enthalten; einen Speicherbereich für
6 Speicherorganisation
 6 Speicherorganisation Der Speicher des Programms ist in verschiedene Speicherbereiche untergliedert Speicherbereiche, die den eigentlichen Programmcode und den Code der Laufzeitbibliothek enthalten; einen
6 Speicherorganisation Der Speicher des Programms ist in verschiedene Speicherbereiche untergliedert Speicherbereiche, die den eigentlichen Programmcode und den Code der Laufzeitbibliothek enthalten; einen
Heap vs. Stack vs. statisch. 6 Speicherorganisation. Beispiel Statische Variablen. Statische Variablen
 Heap vs. vs. statisch Der Speicher des Programms ist in verschiedene Speicherbereiche untergliedert Speicherbereiche, die den eigentlichen Programmcode und den Code der Laufzeitbibliothek enthalten; einen
Heap vs. vs. statisch Der Speicher des Programms ist in verschiedene Speicherbereiche untergliedert Speicherbereiche, die den eigentlichen Programmcode und den Code der Laufzeitbibliothek enthalten; einen
Heap vs. Stack vs. statisch. 6 Speicherorganisation. Beispiel Statische Variablen. Statische Variablen
 Heap vs. vs. statisch Der Speicher des Programms ist in verschiedene Speicherbereiche untergliedert Speicherbereiche, die den eigentlichen Programmcode und den Code der Laufzeitbibliothek enthalten; einen
Heap vs. vs. statisch Der Speicher des Programms ist in verschiedene Speicherbereiche untergliedert Speicherbereiche, die den eigentlichen Programmcode und den Code der Laufzeitbibliothek enthalten; einen
Einführung in die Informatik I
 Einführung in die Informatik I Fortgeschrittene Rekursion Prof. Dr. Nikolaus Wulff Problematische Rekursion Mittels Rekursion lassen sich Spezifikationen recht elegant und einfach implementieren. Leider
Einführung in die Informatik I Fortgeschrittene Rekursion Prof. Dr. Nikolaus Wulff Problematische Rekursion Mittels Rekursion lassen sich Spezifikationen recht elegant und einfach implementieren. Leider
Algorithmen & Programmierung. Rekursive Funktionen (1)
 Algorithmen & Programmierung Rekursive Funktionen (1) Berechnung der Fakultät Fakultät Die Fakultät N! einer nichtnegativen ganzen Zahl N kann folgendermaßen definiert werden: d.h. zur Berechnung werden
Algorithmen & Programmierung Rekursive Funktionen (1) Berechnung der Fakultät Fakultät Die Fakultät N! einer nichtnegativen ganzen Zahl N kann folgendermaßen definiert werden: d.h. zur Berechnung werden
II.3.1 Rekursive Algorithmen - 1 -
 1. Grundelemente der Programmierung 2. Objekte, Klassen und Methoden 3. Rekursion und dynamische Datenstrukturen 4. Erweiterung von Klassen und fortgeschrittene Konzepte II.3.1 Rekursive Algorithmen -
1. Grundelemente der Programmierung 2. Objekte, Klassen und Methoden 3. Rekursion und dynamische Datenstrukturen 4. Erweiterung von Klassen und fortgeschrittene Konzepte II.3.1 Rekursive Algorithmen -
Vorkurs Informatik WiSe 17/18
 Java Rekursion Dr. Werner Struckmann / Stephan Mielke, Nicole Naczk, 10.10.2017 Technische Universität Braunschweig, IPS Überblick Einleitung Türme von Hanoi Rekursion Beispiele 10.10.2017 Dr. Werner Struckmann
Java Rekursion Dr. Werner Struckmann / Stephan Mielke, Nicole Naczk, 10.10.2017 Technische Universität Braunschweig, IPS Überblick Einleitung Türme von Hanoi Rekursion Beispiele 10.10.2017 Dr. Werner Struckmann
Vorlesung Programmieren
 Vorlesung Programmieren Speicherverwaltung und Parameterübergabe Prof. Dr. Stefan Fischer Institut für Telematik, Universität zu Lübeck http://www.itm.uni-luebeck.de/people/fischer Gültigkeitsbereich von
Vorlesung Programmieren Speicherverwaltung und Parameterübergabe Prof. Dr. Stefan Fischer Institut für Telematik, Universität zu Lübeck http://www.itm.uni-luebeck.de/people/fischer Gültigkeitsbereich von
Vorkurs Informatik WiSe 16/17
 Java Rekursion Dr. Werner Struckmann / Stephan Mielke, Jakob Garbe, 11.10.2016 Technische Universität Braunschweig, IPS Überblick Einleitung Beispiele 11.10.2016 Dr. Werner Struckmann / Stephan Mielke,
Java Rekursion Dr. Werner Struckmann / Stephan Mielke, Jakob Garbe, 11.10.2016 Technische Universität Braunschweig, IPS Überblick Einleitung Beispiele 11.10.2016 Dr. Werner Struckmann / Stephan Mielke,
public class Test extends MiniJava { public static void main (String [] args) { write(args[0]+args[1]); } } // end of class Test
![public class Test extends MiniJava { public static void main (String [] args) { write(args[0]+args[1]); } } // end of class Test public class Test extends MiniJava { public static void main (String [] args) { write(args[0]+args[1]); } } // end of class Test](/thumbs/80/81152067.jpg) Manche Funktionen, deren Ergebnistyp void ist, geben gar keine Werte zurück im Beispiel: write() und main(). Diese Funktionen heißen Prozeduren. Das Hauptprogramm hat immer als Parameter ein Feld args
Manche Funktionen, deren Ergebnistyp void ist, geben gar keine Werte zurück im Beispiel: write() und main(). Diese Funktionen heißen Prozeduren. Das Hauptprogramm hat immer als Parameter ein Feld args
11. Rekursion. 1, falls n 1. n (n 1)!, andernfalls. Mathematische Rekursion. Rekursion in Java: Genauso! Unendliche Rekursion. n!
 Mathematische Rekursion 11. Rekursion Mathematische Rekursion, Terminierung, der Aufrufstapel, Beispiele, Rekursion vs. Iteration, Lindenmayer Systeme Viele mathematische Funktionen sind sehr natürlich
Mathematische Rekursion 11. Rekursion Mathematische Rekursion, Terminierung, der Aufrufstapel, Beispiele, Rekursion vs. Iteration, Lindenmayer Systeme Viele mathematische Funktionen sind sehr natürlich
Rekursive Funktionen
 Um Rekursion zu verstehen, muss man vor allem Rekursion verstehen. http://www2.norwalk-city.k12.oh.us/wordpress/precalc/files/2009/05/mona-lisa-jmc.jpg Rekursive Funktionen OOPM, Ralf Lämmel Was ist Rekursion?
Um Rekursion zu verstehen, muss man vor allem Rekursion verstehen. http://www2.norwalk-city.k12.oh.us/wordpress/precalc/files/2009/05/mona-lisa-jmc.jpg Rekursive Funktionen OOPM, Ralf Lämmel Was ist Rekursion?
Rekursion. Sie wissen wie man Programme rekursiv entwickelt. Sie kennen typische Beispiele von rekursiven Algorithmen
 Rekursion Sie wissen wie man Programme rekursiv entwickelt Sie kennen typische Beispiele von rekursiven Algorithmen Sie kennen die Vor-/Nachteile von rekursiven Algorithmen Einführung 2 von 40 Rekursiver
Rekursion Sie wissen wie man Programme rekursiv entwickelt Sie kennen typische Beispiele von rekursiven Algorithmen Sie kennen die Vor-/Nachteile von rekursiven Algorithmen Einführung 2 von 40 Rekursiver
12. Rekursion. 1, falls n 1. n (n 1)!, andernfalls. Lernziele. Mathematische Rekursion. Rekursion in Java: Genauso! n! =
 Lernziele Sie verstehen, wie eine Lösung eines rekursives Problems in Java umgesetzt werden kann. Sie wissen, wie Methoden in einem Aufrufstapel abgearbeitet werden. 12. Rekursion Mathematische Rekursion,
Lernziele Sie verstehen, wie eine Lösung eines rekursives Problems in Java umgesetzt werden kann. Sie wissen, wie Methoden in einem Aufrufstapel abgearbeitet werden. 12. Rekursion Mathematische Rekursion,
Rekursive Funktionen
 Um Rekursion zu verstehen, muss man vor allem Rekursion verstehen. http://www2.norwalk-city.k12.oh.us/wordpress/precalc/files/2009/05/mona-lisa-jmc.jpg Rekursive Funktionen OOPM, Ralf Lämmel Was ist Rekursion?
Um Rekursion zu verstehen, muss man vor allem Rekursion verstehen. http://www2.norwalk-city.k12.oh.us/wordpress/precalc/files/2009/05/mona-lisa-jmc.jpg Rekursive Funktionen OOPM, Ralf Lämmel Was ist Rekursion?
Institut fu r Informatik
 Technische Universita t Mu nchen Institut fu r Informatik Lehrstuhl fu r Bioinformatik Einfu hrung in die Programmierung fu r Bioinformatiker Prof. B. Rost, L. Richter WS 2013/14 Aufgabenblatt 5 2. Dezember
Technische Universita t Mu nchen Institut fu r Informatik Lehrstuhl fu r Bioinformatik Einfu hrung in die Programmierung fu r Bioinformatiker Prof. B. Rost, L. Richter WS 2013/14 Aufgabenblatt 5 2. Dezember
Methoden. Gerd Bohlender. Einstieg in die Informatik mit Java, Vorlesung vom
 Einstieg in die Informatik mit Java, Vorlesung vom 2.5.07 Übersicht 1 2 definition 3 Parameterübergabe, aufruf 4 Referenztypen bei 5 Überladen von 6 Hauptprogrammparameter 7 Rekursion bilden das Analogon
Einstieg in die Informatik mit Java, Vorlesung vom 2.5.07 Übersicht 1 2 definition 3 Parameterübergabe, aufruf 4 Referenztypen bei 5 Überladen von 6 Hauptprogrammparameter 7 Rekursion bilden das Analogon
9. Rekursion. 1 falls n 1 n (n 1)!, andernfalls. Experiment: Die Türme von Hanoi. Links Mitte Rechts. Mathematische Rekursion
 Experiment: Die Türme von Hanoi. Rekursion Mathematische Rekursion, Terminierung, der Aufrufstapel, Beispiele, Rekursion vs. Iteration Links Mitte Rechts Mathematische Rekursion Viele mathematische Funktionen
Experiment: Die Türme von Hanoi. Rekursion Mathematische Rekursion, Terminierung, der Aufrufstapel, Beispiele, Rekursion vs. Iteration Links Mitte Rechts Mathematische Rekursion Viele mathematische Funktionen
Erste Java-Programme (Scopes und Rekursion)
 Lehrstuhl Bioinformatik Konstantin Pelz Erste Java-Programme (Scopes und Rekursion) Tutorium Bioinformatik (WS 18/19) Konstantin: Konstantin.pelz@campus.lmu.de Homepage: https://bioinformatik-muenchen.com/studium/propaedeutikumprogrammierung-in-der-bioinformatik/
Lehrstuhl Bioinformatik Konstantin Pelz Erste Java-Programme (Scopes und Rekursion) Tutorium Bioinformatik (WS 18/19) Konstantin: Konstantin.pelz@campus.lmu.de Homepage: https://bioinformatik-muenchen.com/studium/propaedeutikumprogrammierung-in-der-bioinformatik/
FHZ. K13 Rekursion. Lernziele. Hochschule Technik+Architektur Luzern Abteilung Informatik, Fach Programmieren. Inhalt
 Inhalt 1. Einführung 1. Beispiel: Fakultät 2. Beispiel: Zahlenfolge 3. Beispiel: Formale Sprache 4. Unterschied Iteration/Rekursion 2. Rekursive Methoden 1. Beispiel: Fakultät 2. Beispiel: "Türme
Inhalt 1. Einführung 1. Beispiel: Fakultät 2. Beispiel: Zahlenfolge 3. Beispiel: Formale Sprache 4. Unterschied Iteration/Rekursion 2. Rekursive Methoden 1. Beispiel: Fakultät 2. Beispiel: "Türme
Mathematische Rekursion
 Rekursion Mathematische Rekursion o Viele mathematische Funktionen sind sehr natürlich rekursiv definierbar, d.h. o die Funktion erscheint in ihrer eigenen Definition. Mathematische Rekursion o Viele mathematische
Rekursion Mathematische Rekursion o Viele mathematische Funktionen sind sehr natürlich rekursiv definierbar, d.h. o die Funktion erscheint in ihrer eigenen Definition. Mathematische Rekursion o Viele mathematische
Prof. Dr. Oliver Haase Karl Martin Kern Achim Bitzer. Programmiertechnik Klassenmethoden Teil 2
 Prof. Dr. Oliver Haase Karl Martin Kern Achim Bitzer Programmiertechnik Klassenmethoden Teil 2 Rekursion 2/23 Definition Rekursion, die siehe Rekursion Was ist Rekursion Allgemein: Rekursion ist die Definition
Prof. Dr. Oliver Haase Karl Martin Kern Achim Bitzer Programmiertechnik Klassenmethoden Teil 2 Rekursion 2/23 Definition Rekursion, die siehe Rekursion Was ist Rekursion Allgemein: Rekursion ist die Definition
Einstieg in die Informatik mit Java
 1 / 26 Einstieg in die Informatik mit Java Methoden Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 26 1 Methoden 2 Methodendefinition 3 Parameterübergabe, Methodenaufruf
1 / 26 Einstieg in die Informatik mit Java Methoden Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 26 1 Methoden 2 Methodendefinition 3 Parameterübergabe, Methodenaufruf
Programmiertechnik Klassenmethoden
 Programmiertechnik Klassenmethoden Prof. Dr. Oliver Haase Oliver Haase Hochschule Konstanz 1 Motivation Programm zur Berechung von public class Eval1 { public static void main(string[] args) { java.util.scanner
Programmiertechnik Klassenmethoden Prof. Dr. Oliver Haase Oliver Haase Hochschule Konstanz 1 Motivation Programm zur Berechung von public class Eval1 { public static void main(string[] args) { java.util.scanner
Nachklausur Bitte in Druckschrift leserlich ausfüllen!
 Übungen zur Vorlesung Informatik für Informationsmanager WS 2005/2006 Universität Koblenz-Landau Institut für Informatik Prof. Dr. Bernhard Beckert Dr. Manfred Jackel Nachklausur 24.04.2006 Bitte in Druckschrift
Übungen zur Vorlesung Informatik für Informationsmanager WS 2005/2006 Universität Koblenz-Landau Institut für Informatik Prof. Dr. Bernhard Beckert Dr. Manfred Jackel Nachklausur 24.04.2006 Bitte in Druckschrift
2 Eine einfache Programmiersprache
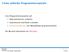 2 Eine einfache Programmiersprache Eine Programmiersprache soll Datenstrukturen anbieten Operationen auf Daten erlauben Kontrollstrukturen zur Ablaufsteuerung bereitstellen Als Beispiel betrachten wir
2 Eine einfache Programmiersprache Eine Programmiersprache soll Datenstrukturen anbieten Operationen auf Daten erlauben Kontrollstrukturen zur Ablaufsteuerung bereitstellen Als Beispiel betrachten wir
Vorlesung Programmieren
 Vorlesung Programmieren 11 Rekursion Jun.-Prof. Dr.-Ing. Anne Koziolek Version 1.1 ARBEITSGRUPPE ARCHITECTURE-DRIVEN REQUIREMENTS ENGINEERING (ARE) INSTITUT FÜR PROGRAMMSTRUKTUREN UND DATENORGANISATION
Vorlesung Programmieren 11 Rekursion Jun.-Prof. Dr.-Ing. Anne Koziolek Version 1.1 ARBEITSGRUPPE ARCHITECTURE-DRIVEN REQUIREMENTS ENGINEERING (ARE) INSTITUT FÜR PROGRAMMSTRUKTUREN UND DATENORGANISATION
2 Eine einfache Programmiersprache. Variablen. Operationen Zuweisung. Variablen
 Variablen Eine Programmiersprache soll Datenstrukturen anbieten Operationen auf Daten erlauben Kontrollstrukturen zur Ablaufsteuerung bereitstellen Variablen dienen zur Speicherung von Daten. Um Variablen
Variablen Eine Programmiersprache soll Datenstrukturen anbieten Operationen auf Daten erlauben Kontrollstrukturen zur Ablaufsteuerung bereitstellen Variablen dienen zur Speicherung von Daten. Um Variablen
Informatik II Übung, Woche 14
 Giuseppe Accaputo 7. April, 2016 Plan für heute 1. Java Klassen Beispiel: Implementation eines Vorlesungsverzeichnis (VVZ) 2. Informatik II (D-BAUG) Giuseppe Accaputo 2 Java Klassen Beispiel: Implementation
Giuseppe Accaputo 7. April, 2016 Plan für heute 1. Java Klassen Beispiel: Implementation eines Vorlesungsverzeichnis (VVZ) 2. Informatik II (D-BAUG) Giuseppe Accaputo 2 Java Klassen Beispiel: Implementation
C++ - Kontrollstrukturen Teil 2
 C++ - Kontrollstrukturen Teil 2 Reiner Nitsch 8417 r.nitsch@fbi.h-da.de Schleife und Verzweigung kombiniert SV initialisieren while(b1) if(b2) w f V1 V2 SV Richtung Ziel verändern Wichtiger Baustein vieler
C++ - Kontrollstrukturen Teil 2 Reiner Nitsch 8417 r.nitsch@fbi.h-da.de Schleife und Verzweigung kombiniert SV initialisieren while(b1) if(b2) w f V1 V2 SV Richtung Ziel verändern Wichtiger Baustein vieler
Inhalt Kapitel 2: Rekursion
 Inhalt Kapitel 2: Rekursion 1 Beispiele und Definition 2 Partialität und Terminierung 3 Formen der Rekursion Endständige Rekursion 4 Einbettung 29 Beispiele und Definition Rekursion 30 Man kann eine Funktion
Inhalt Kapitel 2: Rekursion 1 Beispiele und Definition 2 Partialität und Terminierung 3 Formen der Rekursion Endständige Rekursion 4 Einbettung 29 Beispiele und Definition Rekursion 30 Man kann eine Funktion
Tag 5. Repetitorium Informatik (Java) Dozent: Marius Kamp Lehrstuhl für Informatik 2 (Programmiersysteme)
 Tag 5 Repetitorium Informatik (Java) Dozent: Marius Kamp Lehrstuhl für Informatik 2 (Programmiersysteme) Friedrich-Alexander-Universität Erlangen-Nürnberg Wintersemester 2017/2018 Übersicht Methoden Deklaration
Tag 5 Repetitorium Informatik (Java) Dozent: Marius Kamp Lehrstuhl für Informatik 2 (Programmiersysteme) Friedrich-Alexander-Universität Erlangen-Nürnberg Wintersemester 2017/2018 Übersicht Methoden Deklaration
Klassenvariablen, Klassenmethoden
 Einstieg in die Informatik mit Java, Vorlesung vom 11.12.07 Übersicht 1 Klassenmethoden 2 Besonderheiten von Klassenmethoden 3 Aufruf einer Klassenmethode 4 Hauptprogrammparameter 5 Rekursion Klassenmethoden
Einstieg in die Informatik mit Java, Vorlesung vom 11.12.07 Übersicht 1 Klassenmethoden 2 Besonderheiten von Klassenmethoden 3 Aufruf einer Klassenmethode 4 Hauptprogrammparameter 5 Rekursion Klassenmethoden
Software Entwicklung 1
 Software Entwicklung 1 Annette Bieniusa Peter Zeller AG Softech FB Informatik TU Kaiserslautern Speichermanagement Wie viel Speicher braucht ein Programm? Wofür wird Speicher benötigt? Wie ist der Speicher
Software Entwicklung 1 Annette Bieniusa Peter Zeller AG Softech FB Informatik TU Kaiserslautern Speichermanagement Wie viel Speicher braucht ein Programm? Wofür wird Speicher benötigt? Wie ist der Speicher
7. Verkettete Strukturen: Listen
 7. Verkettete Strukturen: Listen Java-Beispiele: IntList.java List.java Stack1.java Version: 4. Jan. 2016 Vergleich: Schwerpunkte Arrays verkettete Listen Listenarten Implementation: - Pascal (C, C++):
7. Verkettete Strukturen: Listen Java-Beispiele: IntList.java List.java Stack1.java Version: 4. Jan. 2016 Vergleich: Schwerpunkte Arrays verkettete Listen Listenarten Implementation: - Pascal (C, C++):
Schwerpunkte. Verkettete Listen. Verkettete Listen: 7. Verkettete Strukturen: Listen. Überblick und Grundprinzip. Vergleich: Arrays verkettete Listen
 Schwerpunkte 7. Verkettete Strukturen: Listen Java-Beispiele: IntList.java List.java Stack1.java Vergleich: Arrays verkettete Listen Listenarten Implementation: - Pascal (C, C++): über Datenstrukturen
Schwerpunkte 7. Verkettete Strukturen: Listen Java-Beispiele: IntList.java List.java Stack1.java Vergleich: Arrays verkettete Listen Listenarten Implementation: - Pascal (C, C++): über Datenstrukturen
Rekursive Funktionen (1)
 Rekursive Funktionen (1) Rekursive Algorithmen Wenn Gesamtlösung durch Lösen gleichartiger Teilprobleme erzielbar: Rekursion möglich Beispiel: Fakultät einer ganzen Zahl n: n i n! = i=1 für n > 0 1 für
Rekursive Funktionen (1) Rekursive Algorithmen Wenn Gesamtlösung durch Lösen gleichartiger Teilprobleme erzielbar: Rekursion möglich Beispiel: Fakultät einer ganzen Zahl n: n i n! = i=1 für n > 0 1 für
Programmiertechnik Methoden, Teil 2
 Programmiertechnik Methoden, Teil 2 Prof. Dr. Oliver Haase Oliver Haase Hochschule Konstanz 1 Rekursion Oliver Haase Hochschule Konstanz 2 Definition Was ist Rekursion? Allgemein: Rekursion ist die Definition
Programmiertechnik Methoden, Teil 2 Prof. Dr. Oliver Haase Oliver Haase Hochschule Konstanz 1 Rekursion Oliver Haase Hochschule Konstanz 2 Definition Was ist Rekursion? Allgemein: Rekursion ist die Definition
CS1005 Objektorientierte Programmierung
 CS1005 Objektorientierte Programmierung Bachelor of Science (Informatik) Funktionen / statische Methoden - Definition - Verwendung - Ausführung Seite 1 Th Letschert Funktionen: Definition und Verwendung
CS1005 Objektorientierte Programmierung Bachelor of Science (Informatik) Funktionen / statische Methoden - Definition - Verwendung - Ausführung Seite 1 Th Letschert Funktionen: Definition und Verwendung
Objektorientierte Programmierung (ZQ1u2B)
 Objektorientierte Programmierung (ZQ1u2B) Woche 4 Rekursion Christopher Scho lzel Technische Hochschule Mittelhessen 4. November 2015 Inhalt Rekursion Lineare Rekursion Verzweigte Rekursion Verschränkte
Objektorientierte Programmierung (ZQ1u2B) Woche 4 Rekursion Christopher Scho lzel Technische Hochschule Mittelhessen 4. November 2015 Inhalt Rekursion Lineare Rekursion Verzweigte Rekursion Verschränkte
Prof. Dr. Oliver Haase Karl Martin Kern Achim Bitzer. Programmiertechnik Klassenmethoden
 Prof. Dr. Oliver Haase Karl Martin Kern Achim Bitzer Programmiertechnik Klassenmethoden Motivation Programm zur Berechnung von public class Eval1 { public static void main(string[] args) { java.util.scanner
Prof. Dr. Oliver Haase Karl Martin Kern Achim Bitzer Programmiertechnik Klassenmethoden Motivation Programm zur Berechnung von public class Eval1 { public static void main(string[] args) { java.util.scanner
2 Eine einfache Programmiersprache
 2 Eine einfache Programmiersprache Eine Programmiersprache soll Datenstrukturen anbieten Operationen auf Daten erlauben Kontrollstrukturen zur Ablaufsteuerung bereitstellen Als Beispiel betrachten wir
2 Eine einfache Programmiersprache Eine Programmiersprache soll Datenstrukturen anbieten Operationen auf Daten erlauben Kontrollstrukturen zur Ablaufsteuerung bereitstellen Als Beispiel betrachten wir
Rekursive Funktionen (1)
 Rekursive Funktionen (1) Rekursive Algorithmen Wenn Gesamtlösung durch Lösen gleichartiger Teilprobleme erzielbar: Rekursion möglich Beispiel: Fakultät einer ganzen Zahl n: nn ii nn! = ii=1 für nn > 0
Rekursive Funktionen (1) Rekursive Algorithmen Wenn Gesamtlösung durch Lösen gleichartiger Teilprobleme erzielbar: Rekursion möglich Beispiel: Fakultät einer ganzen Zahl n: nn ii nn! = ii=1 für nn > 0
Wiederholung Wozu Methoden? Methoden Schreiben Methoden Benutzen Rekursion?! Methoden. Javakurs 2012, 3. Vorlesung
 Wiederholung Wozu? Schreiben Benutzen Rekursion?! Javakurs 2012, 3. Vorlesung maggyrz@freitagsrunde.org 5. März 2013 Wiederholung Wozu? Schreiben Benutzen Rekursion?! 1 Wiederholung 2 Wozu? 3 Schreiben
Wiederholung Wozu? Schreiben Benutzen Rekursion?! Javakurs 2012, 3. Vorlesung maggyrz@freitagsrunde.org 5. März 2013 Wiederholung Wozu? Schreiben Benutzen Rekursion?! 1 Wiederholung 2 Wozu? 3 Schreiben
4 Rekursionen. 4.1 Erstes Beispiel
 4 Rekursionen Viele Algorithmen besitzen sowohl eine iterative als auch eine rekursive Lösung. Sie unterscheiden sich darin, dass die iterative Version meist einen etwas längeren Kode besitzt, während
4 Rekursionen Viele Algorithmen besitzen sowohl eine iterative als auch eine rekursive Lösung. Sie unterscheiden sich darin, dass die iterative Version meist einen etwas längeren Kode besitzt, während
Einstieg in die Informatik mit Java
 1 / 18 Einstieg in die Informatik mit Java Klassenvariablen, Klassenmethoden Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 18 1 Klassenmethoden 2 Besonderheiten von Klassenmethoden
1 / 18 Einstieg in die Informatik mit Java Klassenvariablen, Klassenmethoden Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 18 1 Klassenmethoden 2 Besonderheiten von Klassenmethoden
EINI WiMa. Einführung in die Informatik für Naturwissenschaftler und Ingenieure. Vorlesung 2 SWS WS 11/12
 EINI WiMa Einführung in die Informatik für Naturwissenschaftler und Ingenieure Vorlesung 2 SWS WS 11/12 Fakultät für Informatik Technische Universität Dortmund lars.hildebrand@udo.edu http://ls1-www.cs.uni-dortmund.de
EINI WiMa Einführung in die Informatik für Naturwissenschaftler und Ingenieure Vorlesung 2 SWS WS 11/12 Fakultät für Informatik Technische Universität Dortmund lars.hildebrand@udo.edu http://ls1-www.cs.uni-dortmund.de
Stack. Seniorenseminar Michael Pohlig
 Stack Seniorenseminar 21.06.2013 Michael Pohlig (pohlig@kit.edu) Übersicht 1. Axiomatik eins Kellers und seine Software- Realisierung 2. Bedeutung der Rekursion in der Mathematik 3. Rekursive Programmierung.
Stack Seniorenseminar 21.06.2013 Michael Pohlig (pohlig@kit.edu) Übersicht 1. Axiomatik eins Kellers und seine Software- Realisierung 2. Bedeutung der Rekursion in der Mathematik 3. Rekursive Programmierung.
8 Anwendung: Suchen. Folge a ganzer Zahlen; Element x. Wo kommt x in a vor?
 8 Anwendung: Suchen Gegeben: Gesucht: Folge a ganzer Zahlen; Element x Wo kommt x in a vor? Naives Vorgehen: Vergleiche x der Reihe nach mit a[0], a[1], usw. Finden wir i mit a[i] == x, geben wir i aus.
8 Anwendung: Suchen Gegeben: Gesucht: Folge a ganzer Zahlen; Element x Wo kommt x in a vor? Naives Vorgehen: Vergleiche x der Reihe nach mit a[0], a[1], usw. Finden wir i mit a[i] == x, geben wir i aus.
Informatik. Pointer (Dynamisch) Vorlesung. 17. Dezember 2018 SoSe 2018 FB Ing - SB Umwelttechnik und Dienstleistung - Informatik Thomas Hoch 1
 Informatik Vorlesung 08 Pointer (Dynamisch) 17. Dezember 2018 SoSe 2018 FB Ing - SB Umwelttechnik und Dienstleistung - Informatik Thomas Hoch 1 Pointer (Zeiger) Dynam. Speicher Bisher: Speicherbedarf muss
Informatik Vorlesung 08 Pointer (Dynamisch) 17. Dezember 2018 SoSe 2018 FB Ing - SB Umwelttechnik und Dienstleistung - Informatik Thomas Hoch 1 Pointer (Zeiger) Dynam. Speicher Bisher: Speicherbedarf muss
Einführung in die Informatik I
 Einführung in die Informatik I LOOP Programme, rekursive Funktionen und der Turm von Hanoi Prof. Dr. Nikolaus Wulff Berechenbarkeit Mitte des 20. Jahrhunderts beantworteten Pioniere, wie Alan M. Turing
Einführung in die Informatik I LOOP Programme, rekursive Funktionen und der Turm von Hanoi Prof. Dr. Nikolaus Wulff Berechenbarkeit Mitte des 20. Jahrhunderts beantworteten Pioniere, wie Alan M. Turing
2. Unterprogramme und Methoden
 2. Unterprogramme und Methoden Durch Methoden wird ausführbarer Code unter einem Namen zusammengefasst. Dieser Code kann unter Verwendung von sogenannten Parametern formuliert sein, denen später beim Aufruf
2. Unterprogramme und Methoden Durch Methoden wird ausführbarer Code unter einem Namen zusammengefasst. Dieser Code kann unter Verwendung von sogenannten Parametern formuliert sein, denen später beim Aufruf
Aufgabe 1 (12 Punkte)
 Aufgabe 1 (12 Punkte) Schreiben Sie eine Klasse public class ZinsesZins, die zu einem gegebenen Anfangskapital von 100,00 die Kapitalentwicklung bei einer jährlichen nachschüssigen Verzinsung in Höhe von
Aufgabe 1 (12 Punkte) Schreiben Sie eine Klasse public class ZinsesZins, die zu einem gegebenen Anfangskapital von 100,00 die Kapitalentwicklung bei einer jährlichen nachschüssigen Verzinsung in Höhe von
2 Eine einfache Programmiersprache
 2 Eine einfache Programmiersprache Eine Programmiersprache soll Datenstrukturen anbieten Operationen auf Daten erlauben Kontrollstrukturen zur Ablaufsteuerung bereitstellen Als Beispiel betrachten wir
2 Eine einfache Programmiersprache Eine Programmiersprache soll Datenstrukturen anbieten Operationen auf Daten erlauben Kontrollstrukturen zur Ablaufsteuerung bereitstellen Als Beispiel betrachten wir
Vorlesung Programmieren
 Vorlesung Programmieren 17 Vom Programm zur Maschine Prof. Dr. Ralf H. Reussner Version 1.0 LEHRSTUHL FÜR SOFTWARE-DESIGN UND QUALITÄT (SDQ) INSTITUT FÜR PROGRAMMSTRUKTUREN UND DATENORGANISATION (IPD),
Vorlesung Programmieren 17 Vom Programm zur Maschine Prof. Dr. Ralf H. Reussner Version 1.0 LEHRSTUHL FÜR SOFTWARE-DESIGN UND QUALITÄT (SDQ) INSTITUT FÜR PROGRAMMSTRUKTUREN UND DATENORGANISATION (IPD),
Institut für Programmierung und Reaktive Systeme 2. Februar Programmieren I. Übungsklausur
 Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme 2. Februar 2017 Hinweise: Klausurtermine: Programmieren I Übungsklausur Programmieren I: 13. März
Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme 2. Februar 2017 Hinweise: Klausurtermine: Programmieren I Übungsklausur Programmieren I: 13. März
2 Eine einfache Programmiersprache
 2 Eine einfache Programmiersprache Eine Programmiersprache soll Datenstrukturen anbieten Operationen auf Daten erlauben Kontrollstrukturen zur Ablaufsteuerung bereitstellen Als Beispiel betrachten wir
2 Eine einfache Programmiersprache Eine Programmiersprache soll Datenstrukturen anbieten Operationen auf Daten erlauben Kontrollstrukturen zur Ablaufsteuerung bereitstellen Als Beispiel betrachten wir
Schnittstellen, Stack und Queue
 Schnittstellen, Stack und Queue Schnittstelle Stack Realisierungen des Stacks Anwendungen von Stacks Schnittstelle Queue Realisierungen der Queue Anwendungen von Queues Hinweise zum Üben Anmerkung: In
Schnittstellen, Stack und Queue Schnittstelle Stack Realisierungen des Stacks Anwendungen von Stacks Schnittstelle Queue Realisierungen der Queue Anwendungen von Queues Hinweise zum Üben Anmerkung: In
Einführung in die Programmierung
 Skript zur Vorlesung: Einführung in die Programmierung WiSe 2009 / 2010 Skript 2009 Christian Böhm, Peer Kröger, Arthur Zimek Prof. Dr. Christian Böhm Annahita Oswald Bianca Wackersreuther Ludwig-Maximilians-Universität
Skript zur Vorlesung: Einführung in die Programmierung WiSe 2009 / 2010 Skript 2009 Christian Böhm, Peer Kröger, Arthur Zimek Prof. Dr. Christian Böhm Annahita Oswald Bianca Wackersreuther Ludwig-Maximilians-Universität
Klausur Kompaktkurs Einführung in die Programmierung Dr. T. Weinzierl & M. Sedlacek 25. März 2011
 Kompaktkurs Einführung in die Programmierung Klausur Seite 1/10 Name, Vorname, Unterschrift: Matrikelnummer: Wichtig: Klausur Kompaktkurs Einführung in die Programmierung Dr. T. Weinzierl & M. Sedlacek
Kompaktkurs Einführung in die Programmierung Klausur Seite 1/10 Name, Vorname, Unterschrift: Matrikelnummer: Wichtig: Klausur Kompaktkurs Einführung in die Programmierung Dr. T. Weinzierl & M. Sedlacek
EINFÜHRUNG IN DIE PROGRAMMIERUNG
 EINFÜHRUNG IN DIE PROGRAMMIERUNG GRUNDLAGEN Tobias Witt!! 24.03.2014 ORGANISATORISCHES 09:00-10:30! Täglich Übungen zur Vertiefung! Laptop hier nicht erforderlich! Linux, OS X! Freitag: http://hhu-fscs.de/linux-install-party/
EINFÜHRUNG IN DIE PROGRAMMIERUNG GRUNDLAGEN Tobias Witt!! 24.03.2014 ORGANISATORISCHES 09:00-10:30! Täglich Übungen zur Vertiefung! Laptop hier nicht erforderlich! Linux, OS X! Freitag: http://hhu-fscs.de/linux-install-party/
Programmieren 1 C Überblick
 Programmieren 1 C Überblick 1. Einleitung 2. Graphische Darstellung von Algorithmen 3. Syntax und Semantik 4. Einstieg in C: Einfache Sprachkonstrukte und allgemeiner Programmaufbau 5. Skalare Standarddatentypen
Programmieren 1 C Überblick 1. Einleitung 2. Graphische Darstellung von Algorithmen 3. Syntax und Semantik 4. Einstieg in C: Einfache Sprachkonstrukte und allgemeiner Programmaufbau 5. Skalare Standarddatentypen
Systemnahe Programmierung in C (SPiC)
 Systemnahe Programmierung in C (SPiC) 9 Funktionen Jürgen Kleinöder, Daniel Lohmann, Volkmar Sieh Lehrstuhl für Informatik 4 Verteilte Systeme und Betriebssysteme Friedrich-Alexander-Universität Erlangen-Nürnberg
Systemnahe Programmierung in C (SPiC) 9 Funktionen Jürgen Kleinöder, Daniel Lohmann, Volkmar Sieh Lehrstuhl für Informatik 4 Verteilte Systeme und Betriebssysteme Friedrich-Alexander-Universität Erlangen-Nürnberg
Grundlagen der Programmierung WS 15/16 (Vorlesung von Prof. Bothe)
 Humboldt-Universität zu Berlin Institut für Informatik Grundlagen der Programmierung WS 15/16 (Vorlesung von Prof. Bothe) Übungsblatt 4: Felder und Rekursion Abgabe: bis 9:00 Uhr am 14.12.2015 über Goya
Humboldt-Universität zu Berlin Institut für Informatik Grundlagen der Programmierung WS 15/16 (Vorlesung von Prof. Bothe) Übungsblatt 4: Felder und Rekursion Abgabe: bis 9:00 Uhr am 14.12.2015 über Goya
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Dynamische Datenobjekte Pointer/Zeiger, Verkettete Liste Eigene Typdefinitionen 1 Zeigeroperatoren & und * Ein Zeiger ist die Speicheradresse irgendeines Objektes. Eine
Algorithmen und Datenstrukturen Dynamische Datenobjekte Pointer/Zeiger, Verkettete Liste Eigene Typdefinitionen 1 Zeigeroperatoren & und * Ein Zeiger ist die Speicheradresse irgendeines Objektes. Eine
Technische Informatik I - HS 18
 Institut für Technische Informatik und Kommunikationsnetze Prof. L. Thiele Technische Informatik I - HS 18 Musterlösung zu Übung 3 Datum : 25.-26. Oktober 2018 Aufgabe 1: Wurzelverfahren nach Heron Das
Institut für Technische Informatik und Kommunikationsnetze Prof. L. Thiele Technische Informatik I - HS 18 Musterlösung zu Übung 3 Datum : 25.-26. Oktober 2018 Aufgabe 1: Wurzelverfahren nach Heron Das
Datenstrukturen und Algorithmen
 Datenstrukturen und Algorithmen VO 708.031 27.10.2011 stefan.klampfl@tugraz.at 1 Wiederholung Wir vergleichen Algorithmen anhand des ordnungsmäßigen Wachstums von T(n), S(n), Asymptotische Schranken: O-Notation:
Datenstrukturen und Algorithmen VO 708.031 27.10.2011 stefan.klampfl@tugraz.at 1 Wiederholung Wir vergleichen Algorithmen anhand des ordnungsmäßigen Wachstums von T(n), S(n), Asymptotische Schranken: O-Notation:
Einführung in die Programmierung WS 2009/10. Übungsblatt 7: Imperative Programmierung, Parameterübergabe
 Ludwig-Maximilians-Universität München München, 04.12.2009 Institut für Informatik Prof. Dr. Christian Böhm Annahita Oswald, Bianca Wackersreuther Einführung in die Programmierung WS 2009/10 Übungsblatt
Ludwig-Maximilians-Universität München München, 04.12.2009 Institut für Informatik Prof. Dr. Christian Böhm Annahita Oswald, Bianca Wackersreuther Einführung in die Programmierung WS 2009/10 Übungsblatt
C++ Teil 5. Sven Groß. 16. Nov Sven Groß (IGPM, RWTH Aachen) C++ Teil Nov / 16
 C++ Teil 5 Sven Groß 16. Nov 2015 Sven Groß (IGPM, RWTH Aachen) C++ Teil 5 16. Nov 2015 1 / 16 Themen der letzten Vorlesung Namensräume Live Programming zu A2 Gleitkommazahlen Rundungsfehler Auswirkung
C++ Teil 5 Sven Groß 16. Nov 2015 Sven Groß (IGPM, RWTH Aachen) C++ Teil 5 16. Nov 2015 1 / 16 Themen der letzten Vorlesung Namensräume Live Programming zu A2 Gleitkommazahlen Rundungsfehler Auswirkung
Rekursion. Annabelle Klarl. Einführung in die Informatik Programmierung und Softwareentwicklung
 Rekursion Annabelle Klarl Zentralübung zur Vorlesung Einführung in die Informatik: http://www.pst.ifi.lmu.de/lehre/wise-12-13/infoeinf WS12/13 Aufgabe 1: Potenzfunktion Schreiben Sie eine Methode, die
Rekursion Annabelle Klarl Zentralübung zur Vorlesung Einführung in die Informatik: http://www.pst.ifi.lmu.de/lehre/wise-12-13/infoeinf WS12/13 Aufgabe 1: Potenzfunktion Schreiben Sie eine Methode, die
Kapitel 7: Rekursion. Inhalt. Rekursion: Technik Rekursion vs. Iteration
 Wintersemester 2007/08 Einführung in die Informatik für Naturwissenschaftler und Ingenieure (alias Einführung in die Programmierung) (Vorlesung) Inhalt Rekursion: Technik Prof. Dr. Günter Rudolph Fakultät
Wintersemester 2007/08 Einführung in die Informatik für Naturwissenschaftler und Ingenieure (alias Einführung in die Programmierung) (Vorlesung) Inhalt Rekursion: Technik Prof. Dr. Günter Rudolph Fakultät
Lösungsvorschlag Serie 2 Rekursion
 (/) Lösungsvorschlag Serie Rekursion. Algorithmen-Paradigmen Es gibt verschiedene Algorithmen-Paradigmen, also grundsätzliche Arten, wie man einen Algorithmus formulieren kann. Im funktionalen Paradigma
(/) Lösungsvorschlag Serie Rekursion. Algorithmen-Paradigmen Es gibt verschiedene Algorithmen-Paradigmen, also grundsätzliche Arten, wie man einen Algorithmus formulieren kann. Im funktionalen Paradigma
n 1. Grundzüge der Objektorientierung n 2. Methoden, Unterprogramme und Parameter n 3. Datenabstraktion n 4. Konstruktoren n 5. Vordefinierte Klassen
 n 1. Grundzüge der Objektorientierung n 2. Methoden, Unterprogramme und Parameter n 3. Datenabstraktion n 4. Konstruktoren n 5. Vordefinierte Klassen II.2.2 Methoden, Unterprogramme und Parameter - 1 -
n 1. Grundzüge der Objektorientierung n 2. Methoden, Unterprogramme und Parameter n 3. Datenabstraktion n 4. Konstruktoren n 5. Vordefinierte Klassen II.2.2 Methoden, Unterprogramme und Parameter - 1 -
Programmieren I. Methoden-Spezial Heusch --- Ratz 6.1, Institut für Angewandte Informatik
 Programmieren I Methoden-Spezial Heusch --- Ratz 6.1, 6.2 KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Parameterübergabe bei primitivem Datentypen (Wertkopie) public class MethodParameters
Programmieren I Methoden-Spezial Heusch --- Ratz 6.1, 6.2 KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Parameterübergabe bei primitivem Datentypen (Wertkopie) public class MethodParameters
Programmieren I. Methoden-Special Heusch --- Ratz 6.1, Institut für Angewandte Informatik
 Programmieren I Methoden-Special Heusch --- Ratz 6.1, 6.2 KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Parameterübergabe: Wertkopie -By- public class MethodParameters { public
Programmieren I Methoden-Special Heusch --- Ratz 6.1, 6.2 KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Parameterübergabe: Wertkopie -By- public class MethodParameters { public
Rekursion. Rekursive Funktionen, Korrektheit, Terminierung, Rekursion vs. Iteration, Sortieren
 Rekursion Rekursive Funktionen, Korrektheit, Terminierung, Rekursion vs. Iteration, Sortieren Mathematische Rekursion o Viele mathematische Funktionen sind sehr natürlich rekursiv definierbar, d.h. o die
Rekursion Rekursive Funktionen, Korrektheit, Terminierung, Rekursion vs. Iteration, Sortieren Mathematische Rekursion o Viele mathematische Funktionen sind sehr natürlich rekursiv definierbar, d.h. o die
Rekursion. Rekursive Funktionen, Korrektheit, Terminierung, Rekursion vs. Iteration, Sortieren
 Rekursion Rekursive Funktionen, Korrektheit, Terminierung, Rekursion vs. Iteration, Sortieren Mathematische Rekursion o Viele mathematische Funktionen sind sehr natürlich rekursiv definierbar, d.h. o die
Rekursion Rekursive Funktionen, Korrektheit, Terminierung, Rekursion vs. Iteration, Sortieren Mathematische Rekursion o Viele mathematische Funktionen sind sehr natürlich rekursiv definierbar, d.h. o die
C++ Teil 5. Sven Groß. 12. Nov IGPM, RWTH Aachen. Sven Groß (IGPM, RWTH Aachen) C++ Teil Nov / 16
 C++ Teil 5 Sven Groß IGPM, RWTH Aachen 12. Nov 2014 Sven Groß (IGPM, RWTH Aachen) C++ Teil 5 12. Nov 2014 1 / 16 Themen der letzten Vorlesung Eingabestrom, Verhalten von cin Namensräume Live Programming
C++ Teil 5 Sven Groß IGPM, RWTH Aachen 12. Nov 2014 Sven Groß (IGPM, RWTH Aachen) C++ Teil 5 12. Nov 2014 1 / 16 Themen der letzten Vorlesung Eingabestrom, Verhalten von cin Namensräume Live Programming
3AA. Prozeduren und Rekursion Prof. Dr. Wolfgang P. Kowalk Universität Oldenburg WS 2005/2006
 3AA Prozeduren und Rekursion 29.11.05 Prof. Dr. Wolfgang P. Kowalk Universität Oldenburg WS 2005/2006 3AA Prozeduren Berechnete Sprungadresse Ausführung bestimmter Anweisungen durch Schleifen Stattdessen:
3AA Prozeduren und Rekursion 29.11.05 Prof. Dr. Wolfgang P. Kowalk Universität Oldenburg WS 2005/2006 3AA Prozeduren Berechnete Sprungadresse Ausführung bestimmter Anweisungen durch Schleifen Stattdessen:
Inhalt. 3. Spezielle Algorithmen
 Inhalt 0. Rechner und Programmierung für Kommunikationstechniker und Mechatroniker 1. Algorithmen - Wesen, Eigenschaften, Entwurf 2. Darstellung von Algorithmen mit Struktogrammen und Programmablaufplänen
Inhalt 0. Rechner und Programmierung für Kommunikationstechniker und Mechatroniker 1. Algorithmen - Wesen, Eigenschaften, Entwurf 2. Darstellung von Algorithmen mit Struktogrammen und Programmablaufplänen
1. Grundzüge der Objektorientierung 2. Methoden, Unterprogramme und Parameter 3. Datenabstraktion 4. Konstruktoren 5. Vordefinierte Klassen
 1. Grundzüge der Objektorientierung 2. Methoden, Unterprogramme und Parameter 3. Datenabstraktion 4. Konstruktoren 5. Vordefinierte Klassen II.2.2 Methoden, Unterprogramme und Parameter - 1 - 2. Methoden
1. Grundzüge der Objektorientierung 2. Methoden, Unterprogramme und Parameter 3. Datenabstraktion 4. Konstruktoren 5. Vordefinierte Klassen II.2.2 Methoden, Unterprogramme und Parameter - 1 - 2. Methoden
Technische Informatik I Übung 3: Assembler
 Technische Informatik I Übung 3: Assembler Roman Trüb Computer Engineering Group, ETH Zürich 1 Lernziele Übung 3 Aufgabe 1 Aufbau und Aufruf von Funktionen in Assembler Assembler Codeanalyse Aufgabe 2
Technische Informatik I Übung 3: Assembler Roman Trüb Computer Engineering Group, ETH Zürich 1 Lernziele Übung 3 Aufgabe 1 Aufbau und Aufruf von Funktionen in Assembler Assembler Codeanalyse Aufgabe 2
Präzedenz von Operatoren
 Präzedenz von Operatoren SWE-30 Die Präzedenz von Operatoren bestimmt die Struktur von Ausdrücken. Ein Operator höherer Präzedenz bindet die Operanden stärker als ein Operator geringerer Präzedenz. Mit
Präzedenz von Operatoren SWE-30 Die Präzedenz von Operatoren bestimmt die Struktur von Ausdrücken. Ein Operator höherer Präzedenz bindet die Operanden stärker als ein Operator geringerer Präzedenz. Mit
Java Virtual Machine (JVM) Bytecode
 Java Virtual Machine (JVM) durch Java-Interpreter (java) realisiert abstrakte Maschine = Softwareschicht zwischen Anwendung und Betriebssystem verantwortlich für Laden von Klassen, Ausführen des Bytecodes,
Java Virtual Machine (JVM) durch Java-Interpreter (java) realisiert abstrakte Maschine = Softwareschicht zwischen Anwendung und Betriebssystem verantwortlich für Laden von Klassen, Ausführen des Bytecodes,
Technische Informatik 1 Übung 2 Assembler (Rechenübung) Georgia Giannopoulou (ggeorgia@tik.ee.ethz.ch) 22./23. Oktober 2015
 Technische Informatik 1 Übung 2 Assembler (Rechenübung) Georgia Giannopoulou (ggeorgia@tik.ee.ethz.ch) 22./23. Oktober 2015 Ziele der Übung Aufgabe 1 Aufbau und Aufruf von Funktionen in Assembler Codeanalyse
Technische Informatik 1 Übung 2 Assembler (Rechenübung) Georgia Giannopoulou (ggeorgia@tik.ee.ethz.ch) 22./23. Oktober 2015 Ziele der Übung Aufgabe 1 Aufbau und Aufruf von Funktionen in Assembler Codeanalyse
Informatik 1 ( ) D-MAVT F2010. Schleifen, Felder. Yves Brise Übungsstunde 5
 Informatik 1 (251-0832-00) D-MAVT F2010 Schleifen, Felder Nachbesprechung Blatt 3 Aufgabe 1 ASCII... A > a Vorsicht: Lösen Sie sich von intuitiven Schlussfolgerungen. A ist nicht grösser als a, denn in
Informatik 1 (251-0832-00) D-MAVT F2010 Schleifen, Felder Nachbesprechung Blatt 3 Aufgabe 1 ASCII... A > a Vorsicht: Lösen Sie sich von intuitiven Schlussfolgerungen. A ist nicht grösser als a, denn in
2. Programmierung in C
 2. Programmierung in C Inhalt: Überblick über Programmiersprachen, Allgemeines zur Sprache C C: Basisdatentypen, Variablen, Konstanten Operatoren, Ausdrücke und Anweisungen Kontrollstrukturen (Steuerfluss)
2. Programmierung in C Inhalt: Überblick über Programmiersprachen, Allgemeines zur Sprache C C: Basisdatentypen, Variablen, Konstanten Operatoren, Ausdrücke und Anweisungen Kontrollstrukturen (Steuerfluss)
Einschub: Anweisungen und Bedingungen für PAP und Struktogramme (1)
 Einschub: Anweisungen und Bedingungen für PAP und Struktogramme (1) Anweisungen: Eingabeanweisungen, z.b. Eingabe: x Ausgabeanweisungen, z.b. Ausgabe: Das Maximum ist, max Die Symbole x und max werden
Einschub: Anweisungen und Bedingungen für PAP und Struktogramme (1) Anweisungen: Eingabeanweisungen, z.b. Eingabe: x Ausgabeanweisungen, z.b. Ausgabe: Das Maximum ist, max Die Symbole x und max werden
Algorithmen und Programmierung II
 Algorithmen und Programmierung II Vererbung Prof. Dr. Margarita Esponda SS 2012 1 Imperative Grundbestandteile Parameterübergabe String-Klasse Array-Klasse Konzepte objektorientierter Programmierung Vererbung
Algorithmen und Programmierung II Vererbung Prof. Dr. Margarita Esponda SS 2012 1 Imperative Grundbestandteile Parameterübergabe String-Klasse Array-Klasse Konzepte objektorientierter Programmierung Vererbung
EINFÜHRUNG IN DIE PROGRAMMIERUNG
 EINFÜHRUNG IN DIE PROGRAMMIERUNG GRUNDLAGEN Tobias Witt 24.03.2014 ORGANISATORISCHES tobias.witt@hhu.de 10:30-12:00 Täglich Übungen zur Vertiefung Laptop hier nicht erforderlich Aber später in den Übungen!
EINFÜHRUNG IN DIE PROGRAMMIERUNG GRUNDLAGEN Tobias Witt 24.03.2014 ORGANISATORISCHES tobias.witt@hhu.de 10:30-12:00 Täglich Übungen zur Vertiefung Laptop hier nicht erforderlich Aber später in den Übungen!
Typ : void* aktuelle Parameter Pointer von beliebigem Typ
 2. Funktionen - Prototypvereinbarung typangabe funktionsname(parameterliste); - Funktionsdefinition typ funktionsname(parameterliste){ Anweisung - Funktionstyp -> Typ der Funktionswertes zulaessige Typangaben
2. Funktionen - Prototypvereinbarung typangabe funktionsname(parameterliste); - Funktionsdefinition typ funktionsname(parameterliste){ Anweisung - Funktionstyp -> Typ der Funktionswertes zulaessige Typangaben
Universität München, Hans-Peter Kriegel und Thomas Seidl Informatik II a[0] a[1] a[2] a[3] a[n 1]
![Universität München, Hans-Peter Kriegel und Thomas Seidl Informatik II a[0] a[1] a[2] a[3] a[n 1] Universität München, Hans-Peter Kriegel und Thomas Seidl Informatik II a[0] a[1] a[2] a[3] a[n 1]](/thumbs/97/133911680.jpg) Universität München, Hans-Peter Kriegel und Thomas Seidl Informatik II -108 Kapitel 5: Arrays Einführung Ein Array ist eine Reihung gleichartiger Objekte. a: a[0] a[1] a[2] a[3] a[n 1] Bezeichner a steht
Universität München, Hans-Peter Kriegel und Thomas Seidl Informatik II -108 Kapitel 5: Arrays Einführung Ein Array ist eine Reihung gleichartiger Objekte. a: a[0] a[1] a[2] a[3] a[n 1] Bezeichner a steht
Algorithmen und Datenstrukturen Tafelübung 4. Jens Wetzl 15. November 2011
 Algorithmen und Datenstrukturen Tafelübung 4 Jens Wetzl 15. November 2011 Folien Keine Garantie für Vollständigkeit und/oder Richtigkeit Keine offizielle Informationsquelle LS2-Webseite Abrufbar unter:
Algorithmen und Datenstrukturen Tafelübung 4 Jens Wetzl 15. November 2011 Folien Keine Garantie für Vollständigkeit und/oder Richtigkeit Keine offizielle Informationsquelle LS2-Webseite Abrufbar unter:
Einführung in die Programmierung Wintersemester 2010/11
 Einführung in die Programmierung Wintersemester 2010/11 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering Fakultät für Informatik TU Dortmund : Rekursion Inhalt Rekursion: Technik Rekursion
Einführung in die Programmierung Wintersemester 2010/11 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering Fakultät für Informatik TU Dortmund : Rekursion Inhalt Rekursion: Technik Rekursion
Rekursive Funktionen sind Funktionen, die sich auf sich selbst beziehen bzw. Funktion, die sich selbst aufrufen.
 Rekursive Funktionen Was sind rekursive Funktionen? Rekursive Funktionen sind Funktionen, die sich auf sich selbst beziehen bzw. Funktion, die sich selbst aufrufen. Wozu braucht man rekursive Funktionen?
Rekursive Funktionen Was sind rekursive Funktionen? Rekursive Funktionen sind Funktionen, die sich auf sich selbst beziehen bzw. Funktion, die sich selbst aufrufen. Wozu braucht man rekursive Funktionen?
Funktionen. mehrfach benötigte Programmteile nur einmal zu schreiben und mehrfach aufzurufen
 Funktionen Funktionen erlauben, dem Programmcode hierarchisch zu strukturieren ein Hauptprogramm steuert dabei die Abfolge von Schritten, die einzelnen Schritte können durch Funktionen realisiert werden
Funktionen Funktionen erlauben, dem Programmcode hierarchisch zu strukturieren ein Hauptprogramm steuert dabei die Abfolge von Schritten, die einzelnen Schritte können durch Funktionen realisiert werden
Das Kontrollfluss-Diagramm für Ò ¼ µ:
 Das Kontrollfluss-Diagramm für Ò ¼ µ: find0(a,x,n1,n2) t = (n1+n2)/2; no a[t]==x yes no n1==n2 yes return t; no x > a[t] yes return 1; no n1 < t yes return find0(a,x,t+1,n2); return 1; return find0(a,x,n1,t
Das Kontrollfluss-Diagramm für Ò ¼ µ: find0(a,x,n1,n2) t = (n1+n2)/2; no a[t]==x yes no n1==n2 yes return t; no x > a[t] yes return 1; no n1 < t yes return find0(a,x,t+1,n2); return 1; return find0(a,x,n1,t
