Albrecht Beutelspacher Kleines Mathematikum Die 101 wichtigsten Fragen und Antworten zur Mathematik
|
|
|
- Markus Kappel
- vor 7 Jahren
- Abrufe
Transkript
1 Unverkäufliche Leseprobe Albrecht Beutelspacher Kleines Mathematikum Die 101 wichtigsten Fragen und Antworten zur Mathematik 189 Seiten, Halbleinen ISBN: Verlag C.H.Beck ohg, München
2 Grundlagen 1 Was ist Mathematik? Die schwierigste Frage zu Beginn! Deshalb gebe ich gleich vier Antworten. 1. Man kann Mathematik dadurch definieren, dass man sie inhaltlich beschreibt, also die Objekte benennt, die in der Mathematik untersucht werden. Traditionell unterscheidet man Geometrie, Algebra, Analysis und Stochastik. Geometrie ist die Lehre des uns umgebenden Raums, den wir dadurch zu erfassen versuchen, dass wir Punkte, Geraden, Ebenen, Dreiecke, Vierecke, Kreise und so weiter definieren und durch deren Studium ein immer besseres Verständnis des Raums erhalten. Wie die Geometrie hatte auch die Algebra ihre erste Blütezeit in der griechischen Antike. Man studiert unter diesem Begriff Zahlen und deren Eigenschaften, zum Beispiel Primzahlen. Die Analysis, auch Differential- und Integralrechnung genannt, ist die Lehre von Größen, die sich kontinuierlich verändern. Sie wurde wesentlich geprägt von Leibniz und Newton. Die Stochastik ist die jüngste der vier Disziplinen; sie ist die mathematische Lehre vom Zufall. 2. Man kann Mathematik auch dadurch definieren, dass man ihre Methode beschreibt, die sie aus der Menge aller anderen Wissenschaften heraushebt. 13
3 Was die Mathematik wirklich auszeichnet, ist der Beweis, also die rein logische Ableitung ihrer Aussagen. Mathematik behandelt Begriffe, die klar definiert sind: Dreiecke, Vierecke, Kreise, ganze Zahlen, Primzahlen, Funktionen und so weiter. Sie behandelt Eigenschaften dieser Begriffe und Beziehungen dieser Eigenschaften: In jedem rechtwinkligen Dreieck gilt der Satz des Pythagoras. Durch diese logischen Beziehungen wird Ordnung in die Welt der Begriffe gebracht. 3. Man kann auch den Blick nach außen wenden und das Augenmerk auf die Beschreibung und Beherrschung der Welt durch die Mathematik richten. Galileo Galilei ( ) war der Überzeugung, dass Mathematik die Sprache der Natur ist. Mathematik ist das mächtigste Instrument, mit dem wir die Welt um uns herum beschreiben, erkennen und strukturieren können. 4. Eine moderne und, wie ich finde, sehr treffende Beschreibung stammt von dem Mathematiker Hans Freudenthal ( ), der gleichermaßen als Fachwissenschaftler und als Didaktiker Herausragendes geleistet hat. Er sagt: «Mathematische Begriffe, Konzepte und Verfahren sind Werkzeuge, mit denen wir Phänomene der physikalischen, der sozialen und der mentalen Welt gedanklich organisieren.» In dieser Definition kommt deutlich zum Ausdruck, dass Mathematik von Menschen gemacht wird: «Wir organisieren.» Mathematik entsteht nicht von alleine, sondern durch aktives Handeln von Menschen. Übrigens: Dieses Buch gibt noch 100 weitere Antworten auf die Frage, was Mathematik ist. 14
4 2 Seit wann gibt es Mathematik? Mathematik ist zusammen mit der Astronomie die älteste Wissenschaft. Trotzdem gibt es mindestens drei Antworten auf die Frage, seit wann es Mathematik gibt. Erste Antwort: seit etwa Jahren. Aus dieser Zeit stammen die ersten Kulturzeugnisse der Menschheit, darunter auch Knochen, die viele Kerben enthalten. Diese sind so sorgfältig, so gleichmäßig und so systematisch ausgeführt, dass die Historiker sicher sind: Dabei handelt es sich um Zahlendarstellungen. Was damit gezählt wurde und warum, wissen wir nicht. Aber klar ist: Schon damals gab es Menschen, die gezählt haben und für die das Ergebnis so wichtig war, dass sie es mühsam in Knochen eingekerbt haben. Die zweite Antwort lautet: Mathematik gibt es seit etwa 5000 Jahren. Damals benutzten sowohl die Babylonier als auch die Ägypter hoch entwickelte mathematische Methoden. Sie konnten Zahlen sinnvoll notieren, gewisse Gleichungen lösen, Kalenderberechnungen durchführen und Land vermessen. Dazu benutzten sie Erkenntnisse wie den Satz des Pythagoras, die wir heute, ohne zu zögern, der Mathematik zuordnen. Soweit wir das beurteilen können, wurden diese Erkenntnisse wie Naturgesetze angenommen. Das heißt, sie wurden an Beispielen überprüft und dann einfach verwendet. Daher ist eine dritte Antwort notwendig. Diese lautet: Vor etwa 2500 Jahren haben die Griechen die Mathematik in unserem Sinne erfunden. Denn ihnen ist damals bewusst geworden, dass man durch genaues Nachdenken, scharfes Argumentieren sowie folgerichtiges Schließen zu Erkennt- 15
5 nissen gelangen kann und nicht nur durch Augenschein, Erfahrung und Intuition. Damals wurden drei Begriffe geprägt: Definition, Satz, Beweis. Dieser Dreiklang ist heute etwas in Misskredit geraten verständlicherweise, denn er wurde jahrzehntelang als didaktisches Allheilmittel benutzt, wofür er nie gedacht war. In einer Definition wird ein Begriff präzise beschrieben und unmissverständlich von anderen abgegrenzt. In der Mathematik wissen wir immer ganz genau, worüber wir reden. Wenn wir «Kreis» sagen, dann meinen wir damit nicht irgendetwas Rundes, dem bei Bedarf irgendwelche Eigenschaften zugesprochen werden, sondern ein Kreis ist definiert als die Menge aller Punkte, die vom Mittelpunkt den gleichen Abstand haben. Und man darf nur diese Eigenschaft benutzen. Die Erkenntnisse der Mathematik werden in Sätzen dargestellt. Hier gilt Ähnliches wie bei den Definitionen: Wir wissen auch immer genau, was wir beweisen müssen oder was wir bewiesen haben. Der Beweis ist die Methode der Mathematik zur Wahrheitssicherung. Das ist das «scharfe Nachdenken» in geordneter Form. Ein Beweis basiert auf rein logischen Schlussfolgerungen, ist also so objektiv wie möglich. Ich weiß, dass viele Schülerinnen und Schüler sowie manche Studierende Beweise nicht mögen, und ich weiß auch, dass im Schulunterricht immer weniger Beweise vorkommen. Das finde ich nicht nur persönlich schade, sondern es ist ein Fehler. Denn genau dadurch zeichnet sich die Mathematik vor allen anderen Wissenschaften aus, dass man in ihr die Ergebnisse durch reine Logik und deshalb mit einem Höchstmaß an Objektivität erhält. Denken Sie mal an den Satz des Pythagoras, den berühmtesten mathematischen Satz: In jedem rechtwinkligen Dreieck, dessen kurze Seiten die Längen a und b haben und des- 16
6 sen lange Seite die Länge c hat, gilt a 2 +b 2 =c 2. Dieser Satz wurde vor 2500 Jahren zum ersten Mal bewiesen, er gilt heute noch wörtlich so wie damals und er wird auch in 2500 Jahren noch genauso gelten wie heute und damals! Welche Wissenschaft kann das von sich behaupten? 3 Welches ist das erste Mathematikbuch? Etwa 300 Jahre vor Christus schrieb ein Mann ein Buch, das zu den Wer ken mit den größten Auswirkungen auf die Geschichte gehört. Es hat zwar keine politischen, gesellschaftlichen oder religiösen Umwälzungen hervorgebracht wie etwa die Bibel, der Koran oder Das Kapital, aber es hat einen kaum vorstellbaren Einfluss auf die Entwicklung der Wissenschaft genommen: Die Geschichte der Mathematik wäre ohne dieses Buch völlig anders verlaufen. Es ist das mit Abstand wichtigste und übrigens auch erfolgreichste Mathematikbuch aller Zeiten. Der Mann hieß Euklid, und das Buch, das er schrieb, heißt Die Elemente. Über den Menschen Euklid wissen wir fast nichts. Er wirkte vermutlich zwischen 320 und 260 v. Chr. in Alexandria, dem damaligen Wissenschaftszentrum der Welt, und gilt als Begründer der mathematischen Schule von Alexandria. Er hat zahlreiche Bücher verfasst, darunter sechs mathematische. Euklids berühmtestes Werk sind zweifellos Die Elemente, ein Werk, das in 13 Bücher eingeteilt ist. Die Bücher I bis IV behandeln die Geometrie der Ebene, Buch V die Proportionenlehre, Buch VI stellt die Ähnlichkeitsgeometrie dar, die Bücher VII bis IX Zahlentheorie, Buch X studiert inkommensurable Strecken, die Bücher XI bis XIII be handeln schließlich räumliche Geometrie. 17
7 Wenn man das Buch aufschlägt, ist man verblüfft von dessen Nüchternheit. Es beginnt nicht mit einer programmatischen Vorrede, nicht mit einem Verweis auf die Vorgänger, nicht mit Danksagungen, sondern es geht direkt los. Definitionen, Axiome, Postulate, nur wenige Seiten und dann Sätze, Aufgaben und Konstruktionen. Vermutlich gibt es kaum Sätze in den Elementen, die Euklid als Erster bewiesen hat. Das war nicht sein Ziel. Das Ziel der Elemente war es, das damalige mathematische Wissen systematisch zusam menzufassen. Schon eine bloße Zusammenfassung wäre eine bewundernswerte Leistung gewesen, die Euklid Unsterblichkeit gesichert hätte. Aber das Buch ist kein Lexikon, auch keine Datenbank, in der alles gleichwertig nebeneinandersteht. Die Leistung Euklids besteht darin, alles in Form gebracht zu haben, in die mathematische Form. Und dies bedeutet, dass eines aus dem anderen folgt, ja folgen muss. Der Aufbau ist folgerichtig so, dass alle Aussagen bewiesen werden und zum Beweis nur logische Schlüsse zugelassen sind, in denen Aussagen benutzt werden, die schon bewiesen sind! Das heißt: Für die Aussage Nummer 29 darf man nur die Sätze 1 bis 28 verwenden. Das kann man natürlich nicht ad infinitum machen, sondern man muss auf irgendwelche Aussagen aufbauen: Dies sind die Grundsätze oder Postulate, zu denen wir heute Axiome sagen. Ein typisches Postulat lautet: Durch je zwei Punkte kann man eine gerade Linie ziehen. Also lautet die Regel: Zum Beweis des Satzes Nummer 29 darf man nur die Sätze 1 bis 28 und die Postulate verwenden. Die Elemente sind ein stilbildendes Werk, das mustergültig den Aufbau einer Wissenschaft zeigt, ein Werk, das Orientierung gibt und Maßstäbe setzt! Euklid hat einen De-facto-Standard geschaffen, der nun 2300 Jahre lang die Mathematik geprägt, ja definiert hat und dies tun wird, solange es Mathematik geben wird. 18
8 4 Was ist ein Punkt? Der erste Satz des ersten Mathematikbuchs der Welt, der Elemente des Euklid, lautet: «Definitionen. 1. Ein Punkt ist, was keine Teile hat.» Natürlich beginnt Euklid mit Definitionen. Damit man genau weiß, worüber man spricht. Dann kommen die Postulate und Axiome, zum Beispiel «Gefordert soll sein, dass man von jedem Punkt nach jedem Punkt die Strecke ziehen kann», und anschließend folgen Sätze, die meist als herausfordernde Aufgabe gestellt sind. Der erste lautet: «Über einer gegebenen Strecke ein gleichseitiges Dreieck errichten.» All diese Sätze werden bewiesen. Das heißt, sie werden mit logischen Schlussregeln aus den Postulaten und Axiomen sowie den schon bewiesenen Sätzen gefolgert. Das ist perfekt und vorbildlich. So wie Mathematik sein soll. Es bleibt nur ein kleiner Makel. Die erste Definition, die Definition eines Punktes, die so klar zu sein scheint, wird nie verwendet. Auch die zweite Definition: «Eine Linie ist eine breitenlose Länge», wird nie benutzt. Nie gibt es ein Argument, das sagt: «Aus der Definition eines Punktes, nämlich dass er keine Teile hat, folgt das und das.» Hat Euklid das vergessen? Die Mathematik hat über 2000 Jahre gebraucht, um dieses Problem zu lösen. Immer wieder hat man versucht zu beschreiben, was denn ein Punkt wirklich ist. Dabei stellte sich allgemeines Unbehagen ein, nicht weil das zu schwierig oder gar unmöglich war, sondern weil man diese Definitionen allesamt nicht verwenden konnte. Das scheint negativ zu sein, aber es ist absolut positiv. Man braucht keine solche Definition. Man muss nicht wissen, was ein Punkt «ist», um Geometrie machen zu können. Das klingt paradox, aber es ist eine befreiende Erkenntnis. 19
9 Der Erste, der diese Erkenntnis klar aussprach, war der Gießener Mathematiker Moritz Pasch im 19. Jahrhundert. Das Problem, was denn ein Punkt sei, wurde nicht gelöst, sondern es hat sich aufgelöst. Es reicht, die Postulate und Axiome zu kennen. Das ist so ähnlich wie beim Schachspiel. Man muss nicht wissen, was ein Turm «ist», sondern muss nur die Regeln kennen, nach denen er zieht, schlägt und geschlagen wird. Unübertrefflich drastisch hat dies David Hilbert zum Ausdruck gebracht, der bedeutendste Mathematiker der ersten Hälfte des 20. Jahrhunderts. Er sagt radikal: «Man muss jederzeit anstelle von Punkten, Geraden und Ebenen Tische, Stühle und Bierseidel sagen können.» 5 Was ist ein Beweis? «Seit der Zeit der Griechen bedeutet Mathematik zu sagen, Beweis zu sagen», schreibt Nicolas Bourbaki, und er muss es wissen. Denn hinter dem Pseudonym «Nicolas Bourbaki» verbirgt sich ein weitgehend französisches Autorenkollektiv höchster mathematischer Qualität, das seit 1934 der Mathematik neue, «strenge» Grundlagen gab. Insbesondere war der Anspruch von Bourbaki, dass alles bewiesen werden muss. Eine Aussage wird bewiesen, indem sie aus schon bewiesenen Aussagen durch rein logische Argumente abgeleitet wird. Wenn wir zum Beispiel den Satz des Thales («Der Winkel im Halbkreis ist ein rechter») beweisen, dann dürfen wir den Basiswinkelsatz («In einem gleichschenkligen Dreieck sind die Basiswinkel gleich groß») und den Winkelsummensatz («In jedem Dreieck ist die Summe der Innenwinkel gleich 180») benutzen, denn diese wurden schon vorher bewiesen. 20
10 C α β A α γ γ M β B Der Beweis funktioniert grob so: Aufgrund des Basiswinkelsatzes sind die beiden mit α beziehungsweise β bezeichneten Winkel gleich groß. Nun nützt man die Winkelsumme in den beiden Dreiecken rechts und links aus sowie die Tatsache, dass die Winkel γ und γ zusammen 180 ergeben. Daraus ergibt sich α+β=90. Entscheidend ist, dass dieser Beweis nur dann Gültigkeit hat, wenn zuvor der Basiswinkelsatz, der Winkelsummensatz und der Satz über die Nebenwinkel («γ+γ =180») bewiesen worden sind. Um diese Sätze zu beweisen, darf man wiederum nur Sätze benutzen, die schon vorher bewiesen wurden. Und so weiter. Aber irgendwann ist dieser Rückgriff auf bereits bewiesene Sätze natürlich ausgeschöpft. Irgendwo muss jeder Beweis schließlich verankert werden. Das bedeutet: Man führt alles auf Sätze zurück, die nicht bewiesen werden. Weil sie nicht mehr bewiesen werden können. Diese Sätze nennt man Axiome. Ein Axiom ist zum Beispiel der Satz: «Je zwei verschiedene Punkte liegen auf genau einer Geraden.» Zusammenfassend gesagt: Zum Beweis eines Satzes darf man zum einen schon bewiesene Sätze verwenden und zum anderen die Axiome und nur diese! Übrigens: Ein Beweis ist weit entfernt von einer rein 21
11 logischen Spielerei. In der Regel liegt ihm eine höchst kreative Leistung zugrunde. Das kann man im Kleinen schon bei obigem Beweis des Satzes von Thales sehen. Der entscheidende Zug bestand darin, die Punkte C und M zu verbinden. Wenn das geschehen ist, läuft der Rest fast automatisch. Jeder, der sich mit Mathematik beschäftigt, weiß, dass Beweise oft schwer nachzuvollziehen sind. Aber noch viel schwieriger ist es, einen Beweis zu finden. Das ist so wie in der Musik: Eine Beethovensonate zu spielen ist eine große Leistung aber unvorstellbar viel größer ist die Leistung, die Sonate zu komponieren! 6 Was sind Axiome? Axiome sind die Grundaussagen, aus denen sich, ausschließlich mit Hilfe logischer Schlüsse, alle gültigen Aussagen einer Theorie ergeben. Diese «axiomatische Methode» wurde bereits im ersten Mathematikbuch der Welt, den Elementen von Euklid, kompromisslos angewandt. Euklid unterscheidet zwischen «Axiomen», die für ihn logische Regeln sind, und «Postulaten», die sich auf die Geometrie beziehen. Wir würden heute beides Axiome nennen. Über viele Jahrhunderte hinweg war man jedoch der Meinung, dass Axiome nicht nur Grundlagen einer Theorie sind, sondern dass sie sich noch durch etwas anderes auszeichnen, nämlich durch ihre unmittelbar einleuchtende Wahrheit. Aristoteles hat auch hier eine enorme Wirkung gehabt. Bei ihm bedeutet axiôma einen Satz, der eines Beweises nicht bedürftig ist. Durch die Verknüpfung beider Aspekte wurde logische Folgerichtigkeit an Wahrheit gekoppelt: Da die Axiome wahr sind, müssen auch die aus den Axiomen logisch abgeleiteten Sätze wahr und nicht nur «richtig» sein. 22
Albrecht Beutelspachers Kleines Mathematikum
 Albrecht Beutelspachers Kleines Mathematikum Buch Das erste mathematische Mitmachmuseum der Welt steht in Gießen, und jährlich überzeugen sich dort über 150.000 Besucher davon, dass Mathematik alles andere
Albrecht Beutelspachers Kleines Mathematikum Buch Das erste mathematische Mitmachmuseum der Welt steht in Gießen, und jährlich überzeugen sich dort über 150.000 Besucher davon, dass Mathematik alles andere
Geometrie 0.1. Homepage zur Veranstaltung: Lehre Geometrie
 Geometrie 0.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 0.2 Inhaltsverzeichnis Geometrie 0 Geometrie!? 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen
Geometrie 0.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 0.2 Inhaltsverzeichnis Geometrie 0 Geometrie!? 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen
Euklid von Alexandria
 Euklid von Alexandria lebte ca. 360 v. Chr. bis ca. 280 v. Chr. systematisierte in 13 Büchern ( Elemente ) das mathematische Wissen der Antike - bis ins 19. Jahrhundert nach Bibel das am meisten verbreitete
Euklid von Alexandria lebte ca. 360 v. Chr. bis ca. 280 v. Chr. systematisierte in 13 Büchern ( Elemente ) das mathematische Wissen der Antike - bis ins 19. Jahrhundert nach Bibel das am meisten verbreitete
Diese Folien bilden kein Skriptum zur Vorlesung.
 Geometrie für Lehramt an beruflichen Schulen MA9925 Vorlesung von Prof. Dr. Johann Hartl Fakultät für Mathematik Technische Universität München Wintersemester 2013/14 Diese Folien bilden kein Skriptum
Geometrie für Lehramt an beruflichen Schulen MA9925 Vorlesung von Prof. Dr. Johann Hartl Fakultät für Mathematik Technische Universität München Wintersemester 2013/14 Diese Folien bilden kein Skriptum
Die Anfänge der Mathematik als Wissenschaft Logik und Geometrie im antiken Griechenland (I) 2010 Prof. Dr. Fridtjof Toenniessen
 Die Anfänge der Mathematik als Wissenschaft Logik und Geometrie im antiken Griechenland (I) Die Anfänge der Mathematik als Wissenschaft Logik und Geometrie im antiken Griechenland (I) Thales von Milet
Die Anfänge der Mathematik als Wissenschaft Logik und Geometrie im antiken Griechenland (I) Die Anfänge der Mathematik als Wissenschaft Logik und Geometrie im antiken Griechenland (I) Thales von Milet
Geometrie Satz des Pythagoras
 TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausgabe:
TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausgabe:
Kapitel 3 Mathematik. Kapitel 3.6 Geometrie Satz des Pythagoras
 TG TECHNOLOGISCHE GRUNDLAGEN LÖSUNGSSATZ Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 877 Nidfurn 055-654 1 87
TG TECHNOLOGISCHE GRUNDLAGEN LÖSUNGSSATZ Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 877 Nidfurn 055-654 1 87
Geometrie Satz des Pythagoras
 TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 877 Nidfurn 055-654 1 87 Ausgabe: November
TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 877 Nidfurn 055-654 1 87 Ausgabe: November
4.15 Buch I der Elemente
 4.15 Buch I der Elemente Das erste Buch der Elemente beginnt mit 23 Definitionen, 5 Postulate und einige Axiomen (von denen man in späteren Ausgaben bis zu 9 findet). Die ersten fünf Definitionen lauten
4.15 Buch I der Elemente Das erste Buch der Elemente beginnt mit 23 Definitionen, 5 Postulate und einige Axiomen (von denen man in späteren Ausgaben bis zu 9 findet). Die ersten fünf Definitionen lauten
Übungsaufgaben Einführung in die Geometrie, mathematische Grundlagen II, Serie 3 SoSe 2013
 Übungsaufgaben Einführung in die Geometrie, mathematische Grundlagen II, Serie 3 SoSe 2013 Gieding 06.05.2013-12.05.2013 Definitionen und Definieren Aufgabe 3.01 SoSe 2013 S Die Begriffe Winkel, Schenkel
Übungsaufgaben Einführung in die Geometrie, mathematische Grundlagen II, Serie 3 SoSe 2013 Gieding 06.05.2013-12.05.2013 Definitionen und Definieren Aufgabe 3.01 SoSe 2013 S Die Begriffe Winkel, Schenkel
Klausur zur Akademischen Teilprüfung, Modul 2,
 PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilprüfung, Modul, GHPO I vom.7.00, RPO vom 4.08.00 Einführung in die Geometrie Wintersemester 1/1, 1. Februar 01 Klausur zur ATP, Modul, Einführung
PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilprüfung, Modul, GHPO I vom.7.00, RPO vom 4.08.00 Einführung in die Geometrie Wintersemester 1/1, 1. Februar 01 Klausur zur ATP, Modul, Einführung
Nichts als die mathematische Wahrheit
 1 Nichts als die mathematische Wahrheit Holger Stephan Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS), Berlin Lange Nacht der Wissenschaften 10. Mai 2014 2 Anregungen zu folgenden Fragen
1 Nichts als die mathematische Wahrheit Holger Stephan Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS), Berlin Lange Nacht der Wissenschaften 10. Mai 2014 2 Anregungen zu folgenden Fragen
Die Anfänge der Logik
 Die Anfänge der Logik Die Entwicklung des logischen Denkens vor Aristoteles Holger Arnold Universität Potsdam, Institut für Informatik arnold@cs.uni-potsdam.de Grundfragen Was ist Logik? Logik untersucht
Die Anfänge der Logik Die Entwicklung des logischen Denkens vor Aristoteles Holger Arnold Universität Potsdam, Institut für Informatik arnold@cs.uni-potsdam.de Grundfragen Was ist Logik? Logik untersucht
Mathematik hat Geschichte. Teil 4 Griechen. Zahlen bei den Griechen vChr. Zahlen bei den Griechen vChr.
 hat Geschichte Zahlen bei den Griechen 500-100vChr. Teil 4 Griechen Pythagoras Griechische Zahlschreibweise Euklid Archimedes 1 2 Zahlen bei den Griechen 500-100vChr. Zahlen bei den Griechen 500-100vChr.
hat Geschichte Zahlen bei den Griechen 500-100vChr. Teil 4 Griechen Pythagoras Griechische Zahlschreibweise Euklid Archimedes 1 2 Zahlen bei den Griechen 500-100vChr. Zahlen bei den Griechen 500-100vChr.
Klausur zur Akademischen Teilprüfung, Modul 2,
 PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilprüfung, Modul, GHPO I vom.7.003, RPO vom 4.08.003 Einführung in die Geometrie Wintersemester 1/13, 1. Februar 013 Klausur zur ATP, Modul, Einführung
PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilprüfung, Modul, GHPO I vom.7.003, RPO vom 4.08.003 Einführung in die Geometrie Wintersemester 1/13, 1. Februar 013 Klausur zur ATP, Modul, Einführung
Einfu hrung in die Geometrie
 PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilpru fung, Modul Einfu hrung in die Geometrie Abbildung 0: Winkelkreuz Abbildung 0: Spannen von gleichschenkligen Trapezen auf dem Winkelkreuz
PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilpru fung, Modul Einfu hrung in die Geometrie Abbildung 0: Winkelkreuz Abbildung 0: Spannen von gleichschenkligen Trapezen auf dem Winkelkreuz
Arbeitskreis Anwendungsorientierter Mathematikunterricht. Nicht anwendungsorientierter Mathematikunterricht" - Was ist das?
 Gymnasium Neureut Dienstag, 16.11.2010 Arbeitskreis Anwendungsorientierter Mathematikunterricht Vortrag zu Nicht anwendungsorientierter Mathematikunterricht" - Was ist das? 1 2 = 1 2 2 = 0,7071...... ist
Gymnasium Neureut Dienstag, 16.11.2010 Arbeitskreis Anwendungsorientierter Mathematikunterricht Vortrag zu Nicht anwendungsorientierter Mathematikunterricht" - Was ist das? 1 2 = 1 2 2 = 0,7071...... ist
Panorama der Mathematik und Informatik
 Panorama der Mathematik und Informatik : Hilberts Probleme Dirk Frettlöh Technische Fakultät 8/60 : Hilberts Probleme Panorama der Mathematik und Informatik Eine sehr kurze Geschichte der Mathematik (aus:
Panorama der Mathematik und Informatik : Hilberts Probleme Dirk Frettlöh Technische Fakultät 8/60 : Hilberts Probleme Panorama der Mathematik und Informatik Eine sehr kurze Geschichte der Mathematik (aus:
Logische Grundlagen der Mathematik, WS 2014/15
 Logische Grundlagen der Mathematik, WS 2014/15 Thomas Timmermann 16. Oktober 2014 1 Einleitung Literatur Paul.R. Halmos, Naive Set Theory Ralf Schindler, Logische Grundlagen der Mathematik Peter J. Cameron,
Logische Grundlagen der Mathematik, WS 2014/15 Thomas Timmermann 16. Oktober 2014 1 Einleitung Literatur Paul.R. Halmos, Naive Set Theory Ralf Schindler, Logische Grundlagen der Mathematik Peter J. Cameron,
Prof. Dr. Dörte Haftendorn Leuphana Universität 2
 Mathematik hat Geschichte Teil 4 Griechen Pythagoras Griechische Zahlschreibweise Euklid Archimedes Prof. Dr. Dörte Haftendorn Leuphana Universität www.mathematik-verstehen.de 1 Zahlen bei den Griechen
Mathematik hat Geschichte Teil 4 Griechen Pythagoras Griechische Zahlschreibweise Euklid Archimedes Prof. Dr. Dörte Haftendorn Leuphana Universität www.mathematik-verstehen.de 1 Zahlen bei den Griechen
Mathematik hat Geschichte. Teil 4 Griechen. Zahlen bei den Griechen vChr. Zahlen bei den Griechen vChr.
 hat Geschichte Zahlen bei den Griechen 500-100vChr. Teil 4 Griechen Pythagoras Griechische Zahlschreibweise Euklid Archimedes Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt
hat Geschichte Zahlen bei den Griechen 500-100vChr. Teil 4 Griechen Pythagoras Griechische Zahlschreibweise Euklid Archimedes Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Grundbildung Trigonometrie. Das komplette Material finden Sie hier:
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Das komplette Material finden Sie hier: School-Scout.de Inhalt Seite Vorwort I. Grundlagen 1. Trigonometrie was ist das? 2. Ein rechtwinkliges
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Das komplette Material finden Sie hier: School-Scout.de Inhalt Seite Vorwort I. Grundlagen 1. Trigonometrie was ist das? 2. Ein rechtwinkliges
Motivation und Geschichte. Geschichte der Logik Logik und Informatik
 Motivation und Geschichte Geschichte der Logik Logik und Informatik Logik für Informatiker, M. Lange, IFI/LMU: Motivation und Geschichte Geschichte der Logik 12 Aufgaben der Logik Logik (aus Griechischem)
Motivation und Geschichte Geschichte der Logik Logik und Informatik Logik für Informatiker, M. Lange, IFI/LMU: Motivation und Geschichte Geschichte der Logik 12 Aufgaben der Logik Logik (aus Griechischem)
Wünsche eines Hochschullehrers an die künftigen Mathematikstudierenden. Albrecht Beutelspacher
 Wünsche eines Hochschullehrers an die künftigen Mathematikstudierenden Albrecht Beutelspacher Mathematikausbildung an Schulen! Selektiert nicht die besten Mathematiker (schwache Korrelation von Schulnote
Wünsche eines Hochschullehrers an die künftigen Mathematikstudierenden Albrecht Beutelspacher Mathematikausbildung an Schulen! Selektiert nicht die besten Mathematiker (schwache Korrelation von Schulnote
Aufgabe 1: Definieren
 Aufgabe 1: Definieren a) Definieren Sie den Begriff Mittelpunkt einer Strecke AB. Der Punkt M ist Mittelpunkt der Strecke AB, wenn er zu dieser gehört und AM = MB gilt b) Definieren Sie den Begriff konvexes
Aufgabe 1: Definieren a) Definieren Sie den Begriff Mittelpunkt einer Strecke AB. Der Punkt M ist Mittelpunkt der Strecke AB, wenn er zu dieser gehört und AM = MB gilt b) Definieren Sie den Begriff konvexes
Mathematische Grundlagen II: Einführung in die Geometrie Sekundarstufe
 PH Heidelberg, Fach Mathematik Klausur zur Akademischen Vorprüfung Mathematische Grundlagen II: Einführung in die Geometrie Sekundarstufe Wintersemester 12/13 12. Februar 2013 Aufgabe 8: Definieren Nr.
PH Heidelberg, Fach Mathematik Klausur zur Akademischen Vorprüfung Mathematische Grundlagen II: Einführung in die Geometrie Sekundarstufe Wintersemester 12/13 12. Februar 2013 Aufgabe 8: Definieren Nr.
PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilpru fung, Modul 2. Einfu hrung in die Geometrie
 PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilpru fung, Modul Einfu hrung in die Geometrie Abbildung 01 Abbildung 0 Wintersemester 011/1 10. Februar 01 Abbildung 0 Klausur zur ATP, Modul,
PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilpru fung, Modul Einfu hrung in die Geometrie Abbildung 01 Abbildung 0 Wintersemester 011/1 10. Februar 01 Abbildung 0 Klausur zur ATP, Modul,
1. LESEPROBE KAPITEL GEOMETRIE
 LESEPROBE KAPITEL GEOMETRIE 1. LESEPROBE KAPITEL GEOMETRIE Beispiel G4.06 Der Kreis k hat den Mittelpunkt M und einen Durchmesser AB (= 2r). Der Halbierungspunkt der Strecke MB heißt C. D ( A, B) sei ein
LESEPROBE KAPITEL GEOMETRIE 1. LESEPROBE KAPITEL GEOMETRIE Beispiel G4.06 Der Kreis k hat den Mittelpunkt M und einen Durchmesser AB (= 2r). Der Halbierungspunkt der Strecke MB heißt C. D ( A, B) sei ein
Axiomatischer Aufbau der Geometrie
 Bei axiomatisch aufgebauten Theorien existieren heute: 2 Arten von Begriffen: Grundbegriffe (werden nicht definiert und das verwendete Axiomensystem legt fest, welche Begriffe Grundbegriffe sind) Abgeleitete
Bei axiomatisch aufgebauten Theorien existieren heute: 2 Arten von Begriffen: Grundbegriffe (werden nicht definiert und das verwendete Axiomensystem legt fest, welche Begriffe Grundbegriffe sind) Abgeleitete
Vorkurs Mathematik 2016
 Vorkurs Mathematik 2016 WWU Münster, Fachbereich Mathematik und Informatik PD Dr. K. Halupczok / Dr. Frank Wübbeling Denkanstoß: Was ist wissenschaftliches Denken? Denkanstoß: Was ist wissenschaftliches
Vorkurs Mathematik 2016 WWU Münster, Fachbereich Mathematik und Informatik PD Dr. K. Halupczok / Dr. Frank Wübbeling Denkanstoß: Was ist wissenschaftliches Denken? Denkanstoß: Was ist wissenschaftliches
4.13 Euklid (um 300 v.chr.) und seine Werke
 4.13 Euklid (um 300 v.chr.) und seine Werke wurde (vermutlich nach Studium in Athen) von einem frühen Vertreter der Dynastie der Ptolemäer nach Alexandria berufen, wo er die dortige mathematische Schule
4.13 Euklid (um 300 v.chr.) und seine Werke wurde (vermutlich nach Studium in Athen) von einem frühen Vertreter der Dynastie der Ptolemäer nach Alexandria berufen, wo er die dortige mathematische Schule
Elementargeometrie Vorlesung von Prof. Dr. Johann Hartl Fakultät für Mathematik Technische Universität München Wintersemester 2014/15
 Elementargeometrie Vorlesung von Prof. Dr. Johann Hartl Fakultät für Mathematik Technische Universität München Wintersemester 2014/15 Diese Folien bilden kein Skriptum zur Vorlesung. Sie sollen das Mitschreiben
Elementargeometrie Vorlesung von Prof. Dr. Johann Hartl Fakultät für Mathematik Technische Universität München Wintersemester 2014/15 Diese Folien bilden kein Skriptum zur Vorlesung. Sie sollen das Mitschreiben
Mathematische Probleme, SS 2015 Montag $Id: dreieck.tex,v /04/27 13:26:30 hk Exp $
 $Id: dreieck.tex,v 1.17 2015/04/27 13:26:30 hk Exp $ 1 Dreiecke 1.5 Einige spezielle Punkte im Dreieck m Ende der letzten Sitzung hatten wir eingesehen das die drei Mittelsenkrechten eines Dreiecks = sich
$Id: dreieck.tex,v 1.17 2015/04/27 13:26:30 hk Exp $ 1 Dreiecke 1.5 Einige spezielle Punkte im Dreieck m Ende der letzten Sitzung hatten wir eingesehen das die drei Mittelsenkrechten eines Dreiecks = sich
24 KAPITEL 2. REELLE UND KOMPLEXE ZAHLEN
 24 KAPITEL 2. REELLE UND KOMPLEXE ZAHLEN x 2 = 0+x 2 = ( a+a)+x 2 = a+(a+x 2 ) = a+(a+x 1 ) = ( a+a)+x 1 = x 1. Daraus folgt dann, wegen x 1 = x 2 die Eindeutigkeit. Im zweiten Fall kann man für a 0 schreiben
24 KAPITEL 2. REELLE UND KOMPLEXE ZAHLEN x 2 = 0+x 2 = ( a+a)+x 2 = a+(a+x 2 ) = a+(a+x 1 ) = ( a+a)+x 1 = x 1. Daraus folgt dann, wegen x 1 = x 2 die Eindeutigkeit. Im zweiten Fall kann man für a 0 schreiben
3. Synthetische Geometrie (synthetein = zusammensetzen)
 3. Synthetische Geometrie (synthetein = zusammensetzen) Wichtig ist in der synthetischen Geometrie das Zusammensetzen von Grundsätzen, Voraussetzungen, Sätzen und Folgerungen. Die SuS lernen die neue Art
3. Synthetische Geometrie (synthetein = zusammensetzen) Wichtig ist in der synthetischen Geometrie das Zusammensetzen von Grundsätzen, Voraussetzungen, Sätzen und Folgerungen. Die SuS lernen die neue Art
Motivation und Geschichte. Geschichte der Logik Logik und Informatik
 Motivation und Geschichte Geschichte der Logik Logik und Informatik Theoretische Informatik: Logik, M. Lange, FB16, Uni Kassel: 2.1 Motivation und Geschichte Geschichte der Logik 13 Aufgaben der Logik
Motivation und Geschichte Geschichte der Logik Logik und Informatik Theoretische Informatik: Logik, M. Lange, FB16, Uni Kassel: 2.1 Motivation und Geschichte Geschichte der Logik 13 Aufgaben der Logik
Definitionen. 1. Ein Punkt ist, was keine Teile hat. 3. Die Enden einer Linie sind Punkte.
 Das erste der dreizehn Bücher von Euklids Elementen beginnt nach der Ausgabe in Ostwald s Klassikern der exakten Wissenschaften (Nr. 235), Leipzig 1933, folgendermaßen: Definitionen. 1. Ein Punkt ist,
Das erste der dreizehn Bücher von Euklids Elementen beginnt nach der Ausgabe in Ostwald s Klassikern der exakten Wissenschaften (Nr. 235), Leipzig 1933, folgendermaßen: Definitionen. 1. Ein Punkt ist,
2. Kongruenzsätze (SWS und SSS) ohne Parallelen.
 2. Kongruenzsätze (SWS und SSS) ohne Parallelen. In diesem Kapitel beginnen wir mit der systematischen ufstellung der Euklidischen Geometrie wie man sie in [Euklid, Elemente] findet. ls erstes Lehrstück
2. Kongruenzsätze (SWS und SSS) ohne Parallelen. In diesem Kapitel beginnen wir mit der systematischen ufstellung der Euklidischen Geometrie wie man sie in [Euklid, Elemente] findet. ls erstes Lehrstück
Pädagogische Hochschule Schwäbisch Gmünd
 Pädagogische Hochschule Schwäbisch Gmünd Institut für Mathematik und Informatik Albrecht: uebung_0_geo.docx: Die Entfernung zum Horizont 1. In der "sonntag aktuell" vom 26.01.2003 wurde in einem Bericht
Pädagogische Hochschule Schwäbisch Gmünd Institut für Mathematik und Informatik Albrecht: uebung_0_geo.docx: Die Entfernung zum Horizont 1. In der "sonntag aktuell" vom 26.01.2003 wurde in einem Bericht
Zwillinge von Archimedes (1)
 Zwillinge von Archimedes (1) Zwillinge von Archimedes (2) Zwillinge von Archimedes (3) DIDAKTIK DER GEOMETRIE Elementargeometrie 2 Prof. Heinz Klemenz Universität Zürich, Kantonsschule Rychenberg Winterthur
Zwillinge von Archimedes (1) Zwillinge von Archimedes (2) Zwillinge von Archimedes (3) DIDAKTIK DER GEOMETRIE Elementargeometrie 2 Prof. Heinz Klemenz Universität Zürich, Kantonsschule Rychenberg Winterthur
1.3 Aussagen. Beispiel: Das Bruttosozialprodukt der Bundesrepublik Deutschland ist höher als das der USA ist eine offenbar falsche Aussage.
 1.3 Aussagen In der Mathematik geht es um Aussagen. Eine Aussage ist ein statement, das entweder wahr oder falsch sein kann. Beides geht nicht! Äußerungen, die nicht die Eigenschaft haben, wahr oder falsch
1.3 Aussagen In der Mathematik geht es um Aussagen. Eine Aussage ist ein statement, das entweder wahr oder falsch sein kann. Beides geht nicht! Äußerungen, die nicht die Eigenschaft haben, wahr oder falsch
Wie bearbeitet man einen Übungszettel?
 Wie bearbeitet man einen Übungszettel? Tipps: Mathematik lernt man nur durch Selbermachen: Übungsaufgaben müssen selbst bearbeitet werden. Das Nachvollziehen einer Lösung reicht nicht aus. Der Weg ist
Wie bearbeitet man einen Übungszettel? Tipps: Mathematik lernt man nur durch Selbermachen: Übungsaufgaben müssen selbst bearbeitet werden. Das Nachvollziehen einer Lösung reicht nicht aus. Der Weg ist
Ästhetik ist die Theorie der ästhetischen Erfahrung, der ästhetischen Gegenstände und der ästhetischen Eigenschaften.
 16 I. Was ist philosophische Ästhetik? instrumente. Die Erkenntnis ästhetischer Qualitäten ist nur eine unter vielen möglichen Anwendungen dieses Instruments. In diesem Sinn ist die Charakterisierung von
16 I. Was ist philosophische Ästhetik? instrumente. Die Erkenntnis ästhetischer Qualitäten ist nur eine unter vielen möglichen Anwendungen dieses Instruments. In diesem Sinn ist die Charakterisierung von
Wissenschaftliche Grundlagen des Mathematischen Schulstoffs III III. Die erste Stunde. Die erste Stunde
 Wissenschaftliche Grundlagen des Mathematischen Schulstoffs III III Was ist ist Mathematik? Der Inhalt Geometrie (seit (seit Euklid, ca. ca. 300 300 v. v. Chr.) Chr.) Die Die Lehre vom vom uns uns umgebenden
Wissenschaftliche Grundlagen des Mathematischen Schulstoffs III III Was ist ist Mathematik? Der Inhalt Geometrie (seit (seit Euklid, ca. ca. 300 300 v. v. Chr.) Chr.) Die Die Lehre vom vom uns uns umgebenden
Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt.
 M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
Prof. Dr. Dörte Haftendorn, Leuphana Universität Lüneburg, 2013
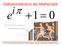 Selbstverständnis der Mathematik i 1 Selbstverständnis der Mathematik Komplexe Zahlen Geometrie i Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 Selbstverständnis der Mathematik : = Menge der Menschen,
Selbstverständnis der Mathematik i 1 Selbstverständnis der Mathematik Komplexe Zahlen Geometrie i Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 Selbstverständnis der Mathematik : = Menge der Menschen,
Mathematische Probleme, SS 2016 Freitag $Id: dreieck.tex,v /04/29 12:45:52 hk Exp $
 $Id: dreieck.tex,v 1.26 2016/04/29 12:45:52 hk Exp $ 1 Dreiecke 1.6 Einige spezielle Punkte im Dreieck Wir beschäftigen uns weiterhin mit den speziellen Punkten eines Dreiecks und haben in der letzten
$Id: dreieck.tex,v 1.26 2016/04/29 12:45:52 hk Exp $ 1 Dreiecke 1.6 Einige spezielle Punkte im Dreieck Wir beschäftigen uns weiterhin mit den speziellen Punkten eines Dreiecks und haben in der letzten
3. Die Existenz des Pentagons.
 3. Die Existenz des Pentagons. In dieser Vorlesung werden wir sehen wie die Griechen bewiesen haben, dass es das Pentagon wirklich gibt. Dieser Beweis ist schon recht anspruchsvoll. So anspruchsvoll, dass
3. Die Existenz des Pentagons. In dieser Vorlesung werden wir sehen wie die Griechen bewiesen haben, dass es das Pentagon wirklich gibt. Dieser Beweis ist schon recht anspruchsvoll. So anspruchsvoll, dass
Achsensymmetrie. Konstruktionen M 7.1
 M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
Referat über Thales, Pythagoras & Euklid. von Steffen Dremel Klasse 9a
 Referat über Thales, Pythagoras & Euklid von Steffen Dremel Klasse 9a Thales von Milet Geboren: ca. 624 v. Chr. in Milet, Kleinasien Gestorben: ca. 546 v. Chr. War ein griechischer Naturphilosoph, Staatsmann,
Referat über Thales, Pythagoras & Euklid von Steffen Dremel Klasse 9a Thales von Milet Geboren: ca. 624 v. Chr. in Milet, Kleinasien Gestorben: ca. 546 v. Chr. War ein griechischer Naturphilosoph, Staatsmann,
Rhetorik und Argumentationstheorie.
 Rhetorik und Argumentationstheorie 2 [frederik.gierlinger@univie.ac.at] Teil 2 Was ist ein Beweis? 2 Wichtige Grundlagen Tautologie nennt man eine zusammengesetzte Aussage, die wahr ist, unabhängig vom
Rhetorik und Argumentationstheorie 2 [frederik.gierlinger@univie.ac.at] Teil 2 Was ist ein Beweis? 2 Wichtige Grundlagen Tautologie nennt man eine zusammengesetzte Aussage, die wahr ist, unabhängig vom
Arbeitsblätter zur Arbeit mit GEOGEBRA in Klasse 6
 Arbeitsblätter zur Arbeit mit GEOGEBRA in Klasse 6 Die folgenden Arbeitsblätter sind für die Arbeit im Mathematikunterricht Klasse 6 bestimmt. Sie kommen im Verlauf von Lernbereich 3 Dreiecke und Vierecke
Arbeitsblätter zur Arbeit mit GEOGEBRA in Klasse 6 Die folgenden Arbeitsblätter sind für die Arbeit im Mathematikunterricht Klasse 6 bestimmt. Sie kommen im Verlauf von Lernbereich 3 Dreiecke und Vierecke
Beispiellösungen zu Blatt 65
 µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 65 Welche regelmäßigen n-ecke der Seitenlänge 1 kann man in kleinere
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 65 Welche regelmäßigen n-ecke der Seitenlänge 1 kann man in kleinere
MAT746 Seminar über Euklidische Geometrie Philipp Becker
 MAT746 Seminar über Euklidische Geometrie Philipp Becker R David Hilbert (1862-1943) Den Begriffen aus der Anschauungswelt fehlt die notwendige mathematische Exaktheit. Gebäude der Geometrie soll nicht
MAT746 Seminar über Euklidische Geometrie Philipp Becker R David Hilbert (1862-1943) Den Begriffen aus der Anschauungswelt fehlt die notwendige mathematische Exaktheit. Gebäude der Geometrie soll nicht
Begründen in der Geometrie
 Nr.6 9.6.2016 Begründen in der Geometrie Didaktische Grundsätze Zuerst die geometrischen Phänomene erkunden und kennenlernen. Viel zeichnen! Vierecke, Kreise, Dreiecke, Winkel, Strecken,... In dieser ersten
Nr.6 9.6.2016 Begründen in der Geometrie Didaktische Grundsätze Zuerst die geometrischen Phänomene erkunden und kennenlernen. Viel zeichnen! Vierecke, Kreise, Dreiecke, Winkel, Strecken,... In dieser ersten
3. Vorlesung. Die Existenz des Pentagons. (*)
 3. Vorlesung. ie Existenz des Pentagons. (*) In dieser Vorlesung werden wir sehen wie die Griechen bewiesen haben, dass es das Pentagon wirklich gibt. ieser eweis ist schon recht anspruchsvoll. So anspruchsvoll,
3. Vorlesung. ie Existenz des Pentagons. (*) In dieser Vorlesung werden wir sehen wie die Griechen bewiesen haben, dass es das Pentagon wirklich gibt. ieser eweis ist schon recht anspruchsvoll. So anspruchsvoll,
Grundwissen JS 7: Geometrie 17. Juli (a) Wann heißt eine Figur achsensymmetrisch? Welche Bedeutung hat die Symmetrieachse anschaulich
 GYMNASIUM MIT SCHÜLERHEIM EGNITZ math-technolog u sprachl Gymnasium WILHELM-VON-HUMBOLDT-STRASSE 7 91257 EGNITZ FERNRUF 09241/48333 FAX 09241/2564 Grundwissen JS 7: Geometrie 17 Juli 2007 1(a) Wann heißt
GYMNASIUM MIT SCHÜLERHEIM EGNITZ math-technolog u sprachl Gymnasium WILHELM-VON-HUMBOLDT-STRASSE 7 91257 EGNITZ FERNRUF 09241/48333 FAX 09241/2564 Grundwissen JS 7: Geometrie 17 Juli 2007 1(a) Wann heißt
Konstruktionen am Dreieck
 Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Symmetrien und Winkel
 Symmetrien und Winkel 20 1 13 Symmetrien Zeichnungen und Konstruktionen zur Symmetrie 401 A Wähle das erste oder das zweite Bild von Vasarely im mathbuch 1 auf Seite 65. Beschreibe es. B Zeichne das Bild
Symmetrien und Winkel 20 1 13 Symmetrien Zeichnungen und Konstruktionen zur Symmetrie 401 A Wähle das erste oder das zweite Bild von Vasarely im mathbuch 1 auf Seite 65. Beschreibe es. B Zeichne das Bild
DER INDIVIDUELLE MYTHOS DES NEUROTIKERS
 DER INDIVIDUELLE MYTHOS DES NEUROTIKERS LACANS PARADOXA Was Sie eine Analyse lehrt, ist auf keinem anderen Weg zu erwerben, weder durch Unterricht noch durch irgendeine andere geistige Übung. Wenn nicht,
DER INDIVIDUELLE MYTHOS DES NEUROTIKERS LACANS PARADOXA Was Sie eine Analyse lehrt, ist auf keinem anderen Weg zu erwerben, weder durch Unterricht noch durch irgendeine andere geistige Übung. Wenn nicht,
7 Gültigkeit und logische Form von Argumenten
 7 Gültigkeit und logische Form von Argumenten Zwischenresümee 1. Logik ist ein grundlegender Teil der Lehre vom richtigen Argumentieren. 2. Speziell geht es der Logik um einen spezifischen Aspekt der Güte
7 Gültigkeit und logische Form von Argumenten Zwischenresümee 1. Logik ist ein grundlegender Teil der Lehre vom richtigen Argumentieren. 2. Speziell geht es der Logik um einen spezifischen Aspekt der Güte
Landeswettbewerb Mathematik Baden-Württemberg Musterlösungen 1. Runde 2007
 Landeswettbewerb Mathematik Baden-Württemberg Musterlösungen Runde 007 Aufgabe Günter bastelt Würfel Jede Seitenfläche färbt er entweder grün oder rot Wie viele Würfel, die sich allein durch ihre Färbung
Landeswettbewerb Mathematik Baden-Württemberg Musterlösungen Runde 007 Aufgabe Günter bastelt Würfel Jede Seitenfläche färbt er entweder grün oder rot Wie viele Würfel, die sich allein durch ihre Färbung
Vorkurs Mathematik 2016
 Vorkurs Mathematik 2016 WWU Münster, Fachbereich Mathematik und Informatik PD Dr. K. Halupczok Skript VK1 vom 8.9.2016 VK1: Logik Die Kunst des Schlussfolgerns Denition 1: Eine Aussage ist ein sprachliches
Vorkurs Mathematik 2016 WWU Münster, Fachbereich Mathematik und Informatik PD Dr. K. Halupczok Skript VK1 vom 8.9.2016 VK1: Logik Die Kunst des Schlussfolgerns Denition 1: Eine Aussage ist ein sprachliches
Die Kapitel 1 und 2.1 haben wir im Jahr 2012 behandelt. Im Zirkel am haben wir mit Kapitel 2.2 begonnen.
 Das vorliegende Skript beschäftigt sich mit dem Thema Elementargeometrie. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft(MSG) im Schuljahr 2012/2013. Die vorliegende
Das vorliegende Skript beschäftigt sich mit dem Thema Elementargeometrie. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft(MSG) im Schuljahr 2012/2013. Die vorliegende
Peripheriewinkelsatz (auch Umfangswinkelsatz)
 Peripheriewinkelsatz (auch Umfangswinkelsatz) Für die Einführung des Peripheriewinkelsatzes (auch Umfangwinkelsatz) machen wir uns mit dem Satz des Thales vertraut. Der Satz des Thales besagt, dass Dreiecke,
Peripheriewinkelsatz (auch Umfangswinkelsatz) Für die Einführung des Peripheriewinkelsatzes (auch Umfangwinkelsatz) machen wir uns mit dem Satz des Thales vertraut. Der Satz des Thales besagt, dass Dreiecke,
Geometrie Modul 4b WS 2015/16 Mi HS 1
 Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Über das Lesen mathematischer Texte Teil 2: Definition, Satz, Beweis
 Über das Lesen mathematischer Texte Teil 2: Definition, Satz, Beweis Hagen Knaf Prof. Dr. H. Knaf, Mathematisches Beweisen 1 Struktur mathematischer Texte Ein mathematischer Text enthält neben dem fortlaufenden
Über das Lesen mathematischer Texte Teil 2: Definition, Satz, Beweis Hagen Knaf Prof. Dr. H. Knaf, Mathematisches Beweisen 1 Struktur mathematischer Texte Ein mathematischer Text enthält neben dem fortlaufenden
[81] Argumentationen mit Winkeln
![[81] Argumentationen mit Winkeln [81] Argumentationen mit Winkeln](/thumbs/76/73203969.jpg) [81] Argumentationen mit Winkeln In: L.Flade, W. Herget (Hrsg), Mathematik lehren und lernen nach TIMSS Anregungen für die Sekundarstufen, Berlin (Volk&Wissen) 2000, 51-58 1. Eine TIMSS-Aufgabe als Ausgangspunkt
[81] Argumentationen mit Winkeln In: L.Flade, W. Herget (Hrsg), Mathematik lehren und lernen nach TIMSS Anregungen für die Sekundarstufen, Berlin (Volk&Wissen) 2000, 51-58 1. Eine TIMSS-Aufgabe als Ausgangspunkt
Aufgabe 1: Multiple Choice Test
 PH Heidelberg, Fach Mathematik, Klausur zur Teilprüfung Modul, Einführung in die Geometrie, SS010, 30.07.010 Aufgabe 1: Multiple Choice Test Kennzeichnen Sie die Ihrer Meinung nach richtigen Antworten.
PH Heidelberg, Fach Mathematik, Klausur zur Teilprüfung Modul, Einführung in die Geometrie, SS010, 30.07.010 Aufgabe 1: Multiple Choice Test Kennzeichnen Sie die Ihrer Meinung nach richtigen Antworten.
7. Klasse. Algebra. 2.1 Kommutativgesetz (KG) der Addition und Multiplikation Für alle rationalen Zahlen a und b gilt: a+b = b+a a b = b a
 Algebra 1. Termen mit Variablen Ein Term ist ein Rechenausdruck, der aus Zahlen, Variablen und Rechenzeichen bestehen kann. Variablen sind Platzhalter für Zahlen oder für Größen. Eine Variable steht immer
Algebra 1. Termen mit Variablen Ein Term ist ein Rechenausdruck, der aus Zahlen, Variablen und Rechenzeichen bestehen kann. Variablen sind Platzhalter für Zahlen oder für Größen. Eine Variable steht immer
Frage 8.3. Wozu dienen Beweise im Rahmen einer mathematischen (Lehramts-)Ausbildung?
 8 Grundsätzliches zu Beweisen Frage 8.3. Wozu dienen Beweise im Rahmen einer mathematischen (Lehramts-)Ausbildung? ˆ Mathematik besteht nicht (nur) aus dem Anwenden auswendig gelernter Schemata. Stattdessen
8 Grundsätzliches zu Beweisen Frage 8.3. Wozu dienen Beweise im Rahmen einer mathematischen (Lehramts-)Ausbildung? ˆ Mathematik besteht nicht (nur) aus dem Anwenden auswendig gelernter Schemata. Stattdessen
Übungen zur Vorlesung Grundlagen der Mathematik II Lösungsvorschlag
 MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr. E. Schörner SS 01 Blatt 7 0.06.01 Übungen zur Vorlesung Grundlagen der Mathematik II Lösungsvorschlag 5. a Um ein rechtwinkliges Dreieck in seiner Gestalt
MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr. E. Schörner SS 01 Blatt 7 0.06.01 Übungen zur Vorlesung Grundlagen der Mathematik II Lösungsvorschlag 5. a Um ein rechtwinkliges Dreieck in seiner Gestalt
2.2 Axiomatische Mathematik
 33 2.2 Axiomatische Mathematik Die deduktive Methode funktioniert folgendermaßen: Der Beweis einer Aussage (A1) wird auf eine offensichtlichere Aussage (A2) zurückgeführt. Dann wird nach einer noch unbedenklicheren
33 2.2 Axiomatische Mathematik Die deduktive Methode funktioniert folgendermaßen: Der Beweis einer Aussage (A1) wird auf eine offensichtlichere Aussage (A2) zurückgeführt. Dann wird nach einer noch unbedenklicheren
Martin Goldstern Der logische Denker Kurt Gödel und sein Unvollständigkeitssatz. 6.
 Martin Goldstern Der logische Denker Kurt Gödel und sein Unvollständigkeitssatz http://www.tuwien.ac.at/goldstern/ 6.September 2006 1 Kurt Gödel, 1906-1978 1906: geboren am 28.April in Brünn (heute Brno)
Martin Goldstern Der logische Denker Kurt Gödel und sein Unvollständigkeitssatz http://www.tuwien.ac.at/goldstern/ 6.September 2006 1 Kurt Gödel, 1906-1978 1906: geboren am 28.April in Brünn (heute Brno)
Kapitel 1. Grundlegendes
 Kapitel 1 Grundlegendes Abschnitt 1.4 Vollständige Induktion Charakterisierung der natürlichen Zahlen Die Menge N 0 = {0, 1, 2, 3,...} der natürlichen Zahlen läßt sich wie folgt charakterisieren: 1. 0
Kapitel 1 Grundlegendes Abschnitt 1.4 Vollständige Induktion Charakterisierung der natürlichen Zahlen Die Menge N 0 = {0, 1, 2, 3,...} der natürlichen Zahlen läßt sich wie folgt charakterisieren: 1. 0
Vierecke. 7.1 Grundwissen Mathematik Geometrie Klasse 7. Drachenviereck: Viereck, bei dem eine Diagonale Symmetrieachse ist
 7.1 Grundwissen Mathematik Geometrie Klasse 7 Vierecke Trapez: Viereck, bei dem zwei Gegenseiten parallel sind gleichschenkliges Trapez: Trapez, bei dem die beiden Schenkel c gleich lang sind (b = d) d
7.1 Grundwissen Mathematik Geometrie Klasse 7 Vierecke Trapez: Viereck, bei dem zwei Gegenseiten parallel sind gleichschenkliges Trapez: Trapez, bei dem die beiden Schenkel c gleich lang sind (b = d) d
Schulmathematik versus Unimathematik : Sichtweisen eines Fachmathematikers
 Schulmathematik versus Unimathematik : Sichtweisen eines Fachmathematikers 25. April 2015 1. Antithesen Warum muss ich mich an der Uni mit Galoistheorie beschäftigen? Die ist so schwer und in der Schule
Schulmathematik versus Unimathematik : Sichtweisen eines Fachmathematikers 25. April 2015 1. Antithesen Warum muss ich mich an der Uni mit Galoistheorie beschäftigen? Die ist so schwer und in der Schule
Klassenstufen 7, 8. Fachbereich Mathematik Tag der Mathematik 9. November 2013
 Fachbereich Mathematik Tag der Mathematik 9. November 2013 Klassenstufen 7, 8 12 Aufgabe 1 (5+++5+2 Punkte). Meister Hora hat eine kuriose Uhr: Bei dieser springt der Stundenzeiger nicht wie üblich jede
Fachbereich Mathematik Tag der Mathematik 9. November 2013 Klassenstufen 7, 8 12 Aufgabe 1 (5+++5+2 Punkte). Meister Hora hat eine kuriose Uhr: Bei dieser springt der Stundenzeiger nicht wie üblich jede
Der Satz des Pythagoras. Kein Darwinscher Zufall
 Der Satz des Pythagoras. Kein Darwinscher Zufall Detlef Dürr duerr@rz.mathematik.uni-muenchen.de 1. Mai 2012 1 Zahlen-Verhältnisse Die Grunderkenntnis der Gesetzmäßigkeit in der Natur ist Harmonie. Heute
Der Satz des Pythagoras. Kein Darwinscher Zufall Detlef Dürr duerr@rz.mathematik.uni-muenchen.de 1. Mai 2012 1 Zahlen-Verhältnisse Die Grunderkenntnis der Gesetzmäßigkeit in der Natur ist Harmonie. Heute
Was ist nichteuklidische Geometrie?
 Mathematisches Institut LMU München 9. Mai 2009 Euklids Stoicheia : Die Elemente (350 v. Chr.) Ein Fragment einer frühen Abschrift Euklids Elemente im 17. Jahrhundert Das Verstehen des Raumes durch primitive
Mathematisches Institut LMU München 9. Mai 2009 Euklids Stoicheia : Die Elemente (350 v. Chr.) Ein Fragment einer frühen Abschrift Euklids Elemente im 17. Jahrhundert Das Verstehen des Raumes durch primitive
Axiomatische Beschreibung der ganzen Zahlen
 Axiomatische Beschreibung der ganzen Zahlen Peter Feigl JKU Linz peter.feigl@students.jku.at 0055282 Claudia Hemmelmeir JKU Linz darja@gmx.at 0355147 Zusammenfassung Wir möchten in diesem Artikel die ganzen
Axiomatische Beschreibung der ganzen Zahlen Peter Feigl JKU Linz peter.feigl@students.jku.at 0055282 Claudia Hemmelmeir JKU Linz darja@gmx.at 0355147 Zusammenfassung Wir möchten in diesem Artikel die ganzen
2. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 8 Saison 1962/1963 Aufgaben und Lösungen
 2. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 8 Saison 1962/1963 Aufgaben und Lösungen 1 OJM 2. Mathematik-Olympiade 2. Stufe (Kreisolympiade) Klasse 8 Aufgaben Hinweis: Der Lösungsweg mit Begründungen
2. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 8 Saison 1962/1963 Aufgaben und Lösungen 1 OJM 2. Mathematik-Olympiade 2. Stufe (Kreisolympiade) Klasse 8 Aufgaben Hinweis: Der Lösungsweg mit Begründungen
Grundlagen der Geometrie
 Grundlagen der Geometrie Vorlesungsausarbeitung zum WS 2010/11 von Prof. Dr. K. Fritzsche ii Inhalt 0 Grundlagen der Schulgeometrie 1 I Die Elemente : Inzidenz und Anordnung 9 1. Die deduktive Methode
Grundlagen der Geometrie Vorlesungsausarbeitung zum WS 2010/11 von Prof. Dr. K. Fritzsche ii Inhalt 0 Grundlagen der Schulgeometrie 1 I Die Elemente : Inzidenz und Anordnung 9 1. Die deduktive Methode
Geometrie Winkel und Vierecke PRÜFUNG 02. Ohne Formelsammlung! Name: Klasse: Datum: Punkte: Note: Klassenschnitt/ Maximalnote : Ausgabe: 2.
 GEOMETRIE PRÜFUNGSVORBEREITUNG Seite 1 Geometrie Winkel und Vierecke PRÜFUNG 02 Name: Klasse: Datum: : Note: Ausgabe: 2. Mai 2011 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle
GEOMETRIE PRÜFUNGSVORBEREITUNG Seite 1 Geometrie Winkel und Vierecke PRÜFUNG 02 Name: Klasse: Datum: : Note: Ausgabe: 2. Mai 2011 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle
Brückenkurs. Beweise. Anja Haußen Brückenkurs, Seite 1/23
 Brückenkurs Beweise Anja Haußen 30.09.2016 Brückenkurs, 30.09.2016 Seite 1/23 Inhalt 1 Einführung 2 Sätze 3 Beweise 4 direkter Beweis Brückenkurs, 30.09.2016 Seite 2/23 Einführung Die höchste Form des
Brückenkurs Beweise Anja Haußen 30.09.2016 Brückenkurs, 30.09.2016 Seite 1/23 Inhalt 1 Einführung 2 Sätze 3 Beweise 4 direkter Beweis Brückenkurs, 30.09.2016 Seite 2/23 Einführung Die höchste Form des
4. Parallelität ohne Metrik
 4. Parallelität ohne Metrik In der Euklidischen Geometrie wird nicht gemessen. as hat zwei Gründe. Erstens, gab es bei den Griechen noch kein entwickeltes Stellenwertsystem. Zweitens, haben sie ja schon
4. Parallelität ohne Metrik In der Euklidischen Geometrie wird nicht gemessen. as hat zwei Gründe. Erstens, gab es bei den Griechen noch kein entwickeltes Stellenwertsystem. Zweitens, haben sie ja schon
Aufgabe G.1: Definitionen, Begriffsbildungen
 Aufgabe G.1: Definitionen, Begriffsbildungen a) Der Begriff Dreieck sei definiert. Definieren Sie den Begriff Innenwinkel eines Dreiecks. (2 Punkte) b) Definieren Sie den Begriff Inneres eines Winkels
Aufgabe G.1: Definitionen, Begriffsbildungen a) Der Begriff Dreieck sei definiert. Definieren Sie den Begriff Innenwinkel eines Dreiecks. (2 Punkte) b) Definieren Sie den Begriff Inneres eines Winkels
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 24 Unter den drei klassischen Problemen der antiken Mathematik versteht man (1) die Quadratur des Kreises, (2) die Dreiteilung
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 24 Unter den drei klassischen Problemen der antiken Mathematik versteht man (1) die Quadratur des Kreises, (2) die Dreiteilung
(Beispiel eines gleichschenkligen Dreiecks aus Gitterpunkten.)
 Fachbereich Mathematik Tag der Mathematik 12. November 2011 Klassenstufen 9, 10 (Beispiel eines gleichschenkligen Dreiecks aus Gitterpunkten.) Aufgabe 1 (5+5+10 Punkte). Wir betrachten sechzehn Punkte
Fachbereich Mathematik Tag der Mathematik 12. November 2011 Klassenstufen 9, 10 (Beispiel eines gleichschenkligen Dreiecks aus Gitterpunkten.) Aufgabe 1 (5+5+10 Punkte). Wir betrachten sechzehn Punkte
Stufen des Begriffsverständnisses (vgl. van-hiele-schema)
 Stufen des Begriffsverständnisses (vgl. van-hiele-schema) intuitives Begriffsverständnis: Kenntnis einfacher Beispiele, Vergleich auf der Ebene von Formulierungen wie sieht aus wie inhaltliches Begriffsverständnis:
Stufen des Begriffsverständnisses (vgl. van-hiele-schema) intuitives Begriffsverständnis: Kenntnis einfacher Beispiele, Vergleich auf der Ebene von Formulierungen wie sieht aus wie inhaltliches Begriffsverständnis:
4.18 Buch IV der Elemente
 4.18 Buch IV der Elemente Buch IV behandelt die folgenden Konstruktionsaufgaben: Buch IV, Einem Kreis ein Dreieck mit vorgegebenen Winkeln einschreiben. Buch IV, 3 Einem Kreis ein Dreieck mit vorgegebenen
4.18 Buch IV der Elemente Buch IV behandelt die folgenden Konstruktionsaufgaben: Buch IV, Einem Kreis ein Dreieck mit vorgegebenen Winkeln einschreiben. Buch IV, 3 Einem Kreis ein Dreieck mit vorgegebenen
Musterlösung zur 3. Hausaufgabe - Unterrichtsanalyse -
 1) Vorkenntnisse: Musterlösung zur 3. Hausaufgabe - Unterrichtsanalyse - Im Rahmen der aktuellen Einheit wurden die folgenden Themen im Unterricht behandelt. Grundkonstruktionen mit Zirkel und Lineal;
1) Vorkenntnisse: Musterlösung zur 3. Hausaufgabe - Unterrichtsanalyse - Im Rahmen der aktuellen Einheit wurden die folgenden Themen im Unterricht behandelt. Grundkonstruktionen mit Zirkel und Lineal;
Vollständige Induktion
 Kantonsschule Olten Hardwald 4600 Olten Vollständige Induktion Andreas Stoll Andreas Pulfer Erfänzungsfach Anwendungen der Mathematik (2017/18) 1 Beweisen 1.1 Axiome und Prämissen Bei einem Beweis wird
Kantonsschule Olten Hardwald 4600 Olten Vollständige Induktion Andreas Stoll Andreas Pulfer Erfänzungsfach Anwendungen der Mathematik (2017/18) 1 Beweisen 1.1 Axiome und Prämissen Bei einem Beweis wird
1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: m (ausgesprochen: T von t und m)
 Grundwissen Mathematik 7. Klasse 1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: Ttm (, ) = ( t 5+ 6) 20+ m (ausgesprochen: T von t und m) Ein Term besteht aus
Grundwissen Mathematik 7. Klasse 1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: Ttm (, ) = ( t 5+ 6) 20+ m (ausgesprochen: T von t und m) Ein Term besteht aus
Geometrie der Polygone Zirkel und Lineal Markus Wurster 1
 Geometrie der Polygone Teil 5 Zirkel und Lineal Geometrie der Polygone Zirkel und Lineal Markus Wurster 1 Die klassische Methode mit Zirkel und Lineal Wenn wir Geometrie treiben, verwenden wir dazu oft
Geometrie der Polygone Teil 5 Zirkel und Lineal Geometrie der Polygone Zirkel und Lineal Markus Wurster 1 Die klassische Methode mit Zirkel und Lineal Wenn wir Geometrie treiben, verwenden wir dazu oft
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2013/14 Inhalt Übungserklärung* Beweis durch Vollständige Induktion 2
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2013/14 Inhalt Übungserklärung* Beweis durch Vollständige Induktion 2
Examen Kurzfragen (sortiert) VI. Dreiecke. 24. Juni 2014
 Examen Kurzfragen (sortiert) VI. Dreiecke 24. Juni 2014 VI. Dreiecke Frage 1 Wie werden im rechtwinkligen Dreieck die beiden Seiten genannt, die dem rechten Winkel anliegen? VI. Dreiecke Frage 1 Wie werden
Examen Kurzfragen (sortiert) VI. Dreiecke 24. Juni 2014 VI. Dreiecke Frage 1 Wie werden im rechtwinkligen Dreieck die beiden Seiten genannt, die dem rechten Winkel anliegen? VI. Dreiecke Frage 1 Wie werden
Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt.
 M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
