4.3 Unterrichtsmaterialien
|
|
|
- Gretel Fuchs
- vor 8 Jahren
- Abrufe
Transkript
1 4.3 Unterrichtsmaterialien Jonathan Jeschke und Ernst Peller Material 1: Karten zum Ausdrucken und Ausschneiden Eigenschaften von Säugetieren I
2 4 Von r-strategen und K-Strategen sowie schnellen und langsamen Lebenszyklen Eigenschaften von Vögeln II
3 4.3 Unterrichtsmaterialien Eigenschaften von Fischen III
4 4 Von r-strategen und K-Strategen sowie schnellen und langsamen Lebenszyklen Material 2: Das Konzept der r- und K-Strategen Aufgabe 1 Beim Vergleich von Organismen, die in den Tropen leben, mit solchen, die in temperierten Gebieten vorkommen, ist dem Evolutionsbiologen Theodosius Dobzhansky etwas aufgefallen: In den Tropen gibt es relativ stabile Umweltbedingungen und eine große Zahl an Arten in großer Populationsdichte, vermutlich nahe der Tragekapazität K. Dobzhansky nahm an, dass bestimmte Eigenschaften von Arten bei unterschiedlichen Populationsdichten von Vorteil sind. Die Wissenschaftler Robert MacArthur und Edward Osborne Wilson knüpften an diese Annahme an und erweiterten das Konzept von Dobzhansky. Sie behaupteten, dass es für Arten, die eine niedrige Populationsdichte aufweisen, von Vorteil ist, wenn sie eine hohe Wachstumsrate r besitzen. Umgekehrt sollte es für Arten mit einer hohen Populationsdichte (nahe der Tragekapazität K) vorteilhaft sein, wenn der Wert K hoch ist. Arten, die in stark wechselnden Umweltbedingungen leben (deren Individuenzahl beispielsweise häufig durch Katastrophen wie das Austrocknen eines Tümpels verändert wird), weisen so üblicherweise niedrige Populationsdichten auf. Sie sind r-selektiert und werden als r-strategen bezeichnet. Sie zeichnen sich durch eine hohe Wachstumsrate, ein niedriges Fortpflanzungsalter und eine oft nur einmalige hohe Anzahl an Nachkommen aus. Sie sind zudem eher klein und haben eine nur kurze Lebensspanne. Das genaue Gegenteil dieser r-strategen nennt man K-Strategen, die unter stabilen Umweltbedingungen leben und hohe Populationsdichten haben (nahe an K). Sie sollten besonders effizient sein, zum Beispiel bei der Verwertung von Nährstoffen. Nach einer Arbeit des Biologen Eric Pianka aus dem Jahr 1970 sind K-Strategen groß, haben ein hohes Fortpflanzungsalter, weniger (dafür mehrmals) Nachkommen und eine längere Lebensspanne. Eine absolute Einteilung von Lebewesen in diese beiden Kategorien ist nicht möglich. Innerhalb einer Verwandtschaftsgruppe wie den Säugetieren kann man die verschiedenen Arten entlang eines r/k-kontinuums aufreihen. So gehören die Nagetiere (z. B. Hausmaus) eher zu den r-strategen und die Primaten (z. B. Mensch) zu den K-Strategen. Seit den 1980er-Jahren wurde viel Kritik an dem Konzept geäußert und es wird empfohlen, auf die Begriffe r- und K-Selektion zu verzichten. a Fasse die wesentlichen Aussagen des r/k-konzepts tabellarisch zusammen. b Suche nach Widersprüchen beziehungsweise unlogischen Aussagen im r/k-konzept. Gibt es Beispiele von Organismen, die nicht in das Konzept passen? Recherchiere! Aufgabe 2 In einem Biologiebuch wurde die folgende Aussage zur Begründung des Konzepts der r- und K- Strategen gemacht: Die optimale Strategie zum Überleben von Populationen hängt wesentlich von der Konstanz der Lebensbedingungen ab. So beherbergt ein See mit seinen gleichbleibenden Lebensbedingungen überwiegend K-Strategen wie Fische. Eine Pfütze dagegen existiert nur kurze Zeit: Sie wird von r-strategen wie Einzellern und Wasserflöhen besiedelt. IV
5 4.3 Unterrichtsmaterialien Tab. 4.3: Arteigenschaften von Hecht und Wasserfloh Hecht Wasserfloh Fortpflanzungsalter 3 Jahre 1 Woche Zeit zwischen 2 Gelegen 12 Monate 3 Tage Gelegegröße Gewicht, Eier 11 mg 0,01 mg Gewicht, Erwachsene 28 kg 0,5 mg Maximalalter 24 Jahre 3 Monate a Recherchiere, welche Lebewesen es in Pfützen und Seen gibt. b Bewerte die oben gemachte Aussage. Ziehe hierfür auch die Arteigenschaften beispielsweise von Hecht und Wasserfloh heran (Tab. 4.3). Material 3: Korrelation von Eigenschaften Evolutionsbiologen und Ökologen betrachten das r/k-konzept seit den 1980er-Jahren als nicht mehr zeitgemäß. Ein pauschaler Zusammenhang zwischen konstanten Umweltbedingungen, einer großen Populationsdichte und zum Beispiel den Arteigenschaften große Individuen und kleine Nachkommenzahl wie im r/k-konzept gefordert konnte nicht bestätigt werden. Nichtsdestotrotz hat man sehr wohl einen Zusammenhang (beziehungsweise eine Korrelation) zwischen bestimmten Eigenschaften von Arten finden können. So gibt es eine lineare Beziehung (Korrelation) zwischen den Arteigenschaften Maximalalter und Anzahl an Nachkommen. Man darf aber nicht vergessen, dass weitere Faktoren Arteigenschaften wie die Anzahl der Nachkommen beeinflussen. Lebewesen, die beispielsweise Brutpflege betreiben, d. h. sich intensiv um ihre Nachkommen kümmern, können nicht gleichzeitig sehr viele (aber relativ große) Nachkommen versorgen. Tiere, die keine Brutpflege betreiben, können dafür mehr (kleinere) Nachkommen auf einmal hervorbringen, da sie sich nicht um jedes einzelne Individuum kümmern müssen. Aufgabe 3 a Erstelle eine Tabelle, aus der das Maximalalter und die Wurfgröße ausgewählter Säugetierarten ersichtlich sind. Die Datengrundlage findest du in den Karten Eigenschaften von Säugetieren (Material 1). b Zeichne unter Verwendung der Tabelle einen Graphen, der die Abhängigkeit der Wurfgröße (y-achse) vom Maximalalter (x-achse) darstellt. c Beschreibe und interpretiere den Graphen. Aufgabe 4 a Erstelle eine Tabelle, aus der das Maximalalter und die Gelegegröße ausgewählter Fischarten ersichtlich sind. Die Datengrundlage findest du in den Karten Eigenschaften von Fischen (Material 1). b Zeichne unter Verwendung der Tabelle einen Graphen, der die Abhängigkeit der Gelegegröße (y-achse) vom Maximalalter (x-achse) darstellt. V
6 4 Von r-strategen und K-Strategen sowie schnellen und langsamen Lebenszyklen c Beschreibe und interpretiere den Graphen. Hinweis: Eine Besonderheit bei Fischen ist, dass sie im Gegensatz zu Vögeln und Säugetieren mit zunehmendem Alter weiterhin wachsen. d Vergleiche die Ergebnisse bei Fischen mit denen von Säugetieren (Aufgabe 3). Material 4: Schnelle und langsame Lebenszyklen fast/slow-konzept In den späten 1980er-Jahren wurde ein Nachfolgekonzept für das r/k-konzept entwickelt. Es sagt aus, dass sich Arten im Tempo ihrer Lebenszyklen unterscheiden. Lebewesen mancher Arten leben schnell (sie haben eine vergleichsweise kurze Lebensspanne), Lebewesen anderer Arten dagegen leben langsam (sie haben eine vergleichsweise lange Lebensspanne). Die Eigenschaften der Arten (Tab. 4.4) mit schnellem Lebenszyklus ähneln denen von r-strategen und die der Arten mit langsamem Lebenszyklus denen von K-Strategen. Doch im Gegensatz zum r/k-konzept sind die Merkmale beim fast/slow-konzept nicht in Zusammenhang mit Populationsdichte und Stabilität der Umweltbedingungen gebracht. Außerdem sind die Korrelationen genauer untersucht und weniger pauschal: Es gibt unterschiedliche fast/slow-kontinua für unterschiedliche Organismengruppen. Tab. 4.4: Eigenschaften von Arten mit schnellem beziehungsweise langsamem Lebenszyklus, gültig für Säugetiere und Vögel (nach Reynolds 2003 und Jeschke et al. 2008) schneller Lebenszyklus (fast life history) langsamer Lebenszyklus (slow life history) Fortpflanzung beginnt früh beginnt spät Abstände zwischen Geburten kurze Abstände lange Abstände Wurf-/Gelegegröße hohe Wurf-/Gelegegröße niedrige Wurf-/Gelegegröße Körpergröße der Nachkommen Nachkommen sind klein Nachkommen sind groß Körpergröße der Erwachsenen Erwachsene sind klein Erwachsene sind groß Lebensspanne kurz lang Wie im r/k-konzept sind die Merkmale der schnellen beziehungsweise langsamen Arten Extremwerte einer großen Bandbreite an Merkmalen, sodass man viele Arten entlang eines Kontinuums von schnell nach langsam aufreihen kann. Aufgabe 5 Sortiere jeweils die neun Karten mit Säugetieren beziehungsweise Vögeln (Material 1) so, dass du eine Reihe beginnend mit Lebewesen mit schnellem Lebenszyklus mit Übergängen zu Lebewesen mit langsamem Lebenszyklus erhältst. Beachte, dass du hier nur eine Arteigenschaft als Hauptkriterium verwendest. Aufgabe 6 a Erstelle analog zu Aufgabe 5 mithilfe der neun Fischkarten (Material 1) eine Reihe, die ein Kontinuum von schnellen zu langsamen Lebenszyklen darstellt. b Vergleiche die Arteigenschaften deiner Reihe mit den Merkmalen in Tabelle 4.4. Modifiziere die Tabelle entsprechend. VI
4.5 Lösungen zu den Unterrichtsmaterialien
 4.5 Lösungen zu den Unterrichtsmaterialien Material 1: Karten zum Ausdrucken und Ausschneiden Eigenschaften von Säugetieren Jonathan Jeschke und Ernst Peller I 4 Von r-strategen und K-Strategen sowie schnellen
4.5 Lösungen zu den Unterrichtsmaterialien Material 1: Karten zum Ausdrucken und Ausschneiden Eigenschaften von Säugetieren Jonathan Jeschke und Ernst Peller I 4 Von r-strategen und K-Strategen sowie schnellen
Die Ökologie beschäftigt sich mit den Wechselwirkungen zwischen abiotischen und biotischen Faktoren.
 6. Ökologie Die Ökologie beschäftigt sich mit den Wechselwirkungen zwischen abiotischen und biotischen Faktoren. biotische Faktoren Fressfeinde Nahrung (Pflanzen) Artgenossen (Vermehrung) Konkurrenten
6. Ökologie Die Ökologie beschäftigt sich mit den Wechselwirkungen zwischen abiotischen und biotischen Faktoren. biotische Faktoren Fressfeinde Nahrung (Pflanzen) Artgenossen (Vermehrung) Konkurrenten
Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n (2k 1) = n 2.
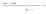 Aufgabe 1. (5 Punkte) Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n k=1 (2k 1) = n 2. Aufgabe 2. (7 Punkte) Gegeben sei das lineare Gleichungssystem x + 2z = 0 ay
Aufgabe 1. (5 Punkte) Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n k=1 (2k 1) = n 2. Aufgabe 2. (7 Punkte) Gegeben sei das lineare Gleichungssystem x + 2z = 0 ay
Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: k = n (n + 1) 2
 Aufgabe 1. (5 Punkte) Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n k = k=1 n (n + 1). 2 Aufgabe 2. (5 Punkte) Bestimmen Sie das folgende Integral mithilfe partieller
Aufgabe 1. (5 Punkte) Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n k = k=1 n (n + 1). 2 Aufgabe 2. (5 Punkte) Bestimmen Sie das folgende Integral mithilfe partieller
Ökologieklausur Zusammenstellung aus möglicherweise3 verschiedenen Klausurvarianten! (Dopplungen wurden weggelassen)
 Ökologieklausur 14.02.2013 Zusammenstellung aus möglicherweise3 verschiedenen Klausurvarianten! (Dopplungen wurden weggelassen) Blaum: 1.Nenne die Ausbreitungsvektoren für invasive Arten (3) 2. Eine in
Ökologieklausur 14.02.2013 Zusammenstellung aus möglicherweise3 verschiedenen Klausurvarianten! (Dopplungen wurden weggelassen) Blaum: 1.Nenne die Ausbreitungsvektoren für invasive Arten (3) 2. Eine in
Buch: Biologie, Wildermuth, S. 54, Objekte: diverse Tiermodelle und Skelette
 TIERE - ANIMALIA Datum Bereich Ziel Sozialform Zeitaufwand Lernorte: Links Material/Hilfsmittel xx. yy. zzzz Schwerpunktbereich Naturwissenschaften: Land und Forstwirtschaft, Grundlagen der Biologie Sie
TIERE - ANIMALIA Datum Bereich Ziel Sozialform Zeitaufwand Lernorte: Links Material/Hilfsmittel xx. yy. zzzz Schwerpunktbereich Naturwissenschaften: Land und Forstwirtschaft, Grundlagen der Biologie Sie
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Die Bevölkerungsentwicklung in Deutschland
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Die Bevölkerungsentwicklung in Deutschland Das komplette Material finden Sie hier: School-Scout.de SCHOOL-SCOUT Statistiken analysieren
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Die Bevölkerungsentwicklung in Deutschland Das komplette Material finden Sie hier: School-Scout.de SCHOOL-SCOUT Statistiken analysieren
Prof. Dr. Elmar Grosse-Klönne Institut für Mathematik
 Prof. Dr. Elmar Grosse-Klönne Institut für Mathematik Lineare Algebra Analytische Geometrie I* Übungsaufgaben, Blatt Musterlösungen Aufgabe. Es seien A, B, C Teilmengen einer Menge X. Zeige: i A B C =
Prof. Dr. Elmar Grosse-Klönne Institut für Mathematik Lineare Algebra Analytische Geometrie I* Übungsaufgaben, Blatt Musterlösungen Aufgabe. Es seien A, B, C Teilmengen einer Menge X. Zeige: i A B C =
Procyte Eucyte Organell Aufgabe Zellorganell Autotrophe Stellen Nährstoffe selbst her Organismen Pflanzen Fotosynthese Bakterien Chemosynthese
 Procyte (die) Eucyte (die) Zellorganell (das; -organellen) Organell Zellkern Ribosomen Mitochondrien Chloroplasten Endoplasmatisches Retikulum (ER) Golgiapparat (Dictyosom) Membran Zellwand Vakuole Aufgabe
Procyte (die) Eucyte (die) Zellorganell (das; -organellen) Organell Zellkern Ribosomen Mitochondrien Chloroplasten Endoplasmatisches Retikulum (ER) Golgiapparat (Dictyosom) Membran Zellwand Vakuole Aufgabe
Variation und Selektion
 2.1 Variation und Selektion: Tiere in ihrer Umwelt (Basiskurs) Variation und Selektion Variation und Selektion 1234 Huhu, hier bin ich wieder euer Urmel Auf unserer spannenden Reise durch das "Abenteuer
2.1 Variation und Selektion: Tiere in ihrer Umwelt (Basiskurs) Variation und Selektion Variation und Selektion 1234 Huhu, hier bin ich wieder euer Urmel Auf unserer spannenden Reise durch das "Abenteuer
Ökologie. Die Lehre vom Haus
 Ökologie Die Lehre vom Haus Übersicht Ökologie 1. Welche Voraussetzungen braucht es für Leben: a. Abiotische Faktoren (Wo findet Leben statt?) b. Biotische Faktoren (Wie beeinflussen sich Lebewesen gegenseitig;
Ökologie Die Lehre vom Haus Übersicht Ökologie 1. Welche Voraussetzungen braucht es für Leben: a. Abiotische Faktoren (Wo findet Leben statt?) b. Biotische Faktoren (Wie beeinflussen sich Lebewesen gegenseitig;
2. Mathematik-Schularbeit für die 6. Klasse Autor: Gottfried Gurtner
 2. Mathematik-Schularbeit für die 6. Klasse Autor: Gottfried Gurtner Arbeitszeit: 100 Minuten Lernstoff: Mathematische Grundkompetenzen: AG2.1, AG2.2, AG2.3 FA1.1, FA1.5, FA1.6, FA1.7, FA1.9 FA2.1, FA2.2,
2. Mathematik-Schularbeit für die 6. Klasse Autor: Gottfried Gurtner Arbeitszeit: 100 Minuten Lernstoff: Mathematische Grundkompetenzen: AG2.1, AG2.2, AG2.3 FA1.1, FA1.5, FA1.6, FA1.7, FA1.9 FA2.1, FA2.2,
Evolutionäre Psychologie
 Evolutionäre Psychologie Von Habib Günesli 15.11.2006 Zum Inhalt Drei Artikel Evolutionsbiologische Mutmaßungen über Vaterschaft Rolle des Vaters für die frühe Entwicklung des Kindes Eltern-Kind-Beziehung
Evolutionäre Psychologie Von Habib Günesli 15.11.2006 Zum Inhalt Drei Artikel Evolutionsbiologische Mutmaßungen über Vaterschaft Rolle des Vaters für die frühe Entwicklung des Kindes Eltern-Kind-Beziehung
3 empfindet Ausbildung als langweilig, bricht Studium mit. Universität Edinburgh. 3 schreibt sich in Cambridge ein, studiert Botanik, schliesst
 Stichwortliste zu Charles Darwin 3 geboren 1809 Shrewsbury, Westengland 3 frühes Interesse an der Natur 3 Vater Arzt schickt Charles zum Medizinstudium an die Universität Edinburgh 3 empfindet Ausbildung
Stichwortliste zu Charles Darwin 3 geboren 1809 Shrewsbury, Westengland 3 frühes Interesse an der Natur 3 Vater Arzt schickt Charles zum Medizinstudium an die Universität Edinburgh 3 empfindet Ausbildung
Wesentliche prozessbezogene Kompetenzen Erkenntnisgewinnung (EG), Kommunikation (KK), Bewertung (BW), den Aufgaben ( 1, 2 ) zugeordnet
 Einführung 1. Allgemeines (Begriffsbestimmung, Mappenführung) Anschauungsmaterial, Buch 2.Arbeitsmethoden in der Biologie 1 Kennzeichen des Lebens Kennzeichen des Lebens (S. 14/15) Die Kennzeichen von
Einführung 1. Allgemeines (Begriffsbestimmung, Mappenführung) Anschauungsmaterial, Buch 2.Arbeitsmethoden in der Biologie 1 Kennzeichen des Lebens Kennzeichen des Lebens (S. 14/15) Die Kennzeichen von
Statistik I für Humanund Sozialwissenschaften
 Statistik I für Humanund Sozialwissenschaften 3. Übung Lösungsvorschlag Gruppenübung G 8 a) Ein Professor möchte herausfinden, welche 5 seiner insgesamt 8 Mitarbeiter zusammen das kreativste Team darstellen.
Statistik I für Humanund Sozialwissenschaften 3. Übung Lösungsvorschlag Gruppenübung G 8 a) Ein Professor möchte herausfinden, welche 5 seiner insgesamt 8 Mitarbeiter zusammen das kreativste Team darstellen.
Populationsstruktur. Wochenstube. Wochenstube. Wochenstube. Individuen. Individuen. Individuen
 Inhalt Evolution und Artenvielfalt Morphologie Ökomorphologie Reproduktionsbiologie Populationsbiologie Ultraschall-Echoorientierung Nahrungsökologie Jagdverhalten Quartierökologie Verhalten Winterschlaf
Inhalt Evolution und Artenvielfalt Morphologie Ökomorphologie Reproduktionsbiologie Populationsbiologie Ultraschall-Echoorientierung Nahrungsökologie Jagdverhalten Quartierökologie Verhalten Winterschlaf
ARBEITSBLATT STUDIUM EINFACHER BEWEGUNGEN
 ARBEITSBLATT STUDIUM EINFACHER BEWEGUNGEN FREIER FALL NAME:.. KLASSE:.. DATUM:. Verwendete die Simulation: http://www.walter-fendt.de/ph14d/wurf.htm Wir untersuchen zum freien Fall folgende Fragestellungen:
ARBEITSBLATT STUDIUM EINFACHER BEWEGUNGEN FREIER FALL NAME:.. KLASSE:.. DATUM:. Verwendete die Simulation: http://www.walter-fendt.de/ph14d/wurf.htm Wir untersuchen zum freien Fall folgende Fragestellungen:
Evolutionspsychologische Emotionstheorien I: Grundlagen
 Evolutionspsychologische Emotionstheorien I: Grundlagen 2. Vererbung 3. natürliche Patricia Buggisch Justus-Liebig-Universität Gießen 2006 2. Vererbung 3. natürliche Einleitung - Biologische Evolution
Evolutionspsychologische Emotionstheorien I: Grundlagen 2. Vererbung 3. natürliche Patricia Buggisch Justus-Liebig-Universität Gießen 2006 2. Vererbung 3. natürliche Einleitung - Biologische Evolution
Ökologie. Die Lehre vom Haus
 Ökologie Die Lehre vom Haus Übersicht Ökologie 1. Welche Voraussetzungen braucht es für Leben: a. Abiotische Faktoren (Wo findet Leben statt?) b. Biotische Faktoren (Wie beeinflussen sich Lebewesen gegenseitig;
Ökologie Die Lehre vom Haus Übersicht Ökologie 1. Welche Voraussetzungen braucht es für Leben: a. Abiotische Faktoren (Wo findet Leben statt?) b. Biotische Faktoren (Wie beeinflussen sich Lebewesen gegenseitig;
Unsere Umwelt ein großes Recyclingsystem
 Unsere Umwelt ein großes Recyclingsystem 1. Der Regenwurm in seinem Lebensraum Im Biologiebuch findest du Informationen über den Regenwurm. Lies den Text durch und betrachte die Abbildung. Regenwürmer
Unsere Umwelt ein großes Recyclingsystem 1. Der Regenwurm in seinem Lebensraum Im Biologiebuch findest du Informationen über den Regenwurm. Lies den Text durch und betrachte die Abbildung. Regenwürmer
Mathem.Grundlagen der Computerlinguistik I, WS 2004/05, H. Leiß 1
 Mathem.Grundlagen der Computerlinguistik I, WS 2004/05, H. Leiß 1 1 Vorbemerkungen Mathematische Begriffe und Argumentationsweisen sind in vielen Fällen nötig, wo man über abstrakte Objekte sprechen und
Mathem.Grundlagen der Computerlinguistik I, WS 2004/05, H. Leiß 1 1 Vorbemerkungen Mathematische Begriffe und Argumentationsweisen sind in vielen Fällen nötig, wo man über abstrakte Objekte sprechen und
Mathematik - 1. Semester. folgenden Zahlenpaare die gegebene Gleichung erfüllen:
 Mathematik -. Semester Wi. Ein Beispiel Lineare Funktionen Gegeben sei die Gleichung y x + 3. Anhand einer Wertetabelle sehen wir; daß die folgenden Zahlenpaare die gegebene Gleichung erfüllen: x 0 6 8
Mathematik -. Semester Wi. Ein Beispiel Lineare Funktionen Gegeben sei die Gleichung y x + 3. Anhand einer Wertetabelle sehen wir; daß die folgenden Zahlenpaare die gegebene Gleichung erfüllen: x 0 6 8
Evolutionsfaktoren. = Gesamtheit der Gene aller Individuen einer Population bleibt nach dem HARDY-WEINBERG-Gesetz unter folgenden Bedingungen
 Evolutionsfaktoren 1 Genpool = Gesamtheit der Gene aller Individuen einer bleibt nach dem HARDY-WEINBERG-Gesetz unter folgenden Bedingungen gleich: keine Mutationen alle Individuen sind für Umweltfaktoren
Evolutionsfaktoren 1 Genpool = Gesamtheit der Gene aller Individuen einer bleibt nach dem HARDY-WEINBERG-Gesetz unter folgenden Bedingungen gleich: keine Mutationen alle Individuen sind für Umweltfaktoren
KORREKTURANLEITUNGEN zum Testheft A2
 Projekt Standardisierte schriftliche Reifeprüfung in Mathematik KORREKTURANLEITUNGEN zum Testheft A2 A201 Aussagen zur quadratischen Gleichung Jede dieser quadratischen Gleichungen hat genau zwei reelle
Projekt Standardisierte schriftliche Reifeprüfung in Mathematik KORREKTURANLEITUNGEN zum Testheft A2 A201 Aussagen zur quadratischen Gleichung Jede dieser quadratischen Gleichungen hat genau zwei reelle
Vorlesung 4: Risikoallokation
 Vorlesung 4: Risikoallokation Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Risikoallokation 1/23 2 / 23 4.1 Einleitung Bisher haben wir uns ausschliesslich
Vorlesung 4: Risikoallokation Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Risikoallokation 1/23 2 / 23 4.1 Einleitung Bisher haben wir uns ausschliesslich
Wettbewerbs- und Symbiose-Modelle Von Jakob Foss
 Wettbewerbs- und Symbiose-Modelle Von Jakob Foss Wettbewerbsmodell Das einfachste Wettbewerbsmodell für zwei Spezies lässt sich aus dem Lotka- Volterra Modell ableiten und sieht folgendermaßen aus: dn1
Wettbewerbs- und Symbiose-Modelle Von Jakob Foss Wettbewerbsmodell Das einfachste Wettbewerbsmodell für zwei Spezies lässt sich aus dem Lotka- Volterra Modell ableiten und sieht folgendermaßen aus: dn1
Kapitel 13. Evolutionäre Spieltheorie. Einleitung. Evolutionäre Biologie. Übersicht 2. Alternative: Biologische Evolutionstheorie
 Übersicht : Evolutionäre Spieltheorie Einleitung Evolutionäre Biologie Evolutionäre Spieltheorie: Idee Gefangenendilemma (Beispiel) Evolutionäre Stabilität Beispiele Wiederholtes Gefangenendilemma Chicken-Spiel
Übersicht : Evolutionäre Spieltheorie Einleitung Evolutionäre Biologie Evolutionäre Spieltheorie: Idee Gefangenendilemma (Beispiel) Evolutionäre Stabilität Beispiele Wiederholtes Gefangenendilemma Chicken-Spiel
Arbeitsblatt: Studium einfacher Bewegungen Freier Fall
 Arbeitsblatt: Studium einfacher Bewegungen Freier Fall NAME:.. Klasse:.. Thema: Freier Fall Öffnen Sie die Simulation mit dem Firefox-Browser: http://www.walter-fendt.de/ph6de/projectile_de.htm Wir untersuchen
Arbeitsblatt: Studium einfacher Bewegungen Freier Fall NAME:.. Klasse:.. Thema: Freier Fall Öffnen Sie die Simulation mit dem Firefox-Browser: http://www.walter-fendt.de/ph6de/projectile_de.htm Wir untersuchen
Kapitel 13. Evolutionäre Spieltheorie. Einleitung. Evolutionäre Biologie. Übersicht 2. Alternative: Biologische Evolutionstheorie
 Übersicht : Evolutionäre Spieltheorie Einleitung Evolutionäre Biologie Evolutionäre Spieltheorie: Idee Gefangenendilemma (Beispiel) Evolutionäre Stabilität Beispiele Wiederholtes Gefangenendilemma Chicken-Spiel
Übersicht : Evolutionäre Spieltheorie Einleitung Evolutionäre Biologie Evolutionäre Spieltheorie: Idee Gefangenendilemma (Beispiel) Evolutionäre Stabilität Beispiele Wiederholtes Gefangenendilemma Chicken-Spiel
5. Weitere wichtige Funktionsklassen
 57 Mathematik für Biologen, Biotechnologen und Biochemiker 5 Weitere wichtige Funktionsklassen 5 Potenzfunktionen und doppelt-logarithmisches Papier Die Funktionen der Form f() = a b (mit reellen Zahlen
57 Mathematik für Biologen, Biotechnologen und Biochemiker 5 Weitere wichtige Funktionsklassen 5 Potenzfunktionen und doppelt-logarithmisches Papier Die Funktionen der Form f() = a b (mit reellen Zahlen
Abiturtraining Physik
 Abiturtraining Physik Aus: Schriftliche Abiturprüfung Physik Sachsen Anhalt 04 Thema G : Auf dem Weg zum Mars Gravitation Die russische Raumsonde Phobos Grunt startete im November 0 zu einem Flug zum Marsmond
Abiturtraining Physik Aus: Schriftliche Abiturprüfung Physik Sachsen Anhalt 04 Thema G : Auf dem Weg zum Mars Gravitation Die russische Raumsonde Phobos Grunt startete im November 0 zu einem Flug zum Marsmond
AF2 Funktionsgraphen interpretieren
 Was kann man aus einem Funktionsgraphen ablesen? Anhand eines Funktionsgraphen kann man viele Informationen ablesen. Der Verlauf des Graphen und besondere Punkte der Funktion werden daran deutlich. Allgemein
Was kann man aus einem Funktionsgraphen ablesen? Anhand eines Funktionsgraphen kann man viele Informationen ablesen. Der Verlauf des Graphen und besondere Punkte der Funktion werden daran deutlich. Allgemein
Beispielaufgaben zum Vorbereitungskurs Mathematik
 Erik Sperfeld, Coronula Grauf & Thomas Massie Beispielaufgaben zum Vorbereitungskurs Mathematik Die folgenden Aufgaben stellen beispielhaft dar, was im Vorbereitungskurs geübt wird. Aufgabe 1 Zwei Bauern
Erik Sperfeld, Coronula Grauf & Thomas Massie Beispielaufgaben zum Vorbereitungskurs Mathematik Die folgenden Aufgaben stellen beispielhaft dar, was im Vorbereitungskurs geübt wird. Aufgabe 1 Zwei Bauern
Kurzinfo. Sachunterricht. Der Igel. Leseverstehen. Klasse 3. Einzel- und Partnerarbeit. Lehrer kopiert: o Material 1 auf Folie o Material 2 und 3
 Kurzinfo Fach Thema Förderbereich Altersstufe Sozialform Sachunterricht Der Igel Leseverstehen Klasse 3 Einzel- und Partnerarbeit Medien Material/ Vorbereitung Lehrer kopiert: o Material 1 auf Folie o
Kurzinfo Fach Thema Förderbereich Altersstufe Sozialform Sachunterricht Der Igel Leseverstehen Klasse 3 Einzel- und Partnerarbeit Medien Material/ Vorbereitung Lehrer kopiert: o Material 1 auf Folie o
Klasse der Säugetiere
 Klasse der Säugetiere Säugetiere gehören zu den Wirbeltieren. Sie besitzen ein Skelett aus Knochen. Säugetiere haben meist 4 Beine. Ihre Körper sind meist von einer Haut mit Haaren bedeckt. Dieses Fell
Klasse der Säugetiere Säugetiere gehören zu den Wirbeltieren. Sie besitzen ein Skelett aus Knochen. Säugetiere haben meist 4 Beine. Ihre Körper sind meist von einer Haut mit Haaren bedeckt. Dieses Fell
Lösungen zur deskriptiven Statistik
 Lösungen zur deskriptiven Statistik Aufgabe 1. Bei einer Stichprobe von n = Studenten wurden folgende jährliche Ausgaben (in e) für Urlaubszwecke ermittelt. 1 58 5 35 6 8 1 6 55 4 47 56 48 1 6 115 8 5
Lösungen zur deskriptiven Statistik Aufgabe 1. Bei einer Stichprobe von n = Studenten wurden folgende jährliche Ausgaben (in e) für Urlaubszwecke ermittelt. 1 58 5 35 6 8 1 6 55 4 47 56 48 1 6 115 8 5
Tutorial: Balken- und Tortendiagramm
 Tutorial: Balken- und Tortendiagramm In der Tabelle ist die Notenverteilung von 510 Teilnehmern an Mathematik Proseminaren angegeben (NA bedeutet einen unbekannten Wert). Der Sachverhalt sollte in zwei
Tutorial: Balken- und Tortendiagramm In der Tabelle ist die Notenverteilung von 510 Teilnehmern an Mathematik Proseminaren angegeben (NA bedeutet einen unbekannten Wert). Der Sachverhalt sollte in zwei
Gymnasium Große Schule, Wolfenbüttel Schulcurriculum Biologie Klasse 5
 1 Gymnasium Große Schule, Wolfenbüttel Schulcurriculum Biologie Klasse 5 Inhalt Wesentliche fachwissenschaftliche Kompetenzen (FW) Vom Wolf zum Dackel (ca. 15-18 Std.) X= in UE Wesentliche prozessbezogene
1 Gymnasium Große Schule, Wolfenbüttel Schulcurriculum Biologie Klasse 5 Inhalt Wesentliche fachwissenschaftliche Kompetenzen (FW) Vom Wolf zum Dackel (ca. 15-18 Std.) X= in UE Wesentliche prozessbezogene
Anforderungsniveau Prüfungsteil Sachgebiet digitales Hilfsmittel erhöht B Lineare Algebra WTR
 Gemeinsame Abituraufgabenpools der Länder Aufgabensammlung Aufgabe für das Fach Mathematik Kurzbeschreibung Anforderungsniveau Prüfungsteil Sachgebiet digitales Hilfsmittel erhöht B Lineare Algebra WTR
Gemeinsame Abituraufgabenpools der Länder Aufgabensammlung Aufgabe für das Fach Mathematik Kurzbeschreibung Anforderungsniveau Prüfungsteil Sachgebiet digitales Hilfsmittel erhöht B Lineare Algebra WTR
Übersicht. Lamarck und Darwin Variation natürliche Selektion, sexuelle, künstliche Gendrift Artbildung adaptive Radiation
 Evolution 1 Übersicht Lamarck und Darwin Variation natürliche Selektion, sexuelle, künstliche Gendrift Artbildung adaptive Radiation 2 Jean Baptiste de LAMARCK... der häufige Gebrauch eines Organs [stärkt]
Evolution 1 Übersicht Lamarck und Darwin Variation natürliche Selektion, sexuelle, künstliche Gendrift Artbildung adaptive Radiation 2 Jean Baptiste de LAMARCK... der häufige Gebrauch eines Organs [stärkt]
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 30.11.2016 5. Teilmengen von R und von R n Der R n ist eine mathematische Verallgemeinerung: R n = {x = (x 1,..., x n ) : x i R} = } R. {{.. R }. n mal Für x R ist x der Abstand zum
Universität Freiburg 30.11.2016 5. Teilmengen von R und von R n Der R n ist eine mathematische Verallgemeinerung: R n = {x = (x 1,..., x n ) : x i R} = } R. {{.. R }. n mal Für x R ist x der Abstand zum
Mechanismen der Evolution. Übersicht. Lamarck und Darwin Variation natürliche Selektion, sexuelle, künstliche Gendrift Artbildung adaptive Radiation
 Mechanismen der Evolution 1 Übersicht Lamarck und Darwin Variation natürliche Selektion, sexuelle, künstliche Gendrift Artbildung adaptive Radiation 2 Jean Baptiste de LAMARCK... der häufige Gebrauch eines
Mechanismen der Evolution 1 Übersicht Lamarck und Darwin Variation natürliche Selektion, sexuelle, künstliche Gendrift Artbildung adaptive Radiation 2 Jean Baptiste de LAMARCK... der häufige Gebrauch eines
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Die Wirbeltierklassen im Vergleich - Material für den Vertretungsunterricht
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Die Wirbeltierklassen im Vergleich - Material für den Vertretungsunterricht Das komplette Material finden Sie hier: School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Die Wirbeltierklassen im Vergleich - Material für den Vertretungsunterricht Das komplette Material finden Sie hier: School-Scout.de
SS 2016 Torsten Schreiber
 SS 01 Torsten Schreiber 15 Ein lineares Gleichungssystem besteht immer aus einer Anzahl an Variablen und Gleichungen. Die Zahlen vor den Variablen werden in der sogenannten zusammen gefasst und die Zahlen
SS 01 Torsten Schreiber 15 Ein lineares Gleichungssystem besteht immer aus einer Anzahl an Variablen und Gleichungen. Die Zahlen vor den Variablen werden in der sogenannten zusammen gefasst und die Zahlen
GRUNDWISSEN BIOLOGIE DER 6. JAHRGANGSSTUFE
 Auszug aus dem Lehrplan: Sie verstehen wichtige Beziehungen zwischen Körperbau und Lebensweise bei Wirbeltieren. Sie können die Verwandtschaft der Wirbeltiere anhand ausgewählter e nachvollziehen. Sie
Auszug aus dem Lehrplan: Sie verstehen wichtige Beziehungen zwischen Körperbau und Lebensweise bei Wirbeltieren. Sie können die Verwandtschaft der Wirbeltiere anhand ausgewählter e nachvollziehen. Sie
Grundwissenkarten Gymnasium Vilsbisburg. 6. Klasse. Natur und Technik. SP Biologie
 Grundwissenkarten Gymnasium Vilsbisburg 6. Klasse Natur und Technik SP Biologie Es sind insgesamt 21 Karten für die 6. Klasse erarbeitet. davon : 21 Karten als ständiges Gundwissen für alle Jahrgangsstufen
Grundwissenkarten Gymnasium Vilsbisburg 6. Klasse Natur und Technik SP Biologie Es sind insgesamt 21 Karten für die 6. Klasse erarbeitet. davon : 21 Karten als ständiges Gundwissen für alle Jahrgangsstufen
Mobiles Lernen am Beispiel des. Sichelschule Balingen. Projekts Fließgewässer- Untersuchung
 Unser Ziel: Sichelschule Balingen Wir wollen den Schülerinnen und Schülern Möglichkeiten anbieten, sich zu verantwortungsvoll handelnden, selbstbewussten und lebenstüchtigen Jugendlichen zu entwickeln
Unser Ziel: Sichelschule Balingen Wir wollen den Schülerinnen und Schülern Möglichkeiten anbieten, sich zu verantwortungsvoll handelnden, selbstbewussten und lebenstüchtigen Jugendlichen zu entwickeln
Übungsblatt 7. Thema: Sortieren, Objektorientierung
 Informatik I WS 05/06 Prof. Dr. W. May Dipl.-Inform. Oliver Fritzen Dipl.-Inform. Christian Kubczak Übungsblatt 7 Ausgegeben am: Abgabe bis: 9.12.2005 6.1.2006 (Theorie) 6.1.2006 (Praktisch) Thema: Sortieren,
Informatik I WS 05/06 Prof. Dr. W. May Dipl.-Inform. Oliver Fritzen Dipl.-Inform. Christian Kubczak Übungsblatt 7 Ausgegeben am: Abgabe bis: 9.12.2005 6.1.2006 (Theorie) 6.1.2006 (Praktisch) Thema: Sortieren,
Standardisierte Vorgehensweisen und Regeln zur Gewährleistung von: Eindeutigkeit Schlussfolgerungen aus empirischen Befunden sind nur dann zwingend
 Standardisierte Vorgehensweisen und Regeln zur Gewährleistung von: Eindeutigkeit Schlussfolgerungen aus empirischen Befunden sind nur dann zwingend oder eindeutig, wenn keine alternativen Interpretationsmöglichkeiten
Standardisierte Vorgehensweisen und Regeln zur Gewährleistung von: Eindeutigkeit Schlussfolgerungen aus empirischen Befunden sind nur dann zwingend oder eindeutig, wenn keine alternativen Interpretationsmöglichkeiten
Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 10 (Kapitel 11)
 Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 10 (Kapitel 11) Hinweis: Dieses Übungsblatt enthält
Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 10 (Kapitel 11) Hinweis: Dieses Übungsblatt enthält
Gymnasium OHZ Schul-KC Mathematik Jahrgang 6 eingeführtes Schulbuch: Lambacher Schweizer 6
 6 Wochen erläutern einfache mathematische Sachverhalte, Begriffe, Regeln, Verfahren und Zusammenhänge mit eigenen Worten und geeigneten Fachbegriffen. begründen durch Ausrechnen. vergleichen verschiedene
6 Wochen erläutern einfache mathematische Sachverhalte, Begriffe, Regeln, Verfahren und Zusammenhänge mit eigenen Worten und geeigneten Fachbegriffen. begründen durch Ausrechnen. vergleichen verschiedene
Problemlösen. Zahl Ebene und Raum Größen Daten und Vorhersagen. Fachsprache, Symbole und Arbeitsmittel anwenden
 Curriculum Mathematik 3. Klasse Aus den Rahmenrichtlinien Die Schülerin, der Schüler kann Vorstellungen von natürlichen, ganzen rationalen Zahlen nutzen mit diesen schriftlich im Kopf rechnen geometrische
Curriculum Mathematik 3. Klasse Aus den Rahmenrichtlinien Die Schülerin, der Schüler kann Vorstellungen von natürlichen, ganzen rationalen Zahlen nutzen mit diesen schriftlich im Kopf rechnen geometrische
Wie kann man große Hunde züchten? Spielregeln zum Simulationsversuch
 Wie kann man große Hunde züchten? Spielregeln zum Simulationsversuch Aufgabe: Spielt das Spiel: Wie kann man große Hunde züchten? Ein Größenmerkmal wird durch einen farbigen Chip simuliert. Es gibt vier
Wie kann man große Hunde züchten? Spielregeln zum Simulationsversuch Aufgabe: Spielt das Spiel: Wie kann man große Hunde züchten? Ein Größenmerkmal wird durch einen farbigen Chip simuliert. Es gibt vier
Folgen und Reihen Folgen
 Folgen und Reihen 30307 Folgen Einstieg: Wir beginnen mit einigen Beispielen für reelle Folgen: (i),, 4, 8, 6, (ii) 4,, 6, 3, 7, (iii) 0,,,, 3,, (iv), 3, 7,,, Aufgabe : Setzt die Zahlenfolgen logisch fort
Folgen und Reihen 30307 Folgen Einstieg: Wir beginnen mit einigen Beispielen für reelle Folgen: (i),, 4, 8, 6, (ii) 4,, 6, 3, 7, (iii) 0,,,, 3,, (iv), 3, 7,,, Aufgabe : Setzt die Zahlenfolgen logisch fort
Zeitliche Zuordnung (Vorschlag) Kompetenzen Wissen.Biologie Seiten
 Vorschlag für das Schulcurriculum bis zum Ende der Klasse 8 Auf der Grundlage von (Die zugeordneten Kompetenzen finden Sie in der Übersicht Kompetenzen ) Zeitliche Zuordnung (Vorschlag) Kompetenzen Wissen.Biologie
Vorschlag für das Schulcurriculum bis zum Ende der Klasse 8 Auf der Grundlage von (Die zugeordneten Kompetenzen finden Sie in der Übersicht Kompetenzen ) Zeitliche Zuordnung (Vorschlag) Kompetenzen Wissen.Biologie
Grundwissenkarten Hans-Carossa-Gymnasium. 8. Klasse. Biologie
 Grundwissenkarten Hans-Carossa-Gymnasium 8. Klasse Biologie Es sind insgesamt 12 Karten für die 8. Klasse erarbeitet. davon : Karten ausschneiden : Es ist auf der linken Blattseite die Vorderseite mit
Grundwissenkarten Hans-Carossa-Gymnasium 8. Klasse Biologie Es sind insgesamt 12 Karten für die 8. Klasse erarbeitet. davon : Karten ausschneiden : Es ist auf der linken Blattseite die Vorderseite mit
Das Wichtigste auf einen Blick... 66
 Inhaltsverzeichnis Bio 5/6 3 Inhaltsverzeichnis 1 Biologie Was ist das?... 8 Kennzeichen des Lebens.... 9 1 Lebendes oder Nichtlebendes?... 10 Arbeitsgebiete und Arbeitsgeräte der Biologen... 11 Tiere
Inhaltsverzeichnis Bio 5/6 3 Inhaltsverzeichnis 1 Biologie Was ist das?... 8 Kennzeichen des Lebens.... 9 1 Lebendes oder Nichtlebendes?... 10 Arbeitsgebiete und Arbeitsgeräte der Biologen... 11 Tiere
Klaus, wie Sie im Vergleich zum Durchschnitt sind
 Kapitel 2 Dieses Kapitel ist ein Auszug aus den 9 Kapiteln Ihres 100-seitigen Persönlichkeits-Gutachtens Klaus, wie Sie im Vergleich zum Durchschnitt sind Einen Vergleich Ihrer Persönlichkeit mit dem Durchschnitt
Kapitel 2 Dieses Kapitel ist ein Auszug aus den 9 Kapiteln Ihres 100-seitigen Persönlichkeits-Gutachtens Klaus, wie Sie im Vergleich zum Durchschnitt sind Einen Vergleich Ihrer Persönlichkeit mit dem Durchschnitt
Expertenpuzzle Quadratische Funktionen
 Phase Aufgaben für die Expertengruppe I Im Folgenden sollen die in IR definierten Funktionen a : x x, b : x,5x, und d: x x untersucht werden. Die Abbildung zeigt den Graphen G a von a. Zeichnet die Graphen
Phase Aufgaben für die Expertengruppe I Im Folgenden sollen die in IR definierten Funktionen a : x x, b : x,5x, und d: x x untersucht werden. Die Abbildung zeigt den Graphen G a von a. Zeichnet die Graphen
Bivariate explorative Datenanalyse in R
 Bivariate explorative Datenanalyse in R Achim Zeileis, Regina Tüchler 2006-10-09 In der LV Statistik 1 haben wir auch den Zusammenhang von 2 Variablen untersucht. Hier werden die dazugehörenden R-Befehle
Bivariate explorative Datenanalyse in R Achim Zeileis, Regina Tüchler 2006-10-09 In der LV Statistik 1 haben wir auch den Zusammenhang von 2 Variablen untersucht. Hier werden die dazugehörenden R-Befehle
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Lernwerkstatt: Mechanik der Bewegungen - Eine Einführung
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lernwerkstatt: Mechanik der Bewegungen - Eine Einführung Das komplette Material finden Sie hier: School-Scout.de SCHOOL-SCOUT Mechanik
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lernwerkstatt: Mechanik der Bewegungen - Eine Einführung Das komplette Material finden Sie hier: School-Scout.de SCHOOL-SCOUT Mechanik
0 [Information] Fibonacci bonacci. Bergstadt-Gymnasium Di Ma/Inf 9 (ht)
![0 [Information] Fibonacci bonacci. Bergstadt-Gymnasium Di Ma/Inf 9 (ht) 0 [Information] Fibonacci bonacci. Bergstadt-Gymnasium Di Ma/Inf 9 (ht)](/thumbs/74/70281495.jpg) 0 [Information] Der italienische Mathematiker (eigentlich Leonardo von Pisa, 1170-1250) stellt in seinem Buch Liber Abaci folgende Aufgabe: Ein Mann hält ein Kaninchenpaar an einem Ort, der gänzlich von
0 [Information] Der italienische Mathematiker (eigentlich Leonardo von Pisa, 1170-1250) stellt in seinem Buch Liber Abaci folgende Aufgabe: Ein Mann hält ein Kaninchenpaar an einem Ort, der gänzlich von
Physikalisches Fortgeschrittenenpraktikum Gammaspektroskopie. Auswertung
 Physikalisches Fortgeschrittenenpraktikum Gammaspektroskopie Auswertung Armin Burgmeier Robert Schittny 1 Energiekalibrierung der Detektoren Zur Energiekalibrierung nahmen wir zunächst die Spektren von
Physikalisches Fortgeschrittenenpraktikum Gammaspektroskopie Auswertung Armin Burgmeier Robert Schittny 1 Energiekalibrierung der Detektoren Zur Energiekalibrierung nahmen wir zunächst die Spektren von
Vorlesung 2: Risikopräferenzen im Zustandsraum
 Vorlesung 2: Risikopräferenzen im Zustandsraum Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie VL 2, FS 12 Risikopräferenzen im Zustandsraum 1/29 2.1 Motivation
Vorlesung 2: Risikopräferenzen im Zustandsraum Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie VL 2, FS 12 Risikopräferenzen im Zustandsraum 1/29 2.1 Motivation
Lernsituation 3.2: Analysis (26 UStd.) Titel: Analysis- Einführung in die Differenzialrechnung
 Bildungsgang: Zweijährige Höhere Berufsfachschule (Höhere Handelsschule) Lernsituation 3.2: Analysis (26 UStd.) Titel: Analysis- Einführung in die Differenzialrechnung Einstiegsszenario 1 Lernergebnis
Bildungsgang: Zweijährige Höhere Berufsfachschule (Höhere Handelsschule) Lernsituation 3.2: Analysis (26 UStd.) Titel: Analysis- Einführung in die Differenzialrechnung Einstiegsszenario 1 Lernergebnis
Inhaltsverzeichnis. Inhaltsverzeichnis
 Inhaltsverzeichnis Inhaltsverzeichnis 1 Beweistechniken 1.1 Prädikatenlogik..................................... 1. Direkter Beweis.................................... 3 1.3 Indirekter Beweis....................................
Inhaltsverzeichnis Inhaltsverzeichnis 1 Beweistechniken 1.1 Prädikatenlogik..................................... 1. Direkter Beweis.................................... 3 1.3 Indirekter Beweis....................................
Arbeitsblatt Rundgang Tropengarten Klasse 7/8
 1 Arbeitsblatt Rundgang Tropengarten Klasse 7/8 Datum: Herzlich willkommen in der Biosphäre Potsdam! Schön, dass du da bist! Auf dem Weg durch die Biosphäre kannst du verschiedene Aufgaben lösen: 1.) Zu
1 Arbeitsblatt Rundgang Tropengarten Klasse 7/8 Datum: Herzlich willkommen in der Biosphäre Potsdam! Schön, dass du da bist! Auf dem Weg durch die Biosphäre kannst du verschiedene Aufgaben lösen: 1.) Zu
Funktionen in der Mathematik
 R. Brinkmann http://brinkmann-du.de Seite 05.0.008 Funktionen in der Mathematik Bei der mathematischen Betrachtung natürlicher, technischer oder auch alltäglicher Vorgänge hängt der Wert einer Größe oft
R. Brinkmann http://brinkmann-du.de Seite 05.0.008 Funktionen in der Mathematik Bei der mathematischen Betrachtung natürlicher, technischer oder auch alltäglicher Vorgänge hängt der Wert einer Größe oft
Mathematik Abivorklausur Probe Wal 2011
 Mathematik Abivorklausur Probe Wal 0 Zugelassene Hilfsmittel: Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit) Mathematische Formelsammlung Wörterbuch zur deutschen Rechtschreibung Aufgabenstellung:
Mathematik Abivorklausur Probe Wal 0 Zugelassene Hilfsmittel: Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit) Mathematische Formelsammlung Wörterbuch zur deutschen Rechtschreibung Aufgabenstellung:
Geschichte und Herkunft
 Geschichte und Herkunft 15 den Menschen auch die anderen Gebiete der Erde besiedelten. So konnte auch klar nachgewiesen werden, dass alle Hunde des amerikanischen Kontinents von den in Europa und Asien
Geschichte und Herkunft 15 den Menschen auch die anderen Gebiete der Erde besiedelten. So konnte auch klar nachgewiesen werden, dass alle Hunde des amerikanischen Kontinents von den in Europa und Asien
Populationspharmakokinetik, Allometrie und Skalierung von Modellparametern. Tillmann Utesch, Axel Rack, U. K., Max von Kleist
 Populationspharmakokinetik, Allometrie und Skalierung von Modellparametern Tillmann Utesch, Axel Rack, U. K., Max von Kleist Übersicht Einleitung Allometrie (Populations-)Pharmakokinetik Zusammenfassung
Populationspharmakokinetik, Allometrie und Skalierung von Modellparametern Tillmann Utesch, Axel Rack, U. K., Max von Kleist Übersicht Einleitung Allometrie (Populations-)Pharmakokinetik Zusammenfassung
Quadratische Gleichungen und Funktionen
 Unterrichtsfach Lehrplan HAK: Mathematik und angewandte Mathematik -- 2. HAK (2. Jahrgang), 3. Semester Kompetenzmodul 3 -- 1. AUL (1. Jahrgang) Lehrplan HLW: Mathematik und angewandte Mathematik -- 3.
Unterrichtsfach Lehrplan HAK: Mathematik und angewandte Mathematik -- 2. HAK (2. Jahrgang), 3. Semester Kompetenzmodul 3 -- 1. AUL (1. Jahrgang) Lehrplan HLW: Mathematik und angewandte Mathematik -- 3.
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg Wahlteil Analysis 2 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com März 2015 1 Aufgabe
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg Wahlteil Analysis 2 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com März 2015 1 Aufgabe
Kapitel 01.01: Einführung in die Biologie
 1 2 Inhalt...1 Inhalt... 2 Was bedeutet Biologie?... 3 Womit beschäftigt sich die Biologie...3 Die Reiche der Biologie... 4 Merkmale des Lebens... 5 Wir betrachten Lebewesen mit dem Mikroskop...6 Mikroskopische
1 2 Inhalt...1 Inhalt... 2 Was bedeutet Biologie?... 3 Womit beschäftigt sich die Biologie...3 Die Reiche der Biologie... 4 Merkmale des Lebens... 5 Wir betrachten Lebewesen mit dem Mikroskop...6 Mikroskopische
2 Funktionen einer Variablen
 2 Funktionen einer Variablen 2.1 Einführende Beispiele Kostenfunktion und Stückkostenfunktion: Das Unternehmen Miel produziert hochwertige Waschmaschinen. Es hat monatliche Fikosten von 170.000. Die sind
2 Funktionen einer Variablen 2.1 Einführende Beispiele Kostenfunktion und Stückkostenfunktion: Das Unternehmen Miel produziert hochwertige Waschmaschinen. Es hat monatliche Fikosten von 170.000. Die sind
KLP Klasse 7. Kap. I. Prozentrechnung. Arg/Komm Problemlösen. Vergleichen und bewerten Darstellungen Nutzen verschiedene Darstellungsformen
 Kap. I Arithmetik Prozentrechnung Umwandlung von Brüchen Dezimalbrüchen Prozentzahlen Vergleichen und bewerten Darstellungen Nutzen verschiedene Darstellungsformen Berechnen von Prozentwert Prozentsatz
Kap. I Arithmetik Prozentrechnung Umwandlung von Brüchen Dezimalbrüchen Prozentzahlen Vergleichen und bewerten Darstellungen Nutzen verschiedene Darstellungsformen Berechnen von Prozentwert Prozentsatz
Einiges zu den Potenzfunktionen. Exponentialfunktionen
 Einiges zu den Potenzfunktionen Es sind zunächst zwei Arten der Potenzfunktionen zu unterscheiden. Erstens die eigentlichen Potenzfunktionen, bei denen die Variable x als Basis von Potenzen vorkommt. Diese
Einiges zu den Potenzfunktionen Es sind zunächst zwei Arten der Potenzfunktionen zu unterscheiden. Erstens die eigentlichen Potenzfunktionen, bei denen die Variable x als Basis von Potenzen vorkommt. Diese
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 05. Dezember 2012 1 Datenpaare Korrelation 2 Lineare Regression Problemstellung Beispiel Bleibelastung 3 Regression
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 05. Dezember 2012 1 Datenpaare Korrelation 2 Lineare Regression Problemstellung Beispiel Bleibelastung 3 Regression
Unterrichtsmaterial. Die Unterrichtssequenz enthält drei verschiedene Teile/ Experimente:
 Unterrichtsmaterial Die Unterrichtssequenz enthält drei verschiedene Teile/ Experimente: I. Mit dem Abkühlungsprozess vertraut werden Idee: Gegebenes Experiment / Beobachtung des Abkühlungsprozesses von
Unterrichtsmaterial Die Unterrichtssequenz enthält drei verschiedene Teile/ Experimente: I. Mit dem Abkühlungsprozess vertraut werden Idee: Gegebenes Experiment / Beobachtung des Abkühlungsprozesses von
Funktionaler Zusammenhang. Lehrplan Realschule
 Funktionaler Bildungsstandards Lehrplan Realschule Die Schülerinnen und Schüler nutzen Funktionen als Mittel zur Beschreibung quantitativer Zusammenhänge, erkennen und beschreiben funktionale Zusammenhänge
Funktionaler Bildungsstandards Lehrplan Realschule Die Schülerinnen und Schüler nutzen Funktionen als Mittel zur Beschreibung quantitativer Zusammenhänge, erkennen und beschreiben funktionale Zusammenhänge
ETWR TEIL B ÜBUNGSBLATT 1 WS14/15
 ETWR TEIL B ÜBUNGSBLATT 1 WS14/15 OTTO-VON-GUERICKE-UNIVERSITÄT MAGDEBURG F A K U L T Ä T F Ü R W I R T S C H A F T S W I S S E N S C H A FT LEHRSTUHL FÜR EMPIRISCHE WIRTSCHAFTSFORSCHUNG & GESUNDHEITSÖKONOMIE,
ETWR TEIL B ÜBUNGSBLATT 1 WS14/15 OTTO-VON-GUERICKE-UNIVERSITÄT MAGDEBURG F A K U L T Ä T F Ü R W I R T S C H A F T S W I S S E N S C H A FT LEHRSTUHL FÜR EMPIRISCHE WIRTSCHAFTSFORSCHUNG & GESUNDHEITSÖKONOMIE,
1. Mathematik-Schularbeit für die 5. Klasse Autor: Gottfried Gurtner
 1. Mathematik-Schularbeit für die 5. Klasse Autor: Gottfried Gurtner Arbeitszeit: 50 Minuten Lernstoff: Mathematische Grundkompetenzen: AG1.1 Wissen über die Zahlenmengen,,, verständig einsetzen können
1. Mathematik-Schularbeit für die 5. Klasse Autor: Gottfried Gurtner Arbeitszeit: 50 Minuten Lernstoff: Mathematische Grundkompetenzen: AG1.1 Wissen über die Zahlenmengen,,, verständig einsetzen können
Ökologie Grundkurs. Unterrichtsvorhaben IV:
 Ökologie Grundkurs Unterrichtsvorhaben IV: Thema/Kontext: Autökologische Untersuchungen Welchen Einfluss haben abiotische Faktoren auf das Vorkommen von Arten? Schwerpunkte der Kompetenzentwicklung: E1
Ökologie Grundkurs Unterrichtsvorhaben IV: Thema/Kontext: Autökologische Untersuchungen Welchen Einfluss haben abiotische Faktoren auf das Vorkommen von Arten? Schwerpunkte der Kompetenzentwicklung: E1
1 Was ist Leben? Kennzeichen der Lebewesen
 1 In diesem Kapitel versuche ich, ein großes Geheimnis zu lüften. Ob es mir gelingt? Wir werden sehen! Leben scheint so selbstverständlich zu sein, so einfach. Du wirst die wichtigsten Kennzeichen der
1 In diesem Kapitel versuche ich, ein großes Geheimnis zu lüften. Ob es mir gelingt? Wir werden sehen! Leben scheint so selbstverständlich zu sein, so einfach. Du wirst die wichtigsten Kennzeichen der
Inhaltsverzeichnis. Haustiere und Nutztiere
 Inhaltsverzeichnis M Aufgaben richtig verstehen 8 M Biologische Prinzipien 10 1 Kennzeichen von Lebewesen 1.1 Biologie ein neues Unterrichtsfach 12 M Mein Biologieheft führen 13 1.2 Lebewesen haben typische
Inhaltsverzeichnis M Aufgaben richtig verstehen 8 M Biologische Prinzipien 10 1 Kennzeichen von Lebewesen 1.1 Biologie ein neues Unterrichtsfach 12 M Mein Biologieheft führen 13 1.2 Lebewesen haben typische
Wir lernen uns kennen
 Erste Wabe im vernetzten Unterricht 1) Die Kriterien des Lebens Wo kommen wir her? 2) Ein Lebewesen meiner Wahl (Plakat) 1) Meine Lebenszeitleiste Wir lernen uns kennen 2) Quellen als Spuren der Vergangenheit
Erste Wabe im vernetzten Unterricht 1) Die Kriterien des Lebens Wo kommen wir her? 2) Ein Lebewesen meiner Wahl (Plakat) 1) Meine Lebenszeitleiste Wir lernen uns kennen 2) Quellen als Spuren der Vergangenheit
AUFGABENSAMMLUNG Lösungen. Laufen: Skelett. Lösungen
 Laufen: Skelett Bei der Fortbewegung spielt das Skelett eine wichtige Rolle. Wirbeltiere zeichnen sich durch ein Innenskelett aus. Beschrifte die Knochen des Hundes. 1 Laufen: Gangarten Die meisten Vierbeiner
Laufen: Skelett Bei der Fortbewegung spielt das Skelett eine wichtige Rolle. Wirbeltiere zeichnen sich durch ein Innenskelett aus. Beschrifte die Knochen des Hundes. 1 Laufen: Gangarten Die meisten Vierbeiner
Aufgabenpaket zum Crashkurs Mathematik
 Wilhelm-Hausenstein-Gymnasium Sprachliches und Naturwissenschaftlich-technologisches Gymnasium Elektrastraße 61 8195 München Telefon (089) 999690 Fa (089) 9996939 Aufgabenpaket zum Crashkurs Mathematik
Wilhelm-Hausenstein-Gymnasium Sprachliches und Naturwissenschaftlich-technologisches Gymnasium Elektrastraße 61 8195 München Telefon (089) 999690 Fa (089) 9996939 Aufgabenpaket zum Crashkurs Mathematik
Kapitel 7. Regression und Korrelation. 7.1 Das Regressionsproblem
 Kapitel 7 Regression und Korrelation Ein Regressionsproblem behandelt die Verteilung einer Variablen, wenn mindestens eine andere gewisse Werte in nicht zufälliger Art annimmt. Ein Korrelationsproblem
Kapitel 7 Regression und Korrelation Ein Regressionsproblem behandelt die Verteilung einer Variablen, wenn mindestens eine andere gewisse Werte in nicht zufälliger Art annimmt. Ein Korrelationsproblem
Kompetenzen Natur und Technik Check S2/S3
 Institut für Bildungsevaluation Assoziiertes Institut der Universität Zürich Kompetenzen Natur und Technik Check S2/S3 Informationen für Lehrpersonen und Eltern 1. Wie sind die Ergebnisse dargestellt?
Institut für Bildungsevaluation Assoziiertes Institut der Universität Zürich Kompetenzen Natur und Technik Check S2/S3 Informationen für Lehrpersonen und Eltern 1. Wie sind die Ergebnisse dargestellt?
violetter Rotkohlsaft mit Wasser Zitronensaft Backpulver Rohrreiniger Entkalker Seife färbt sich violett rot rot blau rot blau grün
 1. Kevin führt im Unterricht einen Versuch mit Rotkohlsaft durch. Dazu gibt er den violetten Rotkohlsaft zu Wasser und zu einigen Haushalts-Chemikalien. Der Rotkohlsaft verändert seine Farbe dabei folgendermaßen:
1. Kevin führt im Unterricht einen Versuch mit Rotkohlsaft durch. Dazu gibt er den violetten Rotkohlsaft zu Wasser und zu einigen Haushalts-Chemikalien. Der Rotkohlsaft verändert seine Farbe dabei folgendermaßen:
Kern- und Schulcurriculum Mathematik Klasse 11/12. Stand Schuljahr 2012/13
 Kern- und Schulcurriculum Mathematik Klasse 11/12 Stand Schuljahr 2012/13 UE 1 Wiederholung Funktionen Änderungsrate Ableitung Ableitung berechnen Ableitungsfunktion Ableitungsregeln für Potenz, Summe
Kern- und Schulcurriculum Mathematik Klasse 11/12 Stand Schuljahr 2012/13 UE 1 Wiederholung Funktionen Änderungsrate Ableitung Ableitung berechnen Ableitungsfunktion Ableitungsregeln für Potenz, Summe
Aufgabe: Laborgeräte II Angepasstheit der Vögel
 Aufgabe: Laborgeräte II Angepasstheit der Vögel Stand: 07.06.2016 Jahrgangsstufe 6 Fach/Fächer Übergreifende Bildungs- und Erziehungsziele Biologie Alltagskompetenz und Lebensökonomie Berufliche Orientierung
Aufgabe: Laborgeräte II Angepasstheit der Vögel Stand: 07.06.2016 Jahrgangsstufe 6 Fach/Fächer Übergreifende Bildungs- und Erziehungsziele Biologie Alltagskompetenz und Lebensökonomie Berufliche Orientierung
Regression und Korrelation
 Kapitel 7 Regression und Korrelation Ein Regressionsproblem behandeltdie VerteilungeinerVariablen, wenn mindestens eine andere gewisse Werte in nicht zufälliger Art annimmt. Ein Korrelationsproblem dagegen
Kapitel 7 Regression und Korrelation Ein Regressionsproblem behandeltdie VerteilungeinerVariablen, wenn mindestens eine andere gewisse Werte in nicht zufälliger Art annimmt. Ein Korrelationsproblem dagegen
