Konstruktionselemente
|
|
|
- Nora Schräder
- vor 9 Jahren
- Abrufe
Transkript
1 Konstruktionselemente Kapitel 14: Getriebe Prof. Dr.-Ing. Andreas Ettemeyer Dipl.-Ing. Otto Olbrich Fachhochschule München Fachbereich 06 Feinwerk- und Mikrotechnik Version 3.02 vom
2 Konstruktionselemente Kapitel 14 - Getriebe Inhalt 14 Getriebe Rad- und Getriebearten Aufgabe eines Zahnradpaares Verzahnungsgesetz Evolventenverzahnung Beschreibung der Zahngeometrie Gegenprofil der Evolvente Bezeichnungen der Stirnradverzahnung Verzahnungseingriff Nullverzahnung Herstellung der Verzahnung Herstellung mit Zahnstangenprofil andere Herstellverfahren Ausführung und Eigenschaften der Evolventenverzahnung Profilverschiebung Prinzip Möglichkeiten durch Profilverschiebung Kenngrößen bei Profilverschiebung Nicht evolvente Verzahnungen Zykloidenverzahnung Kreisbogenverzahnung DIN Triebstockverzahnung Kettenräder Hinweise für die Konstruktion von Zahnradpaaren Beanspruchung von Zahnrädern Biegebeanspruchung des Zahnfußes: Grübchentragfähigkeit: Fresstragfähigkeit Verschleißtragfähigkeit Ettemeyer, Olbrich, Fachhochschule München, V 3.02
3 Konstruktionselemente Kapitel 14 - Getriebe 14 Getriebe 14.1 Rad- und Getriebearten Ein Zahnradpaar besteht immer aus einem treibenden und einem getriebenen Zahnrad. a) Stirnradpaar, geradverzahnt b) Stirnradpaar, schrägverzahnt c) Innenradpaar d) Zahnstangenradpaar e) Kegelradpaar, geradverzahnt f) Kegelradpaar, schrägverzahnt g) Stirnrad- Schraubenräderpaar h) Schneckenradsatz i) Kegel-Schraubräderpaar Weitere Begriffe: - Ritzel oder Kleinrad - Großrad - Treibendes Rad Index a, getriebenes Rad Index b - Getriebezug = Kombination von 2 oder mehr Radpaaren - Getriebe = Baugruppe aus Radpaar(en) und Gehäuse zur Übetragung von Drehmoment und Drehbewegung - Standgetriebe = keine Lageveränderung der Achsen Ettemeyer, Olbrich, Fachhochschule München, V 3.02
4 Konstruktionselemente Kapitel 14 - Getriebe - Umlauf- oder Planetengetriebe siehe Bild Planetengetriebe: a Sonnenb Planetenrad c umlaufender Steg d Hohlrad e Gehäuse Zweistufiger Getriebezug: Zahnverlauf an Stirnrädern: Gerade Stufen Schräg Pfeil Kreisbogen Zahnverlauf an Kegelrädern: Gerade Schräg Spiral Evolventen Kreisbogen Ettemeyer, Olbrich, Fachhochschule München, V 3.02
5 Konstruktionselemente Kapitel 14 - Getriebe 14.2 Aufgabe eines Zahnradpaares Wälzkreis 2 Rad (Großrad) getrieben Wälzachse treibend Wälzkreis 1 Ritzel (Kleinrad) (Im linken Bild ist das Kämmen der Verzahnung der Zahnräder durch das schlupffreie Abrollen auf den Wälzkreisen ersetzt.) Aufgaben sind: 1. Drehmoment wandeln. Die Umfangskraft F u ist für beide Räder gleich. Damit ergibt sich bei der gezeichneten Geometrie: F u r w1 < F u r w2 2. Drehbewegung gleichförmig übertragen. Übersetzung i = ω 1 /ω 2 = konstant (auch innerhalb einer Umdrehung) Abrollen der Zahnräder auf den Wälzkreisen; Berührung der Wälzkreise im Wälzpunkt C. Die Umfangsgeschwindigkeit v ist für beide Räder gleich. Daraus folgt: v = d π n = d π n W W1 1 W2 2 i z = Zähnezahl n d r ω z n d r ω z 1 w2 w2 1 2 = = = = = = 2 w1 w1 2 1 u Ettemeyer, Olbrich, Fachhochschule München, V 3.02
6 Konstruktionselemente Kapitel 14 - Getriebe i > 1 Übersetzung ins Langsame Moment wird vergrößert (außer bei i nahe 1 und schlechtem Wirkungsgrad) i < 1 Übersetzung ins Schnelle Moment wird verkleinert. Die Momentenübersetzung ist: i M M = M 2 1 Bei hohem Wirkungsgrad (geringe Reibung) ist i M fast so groß wie i. Getriebe für Übersetzung und geringe Momente: Zahnräder oft aus Blech oder Kunststoff oft sehr schmal. Kunststoffe wie POM oder PA eignen sich auch zur Übertragung mittelhoher Momente. Getriebe zur Übertragung hoher Momente: Zahnräder aus Stahl, häufig einsatzgehärtet. Ritzel ist etwas breiter als das Rad es trägt immer die gesamte Zahnbreite, auch wenn die Räder infolge von Toleranzen und Spiel seitlich etwas gegeneinander versetzt sind Verzahnungsgesetz Geschwindigkeiten der Berührpunkte B 1 und B 2 zweier Radflanken: Die Zähne gleiten aufeinander Ettemeyer, Olbrich, Fachhochschule München, V 3.02
7 Konstruktionselemente Kapitel 14 - Getriebe Grundlegende Bedingungen bei der Verzahnung: - Berührung der Flankenpunkte B 1 und B 2 - Geschwindigkeitsvektoren stehen senkrecht auf den Radien - Zerlegung der Geschwindigkeit in Normal und Tangentialkomponente auf der Oberfläche - Normalanteil muss bei beiden Rädern gleich groß sein (kein Abheben der Zähne) - Drehgeschwindigkeiten und Übersetzungsverhältnis sind konstant. (i = konst.) Beispiel: willkürlich geformte Zahnflanken: Gewünschte Übersetzung gilt für Wälzpunkt C. Im Beispiel bewegen sich B 1 mit v 1 = ω 1 R 1 bzw. B 2 v = ω R (senkrecht zu den jeweiligen Radien) Bei Zerlegung in Tangential- und Normalenkomponente an den Zahnflanken führt dies zu vn 1 vn2! Bedingung kein Abheben nicht erfüllt. Außerdem ergibt sich in diesem Fall der Wälzpunkt C. Damit wäre das Übersetzungsverhältnis gegenüber dem Wälzpunkt C geändert. Die widerspricht ebenfalls einer Grundforderung der Verzahnung. Daraus folgt: Ettemeyer, Olbrich, Fachhochschule München, V 3.02
8 Konstruktionselemente Kapitel 14 - Getriebe Verzahnungsgesetz: Die Normale im jeweiligen Berührungspunkt (Eingriffspunkt) zweier Zahnflanken muss stets durch den Wälzpunkt C gehen. Ermittlung der Gegenflanke: Unter Anwendung des Verzahnungsgesetzes kann man für eine beliebig gestaltete Flanke die Gegenflanke konstruieren: a) (Willkürlich) gestaltete Flanke F 1 am Rad 1, für die eine Gegenflanke konstruiert werden soll. Voraussetzung: Normalen N zu der Flanke gehen durch den Wälzkreis w 1 und Flanken müssen sich im Wälzpunkt C berühren. b) Beliebiger Punkt B auf der Flanke F 1, daran Tangente und Normale legen, Normale schneidet Wälzkreis in W 1. Dafür zugehörigen Punkt W 2 am Wälzkreis w 2 markieren, so dass der Bogen CW 1 = CW 2. Beim Drehen in Pfeilrichtung bis W 1 und W 2 sich in C treffen. Damit geht Normale N bzw. Strecke n ebenfalls durch C; B 1 ist nach B gewandert. In B berühren sich nun die beiden Flanken: B 1 =B 2 =B; c) Konstruktion von B 2 : Zurückdrehen der beiden Räder um den gleichen Betrag; C wandert von Rad 1 wieder nach W 1 und W 2 von Rad 2, B wandert nach B 1 bzw. B 2. Abstand BC = B 2 W 2 = B 1 W 1 =n; d) Diese Konstruktion wird an vielen Punkten der Flanke durchgeführt und man erhält den jeweiligen Gegenpunkt. Die Verbindungslinie ist die Flanke des Gegenzahns, die das Verzahnungsgesetz erfüllt. g ist die Eingriffslinie (räumlich: Fläche). Sie beschreibt die absolute Bahn des Eingriffspunktes (Berührpunktes). Die Zahnflanken sind die relativen Bahnen des Berührpunktes. Ergebnis: Zu einer gegebenen Zahnflanke gehören immer eine genau definierte Gegenflanke und Eingriffslinie. In der Praxis wählt man die Eingriffslinie vor und bestimmt daraus Flanke und Gegenflanke. Ettemeyer, Olbrich, Fachhochschule München, V 3.02
9 Konstruktionselemente Kapitel 14 - Getriebe 14.4 Evolventenverzahnung Beschreibung der Zahngeometrie Bei einer geraden Eingriffslinie entsteht die Evolventenverzahnung: Tangente Evolvente Normale der Evolvente in Y Zahnflankenform ist Evolvente an den Grundkreis d b Zähne können mit einem einem Werkzeug mit geraden Schneidflanken hergestellt werden Zähne passen zu beliebigen Zähnezahlen des Gegenrades Eingriffslinie ist eine Gerade Konstruktion der Evolvente: (Fadenkonstruktion) Man wickelt von dem Grundkreis einen Faden ab, an dessen Ende sich ein Schreibstift befindet. Hält man den Faden dabei straff gespannt, so beschreibt der Stift eine Evolvente. Mit dem Radius r b des Grundkreises ist die Evolvente eindeutig bestimmt. Die Evolvente ist die Flankenform des Zahnes außerhalb des Grundkreises bei Evolventenverzahnung. Die Flankennormale (= Berührungsnormale) tangiert stets den Grundkreis. Innerhalb des Grundkreises existiert die Evolvente nicht. Evolventenfunktion invα = tanα α (involut α) Gegenprofil der Evolvente Ist wieder eine Evolvente an den Grundkreis des Gegenrades. Jede Evolvente ist nur eine Funktion des ihr zugehörigen Grundkreises, also unabhängig vom Gegenrad. Evolvente als Zahnprofil gibt eine konstante Übersetzung über den gesamten Drehweg. Ettemeyer, Olbrich, Fachhochschule München, V 3.02
10 Konstruktionselemente Kapitel 14 - Getriebe Die Konstanz der Übersetzung bleibt bei der Evolvente auch bei Abweichungen vom theoretischen Achsabstand erhalten. Außer am Wälzpunkt C gleiten die Zahnflanken aufeinander. Gleiten hat den positiven Effekt, dass sich ein Schmierfilm besser ausbildet. Die gestrichelt gezeichnete Fußausrundung innerhalb der Radien r b. wird vom Zahnkopf des Herstellprofils geformt. Hierauf wird später eingegangen. Ettemeyer, Olbrich, Fachhochschule München, V 3.02
11 Konstruktionselemente Kapitel 14 - Getriebe r 1 p e r 2 Die Eingriffsstrecke ist der geometrische Ort aller Berührungspunkte der Zahnflanken von Rad 1 mit Rad 2. Die Profilüberdeckung muss > 1 sein, d.h. bevor ein Zahn außer Eingriff kommt, muss der nachfolgende Zahn eingreifen. Die Eingriffslinie bei Evolventenverzahnung ist eine Gerade Damit ist der Eingriffswinkel α konstant. Profilüberdeckung ε α gα ε α = p e Zwischen Grundkreis und Fußkreis erfolgt kein Eingriff. Ettemeyer, Olbrich, Fachhochschule München, V 3.02
12 Konstruktionselemente Kapitel 14 - Getriebe Bezeichnungen der Stirnradverzahnung Siehe auch Bilder Kap a a d b Achsabstand d, r Teilkreis-, -radius d a, r a Kopfkreis-, -radius d f, r f Fußkreis-, -radius d b, r b Grundkreis-, -radius d w, r w Wälzkreis-, -radius e Lückenweite auf dem Teilkreis g, g α Eingriffsstrecke h Zahnhöhe = h a + h f h a h f i inv m p s x z z min Kopfhöhe von Teilkreis bis Kopfkreis Null-Achsabstand (Summe der Teilkreisradien) Zahnbreite Fußhöhe von Teilkreis bis Fußkreis Übersetzung Evolventenfunktion (sprich involut) Modul Teilung auf dem Teilkreis Zahndicke auf dem Teilkreis Profilverschiebungsfaktor Zähnezahl theoretische Grenzzähnezahl z min praktische Grenzzänezahl A Anfangspunkt des Eingriffs C Wälzpunkt E Endpunkt des Eingriffs F u α α w ε α h a * h f * v Umfangskraft am Teilkreis Eingriffswinkel Betriebseingriffswinkel Profilüberdeckung Zahnkopfhöhenfaktor Zahnfußhöhenfaktor Profilverschiebung in mm, v nicht genormt Die meisten auf den Modul bezogenen Größen werden mit * bezeichnet und Faktor genannt. Z.B. h a * = h a /m (Zahnkopfhöhenfaktor = Zahnkopfhöhe/Modul). Manche auf den Modul bezogenen Größen haben ein eigenes Formelzeichen, z.b. Profilverschiebungsfaktor x. Ettemeyer, Olbrich, Fachhochschule München, V 3.02
13 Verzahnungseingriff Arbeitsflanken (aktive Flanken): hier erfolgt Kraftübertragung (im Bild Rechtsflanken) Rückflanken: keine Kraftübertragung (im Bild Linksflanken)
14 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe 14.5 Nullverzahnung Wichtigste Bestimmungsgrößen Zähnezahl z, Teilkreisdurchmesser d Modul m Teilung p ist die Länge eines Teilkreisbogens zwischen zwei aufeinander folgenden gleichnamigen Flanken (Rechts- oder Linksflanken). Teilkreisumfang U = z p= π d mit z = Zähnezahl, d = Teilkreisdurchmesser p d Modul: m = = [Einheit mm] π z Modul m für Reihe 1 in mm aus DIN 780: Feinwerktechnik: m = 0,05 1 Maschinenbau: m = 1 60 Eingriffwinkel α = 20 (genormt) Grundkreisdurchmesser d = d cosα b
15 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Unterschied Feinwerktechnische Maschinenbau-Verzahnung: Feinwerktechnik Zahnkopfhöhe: h = 1,1 m a ( größere Überdeckung, günstig bei kleinen Zähnezahlen) Maschinenbau: Zahnkopfhöhe: = m ha Fußhöhe h f > m (damit Zahnkopf nicht berührt) (gleich bei Feinwerktechnik und Maschinenbau) Kenngrößen der Null-Verzahnung: Teilkreisdurchmesser d = z m Grundkreisdurchmesser d = d cosα Kopfkreisdurchmesser d = d + 2h Fußkreisdurchmesser d = d 2h Teilung: p = m π Eingriffsteilung p = p cosα = m π cosα Achsabstand: a = r + r = ( z + z ) d b a f e m a f
16 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe 14.6 Herstellung der Verzahnung Herstellung mit Zahnstangenprofil Eine Zahnstange ist im Prinzip ein Zahnrad mit unendlich großem Teilkreis- und Grundkreisdurchmesser. Damit ergeben sich gerade Zahnflanken und 20 Flankenwinkel = Eingriffswinkel. Alle mit so einem Werkzeug hergestellten Räder passen zusammen. Bei der Herstellung ist das Zahnstangenprofil z.b. als Fräser ausgebildet. Die Herstellwälzgerade der Zahnstange wälzt sich dabei auf dem Teilkreis ab. Außerhalb des Grundkreises erzeugt die Zahnstangenflanke eine Evolvente. Innerhalb des Grundkreises erzeugt der Zahnkopf des Herstellprofils die Fußausrundung. Der Bereich der Zahnfußausrundung ist nicht am Eingriff eines Zahnradpaares beteiligt. Er dient als Freiraum für den Zahnkopf des Gegenrades.
17 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Wenn die Zähnezahl mindestens die Grenzzähnezahl bezüglich Unterschnitt ist, schließt die Fußkreiskurve am Grundkreis tangential an die Evolvente an. Unterschreitet die Zähnezahl diese Grenzzähnezahl, dann schließt die Fußkreiskurve etwas außerhalb des Grundkreises mit einem Knick an die Evolvente an. Der Zahnfuß wird auch erheblich geschwächt. Dies bezeichnet man als Unterschnitt. (siehe unterer Teil des Bildes) andere Herstellverfahren Zahnräder aus Stahl weich oder gehärtet werden hauptsächlich durch Wälzfräsen hergestellt. Für hohe Genauigkeiten und nach dem Härten wird geschliffen. Geeignet von 1 Stück bis Großserie. Das Zahnstangenprofil ist wendelförmig auf dem Wälzfräser "aufgewickelt". Der Wälzfräser wird um den Steigungswinkel schräg zur Zahnachse gestellt. Nach einer Fräserumdrehung ist das Zahnstangenprofil um einen Zahn verschoben. Damit muss das Zahnrad während einer Fräserumdrehung um eine Zahnteilung weiter gedreht werden. Die Vorschubrichtung des Fräsers ist in Achsrichtung des Zahnrades. Es wird die ganze Zahnhöhe auf einmal gefräst. Beim Wälzfräsen wird pro Modul nur ein Fräser für alle Zähnezahlen benötigt. Wälzfräsen und für höhere Genauigkeit Wälzschleifen sind die wichtigsten spanenden Herstellverfahren. Wälzfräsen eignet sich ebenso für andere Werkstoffe, z.b. Messing, Aluminium, für Hartgewebe, für Einzelstücke aus Thermoplasten. Wälzschaben verbessert die Oberflächengüte gefräster Räder. Wälzschälen, Wälzhobeln und Wälzstoßen hauptsächlich wo Wälzfräsen wegen der Geometrie nicht möglich ist. Sintern, Strangpressen und Kaltziehen kommt für hohe Stückzahlen und kleine Abmessungen in Frage. Stanzen aus Blech ist billig. Geeignet für niedrige zu übertragende Leistung.. Druckguss für Leichtmetalle und Spritzguss für Kunststoffe liefert hohe Stückzahlen zu niedrigen Kosten bei mittlerer Genauigkeit. Die Tragfähigkeit von Leichtmetall- und Kunststoffzahnrädern ist grob nur 1/10 der von Stahl. Besonders Kunststoffräder ergeben auch in Kombination mit Stahl einen leisen Lauf.
18 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Ausführung und Eigenschaften der Evolventenverzahnung Wenn man immer kleinere Zähnezahlen mit so einem Zahnstangenwerkzeug herstellt, im Beispiel z = 9, wird der Zahn zum Zahnfuß hin immer dünner. Es entsteht Unterschnitt. Unterschnitt sollte normalerweise vermieden werden. Die kleinste Zähnezahl, bei der Unterschnitt gerade noch nicht auftritt, wird mit z min bezeichnet. Auf notwendigerweise ganze Zahlen gerundet, ergeben sich je nach Zahnkopfhöhe des herstellenden Werkzeuges folgende kleinste Grenzzähnezahlen bezüglich Unterschnittfreiheit: * Zahnkopfhöhenfaktor h a theoretische Grenzzähnezahl z min praktische Grenzzähnezahl z' min = 5/6 z min Werte für α = 20 DIN DIN 867 1, Profilverschiebung Prinzip Wenn bei der Herstellung die Zahnstange weiter vom Mittelpunkt weg oder näher zum Mittelpunkt hin gerückt wird, entsteht Profilverschiebung x. Es wälzt sich dann eine Parallele zur Mittellinie auf dem Teilkreis ab. Die Eigenschaften der Verzahnung bleiben erhalten.
19 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Kopfkreis d a und Fußkreis d f werden größer für x > 0 / Kopfkreis d a und Fußkreis d f werden kleiner für x < 0. Teilkreis d und Grundkreis d b ändern sich bei Profilverschiebung nicht. Profilverschiebung v = x m [in mm] Profilverschiebung bis Unterschnittgrenze Profiverschiebung ist eine Maßnahme, um unterschnittfreie Zähne bei kleineren Zähnezahlen als z min zu bekommen. Grenzzähnezahl theoretisch: x= h z * min a zmin z Damit lässt sich Profilverschiebung berechnen, um Unterschnitt gerade zu beseitigen: Für z < z min : z > z min : Die Formel für x ergibt die erforderliche positive Profilverschiebung bis zur Unterschnittsgrenze, wenn z die Zähnezahl ist. Die Formel für x ergibt die größtmögliche negative Profilverschiebung bis Unterschnitt beginnen würde. Ein Rad mit Profilverschiebung wird als V-Rad (V+ oder V-) bezeichnet. Unterschnitt muss vermieden werden, weil Zahnfuß stark geschwächt wird Eingriffsstrecke verkürzt wird. Profilverschiebungsgrenzen Je kleiner die Zähnezahl wird, umso geringer wird die Freiheit für eine Profilverschiebung Bereich wird durch die Grenzkurven für Unterschnitt und zu spitze Zähne begrenzt. Bei negativer Profilverschiebung kommt man an die Unterschnittsgrenze, Bei positiver Profilverschiebung werden die Zähne immer spitzer. In beiden Fällen ergeben sich Festigkeitsprobleme
20 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Möglichkeiten durch Profilverschiebung Positive Profilverschiebung V plus Unterschnitt wird kleiner oder verschwindet. Kleinere Grenzzähnezahl möglich. Zahnfuß wird dicker (größere Zahnfußfestigkeit). Zahnkopf wird spitzer. Größere Krümmungsradien der Flanken bessere Tragfähigkeit. Kopf-/Fußkreis wird größer Zahndicke s > p 2 Negative Profilverschiebung V minus Gefahr von Unterschnitt Zahnfuß wird dünner (geringere Zahnfußfestigkeit). Zahnkopf wird dicker Kopf-/Fußkreis wird kleiner Zahndicke s < p 2 Allgemeine Möglichkeiten durch Profilverschiebung Mit Profilverschiebung kann das Flankenspiel ohne Änderung des Achsabstandes beeinflusst werden Profilverschiebung dient zur Erreichung eines gegebenen Achsabstandes bei gegebener Übersetzung und genormtem Modul. Wegen der breiten Variationsmöglichkeiten mit Hilfe der Profilverschiebung werden überwiegend Zahnräder mit Profilverschiebung hergestellt. Die Wirkungen der Profilverschiebung (außer auf Achsabstand und Flankenspiel) nehmen mit zunehmender Zähnezahl ab und sind bei der Zahnstange Null.
21 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Kenngrößen bei Profilverschiebung Teilkreisdurchmesser d = z m Grundkreisdurchmesser d = d cosα b Kopfkreisdurchmesser a * 2( a) d = d + x+ h m oft mit h = 1 d = d + 2( x+ 1) m * a Fußkreisdurchmesser d = d 2h + 2xm a f f 14.8 Nicht evolvente Verzahnungen Zykloidenverzahnung a) Epizykloide b) Hypozykloide c) Orthozykloide Kreis rollt auf einem anderen Kreis abrollt jeder Punkt des abrollenden Kreises beschreibt eine Zykloide. Der Rollkreis rollt dabei auch innen auf dem Wälzkreis ab. Sowohl Zahnkopf als auch Zahnfuß sind Zykloiden. Eigenschaften: kleinere Mindestzähnezahlen geringere Flächenpressung Herstellwerkzeuge für spanende Herstellung teurer (Hohlflanken) Jede Abweichung vom theoretischen Achsabstand ergibt periodische Übersetzungsschwankungen. Anwendung: Spezialgebiete wie Pumpen- oder Gebläse durch "Zykloidenzahnräder" mit je 2 Zähnen
22 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Kreisbogenverzahnung DIN Die Eigenschaften sind ähnlich wie die der Zykloidenverzahnung Triebstockverzahnung Keine feinwerktechnische Verzahnung. Anwendung bei geringen Drehzahlen der einfachen Herstellbarkeit wegen bei großen Drehkränzen oder Zahnstangenwinden.
23 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Extrem kleine Zähnezahlen des Ritzels Wenn die üblichen Vereinbarungen für die Evolventenverzahnung verlassen werden, und z.b. unterschiedliche Zahnkopfhöhen von Ritzel und Rad eingeführt werden, erreicht man Zähnezahlen bis 3 herunter. Mit versetzten Zahnscheiben oder Schrägverzahnung sind auch wirksame Zähnezahl 1 oder 2 möglich. Mit solchen Getrieben können nur geringe Leistungen übertragen werden Kettenräder Gelenkketten sind für Antriebe sehr verbreitet und es gibt sie in verschiedenen Bauarten. Am meisten verwendet ist die Rollenkette. Durch das Abrollen der Rolle an der Zahnflanke wird der Verschleiß der Kette und des Zahnrades gering gehalten. Eigenschaften von Rollenkettentrieben: Wirkungsgrad 97 bis 99% Hohes übertragbares Moment bei kleinem. Zähnezahlen für Kleinrad 11-25, für Großrad bis etwa 76. große Achsabstände möglich hohe Sicherheit gegen Herausspringen, erspart oft Kettenspanner nahezu konstantes Übersetzungsverhältnis, meist < l% Schwankung Schmierung erforderlich. deutliches Laufgeräusch, steigt mit Umfangsgeschwindigkeit (bis 25 m/s möglich) überproportional. Es gibt auch Zahnketten und Gelenkketten für Antriebe, z.b. für Handhebezeuge.
24 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Zahnriemen (Synchronriemen) Zahnriementriebe ersetzen häufig Kettentriebe, weil sie in vielen Anwendungen überlegene Eigenschaften haben. keine Schmierung leiser Lauf, schwingungsdämpfend geringes Gewicht gute chemische Beständigkeit Lebensdauer oft höher als bei Kette, wenn keine Schmierung möglich ist. Wirkungsgrad ca. 99%. Als Bezugswert für diesen Wirkungsgrad gilt die maximal übertragbare Leistung. Zahnräder aus Al oder Kunststoff möglich bei kleinen Leistungen. konstantes Übersetzungsverhältnis 14.9 Hinweise für die Konstruktion von Zahnradpaaren - Ritzel breiter als das Zahnrad dimensionieren - Überdeckung ausreichend gestalten Maßnahmen zur Minimierung von Laufgeräuschen: - Zähne ballig machen (Eingriffsstoß sanfter machen) - Wahl der Zähnezahlen als Primzahlen oder möglichst keine gemeinsamen Teiler, um periodische Wiederholungen bestimmter Zahnpaarungen zu vermeiden - Anwendung großer Zahnzahlen bei entsprechend kleinen Moduln, um Überdeckung zu vergrößern - Anwendung Schräg- oder Bogenverzahnung (sanfter Eingriffsstoß) - Dämpfende Radwerkstoffe oder Füllen der Radfelgen mit dämpfenden Massen - Versteifen von Getriebegehäusen - Verformungssteife Wellen auswählen - Starres Lagern der Wellen mit kleinstmöglichem Lagerspiel
25 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Materialeinsparungsmöglichkeiten (Risiken beachten) - a) mit abgedrehter Nabe b) Stege c) Bohrungen d) Gussrad mit Scheibensteg e) Aufgepresster Zahnkranz Drehmomentübertragung auf die Welle sicherstellen Beispiel Wellen mit Kunststoffzahnrädern umspritzt: oder Passfedern, Keile, etc. einsetzen Nabe funktionssicher gestalten Zahnrad aus Kunststoff mit Stahlnabe mit eingesetzter Metallbuchse - Verzahnungsqualitäten den Anforderungen anpassen - Schmierung beachten v 1 m/s => Auftragen oder Aufsprühen von Haftschmierstoffen v 4 m/s => Fett-Tauchschmierung v 15 m/s => Öl-Tauchschmierung v > 15 m/s => Öl-Spritzschmierung
26 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Beanspruchung von Zahnrädern Biegebeanspruchung des Zahnfußes: Maximale Beanspruchung im Zahnfuß tritt bei Eingriffsbeginn ein Grübchentragfähigkeit: Hertzsche Pressung: Pittingbildung: Aufgrund der Elastizität des Werkstoffes findet keine Linien- sondern eine Flächenberührung statt. Beim Überschreiten der ertragbaren Hertzschen Pressung bilden sich Grübchen (Pittings). Pittings sind ein Ermüdungsschaden, der frühestens nach Lastwechseln auftritt. Maßnahmen gegen Grübchen hohe Flankenhärte, insbesondere Oberflächenhärtung hohe Profilüberdeckung positive Profilverschiebung bei kleinen Zähnezahlen
27 Feinwerktechnische Konstruktion Kapitel 14 - Getriebe Fresstragfähigkeit Fresserscheinungen (Gallings): : Fressen tritt bei Versagen der Schmierung ein und die Flanken verschweißen durch zu hohen Druck und Temperatur. Es entstehen Narben an den Flanken. Maßnahmen gegen Fressen: Geringe Flankenrauigkeit Einlaufen geschliffener Zahnflanken Härtung EP-Additive zum Öl höhere Ölzähigkeit niedrigere Öltemperatur Kopfrücknahme Verschleißtragfähigkeit Wird durch Gleit- und Verschleißbeanspruchung bestimmt. Bei Misch- oder Trockenreibung tritt Verschleiß auf, bei dem der Werkstoff von den Zahnflanken abgetragen wird. Einlaufverschleiß, oft unterstützt durch niederviskose Einlauföle mit fressverhindernden Zusätzen, ist erwünscht. Damit werden die Rauhigkeit vermindert und kleine Profilabweichungen abgetragen. Zerstörender Verschleiß entsteht bei niedrigen Umfangsgeschwindigkeiten (< 0,5 m/s) oder durch Verunreinigungen des Schmieröls (Abrieb, Staub usw.) Verschleiß (stark übertrieben dargestellt): a) Auskolkung b) Abtrag der gehärteten Randschicht c) Spitzengrenze d) Schwächung des Zahnfußes
Band 4 ZAHNRÄDER QUALITÄTSSICHERUNG. lernen lehren nachschlagen. Rudolf Och
 Band 4 Rudolf Och ZAHNRÄDER QUALITÄTSSICHERUNG lernen lehren nachschlagen Inhalt 1. Zahnradpaar (war OFS19) 5 1.1. Wälzverhalten 5 1.2. Drehzahl, Achsabstand, Profilverschiebung 7 2. Zahnräder, Abmaße
Band 4 Rudolf Och ZAHNRÄDER QUALITÄTSSICHERUNG lernen lehren nachschlagen Inhalt 1. Zahnradpaar (war OFS19) 5 1.1. Wälzverhalten 5 1.2. Drehzahl, Achsabstand, Profilverschiebung 7 2. Zahnräder, Abmaße
Inhaltsverzeichnis.
 Inhaltsverzeichnis 1. Einleitung und Überblick 1 1.1 Zielsetzung 1 1.2 Übertragen der Drehbewegung durch Tangential- und Normalflächenschluß 2 1.3 Aufgaben der Zahnradpaarungen 6 1.4 Einteilung der Zahnradpaarungen
Inhaltsverzeichnis 1. Einleitung und Überblick 1 1.1 Zielsetzung 1 1.2 Übertragen der Drehbewegung durch Tangential- und Normalflächenschluß 2 1.3 Aufgaben der Zahnradpaarungen 6 1.4 Einteilung der Zahnradpaarungen
Zahnräder und Getriebe
 Eigenschaften Zahnradmasse Begriffe, Grössen Übersetzungen Zahnflankenform Unterschneidung und Profilverschiebung Zahnräder und Getriebe Lage der Wellenachse Lage der Zähne Schraubenrad Zahnradarten Kegelrad
Eigenschaften Zahnradmasse Begriffe, Grössen Übersetzungen Zahnflankenform Unterschneidung und Profilverschiebung Zahnräder und Getriebe Lage der Wellenachse Lage der Zähne Schraubenrad Zahnradarten Kegelrad
Eigenschaften. Übersetzungen. Begriffe und Grössen
 Eigenschaften Herstellung Zahnradmasse Zahnräder und Getriebe CVT-Getriebe Sonderfälle Harmonic-Drive-Getriebe Reibradgetriebe Differentialgetriebe Planetengetriebe Schwenkradgetriebe Begriffe, Grössen
Eigenschaften Herstellung Zahnradmasse Zahnräder und Getriebe CVT-Getriebe Sonderfälle Harmonic-Drive-Getriebe Reibradgetriebe Differentialgetriebe Planetengetriebe Schwenkradgetriebe Begriffe, Grössen
21 Grundlagen für Zahnräder und Getriebe
 ahnräder 21 Grundlagen für ahnräder und Getriebe ahnräder übertragen die Drehbewegung von einer Welle auf eine zweite durch Formschluss der im Eingriff befindlichen ähne. Bei verschieden großen ahnrädern
ahnräder 21 Grundlagen für ahnräder und Getriebe ahnräder übertragen die Drehbewegung von einer Welle auf eine zweite durch Formschluss der im Eingriff befindlichen ähne. Bei verschieden großen ahnrädern
Einige Grundlagen der Verzahnungstheorie
 Einige Grundlagen der Verzahnungstheorie 1 Wichtige Kenngrößen Die Relativbewegung zweier Zahnräder entsteht durch das Abrollen der beiden zugrundeliegenden Wälzkreise, aufeinander (Abb. 1). Die Zahnflanken,
Einige Grundlagen der Verzahnungstheorie 1 Wichtige Kenngrößen Die Relativbewegung zweier Zahnräder entsteht durch das Abrollen der beiden zugrundeliegenden Wälzkreise, aufeinander (Abb. 1). Die Zahnflanken,
3 Schrägverzahnte Stirnräder und Stirn-Radpaarungen mit genormten Evolventen-Verzahnungen
 3 Schrägverzahnte Stirnräder und Stirn-Radpaarungen mit genormten Evolventen-Verzahnungen Eine wesentliche Erweiterung der Eigenschuften von Zahnradpaarungen läßt sich durch das Schrägstellen der Zähne
3 Schrägverzahnte Stirnräder und Stirn-Radpaarungen mit genormten Evolventen-Verzahnungen Eine wesentliche Erweiterung der Eigenschuften von Zahnradpaarungen läßt sich durch das Schrägstellen der Zähne
Übersicht Maschinenelemente II
 Maschinenelemente II. BME, GT 3 30.03.2009 1. Folie Übersicht Maschinenelemente II # Vorlesungstermin Thema 1. 10. 02. 2009 Lagerung 2. 17. 02. 2009 Wälzlager und Wälzlagerungen 3. 24. 02. 2009 Wälzlager
Maschinenelemente II. BME, GT 3 30.03.2009 1. Folie Übersicht Maschinenelemente II # Vorlesungstermin Thema 1. 10. 02. 2009 Lagerung 2. 17. 02. 2009 Wälzlager und Wälzlagerungen 3. 24. 02. 2009 Wälzlager
Zahnräder I. Vetr Martin , Bäck Wolfgang , wolfgang Kochbücher für Mechatroniker. 9.
 Zahnräder I Kochbücher für Mechatroniker 9. November 005 Vetr Martin 0355091, [email protected] Bäck Wolfgang 05508, wolfgang [email protected] Zahnräder I Seite 1 1 Mechanik 1.1 Kinematik Die Kinematischen Beziehungen
Zahnräder I Kochbücher für Mechatroniker 9. November 005 Vetr Martin 0355091, [email protected] Bäck Wolfgang 05508, wolfgang [email protected] Zahnräder I Seite 1 1 Mechanik 1.1 Kinematik Die Kinematischen Beziehungen
Stirnzahnräder, gerade verzahnt, Übersicht. Modul Zahnbreite in mm Seite 0,5...3... 199 0,7...6... 200 1,0...9... 201 1,25... 10...
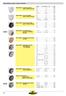 Stirnahnräer, gerae verahnt, Übersicht Stirnahnräer: Aetalhar gespritt gerae verahnt, Stirnahnräer: POM weiß, gefräst gerae verahnt, Stirnahnräer: POM schwar, gefräst gerae verahnt, Stirnahnräer: Kunststoff
Stirnahnräer, gerae verahnt, Übersicht Stirnahnräer: Aetalhar gespritt gerae verahnt, Stirnahnräer: POM weiß, gefräst gerae verahnt, Stirnahnräer: POM schwar, gefräst gerae verahnt, Stirnahnräer: Kunststoff
Stirnräder aus Kunststoff Modul 0,5 geradverzahnt
 Stirnräder aus Kunststoff Modul 0,5 geradverzahnt Werkstoff: Azetalharz (Hostaform C) 48 Zähne- d a d ND B c E b L Bestell- uro / Stück zahl Nr. 12 7,0 6,0 4 2 3 7 390001 12 0,60 13 7,5 6,5 4 2 3 7 390001
Stirnräder aus Kunststoff Modul 0,5 geradverzahnt Werkstoff: Azetalharz (Hostaform C) 48 Zähne- d a d ND B c E b L Bestell- uro / Stück zahl Nr. 12 7,0 6,0 4 2 3 7 390001 12 0,60 13 7,5 6,5 4 2 3 7 390001
- 20.1 - Vordimensionierung (ME-20-01) Aufteilung der Gesamtübersetzung in Stufen i = i I i II...
 - 20.1 - Vorimensionierung (ME-20-01) Gesamtes Getriebe Aufteilung er Gesamtübersetzung in Stufen i = i I i II... Ermittlung er Teilkreisurchmesser er Räer 01, 02,... er einzelnen Stufen I, ΙΙ,... Getriebestufe
- 20.1 - Vorimensionierung (ME-20-01) Gesamtes Getriebe Aufteilung er Gesamtübersetzung in Stufen i = i I i II... Ermittlung er Teilkreisurchmesser er Räer 01, 02,... er einzelnen Stufen I, ΙΙ,... Getriebestufe
Zahnradgetriebe Grundlagen
 Zahnradgetriebe Grundlagen Allgemeines Verzahnungsgesetz Berechnung Herstellung 1 Lernziele Aufgaben von Getrieben Verzahnungsarten kennenlernen Geometrie einer Evolventen- Verzahnung Abmessungen von Verzahnungen
Zahnradgetriebe Grundlagen Allgemeines Verzahnungsgesetz Berechnung Herstellung 1 Lernziele Aufgaben von Getrieben Verzahnungsarten kennenlernen Geometrie einer Evolventen- Verzahnung Abmessungen von Verzahnungen
Inhaltsverzeichnis. 1 Getriebeauslegung Übersetzung Zähnezahlen Zahnradgeometrie Abtriebswelle 5.
 Inhaltsverzeichnis 1 Getriebeauslegung 2 1.1 Übersetzung........................... 2 1.2 Zähnezahlen........................... 3 1.3 Zahnradgeometrie........................ 4 2 Abtriebswelle 5 Literatur
Inhaltsverzeichnis 1 Getriebeauslegung 2 1.1 Übersetzung........................... 2 1.2 Zähnezahlen........................... 3 1.3 Zahnradgeometrie........................ 4 2 Abtriebswelle 5 Literatur
Eigenschaften. Begriffe und Grössen. Übersetzungen
 Eigenschaften Herstellung Zahnradmasse Zahnräder und Getriebe Sonderfälle Harmonic-Drive-Getriebe Reibradgetriebe Differentialgetriebe Planetengetriebe Schwenkradgetriebe Begriffe, Grössen Übersetzungen
Eigenschaften Herstellung Zahnradmasse Zahnräder und Getriebe Sonderfälle Harmonic-Drive-Getriebe Reibradgetriebe Differentialgetriebe Planetengetriebe Schwenkradgetriebe Begriffe, Grössen Übersetzungen
Matura2016-Lösung. Problemstellung 1
 Matura-Lösung Problemstellung. Die Funktion f( = + 9k + müsste bei = den Wert annehmen, also gilt + 9k + = k =. Wir betrachten den Bereich mit positiven Werten. Dann gilt: f ( = 8 + 8 = = ; = Bei liegt
Matura-Lösung Problemstellung. Die Funktion f( = + 9k + müsste bei = den Wert annehmen, also gilt + 9k + = k =. Wir betrachten den Bereich mit positiven Werten. Dann gilt: f ( = 8 + 8 = = ; = Bei liegt
Zahnradtechnik Stirnrad- Evolventenverzahnungen
 Karlheinz Roth Zahnradtechnik Stirnrad- Evolventenverzahnungen Geometrische Grundlagen, Profilverschiebungen, Toleranzen, Festigkeit 2. Auflage Mit 173 Abbildungen Springer Inhaltsverzeichnis 1. Einleitung
Karlheinz Roth Zahnradtechnik Stirnrad- Evolventenverzahnungen Geometrische Grundlagen, Profilverschiebungen, Toleranzen, Festigkeit 2. Auflage Mit 173 Abbildungen Springer Inhaltsverzeichnis 1. Einleitung
Stirnzahnräder: Azetalharz gespritzt gerade verzahnt, mit Nabe. Stirnzahnräder: POM gefräst gerade verzahnt, mit Nabe
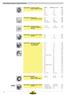 Stirnzahnräder, gerade verzahnt, Übersicht Stirnzahnräder: Azetalharz gespritzt gerade verzahnt, mit Nabe Stirnzahnräder: POM gefräst gerade verzahnt, mit Nabe Modul Zahnbreite in mm Seite 0,5.............3..........
Stirnzahnräder, gerade verzahnt, Übersicht Stirnzahnräder: Azetalharz gespritzt gerade verzahnt, mit Nabe Stirnzahnräder: POM gefräst gerade verzahnt, mit Nabe Modul Zahnbreite in mm Seite 0,5.............3..........
Sehnenlänge. Aufgabenstellung
 Sehnenlänge 1. Drehe die Gerade a um den Punkt A und beachte den grünen Text: a) Wann ist die Gerade eine Sekante, wann ist sie eine Tangente? Wann ist sie weder das eine noch das andere? b) Wie viele
Sehnenlänge 1. Drehe die Gerade a um den Punkt A und beachte den grünen Text: a) Wann ist die Gerade eine Sekante, wann ist sie eine Tangente? Wann ist sie weder das eine noch das andere? b) Wie viele
B Konstruktion. Werktstoff 16MnCr5 (1.7131): Vorgegebene Werte:
 B Konstruktion Tabelle1 Vorgegebene Werte: Drehzahl [1/min] Startleistung [kw] Planetengetriebe Eingang 3520 377 Planetengetriebe Ausgang 565 369 Eingriffswinkel α 20.00 0.3491 Verzahnungsqualität Q 5
B Konstruktion Tabelle1 Vorgegebene Werte: Drehzahl [1/min] Startleistung [kw] Planetengetriebe Eingang 3520 377 Planetengetriebe Ausgang 565 369 Eingriffswinkel α 20.00 0.3491 Verzahnungsqualität Q 5
Kegelschnitte. Evelina Erlacher 13. & 14. M arz 2007
 Workshops zur VO Einfu hrung in das mathematische Arbeiten im SS 2007 Kegelschnitte Evelina Erlacher 13. & 14. M arz 2007 Denken wir uns einen Drehkegel, der nach oben als auch nach unten unbegrenzt ist.
Workshops zur VO Einfu hrung in das mathematische Arbeiten im SS 2007 Kegelschnitte Evelina Erlacher 13. & 14. M arz 2007 Denken wir uns einen Drehkegel, der nach oben als auch nach unten unbegrenzt ist.
Zahnräder. Bewegungen werden durch Formschluss Schlupffrei übertragen Geringer Platzbedarf Höherer Wirkungsgrad
 Zhnräder 1. Vorteile Nchteile Vorteil: Bewegungen werden durch Formschluss Schlupffrei übertrgen Geringer Pltzbedrf Höherer Wirkungsgrd Höhere Kosten Strre Krftübertrgung (entsprechende Kupplungen verwenden)
Zhnräder 1. Vorteile Nchteile Vorteil: Bewegungen werden durch Formschluss Schlupffrei übertrgen Geringer Pltzbedrf Höherer Wirkungsgrd Höhere Kosten Strre Krftübertrgung (entsprechende Kupplungen verwenden)
Maschinenelemente II
 Übungsmitschrift Maschinenelemente II Übung 4 SS 2005 Übung veranstaltet von Dipl.-Ing. Christian Weisel ([email protected]) [zu Übung 4a] Dipl.-Ing. Nick Bretl ([email protected]) [zu Übung 4b] DISCLAIMER
Übungsmitschrift Maschinenelemente II Übung 4 SS 2005 Übung veranstaltet von Dipl.-Ing. Christian Weisel ([email protected]) [zu Übung 4a] Dipl.-Ing. Nick Bretl ([email protected]) [zu Übung 4b] DISCLAIMER
Prof. Dr.-Ing. G. Knauer
 Fachhochschule München Fachbereich 03 Fahrzeugtechnik Prof. Dr.-Ing. G. Knauer Diplomhauptprüfung F a h r z e u g g e t r i e b e WS 02/03 Die Aufgabe umfaßt 7 Angabenblätter und 3 Arbeitsblätter. Überprüfen
Fachhochschule München Fachbereich 03 Fahrzeugtechnik Prof. Dr.-Ing. G. Knauer Diplomhauptprüfung F a h r z e u g g e t r i e b e WS 02/03 Die Aufgabe umfaßt 7 Angabenblätter und 3 Arbeitsblätter. Überprüfen
Gemeinschaftsfachlabor Konstruktions- und Automatisierungstechnik
 Gebäude IB Ebene1 Tel. (0234) 322-4061 Fax (0234) 3214-160 Gemeinschaftsfachlabor Konstruktions- und Automatisierungstechnik Versuch A3 Herstellung und Vermessung eines Evolventenstirnrades Auflage Oktober
Gebäude IB Ebene1 Tel. (0234) 322-4061 Fax (0234) 3214-160 Gemeinschaftsfachlabor Konstruktions- und Automatisierungstechnik Versuch A3 Herstellung und Vermessung eines Evolventenstirnrades Auflage Oktober
Zahnformen in mechanischen Kleinuhren
 Fakultät Maschinenwesen, Institut für Maschinenelemente und Maschinenkonstruktion, Lehrstuhl Maschinenelemente Berechnung, Optimierung und Messung geometrischer und kinematischer Eigenschaften Feinwerktechnische
Fakultät Maschinenwesen, Institut für Maschinenelemente und Maschinenkonstruktion, Lehrstuhl Maschinenelemente Berechnung, Optimierung und Messung geometrischer und kinematischer Eigenschaften Feinwerktechnische
Zahnräder und Getriebe
 Eigenschaften Zahnradmasse Begriffe, Grössen Übersetzungen Zahnflankenform Unterschneidung und Profilverschiebung Lage der Wellenachse Lage der Zähne Herstellung Zahnräder und Getriebe CVT-Getriebe Sonderfälle
Eigenschaften Zahnradmasse Begriffe, Grössen Übersetzungen Zahnflankenform Unterschneidung und Profilverschiebung Lage der Wellenachse Lage der Zähne Herstellung Zahnräder und Getriebe CVT-Getriebe Sonderfälle
Preisliste Zahnräder und Zahnstangen. Kegelräder. Kettenräder mit gehärteten Zähnen. Kettenspannräder. Standard-Kettenräder
 Preisliste 09-08 Zahnräder und Zahnstangen Kegelräder Kettenräder mit gehärteten Zähnen Kettenspannräder Standard-Kettenräder Standard-Kettenradscheiben Taperbuchsen Taper-Kettenräder Stirnräder aus Stahl
Preisliste 09-08 Zahnräder und Zahnstangen Kegelräder Kettenräder mit gehärteten Zähnen Kettenspannräder Standard-Kettenräder Standard-Kettenradscheiben Taperbuchsen Taper-Kettenräder Stirnräder aus Stahl
Aufbau und Wirkungsweise
 1 2 Aufbau und Wirkungsweise Zahnräder übertragen Drehbewegungen von einer Welle auf eine andere durch Formschluss und damit ohne Schlupf. Dabei greifen die Zähne des Antriebs- und des Abtriebsrades ineinander.
1 2 Aufbau und Wirkungsweise Zahnräder übertragen Drehbewegungen von einer Welle auf eine andere durch Formschluss und damit ohne Schlupf. Dabei greifen die Zähne des Antriebs- und des Abtriebsrades ineinander.
Vektoren. Kapitel 3. 3.1 Skalare, Vektoren, Tensoren. 3.2 Vektoren
 Kapitel 3 Vektoren 31 Skalare, Vektoren, Tensoren Viele physikalische Größen lassen sich bei bekannter Maßeinheit durch Angabe ihres Betrages als reelle Zahl vollständig angeben Solche Größen nennt man
Kapitel 3 Vektoren 31 Skalare, Vektoren, Tensoren Viele physikalische Größen lassen sich bei bekannter Maßeinheit durch Angabe ihres Betrages als reelle Zahl vollständig angeben Solche Größen nennt man
GEARPAK Protokoll : Zahnrad Z118
 Seite 1 von 22 Werkstück Zeichnungsnr. Zahnrad Z118 25030_14_01A Qualität ISO 10 Längeneinheit mm Datum Bediener Admin Zähnezahl 118 Schrägungswinkel 0.000 Modul 0.800 Profilversch.-Fakt. -0.250 Zahnradtyp
Seite 1 von 22 Werkstück Zeichnungsnr. Zahnrad Z118 25030_14_01A Qualität ISO 10 Längeneinheit mm Datum Bediener Admin Zähnezahl 118 Schrägungswinkel 0.000 Modul 0.800 Profilversch.-Fakt. -0.250 Zahnradtyp
Berechnung der Eingriffslinie unter Last
 Berechnung der Eingriffslinie unter Last Berechnung der Eingriffslinie unter Last Bei jeder Neukonstruktion gibt es Bauteile, die festigkeitsmässig ausgelegt werden müssen. Hierfür stehen zwei alternative
Berechnung der Eingriffslinie unter Last Berechnung der Eingriffslinie unter Last Bei jeder Neukonstruktion gibt es Bauteile, die festigkeitsmässig ausgelegt werden müssen. Hierfür stehen zwei alternative
1. Mathematikschulaufgabe
 Klasse 8 / I I 1.0 Gib in Mengenschreibweise an: 1.1 Zur Menge M gehören alle Punkte, deren Abstand von parallelen Geraden g und h gleich ist, oder die von einem Punkt A mehr als 4 cm entfernt sind. 1.
Klasse 8 / I I 1.0 Gib in Mengenschreibweise an: 1.1 Zur Menge M gehören alle Punkte, deren Abstand von parallelen Geraden g und h gleich ist, oder die von einem Punkt A mehr als 4 cm entfernt sind. 1.
Herzlich Willkommen zum K2-Tutorium
 Willkommen Herzlich Willkommen zum K2-Tutorium 1. Tutorium SoSe 13 Folie 1 Zeitplan Tutorium Thema 15.04. 22.04. Zahnradgetriebe 29.04. 06.05. Modellbildung Getriebe & Abgabe 1. Testat ANMELDESCHLUSS QISPOS
Willkommen Herzlich Willkommen zum K2-Tutorium 1. Tutorium SoSe 13 Folie 1 Zeitplan Tutorium Thema 15.04. 22.04. Zahnradgetriebe 29.04. 06.05. Modellbildung Getriebe & Abgabe 1. Testat ANMELDESCHLUSS QISPOS
14.5 Wälzlagerstandardisierung
 Hochschule München FK 09 Wirtschaftsingenieurwesen Maschinenlemente II Fettschmierung, häufigste Schmierungsart, da leicht abdichtbar und so häufig Lebensdauerschmierung mit abgedichteten Lagern mit sehr
Hochschule München FK 09 Wirtschaftsingenieurwesen Maschinenlemente II Fettschmierung, häufigste Schmierungsart, da leicht abdichtbar und so häufig Lebensdauerschmierung mit abgedichteten Lagern mit sehr
Vereinfachte Darstellungen in Zeichnungen
 Vereinfachte Darstellungen in Zeichnungen Benennung Beispielzeichnung Anwendung/Bemerkung Geringe Neigungen an Werkstücken Auf die Darstellung geringer Neigungen, z. B. an Schrägen, Kegeln, darf verzichtet
Vereinfachte Darstellungen in Zeichnungen Benennung Beispielzeichnung Anwendung/Bemerkung Geringe Neigungen an Werkstücken Auf die Darstellung geringer Neigungen, z. B. an Schrägen, Kegeln, darf verzichtet
Auslegung einer Getriebestufe Schritt für Schritt
 Auslegung einer Getriebestufe Schritt für Schritt KISSsoft AG Rosengartenstrasse 4 8608 Bubikon Schweiz Tel: +41 55 254 20 50 Fax: +41 55 254 20 51 [email protected] www.kisssoft.ag Folie 1 12.09.2016 WISSEN
Auslegung einer Getriebestufe Schritt für Schritt KISSsoft AG Rosengartenstrasse 4 8608 Bubikon Schweiz Tel: +41 55 254 20 50 Fax: +41 55 254 20 51 [email protected] www.kisssoft.ag Folie 1 12.09.2016 WISSEN
2. Löten 2.1. a) die Lötfläche ist ausreichend, τ a = 1,67 N/mm 2 < τ a zul = 30 N/mm 2 b) Länge 11 mm 2.2. a) 12 kn b) hartgelötet 2.3.
 Lösungen zu Übungen Feinwerktechnische Konstruktion - V.04 Seite 7 2. Löten 2.. a) die Lötfläche ist ausreichend, τ a =,67 N/mm 2 < τ a zul = 30 N/mm 2 b) Länge mm 2.2. a) 2 kn b) hartgelötet 2.3. 2.4.
Lösungen zu Übungen Feinwerktechnische Konstruktion - V.04 Seite 7 2. Löten 2.. a) die Lötfläche ist ausreichend, τ a =,67 N/mm 2 < τ a zul = 30 N/mm 2 b) Länge mm 2.2. a) 2 kn b) hartgelötet 2.3. 2.4.
Lösungen für die Aufgaben zum Zahntrieb
 Lösungen für die Aufgaben zum Zahntrieb 1) Abmessungen am Zahnrad Diese Aufgabe wird nachgereicht: 0 ) Zahnrad gegeben: a) m = 3mm; d = 75mm gesucht: a) z =? Zähnezahl berechnen: z = d m z = 75mm 3mm z
Lösungen für die Aufgaben zum Zahntrieb 1) Abmessungen am Zahnrad Diese Aufgabe wird nachgereicht: 0 ) Zahnrad gegeben: a) m = 3mm; d = 75mm gesucht: a) z =? Zähnezahl berechnen: z = d m z = 75mm 3mm z
Wälzlager. PD M. Ziaei
 Wälzlager Aufgabe und Einteilung Bauformen und Bezeichnungen Lagerauswahl Tragfähigkeit von Wälzlager Reibung und Schmierung Lageranordnung, Gestaltung Quellen: [1] Haberhauer; Bodenstein: Maschinenelemente,
Wälzlager Aufgabe und Einteilung Bauformen und Bezeichnungen Lagerauswahl Tragfähigkeit von Wälzlager Reibung und Schmierung Lageranordnung, Gestaltung Quellen: [1] Haberhauer; Bodenstein: Maschinenelemente,
KISSsoft Tutorial: Stirnrad Festigkeitsrechnung. KISSsoft Tutorial 0010: Stirnrad Festigkeitsrechnung. Aufgabenstellung
 KISSsoft Tutorial: Stirnrad Festigkeitsrechnung KISSsoft Tutorial 0010: Stirnrad Festigkeitsrechnung Für Release 04/2006 Letzte Änderung 05.05.2006 16:45 Aufgabenstellung Aufgabenstellung Es soll ein Stirnradpaar
KISSsoft Tutorial: Stirnrad Festigkeitsrechnung KISSsoft Tutorial 0010: Stirnrad Festigkeitsrechnung Für Release 04/2006 Letzte Änderung 05.05.2006 16:45 Aufgabenstellung Aufgabenstellung Es soll ein Stirnradpaar
Zykloide. Lars Ehrenborg. 15. Januar Definition/Erzeugungsweise 2. 2 Herleitung der Parameterdarstellung 2. 4 Fläche eines Zykloidenbogens 4
 Zykloide Lars Ehrenborg 15. Januar 2017 Inhaltsverzeichnis 1 Definition/Erzeugungsweise 2 2 Herleitung der Parameterdarstellung 2 3 hübsche Eigenschaft 3 4 Fläche eines Zykloidenbogens 4 5 Normale und
Zykloide Lars Ehrenborg 15. Januar 2017 Inhaltsverzeichnis 1 Definition/Erzeugungsweise 2 2 Herleitung der Parameterdarstellung 2 3 hübsche Eigenschaft 3 4 Fläche eines Zykloidenbogens 4 5 Normale und
Flächenpressung. DIMENSIONIEREN I Herbstsemester 2013. 7. Oktober 2013 Paolo Ermanni
 DIMENSIONIEREN I Herbstsemester 2013 Flächenpressung 7. Oktober 2013 Paolo Ermanni Paolo Ermanni, 27.09.13, Seite 1! Lernziele! Laufrad n Spannungszustand an der Kontaktfläche und wesentliche Einflussfaktoren
DIMENSIONIEREN I Herbstsemester 2013 Flächenpressung 7. Oktober 2013 Paolo Ermanni Paolo Ermanni, 27.09.13, Seite 1! Lernziele! Laufrad n Spannungszustand an der Kontaktfläche und wesentliche Einflussfaktoren
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1
 Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
A N T R I E B S T E C H N I K 1. Stirnradverzahnungen. Prof. Dr.-Ing. H. Gruss
 Stirnradverzahnungen Einführung Das Bild zeigt den prinzipiellen Aufbau einer Maschinenanlage. Für die für den Betrieb der Arbeitsmaschine benötigte Energie sind der Wirkort und die spezielle Energieform
Stirnradverzahnungen Einführung Das Bild zeigt den prinzipiellen Aufbau einer Maschinenanlage. Für die für den Betrieb der Arbeitsmaschine benötigte Energie sind der Wirkort und die spezielle Energieform
Köhler/Rögnitz Maschinenteile 2
 Bernd Künne Köhler/Rögnitz Maschinenteile 2 10., neu bearbeitete Auflage Mit 489 Abbildungen sowie zahlreichen Beispielrechnungen STUDIUM VIEWEG+ TEUBNER Inhalt 1 Achsen und Wellen. 1.1 Aufgabe und Einteilungen
Bernd Künne Köhler/Rögnitz Maschinenteile 2 10., neu bearbeitete Auflage Mit 489 Abbildungen sowie zahlreichen Beispielrechnungen STUDIUM VIEWEG+ TEUBNER Inhalt 1 Achsen und Wellen. 1.1 Aufgabe und Einteilungen
am Kopf Auto. Skalierung 600:1. Filter λ c = F α /Q f fα /Q f Hα /Q oben :1. Filter 0.500
 Zahnrad_z40 Werkstück Qualität DIN 6,6,6 Datum 10.10.2015 Teil 1 Längeneinheit mm Bediener Admin Zeichnungsnr. 355522 Zähnezahl 40 Modul 1.250 Schrägungswinkel 0.000 Profilversch.-Fakt. 0.000 Zahnradtyp
Zahnrad_z40 Werkstück Qualität DIN 6,6,6 Datum 10.10.2015 Teil 1 Längeneinheit mm Bediener Admin Zeichnungsnr. 355522 Zähnezahl 40 Modul 1.250 Schrägungswinkel 0.000 Profilversch.-Fakt. 0.000 Zahnradtyp
Prof. Dr.-Ing. G. Knauer
 Fachhochschule München Fachbereich 03 Fahrzeugtechnik Prof. Dr.-Ing. G. Knauer Diplomhauptprüfung F a h r z e u g g e t r i e b e WS 03/04 Die Aufgabe umfasst 7 Angabenblätter und 2 Arbeitsblätter. Überprüfen
Fachhochschule München Fachbereich 03 Fahrzeugtechnik Prof. Dr.-Ing. G. Knauer Diplomhauptprüfung F a h r z e u g g e t r i e b e WS 03/04 Die Aufgabe umfasst 7 Angabenblätter und 2 Arbeitsblätter. Überprüfen
Die Goldene Spirale... 1. Der Goldene Schnitt... 3. Das Goldene Rechteck... 7. Gruppenarbeit... 8
 Die Goldene Spirale Fach: Mathematik Hauptseminar: Spiralen, WS 2005/2006 Dozent: Prof. Dr. R. Deißler Referenten: Judith Stoiber 1389024 Peter Rath 1389345 Handout zum Referat vom 24.01.2006 Inhaltsverzeichnis:
Die Goldene Spirale Fach: Mathematik Hauptseminar: Spiralen, WS 2005/2006 Dozent: Prof. Dr. R. Deißler Referenten: Judith Stoiber 1389024 Peter Rath 1389345 Handout zum Referat vom 24.01.2006 Inhaltsverzeichnis:
4 Reihen und Finanzmathematik
 4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei
4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei
ZAHNRADGENERATOR. Dokumentation über den Zahnradgenerator 5. MÄRZ 2014
 ZAHNRADGENERATOR Dokumentation über den Zahnradgenerator 5. MÄRZ 2014 MEGACAD CENTER (SCHWEIZ) GMBH Chlupfwiesstrasse 31, 8165 Oberweningen Telefon: 044 885 72 33 E-Mail: [email protected] 1 RECHTLICHER
ZAHNRADGENERATOR Dokumentation über den Zahnradgenerator 5. MÄRZ 2014 MEGACAD CENTER (SCHWEIZ) GMBH Chlupfwiesstrasse 31, 8165 Oberweningen Telefon: 044 885 72 33 E-Mail: [email protected] 1 RECHTLICHER
Inhalt.
 Inhalt 1 Achsen und Wellen (Pokorny) 1.1 Aufgabe und Einteilung 11 1.2 Entwicklung des Rechnungsganges für Achsen und Wellen 13 1.2.1 Achsen 13 1.2.2 Wellen 21 1.3 Gestalten und Fertigen 50 1.4 Sonderausführungen
Inhalt 1 Achsen und Wellen (Pokorny) 1.1 Aufgabe und Einteilung 11 1.2 Entwicklung des Rechnungsganges für Achsen und Wellen 13 1.2.1 Achsen 13 1.2.2 Wellen 21 1.3 Gestalten und Fertigen 50 1.4 Sonderausführungen
Horst-W. Grollius. für Maschinenbauer. Technisches Zeichnen. 2., aktualisierte Auflage
 Horst-W. Grollius Technisches Zeichnen für Maschinenbauer 2., aktualisierte Auflage 4.2 Darstellung mittels Schnitten 19 4.2 Darstellung mittels Schnitten 4.2.1 Allgemeines Mithilfe von Schnitten ist es
Horst-W. Grollius Technisches Zeichnen für Maschinenbauer 2., aktualisierte Auflage 4.2 Darstellung mittels Schnitten 19 4.2 Darstellung mittels Schnitten 4.2.1 Allgemeines Mithilfe von Schnitten ist es
Zeichnenkunde mit Problemen
 Zeichnenkunde mit Problemen Die Tipps&Tricks dieses Monats beschäftigen sich mit kleinen Problemen, die bei Konstruktionsarbeiten immer wieder auftauchen. Zunächst soll, wie im Bild rechts dargestellt,
Zeichnenkunde mit Problemen Die Tipps&Tricks dieses Monats beschäftigen sich mit kleinen Problemen, die bei Konstruktionsarbeiten immer wieder auftauchen. Zunächst soll, wie im Bild rechts dargestellt,
V 048. Kegelräder. Lieferung. Bearbeitung, Toleranzen. Kleine Einbau-Anleitung. Übertragbare Leistung. Weiterbearbeitung
 Bearbeitung, Toleranzen Die hier aufgeführten sind allseitig bearbeitet. Die Verzahnung wird im Abwälzverfahren mit balligtragenden Flanken erzeugt. Verzahnungsqualität 8 fs [DIN 3967]. Diese Verzahnungsart
Bearbeitung, Toleranzen Die hier aufgeführten sind allseitig bearbeitet. Die Verzahnung wird im Abwälzverfahren mit balligtragenden Flanken erzeugt. Verzahnungsqualität 8 fs [DIN 3967]. Diese Verzahnungsart
Institut für Mathematik Geometrie und Lineare Algebra J. Schönenberger-Deuel
 Lösungen Übung 7 Aufgabe 1. Skizze (mit zusätzlichen Punkten): Die Figur F wird begrenzt durch die Strecken AB und BC und den Kreisbogen CA auf l. Wir werden die Bilder von AB, BC und CA unter der Inversion
Lösungen Übung 7 Aufgabe 1. Skizze (mit zusätzlichen Punkten): Die Figur F wird begrenzt durch die Strecken AB und BC und den Kreisbogen CA auf l. Wir werden die Bilder von AB, BC und CA unter der Inversion
Papierfalten und Algebra
 Arbeitsblätter zum Thema Papierfalten und Algebra en Robert Geretschläger Graz, Österreich 009 Blatt 1 Lösen quadratischer Gleichungen mit Zirkel und Lineal AUFGABE 1 Zeige, dass die x-koordinaten der
Arbeitsblätter zum Thema Papierfalten und Algebra en Robert Geretschläger Graz, Österreich 009 Blatt 1 Lösen quadratischer Gleichungen mit Zirkel und Lineal AUFGABE 1 Zeige, dass die x-koordinaten der
1. Zykloide. 2. Rollkurven. 3. Tangenten der Zykloide. 4. Bogenlänge der Zykloide. 5. Bogenelement. 6. Zykloidenbogen
 . Zykloide. Rollkurven 3. Tangenten der Zykloide 4. Bogenlänge der Zykloide 5. Bogenelement 6. Zykloidenbogen 7. Krümmungskreisradius der Zykloide 8. Natürliche Gleichung der Zykloide 9. Die natürliche
. Zykloide. Rollkurven 3. Tangenten der Zykloide 4. Bogenlänge der Zykloide 5. Bogenelement 6. Zykloidenbogen 7. Krümmungskreisradius der Zykloide 8. Natürliche Gleichung der Zykloide 9. Die natürliche
Grundlagen der Geometrie
 Grundlagen der Geometrie Vorlesungsausarbeitung zum WS 2010/11 von Prof. Dr. K. Fritzsche ii Inhalt 0 Grundlagen der Schulgeometrie 1 I Die Elemente : Inzidenz und Anordnung 9 1. Die deduktive Methode
Grundlagen der Geometrie Vorlesungsausarbeitung zum WS 2010/11 von Prof. Dr. K. Fritzsche ii Inhalt 0 Grundlagen der Schulgeometrie 1 I Die Elemente : Inzidenz und Anordnung 9 1. Die deduktive Methode
Fertigungstechnik Technische Kommunikation - Technisches Zeichnen
 Eckleinjarten 13a. 7580 Bremerhaven 0471 3416 [email protected] Fertigungstechnik Technische Kommunikation - Technisches Zeichnen 11 Projektionszeichnen 11. Körperschnitte und Abwicklungen 11..4 Kegelige
Eckleinjarten 13a. 7580 Bremerhaven 0471 3416 [email protected] Fertigungstechnik Technische Kommunikation - Technisches Zeichnen 11 Projektionszeichnen 11. Körperschnitte und Abwicklungen 11..4 Kegelige
HAW Hamburg. Fakultät Technik und Informatik. Department Maschinenbau und Produktion. Praktikum - Konstruktion C
 MUT HAW Hamburg Fakultät Technik und Informatik Department Maschinenbau und Produktion Labor für Maschinenelemente und Tribologie W 17 Prof. Dr.-Ing. Andreas Meyer-Eschenbach Dipl.-Ing. Niels Eiben Dipl.-Ing.
MUT HAW Hamburg Fakultät Technik und Informatik Department Maschinenbau und Produktion Labor für Maschinenelemente und Tribologie W 17 Prof. Dr.-Ing. Andreas Meyer-Eschenbach Dipl.-Ing. Niels Eiben Dipl.-Ing.
Fragebogen Kunststoffzahnräder:
 Wolf Kunststoff-Gleitlager GmbH Heisenbergstr. 63-65 Industriegebiet II 50169 Kerpen - Türnich Deutschland Telefon: +49 2237 9749-0 Telefax: +49 2237 9749-20 Email: [email protected] Internet: www.zedex.de
Wolf Kunststoff-Gleitlager GmbH Heisenbergstr. 63-65 Industriegebiet II 50169 Kerpen - Türnich Deutschland Telefon: +49 2237 9749-0 Telefax: +49 2237 9749-20 Email: [email protected] Internet: www.zedex.de
Funktionen in zwei Variablen
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Funktionen in zwei Variablen Literatur: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band 1,
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Funktionen in zwei Variablen Literatur: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band 1,
KUM Workshops Werkzeuge für Stirnräder. Herstellung von Stirnrädern mit Protuberanz. Wissen teilen
 KUM Workshops 2018 Werkzeuge für Stirnräder Herstellung von Stirnrädern mit Protuberanz KISSsoft AG T. +41 55 254 20 50 A Gleason Company F. +41 55 254 20 51 Rosengartenstr. 4, 8608 Bubikon [email protected]
KUM Workshops 2018 Werkzeuge für Stirnräder Herstellung von Stirnrädern mit Protuberanz KISSsoft AG T. +41 55 254 20 50 A Gleason Company F. +41 55 254 20 51 Rosengartenstr. 4, 8608 Bubikon [email protected]
12 Zusammenfassung. Zusammenfassung 207
 Zusammenfassung 207 12 Zusammenfassung Die Arbeit liefert einen Beitrag zur Ermittlung der hydraulischen Verluste von Stirnradverzahnungen. Insbesondere wurde der Einfluss des Flanken- und des Kopfspieles
Zusammenfassung 207 12 Zusammenfassung Die Arbeit liefert einen Beitrag zur Ermittlung der hydraulischen Verluste von Stirnradverzahnungen. Insbesondere wurde der Einfluss des Flanken- und des Kopfspieles
Mit eckigen Rädern fahren
 Mit eckigen Rädern fahren Für Spielfreudige und mathematisch Interessierte Mit eckigen Rädern fahren: Das klingt reichlich unwahrscheinlich, aber möglich ist es. Zugegeben: Die Idee ist etwas wunderlich
Mit eckigen Rädern fahren Für Spielfreudige und mathematisch Interessierte Mit eckigen Rädern fahren: Das klingt reichlich unwahrscheinlich, aber möglich ist es. Zugegeben: Die Idee ist etwas wunderlich
68 by ZIMM Austria 2010
 68 by ZIMM Austria 010 by ZIMM Austria 010 69 Verzahnungstechnik Allgemeine Grundlagen für Schneckenradsätze Allgemeine Beschreibungen: Zur rechtwinkligen Leistungsübertragung bei gleichzeitigem Höhenversatz
68 by ZIMM Austria 010 by ZIMM Austria 010 69 Verzahnungstechnik Allgemeine Grundlagen für Schneckenradsätze Allgemeine Beschreibungen: Zur rechtwinkligen Leistungsübertragung bei gleichzeitigem Höhenversatz
Kö h I e r/rög n i tz Maschinenteile 2
 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Bernd Künne Kö h I e r/rög n i tz Maschinenteile 2 9., überarbeitete
2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Bernd Künne Kö h I e r/rög n i tz Maschinenteile 2 9., überarbeitete
Um vorerst bei den geometrischen Aufgaben zu bleiben, stelle dir folgendes Problem vor:
 Erkläre bitte Extremwertaufgaben... Extremwertaufgaben Sobald man verstanden hat, was ein Extremwert einer Funktion ist (ein lokales Maximum oder Minimum) stellt sich die Frage Und was mach ich damit??.
Erkläre bitte Extremwertaufgaben... Extremwertaufgaben Sobald man verstanden hat, was ein Extremwert einer Funktion ist (ein lokales Maximum oder Minimum) stellt sich die Frage Und was mach ich damit??.
HAW Hamburg. Fakultät Technik und Informatik. Department Maschinenbau und Produktion. Praktikum - Konstruktion 4. Versuch M4
 MUT HAW Hamburg Fakultät Technik und Informatik Department Maschinenbau und Produktion Labor für Maschinenelemente und Tribologie W 16 Prof. Dr.-Ing. Frank Helmut Schäfer Dipl.-Ing. Niels Eiben (Autor)
MUT HAW Hamburg Fakultät Technik und Informatik Department Maschinenbau und Produktion Labor für Maschinenelemente und Tribologie W 16 Prof. Dr.-Ing. Frank Helmut Schäfer Dipl.-Ing. Niels Eiben (Autor)
Handout 3. Grundlegende Befehle und Konstruktionen (Modi) von Cinderella
 Handout 3 Grundlegende Befehle und Konstruktionen (Modi) von Cinderella In dieser Sitzung erfahren Sie mehr über: Grundlegende Befehle von Cinderella Grundlegende Konstruktionen (Modi) von Cinderella Grundlegende
Handout 3 Grundlegende Befehle und Konstruktionen (Modi) von Cinderella In dieser Sitzung erfahren Sie mehr über: Grundlegende Befehle von Cinderella Grundlegende Konstruktionen (Modi) von Cinderella Grundlegende
Ernst Wamer. Das Berechnen von Zahnradern und Getriebe-Verzahnungen Springer Basel A G
 Ernst Wamer Das Berechnen von Zahnradern und Getriebe-Verzahnungen 1981 Springer Basel A G «technica»-reihe Nr. 22 Sonderdruck aus «technica», Nummern 19/1979, 24/1979, 1/1980, 5/1980, 8/1980, 11/1980,
Ernst Wamer Das Berechnen von Zahnradern und Getriebe-Verzahnungen 1981 Springer Basel A G «technica»-reihe Nr. 22 Sonderdruck aus «technica», Nummern 19/1979, 24/1979, 1/1980, 5/1980, 8/1980, 11/1980,
Beschreibung der Anwendung: Jetziger Werkstoff: Jahresbedarf: Aktueller Preis: Warum möchten Sie Kunststoff einsetzen?
 Fragebogen Kunststoffzahnräder Datum: 1. Allgemeine Angaben Unternehmen: Adresse: PLZ: Stadt: Land: Kontakt: Abteilung: Telefon: E-Mail: 2. Anwendungsdaten Beschreibung der Anwendung: Jetziger Werkstoff:
Fragebogen Kunststoffzahnräder Datum: 1. Allgemeine Angaben Unternehmen: Adresse: PLZ: Stadt: Land: Kontakt: Abteilung: Telefon: E-Mail: 2. Anwendungsdaten Beschreibung der Anwendung: Jetziger Werkstoff:
DEUTSCHE NORM DIN Passverzahnungen mit Evolventenflanken und Bezugsdurchmesser Teil 2: Nennmaße und Prüfmaße
 DEUTSCHE NORM DIN 5480-2 D Mai 2006 ICS 21.120.10 Ersatzvermerk siehe unten Passverzahnungen mit Evolventenflanken und Teil 2: e und Prüfmaße Involute splines based on reference diameters Part 2: Nominal
DEUTSCHE NORM DIN 5480-2 D Mai 2006 ICS 21.120.10 Ersatzvermerk siehe unten Passverzahnungen mit Evolventenflanken und Teil 2: e und Prüfmaße Involute splines based on reference diameters Part 2: Nominal
MASCHINENELEMENTE DAS FACHWISSEN DES TECHNIKERS GESTALTUNG UND BERECHNUNG CARL HANSER VERLAG MÜNCHEN 1965
 i DAS FACHWISSEN DES TECHNIKERS OBEBING. KARL-HEINZ DECREE MASCHINENELEMENTE GESTALTUNG UND BERECHNUNG Mit 432 Bildern und 136 Tafeln 2., überarbeitete Auflage CARL HANSER VERLAG MÜNCHEN 1965 Inhaltsverzeichnis
i DAS FACHWISSEN DES TECHNIKERS OBEBING. KARL-HEINZ DECREE MASCHINENELEMENTE GESTALTUNG UND BERECHNUNG Mit 432 Bildern und 136 Tafeln 2., überarbeitete Auflage CARL HANSER VERLAG MÜNCHEN 1965 Inhaltsverzeichnis
Formelsammlung Maschinenkunde II
 Formelsammlung Maschinenkunde II Toleranzen und Passungen Tabelle Skript 6, Seite 10-14 Spielpassungen Friedrich 5-41 Übergangspassungen Presspassungen Oberflächenbeschaffenheit Arithmetischer Mittelrauwert
Formelsammlung Maschinenkunde II Toleranzen und Passungen Tabelle Skript 6, Seite 10-14 Spielpassungen Friedrich 5-41 Übergangspassungen Presspassungen Oberflächenbeschaffenheit Arithmetischer Mittelrauwert
Geometrie. in 15 Minuten. Geometrie. Klasse
 Klasse Geometrie Geometrie 7. Klasse in 5 Minuten Grundbegriffe Wie viele äußere Begrenzungsflächen und ußenkanten haben die Körper? a) Würfel b) risma c) Zylinder d) uader e) yramide f) Kugel 4 M 5 Welche
Klasse Geometrie Geometrie 7. Klasse in 5 Minuten Grundbegriffe Wie viele äußere Begrenzungsflächen und ußenkanten haben die Körper? a) Würfel b) risma c) Zylinder d) uader e) yramide f) Kugel 4 M 5 Welche
KISSsoft 03/2018 Anleitung 053
 KISSsoft 03/2018 Anleitung 053 Schraubradpaar, Paarung Stahlschnecke mit Kunststoff- Rad und Hochverzahnung Erstellt: M. Hoffmann, letztes Update 07.09.2018 KISSsoft AG T. +41 55 254 20 50 A Gleason Company
KISSsoft 03/2018 Anleitung 053 Schraubradpaar, Paarung Stahlschnecke mit Kunststoff- Rad und Hochverzahnung Erstellt: M. Hoffmann, letztes Update 07.09.2018 KISSsoft AG T. +41 55 254 20 50 A Gleason Company
GeoGebra - Kurzanleitung Eine aufgabenorientierte Einführung in GeoGebra
 GeoGebra - Kurzanleitung Eine aufgabenorientierte Einführung in GeoGebra Dynamische Geometrie, Algebra und Analysis ergeben GeoGebra, eine mehrfach preisgekrönte Unterrichtssoftware, die Geometrie und
GeoGebra - Kurzanleitung Eine aufgabenorientierte Einführung in GeoGebra Dynamische Geometrie, Algebra und Analysis ergeben GeoGebra, eine mehrfach preisgekrönte Unterrichtssoftware, die Geometrie und
Physikalische Grundlagen
 Physikalische Grundlagen Gesucht wird F M : Masse m = 1000 kg Beschleunigung a = 7,9 m/s 2 2. 3. Gewichtskraft Eine spezielle Kraft ist die Gewichtskraft (F G ), diese bezeichnet die Kraft, mit der ein
Physikalische Grundlagen Gesucht wird F M : Masse m = 1000 kg Beschleunigung a = 7,9 m/s 2 2. 3. Gewichtskraft Eine spezielle Kraft ist die Gewichtskraft (F G ), diese bezeichnet die Kraft, mit der ein
Euklid ( v. Chr.) Markus Wurster
 Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Punkte und Linien Zwei Linien Markus Wurster Markus Wurster Geometrische Grundbegriffe Winkel Euklid
Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Punkte und Linien Zwei Linien Markus Wurster Markus Wurster Geometrische Grundbegriffe Winkel Euklid
M 3.1. Seite 1. Modul 3.1 Geometrie: Umgang mit dem Geodreieck. Thema. 1. Umgang mit dem Geodreieck. Datum
 Seite. Wie zeichnet man zueinander senkrechte Geraden?. Zeichne zunächst mit deinem Geodreieck eine Gerade von 2 cm. 2. Nun drehst du dein Geodreieck wie rechts abgebildet. Achte darauf, dass die Gerade
Seite. Wie zeichnet man zueinander senkrechte Geraden?. Zeichne zunächst mit deinem Geodreieck eine Gerade von 2 cm. 2. Nun drehst du dein Geodreieck wie rechts abgebildet. Achte darauf, dass die Gerade
Basistext Geometrie Grundschule. Eine Strecke bezeichnet man einer direkte Verbindung zwischen zwei Punkten:
 Basistext Geometrie Grundschule Geometrische Figuren Strecke Eine Strecke bezeichnet man einer direkte Verbindung zwischen zwei Punkten: Gerade Eine Gerade ist eine Strecke ohne Endpunkte. Die Gerade geht
Basistext Geometrie Grundschule Geometrische Figuren Strecke Eine Strecke bezeichnet man einer direkte Verbindung zwischen zwei Punkten: Gerade Eine Gerade ist eine Strecke ohne Endpunkte. Die Gerade geht
Prüfung in Technischer Mechanik 1
 Prüfung in Technischer Mechanik 1 Sommersemester 015 4. August 015, 08:00-10:00 Uhr MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG Bitte beachten Sie die folgenden Punkte: Die Prüfung
Prüfung in Technischer Mechanik 1 Sommersemester 015 4. August 015, 08:00-10:00 Uhr MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG MUSTERLÖSUNG Bitte beachten Sie die folgenden Punkte: Die Prüfung
Exemplar für Prüfer/innen
 Exemplar für Prüfer/innen Kompensationsprüfung zur standardisierten kompetenzorientierten schriftlichen Reifeprüfung AHS Juni 2015 Mathematik Kompensationsprüfung Angabe für Prüfer/innen Hinweise zur Kompensationsprüfung
Exemplar für Prüfer/innen Kompensationsprüfung zur standardisierten kompetenzorientierten schriftlichen Reifeprüfung AHS Juni 2015 Mathematik Kompensationsprüfung Angabe für Prüfer/innen Hinweise zur Kompensationsprüfung
Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen.
 10.1. Ebene Kurven Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen. Parameterdarstellungen einer Kurve sind stetige
10.1. Ebene Kurven Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen. Parameterdarstellungen einer Kurve sind stetige
Prof. Dr. G. Knauer Prof. Dr. H.-J. Plewe
 Fachhochschule München Fachbereich 03 Maschinenbau Prof. Dr. G. Knauer Prof. Dr. H.-J. Plewe Diplomhauptprüfung M a s c h i n e n e l e m e n t e SS 04 Die Aufgabe umfaßt 9 Angabenblätter. Überprüfen Sie
Fachhochschule München Fachbereich 03 Maschinenbau Prof. Dr. G. Knauer Prof. Dr. H.-J. Plewe Diplomhauptprüfung M a s c h i n e n e l e m e n t e SS 04 Die Aufgabe umfaßt 9 Angabenblätter. Überprüfen Sie
Bauformen der Grissongetriebe
 Seite 1 von 5 Bauformen der Grissongetriebe Hans-Erich Maul Im allgemeinen Maschinenbau und anderen Gebieten der Technik werden Getriebe mit Evolventenverzahnung eingesetzt. Die Evolventenverzahnung ist
Seite 1 von 5 Bauformen der Grissongetriebe Hans-Erich Maul Im allgemeinen Maschinenbau und anderen Gebieten der Technik werden Getriebe mit Evolventenverzahnung eingesetzt. Die Evolventenverzahnung ist
Maschinenelemente 2. Teil 2
 Teil 2 Dieses Script ist eine Mitschrift der Vorlesung von Herr Prof. Schlecht. Das Script erhebt weder Anspruch auf Vollständigkeit noch Richtigkeit der in ihm angegebenen Informationen. Ich übernehme
Teil 2 Dieses Script ist eine Mitschrift der Vorlesung von Herr Prof. Schlecht. Das Script erhebt weder Anspruch auf Vollständigkeit noch Richtigkeit der in ihm angegebenen Informationen. Ich übernehme
* KETTENRÄDER UND -SCHEIBEN
 * NRÄDER UND SCHEIBEN TATTECHNOM ANTRIEBSTECHNIK A4060 Leonding Technologiering 15 Tel.: +43.7229.64840.0 Fax: + 43.7229.61817 Email: [email protected] www.tat.at * Inhaltsverzeichnis Technische Daten... 03
* NRÄDER UND SCHEIBEN TATTECHNOM ANTRIEBSTECHNIK A4060 Leonding Technologiering 15 Tel.: +43.7229.64840.0 Fax: + 43.7229.61817 Email: [email protected] www.tat.at * Inhaltsverzeichnis Technische Daten... 03
Das Wort Vektor kommt aus dem lateinischen und heißt so viel wie "Träger" oder "Fahrer".
 Was ist ein Vektor? Das Wort Vektor kommt aus dem lateinischen und heißt so viel wie "Träger" oder "Fahrer". Vektoren sind Listen von Zahlen. Man kann einen Vektor darstellen, indem man seine Komponenten
Was ist ein Vektor? Das Wort Vektor kommt aus dem lateinischen und heißt so viel wie "Träger" oder "Fahrer". Vektoren sind Listen von Zahlen. Man kann einen Vektor darstellen, indem man seine Komponenten
Projekt Stirnrädergetriebe
 Stirnrädergetriebe -1- Projekt Stirnrädergetriebe Stirnrädergetriebe -2- Stirnrädergetriebe -3- Pos. Menge Einheit Benennung Sachnummer / Norm- Bemerkung Kurzbezeichnung 1 1 Stck. Gehäuse 022.01.01 2 1
Stirnrädergetriebe -1- Projekt Stirnrädergetriebe Stirnrädergetriebe -2- Stirnrädergetriebe -3- Pos. Menge Einheit Benennung Sachnummer / Norm- Bemerkung Kurzbezeichnung 1 1 Stck. Gehäuse 022.01.01 2 1
%HUHFKQXQJXQG2SWLPLHUXQJYRQ=DKQUlGHUQPLWPRGHUQHU6RIWZDUH
 Ulrich L. KISSLING KISSsoft AG Frauwis 1 CH-8634 Hombrechtikon %HUHFKQXQJXQG2SWLPLHUXQJYRQ=DKQUlGHUQPLWPRGHUQHU6RIWZDUH (17:,&./81*'(5=$+15$'7(&+12/2*,( Weltweit werden immer mehr Zahnräder aus Kunststoff
Ulrich L. KISSLING KISSsoft AG Frauwis 1 CH-8634 Hombrechtikon %HUHFKQXQJXQG2SWLPLHUXQJYRQ=DKQUlGHUQPLWPRGHUQHU6RIWZDUH (17:,&./81*'(5=$+15$'7(&+12/2*,( Weltweit werden immer mehr Zahnräder aus Kunststoff
Körper- und Galoistheorie
 Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 23 Unter den drei klassischen Problemen der antiken Mathematik versteht man (1) die Quadratur des Kreises, (2) die Dreiteilung
Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 23 Unter den drei klassischen Problemen der antiken Mathematik versteht man (1) die Quadratur des Kreises, (2) die Dreiteilung
Klausur Physik 1 (GPH1) am 8.7.02
 Name, Matrikelnummer: Klausur Physik 1 (GPH1) am 8.7.02 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel: Beiblätter zur Vorlesung Physik 1 im
Name, Matrikelnummer: Klausur Physik 1 (GPH1) am 8.7.02 Fachbereich Elektrotechnik und Informatik, Fachbereich Mechatronik und Maschinenbau Zugelassene Hilfsmittel: Beiblätter zur Vorlesung Physik 1 im
STS. Die ideale Verbindung für Thermoplaste
 STS Die ideale Verbindung für Thermoplaste SCHRIEVER STS Gestern: Probleme mit Verbindungen thermoplastischer Kunststoffe in den Bereichen der Konstruktion, Montage und Belastbarkeit. Heute: Schriever
STS Die ideale Verbindung für Thermoplaste SCHRIEVER STS Gestern: Probleme mit Verbindungen thermoplastischer Kunststoffe in den Bereichen der Konstruktion, Montage und Belastbarkeit. Heute: Schriever
Zweisprachiger Wettbewerb 2007 / 2008 Physik Jahrgang 1 2. Runde
 Zweisprachiger Wettbewerb 2007 / 2008 Physik Jahrgang 1 2. Runde Liebe Schülerin, lieber Schüler, diese Runde des Wettbewerbs hat 20 Fragen, Sie sollen von den vorgegebenen Lösungsmöglichkeiten immer die
Zweisprachiger Wettbewerb 2007 / 2008 Physik Jahrgang 1 2. Runde Liebe Schülerin, lieber Schüler, diese Runde des Wettbewerbs hat 20 Fragen, Sie sollen von den vorgegebenen Lösungsmöglichkeiten immer die
Ferienkurs Experimentalphysik 1
 Ferienkurs Experimentalphysik 1 1 Fakultät für Physik Technische Universität München Bernd Kohler & Daniel Singh Blatt 2 WS 2014/2015 24.03.2015 Ferienkurs Experimentalphysik 1 ( ) - leicht ( ) - mittel
Ferienkurs Experimentalphysik 1 1 Fakultät für Physik Technische Universität München Bernd Kohler & Daniel Singh Blatt 2 WS 2014/2015 24.03.2015 Ferienkurs Experimentalphysik 1 ( ) - leicht ( ) - mittel
