Magnetfeldmessungen P1-80
|
|
|
- Jan Beckenbauer
- vor 9 Jahren
- Abrufe
Transkript
1 Karlsruher Institut für Technologie (KIT) WS 2011 Physikalisches Anfängerpraktikum - P1 Magnetfeldmessungen P1-80 Protkoll von Tobias Renz und Raphael Schmager Gruppe: Do-28 Versuchdatum: 10. November 2011
2 Versuche P1-80: Magnetfeldmessungen Raum F1-16 Aufgaben: 1.) Die folgenden Messungen zeigen, daß die Induktivität einer Eisenkernspule von der Erregung abhängig ist und daß ein Luftspalt im Eisenkern diese Abhängigkeit mindert. 1.1 Entmagnetisieren Sie den Kern. Verwenden Sie dazu die Spule mit Windungen, lassen Sie durch 125 Windungen zunächst den bei geschlossenem Kern maximal möglichen Wechselstrom (ca.0,75a) fließen und regeln Sie dann den Strom langsam auf Null zurück. Überlegen Sie sich Methoden zur Prüfung des Erfolges der Entmagnetisierung. Gute Entmagnetisierung ist wichtig für 2.1! 1.2 Messen Sie den induktiven Widerstand zweier sinnvoll in Serie geschalteter Spulen mit je 1000 Windungen bei geschlossenem gemeinsamen Eisenkern in Abhängigkeit vom Spulenstrom. In einer spannungsrichtigen Schaltung wird der Wechselstrom mit dem Instrument Metravo 2, die Wechselspannung (5V bis 30V in 5V-Schritten) mit dem Instrument Voltcraft gemessen. 1.3 Führen Sie die 1.2 entsprechende Messung nach Einfügen eines Luftspaltes (l S = 2mm) durch. Zwischen U-Kern und Joch wird auf einer Seite eine 2mm-Eisenplatte, auf der anderen Seite ein 2mm- Abstandsstück aus nicht ferromagnetischem Material eingelegt. Tragen Sie in einem Diagramm beide R L (I)-Kurven auf, und begründen Sie die Ergebnisse qualitativ (evtl. nach Erledigung der nächsten Aufgabe). Berechnen Sie jeweils beim größten Meßstrom die Induktivität und daraus sowie aus der Kerngeometrie jeweils die wirksame relative Permeabilität des Kernes. Bei Vorhandensein eines Spaltes ergibt sich allerdings nur ein scheinbarer Wert der Permeabilität. Bei allen Rechnungen dürfen vernachlässigbare Verlustwiderstände und ein vernachlässigbarer Streufluß außerhalb des Kernes angenommen werden. 2.) Die bisher gefundenen Effekte werden durch Messen von Hysteresisschleifen B(H) näher untersucht. 2.1 Messen Sie mit dem Ziel einer B(H)-Kurve für das verwendete Eisen mit Hilfe einer Hallsonde im Luftspalt des Kerns zunächst eine B(I)-Kurve samt Neukurve. Schalten Sie außer dem Strommeßgerät noch einen 600Ω-Widerstand in Serie zu den Spulen, um am Netzgerät den Spulengleichstrom I besser einstellbar zu machen. Beginnen Sie mit dem Strom Null und steigern Sie ihn zunächst (ohne zwischenzeitliche Überhöhungen) schrittweise bis +40mA, dann zurück bis Null, weiter bis -40mA, wieder bis Null und schließlich wieder bis +40mA. Die gewonnene B(I)-Kurve wird nicht einfach durch lineare Umskalierung zu einer Hysteresisschleife des verwendeten Eisens! Es gilt nicht H = n/l I! Der Luftspalt ist zu berücksichtigen: H S l S + H l = n I. (H S = B/μ 0 = H-Wert im Spalt; l S = Feldlinienlänge im Spalt; H = H-Wert im Eisen; l = Feldlinienlänge im Eisen; B = B-Wert im Eisen und im Spalt [Stetigkeit!]) Es folgt: H = n/l {I - (l S / nμ 0 ) B} = n/l I korr Von jedem I-Wert eines Wertepaares (I, B) muß ein B-proportionaler Anteil subtrahiert werden, um den Einfluß des Spaltes auf die Form der Meßkurve zu eliminieren. Eine solche Abbildung heißt Scherung. Führen Sie die Scherung aus, und versehen Sie anschließend die Achsen mit zusätzlichen Skalen für H und B. Berechnen Sie aus der mittleren Steigung der nicht korrigierten Schleife die scheinbare relative Permeabilität und vergleichen Sie das Ergebnis mit dem von Aufgabe 1.3. Entnehmen Sie der korrigierten Schleife wiederum die relative Permeabilität und vergleichen Sie das Ergebnis mit dem von Aufgabe 1.2. Berechnen Sie aus der Schleifenfläche die Verlustleistung im Kern bei Annahmevon 50Hz-Betrieb.
3 2.2 Wiederholen Sie die Messung von Aufgabe 2.1, jedoch bis zu I ±1,2A (ohne 600Ω-Widerstand!). Wieder ist die Scherung der gemessenen Schleife auszuführen und das Ergebnis mit dem von Aufgabe 2.1 zu vergleichen. Nötigenfalls sollte jetzt die Diskussion der Ergebnisse von Aufgabe 1 fortgesetzt werden. Bestimmen Sie außerdem Sättigungsmagnetisierung, Remanenz und Koerzitivkraft. Beim Messen auf konstanten Steuerstrom durch die Hallsonde (temperaturabhängiger Widerstand) achten! 3.) Bei der folgenden Aufgabe geht es um die magnetische Feldstärke in stromdurchflossenen zylindrischen Luftspulen, also um eine Anwendung des Biot-Savartschen Gesetzes. Es zeigt sich, daß bei realen Spulen meist mit beträchtlichen Abweichungen von der nach der Formel für lange Spulen berechneten Feldstärke gerechnet werden muß. 3.1 Eichen Sie eine Longitudinalfeld-Hallsonde. Dazu steht eine Kalibrierspule zur Verfügung, deren Feld im Zentrum aufgrund eines Windungsspaltes ein Minimum aufweist, das mit der Sonde gut zu lokalisieren ist. Stellen Sie einen Steuerstrom von 120mA für die Sonde und einen Spulenstrom von 0,96A ein, bei dem die Feldstärke B im genannten Minimum 10mT beträgt. Nullabgleiche nicht vergessen! 3.2 Messen Sie das Magnetfeld einer Zylinderspule längs der Achse innerhalb und außerhalb mit Hilfe der Hallsonde aus. Tragen Sie die Meßwerte zusammen mit den aus der Spulengeometrie und elektrischen Daten berechneten Werten in ein Diagramm ein. (Spu1enstrom I = 2A). 4.) Diese letzte Aufgabe ist ein reiner Demonstrationsversuch, der die unterschiedliche Wirkung eines inhomogenen Magnetfeldes auf dia-, para- und ferromagnetische Körper zeigt. Bringen Sie in das stark inhomogene Feld zwischen den auf den U-Kern montierten spitzen Polschuhen (ca. 10mm Abstand) nacheinander die an einem sehr dünnen Perlonfaden (Vorsicht!) leicht drehbar hängenden Probestäbchen aus Fe, Al und Bi. Stellen Sie sie ohne Feld auf etwa 45 0 gegen die Verbindungslinie zwischen den Polspitzen gedreht ein. Beobachten und erklären Sie die Effekte beim Einschalten des Feldes (2 x 1000 Windungen, maximal möglicher Gleichstrom). Das diamagnetische Probestäbchen muß extrem sauber sein. Kleinste Verunreinigungen überdecken den diamagnetischen Effekt. Nötigenfalls mit Alkohol reinigen und nur mit der Plastikpinzette anfassen. Vor dem Versuch mit dem ferromagnetischem Material muß der Magnetkern möglichst gut entmagnetisiert werden. Anschließend den Magnetstrom nur sehr vorsichtig von Null her steigern. Zubehör: Netzgerät (regelbar bis ca. 25V=, 30V~) lamellierter Eisen-U-Kern mit Joch (Querschnitt 3,9cm x 4,0cm, mittlere Feldlinienlänge im Fe 48cm) Distanzstücke (4cm x 4cm Fe sowie 4cm x 4cm-U-Form aus Messing, je 2mm dick) Aufsteckspulen ( Wdg., Wdg., Wdg.) 2 spitze, kegelförmige Polschuhe mit Halteklammern Hallsonde, passend zum Distanzstück für den Magnetspalt mit digitaler Anzeige Zylinderspule (Länge 20,8cm; Radius 3,7cm; 814 Wdg.) Hallsonde für Longitudinalfeldmessungen in der Spule; Kalibrierspule zur Hallsonde (10mT bei 0,96A) Hallsonden-Anschlußgerät (mit Versorgungsspannung; Steuerstromregelung; Steuerstrommeßgerät; U H -Nullabgleich; Hallspannungsmeßgerät 100mV; Anschlußbuchsen für externes Hallspannungs-Meßgerät) Millivoltmeter mit Transistorverstärker (Bauart Knick, empfindlichster Bereich 0,l5mV) Universalmeßinstrument Voltcraft; Universalmeßinstrument Metravo 2 Drehspulinstrument Gossen Mavometer (1mA bzw. 100mV) mit la-shunt Kästchen mit Vorschaltwiderständen (2 x 1,2kΩ) Aufbewahrungsgefäß mit Probestäbchen (Fe; Al; Bi) Zeißschiene mit Reitern, Stangen und Klemmen Literatur: Jedes Lehrbuch der Experimentalphysik ist geeignet. Version: Juli
4 Karlsruher Institut für Technologie (KIT) WS 2011 Physikalisches Anfängerpraktikum - P1 Magnetfeldmessungen P1-80 Versuchsvorbereitung von Raphael Schmager Gruppe: Do-28 Druchgeführt am 10. November 2011
5 Versuchsvorbereitung 0 Grundlagen 0.1 Induktion Unter Induktion versteht man das Entstehen einer Spannung durch ein sich änderndes B-Feld. Betrachtet wir eine Spule mit N Windungen durch die ein Magnetfeld B hindurchgeht. Ändert sich nun die magnetische Flussdichte B bzw. der magnetische Fluss Φ = BA durch herausziehen der Spule oder zeitliche Änderung des Feldes, wird eine Spannung in den Spulenenden induziert. U i B Abbildung 1: Induktionsspannung Daraus folgt das Induktionsgesetz: U i = N i Φ (1) 0.2 Induktivität Ändert sich in einem stromdurchflossen Leiter der Stromfluss I, so induziert diese Änderung des Flusses Spannung im Leiter, die der Änderung entgegenwirkt. Wir erhalten: U i = N i Φ = L I (2) L ist die Induktivität der Spule. Diese berechnet sich durch: L = µ r µ 0 N 2 l A. Die Impedanz der Induktivität beträgt Z L = iwl. 0.3 Hall-Effekt Der Hall-Effekt tritt auf, wenn sich ein stromdurchflossener Leiter im Magnetfeld befindet. Hierbei lenkt das Magnetfeld die Elektronen im Leiter ab. Auf Bewegte Elektronen wirkt im Magnetfeld die Lorentzkraft. F L = e v B F L = evb = F el = ee H = e U H b Die dadurch erzeugte Spannung steht senkrecht auf dem Stromfluss I und senkrecht auf dem Magnetfeld B. Sie wird Hallspannung genannt: U H = 1 I ne d B = R H (3) I d B (4) Durch eine Hallsonde kann man die Stärke eines Magnetsfeldes bestimmt werden. Raphael Schmager 1
6 Versuchsvorbereitung B A u F - L F el d I U H Abbildung 2: Hall-Effekt 0.4 Magnetische Materialien Diamagnetismus Liegt kein äußeres Feld an, so besitzen die Atome in einem Diamagnetischen Material kein magnetisches Moment. Diamagnete magnetisieren sich erst in einem externen Magnetfeld, dabei werden auf atomarer Ebene magnetische Dipole induziert. Das Magnetfeld in Ihrem Inneren schwächt sich proportional zum außen angelegten ab. Daher strebt diamagnetisches Material immer in Richtung niedrigerer Feldstärke. Zu den Diamagneten zählen alle Materialien mit negativer magnetischer Suszeptibilität Paramagnetismus Paramegentismus tritt auf, wenn es in einem Stoff viele ungepaarte Elektronen gibt. Damit besitzen die Atome oder Moleküle ein magnetisches Moment. Diese sind jedoch voneinander unabhängig. Im Mittel sind die magnetischen Momente so verteilt, dass sie sich nach außen hin aufheben. Wird nun ein äußeres Magnetfeld angelegt, so orientieren sich diese entsprechend. Paramagnete besitzen eine positive Suszeptibilität Ferromagnetismus Ein Material ist ferromagnetisch, wenn sich im äußeren Magnetfeld eine unabhängige Magnetisierung zeigt. Im Vergleich zu den Paramagneten behalten die Ferromagnete ein Teil ihres Magnetfeldes, nach abschlaten des äußeren Feldes, bei. Sie haben eine sehr große (positive) magnetische Suszeptibilität. Ferromagnetische Materialien werden in den Bereich höhere Feldstärke gezogen. 0.5 Hysterese Hysterese tritt bei ferromagnetischen Materialien auf. Bringt man ein entmagnetisiertes Material in ein Magnetfeld so steigt die magnetische Flussdichte in diesem. Erhöht man nun das umgebende Magnetfeld H, so steigt B im Stoff nur noch langsam an, bis eine Sättigungsgrenze erreicht ist. Das Verhalten bis hin zum Sättigungspunkt wird durch die Neukurve beschrieben. Wird das äußere Magnetfeld wieder langsam auf Null verringert, folgt das B-Feld im Inneren dieser Änderung. B fällt jedoch nicht auf auf Null zurück, sondern nur bis zur einer Restma- Raphael Schmager 2
7 Versuchsvorbereitung B Sättigung B r Neukurve -H c H c H -B r Abbildung 3: Hysteresekurve einer ferromagnetischen Probe gnetisierung, welche Remanenz B R genannt wird. Bei negativen Werten des äußeren Feldes verringert sich das innere Feld wieder, bis es an einem negativen Sättigungspunkt angelangt ist. Man erhält so eine geschlossene Kurve - die Hysteresekurve. Die Feldstärke, die benötigt wird, um das (ferromagnetische) Material wieder vollständig zu entmagnetisieren nennt man Koerzitivfedstärke H C. 1 Induktivität einer Spule 1.1 Entmagnetisierung des Kerns Zur Entmagentisierung eines Eisenkerns soll eine Spule mit Windungen verwendet werden. Es soll bei geschlossenem Kern der maximale Wechselstrom von 0,75A durch die Spule fließen. Danach soll dieser langsam auf Null zurück geregelt werden. Da wir Wechselstrom verwenden, wird andauernd die Hysteresekurve durchlaufen. Durch das langsame herunterregeln des Stroms schafft man es die Remanenz allmählich zu verringern. Abbildung 4: Durchlaufen der Hystereseschleife bis zur Entmagnetisierung Da eine gute Entmagnetisierung wichtig ist, soll diese Überprüft werden. Ob ein messbares Restmagnetfeld besteht lässt sich durch die Magnetfeldmessung mit einer Hall-Sonde oder eines Raphael Schmager 3
8 Versuchsvorbereitung Kompasses zeigen. 1.2 Induktiver Widerstand in Reihe geschalteter Spulen Nun sollen zwei Spulen mit je 1000 Windungen (sinnvoll) in Reihe geschaltet werden. Bei geschlossenen gemeinsamen Eisenkern soll der induktive Widerstand in Abhängigkeit des Spulenstroms berechnet werden. Der Induktive Widerstand einer Spule berechnet sich wie folgt: U L = L I U L = L iwi 0 e iwt = L iwi = Z L I (5) Für die Betrag der Gesamtimpedanz (Scheinwiderstand) ergibt sich somit: Z Ges = U eff = R I 2 + RL 2 = R 2 + w 2 L 2 (6) eff Um nun den induktiven Widerstand der Spulen zu berechnen müssen wir entweder den ohmschen Widerstand vernachlässigen oder er ist gegeben. Es soll dafür eine spannungsrichtige Schaltung verwendet werden: Des Weiteren soll die Permeabilität bestimmt werden. Diese folgt Abbildung 5: Spannungsrichtige Schaltung aus Abschnitt 0.2. L = µ r µ 0 N 2 l A µ r = L l µ 0 N 2 (7) 1.3 Induktiver Widerstand mit Luftspalt Nun wird die Messung wiederholt. Dabei wird der Eisenkern verändert. Zwischen U-Kern und Joch wird auf einer Seite eine 2mm Eisenplatte und auf der anderen Abstandsstück nichtferromagnetischem Material (gleicher Stärke) eingebracht. Dies entspricht einem Luftspalt (l s = 2mm). In einem Diagramm soll die R L (I)-Kurve aufgetragen werden. Anschließend soll der scheinbare Wert der Pereabilität bestimmt werden. Raphael Schmager 4
9 Versuchsvorbereitung 2 Hysterese Im 2. Teil werden die Effekte durch Messung der Hystereseschleife genauer Untersucht. 2.1 Messung mit der Hallsonde Das Ziel ist es eine B(H)-Kurve für das verwendete Eisen zu erhalten. Dazu wird zunächst die B(I)-Kurve samt Neukurve gemessen. Ein 600Ω Widerstand soll mit den Spulen in Reihe geschaltet werden, um am Netzgerät den Spulengleichstrom I besser einstellen zu können. Schrittweise wird nun der Strom von 0A bis +40mA erhöht. Danach allmählich auf -40mA verringert. Und als letztes wieder auf +40mA erhöht. Es muss aufgepasst werden, da die so erhaltene B(I)-Kurve nicht durch lineare Umskalierung in die Hystereseschleife transformiert werden kann. Der Luftspalt ist zu berücksichtigen. Es gilt: H S l S + Hl = ni (8) Mit dem H S = B µ 0, dem Wert im Spalt, der Feldlinienlänge l S im Spalt, dem H-Wert des Eisens und der Feldlinienlänge im Eisen l ergibt sich mit der Stetigkeitsbedingung (B Eisen = B Spalt = B) folgender Zusammenhang. H = n ( I l ) s B = n l nµ 0 l I korr (9) Nun muss bei jedem Wertepaar (I,B) jeweils von der Stromstärke I ein zu B proportionaler Anteil subtrahiert werden. Dies nennt man Scherung. Die Scherung dient dazu, den Einfluss des Spalts zu eliminieren. Anschließend soll aus der mittleren Steigung der nicht korrigierten Schleife die scheinbare relative Permeabilität berechnet und mit dem Ergebnis aus Aufgabe 1.3 verglichen werden. Für die korrigierte Schleife soll gleiches gemacht werden und anschließend mit Aufgabe 1.2 verglichen werden. 2.2 Wiederholung der Messung (nun bis ±1,2A) Der in Reihe geschaltete Widerstand aus Aufgabe 1.2 soll entfernt werden und die Messung bis zu einem Strom von ±1,2A gemessen werden. Es ist erneut eine Scherung durchzuführen und mit Aufgabe 2.1 zu vergleichen. Danach soll die Verlustleistung im Kern bei der Annahme eines 50Hz-Betriebs mit Hilfe der Schleifenfläche berechnet werden. Außerdem soll die Sättigungsmagnetisierung, Remanenz und Koerzitivkraft bestimmt werden. 3 Magnetische Feldstärke in stromdurchflossenen Zylinderspulen 3.1 Eichen der Longitudinalfeld-Hallsonde Wir haben eine Kalibrierspule, die bei einem Spulenstrom von 0,96A in der Mitte ein Minimum es B-Feldes von 10mT aufweist. Dieses Minimum soll mit einer Logitudinalfeld-Hallsonde Raphael Schmager 5
10 Versuchsvorbereitung bestimmt werden. Der Steuerstrom ist auf 120mA zu stellen. Es wird das Minimum der Spannung im inneren der Spule gemessen. Durch den oben erläuterten Zusammenhang zwischen Hallspannung und Strom ergibt sich: I U H = R H d B = k B k = U H B Mit der nun geeichten Sonde kann die Magnetfeldmessung im nächsten Aufgabenteil vollzogen werden. 3.2 Magnetfeldmessung der Zylinderspule Das Magnetfeld einer Zylinderspule soll längs der Achse innerhalb sowie außerhalb gemessen werden. Dabei wird die geeichte Hall-Sonde aus der vorigen Aufgabe verwendet. Die Messwerte der Hallspannung sollen wie auch Werte der Geometrie in eine Tabelle eingetragen werden. Das Magnetfeld einer Spule kann mit dem Biot-Sarvat-Gesetz berechnet werden: db = µ 0I 4πr (d l r) B(z) = NIµ 0 z + l z l 2 2 (11) 3 2l R 2 + (z + l2 )2 R 2 + (z l 2 )2 Die letzte Gleichung ergibt sich aus der Superposition der Magnetfelder der einzelnen stromdruchflossenen Kreisringe. (10) 4 Wirkung eines inhomogenen Magnetfeld Zum Abschluss des Versuchs sollen die Auswirkungen eines inhomogenen Magnetfeldes auf dia-,para- und ferromagnetische Körper untersucht werden. Die Beschreibung der drei magnetischen Materialien fand in der Grundlagen zu Beginn der Vorbereitung statt. Es ist: B = µ 0 ( H + M) = µ 0 (1 + χ) H (12) 5 Quellen H. J. Eichler H.-D. Kronfeldt J. Sahm, Das Neue Physikalische Grundpraktikum, 2. Auflage, Springer-Verlag Vorbereitungsmappe Zur Entmagnetisierung: (Mo, :00Uhr) Stromrichtige Schaltung: (Mo, :00Uhr) Raphael Schmager 6
11 Karlsruher Institut für Technologie (KIT) WS 2011 Physik Praktikum 1 Magnetfeldmessungen Tobias Renz Matrikel Nr November 2011 Versuchsvorbereitung 0
12 Grundlagen Bevor ich die auf die einzelnen Aufgaben eingehe, möchte ich zu Beginn die Hall-Sonde und die Hysteresekurve erläutern. 0.1 Hall-Sonde Eine Hall-Sonde dient zur Messung der Stärke des Magnetfeldes und wir bei diesem Versuch häug verwendet. Der Hall-Eekt basiert auf der Lorentz-Kraft, die eine Ablenkung der Ladungsträger eines Leiters senkrecht zum Magnetfeld und zur Stromrichtung bewirkt ( F L = q v B). Die Ablenkung führt zur Ladungstrennung im Leiter, so dass ein elektrisches Feld entsteht. Die Ladungstrennung dauert so lange bis das elektrische Feld eine gleiche groÿe entgegengesetzte Kraft auf die Ladungsträger bewirkt (qe = F L ). Durch Messung der Spannung des elektrischen Feldes (U H ) kann dann die Stärke des Magnetfeldes bestimmt werden. Aus der Bedingung: q E = q( v B folgt mit der Stromdichte j = n q v ergibt sich die Hallspannung zu: U H = j B b n q In Metallen und den meisten Halbleitern sind die Ladungsträger Elektronen ( q = -e) und mit I = j A = j b d ergibt sich die Hallspannung zu: U H = I B n e d = R H I B d mit R H = Hall-Koezient. 0.2 Hysteresekurve Bei ferromagnetischen Materialien (magnetische Suszeptibilität 1) tritt Hysterese auf. Hysterese bedeutet, dass die Magnetisierung nicht nur von dem äuÿeren Magnetfeld abhängt, sondern auch von der Vorbehandlung des Materials. Hat man ein völlig entmagnetisiertes Material und legt ein äuÿeres Magnetfeld an steigt die Magnetisierung zuerst linear an und geht dann in die Sättigung über. Fährt man das Magnetfeld wieder zurück verläuft die Magnetisierung über einer anderen Kurve bis bei entsprechend groÿem entgegengesetzten Feld wieder Sättigung erreicht wird. Man kann das äuÿere Feld wider ändern wird aber nicht mehr auf die erste Kurve (Neukurve) gelangen. Man erhält eine 1
13 geschlossene Kurve, die Hysteresekurve. Die Restmagnetisierung (bei äuÿerem Feld =0) heiÿt Remanenz, die Feldstärke die benötigt wird um die verbleibende Magnetisierung zu beseitigen heiÿt Koerzitivkraft. Man trägt nun normalerweise das entstehende B-Feld über der äuÿeren magnetischen Erregung auf. Dieser Eekt liegt an den sogenannten Weiÿschen Bezirken in ferromagnetischen Materialien. Diese Bezirke werde durch ein äuÿeres Feld ausgerichtet und das Material wird magnetisch. Wird das äuÿere Feld nun abgeschaltet bleiben diese Bezirke ausgerichtet. 1 Induktivität einer Eisenkernspule 1.1 Entmagnetisierung eines Kerns Zu Beginn des Versuchs soll zuerst ein Kern vollständig entmagnetisiert werden. Dazu wird der Kern in eine Spule gebracht und an die Spule den maximal möglichen Wechselstrom angelegt und der Strom dann langsam auf null herunter geregelt. Durch anlegen des Wechselstroms wird ständig eine Hystersekurve durchlaufen. Durch das herunter regeln des Wechselstroms nimmt die Remanez auch ab und man sollte ein entmagnetisiertes Material erhalten. Es soll dann noch getestet werden ob das Material wirklich entmagnetisiert ist. Dies kann man zum Beispiel mit Sägespäne oder einer Hall-Sonde getestet werden. 1.2 Induktiver Widerstand bei geschlossenem Kern Es soll der induktive Widerstand zweier in Reihe geschalteter Spulen mit je 1000 Windungen bei geschlossenem gemeinsamen Eisenkern in Abhängigkeit vom Spulenstrom gemessen werden. Die Induktionsspannung ist proportional zur Induktivität ( U i nd = L I). Die Impedanz einer Induktivität (Z L ) beträgt Z L = iωl. Der Betrag der Spannung ergibt sich aus U = Z I. Das heiÿt aus Messungen von U und I kann die Induktivität der Spulen gemessen werden. Dazu muss aber der ohmsche 2
14 Widerstand vernachlässigt werden oder bekannt sein, da er in Z rein spielt. R L wird dann über U I berechnet und in einem Diagramm soll die R L(I) Kurve aufgetragen werden. Es soll beim gröÿten Messewert die Induktivität berechnet werden und daraus die wirksame relative Permeabilität (µ R ) Die Induktivität einer langen Spule kann auch theoretisch über L = µ R µ 0 N 2 l A berechnet werden. Daraus kann dann µ R = l L µ 0 A N 2 Es soll mit einer spannungsrichtigen Schaltung gemessen werden. Eine spannungsrichtige Schaltung ist folgendermaÿen aufgebaut: 1.3 Induktiver Widerstand mit Luftspalt Es soll nun die gleiche Messung wie in 1.2 durchgeführt werden aber dieses mal mit einem 2mm breitem Luftspalts zwischen U-Kern und Joch. Auch hier soll dann ein R L (I) Diagramm gezeichnet werden und der nun scheinbare Wert der Permeabilität berechnet werden. 2 Messung von Hysteresechleifen 2.1 Messung einer B(H) Kurve im Luftspalt Das Ziel ist es eine B(H) Kurve für das verwendete Eisen zu bekommen. Dazu wird mit Hilfe einer Hallsonde zunächst im Luftspalt eine B(I) Kurve samt Neukurve gemessen. Um den Spulengleichstrom besser einstellen zu können wird noch ein 600 Ω Widerstand zu den Spulen in Serie geschaltet. Um eine Neukurve zu bekommen benötigen wir nun 3
15 den in 1.1 entmagnetisierten Kern. Es wird nun von Null an der Strom schrittweise auf +40mA gesteigert, dann wieder auf -40mA gesenkt und wieder auf +40mA gesteigert. Es kann jetzt aber nicht durch einfaches Umskalieren die Kurve in eine Hysteresekurve umgewandelt werden, da H = N I nicht gilt. Aus der Stetigkeit der Normalkomponente l des B-Feldes und dem Ampèrschen gesetzt für das H Feld folgt: B F e = B S = B und H s l s + H F e (l l s ) H s l s + H F e l = N I Mit H s = B µ 0 folgt: H = n l (I B s l nµ 0 ) = n I l korr Es muss also von jedem (I,B) Wertepaar ein zu B proportionaler Anteil subtrahiert werden, um den Einuss des Spaltes zu eliminieren. Dies nennt man eine Scherung. Solch eine Scherung sollen für unsere Werte ausführen um eine B(H) Kurve zu bekommen. Aus der mittleren Steigung der nicht korrigierten Schleife soll die scheinbare Permeabilität gemessen werden und mit 1.3 verglichen werden. Die relative Permeabilität aus der korrigierten Schleife soll dann noch mit 1.2 verglichen werden. Es soll nun noch die Verlustarbeit berechnet werden. Zur Änderung des Feldes ist die Arbeit W = H 2 H 1 B dh. Berechnet man die Arbeit für einen vollen Umlauf, so ergibt sich, dass die von der Kurve umschlossene Fläche die Verlustarbeit pro Volumenarbeit darstellt. Bei Wechselstrom ist die Verlustleistung P = V A f 2.2 Messung ohne Widerstand Es soll die selbe Messung wie in 2.1 durchgeführt werden. Es soll jedoch bis ±1, 2 A gemessen werden. Dies erreicht man indem man die Messung ohne den Widerstand durchführt. Es soll dann wieder eine Scherung durchgeführt werden und mit 2.1 verglichen werden. Es soll auch eine Verlustleistung berechnet werden und zusätzlich die Sättigungsmagnetisierung, die Remanenz und die Koerzitivkraft bestimmt werden. 4
16 3 Zylindrische Spulen 3.1 Eichung einer Longitudinalfeld-Hallsonde Es soll eine Hallsonde mit Hilfe einer Kalibrierspule geeicht werden. Das Magnetfeld der Spule weiÿt im Zentrum aufgrund eines Windungsspaltes ein Minimum von 10mT bei einem Spulenstrom von 0,96A auf. Es soll dabei bei einem Steuerstrom von 120mA I B gemessen werden. Die Hallspannung U H = R H = c B. Aus den Messwerten von d U H kann dann die Konstante c bestimmt werden. 3.2 Magnetfeld einer Zylinderspule Es soll das Magnetfeld einer Zylinderspule mit Hilfe der Hallsonde vermessen werden und mit den theoretisch berechneten Werte verglichen werden. Das Magnetfeld einer Spule kann mit dem Biot-Savartschen Gesetz berechnet werden. Bio-Savart-Gesetz: db = µ 0 I (d l r) 4π r 3 Feld einer Spule: B(z) = NIµ 0 [ z+ L 2 2L R 2 +(z+ L 2 )2 L z 2 R ] 2 +(z L 2 )2 (wobei N = Anzahl der Windungen, R= Radius der Spule und L =Länge der Spule) 4 Inhomogenes Magnetfeld In diesem Teil des Versuchs soll die Wirkung eines inhomogenen Magnetfeldes auf dia-,par- und ferromagnetische Körper getestet werden. Bendet sich Materie im Magnetfeld, ist B = µ 0 ( H + M) = µ 0 (1 + χ) H. Mit χ = magnetische Suszeptibilität. Nach dem Wert und Vorzeichen von χ werden nun Materialien in folgende drei Klassen eingeteilt. Diamagnetische Stoe haben eine magnetische Suszeptibilität kleiner als 0. Sie bestehen aus Atomen oder Molekülen, die kein permanentes Dipolmoment. Bringt man sie aber in ein Magnetfeld werden Dipole induziert, die dem äuÿeren Feld ent- 5
17 gegen gerichtet sind. In inhomogenen Feldern werden Diamagnete aus dem Bereich hoher Feldstärken hinausgedrängt. Paramagnetische Stoe besitzen ein positives χ, dass aber kleiner als 1 ist. Paramagnete besitzen Atome mit permanenten Dipolen. Diese Dipole sind aber aufgrund der thermischen Bewegung in alle Richtungen gleich orientiert. Legt man ein äuÿeres Feld an so werden die Dipole teilweise ausgerichtet. In einem inhomogenen Feld werden Paramagnete in Richtung höherer Feldstärken gezogen. Ferromagnetische Materialien haben eine magnetische Suszeptibilität, die viel gröÿer als 1 ist. Ferromagnete besitzen auch ohne äuÿeres Feld magnetische atomare Dipole, die in makroskopischen Raumbereichen (Domänen) parallel ausgerichtet sind. Legt man nun ein äuÿeres Feld an werden die Domänen durch Drehung oder Verschiebung so ausgerichtet, dass das gesamte Material Magnetisiert ist. Ferromagnete werden in Inhomogenen Feldern stark in Richtung der höheren Feldstärken gezogen. 5 Quellen Demtröder, Experimentalphysik physics/praktikum/anleitung/e4.pdf http : // p h10/musteraufgaben/04 w iderstand/strom s pannung r ichtig/s 6
18 Karlsruher Institut für Technologie (KIT) WS 2011 Physikalisches Anfängerpraktikum - P1 Magnetfeldmessungen P1-80 Protkoll von Tobias Renz und Raphael Schmager Gruppe: Do-28 Versuchdatum: 10. November 2011
19 Auswertung 1 Induktivität einer Eisenkernspule 1.1 Entmagnetisierung des Kerns Für die nachfolgenden Aufgaben benötigen wir einen entmagnetisierten Eisenkern. Den Kern haben wir vor jeder neuen Aufgabe nach folgendem Prinzip entmagnetisiert. Wir haben bei geschlossenen Kern mit einer Spule den maximal möglichen Wechselstrom fließen lassen. Bei uns war die maximal erreichte Stromstärke bei 350mA. Die Stromstärke haben wir dann in einer Zeit von 2 bis 3 Minuten auf null herunter geregelt. Durch diese Methode sollten wir eine Magnetisierung von Null erreichen. Nun haben wir mit Hilfe eines Abstandsplättchen einen Luftspalt in den Kern gebracht und dort das Magnetfeld gemessen. Dort hatten wir einen Wert zwischen 0,5 und 0,6mT. Die Magnetisierung verschwindet nicht ganz, aber die Methode bringt ein ganz gutes Ergebnis. 1.2 Induktiver Widerstand bei geschlossenem Kern Wir sollten den induktiven Widerstand R L zweier Spulen mit je 1000 Windungen messen. Die Spulen wurden so in Reihe geschaltet, dass sich die Magnetfelder der Spule im Kern addieren. Über eine spannungsrichtige Schaltung haben wir dann die Spannung an den Spulen und den Strom durch die Spulen gemessen. Da wir den Verlustwiderstand vernachlässigen können ergibt sich der induktive Widerstand sofort aus R L = U I. U / V I / ma R / kω 5 1,53 3, ,46 4, ,26 4, ,94 5, ,54 5, ,1 5,88 Tabelle 1: induktiver Widerstand bei geschlossenem Kern Aus dem Messwert beim höchsten Messstrom soll jetzt noch die Induktivität und die relative Permeabilität berechnet werden. Die Induktivität ergibt sich aus L = R L 2π f und die Permeabilität ergibt sich aus l L µ R = µ 0 A N 2 (1) Mit f = 50Hz, A = 0, 00156m 2, µ 0 = 4π 10 7 N und l = 48cm. Mit unserem Messwert ergibt A 2 sich dann L = 18, 7H und µ R = 1144, 7. Gruppe: Do-28 1
20 Auswertung 6,0 5,5 5,0 R L / k Ω 4,5 4,0 3,5 3,0 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 I / m A Abbildung 1: Induktioniver Widerstand bei geschlossenem Kern 1.3 Induktiver Widerstand mit Luftspalt Bei dieser Messung haben wir nun einen Luftspalt von 2mm in den Kern eingefügt und die Messung analog zu 1.2 durchgeführt. Aus unserem Messwert mit dem größten Messstrom berechnen wir nun die Induktivität und die scheinbare Permeabilität. Die Induktivität ergibt sich zu L = 4, 49H und die Permeabilität zu µ R = 274, 8. U / V I / ma R / kω 5 4,34 1, ,99 1, ,44 1, ,78 1, ,08 1, ,25 1,41 Tabelle 2: induktiver Widerstand mit Luftspalt Wenn man die Induktivität und den induktiven Widerstand theoretisch für eine lange Spule berechnet (siehe Vorbereitung) erwartet man einen konstanten Wert für den induktiven Widerstand. Man erkennt aber in beiden Schaubildern, dass der induktive Widerstand nicht konstant ist. Dies hängt vermutlich damit zusammen, dass bei steigendem Strom die Magnetisierung und somit auch die Induktivität steigt. Man entnimmt aus den Schaubildern, dass der induktive Widerstand für die Spulen mit geschlossenem Kern deutlich höher ist als für den Kern mit Luftspalt. Dies ist auch verständlich, Gruppe: Do-28 2
21 Auswertung 1,4 5 1,4 0 1,3 5 R L / k Ω 1,3 0 1,2 5 1,2 0 1, I / m A Abbildung 2: Induktioniver Widerstand bei Kern mit Luftspalt da dass Magnetfeld im Kern stark absinkt wenn ein Luftspalt vorhanden ist. 2 Hysterese 2.1 Messung einer B(H) Kurve im Luftspalt Um die Hysteresekurve zu bekommen, haben wir den Eisenkern entmagnetisiert und mit einem Vorwiderstand in Reihe geschalten. Für den Widerstand haben wir einen 1,2kΩ und einen 1kΩ Widerstand parallel geschaltet. Dann haben wir das B-Feld im Luftspalt in Abhängigkeit der Stromstärke gemessen. Die Messwerte, sowie die daraus berechneten Werte befinden sich im Anhang. Die erhaltene B(I) Kurve muss dann noch wie in der Vorbereitung beschrieben geschert werden. Wir haben nun die gescherte B(H) Kurve und die ungescherte B(H) Kurve dargestellt. Nun sollte noch aus der mittleren Steigung der nicht korrigierten Schleife die scheinbare relative Permeabilität und aus der korrigierten die relative Permeablität bestimmt werden. Gruppe: Do-28 3
22 Auswertung 0,0 6 0,0 4 0,0 2 B / T 0,0 0-0,0 2-0, H / A m Abbildung 3: Hysteresekurve Aufgabe ,0 4 0,0 2 B K o rrig ie rt / T 0,0 0-0,0 2-0,0 4-0, H S c h e r / A m -1 Abbildung 4: Gescherte Hysteresekurve Aufgabe 2.1 Die Steigung der Ausgleichsgeraden entspricht gerade µ 0 µ R. Wir erhalten dann für µ R = 197,35 (unkorrigiert) und µ R = 907,2 (korrigiert). Vergleicht man diese Werte mit 1.2 und 1.3 Gruppe: Do-28 4
23 Auswertung ergibt sich für die relative Permeabilität entspricht korrigiertem Wert) ein Abweichung von ca. 26% und für die scheinbare relative Permeabilität (entspricht unkorrigiertem Wert) eine Abweichung von ca. 39%. 0,0 6 0,0 4 y=2,48e-4x+4,2e-3 0,0 2 B / T 0,0 0-0,0 2-0, H / A m -1 Abbildung 5: Hysteresekurve Aufgabe 2.1 mit linearer Regression 0,0 4 y=1,14e-3x-7,6e-3 0,0 2 B K o rrig ie rt / T 0,0 0-0,0 2-0,0 4-0, H S c h e r / A m -1 Abbildung 6: Gescherte Hysteresekurve Aufgabe 2.1 mit linearer Regression Gruppe: Do-28 5
24 Auswertung Aus der Schleifenfläche (A i ), dem Volumen des Kerns V = 7, m 3 und der Frequenz (f) von 50Hz kann nun noch die Verlustleistung über P i = V A i f berechnet werden. A 1 = (( x x x ) ( x x x ))dx = 1.43P a (2) A 1Scher = (( x x x 3 ) ( x x x 3 ))dx = 1.40P a (3) Daraus ergeben sich die beiden Werte der Verlustleistung zu: P 1 = 0, 054W und P 1Scher = 0, 052W. 2.2 Messung ohne Widerstand In diesem Aufgabenteil wird die gleiche Messung wie in 2.1 durchgeführt, nur dass wir den Vorwiderstand weg gelassen haben und somit die Stromstärke nicht mehr zwischen ca. ± 40mA sondern zwischen ca. ± 1,2 A variiert. Wir messen also in diesem Teil bei einem deutlich 1,0 0,5 B / T 0,0-0,5-1, H / A m -1 Abbildung 7: Hysteresekurve Aufgabe 2.2 stärkerem Strom. Wir haben auch hier eine nicht korrigierte B(H) Kurve und eine gescherte B(H) Kurve dargestellt. Gruppe: Do-28 6
25 Auswertung 1,0 0,5 B / T 0,0-0,5-1, H S c h e r / A m -1 Abbildung 8: Gescherte Hysteresekurve Aufgabe 2.2 Man sieht im Vergleich zu 2.1 das hier die Sättigungsmagnetisierung erreicht würde. In 2.1 wurde dagegen nur ein Ausschnitt der gesamten Hysteresekurve aufgenommen. Da in 2.2 die Sättigungsmagnetisierung erreicht wurde macht es bei dieser Kurve auch keinen Sinn die Permeabilität zu bestimmen, da bei erreichen der Sättigung durch das Eisen keine Verstärkung mehr zustande kommt. Nun soll auch noch die Verlustleistung im Kern berechnet werden. Leider war es nur möglich 2 Kurven für den ungescherten Fall zu Fitten. Das Integral hierüber ergibt wieder die Fläche: A 2 = (( x x x 3 ) (( x x x 3 )dx = P a (4) Bei der gescherten konnte Origin v8.5.1g keine Kurve finden. Es wurde versucht manuell ein tanh() anzupassen, jedoch waren die Abweichungen noch so groß, das es keinen Sinn gemacht hätte dies für obere und untere Kurve durchzuführen. Aus der Fläche A 2 folgt die Verlustleistung: P = 9, 48W Gruppe: Do-28 7
26 Auswertung Aus dem Schaubild können wir nun die Sättigungsmagnetisierung, die Remanenz und die Koerzitivkraft ablesen. Alle Werte sind im folgenden Schaubild mit aufgeführt. 1,0 0,5 Neg Remanenz Y = -0,5 T B / T 0,0 Pos Remanenz Y = 0,4 T Saettigungsmagnetisierung Y - = Am -1 Y + = Am -1-0,5 Koerzitivkraft x=+-60 Am -1-1, H S c h e r / A m -1 Abbildung 9: Hysteresekurve mit Sättigungsmagnetisierung, Remanenz und Koerzitivkraft Die Messwerte, sowie die daraus berechneten Werte befinden sich im Anhang. 3 magnetische Feldstärke in stromdurchflossenen Zylinderspulen 3.1 Eichung einer Longitudinalfeld-Hallsonde Zur Eichung der Hallsonde stand eine Kalibrierspule zur Verfügung. Diese Spule hat in der Mitte ein Minimum von 10mT. Nun haben wir bei unsere Hallsonde eine Steuerstrom von 112mA eingestellt und mit der Sonde das Magnetfeld in der Spule abgefahren. Beim minimalen Magnetfeld muss auch die minimale Spannung bei der Hallsonde angezeigt werden. Wir haben nun das Spannungsminimum in der Hallsonde gesucht. Wir haben eine Spannung von 0,65mV als Minimum gefunden. Daraus können wir nun die Konstante c in der Gleichung U H = c B bestimmen. Für c ergibt sich ein Wert von 0,065 V T. 3.2 Magnetfeld einer Zylinderspule Es sollte das Magnetfeld einer Zylinderspule gemessen werden und mit den theoretisch berechneten Werten verglichen werden. Das Magnetfeld haben wir mit der in 3.1 geeichten Hallsonde vermessen und immer eine Spannung bei einer bestimmten Position gemessen. Über B = U H c Gruppe: Do-28 8
27 Auswertung wird dann das zugehörige Magnetfeld bestimmt. Da wir bei der Berechnung des Magnetfeldes mit dem Biot-Savart-Gesetz vom Mittelpunkt der Spule ausgehen, haben wir unsere Messwerte so angepasst, dass auch sie vom Mittelpunkt der Spule aus gemessen werden, damit wir unsere Ergebnisse besser vergleichen können. Da unsere Spule warm wurde, hat sich unser Strom während der Messung verändert. Um das B-Feld mit dem Biot-Savart-Gesetz zu berechnen, benötigen wir aber den Strom durch die Spule. Um dieses Problem zu lösen haben wir den Strom zu Beginn des Versuchs gemessen und am Schluss. Zu Beginn also bei einem Abstand von 21,9cm zum Spulenmittelpunkt hatten wir einen Strom von 1,98A. Am Ende unsere Messreihe, bei einem Abstand von -23,1cm von der Spulenmitte hatten wir 1,93A. Nun haben wir angenommen, dass der Strom linear von 1,98 auf 1,93A während unserer Messung abgefallen ist. Deshalb haben wir eine Gerade durch die zwei Punkte (21,9cm / 1,98A) und (-23,1cm / 1,93A) bestimmt und diese Geradengleichung I(t) in das Biot-Savart-Gesetz eingesetzt. db = µ 0I 4πr (d l r) B(z) = NIµ 0 z + l z l 2 2 (5) 3 2l R 2 + (z + l2 )2 R 2 + (z l 2 )2 Mit N=814, l= 20,8cm, R =3,7cm und können wir das Magnetfeld der Spule berechnen. 814 I(t) 4π 10 7 z + B(z) = 0, , 208 I(t) = ( 1 x + 1, 956)A (6) 9 0, (z + l 0,208 )2 Die berechneten Werte befinden sich im Anhang. z 0, , (z l 0,208 )2 T (7) Gruppe: Do-28 9
28 Auswertung In folgendem Schaubild haben wir nun unsere Messpunkte (schwarz) und die theoretisch berechnete Funktion (rot) dargestellt. 0, , ,0 0 6 B / T 0, , , ,3-0,2-0,1 0,0 0,1 0,2 0,3 z / m Abbildung 10: Magnetfeld einer langen Spule Man sieht, dass unsere Messwerte sehr gut mit den theoretisch berechneten Werten übereinstimmen und es so gut wie keine Abweichungen gibt. 4 Inhomogenes Magnetfeld In diesem Teil haben wir die Wirkung eines inhomogenen Feldes auf dia-,para- und ferromagnetische Körper getestet. Dazu haben wir haben wir auf den U-Kern zwei spitze Polschuhe montiert, die ein inhomogenes Feld erzeugen. Das Feld ist direkt zwischen den beiden Spitzen am stärksten. Nun haben wir die drei Stoffe in Form dünner Stäbchen zwischen die Polschuhe gebracht und dann das Magnetfeld eingeschaltet (über die zwei Spulen). Als wir das Aluminium Stäbchen (Paramagnet) zwischen die Polschuhe gebracht haben, wäre zu erwarten gewesen, dass sich das Stäbchen parallel zu den Spitzen dreht. Dieser Effekt war zu erkennen aber leider nur sehr schwach. Beim Eisen (Ferromagnet) war dieser Effekt sehr schön zu sehen. Das Stäbchen hat sich, auch schon bei geringem Strom, parallel zu den Spitzen gedreht. Hier hat man auch gesehen, wie man zwischen einem para- und einem ferromagnetischem Stoff unterscheiden kann. Ein Ferro- Gruppe: Do-28 10
29 Auswertung magnet richtet sich auch schon bei geringerem Magnetfeld (also Stromstärke) aus, wobei eine paramagnetischer Stoff ein stärkeres Magnetfeld benötigt. Als wir das Bismut (diamagnetisch) zwischen die Polschuhe gebracht hatten, hat sich das Stäbchen wie erwartet senkrecht zu den Spitzen ausgerichtet. Gruppe: Do-28 11
30 Auswertung 5 Anhang 5.1 Anhang: Tabelle zu Aufgabe 2.1 I / A B / T B korrigiert / T H / Am -1 H Scher / Am -1 0,0 0, ,00 0,00 5,3 0,011 0,005 22,08 5,48 9,8 0,015 0,009 40,83 10,95 15,0 0,02 0,014 62,50 16,01 20,2 0,025 0,019 84,17 21,08 25,2 0,03 0, ,00 25,32 30,3 0,036 0,03 126,25 26,67 35,3 0,041 0, ,08 30,90 40,0 0,046 0,04 166,67 33,90 35,2 0,042 0, ,67 27,19 29,9 0,036 0,03 124,58 25,01 25,0 0,032 0, ,17 17,88 20,0 0,027 0,021 83,33 13,65 15,0 0,022 0,016 62,50 9,41 8,8 0,017 0,011 36,67 0,19 4,4 0,012 0,006 18,33-1,55 0,0 0,008 0,002 0,00-6,60-5,0 0,002-0,004-20,83-7,54-10,1-0,003-0,009-42,08-12,19-15,0-0,008-0,014-62,50-16,01-20,3-0,014-0,02-84,58-18,19-25,5-0,02-0, ,25-19,96-30,4-0,029-0, ,67-10,57-35,4-0,032-0, ,50-21,41-40,3-0,038-0, ,92-21,93-35,2-0,033-0, ,67-17,28-30,1-0,028-0, ,42-12,63-25,0-0,023-0, ,17-7,98-19,7-0,018-0,024-82,08-2,50-14,6-0,013-0,019-60,83 2,16-10,1-0,009-0,015-42,08 7,62-5,1-0,004-0,01-21,25 11,86 0,0 0-0,006 0,00 19,81 5,5 0, ,92 22,82 9,7 0,011 0,005 40,42 23,74 15,2 0,017 0,011 63,33 26,75 20,2 0,022 0,016 84,17 30,99 24,9 0,028 0, ,75 30,68 30,1 0,033 0, ,42 35,74 35,3 0,04 0, ,08 34,21 40,1 0,045 0, ,08 37,61 Gruppe: Do-28 12
31 Auswertung 5.2 Anhang: Tabelle zu Aufgabe 2.2 I / A B / T B korrigiert / T H / Am -1 H Scher / Am -1 0,00 0, ,00 0,00-0,11-0,125-0,13-475,00-43,77-0,20-0,222-0, ,33-80,33-0,31-0,357-0, ,17-103,44-0,40-0,456-0, ,00-120,95-0,50-0,563-0, ,67-207,47-0,59-0,652-0, ,33-278,74-0,71-0,742-0, ,33-479,49-0,82-0,81-0, ,67-711,38-0,90-0,852-0, ,00-904,65-1,01-0,891-0, , ,31-1,11-0,919-0, , ,79-1,20-0,944-0, , ,68-1,10-0,923-0, , ,09-1,02-0,901-0, , ,78-0,91-0,866-0, ,67-899,92-0,81-0,825-0, ,00-620,36-0,70-0,767-0, ,67-355,44-0,60-0,694-0, ,00-181,55-0,50-0,598-0, ,33-83,60-0,40-0,499-0, ,67 4,44-0,30-0,377-0, ,00 16,54-0,20-0,265-0,27-833,33 61,66-0,10-0,139-0, ,67 60,55 0,00-0,019-0,024 0,00 79,25 0,10 0,109 0, ,67 71,53 0,20 0,226 0, ,33 100,14 0,30 0,348 0, ,00 112,24 0,40 0,457 0, ,67 167,26 0,50 0,568 0, ,33 215,68 0,61 0,666 0, ,67 348,52 0,71 0,741 0, ,33 515,81 0,82 0,813 0, ,67 734,50 0,90 0,851 0, ,00 940,97 1,00 0,888 0, , ,74 1,12 0,923 0, , ,09 1,20 0,944 0, , ,70 1,10 0,923 0, , ,11 1,00 0,889 0, , ,44 0,91 0,865 0, ,67 936,24 0,81 0,824 0, ,00 656,68 0,70 0,767 0, ,67 388,46 Gruppe: Do-28 13
32 0,61 0,698 0, ,67 242,86 0,50 0,596 0, ,33 123,22 0,38 0,471 0, ,33 38,05 0,29 0,373 0, ,33-11,81 0,21 0,268 0, ,00 2,95 0,09 0,123 0, ,00-16,19 0,00 0,019 0,014 0,00-46,23-0,10-0,102-0, ,67-61,63-0,20-0,221-0, ,33-83,63-0,31-0,35-0, ,67-114,11-0,40-0,462-0, ,67-117,73-0,50-0,558-0, ,33-215,68-0,60-0,658-0, ,00-300,42-0,71-0,745-0, ,33-469,58-0,81-0,805-0, ,00-686,40-0,90-0,847-0, ,00-921,16-1,02-0,891-0, , ,80-1,11-0,919-0, , ,79-1,19-0,94-0, , ,40
33 Auswertung 5.3 Anhang: Tabelle zu Aufgabe 3.2 x / cm U / mv z / m B / T 85 0,008 0,219 1,23E ,01 0,209 1,54E ,011 0,199 1,69E ,018 0,189 2,77E ,021 0,179 3,23E ,03 0,169 4,62E ,04 0,159 6,15E ,059 0,149 9,08E ,082 0,139 1,26E ,12 0,129 1,85E ,173 0,119 2,66E ,25 0,109 3,85E ,338 0,099 5,20E ,41 0,089 6,31E ,471 0,079 7,25E ,516 0,069 7,94E ,541 0,059 8,32E ,562 0,049 8,65E ,57 0,039 8,77E ,578 0,029 8,89E ,581 0,019 8,94E ,584 0,009 8,98E ,583-0,001 8,97E ,581-0,011 8,94E ,58-0,021 8,92E ,578-0,031 8,89E ,57-0,041 8,77E ,56-0,051 8,62E ,541-0,061 8,32E ,51-0,071 7,85E ,468-0,081 7,20E ,407-0,091 6,26E ,329-0,101 5,06E ,242-0,111 3,72E ,17-0,121 2,62E ,12-0,131 1,85E ,082-0,141 1,26E ,06-0,151 9,23E ,042-0,161 6,46E ,031-0,171 4,77E ,022-0,181 3,38E ,017-0,191 2,62E ,012-0,201 1,85E ,01-0,211 1,54E ,008-0,221 1,23E ,005-0,231 7,69E-05 Gruppe: Do-28 15
Versuchsvorbereitung P1-80: Magnetfeldmessung
 Versuchsvorbereitung P1-80: Magnetfeldmessung Kathrin Ender Gruppe 10 5. Januar 2008 Inhaltsverzeichnis 1 Induktivität einer Spule 2 1.1 Entmagnetisieren des Kerns............................ 2 1.2 Induktiver
Versuchsvorbereitung P1-80: Magnetfeldmessung Kathrin Ender Gruppe 10 5. Januar 2008 Inhaltsverzeichnis 1 Induktivität einer Spule 2 1.1 Entmagnetisieren des Kerns............................ 2 1.2 Induktiver
N(lT. Datum: tuo*uia*le9. ss/qöi 20.1.a..1.1:1.. (rdüqhne). Fehlerrechnung R 6( Abgabe am: Rückgabe am: I' I
 FAKULTAT FÜR PHYSIK, Universität Karlsruhe (TH) Praktikum Klassische Physik N(lT [email protected] tuo*uia*le9 ss/qöi 20.1.a..1.1:1.. Vers uch :.. Hr,.q.t.ei. f.e!r{.,,n?.\t Li *.J er.r (rdüqhne). Fehlerrechnung
FAKULTAT FÜR PHYSIK, Universität Karlsruhe (TH) Praktikum Klassische Physik N(lT [email protected] tuo*uia*le9 ss/qöi 20.1.a..1.1:1.. Vers uch :.. Hr,.q.t.ei. f.e!r{.,,n?.\t Li *.J er.r (rdüqhne). Fehlerrechnung
Vorbereitung: Ferromagnetische Hysteresis
 Vorbereitung: Ferromagnetische Hysteresis Carsten Röttele 10. Dezember 2011 Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand einer Luftspule 2 1.1 Messung..................................... 2
Vorbereitung: Ferromagnetische Hysteresis Carsten Röttele 10. Dezember 2011 Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand einer Luftspule 2 1.1 Messung..................................... 2
E19 Magnetische Suszeptibilität
 Aufgabenstellung: 1. Untersuchen Sie die räumliche Verteilung des Magnetfeldes eines Elektromagneten und dessen Abhängigkeit vom Spulenstrom. 2. Bestimmen Sie die magnetische Suszeptibilität vorgegebener
Aufgabenstellung: 1. Untersuchen Sie die räumliche Verteilung des Magnetfeldes eines Elektromagneten und dessen Abhängigkeit vom Spulenstrom. 2. Bestimmen Sie die magnetische Suszeptibilität vorgegebener
PD Para- und Diamagnetismus
 PD Para- und Diamagnetismus Blockpraktikum Herbst 2007 (Gruppe 2b) 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Magnetfeld in Materie............................ 2 1.2 Arten von Magnetismus...........................
PD Para- und Diamagnetismus Blockpraktikum Herbst 2007 (Gruppe 2b) 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Magnetfeld in Materie............................ 2 1.2 Arten von Magnetismus...........................
15.Magnetostatik, 16. Induktionsgesetz
 Ablenkung von Teilchenstrahlen im Magnetfeld (Zyklotron u.a.): -> im Magnetfeld B werden geladene Teilchen auf einer Kreisbahn abgelenkt, wenn B senkrecht zu Geschwindigkeit v Kräftegleichgewicht: 2 v
Ablenkung von Teilchenstrahlen im Magnetfeld (Zyklotron u.a.): -> im Magnetfeld B werden geladene Teilchen auf einer Kreisbahn abgelenkt, wenn B senkrecht zu Geschwindigkeit v Kräftegleichgewicht: 2 v
Versuchsvorbereitung: P1-83,84: Ferromagnetische Hysteresis
 Praktikum Klassische Physik I Versuchsvorbereitung: P1-83,84: Ferromagnetische Hysteresis Jingfan Ye Gruppe Mo-11 Karlsruhe, 23. November 2009 Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand einer
Praktikum Klassische Physik I Versuchsvorbereitung: P1-83,84: Ferromagnetische Hysteresis Jingfan Ye Gruppe Mo-11 Karlsruhe, 23. November 2009 Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand einer
E2: Wärmelehre und Elektromagnetismus 18. Vorlesung
 E2: Wärmelehre und Elektromagnetismus 18. Vorlesung 21.06.2018 Barlow-Rad Heute: Telefon nach Bell - Materie im Magnetfeld: Dia-, Para-, Ferromagnetismus - Supraleitung - Faradaysches Induktionsgesetz
E2: Wärmelehre und Elektromagnetismus 18. Vorlesung 21.06.2018 Barlow-Rad Heute: Telefon nach Bell - Materie im Magnetfeld: Dia-, Para-, Ferromagnetismus - Supraleitung - Faradaysches Induktionsgesetz
V 401 : Induktion. Gruppe : Versuchstag: Namen, Matrikel Nr.: Vorgelegt: Hochschule Düsseldorf. Fachbereich EI Testat : Physikalisches Praktikum
 Fachbereich El Gruppe : Namen, Matrikel Nr.: Versuchstag: Vorgelegt: Hochschule Düsseldorf Testat : V 401 : Induktion Zusammenfassung: 01.04.16 Versuch: Induktion Seite 1 von 6 Gruppe : Korrigiert am:
Fachbereich El Gruppe : Namen, Matrikel Nr.: Versuchstag: Vorgelegt: Hochschule Düsseldorf Testat : V 401 : Induktion Zusammenfassung: 01.04.16 Versuch: Induktion Seite 1 von 6 Gruppe : Korrigiert am:
Ferromagnetische Hysterese Versuch P1 83, 84
 Auswertung Ferromagnetische Hysterese Versuch P1 83, 84 Iris Conradi, Melanie Hauck Gruppe Mo-02 19. August 2011 Inhaltsverzeichnis Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand einer Lustspule
Auswertung Ferromagnetische Hysterese Versuch P1 83, 84 Iris Conradi, Melanie Hauck Gruppe Mo-02 19. August 2011 Inhaltsverzeichnis Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand einer Lustspule
Ferromagnetische Hysteresis
 Auswertung Ferromagnetische Hysteresis Stefan Schierle Carsten Röttele 6. Dezember 2011 Inhaltsverzeichnis 1 Induktion und Verlustwiderstand einer Luftspule 2 1.1 Messung.....................................
Auswertung Ferromagnetische Hysteresis Stefan Schierle Carsten Röttele 6. Dezember 2011 Inhaltsverzeichnis 1 Induktion und Verlustwiderstand einer Luftspule 2 1.1 Messung.....................................
3.6 Materie im Magnetfeld
 3.6 Materie im Magnetfeld Vorversuche Die magnetische Feldstärke, gemessen mit einer sog. Hall-Sonde, ist am Ende einer stromdurchflossenen Spule deutlich höher, wenn sich in der Spule ein Eisenkern statt
3.6 Materie im Magnetfeld Vorversuche Die magnetische Feldstärke, gemessen mit einer sog. Hall-Sonde, ist am Ende einer stromdurchflossenen Spule deutlich höher, wenn sich in der Spule ein Eisenkern statt
Ferromagnetische Hysterese Versuch P1-83,84
 Vorbereitung Ferromagnetische Hysterese Versuch P1-83,84 Iris Conradi Gruppe Mo-02 28. November 2010 Inhaltsverzeichnis Inhaltsverzeichnis Grundlegende Erklärungen 3 1 Induktivität und Verlustwiderstand
Vorbereitung Ferromagnetische Hysterese Versuch P1-83,84 Iris Conradi Gruppe Mo-02 28. November 2010 Inhaltsverzeichnis Inhaltsverzeichnis Grundlegende Erklärungen 3 1 Induktivität und Verlustwiderstand
3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P]
![3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P] 3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P]](/thumbs/56/38171884.jpg) 3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P] B = µ 0 I 4 π ds (r r ) r r 3 a) Beschreiben Sie die im Gesetz von Biot-Savart vorkommenden Größen (rechts vom Integral). b) Zeigen Sie, dass das Biot-Savartsche
3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P] B = µ 0 I 4 π ds (r r ) r r 3 a) Beschreiben Sie die im Gesetz von Biot-Savart vorkommenden Größen (rechts vom Integral). b) Zeigen Sie, dass das Biot-Savartsche
Ferromagnetische Hysteresis
 Physikalisches Anfängerpraktikum 1 Gruppe Mo-16 Wintersemester 2005/06 Julian Merkert (1229929) Versuch: P1-83 Ferromagnetische Hysteresis - Vorbereitung - Vorbemerkung Als Hinführung zum Thema Ferromagnetismus
Physikalisches Anfängerpraktikum 1 Gruppe Mo-16 Wintersemester 2005/06 Julian Merkert (1229929) Versuch: P1-83 Ferromagnetische Hysteresis - Vorbereitung - Vorbemerkung Als Hinführung zum Thema Ferromagnetismus
Protokoll zum Versuch
 Protokoll zum Versuch Ferromagnetische Hysterese Kirstin Hübner Armin Burgmeier Gruppe 15 13. Oktober 2008 1 Induktivität und Verlustwiderstand einer Luftspule 1.1 Messungen und Berechnen Wir haben die
Protokoll zum Versuch Ferromagnetische Hysterese Kirstin Hübner Armin Burgmeier Gruppe 15 13. Oktober 2008 1 Induktivität und Verlustwiderstand einer Luftspule 1.1 Messungen und Berechnen Wir haben die
Auswertung des Versuchs P1-83,84 : Ferromagnetische Hysteresis
 Auswertung des Versuchs P1-83,84 : Ferromagnetische Hysteresis Marc Ganzhorn Tobias Großmann Bemerkung Alle in diesem Versuch aufgenommenen Hysteresis-Kurven haben wir gesondert im Anhang an diese Auswertung
Auswertung des Versuchs P1-83,84 : Ferromagnetische Hysteresis Marc Ganzhorn Tobias Großmann Bemerkung Alle in diesem Versuch aufgenommenen Hysteresis-Kurven haben wir gesondert im Anhang an diese Auswertung
Physik 4 Praktikum Auswertung Hall-Effekt
 Physik 4 Praktikum Auswertung Hall-Effekt Von J.W., I.G. 2014 Seite 1. Kurzfassung......... 2 2. Theorie.......... 2 2.1. Elektrischer Strom in Halbleitern..... 2 2.2. Hall-Effekt......... 3 3. Durchführung.........
Physik 4 Praktikum Auswertung Hall-Effekt Von J.W., I.G. 2014 Seite 1. Kurzfassung......... 2 2. Theorie.......... 2 2.1. Elektrischer Strom in Halbleitern..... 2 2.2. Hall-Effekt......... 3 3. Durchführung.........
Physikalisches Anfaengerpraktikum. Hysteresie
 Physikalisches Anfaengerpraktikum Hysteresie Ausarbeitung von Constantin Tomaras & David Weisgerber (Gruppe 10) Montag, 28. November 2005 email: [email protected] 1 (1) Einleitung Eines der interessantesten
Physikalisches Anfaengerpraktikum Hysteresie Ausarbeitung von Constantin Tomaras & David Weisgerber (Gruppe 10) Montag, 28. November 2005 email: [email protected] 1 (1) Einleitung Eines der interessantesten
E2: Wärmelehre und Elektromagnetismus 18. Vorlesung
 E2: Wärmelehre und Elektromagnetismus 18. Vorlesung 21.06.2018 Barlow-Rad Heute: Telefon nach Bell - Materie im Magnetfeld: Dia-, Para-, Ferromagnetismus - Supraleitung - Faradaysches Induktionsgesetz
E2: Wärmelehre und Elektromagnetismus 18. Vorlesung 21.06.2018 Barlow-Rad Heute: Telefon nach Bell - Materie im Magnetfeld: Dia-, Para-, Ferromagnetismus - Supraleitung - Faradaysches Induktionsgesetz
Verwandte Begriffe Maxwell-Gleichungen, elektrisches Wirbelfeld, Magnetfeld von Spulen, magnetischer Fluss, induzierte Spannung.
 Verwandte Begriffe Maxwell-Gleichungen, elektrisches Wirbelfeld, Magnetfeld von Spulen, magnetischer Fluss, induzierte Spannung. Prinzip In einer langen Spule wird ein Magnetfeld mit variabler Frequenz
Verwandte Begriffe Maxwell-Gleichungen, elektrisches Wirbelfeld, Magnetfeld von Spulen, magnetischer Fluss, induzierte Spannung. Prinzip In einer langen Spule wird ein Magnetfeld mit variabler Frequenz
Ferienkurs Experimentalphysik 2
 Ferienkurs Experimentalphysik 2 Lösung Übungsblatt 2 Tutoren: Elena Kaiser und Matthias Golibrzuch 2 Elektrischer Strom 2.1 Elektrischer Widerstand Ein Bügeleisen von 235 V / 300 W hat eine Heizwicklung
Ferienkurs Experimentalphysik 2 Lösung Übungsblatt 2 Tutoren: Elena Kaiser und Matthias Golibrzuch 2 Elektrischer Strom 2.1 Elektrischer Widerstand Ein Bügeleisen von 235 V / 300 W hat eine Heizwicklung
Praktikum Grundlagen der Elektrotechnik 2 (GET2) Versuch 1
 Werner-v.-Siemens-Labor für elektrische Antriebssysteme Prof. Dr.-Ing. Dr. h.c. H. Biechl Prof. Dr.-Ing. E.-P. Meyer Praktikum Grundlagen der Elektrotechnik 2 (GET2) Versuch 1 Magnetisches Feld Lernziel:
Werner-v.-Siemens-Labor für elektrische Antriebssysteme Prof. Dr.-Ing. Dr. h.c. H. Biechl Prof. Dr.-Ing. E.-P. Meyer Praktikum Grundlagen der Elektrotechnik 2 (GET2) Versuch 1 Magnetisches Feld Lernziel:
Ferromagnetische Hysteresis Versuchsvorbereitung
 Versuche P1-32,33,34 Ferromagnetische Hysteresis Versuchsvorbereitung Thomas Keck, Gruppe: Mo-3 Karlsruhe Institut für Technologie, Bachelor Physik Versuchstag: 22.11.2010 1 Inhaltsverzeichnis 1 Begriffsbildung
Versuche P1-32,33,34 Ferromagnetische Hysteresis Versuchsvorbereitung Thomas Keck, Gruppe: Mo-3 Karlsruhe Institut für Technologie, Bachelor Physik Versuchstag: 22.11.2010 1 Inhaltsverzeichnis 1 Begriffsbildung
Ziel: Kennenlernen von Feldverläufen und Methoden der Feldmessung. 1. Elektrisches Feld
 Ziel: Kennenlernen von Feldverläufen und Methoden der Feldmessung 1. Elektrisches Feld 1.1 Nehmen Sie den Potentialverlauf einer der folgenden Elektrodenanordnungen auf: - Plattenkondensator mit Störung
Ziel: Kennenlernen von Feldverläufen und Methoden der Feldmessung 1. Elektrisches Feld 1.1 Nehmen Sie den Potentialverlauf einer der folgenden Elektrodenanordnungen auf: - Plattenkondensator mit Störung
Materie im Magnetfeld
 . Stromschleifen - Permanentmagnet Materie im Magnetfeld EX-II SS007 = > µmag = I S ˆn S = a b µ bahn = e m L µ spin = e m S Stromschleife im Magnetfeld Magnetisierung inhomogenes Magnetfeld = D = µmag
. Stromschleifen - Permanentmagnet Materie im Magnetfeld EX-II SS007 = > µmag = I S ˆn S = a b µ bahn = e m L µ spin = e m S Stromschleife im Magnetfeld Magnetisierung inhomogenes Magnetfeld = D = µmag
Magnetismus. Prof. DI Michael Steiner
 Magnetismus Prof. DI Michael Steiner www.htl1-klagenfurt.at Magnetismus Natürlicher Künstlicher Magneteisenstein Magnetit Permanentmagnete Stabmagnet Ringmagnet Hufeisenmagnet Magnetnadel Temporäre Magnete
Magnetismus Prof. DI Michael Steiner www.htl1-klagenfurt.at Magnetismus Natürlicher Künstlicher Magneteisenstein Magnetit Permanentmagnete Stabmagnet Ringmagnet Hufeisenmagnet Magnetnadel Temporäre Magnete
Versuch 13: Magnetfeld von Spulen
 Versuch 13: Magnetfeld von Spulen Inhaltsverzeichnis 1 Einleitung 3 2 Theorie 3 2.1 Maxwell-Gleichungen.............................. 3 2.2 Biot-Savart-Gesetz............................... 3 3 Durchführung
Versuch 13: Magnetfeld von Spulen Inhaltsverzeichnis 1 Einleitung 3 2 Theorie 3 2.1 Maxwell-Gleichungen.............................. 3 2.2 Biot-Savart-Gesetz............................... 3 3 Durchführung
Magnetisches Feld. Grunderscheinungen Magnetismus - Dauermagnete
 Magnetisches Feld Grunderscheinungen Magnetismus - Dauermagnete jeder drehbar gelagerte Magnet richtet sich in Nord-Süd-Richtung aus; Pol nach Norden heißt Nordpol jeder Magnet hat Nord- und Südpol; untrennbar
Magnetisches Feld Grunderscheinungen Magnetismus - Dauermagnete jeder drehbar gelagerte Magnet richtet sich in Nord-Süd-Richtung aus; Pol nach Norden heißt Nordpol jeder Magnet hat Nord- und Südpol; untrennbar
20. Vorlesung EP. III Elektrizität und Magnetismus. 19. Magnetische Felder Fortsetzung: Materie im Magnetfeld 20. Induktion 21.
 20. Vorlesung EP III Elektrizität und Magnetismus 19. Magnetische Felder Fortsetzung: Materie im Magnetfeld 20. Induktion 21. Wechselstrom Versuche: Induktion: Handdynamo und Thomson-Transformator Diamagnetismus:
20. Vorlesung EP III Elektrizität und Magnetismus 19. Magnetische Felder Fortsetzung: Materie im Magnetfeld 20. Induktion 21. Wechselstrom Versuche: Induktion: Handdynamo und Thomson-Transformator Diamagnetismus:
Physik LK 12, 3. Kursarbeit Induktion - Lösung
 Physik K 1, 3. Kursarbeit Induktion - ösung.0.013 Aufgabe I: Induktion 1. Thomson ingversuch 1.1 Beschreibe den Thomson'schen ingversuch in Aufbau und Beobachtung und erkläre die grundlegenden physikalischen
Physik K 1, 3. Kursarbeit Induktion - ösung.0.013 Aufgabe I: Induktion 1. Thomson ingversuch 1.1 Beschreibe den Thomson'schen ingversuch in Aufbau und Beobachtung und erkläre die grundlegenden physikalischen
III Elektrizität und Magnetismus
 20. Vorlesung EP III Elektrizität und Magnetismus 19. Magnetische Felder 20. Induktion Versuche: Diamagnetismus, Supraleiter Induktion Leiterschleife, bewegter Magnet Induktion mit Änderung der Fläche
20. Vorlesung EP III Elektrizität und Magnetismus 19. Magnetische Felder 20. Induktion Versuche: Diamagnetismus, Supraleiter Induktion Leiterschleife, bewegter Magnet Induktion mit Änderung der Fläche
3. Klausur in K1 am
 Name: Punkte: Note: Ø: Kernfach Physik Abzüge für Darstellung: Rundung: 3. Klausur in K am.. 0 Achte auf gute Darstellung und vergiss nicht Geg., Ges., Formeln herleiten, Einheiten, Rundung...! 9 Elementarladung:
Name: Punkte: Note: Ø: Kernfach Physik Abzüge für Darstellung: Rundung: 3. Klausur in K am.. 0 Achte auf gute Darstellung und vergiss nicht Geg., Ges., Formeln herleiten, Einheiten, Rundung...! 9 Elementarladung:
316 - Magnetfeldmessungen
 316 - Magnetfeldmessungen 1. Aufgaben 1.1 Die magnetische Induktion B eines Elektromagneten auf der Polschuhachse ist mit einer Hall- Sonde in Abhängigkeit vom Magnetisierungsstrom für unterschiedliche
316 - Magnetfeldmessungen 1. Aufgaben 1.1 Die magnetische Induktion B eines Elektromagneten auf der Polschuhachse ist mit einer Hall- Sonde in Abhängigkeit vom Magnetisierungsstrom für unterschiedliche
Magnetismus. Prinzip: Kein Monopol nur Dipole. Kräfte:
 Elektromagnetismus Magnetismus Prinzip: Kein Monopol nur Dipole Kräfte: S N Richtung des Magnetischen Feldes I B Kraft auf Ladungen im B-Feld + Proportionalitätskonstante B FM = q v B Durch Messung: LORENTZ
Elektromagnetismus Magnetismus Prinzip: Kein Monopol nur Dipole Kräfte: S N Richtung des Magnetischen Feldes I B Kraft auf Ladungen im B-Feld + Proportionalitätskonstante B FM = q v B Durch Messung: LORENTZ
Versuchsauswertung: P1-83,84: Ferromagnetische Hysteresis
 Praktikum Klassische Physik I Versuchsauswertung: P1-83,84: Ferromagnetische Hysteresis Christian Buntin, Jingfan Ye Gruppe Mo-11 Karlsruhe, 23. November 2009 Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand
Praktikum Klassische Physik I Versuchsauswertung: P1-83,84: Ferromagnetische Hysteresis Christian Buntin, Jingfan Ye Gruppe Mo-11 Karlsruhe, 23. November 2009 Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand
Magnetische Suszeptibilität: Magnetismusarten
 agnetische Suszeptibilität, agnetismusarten agnetische Suszeptibilität: Im allgemeinen ist H: = χ m H χ m = magnetische Suszeptibilität [χ m ] = 1 Damit wird: at = µ 0 ( H + ) = µ 0 (1 + χ m ) }{{} =µ
agnetische Suszeptibilität, agnetismusarten agnetische Suszeptibilität: Im allgemeinen ist H: = χ m H χ m = magnetische Suszeptibilität [χ m ] = 1 Damit wird: at = µ 0 ( H + ) = µ 0 (1 + χ m ) }{{} =µ
Grundpraktikum der Physik. Versuch Nr. 25 TRANSFORMATOR. Versuchsziel: Bestimmung der physikalischen Eigenschaften eines Transformators
 Grundpraktikum der Physik Versuch Nr. 25 TRANSFORMATOR Versuchsziel: Bestimmung der physikalischen Eigenschaften eines Transformators 1 1. Einführung Für den Transport elektrischer Energie über weite Entfernungen
Grundpraktikum der Physik Versuch Nr. 25 TRANSFORMATOR Versuchsziel: Bestimmung der physikalischen Eigenschaften eines Transformators 1 1. Einführung Für den Transport elektrischer Energie über weite Entfernungen
Institut für Elektrotechnik Übungen zu Elektrotechnik I Version 3.0, 02/2002 Laborunterlagen
 Institut für Elektrotechnik Übungen zu Elektrotechnik I Version 3.0, 0/00 7 Magnetismus 7. Grundlagen magnetischer Kreise Im folgenden wird die Vorgehensweise bei der Untersuchung eines magnetischen Kreises
Institut für Elektrotechnik Übungen zu Elektrotechnik I Version 3.0, 0/00 7 Magnetismus 7. Grundlagen magnetischer Kreise Im folgenden wird die Vorgehensweise bei der Untersuchung eines magnetischen Kreises
Praktikum EE2 Grundlagen der Elektrotechnik Teil 2
 Praktikum EE2 Grundlagen der Elektrotechnik Teil 2 Name: Studienrichtung: Versuch 6 Messen der magnetischen Flussdichte Versuch 7 Transformator Versuch 8 Helmholtzspulen Versuch 9 Leistungsmessung Testat
Praktikum EE2 Grundlagen der Elektrotechnik Teil 2 Name: Studienrichtung: Versuch 6 Messen der magnetischen Flussdichte Versuch 7 Transformator Versuch 8 Helmholtzspulen Versuch 9 Leistungsmessung Testat
Labornetzgerät, Digitalmultimeter, Teslameter mit digitaler axialer Feldsonde (Hallsonde), verschiedene
 Fakultät für Physik und Geowissenschaften Physikalisches Grundpraktikum E 7a Spulenfelder Aufgaben 1. Überprüfen Sie die Kalibrierung des Teslameters mit einer Kalibrierspule.. Nehmen Sie die Flussdichte
Fakultät für Physik und Geowissenschaften Physikalisches Grundpraktikum E 7a Spulenfelder Aufgaben 1. Überprüfen Sie die Kalibrierung des Teslameters mit einer Kalibrierspule.. Nehmen Sie die Flussdichte
Dia- und Paramagnetismus
 Physikalisches Praktikum für das Hauptfach Physik Versuch 19 Dia- und Paramagnetismus Wintersemester 2005 / 2006 Name: Mitarbeiter: EMail: Gruppe: Daniel Scholz Hauke Rohmeyer [email protected] B9 Assistent:
Physikalisches Praktikum für das Hauptfach Physik Versuch 19 Dia- und Paramagnetismus Wintersemester 2005 / 2006 Name: Mitarbeiter: EMail: Gruppe: Daniel Scholz Hauke Rohmeyer [email protected] B9 Assistent:
Übungen zu Experimentalphysik 2
 Physik Department, Technische Universität München, PD Dr. W. Schindler Übungen zu Experimentalphysik 2 SS 13 - Lösungen zu Übungsblatt 4 1 Schiefe Ebene im Magnetfeld In einem vertikalen, homogenen Magnetfeld
Physik Department, Technische Universität München, PD Dr. W. Schindler Übungen zu Experimentalphysik 2 SS 13 - Lösungen zu Übungsblatt 4 1 Schiefe Ebene im Magnetfeld In einem vertikalen, homogenen Magnetfeld
Repetitionen Magnetismus
 TECHNOLOGISCHE GRUNDLAGEN MAGNETISMUS Kapitel Repetitionen Magnetismus Θ = Θ l m = H I I N H µ µ = 0 r N B B = Φ A M agn. Fluss Φ Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1,
TECHNOLOGISCHE GRUNDLAGEN MAGNETISMUS Kapitel Repetitionen Magnetismus Θ = Θ l m = H I I N H µ µ = 0 r N B B = Φ A M agn. Fluss Φ Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1,
Versuch P1-83 Ferromagnetische Hysteresis Auswertung
 Versuch P1-83 Ferromagnetische Hysteresis Auswertung Gruppe Mo-19 Yannick Augenstein Patrick Kuntze Versuchsdurchführung: Montag, 24.10.2011 1 Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand einer
Versuch P1-83 Ferromagnetische Hysteresis Auswertung Gruppe Mo-19 Yannick Augenstein Patrick Kuntze Versuchsdurchführung: Montag, 24.10.2011 1 Inhaltsverzeichnis 1 Induktivität und Verlustwiderstand einer
Vorbereitung: elektrische Messverfahren
 Vorbereitung: elektrische Messverfahren Marcel Köpke 29.10.2011 Inhaltsverzeichnis 1 Ohmscher Widerstand 3 1.1 Innenwiderstand des µa Multizets...................... 3 1.2 Innenwiderstand des AVΩ Multizets.....................
Vorbereitung: elektrische Messverfahren Marcel Köpke 29.10.2011 Inhaltsverzeichnis 1 Ohmscher Widerstand 3 1.1 Innenwiderstand des µa Multizets...................... 3 1.2 Innenwiderstand des AVΩ Multizets.....................
Physikalisches Praktikum 3. Semester
 Torsten Leddig 3.November 004 Mathias Arbeiter Betreuer: Dr.Hoppe Physikalisches Praktikum 3. Semester - Feldmessung - 1 Aufgaben: 1. Elektrisches Feld 1.1 Nehmen Sie den Potenziallinienverlauf einer der
Torsten Leddig 3.November 004 Mathias Arbeiter Betreuer: Dr.Hoppe Physikalisches Praktikum 3. Semester - Feldmessung - 1 Aufgaben: 1. Elektrisches Feld 1.1 Nehmen Sie den Potenziallinienverlauf einer der
Physikalisches Grundpraktikum E13 Hystereseverhalten
 Aufgabenstellung: 1. Messen Sie eine Schar von Hysteresekurven und leiten Sie daraus die Neukurve ab. Ermitteln Sie für jede Hysteresekurve die Koerzitivfeldstärke und die Remanenz. 2. Stellen Sie die
Aufgabenstellung: 1. Messen Sie eine Schar von Hysteresekurven und leiten Sie daraus die Neukurve ab. Ermitteln Sie für jede Hysteresekurve die Koerzitivfeldstärke und die Remanenz. 2. Stellen Sie die
Stromdurchflossene Leiter im Magnetfeld, Halleffekt
 Protokoll zum Versuch Stromdurchflossene Leiter im Magnetfeld, Halleffekt Kirstin Hübner (1348630) Armin Burgmeier (1347488) Gruppe 15 2. Dezember 2007 1 Messung des magnetischen Feldes mit einer Feldplatte
Protokoll zum Versuch Stromdurchflossene Leiter im Magnetfeld, Halleffekt Kirstin Hübner (1348630) Armin Burgmeier (1347488) Gruppe 15 2. Dezember 2007 1 Messung des magnetischen Feldes mit einer Feldplatte
E2: Wärmelehre und Elektromagnetismus 17. Vorlesung
 E2: Wärmelehre und Elektromagnetismus 17. Vorlesung 18.06.2018 Barlow-Rad Elektromagnet Telefon nach Bell Wissenschaftliche Instrumente aus dem 18. und 19. Jahrhundert aus der Sammlung des Teylers Museum
E2: Wärmelehre und Elektromagnetismus 17. Vorlesung 18.06.2018 Barlow-Rad Elektromagnet Telefon nach Bell Wissenschaftliche Instrumente aus dem 18. und 19. Jahrhundert aus der Sammlung des Teylers Museum
Ferienkurs Experimentalphysik 2
 Ferienkurs Experimentalphysik 2 Vorlesung 4 Magnetostatik Andreas Brenneis, Marcus Jung, Ann-Kathrin Straub 16.09.2010 1 Allgemeines In der Magnetostatik gibt es viele Analogien zur Elektrostatik. Ein
Ferienkurs Experimentalphysik 2 Vorlesung 4 Magnetostatik Andreas Brenneis, Marcus Jung, Ann-Kathrin Straub 16.09.2010 1 Allgemeines In der Magnetostatik gibt es viele Analogien zur Elektrostatik. Ein
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 30. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 30. 06.
Elektrizitätslehre und Magnetismus Othmar Marti 30. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 30. 06.
Handout zur Veranstaltung Demonstrationsexperimente: Hallsonde von Leybold
 Handout zur Veranstaltung Demonstrationsexperimente: Hallsonde von Leybold Valentin Conrad 22.12.2006 Didaktik der Physik Universität Bayreuth 1 1 Einführung Die Hallsonde ist ein Messgerät um Magnetfelder
Handout zur Veranstaltung Demonstrationsexperimente: Hallsonde von Leybold Valentin Conrad 22.12.2006 Didaktik der Physik Universität Bayreuth 1 1 Einführung Die Hallsonde ist ein Messgerät um Magnetfelder
Inhalt. Kapitel 4: Magnetisches Feld
 Inhalt Kapitel 4: Magnetische Feldstärke Magnetischer Fluss und magnetische Flussdichte Induktion Selbstinduktion und Induktivität Energie im magnetischen Feld A. Strey, DHBW Stuttgart, 015 1 Magnetische
Inhalt Kapitel 4: Magnetische Feldstärke Magnetischer Fluss und magnetische Flussdichte Induktion Selbstinduktion und Induktivität Energie im magnetischen Feld A. Strey, DHBW Stuttgart, 015 1 Magnetische
Versuch 15 Dia- und Paramagnetismus
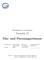 Physikalisches A-Praktikum Versuch 15 Dia- und Paramagnetismus Praktikanten: Gruppe: Julius Strake Niklas Bölter B006 Betreuer: Johannes Schmidt Durchgeführt: 07.09.2012 Unterschrift: E-Mail: [email protected]
Physikalisches A-Praktikum Versuch 15 Dia- und Paramagnetismus Praktikanten: Gruppe: Julius Strake Niklas Bölter B006 Betreuer: Johannes Schmidt Durchgeführt: 07.09.2012 Unterschrift: E-Mail: [email protected]
Induktion. Die in Rot eingezeichnete Größe Lorentzkraft ist die Folge des Stromflusses im Magnetfeld.
 Induktion Die elektromagnetische Induktion ist der Umkehrprozess zu dem stromdurchflossenen Leiter, der ein Magnetfeld erzeugt. Bei der Induktion wird in einem Leiter, der sich in einem Magnetfeld bewegt,
Induktion Die elektromagnetische Induktion ist der Umkehrprozess zu dem stromdurchflossenen Leiter, der ein Magnetfeld erzeugt. Bei der Induktion wird in einem Leiter, der sich in einem Magnetfeld bewegt,
LK Lorentzkraft. Inhaltsverzeichnis. Moritz Stoll, Marcel Schmittfull (Gruppe 2) 25. April Einführung 2
 LK Lorentzkraft Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Magnetfeld dünner Leiter und Spulen......... 2 2.2 Lorentzkraft........................
LK Lorentzkraft Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Magnetfeld dünner Leiter und Spulen......... 2 2.2 Lorentzkraft........................
PHYSIKALISCHES PRAKTIKUM FÜR ANFÄNGER. E 5 - Magnetfeld
 Universität - GH Essen Fachbereich 7 - Physik PHYSIKALISCHES PRAKTIKUM FÜR ANFÄNGER Versuch: E 5 - Magnetfeld 1. Grundlagen Magnetfeld einer Kreisspule (magnetische Feldstärke, magnetische Induktion, Biot-Savartsches
Universität - GH Essen Fachbereich 7 - Physik PHYSIKALISCHES PRAKTIKUM FÜR ANFÄNGER Versuch: E 5 - Magnetfeld 1. Grundlagen Magnetfeld einer Kreisspule (magnetische Feldstärke, magnetische Induktion, Biot-Savartsches
Hysteresekurve und magnetische Suszeptbilität
 M.Links & R.Garreis Hysteresekurve und magnetische Suszeptbilität Anfängerpraktikum SS 2013 Martin Link und Rebekka Garreis 10.06.2013 Universtität Konstanz bei Phillip Knappe 1 M.Links & R.Garreis Inhaltsverzeichnis
M.Links & R.Garreis Hysteresekurve und magnetische Suszeptbilität Anfängerpraktikum SS 2013 Martin Link und Rebekka Garreis 10.06.2013 Universtität Konstanz bei Phillip Knappe 1 M.Links & R.Garreis Inhaltsverzeichnis
Universität Ulm Fachbereich Physik Grundpraktikum Physik
 Universität Ulm Fachbereich Physik Grundpraktikum Physik Versuchsanleitung Transformator Nummer: 25 Kompiliert am: 19. Dezember 2018 Letzte Änderung: 19.12.2018 Beschreibung: Webseite: Bestimmung der physikalischen
Universität Ulm Fachbereich Physik Grundpraktikum Physik Versuchsanleitung Transformator Nummer: 25 Kompiliert am: 19. Dezember 2018 Letzte Änderung: 19.12.2018 Beschreibung: Webseite: Bestimmung der physikalischen
Elektrische Messverfahren
 Vorbereitung Elektrische Messverfahren Carsten Röttele 20. Dezember 2011 Inhaltsverzeichnis 1 Messungen bei Gleichstrom 2 1.1 Innenwiderstand des µa-multizets...................... 2 1.2 Innenwiderstand
Vorbereitung Elektrische Messverfahren Carsten Röttele 20. Dezember 2011 Inhaltsverzeichnis 1 Messungen bei Gleichstrom 2 1.1 Innenwiderstand des µa-multizets...................... 2 1.2 Innenwiderstand
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 26. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 26. 06.
Elektrizitätslehre und Magnetismus Othmar Marti 26. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 26. 06.
Magnetische Induktion Φ = Der magnetische Fluss Φ durch eine Fläche A ist definiert als
 E8 Magnetische Induktion Die Induktionsspannung wird in Abhängigkeit von Magnetfeldgrößen und Induktionsspulenarten untersucht und die Messergebnisse mit den theoretischen Voraussagen verglichen.. heoretische
E8 Magnetische Induktion Die Induktionsspannung wird in Abhängigkeit von Magnetfeldgrößen und Induktionsspulenarten untersucht und die Messergebnisse mit den theoretischen Voraussagen verglichen.. heoretische
Magnetismus der Materie. Bernd Fercher David Schweiger
 Magnetismus der Materie Bernd Fercher David Schweiger Einleitung Erste Beobachtunge in China und Kleinasien Um 1100 Navigation von Schiffen Magnetismus wird durch Magnetfeld beschrieben dieses wird durch
Magnetismus der Materie Bernd Fercher David Schweiger Einleitung Erste Beobachtunge in China und Kleinasien Um 1100 Navigation von Schiffen Magnetismus wird durch Magnetfeld beschrieben dieses wird durch
Ich kann mindestens drei Anwendungsbeispiele von Elektromagneten aufzählen.
 1 MAGNETISMUS 1 Magnetismus Detaillierte Lernziele: 1.1 Dauermagnetismus Ich kann mindestens drei ferromagnetische Werkstoffe aufzählen. Ich kann Nord- und Südpol mit der richtigen Farbe kennzeichnen.
1 MAGNETISMUS 1 Magnetismus Detaillierte Lernziele: 1.1 Dauermagnetismus Ich kann mindestens drei ferromagnetische Werkstoffe aufzählen. Ich kann Nord- und Südpol mit der richtigen Farbe kennzeichnen.
Physikalisches Praktikum II Bachelor Physikalische Technik: Lasertechnik Prof. Dr. H.-Ch. Mertins, MSc. M. Gilbert
 Physikalisches Praktikum II Bachelor Physikalische Technik: Lasertechnik Prof. Dr. H.-h. Mertins, MSc. M. Gilbert FK04 Ferromagnetismus & magnetische Werkstoffe (Pr_PhII_FK04_Magnetismus_7, 24.10.2015)
Physikalisches Praktikum II Bachelor Physikalische Technik: Lasertechnik Prof. Dr. H.-h. Mertins, MSc. M. Gilbert FK04 Ferromagnetismus & magnetische Werkstoffe (Pr_PhII_FK04_Magnetismus_7, 24.10.2015)
Versuch P1-83,84 Ferromagnetische Hysteresis. Auswertung. Von Ingo Medebach und Jan Oertlin. 4. Januar 2010
 Versuch P1-83,84 Ferromagnetische Hysteresis Auswertung Von Ingo Medebach und Jan Oertlin 4. Januar 2010 Inhaltsverzeichnis 1. Induktivität und Verlustwiderstand einer Luftspule...2 1.1. Induktivität und
Versuch P1-83,84 Ferromagnetische Hysteresis Auswertung Von Ingo Medebach und Jan Oertlin 4. Januar 2010 Inhaltsverzeichnis 1. Induktivität und Verlustwiderstand einer Luftspule...2 1.1. Induktivität und
Abiturprüfung Physik, Leistungskurs
 Seite 1 von 8 Abiturprüfung 2013 Physik, Leistungskurs Aufgabenstellung: Aufgabe: Aspekte zur experimentellen Überprüfung des Induktionsgesetzes In der folgenden Aufgabe soll eine Teilaussage des allgemeinen
Seite 1 von 8 Abiturprüfung 2013 Physik, Leistungskurs Aufgabenstellung: Aufgabe: Aspekte zur experimentellen Überprüfung des Induktionsgesetzes In der folgenden Aufgabe soll eine Teilaussage des allgemeinen
Versuch 25: Der Transformator
 Versuch 25: Der Transformator Praktikum der Physik Oliver Heinrich Bernd Kugler L2 11.Mai.2007 Abgabe: 25.Mai.2007, 08.Juni.2007 Betreuer: Andreas Kleiner
Versuch 25: Der Transformator Praktikum der Physik Oliver Heinrich Bernd Kugler L2 11.Mai.2007 Abgabe: 25.Mai.2007, 08.Juni.2007 Betreuer: Andreas Kleiner
Praktikum II TR: Transformator
 Praktikum II TR: Transformator Betreuer: Dr. Torsten Hehl Hanno Rein [email protected] Florian Jessen [email protected] 30. März 2004 Made with L A TEX and Gnuplot Praktikum
Praktikum II TR: Transformator Betreuer: Dr. Torsten Hehl Hanno Rein [email protected] Florian Jessen [email protected] 30. März 2004 Made with L A TEX and Gnuplot Praktikum
Diplomvorprüfung WS 2009/10 Grundlagen der Elektrotechnik Dauer: 90 Minuten
 Diplomvorprüfung Grundlagen der Elektrotechnik Seite 1 von 8 Hochschule München Fakultät 03 Zugelassene Hilfsmittel: Taschenrechner, zwei Blatt DIN A4 eigene Aufzeichnungen Diplomvorprüfung WS 2009/10
Diplomvorprüfung Grundlagen der Elektrotechnik Seite 1 von 8 Hochschule München Fakultät 03 Zugelassene Hilfsmittel: Taschenrechner, zwei Blatt DIN A4 eigene Aufzeichnungen Diplomvorprüfung WS 2009/10
Elektrostaitische Felder
 Elektrostaitische Felder Grundlagen zu den elektrischen Felder 1 homogenes Feld des Plattenkondensators inhomogenes Feld einer Punktladung Bei einem Plattenkondensator verlaufen die Feldlinien parallel
Elektrostaitische Felder Grundlagen zu den elektrischen Felder 1 homogenes Feld des Plattenkondensators inhomogenes Feld einer Punktladung Bei einem Plattenkondensator verlaufen die Feldlinien parallel
Zulassungstest zur Physik II für Chemiker
 SoSe 2016 Zulassungstest zur Physik II für Chemiker 03.08.16 Name: Matrikelnummer: T1 T2 T3 T4 T5 T6 T7 T8 T9 T10 T TOT.../4.../4.../4.../4.../4.../4.../4.../4.../4.../4.../40 R1 R2 R3 R4 R TOT.../6.../6.../6.../6.../24
SoSe 2016 Zulassungstest zur Physik II für Chemiker 03.08.16 Name: Matrikelnummer: T1 T2 T3 T4 T5 T6 T7 T8 T9 T10 T TOT.../4.../4.../4.../4.../4.../4.../4.../4.../4.../4.../40 R1 R2 R3 R4 R TOT.../6.../6.../6.../6.../24
Vorlesung 5: Magnetische Induktion
 Vorlesung 5: Magnetische Induktion, [email protected] Folien/Material zur Vorlesung auf: www.desy.de/~steinbru/physikzahnmed [email protected] 1 WS 2016/17 Magnetische Induktion Bisher:
Vorlesung 5: Magnetische Induktion, [email protected] Folien/Material zur Vorlesung auf: www.desy.de/~steinbru/physikzahnmed [email protected] 1 WS 2016/17 Magnetische Induktion Bisher:
Physik GK ph1, 2. Kursarbeit Elektromagnetismus Lösung =10V ein Strom von =2mA. Berechne R 0.
 Physik GK ph,. Kursarbeit Elektromagnetismus Lösung.04.05 Aufgabe : Stromkreise / Ohmsches Gesetz. Durch einen Widerstand R 0 fließt bei einer Spannung von U 0 =0V ein Strom von I 0 =ma. Berechne R 0.
Physik GK ph,. Kursarbeit Elektromagnetismus Lösung.04.05 Aufgabe : Stromkreise / Ohmsches Gesetz. Durch einen Widerstand R 0 fließt bei einer Spannung von U 0 =0V ein Strom von I 0 =ma. Berechne R 0.
Das magnetische Feld
 Das Magnetfeld wird durch Objekte erzeugt und wirkt gleichzeitig auf Objekte repräsentiert die Kraftwirkung aufgrund des physikalischen Phänomens Magnetismus ist gerichtet und wirkt vom Nordpol zum Südpol
Das Magnetfeld wird durch Objekte erzeugt und wirkt gleichzeitig auf Objekte repräsentiert die Kraftwirkung aufgrund des physikalischen Phänomens Magnetismus ist gerichtet und wirkt vom Nordpol zum Südpol
Elektrizitätslehre Elektromagnetische Induktion Induktion durch ein veränderliches Magnetfeld
 (2013-06-07) P3.4.3.1 Elektrizitätslehre Elektromagnetische Induktion Induktion durch ein veränderliches Magnetfeld Messung der Induktionsspannung in einer Leiterschleife bei veränderlichem Magnetfeld
(2013-06-07) P3.4.3.1 Elektrizitätslehre Elektromagnetische Induktion Induktion durch ein veränderliches Magnetfeld Messung der Induktionsspannung in einer Leiterschleife bei veränderlichem Magnetfeld
Experimentalphysik 2
 Ferienkurs Experimentalphysik 2 Sommer 2014 Vorlesung 2 Thema: Elektrischer Strom und Magnetostatik I Technische Universität München 1 Fakultät für Physik Inhaltsverzeichnis 2 Elektrischer Strom 3 2.1
Ferienkurs Experimentalphysik 2 Sommer 2014 Vorlesung 2 Thema: Elektrischer Strom und Magnetostatik I Technische Universität München 1 Fakultät für Physik Inhaltsverzeichnis 2 Elektrischer Strom 3 2.1
Magnetisches Induktionsgesetz
 Magnetisches Induktionsgesetz Michael Faraday entdeckte, dass ein sich zeitlich veränderndes Magnetfeld eine elektrische Spannung in einer Schleife oder Spule aus leitendem Material erzeugt: die Induktionsspannung
Magnetisches Induktionsgesetz Michael Faraday entdeckte, dass ein sich zeitlich veränderndes Magnetfeld eine elektrische Spannung in einer Schleife oder Spule aus leitendem Material erzeugt: die Induktionsspannung
Physikalisches Anfängerpraktikum Teil 1 Versuch 1 73: Stromdurchflossene Leiter im Magnetfeld, Halleffekt Protokoll
 Physikalisches Anfängerpraktikum eil 1 Versuch 1 73: Stromdurchflossene Leiter im Magnetfeld, Halleffekt Protokoll Gruppe 13: Marc A. Donges , 1060028 Michael Schüssler, 1228119 2004 09
Physikalisches Anfängerpraktikum eil 1 Versuch 1 73: Stromdurchflossene Leiter im Magnetfeld, Halleffekt Protokoll Gruppe 13: Marc A. Donges , 1060028 Michael Schüssler, 1228119 2004 09
Bewegter Leiter im Magnetfeld
 Bewegter Leiter im Magnetfeld Die Leiterschaukel mal umgedreht: Bewegt man die Leiterschaukel im Magnetfeld, so wird an ihren Enden eine Spannung induziert. 18.12.2012 Aufgaben: Lies S. 56 Abschnitt 1
Bewegter Leiter im Magnetfeld Die Leiterschaukel mal umgedreht: Bewegt man die Leiterschaukel im Magnetfeld, so wird an ihren Enden eine Spannung induziert. 18.12.2012 Aufgaben: Lies S. 56 Abschnitt 1
Wechselstromwiderstände (Impedanzen) Parallel- und Reihenschaltungen. RGes = R1 + R2 LGes = L1 + L2
 Wechselstromwiderstände (Impedanzen) Ohm'scher Widerstand R: Kondensator mit Kapazität C: Spule mit Induktivität L: RwR = R RwC = 1/(ωC) RwL = ωl Parallel- und Reihenschaltungen bei der Reihenschaltung
Wechselstromwiderstände (Impedanzen) Ohm'scher Widerstand R: Kondensator mit Kapazität C: Spule mit Induktivität L: RwR = R RwC = 1/(ωC) RwL = ωl Parallel- und Reihenschaltungen bei der Reihenschaltung
ELEKTRIZITÄT & MAGNETISMUS
 ELEKTRIZITÄT & MAGNETISMUS Elektrische Ladung / Coulombkraft / Elektrisches Feld Gravitationsgesetz ( = Gewichtskraft) ist die Ursache von Gravitationskonstante Coulombgesetz ( = Coulombkraft) Elementarladung
ELEKTRIZITÄT & MAGNETISMUS Elektrische Ladung / Coulombkraft / Elektrisches Feld Gravitationsgesetz ( = Gewichtskraft) ist die Ursache von Gravitationskonstante Coulombgesetz ( = Coulombkraft) Elementarladung
Versuch E11 - Hysterese Aufnahme einer Neukurve. Abgabedatum: 24. April 2007
 Versuch E11 - Hysterese Aufnahme einer Neukurve Sven E Tobias F Abgabedatum: 24. April 2007 Inhaltsverzeichnis 1 Ziel des Versuchs 3 2 Physikalischer Zusammenhang 3 2.1 Magnetisches Feld..........................
Versuch E11 - Hysterese Aufnahme einer Neukurve Sven E Tobias F Abgabedatum: 24. April 2007 Inhaltsverzeichnis 1 Ziel des Versuchs 3 2 Physikalischer Zusammenhang 3 2.1 Magnetisches Feld..........................
PN 2 Einführung in die Experimentalphysik für Chemiker
 PN 2 Einführung in die Experimentalphysik für Chemiker 4. Vorlesung 9.5.08 Evelyn Plötz, Thomas Schmierer, Gunnar Spieß, Peter Gilch Lehrstuhl für BioMolekulare Optik Department für Physik Ludwig-Maximilians-Universität
PN 2 Einführung in die Experimentalphysik für Chemiker 4. Vorlesung 9.5.08 Evelyn Plötz, Thomas Schmierer, Gunnar Spieß, Peter Gilch Lehrstuhl für BioMolekulare Optik Department für Physik Ludwig-Maximilians-Universität
18. Magnetismus in Materie
 18. Magnetismus in Materie Wir haben den elektrischen Strom als Quelle für Magnetfelder kennen gelernt. Auch das magnetische Verhalten von Materie wird durch elektrische Ströme bestimmt. Die Bewegung der
18. Magnetismus in Materie Wir haben den elektrischen Strom als Quelle für Magnetfelder kennen gelernt. Auch das magnetische Verhalten von Materie wird durch elektrische Ströme bestimmt. Die Bewegung der
3, wobei C eine Konstante ist. des Zentralgestirns abhängig ist.
 Abschlussprüfung Berufliche Oberschule 00 Physik Technik - Aufgabe I - Lösung Teilaufgabe.0 Für alle Körper, die sich antriebslos auf einer Kreisbahn mit dem Radius R und mit der Umlaufdauer T um ein Zentralgestirn
Abschlussprüfung Berufliche Oberschule 00 Physik Technik - Aufgabe I - Lösung Teilaufgabe.0 Für alle Körper, die sich antriebslos auf einer Kreisbahn mit dem Radius R und mit der Umlaufdauer T um ein Zentralgestirn
Grundkurs Physik (2ph2) Klausur
 1. Ernest O. Lawrence entwickelte in den Jahren 1929-1931 den ersten ringförmigen Teilchenbeschleuniger, das Zyklotron. Dieses Zyklotron konnte Protonen auf eine kinetische Energie von 80 kev beschleunigen.
1. Ernest O. Lawrence entwickelte in den Jahren 1929-1931 den ersten ringförmigen Teilchenbeschleuniger, das Zyklotron. Dieses Zyklotron konnte Protonen auf eine kinetische Energie von 80 kev beschleunigen.
6.4.4 Elihu-Thomson ****** 1 Motivation
 V644 6.4.4 ****** 1 Motivation Ein als Sekundärspule dienender geschlossener Aluminiumring wird durch Selbstinduktion von der Primärspule abgestossen und in die Höhe geschleudert. Ein offener Aluminiumring
V644 6.4.4 ****** 1 Motivation Ein als Sekundärspule dienender geschlossener Aluminiumring wird durch Selbstinduktion von der Primärspule abgestossen und in die Höhe geschleudert. Ein offener Aluminiumring
Vorbereitung zum Versuch
 Vorbereitung zum Versuch elektrische Messverfahren Armin Burgmeier (347488) Gruppe 5 2. Dezember 2007 Messungen an Widerständen. Innenwiderstand eines µa-multizets Die Schaltung wird nach Schaltbild (siehe
Vorbereitung zum Versuch elektrische Messverfahren Armin Burgmeier (347488) Gruppe 5 2. Dezember 2007 Messungen an Widerständen. Innenwiderstand eines µa-multizets Die Schaltung wird nach Schaltbild (siehe
IK Induktion. Inhaltsverzeichnis. Sebastian Diebold, Moritz Stoll, Marcel Schmittfull. 25. April Einführung 2
 IK Induktion Blockpraktikum Frühjahr 2007 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Magnetfelder....................... 2 2.2 Spule............................ 2
IK Induktion Blockpraktikum Frühjahr 2007 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Magnetfelder....................... 2 2.2 Spule............................ 2
