Matrizen ç 2030 II. Quartal æ98766ö. R = ç. B P Preise R R
|
|
|
- Jörg Rothbauer
- vor 6 Jahren
- Abrufe
Transkript
1 Das Doppelelement a ik gibt an, dass das betreffende Element in der i-ten Zeile und k-ten Spalte steht (Wenn nicht anders vereinbart, gilt i,k ³ 0) Bereits das Aufstellen von Tabellen und aus oftmals komplizierten anwendungsbezogenen Texten kann für das Erfassen und ösen eines mathematischen Problems sehr hilfreich sein. Hochschule Hochschule Anwendungsbeispiel Die Elemente einer Matrix können als mehrdimensionale Daten aufgefasst werden. Die Zeilennummer der jeweiligen Matrix stellt die X-Werte und die Spaltennummer die Y-Werte der abzubildenden Zahlentripel dar. Die Matrixelemente selbst bilden die Z-Werte. Auf diese Art können die Daten einer Matrix M als Punktdiagramm oder wie hier als Säulen- oder Flächendiagramm grafisch dargestellt werden. Beispiel: Eine Firma benötigt für die Fertigung zwei Typen von Rohstoffen. Für beide Rohstoffe gibt es fünf Anbieter am Markt. Die erforderlichen Mengen sollen quartalsweise von dem Anbieter mit dem günstigsten Preis bezogen werden. Der Rohstoffbedarf je Quartal sowie die Preise der einzelnen Anbieter für beide Rohstoffarten seien gegeben. Die Bedarfsmatrix B gibt den Bedarf an beiden Rohstoffen R 1 und R 2 quartals- und hier zeilenweise an: In der Preismatrix P sind spaltenweise die von den einzelnen Anbietern für die Rohstoffe R 1 und R 2 pro Mengeneinheit (ME) geforderten Preise erfasst. æ 5 20ö I. Quartal 2030 II. Quartal æ98766ö R = = 1510 III. Quartal è56678ør è30 5 øiv. Quartal R R 1 B P Preise Hochschule Hochschule
2 Stimmen die Anzahl der Zeilen und Spalten einer Matrix A = A (m;n) überein, ist also m = n, so heißt diese Matrix quadratische Matrix vom Typ (n;n) oder n-reihige Matrix. Die Elemente a 11, a 22, a 33,, a nn bilden die Hauptdiagonale der Matrix. æ a 11 a 12 a 1 n ö A(n;n) a21 22 a2n a = è a n 1 a n 2 a nn ø Hochschule Auf Grund ihrer Gestalt sind einige Formen symmetrischer besonders hervorzuheben: Diagonalmatrix Es gilt a ik = 0 für i 0, d.h., alle Elemente außerhalb der Hauptdiagonalen sind gleich 0. (a ii = d ii ) Einheitsmatrix Es gilt a ik = 1 für i = k und a ik = 0 für i 0, d.h., alle Elemente in der Hauptdiagonalen sind gleich 1. æd ö 0 d22 0 D = 0 0 dnn è ø æ ö E = è ø Obere Dreiecksmatrix Es gilt a ik = 0 für i > k, d.h., alle Elemente unterhalb der Hauptdiagonalen sind gleich 0. Untere Dreiecksmatrix Es gilt a ik = 0 für i < k, d.h., alle Elemente unterhalb der Hauptdiagonalen sind gleich 0. Ohne Beschränkung auf einen bestimmten Typ von definiert man außerdem: Nullmatrix Es gilt a ik = 0 für i, k, d.h., alle Elemente sind gleich 0. æ ö 0 a22 0 A U = è ø æa11 a11 a1 n ö 0 a22 a2n A O = 0 è 0 ann ø æa ö a21 a22 0 A U = an è a ann ø 1 2 n Hochschule Transponierte Matrix: Notiert man die Zeilen einer Matrix A vom Typ (m ; n) als Spalten einer Matrix A T, so nennt man A T die zu A transponierte Matrix. Diese ist dann vom Typ (n ; m). æa11 a12 a1 n ö a21 a22 a2n A= a31 a32 a3n am 1 am2 a è mn ø æa11 a21 am 1ö a a a m2 T A = a13 a23 a m3 a1 n a2n a è mn ø Eine quadratische Matrix heißt symmetrisch, wenn Sie mit ihrer Transponierten übereinstimmt. Sie heißt schiefsymmetrisch, wenn die Elemente ihrer Transponierten entgegengesetzte Vorzeichen haben. Bei des Typs n ¹ m entsteht die Transposition durch Schwenk der jeweiligen Spalte in Zeilenlage bzw. durch Schwenk der jeweiligen Zeile in Spaltenlage. Dies erfolgt in der Reihenfolge der Spalten bzw. Zeilen. Bei quadratischen (n = m) entsteht die Transposition der Matrix durch Spiegelung an der Hauptdiagonalen. Hochschule Hochschule
3 Transposition einer Matrix des Typs n ¹ m: æa11 a21 a31... am 1 ö a12 a22 a32... a Das Ergebnis ist eine Matrix des Typs m ¹ n m2 a13 a23 a33... a T m3 A = a14 a24 a34... am a1 n a2n a3n... a è mn ø æa11 a12 a13 a14... a1 n ö a21 a22 a23 a24... a2n A= a31 a32 a33 a34... a 3n am1 am2 am3 am4... a è mn ø Transposition einer Matrix des Typs n = m: Das Ergebnis ist wieder eine Matrix des Typs m = n æa11 a12 a13... a1 n ö æa11 a21 a31... am 1 ö a21 a22 a23... a 2n a12 a22 a32... a m2 T A= a31 a32 a33... a 3n A = a13 a23 a33... a m a a a... a a a a... a è m1 m2 m3 mn ø è 1n 2n 3n mn ø Hochschule Hochschule Übung: Zu den A, B und C sollen die transponierten A T, B T und C T ermittelt werden. æ23-50ö A = Transposition A T æ ö = è ø æ2 3 0ö B = Transposition æ ö = T B Symmetrische Matrix (B = B T ) æ 0 2-1ö C = Transposition æ 0-21ö T C = Schiefsymmetrische Matrix (C = -C T ) Hochschule Hochschule
4 Addition von gleichen Typs A = (a i;k ) und B = (b i;k ) seien (m x n)-. Dann versteht man unter ihrer Summe A + B eine Matrix C mit der Eigenschaft æa11 a12 a1 n ö æb11 b12 b1 n ö a21 a22 a2n b21 b22 b2 n A B C + = = + a a a b b b è m1 m2 mn ø è m1 m2 mn ø Übung: Bilden Sie die Summe der beiden A und B: A = B = æ a11 + b11 a12 + b12 a1 n + b1 n ö a21 + b21 a22 + b22 a2n + b2 n = èam1+ bm 1 am2 + bm2 amn + bmnø Die Summe A + B = C = (c i;k ) ist eine Matrix vom Typ (m x n) mit c ik = a ik + b ik A + B = Hochschule Hochschule Übung skalare Vervielfachung: A = x 8= C = A x 8 = Hochschule Hochschule
5 Übung Vektormultiplikation x 1 A = x3 6x2 3x1 2x2 6x3 5x3 7x2 4x1 2x2 1x3 = 6x3 4x2 3x1 7x2 1x3 2x3 5x2 5x1 1x2 5x3 4x3 1x2 3x1 8x2 4x3 7x3 4x2 4x1 8x2 3x3 Diese Rechenoperation ist nur erlaubt, wenn die Spaltenzahl der Matrix gleich der Spalten- oder Zeilenzahl des Vektors ist x = Hochschule Hochschule Das Produkt zweier A (m x n) und B (p x q) existiert, falls n = p ist! æ a 11 a1 n ö æ b11 b1 n ö æ ö æ b1 k ö A B = a a M M M g M M M = g M i 1 in am 1 a mn bm 1 b mn b è ø è ø è nk ø æ ö = i c ( p= n ) mit c = a b + a b + a b kk ik ik i 1 1 k i 2 2 k in nk Zur Berechnung der Produktmatrix ist es sinnvoll, die höhenversetzt nebeneinander zu schreiben (Falksches Schema). Hochschule Hochschule
6 Falksches Schema Falksches Schema Beispiel Hochschule Hochschule Falksches Schema Beispiel multiplikation Übungen Bitte multiplizieren Sie die folgenden Paare von : æ2 3ö æ9 8ö A = und B = A B =? è4 5ø è7 6ø Hochschule Hochschule
7 multiplikation Übungen multiplikation Übungen Bitte multiplizieren Sie die folgenden Paare von : Bitte multiplizieren Sie die folgenden Paare von : æ5 8 1ö A= æ22, 31, 47, ö B = 52, 48, 39, 63, 70, 27, è ø A B =? 2,2 3,1 4,7 5,2 4,8 3,9 6,3 7,0 2, ,9 60,9 57, ,0 82,9 64, ,1 70,4 52,6 æ23, 41, ö A = 37, 29, 55, 46, æ12, 3 14, 7 11, 9 ö B= 21, 6 13, 7 12, 6 è ø A B =? 12,3 14,7 11,9 21,6 13,7 12,6 2,3 4,1 116,9 90,0 79,0 3,7 2,9 108,2 94,1 80,6 5,5 4,6 167,0 143,9 123,4 Hochschule Hochschule multiplikation Übungen Beispiel: Anwendung auf Quartals-ieferproblem (Folie-Nr.: 3) Bitte multiplizieren Sie die folgenden Paare von : æ173, ö A = 227, 125, æ215, ö B = 189, 125, A B =? æ173, ö T A = 22, 7 B = ( 21, 5 125, 18, 9 12, 5) A B =? 21,5 18,9 12,5 17,3 372,0 327,0 216,3 22,7 488,1 429,0 283,8 12,5 268,8 236,3 156,3 Hochschule Eine Firma benötigt für die Fertigung zwei Typen von Rohstoffen. Für beide Rohstoffe gibt es fünf Anbieter am Markt. Die erforderlichen Mengen sollen quartalsweise von dem Anbieter mit dem günstigsten Preis bezogen werden. Der Rohstoffbedarf je Quartal sowie die Preise der einzelnen Anbieter für beide Rohstoffarten seien gegeben. Die Bedarfsmatrix B gibt den Bedarf an beiden Rohstoffen R 1 und R 2 quartals- und hier zeilenweise an: 1 2 In der Preismatrix P sind spaltenweise die von den einzelnen Anbietern für die Rohstoffe R 1 und R 2 pro Mengeneinheit (ME) geforderten Preise erfasst. æ 5 20ö I. Quartal 2030 II. Quartal æ98766ö R1 B = P = Preise 1510 III. Quartal è56678ør2 è30 5 øiv. Quartal R R Hochschule
8 Falksches Schema Anwendung auf Quartals-ieferproblem (Folie-Nr.: 3) Übung æ 5 20ö I. Quartal II. Quartal æ öR = 1510 III. Quartal = R 2 è30 5 øiv. Quartal A 1 A 2 A 3 A 4 A 5 R R 1 2 P= R R Quartal 1 T P Preise Übung: Beispiel zu multiplikation Wirtschaftsmathematik (Teil 1) Die rechnung wird häufig zur ösung ökonomischer Probleme angewendet. Nehmen wir an, Sie erhalten die Aufgabe die Rohstoffmenge zu ermitteln, die zur Herstellung zweier Endprodukte notwendig ist. Diese Endprodukte wiederum bestehen aus Zwischenprodukten. Es handelt sich also um eine verkettete Beziehung zwischen Rohstoff, Zwischenprodukt und Endprodukt. Die ösung erfolgt über hintereinander erfolgende multiplikation, T = Quartal Quartal Quartal R 1 R 2 wobei gilt: Hochschule Hochschule Übung: Beispiel zu multiplikation Wirtschaftsmathematik (Teil 2) Wir nehmen folgendes an: es handele sich um 2 Endprodukte, die in folgender Anzahl produziert werden sollen: Benötigte Anzahl von Endprodukt 1: 11 Benötigte Anzahl von Endprodukt 2: 5 Zur Herstellung seien folgende Einheiten der Zwischenprodukte notwendig: Für das Endprodukt 1: 3 Einheiten des Zwischenprodukts 1 4 Einheiten des Zwischenprodukts 2 Für das Endprodukt 2: 7 Einheiten des Zwischenprodukts 1 3 Einheiten des Zwischenprodukts 2 Übung: Beispiel zu multiplikation Wirtschaftsmathematik (Teil 3) Um wiederum diese Zwischenprodukte zu erzeugen werden folgende Rohstoffmengen benötigt: Für das Zwischenprodukt 1: 1,5 Einheiten des Rohstoffs 1 4,0 Einheiten des Rohstoffs 2 Für das Zwischenprodukt 2: 1,0 Einheiten des Rohstoffs 1 3,0 Einheiten des Rohstoffs 2 2,5 Einheiten des Rohstoffs 3 Hochschule Hochschule
9 Übung: Beispiel zu multiplikation Wirtschaftsmathematik (Teil 3) Übung: Beispiel zu multiplikation Wirtschaftsmathematik (Teil 4) Tja, geht auch von Hand. Etwas für bekennende Masochisten! Wenn Sie sich dran versuchen wollen, bitte. Ich lass es. Rohstoffe mal Zwischenprodukt mal Endprodukt 1,50 1,00 3,00 7,00 11,00 X X 4,00 3,00 4,00 3,00 5,00 0,00 2,50 Hochschule Hochschule Übung: Beispiel zu multiplikation Wirtschaftsmathematik (Teil 5) Übung: Beispiel zu multiplikation Wirtschaftsmathematik (Teil 6) 1,50 1,00 3,00 7,00 11,00 4,00 3,00 x 4,00 3,00 x 5,00 = ,00 0,00 2,50 ösung mit dem Falk schen Schema 4 3 5,00 1,5 1 8,5 13,5 8,5 13,5 161 ösung mit Excel: 1,50 1,00 3,00 7,00 8,5 13,5 4,00 3,00 x 4,00 3,00 = ,00 2, ,5 0 2,5 10 7,5 10 7,5 147,5 8,5 13,5 11, x 5,00 = ,5 147,5 Hochschule Hochschule
10 Übung: Beispiel Produktionskette (Teil 1) ösung der Aufgabe: Wir nehmen folgendes an: es handele sich um 2 verschiedene Reisen, die an die Frau/den Mann gebracht werden sollen: Benötigte Anzahl von Reise 1: 15 Benötigte Anzahl von Reise 2: 7 Zur Komplettierung jeder Reise seien folgende Einheiten an Zwischentransfers notwendig: Für das Endprodukt 1: 5 Einheiten des Zwischentransfers 1 7 Einheiten des Zwischentransfers 2 Für das Endprodukt 2: 9 Einheiten des Zwischentransfers 1 6 Einheiten des Zwischentransfers 2 Hochschule Hochschule Übung: Beispiel Produktionskette (Teil 2) Übung: Beispiel Produktionskette (Teil 3) Um wiederum diese Zwischentransfers anzumieten, werden folgende Transporteinheiten benötigt: Für Zwischentransfer 1: 3,5 Transporteinheiten 1 6,7 Transporteinheiten 2 Für Zwischentransfer 2: 2,1 Transporteinheiten 1 4,3 Transporteinheiten 2 5,9 Transporteinheiten 3 Transporteinheiten x Zwischentransfer x Reise Hochschule Hochschule
11 Übung: Beispiel Produktionskette (Teil 4) Händische Variante Reise Nr. Zwischentransfers Transporteinheiten Transporteinheiten gesamt/reise Nr.1 15,00 Nr. 1 5,00 Nr. 1 3,50 Nr ,50 Nr ,70 Nr. 2 6,70 Nr ,50 Nr ,70 Nr. 3 0,00 Nr. 3 0,00 Nr ,30 765, ,70 Nr. 2 7,00 Nr. 1 2,10 Nr ,50 Nr. 2 4,30 Nr ,50 Nr. 3 5,90 Nr , ,50 Nr.2 7,00 Nr. 1 9,00 Nr. 1 3,50 Nr ,50 Nr. 2 6,70 Nr ,10 Nr. 3 0,00 Nr. 3 0,00 642,60 Nr. 2 6,00 Nr. 1 2,10 Nr. 1 88,20 Nr. 2 4,30 Nr ,60 Nr. 3 5,90 Nr ,80 516,60 Transporteinheiten gesamt Hochschule Übung: Beispiel Produktionskette (Teil 5) Variante 3,50 2,10 5,00 9,00 15,00 6,70 4,30 x 7,00 6,00 x 7,00 0,00 5,90 32,20 44,10 63,60 86,10 41,30 35,40 791, ,70 867, ,70 Hochschule Übung: Beispiel Produktionskette (Teil 5) Variante 3,50 2,10 5,00 9,00 15,00 6,70 4,30 x 7,00 6,00 x 7,00 0,00 5,90 Übung: Beispiel Produktionskette (Teil 5) Variante 3,50 2,10 5,00 9,00 15,00 6,70 4,30 x 7,00 6,00 x 7,00 0,00 5,90 32,20 44,10 63,60 86,10 41,30 35,40 791, ,70 867, ,70 Hochschule ,20 44,10 63,60 86,10 41,30 35,40 791, ,70 867, ,70 Hochschule
12 Übung: Beispiel Produktionskette (Teil 5) Variante 3,50 2,10 5,00 9,00 15,00 6,70 4,30 x 7,00 6,00 x 7,00 0,00 5,90 32,20 44,10 63,60 86,10 41,30 35,40 791, ,70 867, ,70 Hochschule Übung: Beispiel Produktionskette (Teil 5) Variante 3,50 2,10 5,00 9,00 15,00 6,70 4,30 x 7,00 6,00 x 7,00 0,00 5,90 A B C 32,20 44,10 63,60 86,10 41,30 35,40 A x B = D 791, ,70 867,30 D x C = A x B x C 3215,70 Hochschule
Einführung in die Vektor- und Matrizenrechnung. Matrizen
 Einführung in die Vektor- und Matrizenrechnung Matrizen Definition einer Matrix Unter einer (reellen) m x n Matrix A versteht man ein rechteckiges Schema aus reellen Zahlen, die wie folgt angeordnet sind:
Einführung in die Vektor- und Matrizenrechnung Matrizen Definition einer Matrix Unter einer (reellen) m x n Matrix A versteht man ein rechteckiges Schema aus reellen Zahlen, die wie folgt angeordnet sind:
Materialverflechtung
 Materialverflechtung In einem Unternehmen mit mehrstufigem Fertigungsablauf seien die festen Mengenbeziehungen zwischen Rohstoffen, Zwischen- und Endprodukten durch folgenden Graph gegeben: 00 0 6 E E
Materialverflechtung In einem Unternehmen mit mehrstufigem Fertigungsablauf seien die festen Mengenbeziehungen zwischen Rohstoffen, Zwischen- und Endprodukten durch folgenden Graph gegeben: 00 0 6 E E
Mathematik 1. Inhaltsverzeichnis. Prof. Dr. K. Melzer. karin.melzer@hs-esslingen.de http://www.hs-esslingen.de/de/mitarbeiter/karin-melzer.
 Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Matrizenrechnung 2 11 Matrixbegri 2 12 Spezielle Matrizen 3 13 Rechnen
Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Matrizenrechnung 2 11 Matrixbegri 2 12 Spezielle Matrizen 3 13 Rechnen
Lineare Algebra - alles was man wissen muß
 Statistik für Bioinformatiker SoSe 3 Rainer Spang Lineare Algebra - alles was man wissen muß Der Titel ist natürlich gelogen, aber was wir hier zusammengetragen haben ist zumindest ein Anfang. Weniger
Statistik für Bioinformatiker SoSe 3 Rainer Spang Lineare Algebra - alles was man wissen muß Der Titel ist natürlich gelogen, aber was wir hier zusammengetragen haben ist zumindest ein Anfang. Weniger
Kapitel 15. Lösung linearer Gleichungssysteme
 Kapitel 15. Lösung linearer Gleichungssysteme Lineare Gleichungssysteme Wir befassen uns nun mit der Lösung im allgemeinen nichthomogener linearer Gleichungssysteme in zweifacher Hinsicht. Wir studieren
Kapitel 15. Lösung linearer Gleichungssysteme Lineare Gleichungssysteme Wir befassen uns nun mit der Lösung im allgemeinen nichthomogener linearer Gleichungssysteme in zweifacher Hinsicht. Wir studieren
7 Die Determinante einer Matrix
 7 Die Determinante einer Matrix ( ) a11 a Die Determinante einer 2 2 Matrix A = 12 ist erklärt als a 21 a 22 det A := a 11 a 22 a 12 a 21 Es ist S 2 = { id, τ}, τ = (1, 2) und sign (id) = 1, sign (τ) =
7 Die Determinante einer Matrix ( ) a11 a Die Determinante einer 2 2 Matrix A = 12 ist erklärt als a 21 a 22 det A := a 11 a 22 a 12 a 21 Es ist S 2 = { id, τ}, τ = (1, 2) und sign (id) = 1, sign (τ) =
Leitfaden Lineare Algebra: Determinanten
 Leitfaden Lineare Algebra: Determinanten Die symmetrische Gruppe S n. Eine Permutation σ der Menge S ist eine bijektive Abbildung σ : S S. Ist S eine endliche Menge, so reicht es zu verlangen, dass σ injektiv
Leitfaden Lineare Algebra: Determinanten Die symmetrische Gruppe S n. Eine Permutation σ der Menge S ist eine bijektive Abbildung σ : S S. Ist S eine endliche Menge, so reicht es zu verlangen, dass σ injektiv
LU-Zerlegung. Zusätze zum Gelben Rechenbuch. Peter Furlan. Verlag Martina Furlan. Inhaltsverzeichnis. 1 Definitionen.
 Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Vorlesung 12 22. bzw. 23. Januar 2014. Determinanten 1. Cramersche Regel
 Vorlesung 2 22 bzw 23 Januar 204 Lineares Gleichungssystem a a 2 b b 2 = F a a 2 a 3 b b 2 b 3 c c 2 c 3 = V V =< a, b c > c b a b a F V Seite 70 a x + a 2 x 2 + a 3 x 3 b = 0 < a x + a 2 x 2 + a 3 x 3
Vorlesung 2 22 bzw 23 Januar 204 Lineares Gleichungssystem a a 2 b b 2 = F a a 2 a 3 b b 2 b 3 c c 2 c 3 = V V =< a, b c > c b a b a F V Seite 70 a x + a 2 x 2 + a 3 x 3 b = 0 < a x + a 2 x 2 + a 3 x 3
Tutorial Excel Übung 5&6 Tom s Skater -1- Die Aufgabenstellung ist der folgenden URL zu entnehmen: Übung5&6.
 Tutorial Excel Übung 5&6 Tom s Skater -1-1 Aufgabenstellung Die Aufgabenstellung ist der folgenden URL zu entnehmen: Übung5&6. 2 Ergänzung mit einfachen Formeln Summe der Einnahmen Dieser Betrag ergibt
Tutorial Excel Übung 5&6 Tom s Skater -1-1 Aufgabenstellung Die Aufgabenstellung ist der folgenden URL zu entnehmen: Übung5&6. 2 Ergänzung mit einfachen Formeln Summe der Einnahmen Dieser Betrag ergibt
A Matrix-Algebra. A.1 Definition und elementare Operationen
 A Matrix-Algebra In diesem Anhang geben wir eine kompakte Einführung in die Matrizenrechnung bzw Matrix-Algebra Eine leicht lesbare Einführung mit sehr vielen Beispielen bietet die Einführung in die Moderne
A Matrix-Algebra In diesem Anhang geben wir eine kompakte Einführung in die Matrizenrechnung bzw Matrix-Algebra Eine leicht lesbare Einführung mit sehr vielen Beispielen bietet die Einführung in die Moderne
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Übungskomplex Felder (1) Eindimensionale Felder Mehrdimensionale Felder
 Übungskomplex Felder (1) Eindimensionale Felder Mehrdimensionale Felder Hinweise zur Übung Benötigter Vorlesungsstoff Ab diesem Übungskomplex wird die Kenntnis und praktische Beherrschung der Konzepte
Übungskomplex Felder (1) Eindimensionale Felder Mehrdimensionale Felder Hinweise zur Übung Benötigter Vorlesungsstoff Ab diesem Übungskomplex wird die Kenntnis und praktische Beherrschung der Konzepte
Gleitkommaarithmetik und Pivotsuche bei Gauß-Elimination. Lehrstuhl für Angewandte Mathematik Wintersemester 2009/10. 14.
 Gleitkommaarithmetik und Pivotsuche bei Gauß-Elimination Vorlesung Computergestützte Mathematik zur Linearen Algebra Lehrstuhl für Angewandte Mathematik Wintersemester 2009/0 4. Januar 200 Instabilitäten
Gleitkommaarithmetik und Pivotsuche bei Gauß-Elimination Vorlesung Computergestützte Mathematik zur Linearen Algebra Lehrstuhl für Angewandte Mathematik Wintersemester 2009/0 4. Januar 200 Instabilitäten
Lineare Gleichungssysteme und Gauß'scher Algorithmus
 Zurück Letzter Update 7... Lineare Gleichungssysteme und Gauß'scher Algorithmus In der Mathematik bezeichnet man mit Matrix ein rechteckiges Schema, in dem Zahlen oder Funktionen angeordnet werden. Hier
Zurück Letzter Update 7... Lineare Gleichungssysteme und Gauß'scher Algorithmus In der Mathematik bezeichnet man mit Matrix ein rechteckiges Schema, in dem Zahlen oder Funktionen angeordnet werden. Hier
Numerisches Programmieren
 Technische Universität München SoSe 213 Institut für Informatik Prof. Dr. Thomas Huckle Dipl.-Inf. Christoph Riesinger Dipl.-Math. Jürgen Bräckle Numerisches Programmieren 2. Programmieraufgabe: Lineare
Technische Universität München SoSe 213 Institut für Informatik Prof. Dr. Thomas Huckle Dipl.-Inf. Christoph Riesinger Dipl.-Math. Jürgen Bräckle Numerisches Programmieren 2. Programmieraufgabe: Lineare
Lernzettel Mathe Inhaltsverzeichnis
 Lernzettel Mathe Inhaltsverzeichnis Aufgabe 1 - Vollständige Induktion 2 Aufgabe 2 - Grenzwertbestimmung 2 Aufgabe 3 - Lin/Log 2 Aufgabe 4 - Barwert/Endwert 3 Aufgabe 5 - Maximalstellen, steigend/fallend
Lernzettel Mathe Inhaltsverzeichnis Aufgabe 1 - Vollständige Induktion 2 Aufgabe 2 - Grenzwertbestimmung 2 Aufgabe 3 - Lin/Log 2 Aufgabe 4 - Barwert/Endwert 3 Aufgabe 5 - Maximalstellen, steigend/fallend
Matrixalgebra. mit einer Einführung in lineare Modelle. Stefan Lang Institut für Statistik Ludwigstrasse 33 email: lang@stat.uni-muenchen.
 Matrixalgebra mit einer Einführung in lineare Modelle Stefan Lang Institut für Statistik Ludwigstrasse 33 email: lang@statuni-muenchende 25 August 24 Vielen Dank an Christiane Belitz, Manuela Hummel und
Matrixalgebra mit einer Einführung in lineare Modelle Stefan Lang Institut für Statistik Ludwigstrasse 33 email: lang@statuni-muenchende 25 August 24 Vielen Dank an Christiane Belitz, Manuela Hummel und
Elemente der Analysis II
 Elemente der Analysis II Kapitel 3: Lineare Abbildungen und Gleichungssysteme Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 15. Mai 2009 1 / 35 3.1 Beispiel
Elemente der Analysis II Kapitel 3: Lineare Abbildungen und Gleichungssysteme Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 15. Mai 2009 1 / 35 3.1 Beispiel
2 Matrizen. 2.1 Definition A = a 32... Element in der 3. Zeile und 2. Spalte RP =
 Matrizen James Joseph Sylvester 97 war ein britischer Mathematiker. Eines seiner vielseitigen Arbeitsgebiete war die Theorie von Matrizen und Determinanten. Die ezeichnung Matrix wurde von ihm eingeführt.
Matrizen James Joseph Sylvester 97 war ein britischer Mathematiker. Eines seiner vielseitigen Arbeitsgebiete war die Theorie von Matrizen und Determinanten. Die ezeichnung Matrix wurde von ihm eingeführt.
4. Relationen. Beschreibung einer binären Relation
 4. Relationen Relationen spielen bei Datenbanken eine wichtige Rolle. Die meisten Datenbanksysteme sind relational. 4.1 Binäre Relationen Eine binäre Relation (Beziehung) R zwischen zwei Mengen A und B
4. Relationen Relationen spielen bei Datenbanken eine wichtige Rolle. Die meisten Datenbanksysteme sind relational. 4.1 Binäre Relationen Eine binäre Relation (Beziehung) R zwischen zwei Mengen A und B
Inhaltsverzeichnis. Seite 1: Matrizen. Seite 23: Funktionen. Seite 51: Integralrechnung. Seite 69: Binomialverteilung
 Inhaltsverzeichnis Seite : Matrizen Seite : Funktionen Seite 5: Integralrechnung Seite 69: Binomialverteilung Seite 86: Statistik/Normalverteilung Seite 04: Vektoren Seite 40: Wachstum Lineare Algebra
Inhaltsverzeichnis Seite : Matrizen Seite : Funktionen Seite 5: Integralrechnung Seite 69: Binomialverteilung Seite 86: Statistik/Normalverteilung Seite 04: Vektoren Seite 40: Wachstum Lineare Algebra
Rationale Zahlen. Vergleichen und Ordnen rationaler Zahlen
 Rationale Zahlen Vergleichen und Ordnen rationaler Zahlen Von zwei rationalen Zahlen ist die die kleinere Zahl, die auf der Zahlengeraden weiter links liegt.. Setze das richtige Zeichen. a) -3 4 b) - -3
Rationale Zahlen Vergleichen und Ordnen rationaler Zahlen Von zwei rationalen Zahlen ist die die kleinere Zahl, die auf der Zahlengeraden weiter links liegt.. Setze das richtige Zeichen. a) -3 4 b) - -3
Matlab - eine kurze Einführung
 Matlab - eine kurze Einführung Helke Karen Hesse, Thomas Dunne helke.hesse@iwr.uni-heidelberg.de, thomas.dunne@iwr.uni-heidelberg.de 13.11.2006 1 / Gliederung Überblick Grundlegende Syntax Variablen Vektoren
Matlab - eine kurze Einführung Helke Karen Hesse, Thomas Dunne helke.hesse@iwr.uni-heidelberg.de, thomas.dunne@iwr.uni-heidelberg.de 13.11.2006 1 / Gliederung Überblick Grundlegende Syntax Variablen Vektoren
KAPITEL 3. Lineare Gleichungssysteme, direkte Lösungsverfahren
 KAPITEL 3. Lineare Gleichungssysteme, direkte Lösungsverfahren Beispiel 3.2. Gesucht u(x), das eine Differentialgleichung vom Typ u (x) + λ(x)u(x) = f(x), x [0,], mit den Randbedingungen u(0) = u() = 0
KAPITEL 3. Lineare Gleichungssysteme, direkte Lösungsverfahren Beispiel 3.2. Gesucht u(x), das eine Differentialgleichung vom Typ u (x) + λ(x)u(x) = f(x), x [0,], mit den Randbedingungen u(0) = u() = 0
Numerisches Programmieren
 Technische Universität München SS 2012 Institut für Informatik Prof Dr Thomas Huckle Dipl-Inf Christoph Riesinger Dipl-Math Alexander Breuer Dipl-Math Dipl-Inf Jürgen Bräckle Dr-Ing Markus Kowarschik Numerisches
Technische Universität München SS 2012 Institut für Informatik Prof Dr Thomas Huckle Dipl-Inf Christoph Riesinger Dipl-Math Alexander Breuer Dipl-Math Dipl-Inf Jürgen Bräckle Dr-Ing Markus Kowarschik Numerisches
Dr. Monika Meiler. Inhalt
 Inhalt 11 Dynamische Feldvereinbarung... 11-2 11.1 Dynamische Vereinbarung von Vektoren... 11-3 11.2 Dynamische Vereinbarung von Matrizen... 11-5 11.3 Die Kommandozeile... 11-8 Propädeutikum 11-1/8 11
Inhalt 11 Dynamische Feldvereinbarung... 11-2 11.1 Dynamische Vereinbarung von Vektoren... 11-3 11.2 Dynamische Vereinbarung von Matrizen... 11-5 11.3 Die Kommandozeile... 11-8 Propädeutikum 11-1/8 11
Tipps und Tricks für die tägliche Praxis und zur Vorbereitung auf IHK-Abschlussprüfungen
 EXCEL - GRUNDLAGEN Tipps und Tricks für die tägliche Praxis und zur Vorbereitung auf IHK-Abschlussprüfungen erstellt von Michael Schäfer schulung@michael-schaefer.net Telefon +49 (0)8762 727121 Mobil +49
EXCEL - GRUNDLAGEN Tipps und Tricks für die tägliche Praxis und zur Vorbereitung auf IHK-Abschlussprüfungen erstellt von Michael Schäfer schulung@michael-schaefer.net Telefon +49 (0)8762 727121 Mobil +49
Einführung in die Tensorrechnung
 1. Definition eines Tensors Tensoren sind Grössen, mit deren Hilfe man Skalare, Vektoren und weitere Grössen analoger Struktur in ein einheitliches Schema zur Beschreibung mathematischer und physikalischer
1. Definition eines Tensors Tensoren sind Grössen, mit deren Hilfe man Skalare, Vektoren und weitere Grössen analoger Struktur in ein einheitliches Schema zur Beschreibung mathematischer und physikalischer
Unterprogramme, Pointer und die Übergabe von Arrays
 Unterprogramme, Pointer und die Übergabe von Arrays Unterprogramme Wie schon im Abschnitt über Funktionen erwähnt, versteht man unter einem Unterprogramm im engeren Sinn eine Prozedur, welche die Werte
Unterprogramme, Pointer und die Übergabe von Arrays Unterprogramme Wie schon im Abschnitt über Funktionen erwähnt, versteht man unter einem Unterprogramm im engeren Sinn eine Prozedur, welche die Werte
Lösungen zum 3. Aufgabenblatt
 SS, Lineare Algebra Die Lösungen wurden erstellt von: Isabel Voigt, Vanessa Lamm und Matthias Rehder Hinweis: Eine Liste der zur Bearbeitung verwendeten Literatur ist unter www.mathematiwelt.com aufrufbar.
SS, Lineare Algebra Die Lösungen wurden erstellt von: Isabel Voigt, Vanessa Lamm und Matthias Rehder Hinweis: Eine Liste der zur Bearbeitung verwendeten Literatur ist unter www.mathematiwelt.com aufrufbar.
Einführung in die Kodierungstheorie
 Einführung in die Kodierungstheorie Einführung Vorgehen Beispiele Definitionen (Code, Codewort, Alphabet, Länge) Hamming-Distanz Definitionen (Äquivalenz, Coderate, ) Singleton-Schranke Lineare Codes Hamming-Gewicht
Einführung in die Kodierungstheorie Einführung Vorgehen Beispiele Definitionen (Code, Codewort, Alphabet, Länge) Hamming-Distanz Definitionen (Äquivalenz, Coderate, ) Singleton-Schranke Lineare Codes Hamming-Gewicht
Excel ein Tabellenprogramm
 Excel ein Tabellenprogramm Mit den Tabellen können viele verschiedene Arbeiten erledigt werden: Adressdateien anlegen und verwalten. Sortieren, filtern von Daten. Berechnen von Daten, z.b. Zinsen, Rabatte,
Excel ein Tabellenprogramm Mit den Tabellen können viele verschiedene Arbeiten erledigt werden: Adressdateien anlegen und verwalten. Sortieren, filtern von Daten. Berechnen von Daten, z.b. Zinsen, Rabatte,
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 1. Semester ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN
 ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN Wir wollen nun die Rechengesetze der natürlichen Zahlen auf die Zahlenmenge der ganzen Zahlen erweitern und zwar so, dass sie zu keinem Widerspruch mit bisher geltenden
ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN Wir wollen nun die Rechengesetze der natürlichen Zahlen auf die Zahlenmenge der ganzen Zahlen erweitern und zwar so, dass sie zu keinem Widerspruch mit bisher geltenden
Lineare Algebra (Mathe I) für Wirtschaftsinformatiker; Zusammenfassung
 Lineare Algebra (Mathe I) für Wirtschaftsinformatiker; Zusammenfassung Artur Trzewik sw562@uni-essen.de v1., 26.3.1998 korrigiert 16. Februar 2 Zusammenfassung Warnung: für die Richtigkeit der Definitionnen
Lineare Algebra (Mathe I) für Wirtschaftsinformatiker; Zusammenfassung Artur Trzewik sw562@uni-essen.de v1., 26.3.1998 korrigiert 16. Februar 2 Zusammenfassung Warnung: für die Richtigkeit der Definitionnen
Inhaltsverzeichnis 1 Lineare Gleichungssysteme I
 Inhaltsverzeichnis 1 Lineare Gleichungssysteme I 3 1.1 Mengen und Abbildungen....................................... 3 1.1.1 Mengen und ihre Operationen.............................. 3 1.1.2 Summen- und
Inhaltsverzeichnis 1 Lineare Gleichungssysteme I 3 1.1 Mengen und Abbildungen....................................... 3 1.1.1 Mengen und ihre Operationen.............................. 3 1.1.2 Summen- und
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Datenauswertung mit Hilfe von Pivot-Tabellen in Excel
 Datenauswertung mit Hilfe von Pivot-Tabellen in Excel Begleitendes Manual zu den Workshops zur Datenerfassung und verarbeitung im Juni / Juli 2004 Datenauswertung mit Hilfe von Pivot-Tabellen in Excel...3
Datenauswertung mit Hilfe von Pivot-Tabellen in Excel Begleitendes Manual zu den Workshops zur Datenerfassung und verarbeitung im Juni / Juli 2004 Datenauswertung mit Hilfe von Pivot-Tabellen in Excel...3
Konsolidieren von Daten in EXCEL
 Konsolidieren von Daten in EXCEL Der Begriff der (auch Konsolidation) besitzt in den einzelnen Fachbereichen (Finanzmathematik, Geologie, Medizin usw.) unterschiedliche Bedeutung. Im Sinne dieses Beitrages
Konsolidieren von Daten in EXCEL Der Begriff der (auch Konsolidation) besitzt in den einzelnen Fachbereichen (Finanzmathematik, Geologie, Medizin usw.) unterschiedliche Bedeutung. Im Sinne dieses Beitrages
6 Lösung linearer Gleichungssysteme I: LR-Zerlegung und Verwandte
 Numerik I Version: 240608 40 6 Lösung linearer Gleichungssysteme I: LR-Zerlegung und Verwandte Die zwei wichtigsten Aufgaben der linearen Algebra: Lösung linearer Gleichungssysteme: Ax = b, wobei die n
Numerik I Version: 240608 40 6 Lösung linearer Gleichungssysteme I: LR-Zerlegung und Verwandte Die zwei wichtigsten Aufgaben der linearen Algebra: Lösung linearer Gleichungssysteme: Ax = b, wobei die n
3 FORMELN. 3.1. Formeln erzeugen
 Formeln Excel effektiv 3 FORMELN 3.1. Formeln erzeugen Übungen: Quittung... 136 Kalkulation... 138 Bestellung... 128 Kassenbuch.. 132 Aufmaß... 152 Zum Berechnen verwendet Excel Formeln. Diese sind in
Formeln Excel effektiv 3 FORMELN 3.1. Formeln erzeugen Übungen: Quittung... 136 Kalkulation... 138 Bestellung... 128 Kassenbuch.. 132 Aufmaß... 152 Zum Berechnen verwendet Excel Formeln. Diese sind in
2 Die Darstellung linearer Abbildungen durch Matrizen
 2 Die Darstellung linearer Abbildungen durch Matrizen V und V seien Vektorräume über einem Körper K. Hom K (V, V ) bezeichnet die Menge der K linearen Abbildungen von V nach V. Wir machen Hom K (V, V )
2 Die Darstellung linearer Abbildungen durch Matrizen V und V seien Vektorräume über einem Körper K. Hom K (V, V ) bezeichnet die Menge der K linearen Abbildungen von V nach V. Wir machen Hom K (V, V )
Ausgleichungsrechnung I
 Ausgleichungsrechnung I oder Die Anwendung statistischer Methoden in Vermessungswesen und GIS Gerhard Navratil mit Beiträgen von Martin Staudinger Institute for Geoinformation Technical University Vienna
Ausgleichungsrechnung I oder Die Anwendung statistischer Methoden in Vermessungswesen und GIS Gerhard Navratil mit Beiträgen von Martin Staudinger Institute for Geoinformation Technical University Vienna
Einführung in MATLAB
 Kapitel 4 Einführung in MATLAB 41 Allgemeines MATLAB ist eine kommerzielle mathematische Software zur Lösung mathematischer Probleme und zur graphischen Darstellung der Ergebnisse Die Verfahren in MATLAB
Kapitel 4 Einführung in MATLAB 41 Allgemeines MATLAB ist eine kommerzielle mathematische Software zur Lösung mathematischer Probleme und zur graphischen Darstellung der Ergebnisse Die Verfahren in MATLAB
Beispiel zur Lösung eines Gleichungssystems : 6 y + z = 15 0 6 1. 15 12 x + 3 y 3 z = 15 12 3 3. 15 2 x 3 y = 4 2 3 0.
 Beispiel zur Lösung eines Gleichungssystems : 6 y + z = 5 0 6 5 2 x + 3 y 3 z = 5 2 3 3 5 2 x 3 y = 4 2 3 0 4 z2 /3 z : 3 2 x 3 y = 4 2 3 0 4 4 x + y z = 5 4 5 6 y + z = 5 0 6 5 z2 + 2 z 2 x 3 y = 4 2
Beispiel zur Lösung eines Gleichungssystems : 6 y + z = 5 0 6 5 2 x + 3 y 3 z = 5 2 3 3 5 2 x 3 y = 4 2 3 0 4 z2 /3 z : 3 2 x 3 y = 4 2 3 0 4 4 x + y z = 5 4 5 6 y + z = 5 0 6 5 z2 + 2 z 2 x 3 y = 4 2
Staatlich geprüfte Techniker
 Auszug aus dem Lernmaterial ortbildungslehrgang Staatlich geprüfte Techniker Auszug aus dem Lernmaterial Maschinenbautechnische Grundlagen DAA-Technikum Essen / www.daa-technikum.de, Infoline: 001 83 16
Auszug aus dem Lernmaterial ortbildungslehrgang Staatlich geprüfte Techniker Auszug aus dem Lernmaterial Maschinenbautechnische Grundlagen DAA-Technikum Essen / www.daa-technikum.de, Infoline: 001 83 16
Versand Etiketten / Endlosdruck
 Versand Etiketten / Endlosdruck Dieser Etikettendruck ist nur der Druck mit einem Matrix-Druckern möglich. Bei dem Drucker muss der automatische Zeilenvorschub ausgeschaltet sein (siehe Druckerhandbuch).
Versand Etiketten / Endlosdruck Dieser Etikettendruck ist nur der Druck mit einem Matrix-Druckern möglich. Bei dem Drucker muss der automatische Zeilenvorschub ausgeschaltet sein (siehe Druckerhandbuch).
Einführung in die Java- Programmierung
 Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags Pommes... Praktikum A 230 C 207 (Madeleine) F 112 F 113 (Kevin) E
Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags Pommes... Praktikum A 230 C 207 (Madeleine) F 112 F 113 (Kevin) E
Statistisches Programmieren
 Statistisches Programmieren Session 1 1 Was ist R R ist eine interaktive, flexible Software-Umgebung in der statistische Analysen durchgeführt werden können. Zahlreiche statistische Funktionen und Prozeduren
Statistisches Programmieren Session 1 1 Was ist R R ist eine interaktive, flexible Software-Umgebung in der statistische Analysen durchgeführt werden können. Zahlreiche statistische Funktionen und Prozeduren
in den Microsoft Windows Systemen durch einen Doppelklick auf das Icon von MATLAB oder durch Anwählen des Menüs oder Untermenüs in der Abfolge
 1 Grundkenntnisse von MATLAB 1.1 Bekanntschaft schließen mit MATLAB 1.1.1 Die Arbeitsoberfläche von MATLAB Der Start der Applikation MATLAB 1 erfolgt abhängig vom Betriebssystem auf unterschiedliche Weise:
1 Grundkenntnisse von MATLAB 1.1 Bekanntschaft schließen mit MATLAB 1.1.1 Die Arbeitsoberfläche von MATLAB Der Start der Applikation MATLAB 1 erfolgt abhängig vom Betriebssystem auf unterschiedliche Weise:
1 Lineare Gleichungssysteme
 MLAN1 1 LINEARE GLEICHUNGSSYSTEME 1 Literatur: K Nipp/D Stoffer, Lineare Algebra, Eine Einführung für Ingenieure, VDF der ETHZ, 4 Auflage, 1998, oder neuer 1 Lineare Gleichungssysteme Zu den grundlegenden
MLAN1 1 LINEARE GLEICHUNGSSYSTEME 1 Literatur: K Nipp/D Stoffer, Lineare Algebra, Eine Einführung für Ingenieure, VDF der ETHZ, 4 Auflage, 1998, oder neuer 1 Lineare Gleichungssysteme Zu den grundlegenden
Erzeugung zufälliger Graphen und Bayes-Netze
 Erzeugung zufälliger Graphen und Bayes-Netze Proseminar Algorithmen auf Graphen Georg Lukas, IF2000 2002-07-09 E-Mail: georg@op-co.de Folien: http://op-co.de/bayes/ Gliederung 1. Einleitung 2. einfache
Erzeugung zufälliger Graphen und Bayes-Netze Proseminar Algorithmen auf Graphen Georg Lukas, IF2000 2002-07-09 E-Mail: georg@op-co.de Folien: http://op-co.de/bayes/ Gliederung 1. Einleitung 2. einfache
Skript zur Vorlesung Höhere Mathematik für Bachelorstudiengänge. Prof. Dr. R. Herzog. gehalten im SS2013 Technische Universität Chemnitz
 Skript zur Vorlesung Höhere Mathematik für Bachelorstudiengänge Prof. Dr. R. Herzog gehalten im SS2013 Technische Universität Chemnitz Auszug aus den Studienordnungen zu den Ausbildungszielen der mit dieser
Skript zur Vorlesung Höhere Mathematik für Bachelorstudiengänge Prof. Dr. R. Herzog gehalten im SS2013 Technische Universität Chemnitz Auszug aus den Studienordnungen zu den Ausbildungszielen der mit dieser
XONTRO Newsletter. Kreditinstitute. Nr. 18
 XONTRO Newsletter Kreditinstitute Nr. 18 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische
XONTRO Newsletter Kreditinstitute Nr. 18 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische
Statistische Methoden
 Statistische Methoden Dr CJ Luchsinger 6 Repetition: Rechnen mit Matrizen für die Statistik Matrizen sind aus zwei Gründen für die Statistik sehr wichtig: Sie ermöglichen uns einerseits eine sehr elegante
Statistische Methoden Dr CJ Luchsinger 6 Repetition: Rechnen mit Matrizen für die Statistik Matrizen sind aus zwei Gründen für die Statistik sehr wichtig: Sie ermöglichen uns einerseits eine sehr elegante
Inhalt. Vorwort 3. Literatur 51. c Dr. Etienne Emmrich 2004 1
 Inhalt Vorwort 3 1 Strompreise und lineare Funktionen 5 11 Ökonomisches Problem: Bester Stromtarif 5 12 Mathematischer Exkurs: Funktionsbegriff und lineare Funktionen 6 2 Produktionsplanung, Marktforschung,
Inhalt Vorwort 3 1 Strompreise und lineare Funktionen 5 11 Ökonomisches Problem: Bester Stromtarif 5 12 Mathematischer Exkurs: Funktionsbegriff und lineare Funktionen 6 2 Produktionsplanung, Marktforschung,
Rationale Zahlen. Weniger als Nichts? Ist Null nichts?
 Rationale Zahlen Weniger als Nichts? Ist Null nichts? Oft kann es sinnvoll sein, Werte anzugeben die kleiner sind als Null. Solche Werte werden mit negativen Zahlen beschrieben, die durch ein Minus als
Rationale Zahlen Weniger als Nichts? Ist Null nichts? Oft kann es sinnvoll sein, Werte anzugeben die kleiner sind als Null. Solche Werte werden mit negativen Zahlen beschrieben, die durch ein Minus als
Michael Philippsen 1. Algorithmen und Datenstrukturen. 9. Algorithmenherleitung durch Induktion. 9. Algorithmenherleitung durch Induktion
 9. Algorithmenherleitung durch Induktion Algorithmen und Datenstrukturen 9. Algorithmenherleitung durch Induktion Prof. Dr. Christoph Pflaum Department Informatik Martensstraße 3 958 Erlangen 9. Induktionsformen
9. Algorithmenherleitung durch Induktion Algorithmen und Datenstrukturen 9. Algorithmenherleitung durch Induktion Prof. Dr. Christoph Pflaum Department Informatik Martensstraße 3 958 Erlangen 9. Induktionsformen
Formelsammlung Wirtschaftsmathematik
 Formelsammlung Wirtschaftsmathematik Strobel Stefan 29. Januar 2006 Inhaltsverzeichnis I. Mathematik 2 1. Umrechnung von Dezimalzahlen in Brüche 2 2. Differentiationsregeln 2 2.1. Summenregel..................................
Formelsammlung Wirtschaftsmathematik Strobel Stefan 29. Januar 2006 Inhaltsverzeichnis I. Mathematik 2 1. Umrechnung von Dezimalzahlen in Brüche 2 2. Differentiationsregeln 2 2.1. Summenregel..................................
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
2 Lineare Gleichungssysteme
 Beispiel.5: Funktion von Runge (V) Beispiel Martin-Luther-Universität Halle-Wittenberg, NWF III, Institut für Mathematik Martin Arnold: Grundkurs Numerische Mathematik (WiS 27/8) Abbildung.3: Interpolation
Beispiel.5: Funktion von Runge (V) Beispiel Martin-Luther-Universität Halle-Wittenberg, NWF III, Institut für Mathematik Martin Arnold: Grundkurs Numerische Mathematik (WiS 27/8) Abbildung.3: Interpolation
Canon Nikon Sony. Deutschland 55 45 25. Österreich 40 35 35. Schweiz 30 30 20. Resteuropa 60 40 30 55 45 25 40 35 35 J 30 30 20 60 40 30
 15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
7.1 Einleitung... 2. 7.3 Der kopierfähige Verweis... 7. 7.4 Exakte Übereinstimmung... 9 7.4.1 Übungsaufgabe... 10. 7.5 Zusammenfassung...
 Excel 2007/2010 Lernheft 7 Erweiterte Funktionen 2 Inhaltsverzeichnis: 7.1 Einleitung... 2 7.2 Die Verweis-Funktion... 2 7.2.1 Grundverständnis eines Verweises... 2 7.2.2 Der einfache Verweis... 4 7.2.3
Excel 2007/2010 Lernheft 7 Erweiterte Funktionen 2 Inhaltsverzeichnis: 7.1 Einleitung... 2 7.2 Die Verweis-Funktion... 2 7.2.1 Grundverständnis eines Verweises... 2 7.2.2 Der einfache Verweis... 4 7.2.3
Felder, Rückblick Mehrdimensionale Felder. Programmieren in C
 Übersicht Felder, Rückblick Mehrdimensionale Felder Rückblick Vereinbarung von Feldern: typ name [anzahl]; typ name = {e1, e2, e3,..., en} Die Adressierung von Feldelementen beginnt bei 0 Die korrekte
Übersicht Felder, Rückblick Mehrdimensionale Felder Rückblick Vereinbarung von Feldern: typ name [anzahl]; typ name = {e1, e2, e3,..., en} Die Adressierung von Feldelementen beginnt bei 0 Die korrekte
Algorithmik - Kompaktkurs
 Algorithmik - Kompaktkurs Sommersemester 2012 Steffen Lange 0/1, Folie 1 2012 Prof. Steffen Lange - HDa/FbI - Algorithmik Organisatorisches Vorlesung Folien im Netz (/* bitte zur Vorlesung mitbringen */)
Algorithmik - Kompaktkurs Sommersemester 2012 Steffen Lange 0/1, Folie 1 2012 Prof. Steffen Lange - HDa/FbI - Algorithmik Organisatorisches Vorlesung Folien im Netz (/* bitte zur Vorlesung mitbringen */)
ERP Cloud Tutorial. E-Commerce ECM ERP SFA EDI. Backup. Bilanz- und GuV- Berichte erfassen. www.comarch-cloud.de
 ERP Cloud SFA ECM Backup E-Commerce ERP EDI Bilanz- und GuV- Berichte erfassen www.comarch-cloud.de Inhaltsverzeichnis 1 Ziel des s 3 2 Spaltenschema für Standard-Bilanz- und Standard-GuV erfassen 3 3
ERP Cloud SFA ECM Backup E-Commerce ERP EDI Bilanz- und GuV- Berichte erfassen www.comarch-cloud.de Inhaltsverzeichnis 1 Ziel des s 3 2 Spaltenschema für Standard-Bilanz- und Standard-GuV erfassen 3 3
Didaktik der Zahlbereiche 4. Die Menge der ganzen Zahlen. Mathematikunterricht in der Jahrgangsstufe 7. Zahlbereichserweiterungen in der Hauptschule
 Zahlbereichserweiterungen in der Hauptschule Didaktik der Zahlbereiche 4 Dr. Christian Groß Lehrstuhl Didaktik der Mathematik Universität Augsburg Wintersemester 2006/07 Natürliche Zahlen, : Klasse 5 positive
Zahlbereichserweiterungen in der Hauptschule Didaktik der Zahlbereiche 4 Dr. Christian Groß Lehrstuhl Didaktik der Mathematik Universität Augsburg Wintersemester 2006/07 Natürliche Zahlen, : Klasse 5 positive
Dirk Reinhardt Excel für Einsteiger Teil 1. Einleitung
 Einleitung Excel ist ein sogenanntes Tabellenkalkulationsprogramm. Eine Aufgabe eines Tabellenkalkulationsprogramms ist es, häufig wiederkehrende Rechenoperationen, die in einer Tabelle durchgeführt werden,
Einleitung Excel ist ein sogenanntes Tabellenkalkulationsprogramm. Eine Aufgabe eines Tabellenkalkulationsprogramms ist es, häufig wiederkehrende Rechenoperationen, die in einer Tabelle durchgeführt werden,
Fortgeschrittene Funktionen
 Fortgeschrittene Funktionen Rang Syntax: =Rang(Zahl;Bezug;Reihenfolge) Mit der Funktion RANG lässt sich die Position einer Zahl innerhalb einer Zahlenliste bestimmen. Gleiche Zahlen erhalten den gleichen
Fortgeschrittene Funktionen Rang Syntax: =Rang(Zahl;Bezug;Reihenfolge) Mit der Funktion RANG lässt sich die Position einer Zahl innerhalb einer Zahlenliste bestimmen. Gleiche Zahlen erhalten den gleichen
Die Rotations - Chire Projektdokumentation
 Die Rotations - Chire Projektdokumentation Matthias Wul, Stephan Naterski 19. Juni 2008 Inhaltsverzeichnis 1 Geschichtliche Hintergründe 3 1.1 Die Transpositions-Chire........................... 3 1.1.1
Die Rotations - Chire Projektdokumentation Matthias Wul, Stephan Naterski 19. Juni 2008 Inhaltsverzeichnis 1 Geschichtliche Hintergründe 3 1.1 Die Transpositions-Chire........................... 3 1.1.1
Ingenieurinformatik Diplom-FA (Teil 2, C-Programmierung)
 Hochschule München, FK 03 SS 2014 Ingenieurinformatik Diplom-FA (Teil 2, C-Programmierung) Zulassung geprüft: (Grundlagenteil) Die Prüfung ist nur dann gültig, wenn Sie die erforderliche Zulassungsvoraussetzung
Hochschule München, FK 03 SS 2014 Ingenieurinformatik Diplom-FA (Teil 2, C-Programmierung) Zulassung geprüft: (Grundlagenteil) Die Prüfung ist nur dann gültig, wenn Sie die erforderliche Zulassungsvoraussetzung
ÜBERBLICK ÜBER DAS KURS-ANGEBOT
 ÜBERBLICK ÜBER DAS KURS-ANGEBOT Alle aufgeführten Kurse sind 100 % kostenfrei und können unter http://www.unterricht.de abgerufen werden. ANALYSIS / INFINITESIMALRECHNUNG Nullstellen * Nullstellen einer
ÜBERBLICK ÜBER DAS KURS-ANGEBOT Alle aufgeführten Kurse sind 100 % kostenfrei und können unter http://www.unterricht.de abgerufen werden. ANALYSIS / INFINITESIMALRECHNUNG Nullstellen * Nullstellen einer
Was war vor dem Startwert?
 63 Hans Walser Was war vor dem Startwert? Das mathematische Analogon zur Frage, was vor Adam und Eva war, ist die Frage, ob und wie Folgen und mathematische Strukturen, welche einen natürlichen Anfang
63 Hans Walser Was war vor dem Startwert? Das mathematische Analogon zur Frage, was vor Adam und Eva war, ist die Frage, ob und wie Folgen und mathematische Strukturen, welche einen natürlichen Anfang
Lineare Gleichungssysteme. Lineare Gleichungssysteme. LR Zerlegung ohne Pivotsuche. Zerlegung regulärer Matrizen
 Heinrich Voss voss@tu-harburg.de Hamburg University of Technology Institute for Numerical Simulation Betrachte ein lineares Gleichungssystem Ax = b (1) Es sei A C n n eine gegebene regulär Matrix. Dann
Heinrich Voss voss@tu-harburg.de Hamburg University of Technology Institute for Numerical Simulation Betrachte ein lineares Gleichungssystem Ax = b (1) Es sei A C n n eine gegebene regulär Matrix. Dann
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Kassa-Abschluss buchen. DirectCASH. Dokumentation. DirectCASH Tagesabschluss buchen www.directsoft.at Seite 1 von 16
 Kassa-Abschluss buchen DirectCASH Dokumentation DirectCASH Tagesabschluss buchen www.directsoft.at Seite 1 von 16 Inhaltsverzeichnis 1. Einleitung... 3 2. Abschlussarten... 3 2.1. Tägliche Übergabe...
Kassa-Abschluss buchen DirectCASH Dokumentation DirectCASH Tagesabschluss buchen www.directsoft.at Seite 1 von 16 Inhaltsverzeichnis 1. Einleitung... 3 2. Abschlussarten... 3 2.1. Tägliche Übergabe...
2. Programmierung in C
 2. Programmierung in C Inhalt: Überblick über Programmiersprachen, Allgemeines zur Sprache C C: Basisdatentypen, Variablen, Konstanten Operatoren, Ausdrücke und Anweisungen Kontrollstrukturen (Steuerfluss)
2. Programmierung in C Inhalt: Überblick über Programmiersprachen, Allgemeines zur Sprache C C: Basisdatentypen, Variablen, Konstanten Operatoren, Ausdrücke und Anweisungen Kontrollstrukturen (Steuerfluss)
16. All Pairs Shortest Path (ASPS)
 . All Pairs Shortest Path (ASPS) All Pairs Shortest Path (APSP): Eingabe: Gewichteter Graph G=(V,E) Ausgabe: Für jedes Paar von Knoten u,v V die Distanz von u nach v sowie einen kürzesten Weg a b c d e
. All Pairs Shortest Path (ASPS) All Pairs Shortest Path (APSP): Eingabe: Gewichteter Graph G=(V,E) Ausgabe: Für jedes Paar von Knoten u,v V die Distanz von u nach v sowie einen kürzesten Weg a b c d e
Matrikelnummer. Name: Vorname: Modulklausur: Einführung in die Wirtschaftswissenschaft (31001)
 Name: Vorname: Termin: Prüfer: 27.09.2011, 15.30 17.30 Uhr Aufgabe 1 2 3 4 5 6 Gesamt Maximale Punktzahl 7 9 16 10 4 4 50 Erreichte Punktzahl - 1 - Hinweise zur Bearbeitung der Klausur! 1. Die Klausur
Name: Vorname: Termin: Prüfer: 27.09.2011, 15.30 17.30 Uhr Aufgabe 1 2 3 4 5 6 Gesamt Maximale Punktzahl 7 9 16 10 4 4 50 Erreichte Punktzahl - 1 - Hinweise zur Bearbeitung der Klausur! 1. Die Klausur
3.2 Aufbau des Betriebsabrechnungsbogens
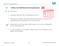 3.2 Aufbau des Betriebsabrechnungsbogens Kennzeichnung: Zentrales Instrument der Kostenstellenrechnung Tabellarischer Aufbau: Der BAB enthält zeilenweise die Kostenarten und spaltenweise die Kostenstellen
3.2 Aufbau des Betriebsabrechnungsbogens Kennzeichnung: Zentrales Instrument der Kostenstellenrechnung Tabellarischer Aufbau: Der BAB enthält zeilenweise die Kostenarten und spaltenweise die Kostenstellen
Wofür braucht man eine Tabellenkalkulation? Das Programm Microsoft Excel gehört in Softwarekategorie der Tabellenkalkulationen.
 Wofür braucht man eine Tabellenkalkulation? Das Programm Microsoft Excel gehört in Softwarekategorie der Tabellenkalkulationen. Was bedeutet das? Man kann damit alles berechnen, was sich irgendwie in Tabellenform
Wofür braucht man eine Tabellenkalkulation? Das Programm Microsoft Excel gehört in Softwarekategorie der Tabellenkalkulationen. Was bedeutet das? Man kann damit alles berechnen, was sich irgendwie in Tabellenform
Einführung in die Tabellenkalkulation Microsoft Excel
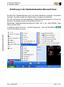 Einführung in die Tabellenkalkulation Microsoft Excel Mit Hilfe einer Tabellenkalkulation kann man Daten tabellarisch auswerten und grafisch darstellen. Die Daten werden als Tabelle erfasst, verwaltet
Einführung in die Tabellenkalkulation Microsoft Excel Mit Hilfe einer Tabellenkalkulation kann man Daten tabellarisch auswerten und grafisch darstellen. Die Daten werden als Tabelle erfasst, verwaltet
klar. Um die zweite Bedingung zu zeigen, betrachte u i U i mit u i = 0. Das mittlere -Zeichen liefert s
 Nachtrag zur allgemeinen Vektorraum-Theorie. 1.5.15. Direkte Summen. Sei V ein Vektorraum, seien U 1,..., U t Unterräume, wir schreiben V = U 1 U 2 U t = t i=1 U i falls die folgenden beiden Bedingungen
Nachtrag zur allgemeinen Vektorraum-Theorie. 1.5.15. Direkte Summen. Sei V ein Vektorraum, seien U 1,..., U t Unterräume, wir schreiben V = U 1 U 2 U t = t i=1 U i falls die folgenden beiden Bedingungen
Java Einführung Operatoren Kapitel 2 und 3
 Java Einführung Operatoren Kapitel 2 und 3 Inhalt dieser Einheit Operatoren (unär, binär, ternär) Rangfolge der Operatoren Zuweisungsoperatoren Vergleichsoperatoren Logische Operatoren 2 Operatoren Abhängig
Java Einführung Operatoren Kapitel 2 und 3 Inhalt dieser Einheit Operatoren (unär, binär, ternär) Rangfolge der Operatoren Zuweisungsoperatoren Vergleichsoperatoren Logische Operatoren 2 Operatoren Abhängig
Kapitel 3 Mathematik. Kapitel 3.3. Algebra Gleichungen
 TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 3 Mathematik Kapitel 3.3 Algebra Gleichungen Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 877 Nidfurn 055-654 1 87 Ausgabe: Februar 009
TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 3 Mathematik Kapitel 3.3 Algebra Gleichungen Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 877 Nidfurn 055-654 1 87 Ausgabe: Februar 009
Bestimmung einer ersten
 Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Prozess und Statistik. Einführung in. Eine R-Übersicht und Motivation R in der täglichen Arbeit zu nutzen. Günter Faes faes.de.
 Einführung in Eine R-Übersicht und Motivation R in der täglichen Arbeit zu nutzen Seite: 1 Präsentationsthemen Was ist R? R Installation R Grundlagen Das Menü Die ersten Schritte R Daten-Objekte und deren
Einführung in Eine R-Übersicht und Motivation R in der täglichen Arbeit zu nutzen Seite: 1 Präsentationsthemen Was ist R? R Installation R Grundlagen Das Menü Die ersten Schritte R Daten-Objekte und deren
Einführung in die Programmierung (EPR)
 Goethe-Center for Scientific Computing (G-CSC) Goethe-Universität Frankfurt am Main Einführung in die Programmierung (EPR) (Übung, Wintersemester 2014/2015) Dr. S. Reiter, M. Rupp, Dr. A. Vogel, Dr. K.
Goethe-Center for Scientific Computing (G-CSC) Goethe-Universität Frankfurt am Main Einführung in die Programmierung (EPR) (Übung, Wintersemester 2014/2015) Dr. S. Reiter, M. Rupp, Dr. A. Vogel, Dr. K.
Einführung in das Arbeiten mit MS Excel. 1. Bearbeitungs
 Einführung in das Arbeiten mit MS Excel 1. Bildschirmaufbau Die Tabellenkalkulation Excel basiert auf einem Rechenblatt, das aus Spalten und Zeilen besteht. Das Rechenblatt setzt sich somit aus einzelnen
Einführung in das Arbeiten mit MS Excel 1. Bildschirmaufbau Die Tabellenkalkulation Excel basiert auf einem Rechenblatt, das aus Spalten und Zeilen besteht. Das Rechenblatt setzt sich somit aus einzelnen
Lineare Gleichungssysteme I (Matrixgleichungen)
 Lineare Gleichungssysteme I (Matrigleichungen) Eine lineare Gleichung mit einer Variable hat bei Zahlen a, b, die Form a b. Falls hierbei der Kehrwert von a gebildet werden darf (a 0), kann eindeutig aufgelöst
Lineare Gleichungssysteme I (Matrigleichungen) Eine lineare Gleichung mit einer Variable hat bei Zahlen a, b, die Form a b. Falls hierbei der Kehrwert von a gebildet werden darf (a 0), kann eindeutig aufgelöst
Mathematik III für Ingenieure
 Mathematik III für Ingenieure im Bachelor-Studiengang Maschinenbau Vorlesung Wintersemester 21/211 B. Schuster aktualisert am 27. Januar 211 Inhalt I. Eigenwerte und Eigenvektoren 1 1. Komplexe Matrizen
Mathematik III für Ingenieure im Bachelor-Studiengang Maschinenbau Vorlesung Wintersemester 21/211 B. Schuster aktualisert am 27. Januar 211 Inhalt I. Eigenwerte und Eigenvektoren 1 1. Komplexe Matrizen
Inhalte: Bestandsveränderungen, Abschlussbuchungen, Umsatzsteuer, Vorsteuer, Zahllast
 1 REWE ÜBUNG 3 Inhalte: Bestandsveränderungen, Abschlussbuchungen, Umsatzsteuer, Vorsteuer, Zahllast 1. Bestandsveränderungen (relev. Abschnitte im Schmole/Deitermann) Bisher: Es wurde unterstellt, dass
1 REWE ÜBUNG 3 Inhalte: Bestandsveränderungen, Abschlussbuchungen, Umsatzsteuer, Vorsteuer, Zahllast 1. Bestandsveränderungen (relev. Abschnitte im Schmole/Deitermann) Bisher: Es wurde unterstellt, dass
Das Kryptosystem von McEliece. auf der Basis von linearen Codes
 Das Kryptosystem von McEliece auf der Basis von linearen Codes Anforderungen Public-Key Kryptosysteme E e (m) = c Verschlüsselung D d (c) = m Entschlüsselung mit Schl. effizient effizient 2/25 Anforderungen
Das Kryptosystem von McEliece auf der Basis von linearen Codes Anforderungen Public-Key Kryptosysteme E e (m) = c Verschlüsselung D d (c) = m Entschlüsselung mit Schl. effizient effizient 2/25 Anforderungen
LINEARE ALGEBRA Ferienkurs. Hanna Schäfer Philipp Gadow
 LINEARE ALGERA Ferienkurs Hanna Schäfer Philipp Gadow INHALT Eigenwerte und Eigenvektoren. asiswechsel.2 Eigenwertgleichung 2.3 Diagonalisierbarkeit 5.4 Trigonalisierung 8.5 Zusatzmaterial 8 Aufgaben 9
LINEARE ALGERA Ferienkurs Hanna Schäfer Philipp Gadow INHALT Eigenwerte und Eigenvektoren. asiswechsel.2 Eigenwertgleichung 2.3 Diagonalisierbarkeit 5.4 Trigonalisierung 8.5 Zusatzmaterial 8 Aufgaben 9
Statistiken und Standardauswertungen
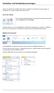 Statistiken und Standardauswertungen Nutzen Sie das ERP von work4all, stehen Ihnen eine Reihe von statistischen Auswertungen zur Verfügung, die in diesem Kapitel beschrieben werden. Aufruf der Statistik
Statistiken und Standardauswertungen Nutzen Sie das ERP von work4all, stehen Ihnen eine Reihe von statistischen Auswertungen zur Verfügung, die in diesem Kapitel beschrieben werden. Aufruf der Statistik
Tipps und Kniffe für MS Excel 2010. Wie Excel denkt und wie wir es sinnvoll nutzen können
 Tipps und Kniffe für MS Excel 2010 Wie Excel denkt und wie wir es sinnvoll nutzen können Die Benutzeroberfläche von Excel Datei >> Optionen die Voreinstellungen Erste Übung mit Excel-Mappe Tabellenblätter
Tipps und Kniffe für MS Excel 2010 Wie Excel denkt und wie wir es sinnvoll nutzen können Die Benutzeroberfläche von Excel Datei >> Optionen die Voreinstellungen Erste Übung mit Excel-Mappe Tabellenblätter
> patienten<-data.frame( c(28,61,79,54,na,48), c(2,2,3,2,1,1), c("pillen","pillen","massage","gymnastik","massage","gymnastik"),
 1 Der Datentyp factor in R 2 Beispieldatensatz > patienten
1 Der Datentyp factor in R 2 Beispieldatensatz > patienten
Folien zum Proseminar Altersvorsorge in Deutschland
 Proseminar im SoSe 2007 Proseminar - Arbeiten mit Excel und Power Point - Dipl.-Kfm. J. Huber 1. Arbeiten mit Excel 2. Erstellen und Formatieren von Grafiken 3. Erstellen einer Präsentation http://www.uni-trier.de/uni/fb4/vwl_amk/index.htm
Proseminar im SoSe 2007 Proseminar - Arbeiten mit Excel und Power Point - Dipl.-Kfm. J. Huber 1. Arbeiten mit Excel 2. Erstellen und Formatieren von Grafiken 3. Erstellen einer Präsentation http://www.uni-trier.de/uni/fb4/vwl_amk/index.htm
