Bilder: Eigenschaften
|
|
|
- Fanny Messner
- vor 8 Jahren
- Abrufe
Transkript
1 Bilder: Eigenschaften Images M. Thaler TG208 Juni
2 Um was geht es? Juni 17 2 Was ist ein Bild? - hier sehen sie verschiedene Ausschnitte eines digitalen Bildes -das Bild besteht aus Farben - näher betrachtet aus Bildpunkten sind quadratisch jeder Punkt hat eine andere Farbe Wie beschreibt man solche Bilder Wie kommen sie zustande Was für Eigenschaften haben Bilder Welche Tpen von Bildern gibt es 2
3 Inhalt Um was geht es? Lehrziele Bildaufnahme Bilder als Funktionen Signale Räumliche Auflösung und Quantisierung Beziehung zwischen Pieln Statistische Eigenschaften von Bildern Rauschmodelle Datentpen und -Strukturen Juni
4 Lehrziele Sie wissen wie Bilder mathematisch dargestellt werden können kennen die Effekte der Quantisierung und können sie diskutieren räumlich und wertemässig kennen Nachbarschaftsbeziehungen zwischen Pieln und können sie erklären und diskutieren kennen die grundlegenden statistischen Eigen-schaften von Bildern und können sie berechnen kennen die zwei wichtigsten Rauschmodelle und können sie diskutieren wissen wie Bilder softwaremässig dargestellt werden und können Problemstellungen diskutieren Juni
5 Bildaufnahme Drei grundlegende Komponenten Lichtquelle Objekt Lichtquelle Kamera Objekt Linse industrielle Kamera Kamera Bildaufnahme optische Achse Sensor Juni
6 Digitale Bildaufnahme Lichtquelle i Objekt Szene i r Optik Projektionsebene intern f' = i r digitalisiertes Bild f Juni 17 6 imaging sstem - Optik visuelle Bereich -Gitter -etc. 6
7 Das Bild als 2-d Funktion Eine 2-dimensionale Funktion f z.b. Intensität als Funktion des Ortes i Intensität entlang einer Bildzeile: f' = f M / 2 Intensität als 3D-Grafik Juni
8 8 Juni 17 8 Funktion: Definitionsbereich a Wertebereich Farbbilder Graustufenbilder Binärbilder Bilder als Funktionen { } oder { } = B G R B G R B G R f r a { } oder { } f f f a {01} f f a Farbbilder - 2^24 Farben ~ 16.7 Mio verschiedene Farben Graustufenbilder -255 Farben Binärbilder -schwarz / weiss
9 Darstellung von digitalen Bildern Farbbilder drei 2-d Matrizen für RGB Graustufenbilder / Binärbilder eine 2-d Matri für Graustufen resp. schwarz / weiss f = A = f00 f01... f0n-1 f10 f11... f1n fm-10 fm fm-1n-1 a 00 a a 0N-1 a 10 a a 1N a M-10 a M a M-10N-1 Juni 17 9 Was sehen Sie auf diesem Bild? -kneiffen Sie Ihre Augen zu... sehen Sie es jetzt? - was haben Sie gemacht?... unsharp masking 9
10 Farbbilder R G B Juni
11 Graustufen- und Binärbilder Binärbild threshold 64 Graustufenbild f {0..255} f {01} Juni
12 Subsampling Juni
13 ... Subsampling Juni
14 Quantisierung Anzahl Bit's pro Piel 256 Graustufen 8 Bit 32 Graustufen 5 Bit 16 Graustufen 4 Bit 8 Graustufen 3 Bit Juni ca Graustufen sind durch das menschliche Auge unterscheidbar 14
15 Quantisierung b 0 b 4 b 1 b 5 Bit-Ebenen: b 7... b 0 Auflösung reduziert b 2 b 3 b 6 b 7 Juni
16 Aliasing Abtasttheorem: 2 höchste Frequenz periodische Funktionen können korrekt abgetastet werden Moiré-Muster Funktionen periodisch Rotation und Überlagerung verletzt Periodizität zusätzliche Frequenzkomponenten BV: das Abtasttheorem wird fast immer verletzt Korrektur nach dem Abtasten kaum mehr möglich Juni Schwarz / Weiss Bilder -Auflösung resp. Anzahl Piel / pro Länge muss 2 grösser als die "kleinste" zu erkennende Struktur sein 16
17 "Beziehung" zwischen Pieln Wie lang ist die Linie? Juni
18 ... Beziehung zwischen Pieln z.b. nur diagonale Verbindungen zulassen welche Piel löschen? nicht ganz eindeutig Juni
19 ... Beziehung zwischen Pieln Mittelpunkte der Piel verbinden Juni
20 Nachbarn eines Piels Nachbarschaft von Piel p und q Nachbarn gleiche Eigenschaften z.b. Graustufen Farbe etc. Mögliche Nachbarschaften N 4 p: die vertikalen und horizontalen Nachbarn des Piels p p 1 p + 1 p 1 p + 1 N D p: die vier diagonalen Nachbarn des Piels p p 1 1 p p p N 8 p: die 8 Nachbarn N 4 p und N D pdes Piel p p p p Juni
21 Zusammenhängende Komponenten zwei verbundene Objekte 1 wenn 4er Nachbarschaft ein verbundenes Objekte wenn 8er Nachbarschaft 1 connected component verbundenes Objekte 4er Nachbarschaft Juni Geben hier Nachbarschaftsbeziehung zwischen Pieln vor und testen welche Piel jeweils diese Beziehung erfüllen -> alle diese Piel werden zu einer verbundenen Komponente zusammengefasst hier farbig markiert 21
22 Nachbarschaften und Pfade Pfad eine Sequenz von benachbarten Punkten 3 Tpen von Nachbarschaften: Piel p und q 4-adjacent - q N 4 p 8-adjacent - q N 8 p m-adjacent - q N 4 p oder - q N D p und N 4 q N 4 p = 0 -connected Pfad -Path -Pfad alle Punkte auf dem Pfad sind -adjacent mit = 4 8 oder m Juni adjacent -> benachbart 22
23 ... Nachbarschaften Beispiel Nachbarschaften 4-adjacent 8-adjacent m-adjacent connected path connected path m-connected path Juni Zeichnen Sie den 4-path den 8-path und den m-path in die entsprechenden Bildausschnitte ein 23
24 Borders and Edges Border / Boundar: Kontur Grenze Menge aller Piel einer Region die mindestens ein Nachbarpiel haben das nicht zur Region gehört geschlossener Pfad wenn Region endlich gross ist global Edge: Kante Ableitung der Intensität übersteigt einen Schwellwert T Ableitung ~ Grauwertänderung lokal Border Kante Juni
25 Distanz-Metriken Gegeben zwei Piel: p und qst wie gross ist die Distanz zwischen den zwei Pieln? Distanzen unabhängig vom Weg Euklidische Distanz D E = 2 s + t Manhattan Distanz D M = s + t Schachbrett Distanz D C 2 s t = ma D E D M D C Juni Hinweis Diagonalabstand - Euklidische Distanz = sqrt2 = wird manchmal mir 1.5 angenähert maimaler Fehler ca. 12% 25
26 Statistische Eigenschaften Histogramm: h'g i Auftretenshäufigkeit eines Pielwertes z.b. des Grauwertes h' g i Anzahl Linien entsprechen der Anzahl Piel mit einem bestimmten Grauwert Grauwert Juni
27 ... statistische Eigenschaften Auftretenshäufigkeit eines Grauwertes Anzahl Piel n i mit einem bestimmen Grauwert g i n i = h' gi gi {0..255} Normierte Auftretenshäufigkeit N M gross Näherung für Wahrscheinlichkeitsverteilung h' gi h gi = p gi M N pg i : Wahrscheinlichkeit dass ein Piel den Grauwert g i hat Juni
28 28 Juni Mittelwert Momente Varianz σ= var Globale statistische Eigenschaften = = 1 0 L i i g i h g m = = 1 0 L i n i i n m g g h g µ = = = M N f N M f = = = M N n n f f N M µ = = var L i i i m g g h g = = = var M N f f N M L: Anzahl Graustufen M N: Bildgrösse Statistische Kenngrössen - Wahrscheinlichkeitsverteilung - Mittelwert oder Erwartungswert - Momente n = 2 Varianz Berechnung der statistischen Grössen - sowohl aus Histogramm -als auch aus Bild = = = 1 0 K z i z i p z z m = = 1 0 K i n i i n m z z p z µ i z p
29 Lokale statistische Eigenschaften Kenngrössen aus lokaler Umgebung berechnen z.b. 33 Umgebung mittleres Piel wird durch Mittelwert der Umgebung ersetzt - Tiefpass-Filterung - m =? Piel wird durch Varianz der Umgebung ersetzt - Mass für Tetur Struktur σ =? Juni m = 1/ *3 + 3*4 + 2*5 + 6 = 1/ = 36/9 = 4 s^2 = = 12/8 = 3/2 s ~
30 Rauschmodelle Zwei wesentliche Rauschemodelle Salt & Pepper Noise Gaussian Noise Salt & Pepper Noise Impulsrauschen Modell für schnelle Transienten bei der Bildaufnahme Transienten oft viel grösser als Signal - werden meist als schwarze und weisse Piel digitalisiert Gaussian Noise Modell für Rauschen von elektr. Komponenten und Sensoren Bildaufnahme: z.b. schlechte Beleuchtung hohe Temperatur Bildübertragung Kamera Framgrabber oft noch analog Verarbeitung: z.b. Verstärker Juni
31 Salt & Pepper Noise Probabilit Densit Function: PDF pz P b P a a b z Pa p z = Pb 0 z = a z = b otherwise wenn P b ~ P a - gleicht zufällig über das Bild verteilten weisse und schwarze Körner salt & pepper Juni
32 Gaussian Noise Probabilit Densit Function: PDF 1 p z = e σ 2π 2 z µ 2 2 σ µ σ 2σ µ µ+σ Parameter: - µ : Mittelwert µ = E{z} - σ 2 : Varianz σ 2 =E{z - µ 2 } ~70% der Rauschwerte liegen im Intervall: [ µ - σ µ + σ ] ~95% der Rauschwerte liegen im Intervall: [ µ - 2σ µ + 2σ] Juni
33 ... Rauschmodelle gaussian noise µ = 0 σ = 0.2 salt & pepper noise 20% verrauschte Piel Juni Weitere Rauschmodelle und Anwendungsgebiete - Range Imaging raleigh noise - Laser Imaging erlang gamma noise eponential noise - Basis für Zufallsgeneratoren sonst wenig praktischer Bezug uniform noise 33
34 Datentpen und -Strukturen Piel Speicherung - meist als 8-Bit unsigned: manchmal double float: Rechenoperationen - Vorsicht mit 8-Bit unsigned Überlauf - besser Casts nach short int oder double - Binärbilder: boolean oder short/int mit 0 und!= 0 - bei Überlauf und Unterlauf oft Sättigung auf Maimal oder Minimalwert abhängig von Anwendung if pi > 255 pi = 255; if pi < 0 pi = 0; Juni
35 ... Datentpen und -Strukturen width N Bilder als Arras 1-d: int img[height*width] heightm - Zugriff auf Element ij: img[i*height+j] i * height j 2-d: int img[height][width] - Zugriff auf Element ij: img[i][j] i j Juni
36 ... Datentpen und -Strukturen Bilder: "Menge" von Attributen meist ein Arra pro Attribut Attribute können sein - Farben R G B und T Transparenz - Graustufen - Teturmass z.b. Varianz oder Standardabweichung - etc. z.b. Farbbilder 1-d: int img[height * width][3] 2-d: int img[height][width][3] - rot img[h][w][1] - grün img[h][w][2] - blau img[h][w][3] Juni
Digitale Bildverarbeitung (DBV)
 Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Grundlagen der Bildverarbeitung: Übung 1
 Grundlagen der Bildverarbeitung: Übung 1 Michael Korn Raum: BC 414, Tel.: 0203-379 - 3583, E-Mail: [email protected] Michael Korn ([email protected]) GBV: Übung 1 1 / 24 Digitale Bilder Michael
Grundlagen der Bildverarbeitung: Übung 1 Michael Korn Raum: BC 414, Tel.: 0203-379 - 3583, E-Mail: [email protected] Michael Korn ([email protected]) GBV: Übung 1 1 / 24 Digitale Bilder Michael
Inhalt. Bildaufnahme / Digitale Bilder. Kameras CCD Sensoren Auge Sampling / Aliasing Quantisierung
 Inhalt Bildaufnahme / Digitale Bilder Kameras CCD Sensoren Auge Sampling / Aliasing Quantisierung Abtastung, Parameter Aliasing-Beispiel: Unterabtastung einer periodischen Funktion. Rekonstruktion ergibt
Inhalt Bildaufnahme / Digitale Bilder Kameras CCD Sensoren Auge Sampling / Aliasing Quantisierung Abtastung, Parameter Aliasing-Beispiel: Unterabtastung einer periodischen Funktion. Rekonstruktion ergibt
Statistische Kenngrößen. Histogramm. Grundlagen zur statistischen Signalverarbeitung. Statistische Beschreibung von Audio
 8.3.6 Statistische Kenngrößen Grundlagen zur statistischen Signalverarbeitung Dr. Detlev Marpe Fraunhofer Institut für achrichtentechnik HHI Histogramm Wahrscheinlichkeitsdichteverteilung Mittelwert µ
8.3.6 Statistische Kenngrößen Grundlagen zur statistischen Signalverarbeitung Dr. Detlev Marpe Fraunhofer Institut für achrichtentechnik HHI Histogramm Wahrscheinlichkeitsdichteverteilung Mittelwert µ
INTELLIGENTE DATENANALYSE IN MATLAB
 INTELLIGENTE DATENANALYSE IN MATLAB Bildanalyse Literatur David A. Forsyth: Computer Vision i A Modern Approach. Mark S. Nixon und Alberto S. Aguado: Feature Extraction and Image Processing. Ulrich Schwanecke:
INTELLIGENTE DATENANALYSE IN MATLAB Bildanalyse Literatur David A. Forsyth: Computer Vision i A Modern Approach. Mark S. Nixon und Alberto S. Aguado: Feature Extraction and Image Processing. Ulrich Schwanecke:
Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt
 Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt im Juni 2016 Themen: Digitale Bilder, Eigenschaften
Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt im Juni 2016 Themen: Digitale Bilder, Eigenschaften
Farbtiefe. Gängige Farbtiefen
 Farbtiefe Die Anzahl der darstellbaren Farben ist abhängig von den Farbabstufungen, die in einem Pixel gespeichert werden. Die Anzahl der darstellbaren Farbtöne wird als Farbtiefe bezeichnet. Die Farbtiefe
Farbtiefe Die Anzahl der darstellbaren Farben ist abhängig von den Farbabstufungen, die in einem Pixel gespeichert werden. Die Anzahl der darstellbaren Farbtöne wird als Farbtiefe bezeichnet. Die Farbtiefe
Adaptive Systeme. Sommersemester Prof. Dr. -Ing. Heinz-Georg Fehn. Prof. Dr. rer. nat. Nikolaus Wulff
 Adaptive Systeme Sommersemester 2015 Prof. Dr. -Ing. Heinz-Georg Fehn Prof. Dr. rer. nat. Nikolaus Wulff Prof. Dr. H.-G. Fehn und Prof. Dr. N. Wulff 1 Adaptive Systeme Adaptives System: ein System, das
Adaptive Systeme Sommersemester 2015 Prof. Dr. -Ing. Heinz-Georg Fehn Prof. Dr. rer. nat. Nikolaus Wulff Prof. Dr. H.-G. Fehn und Prof. Dr. N. Wulff 1 Adaptive Systeme Adaptives System: ein System, das
2. Digitale Codierung und Übertragung
 2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
Motivation. Diskretisierung. Überblick. Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen. Diskretisierung und Quantisierung
 Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
Digitale Bildverarbeitung (DBV)
 Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV)
 Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Bildverarbeitung Herbstsemester 2012. Kanten und Ecken
 Bildverarbeitung Herbstsemester 01 Kanten und Ecken 1 Inhalt Einführung Kantendetektierung Gradientenbasierende Verfahren Verfahren basierend auf der zweiten Ableitung Eckpunkterkennung Harris Corner Detector
Bildverarbeitung Herbstsemester 01 Kanten und Ecken 1 Inhalt Einführung Kantendetektierung Gradientenbasierende Verfahren Verfahren basierend auf der zweiten Ableitung Eckpunkterkennung Harris Corner Detector
Binärbildverarbeitung
 Prof. Dr.-Ing. Thomas Zielke " Binärbildverarbeitung SS 2013 3.1 Anwendungen von Binärbildern" Ein Bild mit nur zwei Grau/Farb-Stufen nennt man Binärbild. In der Regel werden Bildpunkte mit dem Wert Null
Prof. Dr.-Ing. Thomas Zielke " Binärbildverarbeitung SS 2013 3.1 Anwendungen von Binärbildern" Ein Bild mit nur zwei Grau/Farb-Stufen nennt man Binärbild. In der Regel werden Bildpunkte mit dem Wert Null
Übersicht der Vorlesung
 Übersicht der Vorlesung. Einführung. Bildverarbeitung. Morphologische Operationen 4. Bildsegmentierung 5. Merkmale von Objekten 6. Klassifikation 7. Dreidimensionale Bildinterpretation 8. Bewegungsanalyse
Übersicht der Vorlesung. Einführung. Bildverarbeitung. Morphologische Operationen 4. Bildsegmentierung 5. Merkmale von Objekten 6. Klassifikation 7. Dreidimensionale Bildinterpretation 8. Bewegungsanalyse
Der Zentrale Grenzwertsatz
 QUALITY-APPS Applikationen für das Qualitätsmanagement Der Zentrale Grenzwertsatz Autor: Dr. Konrad Reuter Für ein Folge unabhängiger Zufallsvariablen mit derselben Verteilung und endlichem Erwartungswert
QUALITY-APPS Applikationen für das Qualitätsmanagement Der Zentrale Grenzwertsatz Autor: Dr. Konrad Reuter Für ein Folge unabhängiger Zufallsvariablen mit derselben Verteilung und endlichem Erwartungswert
Digitale Bilder. Ein Referat von Jacqueline Schäfer und Lea Pohl Am
 Digitale Bilder Ein Referat von Jacqueline Schäfer und Lea Pohl Am 06.05.2015 Inhaltsverzeichnis Einheiten Grafiktypen Bildformate Farbtiefe Farbbilder/ Farbräume Quellen Einführung in die Bildverarbeitung
Digitale Bilder Ein Referat von Jacqueline Schäfer und Lea Pohl Am 06.05.2015 Inhaltsverzeichnis Einheiten Grafiktypen Bildformate Farbtiefe Farbbilder/ Farbräume Quellen Einführung in die Bildverarbeitung
Inhaltsbasierte Bildsuche. Matthias Spiller. 17. Dezember 2004
 Kantenbasierte Merkmale für die Bildsuche Inhaltsbasierte Bildsuche Matthias Spiller 17. Dezember 2004 Übersicht Übersicht Einleitung Was sind Kanten? Kantenrichtungs Histogramm Der Canny-Algorithmus Feature-Erzeugung
Kantenbasierte Merkmale für die Bildsuche Inhaltsbasierte Bildsuche Matthias Spiller 17. Dezember 2004 Übersicht Übersicht Einleitung Was sind Kanten? Kantenrichtungs Histogramm Der Canny-Algorithmus Feature-Erzeugung
Elektrotechnik II: Kolloquium 4
 Elektrotechnik II: Kolloquium 4 Digitalschaltungen Hubert Abgottspon: [email protected] Markus Imhof: [email protected] Inhalt des Kolloquium: Digitale Messkette Sensor 1) Filter S&H- Versträker
Elektrotechnik II: Kolloquium 4 Digitalschaltungen Hubert Abgottspon: [email protected] Markus Imhof: [email protected] Inhalt des Kolloquium: Digitale Messkette Sensor 1) Filter S&H- Versträker
Bildkompression InTh, 2005, JPEG, Hak, Rur, 1
 Bildkompression InTh, 25, JPEG, Hak, Rur, 1 Referenzen [1] D Salomon, Data Compression, Springer, 24 [2] Prof Dr A Steffen, Kurs SU, ZHW, 1999-24 [3] G Wallace, The JPEG Still Picture Compression Standard,
Bildkompression InTh, 25, JPEG, Hak, Rur, 1 Referenzen [1] D Salomon, Data Compression, Springer, 24 [2] Prof Dr A Steffen, Kurs SU, ZHW, 1999-24 [3] G Wallace, The JPEG Still Picture Compression Standard,
 Bachelor BEE Statistik Übung: Blatt 1 Ostfalia - Hochschule für angewandte Wissenschaften Fakultät Versorgungstechnik Aufgabe (1.1): Gegeben sei die folgende Messreihe: Nr. ph-werte 1-10 6.4 6.3 6.7 6.5
Bachelor BEE Statistik Übung: Blatt 1 Ostfalia - Hochschule für angewandte Wissenschaften Fakultät Versorgungstechnik Aufgabe (1.1): Gegeben sei die folgende Messreihe: Nr. ph-werte 1-10 6.4 6.3 6.7 6.5
Wie es Euch gefällt Pixelvorverarbeitung oder RAW-Format
 Wie es Euch gefällt Pixelvorverarbeitung oder RAW-Format Je nach Anwendung werden an die Bilddaten unterschiedliche Anforderungen gestellt. Beim schnellen Schnappschuss möchte Sie ein fertiges Bild von
Wie es Euch gefällt Pixelvorverarbeitung oder RAW-Format Je nach Anwendung werden an die Bilddaten unterschiedliche Anforderungen gestellt. Beim schnellen Schnappschuss möchte Sie ein fertiges Bild von
Objekterkennung durch Vergleich von Farben. Videoanalyse Dr. Stephan Kopf HWS2007 Kapitel 5: Objekterkennung
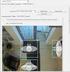 Objekterkennung durch Vergleich von Farben 48 Farbräume (I) Definitionen: Farbe: Sinnesempfindung (keine physikalische Eigenschaft), falls Licht einer bestimmten Wellenlänge auf die Netzhaut des Auges
Objekterkennung durch Vergleich von Farben 48 Farbräume (I) Definitionen: Farbe: Sinnesempfindung (keine physikalische Eigenschaft), falls Licht einer bestimmten Wellenlänge auf die Netzhaut des Auges
Mathematische und statistische Methoden II
 Statistik & Methodenlehre e e Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-206) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden II Dr. Malte
Statistik & Methodenlehre e e Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-206) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden II Dr. Malte
Digitale Bildverarbeitung Einheit 5 Bilder und Statistik
 Digitale Bildverarbeitung Einheit 5 Bilder und Statistik Lehrauftrag SS 2007 Fachbereich M+I der FH-Offenburg Dr. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Verstehen, welche
Digitale Bildverarbeitung Einheit 5 Bilder und Statistik Lehrauftrag SS 2007 Fachbereich M+I der FH-Offenburg Dr. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Verstehen, welche
Vorbereitungsaufgaben
 Praktikum Bildverarbeitung / Bildinformationstechnik Versuch BV 4 / BIT 3: Mustererkennung Paddy Gadegast, CV00, 160967 Alexander Opel, CV00, 16075 Gruppe 3 Otto-von-Guericke Universität Magdeburg Fakultät
Praktikum Bildverarbeitung / Bildinformationstechnik Versuch BV 4 / BIT 3: Mustererkennung Paddy Gadegast, CV00, 160967 Alexander Opel, CV00, 16075 Gruppe 3 Otto-von-Guericke Universität Magdeburg Fakultät
Grundlagen der Bildbearbeitung
 Grundlagen der Bildbearbeitung Voraussetzungen zur Bildbearbeitung Eingabegeräte Scanner Digitale Kameras Ausgabegeräte Speichermedien Index Voraussetzungen zur Bildbearbeitung Um Bilder auf elektronischem
Grundlagen der Bildbearbeitung Voraussetzungen zur Bildbearbeitung Eingabegeräte Scanner Digitale Kameras Ausgabegeräte Speichermedien Index Voraussetzungen zur Bildbearbeitung Um Bilder auf elektronischem
Anleitung: Standardabweichung
 Anleitung: Standardabweichung So kann man mit dem V200 Erwartungswert und Varianz bzw. Standardabweichung bei Binomialverteilungen für bestimmte Werte von n, aber für allgemeines p nach der allgemeinen
Anleitung: Standardabweichung So kann man mit dem V200 Erwartungswert und Varianz bzw. Standardabweichung bei Binomialverteilungen für bestimmte Werte von n, aber für allgemeines p nach der allgemeinen
Einführung in die Medieninformatik 1
 Einführung in die Medieninformatik 1 Wintersemester 2007/08 Prof. Dr. Rainer Malaka, Digitale Medien Medieninformatik 1 1 Plan (vorläufig) 31.10. Einführung 7.11. Menschen: Wahrnehmung 14.11. Menschen:
Einführung in die Medieninformatik 1 Wintersemester 2007/08 Prof. Dr. Rainer Malaka, Digitale Medien Medieninformatik 1 1 Plan (vorläufig) 31.10. Einführung 7.11. Menschen: Wahrnehmung 14.11. Menschen:
Bildtransformationen. Geometrische Transformationen Grauwert-Interpolation
 Bildtransformationen Geometrische Transformationen Grauwert-Interpolation Transformation Transformation zwei Schritte geometrische Transformation (Trafo der Koordinaten) Neuberechnung der Pielwerte an
Bildtransformationen Geometrische Transformationen Grauwert-Interpolation Transformation Transformation zwei Schritte geometrische Transformation (Trafo der Koordinaten) Neuberechnung der Pielwerte an
1.3 Digitale Audiosignale
 Seite 22 von 86 Abb. 1.2.12 - Wirkung der Schallverzögerung Effekte sind: Delay, Echo, Reverb, Flanger und Chorus Hört man ein akustisches Signal im Raum, dann werden die Signale von Wänden und anderen
Seite 22 von 86 Abb. 1.2.12 - Wirkung der Schallverzögerung Effekte sind: Delay, Echo, Reverb, Flanger und Chorus Hört man ein akustisches Signal im Raum, dann werden die Signale von Wänden und anderen
ETWR Teil B. Spezielle Wahrscheinlichkeitsverteilungen (stetig)
 ETWR Teil B 2 Ziele Bisher (eindimensionale, mehrdimensionale) Zufallsvariablen besprochen Lageparameter von Zufallsvariablen besprochen Übertragung des gelernten auf diskrete Verteilungen Ziel des Kapitels
ETWR Teil B 2 Ziele Bisher (eindimensionale, mehrdimensionale) Zufallsvariablen besprochen Lageparameter von Zufallsvariablen besprochen Übertragung des gelernten auf diskrete Verteilungen Ziel des Kapitels
4. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren)
 4. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 4.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
4. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 4.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
Grundlagen von Rasterdaten
 LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS DATABASE Kapitel 7: Grundlagen von Rasterdaten Skript zur Vorlesung Geo-Informationssysteme Wintersemester 2014/15 Ludwig-Maximilians-Universität
LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS DATABASE Kapitel 7: Grundlagen von Rasterdaten Skript zur Vorlesung Geo-Informationssysteme Wintersemester 2014/15 Ludwig-Maximilians-Universität
Was ist Physik? Modell der Natur universell es war schon immer so
 Was ist Physik? Modell der Natur universell es war schon immer so Kultur Aus was sind wir gemacht? Ursprung und Aufbau der Materie Von wo/was kommen wir? Ursprung und Aufbau von Raum und Zeit Wirtschaft
Was ist Physik? Modell der Natur universell es war schon immer so Kultur Aus was sind wir gemacht? Ursprung und Aufbau der Materie Von wo/was kommen wir? Ursprung und Aufbau von Raum und Zeit Wirtschaft
Zusammenfassung Digitale Bildverarbeitung By Fabian Flohrmann
 Zusammenfassung Digitale Bildverarbeitung By Fabian Flohrmann VL01 Stufen der Bildverarbeitung Bildgewinnung => Bildbearbeitung => Bilderkennung Bildgewinnung: Bildaufnahme Bilddiskretisierung Bildbearbeitung:
Zusammenfassung Digitale Bildverarbeitung By Fabian Flohrmann VL01 Stufen der Bildverarbeitung Bildgewinnung => Bildbearbeitung => Bilderkennung Bildgewinnung: Bildaufnahme Bilddiskretisierung Bildbearbeitung:
2. Das digitale Bild und seine Eigenschaften
 2. Das digitale Bild und seine Eigenschaften Digitales Bild: Matrix f = (f m,n ), m = 0; 1;..., m max, n = 0; 1;..., n max Werte f m,n entsprechen Helligkeiten (brightness) oder anderen Größen f m,n {
2. Das digitale Bild und seine Eigenschaften Digitales Bild: Matrix f = (f m,n ), m = 0; 1;..., m max, n = 0; 1;..., n max Werte f m,n entsprechen Helligkeiten (brightness) oder anderen Größen f m,n {
ν und λ ausgedrückt in Energie E und Impuls p
 phys4.011 Page 1 8.3 Die Schrödinger-Gleichung die grundlegende Gleichung der Quantenmechanik (in den bis jetzt diskutierten Fällen) eine Wellengleichung für Materiewellen (gilt aber auch allgemeiner)
phys4.011 Page 1 8.3 Die Schrödinger-Gleichung die grundlegende Gleichung der Quantenmechanik (in den bis jetzt diskutierten Fällen) eine Wellengleichung für Materiewellen (gilt aber auch allgemeiner)
Nichtmonotone Grauwertabbildung
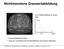 LMU München Medieninformatik Butz/Hilliges 2D Graphics WS2005 02.12.2005 Folie 1 Nichtmonotone Grauwertabbildung Zwei Grauwertfenster in einem Bild. g (g) 0 511 2100 g Erzeugt künstliche Kanten. Grenzen
LMU München Medieninformatik Butz/Hilliges 2D Graphics WS2005 02.12.2005 Folie 1 Nichtmonotone Grauwertabbildung Zwei Grauwertfenster in einem Bild. g (g) 0 511 2100 g Erzeugt künstliche Kanten. Grenzen
Kompression und Datenformate. Grundlagen der Bildspeicherung, Kompressionsverfahren, Datenformate
 Kompression und Datenformate Grundlagen der Bildspeicherung, Kompressionsverfahren, Datenformate AGENDA Digitale Speicherung von Bildern Digitalisierung Informationsgehalt Speicherbedarf Kompression von
Kompression und Datenformate Grundlagen der Bildspeicherung, Kompressionsverfahren, Datenformate AGENDA Digitale Speicherung von Bildern Digitalisierung Informationsgehalt Speicherbedarf Kompression von
Morphologische Bildverarbeitung II
 FAKULTÄT FÜR MATHEMATIK UNIVERSITÄT ULM ABT. STOCHASTIK ABT. ANGEWANDTE INFORMATIONSVERARBEITUNG Seminar Simulation und Bildanalyse mit Java Morphologische Bildverarbeitung II BETREUER: JOHANNES MAYER
FAKULTÄT FÜR MATHEMATIK UNIVERSITÄT ULM ABT. STOCHASTIK ABT. ANGEWANDTE INFORMATIONSVERARBEITUNG Seminar Simulation und Bildanalyse mit Java Morphologische Bildverarbeitung II BETREUER: JOHANNES MAYER
(7) Normal Mapping. Vorlesung Computergraphik II S. Müller. Dank an Stefan Rilling U N I V E R S I T Ä T KOBLENZ LANDAU
 (7) Normal Mapping Vorlesung Computergraphik II S. Müller Dank an Stefan Rilling Einleitung Die Welt ist voller Details Viele Details treten in Form von Oberflächendetails auf S. Müller - 3 - Darstellung
(7) Normal Mapping Vorlesung Computergraphik II S. Müller Dank an Stefan Rilling Einleitung Die Welt ist voller Details Viele Details treten in Form von Oberflächendetails auf S. Müller - 3 - Darstellung
FILTER UND FALTUNGEN
 Ausarbeitung zum Vortrag von Daniel Schmitzek im Seminar Verarbeitung und Manipulation digitaler Bilder I n h a l t. Der Begriff des Filters 3 2. Faltungsfilter 4 2. Glättungsfilter 4 2.2 Filter zur Kantendetektion
Ausarbeitung zum Vortrag von Daniel Schmitzek im Seminar Verarbeitung und Manipulation digitaler Bilder I n h a l t. Der Begriff des Filters 3 2. Faltungsfilter 4 2. Glättungsfilter 4 2.2 Filter zur Kantendetektion
Begriffe aus der Informatik Nachrichten
 Begriffe aus der Informatik Nachrichten Gerhard Goos definiert in Vorlesungen über Informatik, Band 1, 1995 Springer-Verlag Berlin Heidelberg: Die Darstellung einer Mitteilung durch die zeitliche Veränderung
Begriffe aus der Informatik Nachrichten Gerhard Goos definiert in Vorlesungen über Informatik, Band 1, 1995 Springer-Verlag Berlin Heidelberg: Die Darstellung einer Mitteilung durch die zeitliche Veränderung
8. Konfidenzintervalle und Hypothesentests
 8. Konfidenzintervalle und Hypothesentests Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Beispiel. Sie wollen den durchschnittlichen Fruchtsaftgehalt eines bestimmten Orangennektars
8. Konfidenzintervalle und Hypothesentests Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Beispiel. Sie wollen den durchschnittlichen Fruchtsaftgehalt eines bestimmten Orangennektars
Kapitel 12 Stetige Zufallsvariablen Dichtefunktion und Verteilungsfunktion. stetig. Verteilungsfunktion
 Kapitel 12 Stetige Zufallsvariablen 12.1. Dichtefunktion und Verteilungsfunktion stetig Verteilungsfunktion Trägermenge T, also die Menge der möglichen Realisationen, ist durch ein Intervall gegeben Häufig
Kapitel 12 Stetige Zufallsvariablen 12.1. Dichtefunktion und Verteilungsfunktion stetig Verteilungsfunktion Trägermenge T, also die Menge der möglichen Realisationen, ist durch ein Intervall gegeben Häufig
Praktikum 1. Bildverarbeitungs - Software ImageJ LUT Manipulationen Bild - Quantisierung
 Prof. W. Hillen, Medizinische Informatik FH - AC (Jülich)...\image\img_pk_01 ImageJ.doc Praktikum 1 Digitale Bildverarbeitung Bildverarbeitungs - Software ImageJ LUT Manipulationen Bild - Quantisierung
Prof. W. Hillen, Medizinische Informatik FH - AC (Jülich)...\image\img_pk_01 ImageJ.doc Praktikum 1 Digitale Bildverarbeitung Bildverarbeitungs - Software ImageJ LUT Manipulationen Bild - Quantisierung
Einführung in die Fehlerrechnung und Messdatenauswertung
 Grundpraktikum der Physik Einführung in die Fehlerrechnung und Messdatenauswertung Wolfgang Limmer Institut für Halbleiterphysik 1 Fehlerrechnung 1.1 Motivation Bei einem Experiment soll der Wert einer
Grundpraktikum der Physik Einführung in die Fehlerrechnung und Messdatenauswertung Wolfgang Limmer Institut für Halbleiterphysik 1 Fehlerrechnung 1.1 Motivation Bei einem Experiment soll der Wert einer
Kapitel VI - Lage- und Streuungsparameter
 Universität Karlsruhe (TH) Institut für Statistik und Mathematische Wirtschaftstheorie Wahrscheinlichkeitstheorie Kapitel VI - Lage- und Streuungsparameter Markus Höchstötter Lehrstuhl für Statistik, Ökonometrie
Universität Karlsruhe (TH) Institut für Statistik und Mathematische Wirtschaftstheorie Wahrscheinlichkeitstheorie Kapitel VI - Lage- und Streuungsparameter Markus Höchstötter Lehrstuhl für Statistik, Ökonometrie
(Bitte geben Sie bei der Beantwortung von Fragen eine Begründung bzw. bei der Lösung von Kurzaufgaben eine kurze Berechnung an!)
 Teil 1: Fragen und Kurzaufgaben (Bitte geben Sie bei der Beantwortung von Fragen eine Begründung bzw. bei der Lösung von Kurzaufgaben eine kurze Berechnung an!) Frage 1 (6 Punkte) Es wird ein analoges
Teil 1: Fragen und Kurzaufgaben (Bitte geben Sie bei der Beantwortung von Fragen eine Begründung bzw. bei der Lösung von Kurzaufgaben eine kurze Berechnung an!) Frage 1 (6 Punkte) Es wird ein analoges
Datenanalyse. (PHY231) Herbstsemester Olaf Steinkamp
 Datenanalyse (PHY31) Herbstsemester 015 Olaf Steinkamp 36-J- [email protected] 044 63 55763 Einführung, Messunsicherheiten, Darstellung von Messdaten Grundbegriffe der Wahrscheinlichkeitsrechnung und
Datenanalyse (PHY31) Herbstsemester 015 Olaf Steinkamp 36-J- [email protected] 044 63 55763 Einführung, Messunsicherheiten, Darstellung von Messdaten Grundbegriffe der Wahrscheinlichkeitsrechnung und
Klausur zu Methoden der Statistik II (mit Kurzlösung) Sommersemester Aufgabe 1
 Lehrstuhl für Statistik und Ökonometrie der Otto-Friedrich-Universität Bamberg Prof. Dr. Susanne Rässler Klausur zu Methoden der Statistik II (mit Kurzlösung) Sommersemester 2013 Aufgabe 1 In einer Urne
Lehrstuhl für Statistik und Ökonometrie der Otto-Friedrich-Universität Bamberg Prof. Dr. Susanne Rässler Klausur zu Methoden der Statistik II (mit Kurzlösung) Sommersemester 2013 Aufgabe 1 In einer Urne
HDR für Einsteiger Wann brauche ist das? Anregungen aus Fotobuch und ersten eigenen Erfahrungen von Christian Sischka
 HDR für Einsteiger Wann brauche ist das? Anregungen aus Fotobuch und ersten eigenen Erfahrungen von Christian Sischka Thema Was ist HDR? Wann ist es sinnvoll es anzuwenden? Wie mache ich ein HDR? Was stelle
HDR für Einsteiger Wann brauche ist das? Anregungen aus Fotobuch und ersten eigenen Erfahrungen von Christian Sischka Thema Was ist HDR? Wann ist es sinnvoll es anzuwenden? Wie mache ich ein HDR? Was stelle
Graphic Coding. Klausur. 9. Februar 2007. Kurs A
 Graphic Coding Klausur 9. Februar 2007 Kurs A Name: Matrikelnummer: Hinweise - Es sind keine Hilfsmaterialien erlaubt. (Keine Bücher, Taschenrechner, Handys) - Sie haben zwei Stunden Zeit. - Insgesamt
Graphic Coding Klausur 9. Februar 2007 Kurs A Name: Matrikelnummer: Hinweise - Es sind keine Hilfsmaterialien erlaubt. (Keine Bücher, Taschenrechner, Handys) - Sie haben zwei Stunden Zeit. - Insgesamt
Digital meets analog. Analoge Welt Messung physikalischer Größen mittels Sensoren analoge Spannung. Analog-Digital-Wandlung (A/D)
 Überblick Grundlagen: Spannung, Strom, Widerstand, IV-Kennlinien Elektronische Messgeräte im Elektronikpraktikum Passive Filter Signaltransport im Kabel Transistor Operationsverstärker PID-egler Sensorik
Überblick Grundlagen: Spannung, Strom, Widerstand, IV-Kennlinien Elektronische Messgeräte im Elektronikpraktikum Passive Filter Signaltransport im Kabel Transistor Operationsverstärker PID-egler Sensorik
Zufallsgröße. Würfelwurf mit fairem Würfel. Wahrscheinlichkeitsverteilung einer diskreten
 Zufallsgrößen Ergebnisse von Zufallsexperimenten werden als Zahlen dargestellt 0 Einführung Wahrscheinlichkeitsrechnung 2 Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Hypothesentests
Zufallsgrößen Ergebnisse von Zufallsexperimenten werden als Zahlen dargestellt 0 Einführung Wahrscheinlichkeitsrechnung 2 Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Hypothesentests
Computer Graphik I (3D) Dateneingabe
 Computer Graphik I (3D) Dateneingabe 1 3D Graphik- Pipeline Anwendung 3D Dateneingabe Repräsenta
Computer Graphik I (3D) Dateneingabe 1 3D Graphik- Pipeline Anwendung 3D Dateneingabe Repräsenta
die Kunst, mit wenig Farbklexen bunte Bilder zu machen Halftoning, Dithering
 Farbreduktion die Kunst, mit wenig Farbklexen bunte Bilder zu machen Halftoning, Dithering zwei Schritte: geeignete Farben (Repäsentanten) finden Farbreduktion alle Bildfarben den Repräsentanten zuordnen
Farbreduktion die Kunst, mit wenig Farbklexen bunte Bilder zu machen Halftoning, Dithering zwei Schritte: geeignete Farben (Repäsentanten) finden Farbreduktion alle Bildfarben den Repräsentanten zuordnen
EDV-Anwendungen im Archivwesen II
 EDV-Anwendungen im Archivwesen II 070472 UE WS08/09 Grundlagen der Digitalisierung Überblick Allgemeine Grundlagen der Digitalisierung anhand der Ton-Digitalisierung Abtastrate (Samplerate) Wortlänge (Bitrate)
EDV-Anwendungen im Archivwesen II 070472 UE WS08/09 Grundlagen der Digitalisierung Überblick Allgemeine Grundlagen der Digitalisierung anhand der Ton-Digitalisierung Abtastrate (Samplerate) Wortlänge (Bitrate)
Digitale Fotografie. Agfa. R. Wirowski (Agfa-Gevaert AG, FE-Film) 16. Dezember 1998. R. Wirowski. Agfa Lectures - Fachhochschule Köln 1
 Digitale Fotografie (-Gevaert AG, FE-Film) 16. Dezember 1998 Lectures - Fachhochschule Köln 1 Einleitung: Digitale Kamera Halbleiter-Sensor und Elektronik Gehäuse Optik und Verschluß Batteriehalterung
Digitale Fotografie (-Gevaert AG, FE-Film) 16. Dezember 1998 Lectures - Fachhochschule Köln 1 Einleitung: Digitale Kamera Halbleiter-Sensor und Elektronik Gehäuse Optik und Verschluß Batteriehalterung
Dieses Quiz soll Ihnen helfen, Kapitel besser zu verstehen.
 Dieses Quiz soll Ihnen helfen, Kapitel 2.5-2. besser zu verstehen. Frage Wir betrachten ein Würfelspiel. Man wirft einen fairen, sechsseitigen Würfel. Wenn eine oder eine 2 oben liegt, muss man 2 SFr zahlen.
Dieses Quiz soll Ihnen helfen, Kapitel 2.5-2. besser zu verstehen. Frage Wir betrachten ein Würfelspiel. Man wirft einen fairen, sechsseitigen Würfel. Wenn eine oder eine 2 oben liegt, muss man 2 SFr zahlen.
S tandardabweichung : σ= n p 1 p = 200 0,24 0,76 6,04
 R. Brinkmann http://brinkmann-du.de Seite 1 14.10.2007 Wahrscheinlichkeiten von Umgebungen Bei einer Binomialverteilung ist der Erwartungswert der mit der größten Wahrscheinlichkeit. In der Umgebung des
R. Brinkmann http://brinkmann-du.de Seite 1 14.10.2007 Wahrscheinlichkeiten von Umgebungen Bei einer Binomialverteilung ist der Erwartungswert der mit der größten Wahrscheinlichkeit. In der Umgebung des
Die Varianz (Streuung) Definition
 Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Polte, Galina; Rennert, Klaus-Jürgen; Linß, Gerhard: Korrektur von Abbildungsfehlern für optische Messverfahren
 Polte, Galina; Rennert, Klaus-Jürgen; Linß, Gerhard: Korrektur von Abbildungsfehlern für optische Messverfahren Publikation entstand im Rahmen der Veranstaltung: Workshop "Flexible Montage", Ilmenau, 09.
Polte, Galina; Rennert, Klaus-Jürgen; Linß, Gerhard: Korrektur von Abbildungsfehlern für optische Messverfahren Publikation entstand im Rahmen der Veranstaltung: Workshop "Flexible Montage", Ilmenau, 09.
Computergrafik und Bildverarbeitung. Prof. Dr. André Hinkenjann
 Computergrafik und Bildverarbeitung Prof. Dr. André Hinkenjann Organisation Literatur The Computer Image Alan Watt, Fabio Policarpo Addison Wesley Digital Image Processing a practical introduction using
Computergrafik und Bildverarbeitung Prof. Dr. André Hinkenjann Organisation Literatur The Computer Image Alan Watt, Fabio Policarpo Addison Wesley Digital Image Processing a practical introduction using
Multimediatechnik / Video
 Multimediatechnik / Video Video-Farben Pixel, Farben, RGB/YUV http://www.nanocosmos.de/lietz/mtv Helligkeits- und Farb-Pixel s/w-pixel: Wert = Helligkeit Beispiel 8 Bit/Pixel = 256 Stufen 0=schwarz, 255=weiß
Multimediatechnik / Video Video-Farben Pixel, Farben, RGB/YUV http://www.nanocosmos.de/lietz/mtv Helligkeits- und Farb-Pixel s/w-pixel: Wert = Helligkeit Beispiel 8 Bit/Pixel = 256 Stufen 0=schwarz, 255=weiß
Praktikum 2. Grauwert - Histogramme, Bimodalitätsanalyse Bildstatistik
 Prof. W. Hillen, Medizinische Informatik FH - AC (Jülich)...\image\img_pk_02 ImageJ.doc Praktikum 2 Digitale Bildverarbeitung Grauwert - Histogramme, Bimodalitätsanalyse Bildstatistik Themen: Auswertung
Prof. W. Hillen, Medizinische Informatik FH - AC (Jülich)...\image\img_pk_02 ImageJ.doc Praktikum 2 Digitale Bildverarbeitung Grauwert - Histogramme, Bimodalitätsanalyse Bildstatistik Themen: Auswertung
Zufallssignal Stationär (z.b. gleichverteiltes Rauschen) Nicht-stationär (z.b. normalverteiltes Rauschen mit wechselnder Streuung) Deterministisches
 Zufallssignal Stationär (z.b. gleichverteiltes Rauschen) Nicht-stationär (z.b. normalverteiltes Rauschen mit wechselnder Streuung) Deterministisches Signal Periodisch harmonische Schwingung Summe harmonischer
Zufallssignal Stationär (z.b. gleichverteiltes Rauschen) Nicht-stationär (z.b. normalverteiltes Rauschen mit wechselnder Streuung) Deterministisches Signal Periodisch harmonische Schwingung Summe harmonischer
Klausur zur Vorlesung,,Algorithmische Mathematik II
 Institut für angewandte Mathematik, Institut für numerische Simulation Sommersemester 2015 Prof. Dr. Anton Bovier, Prof. Dr. Martin Rumpf Klausur zur Vorlesung,,Algorithmische Mathematik II Bitte diese
Institut für angewandte Mathematik, Institut für numerische Simulation Sommersemester 2015 Prof. Dr. Anton Bovier, Prof. Dr. Martin Rumpf Klausur zur Vorlesung,,Algorithmische Mathematik II Bitte diese
Korrelationsmatrix. Statistische Bindungen zwischen den N Zufallsgrößen werden durch die Korrelationsmatrix vollständig beschrieben:
 Korrelationsmatrix Bisher wurden nur statistische Bindungen zwischen zwei (skalaren) Zufallsgrößen betrachtet. Für den allgemeineren Fall einer Zufallsgröße mit N Dimensionen bietet sich zweckmäßiger Weise
Korrelationsmatrix Bisher wurden nur statistische Bindungen zwischen zwei (skalaren) Zufallsgrößen betrachtet. Für den allgemeineren Fall einer Zufallsgröße mit N Dimensionen bietet sich zweckmäßiger Weise
Farbdarstellung. aber mit einem ausgeprägten Empfindlichkeitsmaximum im roten, grünen bzw. blauen Bereich.
 Erinnerung aus dem Biologieunterricht: Das menschliche Auge hat Stäbchen zur Unterscheidung von Helligkeiten drei verschiedene Arten von Zäpfchen, die für rot, grün und blau empfindlich sind. Genauer:
Erinnerung aus dem Biologieunterricht: Das menschliche Auge hat Stäbchen zur Unterscheidung von Helligkeiten drei verschiedene Arten von Zäpfchen, die für rot, grün und blau empfindlich sind. Genauer:
3. Erfassung und Verarbeitung von Sensordaten
 3. Erfassung und Verarbeitung von Sensordaten Lernziele 3. Erfassung und Verarbeitung von Sensordaten Lernziele: Typische in mobilen Geräten enthaltene Sensorarten kennen, Daten von solchen Sensoren empfangen
3. Erfassung und Verarbeitung von Sensordaten Lernziele 3. Erfassung und Verarbeitung von Sensordaten Lernziele: Typische in mobilen Geräten enthaltene Sensorarten kennen, Daten von solchen Sensoren empfangen
Berechnung des LOG-RANK-Tests bei Überlebenskurven
 Statistik 1 Berechnung des LOG-RANK-Tests bei Überlebenskurven Hans-Dieter Spies inventiv Health Germany GmbH Brandenburger Weg 3 60437 Frankfurt [email protected] Zusammenfassung Mit Hilfe von Überlebenskurven
Statistik 1 Berechnung des LOG-RANK-Tests bei Überlebenskurven Hans-Dieter Spies inventiv Health Germany GmbH Brandenburger Weg 3 60437 Frankfurt [email protected] Zusammenfassung Mit Hilfe von Überlebenskurven
Fragenkatalog Kapitel 1 Fehleranalyse
 Teil 1: Numerik katalog Kapitel 1 Fehleranalyse 1. Zwischen was besteht ein funktionaler Zusammenhang z i? Welche Form hat er? 2. Welche 4 Typen von Fehlerquellen gibt es? Nenne Beispiele! 3. Wie berechnet
Teil 1: Numerik katalog Kapitel 1 Fehleranalyse 1. Zwischen was besteht ein funktionaler Zusammenhang z i? Welche Form hat er? 2. Welche 4 Typen von Fehlerquellen gibt es? Nenne Beispiele! 3. Wie berechnet
Bilder im Zusammenhang mit Geoinformatik sind u.a.: Luftbilder, Satellitenbilder Synthetische Bilder (z.b. digitale Oberflächenmodelle)
 Grundlagen der digitalen Bildverarbeitung Bilder im Zusammenhang mit Geoinformatik sind u.a.: Luftbilder, Satellitenbilder Synthetische Bilder (z.b. digitale Oberflächenmodelle)... dagegen weniger Fotos
Grundlagen der digitalen Bildverarbeitung Bilder im Zusammenhang mit Geoinformatik sind u.a.: Luftbilder, Satellitenbilder Synthetische Bilder (z.b. digitale Oberflächenmodelle)... dagegen weniger Fotos
Morphologie auf Binärbildern
 Morphologie auf Binärbildern WS07 5.1 Konen, Zielke WS07 5.2 Konen, Zielke Motivation Aufgabe: Objekte zählen Probleme: "Salt-&-Pepper"-Rauschen erzeugt falsche Objekte Verschmelzen richtiger Objekte durch
Morphologie auf Binärbildern WS07 5.1 Konen, Zielke WS07 5.2 Konen, Zielke Motivation Aufgabe: Objekte zählen Probleme: "Salt-&-Pepper"-Rauschen erzeugt falsche Objekte Verschmelzen richtiger Objekte durch
Modulklausur Multivariate Verfahren
 Name, Vorname Matrikelnummer Modulklausur 31821 Multivariate Verfahren Datum Punkte Note Termin: 28. März 2014, 9.00-11.00 Uhr Erstprüfer: Univ.-Prof. Dr. H. Singer Hinweise zur Bearbeitung der Modulklausur
Name, Vorname Matrikelnummer Modulklausur 31821 Multivariate Verfahren Datum Punkte Note Termin: 28. März 2014, 9.00-11.00 Uhr Erstprüfer: Univ.-Prof. Dr. H. Singer Hinweise zur Bearbeitung der Modulklausur
Praktikumssemesterarbeit für Numerik Aufgabe 1 HU-Berlin, Sommersemester 2005
 Praktikumssemesterarbeit für Numerik Aufgabe HU-Berlin, Sommersemester 2005 Mario Krell Volker Grabsch 24. Juli 2005 Inhaltsverzeichnis Herleitung aus der Physik. Voraussetzungen und Annahmen Allgemein
Praktikumssemesterarbeit für Numerik Aufgabe HU-Berlin, Sommersemester 2005 Mario Krell Volker Grabsch 24. Juli 2005 Inhaltsverzeichnis Herleitung aus der Physik. Voraussetzungen und Annahmen Allgemein
Bildkorrekturen mit JPGIlluminator:
 Bildkorrekturen mit JPGIlluminator: Mit diesem Programm können Sie gezielt die Lichter und Schatten eines Fotos beeinflussen. Häufig kommt es bei Digitalfotos vor, dass der Kontrastumfang des Bildes einfach
Bildkorrekturen mit JPGIlluminator: Mit diesem Programm können Sie gezielt die Lichter und Schatten eines Fotos beeinflussen. Häufig kommt es bei Digitalfotos vor, dass der Kontrastumfang des Bildes einfach
Die Umsetzung der Lehrplaninhalte in Fokus Mathematik Einführungsphase auf der Basis des Kerncurriculums Mathematik in Nordrhein-Westfalen
 Die Umsetzung der Lehrplaninhalte in auf der Basis des Kerncurriculums Mathematik in Nordrhein-Westfalen Schulinternes Curriculum Schülerbuch 978-3-06-041672-1 Lehrerfassung des Schülerbuchs 978-3-06-041673-8
Die Umsetzung der Lehrplaninhalte in auf der Basis des Kerncurriculums Mathematik in Nordrhein-Westfalen Schulinternes Curriculum Schülerbuch 978-3-06-041672-1 Lehrerfassung des Schülerbuchs 978-3-06-041673-8
Elementare Bildverarbeitungsoperationen
 1 Elementare Bildverarbeitungsoperationen - Kantenerkennung - 1 Einführung 2 Gradientenverfahren 3 Laplace-Verfahren 4 Canny-Verfahren 5 Literatur 1 Einführung 2 1 Einführung Kantenerkennung basiert auf
1 Elementare Bildverarbeitungsoperationen - Kantenerkennung - 1 Einführung 2 Gradientenverfahren 3 Laplace-Verfahren 4 Canny-Verfahren 5 Literatur 1 Einführung 2 1 Einführung Kantenerkennung basiert auf
Belichtung mit Tonwertkorrektur verbessern
 Belichtung mit Tonwertkorrektur verbessern Die meisten Digitalfotos müssen vor dem Ausdruck bearbeitet werden: Helligkeit und Kontrast sollten für ein besseres Ergebnis reguliert werden. Die Tonwertkorrektur
Belichtung mit Tonwertkorrektur verbessern Die meisten Digitalfotos müssen vor dem Ausdruck bearbeitet werden: Helligkeit und Kontrast sollten für ein besseres Ergebnis reguliert werden. Die Tonwertkorrektur
Shape Gradient for Image and Video Segmentation
 Shape Gradient for Image and Video Segmentation [1] S. Jehan-Besson, A. Herbulot, M. Barlaud und G. Aubert 23. Mai 2007 Martin Schröttner und Michael Schneeberger Mat Vis-Gra SS07 1 Überblick Aktive Konturen
Shape Gradient for Image and Video Segmentation [1] S. Jehan-Besson, A. Herbulot, M. Barlaud und G. Aubert 23. Mai 2007 Martin Schröttner und Michael Schneeberger Mat Vis-Gra SS07 1 Überblick Aktive Konturen
Hochschule Bremerhaven Medizintechnik Mathcad Kapitel 6
 6. Diagramme mit Mathcad In diesem Kapitel geht es um andere, als X Y Diagramme. 6.. Kreisdiagramme. Schritt: Die darzustellende Funktion muß zunächst als Funktion definiert werden, zum Beispiel f(x):=
6. Diagramme mit Mathcad In diesem Kapitel geht es um andere, als X Y Diagramme. 6.. Kreisdiagramme. Schritt: Die darzustellende Funktion muß zunächst als Funktion definiert werden, zum Beispiel f(x):=
9 Die Normalverteilung
 9 Die Normalverteilung Dichte: f(x) = 1 2πσ e (x µ)2 /2σ 2, µ R,σ > 0 9.1 Standard-Normalverteilung µ = 0, σ 2 = 1 ϕ(x) = 1 2π e x2 /2 Dichte Φ(x) = 1 x 2π e t2 /2 dt Verteilungsfunktion 331 W.Kössler,
9 Die Normalverteilung Dichte: f(x) = 1 2πσ e (x µ)2 /2σ 2, µ R,σ > 0 9.1 Standard-Normalverteilung µ = 0, σ 2 = 1 ϕ(x) = 1 2π e x2 /2 Dichte Φ(x) = 1 x 2π e t2 /2 dt Verteilungsfunktion 331 W.Kössler,
Prof. Dr. Christoph Kleinn Institut für Waldinventur und Waldwachstum Arbeitsbereich Waldinventur und Fernerkundung
 Systematische Stichprobe Rel. große Gruppe von Stichprobenverfahren. Allgemeines Merkmal: es existiert ein festes, systematisches Muster bei der Auswahl. Wie passt das zur allgemeinen Forderung nach Randomisierung
Systematische Stichprobe Rel. große Gruppe von Stichprobenverfahren. Allgemeines Merkmal: es existiert ein festes, systematisches Muster bei der Auswahl. Wie passt das zur allgemeinen Forderung nach Randomisierung
Software in der Industriellen Bildverarbeitung
 Software in der Industriellen Bildverarbeitung Technologieentwicklung am Beispiel Pattern Matching Dr. Olaf Munkelt MVTec Software GmbH MVTec Software GmbH Firma konzentriert sich auf Building Vision for
Software in der Industriellen Bildverarbeitung Technologieentwicklung am Beispiel Pattern Matching Dr. Olaf Munkelt MVTec Software GmbH MVTec Software GmbH Firma konzentriert sich auf Building Vision for
Bildschirmauflösungen im Vergleich (verkleinert!)
 Bildschirmauflösungen im Vergleich (verkleinert!) nun zur Farbtheorie... Die Farbräume RGB CMYK Rot, Grün, Blau addieren sich zu weißem Licht - Additive Lichtmischung Cyan, Magenta, Yellow verschlucken
Bildschirmauflösungen im Vergleich (verkleinert!) nun zur Farbtheorie... Die Farbräume RGB CMYK Rot, Grün, Blau addieren sich zu weißem Licht - Additive Lichtmischung Cyan, Magenta, Yellow verschlucken
Einführung Aufgabe 1 - Bildverarbeitung. Anton Augsburg 2011
 Einführung Anton Augsburg 2011 Inhalt 1 - Allgemeine Hinweise 2 - Grundlagen 3 - Aufgabenstellung 4 - C# 5 - Einführendes Beispiel 6 - Aufgabenhinweise Medien und Medienströme SS 2011 - Anton Augsburg
Einführung Anton Augsburg 2011 Inhalt 1 - Allgemeine Hinweise 2 - Grundlagen 3 - Aufgabenstellung 4 - C# 5 - Einführendes Beispiel 6 - Aufgabenhinweise Medien und Medienströme SS 2011 - Anton Augsburg
Polaroid DMC an DISKUS
 Carl H. Hilgers Technisches Büro Hauptstraße 82 53693 Königswinter Tel.: 022 23-222 68 Fax: 022 23-275 94 E-Mail: [email protected] Polaroid DMC an DISKUS Die digitale Kamera von Polaroid hat einen SCSI-2
Carl H. Hilgers Technisches Büro Hauptstraße 82 53693 Königswinter Tel.: 022 23-222 68 Fax: 022 23-275 94 E-Mail: [email protected] Polaroid DMC an DISKUS Die digitale Kamera von Polaroid hat einen SCSI-2
Hauptdiplomklausur Informatik August 2006: Multimedia Technology
 Universität Mannheim Fakultät für Mathematik und Informatik Lehrstuhl für Praktische Informatik IV Prof. Dr.-Ing. W. Effelsberg Hauptdiplomklausur Informatik August 2006: Multimedia Technology Name: Matrikel-Nr.:
Universität Mannheim Fakultät für Mathematik und Informatik Lehrstuhl für Praktische Informatik IV Prof. Dr.-Ing. W. Effelsberg Hauptdiplomklausur Informatik August 2006: Multimedia Technology Name: Matrikel-Nr.:
Digitalisierung als Grundlage des Informationszeitalters
 Digitalisierung als Grundlage des Informationszeitalters Prof. Dr.-Ing. Eckehard Steinbach Lehrstuhl für Kommunikationsnetze, Fachgebiet Medientechnik Technische Universität München 80290 München Email:
Digitalisierung als Grundlage des Informationszeitalters Prof. Dr.-Ing. Eckehard Steinbach Lehrstuhl für Kommunikationsnetze, Fachgebiet Medientechnik Technische Universität München 80290 München Email:
Statistik. Jan Müller
 Statistik Jan Müller Skalenniveau Nominalskala: Diese Skala basiert auf einem Satz von qualitativen Attributen. Es existiert kein Kriterium, nach dem die Punkte einer nominal skalierten Variablen anzuordnen
Statistik Jan Müller Skalenniveau Nominalskala: Diese Skala basiert auf einem Satz von qualitativen Attributen. Es existiert kein Kriterium, nach dem die Punkte einer nominal skalierten Variablen anzuordnen
Ü bung GIT- Teil Nachrichtentechnik, 17.11.2015
 Ü bung GIT- Teil Nachrichtentechnik, 17.11.2015 1 OSI Schichtenmodell Systeme der Nachrichtentechnik werden häufig mittels des OSI-Referenzmodells charakterisiert. a) Benennen Sie die Schichten des OSI-Referenzmodells!
Ü bung GIT- Teil Nachrichtentechnik, 17.11.2015 1 OSI Schichtenmodell Systeme der Nachrichtentechnik werden häufig mittels des OSI-Referenzmodells charakterisiert. a) Benennen Sie die Schichten des OSI-Referenzmodells!
Pulse Code Modulation
 Fachbereich Medieninformatik Hochschule Harz Pulse Code Modulation Referat Johannes Bastian 11038 Abgabe: 15.01.2007 Inhaltsverzeichnis Einleitung / Vorwort...1 1 Analoge Signale als Grundlage von PCM...1
Fachbereich Medieninformatik Hochschule Harz Pulse Code Modulation Referat Johannes Bastian 11038 Abgabe: 15.01.2007 Inhaltsverzeichnis Einleitung / Vorwort...1 1 Analoge Signale als Grundlage von PCM...1
Grundlagen Videosignale. Prof. Dr. Ing. Marcus Purat
 Grundlagen Videosignale Prof. Dr. Ing. Marcus Purat Beuth Hochschule fürtechnik Berlin Sommersemester 2012 Grundlagen Videosignale 1. Visuelle Wahrnehmung n 2. Analoge Videosignale 3. Digitale Videosignale
Grundlagen Videosignale Prof. Dr. Ing. Marcus Purat Beuth Hochschule fürtechnik Berlin Sommersemester 2012 Grundlagen Videosignale 1. Visuelle Wahrnehmung n 2. Analoge Videosignale 3. Digitale Videosignale


