bestehenden sind, weiterhin benutzt werden. Oft beleuchten unterschiedliche Formalismen Dinge nämlich von unterschiedlichen Blickwinkeln.
|
|
|
- Hinrich Graf
- vor 7 Jahren
- Abrufe
Transkript
1 2 Endliche Automaten bestehenden sind, weiterhin benutzt werden. Oft beleuchten unterschiedliche Formalismen Dinge nämlich von unterschiedlichen Blickwinkeln. Fragen 1. Sei R = (0 + 1). In welchen Fällen ist w 1 M R und w 2 M R? a) w 1 = 001 und w 2 = 100 b) w 1 = 100 und w 2 = 0011 c) w 1 = 0101 und w 2 = 1010 d) w 1 = 101 und w 2 = Welcher reguläre Ausdruck beschreibt die Menge {a}? a) (a + b) b (a + b) b) b c) (a + b) \ a d) (a + b) b (a + b) 3. Sind die regulären Sprachen gegenüber Vereinigung abgeschlossen? a) Ja b) Nein 4. Welcher reguläre Ausdruck beschreibt die Menge jener Worte, bei denen auf eine 0 stets eine 1 folgt? a) ( ) b) (1 + 01) c) (0 + 1) \ 0 d) (1 + 01) 0 e) (1 + 01) (0 + ) f) (1 + 01) 2.4 Grenzen der regulären Sprachen Mittlerweile haben wir mit DFAs, NFAs, λ-nfas und regulären Ausdrücken vier verschiedene Formalismen kennen gelernt, die die Familie der regulären Sprachen erfassen, d.h. jede von einem dieser drei Automatenmodelle akzeptierte und jede von einem regulären Ausdruck beschriebene Sprache, ist eine reguläre Sprache. Wir haben dann noch die Abschlusseigenschaften kennengelernt und gesehen, dass es auch gar nicht so leicht ist, keine reguläre Sprache 60
2 2.4 Grenzen der regulären Sprachen mehr zu haben. Vereinigt man z.b. zwei reguläre Sprachen, so hat man wieder eine, ebenso beim Durchschnitt und auch das Komplement einer regulären Sprache ist stets regulär. Es erscheint aber unwahrscheinlich, dass alle Sprachen regulär sind. Der DFA kann ja nur endlich viele Informationen speichern und sich auch keine Informationen mehrmals ansehen. Intuitiv kann man also gut vermuten, dass es doch Sprachen geben sollte, die nicht regulär sind. Aber wie könnte eine solche Sprache aussehen? Und wie beweist man, dass eine Sprache tatsächlich nicht regulär ist? Pause to Ponder: Für welche Sprache könnte es unmöglich sein, einen endlichen Automaten zu konstruieren, der sie akzeptiert? Da ein endlicher Automat nur endlich viele Informationen speichern kann, sollten wir dann an die Grenzen endlicher Automaten stossen, wenn wir uns unendlich viele Informationen merken müssen bzw. zwar endlich viele, aber von der Länge des Eingabewortes abhängig viele Informationen. Müssten wir uns z.b. bei einem Eingabewort der Länge 10 gerade 10 Informationen merken, bräuchten wir 10 Zustände. Ist das dann aber auch für ein Eingabewort der Länge 100 und 1000 nötig, dann gibt es keine obere Grenze für die Zustände und es kann keinen endlichen Automaten für die Sprache geben. Ein guter Kandidat ist daher vielleicht die Sprache L = {a n b n n N}. Diese Sprache ist nicht zu kompliziert zu beschreiben und dennoch erfüllt sie intuitiv obiges. Wenn wir nämlich die n bs lesen wollen, so müssen wir uns vorher die Zahl n merken, also die Anzahl der gelesenen as und diese Zahl ist wie oben gewünscht abhängig von der Wortlänge. Wir müssten einen Zustande haben, in dem wir uns merken, dass wir ein a gelesen haben, einen, in dem wir uns merken, dass es zwei waren usw. Da die Zahl beliebig groß werden kann, kann es intuitiv keinen DFA geben, der sich alle diese Zahlen in seinen nur endlich vielen Zuständen merkt. Dies ist aber zunächst nur eine Intuition. Wie beweisen wir nun, dass obiges L tatsächlich nicht regulär ist? Hier hilft uns das sogenannte Pumping Lemma Das Pumping Lemma Das Pumping Lemma macht eine Aussage über alle regulären Sprachen, d.h. es beschreibt eine Eigenschaft, die alle regulären Sprachen haben. Hat eine Sprache diese Eigenschaft also nicht, so kann sie nicht regulär sein. Um uns dem Pumping Lemma zu nähern, machen wir uns einmal selbst auf die Suche nach einer Eigenschaft X, die jede reguläre Sprache haben muss. Wir wissen bisher von regulären Sprachen, das es zu jeder reglären Sprache einen DFA gibt, der sie akzeptiert. Von DFAs wiederum wissen wir, dass sie nur endlich viele Zustände haben. Dies können wir versuchen auszunutzen. 61
3 2 Endliche Automaten Pause to Ponder: Wie können wir dies ausnutzen, um eine Eigenschaft zu erhalten, die jede reguläre Sprache haben muss? Tipp: Man lege dem Automaten ein Wort vor, dass länger ist als die Anzahl der Zustände. Was passiert? Legt man einem Automaten mit n Zuständen ein Wort vor, dass z.b. die Länge 4 n hat, dann muss der Automat, wenn er das Wort akzeptiert, mindestens einen Zustand mehrfach besuchen. Bei jedem gelesene Symbol findet ja ein Zustandswechsel statt und wenn man 4 n Symbole liest, finden also 4 n Zustandswechsel statt. Hat man nur n Zustände zur Auswahl muss zwangsläufig mindestens einer mehrfach auftreten. Das heißt auch, dass beim Lesen des Wortes der Automat Schleifen durchwandert. Diese Schleifen könnte man mehrfach entlang gehen und so neue Worte erzeugen, die alle auch in der Sprache sein müssten. Damit haben wir eine schöne Eigenschaft regulärer Sprachen gefunden. Für alle Worte der Sprache ab einer bestimmten Länge muss gelten, dass man sie so zerlegen kann, dass ein Teilstück des Wortes beliebig oft wiederholt werden kann und das Wort dennoch weiterhin in der Sprache ist. Pause to Ponder: Wie hilft uns das bei der eingangs erwähnten Sprache L = {a n b n n N}? Hätte man für L einen Automaten mit k Zuständen, dann betrachtet man a k b k. Nach obigem müsste schon beim Lesen der ersten k Symbole (also der as) ein Zustand mehrfach auftreten, d.h. wir haben dann bereits beim Lesen der as eine Schleife und könnten diese Schleife auch mehrfach entlang gehen. Nach obigem Überlegungen müssten die dabei entstehenden Wort ja alle in der Sprache L sein (da sie ja weiterhin von unserem angenommenen Automaten akzeptiert werden müssten). Dies klappt aber nicht, da wir ja Worte der Art a k+j b k erzeugen würden, die gerade nicht in L sind. Die oben erarbeitete Vorstellung der speziellen Eigenschaft aller regulären Sprachen wird nachfolgend im Pumping Lemma formalisiert und bewiesen. Im Beweis finden sich etliche der oben schon angedeuteten Argumente wieder. Im Anschluss an den Beweis nutzen wir das Pumping Lemma dann, um für L = {a n b n n N} eindeutig nachzuweisen, dass diese Sprache nicht regulär ist. Auch in dem Beweis finden sich dann die Überlegungen von eben als überzeugende Argumente wieder. Lemma (Pumping Lemma). Sei L REG eine reguläre Sprache. Dann gibt es ein n 1, so dass jedes Wort z L mit z n in die Form z = uvw zerlegt werden kann, wobei 1. uv n 2. v 1 3. uv i w L für jedes i N (inkl. der 0) (Äquivalent zur letzten Aussage ist die Aussage {u}{v} {w} L.) 62
4 2.4 Grenzen der regulären Sprachen Bevor wir zum Beweis kommen, betrachten wir das Lemma noch einmal genauer. Wie oben in den Überlegungen schon beschrieben, macht es eine Aussage über reguläre Sprachen. Wenn eine Sprache also regulär ist, dann gilt das Pumping Lemma. Es sagt dann, dass es eine natürliche Zahl n 1 gibt derart, dass jedes Wort z aus L, das mindestens die Länge n hat, zerlegt werden kann in z = uvw. Wie ein Wort z in Teilworte uvw zerlegt wird, bereitet bisweilen Probleme. Mit z = uvw wird ausgesagt, dass z in drei Teilworte, nämlich u, v und w, zerlegt wird, wobei u, v und w hintereinander geschrieben gerade wieder z ergeben. Hat man z.b. das Wort z = Hausboot, dann ist z.b. u = Hau, v = sb und w = oot eine Zerlegung von z in u, v und w mit z = uvw. Man beachte, dass der erste Buchstabe von u der erste Buchstabe von z ist und der letzte Buchstabe von w der letzte Buchstabe von z. Betrachtet man dann z.b. uv 2 w (was wir bei der dritten Eigenschaft des Pumping Lemmas brauchen), dann ist dies gerade uvvw also mit der obigen Bedeutung von u, v und w dann also Hau sb sb oot = Hausbsboot. Man beachte, dass bei einer Zerlegung z = uvw oft auch z.b. u = λ möglich ist. In diesem Fall ist der erste Buchstabe von v dann der erste Buchstabe von z. Die Zerlegung z = uvw aus dem Pumping Lemma erfüllt dann drei Eigenschaften, von denen wir die dritte oben bereits skizziert haben: Man kann einen Teil des Wortes (hier das v) beliebig oft schreiben und erhält stets ein Wort aus L. Das Wort v entspricht im Automaten aus den vorherigen Überlegungen der Schleife. Dies wird auch gleich im Beweis deutlich werden. Die erste und zweite Eigenschaft besagen, dass die Schleife existieren muss, also mindestens die Länge 1 haben muss (zweite Eigenschaft) und dass diese bis zu einem bestimmten Zeitpunkt das erste Mal entlang gegangen sein muss (erste Eigenschaft). Die erste Eigenschaft rührt daher, dass bei einem Automaten mit n Zuständen nach n gelesenen Symbolen bereits n + 1 Zustände besucht wurden (der Startzustand und nach jedem gelesenen Symbol ein weiterer). Hat man nur n Zustände ist spätestens der n + 1-te Zustand also ein Zustand, den man schon einmal besucht hatte. Man beachte noch, dass die dritte Eigenschaft besagt, dass mit z = uvw L für jedes i 0 auch uv i w L gilt. Insbesondere kann i auch 0 sein und in diesem Fall haben wir uv 0 w = uw. Es müssen also uw ebenso wie uvvw, uvvvw usw. alle in L sein. Wir beweisen nun das Pumping Lemma. Man achte beim Durcharbeiten darauf, wo sich die obigen Ideen überall wiederfinden. Beweis. Sei L regulär. Dann gibt es einen DFA, der L akzeptiert und sogar einen vollständigen DFA, der L akzeptiert. Sei dieser vollständige DFA mit A benannt. Es gilt also L(A) = L und A ist zudem vollständig. A hat eine Menge von Zuständen. Sei n die Anzahl dieser Zustände von A. Wir müssen nun zeigen, dass jedes Wort z aus L, dessen Länge mindestens n ist, in z = uvw zerlegt werden kann, wobei u, v und w die drei Eigenschaften des Lemmas erfüllen. 63
5 2 Endliche Automaten Sei also z L mit z n (gibt es kein solches z ist nichts zu zeigen, da das Pumping Lemma ja nur für Worte mit dieser Eigenschaft etwas fordert; gibt es also keine solchen Worte, gilt das Pumping Lemma sofort). Wir legen nun A das Wort z vor. A beginnt dann eine Rechnung in seinem Startzustand z s. Da A vollständig ist kann z bis zum Ende gelesen werden. (Ferner endet A dann in einem Endzustand, da z L ist. Dies benötigen wir aber jetzt noch nicht.) Da z aus mindestens n Buchstaben besteht, finden mindestens n Zustandsübergänge statt, d.h. es werden inklusive des Startzustandes mindestens n + 1 Zustände besucht. Da es aber nur n Zustände gibt, muss mindestens ein Zustand doppelt auftreten. Sei die Zustandsfolge, die in A vom Startzustand z s zu einem Endzustand z e beim Lesen von z besucht wird durch z 0, z 1, z 2,..., z n,..., z q gegeben. Hier ist also z 0 = z s und z q = z e und die Indizes geben an, der wievielte Zustand gerade besucht wird. Man beachte, dass die Indizierung hier nichts mit den verschiedenen Zuständen aus Z zu tun hat. Es könnte also z.b. z 1 = z 2 sein. Wir wissen nun nach obigem, dass ein Zustand mehrfach auftreten muss. Seien daher z i und z j mit i j und i < j in dieser Folge gleich und außerdem z j der erste Zustand, der ein zweites Mal auftritt. Da von z 0 bis z n bereits n + 1 Zustände in der Zustandsfolge auftreten, es aber nur n Zustände gibt, muss hier bereits ein Zustand doppelt auftreten, d.h. es muss j n gelten. Ferner muss wegen i j und i < j (z i und z j treten in der Folge nicht zum gleichen Zeitpunkt auf und z j ist gerade die erste Wiederholung von z i ) j i 1 gelten. Wir können nun das Wort z, das uns ja von z 0 nach z q in der obigen Zustandsfolge bringt, an i und j zerlegen. Sei dazu u das Wort, das von z 0 bis z i gelesen wird, v das Wort, das von z i bis z j gelesen wird und w das Wort, das von z j bis z q gelesen wird. Damit ist uvw = z. Nach obigen Ausführungen zur Wahl von i und j ist ferner uv n (wegen j n oben) und v 1 (wegen j i 1 oben). Die gewählte Zerlegung von z in uvw erfüllt also schon die ersten beiden Bedingungen im Pumping Lemma. Da z i = z j gilt, aber i j ist, überführt das Wort v den Automaten also von z i zurück nach z i (= z j ). Diese Schleife (bzw. besser: dieser Kreis) im Automaten kann beliebig oft entlang gegangen werden und egal wie oft man diese Schleife entlang geht, also egal wie oft man das Teilwort v liest, man ist im Anschluss in v j und kann von hieraus mit w in einen Endzustand gelangen (erst an dieser Stelle wird benötigt, dass v q ein Endzustand ist, da ursprünglich ja auch v von A akzeptiert wurde). Daraus folgt aber nun, dass uv i w für alle i 0 akzeptiert wird und also auch die dritte Bedingung im Pumping Lemma von unserer gewählten Zerlegung erfüllt wird. Damit haben wir das Pumping Lemma bewiesen. 64
6 2.4 Grenzen der regulären Sprachen Wir wollen nun das Pumping Lemma nutzen, um zu zeigen, dass die Sprache {a n b n n N} nicht regulär ist. Dazu nehmen wir an, die Sprache wäre regulär und zeigen einen Widerspruch. Wir führen den Beweis zunächst sehr ausführlich und bauen etliche Erklärungen in den Beweis ein. Wir betonen aber schon hier, dass wir bei einem Widerspruchsbeweis annehmen, dass das Pumping Lemma gilt und dann einen Widerspruch herstellen wollen. Da das Pumping Lemma sagt, dass alle Worte mit z L und z n zerlegt werden können, genügt es für ein Wort mit z L und z n zu zeigen, dass dem nicht so ist. Da das Pumping Lemma dann sagt, dass eine Zerlegung z = uvw existiert, die die drei Eigenschaften erfüllt (also erstens und zweitens und drittens), muss man dann zeigen, dass jede Zerlegungen von z in uvw mindestens eine der drei Eigenschaften nicht erfüllt (also alle Zerlegungen im Widerspruch zu erstens, zweitens oder drittens stehen). Satz L := {a n b n n N} ist nicht regulär. Beweis. Angenommen L wäre regulär. Dann gilt das Pumping Lemma. Sei k die Zahl aus dem Pumping Lemma. An dieser Stelle bereits der erste Hinweis: Die Zahl k wird nicht genauer spezifiziert. Es geht lediglich darum, dass es k geben müsste, wenn denn das Pumping Lemma gilt. Es macht auch wenig Sinn, diese Zahl hier genauer spezifizieren zu wollen. Sie hing im Beweis des Pumping Lemmas ja mit der Anzahl der Zustände eines Automaten zusammen, der L akzeptiert. Wenn unser Widerspruchsbeweis nachfolgend also erfolgreich ist und wir tatsächlich zeigen, das L nicht regulär ist, dann gibt es ja gerade keinen DFA für L und dann macht es auch keinen Sinn zu versuchen, dessen Anzahl an Zuständen zu ermitteln. Wir betrachten nun das Wort z = a k b k. Es gilt z L und z k. Bei der Wahl von z sind wir recht frei und es ist tatsächlich bei manchen Sprachen viel Kreativität nötig, um auf ein gutes z zu kommen (d.h. eines mit dem man arbeiten kann und das einem nachher tatsächlich erlaubt, zu einem Widerspruch zu kommen). Das z muss aber in L sein und es muss von der Zahl k abhängen (also von jener Zahl, dessen Existenz aus der angenommenen Gültigkeit des Pumping Lemmas folgt). Warum muss z von k abhängen? Weil wir ein Wort benötigen, dass in L ist und z k erfüllt und um sicherzustellen, dass die Länge von z mindestens k ist, muss das k irgendwie in z auftreten. Nun muss es nach dem Pumping Lemma eine Zerlegung z = uvw geben, die die drei Eigenschaften erfüllt. Wir wollen dies zum Widerspruch führen. Wir betrachten dazu nun nur jene Zerlegungen, die die erste und zweite Bedingung erfüllen und zeigen, dass diese im Widerspruch zur dritten stehen. Wir haben dann gezeigt, dass jede Zerlegung von z in uvw im Widerspruch zu einer der drei Bedingungen steht und sind dann fertig. Warum müssen hier alle Zerlegungen betrachtet werden? Im Pumping Lemma ist ja nur von einer die Rede? Letzteres ist zwar richtig, wir wollen ja aber gerade einen Widerspruch erzeugen. Um also zu zeigen, dass es nicht stimmt, 65
7 2 Endliche Automaten dass es eine Zerlegung von z in uvw gibt, die die drei Eigenschaften erfüllt, müssen wir zeigen, dass es keine solche Zerlegung gibt. Dazu müssen wir zeigen, dass alle Zerlegungen einen Widerspruch erzeugen, dass also jede Zerlegung von z in uvw mit mindestens einer der drei Eigenschaften im Widerspruch steht. Und warum genügt es dann nur jene zu betrachten, die die ersten beiden Eigenschaften erfüllen? Das ist ganz einfach: Eine Zerlegung, die nicht die ersten beiden Eigenschaften erfüllt, erfüllt ja bereits mindestens eine der drei Eigenschaften nicht (nämlich eine der ersten beiden). Es genügt also sich die Zerlegungen anzugucken, die die beiden ersten Eigenschaften erfüllen und dann herzuleiten, dass diese Zerlegungen nun aber im Widerspruch zur dritten Eigenschaft stehen. Damit hat man dann gezeigt, dass alle Zerlegungen zu den drei Eigenschaften im Widerspruch stehen. Entweder widerspricht eine Zerlegung dann schon einer der ersten beiden Eigenschaften oder, wenn sie die ersten beiden Eigenschaften erfüllt, dann widerspricht sie der dritten. Der Grund für dieses Vorgehen ist, dass man über Zerlegungen, die die ersten beiden Eigenschaften erfüllen schon etwas weiß (nämlich die Aussagen der ersten beiden Eigenschaften) und dass man dann damit arbeiten kann. Sei also z = a k b k = uvw eine Zerlegung mit i) uv k und ii) v 1. Da uv ja in den ersten Buchstaben von z liegt (wgen z = uvw) und da uv aber höchstens die Länge k hat, muss uv also in den ersten k Buchstaben von z liegen (beginnend bei dem ersten), d.h. in den ersten k as. Beachtet man ferner, dass v 1 gilt, so kann man bereits v {a} + schlussfolgern. Genauer kann man sogar sagen, dass es ein j mit 1 j k geben muss derart, dass v = a j gilt. Man beachte, dass wir an dieser Stelle jede Zerlegung z = uvw, die i) und ii) erfüllt, betrachten. Durch j und dadurch, dass wir nicht genauer spezifizieren, wo v beginnt (bzw. wo u endet), haben wir diese Zerlegungen quasi parametrisiert. Eine Zerlegung ist z.b. u = λ, v = a, w = a k 1 b k, eine weitere ist u = a, v = a, w = a k 2 b k, noch eine ist u = aa, v = a, w = a k 3 b k. Es gibt dann weitere wie z.b. u = aa, v = aaa, w = a k 5 b k usw. Allen diese Zerlegungen ist gemein, dass u in den as liegt (ganz genau: u ist zwischen a 0 = λ und a k 1 ), dass dann v folgt und v nur aus as besteht, mindestens aus einem und maximal aus k vielen, wobei einige Fälle je nach Wahl von u nicht eintreten können und dass w dann den Rest von z ausmacht. Wir betrachten nun das Wort uv 2 w = uvvw, dass nach der dritten Bedingung in L sein müsste. Es ist aber uv 2 w = uvvw = a k+j b k (man beachte, dass wir v = a j ja nun zweimal hintereinander dort stehen haben) und damit ist uv 2 w L, denn j > 1 und damit haben wir nicht mehr gleiche viele as wie bs. Da die dritte Eigenschaft des Pumping Lemmas aber verlangen würde, dass für jedes i 0 dann uv i w L ist, haben wir einen Widerspruch. Die ursprüngliche Annahme muss also falsch sein und daher ist L nicht regulär. Das notieren von v i mit i 0 nennt man Pumpen. Wie die Wahl von z ist es wieder ein kreativer Prozess, auf ein gutes i zu kommen, wobei gut hier 66
8 2.4 Grenzen der regulären Sprachen bedeutet ein i zu finden, das einen Widerspruch erlaubt, mit dem also uv i w L gilt. Es ist manchmal nötig, mehrere Versuche zu unternehmen, bis man auf ein gutes z und ein gutes i kommt. Die i könnten zudem auch unterschiedlich sein, je nachdem welche Zerlegung von z man hat. Es könnte also sein, dass man die Zerlegung von z erst geeignet parametrisieren und dann eine Fallunterscheidung machen muss und für unterschiedliche Fälle unterschiedliche i benötigt. Wichtig ist nur, dass man stets zu einem Widerspruch kommt. Wir betonen hier auch noch einmal, dass auch i = 0 gesetzt werden darf. Auch das Wort uw muss also in L sein und man hat einen Widerspruch, falls dies nicht der Fall ist. Dies ist in machen Fällen die einzige Möglichkeit einen Widerspruch herzustellen, daher sollte man diesen Spezialfall in Erinnerung behalten. Damit haben wir nun gezeigt, dass es tatsächlich Sprachen gibt, die nicht regulär sind! Wir betonen dies im folgenden Satz. Satz Es gibt Sprachen, die nicht regulär sind. Ein Beispiel ist die Sprache L := {a n b n n N}. Es gibt keinen DFA, der L akzeptiert. Das Pumping Lemma hilft uns für Sprachen wie obige und auch für weitere zu zeigen, dass die Sprachen nicht regulär sind. Das Pumping Lemma macht also eine Aussage über eine Eigenschaft, die alle regulären Sprachen haben. Es wird dann aber benutzt, um gerade zu zeigen, dass eine Sprache nicht regulär ist. Wir fassen noch einmal den Ablauf zusammen, wenn man für eine Sprache L mittels Nutzung des Pumping Lemmas zeigen will, dass L nicht regulär ist. 1. Annehmen L wäre regulär 2. Die Zahl aus dem Pumping Lemma benennen (z.b. k). 3. Ein Wort z finden mit z k und z L. Dieses Wort muss gut gewählt sein, damit der nachfolgende Widerspruch gelingt. Hier muss man also u.u. experimentieren. 4. Für alle Zerlegungen von z in uvw zeigen, dass sie im Widerspruch zur ersten, zweiten oder dritten Bedingung sind. Üblicherweise betrachtet man alle Zerlegungen, die die erste und zweite Bedingung erfüllen und zeigt, dass man dann einen Widerspruch zur dritten Bedingung erhält. 5. Also: Alle Zerlegungen z = uvw mit uv k und v 1 betrachten. 6. Zeigen, dass man ein i findet mit uv i w L. (Dies kann auch i = 0 sein!) 67
9 2 Endliche Automaten Wir wollen zum Abschluss noch ein zweites Beispiel betrachten und hier beim Beweis zügig vorgehen. Zur Erinnerung: w rev ist gerade das Wort w von hinten nach vorne gelesen, also z.b. 011 rev = 110. Satz L := {ww rev w {0, 1} } ist nicht regulär. Beweis. Angenommen L wäre regular. Dann gilt das Pumping Lemma. Sei k die Zahl aus dem Pumping Lemma. Wir betrachten z = 0 k 1 k 1 k 0 k. Es ist z L und z k. Sei z = uvw eine Zerlegung von z mit uv k und v 1. Hieraus folgt v = 0 j für ein j mit 1 j k. Nun ist aber uv 0 w = 0 k j 1 k 1 k 0 k nicht mehr in L im Widerspruch zum Pumping Lemma. Die Annahme ist daher falsch und L somit nicht regulär. Man beachte, dass der obige Beweis mit z = 0 k 0 k nicht gelungen wäre. Die Wahl des Wortes ist also wichtig. Wir haben in diesem Abschnitt das Pumping Lemma kennengelernt. Dieses macht eine Aussage über die regulären Sprachen, d.h. alle regulären Sprachen haben die im Pumping Lemma beschriebenen Eigenschaften. Genutzt wird das Pumping Lemma dann, um nachzuweisen, dass eine Sprache nicht regulär ist. Dazu wird gezeigt, dass eine Sprache gerade nicht die im Pumping Lemma beschriebenen Eigenschaften hat. Das Vorgehen ist dabei zu einem gewissen Teil stets gleich. Bei der Wahl des Wortes, das man zerlegen möchte, und bei der Betrachtung aller Zerlegungen und dem Erreichen des Widerspruches ist aber stets Kreativität erforderlich. Fragen 1. Für welche Worte z wird im Pumping Lemma eine Aussage getroffen? a) Für solche mit z n. b) Für solche mit z L und z n. c) Für solche mit z L. d) Für alle z L mit z n. 2. Wie lautet die dritte Eigenschaft im Pumping Lemma? a) uv i w L für jedes i > 0 b) uv i w L für ein i 0 c) uv i w L für jedes i 0 d) uv i w L für ein i > 0 3. Welche Formulierung entspricht der dritten Eigenschaft im Pumping Lemma? a) {u}{v} {w} L 68
10 2.4 Grenzen der regulären Sprachen b) {u}{v} + {w} L c) {u}{v} + {w} L d) {u}{v} {w} L 4. Wovon muss das bei einem Widerspruchsbeweis mittels des Pumping Lemmas gewählte Wort z abhängen? a) Von der Anzahl der Zustände Z des DFA. b) Von der Zahl aus dem Pumping Lemma k, die noch genauer spezifiziert werden muss. c) Von der Zahl aus dem Pumping Lemma k, die nicht genauer spezifiziert werden muss. d) Das Wort muss lediglich in der Sprache sein. 5. Wieviele Zerlegungen von z müssen bei einem Widerspruchsbeweis mittels des Pumping Lemmas betrachtet werden? a) Eine Zerlegung muss zum Widerspruch geführt werden. b) Alle Zerlegungen von z müssen zum Widerspruch gebracht werden. c) Zerlegungen mit bestimmten Eigenschaften müssen zum Widerspruch gebracht werden. d) Man muss eine Zerlegung mit bestimmten Eigenschaften finden und diese zum Widerspruch führen. 6. Kann mit dem Pumping Lemma gezeigt werden, dass eine Sprache regulär ist? a) Ja! b) Nein! 69
Frank Heitmann 2/47. 1 Ein PDA beginnt im Startzustand z 0 und mit im Keller. 2 Ist der Automat
 Formale Grundlagen der Informatik 1 Kapitel 5 Über reguläre Sprachen hinaus und (Teil 2) Frank Heitmann heitmann@informatik.uni-hamburg.de 21. April 2015 Der Kellerautomat - Formal Definition (Kellerautomat
Formale Grundlagen der Informatik 1 Kapitel 5 Über reguläre Sprachen hinaus und (Teil 2) Frank Heitmann heitmann@informatik.uni-hamburg.de 21. April 2015 Der Kellerautomat - Formal Definition (Kellerautomat
Das Pumping Lemma der regulären Sprachen
 Das Pumping Lemma der regulären Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de 1 Das Pumping Lemma Das Pumping Lemma der regulären Sprachen macht eine Aussage der Art wenn eine Sprache L regulär
Das Pumping Lemma der regulären Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de 1 Das Pumping Lemma Das Pumping Lemma der regulären Sprachen macht eine Aussage der Art wenn eine Sprache L regulär
Die mathematische Seite
 Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Formalismen für REG. Formale Grundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen. Das Pumping Lemma. Abschlusseigenschaften
 Formalismen für RE Formale rundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de Satz Zu jeder regulären Sprache L gibt es einen DFA A mit L(A) =
Formalismen für RE Formale rundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de Satz Zu jeder regulären Sprache L gibt es einen DFA A mit L(A) =
Worterkennung in Texten speziell im Compilerbau 14. April Frank Heitmann 2/65
 Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges kennengelernt,
Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges kennengelernt,
Ein deterministischer endlicher Automat (DFA) kann als 5-Touple dargestellt werden:
 Sprachen und Automaten 1 Deterministische endliche Automaten (DFA) Ein deterministischer endlicher Automat (DFA) kann als 5-Touple dargestellt werden: M = (Z,3,*,qo,E) Z = Die Menge der Zustände 3 = Eingabealphabet
Sprachen und Automaten 1 Deterministische endliche Automaten (DFA) Ein deterministischer endlicher Automat (DFA) kann als 5-Touple dargestellt werden: M = (Z,3,*,qo,E) Z = Die Menge der Zustände 3 = Eingabealphabet
Beispiel: A d zum Automaten, der OTTO im Text erkennt. Zur Erinnerung: der nichtdeterministische Automat sieht so aus:
 Endliche Automaten Jörg Roth 80 Beispiel: A d zum Automaten, der TT im Text erkennt. Zur Erinnerung: der nichtdeterministische Automat sieht so aus: T T S 1 S 2 S 3 S 4 immer immer δ d (es sind nur S mit
Endliche Automaten Jörg Roth 80 Beispiel: A d zum Automaten, der TT im Text erkennt. Zur Erinnerung: der nichtdeterministische Automat sieht so aus: T T S 1 S 2 S 3 S 4 immer immer δ d (es sind nur S mit
2.3 Abschlusseigenschaften
 2.3 Abschlusseigenschaften 2.3 Abschlusseigenschaften In diesem Abschnitt wollen wir uns mit Abschlusseigenschaften der regulären Sprachen, d.h. mit der Frage, ob, gegeben eine Operation und zwei reguläre
2.3 Abschlusseigenschaften 2.3 Abschlusseigenschaften In diesem Abschnitt wollen wir uns mit Abschlusseigenschaften der regulären Sprachen, d.h. mit der Frage, ob, gegeben eine Operation und zwei reguläre
Theorie der Informatik
 Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Das Pumping-Lemma Formulierung
 Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
Formale Methoden 1. Gerhard Jäger 23. Januar Uni Bielefeld, WS 2007/2008 1/18
 1/18 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 23. Januar 2008 2/18 Das Pumping-Lemma Sein L eine unendliche reguläre Sprache über ein endliches Alphabet
1/18 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 23. Januar 2008 2/18 Das Pumping-Lemma Sein L eine unendliche reguläre Sprache über ein endliches Alphabet
2.2 Nichtdeterministische endliche Automaten
 2 Endliche Automaten arbeiten und hier kann dann ggf. auch wieder auf die Konstruktion verwiesen werden. Fragen 1. Wie viele Informationen kann man in einem DFA speichern? a) beliebig viele b) endlich
2 Endliche Automaten arbeiten und hier kann dann ggf. auch wieder auf die Konstruktion verwiesen werden. Fragen 1. Wie viele Informationen kann man in einem DFA speichern? a) beliebig viele b) endlich
Fragen 1. Wie viele Startzustände kann ein endlicher Automat haben? 2. Wie viele Endzustände kann ein endlicher Automat haben?
 2 Endliche Automaten Konfigurationsübergang, Rechnung, Erfolgsrechnung, akzeptierte Sprache, reguläre Menge und die Sprachfamilie REG. Alle diese Begriffe sind wichtig und sollten bekannt sein, da wir
2 Endliche Automaten Konfigurationsübergang, Rechnung, Erfolgsrechnung, akzeptierte Sprache, reguläre Menge und die Sprachfamilie REG. Alle diese Begriffe sind wichtig und sollten bekannt sein, da wir
c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} c) {abcabc} d) {abcbc, abc, a} c) {aa, ab, ba, bb} d) {{aa}, {ab}, {ba}, {bb}}
 2 Endliche Automaten Fragen 1. Was ergibt sich bei {a, bc} {de, fg}? a) {abc, defg} b) {abcde, abcfg} c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} 2. Was ergibt sich bei {abc, a} {bc, λ}?
2 Endliche Automaten Fragen 1. Was ergibt sich bei {a, bc} {de, fg}? a) {abc, defg} b) {abcde, abcfg} c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} 2. Was ergibt sich bei {abc, a} {bc, λ}?
a b b a Alphabet und Wörter - Zusammengefasst Formale Grundlagen der Informatik 1 Kapitel 2 Endliche Automaten und reguläre Sprachen
 Formale Grundlagen der Informatik Kapitel 2 und reguläre Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de 5. April 26 Frank Heitmann heitmann@informatik.uni-hamburg.de /52 Alphabet und Wörter
Formale Grundlagen der Informatik Kapitel 2 und reguläre Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de 5. April 26 Frank Heitmann heitmann@informatik.uni-hamburg.de /52 Alphabet und Wörter
Die Nerode-Relation und der Index einer Sprache L
 Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Typ-3-Sprachen. Das Pumping-Lemma
 Das Pumping-Lemma Typ-3-Sprachen Um zu zeigen, daß eine Sprache L regulär ist, kannman einen NFA M angeben mit L(M) = L, oder eine rechtslineare Grammatik G angeben mit L(G) =L, oder einen regulären Ausdruck
Das Pumping-Lemma Typ-3-Sprachen Um zu zeigen, daß eine Sprache L regulär ist, kannman einen NFA M angeben mit L(M) = L, oder eine rechtslineare Grammatik G angeben mit L(G) =L, oder einen regulären Ausdruck
Grenzen der Regularität
 Grenzen der Regularität Um die Mächtigkeit von endlichen Automaten zu verstehen, muss man auch ihre Grenzen kennen. Sei z.b. B = {0 n 1 n n 0} Gibt es einen DEA für B? Es sieht so aus, als müsste sich
Grenzen der Regularität Um die Mächtigkeit von endlichen Automaten zu verstehen, muss man auch ihre Grenzen kennen. Sei z.b. B = {0 n 1 n n 0} Gibt es einen DEA für B? Es sieht so aus, als müsste sich
Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni Christian Franz
 Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni 2 Christian Franz Inhaltsverzeichnis Wiederholung: Vorlesung vom 9.6.2... Beispiele für Äquivalenzklassen... 4.5. Minimierung
Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni 2 Christian Franz Inhaltsverzeichnis Wiederholung: Vorlesung vom 9.6.2... Beispiele für Äquivalenzklassen... 4.5. Minimierung
Das Pumping Lemma: Ein Anwendungsbeispiel
 Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
Worterkennung in Texten speziell im Compilerbau 20. April Frank Heitmann 2/64
 Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges
Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges
Fragen 1. Muss eine DTM ein Wort zu Ende gelesen haben, um es zu akzeptieren? a) Ja! b) Nein!
 4 Turingmaschinen Eingabeband nicht nur lesen, sondern auch schreiben kann und die zudem mit ihrem Lese-Schreib-Kopf (LSK) nach links und rechts gehen kann. Das Eingabeband ist zudem in beide Richtungen
4 Turingmaschinen Eingabeband nicht nur lesen, sondern auch schreiben kann und die zudem mit ihrem Lese-Schreib-Kopf (LSK) nach links und rechts gehen kann. Das Eingabeband ist zudem in beide Richtungen
Theoretische Informatik Mitschrift
 5 Eigenschaften regulärer Sprachen 51: Die Nerode-Relation Theoretische Informatik Mitschrift Definition 51: Sei L * L * * mit L :={u, v * * w *:uw L v w L }heißt Nerode-Relation von L Sei ={0,1}, L= *{00}
5 Eigenschaften regulärer Sprachen 51: Die Nerode-Relation Theoretische Informatik Mitschrift Definition 51: Sei L * L * * mit L :={u, v * * w *:uw L v w L }heißt Nerode-Relation von L Sei ={0,1}, L= *{00}
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Algorithmen mit konstantem Platzbedarf: Die Klasse REG
 Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
Formale Grundlagen der Informatik 1 Kapitel 5 Abschlusseigenschaften
 Formale Grundlagen der Informatik 1 Kapitel 5 Frank Heitmann heitmann@informatik.uni-hamburg.de 18. April 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/64 NFAs - Grundlagen DFAs vs. NFAs Der
Formale Grundlagen der Informatik 1 Kapitel 5 Frank Heitmann heitmann@informatik.uni-hamburg.de 18. April 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/64 NFAs - Grundlagen DFAs vs. NFAs Der
1. Übungsblatt 6.0 VU Theoretische Informatik und Logik
 . Übungsblatt 6. VU Theoretische Informatik und Logik 25. September 23 Aufgabe Sind folgende Aussagen korrekt? Begründen Sie jeweils Ihre Antwort. a) Für jede Sprache L gilt: L < L (wobei A die Anzahl
. Übungsblatt 6. VU Theoretische Informatik und Logik 25. September 23 Aufgabe Sind folgende Aussagen korrekt? Begründen Sie jeweils Ihre Antwort. a) Für jede Sprache L gilt: L < L (wobei A die Anzahl
Informatik IV. Pingo Sommersemester Dozent: Prof. Dr. J. Rothe. J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13
 Informatik IV Sommersemester 2019 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13 Website http://pingo.upb.de/ Code: 1869 J. Rothe (HHU Düsseldorf) Informatik IV 2 / 13 Frage
Informatik IV Sommersemester 2019 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13 Website http://pingo.upb.de/ Code: 1869 J. Rothe (HHU Düsseldorf) Informatik IV 2 / 13 Frage
Theoretische Informatik I (Winter 2017/18) Prof. Dr. Ulrich Hertrampf. Das Pumping Lemma
 Das Pumping Lemma Bisher haben wir eine Reihe von Charakterisierungen der Typ-3 Sprachen kennengelernt. Das erfüllt mehrere Zwecke: Wenn wir von einer Sprache zeigen wollen, dass sie vom Typ-3 ist, dann
Das Pumping Lemma Bisher haben wir eine Reihe von Charakterisierungen der Typ-3 Sprachen kennengelernt. Das erfüllt mehrere Zwecke: Wenn wir von einer Sprache zeigen wollen, dass sie vom Typ-3 ist, dann
Theoretische Informatik I (Winter 2018/19) Prof. Dr. Ulrich Hertrampf. Das Pumping Lemma
 Das Pumping Lemma Bisher haben wir eine Reihe von Charakterisierungen der Typ-3 Sprachen kennengelernt. Das erfüllt mehrere Zwecke: Wenn wir von einer Sprache zeigen wollen, dass sie vom Typ-3 ist, dann
Das Pumping Lemma Bisher haben wir eine Reihe von Charakterisierungen der Typ-3 Sprachen kennengelernt. Das erfüllt mehrere Zwecke: Wenn wir von einer Sprache zeigen wollen, dass sie vom Typ-3 ist, dann
Theoretische Informatik Kap 1: Formale Sprachen/Automatentheorie
 Gliederung der Vorlesung. Grundbegriffe. Formale Sprachen/Automatentheorie.. Grammatiken.2..3. Kontext-freie Sprachen 2. Berechnungstheorie 2.. Berechenbarkeitsmodelle 2.2. Die Churchsche These 2.3. Unentscheidbarkeit
Gliederung der Vorlesung. Grundbegriffe. Formale Sprachen/Automatentheorie.. Grammatiken.2..3. Kontext-freie Sprachen 2. Berechnungstheorie 2.. Berechenbarkeitsmodelle 2.2. Die Churchsche These 2.3. Unentscheidbarkeit
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2013
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2013 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Reguläre Ausdrücke Wozu
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2013 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Reguläre Ausdrücke Wozu
FORMALE SYSTEME. 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten. TU Dresden, 14. November 2016.
 FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
Kontextfreie Grammatiken
 Kontextfreie Grammatiken Bisher haben wir verschiedene Automatenmodelle kennengelernt. Diesen Automaten können Wörter vorgelegt werden, die von den Automaten gelesen und dann akzeptiert oder abgelehnt
Kontextfreie Grammatiken Bisher haben wir verschiedene Automatenmodelle kennengelernt. Diesen Automaten können Wörter vorgelegt werden, die von den Automaten gelesen und dann akzeptiert oder abgelehnt
Theoretische Informatik I
 (702765) Skript zur Vorlesung am 30.6.2000 Aus der vorherigen Vorlesung: Theoretische Informatik I Satz W: Sei X ein Alphabet. Zu jeder regulären Sprache R X * gibt es ein n N, so daß für alle Wörter z
(702765) Skript zur Vorlesung am 30.6.2000 Aus der vorherigen Vorlesung: Theoretische Informatik I Satz W: Sei X ein Alphabet. Zu jeder regulären Sprache R X * gibt es ein n N, so daß für alle Wörter z
WS07/08 Automaten und Formale Sprachen 5. Vorlesung
 WS7/8 Automaten und Formale Sprachen 5. Vorlesung Martin Dietzfelbinger 3. November 27 FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/8 3..27 Stichworte Induktive Definitionen: (i) Basisobjekte,
WS7/8 Automaten und Formale Sprachen 5. Vorlesung Martin Dietzfelbinger 3. November 27 FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/8 3..27 Stichworte Induktive Definitionen: (i) Basisobjekte,
Lösung zur Klausur. Grundlagen der Theoretischen Informatik im WiSe 2003/2004
 Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Folgen und Grenzwerte
 Wintersemester 2015/201 Folgen und Grenzwerte von Sven Grützmacher Dieser Vortrag wurde für den (von der Fachschaft organisierten) Vorkurs für die Studienanfänger an der Fakultät für Mathematik und Informatik
Wintersemester 2015/201 Folgen und Grenzwerte von Sven Grützmacher Dieser Vortrag wurde für den (von der Fachschaft organisierten) Vorkurs für die Studienanfänger an der Fakultät für Mathematik und Informatik
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 20.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch, 10.06.2015, D028,
Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 20.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch, 10.06.2015, D028,
Endliche Automaten. δ : Z Σ Z die Überführungsfunktion, z 0 Z der Startzustand und F Z die Menge der Endzustände (Finalzustände).
 Endliche Automaten Endliche Automaten Definition Ein deterministischer endlicher Automat (kurz DFA für deterministic finite automaton ) ist ein Quintupel M = (Σ, Z, δ, z 0, F), wobei Σ ein Alphabet ist,
Endliche Automaten Endliche Automaten Definition Ein deterministischer endlicher Automat (kurz DFA für deterministic finite automaton ) ist ein Quintupel M = (Σ, Z, δ, z 0, F), wobei Σ ein Alphabet ist,
Satz 90 Sei A = (Q, Σ, δ, q 0, F ) ein DFA. Der Zeitaufwand des obigen Minimalisierungsalgorithmus ist O( Q 2 Σ ).
 Satz 90 Sei A = (Q, Σ, δ, q 0, F ) ein DFA. Der Zeitaufwand des obigen Minimalisierungsalgorithmus ist O( Q 2 Σ ). Beweis: Für jedes a Σ muss jede Position in der Tabelle nur konstant oft besucht werden.
Satz 90 Sei A = (Q, Σ, δ, q 0, F ) ein DFA. Der Zeitaufwand des obigen Minimalisierungsalgorithmus ist O( Q 2 Σ ). Beweis: Für jedes a Σ muss jede Position in der Tabelle nur konstant oft besucht werden.
Einführung in die Computerlinguistik Satz von Kleene
 Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 17.11.2009 Wiebke Petersen Einführung CL (WiSe 09/10) 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von
Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 17.11.2009 Wiebke Petersen Einführung CL (WiSe 09/10) 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von
Informatik III. Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung 17.11.2006 schindel@informatik.uni-freiburg.de 1 Prinzip des Kellerautomats Push-Down-Automaton (PDA) Ein Kellerautomat vereinigt
Informatik III Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung 17.11.2006 schindel@informatik.uni-freiburg.de 1 Prinzip des Kellerautomats Push-Down-Automaton (PDA) Ein Kellerautomat vereinigt
1 Lokale Sprachen. 2 Verallgemeinerung
 1 Lokale Sprachen Es soll um Sprachen gehen die nur aufgrund ihrer Teilworte einer festen Länge entschieden werden können. Anschaulich heisst dies man kann ein Fenster der Länge k über das Eingabewort
1 Lokale Sprachen Es soll um Sprachen gehen die nur aufgrund ihrer Teilworte einer festen Länge entschieden werden können. Anschaulich heisst dies man kann ein Fenster der Länge k über das Eingabewort
Lösungen zum Aufgabenblatt Nr. 1: Konstruktion der reellen Zahlen
 Lösungen zum Aufgabenblatt Nr. 1: Konstruktion der reellen Zahlen Aufgabe 1: Es sei D die Menge aller rationalen Dedekind-Mengen, also D := { M 2 Q M is Dedekind-Menge }. Auf der Menge D definieren wir
Lösungen zum Aufgabenblatt Nr. 1: Konstruktion der reellen Zahlen Aufgabe 1: Es sei D die Menge aller rationalen Dedekind-Mengen, also D := { M 2 Q M is Dedekind-Menge }. Auf der Menge D definieren wir
1 Eliminieren von ɛ-übergängen
 1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
TU Berlin Nachklausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2012)
 Berlin, 05. Oktober 2012 Name:... Matr.-Nr.:... TU Berlin Nachklausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2012) 1 2 3 4 5 6 7 Σ Bearbeitungszeit: 60 min.
Berlin, 05. Oktober 2012 Name:... Matr.-Nr.:... TU Berlin Nachklausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2012) 1 2 3 4 5 6 7 Σ Bearbeitungszeit: 60 min.
Abschlusseigenschaften
 Abschlusseigenschaften Die Klasse der regulären Sprachen hat eine große Zahl nützlicher Eigenschaften, insbesondere die folgenden Abschlusseigenschaften: Satz: Die Klasse der regulären Sprachen ist abgeschlossen
Abschlusseigenschaften Die Klasse der regulären Sprachen hat eine große Zahl nützlicher Eigenschaften, insbesondere die folgenden Abschlusseigenschaften: Satz: Die Klasse der regulären Sprachen ist abgeschlossen
2.6 Stetigkeit und Grenzwerte
 2.6 Stetigkeit und Grenzwerte Anschaulich gesprochen ist eine Funktion stetig, wenn ihr Graph sich zeichnen lässt, ohne den Stift abzusetzen. Das ist natürlich keine präzise mathematische Definition und
2.6 Stetigkeit und Grenzwerte Anschaulich gesprochen ist eine Funktion stetig, wenn ihr Graph sich zeichnen lässt, ohne den Stift abzusetzen. Das ist natürlich keine präzise mathematische Definition und
Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden kann.
 Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
2 Rationale und reelle Zahlen
 2 reelle Es gibt Mathematik mit Grenzwert (Analysis) und Mathematik ohne Grenzwert (z.b Algebra). Grenzwerte existieren sicher nur dann, wenn der Zahlbereich vollständig ist, also keine Lücken aufweist
2 reelle Es gibt Mathematik mit Grenzwert (Analysis) und Mathematik ohne Grenzwert (z.b Algebra). Grenzwerte existieren sicher nur dann, wenn der Zahlbereich vollständig ist, also keine Lücken aufweist
Lösungen zu Übungsblatt 6
 Lösungen zu Übungsblatt 6 Aufgabe 1 Um nachzuweisen, dass eine Sprache L nicht kontextfrei ist, genügt es nach dem (starken) Pumping Lemma für kontextfreie Sprachen zu zeigen: Für jedes n 0 existiert ein
Lösungen zu Übungsblatt 6 Aufgabe 1 Um nachzuweisen, dass eine Sprache L nicht kontextfrei ist, genügt es nach dem (starken) Pumping Lemma für kontextfreie Sprachen zu zeigen: Für jedes n 0 existiert ein
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
8 Konvergenzkriterien und Häufungswerte von Folgen in R
 8 Konvergenzkriterien und Häufungswerte von Folgen in R 8.1 Konvergenz monotoner Folgen 8.2 Die Zahl e 8.3 Existenz monotoner Teilfolgen 8.4 Auswahlprinzip von Bolzano-Weierstraß 8.5 Konvergenzkriterium
8 Konvergenzkriterien und Häufungswerte von Folgen in R 8.1 Konvergenz monotoner Folgen 8.2 Die Zahl e 8.3 Existenz monotoner Teilfolgen 8.4 Auswahlprinzip von Bolzano-Weierstraß 8.5 Konvergenzkriterium
Übung zur Vorlesung Theoretische Information. Pumping Lemma
 Übung zur Vorlesung Theoretische Information Pumping Lemma Folie Ein Endlicher Automat q q, q 2, Akzeptierte Sprache? Folie 2 Ein Endlicher Automat q q, q 2, Akzeptierte Sprache? Am Anfang eine, dannach
Übung zur Vorlesung Theoretische Information Pumping Lemma Folie Ein Endlicher Automat q q, q 2, Akzeptierte Sprache? Folie 2 Ein Endlicher Automat q q, q 2, Akzeptierte Sprache? Am Anfang eine, dannach
Einfache Parkettierungen
 Einfache Definitionen: Unter einer Parkettierung (auch Pflasterung oder Parkett genannt) verstehen wir eine überlappungsfreie Überdeckung der Ebene durch Polygone. Ein Polygon (auch Vieleck oder n-eck
Einfache Definitionen: Unter einer Parkettierung (auch Pflasterung oder Parkett genannt) verstehen wir eine überlappungsfreie Überdeckung der Ebene durch Polygone. Ein Polygon (auch Vieleck oder n-eck
Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (ii) ε ist ein regulärer Ausdruck über Σ.
 Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Theoretische Informatik Mitschrift
 3. Endliche Automaten endliche Zustandsübergangssysteme Theoretische Informatik Mitschrift Beispiel: 2-Bit-Ringzähler: ={Inc} L R ={IncInc Inc,Inc 7, Inc 11,...} n ' mod ' 4=3 ={Inc n k 0.n=4 k3 } 2-Bit-Ringzähler
3. Endliche Automaten endliche Zustandsübergangssysteme Theoretische Informatik Mitschrift Beispiel: 2-Bit-Ringzähler: ={Inc} L R ={IncInc Inc,Inc 7, Inc 11,...} n ' mod ' 4=3 ={Inc n k 0.n=4 k3 } 2-Bit-Ringzähler
b liegt zwischen a und c.
 2 DIE ANORDNUNGSAXIOME 5 (2.4) a, b, c R : (a < b 0 < c) ac < bc Monotoniegesetz der Multiplikation Bezeichnungen a > b : b < a (> wird gelesen: größer als ) a b : a < b oder a = b a b : a > b oder a =
2 DIE ANORDNUNGSAXIOME 5 (2.4) a, b, c R : (a < b 0 < c) ac < bc Monotoniegesetz der Multiplikation Bezeichnungen a > b : b < a (> wird gelesen: größer als ) a b : a < b oder a = b a b : a > b oder a =
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 3 14. Mai 2010 Einführung in die Theoretische
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 3 14. Mai 2010 Einführung in die Theoretische
Ogden s Lemma: Der Beweis (1/5)
 Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Kapitel 4. Reihen 4.1. Definition und Beispiele
 Kapitel 4. Reihen 4.1. Definition und Beispiele Ist (a n ) eine Folge von Zahlen, so heißt der formale Ausdruck a ν = a 0 + a 1 + a 2 +... eine Reihe; die einzelnen a ν sind die Glieder dieser Reihe. Um
Kapitel 4. Reihen 4.1. Definition und Beispiele Ist (a n ) eine Folge von Zahlen, so heißt der formale Ausdruck a ν = a 0 + a 1 + a 2 +... eine Reihe; die einzelnen a ν sind die Glieder dieser Reihe. Um
Wie man eine Sprache versteht
 Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
λ(a n ) n 1 = (λa n ) n 1. Abbildung 1: Graph einer Folge. b n = arctan(n), f n = cos(nπ), g n = n 2, h n = ( 1) n n.
 Folgen Es sei X eine beliebige Menge. Eine Folge mit Werten in X ist eine Abbildung von N nach X. Es wird also jeder natürlichen Zahl n (dem Index) ein Element a n aus X zugeordnet (das n-te Folgenglied).
Folgen Es sei X eine beliebige Menge. Eine Folge mit Werten in X ist eine Abbildung von N nach X. Es wird also jeder natürlichen Zahl n (dem Index) ein Element a n aus X zugeordnet (das n-te Folgenglied).
Eine Aussage kann eine Eigenschaft für ein einzelnes, konkretes Objekt behaupten:
 Aussagen Aussagen Eine Aussage kann eine Eigenschaft für ein einzelnes, konkretes Objekt behaupten: verbale Aussage formale Aussage Wahrheitswert 1) 201 ist teilbar durch 3 3 201 wahre Aussage (w.a.) 2)
Aussagen Aussagen Eine Aussage kann eine Eigenschaft für ein einzelnes, konkretes Objekt behaupten: verbale Aussage formale Aussage Wahrheitswert 1) 201 ist teilbar durch 3 3 201 wahre Aussage (w.a.) 2)
Suche nach einem solchen Kreis. Endlichkeitstest. Vereinigung und Durchschnitt. Abschlusseigenschaften
 Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Mengenlehre und vollständige Induktion
 Fachschaft MathPhys Heidelberg Mengenlehre und vollständige Induktion Vladislav Olkhovskiy Vorkurs 018 Inhaltsverzeichnis 1 Motivation 1 Mengen.1 Grundbegriffe.................................. Kostruktionen
Fachschaft MathPhys Heidelberg Mengenlehre und vollständige Induktion Vladislav Olkhovskiy Vorkurs 018 Inhaltsverzeichnis 1 Motivation 1 Mengen.1 Grundbegriffe.................................. Kostruktionen
Im gesamten Kapitel sei Ω eine nichtleere Menge. Wir bezeichnen die Potenzmenge
 1 Mengensysteme Ein Mengensystem ist eine Familie von Teilmengen einer Grundmenge und damit eine Teilmenge der Potenzmenge der Grundmenge. In diesem Kapitel untersuchen wir Mengensysteme, die unter bestimmten
1 Mengensysteme Ein Mengensystem ist eine Familie von Teilmengen einer Grundmenge und damit eine Teilmenge der Potenzmenge der Grundmenge. In diesem Kapitel untersuchen wir Mengensysteme, die unter bestimmten
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
 Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Homomorphismen. Defnition: Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen:
 Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Kapitel 1: Endliche Automaten Gliederung 1. Endliche Automaten
 Gliederung 0. Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechenbarkeitstheorie 4. Komplexitätstheorie.. Grundlagen.2. Minimierungsalgorithmus.3. /3, S. Gibt es Sprachen, die nicht Automatensprachen
Gliederung 0. Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechenbarkeitstheorie 4. Komplexitätstheorie.. Grundlagen.2. Minimierungsalgorithmus.3. /3, S. Gibt es Sprachen, die nicht Automatensprachen
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Lösungsvorschläge Blatt 4
 Theoretische Informatik Departement Informatik Prof. Dr. Juraj Hromkovič http://www.ita.inf.ethz.ch/theoinf16 Lösungsvorschläge Blatt 4 Zürich, 21. Oktober 2016 Lösung zu Aufgabe 10 (a) Wir zeigen mit
Theoretische Informatik Departement Informatik Prof. Dr. Juraj Hromkovič http://www.ita.inf.ethz.ch/theoinf16 Lösungsvorschläge Blatt 4 Zürich, 21. Oktober 2016 Lösung zu Aufgabe 10 (a) Wir zeigen mit
Theoretische Grundlagen der Informatik. Vorlesung am 17. Januar INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik 0 17.01.2019 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Evaluation Ergebnisse
Theoretische Grundlagen der Informatik 0 17.01.2019 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Evaluation Ergebnisse
Kurz-Skript zur Theoretischen Informatik I
 Kurz-Skript zur Theoretischen Informatik I Inhaltsverzeichnis 1 Grundlagen 2 2 Reguläre Ausdrücke 4 3 Endliche Automaten 5 3.1 Vollständige endliche Automaten................................... 6 3.2 ε
Kurz-Skript zur Theoretischen Informatik I Inhaltsverzeichnis 1 Grundlagen 2 2 Reguläre Ausdrücke 4 3 Endliche Automaten 5 3.1 Vollständige endliche Automaten................................... 6 3.2 ε
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Beweis des Pumping Lemmas
 Beweis des Pumping Lemmas Die Sprache L sei eine Typ-2 Sprache, d.h. es gibt eine Typ-2 Grammatik G =(V,, P, S) in CNF, so dass L = L(G) gilt. Wir fixieren eine solche Grammatik G und wählen n = 2 V. Nun
Beweis des Pumping Lemmas Die Sprache L sei eine Typ-2 Sprache, d.h. es gibt eine Typ-2 Grammatik G =(V,, P, S) in CNF, so dass L = L(G) gilt. Wir fixieren eine solche Grammatik G und wählen n = 2 V. Nun
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 19.
 Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Professur für Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Professur für Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Vorlesung Theoretische Informatik (Info III)
 1 Vorlesung Theoretische Informatik (Info III) Prof. Dr. Dorothea Wagner Dipl.-Math. Martin Holzer 22. Januar 2008 Einleitung Motivation 2 Thema heute Kontextfreie Grammatiken: Lemma von Ogden Eigenschaften
1 Vorlesung Theoretische Informatik (Info III) Prof. Dr. Dorothea Wagner Dipl.-Math. Martin Holzer 22. Januar 2008 Einleitung Motivation 2 Thema heute Kontextfreie Grammatiken: Lemma von Ogden Eigenschaften
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 30.04.2013 Grenzen regulärer Sprachen Wie beweist man, dass eine Sprache nicht regulär
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 30.04.2013 Grenzen regulärer Sprachen Wie beweist man, dass eine Sprache nicht regulär
2. Übungsblatt 6.0 VU Theoretische Informatik und Logik
 2. Übungsblatt 6.0 VU Theoretische Informatik und Logik 25. September 2013 Aufgabe 1 Geben Sie jeweils eine kontextfreie Grammatik an, welche die folgenden Sprachen erzeugt, sowie einen Ableitungsbaum
2. Übungsblatt 6.0 VU Theoretische Informatik und Logik 25. September 2013 Aufgabe 1 Geben Sie jeweils eine kontextfreie Grammatik an, welche die folgenden Sprachen erzeugt, sowie einen Ableitungsbaum
1 Mengen und Aussagen
 Mathematik für Physiker I, WS 010/011 Montag 01.11 $Id: mengen.tex,v 1.4 010/11/01 14:19:48 hk Exp $ $Id: beweise.tex,v 1.3 010/11/05 06:40:11 hk Exp $ 1 Mengen und Aussagen Wir haben jetzt Allaussagen
Mathematik für Physiker I, WS 010/011 Montag 01.11 $Id: mengen.tex,v 1.4 010/11/01 14:19:48 hk Exp $ $Id: beweise.tex,v 1.3 010/11/05 06:40:11 hk Exp $ 1 Mengen und Aussagen Wir haben jetzt Allaussagen
Satz (Abschluß unter der Stern-Operation)
 Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Beispiel Produktautomat
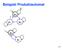 Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M 2. p 1
 Beispiel Produktautomat p Vereinfachte Konstruktion f. NFAs Seien M,M 2 NFAs f. die Sprachen L und L 2. Konstruktion eines NFAs für L L 2 : Erzeuge Kopien von M und M 2. p q q p 2 Erzeuge neuen Startzustand
Beispiel Produktautomat p Vereinfachte Konstruktion f. NFAs Seien M,M 2 NFAs f. die Sprachen L und L 2. Konstruktion eines NFAs für L L 2 : Erzeuge Kopien von M und M 2. p q q p 2 Erzeuge neuen Startzustand
5.2 Endliche Automaten
 114 5.2 Endliche Automaten Endliche Automaten sind Turingmaschinen, die nur endlichen Speicher besitzen. Wie wir bereits im Zusammenhang mit Turingmaschinen gesehen haben, kann endlicher Speicher durch
114 5.2 Endliche Automaten Endliche Automaten sind Turingmaschinen, die nur endlichen Speicher besitzen. Wie wir bereits im Zusammenhang mit Turingmaschinen gesehen haben, kann endlicher Speicher durch
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 19 Algebraisch abgeschlossene Körper Wir haben zuletzt erwähnt, dass ein lineares Polynom X a über einem Körper stets irreduzibel
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 19 Algebraisch abgeschlossene Körper Wir haben zuletzt erwähnt, dass ein lineares Polynom X a über einem Körper stets irreduzibel
Streichholzgeschichten von Dieter Ortner.
 Streichholzgeschichten von Dieter Ortner. 1. Streichholzgeschichte Nr. 1 Aus vier n kann man ein Quadrat bilden. Mit diesem Verfahren sollst du nun selber herausfinden, wie viele es braucht, wenn das grosse
Streichholzgeschichten von Dieter Ortner. 1. Streichholzgeschichte Nr. 1 Aus vier n kann man ein Quadrat bilden. Mit diesem Verfahren sollst du nun selber herausfinden, wie viele es braucht, wenn das grosse
Normalformen boolescher Funktionen
 Normalformen boolescher Funktionen Jeder boolesche Ausdruck kann durch (äquivalente) Umformungen in gewisse Normalformen gebracht werden! Disjunktive Normalform (DNF) und Vollkonjunktion: Eine Vollkonjunktion
Normalformen boolescher Funktionen Jeder boolesche Ausdruck kann durch (äquivalente) Umformungen in gewisse Normalformen gebracht werden! Disjunktive Normalform (DNF) und Vollkonjunktion: Eine Vollkonjunktion
zu der begründeten Vermutung, dass dies auch bei einer beliebig größeren Anzahl von "Bausteinen"
 Unterrichtseinheit 1: Quadratverdopplung In dieser Unterrichtseinheit sollen die Schülerinnen und Schüler erkennen und beweisen, dass sich die Zahl, deren Quadrat 2 ergibt, nicht als Bruch darstellen lässt,
Unterrichtseinheit 1: Quadratverdopplung In dieser Unterrichtseinheit sollen die Schülerinnen und Schüler erkennen und beweisen, dass sich die Zahl, deren Quadrat 2 ergibt, nicht als Bruch darstellen lässt,
Zufallsvariablen: Die allgemeine Definition
 KAPITEL 8 Zufallsvariablen: Die allgemeine Definition 8.1. Zufallsvariablen Bis zu diesem Zeitpunkt haben wir ausschließlich Zufallsvariablen mit endlich oder abzählbar vielen Werten (also diskrete Zufallsvariablen)
KAPITEL 8 Zufallsvariablen: Die allgemeine Definition 8.1. Zufallsvariablen Bis zu diesem Zeitpunkt haben wir ausschließlich Zufallsvariablen mit endlich oder abzählbar vielen Werten (also diskrete Zufallsvariablen)
3. Selbstbehalt und Selbstbeteiligung
 3. Selbstbehalt und Selbstbeteiligung Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie (FS 11) Selbstbehalt und Selbstbeteiligung 1 / 16 1. Modellrahmen 1.1
3. Selbstbehalt und Selbstbeteiligung Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie (FS 11) Selbstbehalt und Selbstbeteiligung 1 / 16 1. Modellrahmen 1.1
Induktive Definitionen
 Priv.-Doz. Dr.rer.nat.habil. Karl-Heinz Niggl Technische Universität Ilmenau Fakultät IA, Institut für Theoretische Informatik Fachgebiet Komplexitätstheorie und Effiziente Algorithmen J Induktive Definitionen
Priv.-Doz. Dr.rer.nat.habil. Karl-Heinz Niggl Technische Universität Ilmenau Fakultät IA, Institut für Theoretische Informatik Fachgebiet Komplexitätstheorie und Effiziente Algorithmen J Induktive Definitionen
2. Vorlesung. Die Theorie der schwarz-weissen Ketten.
 2. Vorlesung. Die Theorie der schwarz-weissen Ketten. Die Theorie der schwarzen Steinchen haben wir jetzt halbwegs vertanden. Statt mit schwarzen Steinen wie die Griechen, wollen wir jetzt mit schwarzen
2. Vorlesung. Die Theorie der schwarz-weissen Ketten. Die Theorie der schwarzen Steinchen haben wir jetzt halbwegs vertanden. Statt mit schwarzen Steinen wie die Griechen, wollen wir jetzt mit schwarzen
Stetige Funktionen. Definition. Seien (X, d) und (Y, ϱ) metrische Räume und f : X Y eine Abbildung. D(f) X sei der Definitionsbereich von f.
 Stetige Funktionen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume), spielen eine zentrale Rolle in der Mathematik. In der Analysis sind Abbildungen
Stetige Funktionen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume), spielen eine zentrale Rolle in der Mathematik. In der Analysis sind Abbildungen
Reguläre Sprachen und endliche Automaten
 Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
