I.5. Kontextfreie Sprachen
|
|
|
- Christel Busch
- vor 9 Jahren
- Abrufe
Transkript
1 I.5. Kontextfreie prachen Zieht man in Betracht, dass BNF-yteme gerade so beschaffen sind, dass auf der linken eite immer genau ein Nichtterminal steht, so sind das also gerade die Ableitungsregeln einer kontextfreien Grammatik. Kontextfreie Grammatiken sind also für die truktur von Programmiersprachen von prinzipieller Bedeutung. (Ein mittels BNF-Regeln abgeleitetes Terminalwort ist ein Programm in der jeweiligen Programmiersprache - mit gewissen Einschränkungen (siehe später). Ableitungsbäume Ableitungen in kontextfreien prachen werden häufig Ableitungsbäume zugeordnet: ei G = (N, T,, P) eine kontextfreie Grammatik. Jeder Ableitung w 1 w 2... w n wird ein Ableitungsbaum mit der Wurzel wie folgt zugeordnet: (induktive Definition über n) Für n = 0 besteht der Baum nur aus dem Knoten Ist B n-1 der Ableitungsbaum von w 1 w 2... w n-1 und entsteht w n aus w n-1 durch Anwendung der Regel A w = x 1... x l, x i N T, d.h. w n-1 = w A w, w n = w w w, so erhält man den Ableitungsbaum B n von w 1... w n aus B n-1, indem man den Knoten A in B n-1 ersetzt durch den Baum A x 1 x 2 x 3 x l Beispiel: ei G = ({}, {a},, { a, }) Der Ableitungsbaum für die Ableitung a aa ist a a
2 Offenbar können verschiedene Ableitungen den gleichen Ableitungsbaum besitzen; z.b. hat die Ableitung a aa den gleichen Ableitungsbaum. Die Zuordnung von Ableitungen zu den Ableitungsbäumen wird eineindeutig, wenn man nur Linksableitungen zulässt: Definition: Die Ableitung w 1 w 2... w n heißt Linksableitung, wenn bei jedem Ableitungsschritt das am weitesten links stehende Nichtterminal vermöge einer Regel aus P ersetzt wird. Es ist aber möglich, dass es für ein Wort w L(G) verschiedene Linksableitungen gibt: Definition: Die (kontextfreie) Grammatik G heißt mehrdeutig, wenn w L(G), so dass w 2 verschiedene Linksableitungen besitzt. Anderenfalls heißt G eindeutig. Die kontextfreie prache L heißt eindeutig, wenn es eine eindeutige kontextfreie Grammatik G mit L = L(G) gibt. Anderenfalls heißt L mehrdeutig. Beispiel: Die Grammatik G = ({}, {a},, { a, }) ist mehrdeutig, denn es gibt für aaa die Linksableitungen a a aa aaa a aa aaa mit den Ableitungsbäumen a a a a a a Es ist L(G) = {a i : i 1}. L(G) ist (natürlich) regulär und wird z.b. von der Grammatik G 1 = ({}, {a},, { a, a}) erzeugt. G 1 ist eindeutig, also auch L(G) = L(G 1 ).
3 Beispiel: für eine mehrdeutige kontextfreie prache: L = {a i b j c k : i = j oder j = k} (o.b.) Dagegen gilt: atz 5.1.: Jede reguläre prache ist eindeutig. ei L regulär. Dann wird (nach Hauptsatz für die regulären prachen) L von einem DA akzeptiert. Im Beweisteil (i) (ii) wird dann gerade eine eindeutige Grammatik G mit L = L(G) konstruiert. Normalformen Es gibt für eine kontextfreie prache L viele verschiedene Grammatiken, die L erzeugen. Für Einsichten in die truktur solcher prachen sind gewisse Normierungen für erzeugende Grammatiken relevant. Hier sei nur eine erwähnt: Definition: Eine kontextfreie Grammatik G = (N, T,, P} ist in Chomsky- Normalform, wenn alle Regeln von der Form X YZ oder X a mit X, Y; Z N, a T sind. atz 5.2.: Zu jeder kontextfreien Grammatik G = (N, T,, P) mit ε L(G) gibt es eine äquivalente kontextfreie Grammatik G in Chomsky-Normalform. (o.b.) Zum Pumping-Lemma für reguläre prachen gibt es ein Analogon: atz 5.3.: (Pumping-Lemma für kontextfreie prachen) ei L kontextfrei. Dann gibt es eine natürliche Zahl n, so dass für jedes Wort w L mit w n gilt: Es gibt w 1, w 2, w 3, w 4, w 5, mit w = w 1 w 2 w 3 w 4 w 5, w 2 w 3 w 4 n, i i w 2 w 4 ε, und w w w w w L i Das P.-Lemma erlaubt häufig den Nachweis, dass eine prache nicht kontextfrei ist.
4 Beispiel: L={v v : v {0,1} * } Angenommen L wäre kontextfrei. Dann existierte eine Zahl n mit den Eigenschaften des Pumping-Lemmas. ei w = L n n n n Dann ist also w = w 1 w 2 w 3 w 4 w 5 mit w 2 w 3 w 4 n. Wenn w 2 w 3 w 4 in der 1.Hälfte von w liegt, so endet im für i = 0 erzeugten Wort die 1. Hälfte mit 1, die 2. mit 0 (falls überhaupt: ein Wort gerader Länge entsteht). Wenn w 2 w 3 w 4 in der 2.Hälfte von w liegt, so beginnt im für i = 0 erzeugten Wort die 1. Hälfte mit 1, die 2. Hälfte mit 0. Wenn w 2 w 3 w 4 die Mitte überlappt, so beginnt im für i = 0 erzeugten Wort die 1. Hälfte mit n Einsen, die 2. nicht. Bemerkung: Dieses Beispiel dokumentiert die mangelnde Kopierfähigkeit kontextfreier Grammatiken. Eine Konsequenz ist, dass die meisten Programmiersprachen nicht kontextfrei sind. Z.B. gibt es in Pascal die Bedingung, dass Anzahl und Typen der formalen Parameter und der aktuellen Parameter übereinstimmen müssen. Diese Bedingung lässt sich - unserem obigen Beispiel entsprechend - nicht durch BNF-Regeln formulieren! Bei Programmiersprachen erzeugt man durch kontextfreie Grammatiken (BNF- Regeln) eine echte Obermenge der zulässigen Programme, aus denen die Programme durch verbale Einschränkungen ausgesondert werden. Abschlusseigenschaften atz 5.4.: Kontextfreie prachen sind abgeschlossen gegenüber den regulären Operationen Vereinigung, Verkettung und Iteration. eien L 1 = L(G 1 ) und L 2 = L(G 2 ) erzeugt von den kontextfreien Grammatiken G 1 = (N 1, T 1, 1, P 1 ), G 2 = (N 2, T 2, 2, P 2 ) und o.b.d.a. sei N 1 N 2 =. eien 3, 4, 5 neue Nichtterminale. G 3 := (N 1 N 2 { 3 }, T 1 T 2, 3, P 3 ) mit P 3 = P 1 P 2 { 3 1, 3 2 }. Offenbar ist L(G 3 ) = L 1 L 2.
5 G 4 := (N 1 N 2 { 4 }, T 1 T 2, 4, P 4 ) mit P 4 = P 1 P 2 { }. Offenbar ist L(G 4 ) = L 1 L 2. G 5 := (N 1 { 5 }, T 1, 5, P 5 ) mit P 5 = P 1 { 5 ε, }. Offenbar ist L(G 5 ) = L 1 *. atz 5.5.: Die kontextfreien prachen sind nicht abgeschlossen gegenüber Durchschnitten. L 2 := {a i b i c j : i 1, j 1} L 3 := {a i b j c j : i 1, j 1} L 2 wird erzeugt von Grammatik mit den Produktionen AB, A aab ab, B cb c (Übung!!) L 3 wird erzeugt von Grammatik mit den Produktionen CD, C ac a, D bdc bc (Übung!!) Aber L 2 L 3 = { a i b i c i : i 1} ist nicht kontextfrei (Übung!)
Grammatiken. Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen
 Grammatiken Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen Grammatiken eignen sich besonders zur Modellierung beliebig tief geschachtelter,
Grammatiken Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen Grammatiken eignen sich besonders zur Modellierung beliebig tief geschachtelter,
Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen
 Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen (Kontextsensitive) Sprachen L 2 Menge aller kontextfreien
Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen (Kontextsensitive) Sprachen L 2 Menge aller kontextfreien
Ein Fragment von Pascal
 Ein Fragment von Pascal Wir beschreiben einen (allerdings sehr kleinen) Ausschnitt von Pascal durch eine kontextfreie Grammatik. Wir benutzen das Alphabet Σ = {a,..., z, ;, :=, begin, end, while, do} und
Ein Fragment von Pascal Wir beschreiben einen (allerdings sehr kleinen) Ausschnitt von Pascal durch eine kontextfreie Grammatik. Wir benutzen das Alphabet Σ = {a,..., z, ;, :=, begin, end, while, do} und
Umformung NTM DTM. Charakterisierung rek. aufz. Spr. Chomsky-3-Grammatiken (T5.3) Chomsky-0-Grammatik Rek. Aufz.
 Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
F2 Zusammenfassung Letzte Tips zur Klausur
 F2 Zusammenfassung Letzte Tips zur Klausur Berndt Farwer FB Informatik, Uni HH F2-ommersemester 2001-(10.6.) p.1/15 Funktionen vs. Relationen Funktionen sind eindeutig, Relationen brauchen nicht eindeutig
F2 Zusammenfassung Letzte Tips zur Klausur Berndt Farwer FB Informatik, Uni HH F2-ommersemester 2001-(10.6.) p.1/15 Funktionen vs. Relationen Funktionen sind eindeutig, Relationen brauchen nicht eindeutig
Übungsblatt 7. Vorlesung Theoretische Grundlagen der Informatik im WS 16/17
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Normalformen für kontextfreie Grammatiken. Noam CHOMSKY, Sheila GREIBACH. Bäume. Ableitungen in kontextfreien Grammatiken. Grammatik G = (N,T,P,S)
 Noam CHOMSKY, Sheila GREIBACH Normalformen für kontextfreie Grammatiken Noam CHOMSKY (*1928 ) Sheila GREIBACH (*1939) Grammatik G = (N,T,P,S) GREIBACH Normalform: A aw, w N* Erweiterte GREIBACH Normalform:
Noam CHOMSKY, Sheila GREIBACH Normalformen für kontextfreie Grammatiken Noam CHOMSKY (*1928 ) Sheila GREIBACH (*1939) Grammatik G = (N,T,P,S) GREIBACH Normalform: A aw, w N* Erweiterte GREIBACH Normalform:
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Kontextfreie Sprachen
 Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Automatentheorie und formale Sprachen
 Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Klammersprache Definiere
 Klammersprache w=w 1...w n {(,)}* heißt korrekt geklammert, falls die Anzahl ( ist gleich der Anzahl ). in jedem Anfangsstück w 1,...,w i (i n) ist die Anzahl ( nicht kleiner als die Anzahl ). Definiere
Klammersprache w=w 1...w n {(,)}* heißt korrekt geklammert, falls die Anzahl ( ist gleich der Anzahl ). in jedem Anfangsstück w 1,...,w i (i n) ist die Anzahl ( nicht kleiner als die Anzahl ). Definiere
Informatik III - WS07/08
 Informatik III - WS07/08 Kapitel 5 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner [email protected] Kapitel 5 : Grammatiken und die Chomsky-Hierarchie Informatik III - WS07/08 Kapitel 5 2 Definition
Informatik III - WS07/08 Kapitel 5 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner [email protected] Kapitel 5 : Grammatiken und die Chomsky-Hierarchie Informatik III - WS07/08 Kapitel 5 2 Definition
Theoretische Informatik und Logik Übungsblatt 2 (2017S) Lösung
 Theoretische Informatik und Logik Übungsblatt 2 (2017) en Aufgabe 2.1 Geben ie jeweils eine kontextfreie Grammatik an, welche die folgenden prachen erzeugt, sowie eine Linksableitung und einen Ableitungsbaum
Theoretische Informatik und Logik Übungsblatt 2 (2017) en Aufgabe 2.1 Geben ie jeweils eine kontextfreie Grammatik an, welche die folgenden prachen erzeugt, sowie eine Linksableitung und einen Ableitungsbaum
Übungsblatt 7. Vorlesung Theoretische Grundlagen der Informatik im WS 16/17
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Kontextfreie Sprachen
 Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Theoretische Grundlagen der Informatik. Vorlesung am 8. Januar INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik 0 08.01.2019 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Letzte Vorlesung Eine
Theoretische Grundlagen der Informatik 0 08.01.2019 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Letzte Vorlesung Eine
Kontextfreie (Typ-2) Sprachen
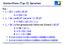 Kontextfreie (Typ-2) prachen Bsp.: L 1 = { n 1 n n>} с {,1}* 1 1 L 2 = {w wє{,1}* und w=w rev } с {,1}* 11 1 ε L 3 = {w w hat genausoviele Nullen wie Einsen} с {,1}* B 1 ε 1 B 1 1 BB 1 11 11 11 11B 111
Kontextfreie (Typ-2) prachen Bsp.: L 1 = { n 1 n n>} с {,1}* 1 1 L 2 = {w wє{,1}* und w=w rev } с {,1}* 11 1 ε L 3 = {w w hat genausoviele Nullen wie Einsen} с {,1}* B 1 ε 1 B 1 1 BB 1 11 11 11 11B 111
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 14.05.2013 Analog zu Linksableitungen definiert man Definition 2.45 Ein Ableitungsschritt
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 14.05.2013 Analog zu Linksableitungen definiert man Definition 2.45 Ein Ableitungsschritt
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (I) 3.06.2015 Viorica Sofronie-Stokkermans e-mail: [email protected] 1 Organisatorisches 1. Teilklausur: Mittwoch,
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (I) 3.06.2015 Viorica Sofronie-Stokkermans e-mail: [email protected] 1 Organisatorisches 1. Teilklausur: Mittwoch,
Automaten und formale Sprachen Klausurvorbereitung
 Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Theoretische Informatik
 Theoretische Informatik Prof. Meer, Dr. Gengler Aufgabenblatt 7 Besprechung in KW 48 / Abgabe in KW 49 Heften Sie unbedingt alle Blätter Ihrer Lösung zusammen und geben Sie oben auf dem ersten Blatt Ihren
Theoretische Informatik Prof. Meer, Dr. Gengler Aufgabenblatt 7 Besprechung in KW 48 / Abgabe in KW 49 Heften Sie unbedingt alle Blätter Ihrer Lösung zusammen und geben Sie oben auf dem ersten Blatt Ihren
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 15.01.2015 INSTITUT FÜR THEORETISCHE 0 KIT 15.01.2015 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 15.01.2015 INSTITUT FÜR THEORETISCHE 0 KIT 15.01.2015 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive
 Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive Grammatik G mit L(G) = L(G ). Beweis im Beispiel (2.): G = (V,Σ, P, S) : P = {S asbc, S abc, CB BC, ab ab, bb bb, bc bc, cc cc}. (i) G
Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive Grammatik G mit L(G) = L(G ). Beweis im Beispiel (2.): G = (V,Σ, P, S) : P = {S asbc, S abc, CB BC, ab ab, bb bb, bc bc, cc cc}. (i) G
Kapitel 2: Formale Sprachen Gliederung
 Gliederung 0. Motivation und Einordnung 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. 2/5, Folie 1 2017 Prof.
Gliederung 0. Motivation und Einordnung 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. 2/5, Folie 1 2017 Prof.
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Kontextfreie Sprachen und Pushdown-Automaten Dozentin: Wiebke Petersen WS 2004/2005 Wiebke Petersen Formale Komplexität natürlicher Sprachen WS 03/04 Wiederholung c
Einführung in die Computerlinguistik Kontextfreie Sprachen und Pushdown-Automaten Dozentin: Wiebke Petersen WS 2004/2005 Wiebke Petersen Formale Komplexität natürlicher Sprachen WS 03/04 Wiederholung c
Schnitt- und Äquivalenzproblem
 Schnitt- und Äquivalenzproblem Das Schnittproblem besteht in der Frage, ob der Schnitt zweier gegebener regulärer Sprachen L 1 und L 2 leer ist. Dabei können die Sprachen durch DEAs oder Typ-3 Grammatiken,
Schnitt- und Äquivalenzproblem Das Schnittproblem besteht in der Frage, ob der Schnitt zweier gegebener regulärer Sprachen L 1 und L 2 leer ist. Dabei können die Sprachen durch DEAs oder Typ-3 Grammatiken,
Musterlösung Informatik-III-Nachklausur
 Musterlösung Informatik-III-Nachklausur Aufgabe 1 (2+2+4+4 Punkte) (a) L = (0 1) 0(0 1) 11(0 1) 0(0 1) (b) Der Automat ist durch folgendes Übergangsdiagramm gegeben: 0, 1 0, 1 0, 1 0, 1 0 s q 1 1 0 0 q
Musterlösung Informatik-III-Nachklausur Aufgabe 1 (2+2+4+4 Punkte) (a) L = (0 1) 0(0 1) 11(0 1) 0(0 1) (b) Der Automat ist durch folgendes Übergangsdiagramm gegeben: 0, 1 0, 1 0, 1 0, 1 0 s q 1 1 0 0 q
Beweisidee: 1 Verwende den Keller zur Simulation der Grammatik. Leite ein Wort. 2 Problem: der Keller darf nicht beliebig verwendet werden, man kann
 Automaten und Formale prachen alias Theoretische Informatik ommersemester 2011 Dr. ander Bruggink Übungsleitung: Jan tückrath Wir beschäftigen uns ab jetzt einige Wochen mit kontextfreien prachen: Kontextfreie
Automaten und Formale prachen alias Theoretische Informatik ommersemester 2011 Dr. ander Bruggink Übungsleitung: Jan tückrath Wir beschäftigen uns ab jetzt einige Wochen mit kontextfreien prachen: Kontextfreie
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie prachen (VI) 25.06.2015 Viorica ofronie-tokkermans e-mail: [email protected] 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie prachen (VI) 25.06.2015 Viorica ofronie-tokkermans e-mail: [email protected] 1 Übersicht 1. Motivation 2. Terminologie
Ogden s Lemma: Der Beweis (1/5)
 Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Einführung in die theoretische Informatik Sommersemester 2017 Übungsblatt Lösungsskizze 7
 Prof. J. Esparza Technische Universität München S. Sickert, J. Krämer KEINE ABGABE Einführung in die theoretische Informatik Sommersemester 2017 Übungsblatt 7 Übungsblatt Wir unterscheiden zwischen Übungs-
Prof. J. Esparza Technische Universität München S. Sickert, J. Krämer KEINE ABGABE Einführung in die theoretische Informatik Sommersemester 2017 Übungsblatt 7 Übungsblatt Wir unterscheiden zwischen Übungs-
6 Kontextfreie Grammatiken
 6 Kontextfreie Grammatiken Reguläre Grammatiken und damit auch reguläre Ausdrücke bzw. endliche Automaten haben bezüglich ihres Sprachumfangs Grenzen. Diese Grenzen resultieren aus den inschränkungen,
6 Kontextfreie Grammatiken Reguläre Grammatiken und damit auch reguläre Ausdrücke bzw. endliche Automaten haben bezüglich ihres Sprachumfangs Grenzen. Diese Grenzen resultieren aus den inschränkungen,
1. Übungsblatt 6.0 VU Theoretische Informatik und Logik
 . Übungsblatt 6. VU Theoretische Informatik und Logik 25. September 23 Aufgabe Sind folgende Aussagen korrekt? Begründen Sie jeweils Ihre Antwort. a) Für jede Sprache L gilt: L < L (wobei A die Anzahl
. Übungsblatt 6. VU Theoretische Informatik und Logik 25. September 23 Aufgabe Sind folgende Aussagen korrekt? Begründen Sie jeweils Ihre Antwort. a) Für jede Sprache L gilt: L < L (wobei A die Anzahl
Definition 4 (Operationen auf Sprachen) Beispiel 5. Seien A, B Σ zwei (formale) Sprachen. Konkatenation: AB = {uv ; u A, v B} A + = n 1 An
 Definition 4 (Operationen auf Sprachen) Seien A, B Σ zwei (formale) Sprachen. Konkatenation: AB = {uv ; u A, v B} A 0 = {ɛ}, A n+1 = AA n A = n 0 An A + = n 1 An Beispiel 5 {ab, b}{a, bb} = {aba, abbb,
Definition 4 (Operationen auf Sprachen) Seien A, B Σ zwei (formale) Sprachen. Konkatenation: AB = {uv ; u A, v B} A 0 = {ɛ}, A n+1 = AA n A = n 0 An A + = n 1 An Beispiel 5 {ab, b}{a, bb} = {aba, abbb,
Kontextfreie Sprachen. Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Kontextfreie Sprachen
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Wortproblem: der CYK-Algorithmus Pumping Lemma für kontextfreie Sprachen
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Wortproblem: der CYK-Algorithmus Pumping Lemma für kontextfreie Sprachen
q 0 q gdw. nicht (q A) (q A) q i+1 q gdw. q i q oder ( a Σ) δ(q, a) i δ(q, a) L = {a n b n : n N} für a, b Σ, a b
 Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
Mehrdeutige Grammatiken
 Mehrdeutige Grammatiken Wir haben gesehen, dass es auch mehr als eine Linksableitung, d.h. mehr als einen Syntaxbaum geben kann, um das selbe Terminalwort zu erzeugen. Eine Grammatik, die für mindestens
Mehrdeutige Grammatiken Wir haben gesehen, dass es auch mehr als eine Linksableitung, d.h. mehr als einen Syntaxbaum geben kann, um das selbe Terminalwort zu erzeugen. Eine Grammatik, die für mindestens
2. Übungsblatt 6.0 VU Theoretische Informatik und Logik
 2. Übungsblatt 6.0 VU Theoretische Informatik und Logik 25. September 2013 Aufgabe 1 Geben Sie jeweils eine kontextfreie Grammatik an, welche die folgenden Sprachen erzeugt, sowie einen Ableitungsbaum
2. Übungsblatt 6.0 VU Theoretische Informatik und Logik 25. September 2013 Aufgabe 1 Geben Sie jeweils eine kontextfreie Grammatik an, welche die folgenden Sprachen erzeugt, sowie einen Ableitungsbaum
Theorie der Informatik. Theorie der Informatik. 6.1 Einführung. 6.2 Alphabete und formale Sprachen. 6.3 Grammatiken. 6.4 Chomsky-Hierarchie
 Theorie der Informatik 17. März 2014 6. Formale Sprachen und Grammatiken Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 6.1 Einführung
Theorie der Informatik 17. März 2014 6. Formale Sprachen und Grammatiken Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 6.1 Einführung
Formale Grundlagen der Informatik
 Formale Grundlagen der Informatik / 2015 1 Reguläre Ausdrücke Kommen in der Praxis immer dann vor, wenn standardisierte Eingaben erforderlich sind: Telefonnummern: +Land (0) Ort Anschluß Dateinamen: (A-Z,
Formale Grundlagen der Informatik / 2015 1 Reguläre Ausdrücke Kommen in der Praxis immer dann vor, wenn standardisierte Eingaben erforderlich sind: Telefonnummern: +Land (0) Ort Anschluß Dateinamen: (A-Z,
Automaten und formale Sprachen Notizen zu den Folien
 Automaten und formale prachen Notizen zu den Folien 10 Kontextfreie Grammatiken Beispiele für kontextfreien Grammatiken ei Σ = {a, b}. Beispiel 1 (Folie 233, oben) Geben ie eine kontextfreie Grammatik
Automaten und formale prachen Notizen zu den Folien 10 Kontextfreie Grammatiken Beispiele für kontextfreien Grammatiken ei Σ = {a, b}. Beispiel 1 (Folie 233, oben) Geben ie eine kontextfreie Grammatik
(Prüfungs-)Aufgaben zu formale Sprachen
 (Prüfungs-)Aufgaben zu formale Sprachen (siehe auch bei den Aufgaben zu endlichen Automaten) 1) Eine Grammatik G sei gegeben durch: N = {S, A}, T = {a, b, c, d}, P = { (S, Sa), (S, ba), (A, ba), (A, c),
(Prüfungs-)Aufgaben zu formale Sprachen (siehe auch bei den Aufgaben zu endlichen Automaten) 1) Eine Grammatik G sei gegeben durch: N = {S, A}, T = {a, b, c, d}, P = { (S, Sa), (S, ba), (A, ba), (A, c),
kontextfreie Grammatiken Theoretische Informatik kontextfreie Grammatiken kontextfreie Grammatiken Rainer Schrader 14. Juli 2009 Gliederung
 Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Automaten und formale Sprachen Notizen zu den Folien
 Automaten und formale prachen Notizen zu den Folien 10 Kontextfreie Grammatiken Beispiele für kontextfreien Grammatiken ei Σ = {a, b}. Beispiel 1 (Folie 211, oben) Geben ie eine kontextfreie Grammatik
Automaten und formale prachen Notizen zu den Folien 10 Kontextfreie Grammatiken Beispiele für kontextfreien Grammatiken ei Σ = {a, b}. Beispiel 1 (Folie 211, oben) Geben ie eine kontextfreie Grammatik
Grammatik Prüfung möglich, ob eine Zeichenfolge zur Sprache gehört oder nicht
 Zusammenhang: Formale Sprache Grammatik Formale Sprache kann durch Grammatik beschrieben werden. Zur Sprache L = L(G) gehören nur diejenigen Kombinationen der Zeichen des Eingabealphabets, die durch die
Zusammenhang: Formale Sprache Grammatik Formale Sprache kann durch Grammatik beschrieben werden. Zur Sprache L = L(G) gehören nur diejenigen Kombinationen der Zeichen des Eingabealphabets, die durch die
Kapitel: Die Chomsky Hierarchie. Die Chomsky Hierarchie 1 / 14
 Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Kapitel IV Formale Sprachen und Grammatiken
 Kapitel IV Formale Sprachen und Grammatiken 1. Begriffe und Notationen Sei Σ ein (endliches) Alphabet. Dann Definition 42 1 ist Σ das Monoid über Σ, d.h. die Menge aller endlichen Wörter über Σ; 2 ist
Kapitel IV Formale Sprachen und Grammatiken 1. Begriffe und Notationen Sei Σ ein (endliches) Alphabet. Dann Definition 42 1 ist Σ das Monoid über Σ, d.h. die Menge aller endlichen Wörter über Σ; 2 ist
Theoretische Informatik I
 Theoretische Informatik I Rückblick Theoretische Informatik I 1. Mathematische Methoden 2. Reguläre Sprachen 3. Kontextfreie Sprachen Themen der Theoretischen Informatik I & II Mathematische Methodik in
Theoretische Informatik I Rückblick Theoretische Informatik I 1. Mathematische Methoden 2. Reguläre Sprachen 3. Kontextfreie Sprachen Themen der Theoretischen Informatik I & II Mathematische Methodik in
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen 19
 Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden kann.
 Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Chomsky-Grammatiken 16. Chomsky-Grammatiken
 Chomsky-Grammatiken 16 Chomsky-Grammatiken Ursprünglich von Chomsky in den 1950er Jahren eingeführt zur Beschreibung natürlicher Sprachen. Enge Verwandschaft zu Automaten Grundlage wichtiger Softwarekomponenten
Chomsky-Grammatiken 16 Chomsky-Grammatiken Ursprünglich von Chomsky in den 1950er Jahren eingeführt zur Beschreibung natürlicher Sprachen. Enge Verwandschaft zu Automaten Grundlage wichtiger Softwarekomponenten
Einführung in die Computerlinguistik Formale Grammatiken rechtslineare und kontextfreie Grammatiken Kellerautomaten
 Einführung in die Computerlinguistik Formale Grammatiken rechtslineare und kontextfreie Grammatiken Kellerautomaten Dozentin: Wiebke Petersen 13. Foliensatz Wiebke Petersen Einführung CL 1 Formale Grammatik
Einführung in die Computerlinguistik Formale Grammatiken rechtslineare und kontextfreie Grammatiken Kellerautomaten Dozentin: Wiebke Petersen 13. Foliensatz Wiebke Petersen Einführung CL 1 Formale Grammatik
Einführung in die Theoretische Informatik
 echnische Universität München Fakultät für Informatik Prof. obias Nipkow, Ph.D. ascha öhme, Lars Noschinski ommersemester 2011 Lösungsblatt 5 6. Juni 2011 Einführung in die heoretische Informatik Hinweis:
echnische Universität München Fakultät für Informatik Prof. obias Nipkow, Ph.D. ascha öhme, Lars Noschinski ommersemester 2011 Lösungsblatt 5 6. Juni 2011 Einführung in die heoretische Informatik Hinweis:
Kontextfreie Grammatiken
 Kontextfreie Grammatiken Bisher haben wir verschiedene Automatenmodelle kennengelernt. Diesen Automaten können Wörter vorgelegt werden, die von den Automaten gelesen und dann akzeptiert oder abgelehnt
Kontextfreie Grammatiken Bisher haben wir verschiedene Automatenmodelle kennengelernt. Diesen Automaten können Wörter vorgelegt werden, die von den Automaten gelesen und dann akzeptiert oder abgelehnt
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten 30.04.2015 Viorica Sofronie-Stokkermans Matthias Horbach e-mail: [email protected], [email protected] 1 Bis jetzt 1. Motivation
Grundlagen der Theoretischen Informatik 3. Endliche Automaten 30.04.2015 Viorica Sofronie-Stokkermans Matthias Horbach e-mail: [email protected], [email protected] 1 Bis jetzt 1. Motivation
Formale Grundlagen der Wirtschaftsinformatik
 Formale Grundlagen der Wirtschaftsinformatik Nikolaj Popov Research Institute for Symbolic Computation [email protected] Sprachen und Grammatiken Teil II Sprache Definition: Ein Alphabet Σ ist
Formale Grundlagen der Wirtschaftsinformatik Nikolaj Popov Research Institute for Symbolic Computation [email protected] Sprachen und Grammatiken Teil II Sprache Definition: Ein Alphabet Σ ist
Kontextfreie Grammatiken. Kontextfreie Grammatiken 1 / 45
 Kontextfreie Grammatiken Kontextfreie Grammatiken 1 / 45 Was kann man mit kontextfreien Grammatiken anfangen? Kontextfreie Grammatiken, kurz: werden zur Modellierung von KFGs beliebig tief geschachtelten
Kontextfreie Grammatiken Kontextfreie Grammatiken 1 / 45 Was kann man mit kontextfreien Grammatiken anfangen? Kontextfreie Grammatiken, kurz: werden zur Modellierung von KFGs beliebig tief geschachtelten
Lösung zur Klausur. Grundlagen der Theoretischen Informatik im WiSe 2003/2004
 Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
2.6 Deterministisches Top-Down-Parsen
 48 2.6 Deterministisches Top-Down-Parsen Als nächstes wollen wir uns mit Methoden zur syntaktischen Analyse befassen. Der lexikale canner eines Compilers liest die Eingabe Zeichen für Zeichen und erzeugt
48 2.6 Deterministisches Top-Down-Parsen Als nächstes wollen wir uns mit Methoden zur syntaktischen Analyse befassen. Der lexikale canner eines Compilers liest die Eingabe Zeichen für Zeichen und erzeugt
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (III) 17.06.2015 Viorica Sofronie-Stokkermans e-mail: [email protected] 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (III) 17.06.2015 Viorica Sofronie-Stokkermans e-mail: [email protected] 1 Übersicht 1. Motivation 2. Terminologie
Tutoraufgabe 1 (ɛ-produktionen):
 Prof aa Dr J Giesl Formale Systeme, Automaten, Prozesse SS 2010 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus dem gleichen Tutorium
Prof aa Dr J Giesl Formale Systeme, Automaten, Prozesse SS 2010 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus dem gleichen Tutorium
Grammatiken. Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V. Startsymbol S V. Kurzschreibweise G = (V, Σ, P, S)
 Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Alphabet, formale Sprache
 n Alphabet Alphabet, formale Sprache l nichtleere endliche Menge von Zeichen ( Buchstaben, Symbole) n Wort über einem Alphabet l endliche Folge von Buchstaben, die auch leer sein kann ( ε leere Wort) l
n Alphabet Alphabet, formale Sprache l nichtleere endliche Menge von Zeichen ( Buchstaben, Symbole) n Wort über einem Alphabet l endliche Folge von Buchstaben, die auch leer sein kann ( ε leere Wort) l
Das Halteproblem für Turingmaschinen
 Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Nachklausur zur Vorlesung Informatik 3 mit einigen Anmerkungen zu Lösungen
 Nachklausur zur Vorlesung Informatik 3 mit einigen Anmerkungen zu Lösungen Aufgabe 1 2 3 4 5 6 7 max. Punkte 6 6 7 7 8 8 12 err. Punkte Gesamtpunktzahl: Note: 1 Aufgabe 1 (3+1+1+1 = 6 Punkte) Es seien
Nachklausur zur Vorlesung Informatik 3 mit einigen Anmerkungen zu Lösungen Aufgabe 1 2 3 4 5 6 7 max. Punkte 6 6 7 7 8 8 12 err. Punkte Gesamtpunktzahl: Note: 1 Aufgabe 1 (3+1+1+1 = 6 Punkte) Es seien
Nichtdeterministischer Kellerautomat
 1 Nichtdeterministischer Kellerautomat endlicher Automat mit Zusatzspeicher in Form eines Kellers (Stapel, Stack) mit Speicheroperationen pro Übergang Keller über X: w X mit den Operationen push, head,
1 Nichtdeterministischer Kellerautomat endlicher Automat mit Zusatzspeicher in Form eines Kellers (Stapel, Stack) mit Speicheroperationen pro Übergang Keller über X: w X mit den Operationen push, head,
Übersicht. 3 3 Kontextfreie Sprachen
 Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
Theoretische Informatik Kap 1: Formale Sprachen/Automatentheorie
 Gliederung der Vorlesung. Grundbegriffe. Formale Sprachen/Automatentheorie.. Grammatiken.2..3. Kontext-freie Sprachen 2. Berechnungstheorie 2.. Berechenbarkeitsmodelle 2.2. Die Churchsche These 2.3. Unentscheidbarkeit
Gliederung der Vorlesung. Grundbegriffe. Formale Sprachen/Automatentheorie.. Grammatiken.2..3. Kontext-freie Sprachen 2. Berechnungstheorie 2.. Berechenbarkeitsmodelle 2.2. Die Churchsche These 2.3. Unentscheidbarkeit
Abschnitt 5. Grammatiken
 Abschnitt 5 Sven Büchel Computerlinguistik I: Übung 148 / 163 Definition Formale Grammatik Eine formale Grammatik G ist eine 4-Tupel G =(N,T,P,S) mit einem Alphabet von Nicht-Terminalsymbolen N einem Alphabet
Abschnitt 5 Sven Büchel Computerlinguistik I: Übung 148 / 163 Definition Formale Grammatik Eine formale Grammatik G ist eine 4-Tupel G =(N,T,P,S) mit einem Alphabet von Nicht-Terminalsymbolen N einem Alphabet
DisMod-Repetitorium Tag 4
 DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (II) 11.06.2015 Viorica Sofronie-Stokkermans e-mail: [email protected] 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (II) 11.06.2015 Viorica Sofronie-Stokkermans e-mail: [email protected] 1 Übersicht 1. Motivation 2. Terminologie
Vorlesung Automaten und Formale Sprachen Sommersemester Beispielsprachen. Sprachen
 Vorlesung Automaten und Formale Sprachen Sommersemester 2018 Prof. Barbara König Übungsleitung: Christina Mika-Michalski Wörter Wort Sei Σ ein Alphabet, d.h., eine endliche Menge von Zeichen. Dann bezeichnet
Vorlesung Automaten und Formale Sprachen Sommersemester 2018 Prof. Barbara König Übungsleitung: Christina Mika-Michalski Wörter Wort Sei Σ ein Alphabet, d.h., eine endliche Menge von Zeichen. Dann bezeichnet
2.1 Allgemeines. Was ist eine Sprache? Beispiele:
 Was ist eine Sprache? Beispiele: (a) Deutsch, Japanisch, Latein, Esperanto,...: Natürliche Sprachen (b) Pascal, C, Java, Aussagenlogik,...: Formale Sprachen Wie beschreibt man eine Sprache? (i) Syntax
Was ist eine Sprache? Beispiele: (a) Deutsch, Japanisch, Latein, Esperanto,...: Natürliche Sprachen (b) Pascal, C, Java, Aussagenlogik,...: Formale Sprachen Wie beschreibt man eine Sprache? (i) Syntax
Informales Beispiel. Formale Grundlagen der Informatik 1 Kapitel 6 Eigenschaften kontextfreier Sprachen. Grammatiken. Anmerkungen
 Informales Beispiel Formale Grundlagen der Informatik 1 Kapitel 6 Eigenschaften kontextfreier Sprachen Frank Heitmann [email protected] 22. April 2014 I L IL ID L a b c D 0 1 2 3 4 Eine
Informales Beispiel Formale Grundlagen der Informatik 1 Kapitel 6 Eigenschaften kontextfreier Sprachen Frank Heitmann [email protected] 22. April 2014 I L IL ID L a b c D 0 1 2 3 4 Eine
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation
 Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform 3.7 Greibach-Normalform
Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform 3.7 Greibach-Normalform
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 18.01.2011 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Vorlesung am 18.01.2011 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
