Lineare Algebra und Numerische Mathematik
|
|
|
- Agnes Esser
- vor 9 Jahren
- Abrufe
Transkript
1 Lineare Algebra und Numerische Mathematik Prof. Dr. P. Grohs Seminar for Applied Mathematics, ETH Zürich Vorlesung für D-BAUG Herbstsemester P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
2 Dozent P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
3 Dozent Prof. Dr. Philipp Grohs P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
4 Dozent Prof. Dr. Philipp Grohs Professor für angewandte Mathematik am Seminar für angewandte Mathematik der ETH Zürich seit 2011 Raum: HG G 59.2 P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
5 Dozent Prof. Dr. Philipp Grohs Professor für angewandte Mathematik am Seminar für angewandte Mathematik der ETH Zürich seit 2011 Raum: HG G 59.2 Forschungsinteressen: Approximationstheorie und numerische harmonische Analysis Numerische Methoden für PDEs Geometrie P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
6 Inhalt P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
7 Inhalt Eine Vorlesung über mathematische und numerische Methoden P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
8 Inhalt Eine Vorlesung über mathematische und numerische Methoden Klar: Mathematische und numerische Methoden spielen eine zentrale Rolle in den (modernen) (Ingenieur-)wissenschaften! P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
9 Inhalt Eine Vorlesung über mathematische und numerische Methoden Klar: Mathematische und numerische Methoden spielen eine zentrale Rolle in den (modernen) (Ingenieur-)wissenschaften! Das wird Ihnen (leider erst) im Laufe des Studiums klar werden P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
10 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
11 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) = ein mathematisches Grundlagenfach P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
12 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) = ein mathematisches Grundlagenfach Lineare Gleichungssysteme und Ausgleichsprobleme P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
13 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) = ein mathematisches Grundlagenfach Lineare Gleichungssysteme und Ausgleichsprobleme Vektoren, Matrizen, Unterräume und Basen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
14 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) = ein mathematisches Grundlagenfach Lineare Gleichungssysteme und Ausgleichsprobleme Vektoren, Matrizen, Unterräume und Basen Lineare Abbildungen und Determinanten P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
15 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) = ein mathematisches Grundlagenfach Lineare Gleichungssysteme und Ausgleichsprobleme Vektoren, Matrizen, Unterräume und Basen Lineare Abbildungen und Determinanten Eigenwerte und Eigenräume P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
16 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) = ein mathematisches Grundlagenfach Lineare Gleichungssysteme und Ausgleichsprobleme Vektoren, Matrizen, Unterräume und Basen Lineare Abbildungen und Determinanten Eigenwerte und Eigenräume Numerik: beschäftigt sich als Teilgebiet der Mathematik mit der Konstruktion und Analyse von Algorithmen zur Lösung kontinuierlicher mathematischer Probleme. P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
17 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) = ein mathematisches Grundlagenfach Lineare Gleichungssysteme und Ausgleichsprobleme Vektoren, Matrizen, Unterräume und Basen Lineare Abbildungen und Determinanten Eigenwerte und Eigenräume Numerik: beschäftigt sich als Teilgebiet der Mathematik mit der Konstruktion und Analyse von Algorithmen zur Lösung kontinuierlicher mathematischer Probleme. Rechenaufwand von Algorithmen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
18 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) = ein mathematisches Grundlagenfach Lineare Gleichungssysteme und Ausgleichsprobleme Vektoren, Matrizen, Unterräume und Basen Lineare Abbildungen und Determinanten Eigenwerte und Eigenräume Numerik: beschäftigt sich als Teilgebiet der Mathematik mit der Konstruktion und Analyse von Algorithmen zur Lösung kontinuierlicher mathematischer Probleme. Rechenaufwand von Algorithmen Rundungsfehler P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
19 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) = ein mathematisches Grundlagenfach Lineare Gleichungssysteme und Ausgleichsprobleme Vektoren, Matrizen, Unterräume und Basen Lineare Abbildungen und Determinanten Eigenwerte und Eigenräume Numerik: beschäftigt sich als Teilgebiet der Mathematik mit der Konstruktion und Analyse von Algorithmen zur Lösung kontinuierlicher mathematischer Probleme. Rechenaufwand von Algorithmen Rundungsfehler Dünnbesetze Matrizen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
20 Inhalt Lineare Algebra: is the branch of mathematics concerning vector spaces and linear mappings between such spaces (Wikipedia) = ein mathematisches Grundlagenfach Lineare Gleichungssysteme und Ausgleichsprobleme Vektoren, Matrizen, Unterräume und Basen Lineare Abbildungen und Determinanten Eigenwerte und Eigenräume Numerik: beschäftigt sich als Teilgebiet der Mathematik mit der Konstruktion und Analyse von Algorithmen zur Lösung kontinuierlicher mathematischer Probleme. Rechenaufwand von Algorithmen Rundungsfehler Dünnbesetze Matrizen Interpolation mit Polynomen und Splines P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
21 Lernziele P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
22 Lernziele ➊ Wissen und Kenntnisse P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
23 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
24 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
25 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung Lösungsverfahren und (numerische) Algorithmen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
26 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung Lösungsverfahren und (numerische) Algorithmen ➋ Fähigkeiten und Fertigkeiten P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
27 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung Lösungsverfahren und (numerische) Algorithmen ➋ Fähigkeiten und Fertigkeiten Analytisches Denken P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
28 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung Lösungsverfahren und (numerische) Algorithmen ➋ Fähigkeiten und Fertigkeiten Analytisches Denken Abstraktes Denken P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
29 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung Lösungsverfahren und (numerische) Algorithmen ➋ Fähigkeiten und Fertigkeiten Analytisches Denken Abstraktes Denken Algorithmisches Denken P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
30 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung Lösungsverfahren und (numerische) Algorithmen ➋ Fähigkeiten und Fertigkeiten Analytisches Denken Abstraktes Denken Algorithmisches Denken Das muss ein ETH-Ingenieur können! P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
31 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung Lösungsverfahren und (numerische) Algorithmen ➋ Fähigkeiten und Fertigkeiten Analytisches Denken Abstraktes Denken Algorithmisches Denken Das muss ein ETH-Ingenieur können! P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
32 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung Lösungsverfahren und (numerische) Algorithmen ➋ Fähigkeiten und Fertigkeiten Analytisches Denken Abstraktes Denken Algorithmisches Denken Das muss ein ETH-Ingenieur können! Schwierig und anspruchsvoll! P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
33 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung Lösungsverfahren und (numerische) Algorithmen ➋ Fähigkeiten und Fertigkeiten Analytisches Denken Abstraktes Denken Algorithmisches Denken Das muss ein ETH-Ingenieur können! Schwierig und anspruchsvoll! P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
34 Lernziele ➊ Wissen und Kenntnisse Begriffe und Konzepte aus der linearen Algebra Resultate, Techniken und deren Anwendung Lösungsverfahren und (numerische) Algorithmen ➋ Fähigkeiten und Fertigkeiten Analytisches Denken Abstraktes Denken Algorithmisches Denken Das muss ein ETH-Ingenieur können! Schwierig und anspruchsvoll! Verständnis: Vorlesung 1/3, Hausaufgaben 1/3, Prüfungsvorbereitung 1/3 P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
35 Vorlesungen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
36 Vorlesungen Vorlesungsstil: Back to the roots: Wandtafel P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
37 Vorlesungen Vorlesungsstil: Back to the roots: Wandtafel Vorlesungszeiten (regulär): Mi 7:45 9:30 HCI G7 Do 10:15-11:55 HG F 1 (14-tägig) Erste Donnerstagvorlesung: 17. September 2015 P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
38 Vorlesungen Vorlesungsstil: Back to the roots: Wandtafel Vorlesungszeiten (regulär): Mi 7:45 9:30 HCI G7 Do 10:15-11:55 HG F 1 (14-tägig) Erste Donnerstagvorlesung: 17. September 2015 Gelegenheit für private Fragen: Vorlesungspause! P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
39 Vorlesungen Vorlesungsstil: Back to the roots: Wandtafel Vorlesungszeiten (regulär): Mi 7:45 9:30 HCI G7 Do 10:15-11:55 HG F 1 (14-tägig) Erste Donnerstagvorlesung: 17. September 2015 Gelegenheit für private Fragen: Vorlesungspause! Anregungen, Fehlermeldungen, Kommentare WIKI P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
40 Prüfungen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
41 Prüfungen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
42 Prüfungen Sessionsprüfung im Sommer, Teil der Basisprüfung, 120 Minuten, schriftlich P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
43 Prüfungen Sessionsprüfung im Sommer, Teil der Basisprüfung, 120 Minuten, schriftlich Mittsemesterprüfung am xx. Oktober 2015, 30-minütige Schnellprüfung, ohne Hilfsmittel P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
44 Prüfungen Sessionsprüfung im Sommer, Teil der Basisprüfung, 120 Minuten, schriftlich Mittsemesterprüfung am xx. Oktober 2015, 30-minütige Schnellprüfung, ohne Hilfsmittel Endsemesterprüfung am yy. Dezember 2015, 30-minütige Schnellprüfung, ohne Hilfsmittel P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
45 Prüfungen Sessionsprüfung im Sommer, Teil der Basisprüfung, 120 Minuten, schriftlich Mittsemesterprüfung am xx. Oktober 2015, 30-minütige Schnellprüfung, ohne Hilfsmittel Endsemesterprüfung am yy. Dezember 2015, 30-minütige Schnellprüfung, ohne Hilfsmittel Die Leistung in Mitt- und Endsemesterprüfungen wird durch Bonuspunkte in der Sessionsprüfung angerechnet! P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
46 Hausaufgaben und Übungen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
47 Hausaufgaben und Übungen Übungen sind ein zentraler Teil der Lehrveranstaltung: P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
48 Hausaufgaben und Übungen Übungen sind ein zentraler Teil der Lehrveranstaltung: in kleinen Gruppen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
49 Hausaufgaben und Übungen Übungen sind ein zentraler Teil der Lehrveranstaltung: in kleinen Gruppen wichtig für gegenseitige Rückmeldungen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
50 Hausaufgaben und Übungen Übungen sind ein zentraler Teil der Lehrveranstaltung: in kleinen Gruppen wichtig für gegenseitige Rückmeldungen dienen der Wissenssicherung P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
51 Hausaufgaben und Übungen Übungen sind ein zentraler Teil der Lehrveranstaltung: in kleinen Gruppen wichtig für gegenseitige Rückmeldungen dienen der Wissenssicherung transformieren passives in aktives Wissen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
52 Hausaufgaben und Übungen Übungen sind ein zentraler Teil der Lehrveranstaltung: in kleinen Gruppen wichtig für gegenseitige Rückmeldungen dienen der Wissenssicherung transformieren passives in aktives Wissen Konsequentes, beharrliches Bearbeiten der Übungsserien essentiell für Prüfungserfolg P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
53 Hausaufgaben und Übungen Übungen sind ein zentraler Teil der Lehrveranstaltung: in kleinen Gruppen wichtig für gegenseitige Rückmeldungen dienen der Wissenssicherung transformieren passives in aktives Wissen Konsequentes, beharrliches Bearbeiten der Übungsserien essentiell für Prüfungserfolg Online-Publikation der Übungsblätter (PDF) jede Woche am Mittwoch P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
54 Hausaufgaben und Übungen Übungen sind ein zentraler Teil der Lehrveranstaltung: in kleinen Gruppen wichtig für gegenseitige Rückmeldungen dienen der Wissenssicherung transformieren passives in aktives Wissen Konsequentes, beharrliches Bearbeiten der Übungsserien essentiell für Prüfungserfolg Online-Publikation der Übungsblätter (PDF) jede Woche am Mittwoch Freiwillige Abgabe der eigenen Lösungen in den Übungsgruppen Arbeitsaufwand: 3-6 Stunden/Übungsblatt P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
55 Übungsleitung P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
56 Übungsleitung Timo Welti MSc Mathematik ETH Zürich, Doktorand am Seminar für Angewandte Mathematik der ETH Zürich Büro: HG J 49 P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
57 Übungsleitung Timo Welti MSc Mathematik ETH Zürich, Doktorand am Seminar für Angewandte Mathematik der ETH Zürich Büro: HG J 49 Franziska Weber PhD Universität Oslo, Postdoc am Seminar für Angewandte Mathematik der ETH Zürich [email protected] Büro: HG J 49 P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
58 Tutoren P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
59 Tutoren Daphné Chopard Andy Disch Ann-Katrin Thamm Silvan Vetter Simon Zeder Elke Spindler Željko Kerata P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
60 Einschreibung in Übungsgruppen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
61 Einschreibung in Übungsgruppen Belegung dieser Vorlesung in mystudies: P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
62 Einschreibung in Übungsgruppen Belegung dieser Vorlesung in mystudies: Erhalt einer mit detailierten Erläuterungen zur Einschreibung von mit Link für Einschreibung in Übungsgruppen. P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
63 Einschreibung in Übungsgruppen Belegung dieser Vorlesung in mystudies: Erhalt einer mit detailierten Erläuterungen zur Einschreibung von mit Link für Einschreibung in Übungsgruppen. Benutzen Sie den Link, um sich in eine freie Übungsgruppe einzuschreiben. Beachten Sie dabei, dass Sie keine Terminüberschneidungen mit Analysis haben! P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
64 Einschreibung in Übungsgruppen Belegung dieser Vorlesung in mystudies: Erhalt einer mit detailierten Erläuterungen zur Einschreibung von mit Link für Einschreibung in Übungsgruppen. Benutzen Sie den Link, um sich in eine freie Übungsgruppe einzuschreiben. Beachten Sie dabei, dass Sie keine Terminüberschneidungen mit Analysis haben! Link behalten! Gilt auch für Übungen Analysis + Informatik. P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
65 Zentralpräsenz P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
66 Zentralpräsenz Flexible Auditorien LFW C4, HG E 41 P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
67 Zentralpräsenz Flexible Auditorien LFW C4, HG E 41 Erklärungen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
68 Zentralpräsenz Flexible Auditorien LFW C4, HG E 41 Erklärungen Diskussion P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
69 Zentralpräsenz Flexible Auditorien LFW C4, HG E 41 Erklärungen Diskussion Micro-Teaching P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
70 Zentralpräsenz Flexible Auditorien LFW C4, HG E 41 Erklärungen Diskussion Micro-Teaching angeboten von den Tutoren P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
71 Zentralpräsenz Flexible Auditorien LFW C4, HG E 41 Erklärungen Diskussion Micro-Teaching angeboten von den Tutoren gemeinsam für drei LA-Vorlesungen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
72 Zentralpräsenz Flexible Auditorien LFW C4, HG E 41 Erklärungen Diskussion Micro-Teaching angeboten von den Tutoren gemeinsam für drei LA-Vorlesungen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
73 Zentralpräsenz Flexible Auditorien LFW C4, HG E 41 Erklärungen Diskussion Micro-Teaching Start: 21. September 2015 Zeiten: Montag, 17-19, LFW C4 Donnerstag, 17-20, HG E41 Freitag, 17-20, HG E41 angeboten von den Tutoren gemeinsam für drei LA-Vorlesungen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
74 Zentralpräsenz Flexible Auditorien LFW C4, HG E 41 Erklärungen Diskussion Micro-Teaching Start: 21. September 2015 Zeiten: Montag, 17-19, LFW C4 Donnerstag, 17-20, HG E41 Freitag, 17-20, HG E41 Nutzen Sie das Angebot! angeboten von den Tutoren gemeinsam für drei LA-Vorlesungen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
75 MATLAB P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
76 MATLAB Vorlesung betont algorithmisches Denken. P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
77 MATLAB Vorlesung betont algorithmisches Denken. P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
78 MATLAB Vorlesung betont algorithmisches Denken. Programmiersprache: MATLAB (kommerzielle Software) P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
79 MATLAB Vorlesung betont algorithmisches Denken. Programmiersprache: MATLAB (kommerzielle Software) MATLAB in der Vorlesung ab 2. Semesterhälfte Demonstration von Algorithmen Programmier-Hausaufgaben P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
80 Literatur P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
81 Literatur K. Nipp und D. Stoffer, LINEARE AL- GEBRA, vdf Hochschulverlag, Zürich G. Strang, LINEARE ALGEBRA, Springer, Berlin P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
82 Literatur K. Nipp und D. Stoffer, LINEARE AL- GEBRA, vdf Hochschulverlag, Zürich G. Strang, LINEARE ALGEBRA, Springer, Berlin Wichtigste Referenz: Vorlesungsunterlagen P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
83 Literatur K. Nipp und D. Stoffer, LINEARE AL- GEBRA, vdf Hochschulverlag, Zürich G. Strang, LINEARE ALGEBRA, Springer, Berlin Wichtigste Referenz: Vorlesungsunterlagen Weitere Informationen Webseite zur Vorlesung P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
84 Mitt- und Endsemesterprüfung LA & NM (D-BAUG) Mitte Oktober bzw. Mitte Dezember, HCI G 7 Um pünktliches Kommen 10 Min. vor Prüfungsbeginn wird gebeten! Bedeutung: Anrechnung für Basisprüfung (Bonuspunkte) VVZ: Im Rahmen der Vorlesungen werden je eine 30 minütige Zwischensemesterpruefung und Endsemesterpruefung durchgeführt, die Teilnahme ist fakultativ. Die dabei erzielten Punkte werden für die Sessionsprüfung als ein Bonus der insgesamt erzielbaren Punkte angerechnet. Dabei kann in der Sessionsprüfung die Bestnote 6.0 auch ohne Bonuspunkte erreicht werden. Besprechung der Prüfung im Anschluss an die Prüfung. P. Grohs (SAM, ETH Zürich) Lin. Alg. & Num. Meth BAUG HS / 14
Lineare Algebra und Numerische Mathematik
Lineare Algebra und Numerische Mathematik Prof. Ralf Hiptmair Seminar for Applied Mathematics, ETH Zürich Vorlesung für D-BAUG Herbstsemester 2014 www.math.ethz.ch/education/bachelor/lectures/hs2014/other/linalgnum_baug
Einführung in die Numerik
Einführung in die Numerik Sommersemester 2017 Dr. Andreas Potschka Ruprecht Karls-Universität Heidelberg Interdisziplinäres Zentrum für Wissenschaftliches Rechnen Im Neuenheimer Feld 205, 69120 Heidelberg
Im Nebenfach Mathematik können zwei Varianten studiert werden. Studiensemester. Kontaktzeit 56 h 28 h
Nebenfach Mathematik 1-Fach Bachelor of Science Geographie Im Nebenfach Mathematik können zwei Varianten studiert werden. Variante I: Analysis I Kennnummer Workload Leistungspunkte Studiensemester Häufigkeit
2.2 Pichtmodule Mathematik
2.2 Pichtmodule Mathematik Für die Vermittlung der mathematischen Grundlagen stehen fünf Module zur Verfügung. Von diesen fünf Modulen müssen drei absolviert werden. Die erste Prüfungsleistung kann entweder
Einführung in die Numerische Lineare Algebra (MA 1304)
Einführung in die Numerische Lineare Algebra (MA 1304) Vorlesung Montags, 16:15-17:45 Uhr Rudolf-Mößbauer - HS (Physik) Homepage zur Vorlesung http://www-m2.ma.tum.de/bin/view/allgemeines/numlinalgws1516
Grundlagen der Numerischen Mathematik Sommersemester Kapitel 0. Jun.-Prof. Dr. Thorsten Raasch (JGU Mainz) 23. April 2014
Grundlagen der Numerischen Mathematik Sommersemester 2014 Kapitel 0 Jun.-Prof. Dr. Thorsten Raasch Johannes Gutenberg-Universität Mainz Institut für Mathematik 23. April 2014 Numerik Was ist das? Was ist
Algorithmische Mathematik und Programmieren
Algorithmische Mathematik und Programmieren Martin Lanser Universität zu Köln WS 2016/2017 Organisatorisches M. Lanser (UzK) Alg. Math. und Programmieren WS 2016/2017 1 Ablauf der Vorlesung und der Übungen
Lineare Algebra und Numerische Mathematik für D-BAUG
P. Grohs T. Welti F. Weber Herbstsemester 2 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Mittsemesterprüfung HS, Typ A Name a a Note Vorname Leginummer Datum 29..2 2 4 6 Total
Informatik I Felix Friedrich
1 Informatik I Felix Friedrich Vorlesung am D-ITET der ETH Zürich HS 2014 W i l l k o m m e n 2 zur Vorlesung Informatik I! am ITET Department der ETH Zürich. Ort und Zeit: Mittwoch 8:15-10:00, ETF E1.
Lineare Algebra und Numerische Mathematik für D-BAUG. Serie 6
R. Hiptmair S. Pintarelli E. Spindler Herbstsemester 2014 Lineare Algebra und Numerische Mathematik für D-BAUG Serie 6 ETH Zürich D-MATH Einleitung. Diese Serie behandelt nochmals das Rechnen mit Vektoren
2.2 Pichtmodule Mathematik
2.2 Pichtmodule Mathematik Die Vermittlung der mathematischen Grundlagen erfolgt durch das Modul Mathematik für Informatiker 1. Ergänzend zur Prüfungsordnung kann das Modul Mathematik für Informatiker
Mathematisch-algorithmische Grundlagen für Big Data
Mathematisch-algorithmische Grundlagen für Big Data Numerische Algorithmen für Datenanalyse und Optimierung Prof. Dr. Peter Becker Fachbereich Informatik Hochschule Bonn-Rhein-Sieg Sommersemester 2017
Logik und diskrete Strukturen
Prof. Dr. Institut für Informatik Abteilung V Wintersemester 2015/16 Dozenten und Tutoren Vorlesung Professor für Theoretische Informatik E-Mail: [email protected] Web: http://www.roeglin.org/ Büro:
Maß- und Integrationstheorie (MA2003)
Maß- und Integrationstheorie (MA2003) Elisabeth Ullmann Zentrum Mathematik Elisabeth Ullmann (TUM) MA2003 1 / 12 Allgemeines Vorlesung: Montag, 14:00 15:30 Uhr im Interimshörsaal 2 Übungsgruppen: Gruppe
Mathematik 1. Studiengang Bachelor Informatik WS 2016/2017. Prof. Dr. Ulrich Tipp
Mathematik 1 Studiengang Bachelor Informatik WS 2016/2017 Prof. Dr. Ulrich Tipp Organisatorisches 4 h Vorlesung Di 8:00 9:30 AM Mi 8:00 9:30 AM 2 h Übung in 4 Gruppen Di 10:00 11:30 BE08 (Gruppe L) Di
STUDIENPLAN FÜR DEN DIPLOM-STUDIENGANG TECHNOMATHEMATIK an der Technischen Universität München. Übersicht Vorstudium
STUDIENPLAN FÜR DEN DIPLOM-STUDIENGANG TECHNOMATHEMATIK an der Technischen Universität München Übersicht Vorstudium Das erste Anwendungsgebiet im Grundstudium ist Physik (1. und 2. Sem.) Im 3. und 4. Sem.
Mathematik I für Maschinenbau etc.
Mathematik I für Maschinenbau etc. Michael Joswig Assistenz: 1 Organisation 2 Klausur 3 Mathematik Katja Kulas Dr. Sören Kraußhar WS 2010/2011 Joswig 1 Persönliche Vorstellung Prof. Dr. Michael Joswig
Grundlagen der Mathematik 1
Grundlagen der Mathematik 1 Thomas Markwig http://www.mathematik.uni-kl.de/ keilen 21. April 2015 (3 x 90 min / Woche) Übung (1 x 90 min / Woche) Tutorium (1 x 90 min / Woche) (Lernzentrum) Yue Ren (AG
Algorithmen und Berechnungskomplexität I
Algorithmen und Berechnungskomplexität I Prof. Dr. Institut für Informatik Wintersemester 2013/14 Organisatorisches Vorlesung Dienstag und Donnerstag, 12:30 14:00 Uhr (HS 1) Übungen 16 Übungsgruppen Anmeldung
Mathematik I. (für die Studiengänge Informatik, Elekrotechnik und Physik) Oliver Ernst. Wintersemester 2017/18. Professur Numerische Mathematik
Mathematik I (für die Studiengänge Informatik, Elekrotechnik und Physik) Oliver Ernst Professur Numerische Mathematik Wintersemester 2017/18 Wir Vorlesung Prof. Oliver Ernst Mo 9:45 Do 11:30 Übungen/Praktika
D-MATH Lineare Algebra und Numerische Mathematik HS 2013 Prof. R. Hiptmair. Serie 9
D-MATH Lineare Algebra und Numerische Mathematik HS 213 Prof. R. Hiptmair Serie 9 Die Aufgaben 1. bis 6. behandeln lineare Abbildungen und deren Matrixdarstellungen bezüglich geeigneter Basen. Die Theorie
Numerik I Einführung in die Numerik
Numerik I Einführung in die Numerik M. Gutting 18. Oktober 2016 Termine Termine Vorlesung: dienstags von 12:15 Uhr bis 13:45 Uhr in ENC-D 201 und freitags von 14:15 Uhr bis 15:45 Uhr in ENC-D 223, Übung:
Mathematik für Ingenieure Teil A: CE, EEI, ET, IuK, ME. Information zur Vorlesung und Übung. PD Dr. Markus Bause
Mathematik für Ingenieure Teil A: CE, EEI, ET, IuK, ME Information zur Vorlesung und Übung PD Dr. Markus Bause Universität Erlangen-Nürnberg Department Mathematik [email protected] http://www1.am.uni-erlangen.de/
Modulhandbuch für. den Bachelor-Studiengang Mathematik. und. den Bachelor-Studiengang Wirtschaftsmathematik. an der Universität Augsburg
Universität Augsburg Institut für Modulhandbuch für den Bachelor-Studiengang und den Bachelor-Studiengang Wirtschaftsmathematik an der Universität Augsburg 29.06.2009 Grundlegend für dieses Modulhandbuch
Willkommen an der ETH! Informationen zum Studium am D-ITET
Willkommen an der ETH! Informationen zum Studium am D-ITET Pre-Study Event 6. Juni 2017 (ETF E 1) Reto Kreuzer, Studienkoordinator und Studienberater, D-ITET Reto Kreuzer 06.06.2017 1 Wo finden Sie Informationen
Georg-August-Universität Göttingen. Modulverzeichnis
Georg-August-Universität Göttingen Modulverzeichnis für den Bachelor-Teilstudiengang "Mathematik" (zu Anlage II.28 der Prüfungs- und Studienordnung für den Zwei-Fächer-Bachelor-Studiengang) (Amtliche Mitteilungen
Mathematische Grundlagen II Lineare Algebra und Differential- und Integralrechnung
Lineare Algebra und Differential- und Integralrechnung Dr. Tim Haga 04. April 2017 1 Persönliches 2 Zur Veranstaltung 3 Organisatorisches 4 Scheinverhandlung Dr. Tim Haga 1 / 10 Zu meiner Person Tim Haga
Mathematische Grundlagen II Lineare Algebra und Differential- und Integralrechnung
Lineare Algebra und Differential- und Integralrechnung Tim Haga 05. April 2016 1 Persönliches 2 Zur Veranstaltung 3 Organisatorisches 4 Scheinverhandlung Tim Haga 1 / 10 Zu meiner Person Tim Haga Studium
Numerik gewöhnlicher Differentialgleichungen Wintersemester 2014/15. Kapitel 0
Numerik gewöhnlicher Differentialgleichungen Wintersemester 2014/15 Kapitel 0 Jun.-Prof. Dr. Thorsten Raasch Johannes Gutenberg-Universität Mainz Institut für Mathematik 29. Oktober 2015 Numerik was ist
Diskrete Strukturen WS Ernst W. Mayr. Wintersemester Fakultät für Informatik TU München
WS 2011 Diskrete Strukturen Ernst W. Mayr Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2011ws/ds/ Wintersemester 2011 Diskrete Strukturen Kapitel 0 Organisatorisches Vorlesung: Di 13:45
PHYSIK I. - Mechanik, Akustik, Wärmelehre - Ablauf der Vorlesung. Übungen. Leistungsnachweis
PHYSIK I - Mechanik, Akustik, Wärmelehre - Ablauf der Vorlesung Übungen Leistungsnachweis Ablauf der Vorlesung Termine: Mo. und Mi. 10:15-12:00 Uhr, Gr. Hörsaal Physik Dozent: Prof. K. Jakobs Gustav-Mie
Praktische Mathematik
Praktische Mathematik im Sommersemester 2015 Dr. rer. nat. Steffen Weißer 1 AG Prof. Dr. S. Rjasanow FR 6.1 Mathematik Universität des Saarlandes 21. April 2015 1 www.num.uni-sb.de/weisser Inhalte der
LP(ECTS): 8 Sekr.: MA 7-6
Titel des Moduls: Analysis I für Ingenieure Verantwortliche/-r für das Modul: Studiendekan für den Mathematikservice 1. Qualifikationsziele LP(ECTS): 8 Sekr.: MA 7-6 Modulbeschreibung Kurzbezeichnung:
Modulhandbuch. Wintersemester 2016/17: Veranstaltungen der Arbeitsgruppe Diskrete Mathematik, Optimierung und Operations Research keine Zuordnung
Universität Augsburg Modulhandbuch Wintersemester 2016/17: Veranstaltungen der Arbeitsgruppe Diskrete Mathematik, Optimierung und Operations Research keine Zuordnung Wintersemester 2016/2017 Lehrveranstaltungen
Informatik für Mathematiker und Physiker Woche 1. David Sommer
Informatik für Mathematiker und Physiker Woche 1 David Sommer David Sommer September 26, 2017 1 Willkommen (an der ETH, in den IFMP Übungen, im ersten Semester,...) David Sommer September 26, 2017 2 Ich
Bachelormodule Zweitfach Mathematik a) Überblick
Bachelormodule Zweitfach Mathematik a) Überblick 1 Mathematik 2 2 Module im Pflichtbereich 1 3 Modul NAT-5541 4 Modul NAT-5542 Mathematik: Elemente der Analysis I (EdA I) (Zweitfach) (Elements of analysis
Einsatz von Scilab in der Analysis für Ingenieure
7 Pierre Colson Einsatz von Scilab in der Analysis für Ingenieure 1. Einführung Der Einsatz eines Softwaresystems in einer Analysis-Vorlesung für Ingenieure ist an sich keine Neuigkeit. Er wird aber zu
Modulnummer Modulname Verantwortlicher Dozent. Lineare Algebra und Analytische Geometrie
MN-SEBS-MAT-LAAG (MN-SEGY-MAT-LAAG) (MN-BAWP-MAT-LAAG) Lineare Algebra und Analytische Geometrie Direktor des Instituts für Algebra n Die Studierenden besitzen sichere Kenntnisse und Fähigkeiten insbesondere
Numerische Mathematik für ingenieurwissenschaftliche Studiengänge
Institut für Numerische Mathematik und Optimierung Folien zur Vorlesung Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Sommersemester 2010 Hörerkreis: 3./4. BEC, 3./4. BMB, 4. BAI, 4.
Lineare Algebra und Numerische Mathematik für D-BAUG
P Grohs T Welti F Weber Herbstsemester 215 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 12 Aufgabe 121 Matrixpotenzen und Eigenwerte Diese Aufgabe ist
Numerische Methoden. Thomas Huckle Stefan Schneider. Eine Einführung für Informatiker, Naturwissenschaftler, Ingenieure und Mathematiker.
Thomas Huckle Stefan Schneider Numerische Methoden Eine Einführung für Informatiker, Naturwissenschaftler, Ingenieure und Mathematiker 2. Auflage Mit 103 Abbildungen und 9 Tabellen 4Q Springer Inhaltsverzeichnis
Kapitel -1 Organisatorisches
Kapitel -1 Organisatorisches 1 Das Team Dozent: Prof. Dr. Friedrich Eisenbrand Übungsbetrieb: Dr. Kai Gehrs Tutoren Hans Biebinger Christian Heinemann Reiner Hermann Christian Michalke Thomas Rothvoß Alexander
Inhalt, Ablauf, Organisation, Prüfung,...
Inhalt, Ablauf, Organisation, Prüfung,... Vorlesung Einführung in das Wissenschaftliche Rechnen Sommersemester 2016 Einführung in das Wissenschaftliche Rechnen Sommersemester 2016, Simon Baumstark, Patrick
Allgemeine Informationen zur Vorlesung
Allgemeine Informationen zur Vorlesung Lineare Algebra Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 11. April 2016 Stefan Ruzika Informationen 11. April 2016 1 / 9 Wenden
WS 2015/16 Diskrete Strukturen Organisatorisches
WS 2015/16 Diskrete Strukturen Organisatorisches Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
Grundlagen der Künstlichen Intelligenz
Grundlagen der Künstlichen Intelligenz 0. Organisatorisches Malte Helmert Universität Basel 16. Februar 2015 Organisatorisches Personen: Dozent Dozent Prof. Dr. Malte Helmert E-Mail: [email protected]
Mathematik für Informatiker: Diskrete Strukturen getting started
Mathematik für Informatiker: Diskrete Strukturen getting started Jens Zumbrägel Institut für Algebra Fachbereich Mathematik TU Dresden WiSe 2016/17 12. Okt. 2016 Jens Zumbrägel (TU Dresden) Diskrete Strukturen
Numerik 1. Ch. Helzel. Vorlesung: Mi. + Do. 10:30-12:15
Numerik 1 Ch. Helzel Vorlesung: Mi. + Do. 10:30-12:15 Organisatorisches Mitarbeiter: David Kerkmann und Marina Fischer (Übungen), Felix Lieder (Organisatorisches), Andreas Troll (Programmierübungen) Organisatorisches
Logik und diskrete Strukturen
Logik und diskrete Strukturen Prof. Dr. Stefan Kratsch Institut f ur Informatik Abteilung I [email protected] Wintersemester 2016/17 S. Kratsch ([email protected]) Logik und diskrete Strukturen
Algorithmen und Datenstrukturen
Algorithmen und Datenstrukturen A1. Organisatorisches Marcel Lüthi and Gabriele Röger Universität Basel 28. Februar 2018 Organisatorisches Personen: Dozenten Marcel Lüthi Gabriele Röger Dozenten Dr. Marcel
Willkommen an der ETH! Informationen zum Studium am D-ITET
Willkommen an der ETH! Informationen zum Studium am D-ITET Pre-Study Event 8. September 2017 (ETF E 1) Reto Kreuzer, Studienkoordinator und Studienberater, D-ITET Reto Kreuzer 06.06.2017 1 Wo finden Sie
Propädeutischen Fächer
Auszug aus dem Studienplan für die Propädeutischen Fächer und die Zusatzfächer angeboten von der Math.-Natw. Fakultät im Rahmen eines Bachelor of Science oder für andere Studiengänge mit diesen Programmen
INSTITUT FÜR INFORMATIK
INSTITUT FÜR INFORMATIK Lehrveranstaltungen Wintersemester 2006/2007 Grundlagen der Praktischen Informatik Vorlesung: Grundlagen der Softwareentwicklung und Programmierung Di.+Fr. 9-11 25.11.00, HS 5C
1 Studienpläne bis zum Vordiplom und Bachelor-Abschluss
1 Studienpläne bis zum Vordiplom und Bachelor-Abschluss Die Pflichtvorlesungen für das Studium Lehramt Mathematik an Gymnasien (LG) stimmen in den ersten Semestern weitgehend mit denen des Studiengangs
Fächer und Prüfungen im Bachelorstudium
Fächer und Prüfungen im Bachelorstudium FSI Informatik Uni Erlangen-Nürnberg 16. Oktober 2017 FSI Informatik (Uni Erlangen-Nürnberg) Fächer und Prüfungen im Bachelorstudium 16. Oktober 2017 1 / 17 Grober
Mein Stundenplan Einführungsvortrag für BSc-StudienanfängerInnen 2007/08
Mein Stundenplan Einführungsvortrag für BSc-StudienanfängerInnen 2007/08 Dr. Ute Vogel Abteilung Umweltinformatik Studienberaterin Schwerpunkt Umweltinformatik [email protected] Fragen
Einführung in die Programmierung
Einführung in die Programmierung Prof. Dr. Peer Kröger, Janina Bleicher, Florian Richter Ludwig-Maximilians-Universität München, Institut für Informatik, LFE Datenbanksysteme Wintersemester 2016/2017 Peer
Vektorräume. Lineare Algebra I. Kapitel Juni 2012
Vektorräume Lineare Algebra I Kapitel 9 12. Juni 2012 Logistik Dozent: Olga Holtz, MA 378, Sprechstunden Freitag 14-16 Webseite: www.math.tu-berlin.de/ holtz Email: [email protected] Assistent: Sadegh
Das Informatikstudium (an der ETH)
Das Informatikstudium (an der ETH) Malte Schwerhoff, Dozent (Mit Folien von Hermann Lehner, Emo Wenzel, Sandra Herkle) Departement Informatik Dr. Malte Schwerhoff, Dozent 13.09.2018 1 Warum sind Sie hier?
Brückenkurs Mathematik
Informationen zur Lehrveranstaltung [email protected] Institute for Mathematics and Scientific Computing Karl-Franzens-Universität Graz Graz, August 5, 2014 Übersicht Motivation Motivation für
Computergestützte Mathematik zur Linearen Algebra
Computergestützte Mathematik zur Linearen Algebra Erste Schritte am Rechner Christiane Helzel Übungsleiter: Pawel Buchmüller Tutoren: Valdrin Bajrami, Janka Heyer, Niclas Janssen, David Kerkmann, Tran
Informationen zum 1. Semester
Informationen zum 1. Semester 1 Agenda Studienplan / Prüfungsordnung Prüfungen Unser Team Fragen 2 Ein Bachelor verschiedene Master 3 Stundenplan Montag Dienstag Mittwoch Donnerstag Freitag 08:00-10:00
Lineare Algebra und analytische Geometrie I (Unterrichtsfach) Lösungsvorschlag
MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr E Schörner WS / Blatt 6 Übungen zur Vorlesung Lineare Algebra und analytische Geometrie I (Unterrichtsfach) Lösungsvorschlag Wir verwenden das Unterraumkriterium,
Diskrete Strukturen WS 2010/11. Ernst W. Mayr. Wintersemester 2010/11. Fakultät für Informatik TU München
WS 2010/11 Diskrete Strukturen Ernst W. Mayr Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2010ws/ds/ Wintersemester 2010/11 Diskrete Strukturen Kapitel 0 Organisatorisches Vorlesungen:
Mathematik-Vorkurs. Philipps-Universität Marburg Wintersemester 2016/17. Dr. Andreas Lochmann. 4. Oktober
Mathematik-Vorkurs Philipps-Universität Marburg Wintersemester 2016/17 Dr. Andreas Lochmann [email protected] 4. Oktober 2016 1 / 12 Vorkurs (4.10. 7.10.) Di 10 12 Di 13 16 Mi 10 12 Mi
Organisatorische Hinweise zur Vorlesung. von Prof. Dr. Vladimir Shikhman im Wintersemester 2017/2018
Organisatorische Hinweise zur Vorlesung Mathematik I für Wirtschaftswissenschaftler und -informatiker von Prof. Dr. Vladimir Shikhman im Wintersemester 2017/2018 URL: http://www.tu-chemnitz.de/mathematik/wima
STUDIENPLAN FÜR DEN BACHELORSTUDIENGANG MATHEMATIK
STUDIENPLAN FÜR DEN BACHELORSTUDIENGANG MATHEMATIK an der Technischen Universität München gemäß FPO vom 12. Januar 2005 Es werden folgende Studienrichtungen angeboten: I W Ph N mit dem Nebenfach Informatik
Mathematikstudium in Regensburg
Mathematikstudium in Regensburg Herzlich Willkommen.. an der Fakultät für Mathematik der Universität Regensburg Die Mathematik an der Universität Regensburg Anfängerzahlen im Fach Mathematik im WS 2015/16
Einführung in die Praktische Informatik WS 09/10
Einführung in die Praktische Informatik WS 09/10 Prof. Dr. Christian Sengstock Institut für Informatik Neuenheimer Feld 348 69120 Heidelberg http://dbs.ifi.uni-heidelberg.de [email protected]
Einführung in die Programmierung. Organisatorisches. Skript zur Vorlesung Einführung in die Programmierung
LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS DATABASE Einführung in die Programmierung Organisatorisches Skript zur Vorlesung Einführung in die Programmierung im Wintersemester
Numerik für Informatiker
Numerik für Informatiker Lars Grüne Lehrstuhl für Angewandte Mathematik Mathematisches Institut Universität Bayreuth 95440 Bayreuth [email protected] www.math.uni-bayreuth.de/ lgruene/ Karl Worthmann
Wissenschaftliche Grundlagen des Mathematischen Schulstoffs III III. Die erste Stunde. Die erste Stunde
Wissenschaftliche Grundlagen des Mathematischen Schulstoffs III III Was ist ist Mathematik? Der Inhalt Geometrie (seit (seit Euklid, ca. ca. 300 300 v. v. Chr.) Chr.) Die Die Lehre vom vom uns uns umgebenden
Vorlesung Logik Wintersemester 2016/17 Universität Duisburg-Essen
Vorlesung Logik Wintersemester 2016/17 Universität Duisburg-Essen Barbara König Übungsleitung: Dennis Nolte, Harsh Beohar Barbara König Logik 1 Das heutige Programm: Organisatorisches Vorstellung Ablauf
Springers Mathematische Formeln
Lennart Rade Bertil Westergren Springers Mathematische Formeln Taschenbuch für Ingenieure, Naturwissenschaftler, Informatiker, Wirtschaftswissenschaftler Übersetzt und bearbeitet von Peter Vachenauer Dritte,
Informatik I. W i l l k o m m e n. Team. Einschreibung in Übungsgruppen. Vorlesung am D-ITET der ETH Zürich. zur Vorlesung Informatik I!
W i l l k o m m e n Informatik I Vorlesung am D-ITET der ETH Zürich Felix Friedrich HS 2017 zur Vorlesung Informatik I! am ITET Department der ETH Zürich. Ort und Zeit: Mittwoch 8:15-10:00, ETF E1. Pause
MA2000 (6) Math. Grundlagen. MA2003 (5) Maß- und Int. MA2004 (5) Vektoranalysis MA2101 (9) Algebra. MA2203 (5) Geo-Kalküle
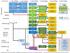weitere Pflichtmodule Reine Mathe frühestes Semester: 1. Sem (WiSe) 2. Sem (SoSe) 3. Sem (WiSe) 4. Sem (SoSe) 5. Sem (WiSe) 6. Sem (SoSe) MA1001 (10) Analysis 1 MA1002 (10) Analysis 2 MA2000 (6) Math.
Datenstrukturen und Algorithmen
Willkommen! Datenstrukturen und Algorithmen Vorlesungshomepage: http://lec.inf.ethz.ch/da/2018 Vorlesung am D-Math (CSE) der ETH Zürich Felix Friedrich FS 2018 Das Team: Chefassistent Assistenten Dozent
Informatik I. Vorlesung am D-ITET der ETH Zürich. Felix Friedrich HS 2017
1 Informatik I Vorlesung am D-ITET der ETH Zürich Felix Friedrich HS 2017 W i l l k o m m e n 2 zur Vorlesung Informatik I! am ITET Department der ETH Zürich. Ort und Zeit: Mittwoch 8:15-10:00, ETF E1.
Vorlesung Logik Wintersemester 2015/16 Universität Duisburg-Essen
Vorlesung Logik Wintersemester 2015/16 Universität Duisburg-Essen Barbara König Übungsleitung: Dennis Nolte, Dr. Harsh Beohar Barbara König Logik 1 Barbara König Logik 2 Das heutige Programm: Organisatorisches
Numerische Mathematik für die Fachrichtungen Informatik und Ingenieurwesen. Andreas Rieder
Numerische Mathematik für die Fachrichtungen Informatik und Ingenieurwesen Andreas Rieder UNIVERSITÄT KARLSRUHE (TH) Institut für Wissenschaftliches Rechnen und Mathematische Modellbildung und Institut
MASTER WIRTSCHAFTSPÄDAGOGIK MIT ZWEITFACH Mathematik
MASTER WIRTSCHAFTSPÄDAGOGIK MIT ZWEITFACH Mathematik Folgendes Curriculum gilt für Master-Studierende, die jeweils nach der neuen Prüfungsordnung studieren. Studierende der alten Prüfungsordnung orientieren
Willkommen an der ETH! Informationen zum Studium am D-ITET
Willkommen an der ETH! Informationen zum Studium am D-ITET Pre-Study Event 9. September 2016 (ETF E 1) Reto Kreuzer, Studienkoordinator und Studienberater, D-ITET Reto Kreuzer 16.06.2016 1 Wo finden Sie