Theoretische Physik IV
|
|
|
- Helene Dresdner
- vor 9 Jahren
- Abrufe
Transkript
1 Sommersemester 2011 heoretische hysik IV hermodynamik und statistische hysik I Skriptum zur Vorlesung von Helmuth Hüffel Umgesetzt in L A EX von Horak Johannes LYX-Version von Bernhard Reiter
2 Kapitel 1 Vorwort Dieses Skriptum enstand nach meiner im Sommersemester 2009 gehaltenen Vorlesung. Es wurde von Johannes Horak gemäß meiner handschriftlichen Unterlagen im Herbst 2010 in L A EX gesetzt und mit Abbildungen versehen, anschließend wurde von Bernhard Reiter eine LYX- Version erstellt. Ich habe den ext weitreichend überarbeitet und stelle ihn für meine Vorlesung im Sommersemester 2011 erneut zur Verfügung. Das Skriptum wird schrittweise alle 1-2 Wochen auf der Wiki Seite ergänzt; zum Semesterende wird eine finale Gesamtversion erscheinen. Für Verbesserungvorschläge und Korrekturen bin ich dankbar und bitte diese per an [email protected] zu senden. Helmuth Hüffel Fakultät für hysik der Universität Wien Wien, am 05. März
3 Kapitel 2 hermodynamik 2.1 Einleitung Grundlegende Begriffe In diesem Abschnitt werden zuerst einige in der hermodynamik gebräuchliche Begriffe angeführt. Die hermodynamik ist eine phänomenologische heorie der Materie und bezieht ihre Konzepte direkt von Experimenten. Ein thermodynamisches System ist jedes makroskopische System (besteht typischerweise aus eilchen / Mol ). Der thermodynamische Zustand eines solchen Systems wird durch experimentell definierte thermodynamische arameter festgelegt. Solche arameter sind zum Beispiel der Druck, das Volumen V, die emperatur, die magnetische Feldstärke H... extensive Größe In diese Kategorie fallen sämtliche Größen, welche proportional zur Substanzmenge im System sind. intensive Größe Diese ist unabhängig von der Substanzmenge im System. Ändert sich ein thermodynamischer Zustand zeitlich nicht (die thermodynamischen aramter, die den Zustand festlegen, sind zeitlich konstant), befindet sich das System im thermodynamischen Gleichgewicht. Wir bezeichnen den thermodynamischen Zustand eines Systems im thermodynamischen Gleichgewicht kurz als Zustand. Im thermodynamischen Gleichgewicht besteht eine Beziehung zwischen den thermodynamischen arametern, die Zustandsgleichung genannt wird. Ein Beispiel für eine mögliche Zustandsgleichung ist f(, V, ) = 0 durch die eine Fläche, die Zustandsfläche, beschrieben wird. unkte, die auf dieser Fläche liegen, stellen Gleichgewichtszustände dar, siehe dazu auch Abbildung (2.1). Die Vorgabe von f ist zur Festlegung des thermodynamischen Systems notwendig. 3
4 4 KAIEL 2. HERMODYNAMIK Eine thermodynamische Zustandsänderung ist nur durch eine Änderung der äußeren Bedingungen des Systems möglich, das System ist ja im thermodynamischen Gleichgewicht und ändert sich - alleine von sich aus - nicht. Eine thermodynamische Zustandsänderung kann zum Beispiel durch eine Veränderung des Systemvolumens bewerkstelligt werden. Werden die äußeren Bedingungen langsam genug verändert, sodass sich das System näherungsweise immer im Gleichgewicht befindet, so wird dies als quasistationäre thermodynamische Zustandsänderung bezeichnet. Es wird von einer reversiblen thermodynamischen Zustandsänderung gesprochen, wenn bei umgekehrter äußerer Änderung des Systems die umgekehrte Reihenfolge der thermodynamischen Zuständsänderungen auftritt. Die Zustandsänderungen können auch als Kreisprozesse erfolgen. Dies bedeutet, dass das System nach einer Folge von Zustandsänderungen am Ende wieder den Anfangszustand erreicht. Bemerkung 2.1 (Reversible Zustandsänderung) Eine reversible thermodynamische Zustandsänderung A B kann durch einen stetigen Weg auf der Zustandsfläche angegeben werden, siehe Abbildung (2.2). Insbesondere gibt es für reversible Zustandsänderungen auch infinitesimale Wege! Bemerkung 2.2 (Irreversible Zustandsänderung) Irreversible Zustandsänderungen können durch keinen Weg auf der Zustandsfläche angegeben werden, obwohl Anfangs- und Endzustand auf der Zustandsfläche liegen, diese sind ja Gleichgewichtszustände. Nicht notwendigerweise müssen während einer irreversiblen Zustandsänderung der Druck, das Volumen V, oder die emperatur wohldefinierte Werte haben. Im Allgemeinen benötigt man zum Beschreiben irreversibler rozesse wesentlich mehr als 2 Freiheitsgrade und daher einen höher dimensionalen Raum zur grafischen Darstellung Abbildung 2.1: Beispiel für eine Zustandsgleichung f(, V, ) = 0, durch sie wird eine Fläche beschrieben. unkte, die auf dieser Fläche liegen, stellen Gleichgewichtszustände dar. In dieser Abbildung sind exemplarisch zwei solche unkte A und B eingezeichnet.
5 2.1. EINLEIUNG 5 Abbildung 2.2: Eine reversible Zustandsänderung A B kann durch einen stetigen Weg auf der Zustandsgleichungsfläche angegeben werden. Definition 2.1 (Mechanische Arbeit W) Mechanische Arbeit ist die vom System geleistete Arbeit durch Volumsvergrößerung. Bei infinitesimaler reversibler Volumsvergößerung dv bei Druck und emperatur gilt für die infinitesimale geleistete Arbeit dw dw = dv (2.1) Bemerkung 2.3 (Reversible Zustandsänderung und geleistete Arbeit) Die vom System bei reversiblen Zustandsänderungen geleistete Arbeit 1. entlang eines endlichen Weges ==> entspricht der Fläche im -V Diagramm W = ˆ B A dv 2. entlang eines geschlossenen Weges ==> entspricht der eingeschlossenen Fläche im -V Diagramm W = dv C
6 6 KAIEL 2. HERMODYNAMIK Bemerkung 2.4 (Irreversible Zustandsänderung und geleistete Arbeit) Für irreversible Zustandsänderungen ist W nicht durch B A Beispiel 2.1 (Freie Expansion eines Gases ins Vakuum) dv beschreibbar! Da an der äußeren Umgebung des Systems keine Arbeit geleistet wird (da kein externes Molekül bewegt wird), folgt, dass W = Wärme Definition 2.2 (Wärme Q) Wärme wird vom System aufgenommen, wenn dessen emperatur steigt, aber dem System keine Arbeit zugeführt wird. Definition 2.3 (Wärmekapazität C) Q = C (2.2) Q entspricht der vom System absorbierten Wärme, der emperaturänderung des Systems. Die Wärmekapazität C hängt vom System ab, sie ist notwendig zu dessen vollständiger Beschreibung! Es wird unterschieden zwischen C V C Erwärmung bei V = konst Erwärmung bei = konst
7 2.1. EINLEIUNG 7 Definition 2.4 (Weitere Begriffe) Wärmereservoir Darunter wird ein thermodynamisches System verstanden welches so groß ist, dass die Zufuhr oder Entnahme einer endlichen Wärmemenge die emperatur des Systems nicht ändert. thermische Isolierung Diese liegt vor wenn zwischen System und Umgebung kein Wärmeaustausch stattfindet. adiabatische Zuständsänderung Zustandsänderung eines Systemes in thermischer Isolation emperaturskala des idealen Gases Die Zustandsgleichung eines idealen Gases definiert eine emperaturskala, die emperaturskala des idealen Gases genannt wird. Definition 2.5 (Das ideale Gas) Dieses ist ein thermodynamisches System mit der Zustandsgleichung N Zahl der Moleküle k Boltzmann Konstante k = J / K V = N k (2.3) ideale Gas emperatur in Kelvin - Beachte dazu Abbildung (2.3) Definition 2.6 (Äquivalente Form der Zustandsgleichung des idealen Gases) Eine äquivalente From der Zustandsgleichung des idealen Gases lautet: n Molzahl, d.h. Anzahl der Mole des Gases V = n R (2.4) (Das Mol ist die Stoffmenge eines Systems, das aus ebenso vielen Einzelteilchen besteht, wie Atome in 12 Gramm des Nuklids Kohlenstoff-12 ( 12 C) enthalten sind) R Gaskonstante mit dem Wert R = J / (K mol). Diese Form der Gleichung setzt die Existenz von Atomen nicht voraus, n stellt eine chemische Eigenschaft des Edelgases dar. Es gilt: wobei R k = mit N k = n R der Einheit Zahl Atome / Mol der Avogadrozahl entspricht.
8 8 KAIEL 2. HERMODYNAMIK Um die emperaturskala des idealen Gases zu konstruieren, misst man V eines idealen N Gases am Siedepunkt und am Gefrierpunkt des Wassers. Man trägt diese unkte auf und verbindet sie durch eine Gerade, siehe Abbildung (2.3). Der Schnittpunkt dieser Geraden mit der Abszisse wird als Nullpunkt der Skala gewählt. Die Intervalle der emperaturskala werden so gewählt, dass der Abstand zwischen Gefrierpunkt undsiedepunkt in 100 gleiche eile zerfällt. Die resultierende Skala ist die KELVIN Skala ( K). Wie wird die emperatur eines Körpers gemessen? Der zu messende Körper wird in thermischen Kontakt mit dem obigen idealen Gas gebracht. Es werden V bestimmt, und die emperatur N des Gases (= emperatur des Körpers) mittels der Abbildung (2.3) abgelesen. Abbildung 2.3: Die ideale Gastemperatur - linearer Abhängigkeit der emperatur von V. Siehe dazu Definition (2.3)
9 2.2. DER ERSE HAUSAZ Der erste Hauptsatz Wir betrachten die Hauptsätze der hermodynamik als mathematische Axiome (die mathematische Modelle definieren) und werden rigorose Konsequenzen aus diesen Axiomen ableiten. Diese mathematischen Modelle entsprechen nicht völlig der realen physikalischen Welt, da die Atomstruktur der Materie nicht erfasst wird; im makroskopischen Bereich jedoch führen sie zu präzisen und weitreichenden Folgerungen. Der Zusammenhang zwischen den Hauptsätzen der hermodynamik und den molekularen Gesetzten wird später in der kinetischen Gastheorie näher besprochen. Definition 2.7 (Erster Hauptsatz der hermodynamik) Wir betrachten eine beliebige (reversible oder irreversible) thermodynamische Zustandsänderung, dabei seien Q die Nettowärmemenge, die vom System absorbiert wird und W die Nettoarbeitsmenge, die vom System geleistet wird. Der erste Hauptsatz der hermodynamik besagt: die durch U := Q W definierte Größe ist gleich für alle thermodynamischen Zustandsänderungen, die von dem gegebenen Anfangs- zu dem gegebenen Endzustand führen. Für reversible Zustandsänderungen gilt überdies (die folgenden unkte sind zueinander äquivalent): für infinitesimale Zustandsänderungen ist du := dq dw ein totales (auch als exakt bezeichnetes) Differential auf der Zustandsfläche. Das bedeutet, dass eine Funktion U auf der Zustandsfläche existiert, deren Differential du ist. Wir nennen U Zustandsfunktion Innere Energie. B du ist unabhängig vom Integrationsweg auf der Zustandsfläche und ist nur A vom Anfangs- und Endpunkt abhängig. für jeden geschlossenen Weg auf der Zustandsfläche ist du = 0 Definition 2.8 (exakte, geschlossene Differentialformen) Seien ω und η Differentialformen, d bezeichne die äußere Ableitung. ω heißt exakt, wenn ω = dη ω heisst geschlossen, wenn dω = 0 Beispiel 2.2 (exakte 1-Form auf R 2, Integrabilitätsbedingung)
10 10 KAIEL 2. HERMODYNAMIK Ist ω eine exakte 1-Form auf R 2 ω = g(x 1, x 2 )dx 1 + h(x 1, x 2 )dx 2 (2.5) so ist die sogenannte Integrabilitätsbedingung erfüllt ( ) ( ) g(x1, x 2 ) h(x1, x 2 ) x 2 x 1 = x 1 x 2 (2.6) Beweis : Für eine exakte 1-Form ω auf R 2 ist die zugehörige Differentialform η eine gewöhnliche Funktion η(x 1, x 2 ), deren äußere Ableitung ( ) ( ) η(x1, x 2 ) η(x1, x 2 ) dη = dx 1 + dx 2 (2.7) x 1 x 2 x 2 x 1 ergibt. Identifizierung von (2.5) und (2.7) sowie Vertauschbarkeit der zweifachen partiellen Ableitungen führt zur Integrabilitätsbedingung (2.6). Bemerkung 2.5 (exakt geschlossen) Es sei O R n ein offenes und einfach zusammenhängendes Gebiet, dann ist auf O jede geschlossene 1-Form auch exakt (Beweis mittels Satz von Stokes). Definition 2.9 (integrierender Faktor) Es sei O R n ein offenes Gebiet. Eine Funktion g in O, mit g(x) 0 für alle x O ist ein integrierender Faktor der 1-Form ω, falls g ω exakt ist, d.h. wenn gilt für eine Funktion f. g ω = df Bemerkung 2.6 (Exaktheit von du, Nicht-Exaktheit von dq oder dw ) Aufgrund des ersten Hauptsatzes ist du eine exakte 1-Form, dq oder dw sind für sich alleine betrachtet jedoch im Allgemeinen nicht exakt! Es gibt im Allgemeinen auf der Zustandsfläche keine Funktion Q, deren Differential dq wäre, ebenso keine Funktion W, deren Differential dw wäre! In historisch bedingter unglücklicher Notation verwenden auch wir symbolisch dq und dw als Namen für spezielle 1-Formen. Es wird sich später im Rahmen des zweiten Hauptsatzes zeigen, dass die dem System reversibel zugeführte infinitesimale Wärmemenge dq durch eine 1-Form beschrieben wird, die nicht exakt ist, aber einen integrierenden Faktor 1 besitzt. 1 dq = ds S bezeichnet die Zustandsfunktion Entropie.
11 2.2. DER ERSE HAUSAZ Folgerungen des ersten Hauptsatzes Wir betrachten in diesem Abschnitt infinitesimale reversible Zustandsänderungen. Sei ein System durch, V, beschrieben. Aufgrund der Zustandsgleichung f(, V, ) = 0 sind je zwei dieser Variablen unabhängig. Wir betrachten zuerst U = U(, V ) du = ( ) ( ) U U d + dv V V Damit ist die absorbierte Wärme eines Systems bei infinitesimaler reversibler Volumsänderung dq = du + }{{} dw = dv d + Nun betrachten wir U = U(, ) V [( ) ] U + dv V du = d + d dq = = ( ) ( ) U U d + [( ) ( ) U V + [( ) V d + ] [ d + ( ) ] V d + d ( ) ] V + d Mit Definition 2.10 (Enthalpie) H = U + V sowie schreiben wir C = ( ) dq d dq = C d + Enthalpie H {}}{ = ( U + V ) = ( ) H (2.8) [( ) ( ) ] U V + d (2.9) schließlich sei U = U(V, )
12 12 KAIEL 2. HERMODYNAMIK du = dv + V Die absorbierte Wärme des Systems ist nun dq = d + sodass sowie V C V = dq = C V d + ( ) dq d V d V [( ) ] U + dv V = V (2.10) [( ) ] U + dv (2.11) V Anwendungen des ersten Hauptsatzes Beispiel 2.3 (Joulesches Expansionsexperiment, innere Energie des idealen Gases) (a) vorher (b) nachher Ein ideales Gas der emperatur 1 befindet sich in einem eilvolumen V 1 eines thermisch isolierten Behälters, während im anderen eil von Volumen V 2 ein Vakuum vorherrscht. Nach dem Öffnen der rennwand verteilt sich das ideale Gas gleichmäßig im gesamten Behälter mit Volumen V 1 + V 2. Experimentell zeigt sich, dass nach der Ausdehnung des Gases die emperatur des Gases unverändert bleibt: 1 = 2 =. Es gilt Q = 0, da emperatur unverändert blieb. Wir wissen bereits (siehe Beispiel 2.1), dass das System keine Arbeit verrichtet hat, also ist W = 0. Mit dem ersten Hauptsatz folgt somit U = Q W = 0 Wir wählen V und als unabhängige Variablen, es muss also gelten (beachte 1 = 2 ) U(V 1, ) = U(V 1 + V 2, ) U = U( ) Durch Gleichung (2.10) erhalten wir, dass C V = V = du( ) d
13 2.2. DER ERSE HAUSAZ 13 Angenommen C V ist konstant (dies gilt bei experimenteller Beobachtung z.b. für einatomige ideale Gase), so ist Die innere Energie eines idealen Gases U = C V (2.12) Wir haben in 2.12 eine aditive Konstante willkürlich gleich Null gesetzt. Betrachten wir nun die Enthalpie (siehe 2.10) H = U( ) + V = (C V + Nk) ( ) H C = = dh d = C V + Nk C C V = Nk C > C V Da die emperaturänderung des Gases umgekehrt proportional zur Wärmekapazität ist, gelingt es also rascher ein ideales Gas bei konstantem Volumen zu erwärmen, als bei konstantem Druck! Beispiel 2.4 (Gleichung für reversible adiabatische Zustandsänderungen des idealen Gases) Wir wissen bereits allgemein, dass (siehe 2.11 und 2.9) [( ) ] U dq = C V d + + dv (2.13) V [( ) ( ) ] U V dq = C d + + d (2.14) Für eine Adiabate gilt dq = 0 und, da ein ideales Gas betrachtet wird (siehe Gleichung 2.12), U V = U = 0 In Gleichung 2.14 ist jedoch noch ein unbekannter erm: ( ) V =? Verwenden Zustandsgleichung 2.3 des ideales Gases damit ergibt sich, dass V = nr V = nr ( ) V = nr ( 1 ) = V 2 All dies wird nun in die Gleichungen 2.13 bzw eingesetzt: 0 = C V d + dv 0 = C d V d
14 14 KAIEL 2. HERMODYNAMIK Wir definieren nun und erhalten γ C C V γ = V d dv d = γ dv V ln = γ ln V + konst = konst V γ Somit lautet die Adiabatengleichung für ein ideales Gas V γ = konst mit γ > 1 (2.15) Im, V -Diagramm sind Adiabaten immer steiler als Isothermen, da γ > 1, siehe Abbildung 2.4. Abbildung 2.4: Adiabaten und Isothermen
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
3 Der 1. Hauptsatz der Thermodynamik
 3 Der 1. Hauptsatz der Thermodynamik 3.1 Der Begriff der inneren Energie Wir betrachten zunächst ein isoliertes System, d. h. es können weder Teilchen noch Energie mit der Umgebung ausgetauscht werden.
3 Der 1. Hauptsatz der Thermodynamik 3.1 Der Begriff der inneren Energie Wir betrachten zunächst ein isoliertes System, d. h. es können weder Teilchen noch Energie mit der Umgebung ausgetauscht werden.
10. Thermodynamik Der erste Hauptsatz Der zweite Hauptsatz Thermodynamischer Wirkungsgrad Der Carnotsche Kreisprozess
 Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Allgemeines Gasgesetz. PV = K o T
 Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
Erinnerung an die Thermodynamik
 2 Erinnerung an die Thermodynamik 2.1 Erinnerung an die Thermodynamik Hauptsätze der Thermodynamik Thermodynamische Potentiale 14 2 Erinnerung an die Thermodynamik 2.1 Thermodynamik: phänomenologische
2 Erinnerung an die Thermodynamik 2.1 Erinnerung an die Thermodynamik Hauptsätze der Thermodynamik Thermodynamische Potentiale 14 2 Erinnerung an die Thermodynamik 2.1 Thermodynamik: phänomenologische
Der Zustand eines Systems ist durch Zustandsgrößen charakterisiert.
 Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Hauptsatz der Thermodynamik
 0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
1 Thermodynamik allgemein
 Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
Winter-Semester 2017/18. Moderne Theoretische Physik IIIa. Statistische Physik
 Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
4 Thermodynamik mikroskopisch: kinetische Gastheorie makroskopisch: System:
 Theorie der Wärme kann auf zwei verschiedene Arten behandelt werden. mikroskopisch: Bewegung von Gasatomen oder -molekülen. Vielzahl von Teilchen ( 10 23 ) im Allgemeinen nicht vollständig beschreibbar
Theorie der Wärme kann auf zwei verschiedene Arten behandelt werden. mikroskopisch: Bewegung von Gasatomen oder -molekülen. Vielzahl von Teilchen ( 10 23 ) im Allgemeinen nicht vollständig beschreibbar
2 Grundbegriffe der Thermodynamik
 2 Grundbegriffe der Thermodynamik 2.1 Thermodynamische Systeme (TDS) Aufteilung zwischen System und Umgebung (= Rest der Welt) führt zu einer Klassifikation der Systeme nach Art der Aufteilung: Dazu: adiabatisch
2 Grundbegriffe der Thermodynamik 2.1 Thermodynamische Systeme (TDS) Aufteilung zwischen System und Umgebung (= Rest der Welt) führt zu einer Klassifikation der Systeme nach Art der Aufteilung: Dazu: adiabatisch
O. Sternal, V. Hankele. 5. Thermodynamik
 5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
Statistische Zustandsgröße Entropie Energieentwertung bei Wärmeübertragungen II. Hauptsatz der Thermodynamik
 Statistische Zustandsgröße Entropie Energieentwertung bei Wärmeübertragungen II. Hauptsatz der hermodynamik Die nachfolgenden Ausführungen stellen den Versuch dar, die zugegeben etwas schwierige Problematik
Statistische Zustandsgröße Entropie Energieentwertung bei Wärmeübertragungen II. Hauptsatz der hermodynamik Die nachfolgenden Ausführungen stellen den Versuch dar, die zugegeben etwas schwierige Problematik
4 Hauptsätze der Thermodynamik
 I Wärmelehre -21-4 Hauptsätze der hermodynamik 4.1 Energieformen und Energieumwandlung Innere Energie U Die innere Energie U eines Körpers oder eines Systems ist die gesamte Energie die darin steckt. Es
I Wärmelehre -21-4 Hauptsätze der hermodynamik 4.1 Energieformen und Energieumwandlung Innere Energie U Die innere Energie U eines Körpers oder eines Systems ist die gesamte Energie die darin steckt. Es
Physik 2 (B.Sc. EIT) 2. Übungsblatt
 Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
2. Thermodynamik Grundbegriffe Hauptsätze Thermodynamische Potentiale response -Funktionen
 2. Thermodynamik 1 2.1 Grundbegriffe 2 2.2 Hauptsätze 3 2.3 Thermodynamische Potentiale 4 2.4 response -Funktionen G. Kahl & B.M. Mladek (E136) Statistische Physik I Kapitel 2 5. März 2012 1 / 25 2.1 Grundbegriffe
2. Thermodynamik 1 2.1 Grundbegriffe 2 2.2 Hauptsätze 3 2.3 Thermodynamische Potentiale 4 2.4 response -Funktionen G. Kahl & B.M. Mladek (E136) Statistische Physik I Kapitel 2 5. März 2012 1 / 25 2.1 Grundbegriffe
Thermodynamische Hauptsätze, Kreisprozesse Übung
 Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Probeklausur STATISTISCHE PHYSIK PLUS
 DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
Thermodynamik der Atmosphäre II
 Einführung in die Meteorologie Teil I Thermodynamik der Atmosphäre II Der erste Hauptsatz der Thermodynamik Die Gesamtenergie in einem geschlossenen System bleibt erhalten. geschlossen steht hier für thermisch
Einführung in die Meteorologie Teil I Thermodynamik der Atmosphäre II Der erste Hauptsatz der Thermodynamik Die Gesamtenergie in einem geschlossenen System bleibt erhalten. geschlossen steht hier für thermisch
2. Thermodynamik Grundbegriffe Hauptsätze Thermodynamische Potentiale response -Funktionen
 2. Thermodynamik 1 2.1 Grundbegriffe 2 2.2 Hauptsätze 3 2.3 Thermodynamische Potentiale 4 2.4 response -Funktionen G. Kahl & F. Libisch (E136) Statistische Physik I Kapitel 2 5. April 2016 1 / 25 2.1 Grundbegriffe
2. Thermodynamik 1 2.1 Grundbegriffe 2 2.2 Hauptsätze 3 2.3 Thermodynamische Potentiale 4 2.4 response -Funktionen G. Kahl & F. Libisch (E136) Statistische Physik I Kapitel 2 5. April 2016 1 / 25 2.1 Grundbegriffe
Die innere Energie and die Entropie
 Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung.
 Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung. Nullter und Erster Hauptsatz der Thermodynamik. Thermodynamische
Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung. Nullter und Erster Hauptsatz der Thermodynamik. Thermodynamische
4.1.1 Kelvin-Planck-Formulierung des 2. Hauptsatzes der Thermodynamik. Thermischer Wirkungsgrad einer Arbeitsmaschine:
 4. Zweiter Hauptsatz der Thermodynamik 4.1. Klassische Formulierungen 4.1.1 Kelvin-Planck-Formulierung des 2. Hauptsatzes der Thermodynamik Thermischer Wirkungsgrad einer Arbeitsmaschine: Beispiel Ottomotor
4. Zweiter Hauptsatz der Thermodynamik 4.1. Klassische Formulierungen 4.1.1 Kelvin-Planck-Formulierung des 2. Hauptsatzes der Thermodynamik Thermischer Wirkungsgrad einer Arbeitsmaschine: Beispiel Ottomotor
Grundlagen der statistischen Physik und Thermodynamik
 Grundlagen der statistischen Physik und Thermodynamik "Feuer und Eis" von Guy Respaud 6/14/2013 S.Alexandrova FDIBA 1 Grundlagen der statistischen Physik und Thermodynamik Die statistische Physik und die
Grundlagen der statistischen Physik und Thermodynamik "Feuer und Eis" von Guy Respaud 6/14/2013 S.Alexandrova FDIBA 1 Grundlagen der statistischen Physik und Thermodynamik Die statistische Physik und die
16 Vektorfelder und 1-Formen
 45 16 Vektorfelder und 1-Formen 16.1 Vektorfelder Ein Vektorfeld v auf D R n ist eine Abbildung v : D R n, x v(x). Beispiele. Elektrisches und Magnetisches Feld E(x), B(x), Geschwindigkeitsfeld einer Strömung
45 16 Vektorfelder und 1-Formen 16.1 Vektorfelder Ein Vektorfeld v auf D R n ist eine Abbildung v : D R n, x v(x). Beispiele. Elektrisches und Magnetisches Feld E(x), B(x), Geschwindigkeitsfeld einer Strömung
II. Wärmelehre. II.2. Die Hauptsätze der Wärmelehre. Physik für Mediziner 1
 II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
Kapitel 4. Thermodynamisches Gleichgewicht zwischen zwei Systemen. 4.1 Systeme im thermischen Kontakt 1; E 1 =? 2; E 2 =?
 Kapitel 4 hermodynamisches Gleichgewicht zwischen zwei Systemen Im letzten Abschnitt haben wir am Beispiel des idealen Gases die Entropie (S(E)) bestimmt, und zwar im Rahmen des mikrokanonischen Ensembles
Kapitel 4 hermodynamisches Gleichgewicht zwischen zwei Systemen Im letzten Abschnitt haben wir am Beispiel des idealen Gases die Entropie (S(E)) bestimmt, und zwar im Rahmen des mikrokanonischen Ensembles
Thermodynamik. Thermodynamics. Markus Arndt. Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008
 Thermodynamik Thermodynamics Markus Arndt Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008 Die Hauptsätze der Thermodynamik & Anwendungen in Wärmekraft und Kältemaschinen
Thermodynamik Thermodynamics Markus Arndt Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008 Die Hauptsätze der Thermodynamik & Anwendungen in Wärmekraft und Kältemaschinen
Physikalische Chemie Physikalische Chemie I SoSe 2009 Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas. Thermodynamik
 Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas Thermodynamik Teilgebiet der klassischen Physik. Wir betrachten statistisch viele Teilchen. Informationen über einzelne Teilchen werden nicht gewonnen bzw.
Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas Thermodynamik Teilgebiet der klassischen Physik. Wir betrachten statistisch viele Teilchen. Informationen über einzelne Teilchen werden nicht gewonnen bzw.
Zur Thermodynamik des idealen Gases (GK Physik 1)
 Zur hermodynamik des idealen Gases (GK Physik 1 Zusammenfassung im Hinblick auf Prozesse. Reinhard Honegger, im Januar 2012. 1 Grundbegriffe 1.1 Zustandsgleichung = Ideale Gasgleichung Druck, olumen, emeratur
Zur hermodynamik des idealen Gases (GK Physik 1 Zusammenfassung im Hinblick auf Prozesse. Reinhard Honegger, im Januar 2012. 1 Grundbegriffe 1.1 Zustandsgleichung = Ideale Gasgleichung Druck, olumen, emeratur
4.1.2 Quantitative Definition durch Wärmekapazitäten
 4 Energie Aus moderner (mikroskopischer Sicht ist klar, daß die Summe U der kinetischen Energien der Moleküle eines Gases (und ggf. ihrer Wechselwirkungsenergien eine thd. Zustandsgröße des Gases ist,
4 Energie Aus moderner (mikroskopischer Sicht ist klar, daß die Summe U der kinetischen Energien der Moleküle eines Gases (und ggf. ihrer Wechselwirkungsenergien eine thd. Zustandsgröße des Gases ist,
Physikalische Chemie 1
 Physikalische Chemie 1 Christian Lehmann 31. Januar 2004 Inhaltsverzeichnis 1 Einführung 2 1.1 Teilgebiete der Physikalischen Chemie............... 2 1.1.1 Thermodynamik (Wärmelehre)............... 2 1.1.2
Physikalische Chemie 1 Christian Lehmann 31. Januar 2004 Inhaltsverzeichnis 1 Einführung 2 1.1 Teilgebiete der Physikalischen Chemie............... 2 1.1.1 Thermodynamik (Wärmelehre)............... 2 1.1.2
Physikdepartment. Ferienkurs zur Experimentalphysik 4. Daniel Jost 10/09/15
 Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 10/09/15 Inhaltsverzeichnis Technische Universität München 1 Kurze Einführung in die Thermodynamik 1 1.1 Hauptsätze der Thermodynamik.......................
Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 10/09/15 Inhaltsverzeichnis Technische Universität München 1 Kurze Einführung in die Thermodynamik 1 1.1 Hauptsätze der Thermodynamik.......................
Thermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden.
 Wärmemenge: hermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden. Sie kann aber unter gewissen oraussetzungen von einem Körer auf einen nderen übertragen werden. Dabei
Wärmemenge: hermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden. Sie kann aber unter gewissen oraussetzungen von einem Körer auf einen nderen übertragen werden. Dabei
Thermodynamik I. Sommersemester 2012 Kapitel 4, Teil 1. Prof. Dr.-Ing. Heinz Pitsch
 Thermodynamik I Sommersemester 2012 Kapitel 4, Teil 1 Prof. Dr.-Ing. Heinz Pitsch Kapitel 4, Teil 1: Übersicht 4 Zweiter Hauptsatz der Thermodynamik 4.1Klassische Formulierungen 4.1.1Kelvin-Planck-Formulierung
Thermodynamik I Sommersemester 2012 Kapitel 4, Teil 1 Prof. Dr.-Ing. Heinz Pitsch Kapitel 4, Teil 1: Übersicht 4 Zweiter Hauptsatz der Thermodynamik 4.1Klassische Formulierungen 4.1.1Kelvin-Planck-Formulierung
Physik I TU Dortmund WS2017/18 Gudrun Hiller Shaukat Khan Kapitel 6
 Physik I U Dortmund WS7/8 Gudrun Hiller Shaukat Khan Kapitel Carnotscher Kreisprozess Modell eines Kreisprozesses (Gedankenexperiment). Nicht nur von historischem Interesse (Carnot 84), sondern auch Prozess
Physik I U Dortmund WS7/8 Gudrun Hiller Shaukat Khan Kapitel Carnotscher Kreisprozess Modell eines Kreisprozesses (Gedankenexperiment). Nicht nur von historischem Interesse (Carnot 84), sondern auch Prozess
Kapitel 8: Thermodynamik
 Kapitel 8: Thermodynamik 8.1 Der erste Hauptsatz der Thermodynamik 8.2 Mechanische Arbeit eines expandierenden Gases 8.3 Thermische Prozesse des idealen Gases 8.4 Wärmemaschine 8.5 Der zweite Hauptsatz
Kapitel 8: Thermodynamik 8.1 Der erste Hauptsatz der Thermodynamik 8.2 Mechanische Arbeit eines expandierenden Gases 8.3 Thermische Prozesse des idealen Gases 8.4 Wärmemaschine 8.5 Der zweite Hauptsatz
1. Wärmelehre 1.1. Temperatur. Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités)
 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für die Temperatur Prinzip
1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für die Temperatur Prinzip
1. Wärme und der 1. Hauptsatz der Thermodynamik 1.1. Grundlagen
 IV. Wärmelehre 1. Wärme und der 1. Hauptsatz der Thermodynamik 1.1. Grundlagen Historisch: Wärme als Stoff, der übertragen und in beliebiger Menge erzeugt werden kann. Übertragung: Wärmezufuhr Joulesche
IV. Wärmelehre 1. Wärme und der 1. Hauptsatz der Thermodynamik 1.1. Grundlagen Historisch: Wärme als Stoff, der übertragen und in beliebiger Menge erzeugt werden kann. Übertragung: Wärmezufuhr Joulesche
1. Thermodynamische Potentiale, Maxwellgleichungen
 69 KAPIEL G hermodynamische Potentiale 1. hermodynamische Potentiale, Maxwellgleichungen hermodynamische Potentiale sind Funktionen von den Zustandsvariablen. Wir haben schon die innere Energie kennengelernt,
69 KAPIEL G hermodynamische Potentiale 1. hermodynamische Potentiale, Maxwellgleichungen hermodynamische Potentiale sind Funktionen von den Zustandsvariablen. Wir haben schon die innere Energie kennengelernt,
Prof. Dr. Peter Vogl, Thomas Eissfeller, Peter Greck. Übung in Thermodynamik und Statistik 4B Blatt 4 Lösung. P + a )
 U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter ogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 4 Lösung. van der Waals Gas, Adiabatengleichung
U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter ogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 4 Lösung. van der Waals Gas, Adiabatengleichung
Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie
 Sommer-Semester 2011 Moderne Theoretische Physik III Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Di 09:45-11:15, Lehmann HS 022, Geb 30.22 Do 09:45-11:15,
Sommer-Semester 2011 Moderne Theoretische Physik III Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Di 09:45-11:15, Lehmann HS 022, Geb 30.22 Do 09:45-11:15,
Entropie und 2. Hauptsatz der Thermodynamik
 Entropie und 2. Hauptsatz der hermodynamik Seminar Didaktik der Physik Datum: 20.11.1006 LV-Nummer: 706099 Vortragende: Markus Kaldinazzi Mathias Scherl Inhalte Reversible und Irreversible Prozesse Drei
Entropie und 2. Hauptsatz der hermodynamik Seminar Didaktik der Physik Datum: 20.11.1006 LV-Nummer: 706099 Vortragende: Markus Kaldinazzi Mathias Scherl Inhalte Reversible und Irreversible Prozesse Drei
22. Entropie; Zweiter Hauptsatz der Wärmelehre
 22. Entropie; Zweiter Hauptsatz der Wärmelehre Nicht alle Prozesse, die dem Energiesatz genügen, finden auch wirklich statt Beispiel: Um alle Energieprobleme zu lösen, brauchte man keine Energie aus dem
22. Entropie; Zweiter Hauptsatz der Wärmelehre Nicht alle Prozesse, die dem Energiesatz genügen, finden auch wirklich statt Beispiel: Um alle Energieprobleme zu lösen, brauchte man keine Energie aus dem
Physikalisch-chemische Grundlagen der Verfahrenstechnik
 Physikalisch-chemische Grundlagen der Verfahrenstechnik Günter Tovar, Thomas Hirth, Institut für Grenzflächenverfahrenstechnik [email protected] Physikalisch-chemische Grundlagen der
Physikalisch-chemische Grundlagen der Verfahrenstechnik Günter Tovar, Thomas Hirth, Institut für Grenzflächenverfahrenstechnik [email protected] Physikalisch-chemische Grundlagen der
I.1.3 b. (I.7a) I.1 Grundbegriffe der Newton schen Mechanik 9
 I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases. f=5 Translation + Rotation. f=7 Translation + Rotation +Vibration. Wiederholung
 1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
2. Hauptsätze der Thermodynamik
 . Hautsätze der hermodynamik ekannt sind vor allem der I. und II. Hautsatz der hermodynamik. Man sricht auch vom 0. Hautsatz und es gibt zusätzlich den III. Hautsatz. 0. HS: Einführung der emeratur als
. Hautsätze der hermodynamik ekannt sind vor allem der I. und II. Hautsatz der hermodynamik. Man sricht auch vom 0. Hautsatz und es gibt zusätzlich den III. Hautsatz. 0. HS: Einführung der emeratur als
Vorlesung Physik für Pharmazeuten PPh Wärmelehre
 Vorlesung Physik für Pharmazeuten PPh - 07 Wärmelehre Aggregatzustände der Materie im atomistischen Bild Beispiel Wasser Eis Wasser Wasserdampf Dynamik an der Wasser-Luft Grenzfläche im atomistischen Bild
Vorlesung Physik für Pharmazeuten PPh - 07 Wärmelehre Aggregatzustände der Materie im atomistischen Bild Beispiel Wasser Eis Wasser Wasserdampf Dynamik an der Wasser-Luft Grenzfläche im atomistischen Bild
Auswahl von Prüfungsfragen für die Prüfungen im September 2011
 Auswahl von Prüfungsfragen für die Prüfungen im September 2011 Was ist / sind / bedeutet / verstehen Sie unter... Wie nennt man / lautet / Wann spricht man von / Definieren Sie... Die anschließenden Fragen
Auswahl von Prüfungsfragen für die Prüfungen im September 2011 Was ist / sind / bedeutet / verstehen Sie unter... Wie nennt man / lautet / Wann spricht man von / Definieren Sie... Die anschließenden Fragen
Statistische Thermodynamik I
 Statistische hermodynamik I Universität Bern FS 2017 R SUSANNE REFFER Institut für theoretische Physik Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 2 1 Einführung in die klassische hermodynamik 4
Statistische hermodynamik I Universität Bern FS 2017 R SUSANNE REFFER Institut für theoretische Physik Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 2 1 Einführung in die klassische hermodynamik 4
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti.
 (c) Ulm University p. 1/1 Grundlagen der Physik 2 Schwingungen und Wärmelehre 10. 05. 2007 Othmar Marti [email protected] Institut für Experimentelle Physik Universität Ulm (c) Ulm University p.
(c) Ulm University p. 1/1 Grundlagen der Physik 2 Schwingungen und Wärmelehre 10. 05. 2007 Othmar Marti [email protected] Institut für Experimentelle Physik Universität Ulm (c) Ulm University p.
Einführung in die Physikalische Chemie: Inhalt. Einführung in die Physikalische Chemie:
 Einführung in die Physikalische Chemie: Inhalt Einführung in die Physikalische Chemie: Inhalt Kapitel 9: Prinzipien der Thermodynamik Inhalt: 9.1 Einführung und Definitionen 9.2 Der 0. Hauptsatz und seine
Einführung in die Physikalische Chemie: Inhalt Einführung in die Physikalische Chemie: Inhalt Kapitel 9: Prinzipien der Thermodynamik Inhalt: 9.1 Einführung und Definitionen 9.2 Der 0. Hauptsatz und seine
6 Thermodynamische Potentiale und Gleichgewichtsbedingungen
 6 hermodynamische Potentiale und Gleichgewichtsbedingungen 6.1 Einführung Wir haben bereits folgende thermodynamische Potentiale untersucht: U(S,V ) S(U,V ) hermodynamische Potentiale sind Zustandsfunktionen
6 hermodynamische Potentiale und Gleichgewichtsbedingungen 6.1 Einführung Wir haben bereits folgende thermodynamische Potentiale untersucht: U(S,V ) S(U,V ) hermodynamische Potentiale sind Zustandsfunktionen
a) Welche der folgenden Aussagen treffen nicht zu? (Dies bezieht sind nur auf Aufgabenteil a)
 Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
11.2 Die absolute Temperatur und die Kelvin-Skala
 11. Die absolute Temperatur und die Kelvin-Skala p p 0 Druck p = p(t ) bei konstantem olumen 1,0 0,5 100 50 0-50 -100-150 -00-73 T/ C Tripelpunkt des Wassers: T 3 = 73,16 K = 0,01 C T = 73,16 K p 3 p Windchill-Faktor
11. Die absolute Temperatur und die Kelvin-Skala p p 0 Druck p = p(t ) bei konstantem olumen 1,0 0,5 100 50 0-50 -100-150 -00-73 T/ C Tripelpunkt des Wassers: T 3 = 73,16 K = 0,01 C T = 73,16 K p 3 p Windchill-Faktor
1 I. Thermodynamik. 1.1 Ideales Gasgesetz. 1.2 Vereinfachte kinetische Gastheorie. 1.3 Erster Hauptsatz der Thermodynamik.
 1 I. hermodynamik 1.1 Ideales Gasgesetz eilchenzahl N Stoffmenge: n [mol], N A = 6.022 10 23 mol 1 ; N = nn A molare Größen: X m = X/n ideales Gasgesetz: V = nr, R = 8.314JK 1 mol 1 Zustandsgrößen:, V,,
1 I. hermodynamik 1.1 Ideales Gasgesetz eilchenzahl N Stoffmenge: n [mol], N A = 6.022 10 23 mol 1 ; N = nn A molare Größen: X m = X/n ideales Gasgesetz: V = nr, R = 8.314JK 1 mol 1 Zustandsgrößen:, V,,
Einführung in die Technische Thermodynamik
 Arnold Frohn Einführung in die Technische Thermodynamik 2., überarbeitete Auflage Mit 139 Abbildungen und Übungen AULA-Verlag Wiesbaden INHALT 1. Grundlagen 1 1.1 Aufgabe und Methoden der Thermodynamik
Arnold Frohn Einführung in die Technische Thermodynamik 2., überarbeitete Auflage Mit 139 Abbildungen und Übungen AULA-Verlag Wiesbaden INHALT 1. Grundlagen 1 1.1 Aufgabe und Methoden der Thermodynamik
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Prof. Dr. U. Schollwöck Sommersemester 2013
 Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Die innere Energie eines geschlossenen Systems ist konstant
 Rückblick auf vorherige Vorlesung Grundsätzlich sind alle möglichen Formen von Arbeit denkbar hier diskutiert: Mechanische Arbeit: Arbeit, die nötig ist um einen Massepunkt von A nach B zu bewegen Konservative
Rückblick auf vorherige Vorlesung Grundsätzlich sind alle möglichen Formen von Arbeit denkbar hier diskutiert: Mechanische Arbeit: Arbeit, die nötig ist um einen Massepunkt von A nach B zu bewegen Konservative
Der Zweite Hauptsatz der TD- Lernziele
 Der Zweite Hauptsatz der D- Lernziele o Einleitung o Entropie (Definition, Entropie als Zustandsfunktion, die Clausius sche Ungleichung) o Der Zweite Hauptzatz der D o Die Entropieänderungen bei speziellen
Der Zweite Hauptsatz der D- Lernziele o Einleitung o Entropie (Definition, Entropie als Zustandsfunktion, die Clausius sche Ungleichung) o Der Zweite Hauptzatz der D o Die Entropieänderungen bei speziellen
Mitschrift Thermodynamik
 Mitschrift hermodynamik Herleitung für den Gasdruck Berechnung des oberen Kreisradius d cosϕ dϕ dψ d N eilchen im Gesamtvolumen dn d N Aufschlagswahrscheinlichkeit eines eilchens Fläche df df sinϕ Gesamte
Mitschrift hermodynamik Herleitung für den Gasdruck Berechnung des oberen Kreisradius d cosϕ dϕ dψ d N eilchen im Gesamtvolumen dn d N Aufschlagswahrscheinlichkeit eines eilchens Fläche df df sinϕ Gesamte
Erinnerung: Intensive, extensive Größen
 Erinnerung: Intensive, extensive Größen Man unterscheidet intensive und extensive Größen: Vorgehen: Man denke sich ein thermodynamisches ystem in zwei eile geteilt: Untersystem Untersystem Extensive Größen
Erinnerung: Intensive, extensive Größen Man unterscheidet intensive und extensive Größen: Vorgehen: Man denke sich ein thermodynamisches ystem in zwei eile geteilt: Untersystem Untersystem Extensive Größen
PCG Grundpraktikum Versuch 4 Neutralisationswärme Multiple Choice Test
 PCG Grundpraktikum Versuch 4 Neutralisationswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Neutralisationswärme wird dieses Vorgespräch durch einen
PCG Grundpraktikum Versuch 4 Neutralisationswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Neutralisationswärme wird dieses Vorgespräch durch einen
Q i + j. dτ = i. - keine pot. und kin. Energien: depot. - adiabate ZÄ: Q i = 0 - keine technische Arbeit: Ẇ t,j = 0
 Institut für hermodynamik hermodynamik - Formelsammlung. Hauptsätze der hermodynamik (a. Hauptsatz der hermodynamik i. Offenes System de = de pot + de kin + du = i Q i + j Ẇ t,j + ein ṁ ein h tot,ein aus
Institut für hermodynamik hermodynamik - Formelsammlung. Hauptsätze der hermodynamik (a. Hauptsatz der hermodynamik i. Offenes System de = de pot + de kin + du = i Q i + j Ẇ t,j + ein ṁ ein h tot,ein aus
ST Der Stirling-Motor als Wärmekraftmaschine
 ST Der Stirling-Motor als Wärmekraftmaschine Blockpraktikum Herbst 2007 Gruppe 2b 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Stirling-Kreisprozess............................. 2 1.2 Technische
ST Der Stirling-Motor als Wärmekraftmaschine Blockpraktikum Herbst 2007 Gruppe 2b 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Stirling-Kreisprozess............................. 2 1.2 Technische
(VIII) Wärmlehre. Wärmelehre Karim Kouz WS 2014/ Semester Biophysik
 Quelle: http://www.pro-physik.de/details/news/1666619/neues_bauprinzip_fuer_ultrapraezise_nuklearuhr.html (VIII) Wärmlehre Karim Kouz WS 2014/2015 1. Semester Biophysik Wärmelehre Ein zentraler Begriff
Quelle: http://www.pro-physik.de/details/news/1666619/neues_bauprinzip_fuer_ultrapraezise_nuklearuhr.html (VIII) Wärmlehre Karim Kouz WS 2014/2015 1. Semester Biophysik Wärmelehre Ein zentraler Begriff
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - Einführung in die Wärmelehre - Prof. Dr. Ulrich Hahn WS 2008/09 Entwicklung der Wärmelehre Sinnesempfindung: Objekte warm kalt Beschreibung der thermische Eigenschaften
Physik III im Studiengang Elektrotechnik - Einführung in die Wärmelehre - Prof. Dr. Ulrich Hahn WS 2008/09 Entwicklung der Wärmelehre Sinnesempfindung: Objekte warm kalt Beschreibung der thermische Eigenschaften
PCG Grundpraktikum Versuch 5 Lösungswärme Multiple Choice Test
 PCG Grundpraktikum Versuch 5 Lösungswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Lösungswärme wird dieses Vorgespräch durch einen Multiple Choice
PCG Grundpraktikum Versuch 5 Lösungswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Lösungswärme wird dieses Vorgespräch durch einen Multiple Choice
4 Entropie. 4.1 Der Zweite Hauptsatz
 4 Entropie 4.1 Der Zweite Hauptsatz In vereinfachter Form besagt der Zweite Hauptsatz(II. HS), daß Wärme nie von selbst von niedriger zu höherer Temperatur fließen kann. Aus dieser schlichten Feststellung
4 Entropie 4.1 Der Zweite Hauptsatz In vereinfachter Form besagt der Zweite Hauptsatz(II. HS), daß Wärme nie von selbst von niedriger zu höherer Temperatur fließen kann. Aus dieser schlichten Feststellung
Formel X Leistungskurs Physik 2001/2002
 Versuchsaufbau: Messkolben Schlauch PI Barometer TI 1 U-Rohr-Manometer Wasser 500 ml Luft Pyknometer 2 Bild 1: Versuchsaufbau Wasserbad mit Thermostat Gegeben: - Länge der Schläuche insgesamt: 61,5 cm
Versuchsaufbau: Messkolben Schlauch PI Barometer TI 1 U-Rohr-Manometer Wasser 500 ml Luft Pyknometer 2 Bild 1: Versuchsaufbau Wasserbad mit Thermostat Gegeben: - Länge der Schläuche insgesamt: 61,5 cm
Thermodynamik Prof. Dr.-Ing. Peter Hakenesch
 hermodynamik _ hermodynamik Prof. Dr.-Ing. Peter Hakenesch [email protected] www.lrz-muenchen.de/~hakenesch _ hermodynamik Einleitung Grundbegriffe 3 Systembeschreibung 4 Zustandsgleichungen 5 Kinetische
hermodynamik _ hermodynamik Prof. Dr.-Ing. Peter Hakenesch [email protected] www.lrz-muenchen.de/~hakenesch _ hermodynamik Einleitung Grundbegriffe 3 Systembeschreibung 4 Zustandsgleichungen 5 Kinetische
Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester
 Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester 1. Temperaturmessung Definition der Temperaturskala durch ein reproduzierbares thermodynam. Phänomen, dem Thermometer Tripelpunkt: Eis Wasser - Dampf
Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester 1. Temperaturmessung Definition der Temperaturskala durch ein reproduzierbares thermodynam. Phänomen, dem Thermometer Tripelpunkt: Eis Wasser - Dampf
5. Zweiter Hauptsatz der Thermodynamik 5.1 Reversible und irreversible Prozesse 5.2 Formulierung des zweiten Hauptsatzes
 5.1 5. Zweiter Hauptsatz der hermodynamik 5.1 Reversible und irreversible Prozesse Stoss zweier Billardkugeln: vorwärts und rückwärts laufender Film ist physikalisch sinnvoll, vom Betrachter nicht zu unterscheiden
5.1 5. Zweiter Hauptsatz der hermodynamik 5.1 Reversible und irreversible Prozesse Stoss zweier Billardkugeln: vorwärts und rückwärts laufender Film ist physikalisch sinnvoll, vom Betrachter nicht zu unterscheiden
6.2 Zweiter HS der Thermodynamik
 Die Änderung des Energieinhaltes eines Systems ohne Stoffaustausch kann durch Zu-/Abfuhr von Wärme Q bzw. mechanischer Arbeit W erfolgen Wird die Arbeit reversibel geleistet (Volumenarbeit), so gilt W
Die Änderung des Energieinhaltes eines Systems ohne Stoffaustausch kann durch Zu-/Abfuhr von Wärme Q bzw. mechanischer Arbeit W erfolgen Wird die Arbeit reversibel geleistet (Volumenarbeit), so gilt W
Spontane und nicht spontane Vorgänge Freiwillig und nicht freiwillig ablaufende Vorgänge
 Prof. Dr. Norbert Hampp 1/7 6. Freie Energie und Freie Enthalphie / 2. Hauptsatz Spontane und nicht spontane Vorgänge Freiwillig und nicht freiwillig ablaufende Vorgänge 1. Empirischer Befund: Bei einer
Prof. Dr. Norbert Hampp 1/7 6. Freie Energie und Freie Enthalphie / 2. Hauptsatz Spontane und nicht spontane Vorgänge Freiwillig und nicht freiwillig ablaufende Vorgänge 1. Empirischer Befund: Bei einer
4.6 Hauptsätze der Thermodynamik
 Thermodynamik.6 Hautsätze der Thermodynamik.6. Erster Hautsatz: Energieerhaltungssatz In einem abgeschlossenen System bleibt der gesamte Energievorrat, also die Summe aus Wärmeenergie, mechanischer Energie
Thermodynamik.6 Hautsätze der Thermodynamik.6. Erster Hautsatz: Energieerhaltungssatz In einem abgeschlossenen System bleibt der gesamte Energievorrat, also die Summe aus Wärmeenergie, mechanischer Energie
2 Wärmelehre. Reibungswärme Reaktionswärme Stromwärme
 2 Wärmelehre Die Thermodynamik ist ein Musterbeispiel an axiomatisch aufgebauten Wissenschaft. Im Gegensatz zur klassischen Mechanik hat sie die Quantenrevolution überstanden, ohne in ihren Grundlagen
2 Wärmelehre Die Thermodynamik ist ein Musterbeispiel an axiomatisch aufgebauten Wissenschaft. Im Gegensatz zur klassischen Mechanik hat sie die Quantenrevolution überstanden, ohne in ihren Grundlagen
Physikalische Chemie Physikalsiche Chemie I SoSe 2009 Prof. Dr. Norbert Hampp 1/10 5. Zustandsfunktionen Idealer und Realer Gase. ZustandsÄnderungen
 Prof. Dr. Norbert Ham 1/10 5. Zustandsfunktionen Idealer und Realer Gase ZustandsÄnderungen Die rennung zwischen unserem System und der ÅUmweltÇ wird durch eine Wand realisiert. WÄnde kånnen unterschiedliche
Prof. Dr. Norbert Ham 1/10 5. Zustandsfunktionen Idealer und Realer Gase ZustandsÄnderungen Die rennung zwischen unserem System und der ÅUmweltÇ wird durch eine Wand realisiert. WÄnde kånnen unterschiedliche
Thermodynamik (Wärmelehre) IV Kreisprozesse und Entropie
 Physik A VL7 (..0) hermodynamik (Wärmelehre) IV Kreisprozesse und Entropie Kreisprozesse Carnot scher Kreisprozess Reale Wärmemaschinen (tirling-motor, Dampfmaschine, Otto- und Dieselmotor) Entropie Der.
Physik A VL7 (..0) hermodynamik (Wärmelehre) IV Kreisprozesse und Entropie Kreisprozesse Carnot scher Kreisprozess Reale Wärmemaschinen (tirling-motor, Dampfmaschine, Otto- und Dieselmotor) Entropie Der.
Allgemeine Gasgleichung und technische Anwendungen
 Allgemeine Gasgleichung und technische Anwendungen Ziele i.allgemeine Gasgleichung: Darstellung in Diagrammen: Begriffsdefinitionen : Iso bar chor them Adiabatische Zustandsänderung Kreisprozess prinzipiell:
Allgemeine Gasgleichung und technische Anwendungen Ziele i.allgemeine Gasgleichung: Darstellung in Diagrammen: Begriffsdefinitionen : Iso bar chor them Adiabatische Zustandsänderung Kreisprozess prinzipiell:
1. Klausur zur Vorlesung Physikalische Chemie I
 1. Klausur zur Vorlesung Physikalische Chemie I Sommersemester 2006 8. Juni 2006 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort... Matrikelnummer...
1. Klausur zur Vorlesung Physikalische Chemie I Sommersemester 2006 8. Juni 2006 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort... Matrikelnummer...
Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke) Übungsblatt 12: Ferromagnet
 Freie Universität Berlin WS 2006/2007 Fachbereich Physik 26.01.2007 Statistische Physik - heorie der Wärme PD Dr. M. Falcke) Übungsblatt 12: Ferromagnet Aufgabe 1 6 Punkte) Ein ferromagnetisches System
Freie Universität Berlin WS 2006/2007 Fachbereich Physik 26.01.2007 Statistische Physik - heorie der Wärme PD Dr. M. Falcke) Übungsblatt 12: Ferromagnet Aufgabe 1 6 Punkte) Ein ferromagnetisches System
Thermodynamik (Wärmelehre) I Die Temperatur
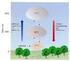 Physik A VL24 (04.12.2012) hermodynamik (Wärmelehre) I Die emperatur emperatur thermische Ausdehnung Festkörper und Flüssigkeiten Gase Das ideale Gas 1 Die emperatur Der Wärmezustand ist nicht mit bisherigen
Physik A VL24 (04.12.2012) hermodynamik (Wärmelehre) I Die emperatur emperatur thermische Ausdehnung Festkörper und Flüssigkeiten Gase Das ideale Gas 1 Die emperatur Der Wärmezustand ist nicht mit bisherigen
P = P(T, v) = k BT v b a v 2 (37.1)
 37 Van der Waals-Gas Das van der Waals-Gas wird als ein Modell für den Phasenübergang gasförmig flüssig vorgestellt und untersucht Van der Waals hat dieses Modell 1873 in seiner Doktorarbeit eingeführt
37 Van der Waals-Gas Das van der Waals-Gas wird als ein Modell für den Phasenübergang gasförmig flüssig vorgestellt und untersucht Van der Waals hat dieses Modell 1873 in seiner Doktorarbeit eingeführt
Wärmelehre Zustandsänderungen ideales Gases
 Wärmelehre Zustandsänderungen ideales Gases p Gas-Gleichung 1.Hauptsatz p V = N k B T U Q W p 1 400 1 isobar 300 200 isochor isotherm 100 p 2 0 2 adiabatisch 0 1 2 3 4 5 V V 2 1 V Bemerkung: Mischung verschiedener
Wärmelehre Zustandsänderungen ideales Gases p Gas-Gleichung 1.Hauptsatz p V = N k B T U Q W p 1 400 1 isobar 300 200 isochor isotherm 100 p 2 0 2 adiabatisch 0 1 2 3 4 5 V V 2 1 V Bemerkung: Mischung verschiedener
4 Der 2. Hauptsatz, Entropie und Gibbs scher Fundamentalsatz
 4 Der 2. Hauptsatz, Entropie und Gibbs scher Fundamentalsatz 4.1 Formulierung des 2. Hauptsatzes Es ist unsere Alltagserfahrung, dass man physikalischen Prozessen in der Regel eine natürliche Zeitabfolge
4 Der 2. Hauptsatz, Entropie und Gibbs scher Fundamentalsatz 4.1 Formulierung des 2. Hauptsatzes Es ist unsere Alltagserfahrung, dass man physikalischen Prozessen in der Regel eine natürliche Zeitabfolge
Onsagersche Gleichung. Energetische Beziehungen
 Onsagersche Gleichung. Energetische Beziehungen R I 4 V t t 1 r 8... D A p l J LX c x Zustandsgrössen sind Grössen, die zur Beschreibung des Zustandes eines stofflichen Systems dienen, T, V, p, m,... T,
Onsagersche Gleichung. Energetische Beziehungen R I 4 V t t 1 r 8... D A p l J LX c x Zustandsgrössen sind Grössen, die zur Beschreibung des Zustandes eines stofflichen Systems dienen, T, V, p, m,... T,
1.2 Zustandsgrößen, Zustandsänderungen, Gleichgewichtszustand
 1.2 Zustandsgrößen, Zustandsänderungen, Gleichgewichtszustand Wie erfolgt die Beschreibung des Zustands eines Systems? über Zustandsgrößen (makroskopische Eigenschaften, die den Zustand eines Systems kennzeichnen)
1.2 Zustandsgrößen, Zustandsänderungen, Gleichgewichtszustand Wie erfolgt die Beschreibung des Zustands eines Systems? über Zustandsgrößen (makroskopische Eigenschaften, die den Zustand eines Systems kennzeichnen)
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke)
 Freie Universität Berlin W 006/007 Fachbereich Physik 8..006 tatistische Physik - heorie der Wärme (PD Dr. M. Falcke) Übungsblatt 9: hermodynamische Identitäten, hermische/kalorische Zustandsgleichung,
Freie Universität Berlin W 006/007 Fachbereich Physik 8..006 tatistische Physik - heorie der Wärme (PD Dr. M. Falcke) Übungsblatt 9: hermodynamische Identitäten, hermische/kalorische Zustandsgleichung,
Modelle zur Beschreibung von Gasen und deren Eigenschaften
 Prof. Dr. Norbert Hampp 1/7 1. Das Ideale Gas Modelle zur Beschreibung von Gasen und deren Eigenschaften Modelle = vereinfachende mathematische Darstellungen der Realität Für Gase wollen wir drei Modelle
Prof. Dr. Norbert Hampp 1/7 1. Das Ideale Gas Modelle zur Beschreibung von Gasen und deren Eigenschaften Modelle = vereinfachende mathematische Darstellungen der Realität Für Gase wollen wir drei Modelle
Kapitel IV Wärmelehre und Thermodynamik
 Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
