Bose-Einstein-Kondensation
|
|
|
- Walther Reuter
- vor 6 Jahren
- Abrufe
Transkript
1 Bose-Einstein-Kondensation Joshua Zelle Physikalisches Proseminar, 2013 J. Zelle Bose-Einstein Kondensation / 14
2 Inhaltsverzeichnis 1 Ursprung 2 erstmalige Herstellung 3 mögliche Anwendungen J. Zelle Bose-Einstein Kondensation / 14
3 Ursprung der Bose-Einstein Kondensation 1924: Postulat von A. Einstein (beruhend auf Arbeit von S. Bose): ideale Bose-Gase kondensieren bei T=0K J. Zelle Bose-Einstein Kondensation / 14
4 Ursprung der Bose-Einstein Kondensation 1924: Postulat von A. Einstein (beruhend auf Arbeit von S. Bose): ideale Bose-Gase kondensieren bei T=0K ideales Bose-Gas: Gas freier, nicht mit einander wechselwirkender Bosonen J. Zelle Bose-Einstein Kondensation / 14
5 Wie entstehen Bose-Einstein Kondensate? Gas wird gekühlt J. Zelle Bose-Einstein Kondensation / 14
6 Wie entstehen Bose-Einstein Kondensate? Gas wird gekühlt de-broglie-wellenlängen der Gasatome werden größer als Atomabstand J. Zelle Bose-Einstein Kondensation / 14
7 Wie entstehen Bose-Einstein Kondensate? Gas wird gekühlt de-broglie-wellenlängen der Gasatome werden größer als Atomabstand alle Atome schwingen im phasenstarr J. Zelle Bose-Einstein Kondensation / 14
8 Wie entstehen Bose-Einstein Kondensate? Gas wird gekühlt de-broglie-wellenlängen der Gasatome werden größer als Atomabstand alle Atome schwingen im phasenstarr die Atome werden ununterscheidbar, es ist ein Bose-Einstein-Kondensat (BEK) entstanden J. Zelle Bose-Einstein Kondensation / 14
9 Beispiel: Rubidium Bsp.: Rb Atome bei T=20nK im Volumen V = mm 3 J. Zelle Bose-Einstein Kondensation / 14
10 Beispiel: Rubidium Bsp.: Rb Atome bei T=20nK im Volumen V = mm 3 λ B = 0.7µm J. Zelle Bose-Einstein Kondensation / 14
11 Beispiel: Rubidium Bsp.: Rb Atome bei T=20nK im Volumen V = mm 3 λ B = 0.7µm r = 4µm J. Zelle Bose-Einstein Kondensation / 14
12 erstmalige Herstellung eines Bose-Einstein Kondensates 1995: 2 Gruppen stellen erstmals ein BEK her: J. Zelle Bose-Einstein Kondensation / 14
13 erstmalige Herstellung eines Bose-Einstein Kondensates 1995: 2 Gruppen stellen erstmals ein BEK her: E. Cornell, C. Wieman: ca Atome 85 Rb bei 20nK J. Zelle Bose-Einstein Kondensation / 14
14 erstmalige Herstellung eines Bose-Einstein Kondensates 1995: 2 Gruppen stellen erstmals ein BEK her: E. Cornell, C. Wieman: ca Atome 85 Rb bei 20nK W. Ketterle: wesentlich mehr Atome, 23 Na im µk-bereich J. Zelle Bose-Einstein Kondensation / 14
15 erstmalige Herstellung eines Bose-Einstein Kondensates 1995: 2 Gruppen stellen erstmals ein BEK her: E. Cornell, C. Wieman: ca Atome 85 Rb bei 20nK W. Ketterle: wesentlich mehr Atome, 23 Na im µk-bereich 2001: Nobelpreis für erstmalige Herstellung und Erforschung eines BEK J. Zelle Bose-Einstein Kondensation / 14
16 Herstellungsprozess von E. Cornell und C. Wieman Laserkühlung in Magneto-Optischer Falle auf mk Abbildung : Magneto-Optische Falle schematisch J. Zelle Bose-Einstein Kondensation / 14
17 Herstellungsprozess von E. Cornell und C. Wieman weitere Kühlung erfolgt durch Evaporationskühlung, d.h.: J. Zelle Bose-Einstein Kondensation / 14
18 Herstellungsprozess von E. Cornell und C. Wieman weitere Kühlung erfolgt durch Evaporationskühlung, d.h.: Magnetfallen werden so manipuliert, dass schnellere Atome entweichen können J. Zelle Bose-Einstein Kondensation / 14
19 Herstellungsprozess von E. Cornell und C. Wieman weitere Kühlung erfolgt durch Evaporationskühlung, d.h.: Magnetfallen werden so manipuliert, dass schnellere Atome entweichen können dabei entweichen über 99% der Atome J. Zelle Bose-Einstein Kondensation / 14
20 Herstellungsprozess von E. Cornell und C. Wieman weitere Kühlung erfolgt durch Evaporationskühlung, d.h.: Magnetfallen werden so manipuliert, dass schnellere Atome entweichen können dabei entweichen über 99% der Atome man erreicht wenige µk bzw. nk J. Zelle Bose-Einstein Kondensation / 14
21 Nachweise BEK fallen lassen; Ausdehnungsgeschwindigkeit erlaubt Rückschlüsse auf Zustand des Materials J. Zelle Bose-Einstein Kondensation / 14
22 Nachweise BEK fallen lassen; Ausdehnungsgeschwindigkeit erlaubt Rückschlüsse auf Zustand des Materials Aufnahme von Fluoreszensbildern, von links nach rechts: 400nK, 200nK, 50nK Abbildung : Fluoreszensbilder der Rb-Atome J. Zelle Bose-Einstein Kondensation / 14
23 mögliche Anwendungen noch genauere Uhren J. Zelle Bose-Einstein Kondensation / 14
24 mögliche Anwendungen noch genauere Uhren Atomlaser bzw. kohärente Materiewellen J. Zelle Bose-Einstein Kondensation / 14
25 mögliche Anwendungen noch genauere Uhren Atomlaser bzw. kohärente Materiewellen sehr kleine Schaltkreise etc. J. Zelle Bose-Einstein Kondensation / 14
26 bisher Erreichtes 1997: erster gepulster Atomlaser (W. Ketterle) J. Zelle Bose-Einstein Kondensation / 14
27 bisher Erreichtes 1997: erster gepulster Atomlaser (W. Ketterle) 1998/99: zunächst gepulster Atomlaser mit höherer Frequenz, dann Atomlaser mit richtigem Strahl J. Zelle Bose-Einstein Kondensation / 14
28 bisher Erreichtes 1997: erster gepulster Atomlaser (W. Ketterle) 1998/99: zunächst gepulster Atomlaser mit höherer Frequenz, dann Atomlaser mit richtigem Strahl kurz darauf: Atomlaser mit 0.1s Bestrahlungszeit J. Zelle Bose-Einstein Kondensation / 14
29 bisher Erreichtes 1997: erster gepulster Atomlaser (W. Ketterle) 1998/99: zunächst gepulster Atomlaser mit höherer Frequenz, dann Atomlaser mit richtigem Strahl kurz darauf: Atomlaser mit 0.1s Bestrahlungszeit BEK mit H, 4 He, 7 Li, 23 Na, 41 K, 52 Cs, 85 Rb, 87 Rb, 133 Cs, 174 Yb J. Zelle Bose-Einstein Kondensation / 14
30 Atomlaser Abbildung : Die ersten Atomlaser J. Zelle Bose-Einstein Kondensation / 14
31 bisherige Probleme nur kleine Mengen herstellbar J. Zelle Bose-Einstein Kondensation / 14
32 bisherige Probleme nur kleine Mengen herstellbar sehr "gutes"vakuum erforderlich; bereits kleine Verunreinigungen können das BEK zerstören J. Zelle Bose-Einstein Kondensation / 14
33 bisherige Probleme nur kleine Mengen herstellbar sehr "gutes"vakuum erforderlich; bereits kleine Verunreinigungen können das BEK zerstören noch nicht möglich, gleichzeitig BEK herzustellen und zu verbrauchen J. Zelle Bose-Einstein Kondensation / 14
34 bisherige Probleme nur kleine Mengen herstellbar sehr "gutes"vakuum erforderlich; bereits kleine Verunreinigungen können das BEK zerstören noch nicht möglich, gleichzeitig BEK herzustellen und zu verbrauchen bisher nicht viele verschiedene BEK J. Zelle Bose-Einstein Kondensation / 14
35 Quellen 1 yorks/pro13/v13.pdf 2 physics/laureates/2001/popular.html P.A. Tipler, R.A. Llewellyn, "Moderne Physik", 3. Auflage, Oldenbourg Verlag, 1999, S J. Zelle Bose-Einstein Kondensation / 14
13. Cornell, Ketterle, Wieman und die 'Bose-Einstein-Kondensation'
13. Cornell, Ketterle, Wieman und die 'Bose-Einstein-Kondensation' Das Ende des 20. Jahrhunderts brachte den ersten experimentellen Nachweis eines schon lange vorhergesagten 'vierten Aggregatzustands'
Kälter als der Weltraum Mit Licht zum Temperaturnullpunkt
Universität Hamburg Institut für Laser-Physik Andreas Hemmerich Kälter als der Weltraum Mit Licht zum Temperaturnullpunkt Was ist Wärme? Warmes und kaltes Licht Kühlen mit Licht Gase am absoluten Nullpunkt:
Kalte Atome. Die kälteste Materie im Universum. Gerhard Birkl. Institut für Angewandte Physik Technische Universität Darmstadt
Kalte Atome Die kälteste Materie im Universum Gerhard Birkl Institut für Angewandte Physik Technische Universität Darmstadt Technische Universität Darmstadt Prof. Dr. Gerhard Birkl SMP 2011 1 Was ist kalt?
Kalte Atome. Gerhard Birkl. Die kälteste Materie im Universum. Institut für Angewandte Physik Technische Universität Darmstadt
Kalte Atome Die kälteste Materie im Universum Saturday Morning Physics 24. 11. 2012 Gerhard Birkl Institut für Angewandte Physik Technische Universität Darmstadt Technische Universität Darmstadt Prof.
Moderne Optik. Schwerpunkt Quantenoptik. Vorlesung im Wintersemester 2012/2013. Prof. Dr. Gerhard Birkl
Moderne Optik Schwerpunkt Quantenoptik Vorlesung im Wintersemester 2012/2013 Prof. Dr. Gerhard Birkl ATOME - PHOTONEN - QUANTEN Institut für Angewandte Physik Raum: S2/15-125 - Telefon: 16-2882 - email:
Kalte Atome. Gerhard Birkl. Die kälteste Materie im Universum. Institut für Angewandte Physik Technische Universität Darmstadt
Kalte Atome Die kälteste Materie im Universum Saturday Morning Physics 22. 11. 2014 Gerhard Birkl Institut für Angewandte Physik Technische Universität Darmstadt Technische Universität Darmstadt Prof.
Kalte Atome. Gerhard Birkl. Die kälteste Materie im Universum. Institut für Angewandte Physik Technische Universität Darmstadt
Kalte Atome Die kälteste Materie im Universum Saturday Morning Physics 21. 11. 2015 Gerhard Birkl Institut für Angewandte Physik Technische Universität Darmstadt Technische Universität Darmstadt Prof.
Bose-Einstein-Kondensat
Bose-Einstein-Kondensat Michael Schnorr Thomas Fischbach 10.11.2008 1 Was ist Bose-Einstein-Kondensat (kurz BEC) 1.1 Vorbemerkungen Aus der Quantenmechanik weiß man, dass man Elementarteilchen in zwei
5. Lichtkräfte und Laserkühlung. 5.1 Lichtkräfte 5.2 Dopplerkühlung 5.3 Konservative Kräfte
Inhalt 5. Lichtkräfte und Laserkühlung 5.1 Lichtkräfte 5.2 Dopplerkühlung 5.3 Konservative Kräfte Kräfte und Potenzial E d F Impulsübertrag E = hω p = hk k E = 0 p = 0 experimentelle Situation Absorption
Motivation Historisches Dopplerkühlen Probleme Quellen. Laserkühlung. Sören Riechers. 28. April 2010
Motivation Historisches Dopplerkühlen Probleme Quellen 28. April 2010 Motivation Historisches Dopplerkühlen Probleme Quellen Inhaltsverzeichnis 1 Motivation Warum? Anwendungen 2 Historisches Beschleunigung
Moderne Optik. Schwerpunkt Quantenoptik. Vorlesung im Wintersemester 2016/2017. Prof. Dr. Gerhard Birkl
Moderne Optik Schwerpunkt Quantenoptik Vorlesung im Wintersemester 2016/2017 Prof. Dr. Gerhard Birkl ATOME - PHOTONEN - QUANTEN Institut für Angewandte Physik Raum: S2/15-125 - Telefon: 16-20410 - email:
Bose-Einstein-Kondensation
Bose-Einstein-Kondensation Zusammenfassung des Seminarvortrags Christian Hauswald 26.11.2007 1. Einleitung Im Jahr 1924 beschäftigte sich der indische Physiker Satyendra N. Bose mit der Quantenstatistik
Bose-Einstein Kondensation und Fermigase. 1924/25 Theorie: S.Bose, A.Einstein Experiment: E.Cornell, C.Wieman, W.Ketterle
Bose-Einstein Kondensation und Fermigase 1924/25 Theorie: S.Bose, A.Einstein 1995 Experiment: E.Cornell, C.Wieman, W.Ketterle Bose-Einstein Kondensation und Fermigase Theorie Quantengase und Grundzüge
Bose-Einstein-Kondensation
Kapitel 10 Bose-Einstein-Kondensation Wenn bosonische Teilchen mit genügend Phasenraumdichte vorliegen, so dass der Abstand zwischen den Teilchen kleiner als die de-broglie Wellenlänge wird, d.h. die Wellen
Schlüsselexperimente der Quantenphysik
Bernd Kugler 15. Mai 2009 Schlüsselexperimente der Quantenphysik Das Zeigermodell Seite 2 Inhalt Optik Problemstellung Zeiger Quantenmechanik Problemstellung Zeiger Interferenz von C 60 -Molekülen Interferenz
Die seltsame Welt der Quanten
Saturday Morning Physics Die seltsame Welt der Quanten Wie spielt Gott sein Würfelspiel? 12. 11. 2005 Gernot Alber und Gerhard Birkl Institut für Angewandte Physik Technische Universität Darmstadt gernot.alber@physik.tu-darmstadt.de
Quantenmaterie in der Atom- und Festkörperphysik
Quantenmaterie in der Atom- und Festkörperphysik József Fortágh, Reinhold Kleiner jeweils Donnerstag, 10-12 Uhr, D6A08 Bose Einstein Kondensate Supraleiter Superfluide T>2.17 K T
Winter-Semester 2017/18. Moderne Theoretische Physik IIIa. Statistische Physik
Winter-Semester 217/18 Moderne heoretische Physik IIIa Statistische Physik Doent: Alexander Shnirman Institut für heorie der Kondensierten Materie Do 11:3-13:, Lehmann Raum 22, Geb 3.22 http://www.tkm.kit.edu/lehre/
EIN TROPFEN LICHT. 1 von :12. von Heinz Horeis
1 von 5 05.03.2012 16:12 Ausgabe: 6/2011, Seite 36 - Erde & Weltall EIN TROPFEN LICHT Kann Licht kondensieren wie Wasserdampf? In der Quantenwelt ist das tatsächlich möglich. Und mit der richtigen Idee
Physik IV Molekülphysik, Kernphysik, Elementarteilchenphysik
Physik IV Molekülphysik, Kernphysik, Elementarteilchenphysik Organisatorisches 1. Kontakt E-mail: bauer@physik.uni-kiel.de RaumNo: LS19/302 2. Infos zur Vorlesung http://www.ieap.uni-kiel.de/solid/ag-bauer
Physik IV Übung 4
Physik IV 0 - Übung 4 8. März 0. Fermi-Bose-Boltzmann Verteilung Ein ideales Gas befinde sich in einer Box mit Volumen V = L 3. Das Gas besteht entweder aus Teilchen, die die Bose-Einstein oder Fermi-Dirac
ALTES UND NEUES VON DER BOSE-EINSTEIN-KONDENSATION
ALTES UND NEUES VON DER BOSE-EINSTEIN-KONDENSATION GERT-LUDWIG INGOLD 1925 von Albert Einstein nach Vorarbeiten von Satyendra Nath Bose zum ersten Mal diskutiert, 1995 vom amerikanischen Wissenschaftsmagazin
Extreme Materie 5 Kompakte Sterne. Suprafluide Neutronensternmaterie
Extreme Materie 5 Kompakte Sterne Suprafluide Neutronensternmaterie Im kanonischen Neutronensternmodell besteht der Mantel aus einer suprafluiden Neutronenflüssigkeit mit einer eingelagerten supraleitfähigen
Bose-Einstein-Kondensation ultrakalter Atome
Bose-Einstein-Kondensation ultrakalter Atome Stephan Hartmann, Rainer Müller und Hartmut Wiesner 22. August 2005 1 Einleitung Am 14. Juli 1995 berichteten die angesehene Wissenschaftszeitschrift Science
Experimtentieren mit den kältesten Objekten des Universums
Experimtentieren mit den kältesten Objekten des Universums - Von Einstein s s Traum zur Realität - QUANTUM Arbeitsgruppe Prof. Immanuel Bloch Email: bloch@uni-mainz.de Internet: www.physik.uni-mainz.de/quantum
Fermi-Dirac-Verteilung
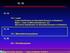
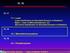
Fermi-Dirac-Verteilung Besetzungsfunktion pro innerem Freiheitsgrad: n(ε) = e (ε µ)/k B T + 6.7.23 Michael Buballa Fermi-Dirac-Verteilung Besetzungsfunktion pro innerem Freiheitsgrad: n(ε) = e (ε µ)/k
Supraleitung, der Walzer der Elektronen
Supraleitung, der Walzer der Elektronen Wolfgang Lang Fakultät für Physik der Universität Wien Forschungsgruppe Elektronische Materialeigenschaften Der elektrische Widerstand Elektronen werden gestreut:
VL 19 VL Laser VL Mehrelektronensysteme VL Periodensystem
VL 19 VL 18 18.1. Laser (Light Amplification by Stimulated Emission of Radiation) Maser = Laser im Mikrowellenbereich, d.h. Microwave Amplification by Stimulated Emission of Radiation) VL 19 19.1. Mehrelektronensysteme
Virialentwicklung. Janek Landsberg Fakultät für Physik, LMU München. Janek Landsberg. Die Virialentwicklung. Verschiedene Potentiale
Die Warum Fakultät für Physik, LMU München 14.06.2006 Die Warum 1 Die Der zweite Virialkoeffizient 2 Hard-Sphere-Potential Lennard-Jones-Potential 3 Warum 4 Bsp. Hard-Sphere-Potential Asakura-Oosawa-Potential
Klausur-Musterlösungen
Klausur-Musterlösungen 9.7.4 Theoretische Physik IV: Statistische Physik Prof. Dr. G. Alber Dr. O. Zobay. Der in Abb. dargestellte Kreisprozess wird mit einem elektromagnetischen Feld ausgeführt. Abb..
Was ist Licht? Einmal Welle-Teilchen und zurück
Was ist Licht? Einmal Welle-Teilchen und zurück Thomas Walther Laser und Quantenoptik Institut für Angewandte Physik 29. Oktober 2011 Thomas Walther Laser und Quantenoptik TU Darmstadt 1 http://antwrp.gsfc.nasa.gov/apod/astropix.html
Quanten 2. Dominik Dillhof, Abraham Hinteregger, Sarah Langer, Lisa Nachtmann
Quanten 2 Seit 50 Jahren grüble ich darüber nach was ein Lichtquant sei, und kann es immer noch nicht sagen. Heute glaubt jeder Lump er wüsste es aber er weiß es nicht. Albert Einstein Dominik Dillhof,
20. Kondensierte Materie was alles noch dazu gehört
20. Kondensierte Materie was alles noch dazu gehört [wikipedia] 1 [http://universe-review.ca] 2 Soft Matter [http://universe-review.ca] 3 Unter dem Begriff der weichen kondensierten Materie fasst man Stoffe
Bose Einstein Kondensation: Physik im Bereich von Picokelvin
Bose Einstein Kondensation: Physik im Bereich von Picokelvin Steyr, Nov 2007 Robert E. Zillich Diana Hufnagl, Dominik Kriegner, Michael Bergmair Institut für Theoretische Physik, Johannes Kepler Universität,
Der Weg zum absoluten Nullpunkt
Leibniz Online, Jahrgang 2013 Zeitschrift der Leibniz-Sozietät e. V. ISSN 1863-3285 http://leibnizsozietaet.de/wp-content/uploads/2013/01/rherrmann.pdf Rudolf Herrmann Der Weg zum absoluten Nullpunkt Vortrag
KOSMISCHE HINTERGRUNDSTRAHLUNG (CMB) Philipp Zilske Universität Bielefeld Physikalisches Proseminar
KOSMISCHE HINTERGRUNDSTRAHLUNG (CMB) Philipp Zilske Universität Bielefeld Physikalisches Proseminar 26.06.2013 26.06.2013 Philipp Zilske - Kosmische Hintergrundstrahlung 2/23 Übersicht 1. Motivation 2.
Bachelorprüfung zur Physik I und II
Bachelorprüfung zur Physik I und II Datum: 09.03.2016 Dauer: 2.0 Stunden 1 Verständnisfragen benutzte Symbole müssen definiert werden alle Zahlenwerte verlangen Einheiten. 1 Punkt pro Aufgabe 1. Nennen
Der Photoelektrische Effekt
Der Photoelektrische Effekt Anna-Maria Klingenböck und Sarah Langer 16.10.2012 Inhaltsverzeichnis 1 Das Licht Welle oder Teilchen? 1 2 Eine einfache Variante 2 3 Versuchsaufbau 3 3.1 1. Versuch...............................
Bose-Einstein Kondensation. Hauptseminar. Bastian Marquardt
Bose-Einstein Kondensation Hauptseminar Bastian Marquardt 21.07.2005 2 Inhaltsverzeichnis 1 Was ist BEK? 1 1.1 Vorbetrachung............................ 1 1.2 Theoretische Grundlagen......................
A t o m e u n t e r K o n t r o l l e
EINSICHTEN 2010 N E W S L E T T E R 0 3 n a t u r w i s s e n s c h a f t e n C h r i s t i n e R ü t h A t o m e u n t e r K o n t r o l l e Der Quantenphysiker Professor Immanuel Bloch baut mit seinem
Physik für Naturwissenschaften. Dr. Andreas Reichert
Physik für Naturwissenschaften Dr. Andreas Reichert Modulhandbuch Modulhandbuch Modulhandbuch Modulhandbuch Modulhandbuch Modulhandbuch Modulhandbuch Modulhandbuch Termine Klausur: 5. Februar?, 12-14 Uhr,
Grundlagen der Physik 3 Lösung zu Übungsblatt 2
Grundlagen der Physik 3 Lösung zu Übungsblatt 2 Daniel Weiss 17. Oktober 2010 Inhaltsverzeichnis Aufgabe 1 - Zustandsfunktion eines Van-der-Waals-Gases 1 a) Zustandsfunktion.................................
MAIUS 1: Erstes Bose-Einstein-Kondensat im All erzeugt
1 von 5 25.01.2017 08:04 Erstmalig interferieren ultrakalte Atome im Weltraum MAIUS 1: Erstes Bose-Einstein-Kondensat im All erzeugt Montag, 23. Januar 2017 Das Experiment MAIUS 1 ist am 23. Januar 2017
Moderne Physik. von Paul A. Tipler und Ralph A. LIewellyn. Oldenbourg Verlag München Wien
Moderne Physik von Paul A. Tipler und Ralph A. LIewellyn Oldenbourg Verlag München Wien Inhaltsverzeichnis I Relativitätstheorie und Quantenmechanik: Die Grundlagen der modernen Physik 1 1 Relativitätstheorie
Interferenz makroskopischer Objekte. Vortragender: Johannes Haupt
Interferenz makroskopischer Objekte Vortragender: Johannes Haupt 508385 1 Inhalt 1. Motivation 2. Geschichtliche Einführung 3. Experiment 3.1. Aufbau 3.2. Resultate 4. Thermische Strahlung 4.1. Grundidee
Supraflüssig, magnetisch, topologisch: Exotische Materie und der Physik-Nobelpreis 2016
Supraflüssig, magnetisch, topologisch: Exotische Materie und der Physik-Nobelpreis 2016 Uwe-Jens Wiese Albert Einstein Center for Fundamental Physics Institut für Theoretische Physik, Universität Bern
Vorlesung Statistische Mechanik: N-Teilchensystem
Virialentwicklung Die Berechnung der Zustandssumme bei realen Gasen ist nicht mehr exakt durchführbar. Eine Möglichkeit, die Wechselwirkung in realen Gasen systematisch mitzunehmen ist, eine Entwicklung
Quantenknistern am absoluten Nullpunkt
Quantenknistern am absoluten Nullpunkt Prof. Dr. rer. nat. Tilman Pfau Magnifizenz, lieber Herr Vorsitzender, meine Damen und Herren, es ist mir eine große Freude hier zu diesem Anlass sprechen zu dürfen.
VL 18 VL Laser VL Mehrelektronensysteme VL Periodensystem
VL 18 VL 17 17.1. Laser (Light Amplification by Stimulated Emission of Radiation) Maser = Laser im Mikrowellenbereich, d.h. Microwave Amplification by Stimulated Emission of Radiation) VL 18 18.1. Mehrelektronensysteme
Fortgeschrittenen Praktikum, SS 2008
selektive Reflexionsspektroskopie (SRS) Fortgeschrittenen Praktikum, SS 2008 Alexander Seizinger, Michael Ziller, Philipp Buchegger, Tobias Müller Betreuer: Reinhardt Maier Tübingen, den 3. Juni 2008 1
Welche Prinzipien bestimmen die quantenmechanischen Zustände, beschrieben durch ihre Quantenzahlen, die die Elektronen eines Atoms einnehmen?
phys4.021 Page 1 12. Mehrelektronenatome Fragestellung: Betrachte Atome mit mehreren Elektronen. Welche Prinzipien bestimmen die quantenmechanischen Zustände, beschrieben durch ihre Quantenzahlen, die
Mott-Isolator-Übergang
-Übergang Patrick Paul Denis Kast Universität Ulm 5. Februar 2009 Seminar zu Theorie der kondensierten Materie II WS 2008/09 Gliederung Festkörper-Modelle 1 Festkörper-Modelle Bändermodell Tight-Binding-Modell
Warum Quantengase anders sind
Warum Quantengase anders sind Schnupperuniversität 5. August 2015 Ute Löw (1) Klassische Gase Luft und Wasserdampf, die Gasgleichung (2) Quantenwelt Teilchen und Wellen (3) Das Pauli-Prinzip Verträgliche
BCS-BEC-CROSSOVER. Hauptseminarvortrag. Silvan Kretschmer
BCS-BEC-CROSSOVER Hauptseminarvortrag Silvan Kretschmer Dresden, 06/2014 1 Fermionische Kondensation: Phänomenologie 2 BCS - Meanfield - Theorie: Gap-Gleichung und chemisches Potential 3 BCS - BEC - Crossover:
H2 1862 mm. H1 1861 mm
1747 mm 4157 mm H2 1862 mm H1 1861 mm L1 4418 mm L2 4818 mm H2 2280-2389 mm H1 1922-2020 mm L1 4972 mm L2 5339 mm H3 2670-2789 mm H2 2477-2550 mm L2 5531 mm L3 5981 mm L4 6704 mm H1 2176-2219 mm L1 5205
Abstract: Vortrag zur Bose-Einstein-Kondensation
Abstract: Vortrag zur Bose-Einstein-Kondensation 1) Was ist ein Bose-Einstein-Kondensat? Grundsätzlich lässt sich jedem Teilchen in einem klassisch betrachteten Gas eine Wellenfunktion zuordnen. Über die
Atom-, Molekül- und Festkörperphysik
Atom-, Molekül- und Festkörperphysik für LAK, SS 2014 Peter Puschnig basierend auf Unterlagen von Prof. Ulrich Hohenester 3. Vorlesung, 20. 3. 2014 Mehrelektronensysteme, Fermionen & Bosonen, Hartree-Fock,
Theoretical Biophysics - Quantum Theory and Molecular Dynamics. 10. Vorlesung. Pawel Romanczuk WS 2016/17
Theoretical Biophysics - Quantum Theory and Molecular Dynamics 10. Vorlesung Pawel Romanczuk WS 2016/17 http://lab.romanczuk.de/teaching Zusammenfassung letzte VL Der Spin Grundlegende Eigenschaften Spin
Stirling sche Näherungsformel
Stirling sche Näherungsformel ln(n!) N ln(n) N für N 6.5.22 Michael Buballa Stirling sche Näherungsformel ln(n!) = N ln(k) k= N dx ln(x) = (x ln(x) x) N = N ln(n) N 6.5.22 Michael Buballa Stirling sche
Max Planck: Das plancksche Wirkungsquantum
Max Planck: Das plancksche Wirkungsquantum Überblick Person Max Planck Prinzip schwarzer Strahler Klassische Strahlungsgesetze Planck sches Strahlungsgesetz Beispiele kosmische Hintergrundstrahlung Sternspektren
13.5 Photonen und Phononen
Woche 11 13.5 Photonen und Phononen Teilchen mit linearem Dispersionsgesetz: E = c p, c - Ausbreitungsgeschwindigkeit (Licht- oder Schallgeschwindigkeit). 13.5.1 Photonen Quantisierung der Eigenschwingungen
Fazit: Wellen haben Teilchencharakter
Die Vorgeschichte Maxwell 1865 sagt elektromagnetische Wellen vorher Hertz 1886 beobachtet verstärkten Funkenüberschlag unter Lichteinstrahlung Hallwachs 1888 studiert den photoelektrischen Effekt systematisch
Institut für Quantenoptik
Institut für Quantenoptik Studium der Wechselwirkung von Licht mit Materie (Atomen) Werkzeug: modernste Lasersysteme Wozu? Kältesten Objekte im Universum
Rätsel in der Welt der Quanten. Leipziger Gespräche zur Mathematik Sächsische Akademie der Wissenschaften
Rätsel in der Welt der Quanten Leipziger Gespräche zur Mathematik Sächsische Akademie der Wissenschaften 1. Februar 2012 Die Klassische Physik Bewegung von Objekten Lichtwellen Bewegung von Objekten Newtonsche
Ein schwarzer Körper und seine Strahlung
Quantenphysik 1. Hohlraumstrahlung und Lichtquanten 2. Max Planck Leben und Persönlichkeit 3. Das Bohrsche Atommodell 4. Niels Bohr Leben und Persönlichkeit 5. Wellenmechanik 6. Doppelspaltexperiment mit
UNIVERSITÄT BIELEFELD
UNIVERSITÄT BIELEFELD 6. Atom- und Molekülphysik 6.7 - Photoeffekt Durchgeführt am 29.11.06 Dozent: Praktikanten (Gruppe 1): Dr. Udo Werner Marcus Boettiger Sarah Dirk Marius Schirmer marius.schirmer@gmx.de
Anderson-Lokalisierung
Anderson-Lokalisierung Hauptseminar: Wechselwirkende Quantengase - WS 2009/2010 David Peter 26. Januar 2010 Unordnung in der Physik Normalerweise störend Reibung in der klassischen Physik BEC: Kühlen um
Übersicht. Laserkühlung. Matthias Pospiech. Universität Hannover
Übersicht Universität Hannover 03.12.2003 Übersicht Teil I: Einführung in die Dopplerkühlung Teil II: Experimentelle Realisierung Übersicht zu Teil I 1 Motivation 2 Photonenrückstoß Einführung Kräfte 3
Ultrakalte Atome in optischen Gittern
Ultrakalte Atome in optischen Gittern Seminarvortrag Matthias Küster Gliederung Motivation Beschreibung des Potentials optischer Gitter Tight-binding-Modell Bloch -Experiment Ausblick 2 Motivation Möglichkeit
Klausur. Physik für Pharmazeuten (PPh) SS Juli 2006
Klausur Physik für Pharmazeuten (PPh) SS06 31. Juli 2006 Name: Matrikel-Nr.: Fachrichtung: Semester: Bearbeitungszeit: 90 min. Bitte nicht mit Bleistift schreiben! Nur Ergebnisse auf den Aufgabenblättern
Kohärente nichtlineare Materiewellendynamik - Helle atomare Solitonen -
Kohärente nichtlineare Materiewellendynamik - Helle atomare Solitonen - Dissertation zur Erlangung des akademischen Grades des Doktors der Naturwissenschaften (Dr. rer. nat.) an der Universität Konstanz
Entartete Fermigase: Handout zum Seminar im Fortgeschrittenen Praktikum
Entartete Fermigase: Handout zum Seminar im Fortgeschrittenen Praktikum Leszek Lupa Johannes Gutenberg Universität zu Mainz (Dated: 12.06.06) Im folgenden soll eine kurze Zusammenfassung für das Thema
Ultrakalte Quantengase. Prof. T. W. Hänsch Dr. Th. Becker, Dr. K. Dieckmann
Ultrakalte Quantengase Prof. T. W. Hänsch Dr. Th. Becker, Dr. K. Dieckmann Zeit, Ort Zeit: Dienstag, Freitag 9 15 Uhr bis 10 23 Uhr Ort: Schellingstrasse 4, Seminarraum 4/16 Persönliche Koordinaten Dr.
Seminar für Fragen der Festkörpertheorie. P.N. Racec
Seminar für Fragen der Festkörpertheorie P.N. Racec WS2003/2004 2 Contents Spezialthemen in Festkörperphysik 5. Fermi-Dirac Verteilungsfunktion........................ 6.2 Bose-Einstein Verteilungsfunktion.......................
Physik für Maschinenbau. Prof. Dr. Stefan Schael RWTH Aachen
Physik für Maschinenbau Prof. Dr. Stefan Schael RWTH Aachen Vorlesung 11 Brechung b α a 1 d 1 x α b x β d 2 a 2 β Totalreflexion Glasfaserkabel sin 1 n 2 sin 2 n 1 c arcsin n 2 n 1 1.0 arcsin
Physik IV - Schriftliche Sessionsprüfung SS 2008
Physik IV - Schriftliche Sessionsprüfung SS 2008 9:00 11:00, Donnerstag, 14. August 2008 Bitte zur Kenntnis nehmen: Es befinden sich insgesamt 6 Aufgaben auf VIER Blättern. Es können insgesamt 60 Punkte
Statistische Mechanik
Kapitel 7 Statistische Mechanik 7.1 Lagrange-Multiplikatoren Fkt fx). Bedingung eines Maximums oder Minimums) df = f x)dx = 0. Fkt von n Variablen: fx 1,x 2,...,x n ). Bedingung des Maximums: Sei df x)
Periodensystem der Elemente (PSE) Z = Ordnungszahl, von 1 bis 112 (hier)
1 1.0079 H 3 Li 6.941 19 39.098 K 23 50.942 V 27 58.933 Co 73 180.95 Ta 78 195.08 Pt 82 207.2 Pb 21 44.956 Sc 25 54.938 Mn 29 63.546 Cu 33 74.922 As 7 14.007 N 75 186.21 Re 80 200.59 Hg 84 208.98 Po* 55
Ziele der physikalischen Forschung. Materialforschung. Fluidphysik. Presseinformation
Ziele der physikalischen Forschung Materialforschung Etwa 90 Prozent der metallischen und halbleitenden Werkstoffe entstammen schmelzmetallurgischen Verfahren. Um die bestehenden Technologien zu optimieren
Statistische Mechanik
David H. Trevena Statistische Mechanik Eine Einführung '«WO«.»vmo i; Übersetzt von Thomas Filk VCH Weinheim New York Basel Cambridge Tokyo Inhaltsverzeichnis Vorwort von H. N. V. Temperley Vorwort des
Konzeption und Aufbau eines hochstabilen Lasers für Präzisionsmessungen an ultrakalten Quantengasen
Department Physik Konzeption und Aufbau eines hochstabilen Lasers für Präzisionsmessungen an ultrakalten Quantengasen Conceptual Design and Setup of a Highly Stable Laser for Precision Measurements on
c n ψ n. (7.1.1) n c n, c n
7 Quantenstatistik All hysikalischen Systeme unterliegen den Gesetzen der Quantenmechanik. Quantenmechanische Effekte haben daher auch einen Einfluss auf die statistische Physik; dies soll im folgenden
Wolfgang Ketterle ist viel beschäftigt. Der in Heidelberg. in die Kälte ging. Der Mann, der. Porträt: Wolfgang Ketterle
Porträt: Wolfgang Ketterle Der Mann, der in die Kälte ging Ein Gespräch mit dem Physiker Wolfgang Ketterle: über zerlegte Radios, Stabhochsprung, den absoluten Nullpunkt sowie den Wissenschaftskrimi, für
Hanbury Brown & Twiss Experiment. Quantenoptik
Hanbury Brown & Twiss Experiment Die Geburtsstunde der Quantenoptik Stellares Michelson Interferometer k d k itöff ist Öffnungswinkel unter dem der Stern erscheint. x 1 x 2. l=d sin( ) ~ d Interferenz
23. Vorlesung EP. IV Optik 26. Beugung (Wellenoptik) V Strahlung, Atome, Kerne 27. Wärmestrahlung und Quantenmechanik
23. Vorlesung EP IV Optik 26. Beugung (Wellenoptik) V Strahlung, Atome, Kerne 27. Wärmestrahlung und Quantenmechanik Strahlung: Stoff der Optik, Wärme-, Elektrizitätslehre u. Quantenphysik Photometrie
Periodensystem. Physik und Chemie. Sprachkompendium und einfache Regeln
Periodensystem Physik und Chemie Sprachkompendium und einfache Regeln 1 Begriffe Das (neutrale) Wasserstoffatom kann völlig durchgerechnet werden. Alle anderen Atome nicht; ein dermaßen komplexes System
Serie 170, Schwingungen und Wellen
Serie 170, Schwingungen und Wellen Brückenkurs Physik donat.adams@fhnw.ch www.adams-science.org Brückenkurs Physik Datum: 10. September 2018 1. Wellenlänge L5XMY5 (a) Berechnen Sie die Wellenlänge bei
T4p: Thermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 3 Lösungsvorschlag
T4p: Thermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 3 Lösungsvorschlag 1. Extremwerte unter Nebenbedingungen In der Vorlesung wurden die mittleren Besetzungszahlen für verschiedene
Der Stern-Gerlach-Versuch
Der Stern-Gerlach-Versuch Lukas Mazur Physik Fakultät Universität Bielefeld Physikalisches Proseminar, 08.05.2013 1 Einleitung 2 Wichtige Personen 3 Motivation 4 Das Stern-Gerlach-Experiment 5 Pauli-Prinzip
Gitter. Schriftliche VORbereitung:
D06a In diesem Versuch untersuchen Sie die physikalischen Eigenschaften eines optischen s. Zu diesen za hlen insbesondere die konstante und das Auflo sungsvermo gen. Schriftliche VORbereitung: Wie entsteht
Hauptseminar Lichtkräfte auf Atome: Fangen und Kühlen
Hauptseminar Lichtkräfte auf Atome: Fangen und Kühlen Dipolfalle und Stehwellenfalle Florian Fimpel 1. Dipolfalle d < λ d.h. elektrodynamische r Beschreibung r r des Lichts (Rayleigh Regime) Kraft des
Doppler Kühlung : Kühlen im 2 Niveausystem. Frank Ziesel. Anwendungen. Optische Melasse. Kühlen in 3 Niveausystemen
Dopplerkühlen von Atomstrahlen und optische Melasse Doppler Kühlung : Kühlen im 2 Niveausystem Anwendungen Zeeman Slower Chirped Slower Institut für Quanteninformationsverarbeitung Universität Ulm Optische
Wir gehen von nichtrelativistischen Bosonen mit dem Spin 0 und der Masse m aus. Die Einteilchenzustände mit dem Impuls p haben die Energie.
3 Ideales Bosegas Wir untersuchen das ideale Bosegas mit fester eilchenzahl. Das ideale Bosegas ist ein bemerkenswertes Modell, weil es zu einem exakt berechenbaren Phasenübergang führt, der so genannten
Experimente mit extrem kalten Gasen Experiments with extremely cold gases
Experimente mit extrem kalten Gasen Experiments with extremely cold gases Prof. Dr. Rempe, Gerhard; Dr. Dürr, Stephan Max-Planck-Institut für Quantenoptik, Garching Korrespondierender Autor E-Mail: stephan.duerr@mpq.mpg.de
Experimentalphysik EP, WS 2012/13
FAKULTÄT FÜR PHYSIK Ludwig-Maximilians-Universität München Prof. O. Biebel, PD. W. Assmann Experimentalphysik EP, WS 0/3 Probeklausur (ohne Optik)-Nummer: 7. Januar 03 Hinweise zur Bearbeitung Alle benutzten