Hanbury Brown & Twiss Experiment. Quantenoptik

Transkript

1 Hanbury Brown & Twiss Experiment Die Geburtsstunde der Quantenoptik

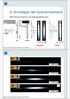
2 Stellares Michelson Interferometer k d k itöff ist Öffnungswinkel unter dem der Stern erscheint. x 1 x 2. l=d sin( ) ~ d Interferenz verschwindet, wenn l =

3 Erste Ordnung Korrelationsfunktion. k k I x 1 x 2 E(x 1 )=E ~k (x 1 )+E ~k 0(x 1 ) d. = D E(x 1 )+E(x 2 ) 2E E D E(x 1 ) 2E D + E(x 2 ) 2E +2Re (he (x 1 )E(x 2 )i) 1+g (1) (d) Erste Ordnung Korrelationsfunktion: g (1) (d) = he (x 1 )E(x 1 + d)i he (x 1 )E(x 1 )i Einsetzen von ebenen Wellen: I E(x 2 )=E ~k (x 2 )+E ~k 0(x 2 ) k k E = E 0 e i(~ k ~x wt) D E ~k (x 1)+E ~k (x 0 1 )+E ~k (x 2)+E ~k (x ) 2E 0 2 E k k k k 1+cos(( ~ k + ~ k 0 ) ~d/2)cos(kdφ/2) A guide to experiments on quantum optics, H. Bachor,T. Ralph (Wiley VCH, 2004)

4 Intensitätsinterferometer mit Radioteleskopen x² x² R. Hanbury Brown and Twiss 1950

5 Zweite Ordnung Korrelationsfunktion k k d x 1 x 2 S = hi(x 1 )I(x 2 )i = he (x 1 )E(x 1 )E (x 2 )E(x 2 )i g (2) (d) Zweite Ordnung Korrelationsfunktion: g (2) (d) = he (x 1 )E(x 1 )E (x 1 + d)e(x 1 + d)i he (x 1 )E(x 1 )i 2 I Einsetzen von ebenen Wellen: E = E 0 e i(~ k ~x wt) D E ~k (x 1)+E ~k (x 0 1 ) 2 E ~k (x 2)+E ~k (x ) 2E k k k k 0 2 E ³ E 2 ~k + E À D 2 2 ~k 0 +2 ( E ~k 2 E 2E ~k 0 cos(kdφ) E(x( 1 ) = E ~k k (x 1 1) ) + E k~k 0(x 1 ) E(x 2 )=E ~k (x 2 )+E ~k 0(x 2 ) R. Hanbury Brown and R. Q.Twiss, Nature 4497,27 (1956)

6 Vergleich Michelson Interferometer I D E ~k (x 1)+E ~k 0 (x 1 )+E ~k (x 2)+E ~k 0 (x 2 ) 2E 1+cos(( ~ k + ~ k 0 ) ~d/2)cos(kdφ/2) Hanbury Brown & Twiss Intensitätsinterferometer I D E ~k (x 1)+E ~k 0 (x 1 ) 2 E ~k (x 2)+E ~k 0 (x 2 ) 2E 2 2 2À 2 2E ³ E 2 ~k + E ~k À D 0 +2 ( E ~k 2 E 2E ~k 0 cos(kdφ) Unempfindlich gegen atmosphärische Fluktuationen

7 Geht das auch mit Licht? Photodetektor detektiert schließlich gequantelte Photonen Herleitung l war für klassische Wellen

8 Hanbury Brown & Twiss mit thermischen h Licht (Bosonen)

9 Hanbury Brown & Twiss mit thermischen h Licht (Bosonen) R. Hanbury Brown and R. Q.Twiss, Nature 4497,27 (1956)

10 Hanbury Brown & Twiss mit thermischen h Licht (Bosonen) Zeitliche 2.Ordnung Korrelationsfunktion: Photonen in Packete (bunched) g (2) (τ) = hi(t)i(t + τ)i hi(t)i 2 R. Hanbury Brown and R. Q.Twiss, Nature 4497,27 (1956)

11 Quantenmechanische Beschreibung Unterscheidbare Teilchen A B Detektorempfindlichkeit sei gleich für beide Teilchen Wahrscheinlichkeitsamplituden: ha 1i = ha 2i = a hb 1i = hb 2i = b Bei Koinzidenz entweder A in 1 und B in 2 oder A in 2 und B in 1 Wahrscheinlichkeit: P u = ha 1ihB 2i 2 + ha 2ihB 1i 2 =2 a 2 b Detektor Detektor U. Fano, American Journal of Physics 29, 539, (1961)

12 Quantenmechanische Beschreibung Bosonen A B Detektorempfindlichkeit sei gleich für beide Teilchen Wahrscheinlichkeitsamplituden: ha 1i = ha 2i = a hb 1i = hb 2i = b Bei Koinzidenz entweder A in 1 und B in 2 oder A in 2 und B in Detektor Detektor Wahrscheinlichkeit: P 2 b = ha 1i hb 2i + ha 2i hb 1i = 2ab 2 = 4 a 2 b 2 = 2P u U. Fano, American Journal of Physics 29, 539, (1961)

13 Hanbury Brown & Twiss mit nicht klassischem Licht aus einzelnen Atomen H.J. Kimble, M. Dagenais, and L. Mandel, Phys. Rev. Lett. 39, 691 (1977)

14 Hanbury Brown & Twiss mit nicht klassischem Licht aus einzelnen Atomen Thermische Photonen Photonen aus einzelnen Atomen H.J. Kimble, M. Dagenais, and L. Mandel, Phys. Rev. Lett. 39, 691 (1977)

15 Hanbury Brown & Twiss mit nicht klassischem Licht aus einzelnen Atomen H.J. Kimble, M. Dagenais, and L. Mandel, Phys. Rev. Lett. 39, 691 (1977)

16 HBT mit Elektronen (Fermionen) H. Kiesel, A.Renz and F. Hasselbach, Nature 418, 392 (2002)

17 HBT mit Elektronen (Fermionen) H. Kiesel, A.Renz and F. Hasselbach, Nature 418, 392 (2002)

18 Quantenmechanische Beschreibung Fermionen A B Detektorempfindlichkeit sei gleich für beide Teilchen Wahrscheinlichkeitsamplituden: ha 1i = ha 2i = a hb 1i = hb 2i = b Bei Koinzidenz entweder A in 1 und B in 2 oder A in 2 und B in Detektor Detektor Wahrscheinlichkeit: P 2 f = ha 1i hb 2i ha 2i hb 1i = 0

19 Hanbury Brown & Twiss mit Atomen(Bosonen) Bose Einstein Kondensat im optischen Gitter Mott Isolator Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Nature 415, (2002)

20 HBT mit Atomen Rb 87 (Bosonen) Abbildung S. Fölling, F. Gerbier, A. Widera, O. Mandel, T. Gericke and I. Bloch, Nature 434, (2005)

21 Absorptionsbilder S. Fölling, F. Gerbier, A. Widera, O. Mandel, T. Gericke and I. Bloch, Nature 434, (2005)

22 Korrelationsfunktion S. Fölling, F. Gerbier, A. Widera, O. Mandel, T. Gericke and I. Bloch, Nature 434, (2005)

23 Bandstruktur Im untersten Energieband sind Atome in Blochzustände Ausgezeichnet durch Kristallimpuls: hq Blochzustände sind Überlagerungszustände g aus mehreren ebenen Wellen mit unterschiedlichen Impuls- Zustände: p n = h hq + n2hk, 2 hk k = 2π/λ x n =( hq + n2 hk)t/m

24 Absorptionsbilder von fermionischen Atomen K 40 The inset shows a Brillouin zone mapping of the cloud, demonstrating that the Fermi gas is in a band insulating state T. Rom, Th. Best, D. van Oosten, U. Schneider, S. Fölling, B. Paredes and I. Bloch, Nature 444, (2006)

25 Korrelationsfunktion T. Rom, Th. Best, D. van Oosten, U. Schneider, S. Fölling, B. Paredes and I. Bloch, Nature 444, (2006)