1.5 Turing-Berechenbarkeit
|
|
|
- Mathias Ulrich Waltz
- vor 8 Jahren
- Abrufe
Transkript
1 A.M. Turing (1937): Maschinenmodell zur exakten Beschreibung des Begriffs effektiv berechenbar Stift Mensch a c b b Rechenblatt a b b c Lese-/Schreibkopf endliche Kontrolle Turingmaschine Eine Turingmaschine arbeitet auf Wörtern, d.h. auf Ketten von Buchstaben (oder Zeichen) über einem endlichen Zeichenvorrat (Alphabet). Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 78 / 140
2 Ein Alphabet Σ ist eine endliche, nicht-leere Menge, deren Elemente Buchstaben, Zeichen oder Symbole genannt werden. Beispiele: Σ 1 := {a, b} Σ 2 := {(,),+,,, /, a} Σ 3 := {0, 1,#} Durch Hintereinanderschreiben von Zeichen erhält man Wörter. n 1 : Σ n = Wörter der Länge n über Σ ε = Wort der Länge 0 (leeres Wort) Σ + := Σ n nicht-leere Wörter über Σ n 1 Σ := Σ + {ε} Wörter über Σ Beispiele: Σ 2 1 Σ 1 = {aa, ab, ba, bb} = {ε, a, b, aa, ab, ba, bb, aaa,...} Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 79 / 140
3 Für w Σ ist w die Länge von w: ε = 0 w = n für alle w Σ n, n 1. Für w Σ und a Σ ist w a die a-länge von w: ε a = 0 wb a = w a für b a wa a = w a + 1 Beachte: u Σ m v Σ n : uv Σ m+n u Σ m : εu = u = uε u, v, w Σ : (uv)w = u(vw) (Σ,, ε) ist Halbgruppe mit neutralem Element ε (d.h. ein Monoid) Jedes w Σ lässt sich eindeutig als Folge von Zeichen aus Σ schreiben. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 80 / 140
4 Lemma 1.25 Seien u, v, x, y Σ mit uv = xy. Dann gilt genau einer der drei folgenden Fälle: (1.) u = x und u = x und v = y. (2.) u > x, und es gibt ein z Σ + mit u = xz und y = zv. (3.) u < x, und es gibt ein z Σ + mit x = uz und v = zy. Abkürzende Schreibweise: u 0 = ε, u 1 = u und u n+1 = u n u für alle u Σ, n 1. Mit R : Σ Σ wird die Spiegelungsfunktion (engl.: reversal) bezeichnet: ε R = ε, (ua) R = au R für alle u Σ und a Σ. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 81 / 140
5 Eine Teilmenge L von Σ heißt eine Formale Sprache über Σ. Beispiele: (1.) L 1 := { w Σ 1 w ist eine ungerade Zahl } (2.) L 2 := { korrekt geklammerte arithmetische Ausdrücke über Σ 2 } z.b.: (a a) a + a/(a + a) a L 2 (((a))) L 2 ((a+) a( L 2 Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 82 / 140
6 Turingmaschine (TM) unendliches Band... a b c # Lese-/Schreibkopf... endliche Kontrolleinheit Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 83 / 140
7 Definition 1.26 Eine Turingmaschine (TM) ist gegeben durch ein 7-Tupel M = (Z,Σ,Γ, δ, z 0,, E): Z endliche Zustandsmenge Σ Eingabealphabet Γ Σ Arbeitsalphabet z 0 Z Startzustand Γ Σ Blank (Leerzeichen) E Z Endzustände δ : ((Z E) Γ) (Z Γ {L, R, N}) Überführungsfunktion Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 84 / 140
8 Rechenschritte von M: δ(z 1, a) = (z 1, b, L): a b c... z b b c... z 1 Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 85 / 140
9 δ(z 2, a) = (z 2, b, R): a b c... z b b c... z 2 Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 86 / 140
10 δ(z 3, a) = (z 3, b, N): a b c... z b b c... z 3 Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 87 / 140
11 Definition 1.27 Eine Konfiguration der TM M ist ein Wort k Γ ZΓ +. k deckt den von verschiedenen Teil des Bandes ab. Beispiele: 10z 1 abc, 10z 2 abc, 10z 3 abc, 1z 1 0bbc, 10bz 2 bc, 10z 3 bbc Startkonfiguration für Eingabe x Σ + : z 0 x Startkonfiguration für Eingabe ε : z 0 Haltekonfiguration: uzv mit z E. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 88 / 140
12 Definition 1.28 (Berechnungsrelation :) a 1...a m z cb 2...b n falls δ(z, b 1 ) = (z, c, N) (m 0, n 1) a a 1...a m zb 1...b n 1...a m cz b 2...b n falls δ(z, b 1 ) = (z, c, R) (m 0, n 2) a 1...a m 1 z a m cb 2...b n falls δ(z, b 1 ) = (z, c, L) (m 1, n 1) Sonderfälle: a 1...a m zb 1 a 1...a m cz zb 1...b n z cb 2...b n falls δ(z, b 1 ) = (z, c, R). falls δ(z, b 1 ) = (z, c, L). bezeichnet den reflexiv-transitiven Abschluss von, d.h. k k gdw. m 0 k 0,...,k m : k = k 0 k 1... k m = k Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 89 / 140
13 Eine Rechnung von M bei Eingabe x Σ ist eine Folge z 0 x = k 0 k 1 k Eine Rechnung kann endlich oder unendlich sein. Eine erfolgreiche Rechnung von M bei Eingabe x Σ ist eine endliche Rechnung z 0 x = k 0 k 1 k 2... k m 1 k m, sodass k m eine Haltekonfiguration ist. T(M) = { x Σ erfolgreiche Rechnung von M mit Eingabe x } ist die von M akzeptierte Sprache. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 90 / 140
14 Beispiel TM für binäres +1 : M = ({z 0, z 1, z 2, z e }, {0, 1}, {0, 1, }, δ, z 0,, {z e }) mit δ(z 0, 0) = (z 0, 0, R), δ(z 0, 1) = (z 0, 1, R), δ(z 0, ) = (z 1,, L) δ(z 1, 0) = (z 2, 1, L), δ(z 1, 1) = (z 1, 0, L), δ(z 1, ) = (z e, 1, N) δ(z 2, 0) = (z 2, 0, L), Beispielrechnung: δ(z 2, 1) = (z 2, 1, L), δ(z 2, ) = (z e,, R) z z z z 0 10z 1 1 1z 1 00 z z z e 110, also z z e 110. Bezeichnung für diese TM: Band := Band +1 Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 91 / 140
15 Definition 1.29 Eine Funktion f : Σ Σ heißt Turing-berechenbar, wenn es eine Turingmaschine M gibt, sodass für alle x, y Σ gilt: f(x) = y gdw. z 0 x M... z ey... (z e E). Ist f(x) undefiniert, so ist die Rechnung von M, die mit der Startkonfiguration z 0 x beginnt, unendlich, d.h., M hält ausgehend von z 0 x nicht an! Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 92 / 140
16 Beispiele: (1) Die Funktion bin_plus1: {0, 1} {0, 1} ist Turing-berechenbar. (2) Die Funktion R : Σ Σ w w R ist Turing-berechenbar. (3) Die Funktion 2 : Σ Σ w ww ist Turing-berechenbar. bin(n) bin(n + 1) Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 93 / 140
17 Definition 1.30 Sei A Σ. Die Menge A heißt entscheidbar, wenn ihre charakteristische Funktion χ A Turing-berechenbar ist: χ A (w) = { 1, falls w A, 0, falls w A. Beispiel: Die Menge A = { w {a, b} w ist gerade } ist entscheidbar. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 94 / 140
18 Definition 1.31 Sei A Σ. Die Menge A heißt semi-entscheidbar, wenn die folgende Funktion χ A Turing-berechenbar ist: χ A (w) = { 1, falls w A, undefiniert, falls w A. Die Turingmaschine zur Berechnung von χ A hält also ausgehend von der Startkonfiguration z 0 w (w Σ ) genau dann an, wenn w A ist. Lemma 1.32 Jede entscheidbare Menge ist semi-entscheidbar. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 95 / 140
19 Definition 1.33 Eine Funktion f : N k N heißt Turing-berechenbar, wenn es eine Turingmaschine M gibt, sodass für alle n 1,...,n k, m N gilt: f(n 1,...,n k ) = m gdw. z 0 bin(n 1 )#bin(n 2 )#...#bin(n k ) M... z ebin(m)... Ist f(n 1,...,n k ) undefiniert, dann hält M ausgehend von der Startkonfiguration z 0 bin(n 1 )#bin(n 2 )#...#bin(n k ) nicht an! (z e E). Beispiel: Die Funktion +1: N N n n + 1 ist Turing-berechenbar. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 96 / 140
20 Eine Mehrband-Turingmaschine mit k 2 Bändern:... a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a b 1 b 2 b 3 b 4 b 5 b 6 b 7 b 8 b 9 b c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9 c endliche Kontrolle δ : (Z Γ k ) (Z Γ k {L, R, N} k ) Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 97 / 140
21 Beispiel: Eine 2-Band-Turingmaschine zur Berechnung der Spiegelungsfunktion M = ( {z 0, z 1, z 2, z 3, z e }, {a, b}, {a, b, }, δ, z 0,, {z e } ) mit: δ z 0 z 1 z 2 z 3 (a, a) (a, b) (a, ) (z 1, a,, R, N) (z 1, a,, R, N) (z 2,, a, L, R) (b, a) (b, b) (b, ) (z 1, b,, R, N) (z 1, b,, R, N) (z 2,, b, L, R) (, a) (z 3,, a, N, L) (, b) (z 3,, b, N, L) (, ) (z e,,, N, N) (z 2,,, L, N) (z 3,,, N, L) (z e,,, N, R) Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 98 / 140
22 Eingabe: w = aab Startkonfiguration: Band 1... a a b Band 2 z 0 Beschreibung: (z 0 aab, z 0 ) Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 99 / 140
23 Rechnung: (z 0 aab, z 0 ) M (az 1 ab, z 1 ) M (aaz 1 b, z 1 ) M (aabz 1, z 1 ) M (aaz 2 b, z 2 ) M (az 2 a, bz 2 ) M (z 2 a, baz 2 ) M (z 2, baaz 2 ) M (z 3, baz 3 a ) M (z 3, bz 3 aa ) M (z 3, z 3 baa ) M (z 3, z 3 baa ) M (z e, z e baa ) Haltekonfiguration: Band b a a... z e Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 100 / 140
24 Satz 1.34 Zu jeder Mehrband-TM M gibt es eine (Einband-) Turingmaschine M, die dieselbe Funktion berechnet wie M. Beweis: Mehrband-Turingmaschine M mit k Bändern:... a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9... Band 1... b 1 b 2 b 3 b 4 b 5 b 6 b 7 b 8 b 9... Band 2... c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9... Band 3 Zustand: z Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 101 / 140
25 Einband-TM M :... a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9... *... b 1 b 2 b 3 b 4 b 5 b 6 b 7 b 8 b 9... *... c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9... * Band mit 2k Spuren Arbeitsalphabet: Γ := Γ (Γ { }) 2k Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 102 / 140
26 Arbeitsweise von M : Startkonfiguration: z 0 w (w Σ ) 1. Phase: w * * * 2. Phase: M simuliert M schrittweise. 3. Phase: Ergebnis von Spur 1 auf das gesamte Band kopieren. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 103 / 140
27 Ist M eine 1-Band-TM, so ist M(i, k) (i k) die k-band-tm, die auf Band i M simuliert, wobei alle anderen Bänder unverändert bleiben. Beispiele: (i) Band := Band + 1(i, k). Schreibweise: Band i := Band i + 1 (ii) Band i := Band i 1. (iii) Band i := 0. (iv) Band i := Band j. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 104 / 140
28 Hintereinanderschalten von TMen M i = (Z i,σ,γ i, δ i, z i,, E i ), i = 1, 2 M : start M 1 M 2 stop M = (Z 1 Z 2,Σ,Γ 1 Γ 2, δ, z 1,, E 2 ) mit δ := δ 1 δ 2 {(z e, a, z 2, a, N) z e E 1, a Γ 1 }. Beispiele: (i) start Band := Band + 1 Band := Band + 1 Band := Band + 1 stop Schreibweise: Band := Band + 3 Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 105 / 140
29 (ii) start M z e 1 M 1 stop M 2 z e2 stop (iii) Band = 0? : Z := {z 0, z 1, ja,nein}, E = {ja,nein}, δ : (z 0, a) (nein, a, N) für a 0 (z 0, 0) (z 1, 0, R) (z 1, a) (nein, a, L) für a (z 1, ) (ja,, L) Hieraus: Band i=0? Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 106 / 140
30 (iv) start Band i = 0? M nein ja stop Schreibweise: WHILE Band i 0 DO M. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 107 / 140
31 Beobachtung: Die Turingmaschinen bilden eine einfache Programmiersprache: Die Funktionen +c und c (c N) sowie f(x 1,...,x n ) = x i (1 i n) sind TM-berechenbar. Diese Sprache enthält einfache Wertzuweisungen. Sie enthält einfache Abfragen und while-schleifen. Das Hintereinanderschalten von Programmen ist möglich. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 108 / 140
32 Satz 1.35 Turingmaschinen können WHILE-Programme simulieren, d.h. jede WHILE-berechenbare Funktion ist auch Turing-berechenbar. Satz 1.36 Jede Turingmaschine kann durch ein GOTO-Programm simuliert werden, d.h. jede Turing-berechenbare Funktion ist auch GOTO-berechenbar. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 109 / 140
33 Beweis: Sei M = (Z,Σ,Γ, δ, z 1,, E) eine TM, die die Funktion f : N k N berechnet. Für alle n 1,...,n k N: f(n 1,...,n k ) ist definiert: z 1 bin(n 1 )#bin(n 2 )#...#bin(n k ) M... z ebin(f(n 1,...,n k ))... f(n 1,...,n k ) ist nicht definiert: z 1 bin(n 1 )#bin(n 2 )#...#bin(n k ) M... M... M... GOTO-Programm M zur Simulation von M: M 1 : P 1 ; M 2 : P 2 ; M 3 : P 3 P 1 : (n 1,...,n k ) Darstellung der Konfiguration z 1 bin(n 1 )#...#bin(n k ) in x, y, z. P 2 : schrittweise Simulation von M auf x, y, z. P 3 : Endwerte von x, y, z f(n 1,...,n k ). Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 110 / 140
34 Kodierung von TM-Konfigurationen Z = {z 1,...,z k }, Γ = {a 1,...,a m }, b > Γ Konfiguration: a i1 a i2...a ip z l a j1 a j2...a jq Kodierung: x = (i 1 i 2...i p ) b y = (j q...j 2 j 1 ) b z = l p mit (i 1...i p ) b := i µ b p µ und (j q...j 1 ) b := µ=1 q ν=1 j ν b ν 1 Beispiel Γ = {a 1, a 2, a 3, a 4 }, b = 5: Konfiguration: a 1 a 2 a 1 z 2 a 3 a 4 Kodierung: x = (a 1 a 2 a 1 ) 5 = = 36 y = (a 4 a 3 ) 5 = = 23 z = 2 P 1 und P 3 : elementare arithmetische Operationen. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 111 / 140
35 Beispiel: Eingabe: (10, 6). Kodierung: 0 a 1, 1 a 2, # a 3, a 4 und b = 5. Eingabekonf.: z 1 bin(10)#bin(6) = z #110 = z 1 a 2 a 1 a 2 a 1 #a 2 a 2 a 1. WHILE-Programm P 1 : z 1; x 0; y 0; WHILE x 2 0 DO x 3 (x 2 MOD 2) + 1; x 2 x 2 DIV 2; y y 5 + x 3 END; y y 5 + 3; WHILE x 1 0 DO x 3 (x 1 MOD 2) + 1; x 1 x 1 DIV 2; y y 5 + x 3 END; Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 112 / 140
36 GOTO-Programm M 2 : P 2 M 2 : a := y MOD b; IF (z = 1) AND (a = 1) THEN GOTO M 1,1 ; IF (z = 1) AND (a = 2) THEN GOTO M 1,2 ;. IF (z = k) AND (a = m) THEN GOTO M k,m ; M 1,1 : Programmstück zur Simulation von δ(z 1, a 1 ) GOTO M 2 ;. M k,m : Programmstück zur Simulation von δ(z k, a m ) GOTO M 2 ; Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 113 / 140
37 Simulation eines TM-Schritts: δ(z i, a j ) = (z i, a j, L): a i1...a ip z i a }{{}}{{} j a j2...a jq }{{} x z y M a i1...a ip 1 z i a }{{}}{{} ip a j a j2...a jq }{{} x z y GOTO-Programmstück: z := i ; y := y DIV b; y := y b + j ; y := y b + (x MOD b); x := x DIV b; Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 114 / 140
38 Übersicht GOTO WHILE TM µ-rekursiv LOOP prim. rekursiv Die Ackermannfunktion a(.,.) ist WHILE-berechenbar und total, aber sie ist nicht LOOP-berechenbar. Prof. Dr. F. Otto (Universität Kassel) Berechenbarkeit und Formale Sprachen 115 / 140
Mächtigkeit von WHILE-Programmen
 Mächtigkeit von WHILE-Programmen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 26. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Mächtigkeit von WHILE-Programmen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 26. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
GTI. Hannes Diener. 6. Juni - 13. Juni. ENC B-0123, [email protected]
 GTI Hannes Diener ENC B-0123, [email protected] 6. Juni - 13. Juni 1 / 49 Die Turingmaschine war das erste (bzw. zweite) formale Modell der Berechenbarkeit. Sie wurden bereits 1936 (also lange
GTI Hannes Diener ENC B-0123, [email protected] 6. Juni - 13. Juni 1 / 49 Die Turingmaschine war das erste (bzw. zweite) formale Modell der Berechenbarkeit. Sie wurden bereits 1936 (also lange
3. Turingmaschinen FORMALISIERUNG VON ALGORITHMEN. Turingmaschinen Registermaschinen Rekursive Funktionen UNTERSCHEIDUNGSMERKMALE DER ANSÄTZE:
 FORMALISIERUNG VON ALGORITHMEN Wegen der beobachteten Zusammenhänge zwischen Berechnungs-, Entscheidungs- und Aufzählungsverfahren genügt es Berechnungsverfahren zu formalisieren. Weiter genügt es Verfahren
FORMALISIERUNG VON ALGORITHMEN Wegen der beobachteten Zusammenhänge zwischen Berechnungs-, Entscheidungs- und Aufzählungsverfahren genügt es Berechnungsverfahren zu formalisieren. Weiter genügt es Verfahren
Zusammenfassung Grundzüge der Informatik 4
 Zusammenfassung Grundzüge der Informatik 4 Sommersemester 04 Thorsten Wink 21. September 2004 Version 1.2 Dieses Dokument wurde in L A TEX 2εgeschrieben. Stand: 21. September 2004 Inhaltsverzeichnis 1
Zusammenfassung Grundzüge der Informatik 4 Sommersemester 04 Thorsten Wink 21. September 2004 Version 1.2 Dieses Dokument wurde in L A TEX 2εgeschrieben. Stand: 21. September 2004 Inhaltsverzeichnis 1
Wortproblem für kontextfreie Grammatiken
 Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Deterministische Turing-Maschinen (DTM) F3 03/04 p.46/395
 Deterministische Turing-Maschinen (DTM) F3 03/04 p.46/395 Turing-Machine Wir suchen ein Modell zur formalen Definition der Berechenbarkeit von Funktionen und deren Zeit- und Platzbedarf. Verschiedene Modelle
Deterministische Turing-Maschinen (DTM) F3 03/04 p.46/395 Turing-Machine Wir suchen ein Modell zur formalen Definition der Berechenbarkeit von Funktionen und deren Zeit- und Platzbedarf. Verschiedene Modelle
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten
 Inhalt 1 Einführung 2 Automatentheorie und Formale Sprachen Grammatiken Reguläre Sprachen und endliche Automaten Kontextfreie Sprachen und Kellerautomaten Kontextsensitive und Typ 0-Sprachen 3 Berechenbarkeitstheorie
Inhalt 1 Einführung 2 Automatentheorie und Formale Sprachen Grammatiken Reguläre Sprachen und endliche Automaten Kontextfreie Sprachen und Kellerautomaten Kontextsensitive und Typ 0-Sprachen 3 Berechenbarkeitstheorie
b) Eine nd. k-band-turingmaschine M zur Erkennung einer m-stelligen Sprache L (Σ ) m ist ein 8-Tupel
 2. Turingmaschinen Zur Formalisierung von Algorithmen benutzen wir hier Turingmaschinen. Von den vielen Varianten dieses Konzeptes, die sich in der Literatur finden, greifen wir das Konzept der on-line
2. Turingmaschinen Zur Formalisierung von Algorithmen benutzen wir hier Turingmaschinen. Von den vielen Varianten dieses Konzeptes, die sich in der Literatur finden, greifen wir das Konzept der on-line
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Turing-Maschine, Berechenbarkeit INSTITUT FÜR THEORETISCHE 0 KIT 07.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen
Theoretische Grundlagen der Informatik Turing-Maschine, Berechenbarkeit INSTITUT FÜR THEORETISCHE 0 KIT 07.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen
Konfiguration einer TM als String schreiben: Bandinschrift zwischen den Blank-Zeichen Links von der Kopfposition Zustand einfügen.
 H MPKP Konfiguration einer TM als String schreiben: Bandinschrift zwischen den Blank-Zeichen Links von der Kopfposition Zustand einfügen. Beispiel: 1234q567 bedeutet: Kopf steht auf 5, Zustand ist q. Rechnung:
H MPKP Konfiguration einer TM als String schreiben: Bandinschrift zwischen den Blank-Zeichen Links von der Kopfposition Zustand einfügen. Beispiel: 1234q567 bedeutet: Kopf steht auf 5, Zustand ist q. Rechnung:
Formale Sprachen. Script, Kapitel 4. Grammatiken
 Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprachen bedeutend für die Syntaxdefinition von Programmiersprachen (Compilerbau) Automaten
Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprachen bedeutend für die Syntaxdefinition von Programmiersprachen (Compilerbau) Automaten
Vorlesung Theoretische Informatik
 Vorlesung Theoretische Informatik Automaten und Formale Sprachen Hochschule Reutlingen Fakultät für Informatik Masterstudiengang Wirtschaftsinformatik überarbeitet von F. Laux (Stand: 09.06.2010) Sommersemester
Vorlesung Theoretische Informatik Automaten und Formale Sprachen Hochschule Reutlingen Fakultät für Informatik Masterstudiengang Wirtschaftsinformatik überarbeitet von F. Laux (Stand: 09.06.2010) Sommersemester
Theoretische Informatik 2
 Theoretische Informatik 2 Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2009/10 Entscheidbare und semi-entscheidbare Sprachen Definition Eine NTM M hält bei Eingabe x, falls
Theoretische Informatik 2 Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2009/10 Entscheidbare und semi-entscheidbare Sprachen Definition Eine NTM M hält bei Eingabe x, falls
Theorie der Informatik
 Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: [email protected] 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: [email protected] 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
5. Varianten des Turingmaschinen-Konzeptes I: Varianten der Programmstruktur
 5. Varianten des Turingmaschinen-Konzeptes I: Varianten der Programmstruktur In der Literatur findet sich eine Vielzahl von Varianten des Turingmaschinen-Konzeptes, die sich alle als äquivalent zum Grundkonzept
5. Varianten des Turingmaschinen-Konzeptes I: Varianten der Programmstruktur In der Literatur findet sich eine Vielzahl von Varianten des Turingmaschinen-Konzeptes, die sich alle als äquivalent zum Grundkonzept
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier [email protected]
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier [email protected] 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier [email protected] 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
3. Ziel der Vorlesung
 3. Ziel der Vorlesung Der Zweck der Vorlesung ist das Studium fundamentaler Konzepte in der Algorithmentheorie. Es werden relevante Maschinenmodelle, grundlegende und höhere Datenstrukturen sowie der Entwurf
3. Ziel der Vorlesung Der Zweck der Vorlesung ist das Studium fundamentaler Konzepte in der Algorithmentheorie. Es werden relevante Maschinenmodelle, grundlegende und höhere Datenstrukturen sowie der Entwurf
Formelsammlung theoretische Informatik I
 Formelsammlung theoretische Informatik I Stand: 27.05.2005 - Version: 1.0.3 Erhältlich unter http://privat.macrolab.de Diese Formelsammlung basiert auf der Vorlesung Theoretische
Formelsammlung theoretische Informatik I Stand: 27.05.2005 - Version: 1.0.3 Erhältlich unter http://privat.macrolab.de Diese Formelsammlung basiert auf der Vorlesung Theoretische
Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung
 Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung Frank Heitmann [email protected] 13. Mai 2014 Frank Heitmann [email protected] 1/17 Überblick Wir hatten
Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung Frank Heitmann [email protected] 13. Mai 2014 Frank Heitmann [email protected] 1/17 Überblick Wir hatten
Theoretische Informatik 1
 Theoretische Informatik 1 Bernhard Nessler Institut für Grundlagen der Informationsverabeitung TU Graz SS 2007 Übersicht 1 Allgemein Teilgebiete der Informatik ohne Theoretische Grundlagen 2 Fragen an
Theoretische Informatik 1 Bernhard Nessler Institut für Grundlagen der Informationsverabeitung TU Graz SS 2007 Übersicht 1 Allgemein Teilgebiete der Informatik ohne Theoretische Grundlagen 2 Fragen an
TEIL III: FORMALE SPRACHEN
 EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 TEIL III: FORMALE SPRACHEN 16. TERMERSETZUNGSSYSTEME UND CHOMSKY-GRAMMATIKEN Theoretische Informatik (SoSe 2011)
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 TEIL III: FORMALE SPRACHEN 16. TERMERSETZUNGSSYSTEME UND CHOMSKY-GRAMMATIKEN Theoretische Informatik (SoSe 2011)
Algorithmen und Programmierung
 Algorithmen und Programmierung Kapitel 5 Formale Algorithmenmodelle A&P (WS 14/15): 05 Formale Algorithmenmodelle 1 Überblick Motivation Formale Algorithmenmodelle Registermaschine Abstrakte Maschinen
Algorithmen und Programmierung Kapitel 5 Formale Algorithmenmodelle A&P (WS 14/15): 05 Formale Algorithmenmodelle 1 Überblick Motivation Formale Algorithmenmodelle Registermaschine Abstrakte Maschinen
Zusammenfassung. Satz. 1 Seien F, G Boolesche Ausdrücke (in den Variablen x 1,..., x n ) 2 Seien f : B n B, g : B n B ihre Booleschen Funktionen
 Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 6 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Satz 1 Seien F, G Boolesche Ausdrücke
Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 6 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Satz 1 Seien F, G Boolesche Ausdrücke
1 Vom Problem zum Programm
 1 Vom Problem zum Programm Ein Problem besteht darin, aus einer gegebenen Menge von Informationen eine weitere (bisher unbekannte) Information zu bestimmen. 1 Vom Problem zum Programm Ein Algorithmus ist
1 Vom Problem zum Programm Ein Problem besteht darin, aus einer gegebenen Menge von Informationen eine weitere (bisher unbekannte) Information zu bestimmen. 1 Vom Problem zum Programm Ein Algorithmus ist
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2013
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2013 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Deterministische Kellerautomaten
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2013 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Deterministische Kellerautomaten
Zusammenfassung. 1 Wir betrachten die folgende Signatur F = {+,,, 0, 1} sodass. 3 Wir betrachten die Gleichungen E. 4 Dann gilt E 1 + x 1
 Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Grundlagen der Informatik II. Teil I: Formale Modelle der Informatik
 Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informatik Woche 10 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Zusammenfassung Zusammenfassung der letzten LV Satz Sei G = (V, Σ, R, S) eine kontextfreie
Einführung in die Theoretische Informatik Woche 10 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Zusammenfassung Zusammenfassung der letzten LV Satz Sei G = (V, Σ, R, S) eine kontextfreie
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Dr. Harald Hempel SS 2006 Inhaltsverzeichnis I. Formale Sprachen 7 1. Sprachen und Grammatiken 8 1.1. Grundlagen................................... 8 1.2. Grammatiken..................................
Grundlagen der theoretischen Informatik Dr. Harald Hempel SS 2006 Inhaltsverzeichnis I. Formale Sprachen 7 1. Sprachen und Grammatiken 8 1.1. Grundlagen................................... 8 1.2. Grammatiken..................................
2: Zahlentheorie / Restklassen 2.1: Modulare Arithmetik
 Stefan Lucks Diskrete Strukturen (WS 2009/10) 57 2: Zahlentheorie / Restklassen 2.1: Modulare Arithmetik Uhr: Stunden mod 24, Minuten mod 60, Sekunden mod 60,... Rechnerarithmetik: mod 2 w, w {8, 16, 32,
Stefan Lucks Diskrete Strukturen (WS 2009/10) 57 2: Zahlentheorie / Restklassen 2.1: Modulare Arithmetik Uhr: Stunden mod 24, Minuten mod 60, Sekunden mod 60,... Rechnerarithmetik: mod 2 w, w {8, 16, 32,
Mathematische Maschinen
 Mathematische Maschinen Ziel: Entwicklung eines allgemeinen Schemas zur Beschreibung von (mathematischen) Maschinen zur Ausführung von Algorithmen (hier: (partiellen) Berechnungsverfahren). Mathematische
Mathematische Maschinen Ziel: Entwicklung eines allgemeinen Schemas zur Beschreibung von (mathematischen) Maschinen zur Ausführung von Algorithmen (hier: (partiellen) Berechnungsverfahren). Mathematische
Theoretische Informatik SS 04 Übung 1
 Theoretische Informatik SS 04 Übung 1 Aufgabe 1 Es gibt verschiedene Möglichkeiten, eine natürliche Zahl n zu codieren. In der unären Codierung hat man nur ein Alphabet mit einem Zeichen - sagen wir die
Theoretische Informatik SS 04 Übung 1 Aufgabe 1 Es gibt verschiedene Möglichkeiten, eine natürliche Zahl n zu codieren. In der unären Codierung hat man nur ein Alphabet mit einem Zeichen - sagen wir die
Codierung. Auszug aus dem Skript von Maciej Liśkiewicz und Henning Fernau
 Codierung Auszug aus dem Skript von Maciej Liśkiewicz und Henning Fernau Ein bisschen Informationstheorie Betrachten wir das folgende Problem: Wie lautet eine sinnvolle Definition für das quantitative
Codierung Auszug aus dem Skript von Maciej Liśkiewicz und Henning Fernau Ein bisschen Informationstheorie Betrachten wir das folgende Problem: Wie lautet eine sinnvolle Definition für das quantitative
Algorithmen II Vorlesung am 15.11.2012
 Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Theoretische Informatik I
 Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Formale Sprachen und Grammatiken
 Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Informatik I. Lutz Donnerhacke [email protected]. PGP:db089309 1c1c 6311 ef09 d819 e029 65be bfb6 c9cb
 Informatik I Lutz Donnerhacke [email protected] PGP:db089309 1c1c 6311 ef09 d819 e029 65be bfb6 c9cb 1 Semesterübersicht Grundbegriffe der theoretischen Informatik Übersicht über Funktionen von Betriebsystemen
Informatik I Lutz Donnerhacke [email protected] PGP:db089309 1c1c 6311 ef09 d819 e029 65be bfb6 c9cb 1 Semesterübersicht Grundbegriffe der theoretischen Informatik Übersicht über Funktionen von Betriebsystemen
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann [email protected]
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann [email protected]
Theoretische Informatik
 Theoretische Informatik Vorlesungsscriptum Sommersemester 2003 Dr Bernd Reichel 1 und Dr Ralf Stiebe 2 Fakultät für Informatik Otto-von-Guericke-Universität Magdeburg 1 Tel: +49 391 67 12851, e-mail: reichel@iwscsuni-magdeburgde,
Theoretische Informatik Vorlesungsscriptum Sommersemester 2003 Dr Bernd Reichel 1 und Dr Ralf Stiebe 2 Fakultät für Informatik Otto-von-Guericke-Universität Magdeburg 1 Tel: +49 391 67 12851, e-mail: reichel@iwscsuni-magdeburgde,
Theoretische Informatik
 Theoretische Informatik für die Studiengänge Ingenieur-Informatik berufsbegleitendes Studium Lehramt Informatik (Sekundar- und Berufsschule) http://theo.cs.uni-magdeburg.de/lehre04s/ Lehrbeauftragter:
Theoretische Informatik für die Studiengänge Ingenieur-Informatik berufsbegleitendes Studium Lehramt Informatik (Sekundar- und Berufsschule) http://theo.cs.uni-magdeburg.de/lehre04s/ Lehrbeauftragter:
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen 19
 Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
THEORETISCHE INFORMATIK
 THEORETISCHE INFORMATIK Vorlesungsskript Jiří Adámek Institut für Theoretische Informatik Technische Universität Braunschweig Januar 2014 Inhaltsverzeichnis 1 Endliche Automaten 1 1.1 Mathematische Grundbegriffe.......................
THEORETISCHE INFORMATIK Vorlesungsskript Jiří Adámek Institut für Theoretische Informatik Technische Universität Braunschweig Januar 2014 Inhaltsverzeichnis 1 Endliche Automaten 1 1.1 Mathematische Grundbegriffe.......................
Reguläre Sprachen Endliche Automaten
 Endliche Automaten (Folie 54, Seite 16 im Skript) Einige Vorteile endlicher deterministischer Automaten: durch Computer schnell simulierbar wenig Speicher benötigt: Tabelle für δ (read-only), aktueller
Endliche Automaten (Folie 54, Seite 16 im Skript) Einige Vorteile endlicher deterministischer Automaten: durch Computer schnell simulierbar wenig Speicher benötigt: Tabelle für δ (read-only), aktueller
effektives Verfahren ~ Algorithmus (Al Chwarismi) Regelsystem, Methode, Rezept, Gebrauchsanleitung Programm (griech. προγραφω, vor-schreiben)
 effektive Verfahren Ein Verfahren ist effektiv, wenn es für jeden Fall, der in einem zuvor abgegrenzten Bereich von eindeutigen Unterscheidungen auftreten kann, eine eindeutige und ausführbare Handlungsanweisung
effektive Verfahren Ein Verfahren ist effektiv, wenn es für jeden Fall, der in einem zuvor abgegrenzten Bereich von eindeutigen Unterscheidungen auftreten kann, eine eindeutige und ausführbare Handlungsanweisung
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Grammatiken und die Chomsky-Hierarchie
 Grammatiken und die Chomsky-Hierarchie Def.: Eine Grammatik G=(Σ,V,S,R) besteht aus endlichem Alphabet Σ endlicher Variablenmenge V mit V Σ= Startsymbol SєV endlicher Menge R с (V Σ) + x(v Σ)* von Ableitungsregeln
Grammatiken und die Chomsky-Hierarchie Def.: Eine Grammatik G=(Σ,V,S,R) besteht aus endlichem Alphabet Σ endlicher Variablenmenge V mit V Σ= Startsymbol SєV endlicher Menge R с (V Σ) + x(v Σ)* von Ableitungsregeln
Endlicher Automat (EA)
 Endlicher Automat (EA) siehe auch Formale Grundlagen 3 1 Motivation: Automaten für die Modellierung, Spezifikation und Verifikation verwenden! Definition Ein Endlicher Automat A = (S,I,Σ,T,F) besteht aus
Endlicher Automat (EA) siehe auch Formale Grundlagen 3 1 Motivation: Automaten für die Modellierung, Spezifikation und Verifikation verwenden! Definition Ein Endlicher Automat A = (S,I,Σ,T,F) besteht aus
Sprachen/Grammatiken eine Wiederholung
 Sprachen/Grammatiken eine Wiederholung Was sind reguläre Sprachen? Eigenschaften regulärer Sprachen Sprachen Begriffe Symbol: unzerlegbare Grundzeichen Alphabet: endliche Menge von Symbolen Zeichenreihe:
Sprachen/Grammatiken eine Wiederholung Was sind reguläre Sprachen? Eigenschaften regulärer Sprachen Sprachen Begriffe Symbol: unzerlegbare Grundzeichen Alphabet: endliche Menge von Symbolen Zeichenreihe:
Einführung in die Informatik I
 Einführung in die Informatik I Algorithmen und deren Programmierung Prof. Dr. Nikolaus Wulff Definition Algorithmus Ein Algorithmus ist eine präzise formulierte Handlungsanweisung zur Lösung einer gleichartigen
Einführung in die Informatik I Algorithmen und deren Programmierung Prof. Dr. Nikolaus Wulff Definition Algorithmus Ein Algorithmus ist eine präzise formulierte Handlungsanweisung zur Lösung einer gleichartigen
Formale Sprachen und deren Grammatiken. Zusammenhang mit der Automatentheorie.
 Formale Sprachen Formale Sprachen und deren Grammatiken. Zusammenhang mit der Automatentheorie. Inhaltsübersicht und Literatur Formale Sprachen: Definition und Darstellungen Grammatiken für formale Sprachen
Formale Sprachen Formale Sprachen und deren Grammatiken. Zusammenhang mit der Automatentheorie. Inhaltsübersicht und Literatur Formale Sprachen: Definition und Darstellungen Grammatiken für formale Sprachen
Informatik I WS 07/08 Tutorium 24
 Info I Tutorium 24 Informatik I WS 07/08 Tutorium 24 20.12.07 Bastian Molkenthin E-Mail: [email protected] Web: http://infotut.sunshine2k.de Rückblick Semi-Thue-Systeme Ein Semi-Thue-System besteht
Info I Tutorium 24 Informatik I WS 07/08 Tutorium 24 20.12.07 Bastian Molkenthin E-Mail: [email protected] Web: http://infotut.sunshine2k.de Rückblick Semi-Thue-Systeme Ein Semi-Thue-System besteht
Programmieren I. Formale Sprachen. www.kit.edu. Institut für Angewandte Informatik
 Programmieren I Formale Sprachen KIT Universität des Landes Baden-Württemberg und nationales Großforschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Formale Sprachen: Allgemeines Sprachen werden
Programmieren I Formale Sprachen KIT Universität des Landes Baden-Württemberg und nationales Großforschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Formale Sprachen: Allgemeines Sprachen werden
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit
 Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Dynamische Optimierung. Kapitel 4. Dynamische Optimierung. Peter Becker (H-BRS) Operations Research II Wintersemester 2014/15 160 / 206
 Kapitel 4 Dynamische Optimierung Peter Becker (H-BRS) Operations Research II Wintersemester 2014/15 160 / 206 Inhalt Inhalt 4 Dynamische Optimierung Allgemeiner Ansatz und Beispiele Stochastische dynamische
Kapitel 4 Dynamische Optimierung Peter Becker (H-BRS) Operations Research II Wintersemester 2014/15 160 / 206 Inhalt Inhalt 4 Dynamische Optimierung Allgemeiner Ansatz und Beispiele Stochastische dynamische
Theoretische Informatik
 Theoretische Informatik - das Quiz zur Vorlesung Teil I - Grundzüge der Logik In der Logik geht es um... (A) die Formen korrekten Folgerns (B) die Unterscheidung von wahr und falsch (C) das Finden von
Theoretische Informatik - das Quiz zur Vorlesung Teil I - Grundzüge der Logik In der Logik geht es um... (A) die Formen korrekten Folgerns (B) die Unterscheidung von wahr und falsch (C) das Finden von
Reguläre Ausdrücke. Prof.Dr.Christian Wagenknecht mit Beiträgen von Herrn Dr.Michael Hielscher
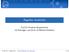 Reguläre Ausdrücke Prof.Dr.Christian Wagenknecht mit Beiträgen von Herrn Dr.Michael Hielscher Prof.Dr.Chr. Wagenknecht Formale Sprachen und Automaten 1/44 Definition reguläre Ausdrücke für reguläre Sprachen
Reguläre Ausdrücke Prof.Dr.Christian Wagenknecht mit Beiträgen von Herrn Dr.Michael Hielscher Prof.Dr.Chr. Wagenknecht Formale Sprachen und Automaten 1/44 Definition reguläre Ausdrücke für reguläre Sprachen
ARBEITSBLATT ZU FORMALEN SPRACHEN
 ARBEITSBLATT ZU FORMALEN SPRACHEN Aufgabe 1: Gegeben ist die folgende Formale Sprache L(G) mit G = (T, N, P, S). Die Produktionen lauten ZUWEISUNG ::= name zuweisungsoperator AUSDRUCK semikolon AUSDRUCK
ARBEITSBLATT ZU FORMALEN SPRACHEN Aufgabe 1: Gegeben ist die folgende Formale Sprache L(G) mit G = (T, N, P, S). Die Produktionen lauten ZUWEISUNG ::= name zuweisungsoperator AUSDRUCK semikolon AUSDRUCK
Theoretische Informatik 2
 Theoretische Informatik 2 Jürgen Koslowski Institut für Theoretische Informatik Technische Universität Braunschweig SS 2015 http://www.iti.cs.tu-bs.de/ koslowj/theo2 Jürgen Koslowski (TU-BS) Theoretische
Theoretische Informatik 2 Jürgen Koslowski Institut für Theoretische Informatik Technische Universität Braunschweig SS 2015 http://www.iti.cs.tu-bs.de/ koslowj/theo2 Jürgen Koslowski (TU-BS) Theoretische
Theoretische Informatik
 Theoretische Informatik Einheit 1 Mathematische Methodik 1. Problemlösen 2. Beweistechniken 3. Wichtige Grundbegriffe Methodik des Problemlösens Klärung der Voraussetzungen Welche Begriffe sind zum Verständnis
Theoretische Informatik Einheit 1 Mathematische Methodik 1. Problemlösen 2. Beweistechniken 3. Wichtige Grundbegriffe Methodik des Problemlösens Klärung der Voraussetzungen Welche Begriffe sind zum Verständnis
Kostenmaße. F3 03/04 p.188/395
 Kostenmaße Bei der TM nur ein Kostenmaß: Ein Schritt (Konfigurationsübergang) kostet eine Zeiteinheit; eine Bandzelle kostet eine Platzeinheit. Bei der RAM zwei Kostenmaße: uniformes Kostenmaß: (wie oben);
Kostenmaße Bei der TM nur ein Kostenmaß: Ein Schritt (Konfigurationsübergang) kostet eine Zeiteinheit; eine Bandzelle kostet eine Platzeinheit. Bei der RAM zwei Kostenmaße: uniformes Kostenmaß: (wie oben);
Syntax (= Satzgefüge), vgl. auch Grammatik
 1 Natürliche Sprachen Natürliche Sprachen bezeichnen wie das Wort "Sprache" ausdrückt zunächst das Gesprochene. Das Schweizerdeutsch etwa ist eine typische natürliche Sprache. Mit der Erfindung der Aufzeichnung
1 Natürliche Sprachen Natürliche Sprachen bezeichnen wie das Wort "Sprache" ausdrückt zunächst das Gesprochene. Das Schweizerdeutsch etwa ist eine typische natürliche Sprache. Mit der Erfindung der Aufzeichnung
1 Syntax von Programmiersprachen
 1 Syntax von Programmiersprachen Syntax ( Lehre vom Satzbau ): formale Beschreibung des Aufbaus der Worte und Sätze, die zu einer Sprache gehören; im Falle einer Programmier-Sprache Festlegung, wie Programme
1 Syntax von Programmiersprachen Syntax ( Lehre vom Satzbau ): formale Beschreibung des Aufbaus der Worte und Sätze, die zu einer Sprache gehören; im Falle einer Programmier-Sprache Festlegung, wie Programme
Automaten und formale Sprachen: Vorlesungsskript G. Brewka, A. Nittka
 Automaten und formale Sprachen: Vorlesungsskript G. Brewka, A. Nittka Literatur: John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman, Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie,
Automaten und formale Sprachen: Vorlesungsskript G. Brewka, A. Nittka Literatur: John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman, Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie,
Entwurf von Algorithmen - Kontrollstrukturen
 Entwurf von Algorithmen - Kontrollstrukturen Eine wichtige Phase in der Entwicklung von Computerprogrammen ist der Entwurf von Algorithmen. Dieser Arbeitsschritt vor dem Schreiben des Programmes in einer
Entwurf von Algorithmen - Kontrollstrukturen Eine wichtige Phase in der Entwicklung von Computerprogrammen ist der Entwurf von Algorithmen. Dieser Arbeitsschritt vor dem Schreiben des Programmes in einer
IT-Basics 2. DI Gerhard Fließ
 IT-Basics 2 DI Gerhard Fließ Wer bin ich? DI Gerhard Fließ Telematik Studium an der TU Graz Softwareentwickler XiTrust www.xitrust.com www.tugraz.at Worum geht es? Objektorientierte Programmierung Konzepte
IT-Basics 2 DI Gerhard Fließ Wer bin ich? DI Gerhard Fließ Telematik Studium an der TU Graz Softwareentwickler XiTrust www.xitrust.com www.tugraz.at Worum geht es? Objektorientierte Programmierung Konzepte
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Ulrich Furbach. Sommersemester 2014
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Ulrich Furbach Institut für Informatik Sommersemester 2014 Furbach Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Ulrich Furbach Institut für Informatik Sommersemester 2014 Furbach Grundlagen d. Theoretischen Informatik:
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Endliche Automaten. Endliche Automaten 1 / 108
 Endliche Automaten Endliche Automaten 1 / 108 Endliche Automaten Endliche Automaten erlauben eine Beschreibung von Handlungsabläufen: Wie ändert sich ein Systemzustand in Abhängigkeit von veränderten Umgebungsbedingungen?
Endliche Automaten Endliche Automaten 1 / 108 Endliche Automaten Endliche Automaten erlauben eine Beschreibung von Handlungsabläufen: Wie ändert sich ein Systemzustand in Abhängigkeit von veränderten Umgebungsbedingungen?
Entscheidungsprobleme. Berechenbarkeit und Komplexität Entscheidbarkeit und Unentscheidbarkeit. Die Entscheidbarkeit von Problemen
 Berechenbarkeit und Komlexität Entscheidbarkeit und Unentscheidbarkeit Wolfgang Schreiner [email protected] Research Institute for Symbolic Comutation (RISC) Johannes Keler University,
Berechenbarkeit und Komlexität Entscheidbarkeit und Unentscheidbarkeit Wolfgang Schreiner [email protected] Research Institute for Symbolic Comutation (RISC) Johannes Keler University,
Aufgabentypen die in der Klausur vorkommen
 Aufgabentypen die in der Klausur vorkommen können 1. Nennen Sie fünf wichtige Anwendungsgebiete der Computerlinguistik. 2. Für welches der drei Anwendungsgebiete Maschinelle Übersetzung, Rechtschreibkorrektur
Aufgabentypen die in der Klausur vorkommen können 1. Nennen Sie fünf wichtige Anwendungsgebiete der Computerlinguistik. 2. Für welches der drei Anwendungsgebiete Maschinelle Übersetzung, Rechtschreibkorrektur
Oft kommt es darauf an, Potenzen a n mod m zu berechnen. Dabei kann n eine sehr groÿe Zahl sein.
 Oft kommt es darauf an, Potenzen a n mod m zu berechnen. Dabei kann n eine sehr groÿe Zahl sein. 3 1384788374932954500363985493554603584759389 mod 28374618732464817362847326847331872341234 Wieso kann ein
Oft kommt es darauf an, Potenzen a n mod m zu berechnen. Dabei kann n eine sehr groÿe Zahl sein. 3 1384788374932954500363985493554603584759389 mod 28374618732464817362847326847331872341234 Wieso kann ein
Tutorium zur theoretischen Informatik Übungsblatt 4 (2006-12-13)
 Ein verständiges Herz erwirbt Kenntnisse, und das Ohr der Weisen lauscht dem Wissen. (Die Bibel, "Buch der Sprüche", Kapitel 18 Vers 15) Inhalt 1. Empfehlenswerte Referenzen 2. Aufgabe 1 CF Grammatik für
Ein verständiges Herz erwirbt Kenntnisse, und das Ohr der Weisen lauscht dem Wissen. (Die Bibel, "Buch der Sprüche", Kapitel 18 Vers 15) Inhalt 1. Empfehlenswerte Referenzen 2. Aufgabe 1 CF Grammatik für
Theoretische Informatik 1 + 2
 AG Theoretische Grundlagen der KI, Fachbereich Informatik, Universität Bremen Skript zu den Lehrveranstaltungen Theoretische Informatik 1 + 2 Prof. Dr. Carsten Lutz Basierend auf einem Skript von Franz
AG Theoretische Grundlagen der KI, Fachbereich Informatik, Universität Bremen Skript zu den Lehrveranstaltungen Theoretische Informatik 1 + 2 Prof. Dr. Carsten Lutz Basierend auf einem Skript von Franz
Mathematik 1. Lösungsvorschläge zum 2. Übungsblatt
 Hochschule Regensburg Fakultät Informatik/Mathematik Christoph Böhm Wintersemester 0/0 Wirtschaftsinformatik Bachelor IW Informatik Bachelor IN Vorlesung Mathematik Mathematik Lösungsvorschläge zum Übungsblatt
Hochschule Regensburg Fakultät Informatik/Mathematik Christoph Böhm Wintersemester 0/0 Wirtschaftsinformatik Bachelor IW Informatik Bachelor IN Vorlesung Mathematik Mathematik Lösungsvorschläge zum Übungsblatt
7. Formale Sprachen und Grammatiken
 7. Formale Sprachen und Grammatiken Computer verwenden zur Verarbeitung von Daten und Informationen künstliche, formale Sprachen (Maschinenspr., Assemblerspachen, Programmierspr., Datenbankspr., Wissensrepräsentationsspr.,...)
7. Formale Sprachen und Grammatiken Computer verwenden zur Verarbeitung von Daten und Informationen künstliche, formale Sprachen (Maschinenspr., Assemblerspachen, Programmierspr., Datenbankspr., Wissensrepräsentationsspr.,...)
Theorie der Informatik (CS206) Fortsetzung LOOP-Programme, primitiv-rekursive Funktionen
 Theorie der Informatik (CS206) Fortsetzung LOOP-Programme, primitiv-rekursive Funktionen 26. März 2012 Proff Malte Helmert und Christian Tschudin Departement Mathematik und Informatik, Universität Basel
Theorie der Informatik (CS206) Fortsetzung LOOP-Programme, primitiv-rekursive Funktionen 26. März 2012 Proff Malte Helmert und Christian Tschudin Departement Mathematik und Informatik, Universität Basel
Einführung. Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Vorlesungen zur Komplexitätstheorie. K-Vollständigkeit (1/5)
 Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
Theoretische Informatik
 Theoretische Informatik Sibylle Schwarz Westsächsische Hochschule Zwickau Dr. Friedrichs-Ring 2a, RII 263 http://www.fh-zwickau.de/~sibsc/ [email protected] SS 2012 1 Einordnung der Theoretischen
Theoretische Informatik Sibylle Schwarz Westsächsische Hochschule Zwickau Dr. Friedrichs-Ring 2a, RII 263 http://www.fh-zwickau.de/~sibsc/ [email protected] SS 2012 1 Einordnung der Theoretischen
Mathematische Grundlagen der Informatik 2
 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss [email protected] 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss [email protected] 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Grafische Interaktionssysteme/ dynamische Visualisierung des endlichen Automaten
 Sprachliche Informationsverarbeitung 29.01.2007 HS Intelligente Systeme Prof. Dr. J. Rolshoven (WS 06/07) Grafische Interaktionssysteme/ dynamische Visualisierung des endlichen Automaten Referentin: Melinda
Sprachliche Informationsverarbeitung 29.01.2007 HS Intelligente Systeme Prof. Dr. J. Rolshoven (WS 06/07) Grafische Interaktionssysteme/ dynamische Visualisierung des endlichen Automaten Referentin: Melinda
8 Diskrete Optimierung
 8 Diskrete Optimierung Definition 8.1. Ein Graph G ist ein Paar (V (G), E(G)) besteh aus einer lichen Menge V (G) von Knoten (oder Ecken) und einer Menge E(G) ( ) V (G) 2 von Kanten. Die Ordnung n(g) von
8 Diskrete Optimierung Definition 8.1. Ein Graph G ist ein Paar (V (G), E(G)) besteh aus einer lichen Menge V (G) von Knoten (oder Ecken) und einer Menge E(G) ( ) V (G) 2 von Kanten. Die Ordnung n(g) von
REG versus CF. Theorem REG ist echt in CF enthalten.
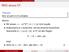 REG versus CF Theorem REG ist echt in CF enthalten. Beweis: Wir wissen: L = {a m b m m 1} ist nicht regulär. Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b}, {S}, S,
REG versus CF Theorem REG ist echt in CF enthalten. Beweis: Wir wissen: L = {a m b m m 1} ist nicht regulär. Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b}, {S}, S,
4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls
 4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls δ(q, a, Z) + δ(q, ɛ, Z) 1 (q, a, Z) Q Σ. Die von einem DPDA, der mit leerem Keller akzeptiert,
4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls δ(q, a, Z) + δ(q, ɛ, Z) 1 (q, a, Z) Q Σ. Die von einem DPDA, der mit leerem Keller akzeptiert,
VBA-Programmierung: Zusammenfassung
 VBA-Programmierung: Zusammenfassung Programmiersprachen (Definition, Einordnung VBA) Softwareentwicklung-Phasen: 1. Spezifikation 2. Entwurf 3. Implementierung Datentypen (einfach, zusammengesetzt) Programmablaufsteuerung
VBA-Programmierung: Zusammenfassung Programmiersprachen (Definition, Einordnung VBA) Softwareentwicklung-Phasen: 1. Spezifikation 2. Entwurf 3. Implementierung Datentypen (einfach, zusammengesetzt) Programmablaufsteuerung
Der Kurs bestand aus zwei Teilen. Mit welchem Teil wollen Sie anfangen? Ich habe mich für Teil A entschieden.
 Mündliche Prüfung in Grundlagen Theoretischer Informatik A + B Prüfer: Prof. Heinemann Dauer: 30 Minuten, 12.09.13 Version: Winter 12/13 und Sommer 13 Der Kurs bestand aus zwei Teilen. Mit welchem Teil
Mündliche Prüfung in Grundlagen Theoretischer Informatik A + B Prüfer: Prof. Heinemann Dauer: 30 Minuten, 12.09.13 Version: Winter 12/13 und Sommer 13 Der Kurs bestand aus zwei Teilen. Mit welchem Teil
Sprachbeschreibung und Erweiterung
 Sprachbeschreibung und Erweiterung Worte, Sprachen, reguläre Ausdrücke, Automaten, BNF, Grammatik, Syntax- Diagramme, Spracherweiterungen do, for, break, switch Formale Beschreibung von Programmiersprachen
Sprachbeschreibung und Erweiterung Worte, Sprachen, reguläre Ausdrücke, Automaten, BNF, Grammatik, Syntax- Diagramme, Spracherweiterungen do, for, break, switch Formale Beschreibung von Programmiersprachen
Theoretische Informatik
 Theoretische Informatik Wolfgang Ertel 28. Oktober 2008 Inhaltsverzeichnis 1 Formale Sprachen und Maschinenmodelle 3 1.1 Grundlagen................................... 3 1.2 Grammatiken..................................
Theoretische Informatik Wolfgang Ertel 28. Oktober 2008 Inhaltsverzeichnis 1 Formale Sprachen und Maschinenmodelle 3 1.1 Grundlagen................................... 3 1.2 Grammatiken..................................
Karlsruher Institut für Technologie Institut für Algebra und Geometrie
 Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. Stefan Kühnlein Dipl.-Math. Jochen Schröder Einführung in Algebra und Zahlentheorie Übungsblatt 2 Aufgabe 1 (4 Punkte) Seien
Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. Stefan Kühnlein Dipl.-Math. Jochen Schröder Einführung in Algebra und Zahlentheorie Übungsblatt 2 Aufgabe 1 (4 Punkte) Seien
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Kapitel 2: Formale Sprachen Gliederung
 Gliederung 0. Einleitung und Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen
Gliederung 0. Einleitung und Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen
1. Der Begriff Informatik 2. Syntax und Semantik von Programmiersprachen. I.2. I.2. Grundlagen von von Programmiersprachen.
 1. Der Begriff Informatik 2. Syntax und Semantik von Programmiersprachen I.2. I.2. Grundlagen von von Programmiersprachen. - 1 - 1. Der Begriff Informatik "Informatik" = Kunstwort aus Information und Mathematik
1. Der Begriff Informatik 2. Syntax und Semantik von Programmiersprachen I.2. I.2. Grundlagen von von Programmiersprachen. - 1 - 1. Der Begriff Informatik "Informatik" = Kunstwort aus Information und Mathematik
Automaten, Formale Sprachen und Berechenbarkeit I. Skript zur Vorlesung im WS 2001/02 an der TU München
 Automaten, Formale Sprachen und Berechenbarkeit I Skript zur Vorlesung im WS 2001/02 an der TU München Ekkart Kindler Steffen Manthey Version: 1.30 vom 30. April 2002 ii Redaktioneller Hinweis: Es gibt
Automaten, Formale Sprachen und Berechenbarkeit I Skript zur Vorlesung im WS 2001/02 an der TU München Ekkart Kindler Steffen Manthey Version: 1.30 vom 30. April 2002 ii Redaktioneller Hinweis: Es gibt
Visual Basic Basisbefehle Hinweis: Der Text in eckigen Klammern [ ] ist variabel, z.b. [var] => 5.3. Eckige Klammern sind stets wegzulassen!
![Visual Basic Basisbefehle Hinweis: Der Text in eckigen Klammern [ ] ist variabel, z.b. [var] => 5.3. Eckige Klammern sind stets wegzulassen! Visual Basic Basisbefehle Hinweis: Der Text in eckigen Klammern [ ] ist variabel, z.b. [var] => 5.3. Eckige Klammern sind stets wegzulassen!](/thumbs/27/12267466.jpg) Visual Basic Basisbefehle Hinweis: Der Text in eckigen Klammern [ ] ist variabel, z.b. [var] => 5.3. Eckige Klammern sind stets wegzulassen! Grundstrukturen: Sub [name]([übergabe]) End Sub [Übergabe] ist
Visual Basic Basisbefehle Hinweis: Der Text in eckigen Klammern [ ] ist variabel, z.b. [var] => 5.3. Eckige Klammern sind stets wegzulassen! Grundstrukturen: Sub [name]([übergabe]) End Sub [Übergabe] ist
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Die Komplexitätsklassen P und NP
 Die Komplexitätsklassen P und NP Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 3. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Die Komplexitätsklassen P und NP Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 3. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
w a is die Anzahl der Vorkommen von a in w Beispiel: abba a = 2
 1 2 Notation für Wörter Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg w a is die Anzahl der Vorkommen von a in w Beispiel: abba
1 2 Notation für Wörter Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg w a is die Anzahl der Vorkommen von a in w Beispiel: abba
