Automaten und formale Sprachen: Vorlesungsskript G. Brewka, A. Nittka
|
|
|
- Sophia Hase
- vor 8 Jahren
- Abrufe
Transkript
1 Automaten und formale Sprachen: Vorlesungsskript G. Brewka, A. Nittka Literatur: John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman, Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie, 2. Auflage, Addison- Wesley, Pearson Studium, 2002, EUR 39,95 Uwe Schöning, Theoretische Informatik - kurzgefasst, 4. Auflage, Spektrum Akademischer Verlag, 2001 Alexander Asteroth, Christel Baier, Theoretische Informatik, Pearson Studium, Einführung 1.1 Was sind Automaten? Beispiele: Geldautomat, Getränkeautomat, Fahrkartenautomat,... hier geht es nicht um konkrete Automaten und wie man sie baut, sondern um abstrakte Modelle von (Klassen von) Automaten und ihre prinzipiellen Eigenschaften Was haben alle Automaten gemeinsam? Möglichkeit der Eingabe Zustände und Übergänge zwischen Zuständen, hervorgerufen durch Eingabe Bsp.: durch Einwurf einer Münze in Kaffeeautomaten wird Zustand "bezahlt" erreicht. Drücken der Taste "Cappuccino" in diesem Zustand führt zu Nachfolgezustand, in dem Cappuccino ausgegeben wird, Drücken der Taste "Geld zurück" in einen Nachfolgezustand, in dem die Münze zurückgegeben wird. Etwas genauer: Automat verfügt über Münzschlitz sowie Tasten "Espresso", "Cappuccino", "Geldrückgabe", die vom Kunden bedient werden können. Außerdem "weiß" der Automat, ob er gerade Geld zurückgegeben oder Cappuccino bzw. Espresso geliefert hat ("Eingaben", die durch eigene Aktion hervorgerufen werden). Insgesamt sind die möglichen Eingaben: M: Münze eingeworfen E: Espresso-Taste gedrückt C: Cappuccino-Taste gedrückt G: Geldrückgabetaste gedrückt R: Geldrückgabe erfolgt LC: Lieferung Cappuccino abgeschlossen LE: Lieferung Espresso abgeschlossen Der Automat hat folgende Zustände: q 0 : q 1 : q 2 : q 3 : q 4 : Anfangszustand Münze eingeworfen Münze eingeworfen und Espresso gedrückt Münze eingeworfen und Cappucino gedrückt Münze eingeworfen und Geldrückgabe gedrückt 1
2 Die durch bestimmte Eingaben hervorgerufenen Übergänge sind im Diagramm veranschaulicht. Die Beschreibung ist so noch nicht vollständig, denn z.b. kann der Kunde ja auch zuerst E oder C eingeben. Um das Bild nicht komplizierter zu machen, gehen wir davon aus, dass für alle nicht explizit genannten Eingaben jeweils der ursprüngliche Zustand erhalten bleiben soll. Ein realistischer Automat sollte natürlich noch verfeinert werden (z.b. merken, wenn zu viele Münzen eingeworfen wurden, oder in einen Fehlerzustand gehen, wenn ohne Anforderung Kaffee geliefert wird). Es geht hier nur um die Verdeutlichung des Prinzips. Anmerkung: q 0 ist insofern ein ausgezeichneter Zustand, als alle Eingabefolgen, die wieder in q 0 landen, vollständige Transaktionen darstellen. Zustände, die durch "gewünschte" Eingabefolgen erreicht werden, heißen finale oder akzeptierende Zustände. Für unsere Zwecke wird es genügen, uns Eingaben als Symbole und Folgen von Eingaben als Zeichenketten aus entsprechenden Symbolen vorzustellen. -> Zusammenhang zu formalen Sprachen Warum sollte man sich als Informatiker mit Automatentheorie auseinander setzen? liefert Grundkonzepte für Design wichtiger Typen von Software (Schaltkreisentwurf, lexikalische Analyse im Compilerbau, Suche von Ausdrücken in Texten, Verifikation von Kommunikationsprotokollen,...) wesentlich für Analyse der (Grenzen der) Berechenbarkeit wesentlich für Analyse der Komplexität von Algorithmen 1.2 Formale Sprachen heißen formal, weil es sich um präzise definierte Kunstsprachen handelt (im Gegensatz zu natürlichen Sprachen) Def.: Ein Alphabet ist eine endliche, nichtleere Menge von Symbolen. Bsp.: {0,1}, {a,b,c}, {,,, },... Def.: Eine Zeichenreihe (auch: Zeichenkette, Wort) über einem Alphabet ist eine endliche Folge von Elementen von. In obiger Definition ist die "leere" Zeichenkette mit eingeschlossen. Diese wird durch das Symbol dargestellt. Die Länge der leeren Zeichenkette ist 0. Sei w eine Zeichenkette der Länge n, a, so ist die Länge der Zeichenkette aw (Notation aw ) n+1. k bezeichnet die Menge der Zeichenketten über der Länge k. * ist die Menge aller Zeichenketten über, d,h, * = ist die Menge aller nichtleeren Zeichenketten über, d,h, + =
3 Def.: Seien x und y Zeichenketten mit x = n x und y = n y. Die Konkatenation von x und y ist die Zeichenkette xy mit xy = n x + n y, die durch Aneinanderreihung von x und y entsteht. Def.: Sei ein Alphabet. S heißt Sprache über gdw. S *. Anmerkung: in der theoretischen Informatik werden Probleme oft gleichgesetzt mit der Frage, ob ein Wort zu entsprechender Sprache gehört. Bsp.: das Problem: "ist n Primzahl?" ist äquivalent zu: gehört Binärdarstellung von n zur Sprache {w w binäre Zahl, die Primzahl ist}. Wie werden Sprachen definiert? a) Aufzählung der Elemente (klappt nur im endlichen Fall) b) Mengenvorschrift: {w w binäre Zahl, die Primzahl ist}. c) Grammatiken: Erzeugung von Zeichenketten durch Menge von Ersetzungsregeln Was haben formale Sprachen und Automaten miteinander zu tun? Automaten können Sprachen erkennen: die von einem Automaten erkannte Sprache besteht aus den Zeichenketten, deren Eingabe vom Anfangs- in einen akzeptierenden Zustand führt. Verschiedene Typen von Automaten entsprechen exakt verschiedenen Typen von Sprachen. Chomsky Hierarchie (Noam Chomsky, Linguist) rek. aufzählbare Sprachen Turing-Maschinen kontext-sensitive Sprachen linear beschränkte Automaten kontext-freie Sprachen Kellerautomaten reguläre Sprachen endliche Automaten weitere Möglichkeit, Sprache zu definieren: Angabe eines Automaten, der sie akzeptiert. Geplante Gliederung der Vorlesung: 1. Einführung 2. Endliche Automaten 3. Reguläre Ausdrücke und Sprachen 4. Eigenschaften regulärer Sprachen 5. Kontextfreie Grammatiken und Sprachen 6. Kellerautomaten 7. Eigenschaften kontextfreier Sprachen 8. Turing-Maschinen 9. Unentscheidbarkeit 3
4 2. Endliche Automaten 2.1 Deterministische endliche Automaten (DEAs) Def.: Ein deterministischer endlicher Automat A = (Q,,, q 0, F) besteht aus einer endlichen Menge von Zuständen Q, einer endlichen Menge von Eingabesymbolen, einer Übergangsfunktion Q -> Q, wobei (q,a) der Zustand ist, der vom Zustand q bei Eingabe a erreicht wird, einem Startzustand q 0 Q, sowie einer Menge F Q von finalen oder akzeptierenden Zuständen. Die Übergangsfunktion lässt sich auf folgende Weise zu einer Funktion Q -> Q erweitern: für alle Zustände q, Zeichenketten w und Eingabesymbole a gilt: *(q, ) = q *(q, wa) = *(q, w), a) *(q, aw) = (q, a), w) Formulierung im Buch, oder zu Formulierung im Buch äquivalent Beispiel: Q = {q 0, q 1 }, = {0,1}, F = {q 0 } (q 0, 0) = q 0 (q 1, 0) = q 1 (q 0, 1) = q 1 (q 1, 1) = q 0 es gilt z.b.: (q 0, 0110) = (q 0, 0), 110) = q 0, 110) = (q 0,1), 10) = q 1, 10) = (q 1,1), 0) = q 0, 0) = (q 0,0), ) = q 0, ) = q 0 Man sagt, die Eingabe 0110 wird von dem Automaten akzeptiert. Def.: Sei A = (Q,,, q 0, F) ein DEA. Die von A akzeptierte Sprache (oder kürzer: die Sprache von A) L(A) wird definiert durch: L(A) = {w *(q 0, w) F} Welche Sprache wird durch den obigen Beispielautomaten akzeptiert? Menge aller Wörter mit gerader Anzahl von 1. 4
5 Übergangsdiagramm: (Startzustand q0 gekennzeichnet durch eingehenden Pfeil ohne Vorgängerzustände, finale durch Doppelkreis) Bemerkung: wird oft in Tabellenform dargestellt. Für obigen Automaten (* bezeichnet akzeptierende Zustände, der Pfeil zeigt auf den Startzustand : 0 1 * q 0 q 0 q 1 q 1 q 1 q Nichtdeterministische endliche Automaten (NEAs) DEA geht bei Eingabe eines Symbols in genau einen definierten Nachfolgezustand über. Ein NEA dagegen kann bei derselben Eingabe mehrere Nachfolgezustände (oder auch keinen) haben. Die verschiedenen möglichen Nachfolgezustände entsprechen Hypothesen über die bisher abgearbeitete Eingabe: DEA NEA q 0 q 0 X q 1 q 11 q 12 q 13 Y q 2 q 21 q 22 q 23 Z q 3 q 31 q 32 q 33 X Y Z Menge der von q 0 bei Eingabe von XYZ erreichbaren Zustände: q 31, q 32, q 33 Wort akzeptiert, wenn mindestens ein akzeptierender Zustand erreichbar. Motivation für NEA: NEAs sind für eine Reihe von praktischen Problemen übersichtlicher und leichter zu entwerfen (und manchmal exponentiell kleiner: siehe weiter unten). 5
6 Beispiel: L 01 ={w01} über dem Alphabet {0,1}, d.h. alle, die mit 01 aufhören: DEA NEA Eingabe von 101: q 0 q q 0 q q 1 q 0 q q 2 q 0 q 2 Beide Automaten akzeptieren 101. Zu beachten: bei NEA genügt es, dass akzeptierender Zustand q 2 unter den erreichbaren ist. Es dürfen auch nicht-akzeptierende erreichbar sein. Def.: Ein nichtdeterministischer endlicher Automat A = (Q,,, q 0, F) besteht aus einer endlichen Menge von Zuständen Q, einer endlichen Menge von Eingabesymbolen, einer Übergangsfunktion Q -> 2 Q, wobei (q,a) die (möglicherweise leere) Menge der Zustände ist, die vom Zustand q bei Eingabe a erreicht wird, einem Startzustand q 0 Q, sowie 1 einer Menge F Q von finalen oder akzeptierenden Zuständen. 2 Q bezeichnet hier die Potenzmenge von Q, also 2 Q = {R R Q}. Die Übergangsfunktion lässt sich wieder zu einer Funktion Q -> 2 Q erweitern: für alle Zustände q, Zeichenketten w und Eingabesymbole a gilt: *(q, ) = {q} *(q, wa) = p, a) oder äquivalent: p *(q,w) *(q, aw) = p, w) p (q,a) 1 Einige Autoren lassen bei NEAs auch mehrere Anfangszustände zu. Wir werden bald endliche Automaten mit -Übergängen einführen. Mit diesen lassen sich mehrere Anfangszustände einfach simulieren. Wir halten uns hier an die Darstellung, die auch von Schöning und Hopcroft/Motwani/Ullman verwendet wird. 6
7 Eingabe 0110 in unserem Beispielautomaten (NEA für L 01 ): *(q 0, ) = *(q 0, ) *(q 1, ) : q 0,0) = {q 0, q 1 } *(q 0, ) *(q 2, ) q 0,1) = {q 0 } = *(q 0, ) q 1,0) = {} = *(q 0, ) *(q 1, ) q 1,1) = {q 2 } = {q 0 } {q 1 } q 2,0) = {} = {q 0, q 1 } q 2,1) = {} Def.: Sei A = (Q,,, q 0, F) ein NEA. Die von A akzeptierte Sprache L(A) wird definiert durch: L(A) = {w *(q 0, w) F }. Bsp. (das zeigt, dass DEA exponentiell größer werden kann als NEA): Folge von Sprachen L i = {w {0,1}* i-tes Symbol von hinten in w ist 1} DEA NEA i=1 i=2 i=3 2 i Zustände i+1 Zustände Hinweis zu i=2: qxx: zuletzt 00 gelesen, oder noch gar nichts, oder nur genau eine 0 qx1: zuletzt 01 gelesen, oder bisher nur genau eine 1 7
8 q11: zuletzt 11 gelesen q10: zuletzt 10 gelesen Jeder DEA kann als NEA aufgefasst werden, bei dem immer eine ein-elementige Menge bestehend aus dem Nachfolgezustand des DEA liefert. Alle Sprachen, die von einem DEA akzeptiert werden, werden deshalb auch von einem NEA akzeptiert. Aber gibt Sprachen, die von einem NEA, aber nicht von einem DEA akzeptiert werden? Nein: zu jedem NEA gibt es einen äquivalenten DEA, den sogenannten Potenzautomaten. Def.: Die Automaten A 1 und A 2 heißen äquivalent, falls L(A 1 ) = L(A 2 ). Konstruktion des Potenzautomaten (Teilmengenkonstruktion): Sei N = (Q N,, N, q 0, F N ) ein nichtdeterministischer endlicher Automat. Wir definieren einen deterministischen endlichen Automaten wie folgt: D = (Q D,, D, q 0D, F D ) wobei: Q D = 2 Q N D (S,a) = p, a) für alle S Q D, a p S q 0D = {q 0 } F D = {S Q D S F N } Bemerkung: wenn n die Anzahl der Zustände von N ist, so besitzt D 2 n Zustände. In vielen Fällen sind aber nicht alle Zustände erreichbar und der DEA lässt sich verkleinern. Anmerkung: die Menge der erreichbaren Zustände R(A) eines Automaten A ist die kleinste Menge mit: 1. q 0 R(A), 2. q R(A) und (q,a) = p für eine Eingabe a impliziert p R(A). Unser Beispielautomat: 0 1 {q 0 } {q 0, q 1 } {q 0 } {q 1 } {q 2 } * {q 2 } {q 0, q 1 } {q 0, q 1 } {q 0, q 2 } * {q 0, q 2 } {q 0, q 1 } {q 0 } * {q 1, q 2 } {q 2 } * {q 0, q 1, q 2 } {q 0, q 1 } {q 0, q 2 } von {q 0 } aus erreichbare Zustände: {q 0 }, {q 0, q 1 }, {q 0, q 2 } 8
9 Graph des Automaten (ohne unerreichbare Zustände): bis auf die Benennung der Zustände identisch mit unserem ursprünglichen DEA (siehe S. 6). Satz: Sei N = (Q N,, N, q 0, F N ) ein nichtdeterministischer endlicher Automat, D = (Q D,, D, {q 0 }, F D ) der Potenzautomat von N. D und N sind äquivalent. Beweis: wir zeigen durch Induktion über die Länge der Eingabe w, dass für alle w D *({q 0 }, w) = N *(q 0, w) Mit diesem Resultat folgt der Satz unmittelbar aus der Definition von L(N) und L(D). Induktionsanfang: für w = gilt D *({q 0 }, ) = N *(q 0, ) = {q 0 } Induktionsschritt: sei w = n+1 und der Satz gelte für Wörter der Länge n. w = xa mit x = n. Damit gilt D *({q 0 }, x) = N *(q 0, x). Nach Definition ist *(q 0, xa) = p, a) = p, a) = D p}, a) = D *({q 0 }, xa) p *(q 0,x) p D *({q 0 },x) p D *({q 0 },x) qed. Def. * Ind.-vor. Def. D Def. D * 2.3 Endliche Automaten mit -Übergängen Es erweist sich als praktisch (z.b. zur Behandlung von optionalen Sprachkonstrukten), Automaten zuzulassen, bei denen Zustandsübergänge auch ganz ohne Eingabe erfolgen können ( -Übergänge). Beispiel: Ein Automat, der ganze Zahlen sowie Dezimalzahlen mit optionalem Vorzeichen erkennt (falls Komma vorkommt, muss mindestens eine Ziffer folgen). Formale Definition: Ein -NEA A = (Q,,, q 0, F) ist definiert wie ein NEA, bis auf den Definitionsbereich von. wird als mögliche Eingabe zugelassen: Q } -> 2 Q Die -Hülle eines Zustands q, -Hülle(q), ist die kleinste Menge von Zuständen für die gilt: 9
10 1. q ist in -Hülle(q), 2. wenn p in -Hülle(q) und r von p aus bei -Eingabe erreichbar, so ist r in -Hülle(q). Beispiel: -Hülle(q 0 ) = {q 0, q 1 } -Hülle(q 2 ) = {q 2, q 4 } Wir erweitern die Definition der -Hülle auf Mengen von Zuständen Q: -Hülle(Q) = -Hülle(q) q Q Wieder erweitern wir zu *. Für alle Zustände q, Zeichenketten w und Eingabesymbole a gilt: *(q, ) = -Hülle(q) *(q, wa) = -Hülle( p, a)) oder äquivalent: p *(q,w) *(q, aw) = p, w) p ( (r,a)), r -Hülle(q) Akzeptierte Sprache definiert wie bei NEA. Wiederum lassen sich -NEAs in äquivalente DEAs überführen: Sei E = (Q E,, E, q 0, F E ) ein -NEA. Wir definieren einen deterministischen endlichen Automaten wie folgt: D = (Q D,, D, q 0D, F D ) wobei: Q D = Menge aller Teilmengen S von Q E, für die S = -Hülle(S) D (S,a) = -Hülle( p, a)) für alle S Q D, a p S q 0D = -Hülle(q 0 ) F D = {S Q D S F E } Unser Beispiel ergibt (nur erreichbare Zustände werden dargestellt): 0,...,9 +,- Komma {q 0,q 1 } {q 2,q 4 } {q 1 } {q 2,q 4 } {q 2,q 4 } {q 3 } {q 1 } {q 2,q 4 } {q 3 } {q 3,q 4 } {q 3,q 4 } {q 3,q 4 } 10
11 Graphische Darstellung des obigen Graphen: Hinweis: der Zustand ist ein Fehlerzustand, aus dem man nicht mehr rauskommt. sowie die zugehörigen Kanten werden häufig bei der Darstellung weggelassen. Konvention: wenn bei DEA Eingaben fehlen, so führen diese zu Fehlerknoten. Satz: Sei E ein -NEA, D der aus ihm nach obigem Verfahren konstruierte DEA. E und D sind äquivalent. Hinweis: Wir haben hier einen -NEA direkt in einen DEA überführt. Die Überführung in einen NEA ist einfacher. Grundidee: bei der Berechnung der Nachfolgerknoten bei Eingabe a berechnet man zunächst die mit erreichbaren Zustände und dann deren mögliche Nachfolger bei Eingabe a. Man muss dann nur noch berücksichtigen, dass akzeptierende Zustände nach Lesen der kompletten Eingabe mit erreichbar sein können: Ein -NEA E=(Q E,,, q 0E, F E ) ist äquivalent zum NEA N= (Q E,,, q 0E, F N ) wobei (q,a) = p,a) und F N = {q Q E -Hülle(q) F E }. p Hülle(q) 2.4 Äquivalenz und Minimierung von Automaten Betrachten Sie folgenden Automaten: Erkennt die Sprache aller Wörter über {a,b}* mit w > 1, die mit b enden. Gibt es einen einfacheren Automaten für diese Sprache? Klar: Wie findet man die einfachsten Automaten für eine Sprache? Suche äquivalente Zustände und ersetze diese durch einen einzigen Zustand. Äquivalent heißt hier selbes Akzeptanzverhalten: 11
12 Def. Sei D = (Q,,, q 0, F) ein DEA. Zwei Zustände p, q aus Q heißen äquivalent, falls für alle w aus * gilt: *(p,w) F genau dann wenn *(q,w) F. Wie findet man äquivalente Zustände in einem Automaten? Die Menge DIFF A aller (ungeordneten) Paare nicht-äquivalenter Zustände in einem Automaten A ist die kleinste Menge, für die gilt: 1. falls p akzeptierender, q nicht-akzeptierender Zustand, so ist {p,q} in DIFF A, 2. falls, für eine Eingabe a, { (r,a), (s,a)} in DIFF A, so ist {r,s} in DIFF A. Entsprechende Algorithmen sind leicht zu realisieren. Entspricht dem Ausfüllen einer Tabelle M. Wir nehmen an, die Zustände seien von 1 bis n durchnummeriert: for i < j n do if i F und j F oder j F und i F then markiere M(i,j) mit X 0 ; if Feld wurde markiert then change:= true else change := false; index:= 0; while change do change := false; index := index + 1; for i < j n, a do if nicht markiert M(i,j) und markiert M( (i,a), (j,a)) mit X index-1 then markiere M(i,j) mit X index ; change := true; Anmerkung: die Indizes der Markierung sind nicht unbedingt nötig, aber hilfreich: man kann zeigen: Algorithmus markiert M(i,j) mit X k genau dann wenn Zustände i, j nicht äquivalent sind und kürzestes Gegenbeispiel hat Länge k. Unser Beispiel: In der Initialisierungsphase werden alle Paare aus akzeptierenden und nichtakzeptierenden Zuständen markiert: 4 3 X 0 X 0 2 X 0 X 0 1 X 0 X Jetzt Zustandspaare p,q zu finden, die für bestimmte Eingabe zu bereits markierten Zustandspaaren führen: (1,b) = 3 (2,b) = 4 (1,b) = 3 (3,b) = 5 M(3,4) bereits markiert, also markiere M(1,2) M(3,5) bereits markiert, also markiere M(1,3) 12
13 Resultat: 4 3 X 0 X 0 2 X 0 X 0 1 X 0 X 0 X 1 X Keine weiteren Markierungen sind möglich: (4,a) = 2 (4,b) = 4 (5,a) = 3 (5,b) = 5 weder M(2,3) noch M(4,5) markiert (2,a) = 2 (2,b) = 4 (3,a) = 3 (3,b) = 5 weder M(2,3) noch M(4,5) markiert Damit sind 4,5 und 2,3 äquivalent. Sei A = (Q A,, A, q 0A, F A ) ein DEA ohne unerreichbare Zustände (gegebenenfalls vorher eliminieren). Erzeugung des minimalen DEA M = (Q M,, M, q 0M, F M ) aus A: 1. Bestimme mit obiger Methode äquivalente Zustände in A. 2. Zustände von M sind die Klassen äquivalenter Zustände von A. 3. M (S, x) = Q gdw A (s, x) = q für ein s S und ein q Q. 4. S = q 0M gdw. q 0A S. 5. S F M gdw. s F A für ein s S. Bemerkung: Zu 3: wenn ein s S in A in Zustand der Äquivalenzklasse Q landet, so gilt das für alle s S. Zu 5: wenn ein s S in A akzeptierender Zustand ist, so gilt das für alle s S. In unserem Beispiel: Äquivalenzklassen {1}, {2,3}, {4,5} Startzustand {1}, F = {{4,5}} ({1},a) = ({1},b) = {2,3} ({2,3},a) = {2,3}, ({2,3},b) = {4,5} ({4,5},a) = {2,3}, ({4,5},b) = {4,5} Satz: Sei A ein DEA, M der nach dem oben beschriebenen Verfahren aus A erzeugte DEA. Es gibt keinen zu A äquivalenten DEA mit weniger Zuständen als M. 13
14 2.5 Kombination endlicher Automaten In diesem Abschnitt wollen wir untersuchen, wie man endliche Automaten für Sprachen L 1 bzw. L 2 so kombinieren kann, dass Automaten für Komplement, Vereinigung, Schnitt, Konkatenation und Kleene-Abschluss (*-Operator) entstehen. Seien M 1 = (Q 1,, 1, q 0,1, F 1 ) und M 2 = (Q 2,, 2, q 0,2, F 2 ) beliebige endliche Automaten, die Sprachen L 1 bzw. L 2 akzeptieren. Annahme: Q 1 und Q 2 disjunkt (sonst Umbenennen von Zuständen). Komplement von L 1 : Voraussetzung: M 1 ist DEA (gegebenenfalls ist Potenzautomat zu konstruieren). Der endliche Automat für *\L 1 entsteht aus dem Automaten M 1 durch Vertauschen von akzeptierenden und nicht-akzeptierenden Zuständen. Beispiel: aus wird Konstruktion klappt nicht für NEAs. Warum? Vereinigung von L 1 und L 2 : Einfügen eines neuen Startzustandes q 0 mit -Übergängen zu den beiden ursprünglichen Startzuständen von M 1 und M 2. q0 q 0,1 M 1 q 0,2 M 2 Schnitt von L 1 und L 2 : Konstruktion des Produktautomaten M 1 M 2 = (Q 1 Q 2,,, (q 0,1, q 0,2 ), F 1 F 2 ) mit ((q 1, q 2 ), a) = { (p 1, p 2 ) p 1 (q 1, a) und p 2 (q 2, a)}. Idee: Zustände des neuen Automaten sind Paare von Zuständen der ursprünglichen Automaten. Neuer Automat nach Eingabe w in Zustand (r, s) gdw. (nach Eingabe w) M 1 in Zustand r und M 2 in Zustand s. Beispiel: aus und 14
15 wird: a b (1, x) (2, y) (2, z) (1, y) (2, y) (2, y) (1, z) (2, z) (2, z) (2, x) (2, y) (3, z) (2, y) (2, y) (3, y) (2, z) (2, z) (3, z) (3, x) (2, y) (3, z) * (3, y) (2, y) (3, y) (3, z) (2, z) (3, z) Konkatenation von L 1 und L 2 (L 1 L 2 = {w 1 w 2 w 1 L 1 und w 2 L 2 }: M 1 M 2 = (Q 1 Q 2,,, q 0,1, F 2 ) mit erreichbar sind nur: (1,x), (2,y), (2, z), (3,y), (3, z) (q, a) = (q, a) falls q Q 1 und (q F 1 oder a ), (q, a) falls q Q 2, {q 0,2 } (q, ) falls q F 1 und a = Illustration: Automat entsteht durch Hintereinanderschalten : Von akzeptierenden Zuständen in M 1 -Übergang zu Startzustand von M 2, akzeptierende Zustände in M 1 und Startzustand von M 2 werden normale Zustände, akzeptierender Zustand von M 2 ist Endzustand des Gesamtautomaten Kleene-Abschluss L* (L 0 ={ }, L n+1 =LL n, L * = L i ): i 0 Sei M = (Q,,, q 0, F) Automat für L. Wir definieren M* = (Q q s,q f },,, q s, {q f }), wobei q s,q f neue Zustände sind und d wie folgt definiert wird: (q, a) = (q, a) falls a und q Q, {q 0, q f } (q, ) falls a = und q F, (q, ) falls a = und q Q\F, {q 0, q f } falls a = und q = q s, sonst Illustration: Automat für L* durch Rückkopplung im ursprünglichen Automaten: -Übergang von alten Endzuständen zu altem Startzustand, neuer Startzustand mit -Übergang zu altem Startzustand und neuem Endzustand, neuer Endzustand auch von alten Endzuständen per -Übergang erreichbar. (Direkter -Übergang von q 0 zu q f klappt nicht: es würde sonst jedes Wort, das zu q 0 führt, akzeptiert werden; ebenso klappt nicht direkter -Übergang von q s zu alten Finalzuständen: Wörter, die von Zuständen in F zu Zuständen in F führen, würden erkannt). 15
Vorlesung Theoretische Informatik
 Vorlesung Theoretische Informatik Automaten und Formale Sprachen Hochschule Reutlingen Fakultät für Informatik Masterstudiengang Wirtschaftsinformatik überarbeitet von F. Laux (Stand: 09.06.2010) Sommersemester
Vorlesung Theoretische Informatik Automaten und Formale Sprachen Hochschule Reutlingen Fakultät für Informatik Masterstudiengang Wirtschaftsinformatik überarbeitet von F. Laux (Stand: 09.06.2010) Sommersemester
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls
 4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls δ(q, a, Z) + δ(q, ɛ, Z) 1 (q, a, Z) Q Σ. Die von einem DPDA, der mit leerem Keller akzeptiert,
4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls δ(q, a, Z) + δ(q, ɛ, Z) 1 (q, a, Z) Q Σ. Die von einem DPDA, der mit leerem Keller akzeptiert,
Theoretische Informatik I
 Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier fernau@uni-trier.de
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Mathematische Grundlagen der Informatik 2
 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss emanuel.duss@gmail.com 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss emanuel.duss@gmail.com 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Informatik IC2. Balazs Simon 2005.03.26.
 Informatik IC2 Balazs Simon 2005.03.26. Inhaltsverzeichnis 1 Reguläre Sprachen 3 1.1 Reguläre Sprachen und endliche Automaten...................... 3 1.2 Determinisieren.....................................
Informatik IC2 Balazs Simon 2005.03.26. Inhaltsverzeichnis 1 Reguläre Sprachen 3 1.1 Reguläre Sprachen und endliche Automaten...................... 3 1.2 Determinisieren.....................................
Deterministische Turing-Maschinen (DTM) F3 03/04 p.46/395
 Deterministische Turing-Maschinen (DTM) F3 03/04 p.46/395 Turing-Machine Wir suchen ein Modell zur formalen Definition der Berechenbarkeit von Funktionen und deren Zeit- und Platzbedarf. Verschiedene Modelle
Deterministische Turing-Maschinen (DTM) F3 03/04 p.46/395 Turing-Machine Wir suchen ein Modell zur formalen Definition der Berechenbarkeit von Funktionen und deren Zeit- und Platzbedarf. Verschiedene Modelle
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen 19
 Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Reguläre Sprachen Endliche Automaten
 Endliche Automaten (Folie 54, Seite 16 im Skript) Einige Vorteile endlicher deterministischer Automaten: durch Computer schnell simulierbar wenig Speicher benötigt: Tabelle für δ (read-only), aktueller
Endliche Automaten (Folie 54, Seite 16 im Skript) Einige Vorteile endlicher deterministischer Automaten: durch Computer schnell simulierbar wenig Speicher benötigt: Tabelle für δ (read-only), aktueller
Grammatiken. Einführung
 Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
Grundlagen der Informatik II. Teil I: Formale Modelle der Informatik
 Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Einführung. Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Vorlesungen zur Komplexitätstheorie. K-Vollständigkeit (1/5)
 Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Die Komplexitätsklassen P und NP
 Die Komplexitätsklassen P und NP Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 3. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Die Komplexitätsklassen P und NP Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 3. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Informatik
 Theoretische Informatik für die Studiengänge Ingenieur-Informatik berufsbegleitendes Studium Lehramt Informatik (Sekundar- und Berufsschule) http://theo.cs.uni-magdeburg.de/lehre04s/ Lehrbeauftragter:
Theoretische Informatik für die Studiengänge Ingenieur-Informatik berufsbegleitendes Studium Lehramt Informatik (Sekundar- und Berufsschule) http://theo.cs.uni-magdeburg.de/lehre04s/ Lehrbeauftragter:
Windows. Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1
 Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1 Wenn der Name nicht gerade www.buch.de oder www.bmw.de heißt, sind Internetadressen oft schwer zu merken Deshalb ist es sinnvoll, die Adressen
Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1 Wenn der Name nicht gerade www.buch.de oder www.bmw.de heißt, sind Internetadressen oft schwer zu merken Deshalb ist es sinnvoll, die Adressen
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
Anmerkungen zur Übergangsprüfung
 DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Wortproblem für kontextfreie Grammatiken
 Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Theoretische Informatik SS 04 Übung 1
 Theoretische Informatik SS 04 Übung 1 Aufgabe 1 Es gibt verschiedene Möglichkeiten, eine natürliche Zahl n zu codieren. In der unären Codierung hat man nur ein Alphabet mit einem Zeichen - sagen wir die
Theoretische Informatik SS 04 Übung 1 Aufgabe 1 Es gibt verschiedene Möglichkeiten, eine natürliche Zahl n zu codieren. In der unären Codierung hat man nur ein Alphabet mit einem Zeichen - sagen wir die
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Formale Sprachen und Grammatiken
 Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Also kann nur A ist roter Südler und B ist grüner Nordler gelten.
 Aufgabe 1.1: (4 Punkte) Der Planet Og wird von zwei verschiedenen Rassen bewohnt - dem grünen und dem roten Volk. Desweiteren sind die Leute, die auf der nördlichen Halbkugel geboren wurden von denen auf
Aufgabe 1.1: (4 Punkte) Der Planet Og wird von zwei verschiedenen Rassen bewohnt - dem grünen und dem roten Volk. Desweiteren sind die Leute, die auf der nördlichen Halbkugel geboren wurden von denen auf
Sprachen/Grammatiken eine Wiederholung
 Sprachen/Grammatiken eine Wiederholung Was sind reguläre Sprachen? Eigenschaften regulärer Sprachen Sprachen Begriffe Symbol: unzerlegbare Grundzeichen Alphabet: endliche Menge von Symbolen Zeichenreihe:
Sprachen/Grammatiken eine Wiederholung Was sind reguläre Sprachen? Eigenschaften regulärer Sprachen Sprachen Begriffe Symbol: unzerlegbare Grundzeichen Alphabet: endliche Menge von Symbolen Zeichenreihe:
Automatentheorie Berechnungsmodell für logische Sprachen
 Automatentheorie Berechnungsmodell für logische Sprachen Thorsten Haupt Betreuer: Tim Priesnitz -Proseminar Theorie kommunizierender Systeme SS 24- Prof. Gert Smolka, PS-Lab, Universität des Saarlandes
Automatentheorie Berechnungsmodell für logische Sprachen Thorsten Haupt Betreuer: Tim Priesnitz -Proseminar Theorie kommunizierender Systeme SS 24- Prof. Gert Smolka, PS-Lab, Universität des Saarlandes
Was ist Sozial-Raum-Orientierung?
 Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Theorie der Informatik
 Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Grundlagen der Theoretischen Informatik - Sommersemester 2012. Übungsblatt 1: Lösungsvorschläge
 Lehrstuhl für Softwaretechnik und Programmiersprachen Professor Dr. Michael Leuschel Grundlagen der Theoretischen Informatik - Sommersemester 2012 Übungsblatt 1: Lösungsvorschläge Disclaimer: Bei Folgendem
Lehrstuhl für Softwaretechnik und Programmiersprachen Professor Dr. Michael Leuschel Grundlagen der Theoretischen Informatik - Sommersemester 2012 Übungsblatt 1: Lösungsvorschläge Disclaimer: Bei Folgendem
3. Zusammenhang. 22 Andreas Gathmann
 22 Andreas Gathmann 3. Zusammenhang Eine der anschaulichsten Eigenschaften eines topologischen Raumes ist wahrscheinlich, ob er zusammenhängend ist oder aus mehreren Teilen besteht. Wir wollen dieses Konzept
22 Andreas Gathmann 3. Zusammenhang Eine der anschaulichsten Eigenschaften eines topologischen Raumes ist wahrscheinlich, ob er zusammenhängend ist oder aus mehreren Teilen besteht. Wir wollen dieses Konzept
Erstellen einer digitalen Signatur für Adobe-Formulare
 Erstellen einer digitalen Signatur für Adobe-Formulare (Hubert Straub 24.07.13) Die beiden Probleme beim Versenden digitaler Dokumente sind einmal die Prüfung der Authentizität des Absenders (was meist
Erstellen einer digitalen Signatur für Adobe-Formulare (Hubert Straub 24.07.13) Die beiden Probleme beim Versenden digitaler Dokumente sind einmal die Prüfung der Authentizität des Absenders (was meist
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
4. AUSSAGENLOGIK: SYNTAX. Der Unterschied zwischen Objektsprache und Metasprache lässt sich folgendermaßen charakterisieren:
 4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Codierungstheorie Rudolf Scharlau, SoSe 2006 9
 Codierungstheorie Rudolf Scharlau, SoSe 2006 9 2 Optimale Codes Optimalität bezieht sich auf eine gegebene Quelle, d.h. eine Wahrscheinlichkeitsverteilung auf den Symbolen s 1,..., s q des Quellalphabets
Codierungstheorie Rudolf Scharlau, SoSe 2006 9 2 Optimale Codes Optimalität bezieht sich auf eine gegebene Quelle, d.h. eine Wahrscheinlichkeitsverteilung auf den Symbolen s 1,..., s q des Quellalphabets
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
THEORETISCHE INFORMATIK
 THEORETISCHE INFORMATIK Vorlesungsskript Jiří Adámek Institut für Theoretische Informatik Technische Universität Braunschweig Januar 2014 Inhaltsverzeichnis 1 Endliche Automaten 1 1.1 Mathematische Grundbegriffe.......................
THEORETISCHE INFORMATIK Vorlesungsskript Jiří Adámek Institut für Theoretische Informatik Technische Universität Braunschweig Januar 2014 Inhaltsverzeichnis 1 Endliche Automaten 1 1.1 Mathematische Grundbegriffe.......................
Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung
 Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung Frank Heitmann heitmann@informatik.uni-hamburg.de 13. Mai 2014 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/17 Überblick Wir hatten
Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung Frank Heitmann heitmann@informatik.uni-hamburg.de 13. Mai 2014 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/17 Überblick Wir hatten
Beweisbar sichere Verschlüsselung
 Beweisbar sichere Verschlüsselung ITS-Wahlpflichtvorlesung Dr. Bodo Möller Ruhr-Universität Bochum Horst-Görtz-Institut für IT-Sicherheit Lehrstuhl für Kommunikationssicherheit bmoeller@crypto.rub.de 6
Beweisbar sichere Verschlüsselung ITS-Wahlpflichtvorlesung Dr. Bodo Möller Ruhr-Universität Bochum Horst-Görtz-Institut für IT-Sicherheit Lehrstuhl für Kommunikationssicherheit bmoeller@crypto.rub.de 6
der Eingabe! Haben Sie das Ergebnis? Auf diesen schwarzen Punkt kommen wir noch zu sprechen.
 Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Endlicher Automat (EA)
 Endlicher Automat (EA) siehe auch Formale Grundlagen 3 1 Motivation: Automaten für die Modellierung, Spezifikation und Verifikation verwenden! Definition Ein Endlicher Automat A = (S,I,Σ,T,F) besteht aus
Endlicher Automat (EA) siehe auch Formale Grundlagen 3 1 Motivation: Automaten für die Modellierung, Spezifikation und Verifikation verwenden! Definition Ein Endlicher Automat A = (S,I,Σ,T,F) besteht aus
Dialognetze. Ziel : Beschreibung von Methoden und Beschreibungstechniken für den Entwurf und die Dokumentation von Dialogabläufen
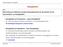 Dialognetze Ziel : Beschreibung von Methoden und Beschreibungstechniken für den Entwurf und die Dokumentation von Dialogabläufen Dialogabläufe auf Fensterebene "grobe Dialogabläufe" d.h. Wechsel zwischen
Dialognetze Ziel : Beschreibung von Methoden und Beschreibungstechniken für den Entwurf und die Dokumentation von Dialogabläufen Dialogabläufe auf Fensterebene "grobe Dialogabläufe" d.h. Wechsel zwischen
EINFACHES HAUSHALT- KASSABUCH
 EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit
 Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Rekursionen. Georg Anegg 25. November 2009. Methoden und Techniken an Beispielen erklärt
 Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
a n + 2 1 auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert:
 Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
15 Optimales Kodieren
 15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
Partitionieren in Vista und Windows 7/8
 Partitionieren in Vista und Windows 7/8 Windows Vista und Windows 7 können von Haus aus Festplatten partitionieren. Doch die Funktion ist etwas schwer zu entdecken, denn sie heißt "Volume verkleinern".
Partitionieren in Vista und Windows 7/8 Windows Vista und Windows 7 können von Haus aus Festplatten partitionieren. Doch die Funktion ist etwas schwer zu entdecken, denn sie heißt "Volume verkleinern".
Das Briefträgerproblem
 Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
t r Lineare Codierung von Binärbbäumen (Wörter über dem Alphabet {, }) Beispiel code( ) = code(, t l, t r ) = code(t l ) code(t r )
 Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
TheGI 1: Grundlagen und algebraische Strukturen Prof. Dr.-Ing. Uwe Nestmann - 09. Februar 2010. 2. Schriftliche Leistungskontrolle (EK)
 TheGI 1: Grundlagen und algebraische Strukturen Prof. Dr.-Ing. Uwe Nestmann - 09. Februar 2010 2. Schriftliche Leistungskontrolle (EK) Punktzahl In dieser schriftlichen Leistungskontrolle sind 100 Punkte
TheGI 1: Grundlagen und algebraische Strukturen Prof. Dr.-Ing. Uwe Nestmann - 09. Februar 2010 2. Schriftliche Leistungskontrolle (EK) Punktzahl In dieser schriftlichen Leistungskontrolle sind 100 Punkte
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Übung Theoretische Grundlagen Nachtrag zur Vorlesung Dirk Achenbach 21.11.2013
 Übung Theoretische Grundlagen Nachtrag zur Vorlesung Dirk Achenbach 21.11.2013 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory of the
Übung Theoretische Grundlagen Nachtrag zur Vorlesung Dirk Achenbach 21.11.2013 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory of the
Theoretische Grundlagen des Software Engineering
 Theoretische Grundlagen des Software Engineering 11: Abstrakte Reduktionssysteme schulz@eprover.org Reduktionssysteme Definition: Reduktionssystem Ein Reduktionssystem ist ein Tupel (A, ) Dabei gilt: A
Theoretische Grundlagen des Software Engineering 11: Abstrakte Reduktionssysteme schulz@eprover.org Reduktionssysteme Definition: Reduktionssystem Ein Reduktionssystem ist ein Tupel (A, ) Dabei gilt: A
Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])
![Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])](/thumbs/29/13170670.jpg) 3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
Punkt 1 bis 11: -Anmeldung bei Schlecker und 1-8 -Herunterladen der Software
 Wie erzeugt man ein Fotobuch im Internet bei Schlecker Seite Punkt 1 bis 11: -Anmeldung bei Schlecker und 1-8 -Herunterladen der Software Punkt 12 bis 24: -Wir arbeiten mit der Software 8-16 -Erstellung
Wie erzeugt man ein Fotobuch im Internet bei Schlecker Seite Punkt 1 bis 11: -Anmeldung bei Schlecker und 1-8 -Herunterladen der Software Punkt 12 bis 24: -Wir arbeiten mit der Software 8-16 -Erstellung
Data Mining: Einige Grundlagen aus der Stochastik
 Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Summenbildung in Bauteiltabellen mit If Then Abfrage
 Summenbildung in Bauteiltabellen mit If Then Abfrage Die in Bauteiltabellen ausgelesenen Werte lassen sich in jeder Spalte als Summe berechnen. So können selbstverständlich die Flächen der in der Tabelle
Summenbildung in Bauteiltabellen mit If Then Abfrage Die in Bauteiltabellen ausgelesenen Werte lassen sich in jeder Spalte als Summe berechnen. So können selbstverständlich die Flächen der in der Tabelle
1. Einführung. 2. Die Abschlagsdefinition
 1. Einführung orgamax bietet die Möglichkeit, Abschlagszahlungen (oder auch Akontozahlungen) zu erstellen. Die Erstellung der Abschlagsrechnung beginnt dabei immer im Auftrag, in dem Höhe und Anzahl der
1. Einführung orgamax bietet die Möglichkeit, Abschlagszahlungen (oder auch Akontozahlungen) zu erstellen. Die Erstellung der Abschlagsrechnung beginnt dabei immer im Auftrag, in dem Höhe und Anzahl der
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Stammdatenanlage über den Einrichtungsassistenten
 Stammdatenanlage über den Einrichtungsassistenten Schritt für Schritt zur fertig eingerichteten Hotelverwaltung mit dem Einrichtungsassistenten Bitte bereiten Sie sich, bevor Sie starten, mit der Checkliste
Stammdatenanlage über den Einrichtungsassistenten Schritt für Schritt zur fertig eingerichteten Hotelverwaltung mit dem Einrichtungsassistenten Bitte bereiten Sie sich, bevor Sie starten, mit der Checkliste
Woche 1: Was ist NLP? Die Geschichte des NLP.
 Woche 1: Was ist NLP? Die Geschichte des NLP. Liebe(r) Kursteilnehmer(in)! Im ersten Theorieteil der heutigen Woche beschäftigen wir uns mit der Entstehungsgeschichte des NLP. Zuerst aber eine Frage: Wissen
Woche 1: Was ist NLP? Die Geschichte des NLP. Liebe(r) Kursteilnehmer(in)! Im ersten Theorieteil der heutigen Woche beschäftigen wir uns mit der Entstehungsgeschichte des NLP. Zuerst aber eine Frage: Wissen
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Ihre Interessentendatensätze bei inobroker. 1. Interessentendatensätze
 Ihre Interessentendatensätze bei inobroker Wenn Sie oder Ihre Kunden die Prozesse von inobroker nutzen, werden Interessentendatensätze erzeugt. Diese können Sie direkt über inobroker bearbeiten oder mit
Ihre Interessentendatensätze bei inobroker Wenn Sie oder Ihre Kunden die Prozesse von inobroker nutzen, werden Interessentendatensätze erzeugt. Diese können Sie direkt über inobroker bearbeiten oder mit
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Handbuch B4000+ Preset Manager
 Handbuch B4000+ Preset Manager B4000+ authentic organ modeller Version 0.6 FERROFISH advanced audio applications Einleitung Mit der Software B4000+ Preset Manager können Sie Ihre in der B4000+ erstellten
Handbuch B4000+ Preset Manager B4000+ authentic organ modeller Version 0.6 FERROFISH advanced audio applications Einleitung Mit der Software B4000+ Preset Manager können Sie Ihre in der B4000+ erstellten
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Guten Morgen und Willkommen zur Saalübung!
 Guten Morgen und Willkommen zur Saalübung! 1 Wie gewinnt man ein Spiel? Was ist ein Spiel? 2 Verschiedene Spiele Schach, Tic-Tac-Toe, Go Memory Backgammon Poker Nim, Käsekästchen... 3 Einschränkungen Zwei
Guten Morgen und Willkommen zur Saalübung! 1 Wie gewinnt man ein Spiel? Was ist ein Spiel? 2 Verschiedene Spiele Schach, Tic-Tac-Toe, Go Memory Backgammon Poker Nim, Käsekästchen... 3 Einschränkungen Zwei
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Absolute Stetigkeit von Maßen
 Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Einfache kryptographische Verfahren
 Einfache kryptographische Verfahren Prof. Dr. Hagen Knaf Studiengang Angewandte Mathematik 26. April 2015 c = a b + a b + + a b 1 11 1 12 2 1n c = a b + a b + + a b 2 21 1 22 2 2n c = a b + a b + + a b
Einfache kryptographische Verfahren Prof. Dr. Hagen Knaf Studiengang Angewandte Mathematik 26. April 2015 c = a b + a b + + a b 1 11 1 12 2 1n c = a b + a b + + a b 2 21 1 22 2 2n c = a b + a b + + a b
Berechnungen in Access Teil I
 in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
Entscheidungsprobleme. Berechenbarkeit und Komplexität Entscheidbarkeit und Unentscheidbarkeit. Die Entscheidbarkeit von Problemen
 Berechenbarkeit und Komlexität Entscheidbarkeit und Unentscheidbarkeit Wolfgang Schreiner Wolfgang.Schreiner@risc.uni-linz.ac.at Research Institute for Symbolic Comutation (RISC) Johannes Keler University,
Berechenbarkeit und Komlexität Entscheidbarkeit und Unentscheidbarkeit Wolfgang Schreiner Wolfgang.Schreiner@risc.uni-linz.ac.at Research Institute for Symbolic Comutation (RISC) Johannes Keler University,
Info zum Zusammenhang von Auflösung und Genauigkeit
 Da es oft Nachfragen und Verständnisprobleme mit den oben genannten Begriffen gibt, möchten wir hier versuchen etwas Licht ins Dunkel zu bringen. Nehmen wir mal an, Sie haben ein Stück Wasserrohr mit der
Da es oft Nachfragen und Verständnisprobleme mit den oben genannten Begriffen gibt, möchten wir hier versuchen etwas Licht ins Dunkel zu bringen. Nehmen wir mal an, Sie haben ein Stück Wasserrohr mit der
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
Fallbeispiel: Eintragen einer Behandlung
 Fallbeispiel: Eintragen einer Behandlung Im ersten Beispiel gelernt, wie man einen Patienten aus der Datenbank aussucht oder falls er noch nicht in der Datenbank ist neu anlegt. Im dritten Beispiel haben
Fallbeispiel: Eintragen einer Behandlung Im ersten Beispiel gelernt, wie man einen Patienten aus der Datenbank aussucht oder falls er noch nicht in der Datenbank ist neu anlegt. Im dritten Beispiel haben
Das Leitbild vom Verein WIR
 Das Leitbild vom Verein WIR Dieses Zeichen ist ein Gütesiegel. Texte mit diesem Gütesiegel sind leicht verständlich. Leicht Lesen gibt es in drei Stufen. B1: leicht verständlich A2: noch leichter verständlich
Das Leitbild vom Verein WIR Dieses Zeichen ist ein Gütesiegel. Texte mit diesem Gütesiegel sind leicht verständlich. Leicht Lesen gibt es in drei Stufen. B1: leicht verständlich A2: noch leichter verständlich
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Hilfe zur Urlaubsplanung und Zeiterfassung
 Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Übung zur Vorlesung Einführung in die Computerlinguistik und Sprachtechnologie
 Übung zur Vorlesung Einführung in die Computerlinguistik und Sprachtechnologie Wintersemester 2009/10, Prof. Dr. Udo Hahn, Erik Fäßler Übungsblatt 3 vom 19.11.2009 Abgabe bis 26.11.2009, 14:30 Uhr; per
Übung zur Vorlesung Einführung in die Computerlinguistik und Sprachtechnologie Wintersemester 2009/10, Prof. Dr. Udo Hahn, Erik Fäßler Übungsblatt 3 vom 19.11.2009 Abgabe bis 26.11.2009, 14:30 Uhr; per
Computeria Rorschach Mit Excel Diagramme erstellen
 Mit Excel Diagramme erstellen 25.12.2010 Roland Liebing Mit Excel Diagramme erstellen Diagramme können Zahlenwerte veranschaulichen, das heisst, mit Hilfe eines Diagramms können Zahlen besser miteinander
Mit Excel Diagramme erstellen 25.12.2010 Roland Liebing Mit Excel Diagramme erstellen Diagramme können Zahlenwerte veranschaulichen, das heisst, mit Hilfe eines Diagramms können Zahlen besser miteinander
