Theoretische Informatik
|
|
|
- Franz Möller
- vor 5 Jahren
- Abrufe
Transkript
1 HTWM Hochschule für Technik und Wirtschaft Mittweida University of Applied Sciences Technikumsplatz 17 0xxxx Mittweida Fachbereich: MPI Fachgruppe Informatik Seminargruppe: IF99P1 Mitschrift von: Isabel Drost Massaneier Str Waldheim Theoretische Informatik Mitschrift von: Drost, Isabel/ if99wp1 Seite 1 von 9
2 Alles was entscheidbar ist, ist auch aufzählbar! Beispiele aufzählbarer Mengen: 1. Natürliche Zahlen 1. Primzahlen Entscheidbar: T Element von M Aufzählbar: T T kein Element von M I Semipositiv entscheidbar: A I M T M Zusammenhänge: (semipositiv=semientscheidbar) 1. entscheidbar=> aufzählbar (Satz x) 2. entscheidbar=> semipositiv entscheidbar 3. entscheidbar=> seminegativ entscheidbar 4. seminegativ+semipositiv <=> entscheidbar 5. Satz 7 6. M semipositiv=> ϕ(m) negativ semientscheidbar 7. M semipositiv=> M aufzählbar (Nachweis: DB von semientscheidbar: M, satz8: M ist aufzählbar, da es semientscheidbar ist. ) X(Kappa)(x)=1 falls x M n.d. sonst (Partielle Charakteristische Funktion von M) Bemerkungen: 1. Aufzählbarkeit und semipositivität sind synonym. 2. Eine Menge ist entscheidbar, wenn die charakt. Fkt. c M berechenbar ist, sie ist aufzählbar, wenn die part. charakt. Fkt. X M berechenbar ist. tϕϕ t ϕϕ A M A M T Μ T ϕ(μ) Zu 6.: ist A m semientscheidbar, ist dessen Komplement semientscheidbar. Damit sind Entscheidungen immer für die gleichen Zahlen möglich. Beispieltabelle: entscheidbar aufzählbar=positiv semientsch. neg. entscheidbar M 3 ={[i,j]: ϕ i, ϕ j Pr,ϕ i ϕ j } i, j=nummern von Funktionen (Programme von Fkt.) M 1 =DBϕ, ϕ P a M 2 ={[i,j]: ϕ i, ϕ j Pr,ϕ i= ϕ j } M2: gibt es einen Algorithmus, der herausfindet, ob beide das gleiche leisten, den gleichen Output liefern (nicht entscheidbar!) M 2 ={[i,j]: ϕ i, ϕ j Pr,ϕ i= ϕ j } aufzählbar hieße, ich kann nacheinander neue Programme erstellen, die den gleichen Algorithmus nach meiner Vorgabe liefern bzw. ich kann bei seminegativ welche finden, die das Gegenteil liefern. Ob sie verschieden sind, krieg ich raus: nach endlicher Zeit kann ich dann nämlich aufhören, zu kontrollieren, ob sie den gleichen Output haben, nämlich an der Stelle, wo sie sich dann unterscheiden. M 3 ={[i,j]: ϕ i, ϕ j Pr,ϕ i ϕ j } ist aufzählbar nach den Dove-tailing-Verfahren. Vorgehensweise: Nimm an, Du hast ein Paar x 1, x 2, wenn die beiden Ausgaben der Funktionen Phi verschieden sind, so kriege ich das nach endlicher Zeit heraus. Wenn sie identisch sind, kriege ich das nicht raus. Also ist M3 positiv entscheidbar, aufzählbar. Nicht aber neg. semientscheidbar. Mitschrift von: Drost, Isabel/ if99wp1 Seite 2 von 9
3 Das Dove-tailing-Verfahren: Ergänzung zum Beweis von Satz8: RE={D ϕ :ϕp a } RE {W ϕ :ϕ P a } und zu zeigen: RE {W ϕ :ϕ P a } Es sei M=W ϕ (ϕ P a) Konstruktion einer Aufzählung f für M mit dovetailing (dt). 1. Fall: W ϕ =φ=m RE (Definition) 1. Fall: W ϕ <>φ=> es gibt ein a W ϕ a falls im x-ten Schritt von dt die Berechnung abbricht f(x)= Df { } ϕ (i) falls die Berechnung von ϕ (i) abbricht f(x)= W ϕ Seminar 2 mit Topflappen Weise nach, das H10={[a 0,...,a n ]:n N a i Z von i=0 bis n a i *x i =0 besitzt ganzzahlige Lösung} H10 REC stimmt REC=RE? Zeige H10 ist aufzählbar (Strategie Dove-tailing) Im x-ten Schritt des Dovetailing wird festgestellt, dass x 0 [1,-1] (entspricht 1-x=0) keine Lösung von t n ist f(x)={ } t n (Neu gefundenes, lösbares Polynom)Im x-ten Schritt des Dovetailing wird festgestellt, dass x 0 eine Lösung von t n ist. to t1... tn x [*] RE (aufzählbar) REC (entscheidbar) ϕ (N) FIN = Menge aller endlichen Mengen Ist A entscheibar, ist auch ihr Komplement entscheidbar. Komplement zu endlichen Mengen ist unendliche, da beide zusammen die natürlichen Zahlen ergibt. Komplement von B kann entweder endlich oder nur entscheidbar sein. Beispiel endlich: B sei Menge der natürlichen Zahlen ohne die 1. Beispiel undendlich: Menge der positiven ganzen Zahlen. Komplement von C liegt nur innerhalb der Menge aller Komplemente ist nicht aufzählbar und nicht entscheidbar (Satz7) Komplement von D kann aufzählbar sein, aber auch außerhalb liegen. card(re/ REC/ FIN)= ℵ 0 (abzählbar) card(ϕ(n))= ℵ 1 (überabzählbar) Mitschrift von: Drost, Isabel/ if99wp1 Seite 3 von 9
4 M N REC (entscheidbar) RE (aufzählbar) unendlich nein nein wiederholungsfrei nummerierbar nein nein monoton nummerierbar nein nein strengmonoton nummerierbar nein nein berechenbar nummerierbar nein ja wiederholgsfrei berechen. num.bar nein ja streng monoton berechn. num.bar ja ja endlich ja ja Das Post sche Korrespondenzproblem: Geg: Folge ((x 0,y 0 ), (x 1,y 1 ),..., (x n,y n )) (Folge von Wortpaaren über einem Alphabet) mit x i,y i X *. Ges: I=(i 1,i 2,... i n ) mit x i1 x i2... x in =y i1... y in Bsp: K1=((1,101),(10,00),(011,11)) I=(1, 3,2,3) x y x y x y geht nicht x y sieht besser aus x y fertig Es ist algorithmisch nicht entscheidbar, ob ein PKP (Post sches Korrespondenzproblem) lösbar ist, oder nicht. K2=((001,0),01,011,(01,101),(10,001)) diese hat als kürzeste Lösung hat 66 Elemente. Ist die Menge der PKP aufzählbar/ entscheidbar? 1. PKP REC 1. PKP RE Beweis mit dem Projektionssatz: Suche entscheidbare Menge B, mit PKP ist Projektion von B. B={[pkp, ind]:pkp ist Post sches Korrespondenzproblem, ind ist endliche Indexfolge} B ={[pkp,ind ]:pkp lösbares PKP und ind ist Lösung} Es gibt einen Algorithmus, der bei vorgegebenen PKP und vorgegebener Indexfolge herausfindet, ob diese Indexfolge Lösung des PKP ist. Vorgehensweise: Ausprobieren. B ist somit entscheidbar. PKP ist Prjektion von B :pkp PKP es gibt eine Lösung ind mit [pkp, ind] B qed. RE H10 REC PKP Dϕ ist aufzählbar (Beweis mit dovetailing) 1. Es ist bekannt: 15 Dϕ 1. Τ berechne ϕ (T ist Turingmaschine) T kommt bei Eingabe von x nach y Schritten in den Finalzustand i in der Zeichnung Ergebnis der Berechnung das Phi Mitschrift von: Drost, Isabel/ if99wp1 Seite 4 von 9
5 i t x ϕ(i) f(0) = 15 (da die 0te Maschine nicht im 1. Takt, sondern im 6. Takt aufhört, somit muß ich mein Standardergebins ausgeben) f(1) = 15 f(2) = f(7) = 15 f(8) = 2 f(13)=3 f(15)=0 f(x)= i falls im x-ten Schritt von dovetailing die Berechnung von ϕ abbricht 15 sonst (denn davon wissen wir, dass bei dessen Eingabe die Berechnung immer abbricht) somit is f überall definiert und somit allgemein rekursiv. W f = Dϕ Eingabe der Turingmaschine ist das, was links der Tabelle steht. Kommt er zum Ende geben wir das i aus. Aufgabe: Zeigen Sie mit dem Projektionsatz, für ϕ Pa gilt: Dϕ RE Benötigt entscheidbare Menge B mit: Dϕ ist Projektion von B x Dϕ <=> es gibt y, es gibt z, es gibt u, mit [x,y,z,u] B Es gibt einen Takt t und es gibt eine Ausgabe y, mit: Die Berechnung von ϕ(x) hört an der Stelle t auf und die Ausgabe ist y. Wenn dem so ist, so gehört x zum Definitionsbereich der Turingmaschine ϕ. B={[x,t,y]:Berechnung von ϕ (x) hört nach t Takten mit Ausgabe von y auf} Dieses B ist entscheidbar: bei bestimmten vorgegebenen Parametern einfach ausprobieren (Nimm die Maschine x, lasse sie 13 Takte rechnen und gucke, ob y rauskommt. B ist entscheidbar, somit ist Dϕ aufzählbar (B REC=> Dϕ RE) PKP={pkp:Menge aller lösbaren Post schen Korrespondenzprobleme} Behauptung: Diese Menge ist aufzählbar PKP n = DF {pkp:pkp PKP und pkp besitzt eine Lösung der Länge n}:pkp n REC (entscheidbar und aufzählbar) Zeige, dass pkp aufzählbar ist: pkp PKP es gibt Lösung l mit [pkp,l] B B={[pkp,l ]:l ist Lösung von pkp} REC PKP ist Projektion von B! B={[a,x,0],[a,y,1],[b,x,1],[c,y,0]} Projektionen von B: P1={[a,x],[a,y],[b,x],[c,y]} P2={[a,0],[a,1],[b,1],[c,0]} P3={[x,0],[y,1],[x,1],[y,0]} PRP REC wurde bewiesen. Mitschrift von: Drost, Isabel/ if99wp1 Seite 5 von 9
6 Es ist relativ einfach, nachzuweisen, dass eine Menge entscheidbar oder aufzählbar ist. (Finde einfach einen Entscheidungs- bzw. Aufzählungsalgorithmus) Schwieriger ist der Nachweis, dass eine Menge nicht entscheidbar/ nicht aufzählbar ist (Weise nach, dass es keinen solchen Algorithmus gibt, c m Pa). Möglichkeiten für den Nachweis der Nicht-Entscheidbarkeit und der Nichtaufzählbarkeit: A,B N; A m B (A auf B m-reduzierbar (transformierbar))= Es gibt f R mit x A<=> f(x) B Eigenschaften: Es sei A m B: a) B REC Ich kriege auch heraus, ob x zu A gehört: berechne f(x). x gehört zu A, wenn f(x) zu B gehört. Ist B entscheidbar, so ist auch A entscheidbar. a) B RE X A (Aufzählbarkeit von A, Semientscheidbarkeit von A) ist herauszufinden, wie oben. Will ich wissen, ob x zu A gehört, muß ich f(x) berechnen. Wenn f(x) zu B gehört, gehört x zu A. B ist aber nur im positiven Falle entscheidbar. Also kann ich die Zuordnung in A auch nur im positiven Falle treffen. A m B positive algorithmische Eigenschaften (Aufzählbarkeit, Entscheidbarkeit) vererben sich von oben nach unten, von rechts nach links. a) A ist nicht entscheidbar, dann muß auch B nicht entscheidbar sein. a) A ist nicht aufzählbar, dann muß auch B nicht aufzählbar sein. A m B, die negativen algorithmischen Eigenschaften vererben sich von oben nach unten/ von links nach rechts. Spezielles Halteproblem K, K ist aufzählbar (RE) und nicht entscheidbar (REC). K m PKP wurde bewiesen. Somit ist PKP nicht entscheidbar. K {[x,y]:x D y } heißt allgemeines Halteproblem (x gehört zum DB der yten Funktion). K={i:i D i } ist das spezielle Halteproblem (i gehört zum DB der iten Fkt.) Halte ich an, oder nicht? Behauptungen: K ist aufzählbar und nicht entscheidbar. 1. Beweis K ist aufzählbar über den Projektionssatz: Projektionsatz: A ist aufzählbar, genau dann, wenn A ist Projektion einer entscheidbaren Menge B. Die Projektion einer Menge ist die Reduktion auf Komponenten dieser Menge. Um diesen Satz anwenden zu können, brauchen wir eine Menge mit mehr Komponenten als K. Turingprädikat : T(y,x,t,z) Suche also von der bekannten Menge K eine entscheidbare Menge und stelle K als Projektion von M dar (M={[i,x,t,y]:T(i,x,t,y)} REC) [x,y] K es gibt eine Taktzahl t und es gibt eine Ausgabe z (oben als y bezeichnet) mit [y,x,t,z] M M ist entscheidbar, somit ist auch K entscheidbar. Halte ich nach t Takten an, oder nicht? 1. Zeige K<= m K (K reduzierbar auf K K ist nichtentscheidbar) Dazu wird die allgemein rekursive Funktion f R mit x K f(x) K. f(x)=[x,x] (ich habe für K zwei Werte als Eingabe, für K nur einen Wert, gebe ich bei K x ein, wird geprüft, ob die xte Maschine bei Eingabe von x anhält, dies erreiche ich, wenn ich bei K x eingebe und intern prüfe, ob die xte Maschine bei Eingabe von x anhält, also die eine Eingabe vorher in eine Eingabe von [x,x] umwandle. Somit gilt: x K f(x) K x D x [x,x] K Somit ist K reduzierbar auf K. M={i: ϕ i ist monoton steigend} Welche algorithmischen Eigenschaften hat M? M ist eine Sammlung von Programmen, die monotone Fkt. berechnen. Ist diese Menge z.b. nicht entscheidbar entscheidbar Mitschrift von: Drost, Isabel/ if99wp1 Seite 6 von 9
7 entscheidbar gibt es einen Algorithmus, der mir sagt, ob ein bestimmtes Programm x eine monotone Funktion beschreibt oder nicht. Nach dem Satz von Rice ist nebenstehende Entscheidung unmöglich. 1. M ist also nicht entscheidbar. 1. Komplement von M aufzählbar (positiv semientscheidbar)? ϕ (M) =M M ={i: ϕ i ist nicht monoton steigend} Beweis über den Projektionssatz: x M Es gibt z mit ϕ x (z) definiert und ϕ x (z-1) definiert und mit ϕ x (z)< ϕ x (z-1) (eine Stelle, die kleiner ist, als die Stelle einen Schritt vorher) Welche Algorithmischen Eigenschaften hat M? es gibt t,t,z mit ϕ x hält bei Eingabe von z nach t Takten (ϕ x ist an der Stelle z definiert), ϕ x hält bei Eingabe von z-1 nach t Takten (ϕ x ist an der vorhergehenden Stelle definiert) und ϕ x (z)< ϕ x (z-1) B{[x,t,t,z]: ϕ x stopt bei Eingabe von z nach t Takten, bei Eingabe von z-1 nach t Takten und es ist ϕ x (z)< ϕ x (z-1)} Diese Menge B ist entscheidbar! (Nimm die Eingabe z und lasse die Maschine x t Takte arbeiten stoppt sie, nimm das Ergebnis, nimm dann die Eingabe z-1 und lasse die Maschine x t Takte arbeiten, ist diese Ergebnis kleiner als das, was Du Dir gemerkt hast, gib true aus!) Ergebnis1 < Ergebnis2 true false x M es gibt z,t,t mit [x,t,t,z] B Spezifikation des H10 mittels Projektionsatz H10={[a 0... a n ]:a i Z 1 Σa i x i (von i=0 bis n) =0 besitzt ganzahlige Lösung} H10 RE (aufzählbar, Beweis mit Projektionssatz) [a 0... a n ] H10 es gibt z Z mit Σa i z i (von i=0 bis n) =0 es gibt z Z mit [a 0... a n ] B qed. Behauptung: M REC M monoton aufzählbar (M ist auch dann entscheidbar, wenn M monoton und nicht streng monoton ist) Beweis: => konstruktiv siehe VO <= a) M ist endlich => M ist entscheidbar nach der Definition a) M ist unendlich => Mitschrift von: Drost, Isabel/ if99wp1 Seite 7 von 9
8 Gibt es einen Algorithmus, der alle Programme auflistet (aufzählt), die 1) an wenigsten 2 Stellen definiert sind 1) niemals den Wert 0 annehmen 1) an keiner Stelle x den Wert x annehmen. 1) 1), 2) und 3) erfüllen? Beweis der Nichtentscheidbarkeit (REC): M REC [ M RE UND ϕ(m) RE (Komplement von M) ] ODER [M RE] REC RE M1= {i: ϕ i an wenigsten 2 Stellen definiert} = nicht entscheidbar nach Satz von Rice aufzählbar (positiv semientscheidbar, mit der Vorgehensweise des Projektionssatzes) B= {[i,x1,x2,t1,t2,y1,y2]:i N und T(i,x1,t1,y1) und T(i,x2,t2,y2)} Diese Menge B ist entscheidbar. Es gilt: i M1 es gibt ein x1,x2, t1,t2, y1, y2 mit [i, x1,x2, t1, t2, y1, y2] B Damit folgt, dass M1 aufählbar ist, M1 RE. M1= {i: Es gibt x 1, es gibt x 2 mit ϕ i (x1) definiert und ϕ i (x 2 ) definiert} M2= {i: ϕ i!= 0 für alle x N} = nicht entscheidbar nach Satz von Rice ϕ(m2)= {i: es gibt ein x mit ϕ i (x)=0} = aufzählbar, aber nicht entscheidbar (Beweis der Aufzählbarkeit mittels Projektionssatz) i ϕ(m2) es gibt x und es gibt t mit T(i,x,t,0) (bzw. B ([i,x,t,0]) Diese Menge ist entscheidbar. B={[x1,x2,x3,x4]:T(x1,x2,x3,x4)} REC. Damit folgt nach dem Projektionssatz, dass das Komplement von M2 aufzählbar, M2 aber nicht aufzählbar ist. ϕ(m3)= {i: ϕ i (x)= x für alle x N} M3= {i: ϕ i (x)!=x für alle x Ν } = aufzählbar, aber nicht entscheidbar nach dem Satz von Rice i ϕ(m3) es gibt x und es gibt t und T(i,x,t,x) Somit ist das Komplement von M3 aufzählbar, damit ist aber M3 selbst nicht aufzählbar, da ja M3 nach dem Satz von Rice nicht entscheidbar ist. Allgemeine Vorgehensweise: Man weise die Nichtaufzählbarkeit folgendermaßen nach: 1) Die Nichtentscheidbarkeit (REC) sei nach dem Satz von Rice gegeben. 2) Die Aufzählbarkeit von M oder dessen Komplement sei nachzuweisen, z.b. via Projektionssatz. 3) Somit kann ich auf die Nichtaufzählbarkeit des jeweils anderen Stücks schließen. Es gilt, M4 ist nicht entscheidbar nach dem Satz von Rice. Es gilt, M4 und sein Komplement sind nicht aufzählbar. Komplement von A RE REC Mitschrift von: Drost, Isabel/ if99wp1 Seite 8 von 9
9 Ist R (Menge der allgemein rekursiven Funktionen) gödeliesierbar? Pr und Pa sind gödelisierbar, R ist nicht gödelisierbar. Pr R Pa Annahme: R sei gödelisierbar (ϕ) f(x) = ϕ x (x)+1 f(x) ist überall definiert und überall berechenbar, das heißt f R Es gibt m mit ϕ m =f (*) f(m)= ϕ m (m) (wegen *) f(m)= ϕ m (m) +1 wegen Definition von f => Widerspruch mit der Zeile drüber! (Klausur) Mitschrift von: Drost, Isabel/ if99wp1 Seite 9 von 9
Theoretische Informatik
 HTWM Hochschule für Technik und Wirtschaft Mittweida University of Applied Sciences Technikumsplatz 17 0xxxx Mittweida Fachbereich: MPI Fachgruppe Informatik Theoretische Informatik Seminargruppe: IF99P1
HTWM Hochschule für Technik und Wirtschaft Mittweida University of Applied Sciences Technikumsplatz 17 0xxxx Mittweida Fachbereich: MPI Fachgruppe Informatik Theoretische Informatik Seminargruppe: IF99P1
Entscheidungsprobleme
 Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge M Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge M Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Entscheidungsprobleme
 Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge U Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge U Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17.November 2011 INSTITUT FÜR THEORETISCHE 0 KIT 17.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17.November 2011 INSTITUT FÜR THEORETISCHE 0 KIT 17.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
2.5 Halteproblem und Unentscheidbarkeit
 38 25 Halteproblem und Unentscheidbarkeit Der Berechenbarkeitsbegriff ist auf Funktionen zugeschnitten Wir wollen nun einen entsprechenden Begriff für Mengen einführen Definition 255 Eine Menge A Σ heißt
38 25 Halteproblem und Unentscheidbarkeit Der Berechenbarkeitsbegriff ist auf Funktionen zugeschnitten Wir wollen nun einen entsprechenden Begriff für Mengen einführen Definition 255 Eine Menge A Σ heißt
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 11 15. Juli 2010 Einführung in die Theoretische
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 11 15. Juli 2010 Einführung in die Theoretische
Theoretische Informatik
 Theoretische Informatik Lektion 10: Entscheidbarkeit Kurt-Ulrich Witt Wintersemester 2013/14 Kurt-Ulrich Witt Theoretische Informatik Lektion 10 1/15 Inhaltsverzeichnis Kurt-Ulrich Witt Theoretische Informatik
Theoretische Informatik Lektion 10: Entscheidbarkeit Kurt-Ulrich Witt Wintersemester 2013/14 Kurt-Ulrich Witt Theoretische Informatik Lektion 10 1/15 Inhaltsverzeichnis Kurt-Ulrich Witt Theoretische Informatik
Referat rekursive Mengen vs. rekursiv-aufzählbare Mengen
 Kapitel 1: rekursive Mengen 1 rekursive Mengen 1.1 Definition 1.1.1 informal Eine Menge heißt rekursiv oder entscheidbar, wenn ihre charakteristische Funktion berechenbar ist. 1.1.2 formal Eine Menge A
Kapitel 1: rekursive Mengen 1 rekursive Mengen 1.1 Definition 1.1.1 informal Eine Menge heißt rekursiv oder entscheidbar, wenn ihre charakteristische Funktion berechenbar ist. 1.1.2 formal Eine Menge A
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Unentscheidbarkeit. 1. Wann sind Sprachen unentscheidbar? 1, A 0, A } = {
 Unentscheidbarkeit 1. Wann sind Sprachen unentscheidbar? Eine Menge A heisst entscheidbar, falls die charakteristische Funktion von A, nämlich A : {0,1}, berechenbar ist, d.h. gilt: A = { 1, A 0, A } Eine
Unentscheidbarkeit 1. Wann sind Sprachen unentscheidbar? Eine Menge A heisst entscheidbar, falls die charakteristische Funktion von A, nämlich A : {0,1}, berechenbar ist, d.h. gilt: A = { 1, A 0, A } Eine
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Der Satz von Rice. Dann ist C(S) eine unentscheidbare Menge.
 Der Satz von Rice Satz: Sei R die Klasse der (Turing-) berechenbaren Funktionen, S eine nichttriviale Teilmenge von R und C(S) ={w Mw berechnet eine Funktion aus S}. Dann ist C(S) eine unentscheidbare
Der Satz von Rice Satz: Sei R die Klasse der (Turing-) berechenbaren Funktionen, S eine nichttriviale Teilmenge von R und C(S) ={w Mw berechnet eine Funktion aus S}. Dann ist C(S) eine unentscheidbare
Theoretische Informatik Mitschrift
 Theoretische Informatik Mitschrift 9. Berechenbarkeit, Entscheidbarkeit, Aufzählbarkeit 9.1 Grundbegriffe bereits gezeigt: Spracherkennung durch Turingmaschine = Berechnung der semi-charakteristischen
Theoretische Informatik Mitschrift 9. Berechenbarkeit, Entscheidbarkeit, Aufzählbarkeit 9.1 Grundbegriffe bereits gezeigt: Spracherkennung durch Turingmaschine = Berechnung der semi-charakteristischen
Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet.
 Rückschau 12.11.04 Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet. Wir haben das Prinzip der Diagonalisierung eingeführt und mit DIAG eine erste nicht rek. aufz. Sprache
Rückschau 12.11.04 Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet. Wir haben das Prinzip der Diagonalisierung eingeführt und mit DIAG eine erste nicht rek. aufz. Sprache
Beispiel: NTM. M = ({q 0,q 1,q 2 }, {0, 1}, {0, 1, #},δ, q 0, #, {q 2 }) q 2
 Beispiel: NTM M = ({q 0,q 1,q 2 }, {0, 1}, {0, 1, #},δ, q 0, #, {q 2 }) 0,1,R 0,0,R q0 1,0,R q1 #,#,R q2 0,0,L Zustand 0 1 # q 0 {(1, R, q 0 )} {(0, R, q 1 )} q 1 {(0, R, q 1 ),(0, L, q 0 )} {(1, R, q
Beispiel: NTM M = ({q 0,q 1,q 2 }, {0, 1}, {0, 1, #},δ, q 0, #, {q 2 }) 0,1,R 0,0,R q0 1,0,R q1 #,#,R q2 0,0,L Zustand 0 1 # q 0 {(1, R, q 0 )} {(0, R, q 1 )} q 1 {(0, R, q 1 ),(0, L, q 0 )} {(1, R, q
Ausgewählte unentscheidbare Sprachen
 Proseminar Theoretische Informatik 15.12.15 Ausgewählte unentscheidbare Sprachen Marian Sigler, Jakob Köhler Wolfgang Mulzer 1 Entscheidbarkeit und Semi-Entscheidbarkeit Definition 1: L ist entscheidbar
Proseminar Theoretische Informatik 15.12.15 Ausgewählte unentscheidbare Sprachen Marian Sigler, Jakob Köhler Wolfgang Mulzer 1 Entscheidbarkeit und Semi-Entscheidbarkeit Definition 1: L ist entscheidbar
Theoretische Informatik für Wirtschaftsinformatik und Lehramt
 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Entscheidungsprobleme Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität Erlangen-Nürnberg
Theoretische Informatik für Wirtschaftsinformatik und Lehramt Entscheidungsprobleme Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität Erlangen-Nürnberg
Die Unentscheidbarkeit extensionaler Eigenschaften von Turingmaschinen: der Satz von Rice
 Die Unentscheidbarkeit extensionaler Eigenschaften von Turingmaschinen: der Satz von Rice Holger Arnold Dieser Text befasst sich mit der Frage, unter welchen Bedingungen das Problem, zu bestimmen, ob die
Die Unentscheidbarkeit extensionaler Eigenschaften von Turingmaschinen: der Satz von Rice Holger Arnold Dieser Text befasst sich mit der Frage, unter welchen Bedingungen das Problem, zu bestimmen, ob die
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
Reduktionen. Formalisierung von Sprache A ist nicht schwerer als Sprache B.
 Reduktionen Formalisierung von Sprache A ist nicht schwerer als Sprache B. Idee: Algorithmus/DTM für B kann genutzt werden, um A zu entscheiden/akzeptieren. WS 2018/19 Reduktionen 1 Zwei einfache Sprachen
Reduktionen Formalisierung von Sprache A ist nicht schwerer als Sprache B. Idee: Algorithmus/DTM für B kann genutzt werden, um A zu entscheiden/akzeptieren. WS 2018/19 Reduktionen 1 Zwei einfache Sprachen
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
Einführung in die Theoretische Informatik Tutorium IX
 Einführung in die Theoretische Informatik Tutorium IX Michael R. Jung 16. & 17. 12. 2014 EThI - Tutorium IX 1 1 Entscheidbarkeit, Semi-Entscheidbarkeit und Unentscheidbarkeit 2 EThI - Tutorium IX 2 Definitionen
Einführung in die Theoretische Informatik Tutorium IX Michael R. Jung 16. & 17. 12. 2014 EThI - Tutorium IX 1 1 Entscheidbarkeit, Semi-Entscheidbarkeit und Unentscheidbarkeit 2 EThI - Tutorium IX 2 Definitionen
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V7, 3.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V7, 3.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Universität Karlsruhe Institut für Theoretische Informatik. Klausur: Informatik III
 Name Vorname Matrikelnummer Universität Karlsruhe Institut für Theoretische Informatik o. Prof. Dr. P. Sanders 10.4.2007 Klausur: Informatik III Aufgabe 1. Multiple Choice 11 Punkte Aufgabe 2. Minimalautomaten
Name Vorname Matrikelnummer Universität Karlsruhe Institut für Theoretische Informatik o. Prof. Dr. P. Sanders 10.4.2007 Klausur: Informatik III Aufgabe 1. Multiple Choice 11 Punkte Aufgabe 2. Minimalautomaten
Übungsblatt 3. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 3 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 21. November 2017 Abgabe 5. Dezember 2017, 11:00 Uhr
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 3 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 21. November 2017 Abgabe 5. Dezember 2017, 11:00 Uhr
Falls H die Eingabe verwirft, so wissen wir, dass M bei Eingabe w nicht hält. M hält im verwerfenden Haltezustand. Beweis:
 1 Unentscheidbarkeit 2 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 #include char *s="include
1 Unentscheidbarkeit 2 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 #include char *s="include
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Übungsblatt 1. Lorenz Leutgeb. 30. März 2015
 Übungsblatt Lorenz Leutgeb 30. März 205 Aufgabe. Annahmen ohne Einschränkungen: P Σ und P Γ. Per Definitionem der Reduktion: P P 2 f : Σ Γ wobei f total und berechenbar, genau so, dass: w Σ : w P f(w)
Übungsblatt Lorenz Leutgeb 30. März 205 Aufgabe. Annahmen ohne Einschränkungen: P Σ und P Γ. Per Definitionem der Reduktion: P P 2 f : Σ Γ wobei f total und berechenbar, genau so, dass: w Σ : w P f(w)
Reduktion / Hilberts 10. Problem
 Reduktion / Hilberts 10. Problem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 9. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Reduktion / Hilberts 10. Problem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 9. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Die Reduktion Hilberts 10. Problem
 Die Reduktion Hilberts 10. Problem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 8. November 2010 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Die Reduktion Hilberts 10. Problem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 8. November 2010 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Theoretische Informatik I
 Theoretische Informatik I Einheit 4.3 Eigenschaften von L 0 /L 1 -Sprachen 1. Abschlußeigenschaften 2. Prüfen von Eigenschaften 3. Grenzen der Sprachklassen Sprachklassen Semi-entscheidbare Sprache Sprache,
Theoretische Informatik I Einheit 4.3 Eigenschaften von L 0 /L 1 -Sprachen 1. Abschlußeigenschaften 2. Prüfen von Eigenschaften 3. Grenzen der Sprachklassen Sprachklassen Semi-entscheidbare Sprache Sprache,
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier
 Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/17 Rekursions- und Lerntheorie
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/17 Rekursions- und Lerntheorie
GTI. Hannes Diener Juli. ENC B-0123,
 GTI Hannes Diener ENC B-0123, diener@math.uni-siegen.de 4.-9. Juli 1 / 29 Entscheidungsprobleme und Halteproblem In diesem Kapitel wollen wir uns an Stelle von Berechenbarkeit von Funktion, welche bei
GTI Hannes Diener ENC B-0123, diener@math.uni-siegen.de 4.-9. Juli 1 / 29 Entscheidungsprobleme und Halteproblem In diesem Kapitel wollen wir uns an Stelle von Berechenbarkeit von Funktion, welche bei
Allgemeines Halteproblem Hilberts 10. Problem
 Allgemeines Halteproblem Hilberts 10. Problem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Allgemeines Halteproblem Hilberts 10. Problem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Automaten, Formale Sprachen und Berechenbarkeit I Wichtige Begriffe
 Automaten, Formale Sprachen und Berechenbarkeit I Wichtige Begriffe Eine partielle Funktion ist eine Relation f A B; für jedes x dom(f) gibt es ein y range(f) mit x f y; wir schreiben statt f A B und x
Automaten, Formale Sprachen und Berechenbarkeit I Wichtige Begriffe Eine partielle Funktion ist eine Relation f A B; für jedes x dom(f) gibt es ein y range(f) mit x f y; wir schreiben statt f A B und x
Informatik III. Arne Vater Wintersemester 2006/ Vorlesung
 Informatik III Arne Vater Wintersemester 2006/07 11. Vorlesung 30.11.2006 1 Beziehungen zwischen den Sprachen Jede reguläre Sprache ist eine kontextfreie Sprache. Jede kontextfreie Sprache ist eine entscheidbare
Informatik III Arne Vater Wintersemester 2006/07 11. Vorlesung 30.11.2006 1 Beziehungen zwischen den Sprachen Jede reguläre Sprache ist eine kontextfreie Sprache. Jede kontextfreie Sprache ist eine entscheidbare
Aufgaben aus den Übungsgruppen 8(Lösungsvorschläge)
 Universität des Saarlandes Theoretische Informatik (WS 2015) Fakultät 6.2 Informatik Team der Tutoren Aufgaben aus den Übungsgruppen 8(Lösungsvorschläge) 1 Berechenbarkeitstheorie Aufgabe 8.1 (Wahr oder
Universität des Saarlandes Theoretische Informatik (WS 2015) Fakultät 6.2 Informatik Team der Tutoren Aufgaben aus den Übungsgruppen 8(Lösungsvorschläge) 1 Berechenbarkeitstheorie Aufgabe 8.1 (Wahr oder
Theoretische Informatik und Logik Übungsblatt 1 (2016S) Lösung
 Theoretische Informatik und Logik Übungsblatt (26S) en Aufgabe. Sei L = {w#w r w {, } }. Geben Sie eine deterministische Turingmaschine M an, welche die Sprache L akzeptiert. Wählen Sie mindestens einen
Theoretische Informatik und Logik Übungsblatt (26S) en Aufgabe. Sei L = {w#w r w {, } }. Geben Sie eine deterministische Turingmaschine M an, welche die Sprache L akzeptiert. Wählen Sie mindestens einen
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion
 Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 26. November 2007 Semi-Entscheidbarkeit
Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 26. November 2007 Semi-Entscheidbarkeit
Wie man eine Sprache versteht
 Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
Prüfungsprotokoll der mündlichen Prüfung Grundlagen der Theoretischen Informatik (Bachelor Informatik)
 Prüfungsprotokoll der mündlichen Prüfung Grundlagen der Theoretischen Informatik 25310 (Bachelor Informatik) Prüfer: Prof. Dr. Verbeek Semester der Prüfung: SS 2010 Datum der Prüfung: 25.11.2010 Dauer:
Prüfungsprotokoll der mündlichen Prüfung Grundlagen der Theoretischen Informatik 25310 (Bachelor Informatik) Prüfer: Prof. Dr. Verbeek Semester der Prüfung: SS 2010 Datum der Prüfung: 25.11.2010 Dauer:
Clevere Algorithmen programmieren
 ClevAlg 2017 Theoretische Informatik Clevere Algorithmen programmieren Dennis Komm, Jakub Závodný, Tobias Kohn 06. Dezember 2017 Die zentralen Fragen sind... Was kann man mit einem Computer nicht machen?
ClevAlg 2017 Theoretische Informatik Clevere Algorithmen programmieren Dennis Komm, Jakub Závodný, Tobias Kohn 06. Dezember 2017 Die zentralen Fragen sind... Was kann man mit einem Computer nicht machen?
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier
 Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/16 Rekursions- und Lerntheorie
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/16 Rekursions- und Lerntheorie
Rekursive Aufzählbarkeit Die Reduktion
 Rekursive Aufzählbarkeit Die Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Rekursive Aufzählbarkeit Die Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Relativierte Berechnungen und die arithmetische Hierachie
 Berechenbarkeit und Komplexität Wintersemester 2010/2011 1 Relativierte Berechnungen und die arithmetische Hierachie Relativierte Berechnungen und Orakel Definition 1 Eine Menge A ist entscheidbar mit
Berechenbarkeit und Komplexität Wintersemester 2010/2011 1 Relativierte Berechnungen und die arithmetische Hierachie Relativierte Berechnungen und Orakel Definition 1 Eine Menge A ist entscheidbar mit
Unentscheidbarkeit von Problemen mittels Turingmaschinen
 Unentscheidbarkeit von Problemen mittels Turingmaschinen Daniel Roßberg 0356177 Roland Schatz 0355521 2. Juni 2004 Zusammenfassung In dieser Arbeit befassen wir uns mit der Unentscheidbarkeit von Problemen
Unentscheidbarkeit von Problemen mittels Turingmaschinen Daniel Roßberg 0356177 Roland Schatz 0355521 2. Juni 2004 Zusammenfassung In dieser Arbeit befassen wir uns mit der Unentscheidbarkeit von Problemen
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK 2. ALGORITHMEN. Prof. Dr. Klaus Ambos-Spies. Sommersemester 2011
 EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 2. ALGORITHMEN Theoretische Informatik (SoSe 2011) 2. Algorithmen 1 / 51 Übersicht 1 Typen von Algorithmen: Entscheidungs-,
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 2. ALGORITHMEN Theoretische Informatik (SoSe 2011) 2. Algorithmen 1 / 51 Übersicht 1 Typen von Algorithmen: Entscheidungs-,
Angewandte Mathematik am Rechner 1
 Angewandte Mathematik am Rechner 1 SOMMERSEMESTER 2017 Kapitel 3 [Bildquellen: Wikipedia User David Madore, Inductiveload ] Grundlagen 2: Funktionen, Berechenbarkeit und emergente Komplexität Michael Wand
Angewandte Mathematik am Rechner 1 SOMMERSEMESTER 2017 Kapitel 3 [Bildquellen: Wikipedia User David Madore, Inductiveload ] Grundlagen 2: Funktionen, Berechenbarkeit und emergente Komplexität Michael Wand
Die Church-Turing-These
 Die Church-Turing-These Elmar Eder () Die Church-Turing-These 1 / 12 Formale Systeme Formale Systeme µ-partiellrekursive Funktionen Logikkalküle SLD-Resolution (Prolog) Chomsky-Grammatiken Turing-Maschinen
Die Church-Turing-These Elmar Eder () Die Church-Turing-These 1 / 12 Formale Systeme Formale Systeme µ-partiellrekursive Funktionen Logikkalküle SLD-Resolution (Prolog) Chomsky-Grammatiken Turing-Maschinen
1 Eine Menge M Σ heißt (rekursiv) aufzählbar genau. 2 Die Familie aller aufzählbaren Mengen wird mit RE
 Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 9 Entscheidbarkeit und Aufzählbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 5. Mai 2014 Definition 1 Eine Menge M Σ heißt (rekursiv)
Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 9 Entscheidbarkeit und Aufzählbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 5. Mai 2014 Definition 1 Eine Menge M Σ heißt (rekursiv)
Das Halteproblem für Turingmaschinen
 Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Berechenbarkeitstheorie 14. Vorlesung
 1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Erinnerung
1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Erinnerung
Einführung in die Theoretische Informatik A Lösungshinweise zur Klausur am
 Einführung in die Theoretische Informatik A Lösungshinweise zur Klausur am 15.03.003 Aufgabe 1 a) Sei die stellige Turingmaschine M durch das folgende Flussdiagramm gegeben: 17 1 1:R 0:R 6 :R 19 0:1 6
Einführung in die Theoretische Informatik A Lösungshinweise zur Klausur am 15.03.003 Aufgabe 1 a) Sei die stellige Turingmaschine M durch das folgende Flussdiagramm gegeben: 17 1 1:R 0:R 6 :R 19 0:1 6
Übungsaufgaben Blatt 3
 Departement Informatik Open Class Sieben Wunder der Informatik Prof Dr Juraj Hromkovič Übungsaufgaben Blatt 3 Zürich, 23 November 26 Zusammenfassung und Aufgaben Ein Entscheidungsproblem besteht darin,
Departement Informatik Open Class Sieben Wunder der Informatik Prof Dr Juraj Hromkovič Übungsaufgaben Blatt 3 Zürich, 23 November 26 Zusammenfassung und Aufgaben Ein Entscheidungsproblem besteht darin,
Theoretische Grundlagen der Informatik. Vorlesung am 16. November INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik 0 16.11.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu KIT-Gedenkfeier für
Theoretische Grundlagen der Informatik 0 16.11.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu KIT-Gedenkfeier für
Satz von Rice. Lemma 39
 Unentscheidbarkeit Satz von Rice Das nächste Resultat zeigt, dass jede Eigenschaft der von einer Turing-Maschine berechneten Funktion unentscheidbar ist. Das bedeutet, es gibt keine Methode, mit der man
Unentscheidbarkeit Satz von Rice Das nächste Resultat zeigt, dass jede Eigenschaft der von einer Turing-Maschine berechneten Funktion unentscheidbar ist. Das bedeutet, es gibt keine Methode, mit der man
VL-06: Unentscheidbarkeit II. (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger
 VL-06: Unentscheidbarkeit II (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger WS 2017, RWTH BuK/WS 2017 VL-06: Unentscheidbarkeit II 1/37 Organisatorisches Nächste Vorlesung: Mittwoch, November
VL-06: Unentscheidbarkeit II (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger WS 2017, RWTH BuK/WS 2017 VL-06: Unentscheidbarkeit II 1/37 Organisatorisches Nächste Vorlesung: Mittwoch, November
Existenz nicht rekursiv aufz. Sprachen
 S : Kardinalität einer Menge S (Anzahl ihrer Elemente) Wie vergleichen wir die Kardinalität unendlicher Mengen? A B : es gibt eine surjektive Abbildung von A nach B A = B : A B und B A Zwei Mengen A und
S : Kardinalität einer Menge S (Anzahl ihrer Elemente) Wie vergleichen wir die Kardinalität unendlicher Mengen? A B : es gibt eine surjektive Abbildung von A nach B A = B : A B und B A Zwei Mengen A und
Einführung in die Informatik Algorithms II
 Einführung in die Informatik Algorithms II Eigenschaften von Algorithmen Wolfram Burgard Cyrill Stachniss 14.1 Was können Computer berechnen? In Kapitel 1 haben wir gesagt, dass Programme die Umsetzung
Einführung in die Informatik Algorithms II Eigenschaften von Algorithmen Wolfram Burgard Cyrill Stachniss 14.1 Was können Computer berechnen? In Kapitel 1 haben wir gesagt, dass Programme die Umsetzung
Klausur zur Vorlesung Einführung in die Theoretische Informatik
 Universität Heidelberg 19. Juli 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Einführung in die Theoretische Informatik LÖSUNGEN Es können
Universität Heidelberg 19. Juli 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Einführung in die Theoretische Informatik LÖSUNGEN Es können
Grundlagen der Theoretischen Informatik Musterlösungen zu ausgewählten Übungsaufgaben
 Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Halteproblem/Kodierung von Turing-Maschinen
 Halteproblem/Kodierung von Turing-Maschinen Unser Ziel ist es nun zu zeigen, dass das sogenannte Halteproblem unentscheidbar ist. Halteproblem (informell) Eingabe: Turing-Maschine M mit Eingabe w. Frage:
Halteproblem/Kodierung von Turing-Maschinen Unser Ziel ist es nun zu zeigen, dass das sogenannte Halteproblem unentscheidbar ist. Halteproblem (informell) Eingabe: Turing-Maschine M mit Eingabe w. Frage:
Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion
 Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 7. Dezember 2006 Rekursiv vs. rekursiv
Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 7. Dezember 2006 Rekursiv vs. rekursiv
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 7.07.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 7.07.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Mächtigkeit von LOOP-Programmen. Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen
 Mächtigkeit von LOOP-Programmen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 23 Die Programmiersprache LOOP Syntax Elemente eines LOOP-Programms Variablen
Mächtigkeit von LOOP-Programmen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 23 Die Programmiersprache LOOP Syntax Elemente eines LOOP-Programms Variablen
Algorithmentheorie 8. Vorlesung
 Algorithmentheorie 8. Vorlesung Martin Dietzfelbinger 1. Juni 2006 1.7 Die Churchsche These Der intuitive Berechenbarkeitsbegriff wird durch die Formalisierung TM-Berechenbarkeit, also Rekursivität von
Algorithmentheorie 8. Vorlesung Martin Dietzfelbinger 1. Juni 2006 1.7 Die Churchsche These Der intuitive Berechenbarkeitsbegriff wird durch die Formalisierung TM-Berechenbarkeit, also Rekursivität von
Algorithmentheorie 9. Vorlesung
 Algorithmentheorie 9. Vorlesung Martin Dietzfelbinger 8. Juni 2006 Turingtafel von M: Gödelnummern TM-Codes (q 0, 0,q 2, 1,R), (q 0, 1,q 0, 0,R), (q 0,B,q 1, 1,N), (q 2, 0,q 2, 0,R), (q 2, 1,q 2, 1,R),
Algorithmentheorie 9. Vorlesung Martin Dietzfelbinger 8. Juni 2006 Turingtafel von M: Gödelnummern TM-Codes (q 0, 0,q 2, 1,R), (q 0, 1,q 0, 0,R), (q 0,B,q 1, 1,N), (q 2, 0,q 2, 0,R), (q 2, 1,q 2, 1,R),
Unentscheidbare Probleme: Existenz, Diagonalsprache, Halteproblem
 Unentscheidbare Probleme: Existenz, Diagonalsprache, Halteproblem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 25. Oktober 2010 Berthold Vöcking, Informatik
Unentscheidbare Probleme: Existenz, Diagonalsprache, Halteproblem Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 25. Oktober 2010 Berthold Vöcking, Informatik
Theoretische Informatik II
 Theoretische Informatik II Einheit 4.6 Elementare Berechenbarkeitstheorie II: Unlösbare Probleme 1. Beweistechniken für Unlösbarkeit 2. Wichtige unlösbare Probleme 3. Der Satz von Rice 4. Unentscheidbare
Theoretische Informatik II Einheit 4.6 Elementare Berechenbarkeitstheorie II: Unlösbare Probleme 1. Beweistechniken für Unlösbarkeit 2. Wichtige unlösbare Probleme 3. Der Satz von Rice 4. Unentscheidbare
Aufgabe Mögliche Punkte Erreichte Punkte a b c d Σ a b c d Σ x1 13
 Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 2003/04 ILKD Prof. Dr. D. Wagner 14. April 2004 2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004 Hier Aufkleber
Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 2003/04 ILKD Prof. Dr. D. Wagner 14. April 2004 2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004 Hier Aufkleber
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 15.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 15.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik. SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch
 Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch 3. Teilklausur 25. 07. 2007 Persönliche Daten bitte gut leserlich
Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch 3. Teilklausur 25. 07. 2007 Persönliche Daten bitte gut leserlich
11. Woche: Turingmaschinen und Komplexität Rekursive Aufzählbarkeit, Entscheidbarkeit Laufzeit, Klassen DTIME und P
 11 Woche: Turingmaschinen und Komplexität Rekursive Aufzählbarkeit, Entscheidbarkeit Laufzeit, Klassen DTIME und P 11 Woche: Turingmaschinen, Entscheidbarkeit, P 239/ 333 Einführung in die NP-Vollständigkeitstheorie
11 Woche: Turingmaschinen und Komplexität Rekursive Aufzählbarkeit, Entscheidbarkeit Laufzeit, Klassen DTIME und P 11 Woche: Turingmaschinen, Entscheidbarkeit, P 239/ 333 Einführung in die NP-Vollständigkeitstheorie
Klausur zur Vorlesung Mathematische Logik
 Universität Heidelberg 13. Februar 2014 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Mathematische Logik Musterlösung Aufgabe 1 (Aussagenlogik
Universität Heidelberg 13. Februar 2014 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Mathematische Logik Musterlösung Aufgabe 1 (Aussagenlogik
Einführung in die mathematische Logik
 Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 19 Entscheidbarkeit und Berechenbarkeit In der letzten Vorlesung haben wir verschiedene mathematische Operationen
Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 19 Entscheidbarkeit und Berechenbarkeit In der letzten Vorlesung haben wir verschiedene mathematische Operationen
Vorname Name Matrikelnummer 1. a) Benennen Sie die übrigen 6 Komponenten einer nicht-deterministischen Turingmaschine (TM): (3 Punkte)
 1 Aufgabe 1 (19 Punkte) a) Benennen Sie die übrigen 6 Komponenten einer nicht-deterministischen Turingmaschine (TM): (3 Punkte) Q, die endliche Zustandsmenge b) Was besagt die Church-Turing-These? (1 Punkt)
1 Aufgabe 1 (19 Punkte) a) Benennen Sie die übrigen 6 Komponenten einer nicht-deterministischen Turingmaschine (TM): (3 Punkte) Q, die endliche Zustandsmenge b) Was besagt die Church-Turing-These? (1 Punkt)
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 15. Vorlesung 14.12.2006 1 Reduktionen Unentscheidbare Probleme Das Halteproblem Das Leerheitsproblem einer Turingmaschine Ein einfaches nicht
Informatik III Christian Schindelhauer Wintersemester 2006/07 15. Vorlesung 14.12.2006 1 Reduktionen Unentscheidbare Probleme Das Halteproblem Das Leerheitsproblem einer Turingmaschine Ein einfaches nicht
Berechenbarkeit/Entscheidbarkeit
 Berechenbarkeit/Entscheidbarkeit Frage: Ist eine algorithmische Problemstellung lösbar? was ist eine algorithmische Problemstellung? formale Sprachen benötigen einen Berechenbarkeitsbegriff Maschinenmodelle
Berechenbarkeit/Entscheidbarkeit Frage: Ist eine algorithmische Problemstellung lösbar? was ist eine algorithmische Problemstellung? formale Sprachen benötigen einen Berechenbarkeitsbegriff Maschinenmodelle
Kapitel 1.4. Exkurs: Entscheidbarkeit und Komplexität. Mathematische Logik (WS 2012/3) K. 1.4: Entscheidbarkeit und Komplexität 1/10
 Kapitel 1.4 Exkurs: Entscheidbarkeit und Komplexität Mathematische Logik (WS 2012/3) K. 1.4: Entscheidbarkeit und Komplexität 1/10 Algorithmen Ein Algorithmus oder eine Rechenvorschrift ist ein effektives
Kapitel 1.4 Exkurs: Entscheidbarkeit und Komplexität Mathematische Logik (WS 2012/3) K. 1.4: Entscheidbarkeit und Komplexität 1/10 Algorithmen Ein Algorithmus oder eine Rechenvorschrift ist ein effektives
Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016)
 Technische Universität Berlin, Berlin, 28.07.2016 Name:... Matr.-Nr.:... Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016) Einlesezeit: Bearbeitungszeit: Max.
Technische Universität Berlin, Berlin, 28.07.2016 Name:... Matr.-Nr.:... Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016) Einlesezeit: Bearbeitungszeit: Max.
Unentscheidbare Probleme: Diagonalisierung
 Unentscheidbare Probleme: Diagonalisierung Prof Dr Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Oktober 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Unentscheidbare Probleme: Diagonalisierung Prof Dr Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Oktober 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Logik und Beweisbarkeit
 Logik und Beweisbarkeit VL 10 Martin Mundhenk Univ. Jena, Institut für Informatik 22. Januar 2019 Vorlesung 11: Beweissysteme 3. Berechenbarkeitstheorie VL08: URM-berechenbare Funktionen und die These
Logik und Beweisbarkeit VL 10 Martin Mundhenk Univ. Jena, Institut für Informatik 22. Januar 2019 Vorlesung 11: Beweissysteme 3. Berechenbarkeitstheorie VL08: URM-berechenbare Funktionen und die These
Wir suchen Antworten auf die folgenden Fragen: Was ist Berechenbarkeit? Wie kann man das intuitiv Berechenbare formal fassen?
 Einige Fragen Ziel: Wir suchen Antworten auf die folgenden Fragen: Wie kann man das intuitiv Berechenbare formal fassen? Was ist ein Algorithmus? Welche Indizien hat man dafür, dass ein formaler Algorithmenbegriff
Einige Fragen Ziel: Wir suchen Antworten auf die folgenden Fragen: Wie kann man das intuitiv Berechenbare formal fassen? Was ist ein Algorithmus? Welche Indizien hat man dafür, dass ein formaler Algorithmenbegriff
Universelle Maschinen und universelle Funktionen
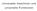 Universelle Maschinen und universelle Funktionen UNIVERSELLE FUNKTIONEN DEFINITION. Sei F eine Klasse von partiellen Funktionen über N. Eine partielle Funktion ϕ (n+1) ist n-universell für F, wenn (i)
Universelle Maschinen und universelle Funktionen UNIVERSELLE FUNKTIONEN DEFINITION. Sei F eine Klasse von partiellen Funktionen über N. Eine partielle Funktion ϕ (n+1) ist n-universell für F, wenn (i)
Nachklausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2012/13
 Institut für Kryptographie und Sicherheit Prof. Dr. Jörn Müller-Quade Nachklausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2012/13 Vorname Nachname Matrikelnummer Hinweise Für
Institut für Kryptographie und Sicherheit Prof. Dr. Jörn Müller-Quade Nachklausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2012/13 Vorname Nachname Matrikelnummer Hinweise Für
Berechenbarkeitsmodelle
 Berechenbarkeit 2 Endliche Automaten erkennen nicht alle algorithmisch erkennbaren Sprachen. Kontextfreie Grammatiken erzeugen nicht alle algorithmisch erzeugbaren Sprachen. Welche Berechnungsmodelle erlauben
Berechenbarkeit 2 Endliche Automaten erkennen nicht alle algorithmisch erkennbaren Sprachen. Kontextfreie Grammatiken erzeugen nicht alle algorithmisch erzeugbaren Sprachen. Welche Berechnungsmodelle erlauben
Durchschnittsleerheitsproblem (DLP)
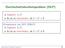 1 Durchschnittsleerheitsproblem (DLP) Gegeben: L, L. Es ist zu entscheiden, ob L L = Komplement von DLP (DNLP) Gegeben: L, L. Es ist zu entscheiden, ob L L Durchschnittsleerheitsproblem (DLP) 2 Nichtentscheidbarkeit
1 Durchschnittsleerheitsproblem (DLP) Gegeben: L, L. Es ist zu entscheiden, ob L L = Komplement von DLP (DNLP) Gegeben: L, L. Es ist zu entscheiden, ob L L Durchschnittsleerheitsproblem (DLP) 2 Nichtentscheidbarkeit
Unentscheidbarkeit. Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: Komplexitätstheorie und effiziente Algorithmen
 Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Prof. Barbara König Übungsleitung: Henning Kerstan & Jan Stückrath Worum geht
Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Prof. Barbara König Übungsleitung: Henning Kerstan & Jan Stückrath Worum geht
1936 von Alan Turing zum theoretischen Studium der Berechenbarkeit eingeführt Besteht aus
 //5 Abstrakte Maschinenmodelle: Turingmaschine (TM) 96 von Alan Turing zum theoretischen Studium der Berechenbarkeit eingeführt Besteht aus einem festen Teil ( "Hardware ) einem variablen Teil ( "Software
//5 Abstrakte Maschinenmodelle: Turingmaschine (TM) 96 von Alan Turing zum theoretischen Studium der Berechenbarkeit eingeführt Besteht aus einem festen Teil ( "Hardware ) einem variablen Teil ( "Software
Diagonalisierung und Reduktion
 Diagonalisierung und Reduktion Sebastian Wild und Markus E. Nebel 13. März 2012 Inhaltsverzeichnis 1 Notationen 1 2 Diagonalisierung 3 2.0 Grundidee..................................... 3 2.1 Beispielaufgabe..................................
Diagonalisierung und Reduktion Sebastian Wild und Markus E. Nebel 13. März 2012 Inhaltsverzeichnis 1 Notationen 1 2 Diagonalisierung 3 2.0 Grundidee..................................... 3 2.1 Beispielaufgabe..................................
Theoretische Informatik: Berechenbarkeit und Formale Sprachen
 Prof. Dr. F. Otto 26.09.2011 Fachbereich Elektrotechnik/Informatik Universität Kassel Klausur zur Vorlesung Theoretische Informatik: Berechenbarkeit und Formale Sprachen SS 2011 Name:................................
Prof. Dr. F. Otto 26.09.2011 Fachbereich Elektrotechnik/Informatik Universität Kassel Klausur zur Vorlesung Theoretische Informatik: Berechenbarkeit und Formale Sprachen SS 2011 Name:................................
Unentscheidbarkeitssätze der Logik
 Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Unentscheidbarkeit des Halteproblems, Unterprogrammtechnik
 Unentscheidbarkeit des Halteproblems, Unterprogrammtechnik Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 26. Oktober 2009 Berthold Vöcking, Informatik 1 () Vorlesung
Unentscheidbarkeit des Halteproblems, Unterprogrammtechnik Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 26. Oktober 2009 Berthold Vöcking, Informatik 1 () Vorlesung
Folgen. Definition. Sei M eine beliebige Menge. Eine Abbildung a : N M oder a : N 0 M heißt eine Folge.
 Folgen Eine Folge stellt man sich am einfachsten als eine Aneinanderreihung von Zahlen (oder Elementen irgendeiner anderen Menge) vor, die immer weiter geht Etwa,,,,,, oder,,, 8,,,, oder 0,,,,,,,, In vielen
Folgen Eine Folge stellt man sich am einfachsten als eine Aneinanderreihung von Zahlen (oder Elementen irgendeiner anderen Menge) vor, die immer weiter geht Etwa,,,,,, oder,,, 8,,,, oder 0,,,,,,,, In vielen
